Как Построить График Функции и Уравнения По Точкам Онлайн?
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник, чтобы построить график функции онлайн.
Содержание
- Что такое график функций
- Сервисы для построения графиков функций онлайн
- Umath.ru
- Yotx.ru
- Graph.reshish.ru
- Desmos.com
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
Пример:
На рисунке мы видим график функции y = x. Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y. Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y.
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро построить график функции онлайн.
Umath.ru
Открывает список самый обычный сервис, позволяющий построить график уравнения. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».

- Нажмите кнопку «Построить график».
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
Перейти на официальный сайт Umath
Yotx.ru
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция, чтобы построить график по точкам онлайн:
:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить».
Огромным плюсом этого сайта можно считать визуализацию графика. Удобно реализована возможность построения нескольких графиков на одной координатной плоскости: можно назначить каждому свой уникальный цвет, толщину линии. Также можно построить несколько графиков в одной плоскости.
Также можно построить несколько графиков в одной плоскости.
Перейти на официальный сайт Yotx
Graph.reshish.ru
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис — калькулятор графика функции с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция, чтобы построить график логарифмической функции онлайн или другой вид:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:».
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Перейти на официальный сайт сервиса
Desmos.com
Desmos безусловно – самый навороченный сервис для построения графика параметрической функции онлайн или любой другой. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция, по построению графиков онлайн по точкам X Y:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График начертится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу, чтобы научиться строить графики онлайн по уравнениям и не только.
Перейти на официальный сайт Desmos
Сайтов для построения графиков функций онлайн с решением великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Last Modified on 21.07.2021 by artikus256
Написано статей
243
y x 1 x 2 1 исследовать функцию и построить
y x 1 x 2 1 исследовать функцию и построитьВы искали y x 1 x 2 1 исследовать функцию и построить? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y x 1 x 2 1 исследовать функцию и построить график, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «y x 1 x 2 1 исследовать функцию и построить».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y x 1 x 2 1 исследовать функцию и построить,y x 1 x 2 1 исследовать функцию и построить график,анализ функции,анализ функции онлайн,график функции для исследования,графики для исследования функций,графики функций для исследования,исследование графика функции,исследование графика функции онлайн,исследование и построение графика функции,исследование и построение графика функции онлайн,исследование и построение графика функции с помощью производной,исследование и построение графика функции с помощью производной онлайн,исследование и построение графиков функции,исследование на непрерывность функции онлайн,исследование на непрерывность функции онлайн калькулятор,исследование функции,исследование функции y 2 x,исследование функции y x 1 x 2,исследование функции y x 2,исследование функции y x 2 x 1,исследование функции и построение графика,исследование функции и построение графика калькулятор онлайн,исследование функции и построение графика онлайн,исследование функции и построение графика онлайн калькулятор,исследование функции и построение графика онлайн с подробным решением,исследование функции и построение графика примеры решения задач,исследование функции и построение графика с помощью производной,исследование функции и построение графика с помощью производной онлайн,исследование функции и построение графика функции с помощью производной,исследование функции и построение графиков,исследование функции и построение графиков функции,исследование функции калькулятор,исследование функции на непрерывность онлайн,исследование функции на непрерывность онлайн калькулятор,исследование функции на непрерывность онлайн с подробным решением,исследование функции онлайн,исследование функции онлайн калькулятор,исследование функции онлайн калькулятор с подробным решением,исследование функции онлайн с подробным решением,исследование функции онлайн с подробным решением онлайн,исследование функции с помощью производной и построение графика,исследование функции с помощью производной и построение графика онлайн,исследование функции с помощью производной онлайн с решением,исследование функции с помощью производной построение графика функции,исследование функции с помощью производной примеры решения,исследование функций,исследование функций и построение графиков,исследование функций онлайн,исследования функции онлайн,исследовать график на непрерывность и построить график онлайн,исследовать график функции,исследовать график функции и построить график,исследовать данные функции на непрерывность и построить их графики онлайн,исследовать и построить график функции,исследовать и построить график функции онлайн с подробным решением,исследовать и построить график функции онлайн с решением,исследовать методами дифференциального исчисления и построить график,исследовать методами дифференциального исчисления и построить график онлайн,исследовать методами дифференциального исчисления функцию,исследовать методом дифференциального исчисления функцию и построить график,исследовать на монотонность функцию онлайн,исследовать на непрерывность и построить график функции онлайн,исследовать на непрерывность функции онлайн,исследовать на непрерывность функцию и построить график онлайн,исследовать на непрерывность функцию онлайн,исследовать на непрерывность функцию онлайн калькулятор,исследовать на непрерывность функцию онлайн с подробным решением,исследовать на ограниченность функцию онлайн,исследовать с помощью производной функцию и построить график,исследовать средствами дифференциального исчисления функцию онлайн,исследовать функции и построить график,исследовать функции и построить график онлайн,исследовать функции на непрерывность онлайн,исследовать функцию,исследовать функцию x y x,исследовать функцию y 2 x 2,исследовать функцию y x 1 x,исследовать функцию y x 2 1 x,исследовать функцию y x 2 1 x 2,исследовать функцию y x 2 x,исследовать функцию y x 3 x 2,исследовать функцию и построить график,исследовать функцию и построить график y x 1 x 2,исследовать функцию и построить график онлайн,исследовать функцию и построить график онлайн решение,исследовать функцию и построить график онлайн с подробным решением,исследовать функцию и построить график онлайн с подробным решением онлайн,исследовать функцию и построить график примеры решения,исследовать функцию и построить график решение онлайн калькулятор,исследовать функцию и построить график с помощью производной,исследовать функцию и построить ее график,исследовать функцию и построить ее график калькулятор онлайн,исследовать функцию и построить ее график онлайн калькулятор,исследовать функцию и построить ее график онлайн с решением,исследовать функцию методами дифференциального исчисления,исследовать функцию методом дифференциального исчисления и построить график,исследовать функцию на монотонность и экстремумы онлайн,исследовать функцию на монотонность онлайн,исследовать функцию на непрерывность и построить график онлайн,исследовать функцию на непрерывность калькулятор онлайн,исследовать функцию на непрерывность онлайн,исследовать функцию на непрерывность онлайн калькулятор,исследовать функцию на непрерывность онлайн с подробным решением,исследовать функцию на ограниченность онлайн,исследовать функцию онлайн,исследовать функцию онлайн с подробным решением,исследовать функцию по графику,исследовать функцию с помощью производной и построить график,исследовать функцию с помощью производной и построить график онлайн,исследовать функцию средствами дифференциального исчисления онлайн,исследовать функцию что значит,исследуйте и постройте график функции,исследуйте и постройте график функции у 3 2х,исследуйте на непрерывность функцию онлайн,исследуйте функции и постройте график,исследуйте функцию,исследуйте функцию y,исследуйте функцию и постройте график,исследуйте функцию и постройте ее график,исследуйте функцию и постройте ее график онлайн,исследуйте функцию на непрерывность онлайн,исследуйте функцию у f x и постройте ее график,как исследовать график функции,как исследовать функцию и построить график,как исследовать функцию и построить ее график,как построить график и исследовать функцию,калькулятор исследование функции,калькулятор исследования функции,калькулятор исследования функции и построения графика,калькулятор онлайн исследование функции на непрерывность,методами дифференциального исчисления исследовать функцию,непрерывность функции онлайн,онлайн анализ функции,онлайн исследование на непрерывность функции онлайн,онлайн исследование функции и построение графика,онлайн исследование функции и построение графика с подробным решением,онлайн исследование функции с помощью производной,онлайн исследования функции,онлайн исследовать функцию на непрерывность и построить график,онлайн калькулятор исследование функции,онлайн калькулятор исследование функции и построение графика,онлайн калькулятор исследование функции на непрерывность,онлайн полное исследование функции и построение графика,периодичность функции онлайн,полное исследование и построение графика функции,полное исследование и построение графика функции онлайн,полное исследование функции,полное исследование функции и построение графика,полное исследование функции и построение графика онлайн,полное исследование функции и построение графика онлайн решение,полное исследование функции и построение графика функции,полное исследование функции онлайн,полное исследование функции онлайн и построение графика,построение графиков и исследование функции,построение графиков функций и исследование,построение и исследование графиков функции,построить график функции используя общую схему исследования функции,построить и исследовать график функции онлайн с подробным решением,примеры исследование функции и построение графика функции,провести исследование и построить график функции,провести исследование и построить график функции онлайн,провести исследование функции и построить график,провести исследование функции и построить график онлайн,провести полное исследование и построить график функции,провести полное исследование и построить график функции онлайн калькулятор,провести полное исследование функции и построить график,провести полное исследование функции и построить график калькулятор онлайн,провести полное исследование функции и построить график онлайн калькулятор,провести полное исследование функции и построить график онлайн решение,провести полное исследование функции и построить график функции,точки пересечения графика функции с осями координат онлайн,функции исследования,что значит исследовать функцию.
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y x 1 x 2 1 исследовать функцию и построить,y x 1 x 2 1 исследовать функцию и построить график,анализ функции,анализ функции онлайн,график функции для исследования,графики для исследования функций,графики функций для исследования,исследование графика функции,исследование графика функции онлайн,исследование и построение графика функции,исследование и построение графика функции онлайн,исследование и построение графика функции с помощью производной,исследование и построение графика функции с помощью производной онлайн,исследование и построение графиков функции,исследование на непрерывность функции онлайн,исследование на непрерывность функции онлайн калькулятор,исследование функции,исследование функции y 2 x,исследование функции y x 1 x 2,исследование функции y x 2,исследование функции y x 2 x 1,исследование функции и построение графика,исследование функции и построение графика калькулятор онлайн,исследование функции и построение графика онлайн,исследование функции и построение графика онлайн калькулятор,исследование функции и построение графика онлайн с подробным решением,исследование функции и построение графика примеры решения задач,исследование функции и построение графика с помощью производной,исследование функции и построение графика с помощью производной онлайн,исследование функции и построение графика функции с помощью производной,исследование функции и построение графиков,исследование функции и построение графиков функции,исследование функции калькулятор,исследование функции на непрерывность онлайн,исследование функции на непрерывность онлайн калькулятор,исследование функции на непрерывность онлайн с подробным решением,исследование функции онлайн,исследование функции онлайн калькулятор,исследование функции онлайн калькулятор с подробным решением,исследование функции онлайн с подробным решением,исследование функции онлайн с подробным решением онлайн,исследование функции с помощью производной и построение графика,исследование функции с помощью производной и построение графика онлайн,исследование функции с помощью производной онлайн с решением,исследование функции с помощью производной построение графика функции,исследование функции с помощью производной примеры решения,исследование функций,исследование функций и построение графиков,исследование функций онлайн,исследования функции онлайн,исследовать график на непрерывность и построить график онлайн,исследовать график функции,исследовать график функции и построить график,исследовать данные функции на непрерывность и построить их графики онлайн,исследовать и построить график функции,исследовать и построить график функции онлайн с подробным решением,исследовать и построить график функции онлайн с решением,исследовать методами дифференциального исчисления и построить график,исследовать методами дифференциального исчисления и построить график онлайн,исследовать методами дифференциального исчисления функцию,исследовать методом дифференциального исчисления функцию и построить график,исследовать на монотонность функцию онлайн,исследовать на непрерывность и построить график функции онлайн,исследовать на непрерывность функции онлайн,исследовать на непрерывность функцию и построить график онлайн,исследовать на непрерывность функцию онлайн,исследовать на непрерывность функцию онлайн калькулятор,исследовать на непрерывность функцию онлайн с подробным решением,исследовать на ограниченность функцию онлайн,исследовать с помощью производной функцию и построить график,исследовать средствами дифференциального исчисления функцию онлайн,исследовать функции и построить график,исследовать функции и построить график онлайн,исследовать функции на непрерывность онлайн,исследовать функцию,исследовать функцию x y x,исследовать функцию y 2 x 2,исследовать функцию y x 1 x,исследовать функцию y x 2 1 x,исследовать функцию y x 2 1 x 2,исследовать функцию y x 2 x,исследовать функцию y x 3 x 2,исследовать функцию и построить график,исследовать функцию и построить график y x 1 x 2,исследовать функцию и построить график онлайн,исследовать функцию и построить график онлайн решение,исследовать функцию и построить график онлайн с подробным решением,исследовать функцию и построить график онлайн с подробным решением онлайн,исследовать функцию и построить график примеры решения,исследовать функцию и построить график решение онлайн калькулятор,исследовать функцию и построить график с помощью производной,исследовать функцию и построить ее график,исследовать функцию и построить ее график калькулятор онлайн,исследовать функцию и построить ее график онлайн калькулятор,исследовать функцию и построить ее график онлайн с решением,исследовать функцию методами дифференциального исчисления,исследовать функцию методом дифференциального исчисления и построить график,исследовать функцию на монотонность и экстремумы онлайн,исследовать функцию на монотонность онлайн,исследовать функцию на непрерывность и построить график онлайн,исследовать функцию на непрерывность калькулятор онлайн,исследовать функцию на непрерывность онлайн,исследовать функцию на непрерывность онлайн калькулятор,исследовать функцию на непрерывность онлайн с подробным решением,исследовать функцию на ограниченность онлайн,исследовать функцию онлайн,исследовать функцию онлайн с подробным решением,исследовать функцию по графику,исследовать функцию с помощью производной и построить график,исследовать функцию с помощью производной и построить график онлайн,исследовать функцию средствами дифференциального исчисления онлайн,исследовать функцию что значит,исследуйте и постройте график функции,исследуйте и постройте график функции у 3 2х,исследуйте на непрерывность функцию онлайн,исследуйте функции и постройте график,исследуйте функцию,исследуйте функцию y,исследуйте функцию и постройте график,исследуйте функцию и постройте ее график,исследуйте функцию и постройте ее график онлайн,исследуйте функцию на непрерывность онлайн,исследуйте функцию у f x и постройте ее график,как исследовать график функции,как исследовать функцию и построить график,как исследовать функцию и построить ее график,как построить график и исследовать функцию,калькулятор исследование функции,калькулятор исследования функции,калькулятор исследования функции и построения графика,калькулятор онлайн исследование функции на непрерывность,методами дифференциального исчисления исследовать функцию,непрерывность функции онлайн,онлайн анализ функции,онлайн исследование на непрерывность функции онлайн,онлайн исследование функции и построение графика,онлайн исследование функции и построение графика с подробным решением,онлайн исследование функции с помощью производной,онлайн исследования функции,онлайн исследовать функцию на непрерывность и построить график,онлайн калькулятор исследование функции,онлайн калькулятор исследование функции и построение графика,онлайн калькулятор исследование функции на непрерывность,онлайн полное исследование функции и построение графика,периодичность функции онлайн,полное исследование и построение графика функции,полное исследование и построение графика функции онлайн,полное исследование функции,полное исследование функции и построение графика,полное исследование функции и построение графика онлайн,полное исследование функции и построение графика онлайн решение,полное исследование функции и построение графика функции,полное исследование функции онлайн,полное исследование функции онлайн и построение графика,построение графиков и исследование функции,построение графиков функций и исследование,построение и исследование графиков функции,построить график функции используя общую схему исследования функции,построить и исследовать график функции онлайн с подробным решением,примеры исследование функции и построение графика функции,провести исследование и построить график функции,провести исследование и построить график функции онлайн,провести исследование функции и построить график,провести исследование функции и построить график онлайн,провести полное исследование и построить график функции,провести полное исследование и построить график функции онлайн калькулятор,провести полное исследование функции и построить график,провести полное исследование функции и построить график калькулятор онлайн,провести полное исследование функции и построить график онлайн калькулятор,провести полное исследование функции и построить график онлайн решение,провести полное исследование функции и построить график функции,точки пересечения графика функции с осями координат онлайн,функции исследования,что значит исследовать функцию.
Где можно решить любую задачу по математике, а так же y x 1 x 2 1 исследовать функцию и построить Онлайн?
Решить задачу y x 1 x 2 1 исследовать функцию и построить вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Исследовать функцию с помощью производной и построить ее график: Математическое Бюро.
 Страница 404 — ЭкоДом: Дом своими руками
Страница 404 — ЭкоДом: Дом своими рукамиДля периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
f(0)=4
Точка:
(0, 4)
5. Найти асимптоты графика — их нет.
6. Вычислить производную функции f'(x)
и определить критические точки.
f'(x) = 4х³ — 12х = 4х(х² — 3).
Приравниваем производную нулю: 4х(х² — 3) = 0.
Получаем 3 корня (это критические точки):
х = 0, х = √3 и х = -√3.
7. Найти промежутки монотонности
функции.
Исследуем знаки производной:
х =
-2
-1.732 -1.5
-0.5
0 0.5
1.5 1.732 2
y’=4х³ — 12х -8 0 4.5
5.5 0
-5.5
-4.5 0
8.
Где производная положительна — там функция возрастает, где отрицательна — там функция убывает.
Возрастает на промежутках [-sqrt(3), 0] U [sqrt(3), oo).
Убывает на промежутках (-oo, -sqrt(3)] U [0, sqrt(3)]
8. Определить экстремумы функции f(x).
Где производная меняет знак с — на + там минимум функции, где меняет знак с + на — там максимум.
экстремумы в точках:
(0, 4) максимум,
(-√ 3, -5) и (√ 3, -5) минимумы.
9. Вычислить вторую производную f»(x).
Приравниваем нулю вторую производную:
f»(x) = 12х²-12 =12(х² — 1) = 0.
Имеем 2 точки перегиба функции: х = 1 и х = -1.
10. Определить направление
выпуклости графика и точки перегиба.
Вогнутая на промежутках (-oo, -1] U [1, oo).
Выпуклая на промежутках [-1, 1]
11. Построить график, используя
полученные результаты исследования — в приложении.
На заданном интервале графика от -1 до 1 будет только выпуклая его часть.
Урок 20. построение графиков функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №20. Построение графиков функций.
Построение графиков функций.
Перечень вопросов, рассматриваемых в теме
- Исследование функций;
- Построение графиков функций;
- Применение производной для решения графических задач.
Глоссарий по теме
Асимптота графика функции y = f(x) – прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1и х2, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Выпуклость вверх. Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка.
Выпуклость вниз. Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.
Максимум функции. Значение функции в точке максимума называют максимумом функции.
Минимум функции. Значение функции в точке минимума называют минимумом функции.
Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Производная второго порядка (вторая производная). Производная второго порядка есть первая производная от производной первого порядка.
Производную определяют, как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к 0, если такой предел существует.
Точка максимума функции. Точку х0называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .
Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .
Точка перегиба. Точки, в которых выпуклость вверх меняется на выпуклость вниз или наоборот, называются точками перегиба.
Точки, в которых выпуклость вверх меняется на выпуклость вниз или наоборот, называются точками перегиба.
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y=f(x) убывает на интервале X, если для любых х1 и х2 , из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.
Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит вышепроведенного отрезка.
Полная схема построения графика функции:
- Найти область определения функции D(f).
- Исследовать функцию на четность (найти f(-x)).
- Найти асимптоты.
- Найти стационарные и критические точки.
- Найти промежутки монотонности.
- Найти интервалы выпуклости вверх и выпуклости вниз.
- Найти точки перегиба
- Составить таблицу значений функции для некоторых точек.
- По полученным данным построить график функции.
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Постройте график функции у = х3 – 3х + 3, используя краткую схему построения. схему построения.
Решение:
1) D(y) = (-∞; +∞)
2) Функция не является ни четной, ни нечетной, т. к.
3) Асимптот нет
4) f’(x) = 3x2 – 3, f’(x) = 0 при х = 1, х = -1.
х = 1, х = -1 – стационарные точки.
5) f’(x)>0 при . Так как в точках х = 1, х = -1 функция непрерывна, то эти точки также включаются в промежутки возрастания.
f’(x)<0 при . Так как в точках х = 1, х = -1 функция непрерывна, то эти точки также включаются в промежутки убывания.
6) Так как в точке х = -1 производная меняет знак с «+» на «-», то х = -1 – точка максимума.
Так как в точке х = 1 производная меняет знак с «-» на «+», то х = 1 – точка минимума.
7) Результаты исследования представим в виде таблицы.
x | (-∞; -1) | -1 | (-1; 1) | 1 | (1; +∞) |
f’(x) | + | 0 | — | 0 | + |
f(x) | 5 | 1 | |||
max | min |
8) Координаты некоторых точек:
9) По полученным данным строим график (рис. 1)
1)
Рисунок 1 – график функции у = х3 – 3х + 3
Пример 2. Постройте график функции, используя подробную схему построения. схему построения.
Решение:
1)
2) Функция не является ни четной, ни нечетной, т. к.
3) х = 1 – вертикальная асимптота
4) , f’(x) = 0 при х = 2, х = 0.
х = 2, х = 0 – стационарные точки.
5) f’(x)>0 при . Так как в точках х = 0, х = 2 функция непрерывна, то эти точки также включаются в промежутки возрастания.
f’(x)<0 при . Так как в точках х = 0, х = 2 функция непрерывна, то эти точки также включаются в промежутки убывания.
Так как в точке х = 0 производная меняет знак с «+» на «-», то х = 0 – точка максимума.
Так как в точке х = 2 производная меняет знак с «-» на «+», то х = 2 – точка минимума.
х = 1 – не является точкой экстремума
6) Найдем интервалы выпуклости функции.
; при функция выпукла вверх.
; при функция выпукла вниз.
7) Результаты исследования представим в виде таблицы.
x | (-∞; 0) | 0 | (0; 1) | 1 | (1; 2) | 2 | (2; +∞) |
f’(x) | + | 0 | — | Не сущ. | — | 0 | + |
f’’(x) | — | — | Не сущ. | + | + | ||
f(x) | -4 | Не сущ. | 0 | ||||
max | min |
8) Координаты некоторых точек:
x | -1 | 0,5 | 1,5 | 3 |
f(x) | -4,5 | -4,5 | 0,5 | 0,5 |
9) По полученным данным строим график (рис. 2)
2)
Рисунок 2 – график функции
Исследование функции с помощью производной /qualihelpy
Рассмотрим функции и , которые непрерывны на отрезке и дифференцируемы на интервале .
Теорема Ферма
: если функция в точке имеет локальный экстремум, то .
Геометрический смысл теоремы: касательная к графику функции в точке параллельна оси абсцисс.
Теорема Лагранжа: , где .
Геометрический смысл теоремы: касательная к графику функции в точке параллельна секущей, соединяющей концы графика этой функции.
Теорема Ролля: если и , то .
Геометрический смысл теоремы: у графика функции существует точка, в которой касательная параллельна оси абсцисс.
Теорема Коши: если , то .
Исследование функции с помощью первой производной
С помощью производной функции можно определить характер монотонности функции, точки экстремума, а также ее наибольшее и наименьшее значение на заданном промежутке.
Достаточное условие возрастания (убывания) функции:
а) если на заданном промежутке , то функция возрастает на этом промежутке;
б) если , то функция убывает на этом промежутке.
Экстремум
функции
Максимумом (минимумом)
функции называют такое ее значение, которое больше (меньше) всех ее других значений в окрестности рассматриваемой точки.
Максимум и минимум функции имеют локальный характер, поскольку отдельные минимумы некоторой функции могут оказаться больше максимумов той же функции (рис. 6.4).
Максимум и минимум функции называются
экстремумом функции
. Значение аргумента, при котором достигается экстремум, называется
точкой экстремума
. На рисунке 6.4 значения , , , и являются точками экстремума рассматриваемой функции.
Критическими точками
функции называют те значения аргумента, при которых производная функции равна нулю или не существует. Критические точки функции находят, решая уравнение: .
Алгоритм нахождения точек экстремума функции:
1) находим область определения функции ;
2) находим ;
3) находим критические точки функции, решая уравнение ;
4) наносим критические точки на область определения функции;
5) определяем знак производной функции на полученных промежутках;
6) определяем точки экстремума функции по правилу:
если при переходе через критическую точку производная меняет знак c «+» на «–», то имеем точку максимума, а если с «–» на «+», то имеем точку минимума.
Рассмотрим функцию на отрезке . Свое наибольшее и наименьшее значение она может принимать либо на концах отрезка, либо в точках экстремума.
Алгоритм нахождения наибольшего и наименьшего
значений
функции на заданном отрезке:
1) находим ;
2) находим критические точки функции, решая уравнение ;
3) находим значение функции на концах отрезка и в критических точках, принадлежащих данному отрезку;
4) определяем наибольшее и наименьшее значение из полученных.
Исследование
функции с помощью второй производной
Критическими точками второго рода
функции называют те значения аргумента, при которых вторая производная этой функции равна нулю или не существует.
Критические точки второго рода функции находят, решая уравнение .
Если при переходе через критическую точку второго рода вторая производная функции меняет знак, то имеем точку перегиба
графика функции.
Если на некотором промежутке выполняется неравенство , то функция вогнута
на этом промежутке, а если , то функция
выпукла
на этом промежутке.
y x 1 x 2 1 исследовать функцию и построить
Вы искали y x 1 x 2 1 исследовать функцию и построить? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y x 1 x 2 1 исследовать функцию и построить график, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «y x 1 x 2 1 исследовать функцию и построить».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y x 1 x 2 1 исследовать функцию и построить,y x 1 x 2 1 исследовать функцию и построить график,анализ функции,анализ функции онлайн,график функции для исследования,графики для исследования функций,графики функций для исследования,исследование графика функции,исследование графика функции онлайн,исследование и построение графика функции,исследование и построение графика функции онлайн,исследование и построение графика функции с помощью производной,исследование и построение графика функции с помощью производной онлайн,исследование и построение графиков функции,исследование на непрерывность функции онлайн,исследование на непрерывность функции онлайн калькулятор,исследование функции,исследование функции y 2 x,исследование функции y x 1 x 2,исследование функции y x 2,исследование функции y x 2 x 1,исследование функции и построение графика,исследование функции и построение графика калькулятор онлайн,исследование функции и построение графика онлайн,исследование функции и построение графика онлайн калькулятор,исследование функции и построение графика онлайн с подробным решением,исследование функции и построение графика примеры решения задач,исследование функции и построение графика с помощью производной,исследование функции и построение графика с помощью производной онлайн,исследование функции и построение графика функции с помощью производной,исследование функции и построение графиков,исследование функции и построение графиков функции,исследование функции калькулятор,исследование функции на непрерывность онлайн,исследование функции на непрерывность онлайн калькулятор,исследование функции на непрерывность онлайн с подробным решением,исследование функции онлайн,исследование функции онлайн калькулятор,исследование функции онлайн калькулятор с подробным решением,исследование функции онлайн с подробным решением,исследование функции онлайн с подробным решением онлайн,исследование функции с помощью производной и построение графика,исследование функции с помощью производной и построение графика онлайн,исследование функции с помощью производной онлайн с решением,исследование функции с помощью производной построение графика функции,исследование функции с помощью производной примеры решения,исследование функций,исследование функций и построение графиков,исследование функций онлайн,исследования функции онлайн,исследовать график на непрерывность и построить график онлайн,исследовать график функции,исследовать график функции и построить график,исследовать данные функции на непрерывность и построить их графики онлайн,исследовать и построить график функции,исследовать и построить график функции онлайн с подробным решением,исследовать и построить график функции онлайн с решением,исследовать методами дифференциального исчисления и построить график,исследовать методами дифференциального исчисления и построить график онлайн,исследовать методами дифференциального исчисления функцию,исследовать методом дифференциального исчисления функцию и построить график,исследовать на монотонность функцию онлайн,исследовать на непрерывность и построить график функции онлайн,исследовать на непрерывность функции онлайн,исследовать на непрерывность функцию и построить график онлайн,исследовать на непрерывность функцию онлайн,исследовать на непрерывность функцию онлайн калькулятор,исследовать на непрерывность функцию онлайн с подробным решением,исследовать на ограниченность функцию онлайн,исследовать с помощью производной функцию и построить график,исследовать средствами дифференциального исчисления функцию онлайн,исследовать функции и построить график,исследовать функции и построить график онлайн,исследовать функции на непрерывность онлайн,исследовать функцию,исследовать функцию x y x,исследовать функцию y 2 x 2,исследовать функцию y x 1 x,исследовать функцию y x 2 1 x,исследовать функцию y x 2 1 x 2,исследовать функцию y x 2 x,исследовать функцию y x 3 x 2,исследовать функцию и построить график,исследовать функцию и построить график y x 1 x 2,исследовать функцию и построить график онлайн,исследовать функцию и построить график онлайн решение,исследовать функцию и построить график онлайн с подробным решением,исследовать функцию и построить график онлайн с подробным решением онлайн,исследовать функцию и построить график примеры решения,исследовать функцию и построить график решение онлайн калькулятор,исследовать функцию и построить график с помощью производной,исследовать функцию и построить ее график,исследовать функцию и построить ее график калькулятор онлайн,исследовать функцию и построить ее график онлайн калькулятор,исследовать функцию и построить ее график онлайн с решением,исследовать функцию методами дифференциального исчисления,исследовать функцию методом дифференциального исчисления и построить график,исследовать функцию на монотонность и экстремумы онлайн,исследовать функцию на монотонность онлайн,исследовать функцию на непрерывность и построить график онлайн,исследовать функцию на непрерывность калькулятор онлайн,исследовать функцию на непрерывность онлайн,исследовать функцию на непрерывность онлайн калькулятор,исследовать функцию на непрерывность онлайн с подробным решением,исследовать функцию на ограниченность онлайн,исследовать функцию онлайн,исследовать функцию онлайн с подробным решением,исследовать функцию по графику,исследовать функцию с помощью производной и построить график,исследовать функцию с помощью производной и построить график онлайн,исследовать функцию средствами дифференциального исчисления онлайн,исследовать функцию что значит,исследуйте и постройте график функции,исследуйте и постройте график функции у 3 2х,исследуйте на непрерывность функцию онлайн,исследуйте функции и постройте график,исследуйте функцию,исследуйте функцию y,исследуйте функцию и постройте график,исследуйте функцию и постройте ее график,исследуйте функцию и постройте ее график онлайн,исследуйте функцию на непрерывность онлайн,исследуйте функцию у f x и постройте ее график,как исследовать график функции,как исследовать функцию и построить график,как исследовать функцию и построить ее график,как построить график и исследовать функцию,калькулятор исследование функции,калькулятор исследования функции,калькулятор исследования функции и построения графика,калькулятор онлайн исследование функции на непрерывность,методами дифференциального исчисления исследовать функцию,непрерывность функции онлайн,онлайн анализ функции,онлайн исследование на непрерывность функции онлайн,онлайн исследование функции и построение графика,онлайн исследование функции и построение графика с подробным решением,онлайн исследование функции с помощью производной,онлайн исследования функции,онлайн исследовать функцию на непрерывность и построить график,онлайн калькулятор исследование функции,онлайн калькулятор исследование функции и построение графика,онлайн калькулятор исследование функции на непрерывность,онлайн полное исследование функции и построение графика,периодичность функции онлайн,полное исследование и построение графика функции,полное исследование и построение графика функции онлайн,полное исследование функции,полное исследование функции и построение графика,полное исследование функции и построение графика онлайн,полное исследование функции и построение графика онлайн решение,полное исследование функции и построение графика функции,полное исследование функции онлайн,полное исследование функции онлайн и построение графика,построение графиков и исследование функции,построение графиков функций и исследование,построение и исследование графиков функции,построить график функции используя общую схему исследования функции,построить и исследовать график функции онлайн с подробным решением,примеры исследование функции и построение графика функции,провести исследование и построить график функции,провести исследование и построить график функции онлайн,провести исследование функции и построить график,провести исследование функции и построить график онлайн,провести полное исследование и построить график функции,провести полное исследование и построить график функции онлайн калькулятор,провести полное исследование функции и построить график,провести полное исследование функции и построить график калькулятор онлайн,провести полное исследование функции и построить график онлайн калькулятор,провести полное исследование функции и построить график онлайн решение,провести полное исследование функции и построить график функции,точки пересечения графика функции с осями координат онлайн,функции исследования,что значит исследовать функцию. На этой странице вы найдёте калькулятор,
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и y x 1 x 2 1 исследовать функцию и построить. Просто введите задачу в окошко и нажмите
«решить» здесь (например, анализ функции).
Где можно решить любую задачу по математике, а так же y x 1 x 2 1 исследовать функцию и построить Онлайн?
Решить задачу y x 1 x 2 1 исследовать функцию и построить вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Исследование функции и построение графика с помощью производной
Пример 1.
Решение
1) Область определения функции
2) Чётность, нечётность функции:
Функция не является ни чётной, ни нечётной.
3) Точки разрыва функции :
— вертикальная
асимптота
Найдём наклонные асимптоты функции :
-
горизонтальная асимптота
4) Промежутки монотонности функции и точки экстремума:
— критическая
точка первого рода
Функция возрастает при и при .
Точек экстремума нет.
5) Промежутки выпуклости и вогнутости и точки перегиба:
— критические
точки второго рода
Функция выпукла при и вогнута при .
— точка
перегиба
6) Точки пересечения с осями координат:
с : — точек
пересечения с нет
с:
7) Построим график функции:
Пример 2.
Исследовать функцию и построить
ее график:
Решение
1) Область определения функции
2) Чётность, нечётность функции:
Функция не является ни чётной, ни нечётной.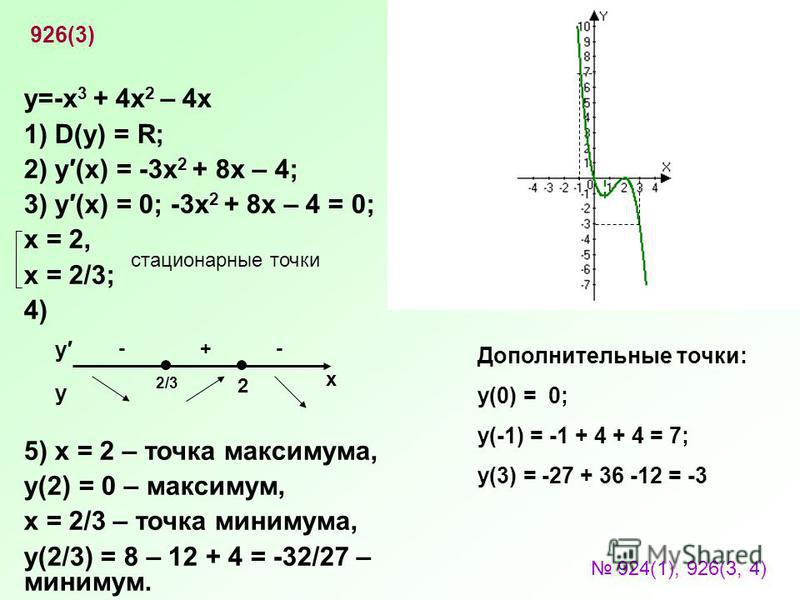
3) Точки разрыва функции :
— вертикальная
асимптота
Найдём наклонные асимптоты функции :
-
горизонтальная асимптота
4) Промежутки монотонности функции и точки экстремума:
— критические
точки первого рода
Функция возрастает при и убывает при и при.
— точка
максимума
5) Промежутки выпуклости и вогнутости и точки перегиба:
— критические
точки второго рода
Функция выпукла при и и вогнута при .
— точка
перегиба
6) Точки пересечения с осями координат:
с :
с:
7) Построим график функции:
3.2 Производная как функция — Объем исчисления 1
Цели обучения
- Определите производную функцию заданной функции.
- Постройте производную функцию от графика заданной функции.
- Укажите связь между производными и непрерывностью.

- Опишите три условия, когда функция не имеет производной.
- Объясните значение производной высшего порядка.
Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке.Если мы дифференцируем функцию положения в данный момент времени, мы получаем скорость в этот момент. Кажется разумным заключить, что знание производной функции в каждой точке может дать ценную информацию о поведении функции. Однако процесс нахождения производной даже для нескольких значений с использованием методов предыдущего раздела быстро стал бы довольно утомительным. В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.
Функция производной дает производную функции в каждой точке области определения исходной функции, для которой определена производная.Мы можем формально определить производную функцию следующим образом.
Определение
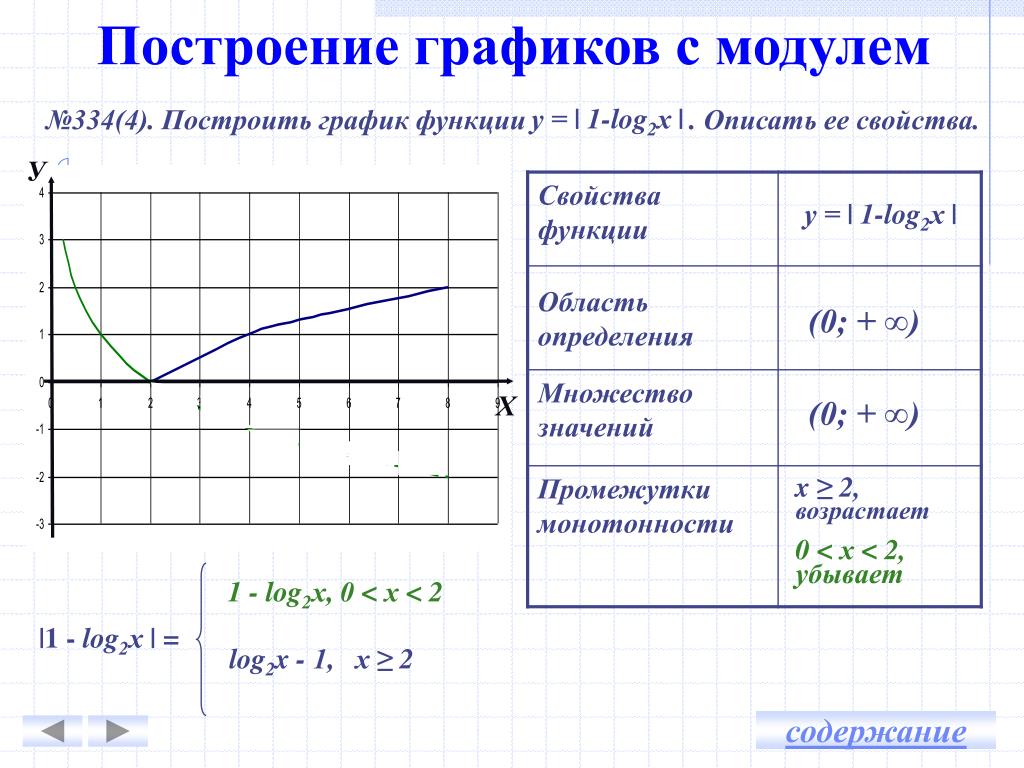
Позвольте быть функцией. Производная функция , обозначенная как, — это функция, область определения которой состоит из таких значений, что существует следующий предел:
.
Говорят, что функция дифференцируема на , если
существует. В более общем смысле, функция называется дифференцируемой на , если она дифференцируема в каждой точке открытого набора, а дифференцируемая функция — это функция, в которой существует в своей области.
В следующих нескольких примерах мы используем (рисунок), чтобы найти производную функции.
Нахождение производной функции квадратного корня
Найдите производную от.
Решение
Начните непосредственно с определения производной функции. Используйте (рисунок).
Нахождение производной квадратичной функции
Найдите производную функции.
Решение
Выполните ту же процедуру, но без умножения на конъюгат.
Найдите производную от.
Решение
Мы используем множество различных обозначений для выражения производной функции. На (Рисунок) мы показали, что если, то. Если бы мы выразили эту функцию в форме, мы могли бы выразить производную как или.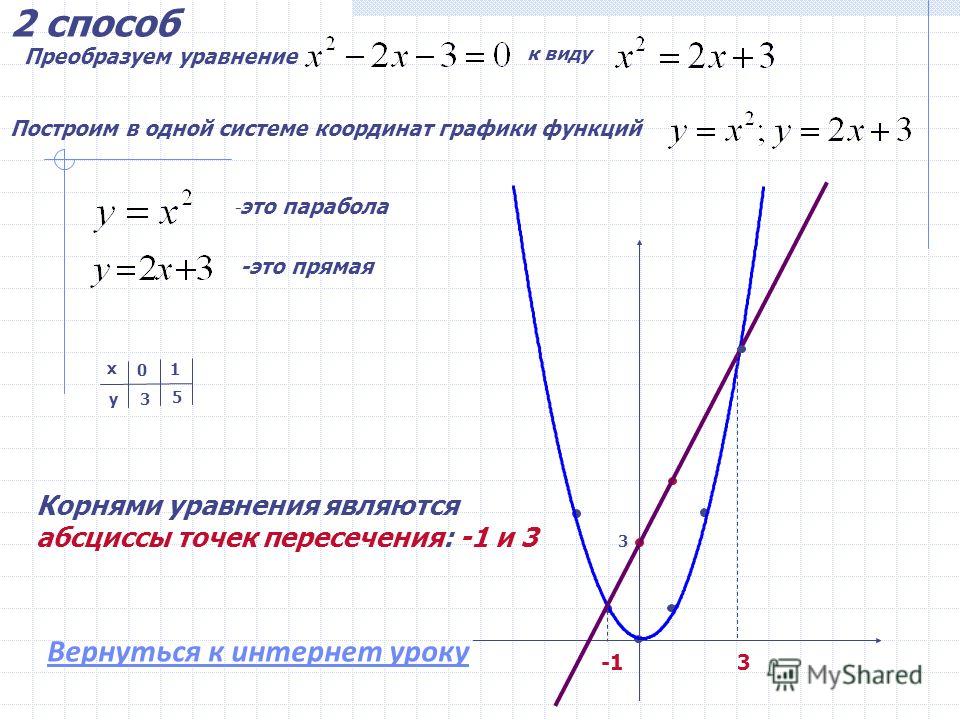 Мы могли бы передать ту же информацию письменно. Таким образом, для функции каждое из следующих обозначений представляет собой производную от:
Мы могли бы передать ту же информацию письменно. Таким образом, для функции каждое из следующих обозначений представляет собой производную от:
.
Вместо мы также можем использовать. Использование обозначений (так называемых обозначений Лейбница) довольно распространено в инженерии и физике.Чтобы лучше понять это обозначение, напомним, что производная функции в точке — это предел наклона секущих линий, когда секущие линии приближаются к касательной. Наклоны этих секущих линий часто выражаются в виде где — разница значений, соответствующая разнице значений, которые выражаются как ((Рисунок)). Таким образом, производная, которую можно представить как мгновенную скорость изменения относительно, выражается как
.
Фигура 1.Производная выражается как.
Мы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение производной функции, мы можем построить график. Учитывая и то, и другое, мы ожидаем увидеть соответствие между графиками этих двух функций, поскольку дает скорость изменения функции (или наклон касательной к).
В (Рисунок) мы обнаружили, что для. Если мы построим график этих функций на тех же осях, что и на (Рисунок), мы сможем использовать графики, чтобы понять взаимосвязь между этими двумя функциями.Во-первых, мы замечаем, что он увеличивается по всей своей области, что означает, что наклон его касательных во всех точках положительный. Следовательно, мы ожидаем для всех значений в его области. Кроме того, по мере увеличения наклон касательных к уменьшается, и мы ожидаем увидеть соответствующее уменьшение. Мы также замечаем, что это не определено и соответствует вертикальной касательной к точке 0.
Рис. 2. Производная везде положительна, потому что функция возрастает.
В (Рисунок) мы обнаружили, что для. Графики этих функций показаны на (Рисунок). Обратите внимание, что для. Для этих же значений. Для значений увеличивается и. Кроме того, имеет горизонтальную касательную в точках и.
Построение производной с помощью функции
Используйте следующий график, чтобы нарисовать график.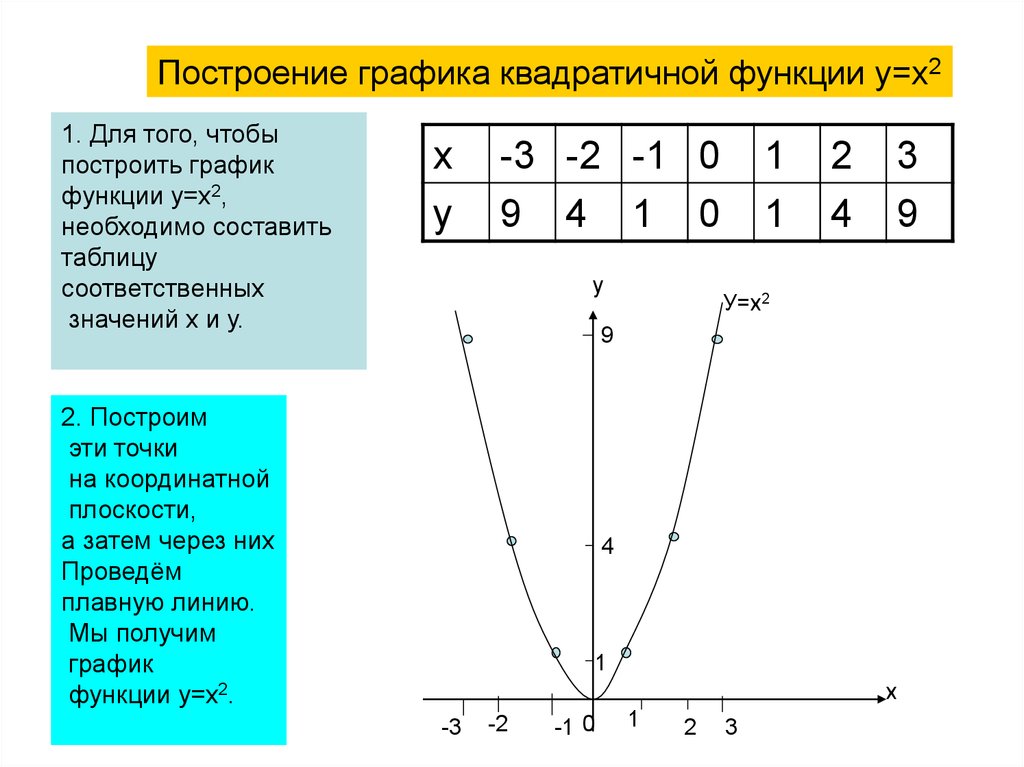
Нарисуйте график. На каком интервале находится график выше оси?
Решение
Теперь, когда мы можем построить график производной, давайте рассмотрим поведение графиков.Во-первых, мы рассматриваем взаимосвязь между дифференцируемостью и непрерывностью. Мы увидим, что если функция дифференцируема в точке, она должна быть непрерывной там; однако функция, непрерывная в какой-то точке, не обязательно должна быть дифференцируемой в этой точке. Фактически, функция может быть непрерывной в точке и не дифференцируемой в этой точке по одной из нескольких причин.
Проба
Если дифференцируем в, то существует и
.
Мы хотим показать, что это непрерывно, показав это.Таким образом,
Следовательно, поскольку определено и, мы заключаем, что непрерывно в точке.
Мы только что доказали, что дифференцируемость предполагает непрерывность, но теперь мы рассмотрим, подразумевает ли непрерывность дифференцируемость. Чтобы определить ответ на этот вопрос, исследуем функцию. Эта функция всюду непрерывна; однако не определено. Это наблюдение приводит нас к мысли, что непрерывность не предполагает дифференцируемости. Давайте изучим дальше. Для,
Эта функция всюду непрерывна; однако не определено. Это наблюдение приводит нас к мысли, что непрерывность не предполагает дифференцируемости. Давайте изучим дальше. Для,
.
Этот предел не существует, потому что
.
См. (Рисунок).
Рисунок 4. Функция непрерывна в 0, но не дифференцируема в 0.
Рассмотрим некоторые дополнительные ситуации, в которых непрерывная функция не дифференцируема. Рассмотрим функцию:
.
Значит, не существует. Беглый взгляд на график проясняет ситуацию. Функция имеет вертикальную касательную в точке 0 ((рисунок)).
Рисунок 5. Функция имеет вертикальную касательную в точке. Он непрерывен в 0, но не дифференцируем в 0.
У функции также есть производная, которая демонстрирует интересное поведение при 0. Мы видим, что
.
Этот предел не существует, в основном потому, что наклон секущих линий непрерывно меняет направление по мере приближения к нулю ((Рисунок)).
Рисунок 6. Функция не дифференцируема в 0.
Итого:
- Заметим, что если функция не является непрерывной, она не может быть дифференцируемой, поскольку каждая дифференцируемая функция должна быть непрерывной. Однако, если функция непрерывна, она все равно не может быть дифференцируемой.
- Мы видели, что это невозможно дифференцировать в 0, потому что предел наклона касательных линий слева и справа не был одинаковым. Визуально это привело к появлению острого угла на графике функции в 0. Отсюда мы заключаем, что для того, чтобы быть дифференцируемой в точке, функция должна быть «гладкой» в этой точке.
- Как мы видели в примере, функция не может быть дифференцируемой в точке, где есть вертикальная касательная.
- Как мы видели, функция может быть не дифференцируемой в точке и более сложными способами.
Непрерывная и дифференцируемая кусочная функция
Производная функции сама по себе является функцией, поэтому мы можем найти производную от производной. Например, производная функции положения — это скорость изменения положения или скорости. Производная скорости — это скорость изменения скорости, которая является ускорением. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать использовать производные для получения третьей производной, четвертой производной и так далее.В совокупности они называются производными более высокого порядка . Обозначения для производных высшего порядка от могут быть выражены в любой из следующих форм:
Производная скорости — это скорость изменения скорости, которая является ускорением. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать использовать производные для получения третьей производной, четвертой производной и так далее.В совокупности они называются производными более высокого порядка . Обозначения для производных высшего порядка от могут быть выражены в любой из следующих форм:
.
Интересно отметить, что обозначение для можно рассматривать как попытку выразить более компактно. Аналогично.
Поиск второй производной
Для, найдите.
В поисках ускорения
Положение частицы вдоль оси координат в момент времени (в секундах) определяется выражением (в метрах).Найдите функцию, описывающую его ускорение во времени.
- Производная функция
В следующих упражнениях используйте определение производной для поиска.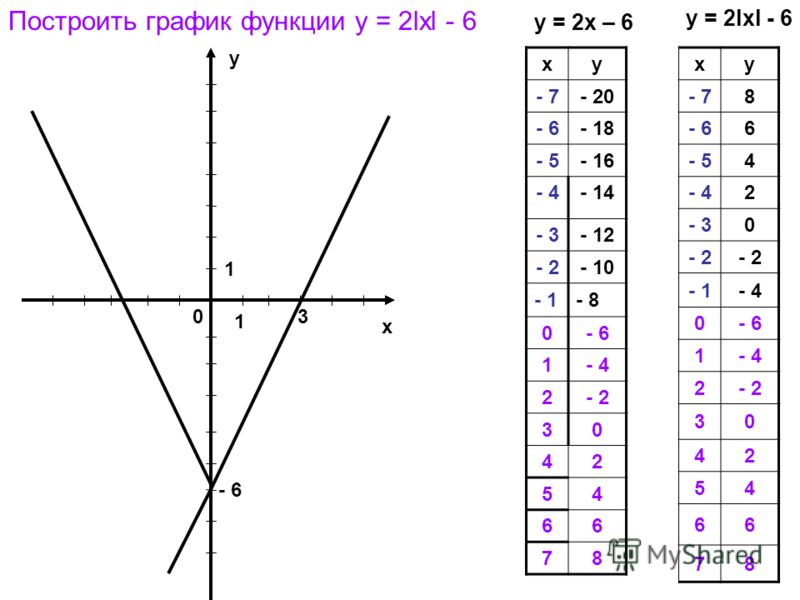
1.
2.
3.
4.
Решение
5.
6.
Решение
7.
8.
Решение
9.
10.
Решение
Для следующих упражнений используйте график, чтобы нарисовать график его производной.
11.
12.
Решение
13.
14.
Решение
Для следующих упражнений данный предел представляет собой производную функции в.Найти и .
15.
16.
Решение
17.
18.
Решение
19.
20.
Решение
Для следующих функций:
- зарисовать график и
- используйте определение производной, чтобы показать, что функция не дифференцируема в.

21.
23
Для следующих графиков
- определяет, для каких значений существует, но не является непрерывным, и
- определить, для каких значений функция является непрерывной, но не дифференцируемой при.
25.
Для следующих функций используйте, чтобы найти.
28.
29.
30.
Решение
Для следующих упражнений используйте калькулятор для построения графиков. Определите функцию, затем используйте калькулятор для построения графика.
31. [Т]
33. [Т]
35. [Т]
Для следующих упражнений опишите, что представляют собой эти два выражения в терминах каждой из данных ситуаций. Обязательно укажите единицы измерения.
37. обозначает население города во время в годах.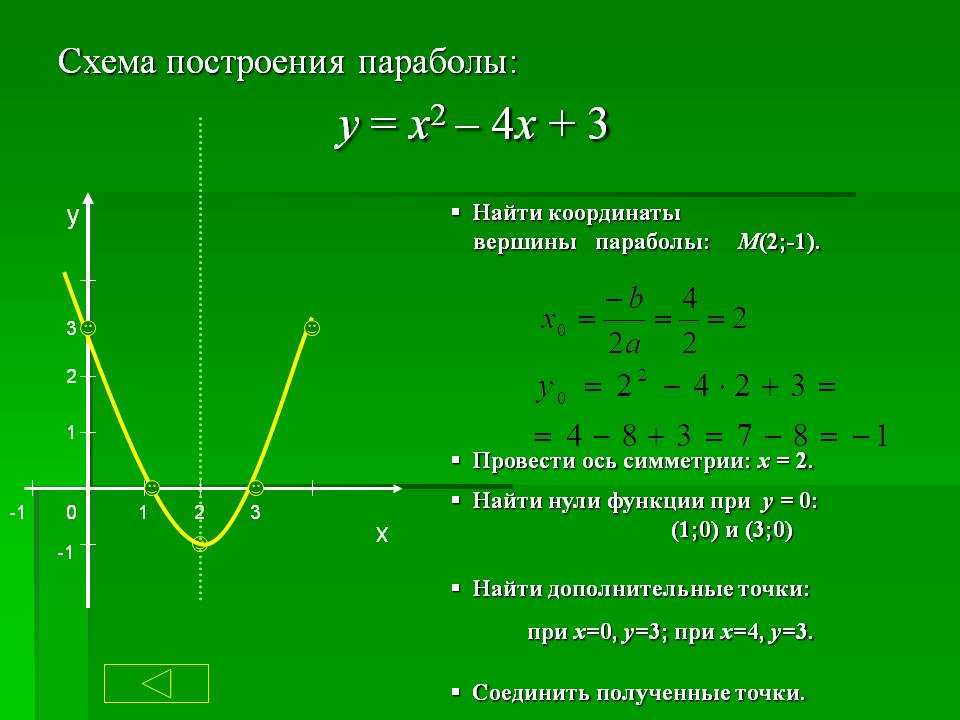
38. обозначает общую сумму денег (в тысячах долларов), потраченную клиентами на концессии в парке развлечений.
Решение
а. Средняя ставка, с которой клиенты потратили на уступки, в тысячах на одного покупателя.
г. Скорость (в тысячах на одного покупателя), по которой клиенты тратили деньги на уступки, в тысячах на одного покупателя.
39. обозначает общую стоимость (в тысячах долларов) производства радиочасов.
40. обозначает оценку (в процентных пунктах), полученную по тесту за количество часов обучения.
Решение
а. Средняя оценка, полученная за тест, при среднем времени обучения между двумя суммами.
г. Скорость (в процентных пунктах в час), с которой оценка по тесту повышалась или понижалась за данное среднее время обучения в часах.
41. обозначает стоимость (в долларах) учебника социологии в университетских книжных магазинах США с 1990 года.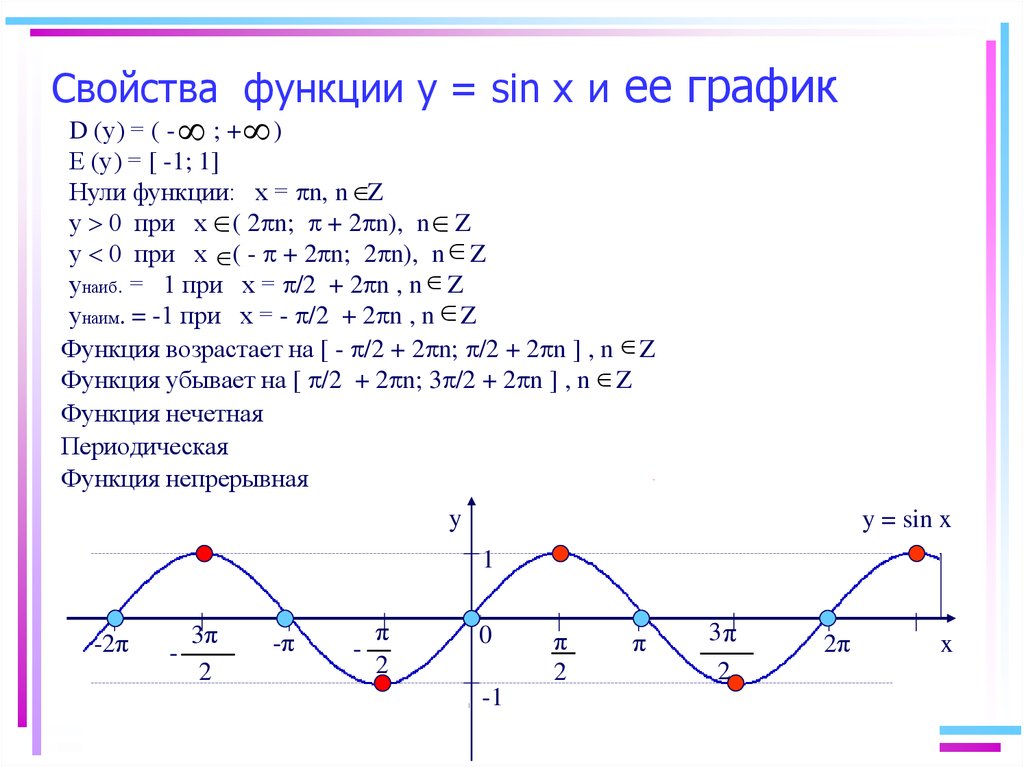
42. обозначает атмосферное давление на высоте футов.
Решение
а. Среднее изменение атмосферного давления между двумя разными высотами.
г. Скорость (торр на фут), с которой атмосферное давление увеличивается или уменьшается на высоте.
Решение
а. Скорость (в градусах на фут), с которой температура повышается или понижается для данной высоты.
г. Скорость изменения температуры при изменении высоты на высоте 1000 футов составляет -0.1 градус на фут.
Решение
а. Скорость, с которой число людей, заболевших гриппом, меняется через несколько недель после первоначальной вспышки.
г. Скорость резко увеличивается до третьей недели, после чего она замедляется, а затем становится постоянной.
Для следующих упражнений используйте следующую таблицу, которая показывает высоту ракеты Saturn V для миссии Apollo 11 через несколько секунд после запуска.
47. В чем физический смысл? Какие единицы?
48. [T] Создайте таблицу значений и нанесите график на одном и том же графике. ( Подсказка: для внутренних точек, оцените и левый предел, и правый предел и усредните их.)
Решение
3.2: Производная как функция
Цели обучения
- Определите производную функцию заданной функции.
- Постройте производную функцию от графика заданной функции.
- Укажите связь между производными и непрерывностью.
- Опишите три условия, когда функция не имеет производной.
- Объясните значение производной высшего порядка.

Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке. Если мы дифференцируем функцию положения в данный момент времени, мы получаем скорость в этот момент. Кажется разумным заключить, что знание производной функции в каждой точке может дать ценную информацию о поведении функции. Однако процесс нахождения производной даже для нескольких значений с использованием методов предыдущего раздела быстро стал бы довольно утомительным.В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.
Производные функции
Функция производной дает производную функции в каждой точке области определения исходной функции, для которой определена производная. Мы можем формально определить производную функцию следующим образом.
Определение: производная функция
Пусть \ (f \) будет функцией. Производная функция , обозначаемая \ (f ‘\), является функцией, область определения которой состоит из таких значений \ (x \), что существует следующий предел:
\ [f ‘(x) = \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h}.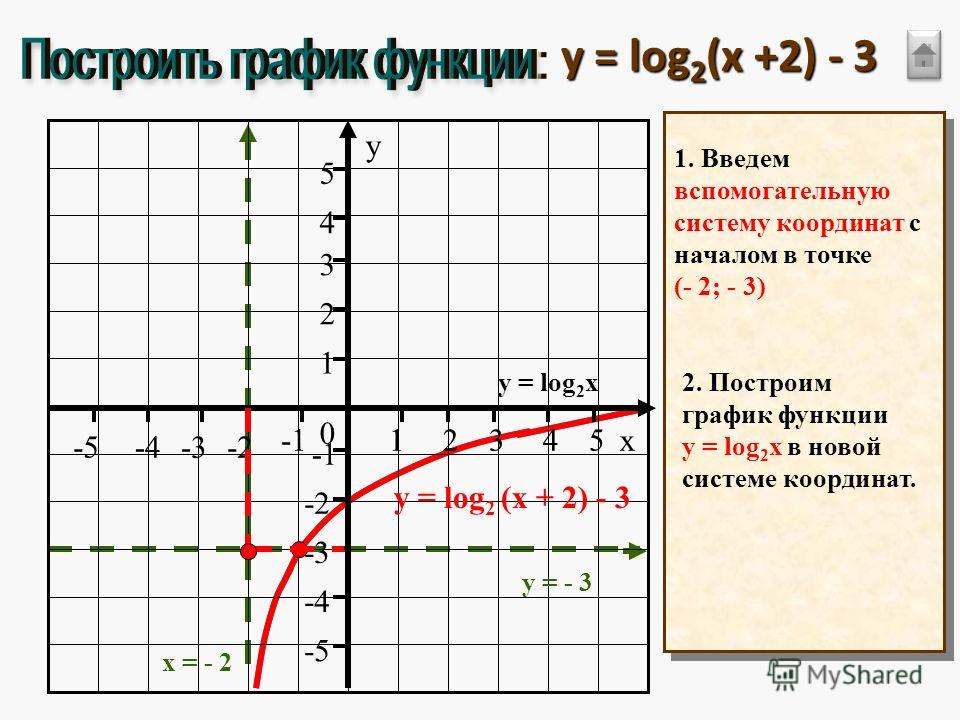 \ label {derdef} \]
\ label {derdef} \]
Функция \ (f (x) \) называется дифференцируемой в точке \ (a \), если существует \ (f ‘(a) \). В более общем смысле, функция называется дифференцируемой на на \ (S \), если она дифференцируема в каждой точке открытого множества \ (S \), а дифференцируемая функция — это функция, в которой \ (f ‘( x) \) существует в своем домене.
В следующих нескольких примерах мы используем уравнение \ ref {derdef}, чтобы найти производную функции.
Пример \ (\ PageIndex {1} \): поиск производной функции извлечения квадратного корня
Найдите производную от \ (f (x) = \ sqrt {x} \).
Решение
Начните непосредственно с определения производной функции.
Заменить \ (f (x + h) = \ sqrt {x + h} \) и \ (f (x) = \ sqrt {x} \) в \ (f ‘(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \).
| \ (f ‘(x) = \ displaystyle \ lim_ {h → 0} \ frac {\ sqrt {x + h} — \ sqrt {x}} {h} \) | ||
| \ (= \ displaystyle \ lim_ {h → 0} \ frac {\ sqrt {x + h} — \ sqrt {x}} {h} ⋅ \ frac {\ sqrt {x + h} + \ sqrt { x}} {\ sqrt {x + h} + \ sqrt {x}} \) | Умножьте числитель и знаменатель на \ (\ sqrt {x + h} + \ sqrt {x} \) без распределения в знаменателе. | |
| \ (= \ displaystyle \ lim_ {h → 0} \ frac {h} {h} left (\ sqrt {x + h} + \ sqrt {x} \ right)} \) | Умножьте числители и упростите. | |
| \ (= \ displaystyle \ lim_ {h → 0} \ frac {1} {\ left (\ sqrt {x + h} + \ sqrt {x} \ right)} \) | Отмените \ (h \). 2 \).2−2x \ справа) = 2x − 2 \). Таким образом, для функции \ (y = f (x) \) каждое из следующих обозначений представляет производную от \ (f (x) \): \ (f ‘(x), \ quad \ dfrac {dy} {dx}, \ quad y’, \ quad \ dfrac {d} {dx} \ big (f (x) \ big) \). Вместо \ (f ‘(a) \) мы также можем использовать \ (\ dfrac {dy} {dx} \ Big | _ {x = a} \). Нотация \ (\ dfrac {dy} {dx} \) (называемая нотацией Лейбница) довольно распространена в технике и физике. Чтобы лучше понять это обозначение, напомним, что производная функции в точке — это предел наклона секущих линий, когда секущие линии приближаются к касательной.Наклоны этих секущих часто выражаются в виде \ (\ dfrac {Δy} {Δx} \), где \ (Δy \) — разность значений \ (y \), соответствующая разнице в \ (x \) значения, которые выражаются как \ (Δx \) (Рисунок \ (\ PageIndex {1} \)). \ (\ Displaystyle \ frac {dy} {dx} = \ lim_ {Δx → 0} \ frac {Δy} {Δx} \). Рисунок \ (\ PageIndex {1} \): производная выражается как \ (\ dfrac {dy} {dx} = \ displaystyle \ lim_ {Δx → 0} \ frac {Δy} {Δx} \). Построение графика производнойМы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение производной функции, мы можем построить график. Учитывая и то, и другое, мы ожидаем увидеть соответствие между графиками этих двух функций, поскольку \ (f ‘(x) \) дает скорость изменения функции \ (f (x) \) (или наклон касательной линия к \ (f (x) \)). В примере \ (\ PageIndex {1} \) мы обнаружили, что для \ (f (x) = \ sqrt {x} \), \ (f ‘(x) = \ frac {1} {2 \ sqrt { Икс}}\).Если мы построим график этих функций на тех же осях, как на рисунке \ (\ PageIndex {2} \), мы сможем использовать графики, чтобы понять взаимосвязь между этими двумя функциями. Рисунок \ (\ PageIndex {3} \): производная \ (f ‘(x) 0 \), где \ (f (x) \) возрастает. Производная равна нулю, если функция имеет горизонтальную касательную. Пример \ (\ PageIndex {3} \): эскиз производной с использованием функции Используйте следующий график \ (f (x) \), чтобы нарисовать график \ (f ‘(x) \).
Деривативы и непрерывностьТеперь, когда мы можем построить график производной, давайте рассмотрим поведение графиков. Во-первых, мы рассматриваем взаимосвязь между дифференцируемостью и непрерывностью.Мы увидим, что если функция дифференцируема в точке, она должна быть непрерывной там; однако функция, непрерывная в какой-то точке, не обязательно должна быть дифференцируемой в этой точке. Фактически, функция может быть непрерывной в точке и не дифференцируемой в этой точке по одной из нескольких причин. Дифференцируемость подразумевает непрерывность Пусть \ (f (x) \) — функция и \ (a \) находится в ее области определения. Если \ (f (x) \) дифференцируема в \ (a \), то \ (f \) непрерывна в \ (a \). Проба Если \ (f (x) \) дифференцируемо в \ (a \), то \ (f ‘(a) \) существует и, если мы положим \ (h = x — a \), имеем \ (x = a + h \), и поскольку \ (h = xa \ to 0 \), мы можем видеть, что \ (x \ to a \). Затем \ [f ‘(a) = \ lim_ {h \ to 0} \ frac {f (a + h) -f (a)} {h} \ nonumber \] можно переписать как \ (F ‘(a) = \ displaystyle \ lim_ {x → a} \ frac {f (x) −f (a)} {x − a} \). Мы хотим показать, что \ (f (x) \) непрерывно в \ (a \), показав, что \ (\ displaystyle \ lim_ {x → a} f (x) = f (a). \) Таким образом, \ (\ begin {align *} \ displaystyle \ lim_ {x → a} f (x) & = \ lim_ {x → a} \; \ big (f (x) −f (a) + f (a)) \ big) \\ [4pt] Следовательно, поскольку \ (f (a) \) определено и \ (\ displaystyle \ lim_ {x → a} f (x) = f (a) \), мы заключаем, что \ (f \) непрерывно в \ (а \). □ Мы только что доказали, что дифференцируемость предполагает непрерывность, но теперь мы рассмотрим, подразумевает ли непрерывность дифференцируемость. Чтобы определить ответ на этот вопрос, исследуем функцию \ (f (x) = | x | \).2}} = + ∞ \). Таким образом, \ (f ‘(0) \) не существует. Быстрый взгляд на график \ (f (x) = \ sqrt [3] {x} \) проясняет ситуацию. Функция имеет вертикальную касательную в точке \ (0 \) (рисунок \ (\ PageIndex {5} \)). Рисунок \ (\ PageIndex {5} \): функция \ (f (x) = \ sqrt [3] {x} \) имеет вертикальную касательную в точке \ (x = 0 \). Он непрерывен в \ (0 \), но не дифференцируем в \ (0 \). Функция \ (f (x) = \ begin {cases} x \ sin \ left (\ frac {1} {x} \ right), & & \ text {if} x ≠ 0 \\ 0, & & \ text {if} x = 0 \ end {ases} \) также имеет производную, которая демонстрирует интересное поведение в \ (0 \). Мы видим, что \ (е ‘(0) = \ displaystyle \ lim_ {x → 0} \ frac {x \ sin \ left (1 / x \ right) −0} {x − 0} = \ lim_ {x → 0} \ sin \ left (\ frac {1} {x} \ right) \). Этот предел не существует, в основном потому, что наклон секущих линий непрерывно меняет направление по мере приближения к нулю (рисунок \ (\ PageIndex {6} \)). Рисунок \ (\ PageIndex {6} \): функция \ (f (x) = \ begin {cases} x \ sin \ left (\ frac {1} {x} \ right), & & \ text {if} x ≠ 0 \\ 0, & & \ text {if} x = 0 \ end {ases} \) не дифференцируемо в \ (0 \). Итого:
| Упростим числитель. |
| \ (= \ displaystyle \ lim_ {h → 0} (4x + h − 3) \) | Выносим за скобки \ (h \) в числителе и сокращаем, добавляя \ (h \) в знаменатель. | |
| \ (= 4x − 3 \) | Возьми предел. |
Затем найдите \ (f » (x) \), взяв производную от \ (f ‘(x) = 4x − 3. \)
| \ (f » (x) = \ displaystyle \ lim_ {h → 0} \ frac {f ‘(x + h) −f’ (x)} {h} \) | Используйте \ (f ‘(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \) с \ (f’ (x) \) в место \ (f (x).3 \), найти \ (a (t). \)
Ключевые понятия
Ключевые уравнения\ (е ‘(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \) Глоссарий
Авторы и авторствоКак сравнить график функции и ее производной — блог Magoosh Чтение производного графика — важная часть учебной программы AP Calculus. Существует ли производная?Во-первых, глядя на график, мы должны знать, существует ли вообще производная функции. В нашем производном посте в блоге есть немного больше информации об этом. Три ситуации, когда дериватив не существуетНет производной, если на кривой есть разрыв.Это любой момент, когда есть разрыв кривой, когда две части кривой не соединяются. Виды несплошностей:Обнаружен устранимый разрыв. Представьте себе линейную функцию, такую как y = x + 3. Если бы мы добавили ограничение, в котором x не определено при x = 0, у нас был бы такой разрыв. Бесконечный разрыв. Это происходит, когда у нас есть какое-либо уравнение, в котором есть разрыв между двумя непрерывными участками кривой из-за того, что асимптоты достигают бесконечности.Например, пусть y = 3 / (x-2). И, наконец, разрыв скачка. Это происходит с кусочными функциями, где две секции просто не соединяются. Производная не существует там, где есть острый угол.Это часто происходит с проблемами абсолютного значения. Посмотрим на график y = √x 2 При x = 0 производной нет, потому что у нас есть резкий изгиб кривой. Наконец, нет производной везде, где есть вертикальный разрез графика.Если есть вертикальный участок графика, наклон не определен; следовательно, производной не существует. Чтение производного графика.Глядя на график, мы должны иметь возможность быстро оценить уклон на любом участке и получить приблизительное представление о том, каким должен быть уклон. Это позволяет легко сопоставить график с его производной. Глядя на первый график, можете ли вы выяснить, какой из трех приведенных ниже графиков является графиком производной? f ‘(x): a б c Несколько ключей к правильному ответу. Построение графика функции на основе производной и двойной производной.Производная и двойная производная говорят нам несколько ключевых вещей о графике: (Надлежащая практика AP: как определить, минимальное оно или максимальное?) Ниже приведен график производной функции f (x). Вот график функции. Можем ли мы увидеть, как они соотносятся? Умение читать графики производной и знать, какой должна быть общая форма исходной функции, является важной частью учебной программы AP Calculus. Убедитесь, что вы знаете, как определять точки перегиба, локальные минимумы и максимумы, а также где функция увеличивается или уменьшается. Гарантированно повысьте свой результат по SAT или ACT. Начните 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep уже сегодня!Между прочим, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT.Нажмите сюда, чтобы узнать больше! О ЗакариЗакари — бывший инженер-механик, а в настоящее время учитель физики, математики и информатики в средней школе. Он окончил университет Макгилла в 2011 году и работал в автомобильной промышленности в Детройте, прежде чем перейти к образованию. Он преподает и занимается репетиторством в течение последних пяти лет, но вы также можете найти его за приключениями, чтением, скалолазанием и путешествиями, когда появляется такая возможность. Как вычислить и построить производную функции с помощью Python — Matplotlib?В этой статье мы построим производную функции с помощью matplotlib и python.Для этого мы используем следующие модули в Python:
Чтобы сначала построить производную функции, мы должны ее вычислить. Библиотека scipy.misc имеет функцию производная () , которая принимает один аргумент как функцию, а другой — переменную w.r.t, от которой мы будем дифференцировать функцию. Итак, мы создадим метод с именем function (), который будет возвращать исходную функцию, и второй метод с именем производное (), который будет возвращать производную этой функции. После этого вычисления производной входной функции мы будем использовать функцию NumPy linspace () , которая устанавливает диапазон оси x. Функция plot () будет использоваться для построения графика функции, а также производной этой функции. Обращение:
Пример 1: (Производная от кубической) В этом примере, мы дадим функцию f (x) = 2x 3 + x + 3 в качестве входных данных, затем вычислим производную и построим график функции и ее производной. Python3
Выход: Пример 2: (Производная полинома степени Poly) В этом примере мы дадим функцию f (x) = x 4 + x 2 +5 в качестве входных данных, затем вычислим производную и построим график функции и ее производной. Python3
Вывод: Пример 3: Производная квадратичной с форматированием по тексту) В этом примере мы построим производную от f (x) = 4x 2 + x + 1. Кроме того, мы будем использовать некоторое форматирование с помощью функции gca () , которая изменит пределы оси так, чтобы обе оси x, y пересекались в начале координат. Python3
Вывод: Внимание компьютерщик! Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы. Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS . И чтобы начать свое путешествие по машинному обучению, присоединитесь к курсу Машинное обучение — базовый уровень 4.5 Производные и форма графика — Исчисление Том 1Цели обучения
Ранее в этой главе мы заявляли, что если функция ff имеет локальный экстремум в точках c, c, то cc должна быть критической точкой f.f. Однако не гарантируется, что функция имеет локальный экстремум в критической точке. Например, f (x) = x3f (x) = x3 имеет критическую точку при x = 0x = 0, поскольку f ′ (x) = 3x2f ′ (x) = 3×2 равно нулю при x = 0, x = 0, но ff не имеет локального экстремума при x = 0.x = 0. Используя результаты из предыдущего раздела, теперь мы можем определить, действительно ли критическая точка функции соответствует локальному экстремальному значению. Первый производный тестСледствие 33 теоремы о среднем значении показало, что если производная функции положительна на интервале II, то функция возрастает на интервале I.I. С другой стороны, если производная функции отрицательна на интервале I, I, тогда функция убывает на интервале II, как показано на следующем рисунке. Рис. 4.30. Обе функции растут в интервале (a, b). (A, b). В каждой точке x, x производная f ′ (x)> 0.f ′ (x)> 0. Обе функции убывают на интервале (a, b). (A, b). В каждой точке x, x производная f ′ (x) Непрерывная функция ff имеет локальный максимум в точке cc тогда и только тогда, когда ff переключается с увеличения на уменьшение в точке c.c. Точно так же ff имеет локальный минимум в точке cc тогда и только тогда, когда ff переключается с уменьшения на увеличение в точке c. Обратите внимание, что ff не обязательно должен иметь локальные экстремумы в критической точке. Рис. 4.31. Функция ff имеет четыре критических точки: a, b, c, andd.a, b, c иd. Функция ff имеет локальные максимумы в точках aa и d, d и локальный минимум в точках b.b. Функция ff не имеет локального экстремума в c.c. Знак f′f ′ меняется на всех локальных экстремумах. Используя рисунок 4.31, мы суммируем основные результаты, касающиеся локальных экстремумов.
Этот результат известен как тест первой производной. Теорема 4.9 Проверка первой производнойПредположим, что ff — непрерывная функция на интервале II, содержащем критическую точку c.c. Если ff дифференцируема над I, I, за исключением, возможно, точки c, c, то f (c) f (c) удовлетворяет одному из следующих описаний:
Мы можем резюмировать тест первой производной как стратегию поиска локальных экстремумов. Стратегия решения проблемСтратегия решения проблем: использование первой производной проверкиРассмотрим функцию ff, непрерывную на интервале I.I.
Теперь давайте посмотрим, как использовать эту стратегию для поиска всех локальных экстремумов для определенных функций. Пример 4.17Использование теста первой производной для поиска локальных экстремумовИспользуйте тест первой производной, чтобы найти расположение всех локальных экстремумов для f (x) = x3−3×2−9x − 1.f (x) = x3−3×2−9x − 1.Используйте графическую утилиту, чтобы подтвердить свои результаты. РешениеШаг 1. Производная равна f ′ (x) = 3×2−6x − 9. f ′ (x) = 3×2−6x − 9. Чтобы найти критические точки, нам нужно найти, где f ′ (x) = 0. f ′ (x) = 0. Разлагая многочлен на множители, мы заключаем, что критические точки должны удовлетворять 3 (x2−2x − 3) = 3 (x − 3) (x + 1) = 0,3 (x2−2x − 3) = 3 (x − 3) ( х + 1) = 0. Следовательно, критическими точками являются x = 3, −1.x = 3, −1. Теперь разделите интервал (−∞, ∞) (- ∞, ∞) на меньшие интервалы (−∞, −1), (- 1,3) и (3, ∞).(−∞, −1), (- 1,3) и (3, ∞). Шаг 2. Поскольку f′f ′ — непрерывная функция, для определения знака f ′ (x) f ′ (x) на каждом подынтервале достаточно выбрать точку на каждом из интервалов (−∞, −1 ), (- 1,3) и (3, ∞) (- ∞, −1), (- 1,3) и (3, ∞) и определяют знак f′f ′ в каждой из этих точек.
Шаг 3. Поскольку f′f ′ меняет знак с положительного на отрицательный, когда xx увеличивается до –1, f – 1, f имеет локальный максимум при x = −1.x = −1. Поскольку f′f ′ меняет знак с отрицательного на положительный при увеличении xx до 3, f3, f имеет локальный минимум при x = 3.х = 3. Эти аналитические результаты согласуются со следующим графиком. Рисунок 4.32. Функция ff имеет максимум при x = −1x = −1 и минимум при x = 3x = 3. КПП 4.16 Используйте тест первой производной, чтобы найти все локальные экстремумы для f (x) = — x3 + 32×2 + 18x.f (x) = — x3 + 32×2 + 18x. Пример 4.18Использование первого производного теста Используйте тест первой производной, чтобы найти расположение всех локальных экстремумов для f (x) = 5×1 / 3 − x5 / 3. РешениеШаг 1. Производная: f ′ (x) = 53x − 2 / 3−53×2 / 3 = 53×2 / 3−5×2 / 33 = 5−5×4 / 33×2 / 3 = 5 (1 − x4 / 3) 3×2 / 3. f ′ (x) = 53x − 2 / 3−53×2 / 3 = 53×2 / 3−5×2 / 33 = 5−5×4 / 33×2 / 3 = 5 (1 − x4 / 3) 3×2 / 3. Производная f ′ (x) = 0f ′ (x) = 0, когда 1 − x4 / 3 = 0,1 − x4 / 3 = 0. Следовательно, f ′ (x) = 0f ′ (x) = 0 при x = ± 1.x = ± 1. Производная f ′ (x) f ′ (x) не определена при x = 0.x = 0. Следовательно, у нас есть три критических точки: x = 0, x = 0, x = 1, x = 1 и x = −1.x = −1. Следовательно, разделим интервал (−∞, ∞) (- ∞, ∞) на меньшие интервалы (−∞, −1), (- 1,0), (0,1), (- ∞, −1), (−1,0), (0,1) и (1, ∞).(1, ∞). Шаг 2: Поскольку f′f ′ непрерывен на каждом подынтервале, достаточно выбрать контрольную точку xx в каждом из интервалов шага 11 и определить знак f′f ′ в каждой из этих точек. Точки x = −2, x = −12, x = 12 и x = 2x = −2, x = −12, x = 12 и x = 2 являются контрольными точками для этих интервалов.
Шаг 3: Поскольку ff убывает на интервале (−∞, −1) (- ∞, −1) и увеличивается на интервале (−1,0), (- 1,0), ff имеет локальный минимум при x = −1.х = -1. Поскольку ff возрастает на интервале (−1,0) (- 1,0) и интервале (0,1), (0,1), ff не имеет локального экстремума при x = 0.x = 0. Поскольку ff возрастает на интервале (0,1) (0,1) и убывает на интервале (1, ∞), f (1, ∞), f имеет локальный максимум при x = 1. Рисунок 4.33. Функция f имеет локальный минимум при x = −1x = −1 и локальный максимум при x = 1.x = 1. КПП 4.17 Используйте тест первой производной, чтобы найти все локальные экстремумы для f (x) = x − 13.е (х) = х-13. Вогнутость и точки перегибаТеперь мы знаем, как определить, где функция увеличивается или уменьшается. Однако есть еще одна проблема, которую следует учитывать в отношении формы графика функции. Если график изгибается, изгибается ли он вверх или вниз? Это понятие называется вогнутостью функции. На рис. 4.34 (a) показана функция ff с графиком, изгибающимся вверх. По мере увеличения xx наклон касательной увеличивается. Таким образом, поскольку производная увеличивается с увеличением xx, f′f ′ является возрастающей функцией.Мы говорим, что эта функция ff вогнута вверх. На рис. 4.34 (b) показана функция ff, которая изгибается вниз. ОпределениеПусть ff — функция, дифференцируемая на открытом интервале I.I. Если f′f ′ возрастает над I, I, мы говорим, что ff вогнута вверх над I.I. Если f′f ′ убывает над I, I, мы говорим, что ff вогнута вниз над I.I. Рис. 4.34 (a), (c) Поскольку f′f ′ возрастает на интервале (a, b), (a, b), мы говорим, что ff вогнутая вверх над (a, b). (A, b). (b), (d) Поскольку f′f ′ убывает на интервале (a, b), (a, b), мы говорим, что ff вогнутая вниз на (a, b). (a, b). В общем, не имея графика функции f, f, как мы можем определить ее вогнутость? По определению функция ff вогнута вверх, если f′f ′ возрастает. Из следствия 3,3 мы знаем, что если f′f ′ — дифференцируемая функция, то f′f ′ возрастает, если ее производная f ″ (x)> 0.f ″ (x)> 0. Следовательно, дважды дифференцируемая функция ff будет вогнутой, когда f ″ (x)> 0. Теорема 4.10 Тест на вогнутостьПусть ff — функция, дважды дифференцируемая на интервале I.I.
Мы заключаем, что мы можем определить вогнутость функции ff, глядя на вторую производную f.f. Кроме того, мы видим, что функция ff может переключать вогнутость (рисунок 4.35). Однако непрерывная функция может переключать вогнутость только в точке xx, если f ″ (x) = 0f ″ (x) = 0 или f ″ (x) f ″ (x) не определено.Следовательно, чтобы определить интервалы, в которых функция ff вогнута вверх и вогнута вниз, мы ищем те значения xx, где f ″ (x) = 0f ″ (x) = 0 или f ″ (x) f ″ (x) равно неопределенный. Когда мы определили эти точки, мы разделим область определения ff на меньшие интервалы и определим знак f ″ f ″ для каждого из этих меньших интервалов. ОпределениеЕсли ff непрерывен в aa, а ff изменяет вогнутость в a, a, точка (a, f (a)) (a, f (a)) является точкой перегиба f.f. Рис. 4.35. Поскольку f ″ (x)> 0f ″ (x)> 0 для x a, x> a, функция ff вогнута вниз на интервале (a, ∞).(а, ∞). Точка (a, f (a)) (a, f (a)) является точкой перегиба f.f. Пример 4.19Испытания на вогнутость Для функции f (x) = x3−6×2 + 9x + 30, f (x) = x3−6×2 + 9x + 30, определите все интервалы, где ff вогнута вверх, и все интервалы, где ff вогнута вниз. Перечислите все точки перегиба для f. РешениеЧтобы определить вогнутость, нам нужно найти вторую производную f ″ (x) .f ″ (x). Первая производная равна f ′ (x) = 3×2−12x + 9, f ′ (x) = 3×2−12x + 9, поэтому вторая производная равна f ″ (x) = 6x − 12.f ″ (x) = 6x − 12. Если функция изменяет вогнутость, это происходит либо когда f ″ (x) = 0f ″ (x) = 0, либо f ″ (x) f ″ (x) не определено. Поскольку f ″ f ″ определено для всех действительных чисел x, x, нам нужно только найти, где f ″ (x) = 0. f ″ (x) = 0. Решая уравнение 6x − 12 = 0,6x − 12 = 0, мы видим, что x = 2x = 2 — единственное место, где ff может изменить вогнутость. Теперь мы проверяем точки на интервалах (−∞, 2) (- ∞, 2) и (2, ∞) (2, ∞), чтобы определить вогнутость f.f. Точки x = 0x = 0 и x = 3x = 3 являются контрольными точками для этих интервалов. Интервал | Контрольная точка | Знак f ″ (x) = 6x − 12f ″ (x) = 6x − 12 в контрольной точке | Заключение | | |||||||||||||||||||||||||||||||||||||||
| (−∞, 2) (- ∞, 2) | х = 0х = 0 | −− | ff вогнутая вниз | |||||||||||||||||||||||||||||||||||||||||
| (2, ∞) (2, ∞) | х = 3х = 3 | ++ | ff вогнутая вверх. |
Мы заключаем, что ff вогнута вниз на интервале (−∞, 2) (- ∞, 2) и вогнута вверх на интервале (2, ∞). (2, ∞). Поскольку ff изменяет вогнутость при x = 2, x = 2, точка (2, f (2)) = (2,32) (2, f (2)) = (2,32) является точкой перегиба. Рисунок 4.36 подтверждает аналитические результаты.
(2, ∞). Поскольку ff изменяет вогнутость при x = 2, x = 2, точка (2, f (2)) = (2,32) (2, f (2)) = (2,32) является точкой перегиба. Рисунок 4.36 подтверждает аналитические результаты.
Рисунок 4.36 Данная функция имеет точку перегиба в (2,32) (2,32), где график меняет вогнутость.
КПП 4.18
Для f (x) = — x3 + 32×2 + 18x, f (x) = — x3 + 32×2 + 18x, найти все интервалы, где ff вогнута вверх, и все интервалы, где ff вогнута вниз.
Теперь мы суммируем в таблице 4.1 информацию, которую первая и вторая производные функции ff предоставляют о графике f, f, и проиллюстрируем эту информацию на рисунке 4.37.
| Знак f′f ′ | Знак f ″ f ″ | Ff увеличивается или уменьшается? | Вогнутость |
|---|---|---|---|
| Положительный | Положительно | Увеличение | Вогнутый вверх |
| Положительно | отрицательный | Увеличение | Вогнутая вниз |
| Отрицательный | Положительно | Уменьшение | Вогнутый вверх |
| Отрицательный | отрицательный | Уменьшение | Вогнутая вниз |
Таблица 4.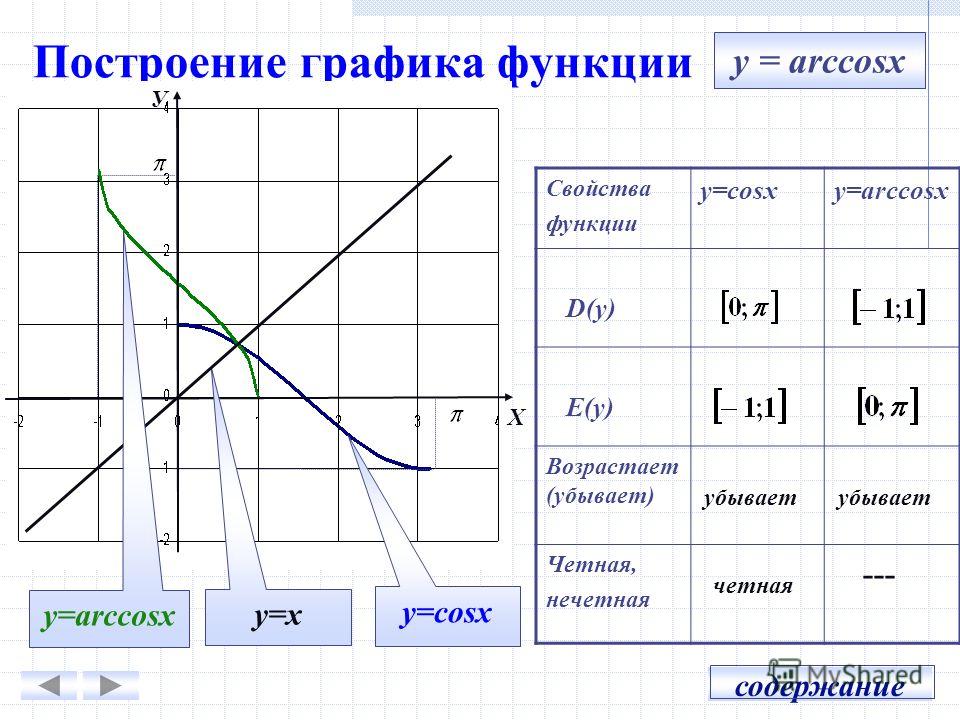 1 Что производные говорят нам о графиках
1 Что производные говорят нам о графиках
Рис. 4.37. Рассмотрим дважды дифференцируемую функцию ff на открытом интервале I.I. Если f ′ (x)> 0f ′ (x)> 0 для всех x∈I, x∈I, функция возрастает по I.I. Если f ′ (x) 0f ″ (x)> 0 для всех x∈I, x∈I, функция вогнута вверх. Если f ″ (x) Тест второй производной
Тест первой производной предоставляет аналитический инструмент для поиска локальных экстремумов, но вторая производная также может использоваться для определения экстремальных значений.Иногда использование второй производной может быть более простым методом, чем использование первой производной.
Мы знаем, что если у непрерывной функции есть локальные экстремумы, это должно происходить в критической точке. Однако функция не обязательно должна иметь локальные экстремумы в критической точке. Здесь мы исследуем, как можно использовать тест второй производной, чтобы определить, имеет ли функция локальный экстремум в критической точке. Пусть ff — дважды дифференцируемая функция такая, что f ′ (a) = 0f ′ (a) = 0 и f ″ f ″ непрерывна на открытом интервале II, содержащем a.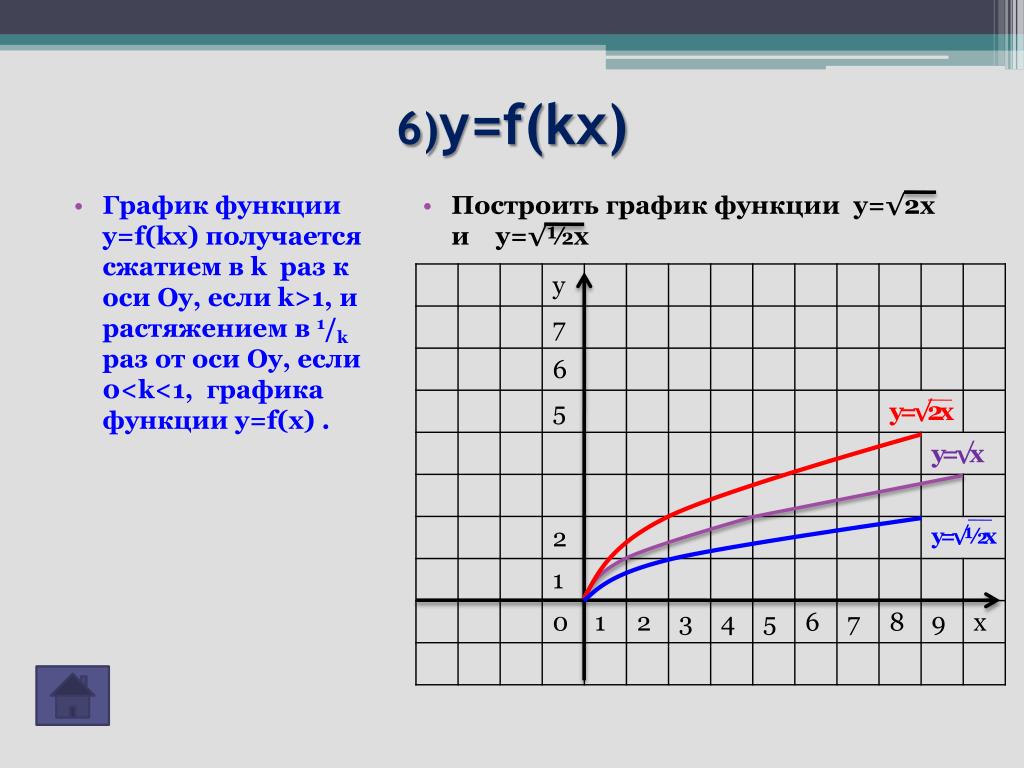 а. Предположим, что f ″ (a) 0x∈I, f ′ (x)> 0, если x ax> a. Следовательно, по тесту первой производной ff имеет локальный максимум при x = a.x = a. С другой стороны, предположим, что существует точка bb такая, что f ′ (b) = 0f ′ (b) = 0, но f ″ (b)> 0. f ″ (b)> 0. Поскольку f ″ f ″ непрерывна на открытом интервале II, содержащем b, b, то f ″ (x)> 0f ″ (x)> 0 для всех x∈Ix∈I (рисунок 4.38). Тогда по следствию 3 f′3, f ′ — возрастающая функция над I.I. Поскольку f ′ (b) = 0, f ′ (b) = 0, мы заключаем, что для всех x∈I, x∈I, f ′ (x) 0f ′ (x)> 0, если x> bx> b. Следовательно, по тесту первой производной ff имеет локальный минимум при x = b.x = b.
а. Предположим, что f ″ (a) 0x∈I, f ′ (x)> 0, если x ax> a. Следовательно, по тесту первой производной ff имеет локальный максимум при x = a.x = a. С другой стороны, предположим, что существует точка bb такая, что f ′ (b) = 0f ′ (b) = 0, но f ″ (b)> 0. f ″ (b)> 0. Поскольку f ″ f ″ непрерывна на открытом интервале II, содержащем b, b, то f ″ (x)> 0f ″ (x)> 0 для всех x∈Ix∈I (рисунок 4.38). Тогда по следствию 3 f′3, f ′ — возрастающая функция над I.I. Поскольку f ′ (b) = 0, f ′ (b) = 0, мы заключаем, что для всех x∈I, x∈I, f ′ (x) 0f ′ (x)> 0, если x> bx> b. Следовательно, по тесту первой производной ff имеет локальный минимум при x = b.x = b.
Рис. 4.38. Рассмотрим дважды дифференцируемую функцию ff такую, что f ″ f ″ непрерывна. Поскольку f ′ (a) = 0f ′ (a) = 0 и f ″ (a) a.х> а. В результате ff имеет локальный максимум при x = a.x = a. Поскольку f ′ (b) = 0f ′ (b) = 0 и f ″ (b)> 0, f ″ (b)> 0, существует интервал II, содержащий bb, такой, что для всех xx в I, I, ff равно уменьшается, если x bx> b.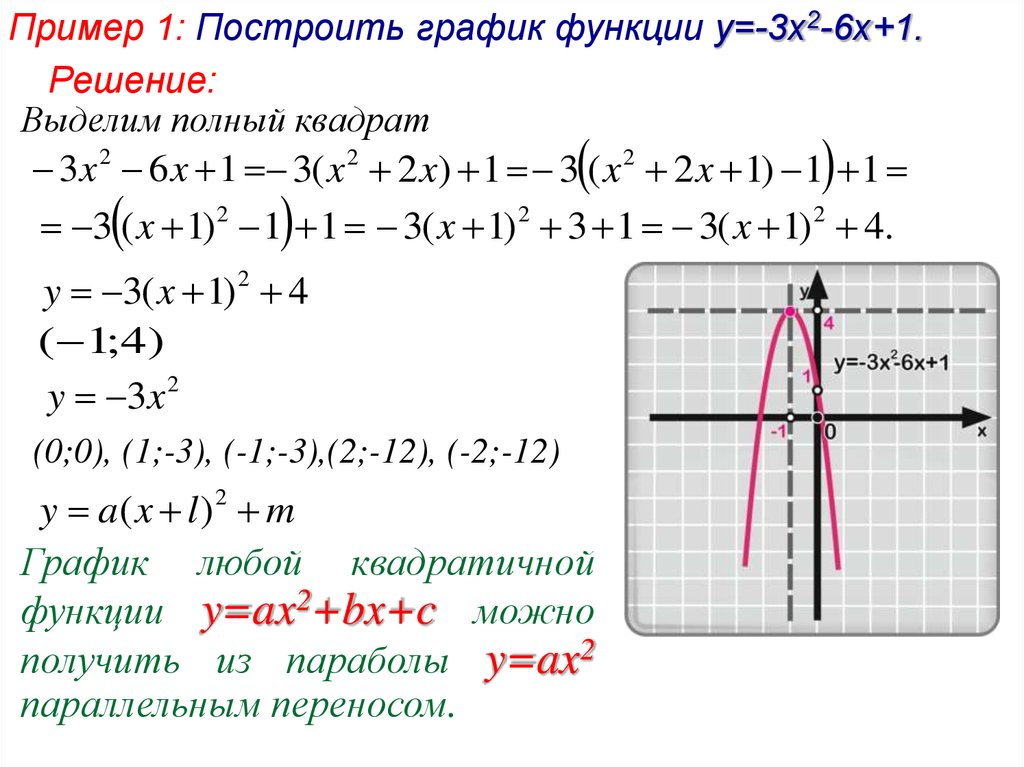 В результате ff имеет локальный минимум при x = b.x = b.
В результате ff имеет локальный минимум при x = b.x = b.
Теорема 4.11
Тест второй производной
Предположим, что f ′ (c) = 0, f ″ f ′ (c) = 0, f ″ непрерывно на интервале, содержащем c.c.
- Если f ″ (c)> 0, f ″ (c)> 0, то ff имеет локальный минимум в c.c.
- Если f ″ (c)
- Если f ″ (c) = 0, f ″ (c) = 0, то проверка не дает результатов.
Обратите внимание, что для случая iii. когда f ″ (c) = 0, f ″ (c) = 0, тогда ff может иметь локальный максимум, локальный минимум или ни одного в c.c. Например, функции f (x) = x3, f (x) = x3, f (x) = x4, f (x) = x4 и f (x) = — x4f (x) = — x4 все имеют критические указывает на x = 0.x = 0. В каждом случае вторая производная равна нулю при x = 0.x = 0. Однако функция f (x) = x4f (x) = x4 имеет локальный минимум при x = 0x = 0, тогда как функция f (x) = — x4f (x) = — x4 имеет локальный максимум при x, x, а функция f (x) = x3f (x) = x3 не имеет локального экстремума при x = 0.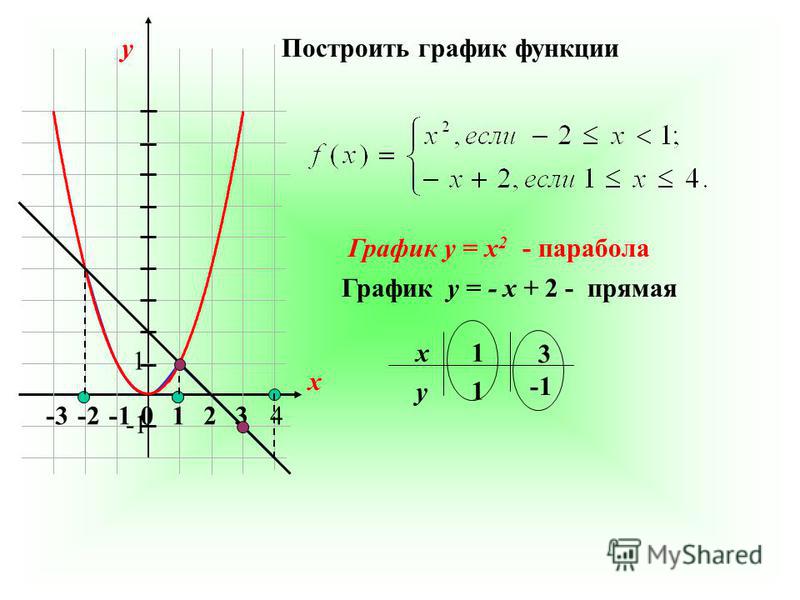 х = 0.
х = 0.
Давайте теперь посмотрим, как использовать тест второй производной, чтобы определить, имеет ли ff локальный максимум или локальный минимум в критической точке cc, где f ′ (c) = 0. f ′ (c) = 0.
Пример 4.20
Использование теста второй производной
Используйте вторую производную, чтобы найти расположение всех локальных экстремумов для f (x) = x5−5×3.f (x) = x5−5×3.
Решение
Чтобы применить тест второй производной, нам сначала нужно найти критические точки cc, где f ′ (c) = 0.f ′ (c) = 0. Производная равна f ′ (x) = 5×4−15×2.f ′ (x) = 5×4−15×2. Следовательно, f ′ (x) = 5×4−15×2 = 5×2 (x2−3) = 0f ′ (x) = 5×4−15×2 = 5×2 (x2−3) = 0, когда x = 0, ± 3.x = 0, ± 3.
Чтобы определить, есть ли у ff локальные экстремумы в любой из этих точек, нам нужно оценить знак f ″ f ″ в этих точках. Вторая производная —
f ″ (x) = 20×3−30x = 10x (2×2−3). f ″ (x) = 20×3−30x = 10x (2×2−3).
В следующей таблице мы оцениваем вторую производную в каждой из критических точек и используем тест второй производной, чтобы определить, имеет ли ff локальный максимум или локальный минимум в любой из этих точек.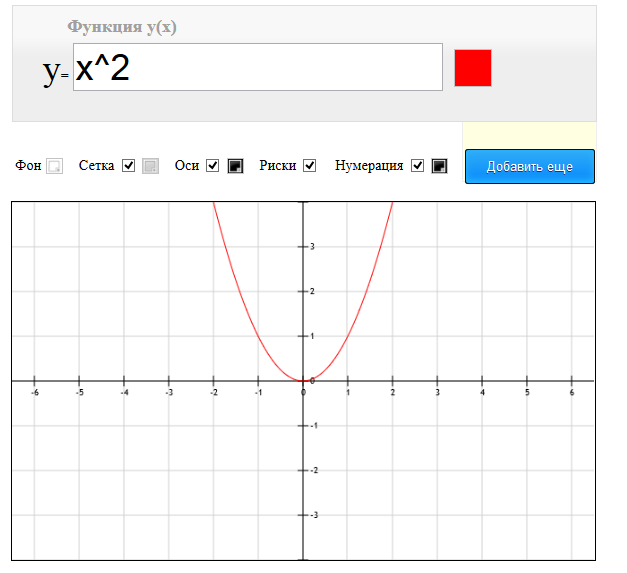
| хх | f ″ (x) f ″ (x) | Заключение |
|---|---|---|
| −3−3 | −303−303 | Местный максимум |
| 00 | 00 | Тест второй производной безрезультатно |
| 33 | 303303 | Местный минимум |
Используя проверку второй производной, мы заключаем, что ff имеет локальный максимум при x = −3x = −3, а ff имеет локальный минимум при x = 3. х = 3. Тест второй производной не дает результатов при x = 0.x = 0. Чтобы определить, есть ли у ff локальные экстремумы при x = 0, x = 0, мы применяем тест первой производной. Чтобы оценить знак f ′ (x) = 5×2 (x2−3) f ′ (x) = 5×2 (x2−3) для x∈ (−3,0) x∈ (−3,0) и x∈ ( 0,3), x∈ (0,3), пусть x = −1x = −1 и x = 1x = 1 — две контрольные точки. Поскольку f ′ (- 1)
х = 3. Тест второй производной не дает результатов при x = 0.x = 0. Чтобы определить, есть ли у ff локальные экстремумы при x = 0, x = 0, мы применяем тест первой производной. Чтобы оценить знак f ′ (x) = 5×2 (x2−3) f ′ (x) = 5×2 (x2−3) для x∈ (−3,0) x∈ (−3,0) и x∈ ( 0,3), x∈ (0,3), пусть x = −1x = −1 и x = 1x = 1 — две контрольные точки. Поскольку f ′ (- 1)
Рисунок 4.39 Функция ff имеет локальный максимум при x = −3x = −3 и локальный минимум при x = 3x = 3.
КПП 4.19
Рассмотрим функцию f (x) = x3− (32) x2−18x.f (x) = x3− (32) x2−18x. Точки c = 3, −2c = 3, −2 удовлетворяют условию f ′ (c) = 0. f ′ (c) = 0. Используйте тест второй производной, чтобы определить, имеет ли ff локальный максимум или локальный минимум в этих точках.
Теперь мы разработали инструменты, необходимые для определения того, где функция увеличивается и уменьшается, а также получили понимание основной формы графика.В следующем разделе мы обсудим, что происходит с функцией при x → ± ∞.x → ± ∞.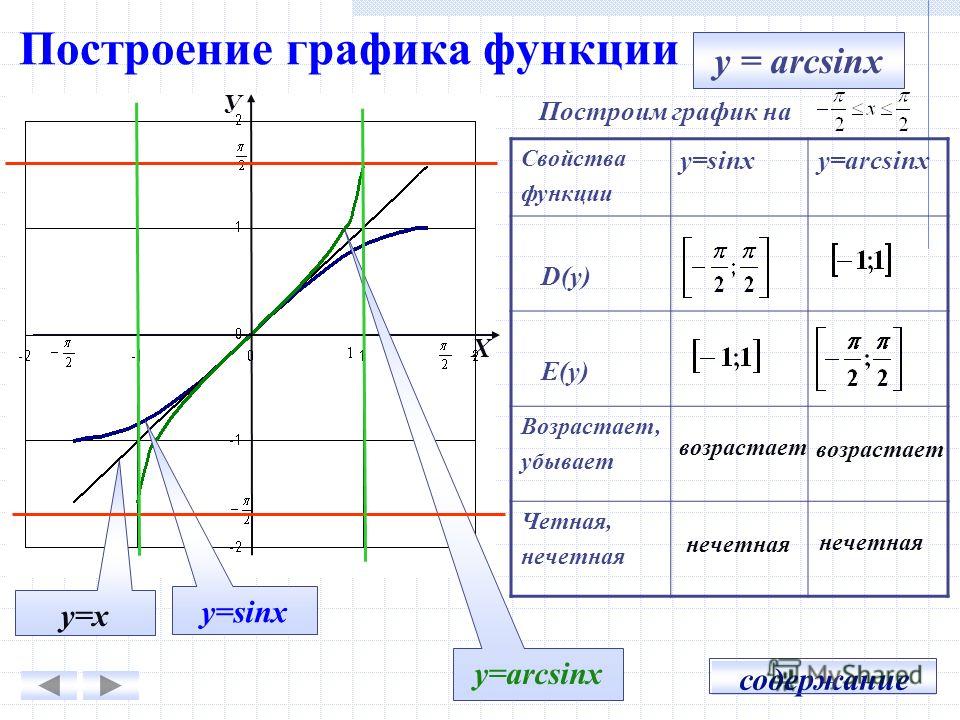 На данный момент у нас есть достаточно инструментов для создания точных графиков большого количества функций.
На данный момент у нас есть достаточно инструментов для создания точных графиков большого количества функций.
Раздел 4.5 Упражнения
194.
Если cc является критической точкой для f (x), f (x), когда нет локального максимума или минимума в c? C? Объяснять.
195.
Для функции y = x3, y = x3, является ли x = 0x = 0 точкой перегиба и локальным максимумом / минимумом?
196.
Для функции y = x3, y = x3, является ли x = 0x = 0 точкой перегиба?
197.
Может ли точка cc быть одновременно точкой перегиба и локальным экстремумом дважды дифференцируемой функции?
198.
Зачем нужна непрерывность для первого производного теста? Придумайте пример.
199.
Объясните, должна ли функция вогнутого вниз пересекать y = 0y = 0 для некоторого значения x.x.
200.
Объясните, может ли многочлен степени 22 иметь точку перегиба.
Для следующих упражнений проанализируйте графики f ‘, f’, затем перечислите все интервалы, в которых ff увеличивается или уменьшается.
202.
204.
Для следующих упражнений проанализируйте графики f ′, f ′, затем перечислите все интервалы, где
- ff увеличивается и уменьшается и
- расположены минимумы и максимумы.
206.
208.
210.
Для следующих упражнений проанализируйте графики f ‘, f’, затем перечислите все точки перегиба и интервалы ff, которые вогнуты вверх и вогнуты вниз.
212.
214.
Для следующих упражнений нарисуйте граф, который удовлетворяет заданным спецификациям для области x = [- 3,3].х = [- 3,3]. Функция не обязательно должна быть непрерывной или дифференцируемой.
216.
f (x)> 0, f ′ (x)> 0f (x)> 0, f ′ (x)> 0 над x> 1, −3 1, −3
217.
f ′ (x)> 0f ′ (x)> 0 над x> 2, −3 2, −3
218.
f ″ (x) 0, −3 0, −3
219.
Имеется локальный максимум при x = 2, x = 2, локальный минимум при x = 1, x = 1, и график не является ни вогнутым вверх, ни вогнутым вниз.
220.
Имеются локальные максимумы при x = ± 1, x = ± 1, функция вогнута вверх для всех x, x, и функция остается положительной для всех x.x.
Для следующих упражнений определите
- интервалов увеличения или уменьшения ff и
- локальных минимумов и максимумов f.f.
221.
f (x) = sinx + sin3xf (x) = sinx + sin3x над −π
Для следующих упражнений определите a.интервалы, где ff вогнута вверх или вогнута вниз, и b. точки перегиба ф.ф.
223.
f (x) = x3−4×2 + x + 2f (x) = x3−4×2 + x + 2
Для следующих упражнений определите
- интервалов увеличения или уменьшения ff,
- локальных минимумов и максимумов f, f,
- интервалов, где ff является вогнутым вверх и вогнутым вниз, и
- точки перегиба ф.ф.
225.
f (x) = x3−6x2f (x) = x3−6×2
226.
f (x) = x4−6x3f (x) = x4−6×3
227.
f (x) = x11−6x10f (x) = x11−6×10
228.
f (x) = x + x2 − x3f (x) = x + x2 − x3
Для следующих упражнений определите
- интервалов увеличения или уменьшения ff,
- локальных минимумов и максимумов f, f,
- интервалов, где ff является вогнутым вверх и вогнутым вниз, и
- точки перегиба ф.ф. Нарисуйте кривую, а затем с помощью калькулятора сравните свой ответ. Если вы не можете определить точный ответ аналитически, воспользуйтесь калькулятором.
231.
[T] f (x) = sin (πx) −cos (πx) f (x) = sin (πx) −cos (πx) над x = [- 1,1] x = [- 1,1 ]
232.
[T] f (x) = x + sin (2x) f (x) = x + sin (2x) над x = [- π2, π2] x = [- π2, π2]
233.
[T] f (x) = sinx + tanxf (x) = sinx + tanx над (−π2, π2) (- π2, π2)
234.
[T] f (x) = (x − 2) 2 (x − 4) 2f (x) = (x − 2) 2 (x − 4) 2
235.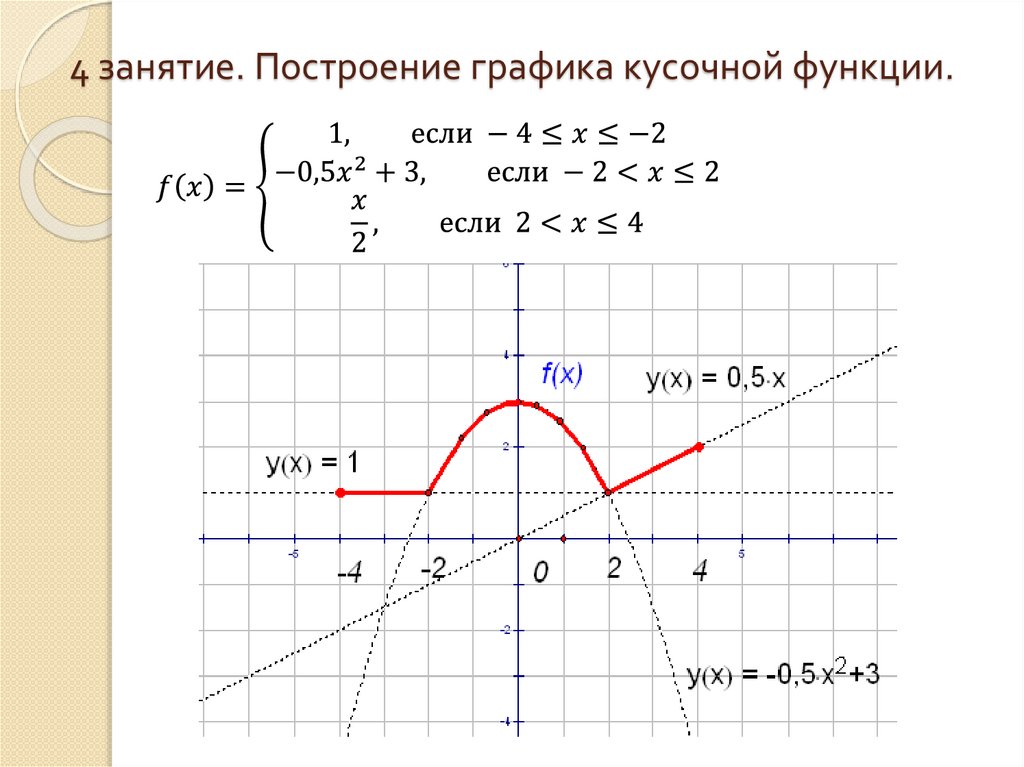
[T] f (x) = 11 − x, x ≠ 1f (x) = 11 − x, x ≠ 1
236.
[T] f (x) = sinxxf (x) = sinxx над x = x = [2π, 0) ∪ (0,2π] [2π, 0) ∪ (0,2π]
237.
f (x) = sin (x) exf (x) = sin (x) ex над x = [- π, π] x = [- π, π]
238.
f (x) = lnxx, x> 0 f (x) = lnxx, x> 0
239.
f (x) = 14x + 1x, x> 0f (x) = 14x + 1x, x> 0
240.
f (x) = exx, x ≠ 0f (x) = exx, x ≠ 0
Для следующих упражнений интерпретируйте предложения в терминах f, f ′ и f ″ .f, f ′ и f ″.
241.
Население растет медленнее. Здесь ff — население.
242.
Велосипед ускоряется быстрее, но машина едет быстрее. Здесь f = f = положение велосипеда минус положение автомобиля.
243.
Самолет плавно приземляется. Здесь ff — высота самолета.
244.
Цены на акции на пике. Здесь ff — цена акции.
245.
Экономика набирает обороты. Здесь ff — это показатель экономики, например ВВП.
Здесь ff — это показатель экономики, например ВВП.
Для следующих упражнений рассмотрим многочлен третьей степени f (x), f (x), который обладает свойствами f ′ (1) = 0, f ′ (3) = 0. f ′ (1) = 0, f ′ (3) = 0. Определите, являются ли следующие утверждения истинными или ложными . Обосновать ответ.
246.
f (x) = 0f (x) = 0 для некоторых 1≤x≤31≤x≤3
247.
f ″ (x) = 0f ″ (x) = 0 для некоторого 1≤x≤31≤x≤3
248.
Абсолютного максимума не существует при x = 3x = 3
249.
Если f (x) f (x) имеет три корня, то у нее 11 точек перегиба.
250.
Если f (x) f (x) имеет одну точку перегиба, то она имеет три действительных корня.
AC Производная функция
Подраздел 1.4.1. Как производная сама по себе является функцией
В вашей работе в предварительном задании 1.2 \ text {,} \) вы могли найти несколько шаблонов. Один из них исходит из наблюдения, что \ (f ‘(0) = 4 \ text {,} \) \ (f’ (1) = 2 \ text {,} \) \ (f ‘(2) = 0 \ text {, } \) и \ (f ‘(3) = -2 \ text {.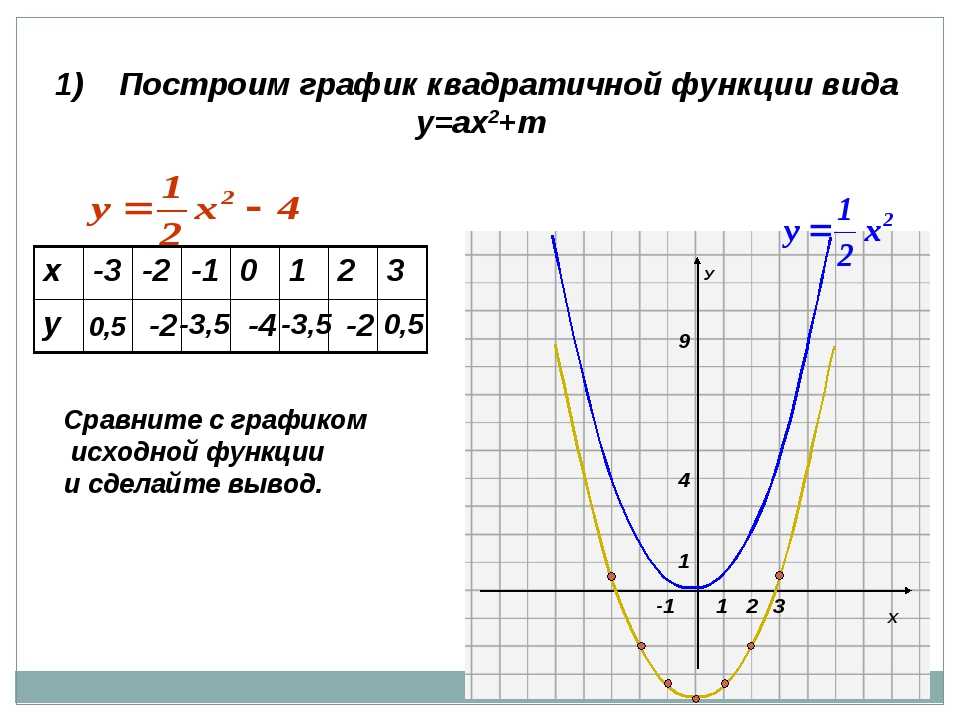 } \) Эта последовательность значений естественным образом приводит нас к предположению, что \ (f’ (4) = -4 \) и \ (f ‘(5 ) = -6 \ text {.} \) Мы также замечаем, что конкретное значение \ (a \) очень мало влияет на процесс вычисления значения производной через определение предела. Чтобы увидеть это более ясно, мы вычисляем \ (f ‘(a) \ text {,} \), где \ (a \) представляет собой число, которое будет названо позже.2} {h} \\
} \) Эта последовательность значений естественным образом приводит нас к предположению, что \ (f’ (4) = -4 \) и \ (f ‘(5 ) = -6 \ text {.} \) Мы также замечаем, что конкретное значение \ (a \) очень мало влияет на процесс вычисления значения производной через определение предела. Чтобы увидеть это более ясно, мы вычисляем \ (f ‘(a) \ text {,} \), где \ (a \) представляет собой число, которое будет названо позже.2} {h} \\
= \ mathstrut \ amp \ lim_ {h \ to 0} \ frac {h (4 — 2a — h)} {h} = \ lim_ {h \ to 0} (4 — 2a — h) \ text {.}
\ end {выровнять *}
Здесь мы видим, что ни \ (4 \), ни \ (2a \) не зависят от значения \ (h \ text {,} \), так как \ (h \ to 0 \ text {,} \) \ (( 4 — 2a — h) \ to (4 — 2a) \ text {.} \) Таким образом, \ (f ‘(a) = 4 — 2a \ text {.} \)
Этот результат согласуется с конкретными значениями, которые мы нашли выше: например, \ (f ‘(3) = 4 — 2 (3) = -2 \ text {.} \) И действительно, наша работа подтверждает, что значение \ (а \) почти не влияет на процесс вычисления производной. 2 \) вместе с набором касательных в рассмотренных выше точках. Справа мы показываем график \ (f ‘(x) = 4 — 2x \) с акцентом на высотах производного графика при том же выборе точек. Обратите внимание на связь между цветами на левом и правом графиках: зеленая касательная линия на исходном графике привязана к зеленой точке на правом графике следующим образом: наклон касательной линии в точке на левом графике совпадает с высотой в соответствующей точке на правом графике.То есть при каждом соответствующем значении \ (x \ text {,} \) наклон касательной к исходной функции такой же, как высота производной функции. Однако обратите внимание, что единицы измерения на вертикальных осях различаются: на левом графике вертикальные единицы — это просто единицы вывода \ (f \ text {.} \) На правом графике \ (y = f ‘ (x) \ text {,} \) единицы на вертикальной оси — это единицы \ (f \) на единицу \ (x \ text {.} \)
2 \) вместе с набором касательных в рассмотренных выше точках. Справа мы показываем график \ (f ‘(x) = 4 — 2x \) с акцентом на высотах производного графика при том же выборе точек. Обратите внимание на связь между цветами на левом и правом графиках: зеленая касательная линия на исходном графике привязана к зеленой точке на правом графике следующим образом: наклон касательной линии в точке на левом графике совпадает с высотой в соответствующей точке на правом графике.То есть при каждом соответствующем значении \ (x \ text {,} \) наклон касательной к исходной функции такой же, как высота производной функции. Однако обратите внимание, что единицы измерения на вертикальных осях различаются: на левом графике вертикальные единицы — это просто единицы вывода \ (f \ text {.} \) На правом графике \ (y = f ‘ (x) \ text {,} \) единицы на вертикальной оси — это единицы \ (f \) на единицу \ (x \ text {.} \)
Отличный способ изучить, как график \ (f (x) \) генерирует график \ (f ‘(x) \), — это использовать java-апплет.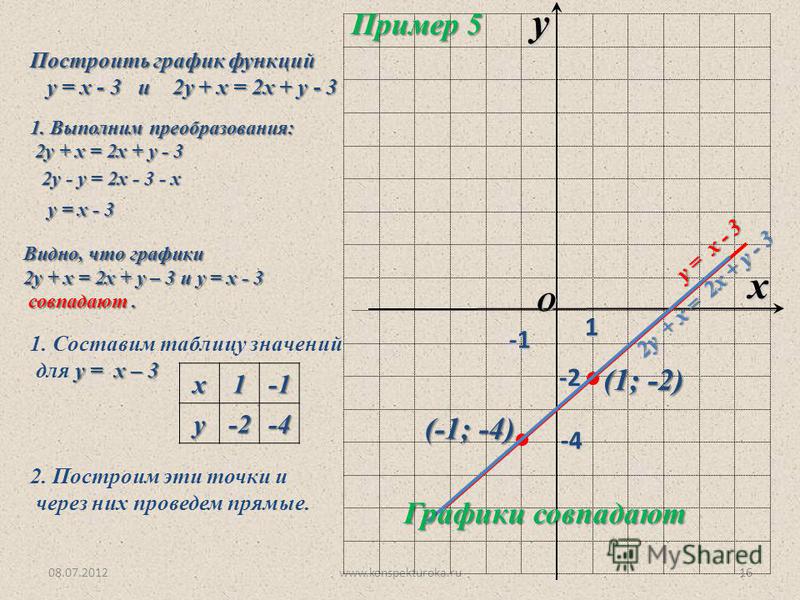 См., Например, апплеты на http://gvsu.edu/s/5C или http://gvsu.edu/s/5D на сайтах Austin и Renault 1 .
См., Например, апплеты на http://gvsu.edu/s/5C или http://gvsu.edu/s/5D на сайтах Austin и Renault 1 .
В разделе 1.3, когда мы впервые определили производную, мы написали определение в терминах значения \ (a \), чтобы найти \ (f ‘(a) \ text {.} \) Как мы видели выше, буква \ (a \) — это просто заполнитель, и часто имеет смысл использовать вместо него \ (x \). Для записи здесь мы повторяем определение производной.
Определение 1.4.2.
Пусть \ (f \) будет функцией, а \ (x \) значением в области определения функции.Мы определяем производную от \ (f \) , новой функции под названием \ (f ‘\ text {,} \) по формуле \ (f’ (x) = \ lim_ {h \ to 0} \ frac { f (x + h) -f (x)} {h} \ text {,} \) при условии, что этот предел существует.
Теперь у нас есть два разных способа думать о производной функции:
- с учетом графика \ (y = f (x) \ text {,} \), как этот график ведет к графику производной функции \ (y = f ‘(x) \ text {?} \) И
- с учетом формулы для \ (y = f (x) \ text {,} \), как определение предела производной генерирует формулу для \ (y = f ‘(x) \ text {?} \)
Обе эти проблемы исследуются в следующих мероприятиях.
Мероприятие 1.4.2.
Для каждого заданного графика \ (y = f (x) \ text {,} \) нарисуйте приблизительный график его производной функции \ (y = f ‘(x) \ text {,} \) сразу на осях ниже. Масштаб сетки для графика \ (f \) равен \ (1 \ times 1 \ text {;} \). Предположим, что горизонтальный масштаб сетки для графика \ (f ‘\) идентичен масштабу для \ (f \ text {.} \) При необходимости отрегулируйте и отметьте вертикальный масштаб по осям для \ (f ‘\ text {.} \)
Когда вы закончите со всеми 8 графиками, напишите несколько предложений, описывающих ваш общий процесс построения эскиза графика производной функции, учитывая, что график является исходной функцией.Какие значения производной функции вы склонны определять в первую очередь? Что ты делаешь после этого? Как ключевые характеристики графика производной функции иллюстрируют свойства графика исходной функции?
Для динамического исследования, которое позволяет вам экспериментировать с построением графика \ (f ‘\) при заданном графике \ (f \ text {,} \), см.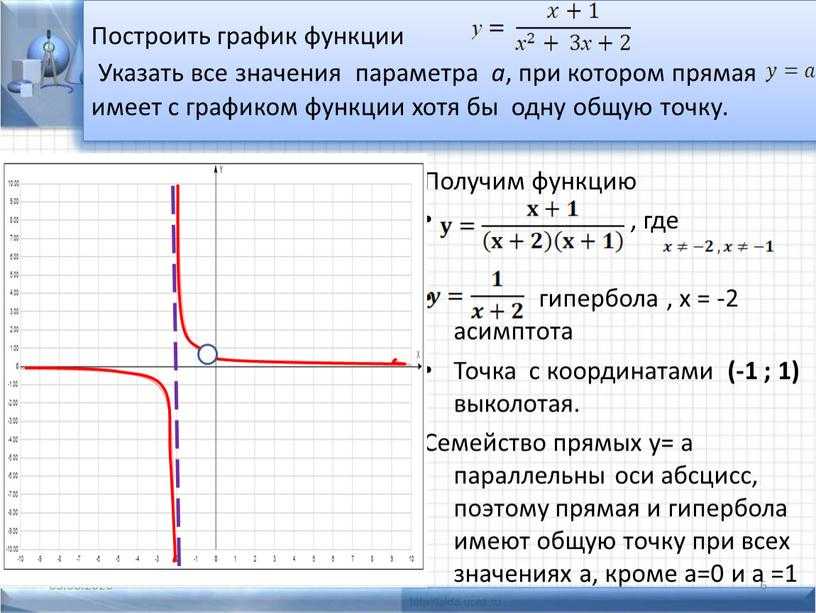 2 \) и использовали предельное определение производной, чтобы показать, что \ (f ‘(a) = 4 — 2a \ text {,} \) или, что то же самое, \ (f ‘(x) = 4 — 2x \ text {.} \) Затем мы построили графики функций \ (f \) и \ (f ‘\), как показано на рисунке 1.4.1. Следуя упражнению 1.4.2, мы теперь понимаем, что могли бы построить довольно точный график \ (f ‘(x) \) без , зная формулу для \ (f \) или \ (f’ \ text {. } \) В то же время полезно знать формулу для производной функции всякий раз, когда ее можно найти.
2 \) и использовали предельное определение производной, чтобы показать, что \ (f ‘(a) = 4 — 2a \ text {,} \) или, что то же самое, \ (f ‘(x) = 4 — 2x \ text {.} \) Затем мы построили графики функций \ (f \) и \ (f ‘\), как показано на рисунке 1.4.1. Следуя упражнению 1.4.2, мы теперь понимаем, что могли бы построить довольно точный график \ (f ‘(x) \) без , зная формулу для \ (f \) или \ (f’ \ text {. } \) В то же время полезно знать формулу для производной функции всякий раз, когда ее можно найти.
В следующем упражнении мы дополнительно исследуем более алгебраический подход к поиску \ (f ‘(x) \ text {:} \) по формуле для \ (y = f (x) \ text {,} \) предела определение производной будет использовано для разработки формулы для \ (f ‘(x) \ text {.} \)
Мероприятие 1.4.3.
Для каждой из перечисленных функций определите формулу производной функции. Для первых двух определите формулу для производной, подумав о природе данной функции и ее наклоне в различных точках; не используйте определение предела. Для последних четырех используйте определение предела. Обратите особое внимание на имена функций и независимые переменные. Важно научиться использовать буквы, отличные от \ (f \) и \ (x \ text {.3 \)
Для последних четырех используйте определение предела. Обратите особое внимание на имена функций и независимые переменные. Важно научиться использовать буквы, отличные от \ (f \) и \ (x \ text {.3 \)
\ (\ Displaystyle F (t) = \ frac {1} {t} \)
\ (\ Displaystyle G (y) = \ sqrt {y} \)
Заметки по исчислению I, раздел 2-10
Заметки по исчислению I, разделы 2-10
Заметки,
Урок 2.10
Что значит f ‘
Про f Сказать?
Первая производная
функции — это выражение, которое сообщает нам наклон касательной
линия к кривой в любой момент.Из-за этого определения первый
производная функции многое говорит нам о функции. Если положительный, то должен увеличиваться. Если отрицательный, то должен уменьшаться. Если равно нулю, то должно быть
при относительном максимуме или относительном минимуме. говорит нам похожие вещи о. также
дает нам ценную информацию о. В
в частности, он сообщает нам, когда функция вогнута вверх, вогнута вниз,
или есть точка перегиба. Такой же тип информации
Такой же тип информации
указал о
по и так далее.
| увеличение | + | ||
| уменьшение | — | ||
| относительный мин. или макс. | 0 | ||
| вогнуться | увеличение | + | |
| вогнуться | уменьшение | — | |
| точка перегиба | относительный мин. или макс. | 0 | |
| вогнуться | увеличение | + | |
| вогнуться | уменьшение | — | |
| точка перегиба | относительный мин.или макс. | 0 | |
| вогнуться | увеличение | ||
| вогнуться | уменьшение | ||
| точка перегиба | относительный мин.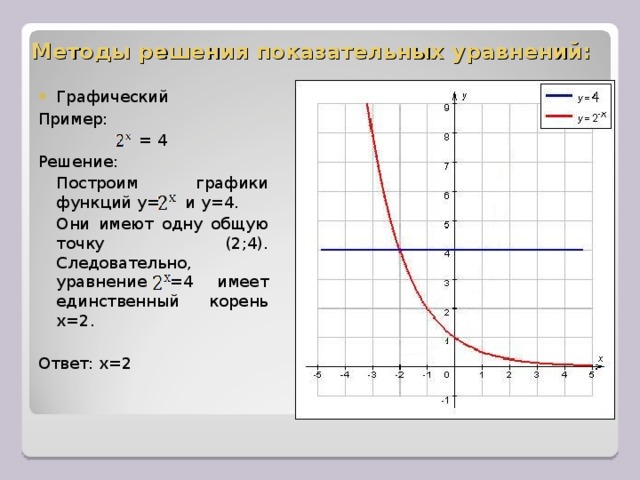 или макс. или макс. | ||
| вогнуться | |||
| вогнуться | |||
| точка перегиба |
| Использование инструментов для обогащения Calculus CD (пришедший вместе с книгой), загрузите и запустите модуль 2.10 . Этот модуль позволит вам попрактиковаться в использовании графической информации. о f ‘определить наклон графика f .. |
Определение:
| Первоначальное | Первоначальная производная f является функция F такая, что F ‘ = f . |
Здесь мы видим процесс, обратный тому, что мы
изучение.Мы начинаем с производной, и мы хотим найти функцию. Этот
Этот
тип
процесса открытия является общим для научных экспериментов и данных
встреча.
Во-первых, нам нужно знать, что разные функции могут
результат в
точно такая же производная. Посмотрите на пример ниже:
| Здесь мы видим семейство кривых, построенных с их общая производная. Семейство параболических функций:, где c принимает | |
| Прямая линия на графике выше. Это производная функция для всех шести параболических функций. | Поскольку дериватив — это прежде всего инструмент для определение формы функции положение графика не влияет на форму. Следовательно совпадающие кривые, которые ориентированы одинаково, но имеют разные должность имеют такую же производную. |
| Проверить концепции |
| # 1: положительная производная что насчет функции? | Выберите одну функцию |
| # 2: отрицательная секунда производная говорит, что насчет функция? | Выберите одну функцию |
# 3: Верно или неверно.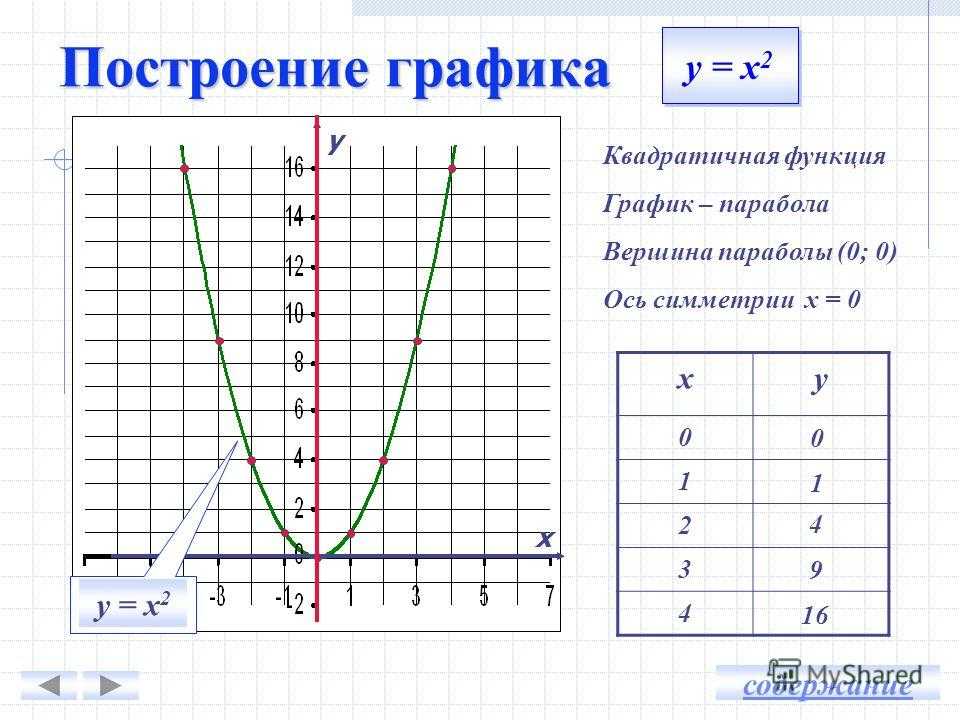 В Впроизводная функции также функция. | Выберите одну истину ложь |
| # 4: Вторая производная нуля говорит, что насчет оригинальная функция? | Выберите там |
| # 5: Верно или неверно.А вторая производная функции дает ценную информацию о функции. | Выберите одну истину ложь |
.
alexxlab
Эпюры онлайн — расчеты по сопромату
Срочная онлайн-помощь
Расчеты по сопромату с подробным ходом решения
Что может сайт — примеры
Примеры основных задач, решаемых сайтом
Обучающие онлайн-тесты
Тренажеры по сопромату — короткие задачи с поэтапным решением
Расчет балки (версия 2018 года)
определение реакций опор, уравнения поперечных сил Q и изгибающих моментов M, вычисление напряжений, подбор сечений, определение перемещений — углов поворота и прогибов
Расчет балки (старая версия)
Примеры расчета »Линии влияния в балке
построение линий влияния (для тех, кто изучает строймеханику). Строит линии влияния всех опорных реакций и моментов на опорах и в любых других указанных сечениях
Строит линии влияния всех опорных реакций и моментов на опорах и в любых других указанных сечениях
Расчет рам, ферм
расчеты статически неопределимых рам, ферм, построение эпюр N, Q, M, построение деформированной схемы, определение реакций опор и многое другое
Примеры расчета »
Центр тяжести и момент инерции
определение моментов инерции, положения центра тяжести, моментов сопротивления, положения главных осей любого сечения. Стандартные фигуры — прямоугольник, круг и профили из сортамента
Примеры расчета »
Расчет стержней
определение продольных сил с учетом собственного веса, вычисление напряжений, подбор сечения стержня построение эпюр продольных сил, напряжений и перемещений
Примеры расчета »
Кручение вала
Построение эпюр крутящих моментов.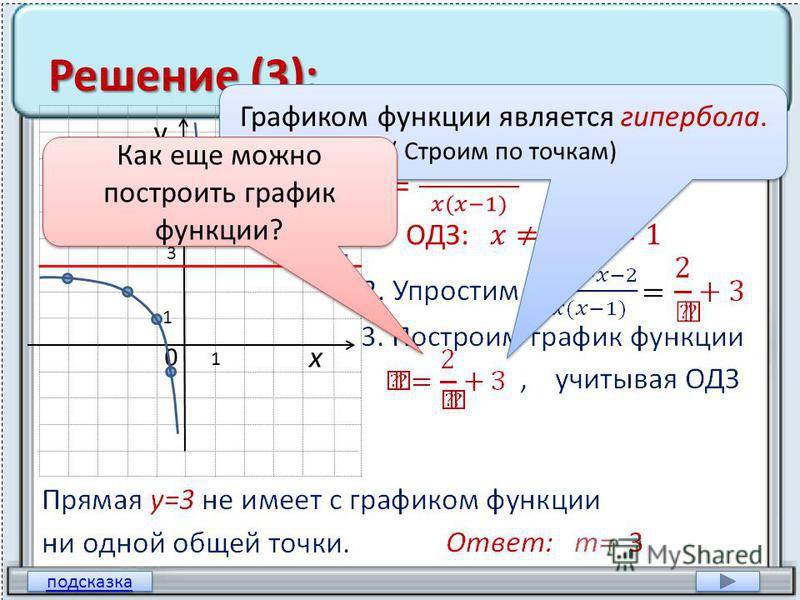 Раскрытие статической неопределимости при кручении, вычисление углов закручивания.
Раскрытие статической неопределимости при кручении, вычисление углов закручивания.
Примеры расчета »
Абсолютно жесткий брус
Статически неопределимая система при растяжении-сжатии. Определение грузоподъемности бруса, закрупленного с помощью двух стержней
Примеры расчета »
Помощь онлайн
Помощь онлайн — сопромат, термех, прикладная механика
Как связаться с нами:
TelegramWhatsAppInstagram
Все калькуляторы
Расчет односкатной фермы
Построение расчетной схемы односкатной фермы для дальнейшего использования в универсальном расчетчике рам/ферм.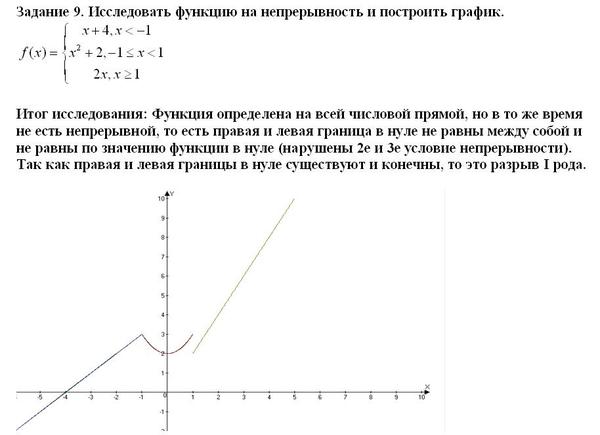
Типовые балки и эпюры
Расчет внутренних усилий для типовых расчетных схем балок, а также вычисление прогибов и углов поворота сечений
Расчет балки / подбор сечения
Подбор сечений балок по нормальным напряжениям — подбор двутавра, прямоугольника, круга и др.
Моменты инерции
Мгновенное вычисление площади, моментов инерции и моментов сопротивления круга, кольца, полукруга, треугольника, трапеции
Умножение эпюр
Умножение эпюр по правилу Симпсона и Верещагина, подробное объяснение расчетов
Интерполяция
Интерполяция часто используется при уточеннии справочных данных
Партнерская программа
Мы согласны отдать Вам 30% своего дохода за рекламу нашего сайта на Вашей площадке ПодробнееПомощь: сопромат, строймеханика, прикладная механика Telegram bluewhite22WhatsAppInstagram
ГДЗ по Алгебре 7 класс: Макарычев
Готовые домашние задания для 7 класса по алгебре Макарычева
Если в прошлом к решебникам относились скептически, то сегодня они стали важным дополнением учебного процесса.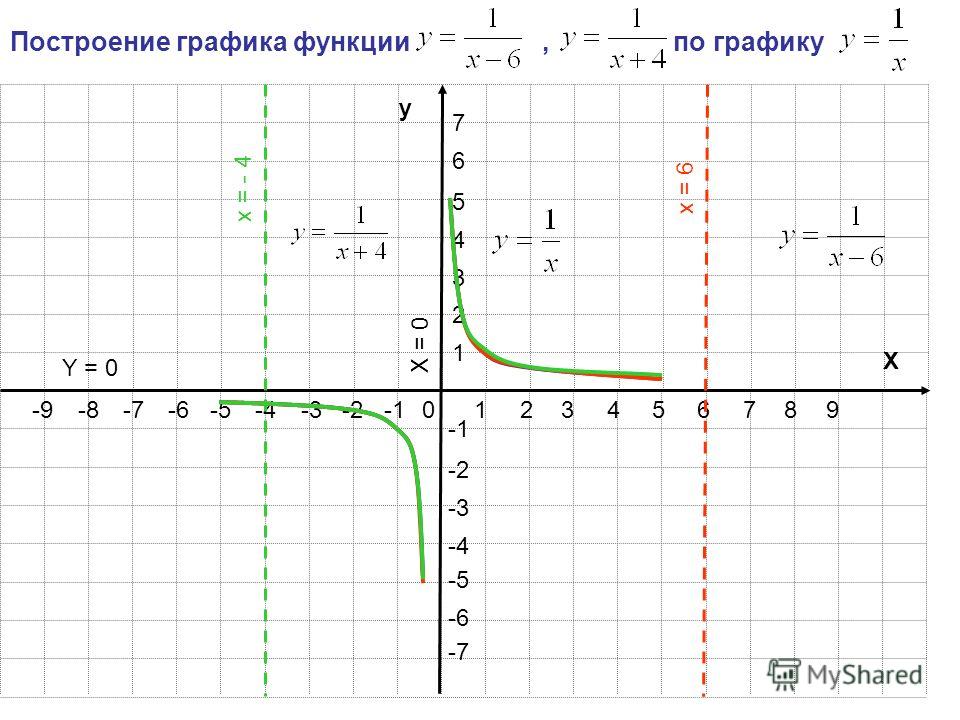 Пособиями с готовыми ответами активно пользуются не только ученики, но и их родители, которые хотят проконтролировать своих детей.
Пособиями с готовыми ответами активно пользуются не только ученики, но и их родители, которые хотят проконтролировать своих детей.
ГДЗ от Ответкина это не просто краткие материалы для списывания. Наш сайт не имеет аналогов, потому что здесь вы можете найти подробный алгоритм решения задач, несколько вариантов ответов, комментарии, благодаря которым можно понять трудную тему.
Что такое Ответкин?
- Это актуальная база данных. В других решебниках школьники вынуждены сверять номера, тратить дополнительное время на поиск нужного ответа. Но на нашем портале мы разместили только свежие ГДЗ к актуальным учебникам, по которым учатся в школах Российской Федерации.
- Подробные решения. Практически к каждому заданию на Ответкине есть короткий ответ и подробный, с алгоритмом выполнения примера, комментариями к нему. Когда нет времени и нужно быстро ответить на уроке, ученик может воспользоваться кратким решением, но если нужно разобраться с непонятной темой – помогут пояснения.

- Бесплатный помощник. Наш сайт бесплатно помогает учащимся и их родителям контролировать правильность выполнения домашней работы. Это позволяет сэкономить деньги на репетиторах.
- Несколько вариантов ответа. Видя альтернативные способы решения – школьник понимает механизм выполнения задачи, ему становятся понятны важные нюансы, которые он пропустил или не усвоил на уроке.
- Удобный поиск по сайту. Учебное пособие с пояснениями можно просматривать как с компьютера, так с мобильного телефона. Чтобы быстро найти определенный номер нужно лишь ввести его в строку поиска. Кроме того, в личном кабинете сохраняется история просмотров, с помощью которой удобно возвращаться к предыдущим заданиям.
ГДЗ от Ответкина становятся незаменимы в конце четверти или учебного года, когда нужно быстро повторить пройденный материал, подтянуть успеваемость.
Уникальные подробные решения с пояснениями Ответкина
С 7 класса школьники начинают изучать новый для них раздел математики – алгебру.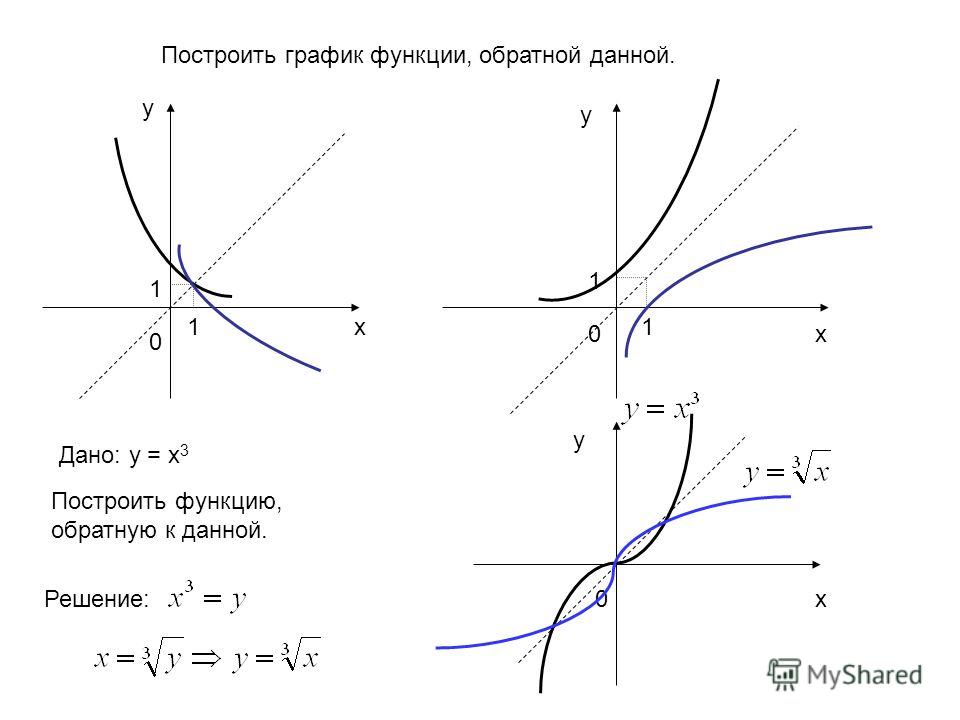 Это важный, но не простой предмет, который тесно связан с экономикой, информатикой, физикой и другими точными науками.
Это важный, но не простой предмет, который тесно связан с экономикой, информатикой, физикой и другими точными науками.
Нередко семиклассники теряются при выполнении разнообразных алгебраических задач. Теперь им нужно решать уравнения не только с одной, но и двумя переменными, строить графики функций, осуществлять разложение многочленов на множители. Далеко не каждый учитель может объяснить эти сложные темы простым и понятным для детей способом. Поэтому родители ломают голову, где бы найти хорошего репетитора, как проверить домашнее задание ребенку, когда сам уже забыл пройденную школьную программу.
С решением этих проблем помогает Ответкин. Он дает возможность узнать правильный ответ и его разные варианты, понять алгоритм выполнения примера.
Почему наш сайт достойная альтернатива занятиям с репетитором?
- Это быстро и бесплатно. Использование учебного пособия с пояснениями позволяет родителям сэкономить деньги. Ученикам не нужно тратить дополнительное время на дорогу к репетитору и обратно домой.
 В любой момент школьник может самостоятельно проверить себя, открыть подробные пояснения, чтобы разобраться в трудном материале. Теперь ему можно не переживать, если он пропустил занятия, был невнимательным на уроке при объяснении новой темы.
В любой момент школьник может самостоятельно проверить себя, открыть подробные пояснения, чтобы разобраться в трудном материале. Теперь ему можно не переживать, если он пропустил занятия, был невнимательным на уроке при объяснении новой темы. - Это удобно. Репетитор занимается с ребенком в назначенное время, поэтому все вопросы школьник вынужден откладывать до следующего дополнительного занятия. А решебником можно воспользоваться в любой момент, как находясь на уроке в школе, так и дома.
- Ответкин приучает к самостоятельности. Готовые домашние задания на нашем сайте — это не просто материалы для списывания, а подробное объяснение важных нюансов школьной программы. Практически каждый номер содержит не только несколько вариантов ответа, на и комментарии, с помощью которых можно восполнить пробелы в знаниях алгебры.
Если говорить о видеоуроках, то они не могут сравниться с нашим порталом по эффективности, удобству и актуальности данных.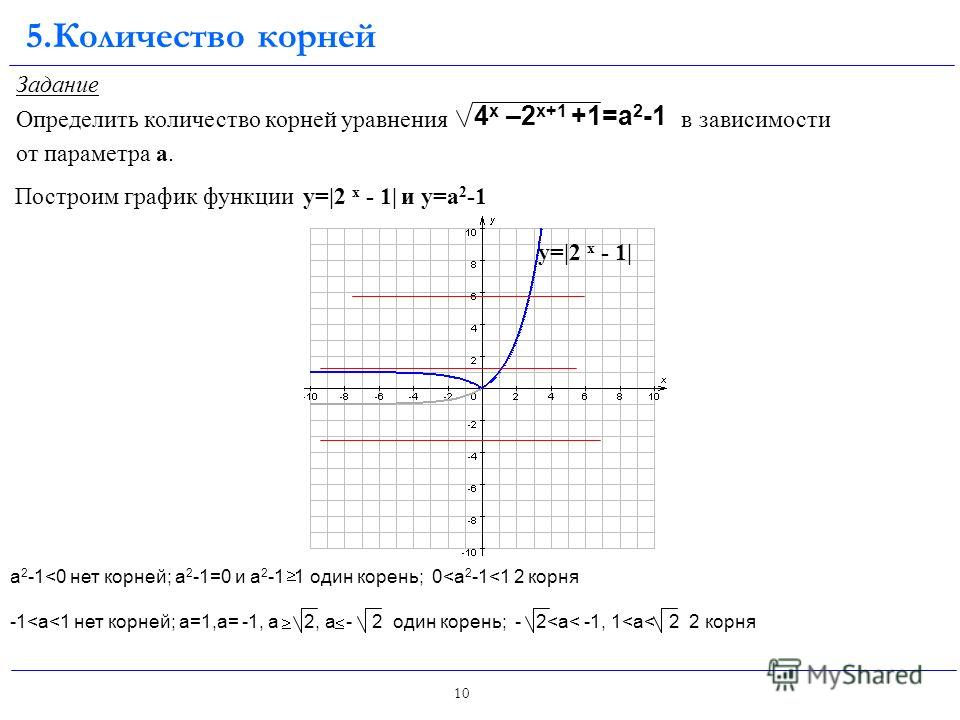 Нередко спикеры объясняют материал 7 класса, не имея опыта преподавания в школе. Они могут говорить много, но без конкретики, не дают подсказок к выполнению домашней работы. Видеоролики нужно проматывать несколько раз, тратить 30-40 минут на усвоение одной только темы. В то время как школьник, возможно, хочет уточнить несколько важных нюансов, а не прослушивать материал всего урока.
Нередко спикеры объясняют материал 7 класса, не имея опыта преподавания в школе. Они могут говорить много, но без конкретики, не дают подсказок к выполнению домашней работы. Видеоролики нужно проматывать несколько раз, тратить 30-40 минут на усвоение одной только темы. В то время как школьник, возможно, хочет уточнить несколько важных нюансов, а не прослушивать материал всего урока.
Как пользоваться сайтом и открывать нужную задачу с комментариями?
Наша команда сделала Ответкин максимально удобным для пользователей. Мы учли, что семиклассники часто просматривают готовые домашние задания в мобильном телефоне. В отличие от других сайтов у нас все материалы размещены на узком полотне, выполнены красивым понятным шрифтом, который комфортно читать со смартфона.
Подсказки как пользоваться сайтом:
- Чтобы найти нужное задание введите его в строку быстрого поиска. Ознакомьтесь с кратким вариантом ответа, который откроется на новой странице. Если вы хотите увидеть подробный алгоритм решения задачи с разными вариантами – зарегистрируйтесь на нашем сайте.

- Вы можете выбрать один из двух, наиболее удобный для вас вариант авторизации. Первый – через социальные сети. Рядом с кнопкой «Войти» нажмите на социальную сеть, например, гугл аккаунт. Подтвердите вход, дайте свое согласие, что ознакомлены с правилами пользования сайтом. Второй вариант – регистрация с нуля с использованием почтового ящика. Напишите адрес вашей почты и ждите письма со ссылкой для активизации аккаунта. Перейдите по ссылке и пользуйтесь сайтом.
- После авторизации вам откроется доступ в личный кабинет. По умолчанию вам будет предоставлена бесплатная подписка, где будет видно количество оставшихся ответов. Каждые сутки пользователь может открывать не более трех заданий. Открытые решения будут храниться в личном кабинете в течение 24 часов, которые можно просматривать неограниченное количество раз.
- Если пользователь желает получить большее число открываний в сутки – ему стоит приобрести подписку на платной основе сроком на месяц. В этом случае в личном кабинете исчезнет реклама.
 В профиле будет видно сколько дней еще действует платная подписка.
В профиле будет видно сколько дней еще действует платная подписка.
Для удобства, чтобы пользователь быстро сориентировался в задании – на белом фоне изображен краткий ответ для записи в тетрадь, на цветном фоне отображена теория и подробные пояснения к номеру. Но даже краткие решения на нашем сайте более подробные, чем в других ГДЗ.
Решебник алгебры седьмого класса к учебнику Ю.Н. Макарычева, Н.Г. Миндюка, К.И. Нешкова, С.Б. Суворова
Решения с пояснениями по алгебре за 7 класс составлены на основе учебника Макарычева 2013 года, который соответствует Федеральным государственным образовательным стандартам. Номера в пособии с готовыми домашними заданиями соответствуют нумерации учебника.
Алгебра седьмого класса содержит 5 глав, состоящих из 16 параграфов, которые в свою очередь в общей сложности разбиты на 46 подпунктов. К каждой теме помимо теории есть практические упражнения. Для коллективного решения предусмотрены «задачи-исследования» и задания для работы в парах. В конце каждого параграфа, для закрепления изученного материала размещены контрольные вопросы. По уровню подготовки среди упражнений есть обязательные, а также повышенной сложности, которые выполняют на добровольной основе.
В конце каждого параграфа, для закрепления изученного материала размещены контрольные вопросы. По уровню подготовки среди упражнений есть обязательные, а также повышенной сложности, которые выполняют на добровольной основе.
Готовые домашние задания по алгебре от Ответкина направлены на усвоение следующих тем и понятий:
- Числовые выражения, сравнение их значений и преобразование.
- Уравнение, решение задач с его помощью, линейные уравнения с одной и двумя переменными, графики и системы линейных уравнений. Линейные неравенства с двумя переменными. Способ подстановки и способ сложения.
- Функция, линейная функция и ее график, вычисление функции по формуле.
- Статистические характеристики: медиана, среднее арифметическое, мода, размах.
- Степень, умножение и деление степеней.
- Стандартный вид одночлена и многочлена. Умножение одночленов, одночлена на многочлен, многочлена на многочлен. Возведение одночлена в степень. Сложение и вычитание многочленов.
 Преобразование целого выражения в многочлен. Разложение многочлена на множители.
Преобразование целого выражения в многочлен. Разложение многочлена на множители. - Квадрат суммы и квадрат разности. Возведение в квадрат разности и суммы двух выражений. Разложение на множители разности квадратов, суммы и разности кубов.
Подробные ответы с комментариями по алгебре за 7 класс помогут школьникам вспомнить пройденный материал: различные действия с дробями и целыми числами, решение текстовых задач, поиск корня уравнения. Но главное, решебник станет надежным советчиком в изучении новых тем, которые впервые вводятся с 7 класса. Это операции с многочленами, решение системных уравнений с двумя переменными, построение графиков функций.
Мы уверены, что учебное пособие от Ответкина поможет полюбить новый предмет – алгебру. С его помощью школьники разберутся в пропущенных темах, подтянут успеваемость, будут уверены в правильности выполнения упражнений.
Популярные решебники
ГДЗ по Алгебре 7 класс: Макарычев Ю.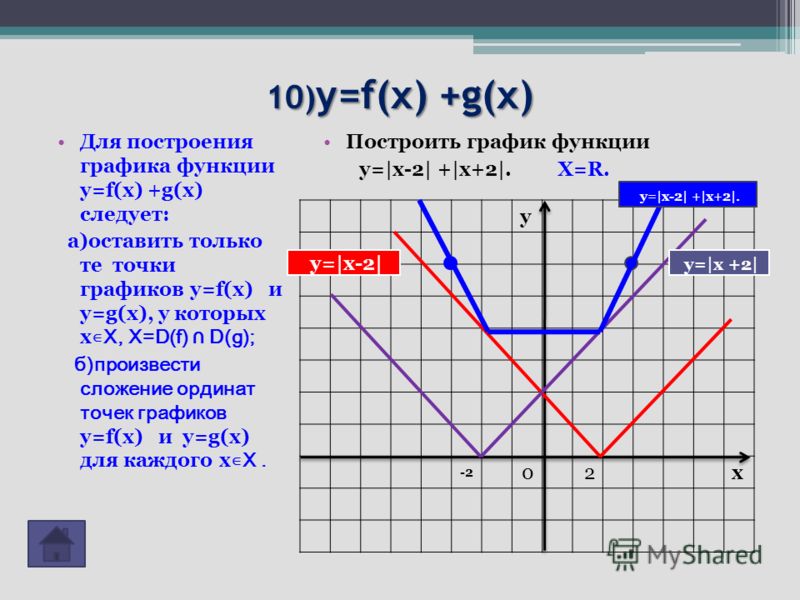 Н.
Н.
Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2013-2022г.
ГДЗ по Алгебре 7 класс: Мордкович А.Г.
Издатель: А.Г. Мордкович и др., 2013-2019г.
ГДЗ по Алгебре 7 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2015-2022г.
15 приложений по физике, математике и информатике, которые позволят забыть про учебники
Искать формулы или рисовать прямой угол куда проще в телефоне, чем в бесконечных конспектах и учебниках. Накануне всероссийской контрольной «Выходи решать!» мы собрали самые удачные приложения по математике, физике и информатике, которые не только помогут подготовиться к тестам и ЕГЭ, но и выучить язык программирования или понять, как работает теория относительности.
Математика
1. «Алгебра»
Справочное приложение, в котором можно быстро найти все необходимые для школьной математики формулы с краткими пояснениями. Искать, конечно, удобнее, чем в тетради. Можно использовать как шпаргалку, но не рекомендуем. Если подглядывать в приложение во время домашнего задания, получается эффективнее.
Можно использовать как шпаргалку, но не рекомендуем. Если подглядывать в приложение во время домашнего задания, получается эффективнее.
Скачать приложение
2. «Пифагория»
Самые увлекательные и наглядные игры, основанные на математических законах, получаются, конечно, из геометрических задач. В приложении «Пифагория» нужно строить фигуры и находить расстояния на координатной сетке. Сначала кажется, что это очень просто, но затем в ход идут довольно непростые построения, а расстояния и углы приходится вычислять на бумажке. Игра поможет по-другому взглянуть на обычный тетрадный листок в клеточку и увидеть новые фигуры и закономерности в сочетании точек.
Скачать приложение
3. Euclidea
Ещё одна игра про геометрические построения, но теперь уже на белом листе, с помощью циркуля и линейки. Решая задачки, чувствуешь себя древним греком и пытаешься додуматься, как построить серединный перпендикуляр, вписать окружность в треугольник или квадрат в окружность. Дополнительная сложность в том, что это нужно сделать за минимальное число элементарных построений. Игра быстро становится сложной, но зато в ней есть подсказки, которые могут сообщить последовательность ходов или полезный для решения факт из геометрии.
Дополнительная сложность в том, что это нужно сделать за минимальное число элементарных построений. Игра быстро становится сложной, но зато в ней есть подсказки, которые могут сообщить последовательность ходов или полезный для решения факт из геометрии.
Скачать приложение
4. Geogebra Classic
Приложение для построений. Если нужно нарисовать картинку к геометрической задаче, то можно сделать это на телефоне. К тому же в приложении проще нарисовать ровный прямой угол и заметить все равные углы и стороны, чем на чертеже от руки в тетради. Отличное приложение в помощь к школьным и более сложным задачам.
Скачать приложение
Приложения, которые решают задачи
Среди приложений по математике помимо обучающих программ много таких, которые помогают решить задачи. При этом многие из них очень полезные, интересные и помогают посмотреть на задачи под новым углом, так что молчать о них не хочется. Итак, приложения для тех, кто привык выводить решение из ответа.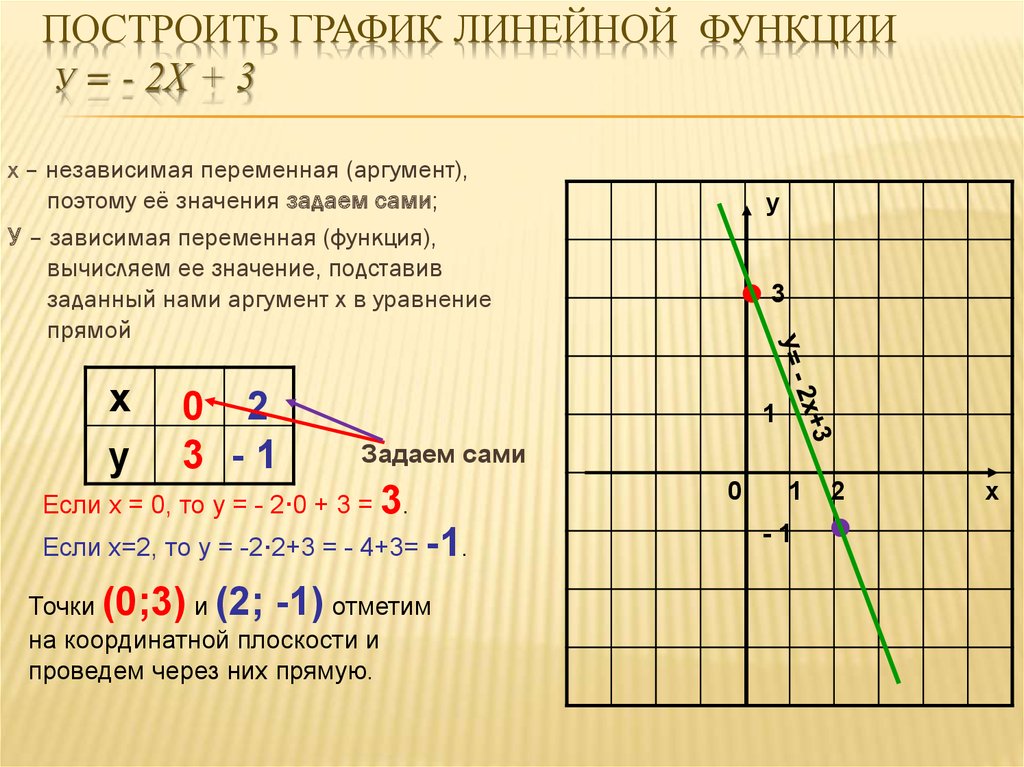
5. Geogebra Graphing Calculator
Строит графики функций, умеет определять нули функций (то есть корни уравнений, умеет находить точки пересечения графиков (то есть решения систем уравнений), умеет находить максимумы и минимумы функций. В целом это просто полезное приложение для построения графиков с большим набором инструментов и простым интерфейсом, но из-за большого «читерского» потенциала в основной список приложений по математике его ставить не хочется.
Скачать приложение
6. Photomath
Приложение, которое по фотографии умеет решать уравнения, сокращать выражения, находить область определения, строить график функции и многое другое. В общем, это калькулятор, в который не нужно напряжённо и скрупулёзно вписывать выражения. Для тех, кто действительно хочет чему-нибудь научиться, есть пошаговый разбор решения задачи и дополнительные факты. Лучше сканировать задачи прямо из учебника — написанное от руки программа воспринимает не всегда хорошо.
Скачать приложение
7.
 Geometryx
GeometryxУмеет определять параметры геометрических фигур. Достаточно вписать всю известную информацию, и если её хватит, приложение выдаст длины всех высот и диагоналей, углы и другие полезные факты о вашей фигуре. Здесь тоже есть полезный раздел со всеми использованными формулами, в который можно заглянуть, чтобы всё-таки разобраться и в следующий раз решить задачу самостоятельно.
Скачать приложение
Физика
8. Snapshots of the universe
Приложений по физике в магазинах Apple и Android очень мало, но тем не менее одна занимательная вещь всё же нашлась. Snapshots of the universe в виде интерактивных экспериментов поясняет работу законов, применяемых в астрофизике. Например, законы Кеплера, по которым вращаются планеты вокруг Солнца, теорию относительности и многое другое. Отлично подходит для того, чтобы проиллюстрировать формулы из учебников. Приложение на английском языке и платное, но стоит недорого. Если вас это не пугает, рекомендуем ознакомиться.
Скачать приложение
9. «Бетафизикс»
«Читерское» приложение есть и по физике. По фотографии задачи оно даёт её решение или по ключевым словам находит основные формулы по теме и табличные значения справочных величин. Идеально, когда не хочется копаться в конспекте, чтобы вспомнить одну маленькую формулу. Пока есть не все темы задач из курса, но основные направления охвачены, а новые задачи должны появиться в следующих обновлениях.
Скачать приложение
10. Slower Light (бонус)
Игра для персональных компьютеров, которая поясняет, как выглядит мир, если двигаться со скоростью, близкой к скорости света. Её разработали учёные из Массачусетского технологического института, так что с научной точки зрения она сделана точно. После прохождения игры все эффекты, которые вы увидите, объяснят доступным языком. Она помогает уложить в голове непонятные концепции теории относительности, такие как замедление времени и сокращение длины. Только на английском языке.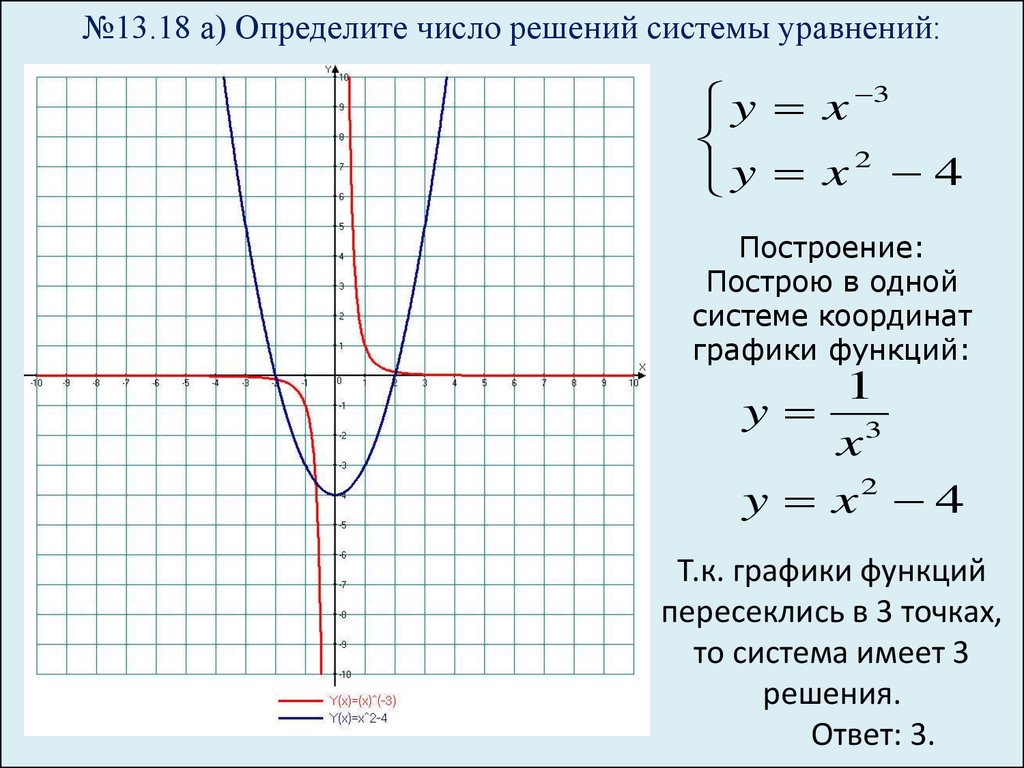
Скачать приложение
Уже в эту субботу, 17 ноября, состоится всероссийская физико-техническая контрольная «Выходи решать!». Чтобы проверить свои знания по физике, математике и информатике за 8 класс вместе с другими участниками, нужно только зарегистрироваться на сайте. Писать контрольную можно как онлайн, так и на одной из очных площадок.
Информатика
11. Sololearn
Очень крутое приложение для обучения программированию. Можно выбрать язык и пройти по нему вводный курс с решением задач и теорией. Кроме того, можно писать тесты по терминологии и командам для лучшего запоминания и соревноваться с другими пользователями. Для начального уровня очень удобно и полезно.
Скачать приложение
12. Learn programming
Хороший текстовый учебник по программированию. К сожалению, только по нему программирование не выучишь, но в дополнение к задачам из других источников он работает как отличный справочный материал. Содержит примеры кода и поддерживает огромное количество языков программирования.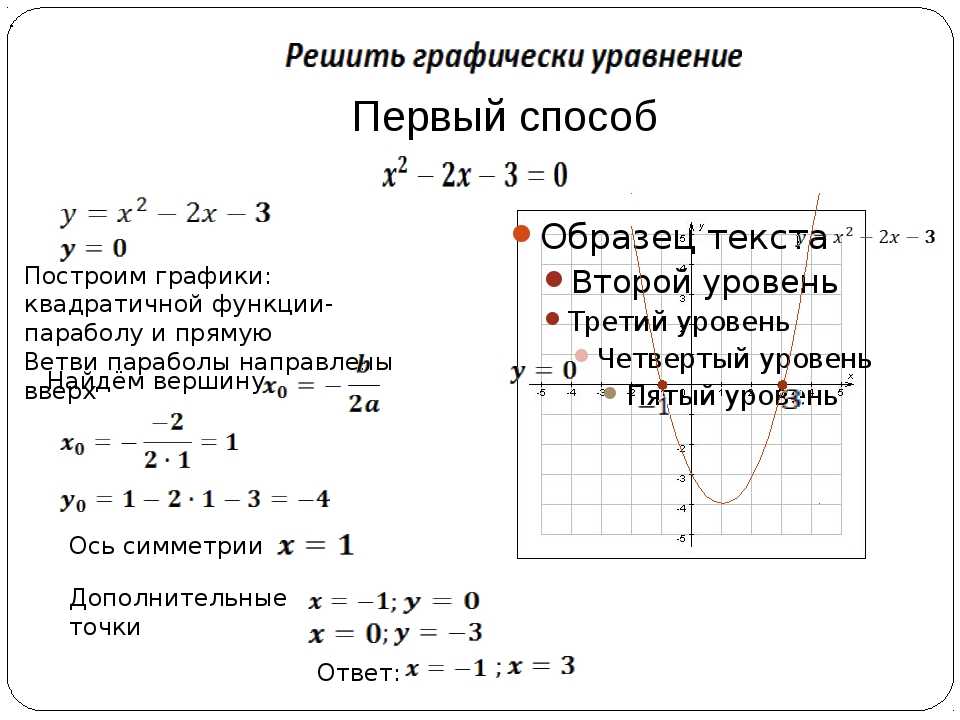 Приложение доступно только на английском.
Приложение доступно только на английском.
Скачать приложение
13. Tynker
Целое семейство игровых приложений для IOS. Цель игры заключается в том, чтобы с помощью кода персонаж на экране выполнил определённую задачу. Такая механика позволяет наглядно и просто объяснить, как работает программирование и строятся алгоритмы. Визуально игра яркая и красочная, поэтому отлично подходит для детей. Она есть только на английском, но текста немного и большинство слов интуитивно понятны при прохождении.
Скачать приложение
Для всех предметов
14. «Супершкольник»
Приложение для подготовки к тестовой части ЕГЭ по математике, физике, химии, биологии, русскому и английскому языкам, истории, обществознанию и литературе. Для теста по каждой теме есть теоретический раздел, где можно повторить основные правила и законы. Кроме того, в приложении есть поисковик по названию формул для математики и физики, что может быть полезно при решении задач.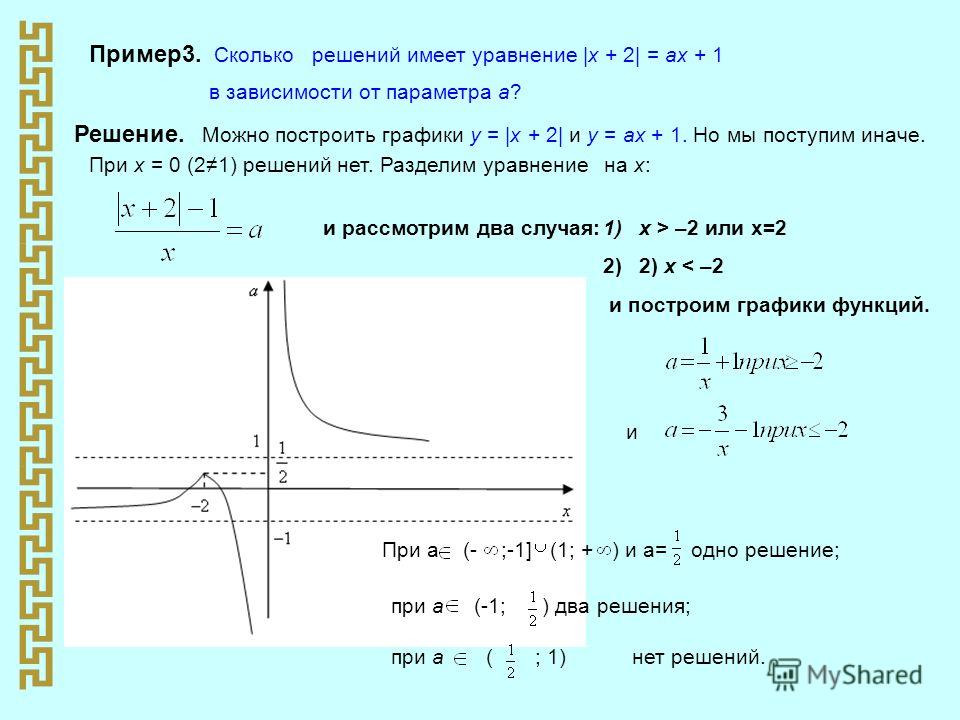 Отличная функция — режим репетитора, который при каждой разблокировке телефона предлагает ответить на вопрос из теста.
Отличная функция — режим репетитора, который при каждой разблокировке телефона предлагает ответить на вопрос из теста.
Скачать приложение
15. «Фоксфорд.Учебник»
Приложение-учебник по математике, физике, информатике, химии, биологии, русскому языку, истории и обществознанию. Всё разбито по темам и разобрано подробно, с примерами и картинками. Отлично работает для повторения теории перед решением задач и для того, чтобы быстро разобраться в неизвестной теме.
Скачать приложение
лучших бесплатных графических программ: для скачивания и онлайн гистограмма и круговая диаграмма, гистограмма, точечная диаграмма, прямоугольная диаграмма и диаграмма с усами) бесплатно.
Бесплатное программное обеспечение для построения графиков и построения графиков представлено в 3 типах:
- локальные программы для создания диаграмм для бесплатной загрузки (для Mac, Windows и Linux)
- онлайн-создатели диаграмм и диаграмм
- программы с открытым исходным кодом.

Кроме того, вы можете найти бесплатное и простое программное обеспечение для создания 3D-графиков, которое позволяет создавать профессиональные диаграммы для различных целей в статистике, математике, науке о данных, маркетинге и т. д.
Вот список лучших бесплатных программ для построения графиков в простой и профессиональный способ.
1. Meta-chart.com
Если вы ищете простой и абсолютно удобный онлайн бесплатное графическое программное обеспечение , Meta-chart.com может быть вашим ответом. Все, что вам нужно, это данные, и вы можете начать строить диаграммы и графики с нуля.
Самое приятное то, что вы можете бесплатно создавать и публиковать свои диаграммы в Интернете. Диаграммы и графики создаются за считанные минуты. Для использования программы не нужно регистрироваться. Однако, если вы решите зарегистрироваться, вы сможете сохранить свои графики и поделиться ими со всем миром.
Основные преимущества и особенности:
- Большое количество возможных типов графиков и диаграмм — вы можете создавать линейные графики, простые и составные гистограммы, круговые диаграммы, гистограммы, точечные диаграммы, прямоугольные диаграммы и диаграммы с усами, диаграммы с областями, сплайны.
 графики, диаграмма «прямоугольник и ус», счетная диаграмма и т. д.
графики, диаграмма «прямоугольник и ус», счетная диаграмма и т. д. - Вы можете вводить данные вручную или импортировать файлы электронных таблиц (CSV) .
- Очень красивый и визуально привлекательный дизайн и графики.
- Абсолютно простое использование онлайн-программы для построения графиков.
- Делитесь бесплатно своими графиками и диаграммами.
- Можно использовать обычную или трехмерную диаграмму .
Веб-сайт: www.meta-chart.com
2. График
График для тех, кому нужна с открытым исходным кодом и бесплатно скачать графическое программное обеспечение для Windows или Mac. Это одна из самых популярных бесплатных программ для построения математических и статистических графиков.
Вы можете рисовать графики функций и выполнять некоторые математические вычисления функций. Система имеет множество встроенных функций, например. sin, cos, log и т. д. Вы можете выбрать цвет, толщину и стиль линий графиков.
sin, cos, log и т. д. Вы можете выбрать цвет, толщину и стиль линий графиков.
Graph — это приложение для Windows, но его также можно запустить на Mac через Wine.
Основные преимущества и особенности:
- Функции рисования — вы можете отображать стандартные функции, параметрические и полярные функции.
- Нарисовать соотношение – программа может показать любое уравнение и неравенство.
- Оттенки , которые можно создавать в различных стилях и цветах.
- Серии точек и линии тренда.
- Взаимодействие с другими программами, такими как Windows Bitmap, Portable Network Graphics, JPEG, Windows Enhanced Metafile, Portable Document Format (PDF) и другими.
- Вы можете создавать свои собственные пользовательские функции.
- Анимации, показывающие, что происходит с функцией.
Веб-сайт: http://www.padowan.dk/
3. Infogr.am
Infogr.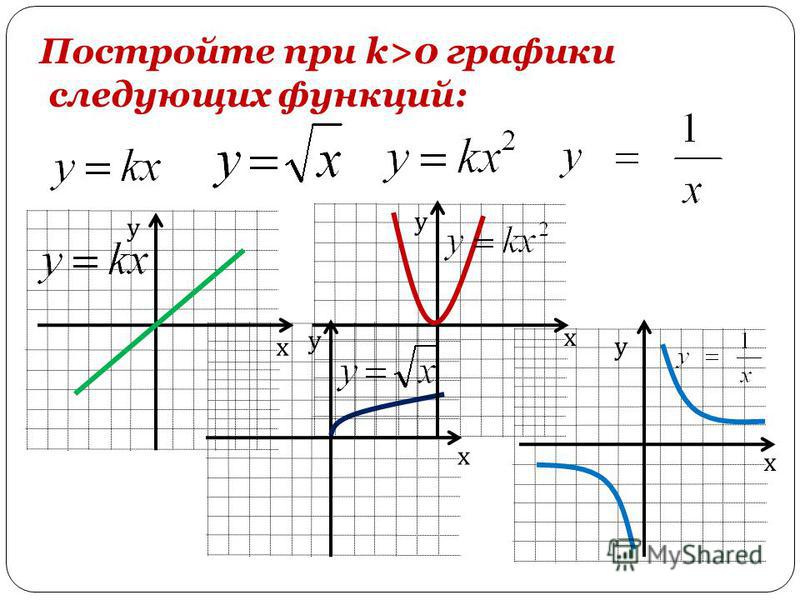 am — это впечатляющая бесплатная программа для построения графиков, доступная онлайн . На самом деле, это платное онлайн-программное обеспечение с бесплатной версией. Они могут предложить вам простоту использования и очень креативные шаблоны графиков.
am — это впечатляющая бесплатная программа для построения графиков, доступная онлайн . На самом деле, это платное онлайн-программное обеспечение с бесплатной версией. Они могут предложить вам простоту использования и очень креативные шаблоны графиков.
Вы можете строить не только красивые диаграммы, но и инфографику, карты и отчеты. Это отличный инструмент для визуализации маркетинговых данных, онлайн-публикаций, образовательных целей, бизнес-отчетности и т. д.
Варианты дизайна видны сразу.
Основные преимущества и возможности бесплатного плана:
- Более 35 типов диаграмм , включая круговые диаграммы, гистограммы и линейные графики, столбчатые таблицы, диаграммы с областями, точечные диаграммы, пузырьковые диаграммы, древовидные карты, финансовые графики и облака слов.
- Опубликуйте свой контент — позволяет добавлять визуализацию данных на ваш веб-сайт с помощью встраивания.
- Импорт данных — вы можете импортировать файлы электронных таблиц (CSV, XLSX) со своего компьютера или из облачного хранилища.

- 2 типа карт – доступ к карте мира и карте США.
- Размер библиотеки 10.
- Простой и удобный интерфейс.
Веб-сайт: https://infogram.com
4.Gnuplot
Gnuplot — это популярная портативная бесплатная программа для построения графиков , которую можно скачать. Он широко используется на многих платформах, включая MS Windows, Linux, Unix и OSX . Он также сохраняет поддержку более старых систем, таких как VMS, Ultrix, OS/2 и MS-DOS. Исходный код защищен авторским правом, но распространяется свободно.
Он был создан, чтобы помочь ученым и студентам визуализировать отношения данных и математические функции. Однако теперь он поддерживает множество неинтерактивных приложений, таких как веб-скрипты.
Gnuplot поддерживает как 2D-, так и 3D-графики. Среди основных стилей 2D-графиков — заполненные кривые, планки погрешностей, гистограммы, гистограммы, ступенчатые функции, шкалы с несколькими осями, круги, ящичные диаграммы и многие другие.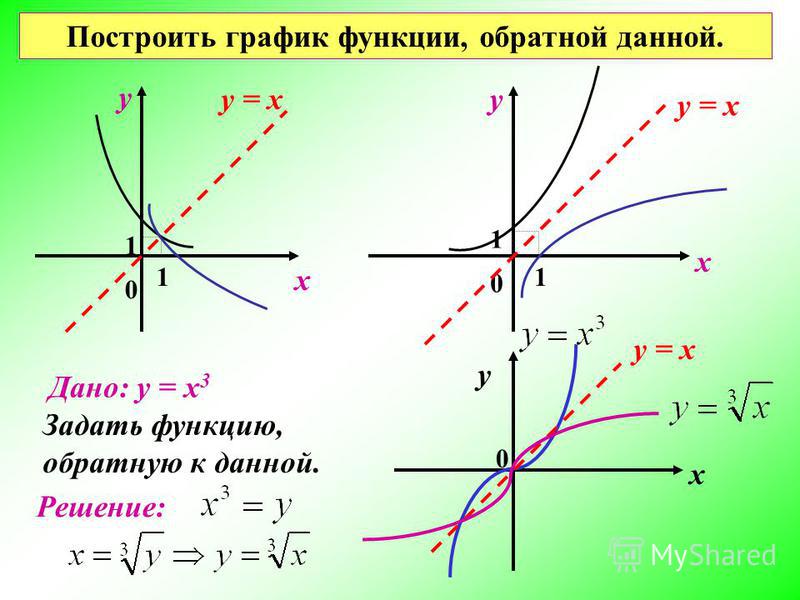
Основные преимущества и возможности:
- Построение 2D-функций и точек данных в различных стилях (точки, линии, планки погрешностей).
- Построение Трехмерных точек данных и поверхностей во многих стилях (контурный график, сетка).
- Алгебраические вычисления.
- Подгонка управляемой данными модели.
- Поддержка многих операционных систем, форматов графических файлов и устройств вывода.
Веб-сайт: http://www.gnuplot.info/
5. Desmos
Desmos – это бесплатный графический калькулятор нового поколения для всех учащихся и преподавателей. Он имеет впечатляющее количество функций и возможностей.
Программа позволяет строить графики функций, исследовать преобразования, отображать данные, оценивать уравнения и многое другое — и все это бесплатно. Вы можете исследовать уравнения, создавать полноцветные графики и делиться ими.
Desmos — невероятно мощный инструмент для построения графиков.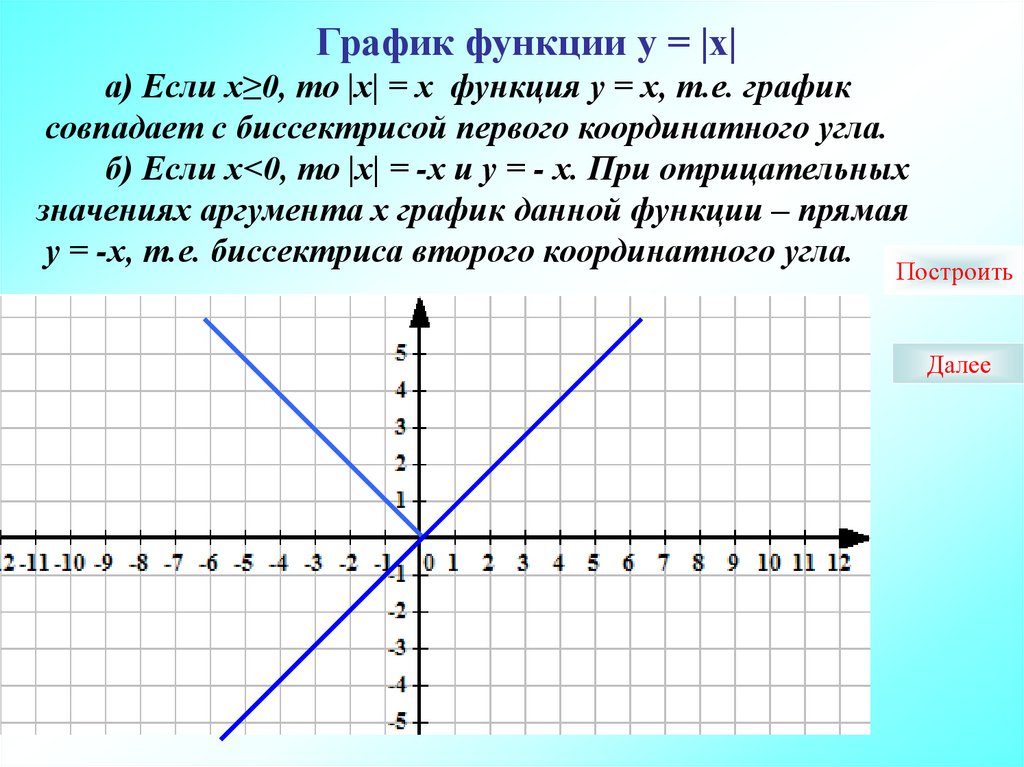 Он также поддерживает виртуальную клавиатуру с часто используемыми математическими символами. Вы также можете использовать физическую клавиатуру.
Он также поддерживает виртуальную клавиатуру с часто используемыми математическими символами. Вы также можете использовать физическую клавиатуру.
Основные преимущества и функции:
- Мощные настройки графика для настройки графика в соответствии с вашими требованиями.
- Производные и дифференциальное исчисление всего несколькими нажатиями клавиш: d/dx.
- Обозначение функций для создания связей между выражениями, таблицами и другими математическими объектами.
- Неравенства для автоматического затенения над или под линиями и кривыми.
- Многие статистические возможности , такие как исследование формы, центра и разброса наборов данных, запуск моделей линейной регрессии, построение и рисование статистических диаграмм, таких как линейный график, гистограммы, точечные диаграммы и многие другие и т. д.
- Интегралы, точки построения, полярные графики и многие другие функции.
Веб-сайт: https://www.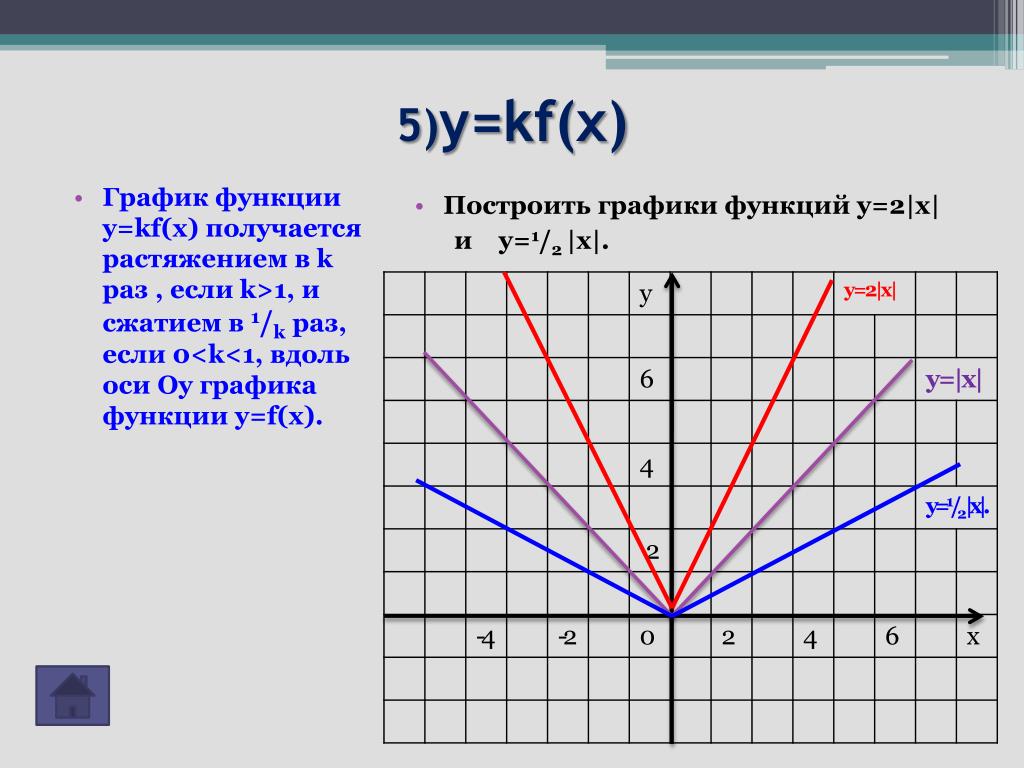 desmos.com/
desmos.com/
6. Orange
Orange — это инструмент машинного обучения, статистики и визуализации данных с открытым исходным кодом для новичков и профессионалов. Он включает визуальное программирование, анализ данных и интерактивную визуализацию данных. Кроме того, его также можно использовать в качестве библиотеки Python.
Вы можете влюбиться в этот инструмент, который позволяет принимать бизнес-решения, не тратя много времени на анализ и сравнение чисел.
Orange идеально подходит для визуализации данных и имеет все необходимое: различные типы графиков, статистические распределения, тепловые карты, деревья решений, иерархическую кластеризацию, линейные проекции, коробчатую диаграмму, точечные диаграммы и многое другое.
Это бесплатно загружаемое программное обеспечение для Windows, Mac OS и Linux .
Основные преимущества и особенности:
- Вы можете выполнять простой анализ данных с продуманной визуализацией данных.

- Большое разнообразие виджетов визуализации, таких как точечная диаграмма, блочная диаграмма, гистограмма, визуализации для конкретных моделей, такие как дендрограмма, силуэтная диаграмма и т. д.
- Визуальное программирование и графический пользовательский интерфейс, позволяющий сосредоточиться на исследовательском анализе данных вместо кодирования.
- Используется в школах, университетах и на курсах профессиональной подготовки по всему миру.
- В Orange доступны различные надстройки для добычи данных.
Веб-сайт: https://orange.biolab.si/
7. GeoGebra
GeoGebra входит в число лучших бесплатных программ для построения графиков с открытым исходным кодом для всех уровней образования, который объединяет электронные таблицы, графики, геометрию, алгебру, статистику, математику и исчисление в одном простом в использовании инструменте.
GeoGebra — ведущий поставщик математического программного обеспечения, поддерживающего образование в области естественных наук, статистики, технологий, инженерии и математики во всем мире.
Вы можете легко решать уравнения, создавать конструкции, строить графики функций, анализировать данные и изучать трехмерную математику! Вы можете использовать программу онлайн или скачать ее на свой компьютер.
Основные преимущества и особенности:
- Очень простой в использовании интерфейс со множеством мощных функций.
- Предоставляет множество различных представлений для математических объектов: представление алгебры, графическое представление, представление электронной таблицы, представление 3D-графики, представление , представление CAS, представление калькулятора вероятностей и т. д.
- Доступно на многих языках для наших миллионов пользователей по всему миру.
- Прямой ввод различных уравнений и координат.
- Вы можете использовать его бесплатно онлайн или загрузить для Windows, Mac и Linux .
Веб-сайт: https://www.geogebra.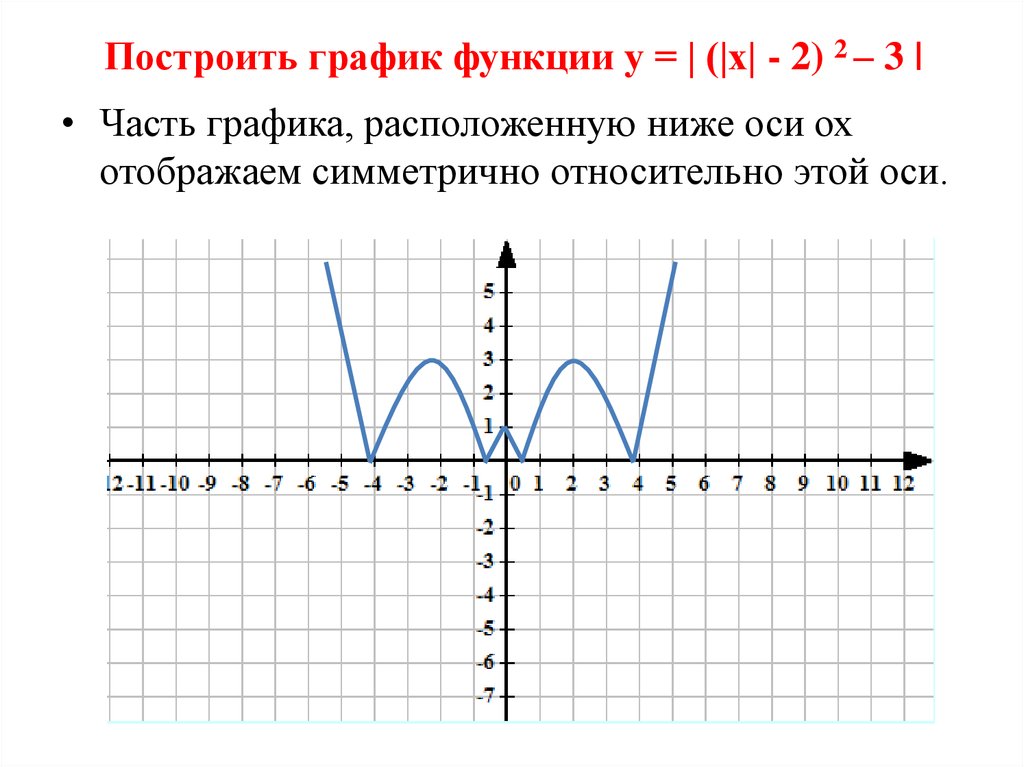 org
org
8. AmCharts
AmCharts также является одним из впечатляющих бесплатных графических инструментов, который может удивить вас своей простотой. Этот продвинутый инструмент построения диаграмм может удовлетворить любые потребности в визуализации данных.
Их решения для построения диаграмм включают линейную диаграмму, площадную диаграмму, диаграмму с прямоугольниками и усами, столбец, гистограмму, водопад, Мекко, цилиндр, трапецию, свечу, с накоплением (обычный, 100% или 3D) и многие другие типы графиков.
Кроме того, AmCharts поддерживает работу как в режиме онлайн, так и в автономном режиме.
Основные преимущества и функции:
- Расширенные серийные диаграммы для визуализации сложных данных. Программное обеспечение объединяет различные типы графиков на одном графике.
- Превосходные шкалы времени.
- Микрографики и спарклайны.
- Функциональный инструмент с интерактивными возможностями, параметрами экспорта и загрузкой внешних данных.

- Адаптивная и мобильная программа.
- Широкие возможности настройки и гибкость, множество вариантов аннотаций. Поддерживает темы и стили CSS.
- Многоязычный — почти 30 языков в комплекте с продуктом.
Веб-сайт: https://www.amcharts.com
Хотите больше бесплатных графических программ?
Вот список других хороших бесплатных решений:
9. Mondrian – универсальное программное обеспечение для визуализации статистических данных. Он предлагает выдающиеся интерактивные методы визуализации данных практически любого типа.
10. LabPlot – KDE-приложение для интерактивного построения графиков и анализа научных данных. Он обеспечивает простой способ создания, управления и редактирования графиков, а также выполнения анализа данных. Доступно для Linux, Windows и Mac OS X.
11. MathGV — бесплатная программа с открытым исходным кодом для построения графиков математических функций для Windows XP, Vista и Windows 7.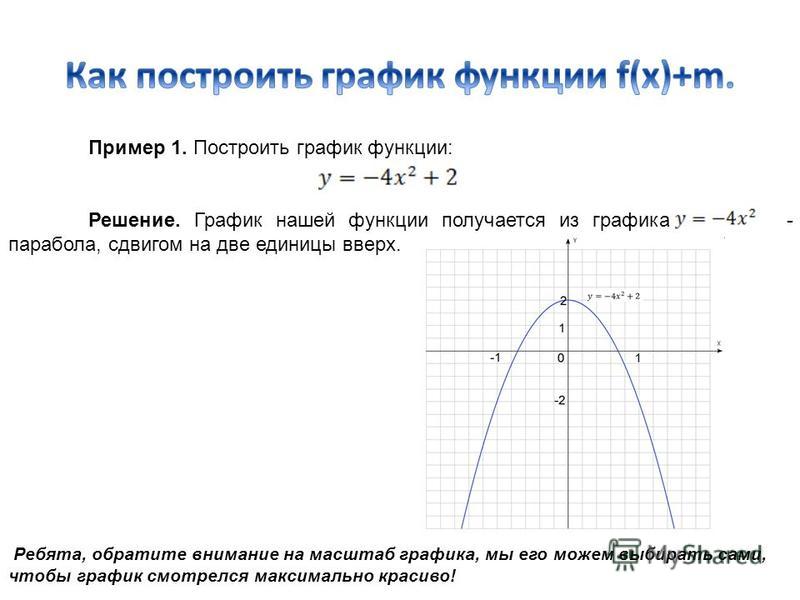
12. Euler Math Toolbox — простая математическая программа объединение числовых и символьных инструментов в одном бесплатном пакете. Программа работает в Windows 7, 8 или 10, 32-битной или 64-битной версии.
13. MagicPlot Student – современная программа для построения графиков для школьников. Легкое приложение для анализа данных, построения графиков и нелинейной подгонки. Доступно для Windows, Mac OS X и Unix-подобных платформ.
14. Meta-calculator.com – бесплатное онлайн-программное обеспечение для построения графиков, которое позволяет отображать любое уравнение, находить его пересечения, создавать таблицы значений и т. д.
15. Mathway – предоставляет учащимся инструменты, должны понимать и решать свои математические задачи.
Если вы являетесь поклонником бесплатного программного обеспечения, вам может пригодиться наш пост о 10 лучших бесплатных программных инструментах для картографирования.
Какая ваша любимая бесплатная программа для построения графиков? Поделитесь своими мыслями в поле ниже.
Prism — GraphPad
Лучшее решение для анализа и построения графиков, специально разработанное для научных исследований. Присоединяйтесь к ведущим мировым ученым и узнайте, как использовать Prism для экономии времени, выбора более подходящего анализа, а также для создания элегантных графиков и представления результатов научных исследований.
Начать бесплатную пробную версию
Цены
Узнайте, что новогоВсеобъемлющий анализ и мощные статистические данные, упрощенные
Эффективная организация данных
Prism специально отформатирован для анализа, который вы хотите выполнить, включая анализ количественных и категорийных данных. Это упрощает правильный ввод данных, выбор подходящего анализа и создание потрясающих графиков.
Начать бесплатную пробную версию
Выполнить правильный анализ
Избегайте статистического жаргона. На понятном языке Prism представляет обширную библиотеку анализов от общих до высокоспецифичных: t-тесты, одно-, двух- и трехфакторный дисперсионный анализ, линейная и нелинейная регрессия, кривые доза-реакция, бинарная логистическая регрессия, анализ выживаемости, главный компонент. анализ и многое другое. Для каждого анализа есть контрольный список, который поможет вам понять необходимые статистические допущения и подтвердить, что вы выбрали подходящий тест.
На понятном языке Prism представляет обширную библиотеку анализов от общих до высокоспецифичных: t-тесты, одно-, двух- и трехфакторный дисперсионный анализ, линейная и нелинейная регрессия, кривые доза-реакция, бинарная логистическая регрессия, анализ выживаемости, главный компонент. анализ и многое другое. Для каждого анализа есть контрольный список, который поможет вам понять необходимые статистические допущения и подтвердить, что вы выбрали подходящий тест.
Начать бесплатную пробную версию
Получайте полезную помощь в процессе работы
Уменьшите сложность статистики. Онлайн-помощь Prism превосходит ваши ожидания. Практически на каждом этапе вы получаете доступ к тысячам страниц руководств пользователя Prism. Учитесь с помощью видеоуроков, руководств и учебных материалов Prism Academy. Просмотрите портфолио графиков и узнайте, как создавать различные типы графиков. Учебные наборы данных также помогут вам понять, почему вы должны выполнять определенные анализы и как интерпретировать ваши результаты.
Начать бесплатную пробную версию
Работайте умнее, а не усерднее
Регрессионный анализ одним щелчком мыши
Никакая другая программа не упрощает подбор кривых так, как Prism. Выберите уравнение, и Prism сделает все остальное — подгонит кривую, отобразит таблицу результатов и параметров функции, нарисует кривую на графике и интерполирует неизвестные значения.
Начните бесплатную пробную версию
Сосредоточьтесь на своих исследованиях, а не на программном обеспечении
Prism выполнит кодирование за вас. Графики и результаты автоматически обновляются в режиме реального времени. Любые изменения в данных и анализах — прямой ввод данных, пропуск ошибочных данных, исправление опечаток или изменение выбора анализа — мгновенно отражаются в результатах, графиках и макетах.
Начать бесплатную пробную версию
Автоматизируйте свою работу без программирования
Автоматически добавляйте несколько парных сравнений в свой анализ одним щелчком мыши. Для настройки параметров этих линий и звездочек просто нажмите кнопку на панели инструментов еще раз. Внесите коррективы в данные или анализ, и результаты, отображаемые на графике, будут обновляться автоматически.
Для настройки параметров этих линий и звездочек просто нажмите кнопку на панели инструментов еще раз. Внесите коррективы в данные или анализ, и результаты, отображаемые на графике, будут обновляться автоматически.
Начать бесплатную пробную версию
Самый быстрый способ создать элегантную графику и поделиться своей работой
Бесчисленные способы настройки графиков
Сосредоточьтесь на истории ваших данных, а не на манипулировании вашим программным обеспечением. Prism позволяет легко создавать нужные вам графики. Выберите тип графика и настройте любую часть — порядок расположения данных, стиль точек данных, метки, шрифты, цвета и многое другое. Варианты настройки безграничны.
Начать бесплатную пробную версию
Исследуйте свои данные
Сосредоточьте свои усилия на анализе наиболее важных данных. Настройте способ представления взаимосвязей в данных, чтобы эффективно исследовать большие наборы данных.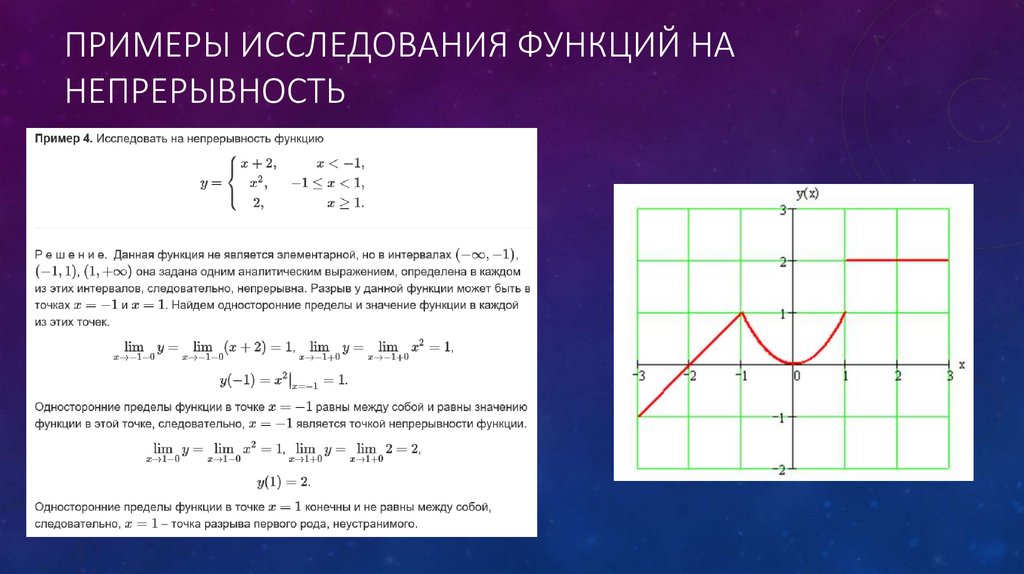
Начать бесплатную пробную версию
Экспорт графиков качества публикации одним щелчком мыши
Сокращение времени публикации. Prism позволяет настраивать экспорт (тип файла, разрешение, прозрачность, размеры, цветовое пространство RGB/CMYK) в соответствии с требованиями журналов. Установите настройки по умолчанию, чтобы сэкономить время.
Начать бесплатную пробную версию
Расширение возможностей совместной работы
Делитесь не только своими графиками. Полная запись ваших данных Prism позволяет эффективно сотрудничать с другими учеными. Все части вашего проекта Prism (необработанные данные, анализы, результаты, графики и макеты) содержатся в одном файле, которым вы можете поделиться одним щелчком мыши. Теперь другие могут легко следить за вашей работой на каждом этапе, повышая четкость ваших выводов и оптимизируя ваши совместные усилия.
Начать бесплатную пробную версию
Узнайте, что нового в Prism!
Представляем еще более мощный Prism с улучшенной визуализацией данных и настройкой графиков, более интуитивно понятной навигацией и более сложным статистическим анализом.
Расширенная визуализация данных и настройка графиков
Пузырьковые диаграммы
Создание пузырьковых диаграмм непосредственно из необработанных данных, кодирование переменных для положения (координаты X и Y), цвета и размера
Скрипичные графики
Визуализация распределения больших наборов данных с помощью расширенных или усеченных скрипичных графиков
Оценочные графики
Автоматическое отображение результатов анализа улучшенный контроль количества узлов или точек перегиба
Подробнее
Улучшенные параметры построения графиков и настройки
Звезды на диаграмме
Автоматическое добавление нескольких результатов сравнения к графикам
Автоматическое добавление меток к гистограммам
Аннотирование гистограмм со значениями средних значений, медиан или размеров выборки, чтобы подчеркнуть, что важно в вашей работе
Улучшенные сгруппированные диаграммы
Легко создавайте графики, которые отображают как отдельные точки (разброс), так и столбцы для среднего (или медианы) и столбцы ошибок
Подробнее
Более интуитивная навигация
Удобный поиск связанных листов
Новая семейная панель показывает семейство листов, связанных с текущим листом, и цепочки анализов автоматически располагаются с отступом
Удобная навигация между несколькими таблицами результатов
Анализы с несколькими таблицами результатов теперь сгруппированы в один лист с вкладками для каждой таблицы результатов; выбрать, какие вкладки показать или скрыть
Улучшенный поиск
Поиск по листам с выделениями или примечаниями заданного цвета
Подробнее
Теперь с восемью типами таблиц данных
Таблица данных с несколькими переменными
Каждая строка представляет отдельный объект, а каждый столбец — отдельную переменную, что позволяет выполнять множественную линейную регрессию (включая регрессию Пуассона), извлекать подмножества данных в другие типы таблиц или выбирать и преобразовывать подмножества данных.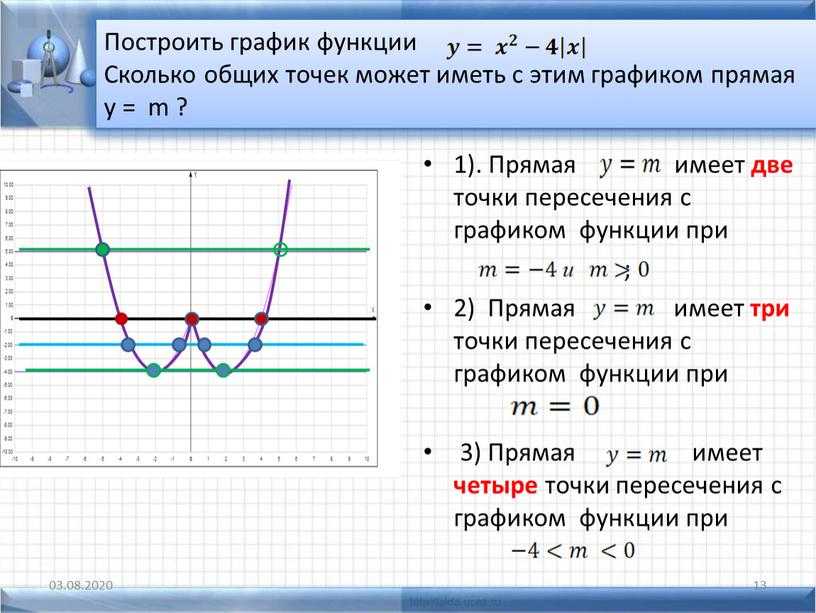 данные. Таблицы с несколькими переменными Prism поддерживают текстовые переменные и позволяют определять типы переменных
данные. Таблицы с несколькими переменными Prism поддерживают текстовые переменные и позволяют определять типы переменных
Вложенная таблица данных
Анализ и визуализация данных, содержащих подмножества в связанных группах; Выполнение вложенных t-тестов и вложенного однофакторного дисперсионного анализа с использованием данных в этих таблицах
Подробнее
Более сложный статистический анализ
Выполнение повторных измерений ANOVA — даже с отсутствующими данными
Теперь Prism автоматически подгонит модель смешанных эффектов для завершения этого анализа
Выполнение простой и множественной логистической регрессии
Подгонка модели к бинарному результату (да/нет, выигрыш/проигрыш, успешно/неудачно) на основе одной переменной-предиктора (простая логистическая регрессия) или множества переменных-предикторов (множественная логистическая регрессия)
Анализ главных компонентов
Рассчитайте и выберите главные компоненты, которые описывают наибольшую дисперсию ваших данных. Выберите один из методов выбора, включая параллельный анализ с помощью моделирования Монте-Карло, порог собственного значения, порог пропорции дисперсии и т. д.
Выберите один из методов выбора, включая параллельный анализ с помощью моделирования Монте-Карло, порог собственного значения, порог пропорции дисперсии и т. д.
Множественный t-критерий (и непараметрический) анализ
Одновременное выполнение нескольких независимых тестов сравнения двух образцов. Выберите из параметрических/непараметрических тестов и укажите, являются ли данные непарными/парными
Анализ категориальных переменных с текстом в множественной линейной и множественной логистической регрессии
Кодирование не требуется! Prism автоматически кодирует категориальные переменные и выполняет анализ. Укажите ссылку и организуйте все уровни категориальных переменных в модели для получения четких, удобочитаемых результатов
Интерполяция на основе множественной линейной и множественной логистической регрессии
Использование указанной модели для прогнозирования значений зависимой переменной на основе данных в таблице данных или с использованием теоретических значений, указанных в анализе
Подробнее
Начать бесплатную 30-дневную пробную версию
Кредитная карта не требуется.
Откройте для себя множество статистических функций, доступных в Prism
Статистические сравнения
- Парные или непарные t-тесты. Сообщает значения P и доверительные интервалы.
- Автоматически генерировать график вулкана (разность со значением P) на основе анализа множественного t-критерия.
- Непараметрический критерий Манна-Уитни, включая доверительный интервал разности медиан.
- Тест Колмогорова-Смирнова для сравнения двух групп.
- Критерий Уилкоксона с доверительным интервалом медианы.
- Выполните сразу несколько t-тестов, используя False Discovery Rate (или множественные сравнения Бонферрони), чтобы выбрать, какие сравнения являются открытиями для дальнейшего изучения.
- Обычные или повторяющиеся измерения ANOVA, за которыми следуют множественные сравнительные тесты Тьюки, Ньюмана-Кеулса, Даннета, Бонферрони или Холма-Сидака, апостериорный тест на тренд или критерий наименьшего значения Фишера.

- Однофакторный дисперсионный анализ без предположения о популяциях с одинаковыми стандартными отклонениями с использованием дисперсионного анализа Брауна-Форсайта и Уэлча с последующими соответствующими тестами сравнения (Games-Howell, Tamhane T2, Dunnett T3)
- Многие тесты множественных сравнений сопровождаются доверительными интервалами и значениями P с поправкой на множественность.
- Коррекция Гринхауса-Гейссера, поэтому повторные измерения одно-, двух- и трехфакторного дисперсионного анализа не должны предполагать сферичность. Когда это выбрано, множественные сравнительные тесты также не предполагают сферичность.
- Непараметрический однофакторный дисперсионный анализ Краскела-Уоллиса или Фридмана с апостериорным критерием Данна.
- Точный критерий Фишера или критерий хи-квадрат.
 Рассчитайте относительный риск и отношение шансов с доверительными интервалами.
Рассчитайте относительный риск и отношение шансов с доверительными интервалами. - Двухфакторный дисперсионный анализ, даже с отсутствующими значениями в некоторых посттестах.
- Двухфакторный дисперсионный анализ с повторными измерениями одного или обоих факторов. Множественные сравнения Tukey, Newman-Keuls, Dunnett, Bonferroni, Holm-Sidak или Fisher’s LSD, проверяющие основные и простые эффекты.
- Трехфакторный дисперсионный анализ (ограничен двумя уровнями по двум факторам и любым количеством уровней по третьему).
- Анализ данных повторных измерений (одно-, двух- и трехфакторных) с использованием модели смешанных эффектов (аналогично повторным измерениям ANOVA, но с возможностью обработки отсутствующих данных).
- Сравнение данных из вложенных таблиц данных с использованием вложенного t-критерия или вложенного однофакторного дисперсионного анализа (с использованием модели смешанных эффектов).

Нелинейная регрессия
- Подберите одно из 105 встроенных уравнений или введите свое собственное. Теперь включает семейство уравнений роста: экспоненциальный рост, экспоненциальное плато, Гомперца, логистическое и бета (рост, а затем спад).
- Введите дифференциальные или неявные уравнения.
- Введите разные уравнения для разных наборов данных.
- Глобальная нелинейная регрессия — общие параметры между наборами данных.
- Надежная нелинейная регрессия.
- Автоматическая идентификация или устранение выбросов.
- Сравните модели, используя F-критерий дополнительной суммы квадратов или AICc.
- Сравните параметры между наборами данных.
- Применить ограничения.

- Различно взвешивайте очки несколькими методами и оцените, насколько хорошо работает ваш метод взвешивания.
- Примите автоматические начальные оценочные значения или введите свои собственные.
- Автоматически отображать кривую в указанном диапазоне значений X.
- Количественная оценка точности подбора параметров с помощью SE или CI. Доверительные интервалы могут быть симметричными (традиционно) или асимметричными (что более точно).
- Количественная оценка симметрии неточности с помощью асимметрии Хоугарда.
- Постройте доверительные интервалы или диапазоны предсказания.
- Проверить нормальность остатков.
- Запускает или повторяет проверку адекватности модели.

- Сообщите ковариационную матрицу или набор зависимостей.
- Простая интерполяция точек из кривой наилучшего соответствия.
- Сопоставьте прямые линии с двумя наборами данных и определите точку пересечения и оба наклона.
Анализ выживания
- Анализ выживаемости Каплана-Мейера. Выполните непараметрический анализ выживаемости для разных групп и сравните расчетные кривые выживаемости для каждой группы с тестом логарифмического ранга (включая тест на тенденцию).
- Регрессия пропорциональных опасностей Кокса. Выполните полупараметрический анализ выживаемости, который позволяет включать дополнительные непрерывные или категориальные переменные-предикторы (ковариаты).
 Автоматически создавайте графики оценочных кривых выживаемости для любого набора значений переменных-предикторов.
Автоматически создавайте графики оценочных кривых выживаемости для любого набора значений переменных-предикторов.
Анализ главных компонентов (АПК)
- Выбор компонентов с помощью параллельного анализа (моделирование методом Монте-Карло), критерия Кайзера (порог собственного значения), порог пропорции дисперсии и т. д.
- Автоматически генерируемые графики осыпи, графики загрузки, двойные графики и многое другое.
- Используйте результаты в последующих приложениях, таких как регрессия основных компонентов.
График нескольких переменных
- Укажите переменные, определяющие координаты оси, цвет и размер.
- Создание пузырьковых графиков.
Статистика столбца
- Расчет описательной статистики: минимум, максимум, квартили, среднее, SD, SEM, CI, CV, асимметрия, эксцесс.

- Среднее или среднее геометрическое с доверительными интервалами.
- Частотные распределения (бин к гистограмме), включая кумулятивные гистограммы.
- Проверка нормальности четырьмя методами (новый: Андерсон-Дарлинг).
- Критерий логарифмической нормальности и вероятность выборки из нормального (гауссовского) распределения по сравнению с логнормальным распределением.
- Создайте график QQ как часть проверки нормальности.
- Один образец t-критерия или критерия Уилкоксона для сравнения среднего значения столбца (или медианы) с теоретическим значением.
- Определите выбросы с помощью метода Граббса или ROUT.
- Проанализируйте набор значений P, используя множественные сравнения Бонферрони или подход FDR для выявления «значительных» результатов или открытий.

Простая линейная регрессия и корреляция
- Расчет наклона и точки пересечения с доверительными интервалами.
- Проведите линию регрессии через указанную точку.
- Подходит для воспроизведения значений Y или среднего значения Y.
- Тест на отклонение от линейности с прогонным тестом.
- Расчет и построение графика остатков четырьмя различными способами (включая график QQ).
- Сравните наклоны и точки пересечения двух или более линий регрессии.
- Интерполировать новые точки вдоль стандартной кривой.
- Корреляция Пирсона или Спирмена (непараметрическая).
Обобщенные линейные модели (GLM)
- Создавайте модели, связывающие несколько независимых переменных с одной зависимой переменной, используя новую таблицу данных с несколькими переменными.

- Множественная линейная регрессия (когда Y является непрерывным).
- Регрессия Пуассона (когда Y считается; 0, 1, 2, …).
- Логистическая регрессия (когда Y бинарный; да/нет, годен/не годен и т. д.).
Клиническая (диагностическая) лабораторная статистика
- Графики Бланда-Альтмана.
- Кривые характеристик оператора приемника (ROC).
- Регрессия Деминга (линейная регрессия II типа).
Моделирование
- Моделирование таблиц XY, столбцов или непредвиденных обстоятельств.
- Повторите анализ смоделированных данных как анализ Монте-Карло.
- График функций из выбранных или введенных вами уравнений и выбранных вами значений параметров.

Прочие расчеты
- Площадь под кривой с доверительным интервалом.
- Преобразование данных.
- Нормализация.
- Определите выбросы.
- Тесты на нормальность.
- Транспонировать таблицы.
- Вычитание базовой линии (и объединение столбцов).
- Вычислить каждое значение как часть его строки, столбца или общей суммы.
Prism доступен для Mac и Windows.
14 лучших типов диаграмм и графиков для визуализации данных [+ Руководство]
Типы диаграмм и графиков для использования с вашими данными
- Гистограмма
- Столбчатая диаграмма
- Линейный график
- Диаграмма с двумя осями
- Таблица зон
- Гистограмма с накоплением
- Карта Мекко
- Круговая диаграмма
- Точечная диаграмма
- Пузырьковая диаграмма
- Карта водопада
- Воронкообразная диаграмма
- Пулевая диаграмма
- Тепловая карта
Существует больше типов диаграмм и графиков, чем когда-либо прежде, потому что данных больше. На самом деле объем данных в 2025 году почти вдвое превысит объем данных, которые мы создаем, собираем, копируем и потребляем сегодня.
На самом деле объем данных в 2025 году почти вдвое превысит объем данных, которые мы создаем, собираем, копируем и потребляем сегодня.
Это делает визуализацию данных необходимой для бизнеса. Вам могут помочь различные типы графиков и диаграмм:
- Мотивируйте свою команду на действия
- Произведите впечатление на заинтересованные стороны прогрессом цели
- Покажите своей аудитории, что вы цените как бизнес
Визуализация данных укрепляет доверие и может объединять различные команды для реализации новых инициатив. Давайте поговорим о типах графиков и диаграмм, которые вы можете использовать для развития своего бизнеса.
Как правильно выбрать диаграмму или график для ваших данных
- Определите цели представления данных.
- Выясните, какие данные вам нужны для достижения цели.
- Соберите свои данные.
- Выберите правильный тип графика или диаграммы.

Каналы, такие как социальные сети или блоги, имеют несколько источников данных, и когда вы управляете этими сложными активами контента, это может стать чрезмерным. Что вы должны отслеживать? Что важнее? Как вы визуализируете и анализируете данные, чтобы вы могли извлечь идеи и полезную информацию?
1. Определите цели представления данных.
Вы хотите убедить или прояснить вопрос? Вы пытаетесь визуализировать данные, которые помогли вам решить проблему, или вы пытаетесь сообщить о происходящих изменениях?
Диаграмма или график могут помочь вам сравнить различные значения, понять, как разные части влияют на целое, или проанализировать тенденции. Диаграммы и графики также могут быть полезны для распознавания данных, которые отклоняются от того, к чему вы привыкли, или помогают вам увидеть отношения между группами.
Уточните свои цели, а затем используйте их при выборе диаграммы.
2. Выясните, какие данные вам нужны для достижения цели.

Различные типы диаграмм и графиков используют различные типы данных. Графики обычно представляют числовые данные, а диаграммы — это визуальное представление данных, которые могут использовать или не использовать числа.
Таким образом, хотя все графики являются разновидностью диаграмм, не все диаграммы являются диаграммами. Если у вас еще нет нужных данных, возможно, вам придется потратить некоторое время на объединение данных, прежде чем строить диаграмму.
3. Соберите данные.
Большинство предприятий регулярно собирают числовые данные, но вам может потребоваться дополнительное время для сбора правильных данных для диаграммы. Помимо инструментов количественных данных, которые измеряют трафик, доход и другие пользовательские данные, вам могут понадобиться некоторые качественные данные.
Вот некоторые другие способы сбора данных для визуализации данных:
- Интервью
- Тесты и опросы
- Отзывы покупателей
- Проверка документов и записей клиентов
- Общественные доски
Избранный ресурс
Бесплатные шаблоны графиков Excel
Заполните форму, чтобы получить шаблоны.
4. Выберите правильный тип графика или диаграммы.
Выбор неправильного визуального пособия или использование по умолчанию наиболее распространенного типа визуализации данных может вызвать путаницу у вашего зрителя или привести к ошибочной интерпретации данных.
Но диаграмма полезна для вас и вашего бизнеса только в том случае, если она четко и эффективно передает вашу точку зрения.
Чтобы найти правильный тип диаграммы или графика, задайте себе вопросы, приведенные ниже.
Затем взгляните на 14 типов диаграмм и графиков, которые можно использовать для визуализации данных и создания диаграммы или графика.
Загрузите упомянутые в видео шаблоны Excel здесь.
5 вопросов, которые следует задать при выборе типа диаграммы для использования
1.
 Хотите сравнить значения?
Хотите сравнить значения?Диаграммы и графики идеально подходят для сравнения одного или нескольких наборов значений, и они могут легко показать низкие и высокие значения в наборах данных. Чтобы создать сравнительную диаграмму, используйте следующие типы графиков:
- Столбец
- Мекко
- Бар
- Пирог
- Строка
- Точечная диаграмма
- Пуля
2. Хотите показать состав чего-либо?
Используйте этот тип диаграммы, чтобы показать, как отдельные части составляют целое, например, тип устройства, используемого для мобильных посетителей вашего веб-сайта, или общий объем продаж с разбивкой по торговым представителям.
Чтобы показать состав, используйте следующие диаграммы:
- Круговая диаграмма
- Многослойный бар
- Мекко
- Район
- Водопад
3. Хотите понять, как распределяются ваши данные?
Диаграммы распределения помогают понять выбросы, нормальную тенденцию и диапазон информации в ваших значениях.
Используйте эти диаграммы, чтобы показать распределение:
- Точечная диаграмма
- Мекко
- Строка
- Столбец
- Бар
4. Заинтересованы ли вы в анализе тенденций в вашем наборе данных?
Если вы хотите узнать больше о том, как набор данных работал в течение определенного периода времени, есть определенные типы диаграмм, которые очень хорошо работают.
Вы должны выбрать:
- Линия
- Двухосевая линия
- Столбец
5. Хотите лучше понять взаимосвязь между наборами значений?
Диаграммы взаимосвязей могут показать, как одна переменная связана с одной или несколькими переменными. Вы можете использовать это, чтобы показать, как что-то положительно влияет, не влияет или отрицательно влияет на другую переменную.
При попытке установить взаимосвязь между вещами используйте следующие диаграммы:
- Точечная диаграмма
- Пузырь
- Строка
Рекомендуемый ресурс: Руководство маркетолога по визуализации данных
Загрузите это бесплатное руководство по визуализации данных, чтобы узнать, какие графики использовать в маркетинге, презентациях или проектах, а также как их эффективно использовать.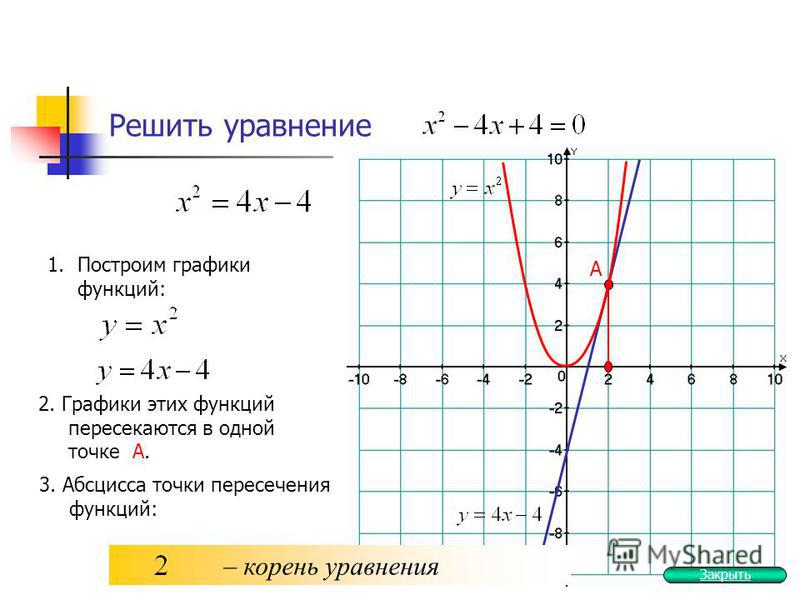
Различные типы графиков и диаграмм для представления данных
Чтобы лучше понять каждую диаграмму и тип графика, а также способы их использования, приведен обзор графиков и типов диаграмм.
1. Гистограмма
Гистограмму следует использовать, чтобы избежать беспорядка, когда одна метка данных длинная или если у вас есть более 10 элементов для сравнения.
Наилучшие варианты использования этих типов диаграмм:
Гистограммы могут помочь вам сравнить данные между различными группами или отслеживать изменения во времени. Гистограммы наиболее полезны, когда происходят большие изменения или чтобы показать, как одна группа сравнивается с другими группами.
В приведенном выше примере сравнивается количество клиентов по бизнес-ролям. Это позволяет легко увидеть, что количество клиентов на роль для отдельных участников более чем в два раза больше, чем для любой другой группы.
Гистограмма также позволяет легко увидеть, какая группа данных является самой высокой или наиболее распространенной.
Например, в начале пандемии трафик онлайн-бизнеса резко вырос. Итак, если вы хотите посмотреть на ежемесячный трафик для онлайн-бизнеса, гистограмма поможет вам легко увидеть этот скачок.
Другие варианты использования гистограмм включают:
- Сравнение продуктов
- Использование продукта
- Сравнение категорий
- Маркетинговый трафик по месяцам или годам
- Маркетинговые конверсии
Рекомендации по проектированию гистограмм:
- Используйте одинаковые цвета на всей диаграмме, выбирая акцентные цвета, чтобы выделить значимые точки данных или изменения во времени.
- Используйте горизонтальные метки для удобства чтения.
- Начните ось Y с 0 , чтобы правильно отразить значения на графике.
2. Столбчатая диаграмма
Используйте столбчатую диаграмму, чтобы показать сравнение между различными элементами или показать сравнение элементов во времени.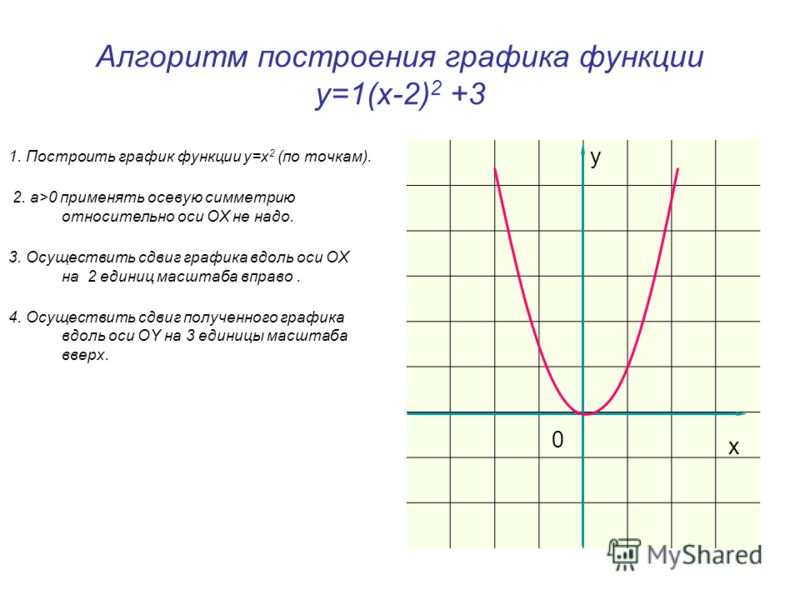 Вы можете использовать этот формат, чтобы увидеть доход на целевую страницу или клиентов по дате закрытия.
Вы можете использовать этот формат, чтобы увидеть доход на целевую страницу или клиентов по дате закрытия.
Наилучшие варианты использования для этого типа диаграммы:
В то время как гистограммы отображают информацию вертикально, а гистограммы отображают данные горизонтально. Хотя вы можете использовать оба варианта для отображения изменений в данных, гистограммы лучше всего подходят для отрицательных данных.
Например, склады часто отслеживают количество несчастных случаев, происходящих в цехах. Когда количество инцидентов падает ниже среднемесячного значения, столбчатая диаграмма может облегчить просмотр этого изменения в презентации.
В приведенном выше примере эта столбчатая диаграмма измеряет количество клиентов по дате закрытия. Столбчатые диаграммы позволяют легко увидеть изменения данных за определенный период времени. Это означает, что у них есть много вариантов использования, в том числе:
- Данные опроса клиентов, например, показывающие, сколько клиентов предпочитают определенный продукт или сколько клиентов используют продукт каждый день.

- Объем продаж, например показывает, какие услуги являются самыми продаваемыми каждый месяц или количество продаж в неделю.
- Прибыли и убытки, показывающие, где растут или падают инвестиции в бизнес.
Рекомендации по проектированию столбчатых диаграмм:
- Используйте одинаковые цвета на всей диаграмме, выбирая акцентные цвета, чтобы выделить значимые точки данных или изменения во времени.
- Используйте горизонтальные метки для удобства чтения.
- Начните ось Y с 0 , чтобы правильно отразить значения на графике.
3. Линейный график
Линейный график показывает тенденции или прогресс с течением времени, и вы можете использовать его для отображения различных категорий данных. Вы должны использовать его, когда рисуете непрерывный набор данных.
Наилучшие варианты использования этих типов графиков:
Линейные графики помогают пользователям отслеживать изменения за короткие и длительные периоды времени.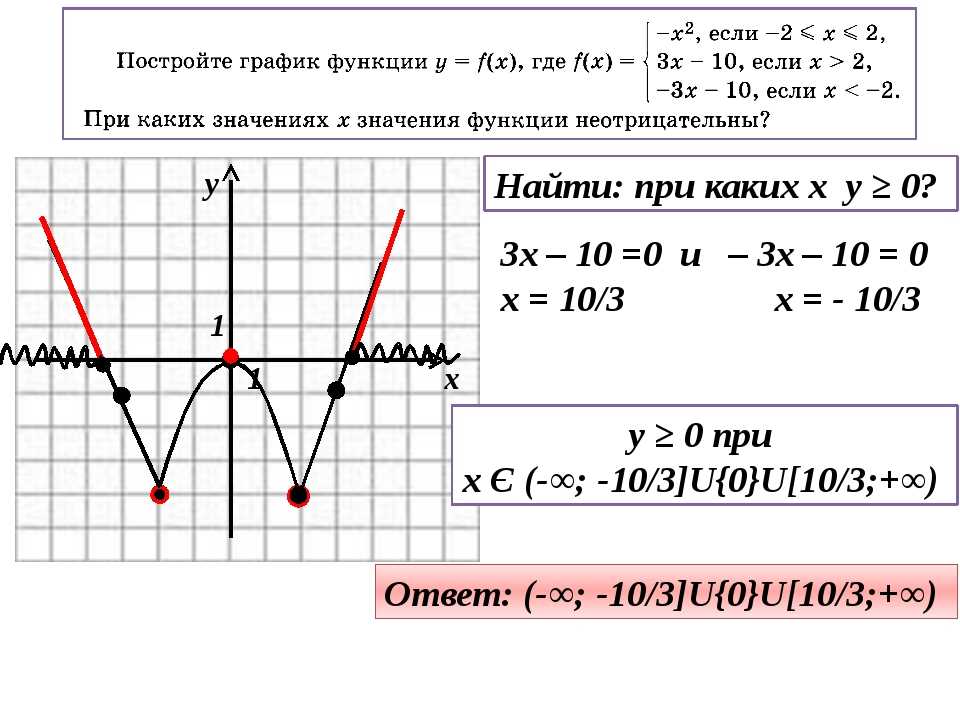 Из-за этого эти типы графиков хороши для наблюдения за небольшими изменениями.
Из-за этого эти типы графиков хороши для наблюдения за небольшими изменениями.
Линейные графики могут помочь вам сравнить изменения для более чем одной группы за один и тот же период. Они также полезны для измерения того, как разные группы относятся друг к другу.
Бизнес может использовать этот тип графика для сравнения уровня продаж различных продуктов или услуг с течением времени.
Эти диаграммы также полезны для измерения производительности сервисного канала. Например, линейный график, который отслеживает, сколько чатов или электронных писем ваша команда отвечает в месяц.
Рекомендации по проектированию линейных графиков:
- Используйте только сплошные линии.
- Не наносите более четырех линий , чтобы не отвлекать внимание.
- Используйте правильную высоту , чтобы линии занимали примерно 2/3 высоты оси Y.
4. Диаграмма с двумя осями
Диаграмма с двумя осями позволяет отображать данные с использованием двух осей Y и общей оси X.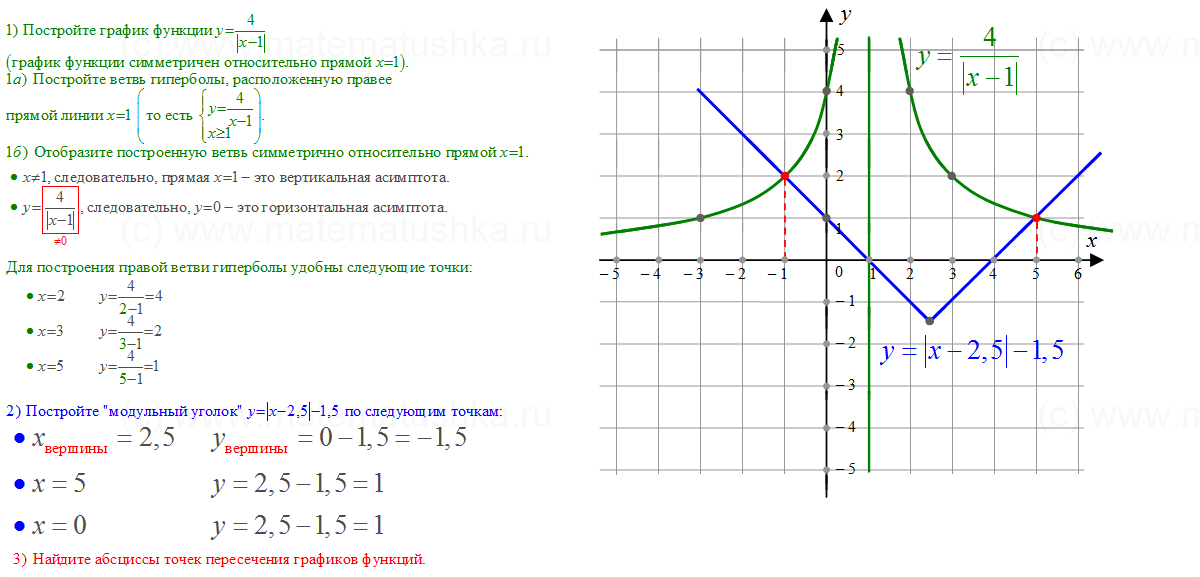 Он имеет три набора данных. Один представляет собой непрерывный набор данных, а другой лучше подходит для группировки по категориям. Используйте эту диаграмму, чтобы визуализировать корреляцию или ее отсутствие между этими тремя наборами данных.
Он имеет три набора данных. Один представляет собой непрерывный набор данных, а другой лучше подходит для группировки по категориям. Используйте эту диаграмму, чтобы визуализировать корреляцию или ее отсутствие между этими тремя наборами данных.
Наилучшие варианты использования для этого типа диаграммы:
Диаграмма с двумя осями позволяет легко увидеть отношения между различными наборами данных. Они также могут помочь в сравнении тенденций.
Например, на приведенной выше диаграмме показано, сколько новых клиентов эта компания привлекает каждый месяц. Он также показывает, какой доход эти клиенты приносят компании.
Это позволяет легко увидеть связь между количеством клиентов и увеличением доходов.
Вы можете использовать двухосевые диаграммы для сравнения:
- Цена и объем вашей продукции
- Доход и количество проданных единиц
- Объем продаж и прибыль
- Эффективность индивидуальных продаж
Рекомендации по проектированию двухосевых диаграмм:
- Используйте ось Y с левой стороны для первичной переменной , потому что мозг естественным образом склонен сначала смотреть влево.

- Используйте разные стили построения графиков для иллюстрации двух наборов данных, как показано выше.
- Выберите контрастные цвета для двух наборов данных.
5. Диаграмма с областями
Диаграмма с областями в основном представляет собой линейную диаграмму, но пространство между осью x и линией заполнено цветом или узором. Это полезно для отображения отношений части к целому, например, для отображения вклада отдельных торговых представителей в общий объем продаж за год. Он помогает анализировать как общую, так и индивидуальную информацию о тенденциях.
Наилучшие варианты использования этих типов диаграмм:
Диаграммы с областями помогают показать изменения с течением времени. Они лучше всего подходят для больших различий между наборами данных, а также помогают визуализировать большие тенденции.
Например, на приведенной выше диаграмме пользователи показаны по дате создания и стадии жизненного цикла.
Линейная диаграмма может показать, что подписчиков больше, чем маркетинговых лидов. Но эта диаграмма с областями подчеркивает, насколько больше количество подписчиков, чем у любой другой группы.
Эти типы диаграмм и графиков делают размер группы и то, как группы связаны друг с другом, визуально более важными, чем изменения данных с течением времени.
Диаграммы с площадями могут помочь вашему бизнесу:
- Визуализировать, какие категории продуктов или продукты внутри категории наиболее популярны
- Показать цели ключевых показателей эффективности (KPI) в сравнении с результатами
- Выявляйте и анализируйте отраслевые тенденции
Рекомендации по проектированию площадных диаграмм:
- Используйте прозрачные цвета , чтобы информация не закрывалась фоном.
- Не отображайте более четырех категорий во избежание беспорядка.

- Организуйте сильно изменяющиеся данные в верхней части диаграммы, чтобы упростить чтение.
6. Столбчатая диаграмма с накоплением
Используйте эту диаграмму, чтобы сравнить множество различных элементов и показать состав каждого элемента, который вы сравниваете.
Лучшие варианты использования для этих типов графиков:
Эти графики полезны, когда группа начинается в одном столбце и со временем переходит в другой.
Например, иногда трудно увидеть разницу между квалифицированным потенциальным клиентом по маркетингу (MQL) и квалифицированным лидом по продажам (SQL). Приведенная выше диаграмма помогает заинтересованным сторонам увидеть эти два типа лидов с единой точки зрения, когда лид переходит с MQL на SQL.
Столбчатые гистограммы отлично подходят для маркетинга. Они упрощают добавление большого количества данных на одну диаграмму или создание точки с ограниченным пространством.
Эти типы графиков могут отображать несколько выводов, поэтому они также отлично подходят для ежеквартальных встреч, когда вам есть что сказать, но не всегда много времени.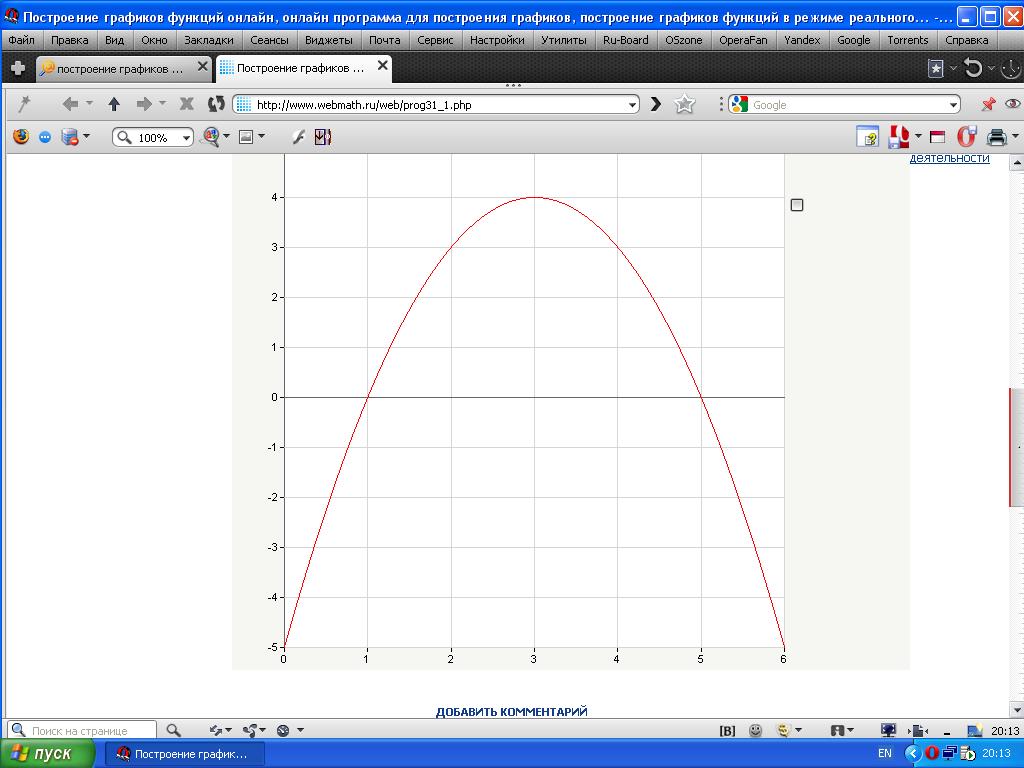
Гистограммы с накоплением также являются разумным вариантом для планирования или стратегических совещаний. Это связано с тем, что эти диаграммы могут отображать много информации одновременно, но они также позволяют легко сосредоточиться на одном стеке за раз или перемещать данные по мере необходимости.
Вы также можете использовать эти диаграммы, чтобы:
- Показать частоту ответов на опросы
- Выявление выбросов в исторических данных
- Сравнение части стратегии с ее эффективностью в целом
Рекомендации по проектированию гистограмм с накоплением:
- Лучше всего использовать для иллюстрации отношений части к целому.
- Используйте контрастных цвета для большей четкости.
- Сделайте масштаб диаграммы достаточно большим для просмотра размеров групп по отношению друг к другу.
7.
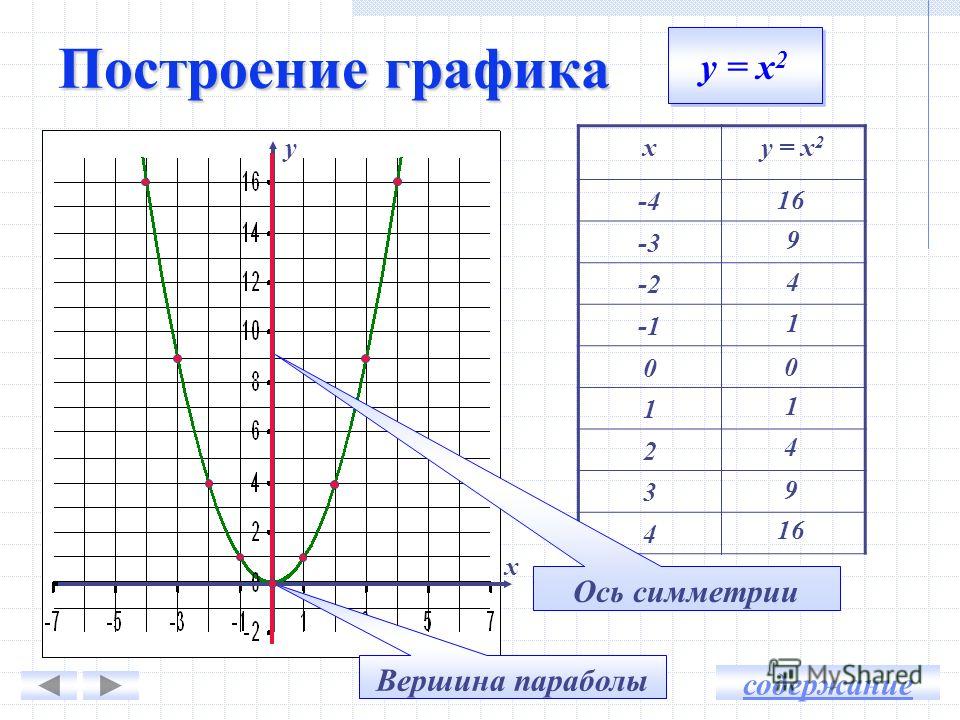 Карта Мекко
Карта МеккоЭтот тип графика, также известный как диаграмма Маримекко, может сравнивать значения, измерять состав каждого из них и отображать распределение данных по каждому из них.
Это похоже на столбчатую гистограмму, за исключением того, что ось X Mekko может отражать другое измерение ваших значений — вместо прогрессии во времени, как это часто делают гистограммы. На приведенном ниже рисунке ось X сравнивает города друг с другом.
Источник изображения
Лучшие варианты использования для этого типа диаграммы:
Вы можете использовать диаграмму Mekko, чтобы показать рост, долю рынка или анализ конкурентов.
Например, на приведенной выше диаграмме Mekko показана рыночная доля управляющих активами, сгруппированных по местонахождению и стоимости их активов. Эта диаграмма показывает, какие фирмы управляют наибольшим количеством активов в различных областях.
Также легко увидеть, какие управляющие активами являются крупнейшими и как они связаны друг с другом.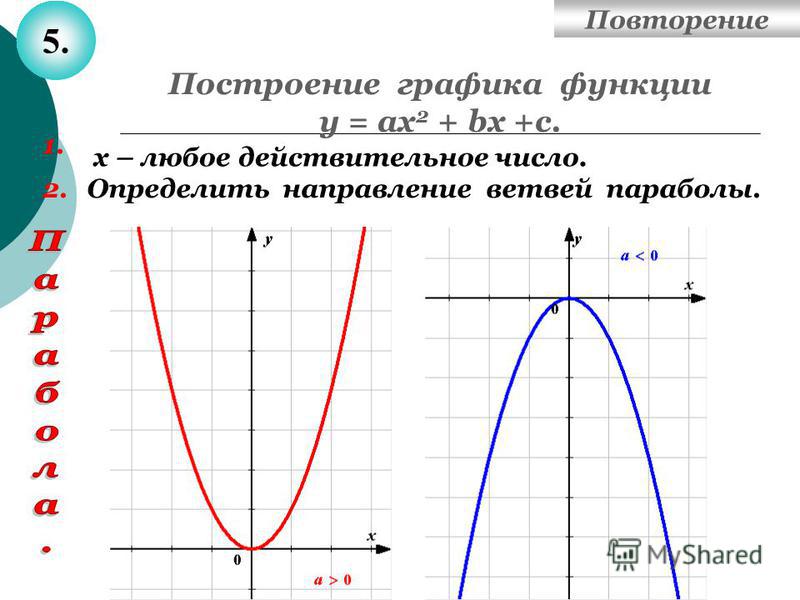
Диаграммы Mekko могут показаться более сложными, чем другие типы диаграмм и графиков. Таким образом, лучше всего использовать их в ситуациях, когда вы хотите подчеркнуть масштаб или различия между группами данных.
Другие варианты использования диаграмм Mekko включают:
- Подробные отчеты о прибылях и убытках
- Доход по брендам и регионам
- Рентабельность продукта
- Доля голоса по отраслям или нишам
Рекомендации по дизайну для диаграмм Mekko:
- Изменяйте высоту стержня , если размер порции является важной точкой сравнения.
- Не включайте слишком много составных значений в каждую полосу. Возможно, вы захотите пересмотреть свою презентацию, если у вас много данных.
- Расположите свои бары с слева направо таким образом, чтобы отображал соответствующий тренд или сообщение .

8. Круговая диаграмма
Круговая диаграмма показывает статическое число и то, как категории представляют часть целого — состав чего-либо. Круговая диаграмма представляет числа в процентах, а общая сумма всех сегментов должна равняться 100%.
Наилучшие варианты использования для этого типа диаграммы:
На изображении выше показан еще один пример распределения клиентов по ролям в компании.
Пример гистограммы показывает, что отдельных участников больше, чем любой другой роли. Но эта круговая диаграмма ясно показывает, что они составляют более 50% ролей клиентов.
Круговые диаграммы позволяют легко увидеть раздел по отношению к целому, поэтому они хороши для отображения:
- Личности клиентов по отношению ко всем клиентам
- Доход от ваших самых популярных продуктов или типов продуктов по отношению ко всем продажам продуктов
- Процент от общей прибыли от разных магазинов
Рекомендации по проектированию круговых диаграмм:
- Не иллюстрируйте слишком много категорий , чтобы обеспечить различие между срезами.

- Убедитесь, что значения среза в сумме составляют 100%.
- Заказывайте ломтики в соответствии с их размером.
9. Точечная диаграмма
Точечная диаграмма или точечная диаграмма покажет взаимосвязь между двумя различными переменными или выявит тенденции распределения. Используйте эту диаграмму, когда есть много разных точек данных, и вы хотите выделить сходство в наборе данных. Это полезно при поиске выбросов или для понимания распределения ваших данных.
Наилучшие варианты использования этих типов диаграмм:
Диаграммы рассеяния полезны в ситуациях, когда у вас слишком много данных, чтобы быстро увидеть закономерность. Лучше всего их использовать, чтобы показать отношения между двумя большими наборами данных.
В приведенном выше примере эта диаграмма показывает, как удовлетворенность клиентов соотносится со временем, которое требуется им для получения ответа.
Прекрасные примеры использования этого типа графика позволяют легко увидеть сравнение двух наборов данных.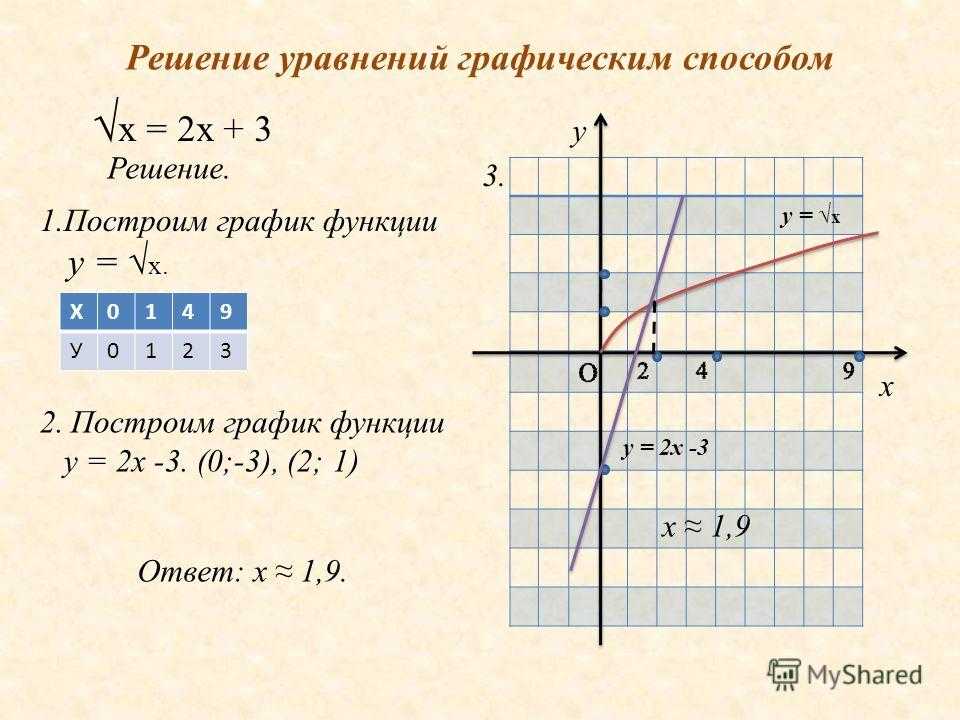 Это может включать:
Это может включать:
- Занятость и производство
- Розничные продажи и инфляция
- Количество посетителей и температура наружного воздуха
- Законы о росте продаж и налогах
Попробуйте выбрать два набора данных, которые уже имеют положительную или отрицательную связь. Тем не менее, этот тип графика также может упростить просмотр данных, выходящих за рамки обычных шаблонов.
Рекомендации по проектированию точечных диаграмм:
- Включить больше переменных , как разные размеры, чтобы включить больше данных.
- Начните ось Y с 0 для точного представления данных.
- Если вы используете линии тренда , используйте не более двух, чтобы упростить понимание вашего графика.
10. Пузырьковая диаграмма
Пузырьковая диаграмма похожа на точечную диаграмму тем, что может отображать распределение или взаимосвязь. Существует третий набор данных, показанный размером пузырька или круга.
Существует третий набор данных, показанный размером пузырька или круга.
Лучшие варианты использования для этого типа диаграммы:
В приведенном выше примере количество часов, проведенных в сети, не просто сравнивается с возрастом пользователя, как это было бы на точечной диаграмме.
Вместо этого вы также можете увидеть, как пол пользователя влияет на время, проведенное в Интернете.
Это делает пузырьковые диаграммы полезными для наблюдения за подъемом или спадом трендов с течением времени. Это также позволяет вам добавить еще одну опцию, когда вы пытаетесь понять отношения между различными сегментами или категориями.
Например, если вы хотите запустить новый продукт, эта диаграмма может помочь вам быстро увидеть стоимость, риск и ценность вашего нового продукта. Это может помочь вам сосредоточить свои усилия на новом продукте с низким уровнем риска и высокой потенциальной отдачей.
Вы также можете использовать пузырьковые диаграммы для:
- Топ продаж по месяцам и местам
- Опросы удовлетворенности клиентов
- Отслеживание производительности магазина
- Обзоры маркетинговых кампаний
Рекомендации по проектированию пузырьковых диаграмм:
- Масштабируйте пузырьки по площади , а не по диаметру.

- Убедитесь, что этикетки четкие и видимые.
- Используйте только круглые формы .
11. Водопадная диаграмма
Используйте каскадную диаграмму, чтобы показать, как начальное значение изменяется с промежуточными значениями — положительными или отрицательными — и приводит к конечному значению.
Используйте эту таблицу, чтобы определить состав числа. Примером этого может быть демонстрация того, как различные отделы влияют на общий доход компании и приводят к определенному показателю прибыли.
Источник изображения
Лучшие варианты использования для этого типа диаграммы:
Эти типы диаграмм и графиков упрощают понимание того, как внутренние и внешние факторы влияют на продукт или кампанию в целом.
В приведенном выше примере диаграмма перемещается от начального баланса в крайнем левом углу к конечному балансу в крайнем правом углу. Факторы в центре включают депозиты, переводы и банковские сборы.
Водопадная диаграмма предлагает быструю визуализацию, которая упрощает просмотр сложных процессов и результатов и устранение неполадок. Например, компании SaaS часто измеряют отток клиентов. Этот формат может помочь визуализировать изменения для новых, текущих пользователей и пользователей бесплатной пробной версии или изменения по пользовательскому сегменту.
Вы также можете попробовать каскадную диаграмму, чтобы показать:
- Изменения выручки или прибыли с течением времени
- Инвентаризация
- Проверка штатного расписания сотрудников
Рекомендации по проектированию каскадных диаграмм:
- Используйте контрастные цвета , чтобы выделить различия в наборах данных.
- Выберите теплые цвета для обозначения увеличения и холодные цвета для обозначения уменьшения.
12. Воронкообразная диаграмма
Воронкообразная диаграмма показывает последовательность шагов и степень выполнения каждого шага.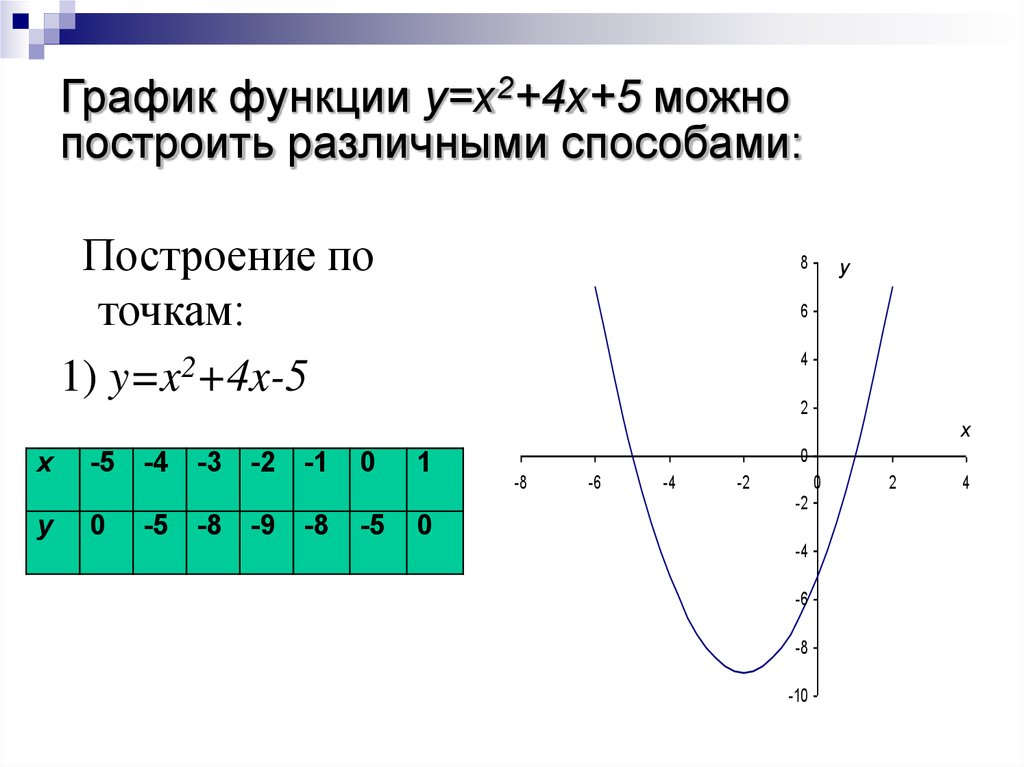 Используйте этот тип диаграммы для отслеживания процесса продаж или коэффициента конверсии по ряду страниц или шагов.
Используйте этот тип диаграммы для отслеживания процесса продаж или коэффициента конверсии по ряду страниц или шагов.
Наилучшие варианты использования этих типов диаграмм:
Наиболее распространенный вариант использования воронкообразной диаграммы — воронка маркетинга или продаж. Но есть много других способов использовать эту универсальную диаграмму.
Если у вас есть как минимум четыре этапа последовательных данных, эта диаграмма поможет вам легко увидеть, какие входные или выходные данные влияют на окончательные результаты.
Например, воронкообразная диаграмма может помочь вам увидеть, как улучшить путь покупателя или рабочий процесс корзины. Это потому, что это может помочь точно определить основные точки падения.
Другие звездные опции для этих типов графиков включают:
- Конвейер сделок
- Анализ преобразования и удержания
- Узкие места в производстве и других многоэтапных процессах
- Эффективность маркетинговой кампании
- Отслеживание конверсий веб-сайта
Рекомендации по проектированию воронкообразных диаграмм:
- Масштабируйте размер каждого раздела , чтобы точно отразить размер набора данных.

- Использовать контрастных цветов или одного цвета в градациях оттенков, от самого темного к самому светлому по мере уменьшения размера воронки.
13. Маркированный график
Маркированный график показывает прогресс в достижении цели, сравнивает его с другим показателем и предоставляет контекст в виде рейтинга или производительности.
Наилучшие варианты использования этих типов диаграмм:
В приведенном выше примере на этой маркированной диаграмме показано количество новых клиентов по отношению к заданной цели клиента. Пулевые графики отлично подходят для сравнения производительности с целями, подобными этой.
Эти типы графиков также могут помочь командам оценить возможные препятствия, поскольку вы можете анализировать данные в узком визуальном представлении.
Например, вы можете создать серию маркированных диаграмм, измеряющих производительность по сравнению с контрольными показателями, или использовать одну маркированную диаграмму для визуализации этих ключевых показателей эффективности в сравнении с их целями:
- Доход
- Прибыль
- Удовлетворенность клиентов
- Средний размер заказа
- Новые клиенты
Одновременный просмотр этих данных вместе с другими поможет командам быстро принимать решения.
Маркированные графики — один из лучших способов отображения анализа данных по годам. Вы также можете использовать маркированные диаграммы для визуализации:
- Оценок удовлетворенности клиентов
- Использование продукта
- покупательские привычки
- Использование социальных сетей по платформам
Рекомендации по проектированию маркированных диаграмм:
- Используйте контрастные цвета , чтобы выделить ход данных.
- Используйте один цвет разных оттенков для оценки прогресса.
14. Тепловая карта
Тепловая карта показывает взаимосвязь между двумя элементами и предоставляет информацию об оценках, например, от высокого к низкому или от плохого к отличному. На этой диаграмме информация о рейтинге отображается с использованием различных цветов или насыщенности.
Варианты оптимального использования тепловых карт:
В приведенном выше примере более темный оттенок зеленого показывает, с чем согласны большинство людей.
При наличии достаточного количества данных тепловые карты могут сделать точку зрения, которая может показаться субъективной, более конкретной. Это облегчает бизнесу действовать в соответствии с настроениями клиентов.
Эти типы диаграмм и графиков можно использовать по-разному. Фактически, многие технологические компании используют инструменты тепловых карт для оценки пользовательского опыта приложений, онлайн-инструментов и дизайна веб-сайтов.
Другим распространенным применением графиков тепловых карт является оценка местоположения. Если вы пытаетесь найти правильное место для своего нового магазина, эти карты могут дать вам представление о том, на что похож этот район, таким образом, что посещение не может сообщить.
Тепловые карты также могут помочь в выявлении закономерностей, поэтому они удобны для анализа быстро меняющихся тенденций, таких как конверсии рекламы. Они также могут помочь с:
- Исследование конкурентов
- Настроение клиентов
- Расширение продаж
- Влияние кампании
- Демография клиентов
Рекомендации по проектированию тепловой карты:
- Используйте базовый и четкий контур карты , чтобы не отвлекаться от данных.

- Используйте один цвет различных оттенков, чтобы показать изменения в данных.
- Избегайте использования нескольких шаблонов.
Примените эти новые типы диаграмм и графиков на практике
Теперь, когда вы выбрали лучший график или диаграмму для своего проекта, попробуйте ресурс визуализации данных, который сделает вашу точку зрения ясной и наглядной.
Визуализация данных — это только часть эффективного общения. Чтобы показать своим клиентам, сотрудникам, руководству и инвесторам, что они важны, продолжайте уделять время обучению.
Примечание редактора: этот пост был первоначально опубликован в ноябре 2020 г. и был обновлен для полноты картины.
Первоначально опубликовано 3 июня 2022 г., 7:00:00, обновлено 11 августа 2022 г.
Темы:
Визуализация данных
Не забудьте поделиться этой публикацией!
Графика — Рисование и программирование на Python
Обзор
Обучение: 15 мин.

Упражнения: 15 минутВопросы
Объективы
матплотлиб — наиболее широко используемая библиотека для построения научных графиков в Python.- Обычно используется подбиблиотека с именем
matplotlib.pyplot. - Блокнот Jupyter по умолчанию отображает графики в строке.
импортировать matplotlib.pyplot как plt
- Тогда простые графики (довольно) просто создать.
время = [0, 1, 2, 3]
позиция = [0, 100, 200, 300]
plt.plot(время, позиция)
plt.xlabel('Время (ч)')
plt.ylabel('Позиция (км)')
Показать все открытые фигуры
В нашем примере Jupyter Notebook запуск ячейки должен сгенерировать рисунок непосредственно под кодом. Рисунок также включен в документ Блокнота для дальнейшего просмотра.
Однако другие среды Python, такие как интерактивный сеанс Python, запускались с терминала. или скрипт Python, выполняемый через командную строку, требует дополнительной команды для отображения рисунка.
Поручить
matplotlibпоказать цифру:плт.показать()Эту команду также можно использовать в блокноте — например, для отображения нескольких рисунков. если несколько созданы одной ячейкой.
- Мы также можем отображать кадры данных Pandas.
- Это неявно использует
matplotlib.pyplot. - Перед построением графика мы преобразуем заголовки столбцов из строки
целочисленный, поскольку они представляют числовые значения
импортировать панды как pd
data = pd.read_csv('data/gapminder_gdp_oceania.csv', index_col='страна')
# Извлечь год из последних 4 символов имени каждого столбца
# Текущие имена столбцов структурированы как 'gdpPercap_(year)',
# поэтому мы хотим сохранить часть (год) только для ясности при построении графика ВВП по годам
# Для этого мы используем strip(), которая удаляет из строки символы, указанные в аргументе
# Этот метод работает со строками, поэтому мы вызываем str перед strip()
лет = data. columns.str.strip('gdpPercap_')
# Преобразование значений года в целые числа, сохранение результатов обратно в фрейм данных
data.columns = years.astype(int)
data.loc['Австралия'].plot()
columns.str.strip('gdpPercap_')
# Преобразование значений года в целые числа, сохранение результатов обратно в фрейм данных
data.columns = years.astype(int)
data.loc['Австралия'].plot()
Выберите и преобразуйте данные, затем нанесите их на график.
- По умолчанию
DataFrame.plotотображает строки как ось X. - Мы можем транспонировать данные для построения нескольких рядов.
данные.T.plot()
plt.ylabel('ВВП на душу населения')
Доступно множество стилей сюжета.
- Например, сделайте гистограмму, используя более причудливый стиль.
plt.style.use('ggplot')
data.T.plot (вид = 'бар')
plt.ylabel('ВВП на душу населения')
Данные также можно вывести на график, вызвав функцию
matplotlib plot напрямую.- Команда
plt.plot(x, y) - Цвет и формат маркеров также можно указать в качестве дополнительного необязательного аргумента, например,
b-— синяя линия,g —— зеленая пунктирная линия.
Получить данные по Австралии из фрейма данных
года = data.columns gdp_australia = data.loc['Австралия'] plt.plot(годы, gdp_australia, 'g--')
Может отображать множество наборов данных вместе.
# Выберите данные по двум странам.
gdp_australia = data.loc['Австралия']
gdp_nz = data.loc['Новая Зеландия']
# График с разноцветными маркерами.
plt.plot(годы, gdp_australia, 'b-', label='Австралия')
plt.plot(годы, gdp_nz, 'g-', label='Новая Зеландия')
# Создать легенду.
plt.legend(loc='верхний левый')
plt.xlabel('Год')
plt.ylabel('ВВП на душу населения ($)')
Добавление легенды
Часто при построении нескольких наборов данных на одном рисунке желательно иметь легенда, описывающая данные.
Это можно сделать в
matplotlibв два этапа:
- Укажите метку для каждого набора данных на рисунке:
plt.plot(годы, gdp_australia, label='Австралия') plt.plot(годы, gdp_nz, label='Новая Зеландия')
- Поручить
matplotlibсоздать легенду.табл.легенда()По умолчанию matplotlib попытается разместить легенду в подходящем месте. если ты скорее указать позицию, это можно сделать с помощью
loc=аргумент, например, для размещения легенду в левом верхнем углу графика указатьloc='upper left'
- Постройте точечный график, коррелирующий ВВП Австралии и Новой Зеландии
- Используйте либо
plt.scatter, либоDataFrame.plot.scatter
plt.scatter(gdp_australia, gdp_nz)
data.T.plot.scatter(x = 'Австралия', y = 'Новая Зеландия')
Минимум и Максимум
Заполните пустые поля ниже, чтобы построить график изменения минимального ВВП на душу населения с течением времени. для всех стран Европы. Измените его снова, чтобы построить график максимального ВВП на душу населения во времени для Европы.
data_europe = pd.read_csv('data/gapminder_gdp_europe.csv', index_col='country') data_europe.____.plot(label='min') data_europe.____ plt.legend(loc='лучший') plt.xticks (поворот = 90)Решение
data_europe = pd.read_csv('data/gapminder_gdp_europe.csv', index_col='country') data_europe.min().plot(label='min') data_europe.max().plot(label='max') plt.legend(loc='лучший') plt.xticks (вращение = 90)
Корреляции
Измените пример в примечаниях, чтобы создать точечную диаграмму, показывающую соотношение между минимальным и максимальным ВВП на душу населения среди стран Азии за каждый год в наборе данных. Какие отношения вы видите (если они есть)?
Решение
data_asia = pd.read_csv('data/gapminder_gdp_asia.csv', index_col='страна') data_asia.describe().T.plot(kind='scatter', x='min', y='max')Между минимальным и максимальным значениями ВВП не видно особых корреляций.
год за годом. Кажется, судьбы азиатских стран не растут и не падают одновременно.
Вы могли заметить, что изменчивость максимума намного выше, чем что из минимума. Взгляните на максимальный и максимальный индексы:
data_asia = pd.read_csv('data/gapminder_gdp_asia.csv', index_col='страна') data_asia.max().plot() печать (data_asia.idxmax()) печать (data_asia.idxmin())Решение
Похоже, что изменчивость этого значения связана с резким падением после 1972 года. Может быть, в игре какая-то геополитика? Учитывая доминирование нефтедобывающих стран, может быть, индекс нефти марки Brent будет интересным сравнением? В то время как Мьянма неизменно имеет самый низкий уровень ВВП, страна с самым высоким уровнем ВВП варьируется более заметно.
Дополнительные корреляции
Эта короткая программа создает график, показывающий корреляция между ВВП и ожидаемой продолжительностью жизни за 2007 г.
, нормализация размера маркера по населению:
data_all = pd.read_csv('data/gapminder_all.csv', index_col='страна') data_all.plot (вид = 'разброс', x = 'gdpPercap_2007', y = 'lifeExp_2007', s=data_all['pop_2007']/1e6)Используя онлайн-справку и другие ресурсы, объясните, что делает каждый аргумент для
сюжета.Решение
Хорошим местом для поиска является документация по сюжетной функции — справка (data_all.plot).
вид — Как уже было видно, это определяет тип рисуемого графика.
x и y — имя столбца или индекс, определяющий, какие данные будут размещены на осях x и y графика
s — подробности можно найти в документации plt.scatter. Одно число или одно значение для каждой точки данных. Определяет размер нанесенных точек.
Сохранение графика в файл
Если вы удовлетворены графиком, который вы видите, вы можете сохранить его в файл, возможно, включить его в публикацию.
В программе есть функция модуль matplotlib.pyplot, который выполняет это: сохранитьрис. Вызов этой функции, например. с
plt.savefig('my_figure.png')сохранит текущую фигуру в файл
my_figure.png. Формат файла будет автоматически выведено из расширения имени файла (другие форматы форматы pdf, ps, eps и svg).Обратите внимание, что функции в
pltссылаются на глобальную цифровую переменную и после того, как цифра была отображена на экране (например, сplt.show) matplotlib заставит эту переменную ссылаться на новую пустую фигуру. Поэтому обязательно позвоните по номеруplt.savefigдо отображения графика на экран, иначе можно найти файл с пустым сюжетом.При использовании фреймов данных данные часто генерируются и выводятся на экран в одну строку, и
.plt.savefigкажется невозможным подходом. Одна из возможностей сохранить фигуру в файл —
- сохранить ссылку на текущую фигуру в локальной переменной (с
plt.)gcf
- вызвать метод класса
savefigиз этой переменной.data.plot(вид='бар') fig = plt.gcf() # получить текущую цифру fig.savefig('my_figure.png')
Обеспечение доступа к вашим участкам
Всякий раз, когда вы создаете графики для статьи или презентации, вы можете сделать несколько вещей, чтобы все могли понять ваши графики.
- Всегда следите за тем, чтобы текст был достаточно большим, чтобы его можно было прочитать. Используйте параметр
fontsizeвxlabel,ylabel,title,legendиtick_paramsсlabelsize, чтобы увеличить размер текста чисел на ваших осях.- Точно так же вы должны сделать так, чтобы ваши элементы графика были легко видны. Используйте
s, чтобы увеличить размер маркеров диаграммы рассеяния, и ширину линии,, чтобы увеличить размеры линий графика.- Использование цвета (и ничего другого) для различения различных элементов графика сделает ваши графики нечитаемыми для дальтоников или тех, у кого есть черно-белый офисный принтер. Для линий 9Параметр 1612 linestyle позволяет использовать различные типы линий. Для точечных диаграмм маркер
позволяет изменить форму точек. Если вы не уверены в своих цветах, вы можете использовать Coblis или Color Oracle, чтобы смоделировать, как ваши графики будут выглядеть для людей с дальтонизмом.
Ключевые моменты
matplotlib— наиболее широко используемая библиотека для построения научных графиков в Python.График данных непосредственно из кадра данных Pandas.
Выберите и преобразуйте данные, затем нанесите их на график.
Доступны многие стили графика: дополнительные параметры см. в галерее Python Graph.
Может отображать множество наборов данных вместе.
Venngage Бесплатная программа для создания графиков | Легко создавайте потрясающие диаграммы и графики
Создавайте красивые диаграммы и графики бесплатно с помощью простых в редактировании шаблонов, интеграции данных и нашего онлайн-конструктора диаграмм. Присоединяйтесь к 40 000 компаний, которые используют Venngage для удобной визуализации сложных данных.
Доверено
Вам не нужно быть экспертом по визуализации данных, чтобы создать график для отчета или презентации.
Excel сложен и выглядит не очень хорошо. Выберите один из наших готовых шаблонов графиков и настройте его за считанные минуты.
Бесплатная программа Venngage для создания графиков избавляет от стресса при создании графиков. Он прост в использовании для новичков, но достаточно мощен для более опытных маркетологов, руководителей и других специалистов.
Необработанные данные для потрясающих графиков. Введите новые данные в простую таблицу, вставьте ссылку на Google Sheets или загрузите файл Excel, чтобы автоматически импортировать информацию с помощью Venngage.
СОСТАВЬТЕ ГРАФИК
1
Создайте учетную запись Venngage — вы можете бесплатно зарегистрироваться с помощью электронной почты или учетной записи Google или Facebook.
2
Создайте график, выбрав один из множества типов графиков: гистограммы, круговые диаграммы, линейные графики, диаграммы рассеяния, пузырьковые диаграммы и т. д.
3
Введите свои данные в нашу таблицу или импортируйте данные из электронной таблицы Google. График будет трансформироваться в соответствии с вашими данными в режиме реального времени.
4
Отредактируйте цвета с помощью нашего цветового круга. Попробуйте различные стили графиков, такие как линейные и гистограммы, одним щелчком мыши. Или оживите свои графики значками.
5
Поделитесь своим графиком с вашей командой с помощью инструмента для создания графиков Venngage. Или обновите, чтобы загрузить свой график.
СОСТАВЬТЕ ГРАФИК
Используйте готовые шаблоны для гистограмм, круговых диаграмм, диаграмм, линейных графиков, диаграмм рассеивания и других типов визуализации данных.
Введите свои данные в наш простой в использовании онлайн-конструктор графиков. Или загрузите файл Excel или вставьте ссылку в свою таблицу Google, чтобы автоматически импортировать данные.
С легкостью делитесь своими графиками в Интернете или в виде изображений, загружая их в форматах PNG, PDF, HTML для отправки по электронной почте или добавляя на слайды в PowerPoint.
Получите доступ к нашей библиотеке тысяч бесплатных иконок и иллюстраций. Добавьте фирменные цвета, шрифты и логотипы одним щелчком мыши с помощью My Brand Kit.
Есть вопрос? Мы здесь, чтобы помочь. Наша служба поддержки работает круглосуточно, поэтому ваша команда может работать как часы.
Интеграция с Pixabay и Pexels поднимает ваши плакаты на новый уровень. Получите доступ к потрясающим профессиональным фотографиям одним щелчком мыши.
СОСТАВЬТЕ ГРАФИК
Новичок в графическом дизайне? Без проблем.
От консервативного, чистого дизайна до креативного, смелого дизайна — у нас есть десятки вариантов, которые вы больше нигде не найдете. И все они легко настраиваются.
И все они легко настраиваются.
СДЕЛАТЬ ГРАФИК
СОСТАВЬТЕ ГРАФИК

СДЕЛАТЬ ГРАФИК
СОСТАВЬТЕ ГРАФИК
Нажмите кнопку «Создать график» ниже. Вы зарегистрируетесь, используя свой адрес электронной почты или учетную запись Google или Facebook. Это бесплатно и кредитная карта не требуется.
Абсолютно. Редактор Venngage автоматически сохраняет вашу работу по ходу работы. Выйдите из нашего бесплатного генератора графиков и вернитесь в любое время, чтобы внести изменения.
Вы можете бесплатно поделиться частной ссылкой с нашего онлайн-конструктора графиков. Для загрузки графика в формате PDF или PNG требуется небольшая ежемесячная плата.
СОСТАВЬТЕ ГРАФИК
Попробуйте Venngage Graph Maker уже сегодня. Выберите любой из наших мощных шаблонов графиков, чтобы начать.
СОСТАВЬТЕ ГРАФИК
СДЕЛАТЬ ГРАФИК
Pauls Online Math Notes
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Добро пожаловать в мои онлайн-уроки и заметки по математике. Целью этого сайта является предоставление полного набора бесплатных онлайновых (и загружаемых) заметок и/или учебных пособий для занятий, которые я преподаю в Университете Ламара. Я пытался написать заметки/учебники таким образом, чтобы они были доступны для всех, кто хочет изучить предмет, независимо от того, посещаете ли вы мои занятия или нет. Другими словами, они не предполагают, что у вас есть какие-либо предварительные знания, кроме стандартного набора предварительных материалов, необходимых для этого класса. Другими словами, предполагается, что вы знаете алгебру и тригонометрию до прочтения примечаний к Исчислению I, знаете исчисление I до прочтения примечаний к Исчислению II, и т. д. . Предположения о вашем прошлом, которые я сделал, даны с каждым описанием ниже.
д. . Предположения о вашем прошлом, которые я сделал, даны с каждым описанием ниже.
Я хотел бы поблагодарить Shane F, Fred J., Mike K. и David A. за все опечатки, которые они нашли и прислали мне! Я пытался проверить эти страницы и найти как можно больше опечаток, однако просто невозможно обнаружить их все, когда вы также являетесь человеком, написавшим материал. Фред, Майк и Дэвид обнаружили довольно много опечаток, которые я пропустил, и были достаточно любезны, чтобы отправить их мне. Еще раз спасибо, Фред, Майк и Дэвид!
Если вы являетесь одним из моих нынешних студентов и ищете домашнее задание, у меня есть набор ссылок, которые приведут вас на нужные страницы, перечисленные здесь.
В настоящее время я получил заметки/учебники для своего класса алгебры (математика 1314), исчисления I (математика 2413), исчисления II (математика 2414), исчисления III (математика 3435) и дифференциальных уравнений (математика 3301) онлайн. У меня также есть пара обзоров/дополнений. Среди обзоров/дополнений, которые у меня есть, есть обзор алгебры/триггеров для моих студентов, изучающих математику, учебник для начинающих по комплексным числам, набор распространенных математических ошибок и несколько советов о том, как изучать математику.
Среди обзоров/дополнений, которые у меня есть, есть обзор алгебры/триггеров для моих студентов, изучающих математику, учебник для начинающих по комплексным числам, набор распространенных математических ошибок и несколько советов о том, как изучать математику.
Я также сделал большинство страниц этого сайта доступными для скачивания. Эти загружаемые версии представлены в формате pdf. Каждая тема на этом сайте доступна для полной загрузки, а в случае очень больших документов я также разделил их на более мелкие части, которые в основном соответствуют каждой из отдельных тем. Чтобы получить загружаемую версию любой темы, перейдите к этой теме, а затем в меню Download вам будет предложено загрузить тему.
Вот полный список всех тем, которые в настоящее время доступны на этом сайте, а также краткое описание каждой из них.
Шпаргалки и таблицы
Шпаргалки по алгебре. Здесь собрано столько общих фактов, свойств, формул и функций по алгебре, сколько я только мог придумать. Также включена страница с распространенными ошибками по алгебре. Доступны две версии шпаргалки. Один полноразмерный и в настоящее время состоит из четырех страниц. Другая версия представляет собой сокращенную версию, которая содержит точно такую же информацию, как и полная версия, за исключением того, что она только что была уменьшена, поэтому две страницы печатаются на лицевой стороне, а две страницы — на обратной стороне одного листа бумаги.
Также включена страница с распространенными ошибками по алгебре. Доступны две версии шпаргалки. Один полноразмерный и в настоящее время состоит из четырех страниц. Другая версия представляет собой сокращенную версию, которая содержит точно такую же информацию, как и полная версия, за исключением того, что она только что была уменьшена, поэтому две страницы печатаются на лицевой стороне, а две страницы — на обратной стороне одного листа бумаги.
Шпаргалки по триггерам. Вот набор общих фактов, свойств и формул триггеров. Единичный круг (полностью заполненный) также включен. Доступны две версии шпаргалки. Один полноразмерный и в настоящее время состоит из четырех страниц. Другая версия представляет собой сокращенную версию, которая содержит точно такую же информацию, как и полная версия, за исключением того, что она только что была уменьшена, поэтому две страницы печатаются на лицевой стороне, а две страницы — на обратной стороне одного листа бумаги.
Шпаргалки по математическому анализу. Это серия памятных листов по математическому анализу, которые охватывают большую часть стандартного курса по математическому анализу I и несколько тем из курса по математическому анализу II. Здесь есть четыре разных шпаргалки. В одном содержится вся информация, в другом — только информация о лимитах, в третьем — только информация о производных, а в последнем — только информация об интегралах. Каждая шпаргалка поставляется в двух версиях. Один полноразмерный, а другой уменьшенный, с точно такой же информацией, что и полноразмерная версия, которая печатает две страницы на передней и / или обратной стороне каждой страницы бумаги.
Это серия памятных листов по математическому анализу, которые охватывают большую часть стандартного курса по математическому анализу I и несколько тем из курса по математическому анализу II. Здесь есть четыре разных шпаргалки. В одном содержится вся информация, в другом — только информация о лимитах, в третьем — только информация о производных, а в последнем — только информация об интегралах. Каждая шпаргалка поставляется в двух версиях. Один полноразмерный, а другой уменьшенный, с точно такой же информацией, что и полноразмерная версия, которая печатает две страницы на передней и / или обратной стороне каждой страницы бумаги.
Общие производные и интегралы. Здесь представлен набор общих производных и интегралов, которые регулярно используются в исчислении I или исчислении II класса. Также включены напоминание о нескольких методах интеграции. здесь доступны две версии шпаргалки. Один полноразмерный и в настоящее время состоит из четырех страниц. Другая версия представляет собой сокращенную версию, которая содержит точно такую же информацию, как и полная версия, за исключением того, что она только что была уменьшена, поэтому две страницы печатаются на лицевой стороне, а две страницы — на обратной стороне одного листа бумаги.
Таблица преобразований Лапласа. Вот список преобразований Лапласа для класса дифференциальных уравнений. В этой таблице приведены многие из часто используемых преобразований и формул Лапласа. В настоящее время он состоит из двух страниц, причем первая страница представляет собой преобразования Лапласа, а вторая — некоторую информацию/факты о некоторых записях.
Заметки для занятий
Во всех классах, за исключением дифференциальных уравнений, есть практические задачи (с решениями), которые вы можете использовать на практике, а также набор задач с заданиями (без решений/ответов), которые могут использовать преподаватели, если они желание.
Алгебра (математика 1314) [Примечания] [Практические задачи] [Задачи с заданиями] — Темы, включенные в этот набор заметок/учебника:
- Предварительные занятия — свойства экспонент, рациональные экспоненты, отрицательные экспоненты, радикалы, многочлены, факторинг, рациональные выражения, комплексные числа
- Решение уравнений и неравенств — Линейные уравнения, Квадратные уравнения, Заполнение квадрата, Квадратные формулы, Применение линейных и квадратных уравнений, Приведение к квадратной форме, Уравнения с радикалами, Линейные неравенства, Полиномиальные и рациональные неравенства, Абсолютные уравнения и неравенства.

- Графики и функции — графические линии, окружности и кусочные функции, определение функции, обозначение функции, композиция функций, обратные функции.
- Общие графики — параболы, эллипсы, гиперболы, абсолютное значение, квадратный корень, постоянная функция, рациональные функции, сдвиги, отражения, симметрия.
- Полиномиальные функции — деление многочленов, нули/корни многочленов, нахождение нулей многочленов, построение графиков многочленов, дроби.
- Экспоненциальные и логарифмические функции — экспоненциальные функции, логарифмические функции, решение экспоненциальных функций, решение логарифмических функций, приложения.
- Системы уравнений — метод подстановки, метод исключения, расширенная матрица, нелинейные системы.
Заметки/учебник по алгебре предполагают, что вы уже знакомы с основами алгебры. В частности, предполагается, что разделы показателей и факторинга будут для вас скорее обзором. Кроме того, предполагается, что вы знакомы с основами графических уравнений. Графики конкретных типов уравнений подробно описаны в примечаниях, однако предполагается, что вы понимаете базовую систему координат и то, как наносить точки на график.
Графики конкретных типов уравнений подробно описаны в примечаниях, однако предполагается, что вы понимаете базовую систему координат и то, как наносить точки на график.
Исчисление I (Математика 2413) [Примечания] [Практические задачи] [Задачи с заданиями] — Темы, включенные в этот набор заметок/учебника:
- Обзор алгебры и триггеров — триггерные функции и уравнения, экспоненциальные функции и уравнения, логарифмические функции и уравнения.
- Пределы — концепции, определение, вычисления, односторонние пределы, непрерывность, пределы, включающие бесконечность, правило L’Hospitals
- Производные — определение, интерпретации, производные формулы, степенное правило, правило произведения, частное правило, цепное правило, производные высшего порядка, неявное дифференцирование, логарифмическое дифференцирование, производные триггерных функций, экспоненциальные функции, логарифмические функции, обратные триггерные функции и гиперболический триггер Функции.

- Применение производных — связанные скорости, критические точки, минимальные и максимальные значения, возрастающие/убывающие функции, точки перегиба, вогнутость, оптимизация
- Интегрирование — Определение, Неопределенные интегралы, Определенные интегралы, Правило замены, Вычисление определенных интегралов, Основная теорема исчисления
- Применение интегралов — среднее значение функции, площадь между кривыми, тела вращения, работа.
Примечания/руководство по исчислению I предполагают, что у вас есть практические знания по алгебре и триггерам. Есть некоторый обзор нескольких тем по алгебре и триггерам, но по большей части предполагается, что у вас есть приличный опыт в алгебре и триггерах. Эти примечания предполагают отсутствие предварительных знаний исчисления.
Исчисление II (Math 2414) [Примечания] [Практические задачи] [Задачи с заданиями] — Темы, включенные в этот набор заметок/учебника:
- Методы интегрирования — интегрирование по частям, интегралы с триггером
Функции, Подстановки триггеров, Интегрирование с использованием дробей, Интегралы
С участием корней, Интегралов с участием квадратов, Стратегия интегрирования, Неправильный
Интегралы, сравнительный тест для несобственных интегралов и аппроксимация определенного
Интегралы.

- Применение интегралов — длина дуги, площадь поверхности, центр масс/центроид, гидростатическое давление и сила, вероятность.
- Параметрические уравнения и полярные координаты — параметрические уравнения и кривые, расчет с помощью параметрических уравнений (касательные, площади, длина дуги и площадь поверхности), полярные координаты, расчет с полярными координатами (касательные, площади, длина дуги и площадь поверхности).
- Последовательности и ряды — Последовательности, ряды, сходимость/расхождение рядов, абсолютные ряды, интегральный тест, сравнительный тест, предельный сравнительный тест, тест чередующихся рядов, тест отношений, тест корня, оценка значения ряда, степенной ряд, ряд Тейлора , Биномиальная серия
- Векторы — Основы, Величина, Единичный вектор, Арифметика, Скалярный продукт, Крест Продукт, Проекция
- Трехмерная система координат — уравнения прямых, уравнения плоскостей, квадратичные поверхности, функции многих переменных, векторные функции, пределы, производные и интегралы векторных функций, касательные векторы, нормальные векторы, бинормальные векторы, кривизна, цилиндрические координаты, сферические Координаты
Примечания/руководство по исчислению II предполагают, что вы уже знакомы с исчислением I, включая пределы, производные и интегрирование (вплоть до базовой подстановки). Также предполагается, что вы достаточно хорошо знаете Trig. Некоторые темы в значительной степени зависят от триггера и знания триггерных функций.
Также предполагается, что вы достаточно хорошо знаете Trig. Некоторые темы в значительной степени зависят от триггера и знания триггерных функций.
Исчисление III (Math 3435) [Примечания] [Практические задачи] [Задачи с заданиями] — Темы, включенные в этот набор заметок/учебника:
- Трехмерная система координат – уравнения прямых, уравнения плоскостей, квадратичные поверхности, функции многих переменных, векторные функции, пределы, производные и интегралы векторных функций, касательные векторы, векторы нормалей, бинормальные векторы, кривизна, цилиндрические координаты , Сферические координаты
- Частичные производные — Пределы, Частичные производные, Частичные высшего порядка Производные, дифференциалы, цепное правило, производные по направлению, градиент.
- Применение частных производных — касательная плоскость, нормальная линия, относительный экстремум, абсолютный экстремум, оптимизация, множители Лагранжа.

- Множественные интегралы — повторные интегралы, двойные интегралы, двойные интегралы в полярных координатах, тройные интегралы, тройные интегралы в цилиндрических координатах, тройные интегралы в сферических координатах, замена переменных, площадь поверхности.
- Линейные интегралы — векторные поля, линейные интегралы по длине дуги, линейные интегралы по отношению к x и y , линейные интегралы векторных полей, основная теорема линейных интегралов, консервативные векторные поля, потенциальные функции, теорема Грина, Завиток, Дивергенция.
- Поверхностные интегралы — параметрические поверхности, поверхностные интегралы, поверхностные интегралы векторных полей, теорема Стокса, теорема о расходимости.
Заметки/руководство по исчислению III предполагают, что у вас есть практические знания исчисления I, включая пределы, производные и интегрирование. Также предполагается, что читатель хорошо знаком с несколькими темами Calculus II, включая некоторые методы интегрирования, параметрические уравнения, векторы и знание трехмерного пространства.
Дифференциальные уравнения (Math 3301) [Примечания]
— Темы, включенные в этот набор заметок/учебника:
- Дифференциальные уравнения первого порядка — линейные уравнения, уравнения с разделителями, точные уравнения, решения равновесия, задачи моделирования.
- Дифференциальные уравнения второго порядка. Однородные и неоднородные дифференциальные уравнения второго порядка, фундаментальный набор решений, неопределенные коэффициенты, вариации параметров, механические колебания
- Преобразования Лапласа — Определение, Обратные преобразования, Ступенчатые функции, Функции Хевисайда, Дельта-функция Дирака, Решение IVP, Неоднородный IVP, Непостоянный коэффициент IVP, Интеграл свертки.
- Системы дифференциальных уравнений — матричная форма, собственные значения/собственные векторы, фазовая плоскость, неоднородные системы, преобразования Лапласа. Решения серии
- — Решения серии, Дифференциальные уравнения Эйлера.

- Дифференциальные уравнения высшего порядка — n th дифференциальные уравнения порядка, неопределенные коэффициенты, вариация параметров, 3 x 3 системы дифференциальных уравнений.
- Краевые задачи и ряды Фурье — Краевые задачи, собственные значения и собственные функции, ортогональные функции, ряды синусоид Фурье, ряды косинусов Фурье, ряды Фурье.
- Уравнения в частных производных — уравнение теплопроводности, волновое уравнение, уравнение Лапласа, разделение переменных.
Эти примечания предполагают отсутствие предварительных знаний дифференциальных уравнений. Однако требуется хорошее понимание исчисления. Это включает в себя практические знания дифференциации и интеграции.
Обзоры и дополнения
Обзор алгебры/триггеров — это обзор алгебры и триггеров
это было первоначально написано для моих студентов исчисления I. Это все еще ориентировано в основном
по отношению к студентам, изучающим исчисление, со случайными комментариями о том, как тема
будет использоваться в классе исчисления. Тем не менее, кому нужен обзор некоторых
базовой алгебры, тригонометрических, экспоненциальных функций и логарифмов следует найти
информация об использовании.
Тем не менее, кому нужен обзор некоторых
базовой алгебры, тригонометрических, экспоненциальных функций и логарифмов следует найти
информация об использовании.
Не все темы, изучаемые на занятиях по алгебре или триггерам, рассматриваются в этом обзор. В основном я освещал темы, которые имеют особое значение для студентов. на уроке исчисления. Я включил пару тем, которые не так важны на занятиях по математическому анализу, но иногда у студентов возникают проблемы с этим. По мере того, как будет время, я буду добавлять и другие разделы.
Обзор представляет собой набор задач с первым решением, содержащим подробную информацию о том, как работать с этим типом задач. Более поздние решения обычно не такие подробные, но могут содержать дополнительную/новую информацию по мере необходимости.
Учебник по комплексным числам. Это краткое введение в некоторые основные идеи, связанные с комплексными числами. Рассматриваемые темы представляют собой краткий обзор арифметики с комплексными числами, комплексного сопряжения, модуля, полярной и экспоненциальной формы, а также вычислительных мощностей и корней комплексных чисел.
Обратите внимание, что в этом учебнике предполагается, что вы, по крайней мере, видели некоторые комплексные числа до чтения. Цель этого документа — немного выйти за рамки того, что видит большинство людей, впервые знакомящихся с комплексными числами, скажем, на уроках алгебры в колледже. Кроме того, этот документ никоим образом не претендует на то, чтобы дать полное представление о комплексных числах, и я не охватываю все используемые концепции (это сам по себе целый класс).
Распространенные математические ошибки. Как и в случае с алгеброй/триггером, просмотрите это
изначально был написан для моего класса исчисления I. Однако только один из пяти
разделы, которые я дал здесь, непосредственно касаются темы исчисления.
другие четыре раздела представляют собой более общие ошибки или охватывают ошибки алгебры и триггеров.
В первых четырех разделах есть пара примеров исчисления, но в
во всех этих случаях я также пытался привести примеры, не связанные с исчислением.

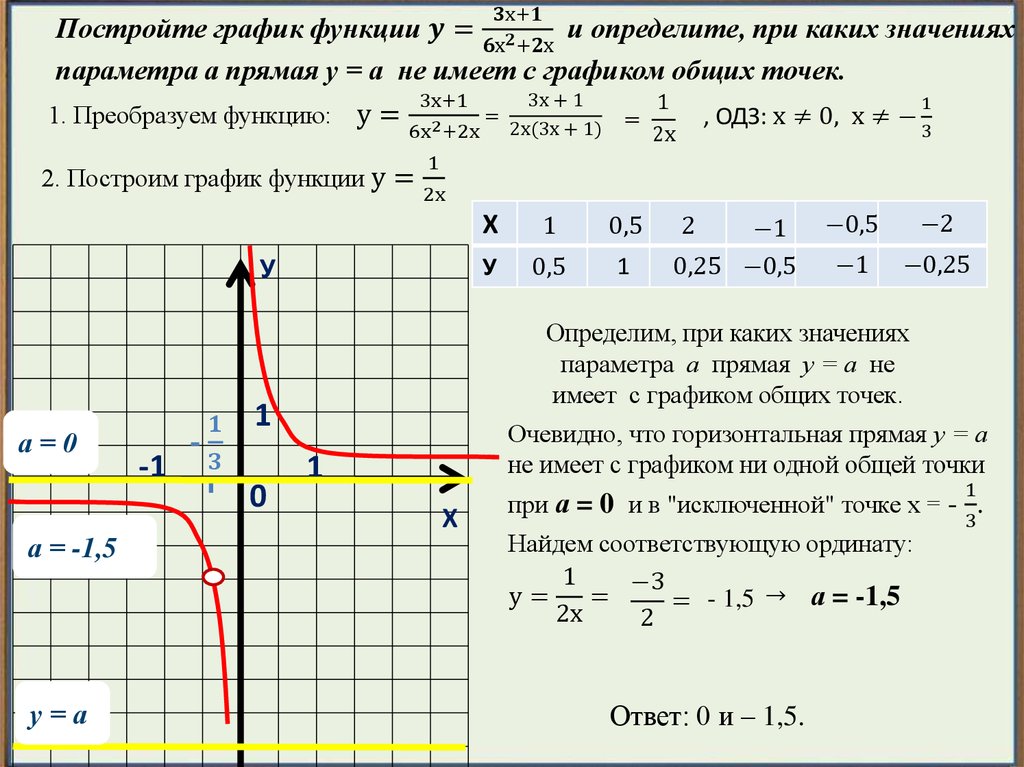
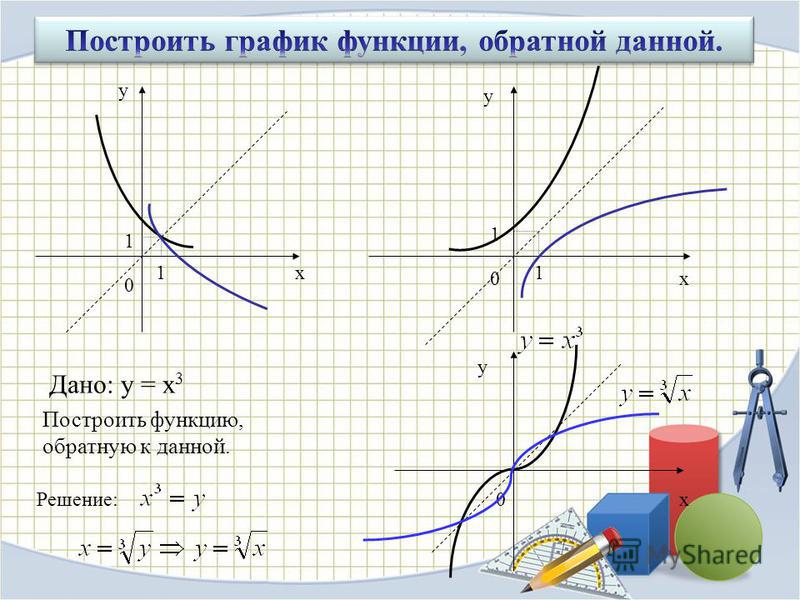
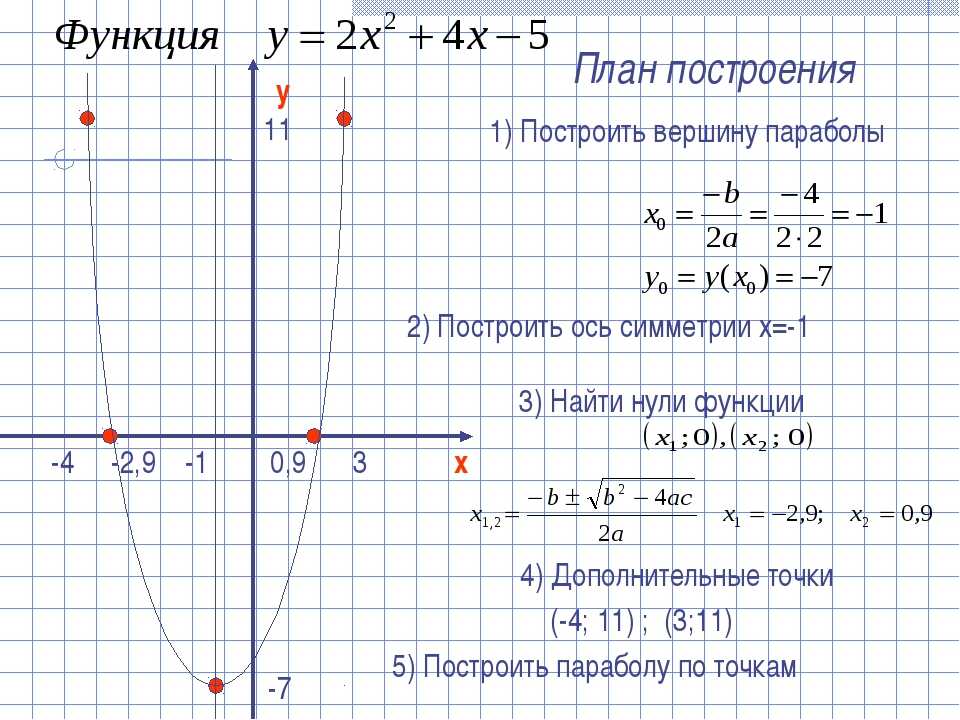
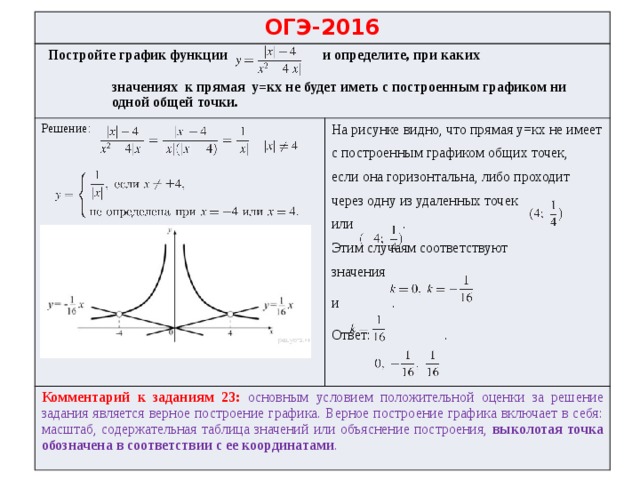
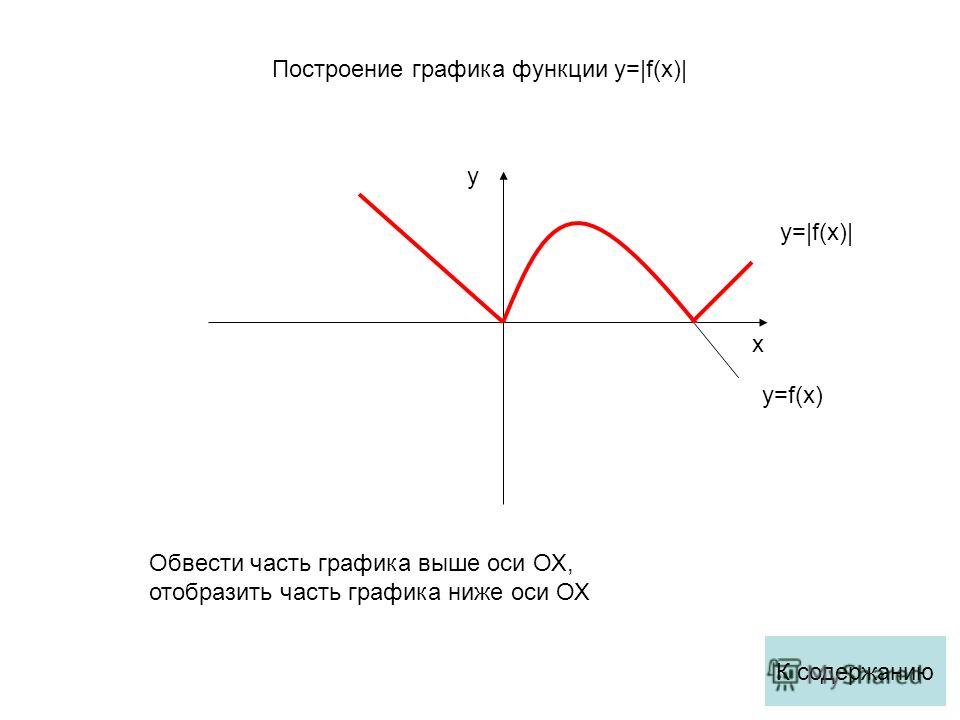 Таким образом, производная, которую можно представить как мгновенную скорость изменения \ (y \) по отношению к \ (x \), выражается как
Таким образом, производная, которую можно представить как мгновенную скорость изменения \ (y \) по отношению к \ (x \), выражается как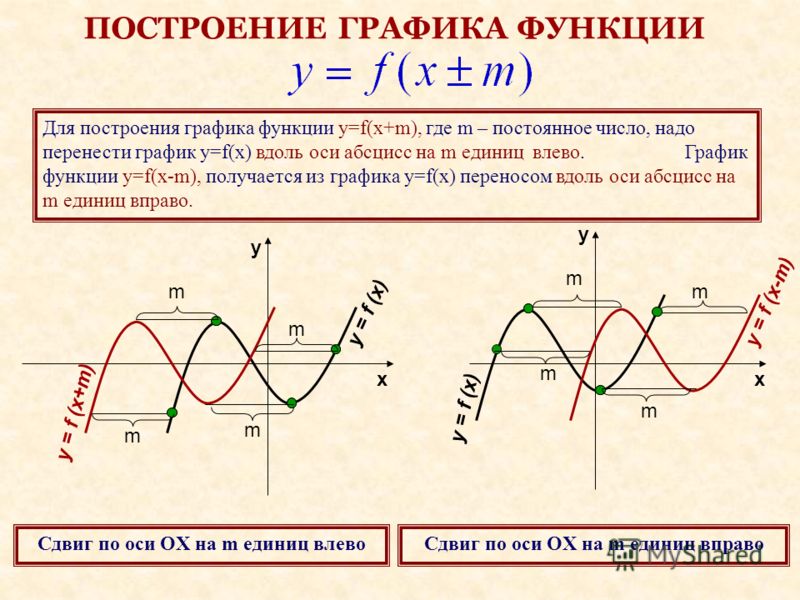 Во-первых, мы замечаем, что \ (f (x) \) увеличивается по всей своей области, а это означает, что наклон его касательных во всех точках положительный. Следовательно, мы ожидаем \ (f ‘(x)> 0 \) для всех значений x в его области определения. Кроме того, по мере увеличения \ (x \) наклон касательных к \ (f (x) \) уменьшается, и мы ожидаем увидеть соответствующее уменьшение \ (f ‘(x) \).2−2x, \; f ‘(x) = 2x − 2 \). Графики этих функций показаны на рисунке \ (\ PageIndex {3} \). Обратите внимание, что \ (f (x) \) убывает при \ (x 1 \), \ (f (x) \) увеличивается и \ (f ‘(x)> 0 \). Кроме того, \ (f (x) \) имеет горизонтальную касательную в \ (x = 1 \) и \ (f ‘(1) = 0 \).
Во-первых, мы замечаем, что \ (f (x) \) увеличивается по всей своей области, а это означает, что наклон его касательных во всех точках положительный. Следовательно, мы ожидаем \ (f ‘(x)> 0 \) для всех значений x в его области определения. Кроме того, по мере увеличения \ (x \) наклон касательных к \ (f (x) \) уменьшается, и мы ожидаем увидеть соответствующее уменьшение \ (f ‘(x) \).2−2x, \; f ‘(x) = 2x − 2 \). Графики этих функций показаны на рисунке \ (\ PageIndex {3} \). Обратите внимание, что \ (f (x) \) убывает при \ (x 1 \), \ (f (x) \) увеличивается и \ (f ‘(x)> 0 \). Кроме того, \ (f (x) \) имеет горизонтальную касательную в \ (x = 1 \) и \ (f ‘(1) = 0 \). 2−4 \). На каком интервале находится график \ (f ‘(x) \) над осью \ (x \)?
2−4 \). На каком интервале находится график \ (f ‘(x) \) над осью \ (x \)?
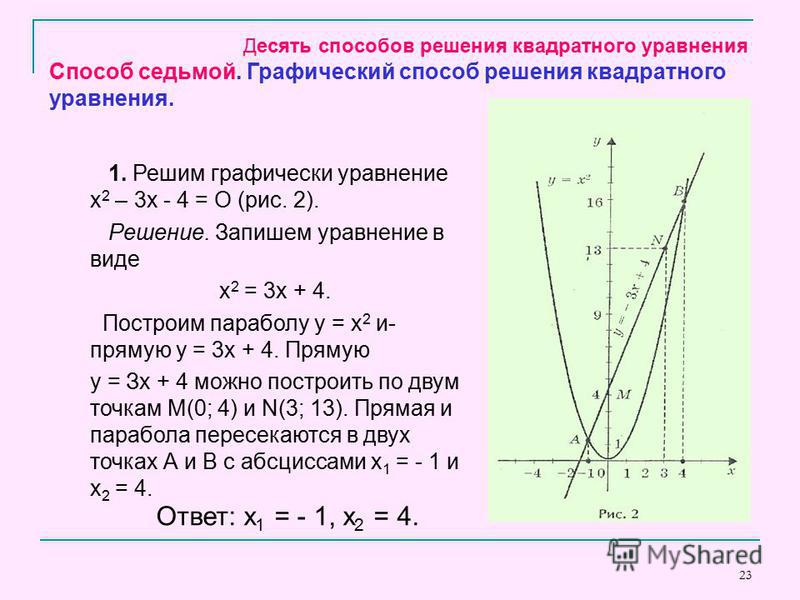 \ end {align *} \)
\ end {align *} \)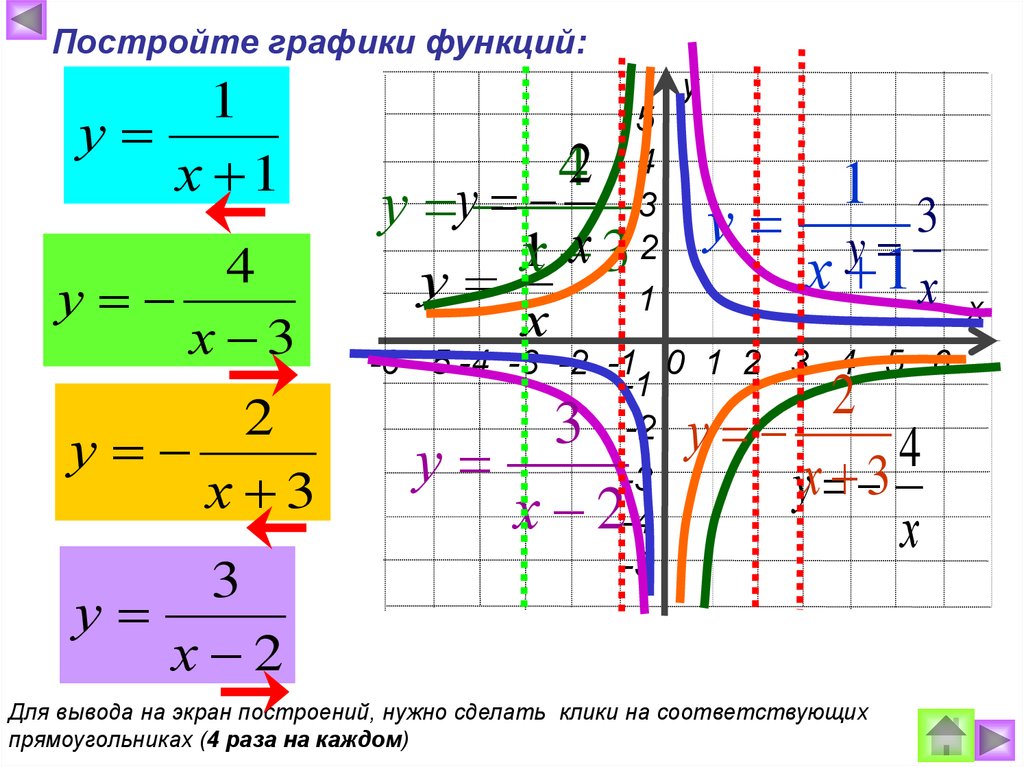
 -} f (x) = f (−10) \). 2 + bx + (10b − 5) −5} {x + 10} & & \ text {Substitute} c = 10b − 5.2, & & \ text {if} x≥3 \ end {cases} \) как непрерывные, так и дифференцируемые в \ (3 \).
-} f (x) = f (−10) \). 2 + bx + (10b − 5) −5} {x + 10} & & \ text {Substitute} c = 10b − 5.2, & & \ text {if} x≥3 \ end {cases} \) как непрерывные, так и дифференцируемые в \ (3 \).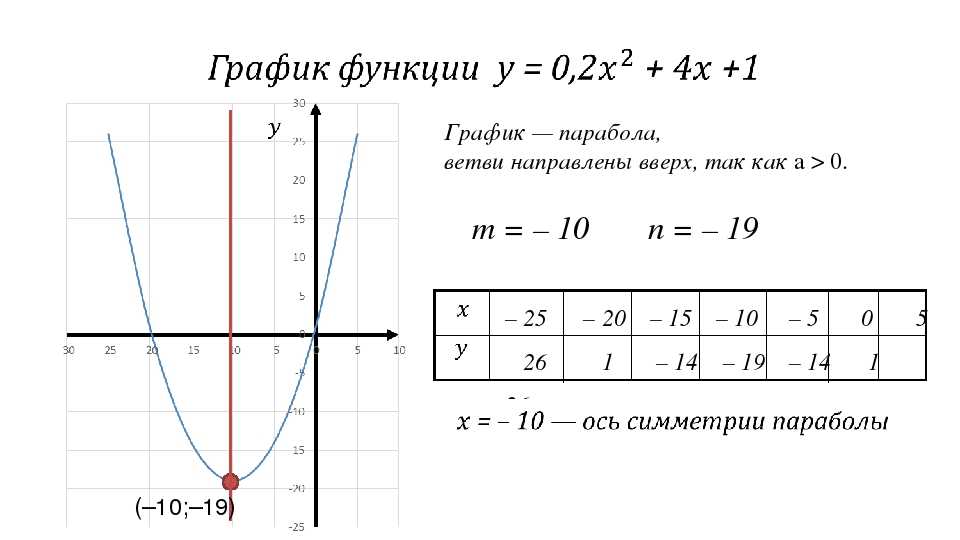 n}.2−3h} {h} \)
n}.2−3h} {h} \)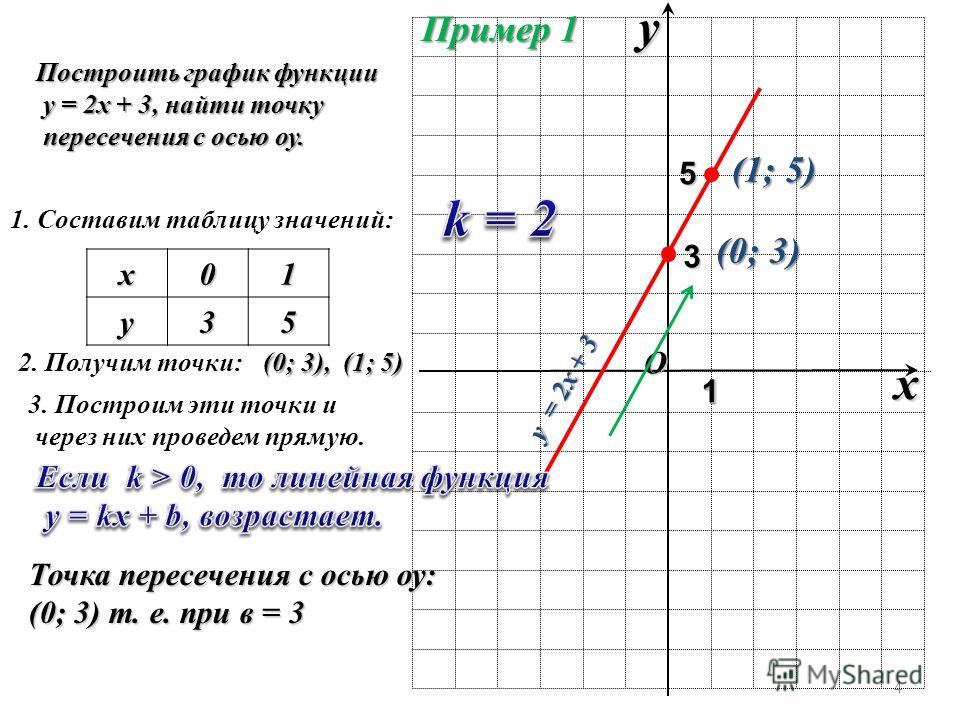 Типичные задачи исчисления включают получение функции или графика функции и поиск информации о точках перегиба, наклоне, вогнутости или существовании производной.
Типичные задачи исчисления включают получение функции или графика функции и поиск информации о точках перегиба, наклоне, вогнутости или существовании производной.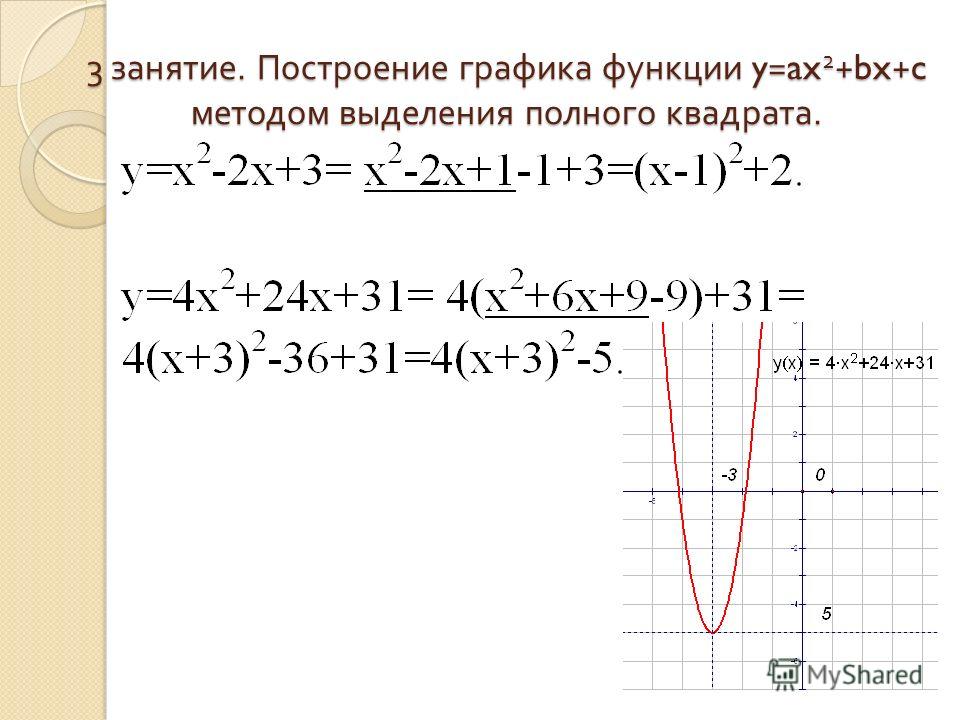 Обратите внимание, у нас есть две вертикальные асимптоты, которые не соединяются.
Обратите внимание, у нас есть две вертикальные асимптоты, которые не соединяются. Сразу должно быть видно, что это какая-то тригонометрическая функция. Мы знаем, что наклон функции равен 0 в нескольких точках; поэтому график производной в какой-то момент должен проходить через ось абсцисс. Также, глядя на график, мы должны увидеть, что это происходит где-то между -2,5 и 0, а также между 0 и 2,5. Одного этого достаточно, чтобы увидеть, что последний график является правильным ответом.
Сразу должно быть видно, что это какая-то тригонометрическая функция. Мы знаем, что наклон функции равен 0 в нескольких точках; поэтому график производной в какой-то момент должен проходить через ось абсцисс. Также, глядя на график, мы должны увидеть, что это происходит где-то между -2,5 и 0, а также между 0 и 2,5. Одного этого достаточно, чтобы увидеть, что последний график является правильным ответом.
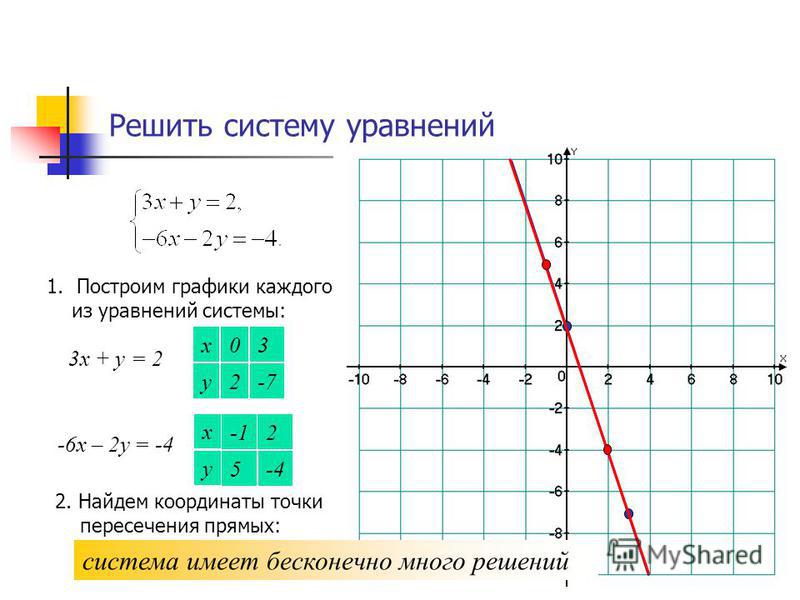 Это кроссплатформенная библиотека для создания 2D-графиков из данных в массивах.
Это кроссплатформенная библиотека для создания 2D-графиков из данных в массивах.
 pyplot as plt
pyplot as plt 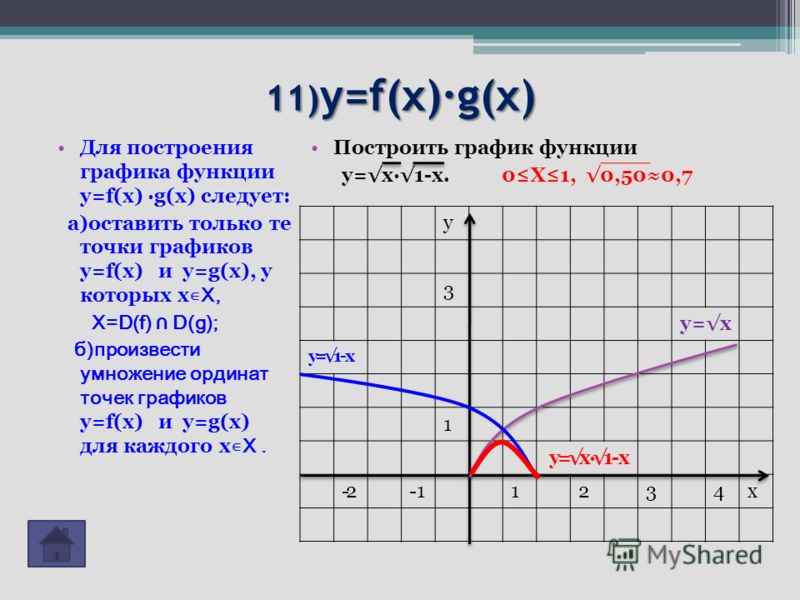 легенда (loc
легенда (loc 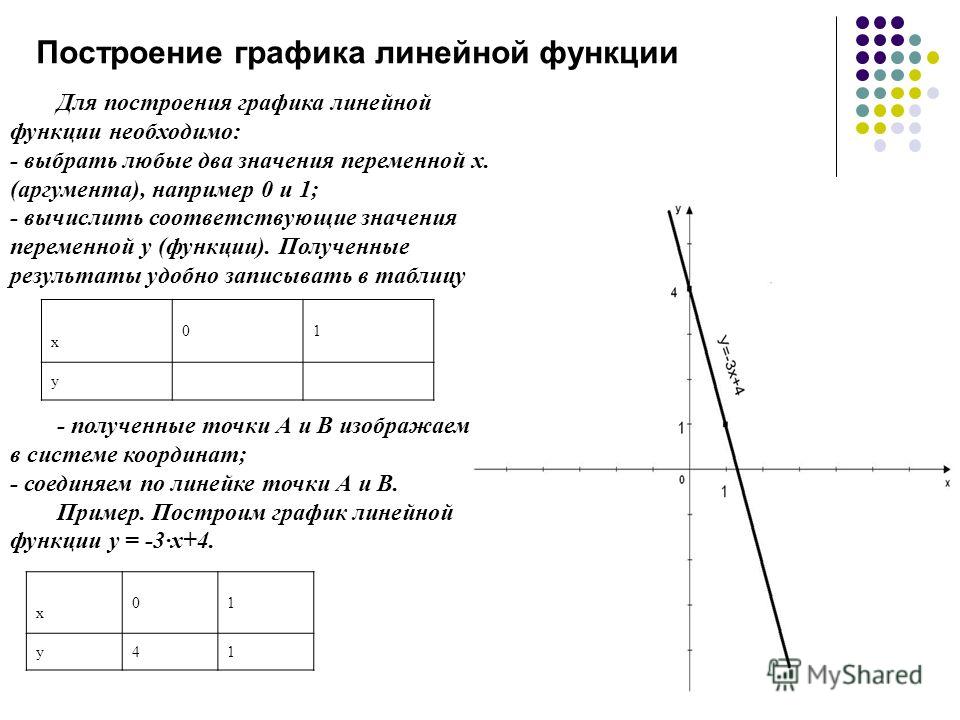 linspace (
linspace (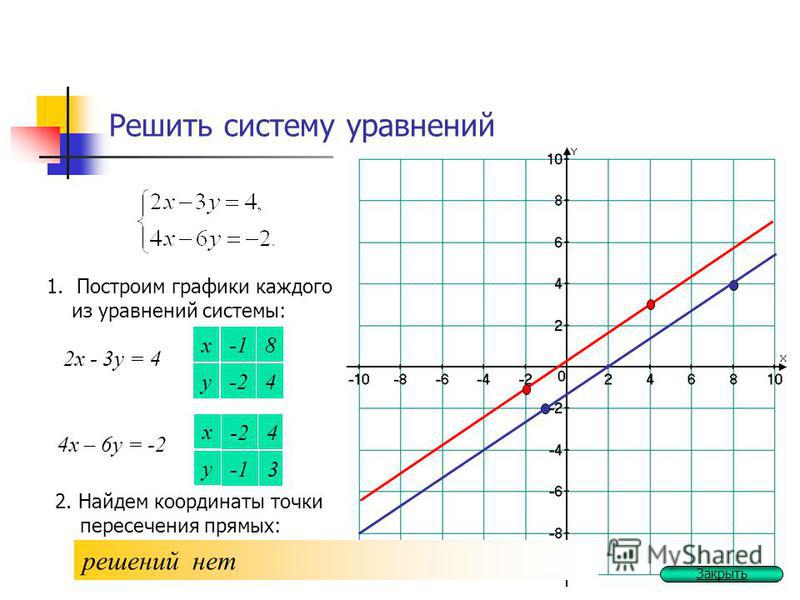 Функция text () , которая входит в библиотеку matplotlib, отображает текст на графике и принимает аргумент в виде координат (x, y). Мы также сделаем некоторое форматирование.
Функция text () , которая входит в библиотеку matplotlib, отображает текст на графике и принимает аргумент в виде координат (x, y). Мы также сделаем некоторое форматирование.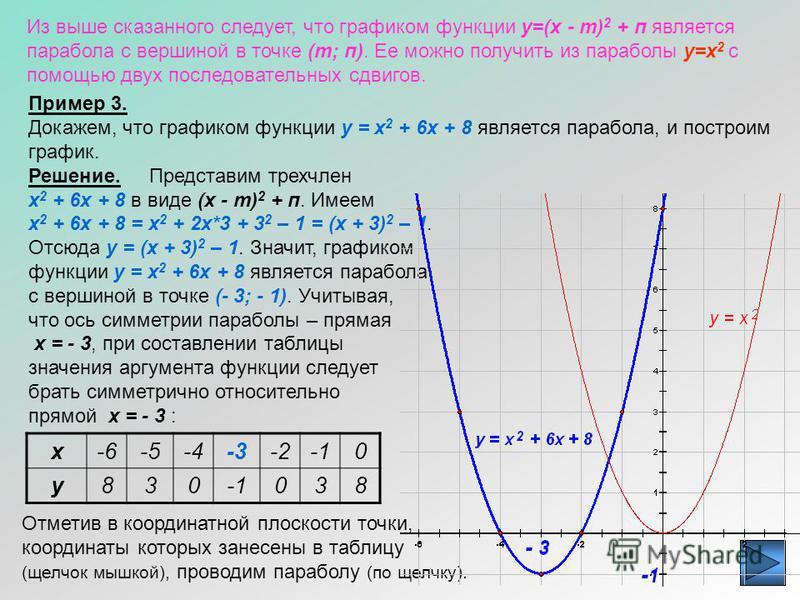 plot (y, функция (y), цвет
plot (y, функция (y), цвет 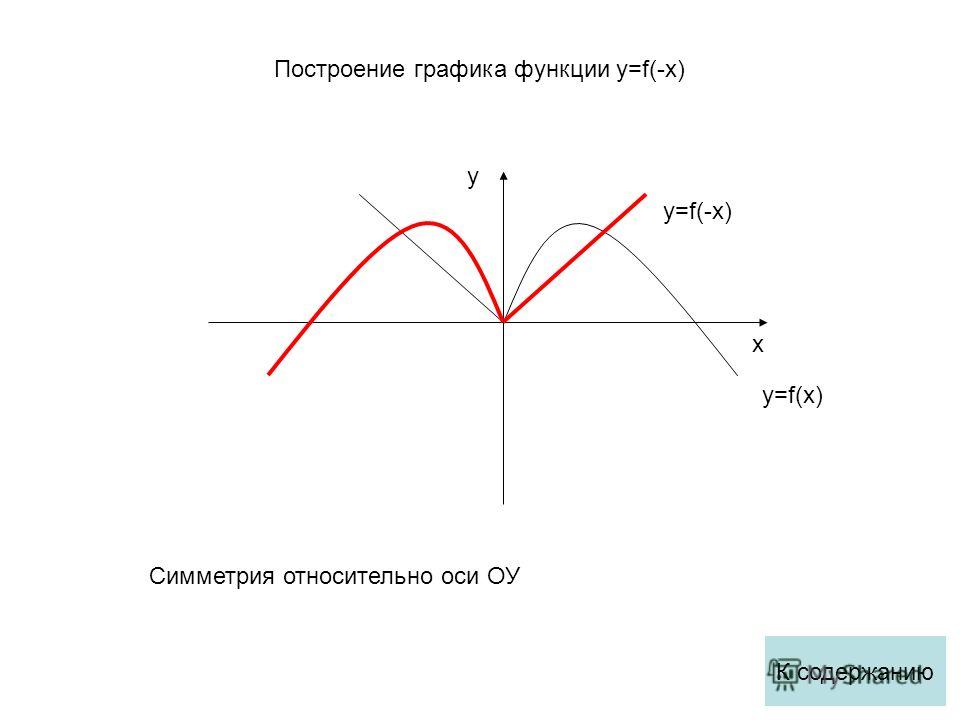 2 + x + 1 $ '
2 + x + 1 $ '
 В этом разделе мы также увидим, как вторая производная предоставляет информацию о форме графика, описывая, изгибается ли график функции вверх или вниз.
В этом разделе мы также увидим, как вторая производная предоставляет информацию о форме графика, описывая, изгибается ли график функции вверх или вниз. c. Если ff — непрерывная функция на интервале II, содержащем cc и дифференцируемая по I, I, за исключением, возможно, точек c, c, единственный способ ff может переключиться с увеличения на уменьшение (или наоборот) в точке cc — это если f′f ′ меняет знак, когда xx увеличивается до c.c. Если ff дифференцируема в c, c, это единственный способ, которым f′.f ′. может менять знак при увеличении xx на cc, если f ′ (c) = 0. f ′ (c) = 0. Следовательно, для функции ff, которая непрерывна на интервале II, содержащем cc и дифференцируема по I, I, за исключением, возможно, точек c, c, единственный способ ff может переключиться с увеличения на уменьшение (или наоборот) — это если f ′ (c ) = 0f ′ (c) = 0 или f ′ (c) f ′ (c) не определено. Следовательно, чтобы найти локальные экстремумы для функции f, f, мы ищем точки cc в области определения ff такие, что f ′ (c) = 0f ′ (c) = 0 или f ′ (c) f ′ (c) равно неопределенный.Напомним, что такие точки называются критическими точками ф.ф.
c. Если ff — непрерывная функция на интервале II, содержащем cc и дифференцируемая по I, I, за исключением, возможно, точек c, c, единственный способ ff может переключиться с увеличения на уменьшение (или наоборот) в точке cc — это если f′f ′ меняет знак, когда xx увеличивается до c.c. Если ff дифференцируема в c, c, это единственный способ, которым f′.f ′. может менять знак при увеличении xx на cc, если f ′ (c) = 0. f ′ (c) = 0. Следовательно, для функции ff, которая непрерывна на интервале II, содержащем cc и дифференцируема по I, I, за исключением, возможно, точек c, c, единственный способ ff может переключиться с увеличения на уменьшение (или наоборот) — это если f ′ (c ) = 0f ′ (c) = 0 или f ′ (c) f ′ (c) не определено. Следовательно, чтобы найти локальные экстремумы для функции f, f, мы ищем точки cc в области определения ff такие, что f ′ (c) = 0f ′ (c) = 0 или f ′ (c) f ′ (c) равно неопределенный.Напомним, что такие точки называются критическими точками ф.ф.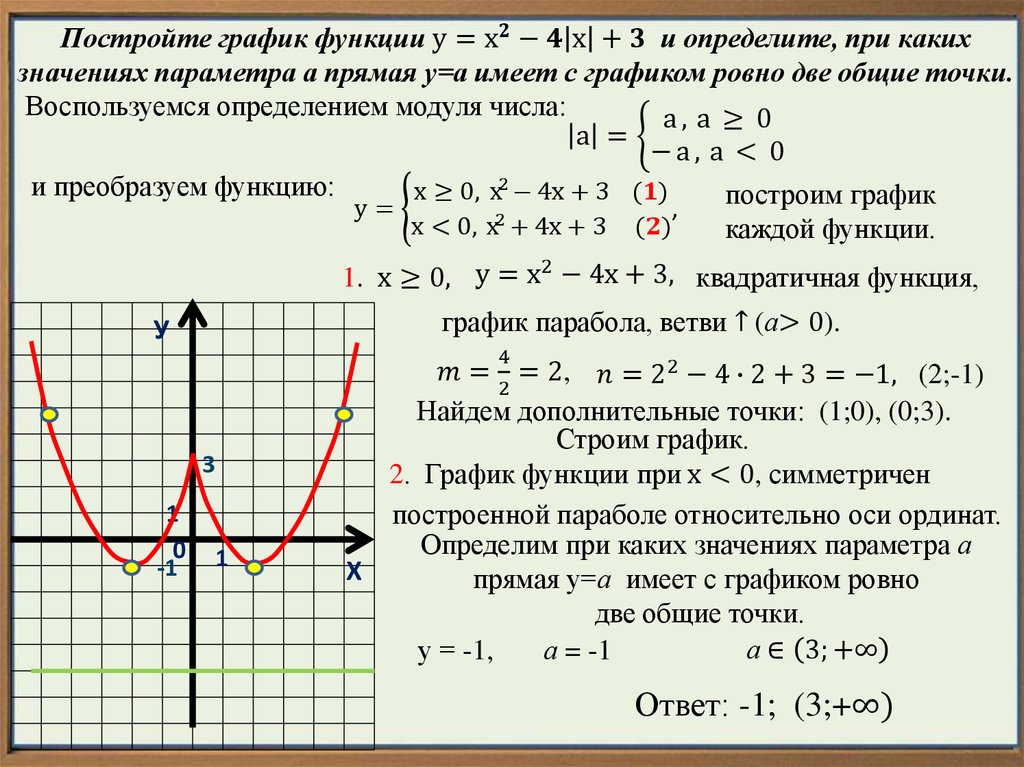 Критические точки являются кандидатами только в локальные экстремумы. На рис. 4.31 мы показываем, что если непрерывная функция ff имеет локальный экстремум, он должен возникать в критической точке, но функция может не иметь локального экстремума в критической точке. Мы показываем, что если ff имеет локальный экстремум в критической точке, то знак f′f ′ меняется по мере увеличения xx через эту точку.
Критические точки являются кандидатами только в локальные экстремумы. На рис. 4.31 мы показываем, что если непрерывная функция ff имеет локальный экстремум, он должен возникать в критической точке, но функция может не иметь локального экстремума в критической точке. Мы показываем, что если ff имеет локальный экстремум в критической точке, то знак f′f ′ меняется по мере увеличения xx через эту точку.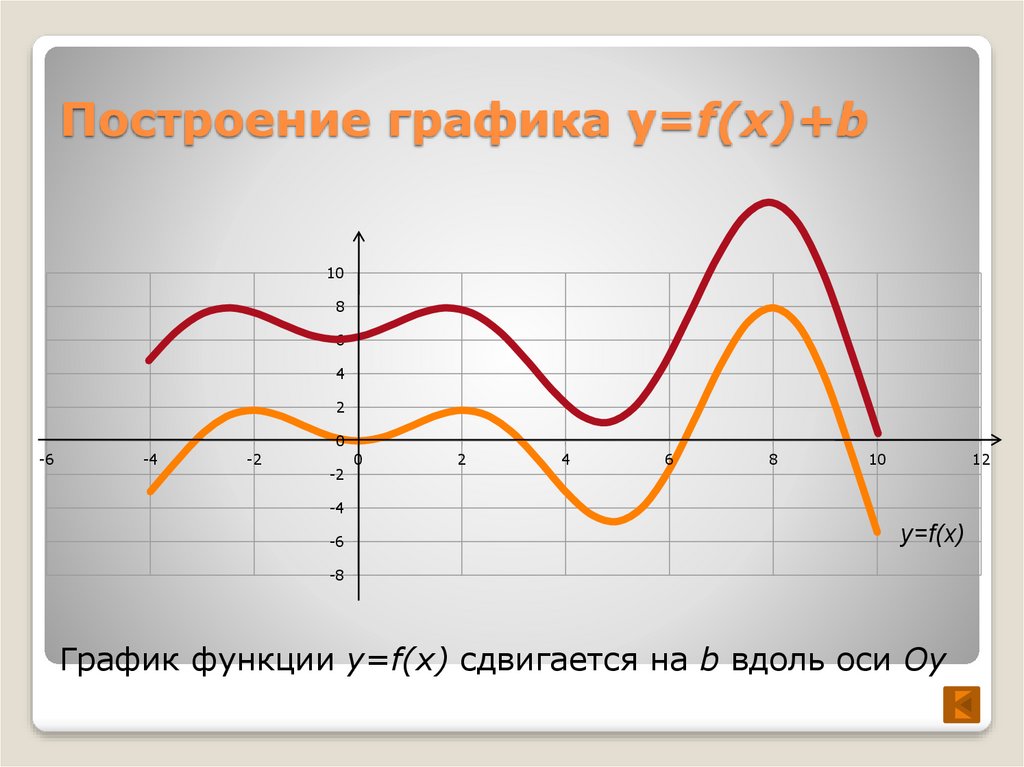 c.
c.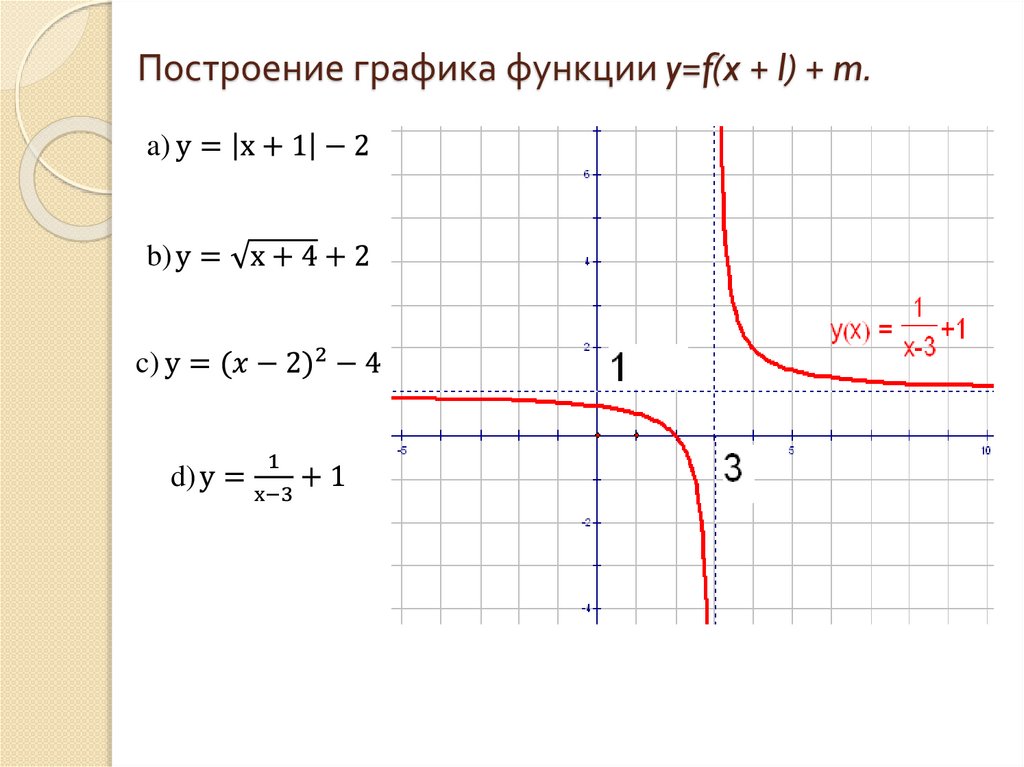
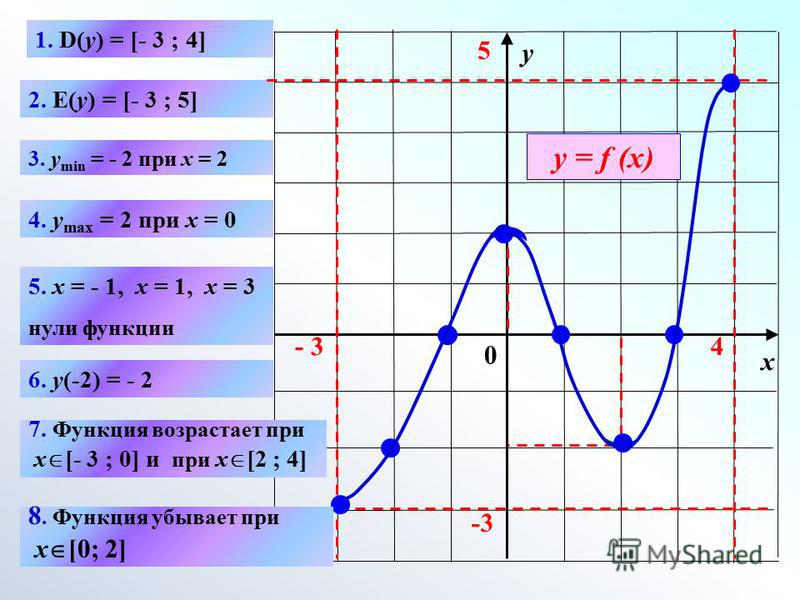
 Например, давайте выберем x = −2, x = 0 и x = 4x = −2, x = 0 и x = 4 в качестве контрольных точек.
Например, давайте выберем x = −2, x = 0 и x = 4x = −2, x = 0 и x = 4 в качестве контрольных точек.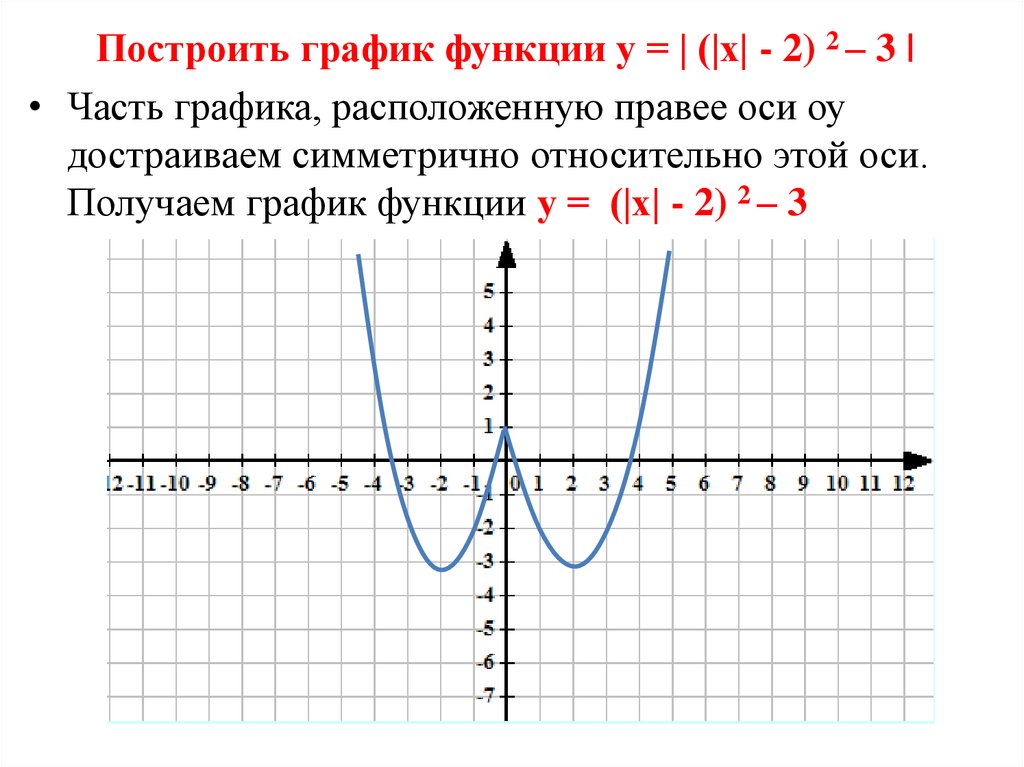
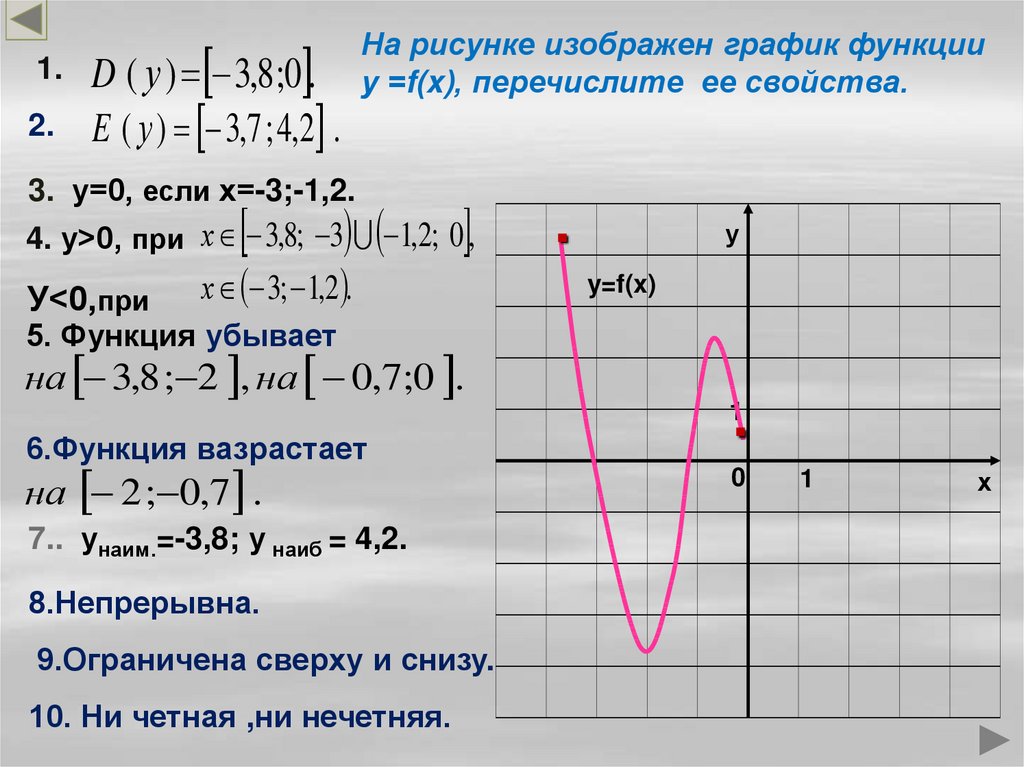 f (x) = 5×1 / 3 − x5 / 3. Используйте графическую утилиту, чтобы подтвердить свои результаты.
f (x) = 5×1 / 3 − x5 / 3. Используйте графическую утилиту, чтобы подтвердить свои результаты.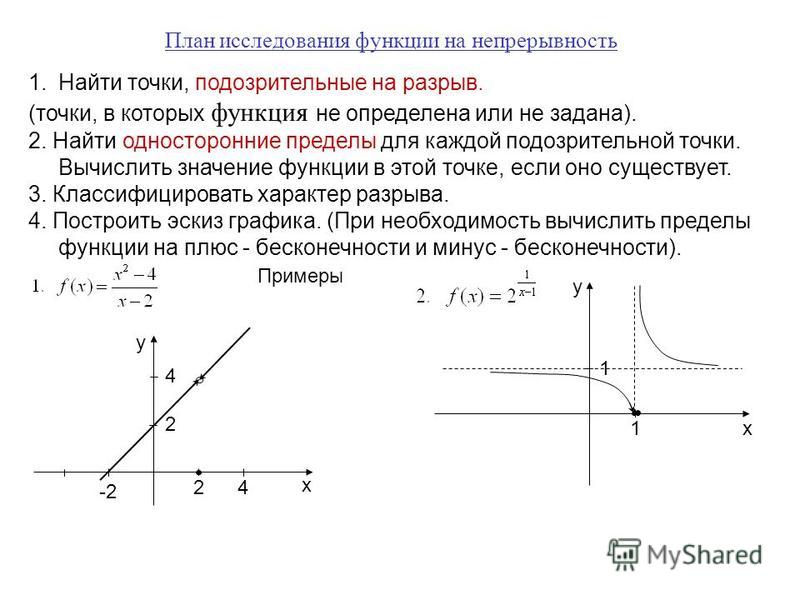
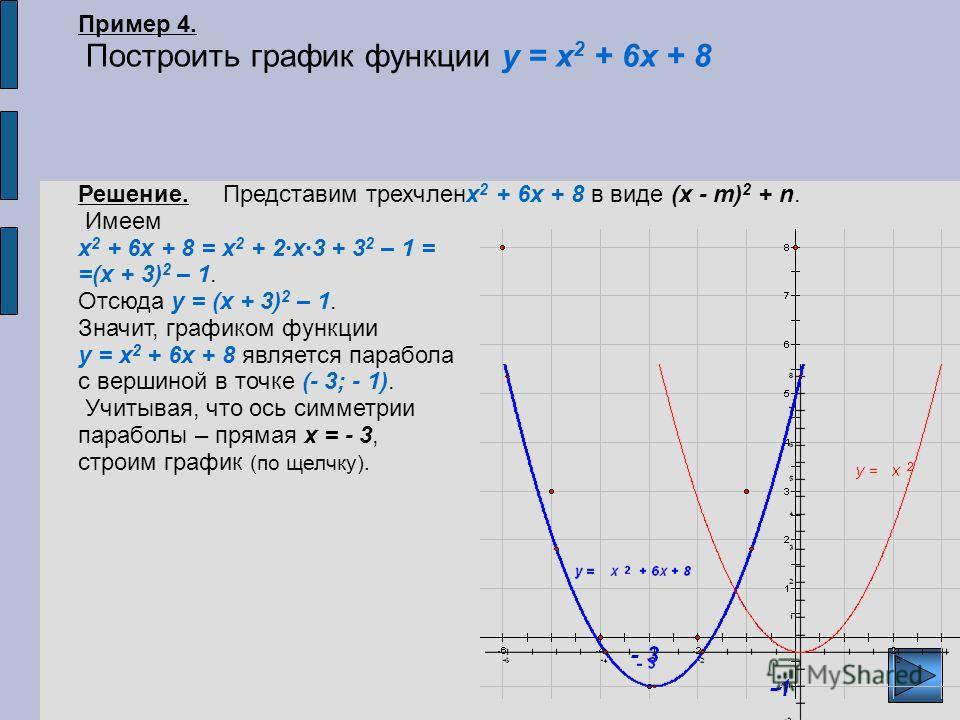
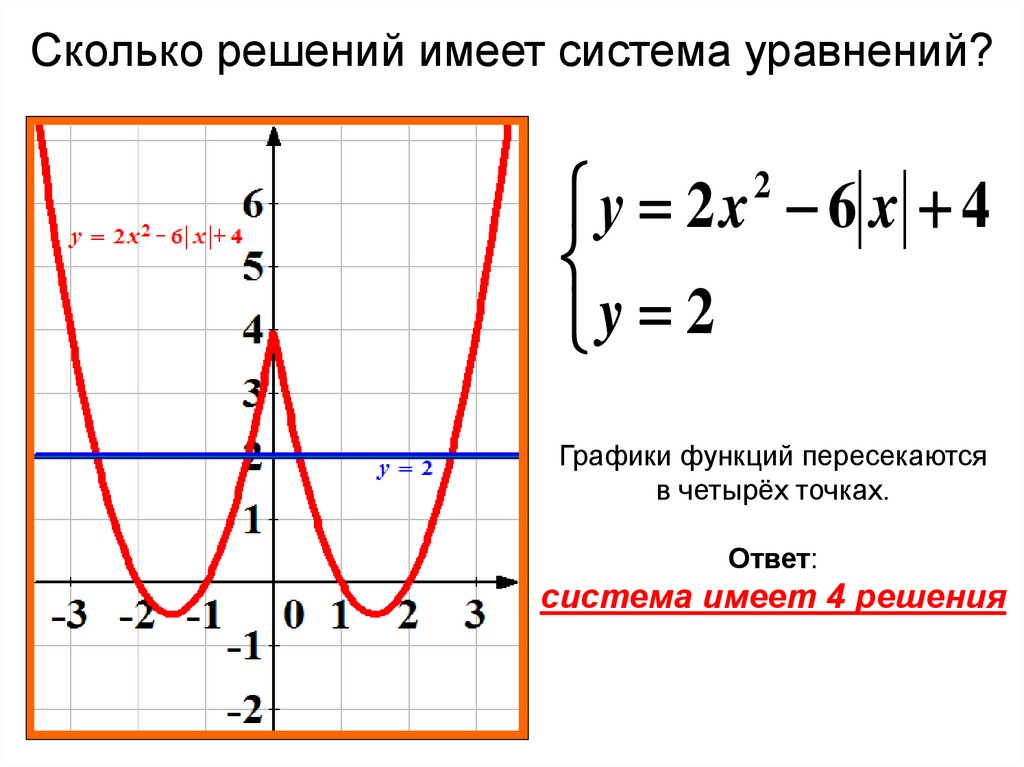 x = 1. Аналитические результаты согласуются со следующим графиком.
x = 1. Аналитические результаты согласуются со следующим графиком.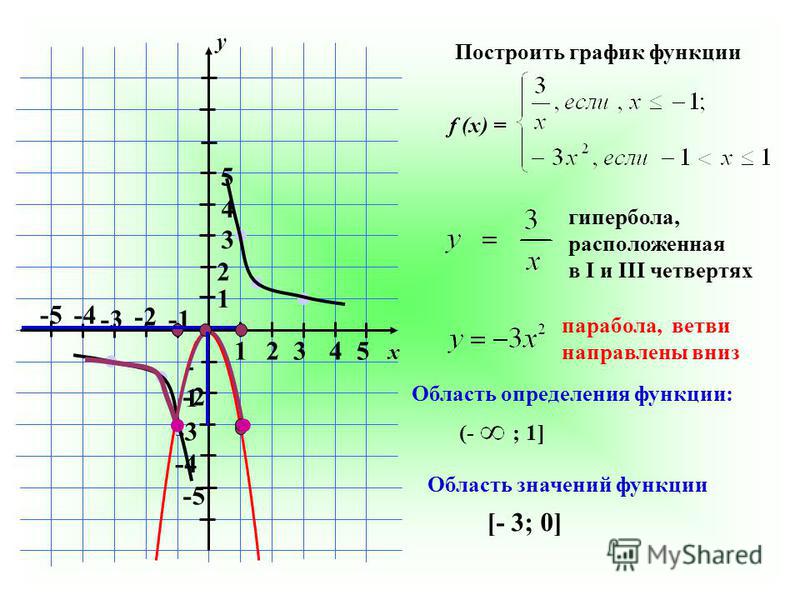 По мере увеличения xx наклон касательной уменьшается. Поскольку производная убывает с увеличением xx, f′f ′ — убывающая функция. Мы говорим, что эта функция ff вогнута вниз.
По мере увеличения xx наклон касательной уменьшается. Поскольку производная убывает с увеличением xx, f′f ′ — убывающая функция. Мы говорим, что эта функция ff вогнута вниз. f ″ (x)> 0. Точно так же функция ff вогнута вниз, если f′f ′ убывает. Мы знаем, что дифференцируемая функция f′f ′ убывает, если ее производная f ″ (x)
f ″ (x)> 0. Точно так же функция ff вогнута вниз, если f′f ′ убывает. Мы знаем, что дифференцируемая функция f′f ′ убывает, если ее производная f ″ (x) Если f ″ f ″ меняет знак при прохождении через точку x, x, то ff меняет вогнутость. Важно помнить, что функция ff не может изменять вогнутость в точке xx, даже если f ″ (x) = 0f ″ (x) = 0 или f ″ (x) f ″ (x) не определено.Если, однако, ff действительно изменяет вогнутость в точке aa и ff непрерывен в a, a, мы говорим, что точка (a, f (a)) (a, f (a)) является точкой перегиба f.f.
Если f ″ f ″ меняет знак при прохождении через точку x, x, то ff меняет вогнутость. Важно помнить, что функция ff не может изменять вогнутость в точке xx, даже если f ″ (x) = 0f ″ (x) = 0 или f ″ (x) f ″ (x) не определено.Если, однако, ff действительно изменяет вогнутость в точке aa и ff непрерывен в a, a, мы говорим, что точка (a, f (a)) (a, f (a)) является точкой перегиба f.f.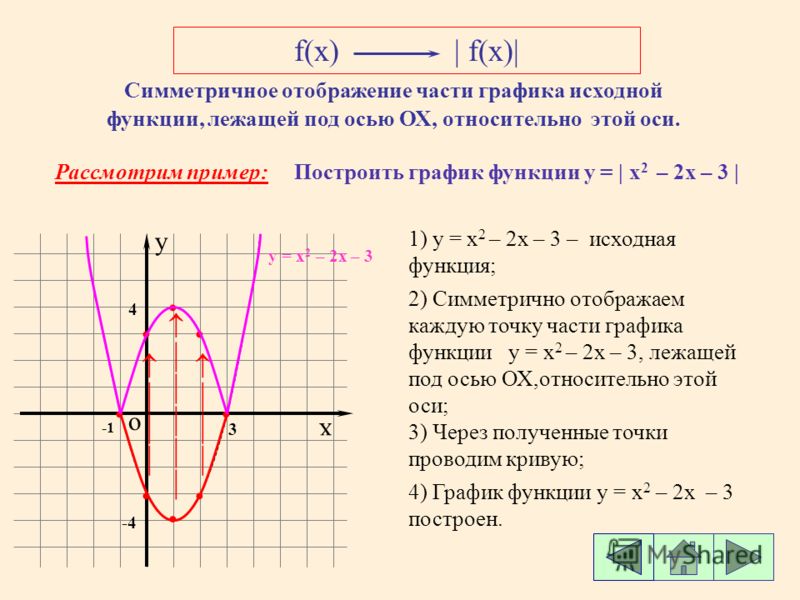 f. Используйте графическую утилиту, чтобы подтвердить свои результаты.
f. Используйте графическую утилиту, чтобы подтвердить свои результаты.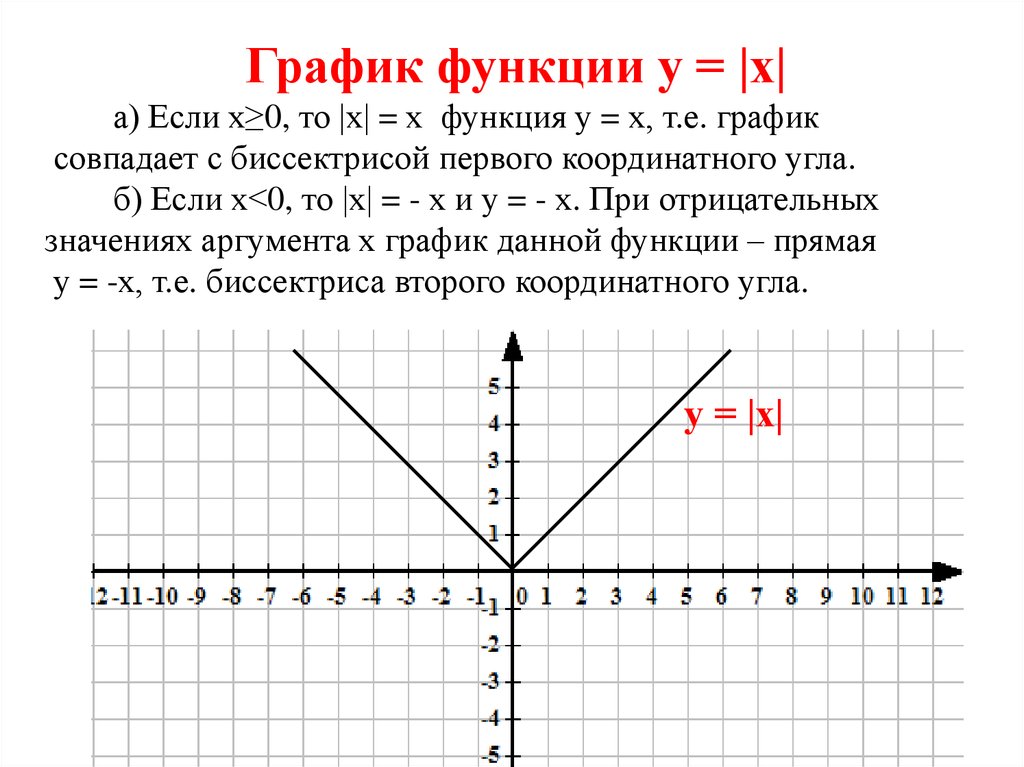
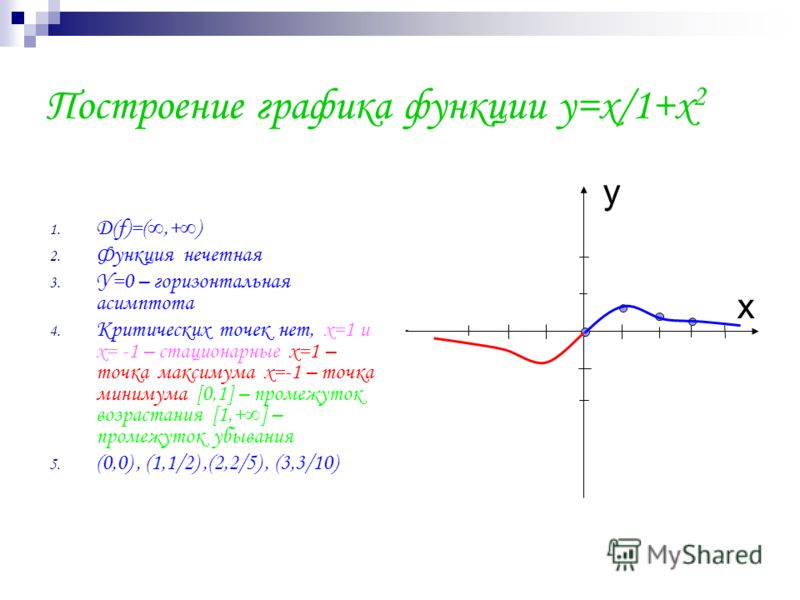 В любой момент школьник может самостоятельно проверить себя, открыть подробные пояснения, чтобы разобраться в трудном материале. Теперь ему можно не переживать, если он пропустил занятия, был невнимательным на уроке при объяснении новой темы.
В любой момент школьник может самостоятельно проверить себя, открыть подробные пояснения, чтобы разобраться в трудном материале. Теперь ему можно не переживать, если он пропустил занятия, был невнимательным на уроке при объяснении новой темы.
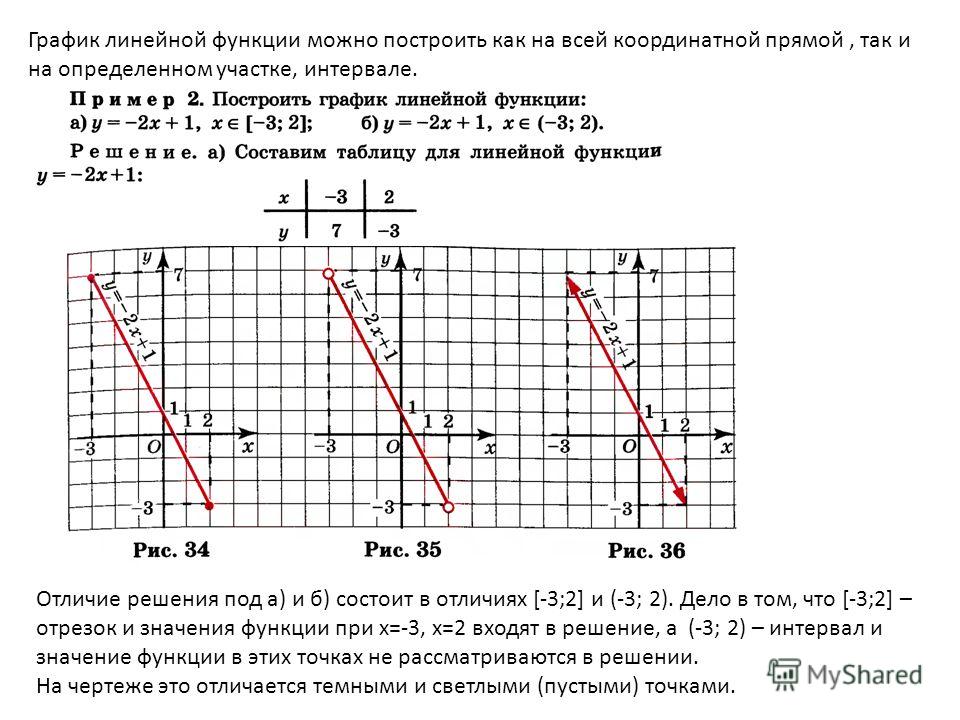 В профиле будет видно сколько дней еще действует платная подписка.
В профиле будет видно сколько дней еще действует платная подписка.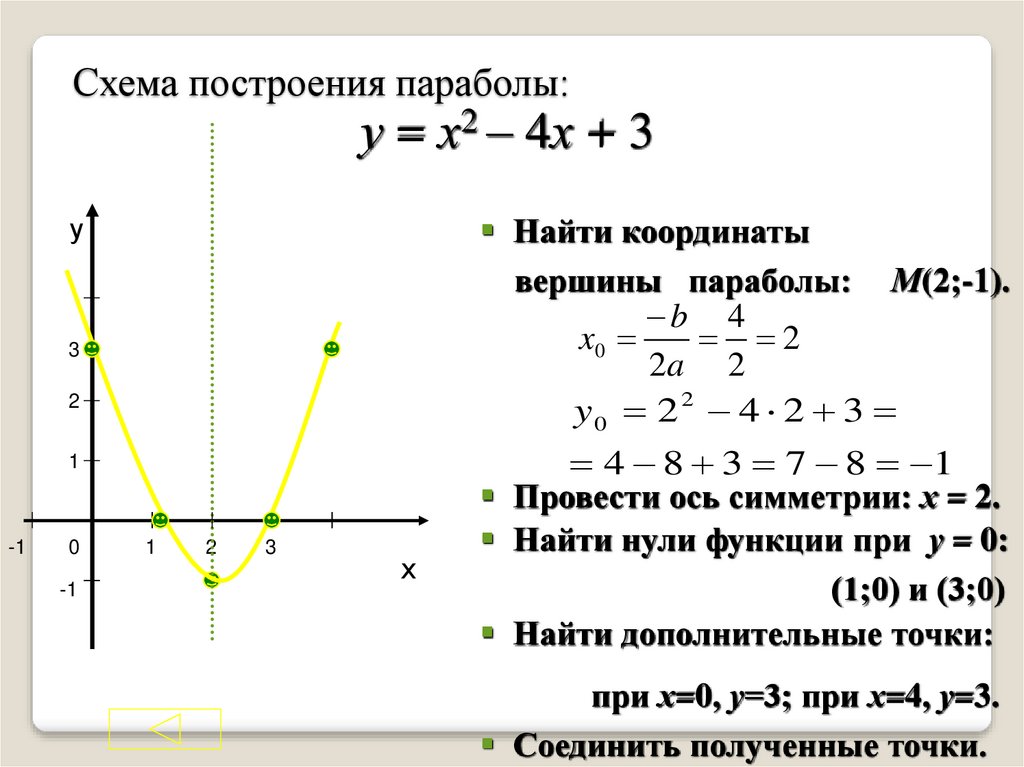 Преобразование целого выражения в многочлен. Разложение многочлена на множители.
Преобразование целого выражения в многочлен. Разложение многочлена на множители.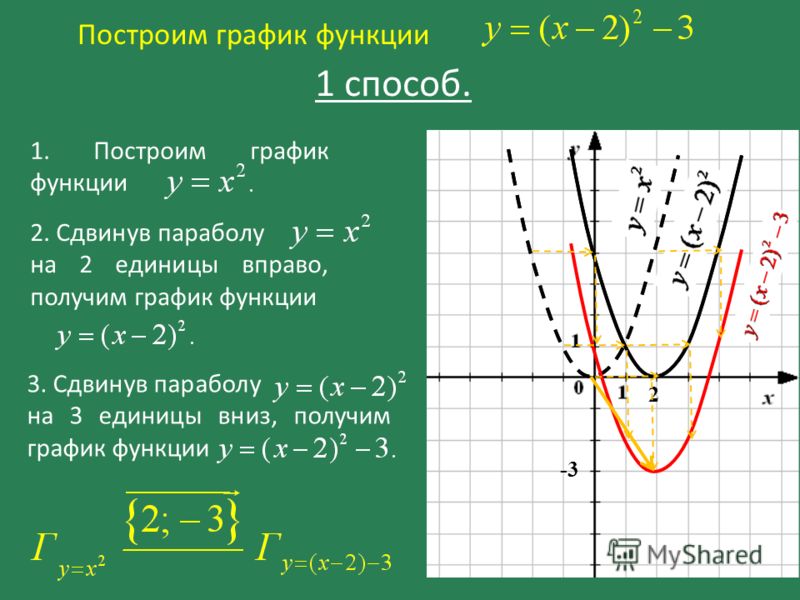
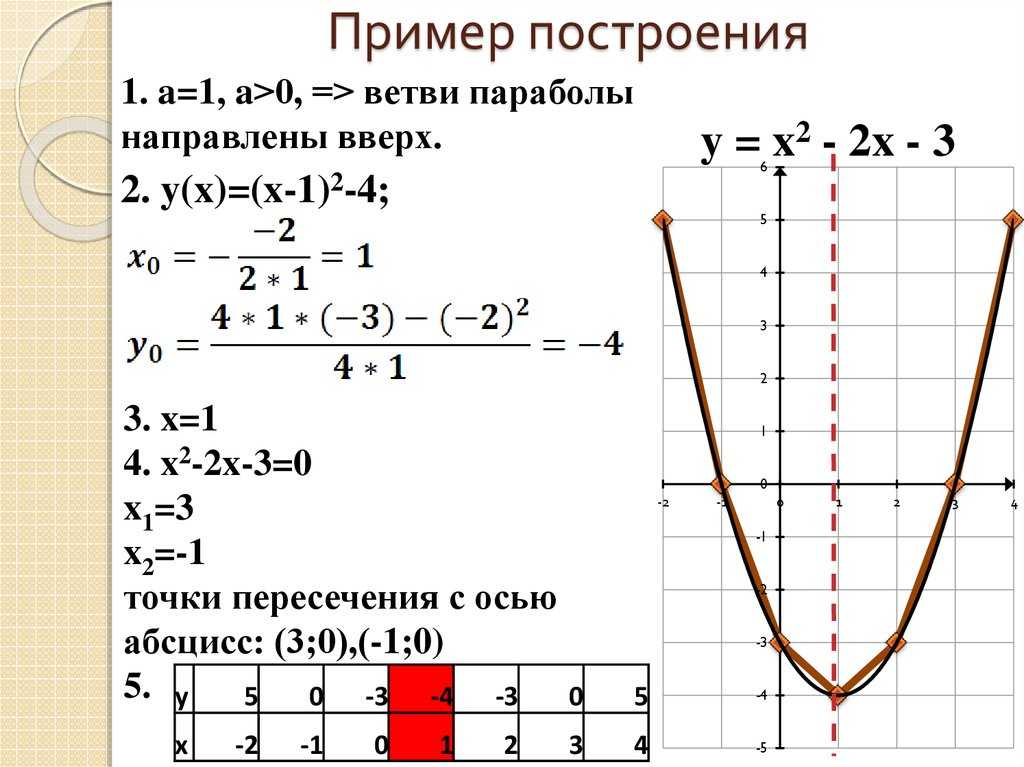 графики, диаграмма «прямоугольник и ус», счетная диаграмма и т. д.
графики, диаграмма «прямоугольник и ус», счетная диаграмма и т. д.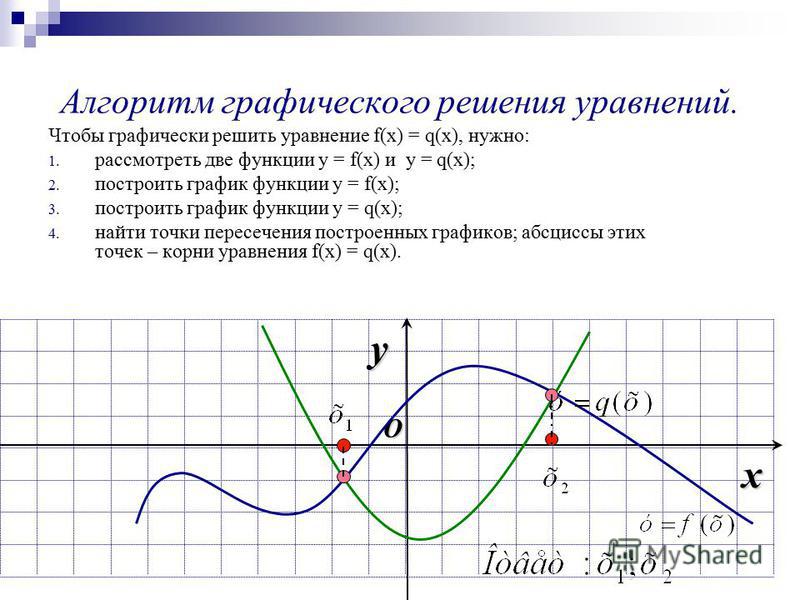

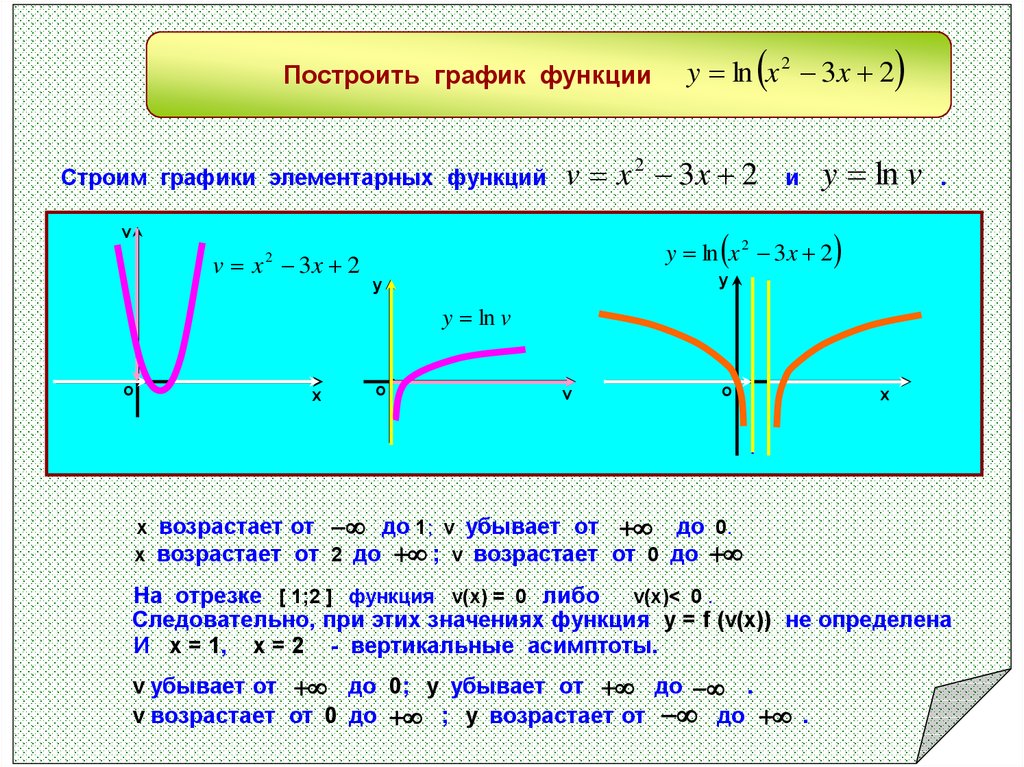

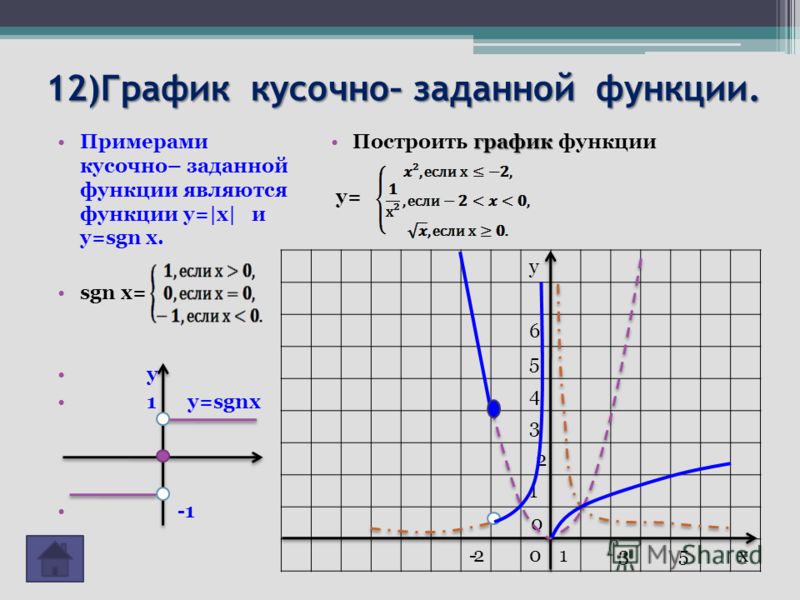 Рассчитайте относительный риск и отношение шансов с доверительными интервалами.
Рассчитайте относительный риск и отношение шансов с доверительными интервалами.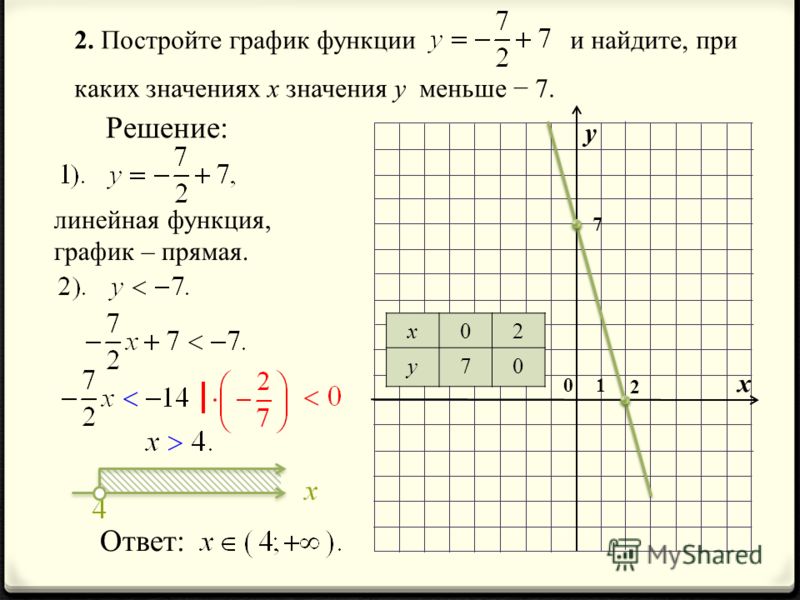

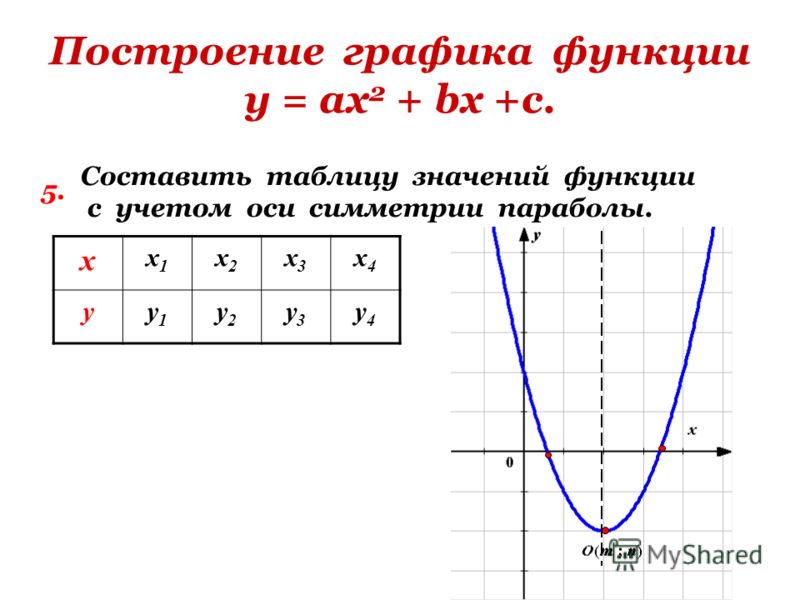
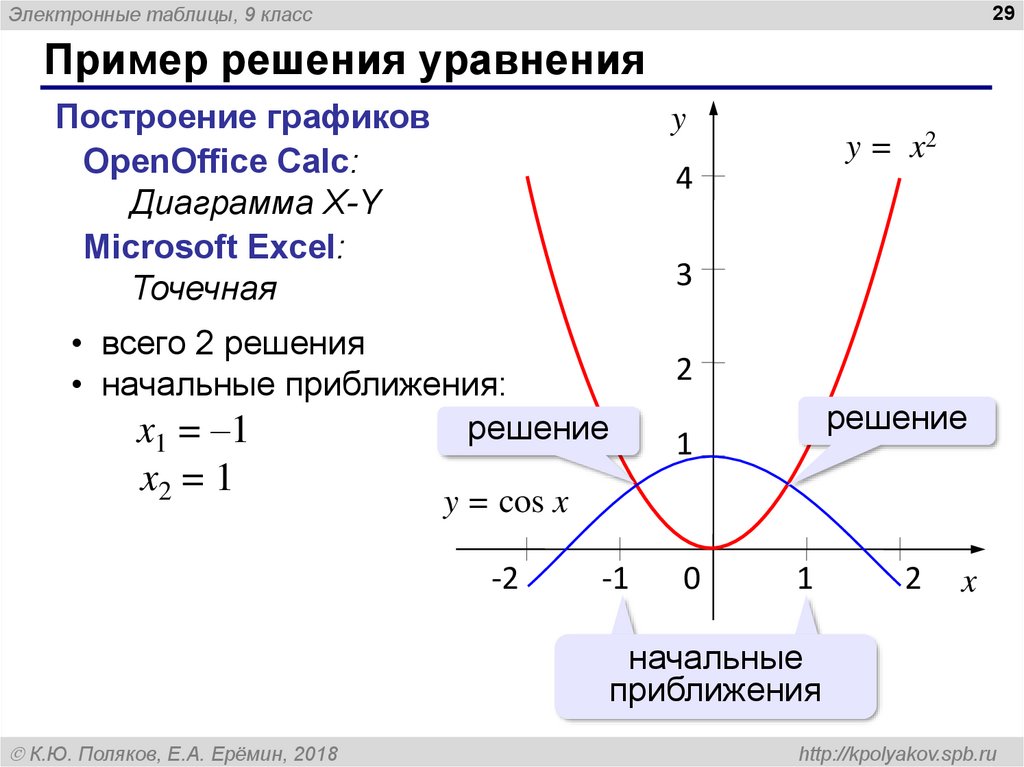 Автоматически создавайте графики оценочных кривых выживаемости для любого набора значений переменных-предикторов.
Автоматически создавайте графики оценочных кривых выживаемости для любого набора значений переменных-предикторов.