Графики в полярной системе координат MatLab
Урок 6. Обычная графика MATLAB
Построение графиков отрезками прямых
Графики в логарифмическом масштабе
Графики в полулогарифмическом масштабе
Столбцовые диаграммы
Построение гистограмм
Лестничные графики — команды stairs
Графики с зонами погрешности
График дискретных отсчетов функции
Графики в полярной системе координат
Угловые гистограммы
Графики векторов
График проекций векторов на плоскость
Контурные графики
Создание массивов данных для трехмерной графики
Графики поля градиентов quiver
Построение графиков поверхностей
Сетчатые 3D-графики с окраской
Сетчатые 3D-графики с проекциями
Построение поверхности столбцами
Построение поверхности с окраской
Построение поверхности и ее проекции
Построение освещенной поверхности
Средства управления подсветкой и обзором фигур
Построение графиков функций трех переменных
График трехмерной слоеной поверхности
Трехмерные контурные графики
Установка осевых надписей
Ввод текста в любое место графика
Позиционирование текста с помощью мыши
Вывод пояснений
Маркировка линий уровня на контурных графиках
Управление свойствами осей графиков
Включение и выключение сетки
Наложение графиков друг на друга
Разбиение графического окна
Изменение масштаба графика
Установка палитры цветов
Установка соответствия между палитрой цветов и масштабом осей
Окраска поверхностей
Установка палитры псевдоцветов
Создание закрашенного многоугольника
Окраска плоских многоугольников
Вывод шкалы цветов
Цветные плоские круговые диаграммы
Другие команды управления световыми эффектами
Окрашенные многоугольники в пространстве
Цветные объемные круговые диаграммы
Построение цилиндра
Построение сферы
Трехмерная графика с треугольными плоскостями
Что нового мы узнали?
В полярной
системе координат любая точка представляется как конец радиус-вектора, исходящего
из начала системы координат, имеющего длину RHO и угол ТНЕТА.
polarCTHETA, RHO) — строит график в полярной системе координат, представляющий собой положение конца радиус-вектора с длиной RHO и углом ТНЕТА;
polarCTHETA,RHO.S) — аналогична предыдущей команде, но позволяет задавать стиль построения с помощью строковой константы S по аналогии с командой plot.
Рис. 6.12
демонстрирует результат выполнения команд:
» t=0:pi/50:2*pi;
» polar(t,sin(5*t))
Рис.
6.12.
График функции в полярной системе координат
Графики функций в полярных координатах могут иметь весьма разнообразный вид, порой напоминая такие объекты природы, как снежинки или кристаллики льда на стекле. Вы можете сами попробовать построить несколько таких графиков — многие получают от этого удовольствие.
Нравится
Твитнуть
Построение графиков функций в полярной системе координат — Энциклопедия современных знаний
Рисунок 19
Полярная система координат на плоскости — это совокупность точки , называемой полюсом, и полупрямой , называемой полярной осью.
Положение точки M в полярной системе координат определяется расстоянием r (полярным радиусом) от точки M до полюса и углом j (полярным углом) между полярной осью и вектором .
(рисунок 19).
Полярный радиус и полярный угол составляют полярные координаты точки M , что записывается в виде M(r,j). Полярный угол измеряется в радианах и отсчитывается от полярной оси:
— в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;
— в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.
Связь между декартовыми и полярными координатами
Пару полярных координат r и j можно перевести в Декартовы координаты x и y по следующим фомулам:
Обратно, полярный радиус r можно найти, зная декартовы координаты x и y , по теореме Пифагора (см. Рис. ??):
,
а полярный угол j в диапазоне [0, 2p), находится при помощи обратной (к тангенсу) тригонометрической функции арктангенс:
Пример № 2. Построить график функции r(j) = 2.
1. Задаём значения j в градусах в диапазоне [0, 2p] с шагом в 5 градусов с использованием автозаполнения (см.
Приложение 1).
2. Перевести j из градусов в радианы с использованием функции РАДИАНЫ (см. Приложение 2).
3. Рассчитать значения r(jрад).
4. По значениям jрад и r(jрад) рассчитать декартовы координаты x и y.
5. По рассчитанным значениям x и y построить график, выбрав тип диаграммы Точечная.
Рисунок 20. Результаты расчёта
Рисунок 21. График функции r(j) = 2
Задание № 4
С помощью пакета Microsoft Excel построить график функций, приведенные в Приложении 5 соответственно варианту. Порядок расчета и результат оформить в виде отчета, содержащего следующие пункты:
a. Первый лист: Титульный лист – пример оформления см в приложении 6,
b. Привести текст задания,
c. Привести расчётные формулы и результаты расчёта,
d. График построенной функции,
e. Указать полярные координаты точки графика, заданной преподавателем.
Построение графиков функций с использованием логарифмической шкалы.
| расстояния |
Шкала называетсялогарифмической,если метками шкалы являются числа, а расстояния между метками –пропорциональны логарифму отношения величин отмеченных на концах этого отрезка (в то время как на шкале в линейном масштабе длина отрезка пропорциональна разности величин на его концах ).
Ни нуль, ни отрицательные числа не могут быть показаны на логарифмической шкале (см. рисунок 22)
Рисунок 22
Логарифмическая шкала исключительно удобна для отображения очень больших диапазонов значений величин.
Пример № 3. Построить график функции . в диапазоне значений [-5, 5] и определить по графику значение функции для х = -3.6 и х = 4.
1. Задаём значения х в диапазоне [-5, 5] с шагом 0.5 с использованием автозаполнения (см. Приложение 1).
2. По заданным х рассчитываем значения функции у.
3. Строим график функции, используя тип диаграммы «точечная» и замечаем, например,что значение функции при отрицательных х очень близко к 0, так что определить его из графика не представляется возможным
Рисунок 23
4. Выделяем ось у.
5. Делаем щелчок правой кнопкой мыши и в раскрывшемся контекстном меню выбираем «формат оси» (см. рисунок 12)
6. В окне «формат оси» помечаем галочкой логарифмическую шкалу.
7. Добавить основные и промежуточные линии сетки.
Результаты представлены на Рисунке 24
Рисунок 24
Из рисунка определяем, что для х = -3.6 значение примерно равно 0.02, а для х = 4 .
6.1.Задание № 5.Построить график функций в диапазоне значений [-10, 10] с шагом 0.5 . Уметь из графика определять значение функции для указанного (преподавателем) аргумента. Порядок расчета и результат оформить в виде отчета, содержащего следующие пункты:
a. Первый лист: Титульный лист – пример оформления см в приложении 6,
b. Привести текст задания,
c. Привести графики без использования логарифмической шкалы,
d. Привести графики с использованием логарифмической шкалы,
e. Сравнить результаты.
Математика Без Ху%!ни. Полярные координаты. Построение графика функции.
Похожие статьи.
Построение графика функции, имеющей разрыв
Построение графика функции по заданным параметрам
Построение графиков функций.
Основные принципы построения и использования автоматизированных информационных систем во внешнеэкономической деятельности
How to Plot Polar Coordinates
By: Yang Kuang and Elleyne Kase and
Updated: 07-09-2021
From The Book: Pre-Calculus For Dummies
Pre-Calculus For Dummies
Исследовать книгу Купить на Amazon
Полярные координаты — чрезвычайно полезное дополнение к вашему набору математических инструментов, поскольку они позволяют решать задачи, которые были бы чрезвычайно уродливыми, если бы вы полагались на стандарт 9.Координаты 0018 x- и y-. Чтобы полностью понять, как строить полярные координаты, вам нужно увидеть, как выглядит плоскость полярных координат.Пустая полярная координатная плоскость (не мишень для дротиков)
На рисунке видно, что плоскость больше не представляет собой сетку прямоугольных координат; вместо этого это серия концентрических окружностей вокруг центральной точки, называемой полюсом .
Плоскость выглядит так, потому что полярные координаты — это заданный радиус и заданный угол в стандартном положении от полюса. Каждый круг представляет одну единицу радиуса, а каждая линия представляет собой специальные углы от единичной окружности.Поскольку вы записываете все точки на полярной плоскости как
, чтобы изобразить точку на полярной плоскости, вы должны сначала найти тета, а затем найти r на этой линии. Этот подход позволяет сузить местоположение точки до одной из линий, представляющих угол. Оттуда вы можете просто отсчитать от полюса радиальное расстояние. Если пойти другим путем и начать с р, можно оказаться в затруднительном положении, когда проблемы усложнятся.
Пример построения полярных координат
Например, чтобы нанести точку E на, которая имеет положительное значение как для радиуса, так и для угла, — вы просто двигаетесь от полюса против часовой стрелки, пока не достигнете соответствующего угла (тета). Вы начинаете там в следующем списке:
Найдите угол в плоскости полярных координат.
Найдите угол по рисунку:
Определите, где радиус пересекает угол.
Поскольку радиус равен 2 ( r
= 2), вы начинаете с полюса и перемещаетесь на 2 точки в направлении угла.Постройте заданную точку.
На пересечении радиуса и угла в плоскости полярных координат поставьте точку и на этом закончите! На этом рисунке показана точка E на плоскости.
Визуализация простых и сложных полярных координат
Поскольку полярные координаты основаны на углах, в отличие от декартовых координат, полярные координаты имеют много различных упорядоченных пар.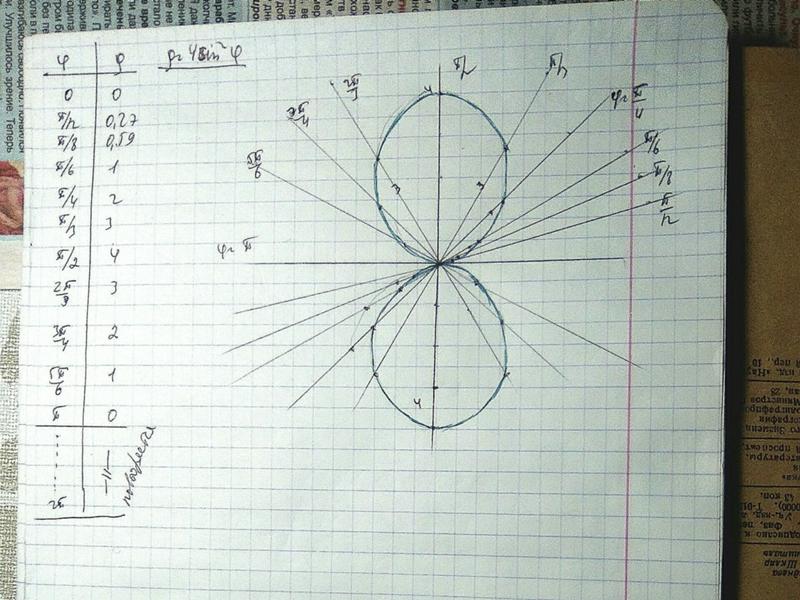
Об этой статье
Эта статья взята из книги:
- Предварительное исчисление для чайников,
Об авторе книги:
Мэри Джейн Стерлинг. Изучала алгебру, бизнес-вычисления, геометрию и конечную математику в Университете Брэдли. в Пеории, штат Иллинойс, более 30 лет. Она является автором нескольких книг для чайников, , в том числе Рабочая тетрадь по алгебре для чайников, Алгебра II для чайников, и Рабочая тетрадь по алгебре II для чайников.
Эту статью можно найти в категории:
- Предварительное исчисление,
6.1: Полярные координаты — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 61269
Цели обучения
- Различать и понимать разницу между прямоугольной системой координат и полярной системой координат.
- Нанесите точки с полярными координатами на полярную плоскость.
На расстоянии более \(12\) километров от порта парусник попадает в непогоду и сбивается с курса ветром силой \(16\) узлов (см.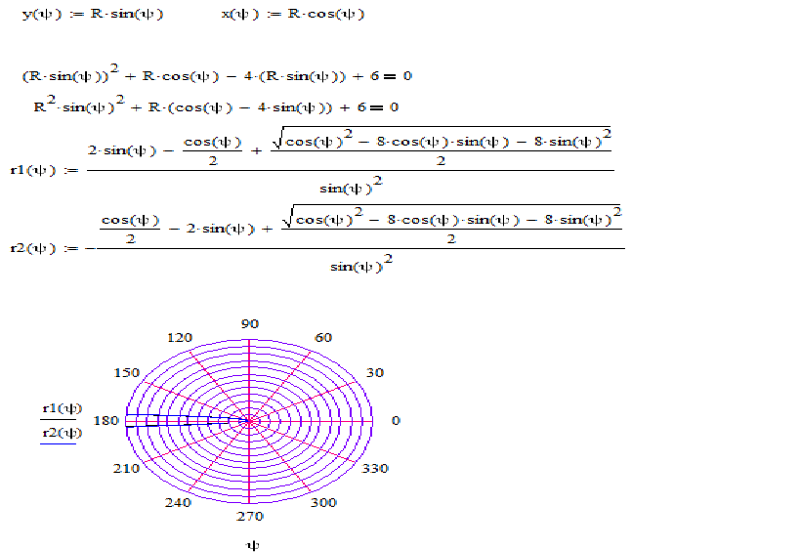
рисунок \(\PageIndex{1}\)). Как моряк может указать свое местонахождение береговой охране? В этом разделе мы исследуем метод представления местоположения, отличный от стандартной сетки координат.
Нанесение точек с использованием полярных координат
Когда мы думаем о построении точек на плоскости, мы обычно думаем о прямоугольных координатах \((x,y)\) в декартовых координатах самолет . Однако существуют и другие способы записи координатной пары и другие типы сеточных систем. В этом разделе мы познакомимся с полярными координатами, которые представляют собой точки, обозначенные \((r,\theta)\) и нанесенные на полярную сетку. Полярная сетка представлена в виде серии концентрических кругов, исходящих из полюса или начала координатной плоскости.
Полярная сетка масштабируется как единичный круг с положительной осью \(x\) — , которая теперь рассматривается как полярная ось, а начало отсчета — как полюс. Первая координата \(r\) — это радиус или длина направленного отрезка прямой от полюса.
Угол \(\theta\), измеренный в радианах, указывает направление \(r\). Мы перемещаемся против часовой стрелки от полярной оси на угол \(\theta\) и измеряем направленный отрезок длиной \(r\) в направлении \(\theta\). Несмотря на то, что мы сначала измеряем \(\theta\), а затем \(r\), полярная точка сначала записывается с координатой \(r\). Например, чтобы нанести точку \(\left(2,\dfrac{\pi}{4}\right)\), мы должны переместить \(\dfrac{\pi}{4}\) единиц против часовой стрелки. а затем длину \(2\) от полюса. Эта точка нанесена на сетку на рисунке \(\PageIndex{2}\).
Пример \(\PageIndex{1}\): Нанесение точки на полярную сетку
Нанесение точки \(\left(3,\dfrac{\pi}{2 }\right)\) на полярной сетке.
Решение
Угол \(\dfrac{\pi}{2}\) находится путем протягивания против часовой стрелки \(90°\) от полярной оси. Точка расположена на расстоянии \(3\) единиц от полюса в направлении \(\dfrac{\pi}{2}\), как показано на рисунке \(\PageIndex{3}\).
Упражнение \(\PageIndex{1}\)
Постройте точку \(\left(2, \dfrac{\pi}{3}\right)\) в полярной сетке.
- Ответить
- Рисунок \(\PageIndex{4}\)
Пример \(\PageIndex{2}\): Нанесение точки в полярной системе координат с отрицательной составляющей
Нанесение точки \(\left(−2, \dfrac{\pi}{6}\right) \) на полярной сетке.
Решение
Мы знаем, что \(\dfrac{\pi}{6}\) находится в первом квадранте. Однако \(r=−2\). Мы можем подойти к построению точки с отрицательным \(r\) двумя способами:
- Постройте точку \(\left(2,\dfrac{\pi}{6}\right)\), переместив \(\dfrac{\pi}{6}\) против часовой стрелки и протянув направленную отрезок \(2\) единиц в первый квадрант. Затем проследите направленный отрезок обратно через полюс и продолжайте движение на \(2\) единиц в третий квадрант;
- Переместите \(\dfrac{\pi}{6}\) в направлении против часовой стрелки и нарисуйте направленный отрезок от полюса \(2\) единиц в отрицательном направлении в третий квадрант.
См. рисунок \(\PageIndex{5a}\). Сравните это с графиком полярной координаты \(\left(2,\dfrac{\pi}{6}\right)\), показанным на рисунке \(\PageIndex{5b}\).
Рисунок \(\PageIndex{5}\)Упражнение \(\PageIndex{2}\)
Нанесите точки \(\left(3,−\dfrac{\pi}{6}\right)\) и \(\left(2,\dfrac{9\pi}{4}\right)\) на той же полярной сетке.
- Ответить
- Рисунок \(\PageIndex{6}\)
Преобразование полярных координат в прямоугольные координаты
Когда задан набор из полярных координат , нам может понадобиться преобразовать их в прямоугольные координаты. Для этого мы можем вспомнить отношения, существующие между переменными \(x\), \(y\), \(r\) и \(\theta\).
\(\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\)
\(\sin \theta=\dfrac{y}{r}\rightarrow y=r \sin \theta\)
При опускании перпендикуляра из точки плоскости на ось x- образуется прямоугольный треугольник, как показано на рисунке \(\PageIndex{7}\).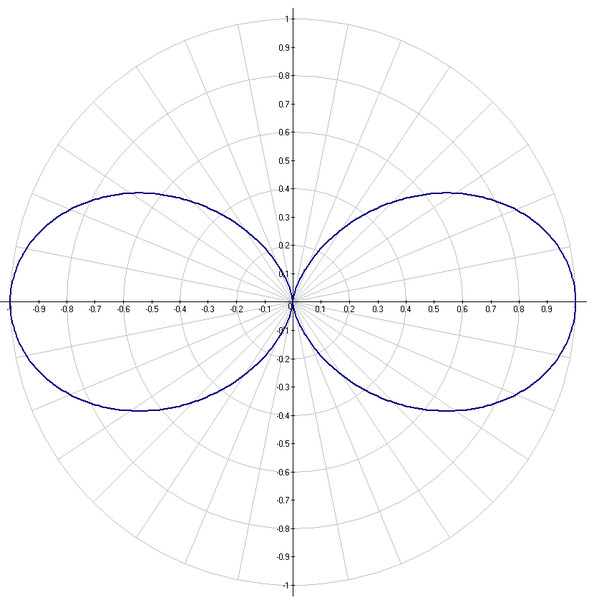
Простой способ запомнить приведенные выше уравнения — представить \(\cos\theta\) как примыкающую сторону к гипотенузе и \(\sin\theta\) как противоположную сторону к гипотенузе.
ПРЕОБРАЗОВАНИЕ ПОЛЯРНЫХ КООРДИНАТ В ПРЯМОУГОЛЬНЫЕ
Чтобы преобразовать полярные координаты \((r, \theta)\) в прямоугольные координаты \((x, y)\), введите
\[\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\]
\[\sin \theta=\dfrac{y}{r}\rightarrow y=r \ sin \theta\]
Как: Данные полярные координаты преобразовать в прямоугольные координаты.
- Учитывая полярную координату \((r,\theta)\, запишите \(x=r \cos \theta\) и \(y=r \sin \theta\).
- Оцените \(\cos \theta\) и \(\sin \theta\).
- Умножьте \(\cos \theta\) на \(r\), чтобы найти \(x\) — координату прямоугольной формы.
- Умножьте \(\sin\theta\) на \(r\), чтобы найти \(y\) — координату прямоугольной формы.
Пример \(\PageIndex{3A}\): запись полярных координат в виде прямоугольных координат
Запись полярных координат \(\left(3,\dfrac{\pi}{2}\right)\) в виде прямоугольных координат.
Решение
Используйте эквивалентные соотношения.
\[\begin{align*} x&= r \cos \theta\\ x&= 3 \cos \dfrac{\pi}{2}\\ &= 0\\ y&= r \sin \theta\\ y& = 3 \sin \dfrac{\pi}{2}\\ &= 3 \end{align*}\]
Прямоугольные координаты равны \((0,3)\). См. рисунок \(\PageIndex{8}\).
Рисунок \(\PageIndex{8}\)Пример \(\PageIndex{3B}\): запись полярных координат в виде прямоугольных координат
Запись полярных координат \((−2,0)\) в виде прямоугольных координат.
Решение
См. рисунок \(\PageIndex{9}\). Записав полярные координаты в виде прямоугольника, мы имеем
\[\begin{align*} x&= r \cos \theta\\ x&= -2 \cos(0)\\ &= -2\\ y&= r \sin \theta\\ y&= -2 \sin(0)\\ &= 0 \end{align*}\]
Прямоугольные координаты также равны \((−2,0)\).
Рисунок \(\PageIndex{9}\)Упражнение \(\PageIndex{3}\)
Запишите полярные координаты \(\left(−1,\dfrac{2\pi}{3}\right)\ ) в виде прямоугольных координат.
- Ответить
\((x,y)=\left(\dfrac{1}{2},−\dfrac{\sqrt{3}}{2}\right)\)
Преобразование прямоугольных координат в полярные координаты
Для преобразования прямоугольных координат в полярные координаты мы будем использовать два других знакомых соотношения. Однако при таком преобразовании мы должны знать, что набор прямоугольных координат даст более одной полярной точки.
ПРЕОБРАЗОВАНИЕ ПРЯМОУГОЛЬНЫХ КООРДИНАТ В ПОЛЯРНЫЕ КООРДИНАТЫ 92\)
\(\tan \theta=\dfrac{y}{x}\)
Рисунок \(\PageIndex{10}\)Пример \(\PageIndex{4}\): Запись прямоугольных координат как полярных Координаты
Преобразование прямоугольных координат \((3,3)\) в полярные координаты.
Решение
Мы видим, что исходная точка \((3,3)\) находится в первом квадранте. Чтобы найти \(\theta\), используйте формулу \(\tan \theta=\dfrac{y}{x}\). Это дает
\[\begin{align*} \tan \theta&= \dfrac{3}{3}\\ \tan \theta&= 1\\ {\tan}^{-1}(1)&= \ dfrac{\pi}{4} \end{align*}\] 92}\\ r&= \sqrt{9+9}\\ r&= \sqrt{18}\\ &= 3\sqrt{2} \end{align*}\]
Итак, \(r=3\ sqrt{2}\) и \(\theta=\dfrac{\pi}{4}\), что дает нам полярную точку \((3\sqrt{2},\dfrac{\pi}{4})\ ).
См. рисунок \(\PageIndex{11}\).
Анализ
Существуют и другие наборы полярных координат, которые будут такими же, как наше первое решение. Например, точки \(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) и \(\left(3\sqrt{2},−\dfrac{ 7\pi}{4}\right)\) будет совпадать с исходным решением \(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка \(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) указывает на движение против часовой стрелки на \(\pi\), что прямо противоположно \(\ dfrac{\pi}{4}\). Радиус выражается как \(−3\sqrt{2}\). Однако угол \(\dfrac{5\pi}{4}\) расположен в третьем квадранте, и, поскольку \(r\) отрицательно, мы продолжаем направленный отрезок в противоположном направлении, в первый квадрант . Это та же точка, что и \(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка \(\left(3\sqrt{2}, −\dfrac{7\pi}{4}\right)\) – это перемещение по часовой стрелке на \(−\dfrac{7\pi}{4}\ ), из \(\dfrac{\pi}{4}\). Радиус, \(3\sqrt{2}\), такой же.
Дополнительная практика
- Нанесите точку с полярными координатами \(\left(3, \frac{\pi}{6}\right)\).
- Нанесите точку с полярными координатами \(\left(5,-\frac{2 \pi}{3}\right)\)
- Преобразование \(\left(6,-\frac{3 \pi}{4}\right)\) в прямоугольные координаты.
- Преобразование \(\left(-2, \frac{3 \pi}{2}\right)\) в прямоугольные координаты.
- Преобразование (7,-2) в полярные координаты.
- Преобразование (-9,-4) в полярные координаты. 92\)
\(\тангенс\тета=\dfrac{y}{x}\)
Ключевые понятия
- Полярная сетка представлена в виде ряда концентрических кругов, исходящих из полюса или источника.
- Чтобы нанести точку в виде \((r,\theta)\), \(\theta>0\), переместитесь против часовой стрелки от полярной оси на угол \(\theta\), а затем продлите направленный отрезок от полюса на длину \(r\) в направлении \(\theta\). Если \(\theta\) отрицательное, двигайтесь по часовой стрелке и продлите направленный отрезок на длину \(r\) в направлении \(\theta\).
