Построение поверхностей второго порядка онлайн: Построение поверхности 3D online

alexxlab / / Разное
(1/2))

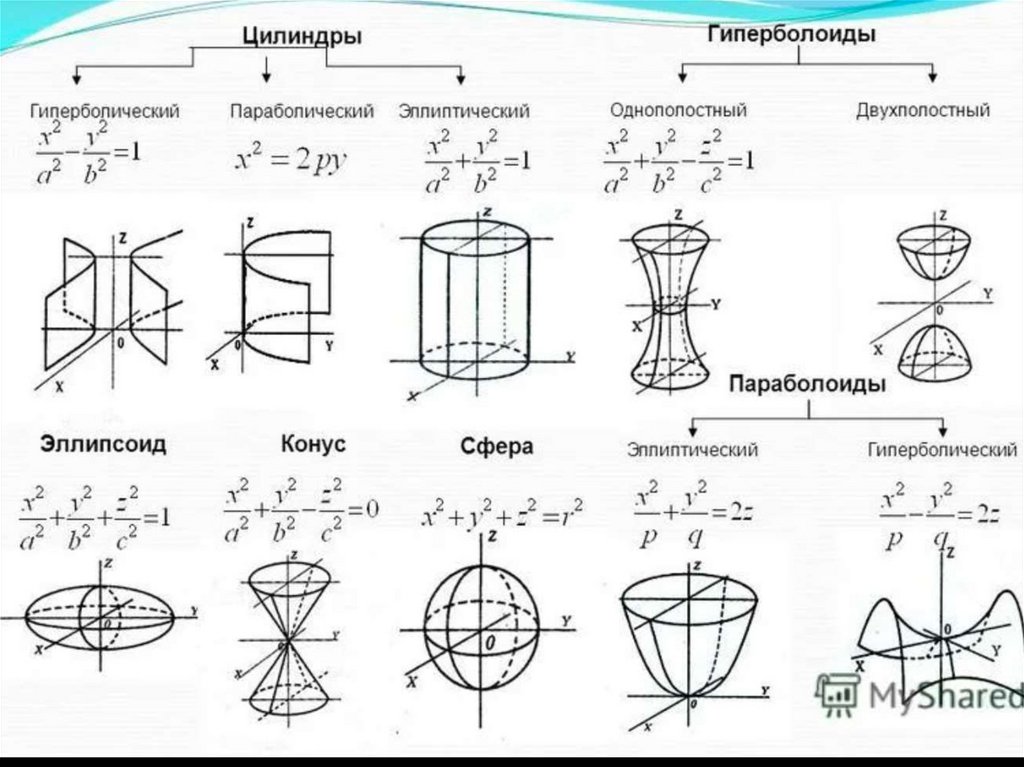
Указанные выше примеры содержат также:

  • модуль или абсолютное значение: absolute(x) или |x|
  • квадратные корни sqrt(x),
    кубические корни cbrt(x)
  • тригонометрические функции:
    синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
  • показательные функции и экспоненты exp(x)
  • обратные тригонометрические функции:
    арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс acot(x)
  • натуральные логарифмы ln(x),
    десятичные логарифмы log(x)
  • гиперболические функции:
    гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
  • обратные гиперболические функции:
    гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x), гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x)
  • другие тригонометрические и гиперболические функции:
    секанс sec(x), косеканс csc(x), арксеканс asec(x), арккосеканс acsc(x), гиперболический секанс sech(x), гиперболический косеканс csch(x), гиперболический арксеканс asech(x), гиперболический арккосеканс acsch(x)
  • функции округления:
    в меньшую сторону floor(x), в большую сторону ceiling(x)
  • знак числа:
    sign(x)
  • для теории вероятности:
    функция ошибок erf(x) (интеграл вероятности), функция Лапласа laplace(x)
  • Факториал от x:
    x! или factorial(x)
  • Гамма-функция gamma(x)
  • Функция Ламберта LambertW(x)
  • Тригонометрические интегралы: Si(x), Ci(x), Shi(x), Chi(x)
Правила ввода

Можно делать следующие операции

2*x
— умножение
3/x
— деление
x^2
— возведение в квадрат
x^3
— возведение в куб
x^5
— возведение в степень
x + 7
— сложение
x — 6
— вычитание
Действительные числа
вводить в виде 7. {2} + 2 a_{34} z + a_{44} = 0$$ где $$a_{11} = 1$$ $$a_{12} = 0$$ $$a_{13} = 0$$ $$a_{14} = -1$$ $$a_{22} = 1$$ $$a_{23} = 0$$ $$a_{24} = -1$$ $$a_{33} = -1$$ $$a_{34} = 1$$ $$a_{44} = 2$$ Инвариантами данного уравнения при преобразовании координат являются определители: $$I_{1} = a_{11} + a_{22} + a_{33}$$


     |a11  a12|   |a22  a23|   |a11  a13|
I2 = |        | + |        | + |        |
     |a12  a22|   |a23  a33|   |a13  a33|

$$I_{3} = \left|\begin{matrix}a_{11} & a_{12} & a_{13}\\a_{12} & a_{22} & a_{23}\\a_{13} & a_{23} & a_{33}\end{matrix}\right|$$ $$I_{4} = \left|\begin{matrix}a_{11} & a_{12} & a_{13} & a_{14}\\a_{12} & a_{22} & a_{23} & a_{24}\\a_{13} & a_{23} & a_{33} & a_{34}\\a_{14} & a_{24} & a_{34} & a_{44}\end{matrix}\right|$$ $$I{\left (\lambda \right )} = \left|\begin{matrix}a_{11} — \lambda & a_{12} & a_{13}\\a_{12} & a_{22} — \lambda & a_{23}\\a_{13} & a_{23} & a_{33} — \lambda\end{matrix}\right|$$


     |a11  a14|   |a22  a24|   |a33  a34|
K2 = |        | + |        | + |        |
     |a14  a44|   |a24  a44|   |a34  a44|


     |a11  a12  a14|   |a22  a23  a24|   |a11  a13  a14|
     |             |   |             |   |             |
K3 = |a12  a22  a24| + |a23  a33  a34| + |a13  a33  a34|
     |             |   |             |   |             |
     |a14  a24  a44|   |a24  a34  a44|   |a14  a34  a44|

подставляем коэффициенты $$I_{1} = 1$$


     |1  0|   |1  0 |   |1  0 |
I2 = |    | + |     | + |     |
     |0  1|   |0  -1|   |0  -1|

$$I_{3} = \left|\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & -1\end{matrix}\right|$$ $$I_{4} = \left|\begin{matrix}1 & 0 & 0 & -1\\0 & 1 & 0 & -1\\0 & 0 & -1 & 1\\-1 & -1 & 1 & 2\end{matrix}\right|$$ $$I{\left (\lambda \right )} = \left|\begin{matrix}- \lambda + 1 & 0 & 0\\0 & — \lambda + 1 & 0\\0 & 0 & — \lambda — 1\end{matrix}\right|$$


     |1   -1|   |1   -1|   |-1  1|
K2 = |      | + |      | + |     |
     |-1  2 |   |-1  2 |   |1   2|


     |1   0   -1|   |1   0   -1|   |1   0   -1|
     |          |   |          |   |          |
K3 = |0   1   -1| + |0   -1  1 | + |0   -1  1 |
     |          |   |          |   |          |
     |-1  -1  2 |   |-1  1   2 |   |-1  1   2 |

$$I_{1} = 1$$ $$I_{2} = -1$$ $$I_{3} = -1$$ $$I_{4} = -1$$ $$I{\left (\lambda \right )} = — \lambda^{3} + \lambda^{2} + \lambda — 1$$ $$K_{2} = -1$$ $$K_{3} = -4$$ Т. {2}} = -1$$ это уравнение для типа двусторонний гиперболоид
— приведено к каноническому виду

Урок 11: Методы и схемы поверхности отклика

Давайте рассмотрим ситуацию первого порядка — метод наискорейшего подъема. Теперь помните, во-первых, мы не знаем, существует ли вообще «холм», поэтому мы начнем с того места, где, по нашему мнению, существует оптимум. Мы начинаем с натуральных единиц и используем закодированные единицы для проведения нашего эксперимента. Рассмотрим пример 11.1 в учебнике. Мы хотим начать в области, где \(x_{1} = \) время реакции (30-40 секунд) и \(x_{2} = \) температура (150-160 градусов), и мы хотим посмотреть на выход процесса в зависимости от этих факторов. В некотором смысле, с целью иллюстрации этой концепции, мы можем наложить эту область экспериментов на наш участок нашего неизвестного «холма». Очевидно, что мы проводим эксперимент в его натуральных единицах, но планы будут указаны в закодированных единицах, чтобы мы могли применить их к любой ситуации. 92\) дизайн и пять центральных точек. Теперь мы подгоняем эту модель первого порядка и исследуем ее.

Вводим фактические данные для A и B и измерения отклика Y.

Сначала подгоняем полную модель: См. Ex-11-1-output.doc

Подгоняем поверхность. Модель имеет два основных эффекта: один член перекрестного произведения, а затем один дополнительный параметр в виде среднего значения для центральной точки. Остатки в этом случае имеют четыре \(df\) , которые происходят от повторения центральных точек . Так как центральных точек пять, т. е. четыре \(df\) среди пяти центральных точек. Это мера чистой ошибки.

Начнем с проверки кривизны. Вопрос заключается в том, отличается ли среднее значение центральных точек от значений при \(x_{1},x_{2} = (0,0)\), предсказанных на основе модели отклика скрининга (основные эффекты плюс взаимодействие). Мы проверяем, находятся ли средние значения точек в центре на плоскости, соответствующей четырем угловым точкам. Если бы p-значение было небольшим, это могло бы сказать вам, что среднее значение центральных точек находится выше или ниже плоскости, указывающей на кривизну поверхности отклика. Тот факт, что в данном случае он не имеет значения, указывает на отсутствие кривизны. Действительно, центральные точки ложатся точно на плоскость, соответствующую четвертным точкам.

В этом тесте есть только одна степень свободы, потому что в проекте есть только одно дополнительное место с точки зрения размеров x .

Далее мы проверяем значительное влияние факторов. Из дисперсионного анализа мы видим, что взаимодействия нет. Итак, давайте переделаем эту модель без члена взаимодействия, оставив только члены A и B. У нас все еще есть среднее значение центральных точек, и наш AOV теперь показывает \(5\df\) для остаточной ошибки. Одним из них является несоответствие аддитивной модели, и, как и прежде, есть \(4\df\) чистой ошибки. У нас есть \(1\ df\) для кривизны, и несоответствие в этом случае — это просто взаимодействия из модели.

Что нам с этим делать? См. анализ Minitab и повторите эти результаты в EX11-1.mpx  | Ex11-1.csv

Наша оценочная модель: \(\hat{y} = 40,34 + 0,775x_{1} + 0,325x_{2}\)

Таким образом, для любых \(x_{1}\) и \(x_{2}\) мы можем предсказать \(y\). Это соответствует плоской поверхности и говорит нам, что предсказанное \(y\) является функцией \(x_{1}\) и \(x_{2}\), а коэффициенты являются градиентом этой функции. В настоящее время мы работаем с закодированными переменными, поэтому эти коэффициенты безразмерны.

Если мы переместимся на 0,775 в направлении \(x_{1}\), а затем на 0,325 в направлении \(x_{2}\), это будет направление наискорейшего подъема. Все, что мы знаем, это то, что эта плоская поверхность является одной стороной «холма».

Метод наискорейшего подъема предлагает нам провести эксперимент первого порядка и найти направление, в котором «холм» идет вверх, и начать движение вверх по холму, выполняя дополнительные измерения в каждом \((x_{1}, x_{2}) \) до тех пор, пока отклик не начнет уменьшаться. Если мы начнем с 0 в закодированных единицах, то сможем провести серию одиночных экспериментов на этом пути вверх по «холму» самого крутого спуска. Если мы сделаем это с размером шага \(x_{1} = 1\), то:

\(1\ /\ 0,775 = x_{2}\ /\ 0,325 \rightarrow x_{2} = 0,325\ /\ 0,775 = 0,42 \)

и, таким образом, размер нашего шага \(x_{1} = 1 \) определяет, что \(x_{2} = 0,42\), чтобы двигаться в направлении, определяемом как самый крутой подъем. Если мы сделаем шаги 1 в кодированных единицах, это будет пять минут с точки зрения единиц времени. И для каждого шага на этом пути мы поднимались бы на 0,42 закодированных единицы в \(x_{2}\) или примерно на 2 градуса по шкале температур.

Шаги Кодированные переменные Естественные переменные Всего лечения
\(x_1\) \(x_1\) \(\xi_1\) \(\xi_1\) г
Происхождение 0 0 35 155  
\(\Дельта\) 1,00 0,42 5 2  
Начало + \(\Дельта\) 1,00 0,42 40 157 41,0
Начало + \(2 \Дельта\) 2,00 0,84 45 159 42,9
Начало + \(3 \Дельта\) 3,00 1,26 50 161 47,1
Начало + \(4 \Дельта\) 4,00 1,68 55 163 49,7
Начало + \(5 \Дельта\) 5,00 2. 10 60 165 53,8
Начало + \(6 \Дельта\) 6,00 2,52 65 167 59,9
Начало + \(7 \Дельта\) 7,00 2,94 70 169 65,0
Начало + \(8 \Дельта\) 8,00 3,36 75 171 70,4
Начало + \(9 \Дельта\) 9,00 3,78 80 173 77,6
Начало + \(10 \Дельта\) 10.00 4,20 85 175 80,3
Начало + \(11 \Дельта\) 11.00 4,62 90 179 76,2
Начало + \(12 \Дельта\) 12.00 5,04 95 181 75,1
Таблица 11-3 Эксперимент с самым крутым подъемом для примера 11-1

Вот ряд шагов в дополнительных мерах пяти минут и 2º температуры. Отклик нанесен на график и показывает увеличение, которое падает к концу.

Рисунок 11-5 Урожайность в зависимости от количества шагов на пути наискорейшего подъема для примера 11-1 1 2 3 4 5 6 7 8 9 10 11 12 40 50 60 70 80 90 шагов Урожайность

Это довольно плавная кривая, и в действительности, вам, вероятно, следует пройти немного дальше пика, чтобы убедиться, что вы находитесь на пике. Но все, что вы пытаетесь сделать, это приблизительно выяснить, где находится вершина «холма». Если ваш первый эксперимент оказался не совсем правильным, возможно, вы пошли не в том направлении!

Возможно, вы захотите провести еще один эксперимент первого порядка, чтобы убедиться. Или вы можете провести эксперимент второго порядка, предполагая, что вы близки к вершине. Это то, что мы обсудим в следующем разделе. Эксперимент второго порядка поможет найти более точное положение пика.

Дело в том, что это довольно дешевый способ «обследовать гору», чтобы попытаться найти оптимальные условия.

Помните, что этот пример показан в двух измерениях, но вы можете работать в трех- или четырехмерном пространстве! Вы можете использовать тот же метод, подобрав модель первого порядка, а затем двигаясь вверх по поверхности отклика на k пространственных измерений, пока вы не подумаете, что находитесь близко к оптимальным условиям.

Если вы находитесь в более чем 2-х измерениях, вы не сможете получить хороший сюжет. Но это нормально. Метод наискорейшего подъема подскажет, где провести новые измерения, и вы узнаете отклик в этих точках. Вы можете продвинуться на несколько шагов и увидеть, что реакция продолжает расти или, возможно, нет, — тогда вы можете провести еще один эксперимент первого порядка и перенаправить свои усилия. Дело в том, что когда мы проводим эксперимент для модели второго порядка, мы надеемся, что оптимум будет в диапазоне эксперимента, а если нет, то мы экстраполируем, чтобы найти оптимум. В этом случае безопаснее всего провести еще один эксперимент вокруг этого предполагаемого оптимума.

Поскольку эксперимент для модели второго порядка требует большего количества запусков, чем эксперименты для модели первого порядка, мы хотим перейти в правую область до начинаем комплектовать модели второго порядка.

Свойства поверхности Civil 3D