Построить функции онлайн: Построение графика функции онлайн

(1/n) () скобки |  | скобки модуля: |x|

Список функций

Имя	Описание
log2(x)	логарифм по основанию 2 от x
lg(x) или log10(x)	логарифм по основанию 10 от x
log(x;b)	логарифм x по основанию b log(x;3)
ln(x)	натуральный логарифм (логарифм по основанию e (2. x	экспонента от х (e в степени x)
sqrt(x)	квадратный корень из x
sign(x)	функция знака: -1 если x<0, 1 если x>0 и 0 если x=0
Тригонометрические функции
sin(x)	синус х
cos(x)	косинус х
tg(x) или tan(x)	тангенс х
ctg(x) или cot(x)	котангенс х
arcsin(x) или asin(x)	арксинус х
arccos(x) или acos(x)	арккосинус х
arctg(x) или atan(x)	арктангенс х
arcctg(x) или acot(x)	арккотангенс х
sinh(x) или sh(x)	гиперболический синус х
cosh(x) или ch(x)	гиперболический косинус х
tanh(x) th(x)	гиперболический тангенс х
coth(x) или cth(x)	гиперболический котангенс х
asinh(x)	гиперболический арксинус х
acosh(x)	гиперболический арккосинус х
atanh(x)	гиперболический арктангенс х
acoth(x)	гиперболический арккотангенс х

Встроенные константы

Имя	Описание
pi	Пи = 3,14. ..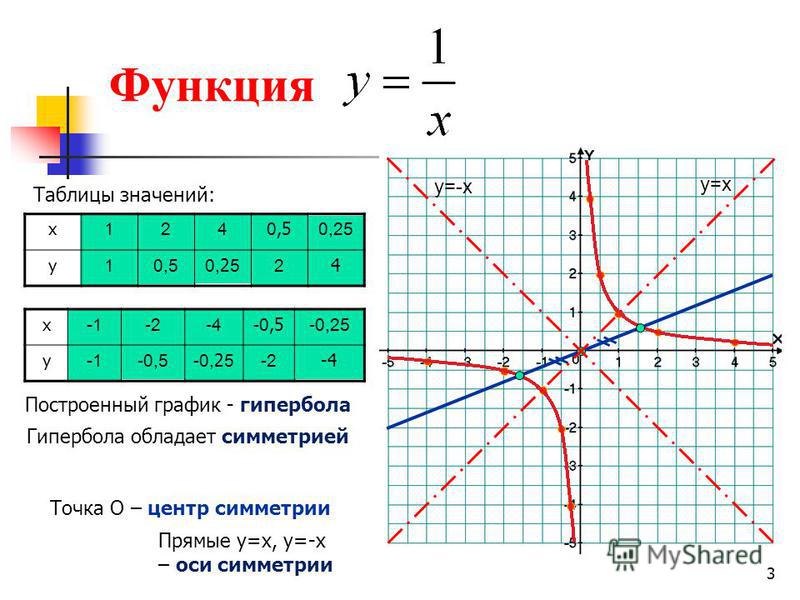
e	e = 2,71828… число Эйлера

Построить график тангенса онлайн. Строим график функций онлайн

«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.

«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).

«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а

«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.

«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.

Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.

1. Построение графика функции y = |f(x)|

Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.

Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.

1) Построить аккуратно и внимательно график функции y = f(x).

2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.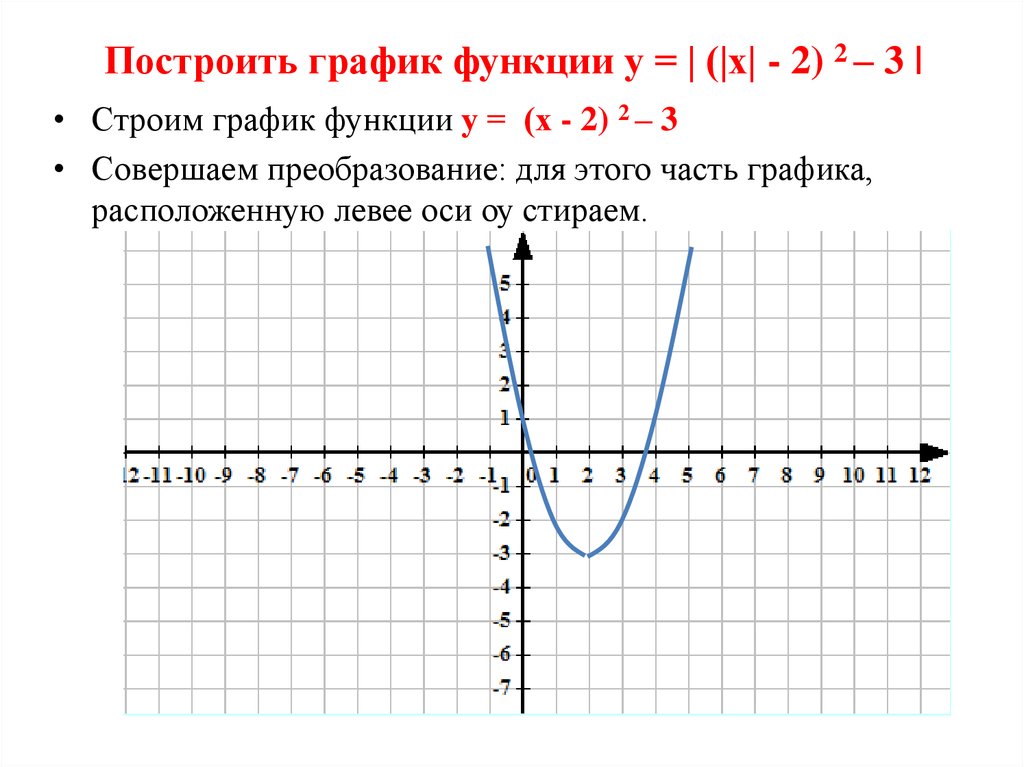

3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

Пример 1. Изобразить график функции y = |x 2 – 4x + 3|

1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.

x 2 – 4x + 3 = 0.

x 1 = 3, x 2 = 1.

Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).

y = 0 2 – 4 · 0 + 3 = 3.

Следовательно, парабола пересекает ось 0y в точке (0, 3).

Координаты вершины параболы:

x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.

Следовательно, точка (2, -1) является вершиной данной параболы.

Рисуем параболу, используя полученные данные (рис. 1)

2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.

3) Получаем график исходной функции (рис. 2 , изображен пунктиром).

2. Построение графика функции y = f(|x|)

Заметим, что функции вида y = f(|x|) являются четными:

y(-x) = f(|-x|) = f(|x|) = y(x).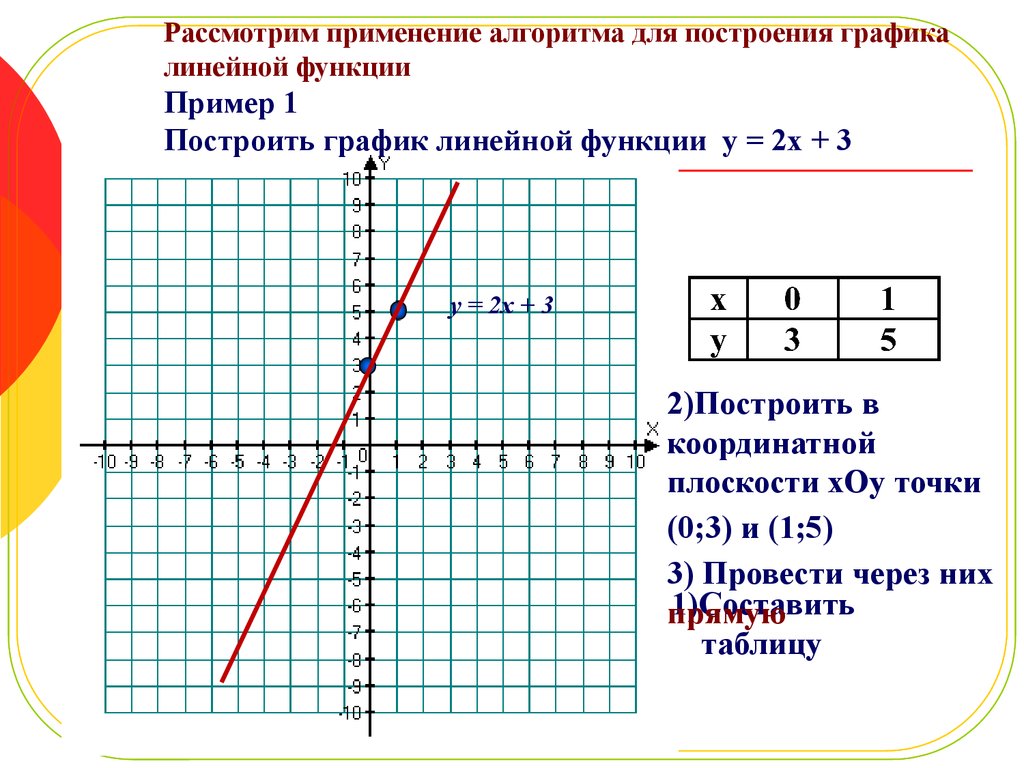 Значит, графики таких функций симметричны относительно оси 0y.

Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.

1) Построить график функции y = f(x).

2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3

Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.

1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).

2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отображаем правую часть графика симметрично оси 0y.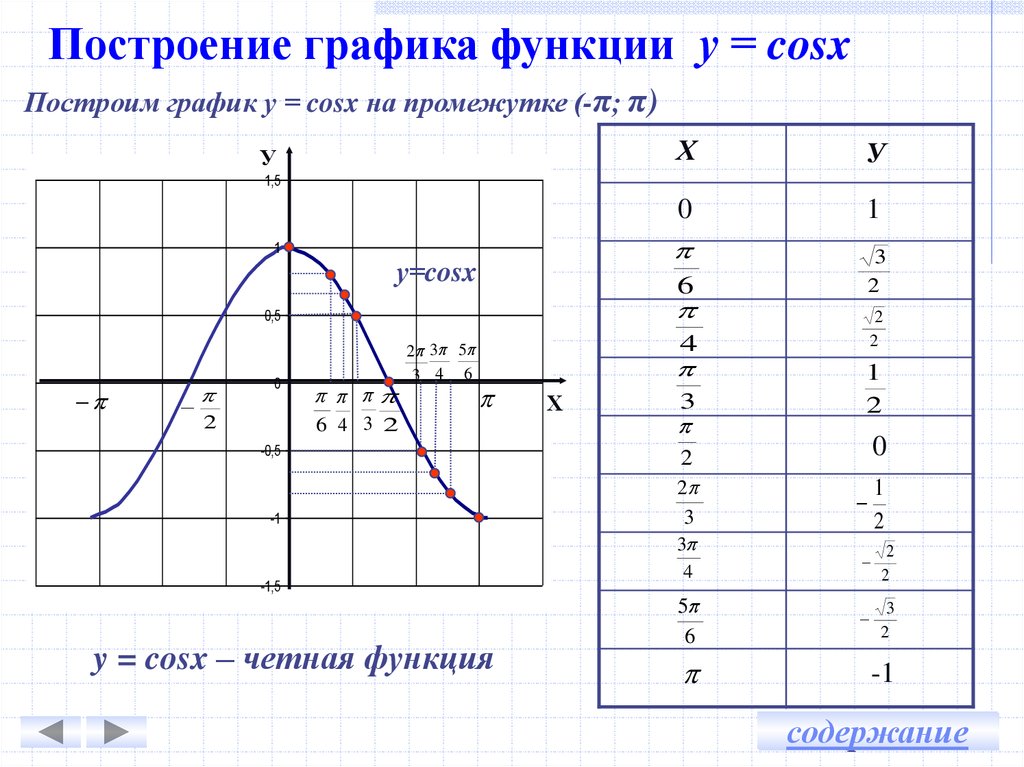

(рис. 3) .

Пример 3. Изобразить график функции y = log 2 |x|

Применяем схему, данную выше.

1) Строим график функции y = log 2 x (рис. 4) .

3. Построение графика функции y = |f(|x|)|

Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Чтобы построить график функции y = |f(|x|)|, необходимо:

1) Построить аккуратно график функции y = f(|x|).

2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.

3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.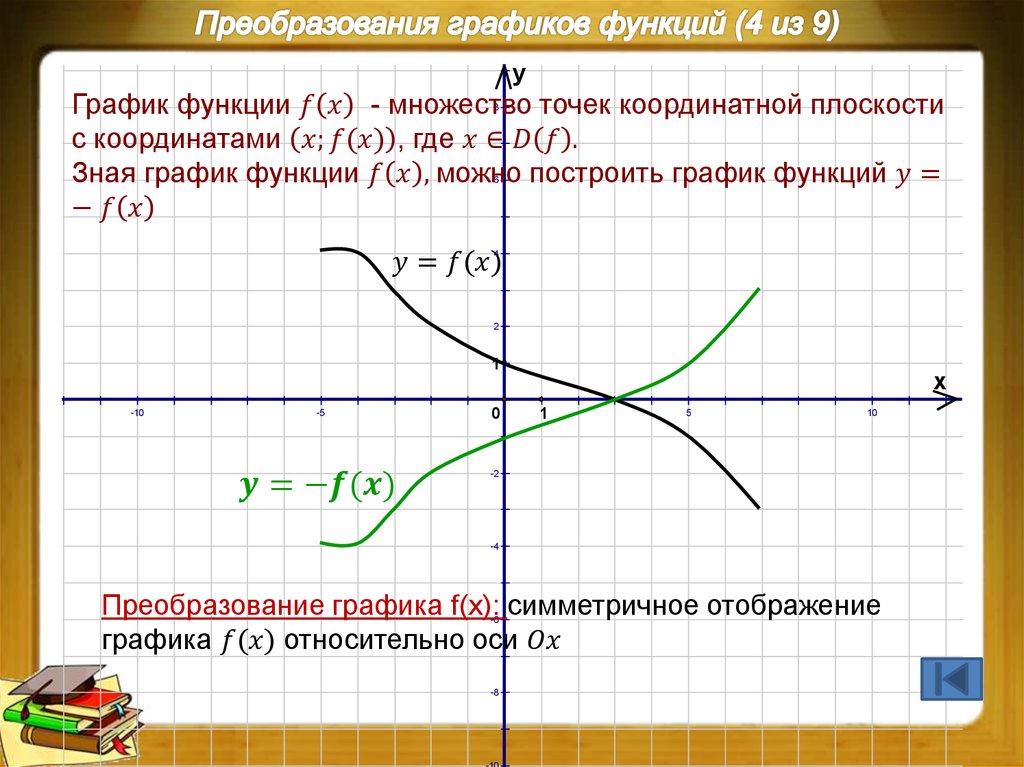

1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1

можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.

Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.

a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .

b) Оставляем ту часть графика, которая расположена в правой полуплоскости.

c) Отображаем полученную часть графика симметрично оси 0y.

d) Полученный график изображен на рисунке пунктиром (рис. 7) .

2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.

3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.

4) Полученный график изображен на рисунке пунктиром (рис. 8) .

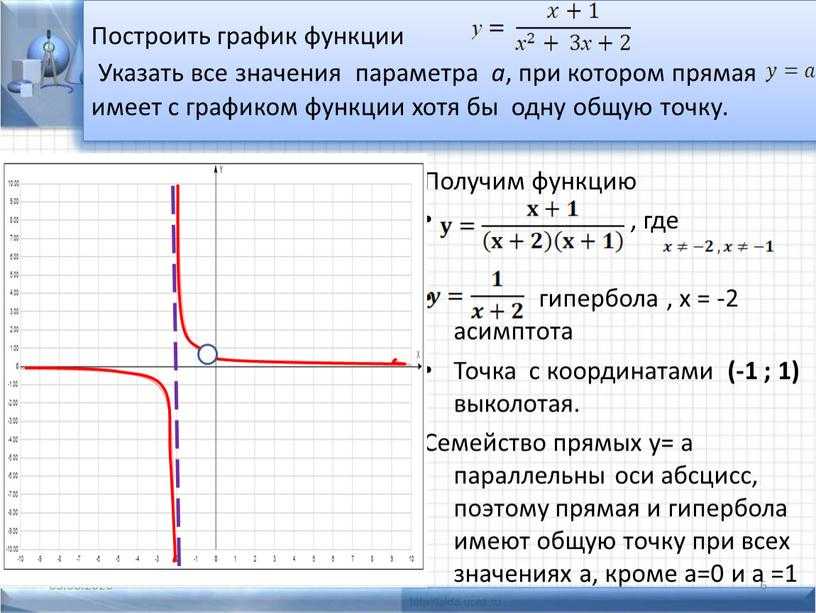
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|

1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.

a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .

Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.

2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.

3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.

4) Окончательный график изображен на рисунке (рис. 11) .

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.

Что такое график функций

Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.

На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .

Сервисы для построения графиков функций онлайн

Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.

Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн.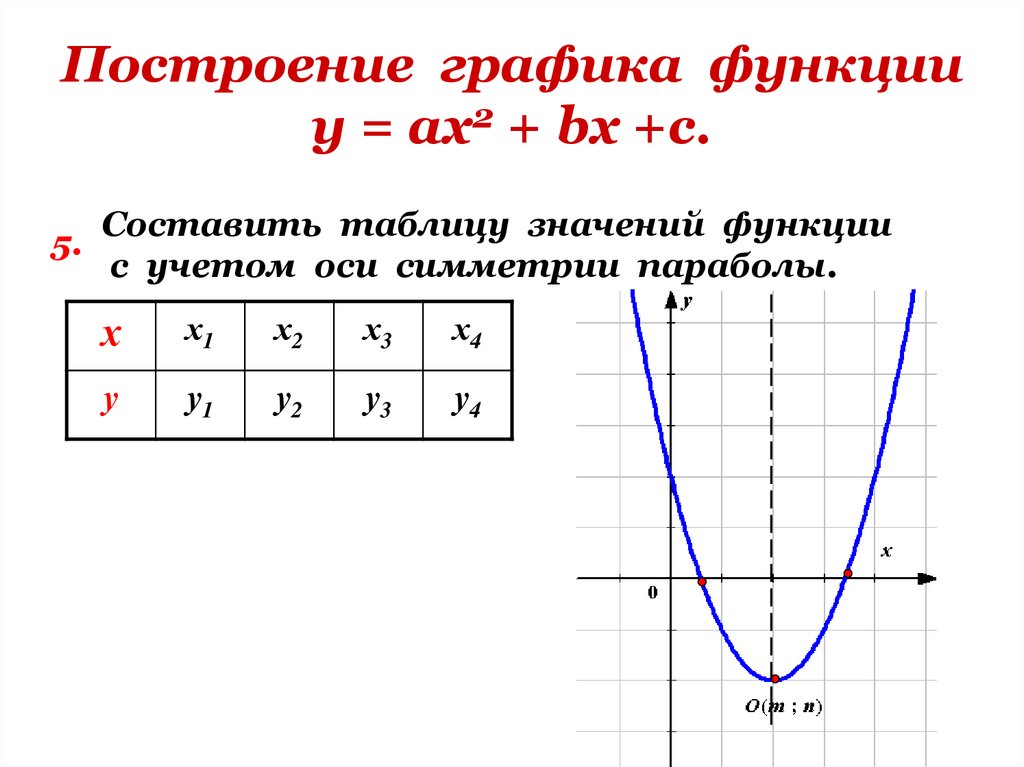 Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.

Инструкция:

1. Введите ваше уравнение в поле после знака «=».
2. Нажмите кнопку «Построить график» .

Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.

В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.

Инструкция:

1. Выберите необходимый способ задания графика.
2. Введите уравнение.
3. Задайте интервал.
4. Нажмите кнопку «Построить» .

Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.

Инструкция:

1. Найдите в списке необходимую вам функцию.
2. Щелкните на нее левой кнопкой мыши
3. При необходимости введите коэффициенты в поле «Функция:» .
4. Нажмите кнопку «Построить» .

В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.

Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).

Инструкция:

1. В левом столбце кликните правой кнопкой мыши по свободной строке.
2. В нижнем левом углу нажмите на значок клавиатуры.
3. На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
4. График строится в реальном времени.

Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.

Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!

функций DigitalOcean | Запуск функций по запросу. Автоматическое масштабирование.

Функции DigitalOcean | Запуск функций по запросу. Автоматическое масштабирование.

DigitalOcean Functions — это решение для бессерверных вычислений, которое запускается по требованию и позволяет вам сосредоточиться на своем коде, мгновенно и уверенно масштабироваться и экономить средства, устраняя необходимость в обслуживании серверов.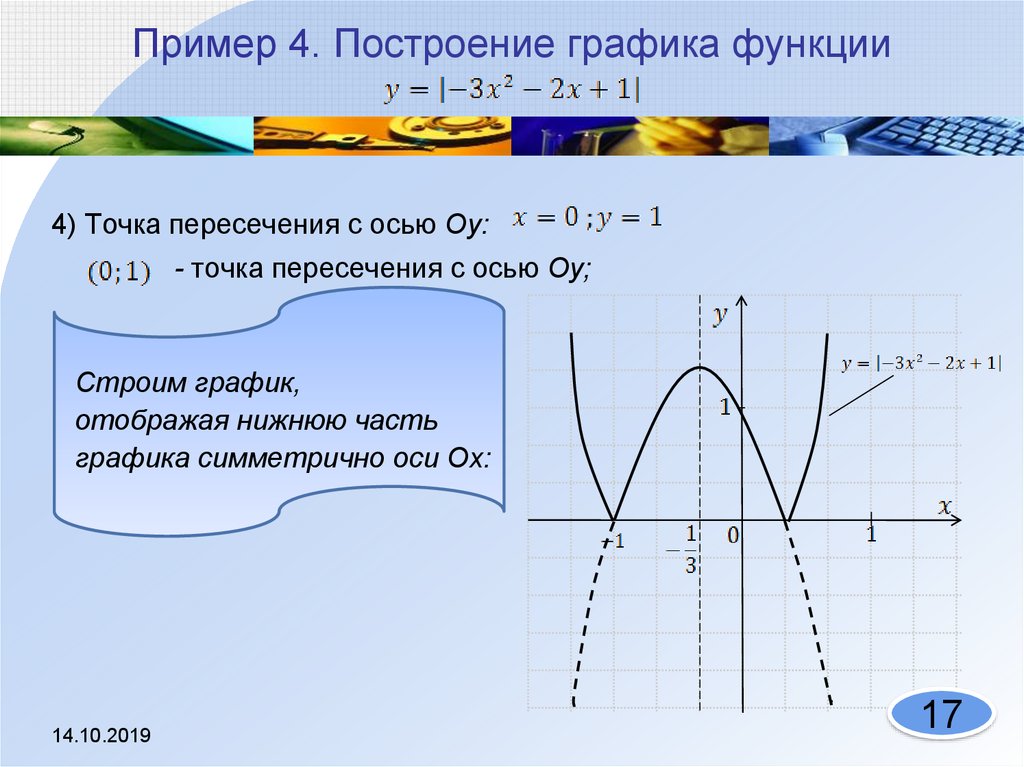

Быстро создавайте или улучшайте свои приложения без управления ресурсами

Сосредоточьтесь на создании отличных приложений

Быстро разрабатывайте и запускайте современные приложения без подготовки или управления серверами. С легкостью создавайте или расширяйте свои приложения, не изучая новые платформы или языки.

Узнайте, как

Платите только тогда, когда ваши ресурсы активны

Вызов функций (фрагментов кода) в ответ на веб-события. Вы будете платить только тогда, когда ваши ресурсы активны, что экономит ваши деньги.

Посмотреть цены

Автоматическое масштабирование в зависимости от спроса

Мгновенное и автоматическое масштабирование в зависимости от спроса без необходимости в предварительно выделенных ресурсах.

Прочесть документацию

Автоматическое развертывание с помощью App Platform

Легко добавляйте функции в качестве компонентов вашего приложения или веб-сайта и развертывайте их в рабочей среде с помощью App Platform.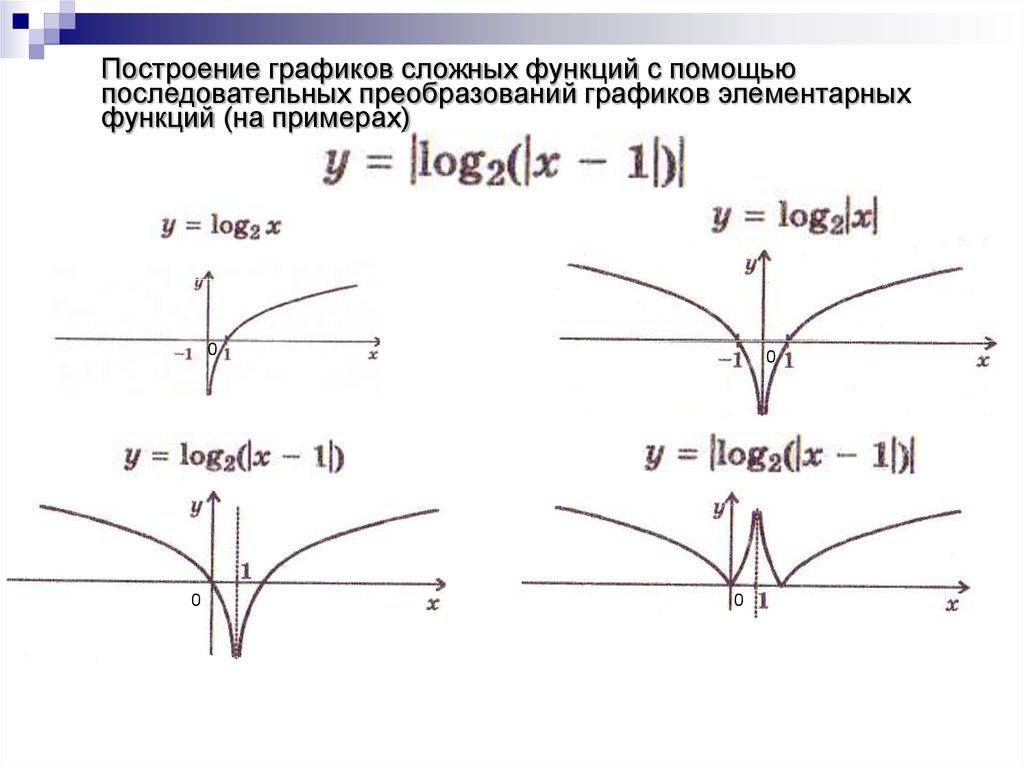

Попробуйте App Platform

Что вы можете создать с помощью функций DigitalOcean

Быстро создавайте API-интерфейсы и добавляйте их на свой веб-сайт или в приложение без изучения нового языка или инфраструктуры ценообразование

DigitalOcean Functions — это решение для бессерверных вычислений, которое запускается по требованию и позволяет вам сосредоточиться на коде, мгновенно и уверенно масштабироваться и экономить средства за счет устранения необходимости в обслуживании серверов.

Посмотреть все цены

90 000

Gib-Seconds of Compute на месяц на счет

$ 0,0000185

за Gib-Seconds для дополнительной памяти и времени выполнения

100 мс

Минимальное время выполнения на функцию

.0003

It enables us to quickly add serverless APIs to our website resulting in increased team productivity and faster time to market.»> DigitalOcean Functions — это отличное сочетание гибкости и простоты использования, которое позволяет моей команде управлять всеми проектами у одного поставщика. Это позволяет нам быстро добавлять бессерверные API-интерфейсы на наш веб-сайт, что повышает производительность команды и ускоряет выход продукта на рынок.

Джонатан Хсу

Директор по работе с клиентами Zerion Software

«> Мы работаем на бессерверной платформе Nimbella уже несколько лет. Мы рады, что теперь мы можем использовать функции DigitalOcean с той же простотой и производительностью для разработчиков, на которую мы рассчитывали. Добавление собственной базы данных, автоматических сборок, статических сайтов и наших собственных доменов, интегрированных с платформой приложений DigitalOcean, позволяет нам еще больше сосредоточиться на повышении ценности для наших клиентов и развитии нашего бизнеса.

Робин Аззам

Генеральный директор Caputron

Узнайте, как легко создавать и добавлять функции в свои приложения

Узнайте, как использовать App Platform для добавления функций в качестве компонентов ваших приложений. Узнайте, как можно использовать консоль разработчика функций и интерфейс командной строки для быстрого создания, тестирования и развертывания функций.

Ознакомьтесь с нашими продуктами

Начните создавать сегодня

Зарегистрируйтесь сейчас, и вы сможете начать работу с DigitalOcean всего за несколько минут.

Зарегистрируйтесь, чтобы начать работу

Разрабатывайте и внедряйте лучшие веб-интерфейсы в рекордно короткие сроки

Самый быстрый способ объединить ваши любимые инструменты и API для создания самых быстрых сайтов, магазинов и приложений для Интернета.

• Начать сборку бесплатно
• Запросить демонстрацию

3 000 000 разработчики и бизнес
отправляются быстрее на Netlify.

Оптимизируйте рабочий процесс

Благодаря Netlify наши команды внедряют изменения 10-15 раз в день.

Харрисон Харниш,
Principal Software Engineer, Twilio

Your team’s tasks

• Scaling
• Devops
• Staging environment
• Global CDN
• Backups/rollbacks
• Production servers
• CI/CD
• Push code to git

Netlify solves

Все готово, уже

Пропустите мучительную настройку и devops.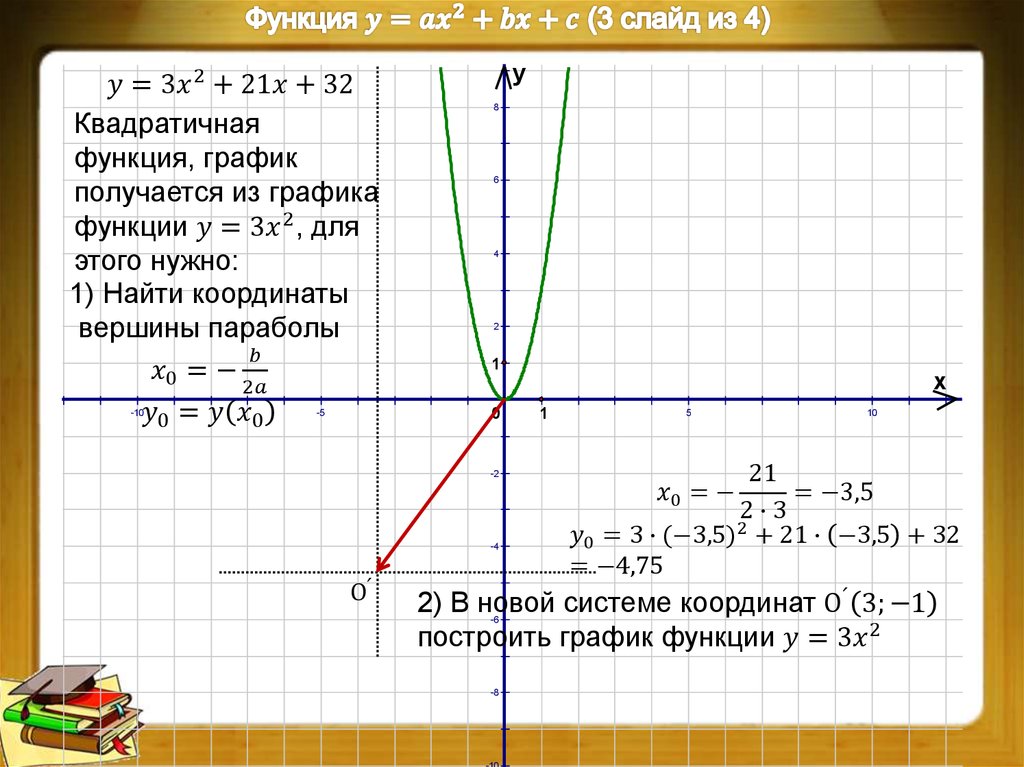 Netlify — это глобальная, готовая к работе среда с самого начала. Пропустите всю настройку сервера и сразу приступайте к сборке.

Развернуть сейчас

Мы можем запускать веб-сайты и кампании за считанные минуты без каких-либо операций, цель, которая часто была несбыточной мечтой в нашей отрасли.

Запустите что-то потрясающее

Быстро начните работу с одним из этих шаблонов. Нажмите, чтобы подключить поставщика Git. Netlify клонирует репозиторий и автоматически развернет ваш новый сайт.

Захватывающая разработка для местного развития

Полная платформа Netlify в вашем терминале. Разверните проект за считанные секунды, настройте сборку, протестируйте пограничные и бессерверные функции и разверните глобально — и все это из командной строки.

Запустите свой проект сейчас

Мы никак не могли разработать наш сайт за то время, когда обходились без Netlify.

◈ Разработчик Netlify ◈ $ netlify разработчик ◈ Запуск Netlify Dev с Eleventy > alt-opt@1. 0.0 смотреть:11ty > одиннадцать —служить —тихо Просмотр файлов…

Стройте из чего угодно, подключайтесь ко всему

Все ваши инструменты. Все ваши данные. Вместе. Благодаря первоклассной поддержке всех современных веб-фреймворков и широкой экосистеме интеграций API Netlify поможет вам создать сайт или приложение любого типа, которые вы только можете себе представить, используя лучшие инструменты для работы.

Ознакомьтесь с нашими интеграциями

Используя Next.js с Netlify, наш клиент упростил рабочий процесс своей веб-команды и повысил общую производительность.

Время развертывания: нажмите на Git, и готово

Быстрая и отказоустойчивая сеть для веб-приложений. При каждом развертывании ваши приложения публикуются для обслуживания во всех наших глобальных периферийных местоположениях. Ваши собственные веб-серверы и CDN больше не требуются.

Начните строить сейчас

Наш веб-сайт стал более гибким и надежным и работает в три раза быстрее, чем раньше.

No related posts.