С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
Построить кривую, заданную параметрическими уравнениями \
Исследуем сначала графики функций \(x\left(t \right)\) и \(x\left(t \right)\).
На втором промежутке \(\left({ — 2, — 1} \right)\) переменная \(x\) возрастает от \(x\left({ — 2} \right) = — 2\)
до \(x\left({ — 1} \right) = 1,\) а переменная \(y\) убывает от \(y\left({ — 2} \right) = 8\) до
\(y\left({ — 1} \right) = 5.
На третьем интервале \(\left({ — 1,\large\frac{1}{3}\normalsize} \right)\) обе переменные убывают. Значение \(x\) изменяется от \(x\left({ — 1} \right) = 1\) до \(x\left({\large\frac{1}{3}\normalsize} \right) = — \large\frac{5}{{27}}\normalsize.\) Соответственно, значение \(y\) уменьшается от \(y\left({ — 1} \right) = 5\) до \(y\left({\large\frac{1}{3}\normalsize} \right) = — \large\frac{29}{{27}}\normalsize.\) Кривая \(y\left(x \right)\) при этом пересекает начало координат.
На четвертом интервале \(\left({\large\frac{1}{3}\normalsize,\large\frac{2}{3}\normalsize} \right)\)
переменная \(x\) возрастает от \(x\left({\large\frac{1}{3}\normalsize} \right) = — \large\frac{5}{{27}}\normalsize\)
до \(x\left({\large\frac{2}{3}\normalsize} \right) = \large\frac{2}{{27}}\normalsize,\)
а переменная \(y\) убывает от \(y\left({\large\frac{1}{3}\normalsize} \right) = — \large\frac{29}{{27}}\normalsize\)
до \(y\left({\large\frac{2}{3}\normalsize} \right) = — \large\frac{40}{{27}}\normalsize.
Исследуем также выпуклость данной кривой. Вторая производная
\(y»»\left(x \right)\) имеет вид:
\[
y»»\left(x \right) = {y»»_{xx}} = \frac{{{{\left({{y»_x}} \right)}»_t}}}{{{x»_t}}}
= \frac{{{{\left({\frac{{3{t^2} + 4t — 4}}{{3{t^2} + 2t — 1}}} \right)}^\prime }}}{{{{\left({{t^3} + {t^2} — t} \right)}^\prime }}}
= \frac{{\left({6t + 4} \right)\left({3{t^2} + 2t — 1} \right) — \left({3{t^2} + 4t — 4} \right)\left({6t + 2} \right)}}{{{{\left({3{t^2} + 2t — 1} \right)}^3}}}
= \frac{{18{t^3} + 12{t^2} + 12{t^2} + 8t — 6t — 4 — \left({18{t^3} + 24{t^2} — 24t + 6{t^2} + 8t — 8} \right)}}{{{{\left({3{t^2} + 2t — 1} \right)}^3}}}
= \frac{{\cancel{\color{blue}{18{t^3}}} + \color{red}{24{t^2}} + \color{green}{2t} — \color{maroon}{4} — \cancel{\color{blue}{18{t^3}}} — \color{red}{30{t^2}} + \color{green}{16t} + \color{maroon}{8}}}{{{{\left({3{t^2} + 2t — 1} \right)}^3}}}
= \frac{{ — \color{red}{6{t^2}} + \color{green}{18t} + \color{maroon}{4}}}{{{{\left({3{t^2} + 2t — 1} \right)}^3}}}
= \frac{{ — 6\left({t — \frac{{9 — \sqrt {105} }}{6}} \right)\left({t — \frac{{9 + \sqrt {105} }}{6}} \right)}}{{{{\left({t + 1} \right)}^3}{{\left({3t — 1} \right)}^3}}}.
\]
Следовательно, вторая производная меняет свой знак на противоположный при переходе через следующие точки (рис.\(15с\)):
\[
{{t_1} = — 1:\;\;x\left({ — 1} \right) = 1,}\;\;
{y\left({ — 1} \right) = 5;}
\]
\[
{{t_2} = \frac{{9 — \sqrt {105} }}{6}:}\;\;
{x\left({\frac{{9 — \sqrt {105} }}{6}} \right) \approx 0,24;}\;\;
{y\left({\frac{{9 — \sqrt {105} }}{6}} \right) \approx 0,91;}
\]
\[
{{t_3} = \frac{1}{3}:}\;\;
{x\left({\frac{1}{3}} \right) = — \frac{5}{{27}},}\;\;
{y\left({\frac{1}{3}} \right) = — \frac{{29}}{{27}};}
\]
\[
{{t_4} = \frac{{9 + \sqrt {105} }}{6}:}\;\;
{x\left({\frac{{9 + \sqrt {105} }}{6}} \right) \approx 40,1;}\;\;
{y\left({\frac{{9 + \sqrt {105} }}{6}} \right) \approx 40,8.}
\]
Поэтому указанные точки представляют собой точки перегиба кривой \(y\left(x \right).\)
Схематический график кривой \(y\left(x \right)\) показан выше на рисунке \(15b.\)
«Преобразование функций» — Качелями. Сдвиг по оси y вверх. Включи полную громкость – увеличишь a (амплитуду) колебаний воздуха.
Сдвиг по оси x влево. Задачи урока. 3 балла. Музыкой. Постройте график функции и определите D(f), E(f) и T: Сжатие по оси x. Сдвиг по оси y вниз. Добавь красного цвета в палитру – уменьшишь k (частоту) электромагнитных колебаний.
«Функции нескольких переменных» — Производные высших порядков. Функцию двух переменных можно изобразить графически. Дифференциальное и интегральное исчисления. Внутренние и граничные точки. Определение предела функции 2-х переменных. Курс математического анализа. Берман. Предел функции 2-х переменных. График функции. Теорема. Ограниченная область.
«Понятие функции» — Способы построение графиков квадратичной функции. Изучение разных способов задания функции – важный методический прием. Особенности изучения квадратичной функции. Генетическая трактовка понятия «функция». Функции и графики в школьном курсе математики. Представление о линейной функции выделяется при построении графика некоторой линейной функции.
«Тема Функция» — Анализ. Нужно выяснить не то, что ученик не знает, а то, что он знает.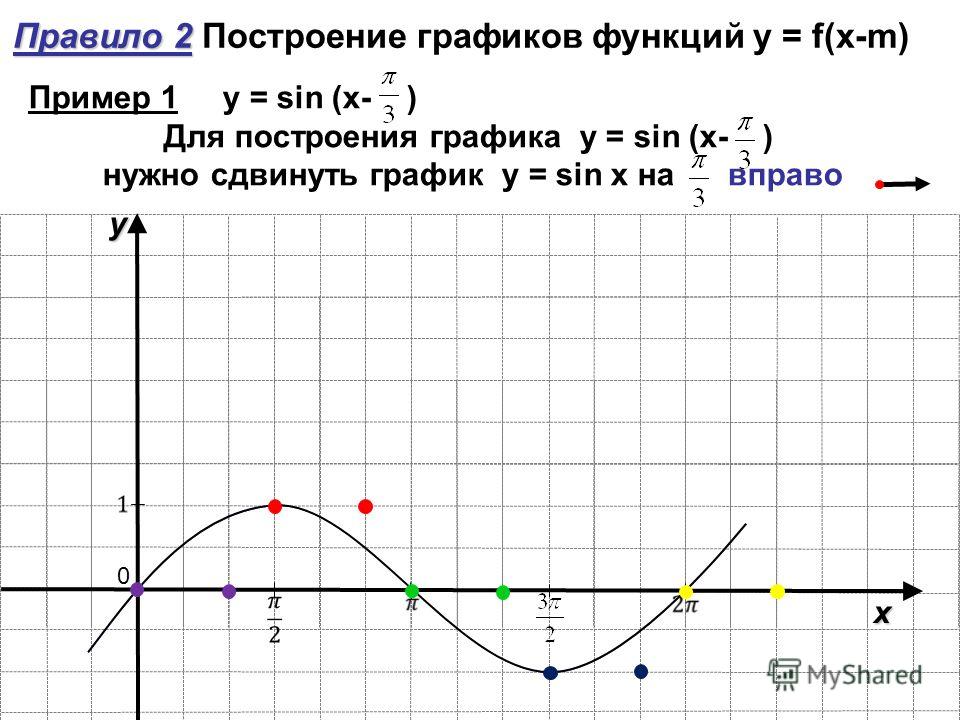
Заложение основ для успешной сдачи ЕГЭ и поступление в ВУЗы. Синтез. Если ученики работают по-разному, то и учитель должен с ними работать по-разному. Аналогия. Обобщение. Распределение заданий ЕГЭ по основным блокам содержания школьного курса математики.
«Преобразование графиков функций» — Повторить виды преобразований графиков. Сопоставить каждому графику функцию. Симметрия. Цель урока: Построение графиков сложных функций. Рассмотрим примеры преобразований, объясним каждый вид преобразования. Преобразование графиков функций. Растяжение. Закрепить построение графиков функций с использованием преобразований графиков элементарных функций.
«Графики функций» — Функция вида. Область значений функции – все значения зависимой переменной у. Графиком функции является парабола. Графиком функции является кубическая парабола. Графиком функции является гипербола. Область определения и область значений функции. Каждую прямую соотнесите с её уравнением: Область определения функции – все значения независимой переменной х.
План построения квадратичной функции.
1. Область определения функции (D (y )).
2. Графиком данной функции является парабола, ветви которой направлены вверх (вниз), т.к. а = __ > 0 (а = __
3. Координаты вершины параболы.
4. Уравнение оси симметрии.
5. Точка пересечения графика с осью OY .
6. Нули функции.
7. Таблица значений функции.
8. График.
Пример построения графика функции y = x 2 – 4 x + 3
1. D (y ) = (- ∞; + ∞).
2. Графиком данной функции является парабола, ветви которой направлены вверх, т. к. а = 1 > 0.
3. Координаты вершины параболы:
x 0 = — , y 0 = 2 2 — 4·2 + 3 = 4 – 8 + 3 = — 1.
4. Уравнение оси симметрии x = 2.
5. Точка пересечения с осью OY (0; 3).
6. Нули функции:
x 2 – 4 x + 3 = 0 D = (- 4) 2 – 4 ·1·3 = 16 -12 = 4 = 2 2
x 1 = = 1 x 2 = = 3
7.
Составим таблицу значений функции:
0
1
2
3
3
0
— 1
0
8. Построим график
Свойства функции:
1. Множество значений функции (E (y )).
2. Промежутки знакопостоянства функции (y >0, y
3. Промежутки монотонности функции (возрастает, убывает).
4. Точки максимума и минимума функции.
Свойства функции y = x 2 – 4 x + 3.
1. E (y ) = [-1; + ∞).
2. y
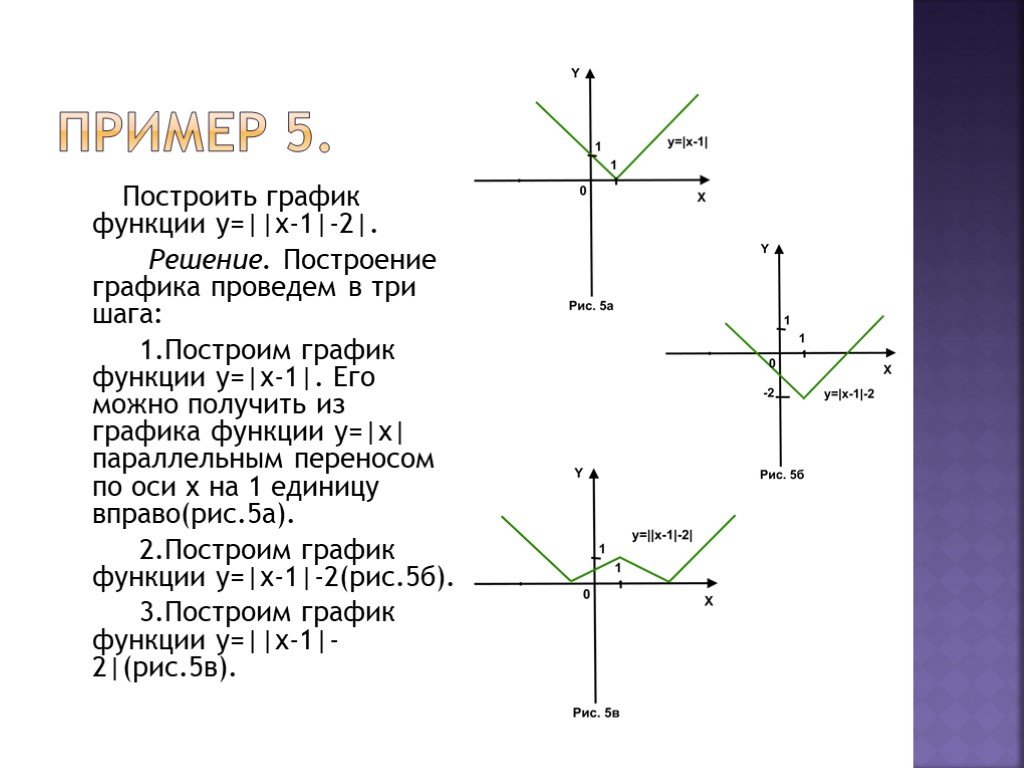
Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=— (x-3)-(— (x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+ (x-3)-(+ (x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5.
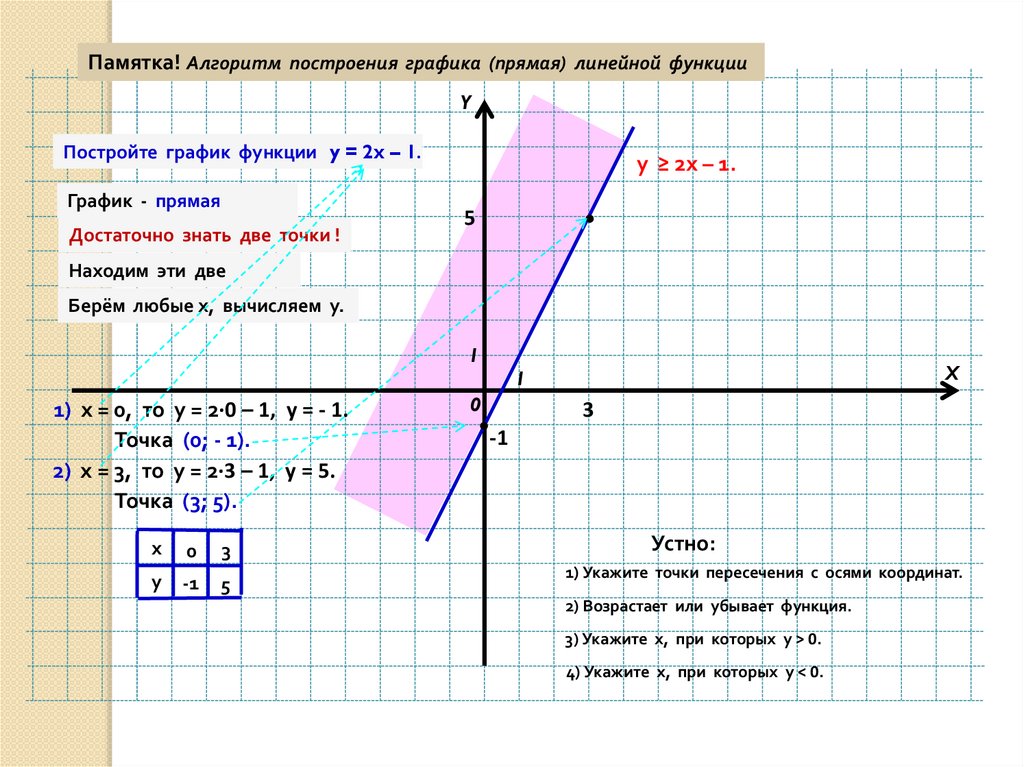Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.
Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U}
ДИАГРАММА РАСПРЕДЕЛЕНИЯ в программировании R 🟢 [С ПРИМЕРАМИ]
Диаграммы рассеяния — это дисперсионных графика, построенных для представления точек данных переменных (обычно двух, но также может быть и три). Основное использование точечной диаграммы в R — визуально проверить, существует ли какая-то связь между числовыми переменными.
- 1 Как сделать точечный график в R?
- 1.1 Диаграмма рассеяния в R с разными цветами
- 1.2 Диаграмма рассеяния с линией регрессии
- 1.3 Добавление нескольких рядов к диаграмме рассеяния R
- 1,4 График рассеяния с стержнями ошибок в R
- 1.5 Подключенный рассеянный диаграмм в R
- 2 гладкий диаграмм рассеяния с функцией гладкого рассеяния
- 2.1 Heat Map R Scatter Drise
- 3 Функция Scatterplot в R 9007 40010
- 3 Функция Scatterplot в R
- 40010
- матрица в R
- 5 Точечная диаграмма в ggplot2
- 6 3D R точечная диаграмма
Как сделать точечную диаграмму в R?
Вы можете создать точечную диаграмму в R с графиком , указав значения x в первом аргументе и значения y во втором, являющиеся числовыми векторами x и y одинаковой длины.
При передаче этих параметров функция plot по умолчанию создаст точечную диаграмму. Вы также можете указать символ точек данных или даже цвет среди других графических параметров. Вы можете просмотреть, как настроить все доступные аргументы в нашем руководстве по созданию графиков в R. 92 + eps
Для построения графика наблюдений введите:
plot(x, y, pch = 19, col = "черный")
plot(y ~ x, pch = 19, col = "black") # Эквивалент Кроме того, вы можете использовать функцию идентификации , чтобы вручную пометить некоторые точки данных графика , например, некоторые выбросы. В аргументе labels вы можете указать нужные метки для каждой точки.
В этом примере мы собираемся определить координаты выбранных точек. Когда закончите, вам нужно будет нажать Esc . Если вам нужно найти дополнительные аргументы или более подробные объяснения функции, введите ?identify в командной консоли.
определить(y ~ x, labels = paste0("(", round(x, 2), ", ", round(y, 2), ")")) Точечная диаграмма в R с разными цветами
Если у вас есть переменная, которая классифицирует точки данных по некоторым группам, вы можете установить ее в качестве параметра аргумента col , чтобы отображать точки данных разными цветами , в зависимости от его группы, или даже установить разные символы по группам.
group <- as.factor(ifelse(x < 0,5, "Группа 1", "Группа 2")) plot(x, y, pch = as.numeric(group), col = group) Scatter график с линией регрессии
Как мы уже говорили во введении, основное использование диаграмм рассеяния в R — проверка связи между переменными . Для этого вы можете добавить линии регрессии (или добавить кривые в случае нелинейных оценок) с 92, столбец = "2", lwd = 3, lty = 2) # Линейная подгонка abline(lm(y ~ x), col = "оранжевый", lwd = 3) # Гладкая посадка линии (lowess (x, y), col = "синий", lwd = 3) # Легенда legend("topleft", legend = c("Теоретическая", "Линейная", "Гладкая"), lwd = 3, lty = c(2, 1, 1), col = c("красный", "оранжевый", "синий"))
Кроме того, вы можете добавить корреляцию Пирсона между переменными, которую вы можете вычислить с помощью функция соответствует функции .
Затем вы можете поместить вывод в некоторые координаты графика с помощью текст функция.
# Рассчитать корреляцию
Исправить <- кор (х, у)
# Создайте график и добавьте вычисленное значение
график (х, у, pch = 19)
text(paste("Correlation:", round(Corr, 2)), x = 0,2, y = 4,5) Добавить несколько рядов к диаграмме рассеяния R
Вы также можете добавить больше данных к исходному графику с помощью точек функция, которая добавит новые точки поверх предыдущего графика, соблюдая исходный масштаб.
набор семян(1)
# Построить первую переменную
сюжет (х, у, pch = 19)
# Новая переменная
п <- 200
x2 <- runif(n)
у2 <- 2,5 + х2 + гнорм(п, 0, 0,1)
# Добавляем новую переменную
points(x2, y2, col = "green", pch = 19) Точечная диаграмма с планками погрешностей в R
Добавление погрешностей на точечную диаграмму в R довольно просто. Предположим, у вас есть 10 групп со средним по Гауссу и стандартным отклонением по Гауссу, как в следующем примере.
Вы можете построить данные и указать предел оси Y как диапазон нижнего и верхнего столбца. Затем вам нужно будет использовать стрелки функционируют следующим образом для создания планок погрешностей.
мои_данные <- 1:10
Среднее значение <- rnorm(10)
Sd <- rn(10, 1, 0,1)
сюжет (my_data, среднее значение,
ylim = диапазон (c (среднее - Sd, среднее + Sd)),
пч = 16)
# Планки ошибок
стрелки (x0 = мои_данные, y0 = среднее значение - Sd, x1 = мои_данные, y1 = среднее значение + Sd,
длина = 0,15, код = 3, угол = 90) Связная диаграмма рассеяния в R
Связная диаграмма рассеяния похожа на линейную диаграмму, но контрольных точек отмечены точками или другим символом. Для этого можно установить 91,05 + рнорм(11) график (x3, y3, type = "b", col = 2, lwd = 3, pch = 1) строки (x3, y4, type = "b", col = 3, lwd = 3, pch = 1) lines(x3, y5, type = "b", col = 4, lwd = 3, pch = 1)
Альтернативой является соединение точек стрелками:
# Функция для соединения точек стрелками
arrowsPlot <- function(x, y, lwd = 1, col = 1, angle = 20, length = 0.
2) {
невидимый (сочный (1: длина (x),
функция (i) стрелки (x[i], y[i], x[i + 1], y[i + 1], lwd = lwd,
col=col, angle=угол, length=длина)))
}
график (x3, y3, col = 2, lwd = 3, pch = "")
arrowsPlot(x3, y3, col = 2, lwd = 3)
строки (x3, y4, столбец = 3, lwd = 3)
arrowsPlot(x3, y4, col = 3, lwd = 3)
линии (x3, y5, столбец = 4, lwd = 3)
arrowsPlot(x3, y5, col = 4, lwd = 3) 93, об.(у3 + 5))
# Создаем подключенную диаграмму рассеяния
график (x4, y5, yaxt = "n", xaxt = "n", pch = "",
xlab = "Популярность", ylab = "Продажи", xlim = c(-1, 5.5))
arrowsPlot(x4, y5, col = 3, lwd = 3)
# Добавление лет к каждой точке
text(x4 + 0.3, y5, 1970:1980) 
2) {
невидимый (сочный (1: длина (x),
функция (i) стрелки (x[i], y[i], x[i + 1], y[i + 1], lwd = lwd,
col=col, angle=угол, length=длина)))
}
график (x3, y3, col = 2, lwd = 3, pch = "")
arrowsPlot(x3, y3, col = 2, lwd = 3)
строки (x3, y4, столбец = 3, lwd = 3)
arrowsPlot(x3, y4, col = 3, lwd = 3)
линии (x3, y5, столбец = 4, lwd = 3)
arrowsPlot(x3, y5, col = 4, lwd = 3) 93, об.(у3 + 5))
# Создаем подключенную диаграмму рассеяния
график (x4, y5, yaxt = "n", xaxt = "n", pch = "",
xlab = "Популярность", ylab = "Продажи", xlim = c(-1, 5.5))
arrowsPlot(x4, y5, col = 3, lwd = 3)
# Добавление лет к каждой точке
text(x4 + 0.3, y5, 1970:1980) Гладкая диаграмма рассеяния с функцией smoothScatter
Функция smoothScatter — это базовая функция R, которая создает сглаженную оценку плотности ядра цвета R-диаграммы рассеяния.
В следующих примерах показано, как использовать самые основные аргументы функции. Обратите внимание, что, как и в других непараметрических методах, вам нужно будет выбрать полосу пропускания.
Хотя функция обеспечивает пропускную способность по умолчанию, вы можете настроить ее с помощью 90,4,
colramp = colorRampPalette(c("#000099", "#00FEFF", "#45FE4F",
"#FCFF00", "#FF9400", "#FF3100")))
Можно даже добавить контур с помощью функции контур .
# install.packages("МАССА")
библиотека (МАСС)
керн <- kde2d(x, y)
контур (kern, drawlabels = FALSE, nlevels = 6,
col = rev(heat.colors(6)), add = TRUE, lwd = 3) Функция диаграммы рассеяния в R
Альтернативой для создания диаграмм рассеяния в R является использование функции диаграмма рассеяния Функция R из пакета car , которая автоматически отображает кривые регрессии и позволяет добавлять маргинальные диаграммы в точечную диаграмму.
# install.packages("car")
библиотека (машина)
диаграмма рассеяния (у ~ х)
scatterplot(x, y) # Эквивалент По умолчанию функция строит три оценки (линейное и непараметрическое среднее и условную дисперсию) с маргинальными ящичковыми диаграммами, и все они одного цвета.
Для того, чтобы настроить диаграмму рассеяния , вы можете использовать аргументы col и pch для изменения цвета и символа точек соответственно. Вы также можете передать аргументы в виде списка аргументам regLine и smooth , чтобы настроить графические параметры соответствующих оценок.
диаграмма рассеяния (х, у,
col = 1, # Изменить цвет точек
pch = 15, # Изменить символы
regLine = list(col = "green", # Цвет линии линейной регрессии
lwd = 3), # Толщина линии линейной регрессии
smooth = list(col.smooth = "red", # Непараметрический средний цвет
col.spread = "blue")) # Цвет непараметрической дисперсии Кроме того, если вы хотите удалить какую-либо из оценок, установите соответствующий аргумент равным FALSE .
диаграмма рассеяния (х, у,
smooth = FALSE, # Удаляет гладкую оценку
regLine = FALSE) # Удаляет линейную оценку Вы также можете установить только один предельный ящик с аргументом boxplots , который по умолчанию равен "xy" .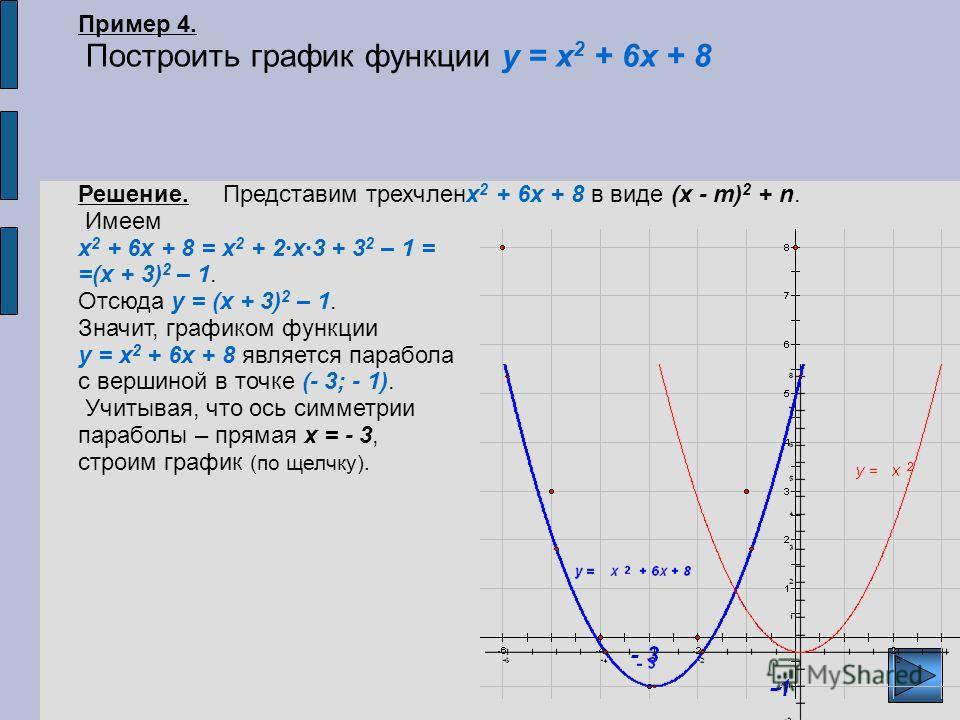
Если вы установите его на "x" , будет отображаться только ящичковая диаграмма оси X. То же самое для оси Y, если вы установите аргумент равным "у" . Если вам не нужен коробочный график, установите для него значение "" .
диаграмма рассеяния (х, у,
boxplots = "x") # Предельная диаграмма для оси x Если у вас есть группы, которые классифицируют данные, вы можете создать оценки регрессии для каждой группы, набрав:
Scatterplot(y ~ x | group) Обратите внимание, можно отключить легенду, установив для аргумента легенды значение FALSE .
Кроме того, вы можете отключить сетку графика или даже добавить эллипс с помощью сетка и эллипс аргументы соответственно.
диаграмма рассеяния (х, у,
boxplots = "", # Отключить boxplots
grid = FALSE, # Отключить сетку графика
ellipse = TRUE) # Рисование эллипсов Есть и другие аргументы, которые вы можете настроить, так что не забудьте ввести ?scatterplot для получения дополнительных сведений.
Матрица рассеяния в R
При работе с несколькими переменными обычно строят несколько диаграмм рассеяния в 9 матрице.0003 отображает каждую переменную по сравнению с другими , чтобы визуализировать корреляцию между переменными. Вы можете создать диаграмму рассеяния в R с несколькими переменными, известную как попарная диаграмма рассеяния или матрица диаграммы рассеяния, с помощью функции пар .
пары (~disp + wt + mpg + hp, data = mtcars) Кроме того, если ваш набор данных содержит факторную переменную, вы можете указать переменную в аргументе col следующим образом, чтобы построить группы с разными цвет.
пары(~disp + wt + mpg + hp, col = factor(mtcars$am), pch = 19, data = mtcars) Альтернативой является использование функции scatterplotMatrix пакета car , который добавляет оценки плотности ядра по диагонали.
install.packages("автомобиль")
библиотека (машина)
scatterplotMatrix(~ disp + wt + mpg + hp, data = mtcars) Вы можете настроить цвета предыдущего графика с соответствующими аргументами:
scatterplotMatrix(~ disp + wt + mpg + hp, data = mtcars,
диагональ = ЛОЖЬ, # Удалить оценки плотности ядра
regLine = list(col = "green", # Цвет линии линейной регрессии
lwd = 3), # Толщина линии линейной регрессии
smooth = list(col.smooth = "red", # Непараметрический средний цвет
col.spread = "blue")) # Цвет непараметрической дисперсии Другой альтернативой является использование функции cpairs пакета gclus .
# install.packages("gclus")
библиотека (gclus)
data <- mtcars[c(1, 3, 5, 6)] # Некоторые числовые переменные
# cpairs(data) # альтернатива pairs()
corr <- abs(cor(data)) # Корреляция по модулю
корр
цвета <- dmat. color(corr)
заказ <- заказ.сингл (корр.)
cpairs(data, order, panel.colors = colors, gap = 0.5,
main = "Отсортированные и окрашенные переменные по корреляции") 
color(corr)
заказ <- заказ.сингл (корр.)
cpairs(data, order, panel.colors = colors, gap = 0.5,
main = "Отсортированные и окрашенные переменные по корреляции") Точечная диаграмма в ggplot2
Создание точечной диаграммы с помощью библиотеки ggplot2 может быть достигнуто с помощью функции geom_point , и вы можете разделить группы по цвету, передав функцию aes с группой в качестве параметра цвета аргумент.
# install.packages("ggplot2")
библиотека (ggplot2)
my_df <- data.frame(x = x, y = y, group = group)
ggplot (my_df, aes (х = х, у = у)) +
geom_point(aes(color = group)) + # Точки и цвет по группе
scale_color_discrete("Группы") + # Изменить заголовок легенды
xlab("Переменная X") + # Метка оси X
ylab("Переменная Y") + # Метка оси Y
theme(axis.line = element_line(color = "black", # Изменяет тему по умолчанию
размер = 0,24)) 3D R scatterplot
С библиотеками scatterplot3d и rgl вы можете создать 3D точечных диаграмм в R .