Построить график функции x 3: Постройте график функции y = x-3

Функции y=x2 и y=x3 и их графики

Урок 23. Алгебра 7 класс

На этом уроке мы говорим о функциях y=x2и y=x3. Строим их графики. Выясняем некоторые свойства этих функций.

Конспект урока «Функции y=x2 и y=x3 и их графики»

Вопросы занятия:

·  рассмотреть функцию y = x², её свойства и график;

·  рассмотреть функцию y = х³, её свойства и график.

Материал урока

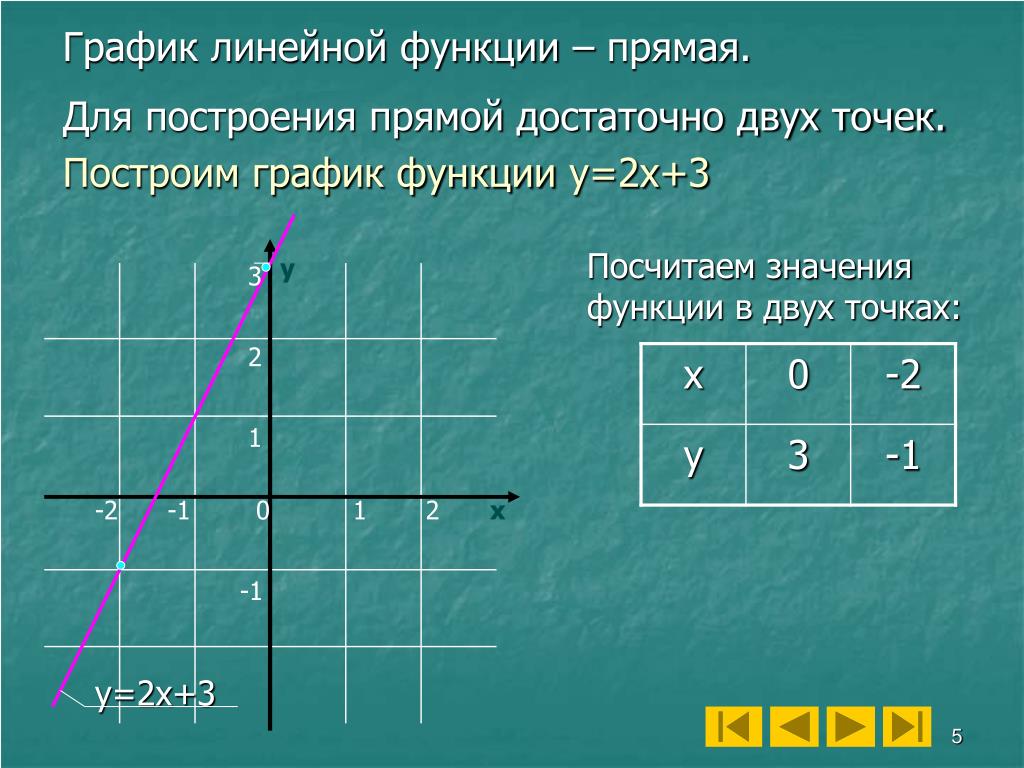
На одном из предыдущих уроков мы с вами познакомились с линейной функцией, которую можно задать формулой вида:

Также вспомним, что графиком линейной функции является прямая.

На этом уроке мы рассмотрим  функции:

А точнее, мы научимся строить графики этих функций и выясним некоторые их свойства.

Начнём с того, что выразим формулой зависимость площади квадрата от длины его стороны.

Таким образом, зависимость площади квадрата от его стороны является примером функции.

Давайте построим график этой функции.

Составим таблицу значений x, y.

Далее полученные точки изобразим на координатной плоскости и проведём через них плавную линию.

Обратите внимание, что этот график неограниченно продолжается вверх справа и слева от оси игрек.

Теперь выясним некоторые свойства функции y = x².

Из последнего свойства графика следует, что точки графика, имеющие противоположные абсциссы, симметричны относительно оси игрек.

Теперь давайте выразим формулой зависимость объёма куба от длины его ребра.

 Если мы будем менять длину ребра, то и его объём будет меняться.

Зависимость объёма куба от длины его ребра является примером функции.

Построим график этой функции.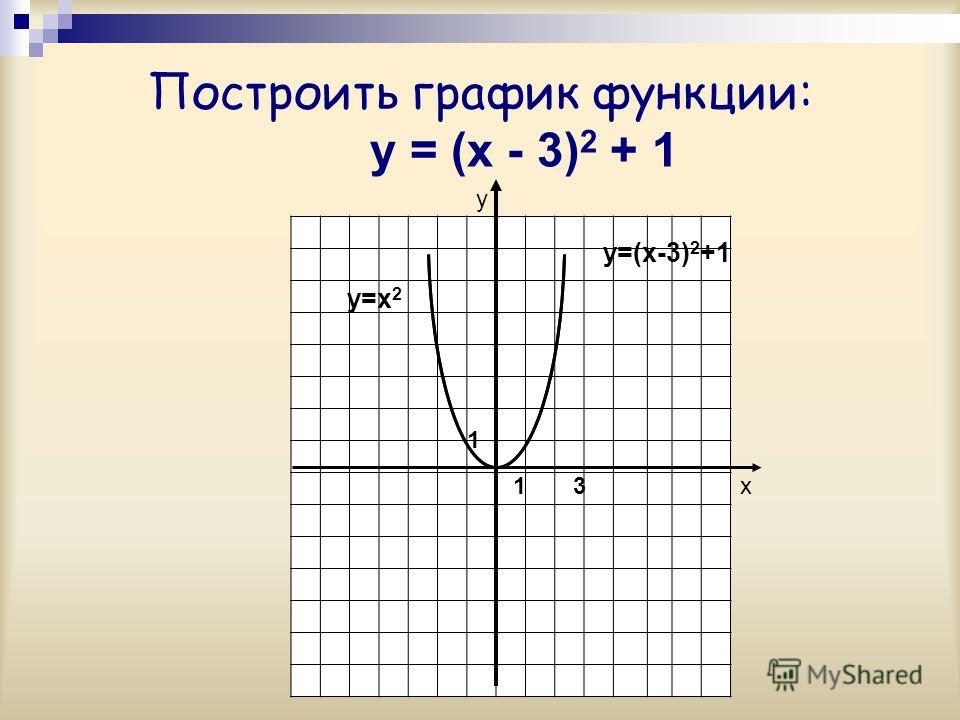

Для этого придадим несколько значений аргументу икс и вычислим соответствующие значения функции.

Изобразим точки с полученными координатами на координатной плоскости и проведём через них плавную линию.

Обратите внимание, что этот график можно неограниченно продолжать справа от оси игрек вверх и слева от оси игрек вниз.

Поговорим о свойствах функции игрек равняется икс в кубе.

Следовательно, точки графика, которые имеют противоположные абсциссы, расположены симметрично относительно начала координат.

В повседневной жизни представление о параболе дают нам, например, траектории прыжков животных, радуга. Тросы висячего моста напоминают нам параболы.

Также параболу часто можно встретить в архитектуре.

Предыдущий урок 22 Умножение одночленов. Возведение одночлена в степень

Следующий урок 24 Многочлен и его стандартный вид

Получите полный комплект видеоуроков, тестов и презентаций Алгебра 7 класс

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Степенная функция, ее свойства и график

Степенная функция, ее свойства и график

Вы знакомы с функциями y=x, y=x², y=x³, y=1/x и т. д. Все эти функции являются частными случаями степенной функции, т. е. функции y=x

p, где p — заданное действительное число.
Свойства и график степенной функции существенно зависит от свойств степени с действительным показателем, и в частности от того, при каких значениях x и p имеет смысл степень x^p. Перейдем к подобному рассмотрению различных случаев в зависимости от
показателя степени p.

1. Показатель p=2n -четное натуральное число.

В этом случае степенная функция y=x²ⁿ, где n — натуральное число, обладает следующими

свойствами:

• область определения — все действительные числа, т. е. множество R;
• множество значений — неотрицательные числа, т. е. y больше или равно 0;
• функция y=x²ⁿ  четная, так как x²ⁿ=(-x)²ⁿ
• функция является убывающей на промежутке x<0 и возрастающей на промежутке x>0.

График функции y=x²ⁿ имеет такой же вид, как например график функции y=x⁴.

        2. Показатель p=2n-1— нечетное натуральное число
В этом случае степенная функция  y=x^2n-1 , где натуральное число, обладает следующими свойствами:

• область определения — множество R;
• множество значений — множество R;
• функция y=x^2n-1 нечетная, так как (-x)^2n-1=x^2n-1;
• функция является возрастающей на всей действительной оси.

График функции y=x^2n-1 имеет такой же вид, как, например, график функции y=x³.

       3.Показатель p=-2n, где n — натуральное число.

В этом случае степенная функция y=x^-2n=1/x

2nобладает следующими свойствами:

• область определения — множество R, кроме x=0;
• множество значений — положительные числа y>0;
• функция  y=1/x²ⁿ четная, так как 1/(-x)²ⁿ=1/x²ⁿ;
• функция является возрастающей на промежутке x<0 и убывающей на промежутке x>0.

График функции y=1/x²ⁿ имеет такой же вид, как, например, график функции y=1/x².

       4.Показатель p=-(2n-1), где n — натуральное число.
В этом случае степенная функция y=x^-(2n-1) обладает следующими свойствами:

• область определения — множество R, кроме x=0;
• множество значений — множество R, кроме y=0;
• функция y=x^-(2n-1)
   нечетная, так как (-x)^-(2n-1) =-x^-(2n-1);
• функция является убывающей на промежутках x<0 и x>0.

График функции y=x^-(2n-1) имеет такой же вид, как, например, график функции y=1/x³.

Следующее Предыдущее Главная страница

Подписаться на: Комментарии к сообщению (Atom)

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Графики кубических функций – объяснение и примеры

Графики кубических функций дают двумерную модель функций, где x возведен в третью степень.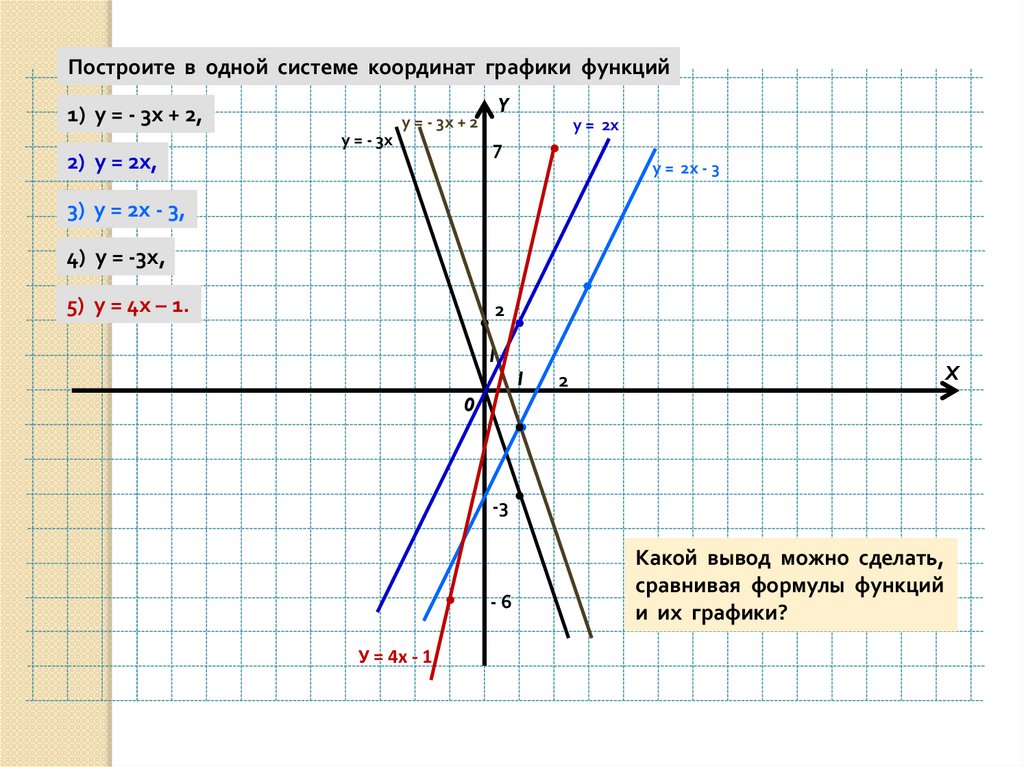

Графики кубических функций в некоторых отношениях аналогичны графикам квадратичных функций. В частности, мы можем использовать базовую форму кубического графика для создания моделей более сложных кубических функций.

Прежде чем научиться строить графики кубических функций, полезно ознакомиться с преобразованиями графиков, геометрией координат и построением графиков квадратичных функций. Графики кубических функций также потребуют приличного знакомства с алгеброй и алгебраическими манипуляциями с уравнениями.

В этом разделе мы рассмотрим:

• Как построить график кубической функции

Как построить график кубической функции

Перед построением графика кубической функции важно ознакомиться с исходной функцией , у=х ³ .

Существуют методы исчисления, позволяющие легко находить локальные экстремумы. В частности, мы можем найти производную кубической функции, которая будет квадратичной функцией.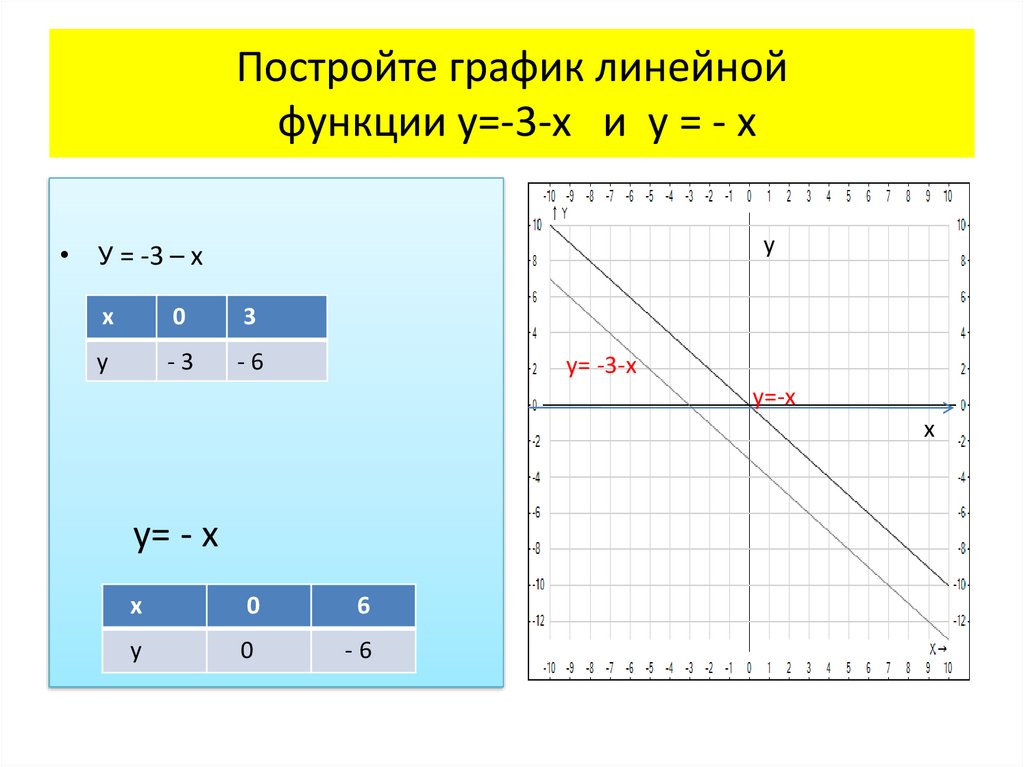 Затем мы можем использовать ключевые точки этой функции, чтобы выяснить, где находятся ключевые точки кубической функции. Однако это будет рассмотрено более подробно в разделах исчисления об использовании производной.

Здесь мы сосредоточимся на том, как мы можем использовать преобразования графа, чтобы найти форму и ключевые точки кубической функции.

Ключевые точки родительской функции

Родительская функция x ³ проходит через начало координат. Он имеет форму, похожую на две половинки параболы, направленные в противоположные стороны, склеенные вместе.

Вершина

Вершина кубической функции — это точка, в которой функция меняет направление. В родительской функции эта точка является исходной.

Чтобы сдвинуть эту вершину влево или вправо, мы можем добавлять или вычитать числа из куба функции. Например, функция (x-1) ³ — это кубическая функция, сдвинутая на одну единицу вправо. В этом случае вершина находится в (1, 0).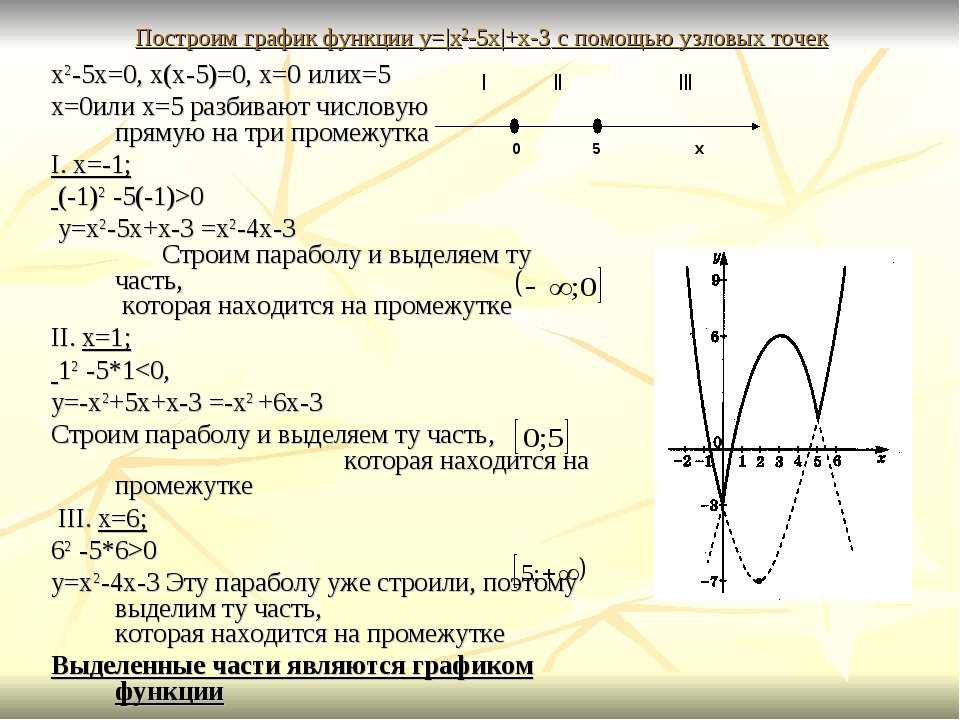

Чтобы сдвинуть эту функцию вверх или вниз, мы можем добавлять или вычитать числа после кубической части функции. Например, функция x ³ +1 — это кубическая функция, сдвинутая на единицу вверх. Его вершина (0, 1).

Reflection

Как и прежде, если мы умножим возведённую в куб функцию на число a, мы сможем изменить растяжку графика. Например, 0,5x ³ сжимает функцию, а 2x ³ расширяет ее.

Если это число a отрицательное, оно переворачивает график вверх дном, как показано на рисунке.

Точка пересечения с осью y

Как и в случае с квадратичными и линейными функциями, точка пересечения с осью y — это точка, в которой x=0. Чтобы найти его, вы просто находите точку f(0).

В родительской функции точка пересечения по оси Y и вершина совпадают. В функции (х-1) ³ , y-пересечение (0-1) ³ =-(-1) ³ =-1.

Х-перехваты.

В отличие от квадратичных функций кубические функции всегда имеют хотя бы одно действительное решение. Их может быть до трех. Например, функция x(x-1)(x+1) упрощается до x ³ -x. Однако из исходной формы функции видно, что эта функция будет равна 0, когда x=0, x=1 или x=-1.

Существует формула для решения кубического уравнения, но она намного сложнее, чем соответствующая формула для квадратного уравнения:

³ √ _{(( ^-b³ / 27a³ + ^bc / 6a² – ^d / 2a² )+√ (( ^-b³ / 27a³ + ^bc / 6a² – ^d / 2a² )²+( ^c / 3a – ^b² / 9a² )³))} + ³ √ _{(( ^-b³ / 27a³ + ^bc / 6a² – ^d / 2a² )+√ (( ^-b³ / 27a³ + ^bc / 6a² – ^d / 2a² )²-( ^c / 3a – ^b² / 9a² )³))} – ^б / _3а .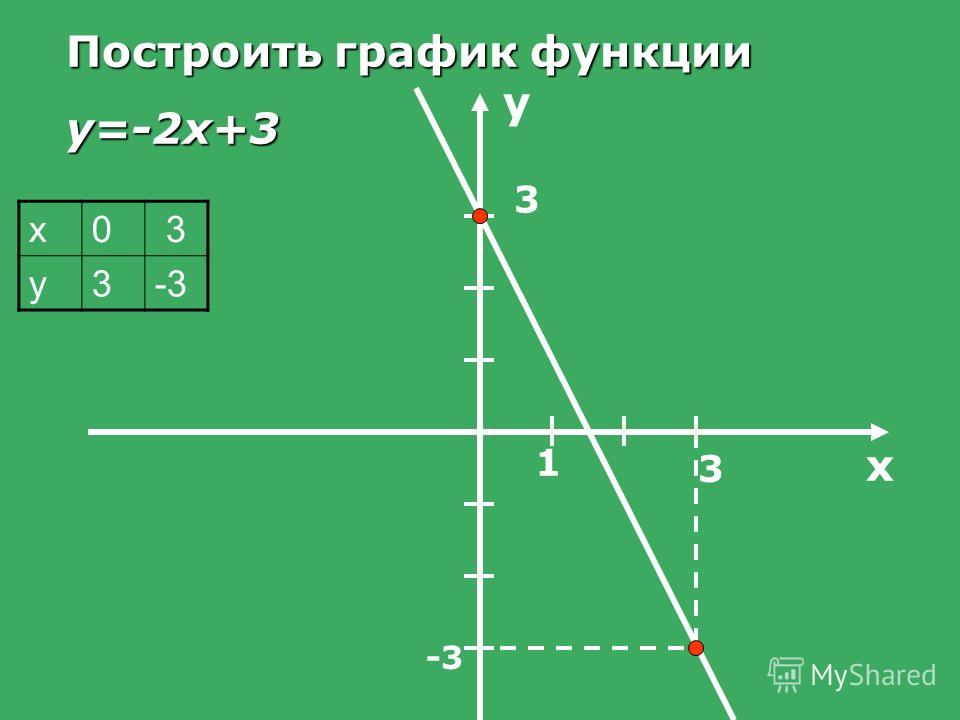

Это довольно длинная формула, поэтому многие люди полагаются на калькуляторы, чтобы найти нули кубических функций, которые нелегко разложить на множители.

Примеры

В этом разделе рассказывается, как строить графики простых примеров кубических функций без использования производных.

Пример 1

График функции -x ³ .

Пример 1 Решение

Единственным отличием данной функции от родительской функции является наличие отрицательного знака. Если мы умножаем кубическую функцию на отрицательное число, она отражает функцию по оси X.

Таким образом, функция -x ³ — это просто функция x ³ , отраженная по оси x. Его вершина по-прежнему (0, 0). Эта точка также является единственной точкой пересечения x или y в функции.

Пример 2

График функции (x-2) ³ -4.

Пример 2 Решение

Опять же, мы будем использовать родительскую функцию x ³ , чтобы найти график заданной функции.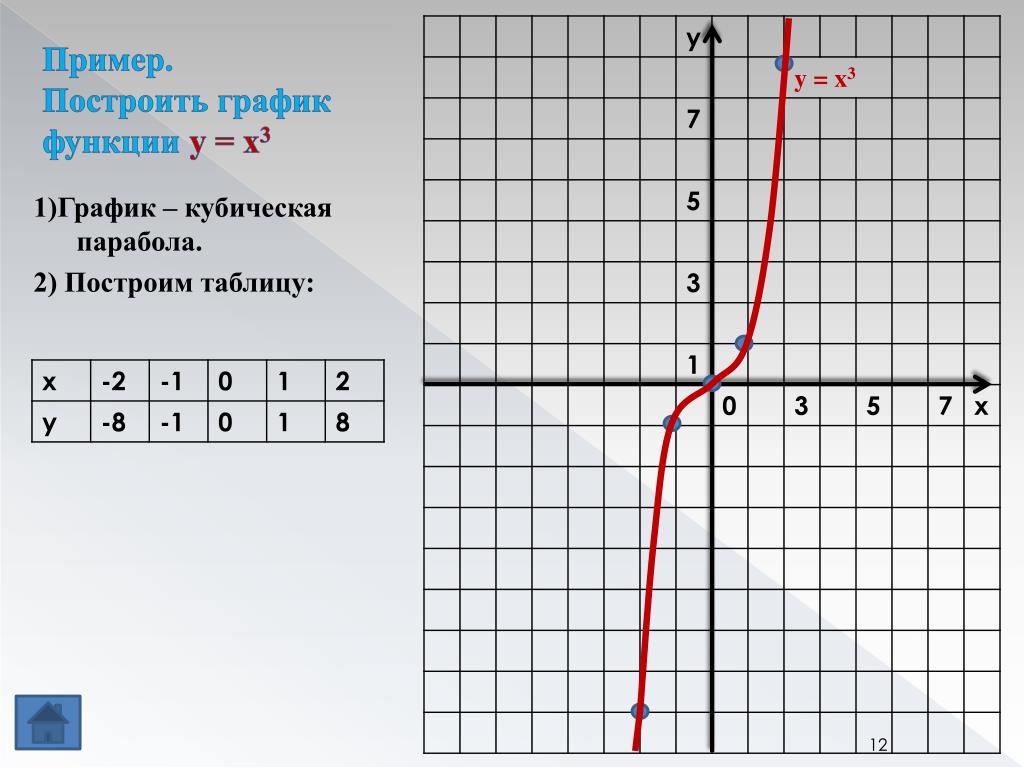

В этом случае нам нужно помнить, что все числа, добавленные к x-члену функции, представляют сдвиг по горизонтали, а все числа, добавленные к функции в целом, представляют сдвиг по вертикали.

В данной функции мы вычитаем 2 из x, что представляет собой сдвиг вершины на две единицы вправо. Это может показаться нелогичным, потому что, как правило, отрицательные числа представляют движение влево, а положительные числа представляют движение вправо. Однако при преобразованиях графа все преобразования, выполняемые непосредственно с x, имеют противоположное ожидаемому направление.

Также вычитаем 4 из функции в целом. Это означает, что мы сдвинем вершину на четыре единицы вниз.

За исключением этих двух сдвигов, функция очень похожа на родительскую функцию. Вершина будет в точке (2, -4).

Новый y-отрезок будет:

(0-2) ³ -4

-8-4

Таким образом, точка (0, -12).

Мы можем решить это уравнение для x, чтобы найти точку пересечения с x:

0=(x-2) ³ -4

4=(x-2) ³ .

На данный момент мы должны взять кубический корень с обеих сторон. Это дает нам:

∛(4)=x-2

∛(4)+2=x.

Десятичное приближение этого числа равно 3,59, поэтому точка пересечения по оси x приблизительно равна (3,59, 0).

Таким образом, мы построили график функции, как показано ниже.

Пример 3

Упростите функцию x(x-2)(x+2). Затем найдите ключевые точки этой функции.

Пример 3 Решение

В текущей форме легко найти точки пересечения x и y этой функции.

Установка x=0 дает нам 0(-2)(2)=0. Таким образом, точка пересечения по оси y равна (0, 0). Следовательно, это также будет x-intercept.

В этом случае, однако, у нас фактически есть больше чем один x-пересечение. Если x=2, средний член (x-2) будет равен 0, а функция будет равна 0. Аналогично, если x=-2, последний член будет равен 0, и, следовательно, функция будет равна 0.

Таким образом, у нас есть три x-перехвата: (0, 0), (-2, 0) и (2, 0).

Расширение функции дает нам x ³ -4x. Поскольку мы ничего не добавляем непосредственно к кубу x или к самой функции, вершиной является точка (0, 0).

Следовательно, функция соответствует графику ниже.

Пример 4

Упростите и нарисуйте график функции x(x-1)(x+3)+2. Затем найдите ключевые точки этой функции.

Пример 4 Решение

Предположим на мгновение, что эта функция не содержит двойки в конце. Пересечения по оси x функции x(x-1)(x+3) равны 0, 1 и -3, поскольку, если x равно любому из этих чисел, вся функция будет равна 0. Пересечение по оси y такой функции равен 0, потому что, когда x=0, y=0.

Расширение функции x(x-1)(x+3) дает нам x ³ +2x ² -3x. Опять же, поскольку непосредственно к x ничего не добавляется и в конце функции ничего нет, вершина этой функции равна (0, 0).

Теперь давайте добавим 2 в конец и подумаем, что это делает.

По сути, мы просто сдвигаем функцию x(x-1)(x+3) вверх на две единицы. Мы можем добавить 2 ко всем значениям y в наших перехватах.

То есть мы теперь знаем точки (0, 2), (1, 2) и (-3, 2). Первая точка (0, 2) является точкой пересечения с осью y.

X-пересечение этой функции более сложное. Для построения графика мы можем просто аппроксимировать его, сдвинув график функции x(x-1)(x+3) вверх на две единицы, как показано.

Пример 5

Определите алгебраическое выражение для показанной кубической функции. Не забудьте также определить любые ключевые моменты.

Пример 5 Решение

Форма этой функции очень похожа на функцию and x ³ . Мы можем увидеть, является ли это просто функцией в кубе x со смещенной вершиной, определив вершину и проверив некоторые точки.

Похоже, вершина находится в точке (1, 5). Мы также можем видеть точки (0, 4), которые являются точкой пересечения с осью y, и (2, 6).

Если функция действительно является просто сдвигом функции x ³ , расположение вершины означает, что ее алгебраическое представление равно (x-1)

3 +5.