Ответов пока нет | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Преобразование графиков тригонометрических функций
Конспект урока по теме:
«Преобразование графиков тригонометрических функций»
Урок – объяснения нового материала.
Цели:
Образовательные: Организовать работу учащихся по изучению и первичному закреплению темы
Развивающие: Способствовать дальнейшему развитию у учащихся логического мышления, познавательного интереса, а также универсальных способов мыслительной деятельности: анализа, обобщения, планирования, конкретизации и рефлексии.
Воспитательные: Воспитание у учащихся культуры труда.
Оборудование: экран, мультимедиапроектор, компьютер, компьютерная программа GeoGebra, файл GeoGebra (приложение 1), буклет (приложение 2), лист-конспект урока (приложение 3), карточки-задания (приложение 4, 5),
Приветствие
Актуализация знаний
Разминка, краткое повторение сведений об основных тригонометрических функциях и известных преобразованиях графиков функций. (y=f(x+a) и y=f(x)+b) Можно проводить в любой форме. Например, разбить учащихся на две команды вариант 1 – вариант 2 и организовать между ними «дуэль», на которой представители команд по очереди будут задавать другой команде вопросы по представленному в данный момент на слайде графику функции.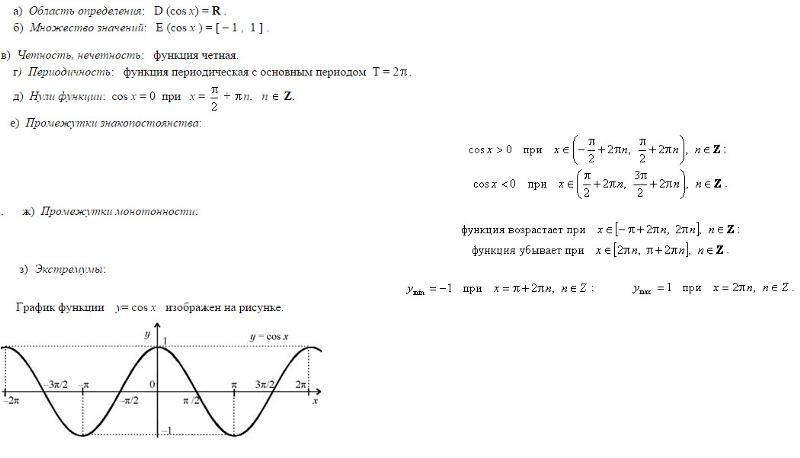
Приложение 1 (файл GeoGebra на экране проектора)
y=sinx
y=cosx
y=sinx+2
y=sin(x-π/6)
y=1+cos(x- π/3)
Исследовательская работа (15 мин)
Я предлагаю вам следующую исследовательскую работу в программе GeoGebra: (по группам) для рассмотрения вопроса преобразования графиков y=mf(x) и y=f(kx) на примере тригонометрических функций. (Задания выполняются за компьютерами в программе GeoGebra) Начертить графики данных функций.
Приложение 2 (карточки-задания)
Группа 1 y=mf(x) | Группа 2 y=f(kx) |
y=cosx y=2cosx y=3cosx y=0,5cosx y=-1cosx y=-2cosx y=-0,5 cosx | y=sinx y=sin2x y=sin3x y=sin0,5x y=sin(-x) y=sin(-2x) y=sin(-0,5x) |
Проанализируем результаты
Группа 1
Можно ли увидеть закономерность?
Как получить из графика y=cosx график y=2cosx?
Какое преобразование если m=-1?
Попробуйте эти визуальные данные объяснить.
Какое утверждение можно сформулировать?
Группа 2
Можно ли увидеть закономерность?
Как получить из графика y=sinx график y=sin2x?
Какое преобразование если k=-1?
Попробуйте эти визуальные данные объяснить.
Какое утверждение можно сформулировать?
Формулировка
Группа 1: Растяжение (сжатие) от(к) оси х с коэффициентом m (1/m)
Группа 2: Растяжение (сжатие) от (к) оси у с коэффициентом k (1/k)
Молодцы!
Первичное закрепление
Построить в тетрадях графики функций
№1. y=1,5cosx
№2. y=sin(x/4)
Перекрёстная проверка графиков с экрана проектора.
Включение в систему знаний
Решение примеров из задачника (фронтальная работа на доске)
Творчество
Пример создание динамических узоров в GeoGebra с использованием тригонометрических функций
А домашнее задание, ребята, у нас будет §13 N13.5, 13.7(a), 13.11(в, г)
Необязательное задание:
Рефлексия
Продолжите фразы:
«Сегодня на уроке я повторил…»
«Сегодня на уроке я узнал…»
«Сегодня на уроке я научился…»
Спасибо за урок!
3
Графики тригонометрической функции — 2022
youtube.com/embed/8oEjxGjAeQI?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Рассмотрим график следующих
(а) y = sinѳ, 0◦ ≤ ѳ ≤ 360◦ ◦
(c) y = tanѳ, 0◦ ≤ ѳ ≤ 360◦
График зависимости y = sinѳ, ѳ◦ ≤ ѳ ≤ 360◦
На листе графика проведите длинную горизонтальную ось посередине. Отметьте точку 0′, на 3 см левее начала координат 0. С центром 0′ нарисуйте окружность радиусом 2 см. Проведите вертикальную ось через 0. Назовите горизонтальную ось ѳ – осью, а вертикальную ось y – осью.
По оси ѳ выберите масштаб от 2см до 1 единицы. С помощью транспортира отметьте углы: 0◦, 30◦, 60◦, 90◦, 120◦, 150◦ … 330◦, как показано на
Проведите горизонтальную линию через 30◦ на окружности. Проведите вертикальную линию через 30◦ на окружности. Проведите вертикальную линию через 30◦ по оси ѳ до пересечения с горизонтальной линией. Отметьте точку пересечения этих двух линий маленьким аккуратным крестиком. Повторите вышеуказанную процедуру для углов 60◦, 90◦, 120◦, … 330◦. Вы получите ряд очков. Соедините точки плавной кривой. Полученная вами кривая является графиком y = sinѳ.
Повторите вышеуказанную процедуру для углов 60◦, 90◦, 120◦, … 330◦. Вы получите ряд очков. Соедините точки плавной кривой. Полученная вами кривая является графиком y = sinѳ.
Существенные признаки графика y = sinѳ:
(a) График y = sinѳ образует волнообразную форму. Говорят, что колеблются.
(б) Максимальное значение y = sinѳ равно 1 и возникает при ѳ = 90◦.
(c) Минимальное значение y = sinѳ равно -1, оно возникает при ѳ = 270◦.
(d) График повторяется с интервалом в 360◦. Функция синуса является примером периодической функции, поскольку она повторяется с интервалом в 360°. Говорят, что функция имеет периодичность 360◦.
(e) Длина AE на графике называется амплитудой функции.
График y = cosѳ, ѳ◦ ≤ ѳ ≤ 360◦
График y = cosѳ можно нарисовать так же, как и y = sinѳ, за исключением того, что углы измеряются от ИЛИ по часовой стрелке, как показано на рис. 14.17. Это так, потому что cosѳ = sin(90◦ – ѳ).
14.17. Это так, потому что cosѳ = sin(90◦ – ѳ).
Существенные признаки графика y = cosѳ:
(a) Все существенные особенности, которые справедливы для графика y = sinѳ, справедливы и для графика y = cosѳ.
(б) Кроме того, косинус отстает от синусоиды на 90◦. Разность обычно называется разностью фаз . Другими словами, косинусоидальная кривая отстает от синусоиды на разность фаз 90◦.
(c) И синусоида, и косинусоидальная кривая демонстрируют некоторые физические явления, такие как приливные волны, звуковые волны, переменные течения и т.д.
График y = tanѳ, ѳ◦ ≤ 360◦
График y = tanѳ легче построить с помощью таблицы значений, чем с помощью проекций единичного круга. Составьте таблицу значений y = tanѳ от 0° до 360°, как показано в Таблице 14.2.
(b) Поскольку касательная функция не определена при 90◦ и 270◦, функция называется разрывной в этих точках. (c) Кривая быстро поднимается и спадает под углами, очень близкими к 90° и 270° соответственно.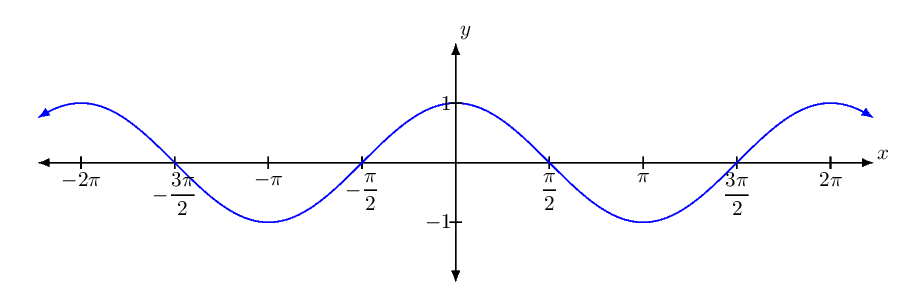 Кривая приближается к вертикальным линиям под углами 90° и 270°, но никогда их не касается. Эти вертикальные линии на 90° и 270° называются
Кривая приближается к вертикальным линиям под углами 90° и 270°, но никогда их не касается. Эти вертикальные линии на 90° и 270° называются
(d) Касательная функция также является периодической функцией. Он имеет периодичность 180◦.
| 0 | 0◦ | 30◦ | 60◦ | 75◦ | 105◦ | 120◦ | 150◦ | 180◦ | 210◦ | 240◦ | 255◦ | 285◦ | 315◦ | 330◦ | 300◦ | 360◦ |
| y = tanѳ | 0 | 0.58 | 1.73 | 3.73 | -3.73 | -1.73 | -0.58 | 0 | 0.58 | 1.73 | 3.73 | -3.73 | -1 | 0,58 | -1,73 | 0 |
Возьмите масштаб 1 см для представления 30° по оси ѳ и 1 см для представления 1 единицы по оси y.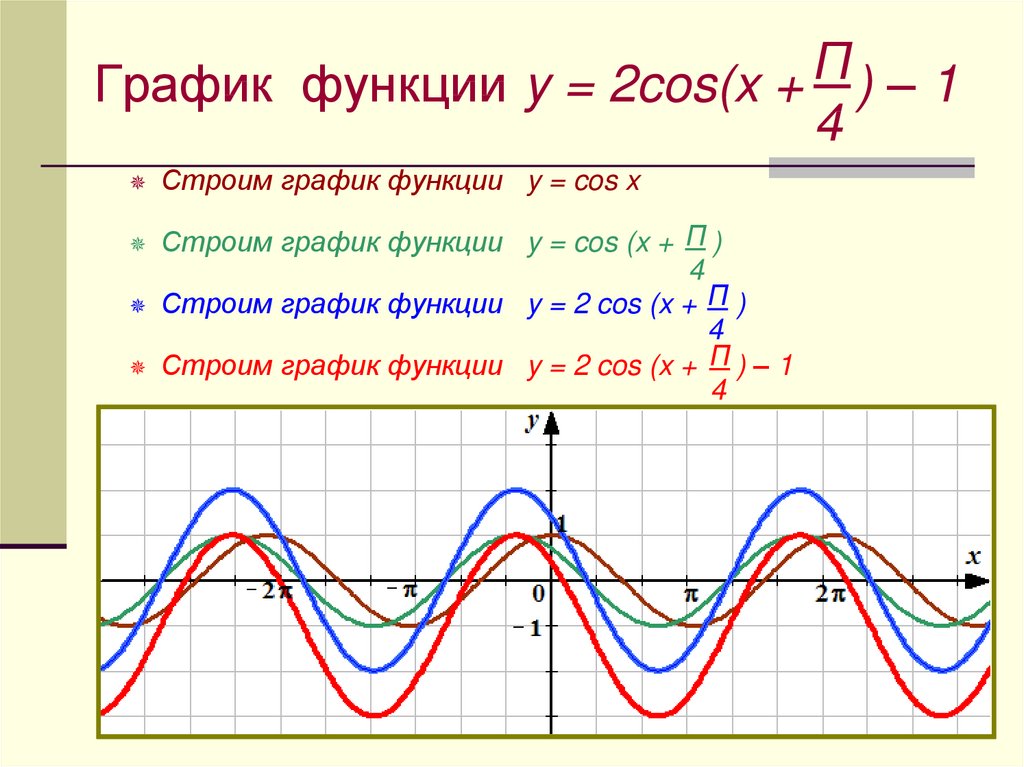
Пример
Используя ту же ось, масштаб 1 см для представления 30◦ по оси ѳ и 2 см для представления 1 единицы по оси Y, нарисуйте графики следующих отношений.
(а) y = sinѳ
(б) y = 2sinѳ
(в)y = ½ sinѳ в интервале 0◦ ≤ ѳ ≤ 360◦.
Раствор
(см. табл. 14.3 и рис. 14.19)
Заметим, что кривые:
y = sinѳ
y = 2sinѳ
y = ½ sinѳ
, но6 отличаются по периодичности амплитуды.Амплитуда y = sinѳ равна 1.
Амплитуда y = 2sinѳ равна 2.
Амплитуда y = ½ sinѳ равна ½.
В общем случае кривая y = A sinѳ имеет амплитуду / A / abd периодичность 360◦. Это свойство той же кривой является также характеристикой косинусоидальной кривой.
Оценка
- Докажите, что sec 2 ѳ + cosec 2 ѳ = (tanѳ + cotѳ)
Общая оценка
(1) Нарисуйте график зависимости y = 2cosx – 1 в диапазоне 0◦ ≤ x ≤ 360◦ с интервалом 30◦.
(2) Нарисуйте график y = 3sin x — 1 в диапазоне 0◦ ≤ x ≤ 360◦ с интервалами 30◦
(3) Нарисуйте график:
(i) y = sin2x ( ii) у = cosx
(iii) y = sec x (iv) cosec x
Все с интервалами 30◦ диапазон 0≤ x ≤ 360.
Присоединяйтесь к дискуссионному форуму и выполните свое назначение : Найдите вопросы в конце каждого урока. Нажмите здесь, чтобы обсудить свои ответы на форуме
Объявление: Получите БЕСПЛАТНУЮ Библию : Обрести истинный покой. Нажмите здесь, чтобы узнать, как получить БЕСПЛАТНУЮ Библию.
По вопросам размещения рекламы/партнерства пишите [email protected]
Загрузите наше бесплатное мобильное приложение для Android : Сохраняйте свои данные при использовании нашего бесплатного приложения. Нажмите на картинку, чтобы скачать. Нет подписки.
Мы заинтересованы в продвижении БЕСПЛАТНОГО обучения. Расскажите своим друзьям о Stoplearn.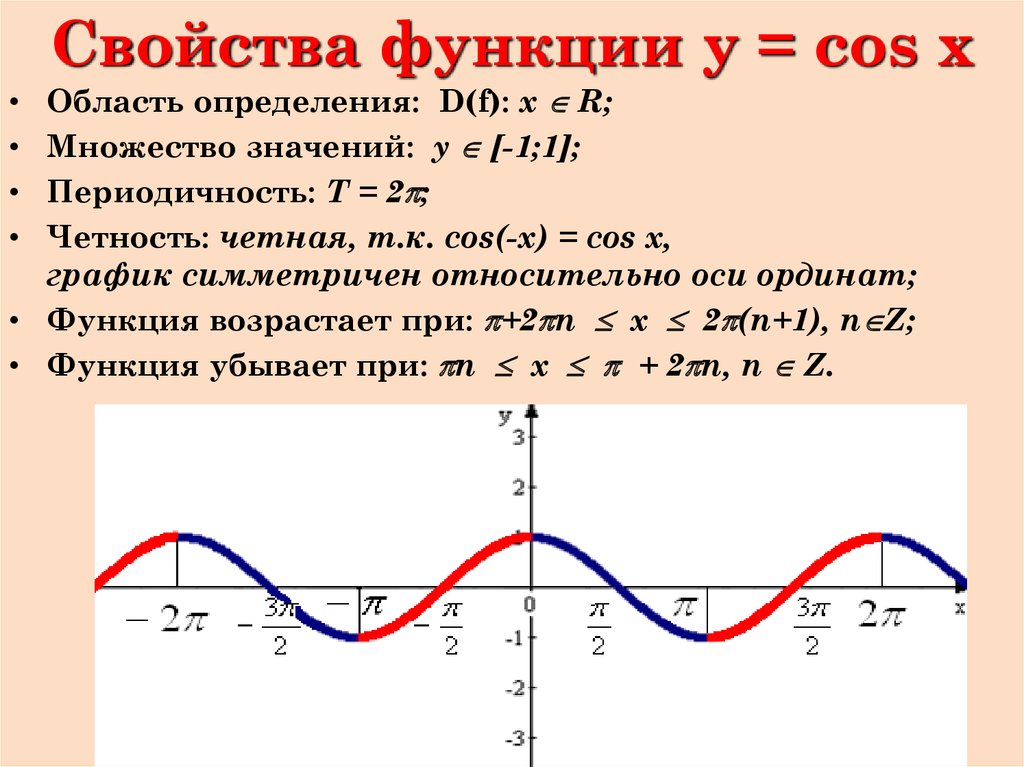 com. Нажмите кнопку «Поделиться» ниже!
com. Нажмите кнопку «Поделиться» ниже!
График с добавлением ординат
График с добавлением ординатВведение
Цель: Построить график функций, которые суммы или разности двух функций синуса, двух функций косинуса, или функция синуса и косинуса.
«Функция y = 2x + 4 на самом деле является сумма двух функций, y = 2x и y = 4. Для каждого значения в домен, в диапазоне есть соответствующее значение, так что точка (x, 2x + 4) находится на графике y = 2x + 4. Суммы тригонометрических функции также можно изобразить в виде графика».
Ресурс: Хейден, Джером Д. и Холл, Бетти С. (1993). Тригонометрия . Прентис-холл: Энглвудские скалы, Нью-Джерси.
Студенческая деятельность
I. Построение графика добавлением ординат на графике Калькулятор.
1. График y = sinx на интервале [-2p, 2p].
Затем на та же координатная плоскость (но другим цветом), график y = cosx на том же интервале. Наконец, по той же координате плоскости (но другого цвета), график y = sinx + cosx над тот же интервал. Как для каждого значения в домене значения диапазона y = sinx + cosx сравнить со значениями диапазонов y = sinx и y = cosx?
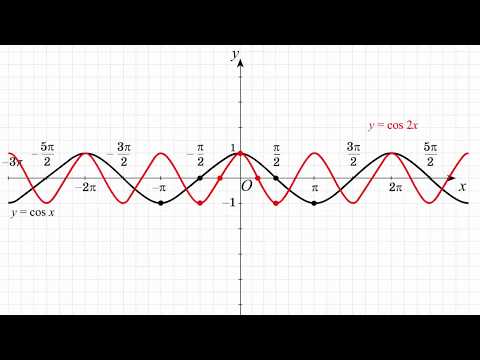
2. График y = 2cosx на интервале [-2p, 2p]. Затем на та же координатная плоскость (но другим цветом), график y = cos2x на том же интервале. Наконец, по той же координате плоскости (но другого цвета), график y = 2cosx + cos2x над тот же интервал. Как для каждого значения в домене значения диапазона y = 2cosx + cos2x сравнить со значениями диапазонов y = 2cosx и y = cos2x?
II. График путем добавления ординат вручную.
1. Откройте файл Excel. Обозначьте первый столбец «x-координаты», второй столбец «y = 2sinx», третий столбец «y = -sin0.5x» и четвертый столбец «y = 2sinx — sin0,5x.
» Установите для каждого столбца округление до четыре десятичных знака.
2. Настройте первый столбец в диапазоне от -2p до 2p с интервалами стр/4.
3. Заполните вторую и третью колонки по используя уравнения y = 2sinx и y = 0,5sinx соответственно.
4. Заполните четвертый столбец, просто добавив второй и третий столбцы.
5. Постройте график y = 2sinx + sin0,5x с помощью координаты x из столбца A и координаты y из столбца Д.
Ключ учителя для активности учащихся
И.
1. y = sinx выделен красным цветом, y = cosx выделен синим цветом, а y = sinx + cosx выделен фиолетовым цветом
Ответ: В каждой координате x координаты y y = sinx + cosx является суммой y-координат y = sinx и у = cosx.
2. y = 2cosx выделено красным цветом, y = cos2x выделено синим цветом, а y = 2cosx + cos2x выделен фиолетовым цветом
Ответ: В каждой координате x координаты y y = sinx + cosx является суммой y-координат y = sinx и у = cosx.
II.
2. В ячейке A2 введите «=-2*pi()». В ячейке A3 введите «=A2+pi()/4». Перетащите, чтобы заполнить ряд 18.
3. В ячейке B2 введите «=2*sin(A2)». Перетащите, чтобы заполнить строку 18. В ячейке C2 введите «=-1*sin(A2/2)». Перетащите, чтобы заполнить строку 18.
4. В ячейке D2 введите «=B2+C2». Тяга заполнить до строки 18.
Вот пример таблицы:
| -6,2832 | 0 | 0 | 0 |
| -5,4978 | 1.4142 | 0,3827 | 1,7969 |
| -4.7124 | 2 | 0,7071 | 2,7071 |
| -3,9270 | 1.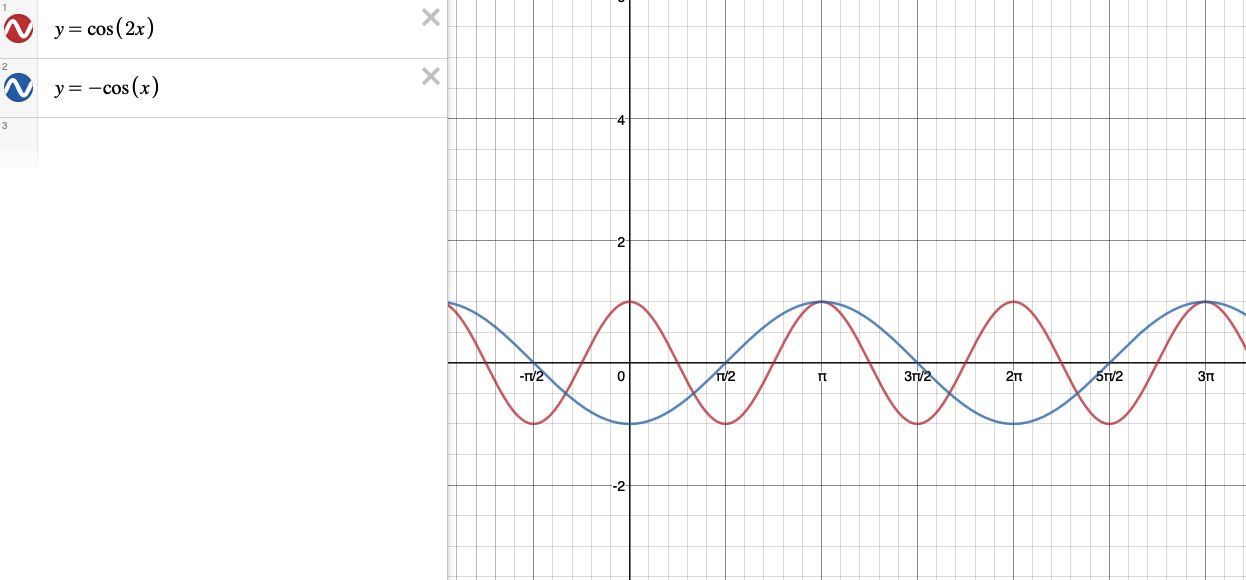 4142 4142 | 0,9239 | 2,3381 |
| -3,1416 | 0 | 1 | 1 |
| -2,3562 | -1,4142 | 0,9239 | -0,4903 |
| -1,5708 | -2 | 0,7071 | -1,2929 |
| -0,7854 | -1,4142 | 0,3827 | -1,0315 |
| 0 | 0 | 0 | 0 |
| 0,7854 | 1.4142 | -0,3827 | 1.0315 |
| 1.5708 | 2 | -0,7071 | 1,2929 |
| 2,3562 | 1.4142 | -0,9239 | 0,4903 |
| 3.1416 | 0 | -1 | -1 |
| 3,9270 | -1,4142 | -0,9239 | -2,3381 |
4. |


%20equals%201%20%2B%20Cos(x).png)

 К какому числу Женя случайно приписала 0?
К какому числу Женя случайно приписала 0? Затем на
та же координатная плоскость (но другим цветом), график y
= cosx на том же интервале. Наконец, по той же координате
плоскости (но другого цвета), график y = sinx + cosx над
тот же интервал. Как для каждого значения в домене
значения диапазона y = sinx + cosx сравнить со значениями
диапазонов y = sinx и y = cosx?
Затем на
та же координатная плоскость (но другим цветом), график y
= cosx на том же интервале. Наконец, по той же координате
плоскости (но другого цвета), график y = sinx + cosx над
тот же интервал. Как для каждого значения в домене
значения диапазона y = sinx + cosx сравнить со значениями
диапазонов y = sinx и y = cosx? 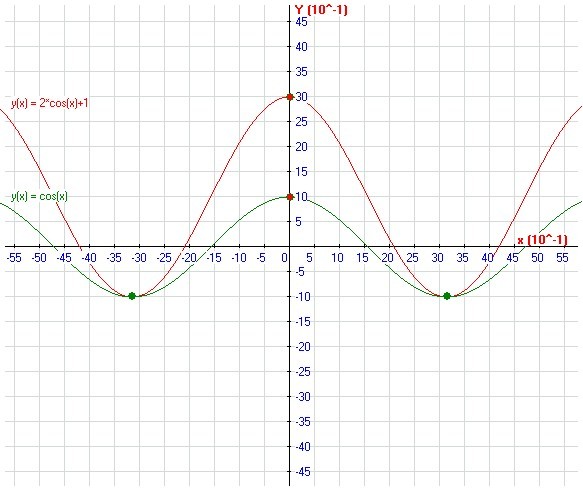 » Установите для каждого столбца округление до
четыре десятичных знака.
» Установите для каждого столбца округление до
четыре десятичных знака.