Построить график функции y 2×2: Постройте график функции y = 2x – 2

2$

9

6,25

4

2,25

1

0,25

0

0,25

1

2,25

4

6,25

9

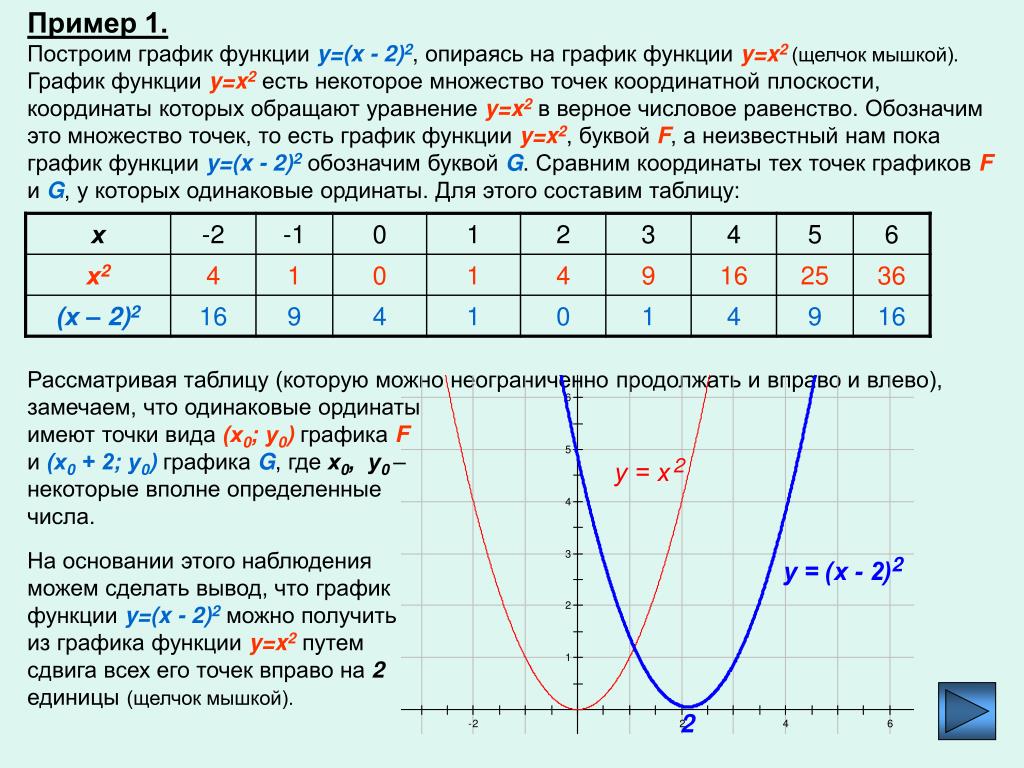
Отметим полученные точки на координатной плоскости и соединим их кривой:

Полученный график называют параболой. Точка (0;0) — это вершина параболы. Вершина делит график на левую и правую части, которые называют ветвями параболы.

Свойства параболы y=x²

1. Область определения $x \in (- \infty;+ \infty)$ — все действительные числа.

2. Область значений $y \in [0;+ \infty)$ — все неотрицательные действительные числа.

3. Функция убывает при $x \lt 0$, функция возрастает при $x \gt 0$.

4. Наименьшее значение функции y = 0 — в вершине параболы при x = 0. Вершина параболы совпадает с началом координат.

5. Все точки на ветвях параболы лежат выше оси абсцисс, для них $y \gt 0$. 2$, кроме двух точек с $ x \neq \pm 1 $.

построение графика

построение графика

y = x2 — 4x + 3

Ветви направлены вверх, т.к. a = 1 > 0 Координаты вершины (2;-1), т.к. Ось симметрии параболы: Координаты точек пересечения с осью х: (x1; 0) = (1; 0) и (x2; 0) = (3; 0) Координаты точки пересечения с осью у: (0; c) = (0; 3) симметричная ей точка относительно оси параболы:

y= -x2 — 6x — 9

Ветви направлены вниз, т.к. a = -1 < 0 Координаты вершины (-3;0), т. к. Ось симметрии параболы: Координаты точки касания с осью х: (x1; 0) = (-3; 0). Координаты точки пересечения с осью у: (0; c) = (0;-9) симметричная ей точка относительно оси параболы:

ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
С ПОМОЩЬЮ ЭЛЕМЕНТАРНЫХ ПРЕОБРАЗОВАНИЙ ГРАФИКА ФУНКЦИИ

y = x²
С помощью выделения полного квадрата любую квадратичную функцию можно представить в виде:
Это свойство позволяет построить график квадратичной функции с помощью элементарных преобразований графика функции y = x².
Построение графика y = a(x — m)² + n можно произвести в три этапа:

	1. Растяжение графика y = x2 вдоль оси у в а раз (при |a|< 1 — это сжатие в 1/|a| раз). Если a< 0, произвести ещё и зеркальное отражение графика относительно оси х (ветви параболы будут направлены вниз). Результат преобразования: график функции y = ax2
	2. Произвести параллельный перенос графика функции y = ax2 вдоль оси x на |m| (вправо при m > 0 и влево при m < 0). Результат преобразования: график функции y = a(x-m)2
	3. Параллельный перенос графика функции y = a(x — m)2 вдоль оси y на |n| (вверх при n > 0 и вниз при n < 0)

Результат преобразования: график функции y = a(x — m)²+n

Примеры:

1.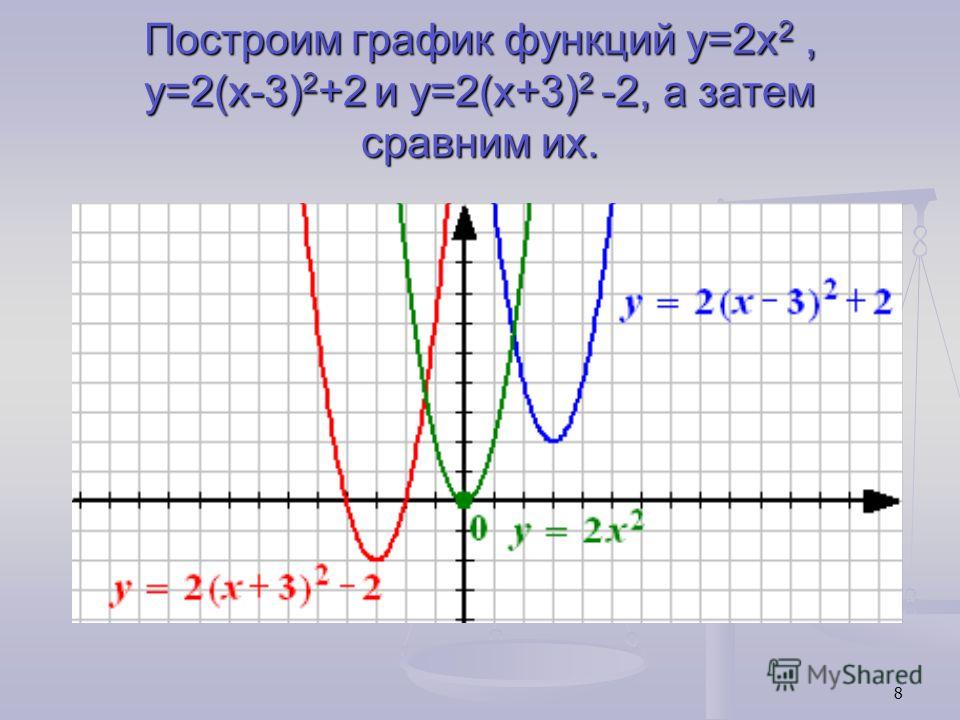 Растяжение графика функции y = x 2 вдоль оси y в 2 раза	2. Параллельный перенос графика функции y = 2x2 вдоль оси x на 3 вправо	Параллельный перенос графика функции y = 2(x — 3)2 вдоль оси y на 1 вверх.

1. Сжатие графика функции y = x 2 вдоль оси y в 2 раза и преобразование симметрии относительно оси x	2. Параллельный перенос графика функции y = — x2 вдоль оси x на 2 влево	Параллельный перенос графика функции y = — (x + 2)2/ 2

Используются технологии uCoz

Графики функций y = x2, y = 2×2 и y = -2×2 фиолетового, красного и синий, соответственно

Исследование парабол что происходит, когда мы строим графики для параболы y = ax ² + bx + c с разными значениями a, b и c.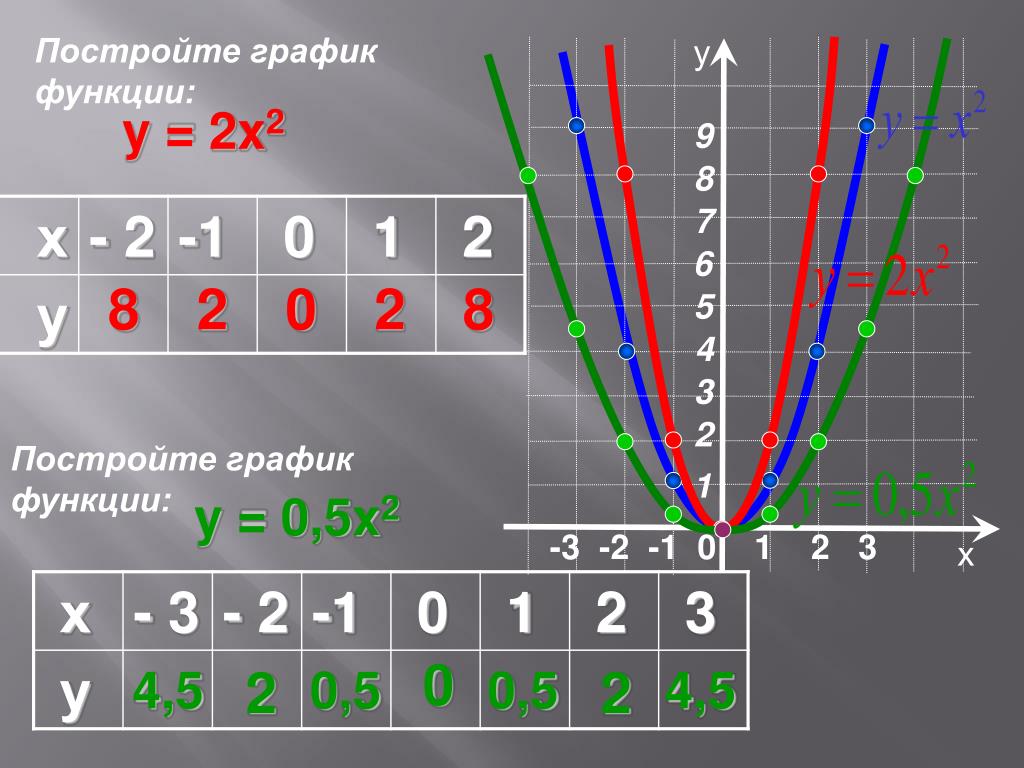 Хорошо начнем сначала с построения графиков для y = ax ² с разными значениями а. ниже приведены графики для a = -2, 1, 2, выделенные синим, фиолетовым и красным цветом соответственно:

 

 

Сначала заметим, что когда a является отрицательным значением, график отражается по оси x, и вершина становится точкой максимума. Далее отметим, что в качестве значения a увеличивается, парабола сужается относительно оси x.

 

            Сейчас мы хотим зафиксировать a (пусть a = 1) и исследовать уравнение y = x ² + bx. Пусть b = -2, 1, 3 в красном, синем и фиолетовый соответственно на следующем графике:

Мы видим, что значения b влияют на то, где парабола пересекает ось x. Теперь давайте посмотрим, что произойдет, если мы изменим оба значения a = 2, 4, 6. и b = -2, 1, 3:

Ага! Итак парабола имеет две точки пересечения: (0,0) и (-(б/а),0).

 

            Наконец, мы хотим изучить, как значения c могут повлиять на параболу.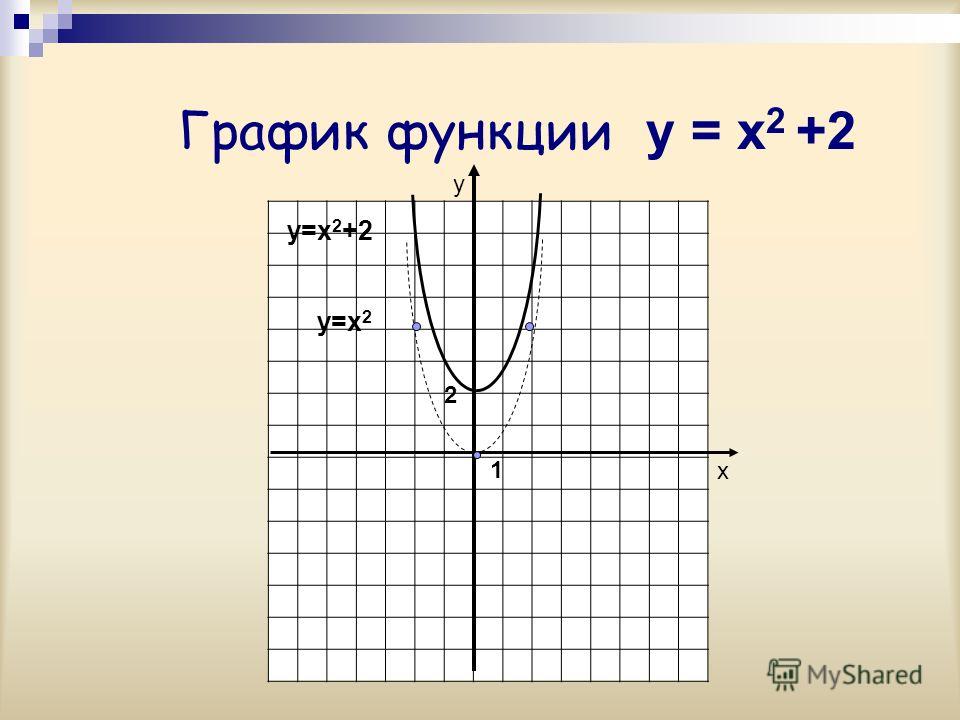 Мы зафиксируем a = 1 и b = 0 и будем варьировать c = -2, ½, 2 красного, синего, фиолетового цвета соответственно:

Сразу видно, что с определяет пересечение парабола на оси у. То есть, парабола y = ax ² + bx + c пересекает ось y в точке y = c. Посмотрим, что произойдет, если мы изменим значения a:

 

y = 10 x ² + x + 2, фиолетовый

y = -10 x ²

+ x + 2, синий

y = 2 x ^{2 + x 90 15 2 + 90 , зеленый}

y = 1/2 x ² + x + 2, бирюзовый

y = 1/20 x ² + x + 2, темно-серый

y = 1/100 x ² + x + 2, красный

 

 вводится в уравнение y = ax ² + bx + c, уже неверно, что парабола пересекает ось x в точках x = 0 и x = -(b/a). Но мы можем установить связь с b с графом, когда введено c: Вершина параболы (b/2a, b ² /4a — б ² /2а + в). Координату x в вершине мы получаем путем рассмотрения графов и при x = -b/2a, тогда y = a(bb/4aa) + -bb/2a + c = bb/4a – bb/2a + c = b ² /4a — б ² /2а + в. Давайте сделаем пример! Пусть а = 2, Ь = 3, с = 2.  Тогда мы должны иметь

 

vertex = (-b/2a, b ² /4a — b ² /2a + c)

           = (-3/4, 9/8 – 9/4 + 2)

           = (-0,75, 0,875)

 

Graphing Calculator согласен с нашим ответом:

Возврат

квадратичная функция

какой ответ для y=2×2 в квадратичной функции
Связанные темы:
доказательство логарифма в алгебре | математические исследовательские проекты | алгебра трехчленный калькулятор | шпаргалка по предварительному исчислению | калькулятор десятичных и смешанных чисел | гиперболический график | рабочий лист для GMAT по математике | ПО для помощи по алгебре | как найти хорошего репетитора по математике ирвин, ca | программа для решения заданных двух линейных уравнений

Автор	Сообщение
Solbe Deen Дата регистрации: 10. 12.2002 От кого:	Размещено: Пятница, 03 августа, 19:31 Здравствуйте, волшебники математики, мне срочно нужна помощь. У меня есть набор математических вопросов, которые мне нужно решить, и я безнадежно потерян. Я не знаю, с чего начать и что делать, а эта статья должна быть готова на следующей неделе. Пожалуйста, дайте мне знать, хорошо ли вы разбираетесь в функциональной области или есть хороший сайт, который может мне помочь.
Наверх
oc_rana Зарегистрирован: 08. 03.2007 Откуда: Египет, Александрия	Размещено: Воскресенье, 05 августа, 11:24 Ааааааааааааааааааааааааааааааааааааааааааааааааа ни нас, студентов, от гнева того, что является ответом для y=2×2 в квадратичной функции). Когда я был там, я сталкивался с теми же проблемами, что и вы. Я всегда путался в базовой математике, промежуточной алгебре и промежуточной алгебре. Я был худшим в ответе для y = 2×2 в квадратичной функции, пока не узнал об алгебраике. Это действительно здорово, и я искренне рекомендую его. Лучшая особенность программного обеспечения заключается в том, что оно также поможет вам выучить алгебру, а не просто давать ответы. Я нашел Algebrator эффективным и уверен, что он поможет и вам. Ваше здоровье.
Наверх
Пооме Дата регистрации: 18.04.2004 Откуда: Среди звезд… где ты оставил меня, и где я буду ждать тебя… всегда…	Размещено: Воскресенье, 05 августа, 15:32 Даже я получил помощь от Algebrator, чтобы познакомиться с концепциями College Algebra месяц назад. Стоит вложить деньги в покупку Algebrator, поскольку он предлагает эффективное обучение алгебре в колледже и доступен по доступной цене.
Наверх
СанГ Зарегистрирован: 31.08.2001 Откуда: красивый северо-запад Нижнего Мичигана	Размещено: Воскресенье, 05 августа, 21:19 Я помню, что часто сталкивался с трудностями с правилом Крамера, добавлением функций и абсолютных значений. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт