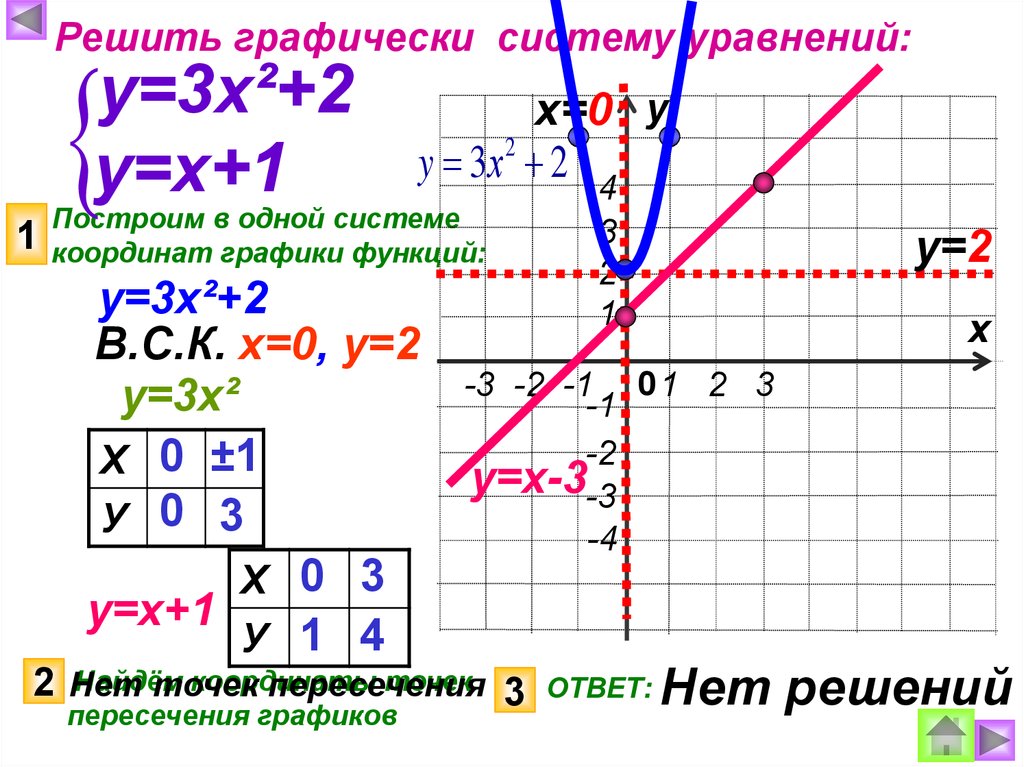
Графики уравнений, содержащих модули — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Тема урока : «Графики уравнений, содержащих модули».
Учитель: Видмонт Татьяна КонстантиновнаМБОУ СОШ №15
город Ростов-на-Дону
1
х2 — 2у = 2
ху = — 6
х2+у2 = 16
х+2у = 4
2у-5 = 0
3. Когда в «стандартные» уравнения прямых, парабол, гипербол включают знак модуля, их графики становятся необычными и даже
красивыми.
Чтобы научиться строить такие
графики:
надо владеть приемами построения
базовых фигур;
твердо знать и понимать
определение модуля числа.
Повторение понятия модуля числа.
Построение графика функции у=│х│
Если х≥ 0, то у = х;
Если х< 0, то у = −х.
х, если х≥ 0;
у=
х, если х≥ 0;
-х, если х< 0.
В результате имеем дело с кусочным заданием
зависимости.
Приемы построения графиков уравнений с
модулями.
Кусочный
Геометрические
преобразования
Сдвиг
Задание 1. Построить график функции у=│х2- 4│.
Используем прием геометрического преобразования.
Строим параболу у = х2- 4.
Часть параболы, расположенную ниже оси х,
нужно заменить линией, ей симметричной
относительно оси х, т.е. геометрическое
преобразование.
Построить график функции у = х2-2 |х|.
Используем прием кусочного построения.
Если х≥0, то у = х2-2х;
Если х<0, то у = х2+2х.
х2-2х, если х ≥ 0;
у=
х2+2х, если х < 0.
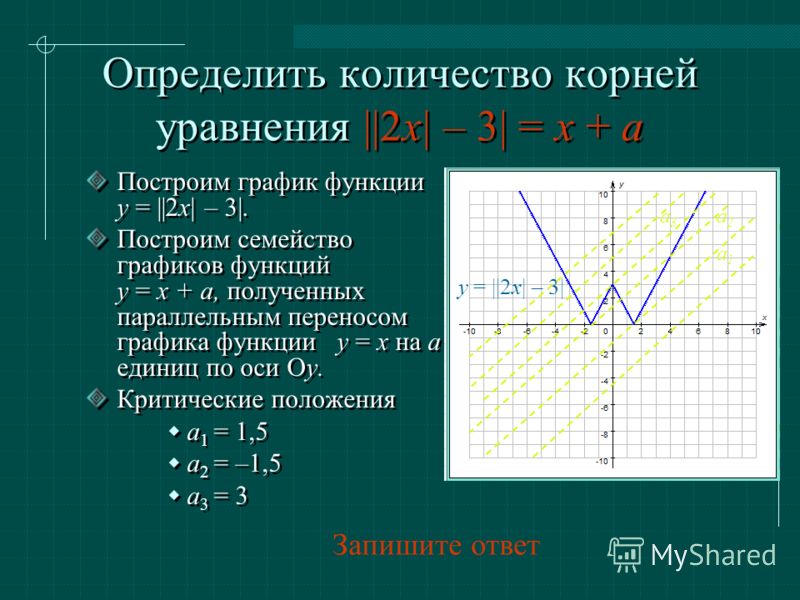
Итак, мы имеем дело с кусочным
заданием зависимости.
Рис.2.49 (9 кл. алгебра).
Алгоритм построения.
Построим параболу у=х2-2х и обведем ту ее часть, которая соответствует
неотрицательным значениям х, то есть часть, расположенную правее оси у.
В той же координатной плоскости построим параболу у=х2+2х и обведем ту ее
часть, которая соответствует отрицательным значениям х, то есть часть,
расположенную левее оси у.
Построить график функции у=│2х-4│+│6+3х│.
Используем прием кусочного построения.
Находим корни каждого выражения, стоящего под знаком
модуля:
2х-4=0, х=2.
6+3х=0, х=-2.
Разобьем ось х на три промежутка:
1) х<-2; 2) -2≤ х < 2; 3) х≥ 2.
х < −2
y=- (2x – 4) – ( 6x + 3x)=-5x- 2
-2 ≤ х < 2
y=- ( 2x -4 )+ (6x + 3x) = x + 10
х ≥2
у=2х-4+6+3х=5х+2.
Итак, мы имеем дело с кусочным заданием
зависимости.
-5х-2, х< −2;
у=
х+10, -2≤ х < 2;
5х+2,х≥ 2.
Построить график функции у=││х-4│-2│.
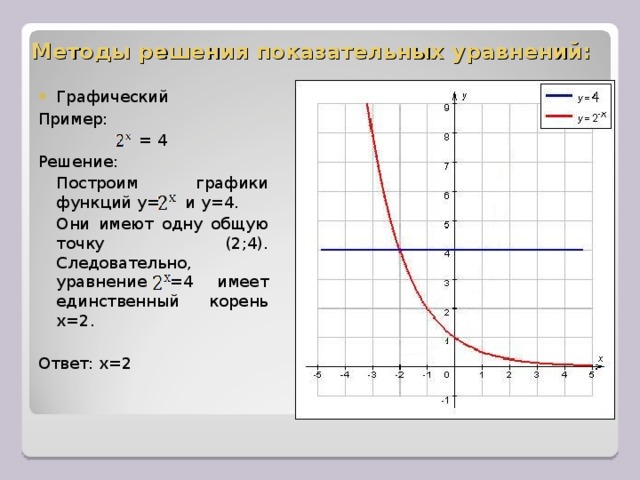
При построении этого графика удобно использовать способ
сдвига вдоль осей координат.
Строим график
уравнения у = │х│.
у
у
-1 0
1
х
0
у
4
х
0
х
-2
Сдвигаем его
по оси х на 4 единицы вправо
и по оси у на 2 единицы вниз..
Часть графика, расположенную
ниже оси х, отображаем
симметрично относительно оси х.
Построить график функции у=│││х│-2│-2│.
При построении этого графика удобно использовать способ
сдвига вдоль осей координат.
Алгоритм построения.
Строим график уравнения у=│х│.
Сдвинем построенный график на 2 ед. вниз.
Часть графика, расположенную ниже оси х
отображаем симметрично относительно
оси х.
Часть графика,
расположенного ниже оси х,
отобразим симметрично
относительно этой оси.
Сдвигаем построенный график на 2
единицы вниз.
13. Каждой группе построить график одной функции.
Задания для самостоятельной работы.1)у=│2х-4│;
2)у=│9-х2│;
3)у=│х2-5х+6│;
4)у=│3-0,5х2│;
5)у=│х2-4│+3;
6)у=│х│-2х;
7) у=х2+ 3│х│.
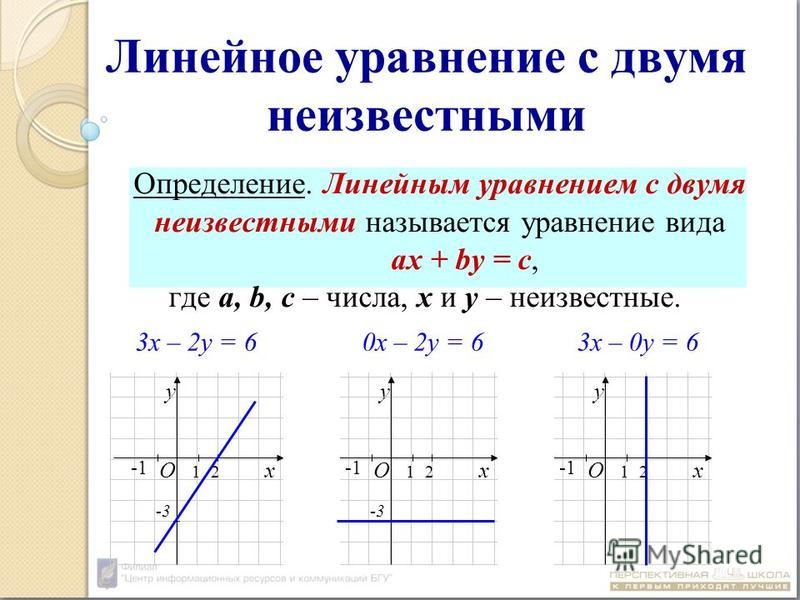
14. Заполнить таблицы.
ГрафикиЗнаю
определение
модуля
числа.
Установите соответствие между графиками
функций и формулами, которые их задают.
Владею
приемами
построения
базовых
фигур.
Знаю
свойства
этих
функций.
Умею
сопоставлять
уравнения с
графиками
функций.
Умею
строить
кусочные
функции.
строить
графики
функций.
Знаю
способы
построения
графиков
уравнений с
модулями.
English Русский Правила
Строим график функции, заданный системой уравнений, в EXCEL. Примеры и описание
Построим в MS EXCEL график функции, заданный системой уравнений. Эта задача часто встречается в лабораторных работах и почему-то является «камнем преткновения» для многих учащихся.
Пусть дана система уравнений
Требуется на отрезке [-1; 4] построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.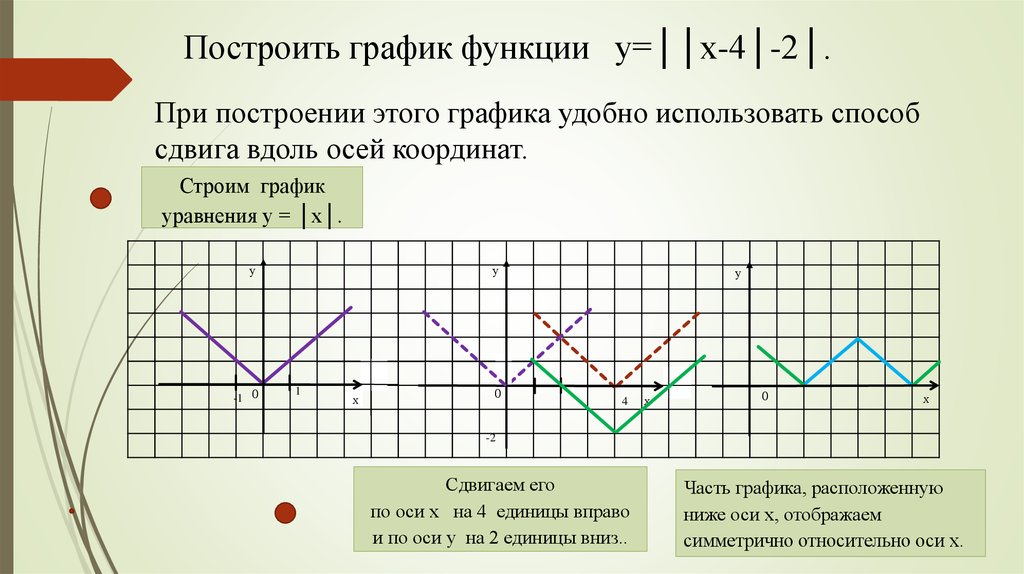
Решение (1 ряд данных)
Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.
СОВЕТ : О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL . О различии диаграмм Точечная и График см. статью График vs Точечная диаграмма в MS EXCEL .
Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см. файл примера, лист Ряд1 ):
Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.
Чтобы построить диаграмму типа Точечная:
- выделите любую ячейку таблицы;
- во вкладке Вставка в группе Диаграммы выберите диаграмму Точечная с прямыми отрезками и маркерами .
Чтобы построить диаграмму типа График:
- выделите любую столбец f(x) вместе с заголовком;
- во вкладке Вставка в группе Диаграммы выберите диаграмму График маркерами .
У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график используя 2 ряда данных .
Решение (2 ряда данных)
Создадим другую таблицу с исходными данными в файле примера, лист График :
Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола. Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы. При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.
У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.
Решение (3 ряда данных)
Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .
Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).
Desmos Graphing Calculator в App Store
Описание
Изучайте математику с помощью быстрого и мощного графического калькулятора Desmos. Постройте любое уравнение, от линий и парабол до производных и рядов Фурье.
Особенности:
Графики: построение полярных, декартовых или параметрических графиков. Нет ограничений на количество выражений, которые вы можете отображать одновременно, и вам даже не нужно вводить выражения в форме y=!
Ползунки: регулируйте значения в интерактивном режиме, чтобы создать интуицию, или анимируйте любой параметр, чтобы визуализировать его влияние на графике.
Таблицы: ввод и построение данных или создание таблицы ввода-вывода для любой функции.
Статистика: Найдите наиболее подходящие линии, параболы и многое другое.
Масштабирование: Масштабируйте оси независимо или одновременно, сводя два пальца, или отредактируйте размер окна вручную, чтобы получить идеальное окно.
Точки интереса: Коснитесь кривой, чтобы показать максимумы, минимумы и точки пересечения.
Коснитесь серых точек интереса, чтобы увидеть их координаты. Удерживайте и перетащите вдоль кривой, чтобы увидеть, как координаты меняются под вашим пальцем.
Научный калькулятор: Просто введите любое уравнение, которое хотите решить, и Desmos покажет вам ответ. Он может обрабатывать квадратные корни, журналы, абсолютное значение и многое другое.
Неравенства: Постройте декартовы и полярные неравенства.
Специальные возможности: читайте и редактируйте математические данные с помощью программы чтения с экрана или обновляемого дисплея Брайля, а также используйте звуковую трассировку для изучения графиков и данных с помощью звука.
Не в сети: доступ в Интернет не требуется.
Посетите сайт www.desmos.com, чтобы узнать больше и ознакомиться с бесплатной браузерной версией нашего калькулятора.
Версия 6.14.0
* Существует новый способ создания списков многоугольников: когда функции многоугольника задано несколько аргументов, и один или несколько из этих аргументов являются списком точек, список полигоны будут созданы.
* Исправлена ошибка, которая могла препятствовать воспроизведению звука.
Рейтинги и обзоры
215 оценок
Лучшее графическое приложение
Будучи студентом, я часто использовал это приложение для квадратичной оптимизации. Он абсолютно бесплатный со всеми важными функциями и работает на всех устройствах. Единственная техническая претензия заключается в том, что он выводит вас из системы каждый раз, когда вы перезагружаете устройство. Кроме того, хотя это не совсем его вина, я провалил модульный тест квадратичной регрессии, потому что использовал «=» вместо «~».
Если бы он только показывал мне, что пошло не так, как проверка орфографии…
Затхлое приложение
Это приложение о том, как tf x=5 идет на 3.5, а не 5, где 3.5 исходит от mf 🤨🤨 тоже столкнул с лестницы мою любимую рыбку, рип Дешон 😔💔
Удивительно
Я использую Desmos с 9 класса, и мне это очень нравится. От возможности отображать обратные функции до производных, это помогает мне лучше понять концепции. Однозначно рекомендую.
Разработчик Desmos указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Данные, не связанные с вами
Могут быть собраны следующие данные, но они не связаны с вашей личностью:
Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста.
Узнать больше
Информация
- Продавец
- Десмос, Инк.
- Размер
- 11,9 МБ
- Категория
- Образование
- Возрастной рейтинг
- 4+
- Авторское право
- © 2021 Desmos Inc.
- Цена
- Бесплатно
- Сайт разработчика
- Тех. поддержка
- Политика конфиденциальности
Еще от этого разработчика
Вам также может понравиться
Пункты графика графического калькулятора онлайн
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
jpg»>
05.2003 
03.2005 
Мой друг хорошо разбирается в математике, и я нашел эту программу в его карманном компьютере. Только тогда я понял, почему он находит этот предмет таким легким.
Заслуживающее внимания обучение, предлагаемое Алгебратором по построению графиков, процентам, свойствам уравнений и решению треугольника, не имеет себе равных. Я пробовал 3-4 программы для домашнего обучения математике, и я нашел это необычным. Алгебратор не только предлагает вам основные принципы, но также помогает с легкостью решить любой сложный вопрос по алгебре среднего уровня. Краткий справочник формул, поставляемый с Algebrator, очень информативен и содержит почти все формулы, относящиеся к Algebra 2.