Площадь сферы
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о сфере). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом на форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√». ЗадачаВ сферу вписан конус, образующая которого равна l, а угол при вершине осевого сечения равен 60 градусов. Найдите площадь сферы.
Решение.
Площадь сферы найдем по формуле:
S = 4πr2
Поскольку в сферу вписан конус, проведем сечение через вершину конуса, которое будет равнобедренным треугольником. Поскольку угол при вершине осевого сечения равен 60 градусам, то треугольник — равносторонний (сумма углов треугольника — 180 градусов, значит остальные углы ( 180-60 ) / 2 = 60 , то есть все углы равны ).
Откуда радиус сферы равен радиусу окружности, описанного вокруг равностороннего треугольника. Сторона треугольника по условию равна l . То есть
R = √3/3 l
Таким образом площадь сферы
S = 4π(√3/3 l)2
S = 4/3πl2
Ответ: площадь сферы равна 4/3πl2.
Задача
Емкость имеет форму полусферы (полушара). Длина окружности основания равна 46 см. На 1 квадратный метр расходуется 300 граммов краски. Сколько необходимо краски, чтобы покрасить емкость?
Решение.
Площадь поверхности фигуры будет равна половине площади сферы и площади сечения сферы.
Поскольку нам известна длина окружности основания, найдем ее радиус:
L = 2πR
R = L / 2π
R = 46 / 2π
R = 23 / π
Откуда площадь основания равна
S = πR2
S = π (23/π) 2
S = 529 / π
Площадь сферы найдем по формуле:
S = 4πr2
Соответственно площадь полусферы
S = 4πr2 / 2
S = 2π (23/π) 2
S = 1058 / π
Общая площадь поверхности фигуры равна:
529 / π + 1058 / π = 1587 / π
Теперь вычислим расход краски (учтем, что расход дан на квадратный метр, а вычисленное значение в квадратных сантиметрах, то есть в одном метре 10 000 квадратных сантиметров)
1587 / π * 300 / 10 000 = 47,61 / π граммов ≈ 15,15 г
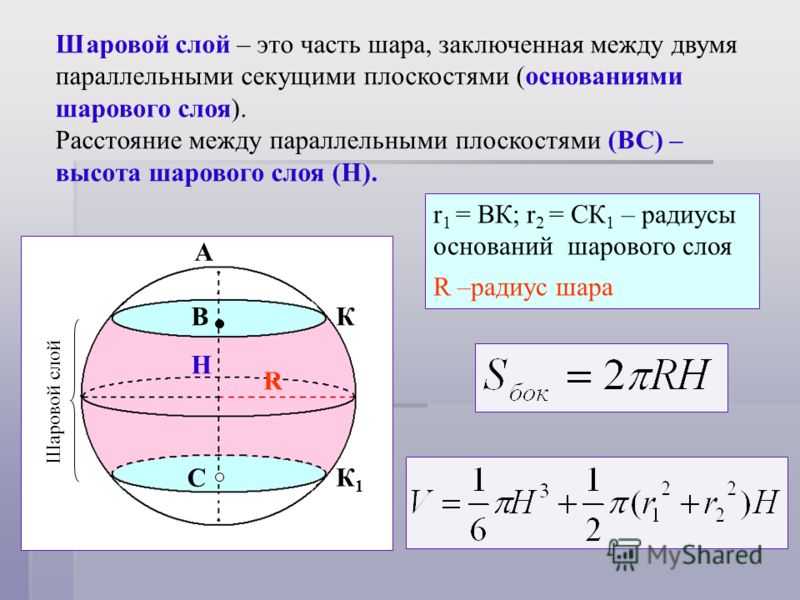
Задача
|
Поверхности двух шаров относятся как m:n. |
Поверхні двох куль відносяться як m:n. Як відносяться їх об’єми? |
Решение. Рiшення.
Для пояснения решения прокомментируем каждую из приведенных формул
| Для пояснення рішення прокоментуємо кожну з приведених формул
| |
| 8. Разделим объемы первого и второго шара друг на друга
9. Сократим получившуюся дробь. Заметим, что соотношение объема двух шаров равно соотношению кубов их радиусов. Учтем выражение, полученное нами ранее в формуле 4 и подставим его. Поскольку корень квадратный — это число в степени 1/2, преобразуем выражение 10. Раскроем скобки и запишем полученное соотношение в виде пропорции. Ответ получен. | 8. Розділимо об’єми першої і другої кулі один на одного
9. Скоротимо дріб, що вийшов. 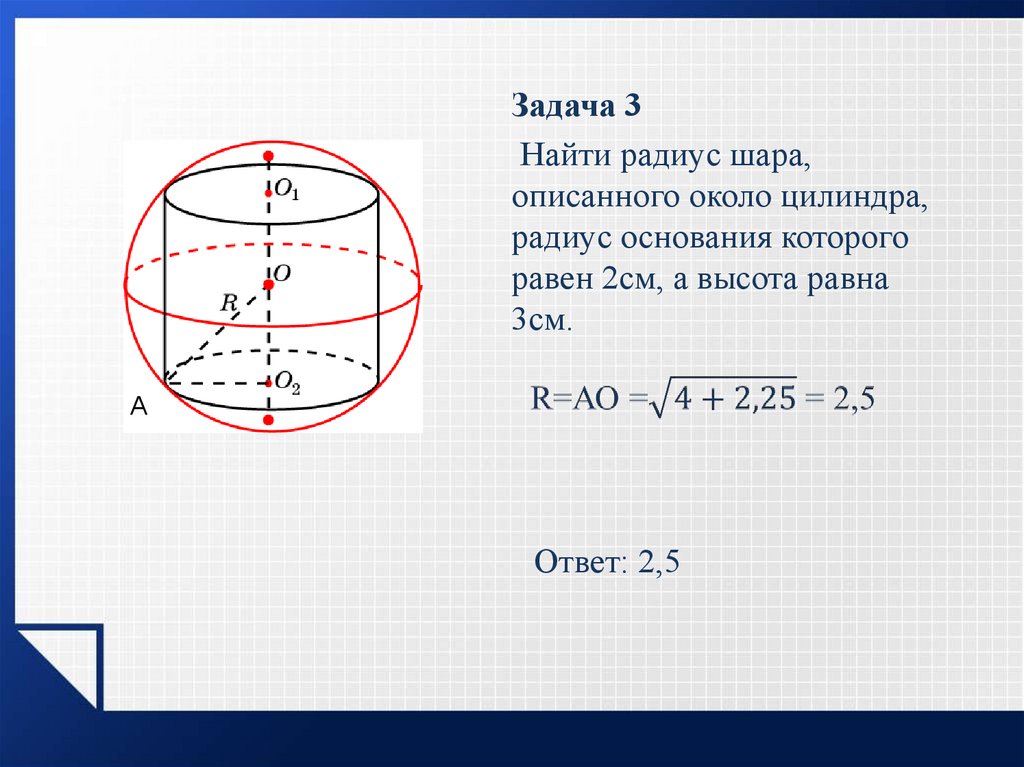 Відмітимо, що співвідношення об’єму двох куль дорівнює співвідношенню кубів їх радіусів. Врахуємо вираження, отримане нами раніше у формулі 4 і підставимо його. Оскільки корінь квадратний — це число в мірі 1/2, перетворимо вираження Відмітимо, що співвідношення об’єму двох куль дорівнює співвідношенню кубів їх радіусів. Врахуємо вираження, отримане нами раніше у формулі 4 і підставимо його. Оскільки корінь квадратний — це число в мірі 1/2, перетворимо вираження
|
0
Сфера (Шар) | Описание курса | Полусфера
сферы, шапочки, кольца / Этюды // Математические этюды
Площадь на сфере: сферы, шапочки, кольца / Этюды // Математические этюдыМатематические этюды
К списку
Площадь всей сферы, шапочки или кольца на сфере посчитать не так просто. Помогает сравнение сферы с «плоскими» поверхностями — плоскостью, конусом и цилиндром.
Если плоскость касается сферы в полюсе, то площадь сферической шапочки и круга на плоскости, высекаемых «вспомогательной»
сферой с центром в полюсе, — одинакова.
«Считывая» с глобуса информацию по приведённому алгоритму, можно построить равновеликую азимутальную картографическую проекцию Земли. Такая проекция сохраняет площади всех областей. Разработал её математик и астроном Иоганн Ламберт — тот самый, который доказал иррациональность числа $\pi$. Заметный недостаток проекции — значительное искажение на общей карте Земли контуров крупных областей, например, континентов.
Круг, касающийся сферы в полюсе, можно считать предельным случаем конуса, касающегося сферы.
Рассмотрим две вспомогательные концентрические сферы с центром в вершине конуса. И на сфере, и на конусе эти сферы высекают кольца. Оказывается, что площади этих колец — на сфере и на конусе — равны.
Равенство остаётся верным для любого положения концентрических сфер. Рассмотренный случай равенства площадей шапочки на сфере
и соответствующего круга, касающегося сферы, получается из конического: радиус одной из концентрических сфер следует положить
нулю, а вершину конуса поместить в полюс сферы.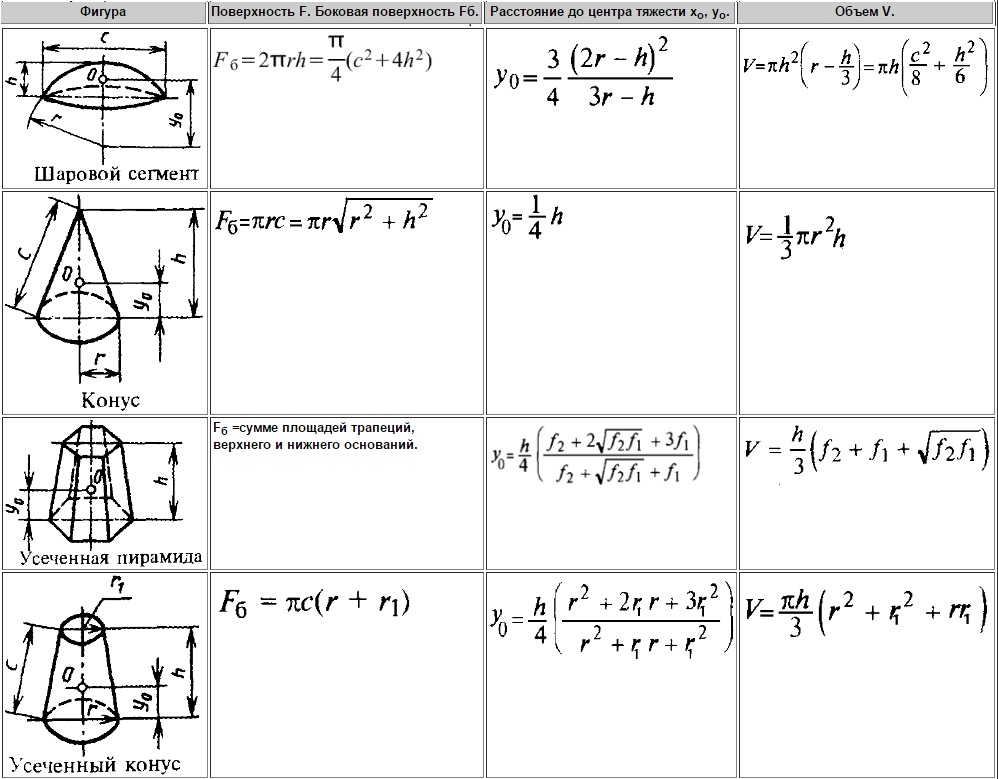
Если же вершину конуса «угнать» на бесконечность, то конус перейдёт в цилиндр, касающийся сферы по экватору. Концентрические вспомогательные сферы перейдут в плоскости.
Площадь сферического кольца, вырезаемого двумя параллельными плоскостями, равна площади соответствующего цилиндрического кольца (плоскости перпендикулярны оси цилиндра). Это приводит к интересному наблюдению: площадь кольца на глобусе зависит только от расстояния между секущими плоскостями, но не зависит от близости кольца к экватору или полюсу. «Съедобное» толкование: если круглый неочищенный апельсин нарезать на ломтики одинаковой толщины, то и площадь шкурки у всех кусков будет одинакова.
Сравнение площади кольца на сфере и кольца на цилиндре позволяет посчитать площадь всей сферы. Когда плоскости касаются полюсов
сферы расстояние между ними равно $2R$. А длина окружности цилиндра, касающегося сферы равна $2\pi R$. 2$.
2$.
Перенося информацию с глобуса на сферу с сохранением высоты получаем равновеликую цилиндрическую картографическую проекцию Земли. Такая проекция, по рассмотренному выше свойству, сохраняет площади всех областей и тоже была разработана Ламбертом.
Утверждение про равенство площадей колец на сфере и на цилиндре называется леммой Архимеда и известно с давних времён. Утверждение про площадь сферической шапочки и площадь круга тоже довольно известно. Удивительно, что связывающая эти два случая конструкция — сравнение площадей колец на сфере и на конусе, заключённых между концентрическими сферами с центрами в вершине конуса — малоизвестна и, возможно, была открыта только в XXI веке.
Литература
Акопян А. Апельсины, канализационные люки и разрезание длинного прямоугольника // Журнал «Квант». — 2021. — № 9. — Стр. 40—43.
Vin De Silva. A Generalisation of Archimedes’ Hatbox Theorem // The Mathematical Gazette. — 2006. — Vol. 90, № 517. — P. 132—134.
— 2006. — Vol. 90, № 517. — P. 132—134.
Картографические проекции // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 136—145, 342, 343.
Теорема о косточке // Математические этюды.
Другие этюды раздела «Площади и объёмы»
Площади фигурОбновлено Формула ПикаТеорема Пифагора: доказательство ЕвклидаОбновлено Теорема Пифагора: интерактивная головоломка Объём шара: весы Архимеда Объём шара Теорема о косточке Сапог ШварцаМатематические этюды
Калькулятор площади поверхности полушария
Автор Dominik Czernia, PhD
Рассмотрение Богной Шик и Аденой Бенн
Последнее обновление: 22 ноября 2022 г.
Содержание:- Как найти площадь поверхности полушария?
- Какова площадь полушария?
Наш калькулятор площади поверхности полушария представляет собой удобный инструмент, который находит различные типы площади поверхности полушария.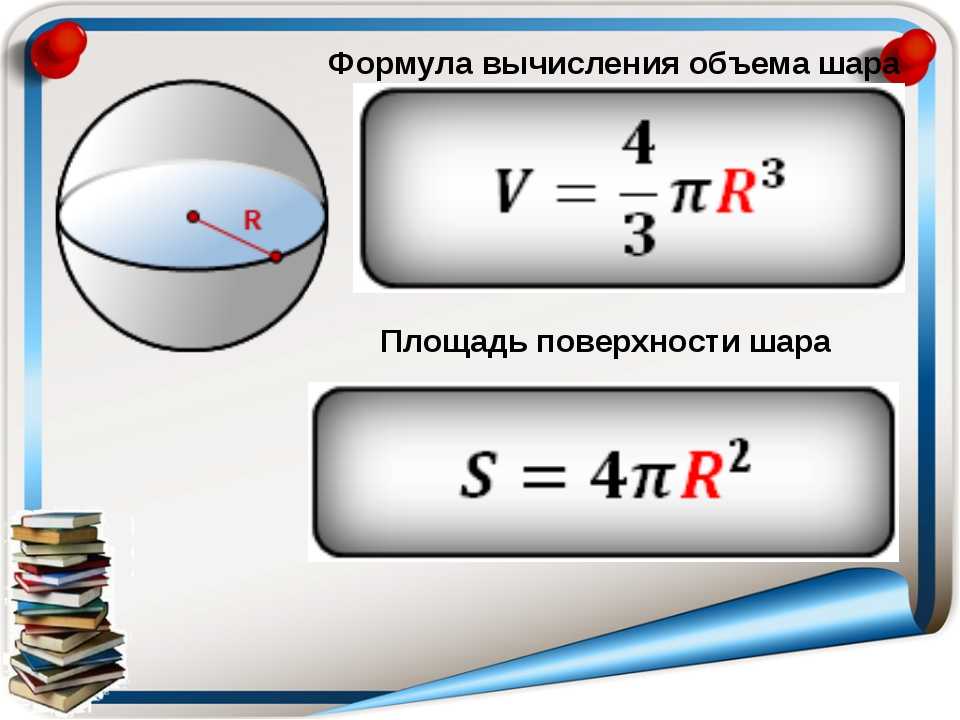 Вы ищете ответ на вопрос, как найти площадь поверхности полушария? Или, может быть, вам просто нужно быстро оценить его? Что бы вы ни планировали сделать, попробуйте этот калькулятор полушарий, который включает в себя несколько различных площадей полушария формулы .
Вы ищете ответ на вопрос, как найти площадь поверхности полушария? Или, может быть, вам просто нужно быстро оценить его? Что бы вы ни планировали сделать, попробуйте этот калькулятор полушарий, который включает в себя несколько различных площадей полушария формулы .
Полусферы создаются путем разделения сферы на две равные половины, как вы можете видеть на рисунке ниже. В отличие от полной сферы, полусфера имеет два типа площадей поверхности: площадь основания (которая представляет собой круг) и площадь крышки . Обозначения, которые мы использовали в этом калькуляторе площади поверхности полушария, следующие:
- r — радиус полушария;
- d — диаметр полусферы;
- V — объем полусферы;
- А — общая площадь поверхности полушария;
- Ab — площадь базовой поверхности полушария;
- Ac — площадь поверхности крышки полусферы; и
- A/V — отношение поверхности к объему полусферы.

🙋 Интересно, что суммарный объем двух полушарий равен объему одной полной сферы. Однако это не относится к площади поверхности. Суммарная площадь двух полушарий больше площади сферы. Причина проста: полушария имеют дополнительных площадей основания .
Если вам нужно проанализировать полные сферы, наш калькулятор сфер — это то, что вам нужно!
Как найти площадь поверхности полушария?
Когда мы разделим сферу пополам и возьмем одну из получившихся частей , мы получим полусферу. В каждом полушарии мы можем назвать две области поверхности: основания и крышки (см. рисунок выше). Из калькулятора площади сферы мы знаем, что площадь поверхности сферы следующая:
A(сфера) = 4 × π × r² .
Вы можете думать об этом как о , в два раза превышающем площадь поверхности крышки полушария . Следовательно, площадь шапки полушария равна:
Ac = A(сфера) / 2 ,
Ac = 2 × π × r² .
Площадь базовой поверхности представляет собой круг с таким же радиусом, как полусфера . Таким образом, согласно кругу вычислить: найти A, можно выразить так:
Ab = π × r² .
Наконец, общая площадь поверхности равна сумма этих двух вкладов :
A = Ac + Ab ,
A = 2 × π × r² + π × r² ,
A = 3 × π × r² 9000.
Калькулятор площади полушария позволяет найти все три типа площадей поверхности определенного полушария. Более того, вы можете выполнять все расчеты в различных единицах измерения (СИ и имперские единицы). Если вы хотите узнать больше о преобразовании единиц площади, ознакомьтесь с нашим конвертером площади!
Какова площадь полушария?
Теперь, когда мы знаем, что такое площадь поверхности полушария и как ее найти, давайте попробуем вывести различные формулы площади полушария. Они могут быть полезны в ситуациях, когда у нас нет радиуса . Прежде всего, есть некоторые основные уравнения полушария, которые вы должны знать:
Прежде всего, есть некоторые основные уравнения полушария, которые вы должны знать:
- Диаметр полушария:
d = 2 × r, - Объем полушария:
В = 2/3 × π × r³, - Площадь основания полушария:
Ab = π × r², - Площадь поверхности крышки полусферы:
Ac = 2 × π × r², - Полная площадь поверхности полушария:
A = 3 × π × r², - Отношение поверхности к объему полушария:
A / V = 9 / (2 × r).
Формула площади полушария (для общей площади) может быть получена из приведенных выше уравнений. Мы можем получить даже шесть из них! Уравнения, используемые вычислителем площади полушария, следующие:
- Учитывая радиус :
A = 3 × π × r²; - Дан диаметр :
A = 3/4 × π × d²; - Учитывая объемов :
A = ³√[243/4 × π × V²]; - Дана базовая площадь :
A = 3 × Ab; - Учитывая площадь крышки :
A = 3/2 × Ac; и - Учитывая отношение поверхности к объему :
A = 243 × π / (4 × (A/V)²).
Как известно, Земля приблизительно представляет собой шар с радиусом почти 6400 км , в котором можно указать северное и южное полушария (конкретно говоря, Земля - геоид). Этот раздел играет важную роль в географии и физике. Например, существует сила, называемая эффектом Кориолиса, которая действует на вас всякий раз, когда вы путешествуете на самолете, заставляя вас сбиться с курса. Когда вы находитесь в северном полушарии, вы будете отклоняться вправо, а в южном полушарии — влево. Вы можете найти больше информации по этой теме в нашем калькуляторе эффекта Кориолиса.
Dominik Czernia, PhD
Радиус
Диаметр
Том
Коэффициент поверхности к объему
Области поверхности
Проверьте 21 Аналогичные калькуляторы 3D Geometry 📦
Кубики. Callced: Найти vo, dellips void geallet geallet Zoide Zoide Zoide xolead. 18 more
Площадь поверхности полушария
Площадь поверхности полушария определяется как область, покрытая гранями полушария. Общая площадь поверхности полушария включает площадь криволинейной поверхности и площадь основания полусферы. Давайте узнаем больше об общей площади поверхности полушария и площади криволинейной поверхности полушария вместе с решенными примерами.
Общая площадь поверхности полушария включает площадь криволинейной поверхности и площадь основания полусферы. Давайте узнаем больше об общей площади поверхности полушария и площади криволинейной поверхности полушария вместе с решенными примерами.
| 1. | Какова площадь поверхности полушария? |
| 2. | Площадь поверхности полусферы Формула |
| 3. | Как найти площадь поверхности полушария? |
| 4. | Часто задаваемые вопросы о площади поверхности полушария |
Какова площадь поверхности полушария?
Площадь поверхности полушария равна сумме площадей всех его граней. Полусфера — это трехмерная фигура, которая получается при разрезании сферы по плоскости, проходящей через центр сферы. Другими словами, полушарие — это половина сферы. Полусфера может быть полой или сплошной. Площадь поверхности полушария измеряется в квадратных единицах. Обратите внимание на рисунок, приведенный ниже, чтобы увидеть сферу и полусферу.
Площадь поверхности полушария измеряется в квадратных единицах. Обратите внимание на рисунок, приведенный ниже, чтобы увидеть сферу и полусферу.
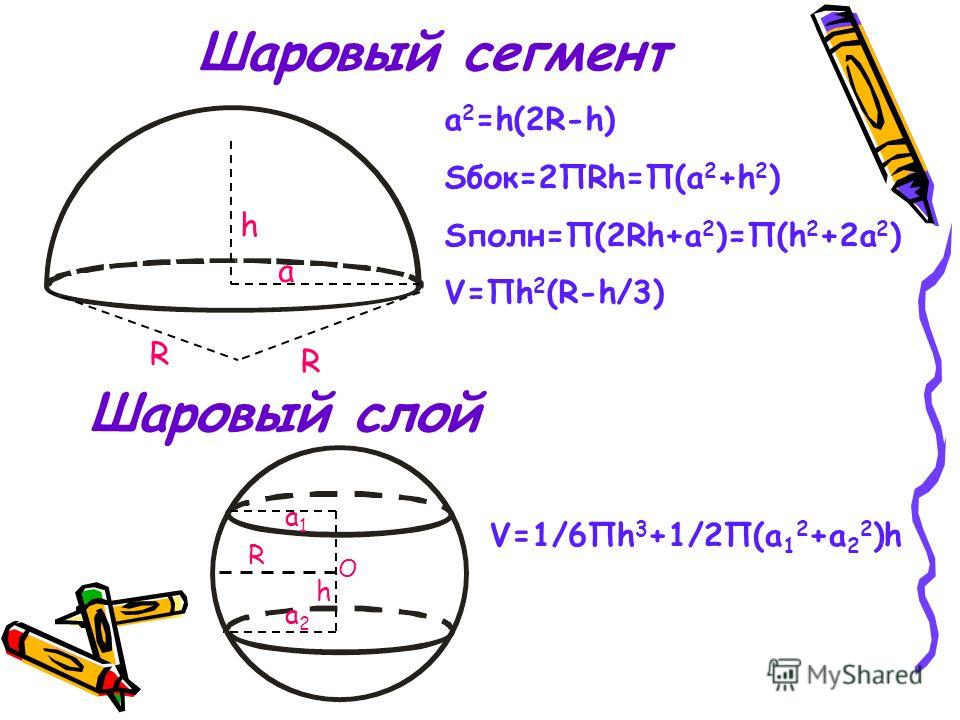
Площадь поверхности полушария Формула
Формула площади поверхности полушария может быть дана как для твердого, так и для полого полушария. Площадь поверхности полушария — это общая площадь, которую покрывают его грани. Его можно разделить на две категории:
- Площадь искривленной поверхности полушария (CSA)
- Общая площадь поверхности полушария (TSA)
Площадь криволинейной поверхности полусферы Формула
Площадь криволинейной поверхности полусферы — это площадь, покрытая ее криволинейной поверхностью. Это ровно половина площади поверхности шара. Площадь криволинейной поверхности полусферы радиуса r можно рассчитать по следующей формуле.
Площадь криволинейной поверхности полушария = 1/2 (площадь криволинейной поверхности сферы) = 1/2 (4 π r 2 ) = 2 π r 2
Где r – радиус полушария .
Общая площадь поверхности полусферы Формула
Общая площадь поверхности полусферы определяется как общее пространство, занимаемое криволинейной поверхностью и базовой поверхностью полусферы. Полную площадь поверхности полушария можно рассчитать, найдя сумму площадей его криволинейной поверхности и поверхности основания. Следует отметить, что основанием полушария является круг. Для полушария, если дан его радиус, то его общую площадь поверхности можно рассчитать по формуле:
Площадь поверхности полушария = Площадь изогнутой поверхности + Площадь основания = 2 π r 2 + π r 2 = 3 π r 2
Где r — радиус полушария.
Площадь поверхности полого полушария Формула
Формула площади поверхности полого полушария: TSA полого полушария = 3πR 2 + πr 2 . Давайте разберемся с выводом этой формулы.
Следует отметить, что существуют два диаметра для круглых оснований полой полусферы: один для внутреннего круглого основания (полая область) и один для внешнего круглого основания. Если «r» — радиус внутренней полусферы, а «R» — радиус внешней полусферы, мы можем вывести следующие формулы.
Если «r» — радиус внутренней полусферы, а «R» — радиус внешней полусферы, мы можем вывести следующие формулы.
- Площадь искривленной поверхности внешней полусферы = 2πR 2
- Площадь искривленной поверхности внутренней полусферы = 2πr 2
- Если мы посмотрим на рисунок, приведенный ниже, мы увидим, что кольцо образовано. Площадь кольца = π(R 2 - r 2 )
- Итак, Полную площадь поверхности полого полушария можно рассчитать, если сложить приведенные выше формулы, то есть TSA полого полушария = 2πR 2 + 2πr 2 + π(R 2 - r 2 ). Это можно записать как TSA полого полушария = 2π (R 2 + r 2 ) + π (R 2 - r 2 ). И если мы хотим еще больше упростить, то получается 3πR 2 + πr 2
Как найти площадь поверхности полушария?
Как мы узнали из предыдущего раздела, площадь поверхности полушария может быть рассчитана с использованием различных формул для полого или твердого полушария, в зависимости от того, находим ли мы площадь изогнутой поверхности или общую площадь поверхности.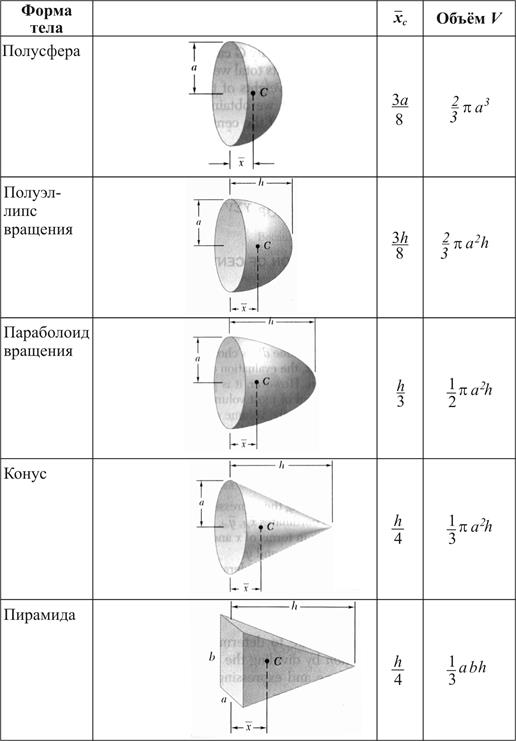
Площадь криволинейной поверхности полушария
Формула для расчета площади криволинейной поверхности (CSA) полушария с радиусом 'r' дается как CSA полушария = 2πr 2 . Следующие шаги показывают, как найти площадь криволинейной поверхности полусферы.
- Шаг 1: Определите радиус (r) полушария.
- Шаг 2: Подставьте значение радиуса (r) и найдите площадь криволинейной поверхности полушария по формуле CSA полушария = 2πr 2
- Шаг 3: Представьте полученный окончательный ответ в квадратных единицах.
Пример: Найдите площадь криволинейной поверхности полушария, радиус которого равен 8 единицам. (Используйте π = 3,14)
Решение:
Радиус (r) полушария = 8 единиц. Итак, подставим в формулу значение r = 8.
Площадь криволинейной поверхности полушария = 2 π r 2 = 2 × 3,14 × 8 2 = 2 × 3,14 × 64 = 401,92 единицы 2
Следовательно, площадь криволинейной поверхности полушария = 401,92 единицы 2
Общая площадь поверхности полушария
Формула для расчета общей площади поверхности (TSA) полушария с радиусом 'r' определяется как TSA полушария = 3πr 2 . Таким образом, мы следуем шагам, показанным ниже, чтобы найти общую площадь полушария.
Таким образом, мы следуем шагам, показанным ниже, чтобы найти общую площадь полушария.
- Шаг 1: Определите радиус (r) полушария.
- Шаг 2: Подставьте значение радиуса (r) и найдите общую площадь поверхности полушария по формуле TSA полушария = 3πr 2
- Шаг 3: Представьте ответ в квадратных единицах.
Пример: Найдите общую площадь поверхности полушария, радиус которого равен 7 единицам. (Используйте π = 22/7)
Решение:
Радиус (r) полушария = 7 единиц. Итак, подставим в формулу значение r = 7.
Общая площадь поверхности полушария = 3 π r 2 = 3 × (22/7) × 7 2 = 3 × 22 × 7 = 462 единицы 2
Следовательно, общая площадь поверхности полушария = 462 единицы 2
Площадь поверхности полого полушария
Площадь поверхности полого полушария можно рассчитать, используя следующие шаги:
- Шаг 1: Определите внутренний радиус (r) и внешний радиус (R ) полого полушария.

- Шаг 2: Найдите общую площадь поверхности полусферы по формуле TSA полой полусферы = 3πR 2 + πr 2
- Шаг 3: Представьте окончательный ответ в квадратных единицах.
Пример: Найдите площадь поверхности полого полушария, внешний радиус которого равен 14 единицам, а внутренний радиус равен 10 единицам. (Используйте π = 3,14)
Решение:
Внешний радиус (R) полушария = 14 единиц, внутренний радиус (r) = 10 единиц. Итак, подставим в формулу значение R = 14, а r = 10.
ТСА полой полусферы = 3πR 2 + πr 2
= [3π × (14) 2 ] + [π × (10) 2 ] 6 1,0003
+ (3,14 × 100)
= 1846,32 + 314
= 2160,32 Единицы 2
Следовательно, площадь поверхности пологом полушарина = 2160,32 Единицы 2
. 6669
6669
- 9000 2 ☛ Связанные
- Площадь поверхности куба
- Площадь поверхности цилиндра
- Площадь поверхности призмы
- Площадь поверхности конуса
- Площадь поверхности сферы
- Разница между площадью и площадью поверхности
- Формулы площади поверхности
9000 2 . Прямоугольник
Примеры площади поверхности полушария
Пример 1: Найдите общую площадь поверхности полушария с радиусом = 21 единица. (Используйте π = 22/7)
Решение:
Радиус полушария = 21 ед. 3 × 22 × 21 × 3 = 4158 единиц 2
Следовательно, общая площадь поверхности полушария = 4158 единиц 2
Пример 2: Используя формулу площади поверхности полушария, найдите радиус полушария, если его общая площадь поверхности = 648 единиц 2 .
 (Use π = 3.14)
(Use π = 3.14)Solution:
The total surface area of a hemisphere = 648 units 2
3 π r 2 = 648
3 × 3.14 × r 2 = 648
9,42 × r 2 = 648
r 2 = 648/9,42 = 68,78
r = 8,29 ед.
Следовательно, радиус полушария = 90,293 ед.
Пример 3: Найдите площадь криволинейной поверхности полусферы, радиус которой равен 9единицы измерения. (Используйте π = 3,14)
Решение:
Радиус (r) полушария = 9 единиц. Итак, подставим в формулу значение r = 9.
Площадь криволинейной поверхности полушария = 2 π r 2 = 2 × 3,14 × 9 2 = 2 × 3,14 × 81 = 508,68 единиц 2
Следовательно, площадь криволинейной поверхности полушария равна 508,8 единиц. 2
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Записаться на бесплатный пробный урок
Практические вопросы по площади поверхности полушария
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади поверхности полушария
Какова площадь поверхности полушария?
площадь поверхности полушария — сумма площадей всех его граней. Поскольку полусфера состоит из изогнутой поверхности и плоской круглой поверхности, нам нужно объединить эти площади, чтобы получить общую площадь поверхности полусферы.
Какова формула площади поверхности полушария?
Формула, используемая для нахождения общей площади поверхности полушария, выражается следующим образом: общая площадь поверхности полушария = 3πr 2 ; где «r» — радиус полушария.
Как найти площадь криволинейной поверхности полушария?
Площадь криволинейной поверхности (CSA) полусферы можно рассчитать, выполнив следующие действия.
- Шаг 1: Определите радиус (r) полушария.
- Шаг 2: Подставьте значение радиуса (r) и найдите площадь криволинейной поверхности полушария по формуле CSA полушария = 2πr 2
- Шаг 3: Выразите площадь в квадратных единицах.
Как найти площадь поверхности полушария?
Площадь поверхности полусферы можно рассчитать в зависимости от типа полусферы, которая может быть полой или сплошной, а также от требуемой площади поверхности. В следующем списке показаны формулы, которые используются для нахождения общей площади поверхности, площади криволинейной поверхности полусферы и общей площади поверхности полой полусферы.
- Общая площадь поверхности полушария = 3πr 2 , где r — радиус полушария.
- Площадь искривленной поверхности полушария = 2πr 2 , где 'r' — радиус полушария.
- Общая площадь поверхности полого полушария = 2π (R 2 + r 2 ) + π(R 2 - r 2 ), где R — внешний радиус полушария, а «r» — внутренний радиус полушария.
 Эта формула также может быть выражена как 3πR 2 + πr 2
Эта формула также может быть выражена как 3πR 2 + πr 2
Какова общая площадь поверхности полого полушария?
Общая площадь, занимаемая или покрытая криволинейной поверхностью и базовой поверхностью полусферы, определяется как общая площадь поверхности полусферы. Для полой полусферы, если заданы ее внутренний радиус (r) и внешний радиус (R), то ее площадь можно рассчитать по формуле: общая площадь поверхности полой полусферы = площадь внешней криволинейной поверхности + площадь внутренней криволинейной поверхности + основание область. Это записывается как ВПС полой полусферы = 2π (R 2 + r 2 ) + π(R 2 - р 2 ). Его также можно упростить и записать как TSA полого полушария = 3πR 2 + πr 2
Какова площадь основания полушария?
Площадь основания полушария – это площадь его основания, которое представляет собой круг. Итак, если радиус (r) полушария дан, то площадь его основания можно рассчитать по формуле: площадь основания полушария = площадь основания круга = π r 2
Что такое площадь боковой поверхности полушария?
Площадь боковой поверхности полушария также известна как изогнутая поверхность полушария. Для полусферы, если ее радиус (r) дан, то площадь ее боковой поверхности можно рассчитать по формуле: площадь боковой поверхности = 1/2 (площадь боковой поверхности сферы) = 1/2 (4 π r 2 ) = 2πr 2
Для полусферы, если ее радиус (r) дан, то площадь ее боковой поверхности можно рассчитать по формуле: площадь боковой поверхности = 1/2 (площадь боковой поверхности сферы) = 1/2 (4 π r 2 ) = 2πr 2
Какова общая площадь поверхности полусферической оболочки?
Общая площадь поверхности полусферической оболочки может быть рассчитана по формуле для общей площади поверхности полой полусферы, поскольку полусферическая оболочка является полой полусферой. Это можно рассчитать по формуле TSA полой полусферы = 3πR 2 + πr 2 , где r – радиус внутренней полусферической оболочки, R – радиус внешней полусферической оболочки.
В чем разница между площадью криволинейной поверхности и площадью поверхности полушария?
Изогнутая поверхность (CSA) — это искривленная часть полушария. Формула, используемая для расчета площади криволинейной поверхности полушария: CSA полушария = 2πr 2 . Принимая во внимание, что общая площадь поверхности полушария включает изогнутую площадь и остальную часть площади полушария.

 Как относятся их объемы?
Как относятся их объемы? Полученное равенство запомним
Полученное равенство запомним Отриману рівність запам’ятаємо
Отриману рівність запам’ятаємо 


 (Use π = 3.14)
(Use π = 3.14)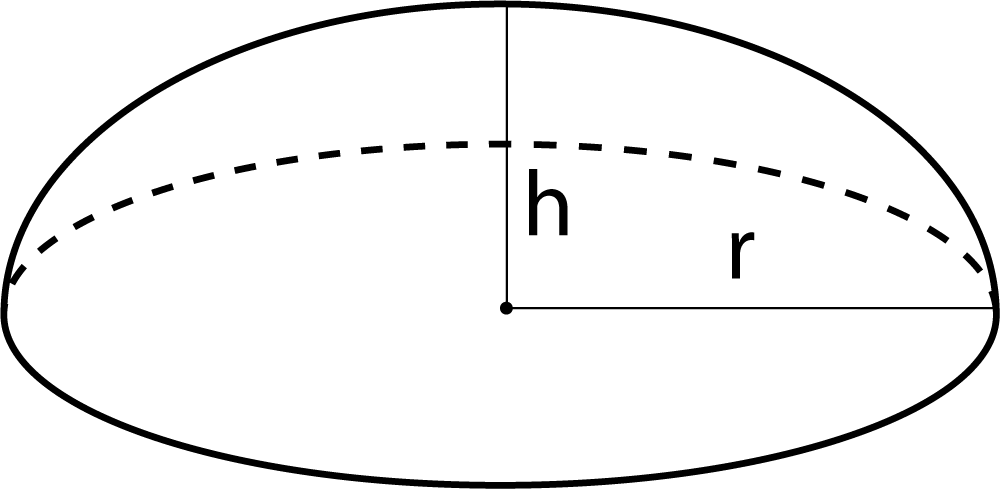 Эта формула также может быть выражена как 3πR 2 + πr 2
Эта формула также может быть выражена как 3πR 2 + πr 2