Тест 4 подобие треугольников и произвольных фигур: О подобии произвольных фигур

Подобие треугольников 8 класс с ответами

Тесты по геометрии 8 класс. Тема: «Подобие треугольников»

Правильный вариант ответа отмечен знаком +

1. На рисунке изображены две похожие фигуры. В каком из вариантов они будут подобными?

— а;

— г;

— б;

+ в.

2. Отношение сторон одного треугольника было задано как 2:4:6. Меньшая из сторон, подобного ему второго треугольника, равняется 4 см. Определите, чему будет равняться периметр этого треугольника.

— 18 см;

— 22 см;

— 20 см;

+ 24 см.

3. Сколько подобных треугольников изображено на этом рисунке?

— 2;

— 4;

— 1;

+3.

4. Треугольники KLM и K₁L₁M₁ подобны. Известно, что отношение площади треугольника KLM к площади K₁L₁M₁ равно 3.

Чему равно отношение сходственных сторон KL к K₁L₁?

+ √3;

— 3;

— 6;

— 9.

5. Сходственные стороны треугольников MKE и M₁K₁E₁ равны соответственно 9 и 3. Площадь треугольника MKE равна 27. Чему равняется площадь треугольника M₁K₁E₁?

— 27;

— 9;

— √27;

+ 3.

6. Отношение площадей подобных треугольников ABC и MNL равно 81. Сторона АВ равна 18. Найдите длину сходственной ей стороны MN.

— 0,22;

— 4,5;

+ 2;

— 9.

7. Стороны треугольников KLM и FER равны: KL = 5, LM = 2, MK = 4; FE = 2,5, ER = 1, RF = 2. Подобны ли данные треугольники? Если да, чему равняется коэффициент подобия?

— треугольники не будут подобными;

+ треугольники подобны, их коэффициент подобия 2;

— они будут подобными, коэффициент подобия 3;

— треугольники являются подобными, с коэффициентом подобия 5.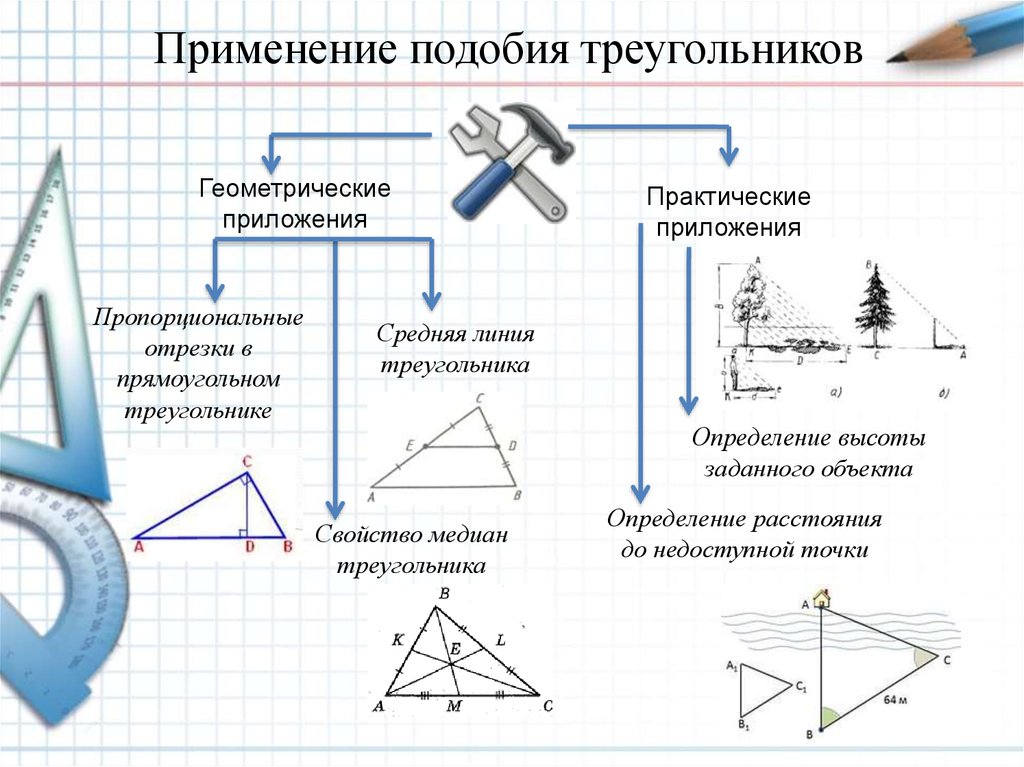

8. В треугольнике ABC угол А = 80°, угол B=15°, сторона АВ = 3. В треугольнике A₁B₁C₁ угол В₁ = 80°, угол С₁=85°, сторона A₁B₁ равна 9. Являются ли треугольники ABC и A₁B₁C₁ подобными? Почему?

— не являются, так как не справедлив ни один из признаков подобия;

+ являются, так как 2 угла 1-го треугольника соответственно равны 2-м углам другого треугольника;

— являются, так как 2 стороны одного треугольника пропорциональны 2-м сторонам другого треугольника, а углы между этими сторонами равны;

— являются, так как 3 стороны одного треугольника пропорциональны 3-м сторонам другого треугольника.

9. Подобны ли равнобедренные треугольники, приведённые на рисунке?

— Треугольники не являются подобными;

— треугольники являются подобными по 2-м пропорциональным сторонам и равным углам между ними;

+ треугольники являются подобными по 2-м равным углам;

— в условии не хватает данных для решения задачи.

10. Треугольники KLM и K₁L₁M₁ подобны. Площадь треугольника KLM меньше площади треугольника K₁L₁M₁ на 5 единиц. Коэффициент подобия равен √6. Чему равна площадь треугольника KLM?

— 5*√6;

— 5: √6;

— 7;

+2.

11. Дана задача: «Треугольники MKE и M

1K₁E₁ подобны. MK = 4, KE = 5, EM=3. Коэффициент подобия равен 2 (треугольник M₁K₁E₁ больше). Найдите отношение периметров этих треугольников». Ниже приведено ее решение. В одном из этапов допущена ошибка. В ответе укажите номер этого этапа.

Решение:

1) Периметр треугольника MKE = MK + KE + EM = 4 + 5 + 3 = 12.

2) Так как треугольники подобны, стороны треугольника M₁K₁E₁ можно найти по формулам:

M₁K₁ = MK/2 =4/2=2;

K₁E₁ = KE/2=5/2=2,5;

E₁M₁ = EM/2=3/2=1,5.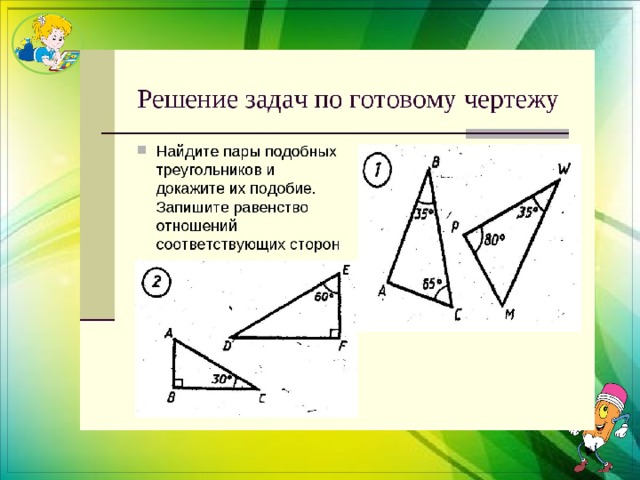

3) Периметр треугольника M₁K₁E₁ = M₁K₁ + K₁E₁ + E₁M₁ = 2 + 2,5 + 1,5 = 6.

4) Отношение периметров треугольников MKE и M₁K₁E₁ равно 12:6=2.

Выберите правильный ответ:

-1;

+2;

— 3;

— 4.

12. Имеются подобные треугольники MKE и M₁K₁E₁. Причем, MK = 4, KE = 5, EM=3. Известен коэффициент подобия данных треугольников. Он равен 2, M₁K₁E₁ — больший треугольник. Требуется найти отношение периметров рассматриваемых треугольников.

+2;

— 4;

— 6;

— 8.

13. На рисунках изображены два треугольника. Являются ли они подобными? Если да, чему равен коэффициент подобия? Учитывайте размер клеток на рисунках — 1х1.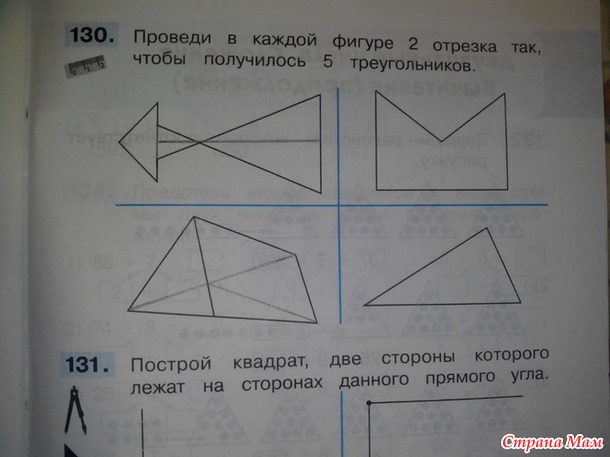

— треугольники подобными не будут;

— треугольники считаются подобными, коэффициент подобия 1,5;

+ треугольники подобные, с коэффициентом подобия 2;

— треугольники подобные, их коэффициент подобия 4.

14. Треугольники ABC и LRE подобны: MN = средняя линия в треугольнике ABC. Найдите коэффициент подобия треугольников LRE и MBN.

+1,5;

— 2;

— 4;

— эти треугольники не будут подобными.

15. В треугольнике EDF был проведён отрезок MN параллельно отрезку DF. Чему будет равен коэффициент подобия получившихся треугольников, если известно, что длина EN = 4 см, а NF= 1 см.

— 4;

— 1/4;

— 5;

+ 4/5 или 5/4.

16. В прямоугольном треугольнике ABC провели отрезок MN, перпендикулярный гипотенузе AB. Какое утверждение будет верным?

Треугольники ABC и MNB будут:

— подобными по 2-м пропорциональным сторонам, а также углу между ними;

— они подобные по паре сторон;

— не подобные;

+ подобные по паре углов.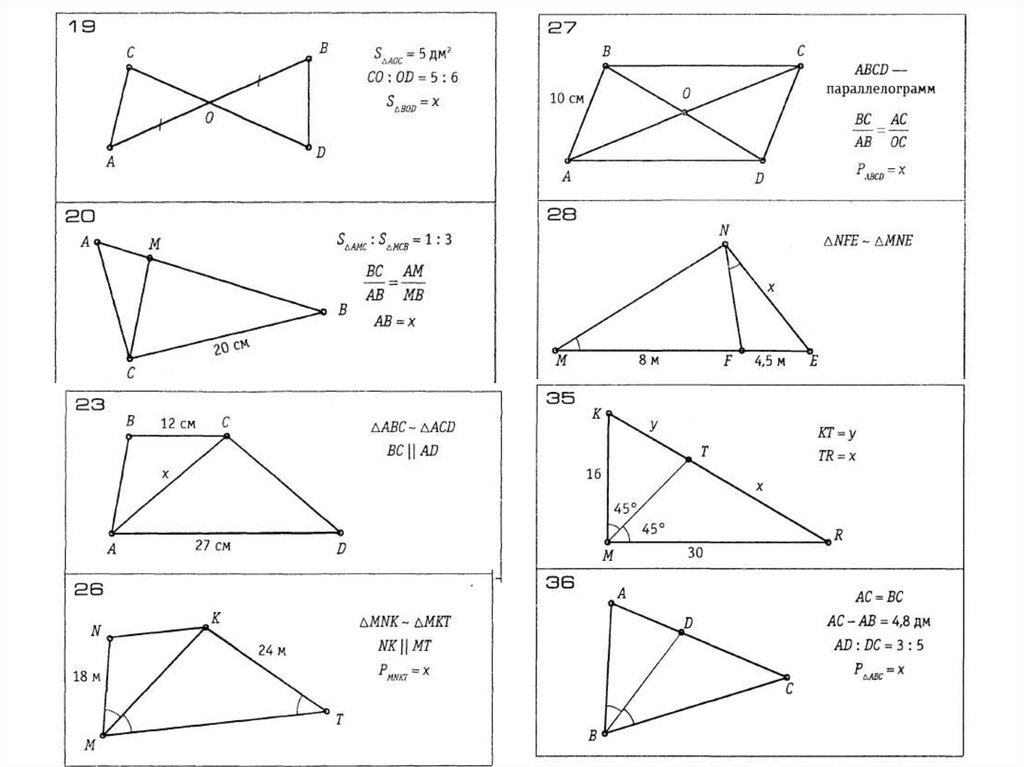

17. Ученик 8 класса средней школы, ростом 1 м 75 см, стоит рядом со столбом. Длина тени школьника равняется 95 см, а длина тени столба составляет 3 м 80 см. Чему будет равна высота столба?

— 7 м;

— 6 м 95 см;

— 7 м 10 см;

+ 7 м 40 см.

18. Треугольники ABC и AB1C подобны, а отрезки AB и A1B1 являются сходственными сторонами. Чему будет равно отношение ?

— 6;

— 3;

— 2;

+ 9.

19. В треугольнике ABC биссектриса CD проведена из угла C. Какое равенство будет верным?

— AC/CD= CD/DB;

— AD/DC= CD/DB;

— AC/CB= DB/AD;

+ AD/BD= AC/BC.

20. На рисунке изображены подобные отрезки. Какое из выражений будет верным для этих отрезков?

— KL/EF= CD/AB;

— AB/CD= EF/KL;

-AB/EF= CD/KL;

+CD/KL= EF/AB.

21. В треугольнике ABC были проведены высоты BB₁ и CC₁. Назовите подобный треугольник для треугольника ABB₁.

— BB₁C;

— BC₁C;

— CC₁B;

+ ACC₁.

22. Чему будет равна длина основания AD у трапеции ABCD?

— 4;

— 8;

— 12;

+ 6.

23. Дана равнобедренная трапеция ABCD, в которой диагональ AC перпендикулярна боковой стороне CD, а сторона BE перпендикулярна диагонали AC, E принадлежит AC. Длина основания трапеций равняется 6 см и 10 см. Необходимо определить соотношение AE:EC.

— 1:3;

— 3:2;

— 3:1;

+ 2:3.

24. В треугольнике ABC проведена средняя линия XY. Длина отрезка AB = 8 см. Чему будет равна длина отрезка XY?

— 2 см;

— 1 см;

— 6 см;

+ 4 см.

25. Выберите верное соотношение между элементами треугольника ABC

26. На рисунке изображены два подобных треугольника. Чему равен отрезок MN?

— 5;

— 4;

— 9;

+ 6.

27. На рисунке изображены два треугольника ABC и MNK. Эти два треугольника считаются подобными. Какому углу соответствует угол A первого треугольника?

— ∠ B;

— ∠ N;

— ∠ K;

+ ∠ M.

28. Согласно признакам подобия, два треугольники подобны, если:

— в треугольниках имеются равные углы;

— у каждого из треугольников стороны пропорциональны сходственным сторонам другого;

— они равны;

+ у этих треугольников углы соответственно равны, а стороны пропорциональны сходственным сторонам другого.

29. Отрезки АВ и СК пропорциональны отрезкам МР и ЕО, если:

— АВ : ЕО = СК : МР;

— АВ : МР = ЕО : СК;

— АВ : СК = ЕО : МР;

+ АВ : МР = СК : ЕО.

30. Треугольник АВС подобен треугольнику А₁В₁С₁, АВ = 4 см, ВС = 6 см, АС = 7 см, А₁В₁ = 8 см. Чему равна сторона В₁С₁?

— 14 см;

— 3 см;

— 3,5 см;

+ 12 см.

Тесты по теме «Треугольник» онлайн

• Треугольники и элементы. Признаки равенства треугольников (7 класс. Повторение)

  27.10.2021 3122

  Тест на знание теоретического материала по теме «Треугольники» для 7 класса

• Равнобедренный треугольник и его свойства

  18.11.2020 13756

  Проверочный тест по теме «Равнобедренный треугольник». Геометрия 7 класс.

• Медиана, биссектриса и высота треугольника

  12.11.2020 6443

  Проверочный тест по теме «Медианы биссектрисы и высоты треугольника»

• 7 класс Глава 2 Треугольники

  18.10.2020 10562 0

  7 класс геометрия учебник Л.С.Атанасян. Данный тест предназначен для повторения Главы 2 «Труегольники». Вопросы двух типов — по теории и практические задания. В тест случайным образом выбираются 5 теоретических вопросов и 5 практических.

• Подобные треугольники.

  ..

  17.03.2019 4948

  Здравствуйте уважаемые ученики. Данный тест предназначен для повторения темы «Подобные треугольники»

• Вычисление площади треугольников. Формула Герона

  21.01.2019 1543

  Тест по геометрии для учащихся 8 класса и старше. Тест полезен в качестве проверки знаний при подготовке к экзаменам. Контактные данные не обязательны и нужны только если вы желаете получить комментарии после проверки (ссылка на страницу VK,  электронная почта, WA). В случае неудачного прохождения научиться решать подобные задачи можно перейдя по ссылке: https://vk.com/stairway5?z=video-172013600_456239026%2F92e52302ee6bf7948a%2Fpl_wall_-172013600    Затем прохождение теста можно повторить.

• 5 класс. Математика. Углы. Прямоугольник. Треугольник.

  08.12.2018 4321

  Тест предназначен для учащихся 5 классов при повторении тем: «Углы», «Прямоугольник и квадрат», «Треугольник».

• Прямоугольные треугольники

  16.04.2020 20726

  Тест по теме «Прямоугольные треугольники» для 7 класса. Содержит 10 вопросов, расположенных в последовательности от простых к более сложным

• 7 класс. Признаки равенства прямоугольных треугольников

  10. 04.2020 5455 0

  Тест — тренинг на применение признаков равенства прямоугольных треугольников. Тест содержит 5 задач на готовых чертежах.

• Виды треугольников

  26.03.2020 3033

  Ребята! Я предлагаю вам ответить на вопросы теста по теме «Виды треугольников»

• Входной тест Геометрия 8

  23.07.2020 269 0

  Входной тест по геометрии, нацеленный на проверку остаточных знаний по геометрии в начале учебного года, проверяет программу по геометрии 7 класса.

• Медиана, биссектриса и высота треугольника.

  

  25.10.2020 10531

  Данный тест будет полезным  учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.

• Геометрия 7 класс. Итоговый тест №2

  20.05.2020 367 0

  Итоговый тест по теме «Признаки равенства треугольников. Медиана, биссектриса и высота треугольника»

• Свойства равнобедренного треугольника.

  25.10.2020 3265 0

  Данный тест будет полезным  учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.

• Первый и второй признаки равенства треугольников

  06.12.2020 799 0

  Тест по геометрии, тема «Первый и второй признаки равенства треугольников»

• Медиана, биссектриса треугольника. Равнобедренный и равносторонний треугольники.

  19.10.2017 101 0

  Задачи этого теста предназначены для отработки и повторения основных свойств треугольников

• Треугольники. Обобщение 7 класс

  19. 07.2019 4772 0

  Данный тест предназначен для проверки знаний учащихся по темам «Треугольники», «Равнобедренный треугольник и его свойства», «Прямоугольный треугольник»

• Остроугольный, прямоугольный и тупоугольный треугольники. 7 класс

  20.12.2020 204 0

  Ребята! Я предлагаю вам ответить на вопросы теста по теме «Виды треугольников». Будьте внимательны!

• Практические задачи на тему: «Подобие треугольников».

  03.02.2022 731 0

  Тестовые задания, проверяющие умение применять подобие треугольников для решения практических задач.

• Треугольник. Элементы треугольника. 7 класс.

  08.05.2018 285 0

  Тест по теме «Треугольник», предназначен для учащихся 7 класса.

• Сумма углов треугольника

  10.05.2020 287 0

  В тесте представлены задачи по теме «Сумма углов треугольника» для учащихся 7 класса.

• Неравенство треугольника. Соотношение между сторонами и углами треугольника.

  22.02.2021 418 0

  Тест содержит 10 заданий по темам «Неравенство треугольника», «Соотношение между сторонами и углами треугольника «

• Геометрия 8-9 класс.

  Треугольники

  04.08.2021 819 0

  Задание 16 ОГЭ несложная планиметрическая задача в одно -два действия, проверяющая владение базовыми знаниями по теме «Треугольники»

• Произвольный треугольник

  08.06.2022 20 0

  Данный тест даст возможность проверить свои знания по методам решения задач на нахождение различных элементов треугольника

• Начальные понятия планиметрии

  06.12.2017 8 0

  Для прохождения теста необходимо повторить следующие вопросы:  Свойства смежных и вертикальных углов. Признаки параллельности прямых. Свойства параллельных прямых. Линии треугольника. Сумма углов треугольника. Внешний угол треугольника.

• Сумма углов треугольника. Неравенство треугоььника.

  12.03.2018 1116 0

  Теоретический тест по теме: Соотношение между сторонами и углами треугольника. 7 класс

• Задача 6. ЕГЭ по математике. Профиль.

  01.07.2019 30 0

  Задача 6, входящая в ЕГЭ по математике профильного уровня. Темы «Треугольники», «Сумма углов треугольника».

• Геаметрыя 7 клас.

  Трохвугольнікі.

  28.11.2019 7 0

  Тэст прызначаны для навучэнцаў 7 класаў пры адпрацоўцы навыкаў рашэня задач па тэме .

• Прямоугольные треугольники. Вариант 2

  16.04.2020 2495 0

  Тест по теме «Прямоугольные треугольники» для 7 класса. Содержит 10 вопросов, расположенных в последовательности от простых к более сложным

• Построение треугольника по трем элементам (проверочная работа)

  24.05.2020 783 0

  Обобщающий тест по теме «Построение треугольника по трем элементам». Состоит из 6 вопросов с выбором ответа и заполнением пропусков.

• Тест по модулю 6

  21.08.2020 2 0

  Привет, ребята! Как всегда, финальный этап каждого модуля — тест. Итоговый тест по первому геометрическому модулю в нашем курсе содержит задачи, для решения которых понадобятся все знания, полученные на протяжении модуля. Удачи!

• Треугольник и его виды

  25.11.2020 351 0

  Данный тест предназначен для проверки знаний по математике 5 класса.

• Олимпиадные задачи «на подсчёт треугольников»

  11. 12.2020 54 0

  Олимпиады — это не просто проверка знаний по пройденным темам. Это стимул изучать предметы шире и глубже, чем требуется по программе. Математика в начальной школе ещё не делится на алгебру и геометрию, но  основные геометрические фигуры  ребятам уже знакомы. Решение задач «на подсчет треугольников» направлен на выявление «геометрического зрения», развитие внимания и логики. Цепочка задач построена таким образом, что при переходе к каждой последующей фигуре, увеличивается число искомых треугольников. При решении задач «на подсчёт треугольников» вырабатываются предметные умения: оценивать взаимопроникающие элементы геометрических фигур с различных точек зрения; выделять элементы фигур и фигуры из фона; включать один и тот же элемент в разные фигуры и соответственно давать им различную интерпретацию. В  тест включено 12 вопросов с одним вариантом ответов. После каждого вопроса следует проверка ответа. Для успешного прохождения необходимо ответить правильно не менее 70% вопросов.

• Подготовка к ОГЭ. ТЕСТ №3

  07.01.2021 27 0

  Подготовка к ОГЭ (тест 3)   Тест для подготовки к ОГЭ по 3 разделам.  Для эфективного результата рекомендую подготовиться по обучающей системе Г.Г. Левитаса «Карточки для коррекции знаний по математике для 7 класса. Левитас Г.Г.» https://multiurok.ru/files/kartochki-dlia-korrektsii-znanii-po-matematike-d-1.html

• Кері байланыс

  04.11.2021 42

  Рефлексия ______________________________________________________________________________________________________

• Треугольники.

  Геометрия 7 класс.

  05.11.2021 46 0

  Тест по теме «Треугольники» проверяет умение находить периметр треугольника, определять виды треугольников, его высоты, медианы и биссектрисы. 

• Геометрические фигуры. Треугольник. Прямоугольный, равнобедренный, равносторонний.

  23.11.2021 19 0

  Треугольник определение. Прямоугольный, равносторонний, равнобедренный треугольники. 

• Многоугольник. Определение, обозначение. Треугольник, прямоугольник, квадрат.

  29.11.2021 39 0

  Многоугольник. Треугольник, квадрат, четырехугольник. Наименование, обозначение.

• Контрольное тестирование

  10.12.2021 21 0

  Тест предназначен для установки степени освоения темы: «Подобные треугольники»

• Равнобедренный и равносторонний треугольник

  07.06.2022 1 0

  Тренажер по решению задач на вычисление элементов равнобедренного и равностороннего треугольника

• Самостоятельная работа «Произвольный треугольник» (ОГЭ)

  25. 08.2022 12 0

  Самостоятельная работа «Произвольный треугольник» (ОГЭ) может быть использована для проверки знаний учащихся по теме.

• начальные сведения о геометрии

  28.11.2022 5 0

  тест по теме «Начальные геометрические сведения» предназначен для обучающихся 7 класса,

Сходство: смысл, теорема, примеры и символы

С Земли солнце и луна кажутся одинакового размера. Хотя Солнце затмевает Луну, похоже, это происходит потому, что обе сферы представляют собой одинаковые фигуры!

В этой статье будет рассмотрено определение сходства в геометрии и его приложениях.

Сходство в определении геометрии

Сходство можно определить как атрибут, проявляемый двумя или более фигурами, когда их формы одинаковы.

Индивидуум участвует в игре «красная ночь» со своими друзьями, требуя, чтобы они завязали друг другу глаза и сделали выбор на похожую пару среди 4 пирожных; пончик, хлеб для гамбургеров, нарезанный хлеб и самоса. Определите подходящий вариант.

Решение:

Самоса имеет треугольную форму; ломтик хлеба прямоугольной формы; хлеб для гамбургеров имеет круглую форму, а пончик — круглую форму.

Таким образом, подходящая аналогичная пара — хлеб для гамбургеров и пончик.

Свойства подобия

Две фигуры называются подобными, если они имеют одинаковую форму, но разные размеры. Следовательно, подобные фигуры обладают следующими свойствами:

• Соответствующие углы равны.
• Соответствующие стороны находятся в одинаковом соотношении: это означает, что все стороны одной фигуры нужно умножить на одно и то же число, чтобы получить соответствующие стороны другой фигуры.

Чтобы лучше понять применение подобия в геометрии, представьте теоремы подобия для треугольников.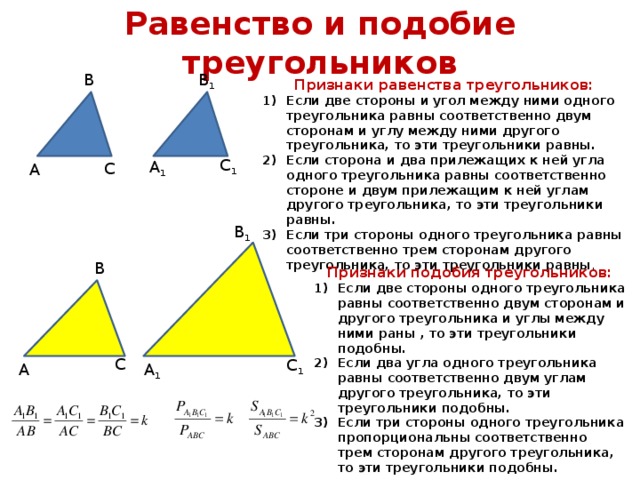

Формулы подобия

Многие люди (возможно, вы) приходят в восторг, когда есть формула для решения задач по теме. Эти формулы становятся отличительной чертой этих тем и служат для улучшения сохранения памяти. Однако в понятии подобия отсутствует такой подход. Проще говоря, едва ли существует какая-либо формула(ы), которая может быть использована для решения проблем подобия.

Тем не менее, проблемы со сходством в первую очередь зависят от понимания и применения свойства подобия , которые обсуждались в предыдущем разделе. Более того, и что более важно, понимание, а также применение теорем , которые обсуждаются ниже, действительно намного больше, чем запоминание формул.

Теоремы подобия в геометрии

Есть несколько способов определить, подобны ли два треугольника, используя одну из четырех теорем треугольника.

Подобие угол-угол

Если два угла в треугольнике равны двум углам в другом треугольнике, то эти два треугольника подобны.

Треугольники ABC и DEF подобны, так как

∠BCA=∠DFE

и

∠CAB=∠FDE.

Сходство между углами, StudySmarter Originals

Сходство между сторонами и углами

Если угол в одном треугольнике равен углу в другом треугольнике и стороны, составляющие этот угол, пропорциональны, то эти два треугольника подобны.

Под пропорциональностью сторон понимается то, что обе стороны треугольника ABC должны быть умножены на одно и то же число, чтобы получить стороны треугольника DEF.

Сторона- Угол- Сходство сторон, StudySmarter Originals

Указанные стороны на приведенном выше рисунке имеют общее отношение, то есть

DEAB=EFBC

и соответствующие углы, образованные этими соответствующими сторонами, равны,

∠ АВС=∠DEF.

Сходство сторона-сторона-сторона

Два треугольника также могут быть классифицированы как подобные в том случае, если их стороны AC, AB и BC, которые соответствуют сторонам другого треугольника DF, DE и FE, действительно пропорциональны.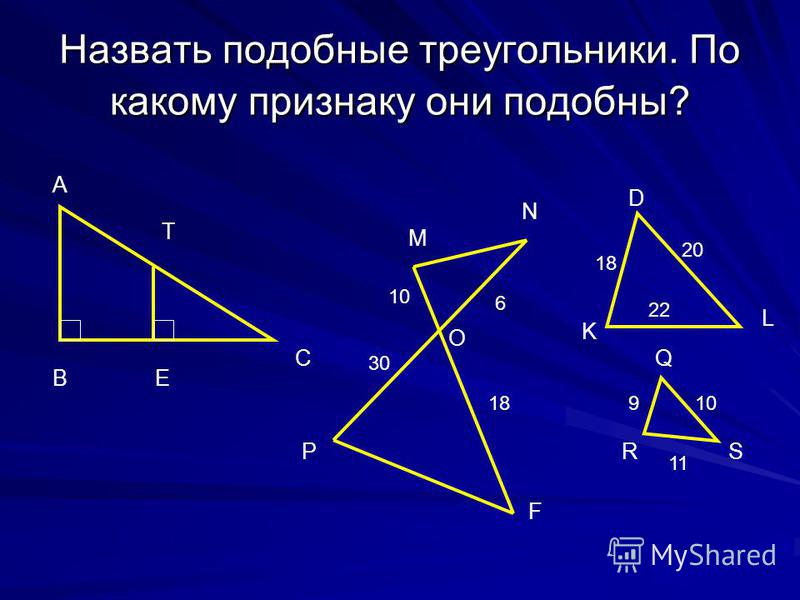

Теорема подобия стороны-стороны-стороны (www.draw.io)

На диаграмме все линии, образующие треугольник DEF, представляют собой длину соответствующей стороны в треугольнике ABC, умноженную на постоянный коэффициент r.

Прямой угол — Гипотенуза — Подобие сторон

Эта теорема верна только для прямоугольных треугольников.

Два треугольника подобны, если длина гипотенузы и длина другой стороны одного треугольника пропорциональны длине гипотенузы и другой стороны другого треугольника. это

BCAC=EFDF

Теорема подобия прямого угла-гипотенуза-сторона (www.draw.io)

Когда мы используем сторону в теореме подобия (например, в теореме SAS), мы не имеем в виду, что стороны равны равны, но отношение сторон треугольника постоянно.

Символ подобия

Символ, который мы используем, чтобы показать, что две вещи подобны, это ∼ . Предположим, что треугольники ABC и DEF подобны, тогда мы могли бы написать

Δ ABC ∼ Δ DEF.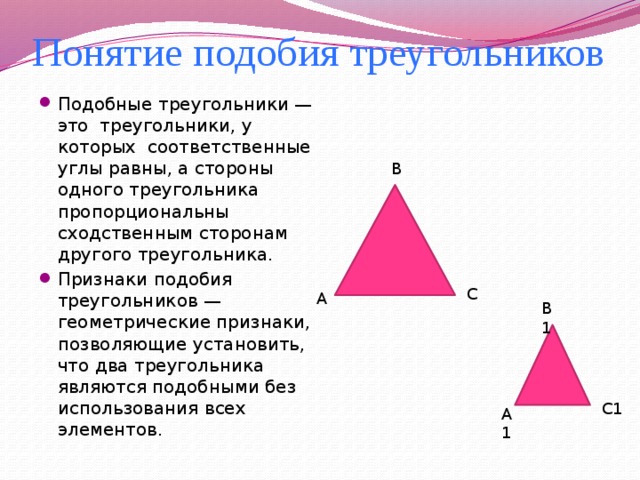

Треугольник ABC имеет стороны AB = 6 см, AC = 4 см и BC = 10 см. Треугольник DEF имеет стороны DE=3 см, DF = 2 см и EF = 5 см. Докажите, что эти треугольники подобны.

Решение:

Поскольку нам даны только стороны, мы хотим использовать теорему подобия SSS.

Чтобы мы могли применить эту теорему, нам нужно найти общее отношение между сторонами треугольника ABC и треугольника DEF.

Отношение сторон AB и DE равно

ABDE=63=2:1

Отношение сторон AC и DF равно

ACDF=42=2:1

Отношение сторон BC и EF равно

БКЭФ=105=2:1

Поскольку отношение между сторонами треугольника ABC к соответствующим сторонам треугольника DEF постоянно, мы можем сказать, что △ABC~△DEF

Подобие многоугольников

Многоугольники — это плоские фигуры, имеющие три или более сторон. Это означает, что треугольник также является многоугольником. Понятие сходства также встречается в других многоугольниках, отличных от треугольников.

По сути, подобие треугольников является частным случаем подобия многоугольников.

Однако для сходства между полигонами необходимо выполнение двух условий:

1. Соответствующие углы пары при сравнении должны быть эквивалентны.

2. Соответствующие стороны пары при сравнении должны иметь равные пропорции.

Докажите, что эти два прямоугольника подобны.

Иллюстрация похожих многоугольников, StudySmarter Original

Решение:

У обоих прямоугольников все внутренние углы прямые. Это означает, что первый критерий, который говорит, что всех соответствующих углов должно быть равно.

Далее нам нужно убедиться, что отношение их соответствующих сторон равно.

Отношение обеих ширин равно

93=3:1

и отношение обеих длин равно

155=3:1

Определите сходство между следующими парами,

(a)

Используя угол Правило угла, StudySmarter Originals

(b)

Использование правила стороны-угла-стороны, StudySmarter Originals

(c)

Используя правило стороны-стороны, StudySmarter Originals

(d)

Используя правило прямой угол-гипотенуза-сторона, StudySmarter Originals

Решение:

(a) Используя правило угла-угла, мы можем скажите, что оба треугольника на рисунке (а) подобны, потому что, зная, что сумма углов в треугольнике равна 180º, следовательно, третий угол в первом треугольнике равен

180°-(63°+73°)=180°-136 °=44°

Это подтверждает, что оба треугольника подобны, так как все соответствующие углы равны.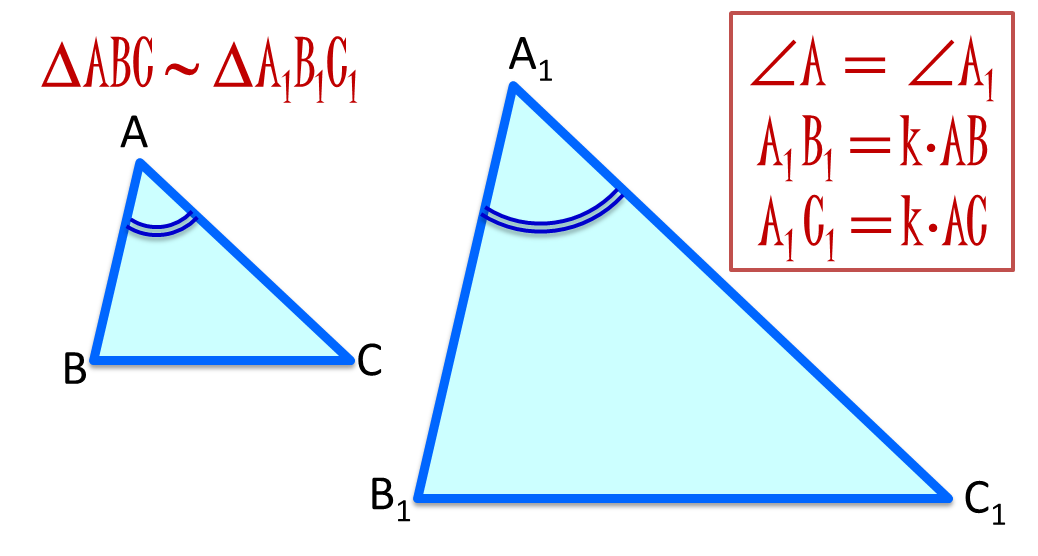

(b) Пара на рисунке (b) не подобна, хотя отношение между соответствующими сторонами равно 2:1, соответствующие углы между ними различны, и поэтому, используя правило стороны-угла-стороны, мы можем подтвердить что треугольные пары не подобны.

(c) Пара на рисунке (c) не подобна, потому что отношение двух сторон равно 2:1, а отношение третьей стороны равно 5:3. Согласно правилу стороны-стороны, отношение всех соответствующих сторон должно быть эквивалентным, поэтому эта пара треугольников не подобна.

(d) Пара на рисунке (d) похожа, потому что они оба являются прямоугольными треугольниками, а отношение соответствующих гипотенуз и противоположных сторон составляет 1:4. Это соответствует правилу подобия прямого угла и гипотенузы.

Сходство — основные выводы

• Фигуры подобны, если они имеют одинаковую форму.
• Существуют четыре теоремы подобия для треугольников: угол-угол, сторона-угол-сторона, сторона-сторона-сторона и прямой угол-гипотенуза-сторона.
• Если два треугольника подобны, их соответствующие стороны имеют пропорциональную длину.
• Для двух подобных треугольников ABC и DEF запишем Δ ABC ∼ Δ DEF.

Конгруэнтность и подобие

Обзор

[Вернитесь к началу страницы]

В области математики и, в частности, геометрии конгруэнтность и подобие являются родственными терминами. Конгруэнтность по существу означает, что две фигуры или предметы имеют одинаковую форму и размер. Хотя конгруэнтные объекты идентичны, их ориентация относительно друг друга и их физические координаты на плоскости или в трехмерном пространстве часто различаются. Например, два треугольника, показанные ниже, являются равносторонними треугольниками и имеют стороны одинаковой длины. Таким образом, они конгруэнтны, несмотря на то, что треугольник справа перевернут.

Треугольники равны, потому что они имеют одинаковую форму и размеры

Сходство означает, что две фигуры или предметы имеют одинаковую форму, но обычно разного размера. Два круга всегда будут похожи, например, потому что по определению они имеют одинаковую форму. Однако, если окружности имеют радиусы разной длины, они не будут конгруэнтными.

Два круга всегда подобны, потому что они имеют одинаковую форму

Конгруэнтность

[Вернитесь к началу страницы]

Слово конгруэнтность происходит от латинского слова congruo , что по существу означает , я согласен . В геометрии, если два объекта описываются как конгруэнтные, подразумевается, что один может быть точно отображен на другой. Другими словами, они имеют одинаковую форму и размер, но часто имеют разное расположение или ориентацию. Например, две конгруэнтные двумерные формы могут сосуществовать в одной плоскости или находиться в разных плоскостях. Две конгруэнтные трехмерные формы могут сосуществовать в одном и том же трехмерном пространстве, но иметь разные пространственные координаты и могут быть по-разному ориентированы вокруг x , y и z оси.

Любая простая двух- или трехмерная фигура может быть задана координатами x , y и (для трехмерных фигур) z точек, определяющих ее границы. Окружность, например, представляет собой двумерную фигуру с определенным центром (или началом координат ) и периметром, состоящим из всех точек, находящихся на заданном расстоянии ( радиус ) от центра в одной плоскости. Точно так же треугольник — это двумерная фигура, которая определяется тремя точками на плоскости. На самом деле, любые три точки на плоскости могут образовывать треугольник, если только они не лежат на одной прямой. Куб определяется восемью точками в трехмерном пространстве, тогда как сфера определяется одной точкой в ​​трехмерном пространстве и всеми точками, которые лежат на заданном расстоянии от этой точки в любом направлении.

В оставшейся части этого обсуждения мы будем заниматься только двумерными формами, хотя те же самые принципы могут быть одинаково хорошо применены к трехмерным объектам. Для любой двумерной формы точки, определяющие эту форму, можно рассматривать как сопоставление , потому что они могут быть указаны как набор координат x и y . Чтобы две фигуры были конгруэнтными, должна быть возможность точно отобразить одну фигуру на другую, используя последовательность из 90 215 перемещений 90 216 , 90 215 поворотов 90 216 и 90 215 отражений 90 216 . Каждый из этих терминов представляет некоторое действие, которое можно применить к фигуре, чтобы изменить ее положение или ориентацию, и они будут подробно обсуждаться в другом месте. На данный момент, вероятно, проще всего сказать, что мы должны иметь возможность перемещать одну фигуру и, при необходимости, поворачивать ее на угол или переворачивать так, чтобы она лежала точно над другой фигурой, при этом все соответствующие точки имели одинаковые 9Координаты 0215 x и y .

Конгруэнтные треугольники с разными координатами и ориентацией

Две фигуры, нарисованные в разных местах на одной плоскости, возможно, с разной ориентацией, очевидно, будут иметь разные отображения. Как же тогда мы можем доказать конгруэнтность? На самом деле это относительно легко. Два отображения конгруэнтны, если и 90 215 только в том случае, если 90 216 , расстояние между любыми двумя точками в одном отображении такое же, как расстояние между соответствующими двумя точками в другом отображении. Это определение конгруэнтности работает для любой двумерной формы.

На приведенном ниже рисунке два неправильных многоугольника ABCD и A’B’C’D’ конгруэнтны. Если вы внимательно изучите изображение, вы сможете увидеть, что если многоугольник ABCD повернуть по часовой стрелке на угол девяносто градусов (90°) вокруг точки C, а затем сдвинуть по горизонтали вправо на три клетки сетки, его точки точно совпадут с полигоном A’B’C’D’. Чтобы доказать конгруэнтность, необходимо показать, что расстояние между любыми двумя точками многоугольника A’B’C’D’ равно расстоянию между соответствующими двумя точками многоугольника ABCD. Это включает в себя пары несмежных точек, таких как A и C и A’ и C’.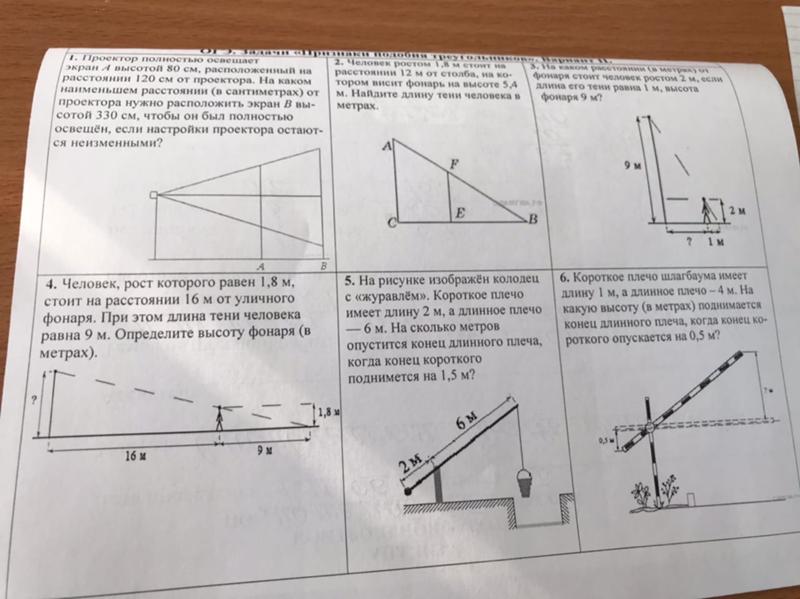 Опять же, внимательное изучение изображения должно показать, что это так (посмотрите на расстояние между двумя точками с точки зрения количества квадратов между ними на сетке как в горизонтальном, так и в вертикальном направлениях).

Два неправильных многоугольника конгруэнтны

Как вы можете видеть из вышеизложенного, если мы возьмем точную копию двумерной фигуры и поместим ее в другое место на той же (или на другой) двумерной плоскости, и даже если мы изменим ориентацию форму (например, перевернуть его вверх дном или на бок, или повернуть на какой-то произвольный угол) форма останется прежней. То же самое применимо, если мы возьмем копию некоторой трехмерной формы и поместим ее в другое место в трехмерном пространстве, даже если мы повернем ее на различные произвольно выбранные углы по всем трем осям. Размеры и форма объекта остаются неизменными. Эти свойства часто называют инвариантов . Примеры инвариантов в конгруэнтных объектах включают соответствующие углы и длины сторон треугольника, длину и высоту прямоугольника и радиус круга или сферы.

Для некоторых двумерных фигур существуют другие тесты, которые можно применить для доказательства конгруэнтности. Одной из таких фигур является треугольник. Два треугольника равны, если можно показать, что соответствующие стороны имеют одинаковую длину и соответствующие углы имеют одинаковую величину. Это включает в себя сравнение всего шести атрибутов (три стороны и три угла), но обычно мы можем доказать конгруэнтность, используя меньшее количество атрибутов. Конгруэнтность часто можно доказать, если мы можем показать, что длины двух сторон и величина одного угла или длина одной стороны и величина двух углов одинаковы для обоих треугольников. Это не работает для всех возможных комбинаций сторон и углов, но комбинации, для которых это работает, описаны на странице «Треугольники». Если два треугольника, ΔABC и ΔDEF, конгруэнтны, мы можем выразить это с помощью символа конгруэнтности (≅):

ΔАВС ≅ ΔDEF

Сходство

[Вернитесь к началу страницы]

Сходство , как и конгруэнтность, требует, чтобы два объекта имели одинаковую форму. Однако для того, чтобы существовало сходство, размеры не обязательно должны быть одинаковыми. Здесь есть несколько следствий. Во-первых, хотя два конгруэнтных объекта должны по определению быть похожими, два подобных объекта не обязательно должны быть конгруэнтными. Во-вторых, если два объекта похожи, то второй объект является либо увеличенной версией, либо уменьшенной версией первого (или, возможно, даже того же размера, и в этом случае объекты также конгруэнтны). Ориентация и расположение двух объектов часто различаются, но это не влияет на то, похожи они или нет. Ранее мы говорили, что все окружности подобны. Также должно быть довольно легко увидеть, что все правильные многоугольники того же типа тоже всегда будут похожи.

Все правильные многоугольники одного типа подобны

Чтобы два неправильных многоугольника были похожи, все соответствующие стороны должны различаться по длине в одинаковой пропорции, а все соответствующие внутренние углы должны иметь одинаковую величину. Мы видели, что мы можем взять два конгруэнтных объекта и отобразить один в другой с помощью процесса вращения и перемещения (т. е. поворота одного объекта и изменения его положения так, чтобы все его точки лежали над соответствующими точками другого объекта). Мы можем сделать то же самое с двумя похожими объектами, если включим дополнительный шаг масштабирования одного из объектов, чтобы его размеры совпадали с размерами другого объекта (это должно произойти до любого поворота и перемещения, которые могут потребоваться). На изображении ниже показаны два подобных неравносторонних треугольника.

Два подобных неравносторонних треугольника

Треугольники, показанные выше, на самом деле являются разносторонними треугольниками (т. Е. Треугольниками, в которых нет двух углов и двух равных сторон). Можно сказать, что два треугольника (фактически любые два треугольника) подобны, если длины соответствующих сторон различаются в той же пропорции. Применительно к треугольникам ABC и DEF это можно выразить так:

AB	=	BC	=	CA
DE		EF		FD

Можно также сказать, что два треугольника подобны, если можно показать, что любые 90 215 двух 90 216 соответствующих углов равны по величине (что автоматически потребовало бы, чтобы третья пара соответствующих углов была равна по величине, поскольку внутренние углы треугольника всегда в сумме составляет сто восемьдесят градусов):

∠ ABC   =  ∠ DEF     и    ∠ BCA   =  ∠ EFD

или:

∠ ABC   =  ∠ DEF     и    ∠ CAB   =  ∠ FDE

или:

∠ BCA   =  ∠ EFD     и    ∠ CAB   =  ∠ FDE

Дополнительно можно показать, что два треугольника подобны, если любые две соответствующие пары сторон различаются по длине на одну и ту же пропорцию, а углы между ними равны.