|
Для изучения сегодняшней темы нам необходимо вспомнить, какие способы решения систем уравнений с двумя переменными нам известны.
|
Текст. Тема урока «Системы уравнений»
|
|
Для решения систем уравнений с двумя переменными использовались такие способы, как метод подстановки, алгебраического сложения, введения новых переменных, графический метод. Сегодня на уроке мы рассмотрим несколько необычные применения этих методов, другие способы решения систем уравнений. |
Текст. Для решения систем уравнений с двумя переменными использовались такие способы, как метод подстановки, алгебраического сложения, введения новых переменных, графический метод.
|
|
пэ от икс игрек равно нулю кю от икс игрек равно нулю |
Текст Определение1.Если поставлена задача – найти такие пары (х;у), которые одновременно удовлетворяют уравнению р(х;у) =0 и уравнению q(х;у) =0, то говорят, что данные уравнения образуют систему уравнений Картинка. р(х;у) =0, q(х;у) =0. |
|
Определение второе. Пару значений икс и игрек, которая одновременно является решением и первого и второго уравнения системы, называют решением системы уравнений. |
Текст Определение2. Пару значений (х;у), которая одновременно является решением и первого и второго уравнения системы, называют решением системы уравнений. |
|
Определение третье. Решить систему уравнений – значит найти все ее решения или установить, что решений нет. |
Текст Определение3. Решить систему уравнений – значит найти все ее решения или установить , что решений нет. |
|
По аналогии можно говорить и о системе трех уравнений с тремя неизвестными. Кю от икс игрек зэт равно нулю эр от икс игрек зэт равно нулю При этом надо найти тройки чисел икс игрек зэт, удовлетворяющие каждое уравнение системы. Вообще, можно говорить о системах с любым количеством уравнений и неизвестных. |
Текст. Система трех уравнений с тремя неизвестными. р(х;у;z) =0, q(х;у;z) =0. r(х;у;z) =0.
|
|
Алгоритм решения системы уравнений прост: постепенный переход от сложного уравнения к более простому, но при этом выполнять равносильные преобразования. Стремиться получить хотя бы одно линейное уравнение, а если происходит переход к уравнению-следствию, то обязательна проверка корней. |
|
|
Определение четвертое. Две системы уравнений называют равносильными, если они имеют одни и те же решения или решений не имеют.
|
Текст. Определение 4. Две системы уравнений называют равносильными, если они имеют одни и те же решения или решений не имеют. |
|
Какие же способы решения систем уравнений являются равносильными?
|
|
|
Методы подстановки, алгебраического сложения, введения новых переменных приводят к равносильным преобразованиям |
Текст. Методы подстановки, алгебраического сложения, введения новых переменных приводят к равносильным преобразованиям системы уравнений. |
|
Запомните! Если в процессе решения используются неравносильные преобразования хотя бы одного уравнения, к ним относятся возведение в квадрат обеих частей уравнения, умножение уравнений системы, преобразования, приводящие к расширению области определения, то необходима проверка решений их подстановкой в исходную систему. |
Текст. Запомните! Неравносильные преобразования, например такие:
Проверка решений их подстановкой в исходную систему обязательна. |
|
Рассмотрим примеры. Обратите внимание на рациональность решения системы. Задание 1 Решить систему уравнений: Первое уравнение — икс плюс игрек плюс два зэт равно четырем. Второе уравнение – два икс плюс игрек плюс зэт равно единице. Третье уравнение — икс плюс два игрек плюс зэт равно трем. Решение Можно заметить, что каждая переменная входит в систему четыре раза. Разделим почленно обе части уравнения на четыре, получим: икс плюс игрек плюс зэт равно двум. В каждом уравнении системы будем выделять это равенство. Тогда из второго уравнения системы имеем: икс равен минус единице. Из третьего уравнения получаем: игрек равен единице. Из первого уравнения имеем: зэт равен двум. Итак, система уравнений имеет единственное решение — тройку чисел: минус один, один, два. Решение в проверке не нуждается, так как преобразования выполнялись равносильные. Ответ: тройка чисел: минус один, один, два. |
Текст. Рассмотрим примеры. Пример1. Обратите внимание на рациональность решения системы. Решить систему уравнений х+у+2z =4, 2х+ у+z =1, х+2у+ z =3. Решение. Сложим все три уравнения( это равносильное преобразование) и получим:4х+4у+4 z=8. Разделим почленно обе части уравнения на четыре, получим; х+у+ z =2. Из второго уравнения системы имеем: х+( х+у+ z)=1 или х+2=1, х=-1. Из третьего уравнения получаем: (х+у+ z)+у=3 или 2+у=3,у=1. Из первого уравнения имеем: ( х+у+ z)+ z=4 или 2+ z=4, z=2. Итак, система уравнений имеет единственное решение (-1;1;2). Ответ: (-1;1;2). |
|
Задание 2 Решить систему уравнений Первое уравнение – икс плюс игрек равно единице. Второе уравнение логарифм икс по основанию три равно логарифму выражения один минус игрек по основанию три. Решение Выразим игрек через икс из первого уравнения системы и, подставляя его вместо игрека во второе уравнение, получаем уравнение: логарифм икс по основанию три равно логарифму икс по основанию три. Решениями этого уравнения являются все положительные числа. Каждому такому значению икс равное альфа, где альфа больше нуля, соответствует значение игрек равное один минус альфа. Следовательно, решениями исходной системы являются все пары чисел альфа и один минус альфа, где альфа — положительное число. Способ подстановки – равносильное преобразование. Ответ: пара чисел: альфа и один минус альфа, где альфа — положительное число. |
Текст. Пример2. Решить систему уравнений х+у=1, log3х= log3(1-у). Решение. у=1-х, log3х= log3х. Получаем уравнение log3х= log3х. Решениями этого уравнения являются все положительные числа. Каждому такому значению х=α(α>0) соответствует значение у=1-α. Следовательно, решениями исходной системы являются все пары чисел (α; 1-α),где α- положительное число. Ответ:(α;1-α),α>0. |
|
Задание 3 Решить систему уравнений: игрек квадрат плюс два икс игрек минус три икс квадрат равно нулю и игрек квадрат плюс три икс в квадрате равно четырем. Решение Можно заметить, что первое уравнение системы – однородное. Считая игрек неизвестной величиной, а икс – постоянной, решим его. Получим: игрек первое равно икс и игрек второе равно минус три икс. Тем самым мы получили линейные уравнения. Исходная система сводится к совокупности двух систем уравнений: первая система состоит из уравнений: игрек равен икс, игрек квадрат плюс три икс в квадрате равно четырем. Вторая система состоит из уравнений: игрек равен минус три икс, игрек квадрат плюс три икс в квадрате равно четырем. Решения первой системы — пара чисел: один и один и пара чисел: минус один, минус один. Вторую систему решаем способом подстановки. Решениями системы является пара чисел: один, деленное на квадратный корень из трех и минус квадратный корень из трех, вторая пара: минус один, деленное на квадратный корень из трех и квадратный корень из трех. При решении исходной системы все преобразования были равносильными, поэтому проверка не нужна. Ответ: пара чисел: один и один; пара чисел: минус один, минус один; пара чисел: один, деленное на квадратный корень из трех, и минус квадратный корень из трех; пара: минус один, деленное на квадратный корень из трех, и квадратный корень из трех. |
Текст.
|
|
Задание 4 Решить систему уравнений Первое уравнение – икс плюс игрек равно единице. Второе — два икс в квадрате плюс два квадратных корней из икс минус икс равно игрек в квадрате минус один плюс два, умноженное на один плюс квадратный корень из икс. Решение Выразим игрек из первого уравнения и подставим во второе, перенесем во втором уравнении все члены в левую часть и, приведя подобные слагаемые, получим систему уравнений: игрек равен один минус икс и икс в квадрате плюс икс минус два равно нулю. Решением системы является пара чисел: один и ноль и пара чисел: минус два и три. Эта система является следствием исходной, поэтому проверка обязательна. Проверка Проверим подстановкой в исходную систему уравнений, является ли каждая пара чисел решением данной системы. Проверим первое уравнение. Если икс равен единице, игрек равен нулю, то получаем верное равенство, и во втором уравнении получаем верное равенство. Значит, пара чисел: один и ноль — решение системы. Проверяем вторую пару чисел: минус два и три. Если икс равен минус двум, игрек равен трем, то первое уравнение системы — верное равенство. А второе уравнение неверно, так как квадратный корень из минус двух не определён, поэтому пара чисел: минус два и три не является решением системы. Ответ: пара чисел: один и ноль. |
Текст. Пример 4. Решить систему уравнений х+у =1, 2х2+2 √х –х =у2-1 +2(1+√х). Решение. у=1-х, 2х2+2 √х –х =(1-х) 2-1 +2(1+√х). у=1-х, х2+х -2=0. Решением системы являются пары чисел(1;0),(-2;3). Эта система является следствием исходной, поэтому проверка обязательна. Проверка. Если х=1,у=0, то 1+0=1,1=1 – верное равенство, и 2·12+2√1-1=02-1+2(1+√1), 3=3 — верное равенство. Значит, пара чисел (1;0)- решение системы. Если х=-2.у=3, то 1=1- верное равенство. а второе уравнение неверно, так как √-2 неопределен. Ответ: (1;0) |
Поэтому сложим все три уравнения (это равносильное преобразование) и получим: четыре икс плюс четыре игрек плюс четыре зэт равно восьми.
Алгебра, 7 класс «системы линейных уравнений и способы их решения» (27 слайдов)
Слайд 1
Алгебра, 7 класс «Системы линейных уравнений и способы их решения»
Слайд 2
Знаете ли вы?
1.
Какую математическую модель называют линейным уравнением с двумя переменными?
2. Что является решением системы уравнений с двумя переменными?
3. Что значит решить систему уравнений?
Слайд 3
Способы решения систем уравнений
1. Графический способ.
2. Способ подстановки.
3. Способ сложения.
Слайд 4
Алгоритм решения системы уравнений графическим способом
Слайд 5
Решить систему уравнений
Рассмотрим первое уравнение
Выразим из этого уравнения y через x .
Для построения графика найдем две точки.
Слайд 6
Построим график
Слайд 7
Рассмотрим второе уравнение
Выразим из этого уравнения y через x .
Слайд 8
Построим график второй функции
Слайд 9
Найдем координаты точки пересечения прямых
Слайд 10
Координаты точки пересечения прямых ― это решение системы
В этом случае говорят, что система решена графически
Слайд 11
Три случая взаимного расположения двух прямых
1.
Прямые пересекаются.
То есть имеют одну общую точку.
Тогда система уравнений имеет единственное решение.
Например, как в рассмотренной системе
Слайд 12
Три случая взаимного расположения двух прямых
2. Прямые параллельны.
То есть не имеют общих точек.
Тогда система уравнений решений не имеет.
Например:
Слайд 13
Три случая взаимного расположения двух прямых
3. Прямые совпадают.
Например:
Тогда система уравнений имеет бесконечно много решений.
Слайд 14
Но
при графическом способе решения системы уравнений обычно получается приближенное решение
Слайд 15
Алгоритм решения системы уравнений способом подстановки
Слайд 16
Способ подстановки
Этот способ удобен тогда, когда хотя бы один из коэффициентов при x или y равен 1 или -1.
Дана система уравнений
Рассмотрим каждое уравнение в отдельности.
1) Выразим одно из неизвестных через другое неизвестное из любого уравнения.
Слайд 17
Способ подстановки
Вернемся в систему:
2) Полученное для y выражение подставим вместо данной неизвестной во второе уравнение.
Получилось уравнение с одной неизвестной
Слайд 18
Способ подстановки
3) Решаем уравнение с одной неизвестной:
Возвращаемся к системе:
Слайд 19
Способ подстановки
Возвращаемся к системе:
4) Подставим найденное значение x в первое уравнение и найдем вторую неизвестную
Запишем ответ.
Ответ:
Слайд 20
Алгоритм решения системы уравнений способом сложения
Слайд 21
Способ сложения
Задача 1. Решить систему уравнений
В тех случаях, когда в обоих линейных уравнениях системы при каком-либо из неизвестных коэффициентами являются противоположные числа, удобно применять способ алгебраического сложения уравнений.
Слайд 22
Способ сложения
Сложим эти равенства почленно. В результате получим тоже верное равенство
+
Слайд 23
Способ сложения
Вернемся в систему, записав одно из исходных уравнений и полученное значение x.
Подставим найденное значение x во второе уравнение, найдем вторую неизвестную.
Тогда пара чисел (5; 4) и будет решением системы.
Ответ:
Слайд 24
Способ сложения
Задача 2. Решить систему уравнений
1) Выберем неизвестную (например x).
уравняем коэффициенты умножением на соответствующие числа.
2) Вычтем одно уравнение из другого.
3) Решим полученное уравнение с одним неизвестным
Слайд 25
Способ сложения
4) Вернемся в систему, записав одно из исходных уравнений и полученное значение y
5) Подставим найденное значение y в первое уравнение, найдем вторую неизвестную.
Тогда пара чисел (-3; 1) и будет решением системы.
Ответ:
Слайд 26
Решите следующие системы уравнений:
Слайд 27
Урок закончен.
Спасибо за внимание.
систем уравнений | Предварительная алгебра | Линейные функции и графики
Дополнительные темы
по системам уравненийПопулярные учебные пособия
по системам уравнений-
Как решить систему уравнений с помощью графика?
Существует множество различных способов решения системы линейных уравнений. В этом уроке вы увидите, как решить систему линейных уравнений, построив обе линии и найдя их пересечение. Взглянем!
-
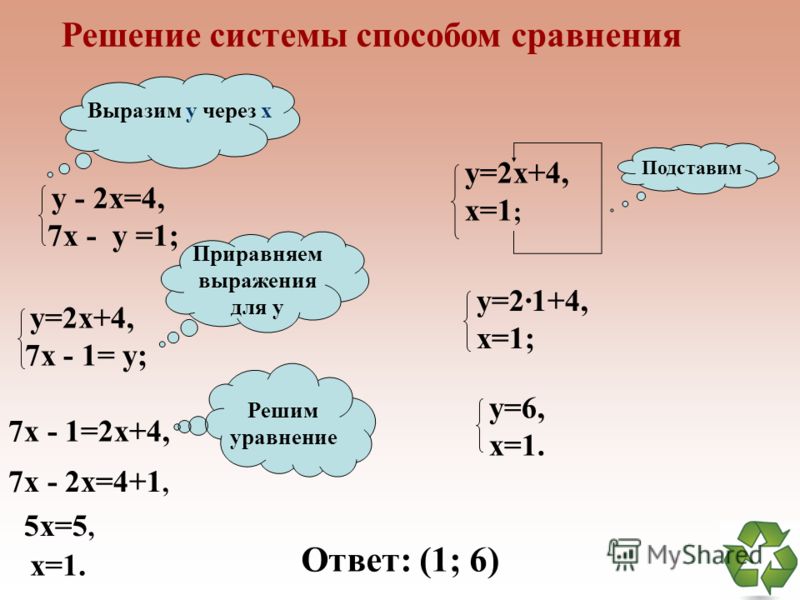
Как решить систему уравнений методом подстановки?
Существует множество различных способов решения системы линейных уравнений. В этом уроке вы увидите, как решить систему линейных уравнений, подставив одно уравнение в другое и найдя переменную. Затем посмотрите, как использовать это значение переменной, чтобы найти значение другой переменной.
Проверьте это! -
Как показать, что система уравнений не имеет решения?
Существует множество различных способов решения системы линейных уравнений. В этом уроке вы увидите, как решить систему линейных уравнений, построив обе линии и найдя их пересечение. Взглянем!
-
Что такое система линейных уравнений?
Система уравнений представляет собой набор уравнений с одинаковыми переменными. Если все уравнения линейные, то у вас есть система линейных уравнений! Чтобы решить систему уравнений, вам нужно выяснить значения переменных, которые решают все задействованные уравнения. Этот учебник познакомит вас с этими системами.
-
Что такое решение системы линейных уравнений?
Если у вас есть система уравнений, содержащая два уравнения с двумя одинаковыми неизвестными переменными, то решением этой системы является упорядоченная пара, которая делает оба уравнения истинными одновременно.
Следуйте инструкциям, поскольку в этом руководстве используется пример для объяснения решения системы уравнений! -
Как решить два уравнения с двумя переменными?
Пытаетесь решить два уравнения с одними и теми же двумя неизвестными переменными? Возьмите одно из уравнений и решите его для одной из переменных. Затем подставьте это в другое уравнение и найдите переменную. Подставьте это значение в любое уравнение, чтобы получить значение для другой переменной. Этот учебник проведет вас через этот процесс замены шаг за шагом!
Системы уравнений — Алгебра для колледжей
Все ресурсы по алгебре для колледжей
5 Диагностические тесты 84 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
Справка по алгебре колледжа » Системы уравнений
Решите систему уравнений.
Возможные ответы:
Ни один из других ответов не является правильным.
Правильный ответ:
Объяснение:
Изолировать в первом уравнении.
Подставьте во второе уравнение, чтобы найти .
Подставьте в первое уравнение, чтобы найти .
Теперь у нас есть значения и и мы можем выразить их в виде точки: .
Сообщить об ошибке
Решить для и .
Возможные ответы:
Невозможно определить.
Правильный ответ:
Объяснение:
1-е уравнение:
2-е уравнение:
Вычтите 2-е уравнение из 1-го уравнения, чтобы исключить «2y» из обоих уравнений и получить ответ для x:
Подключение значения в уравнение и решить для:
Отчет о ошибке
Что является Aslion As System Appations?
Возможные ответы:
Правильный ответ:
Объяснение:
Подставляем уравнение 2.
в уравнение 1.,
итак,
Подставляем в уравнение 2:
итак, решение есть.
Сообщить об ошибке
Человек в каноэ проплыл вверх по течению 400 метров за 2 часа. В том же каноэ этот человек проплыл вниз по течению 600 метров за 2 часа.
Какова скорость течения, , и какова скорость лодки в стоячей воде, ?
Возможные ответы:
Требуется дополнительная информация
Правильный ответ:
Объяснение:
Эта задача представляет собой систему уравнений и использует уравнение .
Начните с назначения переменных. Пусть обозначает скорость лодки, пусть обозначает скорость течения.
Когда лодка идет против течения, общая скорость равна . Вы должны вычесть, потому что скорости работают против друг друга — лодка движется медленнее, чем должна была бы, потому что она должна работать против течения.
Используя наше расстояние вверх по течению (400 м) и время (2 часа) из вопроса, мы можем составить уравнение скорости:
Когда лодка движется вниз по течению, общая скорость равна потому что лодка и течение работают друг с другом, заставляя лодку двигаться быстрее.
Мы можем обратиться к расстоянию вниз по течению (600 м) и времени (2 часа), чтобы составить второе уравнение:
Отсюда используйте исключение, чтобы найти и .
1. Составьте систему уравнений и найдите .
2. Подставьте в одно из уравнений для решения .
Сообщить об ошибке
Сестра Ника Сара в три раза старше его, а через два года будет вдвое старше его. Сколько им сейчас лет?
Возможные ответы:
Нику 4 года, Саре 8 лет
Нику 4 года, Саре 12 лет
Нику 2 года, Саре 6 лет
Нику 3 года, Саре 9 лет
Нику 5 лет, Саре 15 лет
Правильный ответ:
Нику 2 года, Саре 6 лет
Объяснение:
Шаг 1: Составление уравнений
Пусть = возраст Ника на данный момент
Пусть = возраст Сары на данный момент
В первой части вопроса говорится: «Сестра Ника в три раза старше его».
Это означает:
Вторая часть уравнения говорит: «Через два года она будет вдвое старше его». Это означает:
Добавьте 2 к каждой из переменных, потому что каждая из них будет на два года старше, чем сейчас.
Шаг 2: Решите систему уравнений с помощью подстановки
Подставьте во втором уравнении. Решите для
Подключение в первое уравнение, чтобы найти
Отчет о ошибке
Решить систему уравнения:
0020
Возможные ответы:
Правильный ответ:
Объяснение:
Решите методом исключения:
умножьте второе уравнение на два, чтобы сделать возможным исключение
Отчет о ошибке
Решение для и:
Возможные ответы:
Правильный ответ:
Объяснение:
Есть два способа решить это:
— 1-е уравнение можно умножить на , а 2-е уравнение можно умножить на и добавить к 1-му уравнению, чтобы получить уравнение с одной переменной, где
.
Это можно подставить в любое уравнение, чтобы получить
или
. Второе уравнение можно упростить до
.
Затем это значение для можно подставить в первое уравнение, чтобы сделать уравнение единственной переменной в .
Решение дает , которое можно подставить в любое исходное уравнение, чтобы получить
Сообщить об ошибке
If
и
Решить для и .
Возможные ответы:
Нет ответов Explanation:
rearranges to
and
, so
Report an Error
Solve for in the system of equations:
Possible Ответов:
Система не имеет решений Объяснение:
Во втором уравнении можно заменить на из первого.