Синус свойства функции: Свойства функции y = sinx и её график — урок. Алгебра, 10 класс.

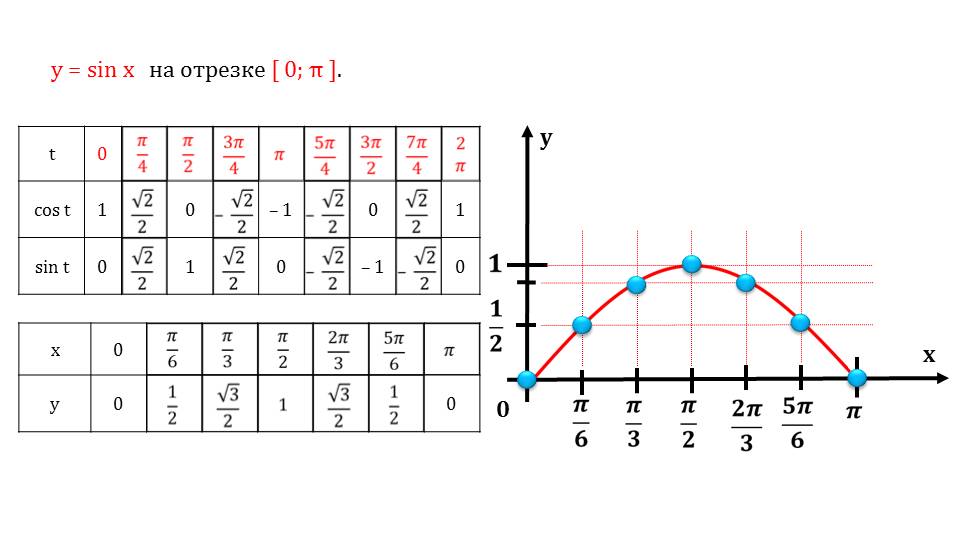
Свойства функции синуса

Используй поиск, чтобы найти научные материалы и собрать список литературы

База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны

Содержание статьи

1. Понятие синуса

2. Свойства функции $f(x)=sinx$

3. График функции $y=sinx$

4. Задачи на построение синусоид

Понятие синуса

Перед изучением функции синуса и её свойств, вспомним понятие самого синуса. Определение синуса можно ввести двумя способами: с помощью прямоугольного треугольника и с помощью тригонометрической окружности.

Определение 1

Синусом острого угла называется отношение длины противолежащего катета к гипотенузе прямоугольного треугольника (рис 1):

\[cos\alpha =\frac{a}{c}\]

Рисунок 1.

Прямоугольный треугольник.

Определение 2

Синусом острого угла называется ордината единичной окружности, которая получается из точки $(1,\ 0)$ путем поворота на угол $\alpha $ радиан (рис. 2).

Рисунок 2. Значение синуса с помощью единичной окружности.

Введем таблицу некоторых значений синуса (таблица 1).

Рисунок 3. Значения синуса.

Свойства функции $f(x)=sinx$

Рассмотрим теперь свойства функции $f\left(x\right)=sinx$.

1. Область определения — все числа.
2. Так как по определению 2 значение синуса определяется с помощью единичной окружности, то область значения данной функции отрезок $[-1,\ 1]$.
3. $f\left(-x\right)={sin \left(-x\right)\ }=-sinx=-f(x)$, следовательно, функция$f\left(x\right)=sinx$ нечетна.
4. $f\left(x+2\pi \right)={sin \left(x+2\pi \right)\ }=sinx=f(x)$, следовательно, функция $f\left(x\right)=sinx$ периодическая с минимальным периодом $2\pi $.
5. Пересечение с осями координат: При $x=0$, $f\left(0\right)=sin0=0$.
   При $y=0$, $x=\pi n,n\in Z$.
6. Функция выше оси $Ox$ при $x\in (2\pi n,\pi +2\pi n),n\in Z$.
7. Функция ниже оси $Ox$ при $x\in (-\pi +2\pi n,2\pi n),n\in Z$.
8. $f’ (x)=(sinx)’=cosx$.\[cosx=0\] \[x=\frac{\pi }{2}+\pi n,\ n\in Z\]

Функция $f\left(x\right)=sinx$ возрастает, при $x\in \left(-\frac{\pi }{2}+2\pi n,\frac{\pi }{2}+2\pi n\right)$.

Функция $f\left(x\right)=sinx$ убывает при $x\in \left(\frac{\pi }{2}+2\pi n,\frac{3\pi }{2}+2\pi n\right)$.

Точки максимума $(\frac{\pi }{2}+2\pi n,1)$.

Точки минимума $(\frac{3\pi }{2}+2\pi n,-1)$.

1. Функция непрерывна на всей области определения.

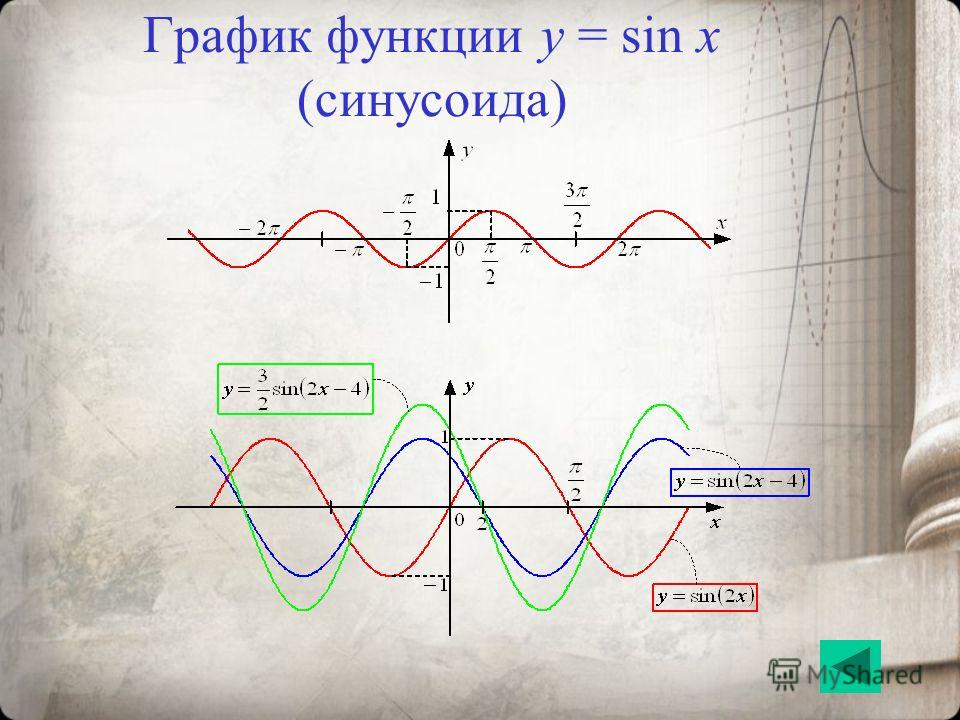
График функции $y=sinx$

Графиком функции $y=sinx$ является синусоида (рис. 3).

Рисунок 4. Синусоида.

Задачи на построение синусоид

Пример 1

Построить график функции $y=sinx-1$.

График данной функции получается из функции $y=sinx$ путем смещения вдоль оси $Oy$ на 1 единицу вниз:

Рисунок 5.

Пример 2

Построить график функции $y=sin\left(x+\frac{\pi }{2}\right)$.

График данной функции получается из функции $y=sinx$ путем смещения вдоль оси $Ox$ на $\frac{\pi }{2}$ единиц влево.

Рисунок 6.

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 18.02.2022

Выполнение любых типов работ по математике

Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами

Подбор готовых материалов по теме

Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы

Функции и Графики — сайт по математике и не только!!! Всё о Математических функциях и их графиках.

.. Функции и Графики — сайт по математике и не только!!! Всё о Математических функциях и их графиках…

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ ОПРЕДЕЛЕНИЕ ФУНКЦИИ СВОЙСТВА ФУНКЦИЙ ЛИНЕЙНАЯ КВАДРАТИЧНАЯ СТЕПЕННЫЕ ФУНКЦИИ ФУНКЦИИ y = ТРИГОНОМЕТРИЧЕСКИЕ ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ПОКАЗАТЕЛЬНАЯ ЛОГАРИФМИЧЕСКАЯ ГРАФИКИ ТЕСТЫ КОНТАКТЫ КАРТА САЙТА НА ГЛАВНУЮ ПРОГРАММИРОВАНИЕ TURBO PASCAL C++

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ y = sin x график — синусоида Свойства функции Область определения: R Область значений: [-1; 1] Четность, нечетность: функция нечетная Период: 2 Нули: sin x = 0 при x = n, n Z Промежутки знакопостоянства: sin x > 0 при x (2n; n + 2n), n Z sin x x (- + 2n; 2n), n Z Экстремумы: xmin = + 2 n, n Z; ymin = -1 xmax = + 2 n, n Z; ymin = 1 Промежутки монотонности: y = cos x график — косинусоида Свойства функции Область определения: R Область значений: [-1; 1] Четность, нечетность: функция четная Период: 2 Нули: Промежутки знакопостоянства: Экстремумы: xmin = + 2 n, n Z; ymin = -1 xmax = 2n, n Z; ymin = 1 Промежутки монотонности: Преобразования графиков y = sinx и y = cosx : Графики функций y = sinx и y = cosx можно получить друг из друга путем параллельных переносов вдоль оси x на /2: y = tg x график — тангенсоида Свойства функции Область определения: объединение интервалов Область значений: R Четность, нечетность: функция нечетная Период: Нули: y = 0 при x = n, n Z Промежутки знакопостоянства: Экстремумов нет Промежутки монотонности: функция возрастает на каждом интервале области определения Асимптоты: x = + n, n Z y = ctg x график — катангенсоида Свойства функции Область определения: объединение интервалов Область значений: R Четность, нечетность: функция нечетная Период: Нули: Промежутки знакопостоянства: Экстремумов нет Промежутки монотонности: функция убывает на каждом интервале области определения Асимптоты: x = n , n Z Преобразования графика y = ctgx : График функци y = ctgx получается из графика y = tgx путем отражения относительно любой из координатныхосей и последующим параллельным переносом вдоль оси x на /2. Используются технологии uCoz

\circ\text{.}\) В каком направлении движется точка?

(iii)

Обратите внимание на угол, отображаемый в начале координат: объясните, почему это разумно.

Используйте ползунок, чтобы изменить угол. Обратите внимание, как рисуется угол и как меняются значения синуса и косинуса.

Вы можете перетащить ползунок или нажать на него и использовать клавиши со стрелками.

Рисунок 7.4.1. Большие углы

Мы можем использовать определение синуса как отношения и это понимание углов для построения графика. На рисунке 7.4.2 перетаскивайте ползунок, пока не получите полный график. График, который простирается на более длинный диапазон (и помечен в градусах), показан на рисунке 7.4.3. 9\circ\), как показано на рисунке 7.4.2.

Длина цикла может быть изменена. В зависимости от приложения мы интерпретируем и измеряем длину цикла по-разному.

Определение 7.4.4. Период.

Длина цикла, измеренная во времени, называется периодом .

Определение 7.4.5. Длина волны.

Длина цикла, измеренная на расстоянии, называется длиной волны .

Иногда вместо измерения продолжительности одного цикла в единицах времени мы измеряем, сколько циклов происходит в фиксированную единицу времени. это называется частота .

Определение 7.4.6. Частота.

Количество волн (периодов), возникающих в секунду, называется

частотой . Обычно это измеряется в герцах (Гц). 1 Гц — это один цикл в секунду.

Обратите внимание, что частота обратно пропорциональна периоду, как показано в таблице 7.4.7

Таблица 7.4.7. Период и частота обратны

Период	Частота
\(\frac{1\text{цикл}}{n\text{секунды}}\)	\(\frac{n\text{циклы}}{1\text{секунда}}\)

Пример 7.

4.8.

Если волна имеет период \(1/3\) секунды, какова ее частота?

Решение 1.

Мы можем увидеть, сколько \(1/3\) секунд содержится в одной секунде. Это

\begin{align*} f \cdot \frac{1}{3} \amp = 1\\ f амп = 3 \end{align*}

Частота равна 3.

Решение 2.

Мы можем считать это преобразованием единиц. Если период равен

\begin{уравнение*} \frac{1/3 \text{ секунд}}{\text{цикл}} \end{equation*}

и частота выражена в циклах в секунду, мы можем инвертировать меру.

\begin{выравнивание*} \frac{\text{циклы}}{1/3 \text{секунды}} \amp = \\ \frac{\text{циклы}}{1/3 \text{секунды}} \cdot \frac{3}{3} \amp = \frac{3 \text{циклы}}{\text{секунды}} \end{align*}

Обычно, если период равен \(T\), то частота равна

\begin{уравнение*} f=\frac{1}{T}. \end{уравнение*}

Пример 7.4.9.

Каковы период и длина волны среднего C, имеющего частоту 261,63 Гц?

Раствор.

Поскольку мы знаем частоту, мы можем напрямую рассчитать период.

\begin{выравнивание*} 261,63 \amp = \frac{1}{T}\\ T \cdot 261,63 \amp = T \cdot \frac{1}{T}\\ \frac{T \cdot 261,63}{261,33} \amp = \frac{1}{261,33}\\ T \amp = \frac{1}{261,63}\\ T \ amp \ приблизительно 0,0038222 \end{align*}

Для длины волны нам нужно вспомнить, что скорость звука составляет 1116 футов в секунду. Теперь мы можем использовать тот факт, что Гц — это число циклов в секунду, чтобы преобразовать частоту (циклов в секунду) в длину волны (футов в цикл). 95 \frac{\text{футы}}{\text{цикл}}. \end{уравнение*}

КПП 7.4.11.

Рассмотрим букву D с частотой 293,66 Гц.

Каков период?

Какова длина волны?

Ответ 1.

\(0,0034053\)

Ответ 2.

\(3,8\)

Решение.

Поскольку мы знаем частоту, мы можем напрямую рассчитать период.

\begin{уравнение*} \begin{выровнено} 293,66 \amp = \frac{1}{T}\\ T \cdot 293,66 \amp = T \cdot \frac{1}{T}\\ \frac{T \cdot 293,66}{293,66} \amp = \frac{1}{293,66}\\ T \amp = \frac{1}{293,66}\\ Т \ ампер \ прибл 0,0034053 \end{выровнено} \end{equation*}

Для длины волны нам нужно вспомнить, что скорость звука составляет 1116 футов в секунду. Теперь мы можем использовать тот факт, что Гц — это число циклов в секунду, чтобы преобразовать частоту (циклов в секунду) в длину волны (футов в цикл).

\begin{уравнение*} \frac{\text{секунды}}{293,66 \text{циклов}} \cdot \frac{1116 \text{футов}}{\text{секунд}} \приблизительно 3,800 \frac{\text{футов}}{\ текст{цикл}}. \end{уравнение*}

Определение 7.4.12. Амплитуда.

Высота волны (от центра к вершине) называется амплитудой .

Пример 7.4.13.

Амплитуда этой синусоиды равна 2. Период равен 180. Обратите внимание, что без контекста период и длина волны совпадают. Частота

\begin{уравнение*} f=\frac{1}{180} \приблизительно 0,0056 \end{уравнение*}

Подраздел 7.

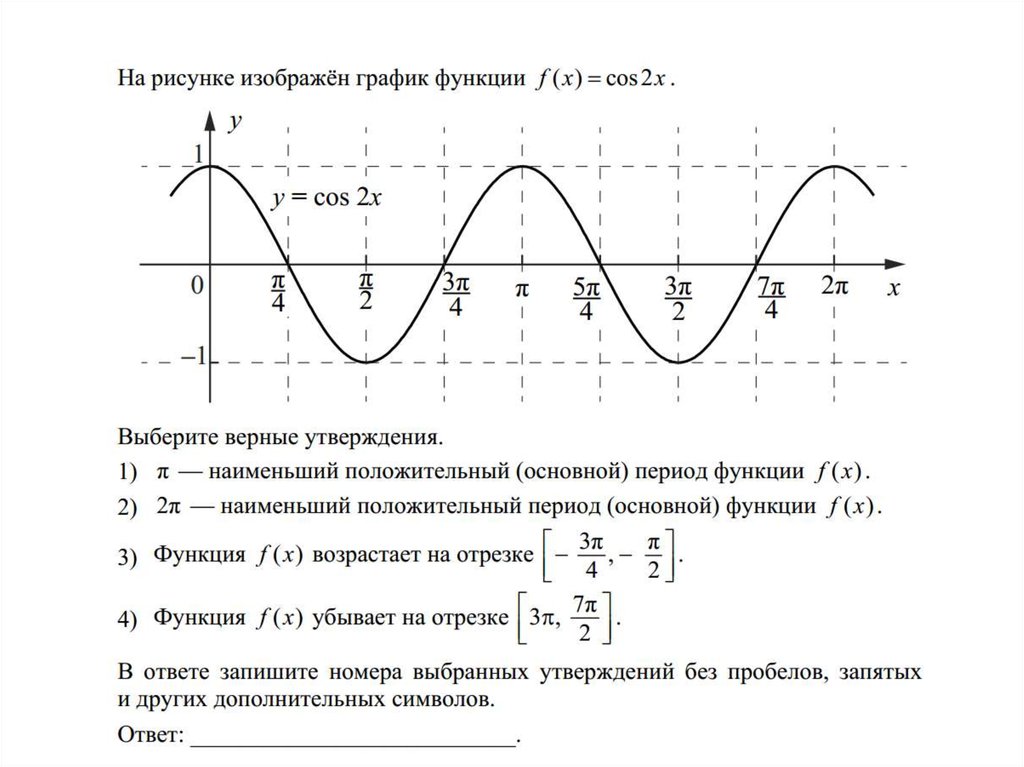4.3 Преобразования синуса

В подразделе 5.4.2 и подразделе 6.2.2 мы научились преобразовывать граф, сдвигая его и отражая. Это относится и к тригонометрическим графикам. Здесь мы научимся изменять амплитуду и частоту синусоид.

Используйте ползунки, чтобы увидеть, как умножение внутреннего и внешнего синуса влияет на кривую.

Рисунок 7.4.14. Амплитуда и длина волны

КПП 7.4.15.

Используйте рисунок 7.4.14, чтобы ответить на следующие вопросы. Обратите внимание, что амплитуда немодифицированного графика равна 1,

.

(а)

Если установить \(a=2\text{,}\), то есть график \(2\sin(\pi x)\), какова будет амплитуда?

(б)

Если вы установите \(a=3\text{,}\), то есть график \(3\sin(\pi x)\), какова будет амплитуда?

(в)

Как можно получить амплитуду 1/2?

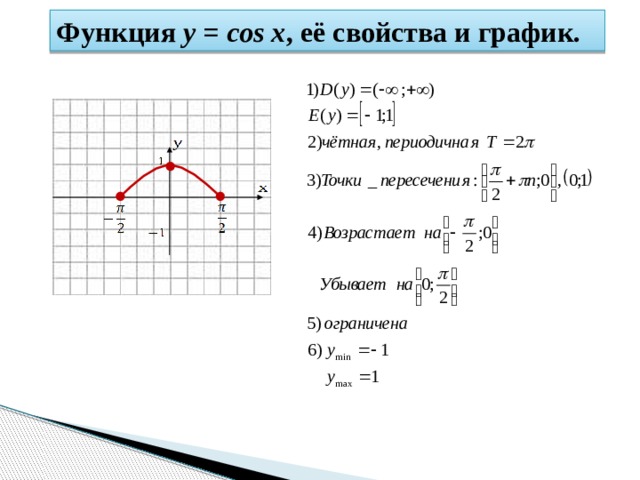
КПП 7.4.16.

Используйте рисунок 7.4.14, чтобы ответить на следующие вопросы. Обратите внимание, что длина волны немодифицированного графика равна 2,

.

(а)

Если вы установите \(f=2\text{,}\), то есть график \(\sin(2 \pi x)\), какова длина волны?

(б)

Если вы установите \(f=3\text{,}\), то есть график \(\sin(3 \pi x)\), какова длина волны?

(в)

Как можно получить длину волны 4?

Упражнения 7.4.4 Упражнения

1. Бесконтекстный.

2. Бесконтекстный.

3. Бесконтекстный.

4. Бесконтекстный.

5. Приложение.

6. Применение.

7. Приложение.

8. Бесконтекстный.

9. Приложение.

10. Бесконтекстный.

Свойства функций комплексного косинуса и синуса

Свойства функций комплексного косинуса и синуса

9{-ix}}{2i} = \frac{1}{2i} \left [ \left ( \cos x + i \sin x \right ) — \left ( \cos (-x) + i \sin (- x) \right ) \right ] = \frac{1}{2i} \left [ 2i \sin x \right ] = \sin x \end{align}

Теперь мы рассмотрим некоторые свойства комплексного косинуса и синусоидальные функции.