Построить кривую в полярной системе координат онлайн: Построить график в полярных координатах на плоскости

Исследовательская работа «Построение кривых в полярной системе координат» • Наука и образование ONLINE

Главная Работы на конкурс Предметное образование Физико-математические дисциплины Исследовательская работа «Построение кривых в полярной системе координат»

Автор: Джикибаев Данияр Хакимович

Место работы/учебы (аффилиация): СОШ № 10 г. Экибастуз Павлодарской области Республики Казахстан, 11 класс

Научный руководитель: Зубко Светлана Алексеевна, учитель математики

Цель исследования – показать принцип построения кривых в полярной системе координат с помощью формул перехода от декартовых координат к полярным координатам. Выявить преимущества полярной системы координат.

Гипотеза — если для  построения кривых, заданных уравнениями третьей (и выше) степеней с двумя переменными ввести новые переменные и новую систему координат  и использовать при этом компьютерные  программы, то это даст возможность рассмотреть большое количество примеров на построение различных кривых с минимальными усилиями.

Этапы исследования  — изучение  и анализ теоретических сведений по данной теме, обзор литературы, сбор материала, наблюдение, систематизация материала.

Задачи исследования:

1. Ознакомиться с историей появления полярной системы координат;
2. Изучить переход от декартовой системы координат к полярной и обратно;
3. Исследовать изменения вида кривой, в зависимости от параметров входящих в её уравнение;
4. Познакомиться с некоторыми замечательными кривыми известных математиков.
5. Выяснить, какие кривые встречаются в окружающем нас мире;
6. Познакомиться с компьютерными программами, необходимыми для построения графиков кривых;
7. Построить графики кривых с помощью компьютерных программ;
8. Подготовить презентацию по теме проекта

Научная новизна. Особенность работы состоит в том, что в ней рассматривается механизм построения кривых, заданных уравнениями третьей (и выше) степеней с двумя переменными, в полярной системе координат  с помощью компьютерных программ, что представляет интерес для учащихся, увлекающихся математикой и информатикой, так как  в школьных учебниках механизм построения таких кривых не оговаривается.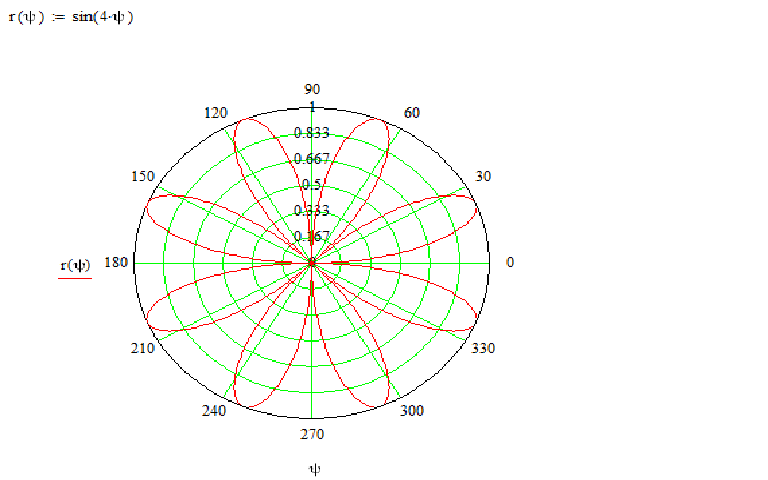

Объектом исследования является полярная система координат, предметом — полярные уравнения кривых и их построение с помощью программ Microsoft  Excel и Visual Basic.

Практическая ценность данной работы заключается в том, что использование компьютерных программ для построения графиков функций,  изучения  их свойств и закономерностей, дает возможность рассмотреть большое количество примеров  с минимальными усилиями.

Результат  работы: обобщение материала, написание программы построения кривых в среде Microsoft  Excel и Visual Basic.

.

Физико-математические дисциплины

Научно-исследовательская работа «Водный свет»

Доступна к просмотру полнотекстовая версия работы

Когда в преддверии международного дня энергосбережения нам рассказывали о рациональном использовании электроэнергии в быту, я вспомнил сразу слова моей мамы. Наверняка, каждый слышал от своих родителей, бабушек и дедушек тоже, что и я: «Не забудь вык…

Посмотреть работу

Естественно-научные дисциплины, Физико-математические дисциплины

Исследовательская работа «Уроки Времени»

Психологи и педагоги считают так, что умение ребенка определять время по часам со стрелкой говорит о зрелости коры головного мозга: сформированности зрительно-пространственного восприятия (понимание пространственных координат «право-лево», «верх-низ»…

Посмотреть работу

Физико-математические дисциплины

Исследовательская работа «Решето Эратосфена»

Доступна к просмотру полнотекстовая версия работы

Решето Эратосфена — это алгоритм, который позволяет фильтровать простые числа и составные. Название «решето» произошло из-за того, что древние греки писали числа на дощечках, покрытых воском, и делали отверстия в тех местах, где оказывались простые ч. ..

Посмотреть работу

Физико-математические дисциплины

Исследовательская работа «География Пермского края в некоторых математических задачах»

Доступна к просмотру полнотекстовая версия работы

В данной работе главное место занимает понятие задачи. Школьники с первых дней занятий в школе встречаются с задачей. Она помогает понять суть математических понятий, выяснять различные стороны взаимосвязей в окружающем мире и способствует развитию л…

Посмотреть работу

Физико-математические дисциплины

Исследовательская работа «Математическая статистика в жизни одного класса»

Актуальность работы заключается в том, что статистические данные нужны не только в математике, но и в обыденной повседневной жизни. Для того, чтобы нам, ученикам, посчитать среднюю отметку за четверть, среднее время класса при сдаче нормативов по физ. ..

Посмотреть работу

Мероприятие завершено

Полярные координаты. Параметрическая форма кривых

Похожие презентации:

Кривые второго порядка

Кривые второго порядка

Кривые второго порядка

Приведение квадратичной формы к главным осям

Кривые и поверхности второго порядка. Методические материалы

Кривые второго порядка

Кривые второго порядка. Лекция 7

Поверхности второго порядка. Поверхности, образованные вращением некоторых кривых второго порядка. Цилиндрические поверхности

Поверхности второго порядка

Кривые второго порядка. Уравнение кривой второго порядка

1. Линейная алгебра и аналитическая геометрия

Тема: Полярные координаты.
Параметрическая форма кривых.
Лектор Имас О.Н.
2018 г.
Кривой 2-го порядка на плоскости называют геометрическое место точек
M(x;y), удовлетворяющих уравнению F(x;y)=0.
Или
i j
a
x
ij y 0, max(i j ) 2
i , j n
Q( x1; x2 ;. ..; xn )
a xx
i , j n
Рассмотрим Q(x1;x2)
ij i
j
Функция Q называется квадратичной формой
a xx
i , j n
ij i
j
a11x12 a12 x1x2 a21x2 x1 a22 x2 2
a11 a12
Матрица A
называется матрицей квадратичной формы, где aij a ji
a21 a22
1 0
Диагональная матрица вида
, полученная из матрицы А путем
0
2
преобразования координат, называется канонической формой матрицы А
Вопрос. Как найти эти новые координаты, т.е этот новый базис?
Очевидно, должно выполняться: АХ= X AX- X=0 (A- E)X=0
(A- E)X=0 – система линейных однородных уравнений, из которой и
найдем фундаментальную систему решений Х, они-то и будут новым
базисом, в котором квадратичная форма примет каноническую форму
Определение. Матрица A- E называется характеристической матрицей
| A- E | называется характеристическим
Определение. Определитель
многочленом от .
a11
a12
a21
a22
Определение. Корни характеристического многочлена | A- E | 0 называются
собственными числами, а ненулевые решения системы (A- E)X=0
называются собственными векторами.
пропустить 3 страницы

4. Поверхности второго порядка

Поверхностью второго порядка называется геометрическое
место точек в пространстве, декартовы координаты которых
удовлетворяют уравнению F(x,y,z) = 0,
F(x,y,z) – многочлен степени 2.
В общем случае :
a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz+2a10x+2a20y+2a30z+a00=0 .
Поверхности второго порядка делятся на
1) вырожденные
и
2) невырожденные
Вырожденные — это плоскости, точки и вырожденные (мнимые)
поверхности (уравнению не удовлетворяет ни одна точка
пространства).
Невырожденными
поверхности
второго
порядка
подразделяются на пять типов.
Эллипсоид,
Гиперболоид (однополосный и двуполостный),
Конус,
Параболоид
Цилиндрическая поверхность
Название
поверхности
Сфера
Аналитический вид
( x x0 )2 ( y y0 )2 ( z z0 )2 r 2
M0(x0;y0;z0) – центр сферы, r – радиус
Эллипсоид
Цилиндр
Конус
( x x0 )2 ( y y0 )2 ( z z0 )2
1
a2
b2
c2
M0(x0;y0;z0) – центр эллипсоида, a, b, с – полуоси
( x x0 ) 2 ( z z0 ) 2
1 Ось l | | Oy
а)
a2 2
b2 2
( x x0 )
( y y0 )
1
2
б)
Ось l | | Oz
a
b2
( x x0 )2 ( y y0 )2 ( z z0 )2
M0(x0;y0) – вершина конуса
Эллиптический
параболоид
( x x0 )2 ( y y0 )2 2 p( z z0 )
Гиперболоид
(однополостный)
( x x0 )2 ( y y0 )2 ( z z0 ) 2
1
2
2
2
a
b
c
Гиперболоид
(двуполостный)
( x x0 )2 ( y y0 )2 ( z z0 ) 2
1
2
2
2
a
b
c
Графическое изображение
x2 y
2 z, p, q 0
p q
Гиперболический параболоид
z
x
пропустить 0,5 страницы
y
Полярная система координат
y
ОПРЕДЕЛЕНИЕ.
Полярная система координат – это
M ( x, y) M ( , ) точка О (полюс) и ось – полярный
луч (совпадает по направлению с
осью Ох).
Связь полярной и декартовой системы координат
x cos
x x
y sin
y
O
Декартова сетка
Полярная сетка
y
3 / 8
/4
1
2
/8
3
O
4
O
1
2
3
4 x
1 2 3 4
пропустить 2 страницы

8. 5. Построение графиков функций, заданных параметрически

Пример.
Построить кривую, заданную уравнением x a cos t ,
y b sin t
Подготовим таблицу значений x и y
t
x
y
0
a
0
/6
√3/2 a
½b
/4
√2/2 a
√2/2 b
/3
½a
√3/2 b
/2
0
b
пропустить 1 страницу
в I четверти
y
O
x

English     Русский Правила

Полярные уравнения

Полярные уравнения и их графики

по

Джанет Дробье собираемся построить несколько различных полярных кривых и изучить их поведение.

---

Справочная информация: Система координат используется для определения местоположения точка в пространстве. Часто в математике мы используем прямоугольную или декартову система координат. Эта система использует прямоугольную сетку для описания местоположения. точки. Другой метод описания местоположения точки заключается в использовании расстояние и направление от фиксированной точки отсчета. Для этого мы будем использовать полярную систему координат. Чтобы настроить систему, мы должны сначала выбрать неподвижную точку, называемую началом координат, и провести луч из этой точки. Это будет быть полярной осью. Далее мы выберем любую точку p на плоскости и повернем отрезок от полярной оси до этой точки. Образующийся угол будет равен θ и расстояние от начала до точки будет r. Таким образом, точка (r, θ) указывает местоположение точки.

---

Общие полярные кривые

Начнем наш взгляд на полярных кривых с некоторыми основными графиками.

Спираль Архимеда

Спираль Архимеда образуется из уравнения г = аθ. График выше был создан с a = .

r = .1θ и r = θ

Изменяя значения a, мы видим, что спираль становится более узкой для меньших значений и шире для больших значений.

---

Круги

Графики уравнения r = a sin θ и r = a cos θ будут окружностями.

r = a sin θ и r = a cos θ

Уравнения вида r = a sin nθ и r = a cos nθ дают розы.

Как график r = a sin nθ отличается от график r = a cos n θ?

r = cos 2θ r = sin 2θ

Синус и косинус графики имеют одинаковый вид. Однако вы заметите, что синус график был повернут на 45 градусов относительно графика косинуса. Это тоже самое результат, найденный в прямоугольной системе координат, где функция синуса была смещена на 45 градусов от функции косинуса.

Теперь посмотрим, что произойдет когда мы сохраняем константу, но варьируем значение n.

r = 2cos 2θ

r = 2 sin 3θ

r = 2 sin 4θ

что когда n — нечетное число, у розы будет n лепестков, а когда n — четное число у розы будет 2n лепестков. Почему это происходит? Когда n равно нечетное число, точки в каждом лепестке на самом деле прослеживаются дважды от 0 до 2pi, однако, когда n равно четному, лепестки прослеживаются только один раз.

Далее давайте рассмотрим, что происходит, когда n остается постоянным, а значение a варьируется.

r = sin 4θ r = 2 sin 4θ r = 3 sin 4θ

Оказывается, что значение а — длина каждого лепестка розы.

Кардиоиды и лимаконы

Уравнения вида r = a + b sin θ, a b sin θ, a + b cos θ и a b cos θ будут производить лимаконы.

Давайте посмотрим, что происходит при различных значениях a и б.

r = 2 + 3sin θ

Когда значение a меньше значения b, граф представляет собой лимакон с внутренней петлей и .

r = 5 + cos 4θ

Когда значение a больше значения b, график представляет собой лимакон с ямочками.

r = 5 2 sin θ

Когда значение a больше или равно значение 2b, граф представляет собой выпуклый лимакон.

г = 2 2 грех θ

Когда значение a равно значению b, график является частным случаем лимакона. Он называется кардиоидным.

Обратите внимание, что в каждом графе лиамсонов переход от синуса к косинусу не влияет на форму графика, просто его направленность. Уравнения, использующие синус, будут симметричны относительно вертикальной оси. в то время как уравнения с использованием косинуса симметричны относительно горизонтальной оси. Знак b также повлияет на их ориентацию.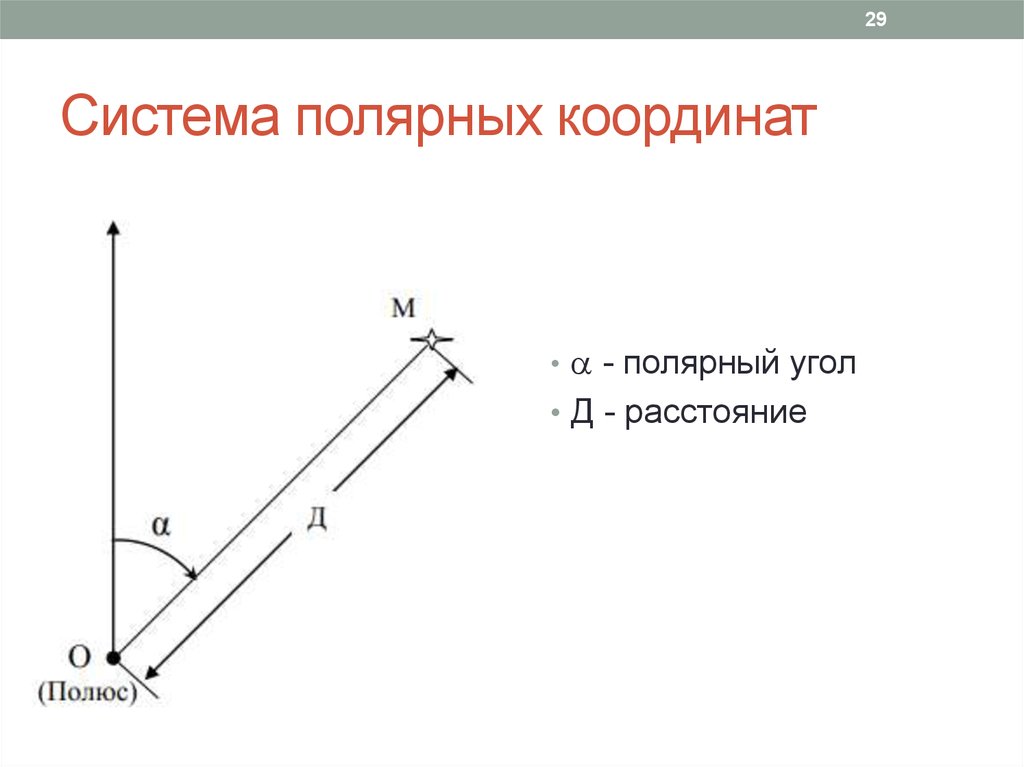

---

Лемнискат

Графики уравнений вида и будут лемнискатами.

Это график лемниската Бернулли.

---

Еще один интересный график

Следующий график довольно интригующе. После работы с несколькими полярными графами и наблюдения за их общей формы, периодичности и симметрии, было довольно неожиданно закончить с графиком прямой линии. График ниже выглядит как график уравнения y = x+1.

Чтобы доказать, что это действительно правильный график для этого уравнения, мы вернемся к взаимосвязи между полярные и декартовы координаты. Воспользуемся тем, что x = r cosθ и y = r sinθ, чтобы показать, что полярное уравнение на самом деле эквивалентно уравнение y = x + 1.

Так как,

Таким образом, y = x +1.

Просто для удовольствия!

Пока я исследовал полярные кривые, я наткнулся на много других интересных графиков.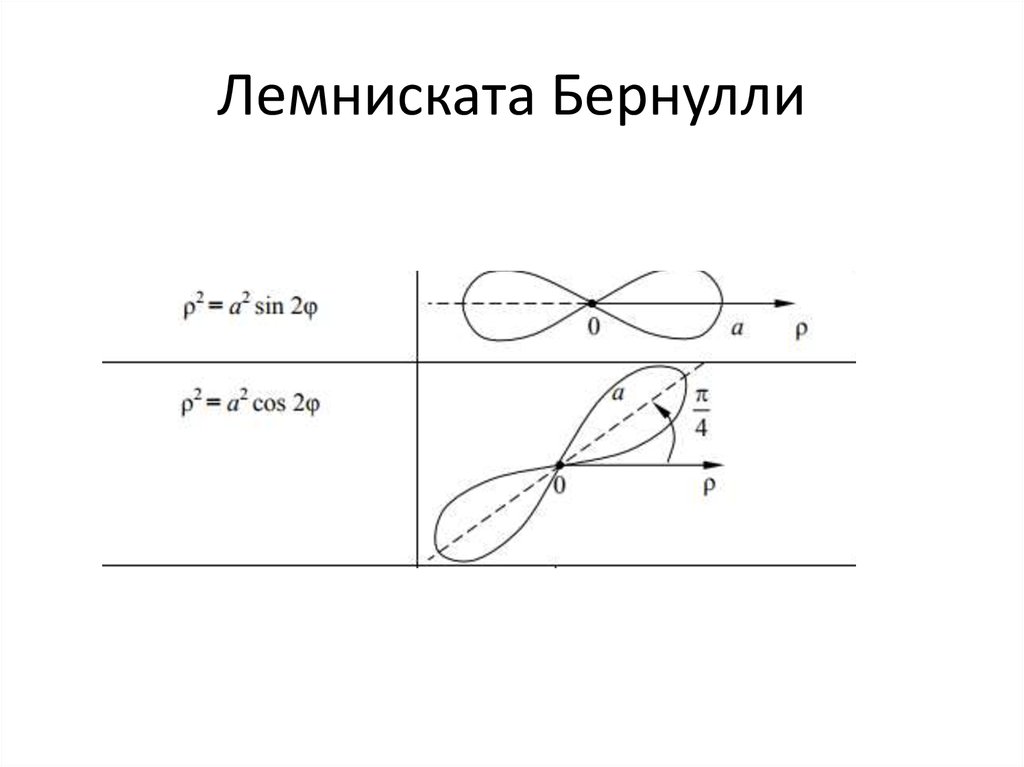 Я включил некоторые из моих любимых ниже. Наслаждаться!

The Conchoid of Nicomedes

Untitled

Hyperbolic Spiral

Untitled

Оскар Баттерфляй

5

2 Домашняя страница

Калькулятор полярных координат с шагами — Декартова координата

Калькулятор полярных координат — идеальный способ для быстрых расчетов при работе с такой системой координат . С помощью стандартного калькулятора может быть трудно увидеть взаимосвязь между углами и радиусом. Это не линейное преобразование. Калькулятор решает эту проблему, отображая углы и радиусы по окружности.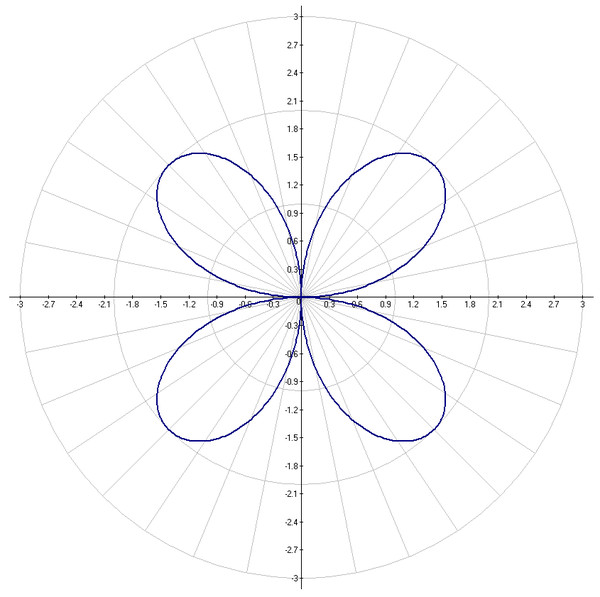

Этот калькулятор также может преобразовывать координаты из полярных в прямоугольные и наоборот. Если вас интересует вычисление прямоугольника, вы можете выполнить уравнения с помощью нашего калькулятора прямоугольников. В этой статье кратко объясняются оба типа координат и формула быстрого преобразования.

Полярные координаты – определение?

Полярные координаты в двумерной системе координат. Полярная система координат состоит из двух перпендикулярных линий, одной горизонтальной и одной вертикальной. Горизонтальная линия называется осью r, а вертикальная линия называется тета-9.0279 θ .

Координаты можно прочитать как (r, θ). Эта система координат основана на измерении расстояния от точки до фиксированной точки на окружности.

Полярные координаты — это метод построения сложных графических чисел в r = (a, b), где a и b — действительные числа. Эта система координат имеет то преимущество, что не требует приведения комплексных чисел к их прямоугольной форме.

Полярные и декартовы (прямоугольные) координаты

Вы можете использовать полярную систему координат в двух измерениях, где вы рисуете линию от начала до конца, чтобы создать систему координат. Это точка пересечения прямой и оси. Угол линии x всегда горизонтален. Эта система координат представляет два числа: расстояние от начала координат и угол линии x .

Важно подчеркнуть, что полюс является источником системы. Чтобы найти полярные координаты, нужно провести линию, которая сольется с полюсом. В этом случае координатами является длина линии p , а также содержит угол, образующий полярную ось.

Декартова система координат — это сетка, которую можно создать в любом количестве измерений. В декартовых системах используются линейные расстояния. Вы можете идентифицировать точки по упорядоченной паре чисел, и вы можете использовать их оба для определения своего местоположения в сети. Первое число — это координата x, и оно определяет горизонтальное положение на сетке. Ось Y представляет собой вертикальную линию, проходящую сверху вниз. Расстояние точки от начала координат можно назвать величиной. Величина точки всегда является положительным числом.

Преобразование декартовых координат в полярные координаты создание точки (x, y) и преобразование ее в (r, θ). Это преобразование часто необходимо при решении математических задач, связанных с преобразованием прямоугольных координат в полярные.

Связь между полярными и декартовыми координатами

Полярные координаты в прямоугольные – формула

Формула полярных координат в прямоугольные представляет собой инструмент преобразования сетки, который позволяет пользователям преобразовывать полярные координаты в прямоугольные координаты. Это отличный инструмент для учащихся математических классов, изучающих эти системы. Для преобразования полярных координат в прямоугольные используйте следующие формулы: 9{2}}

Радиус r — расстояние от начала координат, θ — угол от оси x.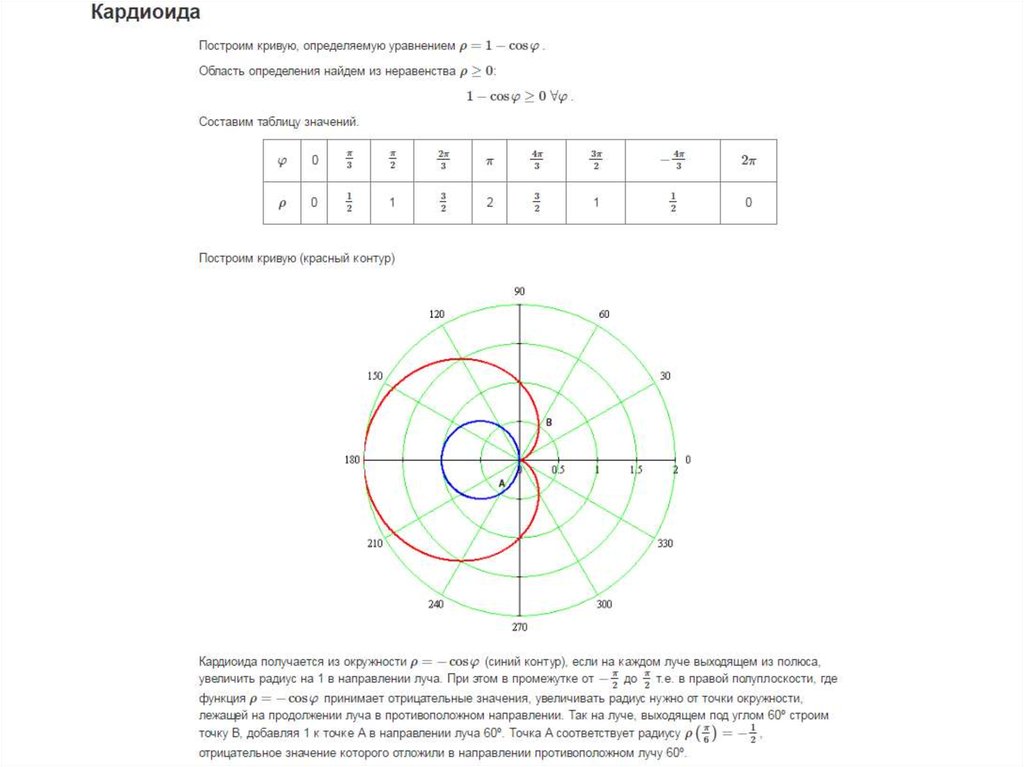

\theta = \arctan \frac{y}{x}

где:

(x, y) – представляют декартовы координаты;
(r, θ) – представляют полярные координаты.

К полярным координатам применяются следующие ограничения:

• r — должно быть больше или равно 0
• θ — положение должно быть в диапазоне [−π, π]

Интеграл в полярных координатах – как интегрировать?

Полярные координаты Интеграл — это простой способ решения интегралов вида. Вы можете использовать интеграл для вычисления площади области, ограниченной двумя кривыми. Область может быть прямоугольной или эллиптической. Вы можете определить область с двумя полярными кривыми, r (θ) и r ‘(θ).

Интеграл в полярных координатах можно использовать для вычисления площади области, ограниченной двумя полярными кривыми. Область может быть прямоугольной или эллиптической.

Площадь в полярных координатах

Вы можете использовать полярную систему координат для построения окружностей, эллипсов и других конических сечений. Также вы можете решать задачи на площадь кругов. Координаты записываются в виде r , θ , где r — расстояние от центра окружности до точки, а θ — угол, измеряемый от центра до точки. Вы можете идентифицировать точки комплексной плоскости по их действительной и мнимой частям.

Если вам нужно визуализировать координаты, попробуйте с помощью транспортира создать окружность радиусом в 1 единицу. Нарисуйте X в центре круга. Обозначьте X как полюс, а область вокруг X как экватор.

• В точке P на экваторе ваши координаты (0,1).
• Если вы находитесь в точке Q на экваторе, они равны (1,0).
• Если вы находитесь в точке R на экваторе, они равны (1,1).

Площадь в полярных координатах — это особый тип плоскостной геометрии, представляющий плоскость с круговой границей. Центр круга — это полюс, а окружность — экватор.

Площадь с полярными координатами

Калькулятор полярных координат – Как пользоваться?

Калькулятор полярных координат помогает математикам вычислять координаты точки на декартовой плоскости. Приложение простое в использовании. Пользователю предоставляется возможность ввести координаты точки в декартовых или полярных координатах и ​​вычислить другие.

Для ввода декартовых координат пользователь вводит координаты x и y. Чтобы ввести полярные координаты, пользователь вводит угол и радиус, таким образом, вы получаете результаты в кратчайшие сроки. 9{2}} = \sqrt{121+16}=\sqrt{137}

Но если вы используете функцию касательной для нахождения угла, это будет выглядеть так: 

\тангенс \тета = 4 \дел 11 =19,8 \градус

Родственное уравнение для выражения мер в декартовой системе координат (x, y), использует прямоугольный треугольник с известной длинной стороной и углом, и тогда оно выглядит так:

х=12\cdot\cos 19,8\градус = 11,28

Кроме того, вы можете использовать функцию синуса для и .

у=12 \cdot \sin 19.8 \градус = 4,08

В заключение, ответ: точка (12, 19. 8) почти точно равна (11, 4.08) в декартовых координатах.

Подводя итог, вам также следует обратиться к нашему калькулятору сферических координат.

Часто задаваемые вопросы

Как найти полярные координаты?

Найти уравнение полярных координат легко с помощью нашего калькулятора. Введите радиус, угол и градусы для преобразования в полярные координаты.

Чем полярные координаты отличаются от прямоугольных?

Прямоугольные координаты — это координаты с осями x и y. Полярные координаты отличаются от прямоугольных координат, поскольку они используют угол и радиус вместо осей x и y.

Могут ли полярные координаты быть трехмерными?

Этот калькулятор может быть полезен для тех, кому нужно отобразить точки на поверхности или для решения задач, связанных с трехмерным пространством.