Как найти обратную матрицу в Excel
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Уроки Excel Нахождение обратной матрицы в Excel
Excel обладает мощным инструментарием, позволяющим выполнять множество математических, статистических, логических и прочих задач. В программе также можно выполнить такое действие, как нахождение обратной матрицы. Ниже мы на практическом примере рассмотрим, как именно это сделать.
Примечание: Найти обратную матрицу можно только при условии, что исходная является квадратной (количество столбцов и строк одинаковое). К тому же, ее определитель не должен равняться цифре 0.
Содержание
- Этап 1. Вычисляем определитель
- Этап 2. Находим обратную матрицу
- Заключение
Этап 1. Вычисляем определитель
Смотрите также: “Как посчитать среднее значение в Excel: формула, функции, инструменты”
В программе данное действие выполняется с помощью функции МОПРЕД.
- Переходим в свободную ячейку, в которой планируем производить расчеты, после чего кликаем по кнопке “Вставить функцию” (fx) слева от строки формул.
- В открывшемся окне вставки функций выбираем категорию “Математические”, в которой кликаем по оператору “МОПРЕД”, затем – по кнопке OK.
- В следующем окне нужно заполнить единственный аргумент функции – “Массив”, в значении которого указываем координаты нашей матрицы. Сделать это можно вручную, прописав адреса ячеек, используя клавиши клавиатуры. Либо можно сначала кликнуть внутри области ввода информации, затем зажав левую кнопку мыши выделить диапазон ячеек непосредственно в самой таблице. Когда все готово, нажимаем кнопку OK.
- В выбранной ячейке отобразился результат, а именно, определитель матрицы. С учетом наших данных получилось число 157894, что значит, что у нашей матрицы обратная матрица существует, так как определитель не равен нулю.
Этап 2.
 Находим обратную матрицу
Находим обратную матрицуСмотрите также: “Подбор параметра в Excel: где находится, как сделать “
Итак, после того, как мы вычислили, что определитель матрицы не равен нулю, можно приступить к нахождению обратной.
- Встаем в ячейку, которая станет самым верхним левым элементом новой обратной матрицы. Заходим в окно Вставки функции, нажав на соответствующую кнопку.
- В категории “Математические” выбираем функцию “МОБР”, после чего щелкаем по кнопке OK.
- Аналогично заполнению значения аргумента “Массив” для функции МОПРЕД, рассмотренной в первом разделе, указываем координаты первичной матрицы, после чего нажимаем OK.
- Получаем требуемый результат в выбранной ячейке.
- Чтобы скопировать функцию в другие ячейки, выделяем область, которая совпадает по количеству столбцов и строк с начальной матрицей. Затем нажимаем клавишу F2 на клавиатуре, после чего жмем комбинацию Ctrl+Shift+Enter.

- Все готово. В результате выполненных действий нам удалось найти обратную матрицу.
Заключение
Смотрите также: “Как разъединить объединенные ячейки в Excel”
Нахождение обратной матрицы – не такая распространенная математическая задача, как, например, сложение, вычитание, умножение, деление, расчеты с процентами и т.д. Но, если все же возникнет такая потребность, вовсе необязательно делать это вручную на листке бумаги, ведь Эксель позволяет быстро и безошибочно справиться с этой задачей.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Обратная матрица в Excel.
 Как найти обратную матрицу в Эксель в 2 этапа
Как найти обратную матрицу в Эксель в 2 этапаГлавная » Уроки MS Excel
Автор Елизавета КМ На чтение 4 мин Опубликовано
Обратная матрица – это сложное математическое понятие, для нахождения которой необходимо выполнить множество непростых действий на бумаге. Однако программа Excel решает данную задачу в более короткие сроки и без особых усилий со стороны исполнителя. Давайте разберемся, каким образом можно найти обратную матрицу в несколько этапов на одном из примеров.
Замечание эксперта! Обязательным условием для нахождения обратной матрицы, является соответствие исходных данных квадратной матрице, а определителя нулю.
Содержание
- Находим значение определителя
- Определяем значение обратной матрицы
- Сферы использования расчетов с обратной матрицей
- Заключение
Находим значение определителя
Чтобы выполнить это действие, необходимо воспользоваться функцией МОПРЕД. Как именно это делается, рассмотрим на примере:
Как именно это делается, рассмотрим на примере:
- Записываем квадратную матрицу в любом свободном месте.
- Выбираем свободную ячейку, после чего находим напротив строки формул кнопку «fx» («Вставить функцию») и кликаем по ней ЛКМ.
- Должно открыться окно, где в строке «Категория:» останавливаемся на «Математические», а ниже выбираем функцию МОПРЕД. Соглашаемся с выполненными действиями кликнув по кнопке «ОК».
- Далее в открывшемся окне заполняем координаты массива.
Совет! Заполнить адресацию можно одним из двух способов: вручную или кликнув кнопкой мыши в месте ввода информации о массиве и, определив выделением зоны место расположения квадратной матрицы, получить адрес массива автоматически.
- После проверки введенных ручным или автоматическим образом данных жмите «ОК».
- После всех проведенных манипуляций свободная ячейка должна отобразить определитель матрицы, значение которого понадобится для нахождения обратной матрицы.
 Как видно по скриншоту, после вычислений получилось число 338, а, следовательно, потому как определитель не равен 0, то обратная матрица существует.
Как видно по скриншоту, после вычислений получилось число 338, а, следовательно, потому как определитель не равен 0, то обратная матрица существует.
Определяем значение обратной матрицы
Как только вычисление определителя закончено, можно переходить к определению обратной матрицы:
- Выбираем место расположения верхнего элемента обратной матрицы, открываем окно «Вставка функции».
- Выбираем категорию «Математические».
- В расположившихся снизу функциях пролистываем список и останавливаем выбор на МОБР. Кликаем по кнопке «ОК».
- Аналогично ранее выполняемым действиям при нахождении значений определителя вписываем координаты массива с квадратной матрицей.
- Убеждаемся в правильности выполненных действий и жмем «ОК».
- В выбранной верхней левой ячейке будущей обратной матрицы появится результат.
- Для копирования формулы для нахождения значений в других ячейках используем свободное выделение. Для этого, зажав ЛКМ, растягиваем на всю область будущей обратной матрицы.

- Жмем на клавиатуре кнопку F2 и переходим к набору комбинации «Ctrl+Shift+Enter». Готово!
7Рекомендация эксперта! Для удобства выполнения действий по нахождению обратной матрицы в таблице Excel расположение массива с квадратной матрицей и выбранная область для ячеек с обратной матрицей должны располагаться на одном уровне по отношению к столбцам. Таким образом будет проще определить границы адресации второго массива. Пример указан на иллюстрации ниже.
Сферы использования расчетов с обратной матрицей
Экономика – это область, которая требует проведения постоянных и очень сложных расчетов. Для облегчения используется матричная система расчетов. Нахождение обратной матрицы – это быстрый способ обработки большого объема информации за максимально короткие сроки, конечный результат которого будет представлен в наиболее удобном для восприятия виде.
Другая область применения – это 3D моделирование изображений. Всевозможные программы имеют встроенные инструменты для проведения подобного рода расчетов, что в значительной степени облегчает работу конструкторам при производстве расчетов. Наиболее популярной программой среди 3D моделистов считается Компас-3D.
Всевозможные программы имеют встроенные инструменты для проведения подобного рода расчетов, что в значительной степени облегчает работу конструкторам при производстве расчетов. Наиболее популярной программой среди 3D моделистов считается Компас-3D.
Существуют и другие сферы деятельности, где можно применить систему расчетов обратной матрицы, но все же основной программой для проведения матричных расчетов можно считать Excel.
Заключение
Нахождение обратной матрицы нельзя назвать такой же распространенной математической задачей, как вычитание, сложение или деление, но если появилась необходимость в ее решении, то все действия могут произведены в табличном процессоре Excel. Если человеческий фактор склонен допускать ошибки, то компьютерная программа выдаст 100% точный результат.
Оцените качество статьи. Нам важно ваше мнение:
Excel как найти обратную матрицу матрица обратная матрица Эксель
Обратные матрицы — Как найти обратную матрицу
Каталин Дэвид
Матрица обратима, если ее определитель отличен от нуля.
Матрицы Умножение матриц Определители Ранг матрицы Матричные уравнения Системы уравнений Калькуляторы для матриц
Подборка по базе: Тема 6. Типы хозяйственных операций и их влияние на баланс.pdf, Актуальность лизинговых операций в деятельности коммерческого ба, 1 урок Свойства информации.docx, 20 операций — НЭБзу_19 Бабкина А.В.doc, ОРГАНИЗАЦИИ СКЛАДСКИХ ОПЕРАЦИЙ профпереподготовка к высшему обра, ОАиП 1 Понятие алгоритма свойства алгоритма.docx, Лекция 2 Психофизиологические свойства специалиста организации.d, 08. Ссылки на некоторые ресурсы для технологии.  docx, Понятие алгоритма. Свойства алгоритмов.ppt, Восприятие и его свойства.pptx docx, Понятие алгоритма. Свойства алгоритмов.ppt, Восприятие и его свойства.pptxНекоторые свойства операций над матрицами. Вернёмся к действиям с матрицами. Можно ли к матрице прибавить число? Например: . Ну, или наоборот: Нет. К матрице можно прибавить только другую матрицу, причём точно такого же размера. Матрицу можно умножить на число. Но сложить их нельзя. Следует отметить, что допустимо сложение определителя матрицы с числом: Результат вычисления определителя – число (справедливо и для разности). Как возвести матрицу в квадрат? Операция определена только для квадратных матриц – «два на два», «три на три» и т.д. Возвести квадратную матрицу в квадрат – это значит, умножить её саму на себя: Пример 1 Возвести в квадрат матрицу Решение: – последовательно (слева направо) перебираем столбцывторой матрицы и «пристраиваем» их к Ответ: Немного о некоммутативности матричного умножения и единичной матрице Коммутативность = Перестановочность. Обычные числа переставлять можно , а матрицы в общем случае не перестановочны: . Рассмотрим некоторые исключения из правила, которые потребуются для выполнения практических задач. Справедливо следующее свойство: если произвольную матрицу умножить слева или справа на единичную матрицу подходящих размеров, то в результате получится исходная матрица: Коммутативность числового множителя относительно умножения матриц Для матриц и действительного числа справедливо следующее свойство: То есть числовой множитель можно (и нужно) вынести вперёд. Правило остаётся справедливым, если перемножаются три либо большее количество матриц. Пример 2 Вычислить произведение Решение: (1) Согласно свойству перемещаем числовой множитель вперёд. Сами матрицы переставлять нельзя! (2) – (3) Выполняем матричное умножение. (4) Здесь можно поделить каждое число 10, но тогда среди элементов матрицы появятся десятичные дроби, что не есть хорошо. Однако замечаем, что все числа матрицы делятся на 5, поэтому умножаем каждый элемент на . Окончательный ответ лучше оставить в виде , хотя, в принципе, годится и внесение дроби: . Ответ: Как умножить три матрицы? Произведение трёх матриц можно вычислить двумя способами: 1) найти , а затем домножить на матрицу «цэ»: ; 2) либо сначала найти , потом выполнить умножение . Результаты обязательно совпадут, и в теории данное свойство называют ассоциативностью матричного умножения Пример 3 Перемножить матрицы двумя способами Алгоритм решения двухшаговый: находим произведение двух матриц, затем снова находим произведение двух матриц. 1) Используем формулу . Действие первое: Действие второе: 2) Используем формулу . Действие первое: Действие второе: Ответ: Как возвести матрицу в куб и более высокие степени? Данные операции также определены только для квадратных матриц. Фактически это частный случай умножения трёх матриц, по свойству ассоциативности матричного умножения: . А матрица, умноженная сама на себя – это квадрат матрицы: Таким образом, получаем рабочую формулу: Пример 4 Возвести матрицу в куб. Решение : Сначала возведём матрицу в квадрат:Возведём матрицу в куб: Возведём матрицу в четвёртую степень двумя способами: Ответ: Матричные выражения Рассмотрим матричное выражение , где – некоторые матрицы. В данном матричном выражении три слагаемых и операции сложения/вычитания выполняются в последнюю очередь. В первом слагаемом сначала нужно транспонировать матрицу «бэ»: , потом выполнить умножение и внести «двойку» в полученную матрицу. Операция транспонирования имеет более высокий приоритет, чем умножение. Скобки, как и в числовых выражениях, меняют порядок действий: – тут сначала выполняется умножение , потом полученная матрица транспонируется и умножается на 2. Во втором слагаемом в первую очередь выполняется матричное умножение , и обратная матрица находится уже от произведения. Если скобки убрать: , то сначала необходимо найти обратную матрицу , а затем перемножить матрицы: . С третьим слагаемым всё очевидно: возводим матрицу в куб и вносим «пятёрку» в полученную матрицу. Если матричное выражение имеет смысл, то результат его вычисления является матрицей. Пример 5 Вычислить значение матричного многочлена , если . Решение: Как найти обратную матрицу? Что такое обратная матрица? Здесь можно провести аналогию с обратными числами: рассмотрим, например, оптимистичное число 5 и обратное ему число . Существует два основных метода нахождения обратной матрицы: Рассмотрим квадратную матрицу . Обратную матрицу можно найти по следующей формуле: , где – определитель матрицы , – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы . Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д. Обозначения: обратная матрица обозначается надстрочным индексом Пример 6: Найти обратную матрицу для матрицы Решаем. 1) Сначала находим определитель матрицы. Если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ. В рассматриваемом примере , а значит, всё в порядке. 2) Находим матрицу миноров . Матрица миноров имеет такие же размеры, как и матрица , то есть в данном случае . Возвращаемся к нашей матрице 3) Находим матрицу алгебраических дополнений . 4) Находим транспонированную матрицу алгебраических дополнений . – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы . 5) Ответ. Вспоминаем нашу формулу Таким образом, обратная матрица: . Как проверить решение? Необходимо выполнить матричное умножение либо Проверка: Получена единичная матрица– это матрица с единицами на главной диагонали и нулями в остальных местах. Таким образом, обратная матрица найдена правильно. Пример7: Найти обратную матрицу для матрицы Алгоритм точно такой же, как и для случая «два на два». Обратную матрицу найдем по формуле: , где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы . 1) Находим определитель матрицы.
2) Находим матрицу миноров . Матрица миноров имеет размерность «три на три» , и нам нужно найти девять чисел. Рассмотрим несколько миноров: Рассмотрим следующий элемент матрицы: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент: необходимо вычислить девять определителей «два на два». Найдем еще один минор в картинках: Окончательный результат: решаем самостоятельно– матрица миноров соответствующих элементов матрицы . 3) Находим матрицу алгебраических дополнений . В матрице миноров необходимо СМЕНИТЬ ЗНАКИ строго у следующих элементов: |
Как найти обратную матрицу 3х3 ?
Данное решение сделано калькулятором, представленным на сайте.
Найдем матрицу A-1, обратную исходной:
| A = | 4 | 3 | 2 | |||
| 2 | 1 | -1 | ||||
| 3 | 3 | 2 |
Запишем формулу для нахождения обратной матрицы:
| A-1 = 1 / det A * | A11 | A21 | A31 | |||
| A12 | A22 | A32 | ||||
| A13 | A23 | A33 |
A11 … A33 — это числа (алгебраические дополнения), которые будут найдены позже.
На ноль делить нельзя. Поэтому если det A равен нулю, то найти обратную матрицу невозможно.
Вычислим det A.
| det A = | 4 | 3 | 2 | = | ||
| 2 | 1 | -1 | ||||
| 3 | 3 | 2 |
К элементам строки 1 прибавляем соответствующие элементы строки 3, умноженные на -1. подробнее
| = | 1 | 0 | 0 | = | ||
| 2 | 1 | -1 | ||||
| 3 | 3 | 2 |
Разложим определитель по элементам строки 1. подробнее
| = ( -1) 1 + 1 * 1 * | 1 | -1 | = | ||
| 3 | 2 |
| = | 1 | -1 | = | ||
| 3 | 2 |
= 1 * 2 — ( -1) * 3 =
= 2 + 3 =
= 5
det A не равен нулю. Следовательно, найти обратную матрицу возможно.
Следовательно, найти обратную матрицу возможно.
Вычислим числа (алгебраические дополнения) A11 … A33
= 1 * 2 — ( -1) * 3 = 2 + 3 = 5
= — ( 2 * 2 — ( -1) * 3 ) = — (4 + 3) = -7
= 2 * 3 — 1 * 3 = 6 — 3 = 3
= — ( 3 * 2 — 2 * 3 ) = — (6 — 6) = 0
= 4 * 2 — 2 * 3 = 8 — 6 = 2
= — ( 4 * 3 — 3 * 3 ) = — (12 — 9) = -3
= 3 * ( -1) — 2 * 1 = -3 — 2 = -5
= — ( 4 * ( -1) — 2 * 2 ) = — (-4 — 4) = 8
= 4 * 1 — 3 * 2 = 4 — 6 = -2
Ответ:
| A-1 = 1 / det A * | A11 | A21 | A31 | |||
| A12 | A22 | A32 | ||||
| A13 | A23 | A33 |
| A-1 = 1 / 5 * | 5 | 0 | -5 | |||
| -7 | 2 | 8 | ||||
| 3 | -3 | -2 |
| A-1 = | 1 | 0 | -1 | |||
| -7/5 | 2/5 | 8/5 | ||||
| 3/5 | -3/5 | -2/5 |
Проверим ответ
Необходимо проверить, что выполняется условие: A-1 * A = E.
Мы будем использовать предпоследнюю форму записи обратной матрицы A-1.
Это позволит нам избежать вычислений с дробями.
b11 = 5 * 4 + 0 * 2 + ( -5) * 3 = 20 + 0 — 15 = 5
b12 = 5 * 3 + 0 * 1 + ( -5) * 3 = 15 + 0 — 15 = 0
b13 = 5 * 2 + 0 * ( -1) + ( -5) * 2 = 10 + 0 — 10 = 0
b21 = -7 * 4 + 2 * 2 + 8 * 3 = -28 + 4 + 24 = 0
b22 = -7 * 3 + 2 * 1 + 8 * 3 = -21 + 2 + 24 = 5
b23 = -7 * 2 + 2 * ( -1) + 8 * 2 = -14 — 2 + 16 = 0
b31 = 3 * 4 + ( -3) * 2 + ( -2) * 3 = 12 — 6 — 6 = 0
b32 = 3 * 3 + ( -3) * 1 + ( -2) * 3 = 9 — 3 — 6 = 0
b33 = 3 * 2 + ( -3) * ( -1) + ( -2) * 2 = 6 + 3 — 4 = 5
Необходимо умножить получившуюся матрицу на 1/5
Таким образом, найденная матрица A-1 является обратной для исходной матрицы A.
Как инвертировать матрицу с помощью NumPy
Просмотреть обсуждение
Улучшить статью
Сохранить статью
- Последнее обновление: 18 авг, 2020
Посмотреть обсуждение
Улучшить статью
Сохранить статью
Обратная матрица — это просто обратная матрица, как это делается в обычной арифметике для одного числа, которое используется для решения уравнений для нахождения значений неизвестных переменных. Обратная матрица — это та матрица, которая при умножении на исходную матрицу дает единичную матрицу. Обратная матрица существует, только если матрица равна неединственное число, т. е. определитель не должен быть равен 0 . Используя определитель и сопряженное, мы можем легко найти обратную квадратную матрицу, используя приведенную ниже формулу:
, если det(A) != 0
A -1 = прил(А)/прил(А)
еще
«Обратно не существует» Уравнение матрикса
Где,
A -1 : 0003
B: Матрица решений
Обратная матрица с использованием NumPy
Python предоставляет очень простой метод вычисления обратной матрицы. Функция numpy.linalg.inv() , доступная в модуле python NumPy, используется для вычисления обратной матрицы.
Функция numpy.linalg.inv() , доступная в модуле python NumPy, используется для вычисления обратной матрицы.
Синтаксис:
numpy.linalg.inv ( a ) Параметр
0026
a: Инвертируемая матрица
Возвраты:
Обратная матрица a .
Example 1:
Python
|
Output:
[[ 0.17647059-0,00326797 -0,02287582] [ 0,05882353 -0,13071895 0,08496732] [-0.11764706 0.1503268 0.05228758]]
Example 2:
Python
|
Output:
[[ 0,13368984 0,10695187 0,02139037 -0,009] [-0,00229183 0,02673797 0,14820474 -0,12987013] [-0,12987013 0,18181818 0,06493506 -0,02597403] [ 0,11000764 -0,28342246 -0,11382735 0,23376623]]
Пример 3:
Python
|
Output:
[[[-2 . 1.] [ 1,5 -0,5 ]] [[-1,25 0,75] [ 0,75 -0,25]]]
Обратная матрица в Excel | Как создать обратную матрицу в Excel?
Обратная матрица Excel (оглавление)
- Введение в обратную матрицу в Excel
- Примеры обратной матрицы в Excel
Матрица, для которой вы хотите вычислить обратную, должна быть квадратной матрицей. Это означает, что матрица должна иметь равное количество строк и столбцов. Определитель матрицы не должен быть равен нулю. Если он равен нулю, вы можете найти обратную матрицу. Теоретическая формула для вычисления обратной матрицы A выглядит следующим образом:
Где,
|A| = Определитель матрицы A.
(adj A) = Сопряженная матрица A.
Если мы подставим оба этих значения в приведенную выше формулу, мы можем получить обратную любую матрицу A. Иногда вычисление обратной матрицы становится очень утомительным. . Математики будут рады узнать, может ли какая-либо функция работать для них и вычислить для них обратную матрицу.
Иногда вычисление обратной матрицы становится очень утомительным. . Математики будут рады узнать, может ли какая-либо функция работать для них и вычислить для них обратную матрицу.
Функция MINVERSE для вычисления обратной матрицы
Функция Excel MINVERSE позволяет пользователю вычислить обратную любую квадратную матрицу с ненулевым определителем. Обратная матрица имеет тот же размер, что и исходная матрица. Вычисленная обратная матрица имеет тот же размер, что и исходная матрица.
Синтаксис:
=MINVERSE(массив)
Аргумент:
массив — массив значений, представляющих матрицу.
В этой статье мы увидим, как вычислить обратную квадратную матрицу.
Примеры обратной матрицы в Excel
Давайте разберемся, как создать обратную матрицу в Excel на нескольких примерах.
Вы можете скачать этот шаблон обратной матрицы Excel здесь — Шаблон обратной матрицы Excel
Пример №1.
 Вычисление обратной матрицы 2X2
Вычисление обратной матрицы 2X2Матрица 2X2 состоит из двух строк и двух столбцов. Предположим, у нас есть квадратная матрица 2X2, как показано на изображении ниже.
Шаг 1: Определите диапазон из 4 ячеек (поскольку у нас есть матрица 2X2) на том же листе Excel, который будет содержать вашу обратную матрицу A. Здесь я выбрал ячейки A1: C5 в качестве диапазона для обратной матрицы A.
Это диапазоны, в которых будет вычисляться обратная матрица A.
Шаг 2: В ячейке B4 начните вводить формулу обратной матрицы =MINV . Вы увидите диапазон формул, связанных с ключевым словом. Дважды щелкните, чтобы выбрать MINVERSE из них, чтобы вы могли вычислить обратную матрицу A. Обязательно выберите все ячейки, в которых будет вычислена ваша обратная.
Шаг 3: Укажите аргумент массива для функции MINVERSE как B1:C2 и закройте круглые скобки, чтобы завершить формулу. Обратите внимание, что массив, который мы предоставляем в качестве аргумента функции MINVERSE, состоит из ячеек со значениями исходной матрицы A.
Обратите внимание, что массив, который мы предоставляем в качестве аргумента функции MINVERSE, состоит из ячеек со значениями исходной матрицы A.
Шаг 4: Чтобы каждый раз видеть вывод формулы, нам нужно нажимать клавишу Enter. Но в этом случае вам нужно нажать Ctrl + Shift + Enter клавиш, чтобы формула была преобразована в формулу массива, которая выглядит следующим образом {=MINVERSE(B1:C2)} и работает вместе со всеми связанными ячейками. с инверсией A.
Вы можете видеть в ячейках B1:C2 матрицу, обратную исходной матрице A.
Мы также можем проверить, правильно ли получена обратная, которую мы получаем через функцию MINVERSE, или нет. Проверить это можно, умножив матрицы A и A на 9.0029 -1 . Результатом умножения должна стать единичная матрица.
Мы можем добиться умножения матриц, используя функцию МУМНОЖ в Excel. Он умножает матрицы. Смотрите вывод в массиве ячеек B1:C5.
Пример №2. Вычисление обратной матрицы 4X4
Шаг 1: Введите матрицу 4X4 по ячейкам A1:E4, как показано на снимке экрана ниже. Это матрица, для которой нам нужно вычислить обратную матрицу.
Шаг 2: Выберите ячейки от A6 до E9. Это ячейки, в которых мы будем вычислять обратную матрицу 4X4 с именем A.
Шаг 3: Не снимая выделения со всех ячеек, в ячейке B6 начните вводить формулу обратной матрицы от = MINV до список формул, связанных с ключевым словом, дважды щелкните, чтобы выбрать MINVERSE.
Шаг 4: Используйте ссылку на массив B1:E4 в качестве аргумента массива для этой функции и закройте круглые скобки, чтобы завершить формулу.
Шаг 5: Вместо нажатия клавиши Enter, как обычно, одновременно нажмите Ctrl + Shift + Enter клавиш, чтобы вычислить обратные значения для всех ячеек в B1:E4. Если этого не сделать, то формула не будет преобразована в формулу массива и либо будет применена только к текущей ячейке и если вы попытаетесь перетащить ее на другие ячейки, то выдаст ошибку.
Если этого не сделать, то формула не будет преобразована в формулу массива и либо будет применена только к текущей ячейке и если вы попытаетесь перетащить ее на другие ячейки, то выдаст ошибку.
Вот как мы можем вычислить обратную матрицу в Excel, используя функцию MINVERSE. Мы также можем проверить с помощью функции MMLUT, правильно ли вычисляется обратное значение.
Выберите диапазоны от B1 до E9, где мы можем проверить, является ли умножение этих двух матриц идентичной матрицей или нет.
Поставляется как идентичная матрица. Следовательно, мы можем сказать, что обратное, которое мы зафиксировали, получено правильно. Это из этой статьи. Давайте закончим с некоторыми моментами, которые следует запомнить.
Что нужно помнить
- Если в заданной матрице есть пустая ячейка или нечисловое значение, MINVERSE выдаст вам #ЗНАЧ! Ошибка.
- Если в результирующей матрице выделить несколько лишних ячеек, будет получена ошибка #Н/Д.

- Если данная матрица является единственной матрицей (для которой не существует обратной), вы получите #ЧИСЛО! Ошибка.
- В качестве формулы массива рекомендуется использовать MINVERSE. В противном случае вы можете получить странные результаты по ячейкам. Как получение ошибок значения, когда вы перетаскиваете формулу по строкам.
- Если вы не хотите, чтобы она использовалась в качестве формулы массива, вам нужно ввести одну и ту же формулу во все ячейки, чтобы получить результат.
Рекомендуемые статьи
Это руководство по обратной матрице в Excel. Здесь мы обсуждаем, как создать обратную матрицу в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете просмотреть другие наши рекомендуемые статьи —
- Матрица в Excel
- Корреляционная матрица Excel
- МИНВЕРС в Excel
- ММУЛЬТ в Excel
Обратная матрица в Excel | Найти обратную матрицу с помощью функции MINVERSE()
Обратная матрица — это обратная квадратная матрица, которая является невырожденной матрицей или обратимой матрицей (определитель не равен нулю).
Трудно определить обратную для сингулярной матрицы. Обратная матрица в Excel имеет такое же количество строк и столбцов, что и исходная матрица.
Одна интересная особенность обратной матрицы заключается в том, что умножая ее на исходную матрицу, мы получим единичную матрицу, в которой все диагональные значения равны единице. Это связано с тем, что обратные матрицы применяются в линейной алгебре при решении уравнений. Для определения обратной матрицы доступны различные методы, включая расчет вручную и автоматический расчет. Автоматизированный анализ включает использование функций ExcelФункции ExcelФункции Excel помогают пользователям экономить время и вести обширные рабочие листы. Существует более 100 функций Excel, классифицированных как финансовые, логические, текстовые, дата и время, поиск и справочная информация, математические, статистические и информационные функции. Подробнее. В Excel процесс обратного вычисления матрицы упрощается за счет применения встроенной функции MINVERSE в Excel.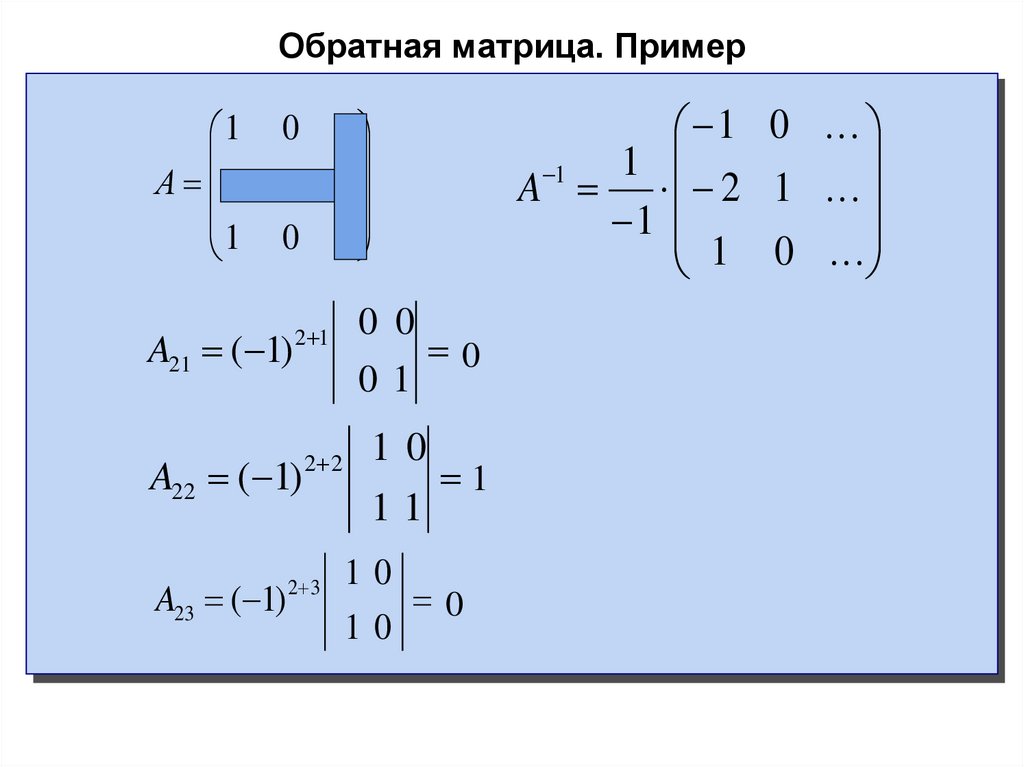 MINVERSE в Excel. MINVERSE означает «обратная матрица» в Excel. Он превращает заданную матрицу в обратную матрицу с идентичными массивами.Подробнее
MINVERSE в Excel. MINVERSE означает «обратная матрица» в Excel. Он превращает заданную матрицу в обратную матрицу с идентичными массивами.Подробнее
Содержание
- Обратная матрица Excel
- Как инвертировать матрицу в Excel?
- Использует
- Примеры
- Пример № 1
- Пример № 2
- Пример № 3
- Вещи. , и т. д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: обратная матрица в Excel (wallstreetmojo.com)Как инвертировать матрицу в Excel?
Функция Excel MINVERSE помогает вернуть массив или обратную матрицу. Входная матрица должна быть квадратной матрицей со всеми числовыми значениями с равным количеством столбцов и строк по размеру. ОБРАТНАЯ матрица будет иметь те же размеры, что и входная матрица.
Назначение : Эта функция направлена на поиск инверсии заданного массива.

Возвращаемое значение: Эта функция возвращает обратную матрицу с одинаковыми размерностями.
Синтаксис : Синтаксис функции MINVERSE:
Массив : Массив должен состоять только из положительных или отрицательных числовых значений.
Функция ИНВЕРС используется двумя способами в Excel, включая ввод вручную и вставку из математических и триггерных функций на вкладке «Формула».
Использование
Обратная матрица в Excel используется для различных целей. Среди них:
- Система линейных уравнений решается в Excel с использованием обратной матрицы
- Обратные матрицы используются в нелинейных уравнениях, линейном программировании в excelЛинейное программирование в ExcelЛинейное программирование в Excel помогает реализовать этот аспект прикладной математики в таблице Excel для решения бизнес-задач за счет оптимизации ресурсов. Для этой цели пользователь может выбрать «Excel Solver».
 Подробнее и нахождение целочисленных решений системных уравнений.
Подробнее и нахождение целочисленных решений системных уравнений. - Обратные матрицы находят применение в анализе данных, особенно в регрессии наименьших квадратов. Для этой функции квадратного корня используется терминология SQRT. Например, пользователь может определить квадратный корень из 70 как 8,366602, используя эту функцию VBA, чтобы определить различные статистические параметры и значения дисперсий и ковариаций.
- Обратные матрицы используются для решения задач, связанных с анализом затрат и результатов в экономике и бизнесе.
Примеры
Вы можете скачать этот шаблон обратной матрицы Excel здесь – Шаблон обратной матрицы Excel
Пример №1 следующую матрицу A.
Выполните следующие шаги, чтобы создать матрицу в Excel.
- Введите матрицу A в лист Excel, как показано на рисунке ниже.
Диапазон матрицы B2:C3. - Выберите диапазон ячеек для размещения обратной матрицы A-1 на том же листе.

- После выбора необходимых ячеек мы должны вставить формулу функции MINVERSE в строку формул. Необходимо убедиться, что формула введена, когда ячейки все еще выделены.
- Затем введите диапазон массива или матрицы, как показано на скриншоте.
- После ввода формулы мы должны нажать клавишу «Ввод» в сочетании с клавишами «CTRL» и «SHIFT», чтобы преобразовать обычную формулу в формулу массива для получения всех элементов обратной матрицы в время. Формула будет изменена на {=MINVERSE (B2:C3)}
- Результирующая обратная матрица получается как:
Здесь мы можем заметить, что размер входной матрицы и обратной матрицы то же, что 2×2.
Пример #2
Определение обратной квадратной матрицы 3×3 в Excel
Для этого примера рассмотрим следующую матрицу A.
 в лист Excel, как показано на рисунке ниже.
в лист Excel, как показано на рисунке ниже.Диапазон матрицы A: B2: D4.
Шаг 2: Выберите диапазон ячеек для размещения обратной матрицы A-1 на том же листе.
Шаг 3: После выбора необходимых ячеек введите формулу функции МИНВЕРС в строку формул. Необходимо убедиться, что формула введена, когда ячейки все еще выделены.
Шаг 4: Введите диапазон массива или матрицы, как показано на скриншоте.
Шаг 5: После ввода формулы нажмите клавишу « ENTER» в сочетании с клавишами «CTRL» и «SHIFT» , чтобы преобразовать обычную формулу в формулу массива для получения всех элементов обратной матрицы в время. Формула будет изменена следующим образом: {=MINVERSE (B2: D4)}
Шаг 6: Результирующая обратная матрица получается как:
Здесь мы можем заметить, что размер входной матрицы и обратной матрицы такой же, как 3× 3.
Пример №3
Определение обратной единичной матрицы
Рассмотрим единичную матрицу 2×2 для этого примера.

Шаг 1: Введите матрицу I на лист Excel.
Шаг 2: Выберите диапазон ячеек для размещения обратной матрицы I -1 на том же листе.
Шаг 3: После выбора необходимых ячеек мы должны вставить формулу функции MINVERSE в строку формул.
Шаг 4: Введите диапазон массива или матрицы, как показано на скриншоте.
Шаг 5: Нажмите клавишу ENTER в сочетании с клавишами CTRL и SHIFTENTER В сочетании с CTRL и SHIFTCtrl-Shift Enter In Excel — это команда быстрого доступа, которая упрощает реализацию формулы массива в функции Excel для выполнения сложных вычислений приведенные данные. В целом он преобразует определенные данные в формат массива в Excel с несколькими значениями данных для этой цели.Подробнее клавиши для преобразования обычной формулы в формулу массива. Формула будет изменена следующим образом: {=MINVERSE (B2:C3)}
Шаг 6: Результирующая обратная матрица получается как:
Из этого видно, что обратная единичная матрица и единичная матрицы одинаковые.

Что нужно помнить
- Если при использовании функции МИНВЕРС в Excel матрица содержит нечисловые значения, пустые ячейки и разное количество столбцов и строк, это может привести к ошибке #Value! Ошибка.
- Ошибка #ЧИСЛО, показанная в предоставленной матрице, является сингулярной матрицей.
- #Н/Д Ошибка, отображаемая в ячейках результирующей обратной матрицы, выходит за допустимые пределы. Функция MINVERSE приводит к ошибке #N/A в выбранных дополнительных ячейках.
- Функцию MINVERSE необходимо вводить как формулу массива в excelArray Формула В ExcelArray формулы являются чрезвычайно полезными и мощными формулами, которые используются в Excel для выполнения некоторых из самых сложных вычислений. Существует два типа формул массива: один возвращает один результат, а другой возвращает несколько результатов. Подробнее читайте в электронной таблице.
Рекомендуемые статьи
Эта статья представляет собой руководство по обратной матрице Excel.
 Мы обсудили обратную матрицу в Excel с использованием функции MINVERSE() с примерами и загружаемым шаблоном Excel. Вы можете узнать больше об Excel из следующих статей: –
Мы обсудили обратную матрицу в Excel с использованием функции MINVERSE() с примерами и загружаемым шаблоном Excel. Вы можете узнать больше об Excel из следующих статей: –- Ковариационная матрица в Excel
- Новая строка в Excel
- Умножение матриц в Excel
- Создание корреляционной матрицы в Excel
Простая инверсия матрицы в Pure Python без Numpy или Scipy — интегрированное машинное обучение и искусственный интеллект
Опубликовано Thom Ives на
Чтобы помочь с инсайтами и инструментами будущих исследований
Загрузите его на GitHub И ознакомьтесь с Интегрированное машинное обучение и искусственный интеллект , который скоро появится на YouTube.
Обзор
Мы рассмотрим процедурный метод грубой силы для инвертирования матрицы с помощью чистого Python.
 Почему бы нам просто не использовать numpy или scipy? Отличный вопрос. Этот блог посвящен инструментам, повышающим эффективность И ясность . Я люблю numpy, pandas, sklearn и все замечательные инструменты, которые предлагает нам сообщество специалистов по данным Python, но я понял, что чем лучше я понимаю «принципы» того или иного предмета, тем лучше я знаю, как его применять. Кроме того, завтрашние инструменты машинного обучения будут разрабатываться теми, кто понимает принципы математики и кодирования сегодняшних инструментов.
Почему бы нам просто не использовать numpy или scipy? Отличный вопрос. Этот блог посвящен инструментам, повышающим эффективность И ясность . Я люблю numpy, pandas, sklearn и все замечательные инструменты, которые предлагает нам сообщество специалистов по данным Python, но я понял, что чем лучше я понимаю «принципы» того или иного предмета, тем лучше я знаю, как его применять. Кроме того, завтрашние инструменты машинного обучения будут разрабатываться теми, кто понимает принципы математики и кодирования сегодняшних инструментов. Кроме того, как только вы поймете эффективный метод обращения матриц, вы на ~ 80 % пути к тому, чтобы иметь свой собственный решатель метода наименьших квадратов и компонент для многих других персональных аналитических модулей, которые помогут вам лучше понять, как много наших замечательных создаются инструменты машинного обучения. Могу ли я порекомендовать вам использовать то, что мы собираемся разработать, для реального проекта? Все эти модули Python, упомянутые выше, молниеносно работают, поэтому, как правило, нет.
 Я бы не рекомендовал вам использовать такие инструменты самостоятельно , ЕСЛИ вы работаете с более мелкими проблемами, ИЛИ вы исследуете какой-то новый подход, который требует небольших изменений в вашем личном наборе инструментов. Таким образом, приведенное выше утверждение заслуживает повторения: средства машинного обучения завтрашнего дня будут разрабатываться теми, кто понимает принципы математики и кодирования сегодняшних инструментов. Я хочу быть частью или, по крайней мере, поддерживать тех, кто будет создавать инструменты следующего поколения. Кроме того, если вы гик, знание того, как запрограммировать инверсию матрицы, является отличным правом прохода! Мы также рассмотрим, как использовать numpy/scipy для инвертирования матрицы в конце этого поста.
Я бы не рекомендовал вам использовать такие инструменты самостоятельно , ЕСЛИ вы работаете с более мелкими проблемами, ИЛИ вы исследуете какой-то новый подход, который требует небольших изменений в вашем личном наборе инструментов. Таким образом, приведенное выше утверждение заслуживает повторения: средства машинного обучения завтрашнего дня будут разрабатываться теми, кто понимает принципы математики и кодирования сегодняшних инструментов. Я хочу быть частью или, по крайней мере, поддерживать тех, кто будет создавать инструменты следующего поколения. Кроме того, если вы гик, знание того, как запрограммировать инверсию матрицы, является отличным правом прохода! Мы также рассмотрим, как использовать numpy/scipy для инвертирования матрицы в конце этого поста.То, как меня учили обращенным матрицам, в темные века, то есть , было чистой пыткой и трудно запоминалось! Если вы сделаете это так, как вы бы запрограммировали, на мой взгляд, это НАМНОГО проще.
 Я бы даже подумал, что легче сделать метод, который мы будем использовать, когда делаем это вручную, чем древнее учение о том, как это сделать. На самом деле, это настолько просто, что мы начнем с матрицы 5×5, чтобы сделать ее «понятнее», когда мы перейдем к кодированию.
Я бы даже подумал, что легче сделать метод, который мы будем использовать, когда делаем это вручную, чем древнее учение о том, как это сделать. На самом деле, это настолько просто, что мы начнем с матрицы 5×5, чтобы сделать ее «понятнее», когда мы перейдем к кодированию.НЕ ПАНИКУЙТЕ. Единственная действительно неприятная вещь в этом методе инвертирования матрицы заключается в том, что, хотя он очень прост, он немного утомителен и скучен. Однако, по сравнению с древним методом, он прост и НАМНОГО легче запомнить. Или, как обычно говорил один из моих любимых наставников: «Это просто, это просто непросто». Мы будем использовать python, чтобы уменьшить скуку, не теряя представления о методе.
Математика
Давайте начнем с базовой линейной алгебры, чтобы понять, почему нам нужна обратная матрица.
Рассмотрим типичную задачу линейной алгебры, например:
AX=B,\hspace{5em}\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32} &a_{33}\end{bmatrix}\begin{bmatrix}x_{11}\\x_{21}\\x_{31}\end{bmatrix}=\begin{bmatrix}b_{11}\\b_{21 }\\b_{31}\end{bmatrix}
Мы хотим найти X, поэтому получаем обратное значение A и делаем следующее: 9{-1} готовым к написанию кода? Давайте начнем с логотипа репозитория github, в котором хранится вся эта работа, потому что он действительно говорит сам за себя:
Мы часто ловко используем « умножить на 1 », чтобы упростить алгебру.
 {-1}. Важно отметить, что матрица A должна быть квадратной, чтобы ее можно было инвертировать. Это означает, что количество строк A и количество столбцов A должны быть равны. 9{-1} легко, предварительно умножьте B на единичную матрицу и выполните операции со строками над A, чтобы преобразовать его в единичную матрицу. Вы хотите сделать это по одному элементу за раз для каждого столбца слева направо.
{-1}. Важно отметить, что матрица A должна быть квадратной, чтобы ее можно было инвертировать. Это означает, что количество строк A и количество столбцов A должны быть равны. 9{-1} легко, предварительно умножьте B на единичную матрицу и выполните операции со строками над A, чтобы преобразовать его в единичную матрицу. Вы хотите сделать это по одному элементу за раз для каждого столбца слева направо.AX=IB,\hspace{5em}\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32} &a_{33}\end{bmatrix}\begin{bmatrix}x_{11}\\x_{21}\\x_{31}\end{bmatrix}= \begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end {bmatrix} \begin{bmatrix}b_{11}\\b_{21}\\b_{31}\end{bmatrix} 9{-1}B,\hspace{5em} \begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix} \begin{bmatrix}x_{11}\\x_{21}\\x_{31}\ end{bmatrix} =\begin{bmatrix}ai_{11}&ai_{12}&ai_{13}\\ai_{21}&ai_{22}&ai_{23}\\ai_{31}&ai_{32}&ai_{33} \end{bmatrix}\begin{bmatrix}b_{11}\\b_{21}\\b_{31}\end{bmatrix}
Вот шаги, S, которые мы должны выполнить, чтобы сделать это для матрицы любого размера.
 Это просто обзор высокого уровня. Вскоре после этого мы сделаем подробный обзор с цифрами. Думайте о методе инверсии как о наборе шагов для каждого столбца слева направо и для каждого элемента в текущем столбце, и в каждом столбце есть один из диагональных элементов, которые представлены как диагональные элементы S_{k1}, где к=1\, к\, п. Мы начнем с самого левого столбца и будем работать справа. Обратите внимание, что каждая буква S представляет собой элемент, который мы используем для масштабирования. Когда мы находимся на определенном шаге, S_{ij}, где i \ и \, j = 1 \, до \, n независимо от того, где мы находимся в матрице, мы выполняем этот шаг для всей строки и используя строку с диагональю S_{k1} как часть этой операции.
Это просто обзор высокого уровня. Вскоре после этого мы сделаем подробный обзор с цифрами. Думайте о методе инверсии как о наборе шагов для каждого столбца слева направо и для каждого элемента в текущем столбце, и в каждом столбце есть один из диагональных элементов, которые представлены как диагональные элементы S_{k1}, где к=1\, к\, п. Мы начнем с самого левого столбца и будем работать справа. Обратите внимание, что каждая буква S представляет собой элемент, который мы используем для масштабирования. Когда мы находимся на определенном шаге, S_{ij}, где i \ и \, j = 1 \, до \, n независимо от того, где мы находимся в матрице, мы выполняем этот шаг для всей строки и используя строку с диагональю S_{k1} как часть этой операции.S = \begin{bmatrix}S_{11}&\dots&\dots&S_{k2} &\dots&\dots&S_{n2}\\S_{12}&\dots&\dots&S_{k3} &\dots&\dots &S_{n3} \\\vdots& & &\vdots & & &\vdots\\ S_{1k}&\dots&\dots&S_{k1} &\dots&\dots &S_{nk}\\ \vdots& & &\vdots & & &\vdots\ \S_{1 n-1}&\dots&\dots&S_{k n-1} &\dots&\dots &S_{n n-1}\\ S_{1n}&\dots&\dots&S_{kn} &\dots&\dots &S_{n1}\\\конец{bmatrix}
Если к этому моменту вы видите достаточно сил, дерзайте! Затем вернитесь и сравните с тем, что мы сделали здесь.

Обобщенный порядок шагов
Мы будем называть текущий диагональный элемент фокусным диагональным элементом, или для краткости fd . Первым шагом (S_{k1}) для каждого столбца является умножение строки, содержащей fd , на 1/fd . Затем мы работаем с оставшимися строками (от S_{k2} до S_{kn}), без fd в них следующим образом:
- используйте элемент, который находится в том же столбце, что и fd , и сделайте его множителем;
- замените строку результатом … [текущая строка] – множитель * [строка, имеющая fd ], и проделайте эту операцию также с матрицей I .
- это оставит ноль в столбце, разделяемом fd в матрице A.
Мы делаем это для всех столбцов слева направо в обеих матрицах A и I. Когда это завершено, A является единичной матрицей, а I становится обратной A.
Давайте подробно рассмотрим эти шаги на матрице 3 x 3 с реальными числами.
 Начнем с матриц A и I, показанных ниже. Затем с помощью кода мы делаем копии матриц, чтобы сохранить исходные матрицы A и I, называя копии A_M и I_M.
Начнем с матриц A и I, показанных ниже. Затем с помощью кода мы делаем копии матриц, чтобы сохранить исходные матрицы A и I, называя копии A_M и I_M.Наши исходные матрицы:
A=\begin{bmatrix}5&3&1\\3&9&4\\1&3&5\end{bmatrix}\hspace{5em} I=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{ bmatrix}
A_M и I_M , изначально такие же, как A и I соответственно:
A_M=\begin{bmatrix}5&3&1\\3&9&4\\1&3&5\end{bmatrix}\hspace{4em} I_M=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}
1. Использование шаги и методы, которые мы только что описали, масштабируют строку 1 обеих матриц на 1/5,0
A_M=\begin{bmatrix}1&0.6&0.2\\3&9&4\\1&3&5\end{bmatrix}\hspace{5em} I_M=\begin{bmatrix}0.2&0&0\\0&1&0\\0&0&1\end{bmatrix}
2. Вычтите 3,0 * 1-й ряд A_M из 2-го ряда A_M и
Вычтите 3,0 * строка 1 I_M из строки 2 I_MA_M=\begin{bmatrix}1&0,6&0,2\\0&7,2&3,4\\1&3&5\end{bmatrix}\hspace{5em} I_M=\begin{bmatrix}0,2&0&0\\-0,6&1&0\\0&0&1\ конец {bmatrix}
3.
 Вычтите 1,0 * 1-я строка A_M из 3-й строки A_M и
Вычтите 1,0 * 1-я строка A_M из 3-й строки A_M и
Вычтите 1,0 * 1-я строка I_M из 3-й строки I_MA_M=\begin{bmatrix}1&0,6&0,2\\0&7,2&3,4\\0&2,4&4,8\end{bmatrix}\hspace{5em} I_M=\begin{bmatrix}0,2&0&0\\-0,6&1&0 \\-0.2&0&1\end{bmatrix}
4. Масштабировать строку 2 обеих матриц на 1/7,2
A_M=\begin{bmatrix}1&0,6&0,2\\0&1&0,472\\0&2,4&4,8\end{bmatrix}\hspace{5em} I_M=\begin{bmatrix}0,2&0&0\\-0,083&0,139&0 \\-0.2&0&1\end{bmatrix}
5. Вычесть 0,6 * 2-й ряд A_M из 1-го ряда A_M
Вычесть 0,6 * 2-й ряд I_M из 1-го ряда I_MA_M=\begin{bmatrix}1&0&-0,083\\0&1&0,472\\0&2,4&4,8\end{bmatrix}\hspace{5em} I_M=\begin{bmatrix}0,25&-0,083&0\\-0,083&0. 139&0\\-0.2&0&1\end{bmatrix}
6. Вычесть 2,4 * 2-я строка A_M из 3-й строки A_M
Вычесть 2,4 * 2-я строка I_M из 3-й строки I_MA_M=\begin{bmatrix}1&0&-0,083\\0&1&0,472\\0&0&3,667\end{bmatrix}\hspace{5em} I_M=\begin{bmatrix}0,25&-0,083&0\\-0,083&0,139&0\ \0&-0,333&1\end{bmatrix}
7.
 Масштабируйте строку 3 обеих матриц на 1/3,667
Масштабируйте строку 3 обеих матриц на 1/3,667A_M=\begin{bmatrix}1&0&-0,083\\0&1&0,472\\0&0&1\end{bmatrix}\hspace{5em} I_M=\begin{bmatrix}0,25&-0,083&0\\-0,083&0,139&0\\0&-0,091&0,273\end{bmatrix}
8. Вычесть -0,083 * 3-я строка A_M из 1-й строки A_M
Вычесть -0,083 * 3-я строка I_M из 1-й строки I_MA_M=\begin{bmatrix}1&0&0\\0&1&0,472\\0&0&1\end{bmatrix}\hspace{5em} I_M=\begin{bmatrix}0,25&-0,091&0,023\\-0,083&0,139&0\\0& -0,091&0,273\end{bmatrix}
9. Вычтите 0,472 * 3-я строка A_M из 2-й строки A_M
Вычтите 0,472 * 3-я строка I_M из 2-й строки I_MA_M=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\hspace{5em} I_M=\begin{bmatrix}0,25&-0,091&0,023\\-0,083&0,182&-0,129\\0& -0,091&0,273\end{bmatrix}
Вроде все хорошо, но давайте проверим A \cdot IM = I.
A \cdot IM=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}
Да! Исходная матрица A, умноженная на нашу матрицу I_M, является единичной матрицей, и это подтверждает, что наша матрица I_M является обратной матрицей A.

Код
Я хочу призвать вас в последний раз попытаться закодировать это самостоятельно. Пожалуйста, не чувствуйте себя виноватым, если вы хотите немедленно взглянуть на мою версию, но с небольшими пошаговыми усилиями и с тем, что вы узнали выше, вы можете это сделать. Если вы застряли, взгляните, но это будет очень полезно для вас, если вы поймете, как это написать самостоятельно.
Когда вы будете готовы посмотреть на мой код, перейдите в блокнот Jupyter под названием MatrixInversion.ipynb , который можно получить из репозитория github для этого проекта. Вам не нужно использовать Jupyter, чтобы следовать дальше. Я также сохранил ячейки как MatrixInversion.py в том же репозитории. Давайте сначала определим некоторые вспомогательные функции, которые помогут в нашей работе.
В репозитории также есть несколько интересных блокнотов Jupyter и файлы .py. Я призываю вас проверить их и поэкспериментировать с ними. Один из них может генерировать макеты формул в форматах LibreOffice Math.
 Если вы не используете блокноты Jupyter, для каждого блокнота есть дополнительные файлы .py.
Если вы не используете блокноты Jupyter, для каждого блокнота есть дополнительные файлы .py.Давайте сначала представим некоторые вспомогательные функции для использования в нашей работе с блокнотом. ПОЖАЛУЙСТА, ОБРАТИТЕ ВНИМАНИЕ: Загрузка приведенных ниже описаний может занять некоторое время.
Посмотреть код на Gist.
ПРИМЕЧАНИЕ: Последний оператор печати в print_matrix использует трюк добавления +0 к округлению (x,3), чтобы избавиться от -0,0. Попробуйте с «+0» и без него, чтобы понять, что я имею в виду.
Давайте подготовим несколько матриц для использования.
Посмотреть код на Gist.
Как было сказано ранее, мы делаем копии исходных матриц:
Посмотреть код на Gist.
Давайте выполним только первый шаг, описанный выше, где мы масштабируем первую строку каждой матрицы на первый диагональный элемент в матрице A_M.
Посмотреть код на Gist.

Теперь мы можем использовать эту первую строку, в первой диагональной позиции которой теперь стоит 1, чтобы привести остальные элементы в первом столбце к 0.
Посмотрите код на Gist.
Давайте просто выполним эти шаги для оставшихся столбцов:
Посмотреть код на Gist.
На этом все шаги для нашего 5×5 завершены. Теперь I_M должно быть обратным A. Давайте проверим, что A \cdot I_M = I .
Посмотреть код на Gist.
Успех! A_M превратился в матрицу идентичности, а I_M стал обратным A. Да! Когда мы умножаем исходную матрицу A на нашу обратную матрицу, мы получаем единичную матрицу.
Мне нравятся блокноты Jupyter, но теперь я хочу использовать их и в сценариях. См. код ниже. Это последняя функция в LinearAlgebraPurePython.py в репозитории. Он импортируется и реализуется LinearAlgebraPractice.py . Обратите внимание, что внутри этой функции invert_matrix вызываются другие функции из LinearAlgebraPurePython.
 py . Обратите внимание, что вся реальная работа по обращению происходит в разделе 3, который удивительно короток. Остальные секции выполняют подготовку и проверки.
py . Обратите внимание, что вся реальная работа по обращению происходит в разделе 3, который удивительно короток. Остальные секции выполняют подготовку и проверки.def invert_matrix(A, tol=Нет): """ Возвращает инверсию переданной матрицы. :param A: инвертируемая матрица :return: обратная матрица A """ # Раздел 1: Убедитесь, что A можно инвертировать. check_squareness(A) check_non_singular(A) # Раздел 2: Сделайте копии A & I, AM & IM, чтобы использовать их для строковых операций п = лен (А) AM = копирующая_матрица (A) I = идентификационная_матрица (n) IM = копирующая_матрица (I) # Раздел 3: Выполнение операций со строками index = list(range(n)) # чтобы разрешить гибкие ссылки на строки *** для fd в диапазоне (n): # fd обозначает диагональ фокуса fdScaler = 1,0 / AM[fd][fd] # ПЕРВОЕ: масштабировать строку fd с помощью обратного fd. for j in range(n): # Используйте j для обозначения зацикливания столбцов. AM[fd][j] *= fdScaler
IM[fd][j] *= fdScaler
# ВТОРОЙ: работа со всеми строками, кроме строки fd, следующим образом:
для i в index[0:fd] + index[fd+1:]:
# *** пропустить строку с fd в ней.
crScaler = AM[i][fd] # cr означает "текущая строка".
для j в диапазоне (n):
# cr - crScaler * fdRow, но по одному элементу за раз.
AM[i][j] = AM[i][j] - crScaler * AM[fd][j]
IM[i][j] = IM[i][j] - crScaler * IM[fd][j]
# Раздел 4: Убедитесь, что IM является инверсией A с указанным допуском
если check_matrix_equality(I,matrix_multiply(A,IM),tol):
вернуть мгновенное сообщение
еще:
поднять ArithmeticError("Матрица, обратная за пределами допуска.")
AM[fd][j] *= fdScaler
IM[fd][j] *= fdScaler
# ВТОРОЙ: работа со всеми строками, кроме строки fd, следующим образом:
для i в index[0:fd] + index[fd+1:]:
# *** пропустить строку с fd в ней.
crScaler = AM[i][fd] # cr означает "текущая строка".
для j в диапазоне (n):
# cr - crScaler * fdRow, но по одному элементу за раз.
AM[i][j] = AM[i][j] - crScaler * AM[fd][j]
IM[i][j] = IM[i][j] - crScaler * IM[fd][j]
# Раздел 4: Убедитесь, что IM является инверсией A с указанным допуском
если check_matrix_equality(I,matrix_multiply(A,IM),tol):
вернуть мгновенное сообщение
еще:
поднять ArithmeticError("Матрица, обратная за пределами допуска.")
Я надеюсь, что вы в полной мере воспользуетесь кодом из репозитория и проведете рефакторинг кода, чтобы написать его в своем собственном стиле, И я особенно надеюсь, что это было полезно и познавательно.

Интересно отметить, что с помощью этих методов определение функции можно выполнить всего за 10–12 строк кода Python. Этот тип усилий показан в файле ShortImplementation.py. Я не рекомендую использовать это. Самый короткий код редко бывает лучшим. Но примечательно, что python может выполнить такую задачу, написав всего несколько строк кода.
В будущих сообщениях мы начнем отсюда, чтобы увидеть из первых рук, как это можно применить к базовому машинному обучению и как это применимо к другим методам, помимо базовой линейной линейной регрессии наименьших квадратов. Тем не менее, мы можем использовать тесно связанный пост о «решении системы уравнений», где мы обходим поиск обратной задачи A и используем те же основные методы, чтобы перейти прямо к решению для X.
Это отличное право прохода, чтобы иметь возможность закодировать свою собственную процедуру обращения матрицы, но давайте убедимся, что мы также знаем, как это сделать, используя numpy / scipy из документации ЗДЕСЬ .
 Посмотрите, сможете ли вы закодировать это, используя нашу матрицу (или матрицы), и сравните свой ответ с нашим ответом на грубую силу. Мой подход с использованием numpy/scipy приведен ниже.
Посмотрите, сможете ли вы закодировать это, используя нашу матрицу (или матрицы), и сравните свой ответ с нашим ответом на грубую силу. Мой подход с использованием numpy/scipy приведен ниже.После того, как вы прочитали краткую документацию и попробовали сами, сравните с тем, что я сделал ниже:
импортировать numpy как np из numpy.linalg импортировать запрос a = np.array([[5., 3., 1.], [3., 9., 4.], [1., 3., 5.]]) напечатать (а, '\n') аинв = инв(а) ainv = ainv.раунд (3) распечатать (аинв)
Обратите внимание на метод округления, примененный к матричному классу. Python безумно точен, и округление позволяет нам сравнивать с нашим ответом на человеческом уровне. Ниже приведен вывод вышеуказанного скрипта.
[[5. 3. 1.] [3. 9. 4.] [1. 3. 5.]] [[ 0,25 -0,091 0,023] [-0,083 0,182 -0,129] [ 0. -0.091 0.273]]
Первая матрица в приведенном выше выводе является нашей входной матрицей A. Вторая матрица, конечно же, является нашей обратной матрицей A.

Заключительные замечания
Если вы сделали большую часть этого самостоятельно и по сравнению с тем, что сделал я, поздравляю! Я знаю, что ты чувствуешь, и это здорово! Если вы этого не сделали, не расстраивайтесь. Таких упражнений будет еще много. Я призываю вас сделать основные математические выводы вашими главными выводами. Главное, что нужно научиться осваивать, это то, что как только вы поймете математические принципы как серию небольших повторяющихся шагов, вы сможете кодировать их с нуля и ПО-НАСТОЯЩЕМУ глубоко понять эти математические принципы. Выполнение такой работы также быстро улучшит ваши навыки работы с Python. Если вы нашли этот пост ценным, я уверен, что вы оцените следующие.
Понимание псевдоинверсии Мура Пенроуза с помощью Python | Программа инженерного образования (EngEd)
Псевдоинверсия Мура-Пенроуза — это метод линейной алгебры, используемый для аппроксимации обратной необратимой матрицы. Этот метод может аппроксимировать обратную любую матрицу, независимо от того, является ли матрица квадратной или нет.
 {-1}b$
{-1}b$Предпосылки:
- Разложение по сингулярным числам
- Возможность работы с матрицами либо в блокноте Jupyter, либо в Google Colab.
- Знание систем линейных уравнений.
Введение в псевдоинверсию
В большинстве случаев матрица коэффициентов линейных систем уравнений не всегда квадратная, и определить ее обратную невозможно. Это означает, что мы не можем напрямую найти решение линейной системы, если это так. Эти ситуации могут возникнуть двумя возможными способами. Один из них, когда линейная система равна занижено (короткожирная матрица).
Система называется недоопределенной, если количество переменных в системе превышает количество уравнений. В этом случае система может иметь бесконечное число решений. Следующий случай — это система Overdetermined (высокая тощая матрица).
Система называется переопределенной , если количество уравнений в ней значительно превышает количество переменных.
 В этом случае система может иметь много решений или не иметь решений. Теперь, чтобы аппроксимировать наилучшее решение для таких систем без уникальных решений, мы используем разложение по сингулярным значениям (SVD). 9\dagger A$
В этом случае система может иметь много решений или не иметь решений. Теперь, чтобы аппроксимировать наилучшее решение для таких систем без уникальных решений, мы используем разложение по сингулярным значениям (SVD). 9\dagger A$Мы не будем доказывать эти условия, но вы можете найти доказательства здесь.
Теперь давайте рассмотрим пример, чтобы понять, как эта техника работает интуитивно.
Предположим, нам дана следующая матрица:
$A=\begin{bmatrix} 1&1&1&-1\ 0&1&1&0\ -1&1&1&1 \end{bmatrix}$
Требуется найти ее псевдообратную.
Эта матрица не является квадратной, поэтому мы не можем вычислить ее обратную. Вместо этого мы можем аппроксимировать его, используя псевдоинверсию. Для этого мы сначала вычисляем его разложение по сингулярным значениям.
Разложение по единственному значению этой матрицы должно возвращать выходные данные, аналогичные приведенным ниже.
$U=\begin{bmatrix} \frac{1}{\sqrt 3} & \frac{1}{\sqrt 2} & \frac{1}{\sqrt 6}\ \frac{1}{\sqrt 3} & 0 &\frac{-2}{\sqrt 6}\ \frac{1}{\sqrt 3} & \frac{-1}{\sqrt 2} & \frac{1}{\sqrt 6} \end{bmatrix}$
$\sum = \begin{bmatrix} \sqrt6 & 0& 0&0\ 0&2&0&0\ 0&0&0&0 \end{bmatrix}$
$V=\begin{bmatrix} 0&1&0&1\ 1&0&1&0\ 1&0&-1&0\ 0&-1&0&1 \end{bmatrix}$ 9Т =\frac{1}{\sqrt 2}\begin{bmatrix} 0&1&0&1\\ 1&0&1&0\\ 1&0&-1&0\\ 0&-1&0&1 \end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt6} & 0& 0\\ 0&\фракция{1}{2}&0\\ 0&0&0\\ 0&0&0 \end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt 3} & \frac{1}{\sqrt 3} & \frac{1}{\sqrt 3}\\ \frac{1}{\sqrt 2} & 0 &\frac{-1}{\sqrt 2}\\ \frac{1}{\sqrt 6} & \frac{-2}{\sqrt 6} & \frac{1}{\sqrt 6} \end{bmatrix}$
$=\begin{bmatrix} 0&1&0&1\\ 1&0&1&0\\ 1&0&-1&0\\ 0&-1&0&1 \end{bmatrix}\begin{bmatrix} \frac{1}{6} & \frac{1}{6}& \frac{1}{6}\\ \frac{1}{4}&0&\frac{-1}{4}\\ 0&0&0\\ 0&0&0 \end{bmatrix}=\frac{1}{12}\begin{bmatrix} 3&0&-3\\ 2&2&2\\ 2&2&2\\ -3&0&3 \end{bmatrix}$Это решение является псевдообратным к $A$.

Рассмотрим еще один пример.
Пусть у нас есть $m\times n$ матрица $A$, где, $m\neq n$, найдем ее псевдообратную.
$A=\begin{bmatrix} -1&2\ 3&-2\ 5 и 7 \end{bmatrix}$
На этот раз мы используем и в то же время учимся вычислять псевдообратную матрицу Мура-Пенроуза с помощью программного обеспечения. В нашем случае мы будем выполнять наши вычисления в Python.
Python-реализация Moore Penrose Pseudoinverse
Здесь нам нужен только
numpy, так как она содержит пакет, посвященный линейной алгебре. Итак, давайте импортируем эту библиотеку.импортировать numpy как np
Следующим шагом будет создание нашей матрицы $A$. Делаем это, как показано ниже.
A = np.массив([[-1,2],[3,-2],[5,7]]) печать(А)
Вывод:
[[-1 2] [ 3 -2] [ 5 7]]
Мы получили матрицу 3 х 2, как и ожидалось, но поскольку эта матрица не квадратная, мы не можем найти ее обратную.

Однако у него есть псевдообратное. Чтобы определить его псевдообратное, давайте сначала получим его разложение по сингулярным значениям.
U,d,VT = np.linalg.svd(A)
Теперь мы можем вывести эти три матрицы в явном виде следующим образом.
печать(U)
Вывод: массив
([[ 0,12708324, 0,47409506, 0,87125411], [0,00164602, -0,87847553, 0,47778451], [0,99189069, -0,0592843, -0,11241989]])печать(г)
Вывод: массив
([8.66918448, 4.10429538])
печать (VT)
Вывод: массив
([[ 0.55798885, 0.82984845], [-0,829\dagger$ сначала создадим диагональную матрицу D, используя сингулярные значения вектора d, полученные выше.D = np.diag(d) печать (Д)
Этот код создает искомую диагональную матрицу.
 {\dagger}$ совпадает с количеством строк U. 9†$ следующим образом.
{\dagger}$ совпадает с количеством строк U. 9†$ следующим образом.Aplus = np.dot (VT.T, np.dot (Dplus, UT)) печать (Аплюс)
Вывод: массив
([[-0,08767773, 0,17772512, 0,07582938], [0,07661927, -0,1192733, 0,08688784]])Выше находится Псевдоинверсия нашей матрицы. Мы можем проверить, что он дает, умножив его на исходную матрицу.
Предоставляет ли он единичную матрицу, как мы ожидаем, когда мы умножаем матрицу на обратную или нет? Давайте посмотрим это на практике.
нп.точка (Аплюс, А)
Вывод: массив
([[ 1.00000000e+00, -2.544e-16], [-2.77555756e-17, 1.00000000e+00]])Действительно, результат недалеко от единичной матрицы. Обратите внимание, что на ведущей диагонали есть единицы, а все остальные элементы вне диагонали настолько незначительны, что их можно считать равными нулю.
Итак, мы можем заключить, что псевдообратная матрица очень точно аппроксимирует обратную матрицу.
 К сожалению, выполнение всех этих шагов по одному, как мы заметили, занимает много времени.
К сожалению, выполнение всех этих шагов по одному, как мы заметили, занимает много времени.Если вас интересует только получение окончательного ответа, в
Numpyсуществует метод в рамках модели линейной алгебры, который автоматически вычисляет псевдоинверсию. Давайте посмотрим, сможем ли мы использовать этот метод, чтобы получить тот же ответ, что и выше.нп.линалг.пинв(А)
Вывод: массив
([[-0,08767773, 0,17772512, 0,07582938], [0,07661927, -0,1192733, 0,08688784]])Метод
pinv()дал нам тот же ответ, который мы вычислили ранее.Заключение
Эта статья познакомила нас с Псевдообратным Мура Пенроуза. Используя эту концепцию, мы можем аппроксимировать обратную неквадратную матрицу как вручную, так и практически. Важно выполнять такую операцию, особенно с реальными данными.
Это включает в себя поиск решения для переменных, когда данные представляют собой неквадратную матрицу.
 Кроме того, мы объяснили, как псевдоинверсия может упростить работу. Теперь, когда вы знаете, как выполнить псевдоинверсию, вы можете продолжить и бросить себе вызов, решив систему линейных уравнений, применяя знания, полученные в этом материале. Это укрепит ваше понимание.
Кроме того, мы объяснили, как псевдоинверсия может упростить работу. Теперь, когда вы знаете, как выполнить псевдоинверсию, вы можете продолжить и бросить себе вызов, решив систему линейных уравнений, применяя знания, полученные в этом материале. Это укрепит ваше понимание.Дальнейшее чтение
- Подробнее о псевдоинверсии
Экспертная оценка Вклад: Мерси Мив
Разложение по сингулярным числам (SVD) и псевдоинверсия
В двух словах, учитывая сингулярную декомпозицию матрицы A ,
псевдоинверсия Мура-Пенроуза задается как
3 выше, и как их вычислить в Python и Mathematica.
Разложение по сингулярным числам (SVD)
Разложение по сингулярным значениям матрицы — это своего рода замена координат, делающая матрицу простой, обобщение диагонализации.
Диагонализация матрицы
Если квадратная матрица A диагонализируема, то существует матрица P такая, что
, где матрица D является диагональной.
 Вы могли бы думать о P как об изменении координат, которое делает действие A как можно проще. Элементы на диагонали D являются собственными значениями A , а столбцы P являются соответствующими собственными векторами.
Вы могли бы думать о P как об изменении координат, которое делает действие A как можно проще. Элементы на диагонали D являются собственными значениями A , а столбцы P являются соответствующими собственными векторами.К сожалению, не все матрицы можно диагонализовать. Разложение по сингулярным числам — это способ сделать что-то вроде диагонализации для 90 872 любой матрицы 90 873, даже неквадратной матрицы.
Обобщение до SVD
Разложение по сингулярным числам обобщает диагонализацию. Матрица Σ в SVD аналогична D в диагонализации. Σ является диагональным, хотя может и не быть квадратным. Матрицы по обе стороны от Σ аналогичны матрице P в диагонализации, хотя теперь есть две разные матрицы, и они не обязательно являются обратными друг другу. Матрицы U и V квадратные, но не обязательно одинаковой размерности.
Элементы по диагонали Σ не обязательно являются собственными значениями, но сингулярными значениями , которые являются обобщением собственных значений.
 Точно так же столбцы U и V не обязательно являются собственными векторами, а являются левыми сингулярными векторами и правыми сингулярными векторами соответственно.
Точно так же столбцы U и V не обязательно являются собственными векторами, а являются левыми сингулярными векторами и правыми сингулярными векторами соответственно.Звездочка в верхнем индексе указывает на сопряженное транспонирование . Если матрица имеет все действительные компоненты, то сопряженное транспонирование — это просто транспонирование. Но если в матрице есть сложные записи, вы берете сопряжение и транспонируете каждую запись.
Матрицы U и V являются унитарными . Матрица M является унитарным, если его инверсия является сопряженной транспонированной, то есть M * M = M M * = I .
Псевдообратная и SVD
(Мура-Пенроуза) псевдообратная матрицы обобщает понятие обратной, что-то вроде того, как SVD обобщает диагонализацию.
 Не у каждой матрицы есть обратная, но у каждой матрицы есть псевдообратная, даже у неквадратных матриц.
Не у каждой матрицы есть обратная, но у каждой матрицы есть псевдообратная, даже у неквадратных матриц.Вычислить псевдоинверсию из SVD просто.
Если
, то
, где Σ + образуется из Σ путем взятия обратной величины всех ненулевых элементов, оставления всех нулей и придания матрице правильной формы: если Σ равно матрица м на n , тогда Σ + должна быть матрицей n на м .
Ниже мы приведем примеры в Mathematica и Python.
Вычисление SVD в системе Mathematica
Начнем с матрицы А ниже.
Мы можем найти SVD A с помощью следующих команд Mathematica.
А = {{2, -1, 0}, {4, 3, -2}} {U, S, V} = SingularValueDecomposition[A]Из этого мы узнаем, что сингулярное разложение A равно
Обратите внимание, что последняя матрица не V , а транспонирование V .
 Mathematica возвращает само V , а не его транспонирование.
Mathematica возвращает само V , а не его транспонирование.Если мы перемножим матрицы вместе, мы можем убедиться, что мы получаем A обратно.
У . S. Транспонировать[V]
Это возвращает
{{2, -1, 0}, {4, 3, -2}}, как и следовало ожидать.
Вычисление псевдоинверсии в системе Mathematica
Команда Mathematica для вычисления псевдоинверсии выглядит просто как
PseudoInverse. (Лучшее в системе Mathematica — это последовательные и предсказуемые имена.)PseudoInverse[A]
Это возвращает
{{19/60, 1/12}, {-(11/30), 1/6}, {1/12, -(1/12)}}И мы можем подтвердить, что вычисление псевдоинверсии через SVD
Sp = {{1/Sqrt[30], 0}, {0, 1/2}, {0, 0}} В . Сп . Транспонировать[U]дает тот же результат.
Вычисление SVD в Python
Далее мы вычисляем разложение по сингулярным числам в Python (NumPy).
>>> a = np.
 matrix([[2, -1, 0],[4,3,-2]])
>>> u, s, vt = np.linalg.svd(a, full_matrices=True)
matrix([[2, -1, 0],[4,3,-2]])
>>> u, s, vt = np.linalg.svd(a, full_matrices=True)
Обратите внимание, что
np.linalg.svdвозвращает транспонирование из V , а не V в определении разложения по сингулярным числам.Кроме того, объект
s— это не диагональная матрица Σ, а вектор, содержащий только диагональные элементы, то есть только сингулярные числа. Это может сэкономить много места, если матрица большая. У метода NumPysvdесть другие параметры, связанные с эффективностью, которые я не буду здесь рассматривать.Мы можем проверить правильность СВД, повернув
sобратно в матрицу и перемножить компоненты вместе.>>> сс = np.matrix([[s[0], 0, 0], [0, s[1], 0]]) >>> у*сс*втВозвращает матрицу A с точностью до плавающей запятой. Поскольку Python выполняет вычисления с плавающей запятой, а не символьные вычисления, как Mathematica, ноль в A превращается в
-3.


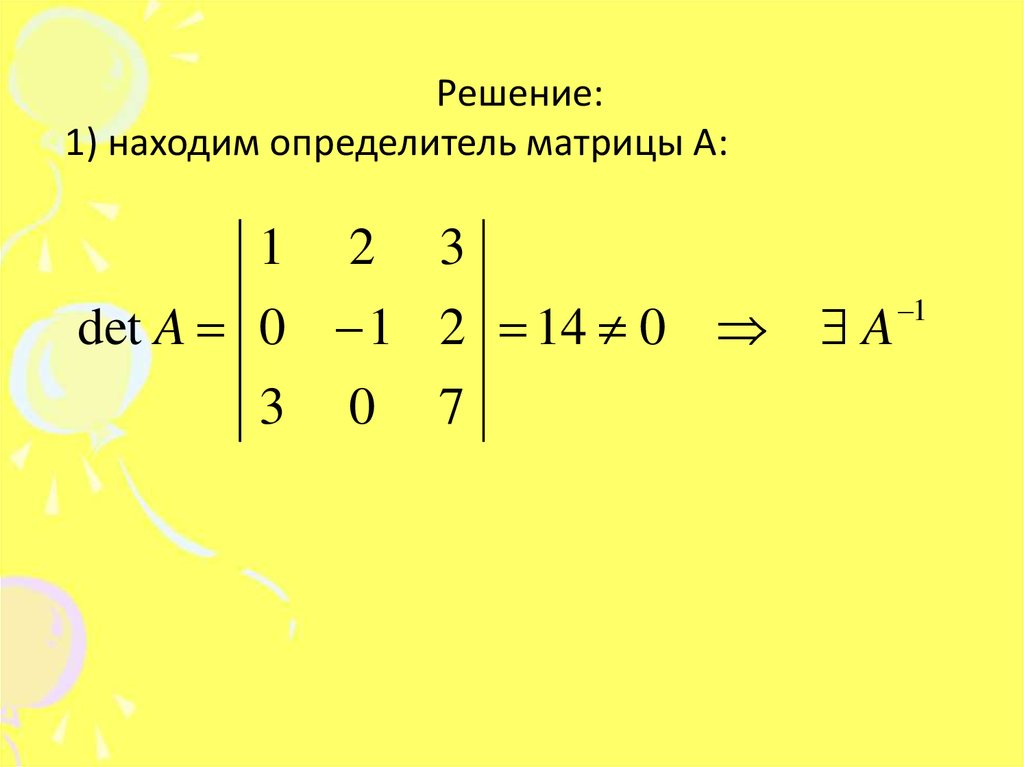 Как видно по скриншоту, после вычислений получилось число 338, а, следовательно, потому как определитель не равен 0, то обратная матрица существует.
Как видно по скриншоту, после вычислений получилось число 338, а, следовательно, потому как определитель не равен 0, то обратная матрица существует.


 Чтобы возвести квадратную матрицу в куб, нужно вычислить произведение:
Чтобы возвести квадратную матрицу в куб, нужно вычислить произведение: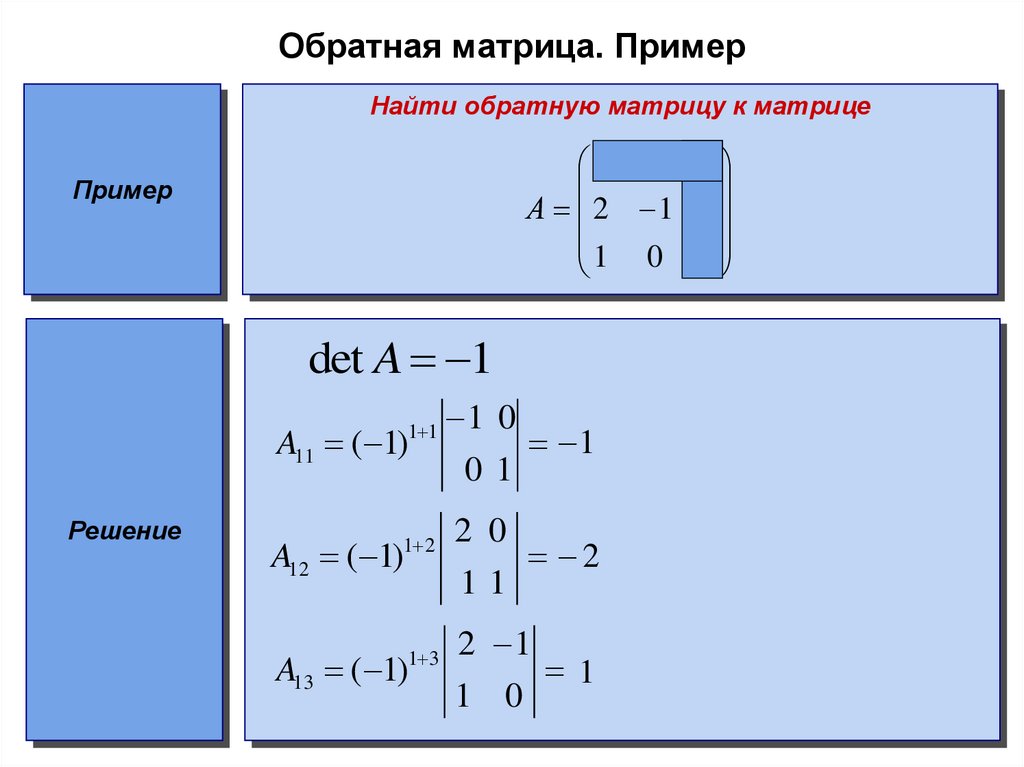
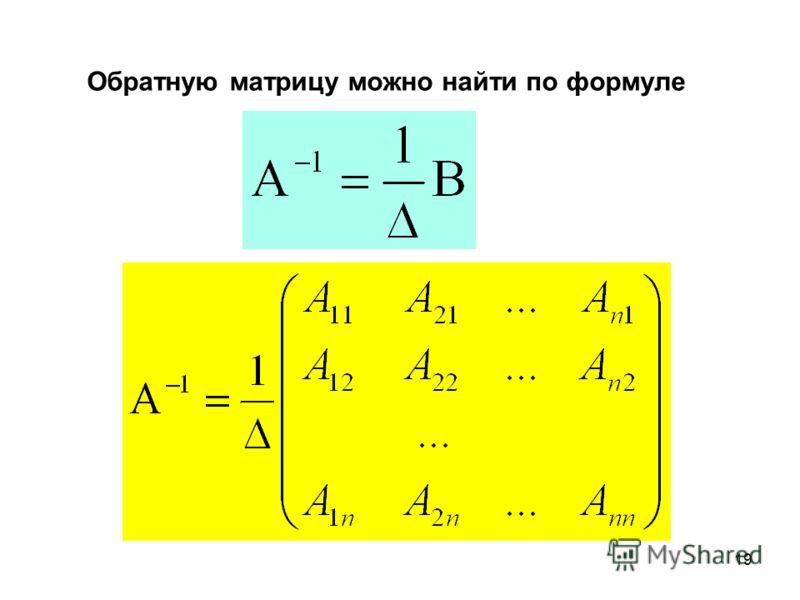
 Произведение данных чисел равно единице: . С матрицами всё похоже! Произведение матрицы на обратную ей матрицу равно – единичной матрице, которая является матричным аналогом числовой единицы. Что необходимо знать и уметь для нахождения обратной матрицы? Вы должны уметь решать определители. Вы должны понимать, что такое матрица и уметь выполнять некоторые действия с ними.
Произведение данных чисел равно единице: . С матрицами всё похоже! Произведение матрицы на обратную ей матрицу равно – единичной матрице, которая является матричным аналогом числовой единицы. Что необходимо знать и уметь для нахождения обратной матрицы? Вы должны уметь решать определители. Вы должны понимать, что такое матрица и уметь выполнять некоторые действия с ними.
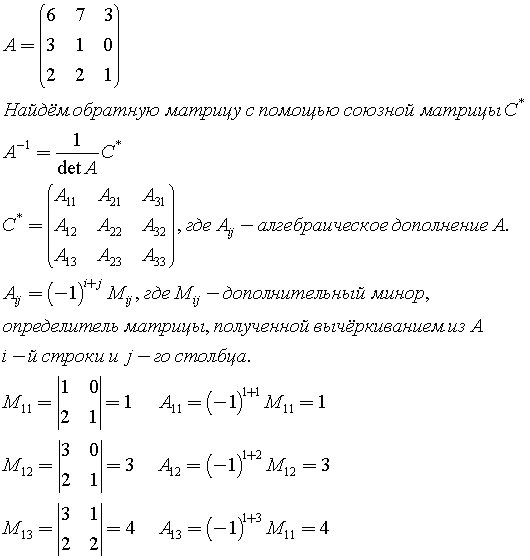 Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: – матрица алгебраических дополнений соответствующих элементов матрицы .
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: – матрица алгебраических дополнений соответствующих элементов матрицы . – обратная матрица существует.
– обратная матрица существует. 2
2 linalg.inv(A))
linalg.inv(A))  linalg.inv(A))
linalg.inv(A))  linalg.inv(A))
linalg.inv(A)) 
 Трудно определить обратную для сингулярной матрицы. Обратная матрица в Excel имеет такое же количество строк и столбцов, что и исходная матрица.
Трудно определить обратную для сингулярной матрицы. Обратная матрица в Excel имеет такое же количество строк и столбцов, что и исходная матрица.
 Подробнее и нахождение целочисленных решений системных уравнений.
Подробнее и нахождение целочисленных решений системных уравнений.
 в лист Excel, как показано на рисунке ниже.
в лист Excel, как показано на рисунке ниже.
 Мы обсудили обратную матрицу в Excel с использованием функции MINVERSE() с примерами и загружаемым шаблоном Excel. Вы можете узнать больше об Excel из следующих статей: –
Мы обсудили обратную матрицу в Excel с использованием функции MINVERSE() с примерами и загружаемым шаблоном Excel. Вы можете узнать больше об Excel из следующих статей: – Почему бы нам просто не использовать numpy или scipy? Отличный вопрос. Этот блог посвящен инструментам, повышающим эффективность И ясность . Я люблю numpy, pandas, sklearn и все замечательные инструменты, которые предлагает нам сообщество специалистов по данным Python, но я понял, что чем лучше я понимаю «принципы» того или иного предмета, тем лучше я знаю, как его применять. Кроме того, завтрашние инструменты машинного обучения будут разрабатываться теми, кто понимает принципы математики и кодирования сегодняшних инструментов.
Почему бы нам просто не использовать numpy или scipy? Отличный вопрос. Этот блог посвящен инструментам, повышающим эффективность И ясность . Я люблю numpy, pandas, sklearn и все замечательные инструменты, которые предлагает нам сообщество специалистов по данным Python, но я понял, что чем лучше я понимаю «принципы» того или иного предмета, тем лучше я знаю, как его применять. Кроме того, завтрашние инструменты машинного обучения будут разрабатываться теми, кто понимает принципы математики и кодирования сегодняшних инструментов.  Я бы не рекомендовал вам использовать такие инструменты самостоятельно , ЕСЛИ вы работаете с более мелкими проблемами, ИЛИ вы исследуете какой-то новый подход, который требует небольших изменений в вашем личном наборе инструментов. Таким образом, приведенное выше утверждение заслуживает повторения: средства машинного обучения завтрашнего дня будут разрабатываться теми, кто понимает принципы математики и кодирования сегодняшних инструментов. Я хочу быть частью или, по крайней мере, поддерживать тех, кто будет создавать инструменты следующего поколения. Кроме того, если вы гик, знание того, как запрограммировать инверсию матрицы, является отличным правом прохода! Мы также рассмотрим, как использовать numpy/scipy для инвертирования матрицы в конце этого поста.
Я бы не рекомендовал вам использовать такие инструменты самостоятельно , ЕСЛИ вы работаете с более мелкими проблемами, ИЛИ вы исследуете какой-то новый подход, который требует небольших изменений в вашем личном наборе инструментов. Таким образом, приведенное выше утверждение заслуживает повторения: средства машинного обучения завтрашнего дня будут разрабатываться теми, кто понимает принципы математики и кодирования сегодняшних инструментов. Я хочу быть частью или, по крайней мере, поддерживать тех, кто будет создавать инструменты следующего поколения. Кроме того, если вы гик, знание того, как запрограммировать инверсию матрицы, является отличным правом прохода! Мы также рассмотрим, как использовать numpy/scipy для инвертирования матрицы в конце этого поста. Я бы даже подумал, что легче сделать метод, который мы будем использовать, когда делаем это вручную, чем древнее учение о том, как это сделать. На самом деле, это настолько просто, что мы начнем с матрицы 5×5, чтобы сделать ее «понятнее», когда мы перейдем к кодированию.
Я бы даже подумал, что легче сделать метод, который мы будем использовать, когда делаем это вручную, чем древнее учение о том, как это сделать. На самом деле, это настолько просто, что мы начнем с матрицы 5×5, чтобы сделать ее «понятнее», когда мы перейдем к кодированию. {-1}. Важно отметить, что матрица A должна быть квадратной, чтобы ее можно было инвертировать. Это означает, что количество строк A и количество столбцов A должны быть равны. 9{-1} легко, предварительно умножьте B на единичную матрицу и выполните операции со строками над A, чтобы преобразовать его в единичную матрицу. Вы хотите сделать это по одному элементу за раз для каждого столбца слева направо.
{-1}. Важно отметить, что матрица A должна быть квадратной, чтобы ее можно было инвертировать. Это означает, что количество строк A и количество столбцов A должны быть равны. 9{-1} легко, предварительно умножьте B на единичную матрицу и выполните операции со строками над A, чтобы преобразовать его в единичную матрицу. Вы хотите сделать это по одному элементу за раз для каждого столбца слева направо. Это просто обзор высокого уровня. Вскоре после этого мы сделаем подробный обзор с цифрами. Думайте о методе инверсии как о наборе шагов для каждого столбца слева направо и для каждого элемента в текущем столбце, и в каждом столбце есть один из диагональных элементов, которые представлены как диагональные элементы S_{k1}, где к=1\, к\, п. Мы начнем с самого левого столбца и будем работать справа. Обратите внимание, что каждая буква S представляет собой элемент, который мы используем для масштабирования. Когда мы находимся на определенном шаге, S_{ij}, где i \ и \, j = 1 \, до \, n независимо от того, где мы находимся в матрице, мы выполняем этот шаг для всей строки и используя строку с диагональю S_{k1} как часть этой операции.
Это просто обзор высокого уровня. Вскоре после этого мы сделаем подробный обзор с цифрами. Думайте о методе инверсии как о наборе шагов для каждого столбца слева направо и для каждого элемента в текущем столбце, и в каждом столбце есть один из диагональных элементов, которые представлены как диагональные элементы S_{k1}, где к=1\, к\, п. Мы начнем с самого левого столбца и будем работать справа. Обратите внимание, что каждая буква S представляет собой элемент, который мы используем для масштабирования. Когда мы находимся на определенном шаге, S_{ij}, где i \ и \, j = 1 \, до \, n независимо от того, где мы находимся в матрице, мы выполняем этот шаг для всей строки и используя строку с диагональю S_{k1} как часть этой операции.
 Начнем с матриц A и I, показанных ниже. Затем с помощью кода мы делаем копии матриц, чтобы сохранить исходные матрицы A и I, называя копии A_M и I_M.
Начнем с матриц A и I, показанных ниже. Затем с помощью кода мы делаем копии матриц, чтобы сохранить исходные матрицы A и I, называя копии A_M и I_M. Вычтите 1,0 * 1-я строка A_M из 3-й строки A_M и
Вычтите 1,0 * 1-я строка A_M из 3-й строки A_M и  Масштабируйте строку 3 обеих матриц на 1/3,667
Масштабируйте строку 3 обеих матриц на 1/3,667
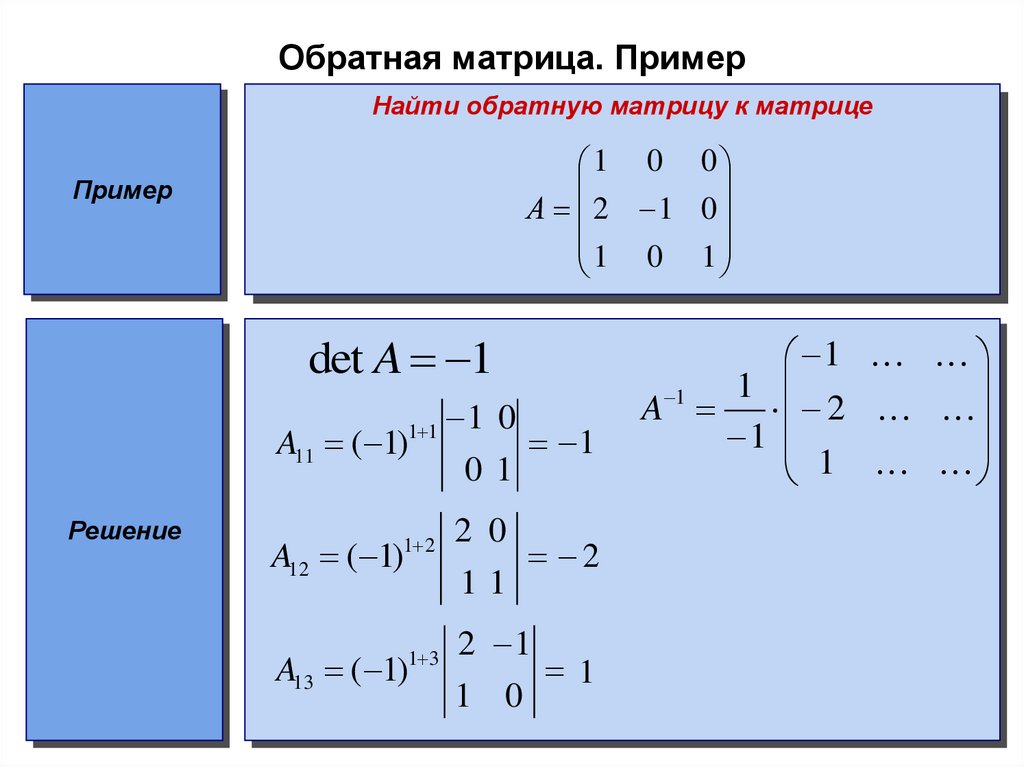 Если вы не используете блокноты Jupyter, для каждого блокнота есть дополнительные файлы .py.
Если вы не используете блокноты Jupyter, для каждого блокнота есть дополнительные файлы .py.
 py . Обратите внимание, что вся реальная работа по обращению происходит в разделе 3, который удивительно короток. Остальные секции выполняют подготовку и проверки.
py . Обратите внимание, что вся реальная работа по обращению происходит в разделе 3, который удивительно короток. Остальные секции выполняют подготовку и проверки. AM[fd][j] *= fdScaler
IM[fd][j] *= fdScaler
# ВТОРОЙ: работа со всеми строками, кроме строки fd, следующим образом:
для i в index[0:fd] + index[fd+1:]:
# *** пропустить строку с fd в ней.
crScaler = AM[i][fd] # cr означает "текущая строка".
для j в диапазоне (n):
# cr - crScaler * fdRow, но по одному элементу за раз.
AM[i][j] = AM[i][j] - crScaler * AM[fd][j]
IM[i][j] = IM[i][j] - crScaler * IM[fd][j]
# Раздел 4: Убедитесь, что IM является инверсией A с указанным допуском
если check_matrix_equality(I,matrix_multiply(A,IM),tol):
вернуть мгновенное сообщение
еще:
поднять ArithmeticError("Матрица, обратная за пределами допуска.")
AM[fd][j] *= fdScaler
IM[fd][j] *= fdScaler
# ВТОРОЙ: работа со всеми строками, кроме строки fd, следующим образом:
для i в index[0:fd] + index[fd+1:]:
# *** пропустить строку с fd в ней.
crScaler = AM[i][fd] # cr означает "текущая строка".
для j в диапазоне (n):
# cr - crScaler * fdRow, но по одному элементу за раз.
AM[i][j] = AM[i][j] - crScaler * AM[fd][j]
IM[i][j] = IM[i][j] - crScaler * IM[fd][j]
# Раздел 4: Убедитесь, что IM является инверсией A с указанным допуском
если check_matrix_equality(I,matrix_multiply(A,IM),tol):
вернуть мгновенное сообщение
еще:
поднять ArithmeticError("Матрица, обратная за пределами допуска.")

 Посмотрите, сможете ли вы закодировать это, используя нашу матрицу (или матрицы), и сравните свой ответ с нашим ответом на грубую силу. Мой подход с использованием numpy/scipy приведен ниже.
Посмотрите, сможете ли вы закодировать это, используя нашу матрицу (или матрицы), и сравните свой ответ с нашим ответом на грубую силу. Мой подход с использованием numpy/scipy приведен ниже.
 {-1}b$
{-1}b$ В этом случае система может иметь много решений или не иметь решений. Теперь, чтобы аппроксимировать наилучшее решение для таких систем без уникальных решений, мы используем разложение по сингулярным значениям (SVD). 9\dagger A$
В этом случае система может иметь много решений или не иметь решений. Теперь, чтобы аппроксимировать наилучшее решение для таких систем без уникальных решений, мы используем разложение по сингулярным значениям (SVD). 9\dagger A$