Построить параметрический график онлайн: Построить график функции, параметрической функции, график в полярной системе координат онлайн

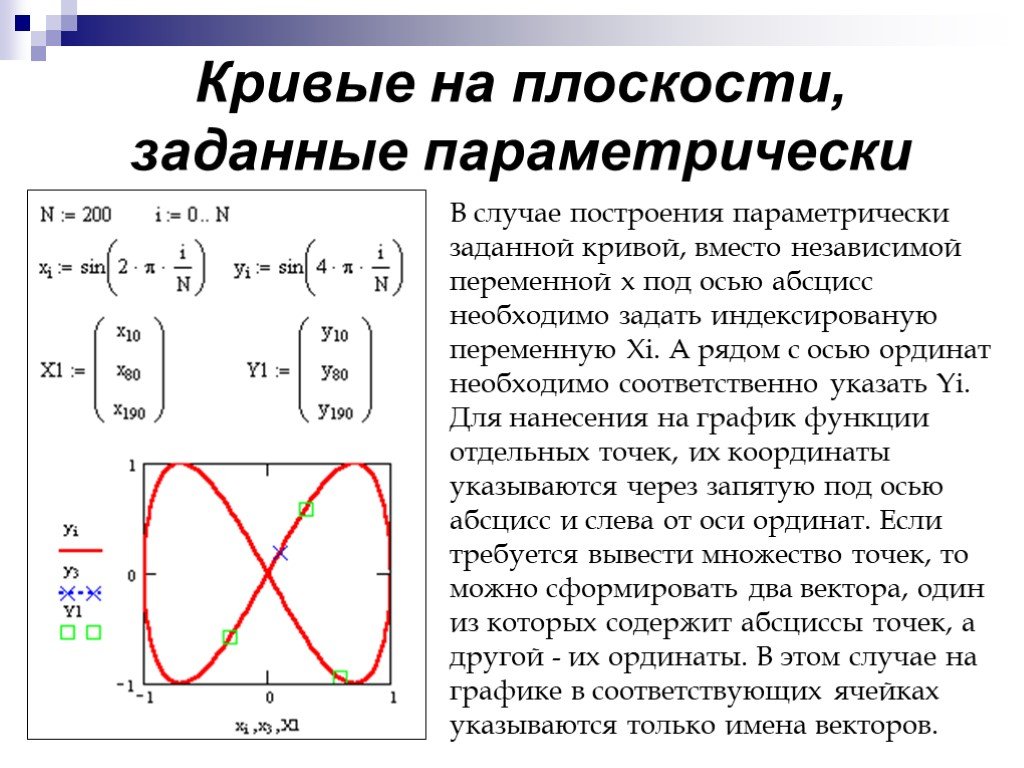
График y 8. Строим график функций онлайн

Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .

Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.

Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .

На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .

Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».

С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).

Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.

График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 у = х 2 — 2х принимает при х = 1 .

Для построения графика функции

f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.

Таблица выглядит следующим образом:

Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).

Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.

Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:

Соответствующие пять точек показаны на рис. 48.

На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.

Для обоснования своего утверждения рассмотрим функцию

.

Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция

y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.

Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика.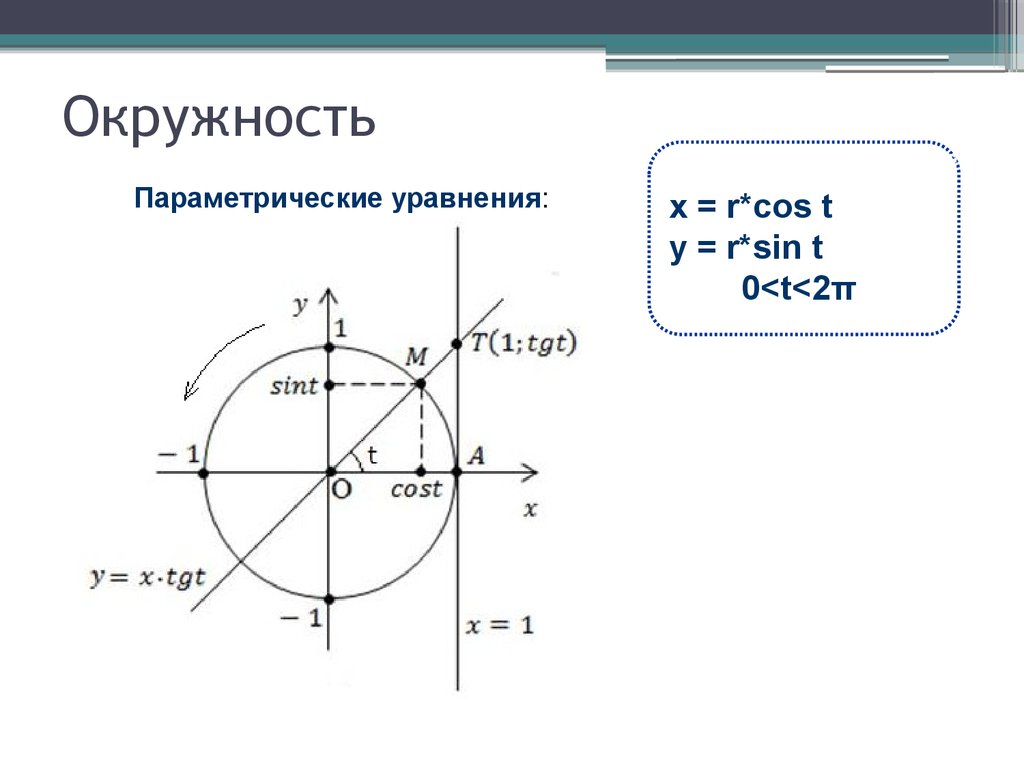 И, наконец, через построенные точки проводят кривую, используя свойства данной функции.

Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.

График функции у = |f(x)|.

Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать

Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).

Пример 2. Построить график функции у = |х|.

Берем график функции

у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).

Пример 3 . Построить график функции y = |x 2 — 2x|.

Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x

График функции y = f(x) + g(x)

Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .

Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).

Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (

х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .

Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)

Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .

При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.

В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая.

Потому компьютер в данном случае – незаменимый помощник.

Что такое график функций

Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.

На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси

X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .

Сервисы для построения графиков функций онлайн

Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.

Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.

Инструкция:

1. Введите ваше уравнение в поле после знака «=».
2. Нажмите кнопку «Построить график» .

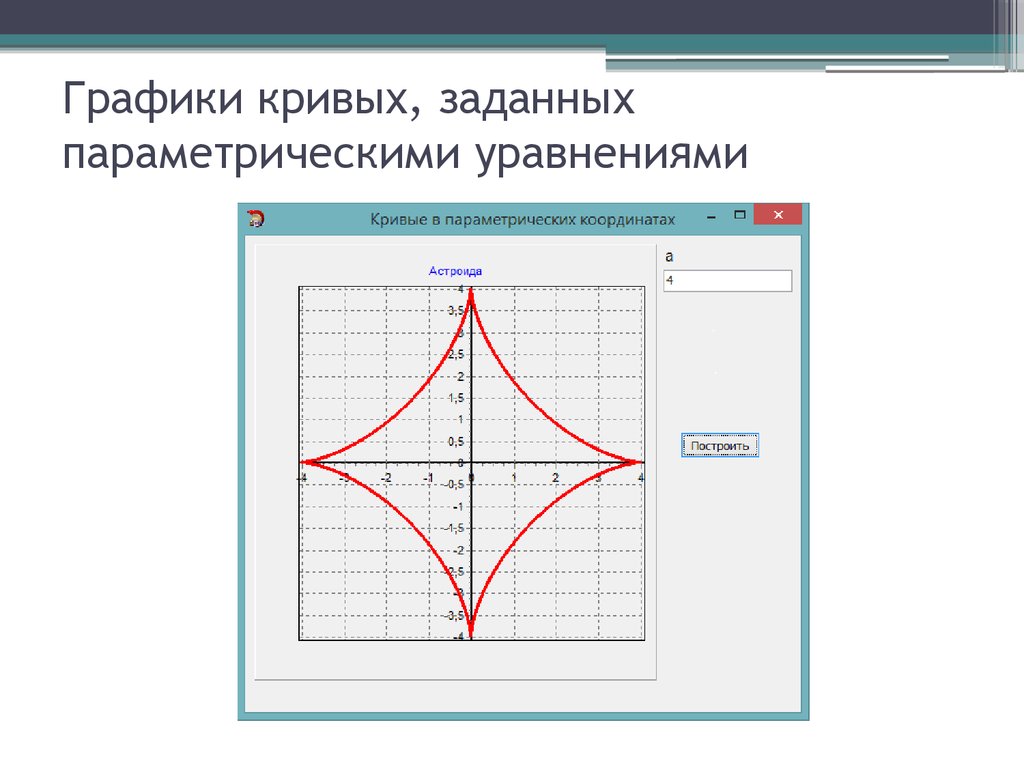
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.

В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.

Инструкция:

1. Выберите необходимый способ задания графика.
2. Введите уравнение.
3. Задайте интервал.
4. Нажмите кнопку «Построить» .

Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.

Инструкция:

1. Найдите в списке необходимую вам функцию.
2. Щелкните на нее левой кнопкой мыши
3. При необходимости введите коэффициенты в поле «Функция:» .
4. Нажмите кнопку «Построить» .

В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.

Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).

Инструкция:

1. В левом столбце кликните правой кнопкой мыши по свободной строке. 2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.

   Квадратичная функция

   Рис 1. Общий вид параболы

   Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.

   Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).

   Основные свойства квадратичной функции

   1. При х =0, у=0, и у>0 при х0

   2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.

   3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }

   Нахождение касательной к параметрической кривой — Криста Кинг Математика

   Формулы, которые мы будем использовать, чтобы найти уравнение касательной линии к параметрической кривой

   Мы будем использовать ту же формулу точки-наклона, чтобы определить уравнение касательной линии к параметрической кривой, которую мы использовали для определения касательной линии к декартовой кривой, которая равна

   ???y-y_1=m(x-x_1)???

   Привет! Я Криста.

   Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать больше.

   где ???м??? это наклон и ???(x_1,y_1)??? точка пересечения касательной с кривой.

   Чтобы найти наклон ???m???, воспользуемся формулой производной параметрической кривой.

   ???m = \ frac {dy} {dx} = \ frac {\ frac {dy} {dt}} {\ frac {dx} {dt}}???

   Как только мы найдем производную параметрической кривой с помощью этой формулы, мы подставим заданную точку в производную, чтобы найти наклон в этой конкретной точке.

   Затем мы подставим наклон и заданную точку в формулу наклона точки для уравнения прямой и упростим ее, чтобы получить уравнение касательной линии.

   Как построить уравнение касательной для параметрической кривой в конкретной точке

   Пройти курс

   Хотите узнать больше об исчислении 2? У меня есть пошаговый курс для этого. 🙂 92???

   ???t=\pm2???

   Как только мы найдем производную параметрической кривой с помощью этой формулы, мы подставим заданную точку в производную, чтобы найти наклон в этой конкретной точке.

   Чтобы значение параметра было действительным, оно должно быть решением обоих уравнений, что означает, что значение интересующего нас параметра равно ???t=\pm2???. Поскольку у нас есть два решения, у нас будет две касательные линии.

   Чтобы определить наклон каждой касательной, подставим ???t=\pm2??? в уравнение производной, которое мы нашли выше. 92}???

   ???f(-2)=\frac{-4}{80-48}???

   ???f(-2)=-\frac18???

   Наконец, соединяя найденные склоны и заданную точку ???(0,4)??? в формулу точки-наклона для уравнения линии мы получаем следующие две касательные линии.

   ???y-y_1=m(x-x_1)???

   ???y-4=\frac18(x-0)???

   ???y=\frac18x+4???

   и

   ???y-y_1=m(x-x_1)???

   ???y-4=-\frac18(x-0)???

   ???y=-\frac18x+4???

   Уравнения также можно преобразовать в следующую форму:

   ???8y=x+32???

   ???-x+8y=32???

   и

   ???8y=-x+32???

   ???x+8y=32???

   Получить доступ к полному курсу Calculus 2

   Изучайте математикуКриста Кинг 8 июля 2021 г. математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление II, исчисление 2, исчисление II, вычисление 2, полярные и параметрические, параметрические кривые, касательная к параметрической кривой, параметрическая касательная , касательная параметрическая кривая, параметрические касательные

   0 лайков

   Справка онлайн — Справка Origin

   Все книгиКниги, не связанные с программированием　Руководство пользователя　Учебники　Быстрая справка　Справка OriginКниги по программированию　X-Function　Origin C　LabTalk Programming　Python　Python (внешний)　Automation Server　LabVIEW VI　Приложения　Разработка приложений　Code Builder　Лицензия Orlab 9　gMOCA0005
   При создании трехмерного графика параметрической функции одновременно создается матрица значений Z. Содержимое 1 сетка 2 Шкала 2.1 Параметр 2.2 Откуда и куда 3 X(u,v), Y(u,v) и Z(u,v) 4 Определение 4.1 Показать сценарий LabTalk 5 График выходной функции Сетка Сетка При построении графика 3D-функции Origin сначала создает матрицу, на основе которой создается график. Укажите размеры матрицы в поле редактирования Columns and Rows. Это определит плотность сетки 3D-поверхности. Весы Параметр Укажите параметр графика. От и до Укажите начало и конец диапазонов u и v. X(u,v), Y(u,v) и Z(u,v) Введите здесь формулу параметров X, Y и Z. Общие математические и статистические функции распределения доступны при нажатии кнопки треугольника справа от текстовых полей X(u,v), Y(u,v) и Z(u,v). Подробную информацию об этих функциях см. в описании встроенных функций LabTalk. Кроме того, вы можете ввести функцию прямо в текстовое поле, используя любые операторы, распознаваемые Origin. Для умножения необходимо включить оператор умножения (*). Вы также можете вызвать любой из источников, даже недоступный из всплывающего меню с треугольной кнопкой или из любых функций, которые вы определили. Вы также можете использовать именованный диапазон в своем выражении. Если нажать кнопку Показать в отдельном окне под треугольной кнопкой, откроется диалоговое окно с более широким полем ввода и панелью предварительного просмотра. На панели предварительного просмотра отображается матрица, рассчитанная по заданной вами формуле. Вы можете проверить результат и при необходимости отредактировать формулу в поле ввода. Определение Определите имена и значения переменных. Эти переменные можно использовать в определении функции. Если переменная еще не определена, но используется в теле функции, она будет выделена красным цветом. Показать сценарий LabTalk Установите этот флажок, чтобы определить переменные с помощью сценариев LabTalk. Если вы уже определили некоторые переменные в таблице Definition , установите этот флажок, чтобы отобразить эквиваленты этих определений в сценариях LabTalk. В дополнение к встроенным функциям или функциям, определяемым пользователем, здесь поддерживаются любые сценарии LabTalk. Вы можете использовать переменные диапазона, строковые переменные, циклы и X-функции, доступные в LabTalk. Сценарии, введенные здесь, будут выполняться перед определением формулы. Существует быстрый способ загрузить условный элемент управления или сценарий цикла, когда вы выполняете сценарий в поле Перед формулой Script . Щелкните правой кнопкой мыши поле Перед формулой Script , чтобы выбрать Conditional/Loop в нижней части контекстного меню, а затем выберите нужную условную структуру или цикл во всплывающем меню. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт