Ответов пока нет
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
Помогите пожалуйста решить задачу 4-го класса. Если около каждого дома посадить по 9 саженцев, то не зватит 100 саженцев, а если по 5 саженцев, то 20 саженцев останется. Сколько домов? Сколько
Решено
На сторонах угла D отмечены точки М и К так, что DМ = DК.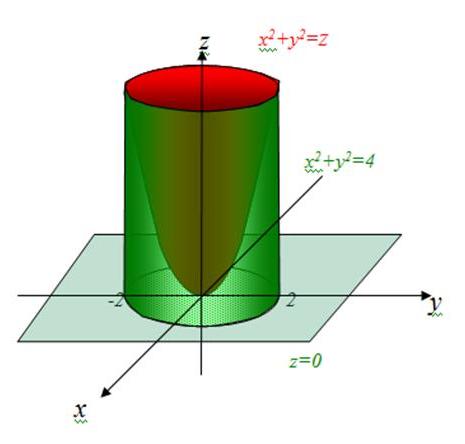 Точка Р лежит внутри угла D, и РК = РМ. Докажите, что луч DР – биссектриса угла МDК.
Точка Р лежит внутри угла D, и РК = РМ. Докажите, что луч DР – биссектриса угла МDК.
Начертите равнобедренный треугольник АВС с основанием АС и острым углом В.С помощью циркуля и линейки проведите высоту из вершины угла А
В треугольнике ABC угол A равен 45 градусов, угол B равен 60 градусов, BC= 6√6. Найдите AC.
Вычислить площадь и высоту параллелограмма, построенного на векторах а=2j+k и b=j+2k
Пользуйтесь нашим приложением
Ответов пока нет | |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||





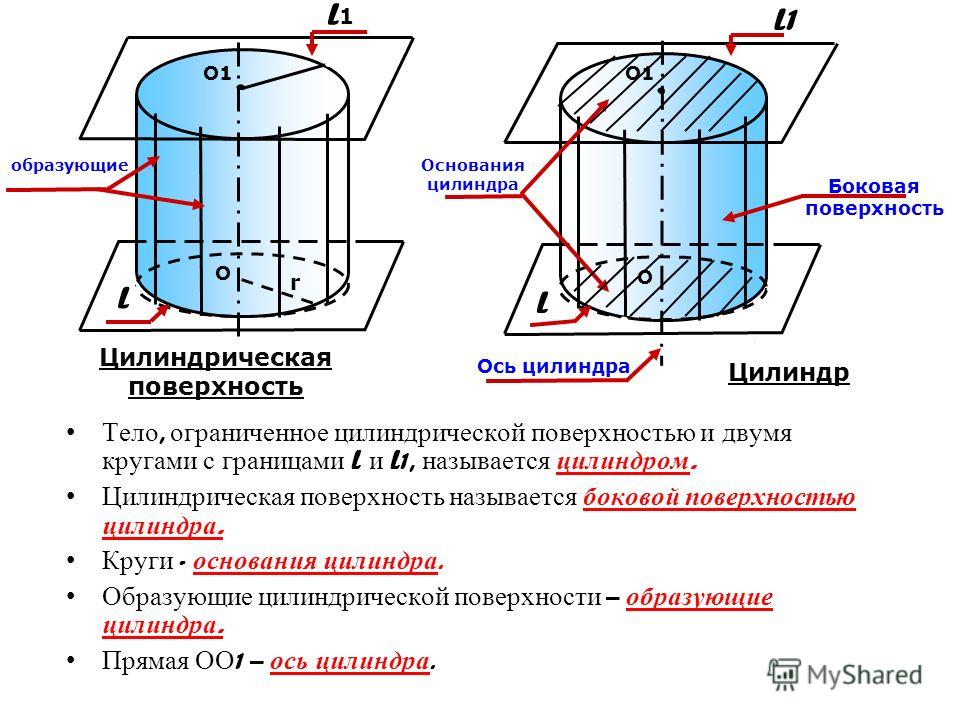
 2. Найдите площадь полной поверхности цилиндра.
2. Найдите площадь полной поверхности цилиндра.