В одной системе координат построить графики функций. Упр. 698, Алгебра, 8 класс, Алимов Ш.А. – Рамблер/класс
В одной системе координат построить графики функций. Упр. 698, Алгебра, 8 класс, Алимов Ш.А. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Привет, очень нужна помощь знатоков!
В одной системе координат построить графики функций и выяснить, при каких х значения одной функции больше (меньше) значений другой, результат проверить, решив соответствующее неравенство:
2) у = х2 — 2, у= 1 — 2х;
3) у = х2 — 5х + 4, у= 7 — 3x;
4) у = 3х2 — 2х + 5, у = 5х + 3;
5) у=х2 — 2х, у = -х2 + х + 5;
6) у = 2х2 — 2x + 5, у = х2 + 4х — 5.

Лучший ответ
Есть помощь, я пришел!
еще ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
ЕГЭ
10 класс
9 класс
похожие вопросы 5
Алгебра. 9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательствоДаровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)
ГДЗАлгебраАлимов Ш.А.Школа9 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее. ..)
..)
ГДЗ11 классКолмогоров А.Н.Алгебра
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.
Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
(Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Вариант 1 Функция задана формулой у= — 6х+14. Определить: а) значение у, если х=0,5; б) значение х, при котором у=2; в) проходит ли график функции через точку А(-5; 44)? Построить график функции у= х+6. а) Принадлежит ли графику точка В(-2; 7) б) указать с помощью графика значение х, при котором у=7; у=0. В одной системе координат построить графики функций: а) у= б) у= 5. Найти координаты точки пересечения графиков функций: у=14х – 24 и у= – 16х + 36. Известно, что график функции у=kх+1 проходит через точку C(2;5). Найдите значение k. | Вариант 2 Функция задана формулой . Определить: а) значение у, если х = — 2,5; б) значение х, при котором у = 5; в) проходит ли график функции через точку А(-15; -39)? Построить график функции а) Принадлежит ли графику точка В(-2; 7) б) указать с помощью графика значение х, при котором у=1; у=0. В одной системе координат построить графики функций: а) б) . Найти координаты точки пересечения графиков функций: и . Известно, что график функции проходит через точку C(3; 1). Найдите значение k. |
Вариант 1 1.Функция задана формулой у= — 6х+14. Определить: а) значение у, если х=0,5; б) значение х, при котором у=2; в) проходит ли график функции через точку А(-5; 44)? 2.Построить график функции у= х+6. а) Принадлежит ли графику точка В(-2; 7) б) указать с помощью графика значение х, при котором у=7; у=0. 3.В одной системе координат построить графики функций: а) у= б) у= 5. 4.Найти координаты точки пересечения графиков функций: у=14х – 24 и у= – 16х + 36. 5.Известно, что график функции у=kх+1 проходит через точку C(2;5). Найдите значение k. | Вариант 2 1. а) значение у, если х = — 2,5; б) значение х, при котором у = 5; в) проходит ли график функции через точку А(-15; -39)? 2.Построить график функции а) Принадлежит ли графику точка В(-2; 7) б) указать с помощью графика значение х, при котором у=1; у=0. 3.В одной системе координат построить графики функций: а) б) . 4.Найти координаты точки пересечения графиков функций: и . 5.Известно, что график функции проходит через точку C(3; 1). Найдите значение k. |
Домашнее задание Построить графики функции в одной системе координат: а) у= б) у = 3. При каком значении x функции принимает значение, равное 22. Постройте график функции . С помощью графика укажите значение функции, соответствующее значению аргумента -2,5. Проходит ли график функции через точку С(20; -36). Пересекаются ли графики функций и ? Если графики функций пересекаются, то найдите координаты точки их пересечения. 6 . Найти точки пересечения графика функции с осями координат. | Домашнее задание Построить графики функции в одной системе координат: а) у= б) у = 3. При каком значении x функции принимает значение, равное 22. Постройте график функции . С помощью графика укажите значение функции, соответствующее значению аргумента -2,5. Проходит ли график функции через точку С(20; -36). Пересекаются ли графики функций и ? Если графики функций пересекаются, то найдите координаты точки их пересечения. 6 . Найти точки пересечения графика функции с осями координат. |
Домашнее задание Построить графики функции в одной системе координат: а) у= б) у = 3. При каком значении x функции принимает значение, равное 22. Постройте график функции . С помощью графика укажите значение функции, соответствующее значению аргумента -2,5. Проходит ли график функции через точку С(20; -36). Пересекаются ли графики функций и ? Если графики функций пересекаются, то найдите координаты точки их пересечения. 6 . Найти точки пересечения графика функции с осями координат. | Домашнее задание Построить графики функции в одной системе координат: а) у= б) у = 3. При каком значении x функции принимает значение, равное 22. Постройте график функции . С помощью графика укажите значение функции, соответствующее значению аргумента -2,5. Проходит ли график функции через точку С(20; -36). Пересекаются ли графики функций и ? Если графики функций пересекаются, то найдите координаты точки их пересечения. 6 . Найти точки пересечения графика функции с осями координат. |
4.1.5: Графики на координатной плоскости
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4305
Предположим, у вас есть набор точек, где координаты x представляют количество месяцев, прошедших с момента покупки компьютера, а координаты y представляют стоимость компьютера. Вы знаете, как нанести эти точки на 9?0024 Декартова плоскость ? Как насчет того, чтобы ситуация была обратной, и у вас были нанесенные на график точки? Не могли бы вы придумать координаты точек и правило функции , которое бы генерировало эти точки?
Функции на декартовой плоскости После того, как таблица для функции создана, следующим шагом будет визуализация взаимосвязи путем графического отображения координат каждой точки данных.
Для построения координатной точки, такой как (4, 2), мы начинаем с начала координат.
Поскольку первая координата равна положительной четвёрке, мы перемещаемся на 4 единицы вправо.
Из этого места, поскольку вторая координата положительна два, мы перемещаемся на 2 единицы вверх.
Рисунок 4.1.5.2Нанесите на декартовой плоскости следующие координатные точки:
- (5, 3)
- (-2, 6)
- (3, -4)
- (-5, -7)
Мы показываем все точки координат на одном графике.
Рисунок 4.1.5.3Обратите внимание, что:
При положительном значении x мы двигаемся вправо.
При отрицательном значении x мы двигаемся влево.
При положительном значении y мы двигаемся вверх.
При отрицательном значении y мы двигаемся вниз.
Когда речь идет о координатной плоскости , также называемой декартовой плоскостью, четыре сечения называются квадрантами . Первый квадрант — это верхний правый сектор, второй квадрант — верхний левый, третий квадрант — нижний левый и четвертый квадрант — нижний правый.
Рисунок 4.1.5.4Рассмотрим студента по имени Джозеф, который собирается в тематический парк, где каждая поездка стоит 2 доллара. Функция, представляющая стоимость проезда на r поездках, равна J(r)=2r.
Предположим, мы хотим визуализировать общую стоимость поездки Джозефа в парке развлечений. Используя приведенную ниже таблицу, построим график функции таким образом, что
| r | Дж(р)=2р |
|---|---|
| 0 | 2(0)=0 |
| 1 | 2(1)=2 |
| 2 | 2(2)=4 |
| 3 | 2(3)=6 |
| 4 | 2(4)=8 |
| 5 | 2(5)=10 |
| 6 | 2(6)=12 |
 1.5.5
1.5.5Зеленые точки обозначают комбинацию (r,J(r)). Точки не связаны, потому что областью определения этой функции являются все целые числа. Соединив точки, мы указываем, что все значения между упорядоченными парами также являются решениями этой функции. Может ли Джозеф прокатиться на 212 аттракционах? Конечно нет! Поэтому мы оставляем эту ситуацию как график рассеяния .
Запись функционального правила с использованием графика
В этом курсе вы научитесь распознавать различные виды функций. Будут определенные методы, которые вы можете использовать для каждого типа функции, которые помогут вам найти правило функции. А пока мы рассмотрим несколько основных примеров и найдем закономерности, которые помогут нам выяснить взаимосвязь между зависимыми и независимыми переменными.
На приведенном ниже графике показано расстояние, которое дюймовый червь преодолевает с течением времени.
Рисунок 4.1.5.6Найдите правило функции, которое показывает, как расстояние и время связаны друг с другом для приведенного выше графика о дюймовых червях:
Составьте таблицу значений нескольких точек координат, чтобы определить шаблон.
Время 0 1 2 3 4 5 6
Расстояние 0 1,5 3 4,5 6 7,5 9
Мы видим, что каждую минуту расстояние увеличивается на 1,5 фута. Мы можем записать правило функции как:
Расстояние=1,5× время
Уравнение функции f(x)=1,5x.
Во многих случаях вам дают график и просят определить взаимосвязь между независимыми и зависимыми переменными. Из графика можно прочитать пары координатных точек, которые находятся на кривой функции. Координатные точки дают значения зависимых и независимых переменных. Эти переменные связаны друг с другом правилом. Важно убедиться, что это правило работает для все точек на кривой. Поиск правила функции для реальных данных позволяет вам делать прогнозы о том, что может произойти.
Анализ графика реальной ситуации
Графики используются для представления данных во всех сферах жизни. Вы можете найти графики в газетах, политических кампаниях, научных журналах и бизнес-презентациях.
Например, большинство ведущих ученых считают, что увеличение выбросов парниковых газов, особенно двуокиси углерода, способствует потеплению планеты. На приведенном ниже графике показано, как уровень углекислого газа увеличился по мере индустриализации мира.
На приведенном ниже графике показано, как уровень углекислого газа увеличился по мере индустриализации мира.
По этому графику мы можем найти концентрацию углекислого газа в атмосфере в разные годы.
1900 — 285 деталей на миллион
1930 — 300 частей на миллион
1950 — 310 деталей на миллион
1990 — 350 частей на миллион
Примеры. нам сказали, что у вас есть набор точек, где координаты x представляют количество месяцев, прошедших с момента покупки компьютера, а координаты y — стоимость компьютера. Как нанести эти точки на декартову плоскость? Не могли бы вы придумать координаты точек и правило функции, которое генерировало бы эти точки, если бы вам просто дали точки на графике?
Решение
Чтобы нанести заданные точки на декартову плоскость, помните, что первая координата представляет собой горизонтальное расстояние от начала координат, а вторая координата представляет собой вертикальное расстояние от начала координат. Если первая координата положительна, переместитесь вправо на соответствующее количество единиц, а если она отрицательна, переместитесь влево на соответствующее количество единиц. С этой точки, если вторая координата положительна, переместитесь вверх на соответствующее количество координат или, если она отрицательна, переместитесь вниз на соответствующее количество координат.
Если первая координата положительна, переместитесь вправо на соответствующее количество единиц, а если она отрицательна, переместитесь влево на соответствующее количество единиц. С этой точки, если вторая координата положительна, переместитесь вверх на соответствующее количество координат или, если она отрицательна, переместитесь вниз на соответствующее количество координат.
Чтобы создать функциональное правило из графика точек, первым делом необходимо поместить данные в таблицу, чтобы было легче увидеть закономерности. Затем найдите закономерность и опишите взаимосвязь в функциональной форме, как в задаче о дюймовом червя выше.
Пример 4.1.5.2
Нарисуйте график функции, которая имеет следующую таблицу значений. Найдите правило функции.
0 1 2 3 4
0 1 4 9 16
Решение
Таблица дает нам пять наборов координатных точек:
(0, 0), (1, 1), (2, 4), (3, 9), (4, 16).
Для построения графика функции мы наносим все координатные точки.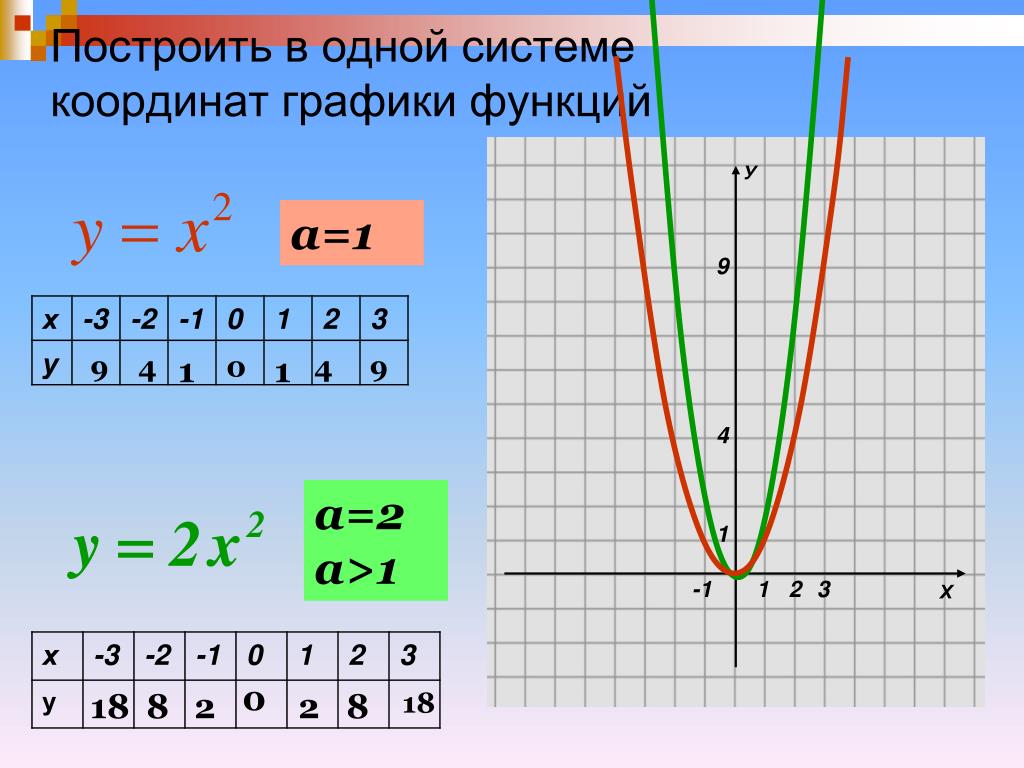 Мы видим, что закономерность такова, что зависимые значения представляют собой квадраты независимых значений.
Мы видим, что закономерность такова, что зависимые значения представляют собой квадраты независимых значений.
Поскольку возведение чисел в квадрат всегда дает положительный результат, а возведение дроби в квадрат дает дробь, областью определения этой функции являются все положительные действительные числа, или x≥0. Это означает, что упорядоченные пары можно соединить плавной кривой. Эта кривая всегда будет продолжаться в положительном направлении, показанном стрелкой.
Рисунок 4.1.5.8Поскольку зависимые значения представляют собой квадраты независимых значений, правилом функции является f(x)=x2.
Обзор
В 1–5 нанесите координатные точки на декартовой плоскости.
- (4, –4)
- (2, 7)
- (–3, –5)
- (6, 3)
- (–4, 3)
6. Используя координатную плоскость ниже, задайте координаты для a – e.
Рисунок 4.1.5.9 В 7–9 нарисуйте зависимость на координатной плоскости. По ситуации определите, соединять ли упорядоченные пары плавной кривой или оставить график в виде точечной диаграммы.
x -10 -5 0 5 10
y -3 -0,5 2 4,5 7
7.
| Сторона куба (в дюймах) | Объем куба (в дюймах3) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 8 |
| 3 | 27 |
| 4 | 64 |
8.
| Время (в часах) | Расстояние (в милях) |
|---|---|
| –2 | –50 |
| –1 | 25 |
| 0 | 0 |
| 1 | 5 |
| 2 | 50 |
В 9-11 постройте график функции.
9. Брэндон является членом киноклуба. Он платит 50 долларов за годовое членство и 8 долларов за фильм.
10.f(x)=(x−2)2
11.f(x)=3,2x
- Учащиеся местной средней школы приняли участие в опросе о рискованном поведении молодежи. На приведенном ниже графике показан процент учащихся старших классов, которые сообщили, что они в настоящее время курят. Человек считается нынешним курильщиком, если он выкурил одну или несколько сигарет за последние 30 дней. Какой процент старшеклассников курил в последующие годы?
- 1991
- 1996
- 2004
- 2005
- На приведенном ниже графике показана средняя продолжительность жизни людей в зависимости от года их рождения. Эта информация взята из Национального отчета по статистике естественного движения населения Центра по контролю за заболеваниями. Какова средняя продолжительность жизни человека, родившегося в последующие годы?
- 1940
- 1955
- 1980
- 1995
 1.5.11
1.5.11- На приведенном ниже графике показан средний доход человека в зависимости от количества лет обучения. Верхняя кривая показывает средний доход мужчин, а нижняя кривая показывает средний доход женщин (Источник: перепись населения США, 2003 г.). Каков средний доход следующих людей:
- Мужчина, 10 лет образования
- Мужчина, 17 лет образования
- Женщина, 10 лет образования
- Женщина, 17 лет образования
Обзор (ответы)
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 1.13.
Словарь
| Срок | Определение |
|---|---|
| квадрант | Квадрант — это четверть координатной плоскости. Четыре квадранта пронумерованы римскими цифрами I, II, III и IV, начиная с правого верхнего угла и увеличиваясь против часовой стрелки.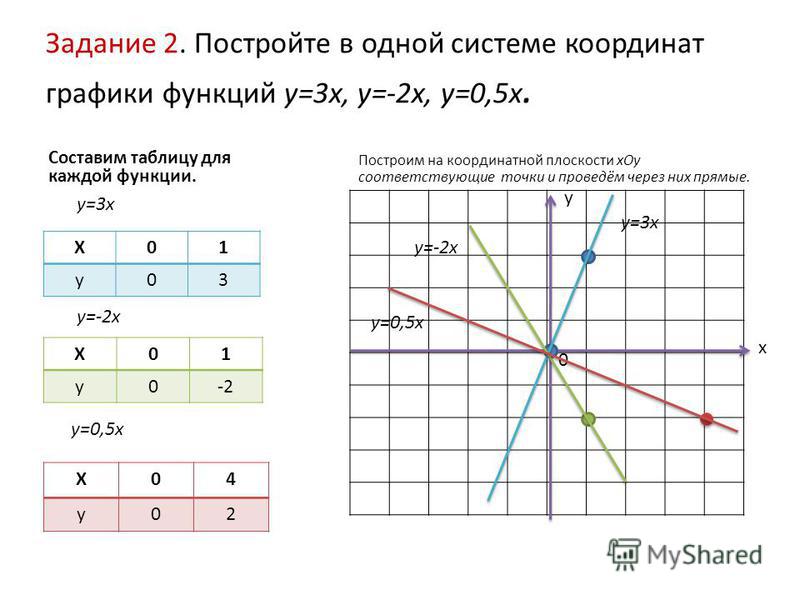 |
| Декартова плоскость | Декартова плоскость представляет собой сетку, образованную горизонтальной числовой линией и вертикальной числовой линией, которые пересекаются в точке (0, 0), называемой началом координат. |
| Координатная плоскость | Координатная плоскость представляет собой сетку, образованную горизонтальной числовой линией и вертикальной числовой линией, которые пересекаются в точке (0, 0), называемой началом координат. Координатная плоскость также называется декартовой плоскостью. |
| Функция | Функция — это отношение, в котором есть только один выход для каждого входа. Другими словами, для каждого значения x существует только одно значение y. |
Дополнительные ресурсы
PLIX: играй, учись, взаимодействуй, исследуй: Функции на декартовой плоскости
Видео: Построение точек на декартовой плоскости — задание 3
24 Функции на декартовой плоскости Вопросы для обсуждения
Практика: Графики на координатной плоскости
Применение в реальных условиях: Nike
Эта страница под названием 4. 1.5: Графики на координатной плоскости публикуется в соответствии с лицензией CC BY-NC и была создана, изменена и/или курирована Фондом CK-12 через исходный контент, отредактированный в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.
1.5: Графики на координатной плоскости публикуется в соответствии с лицензией CC BY-NC и была создана, изменена и/или курирована Фондом CK-12 через исходный контент, отредактированный в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- СК12
- Лицензия
- CC BY-NC
- Программа OER или Publisher
- СК-12
- Показать оглавление
- нет
- Теги
- источник@https://www.
 ck12.org/c/алгебра
ck12.org/c/алгебра - источник@https://www.ck12.org/c/алгебра/
- источник@https://www.
х | у = х 2 | (х, у) |
0 | 0 | (0,0) |
1 | 1 | (1,1) |
2 | 4 | (2,4) |
3 | 9 | (3,9) |
-1 | 1 | (-1,1) |
-2 | 4 | (-2,4) |
-3 | 9 | (-3,9) |
х | у=1/х | (х, у) |
1/3 | 3 | (1/3,3) |
1/2 | 2 | (1/2,2) |
1 | 1 | (1 ,1) |
2 | 1/2 | (2,1/2) |
3 | 1/3 | (3,1/3) |
-1/3 | -3 | (-1/3, -3) |
-1/2 | -2 | (-1/2, -2) |
-1 | -1 | (-1 , -1) |
-2 | -1/2 | (-2, -1/2) |
-3 | -1/3 | (-3,-1/3) |
| |х| знак равно | x, если x ≥ 0, т. -х если х |
График совпадает с линией y = x при x > 0 и с линией y = -x
для х < 0 .
график f(x) = -x
Объединив эти два графика, мы получим
график f(x) = |x|
Пример: 4 Нарисуйте график числа
.т(х) = (х 2 — 4)/(х — 2) =
= ((х — 2)(х + 2)/(х — 2)) =
= (х + 2) х ≠ 2
Следовательно, эту функцию можно записать как
.у = х + 2 х ≠ 2
График h(x)= x 2 — 4 Или x — 2
график у = х + 2 х ≠ 2
Пример: 4 Нарисуйте график числа
.| г (х) = | 1 если x ≤ 2 x + 2 если x > 2 |
Графические функции по переводам
– Предположим, что график функции f(x) известен
.— Тогда мы можем найти графики
у = f(x) + с
у = f(x) — с
у = f(х + с)
у = f(х — с)
y = f(x) + c график f(x) переводит
UP c шт.
y = f(x) — c график f(x) переводит
ВНИЗ на c единиц
y = f(x + c) график f(x) переводит
ВЛЕВО на c единиц
y = f(x — c) график f(x) переводит
ВПРАВО c шт.
Пример: 5 Нарисуйте
график y = f(x) = |x — 3| + 2
Перевести график y = |x| 3 единицы ВПРАВО, чтобы получить график
у = |х-3|
Перевести график y = |x — 3| 2 единицы вверх, чтобы получить график y = |x — 3| + 2
Пример: 8
Нарисуйте график
у = х 2 — 4х + 5
— заполните квадрат
у + 4 = (х 2 — 4х + 5) + 4 у = (х 2 — 4x + 4) + 5 — 4
у = (х — 2) 2 + 1
В таком виде мы видим, что график можно получить, переведя график y = x 2 вправо на 2 единицы из-за x — 2 и вверх на 1 единицу из-за +1.
у = х 2 — 4х + 5
Отражения
(-x, y) — это отражение (x, y) относительно оси y
(x, -y) — это отражение (x, y) относительно оси x
Графики y = f(x) и y = f(-x) являются отражением друг друга относительно оси y
Графики y = f(x) и y = -f(x) являются отражением друг друга относительно оси x
Граф можно получить отражением и переводом:
– Нарисуйте график числа
.


 Функция задана формулой . Определить:
Функция задана формулой . Определить: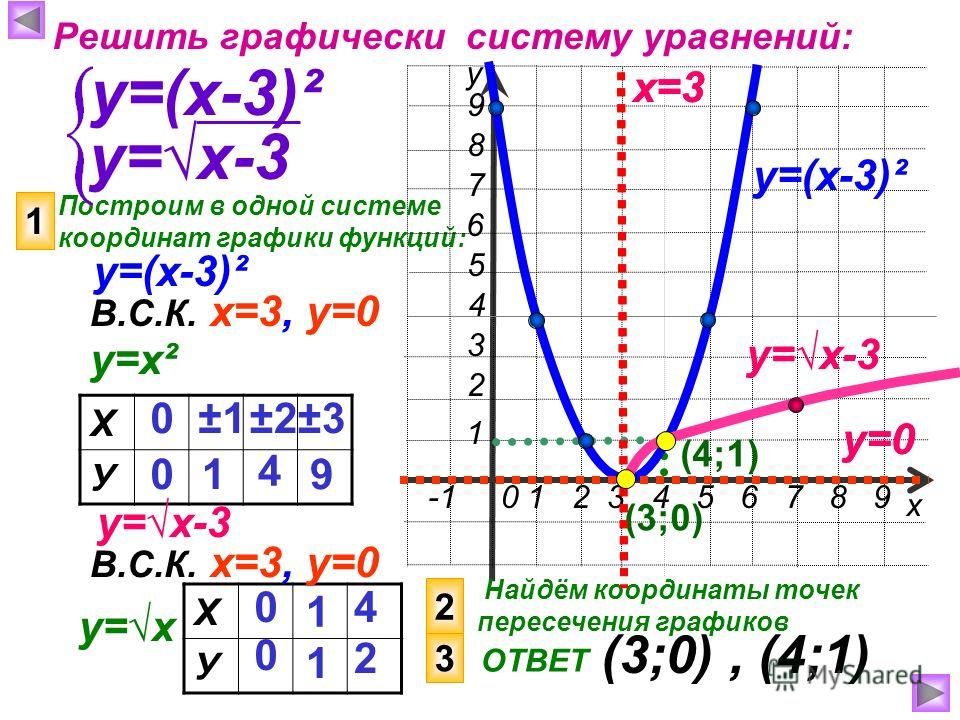


 ck12.org/c/алгебра
ck12.org/c/алгебра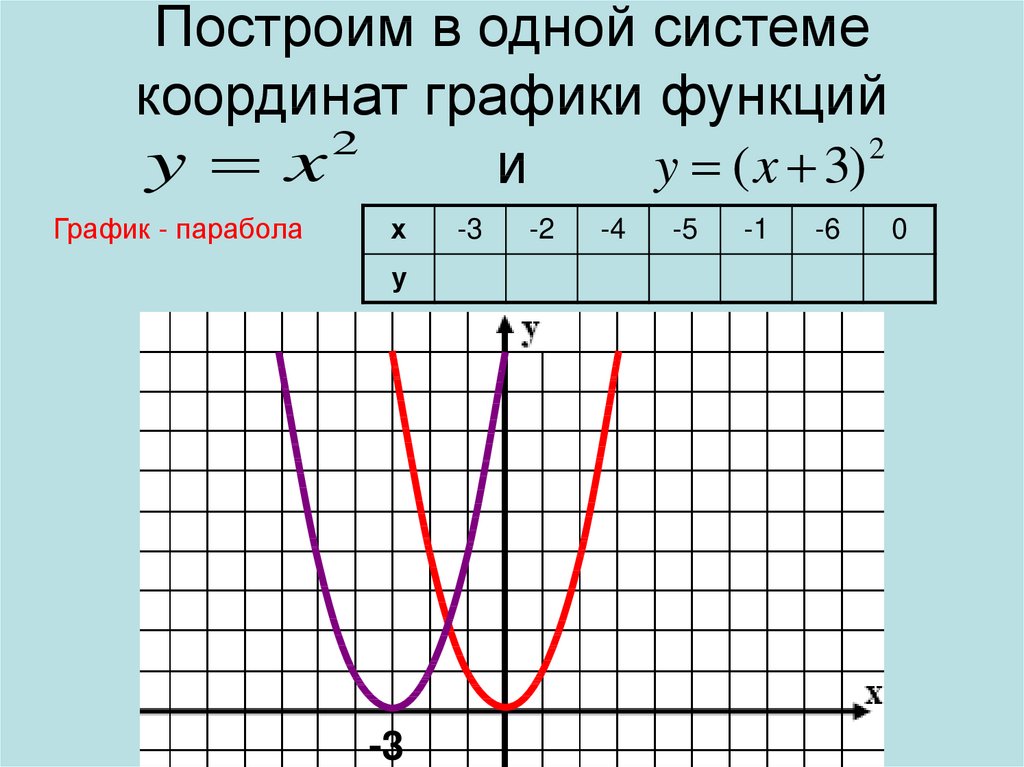
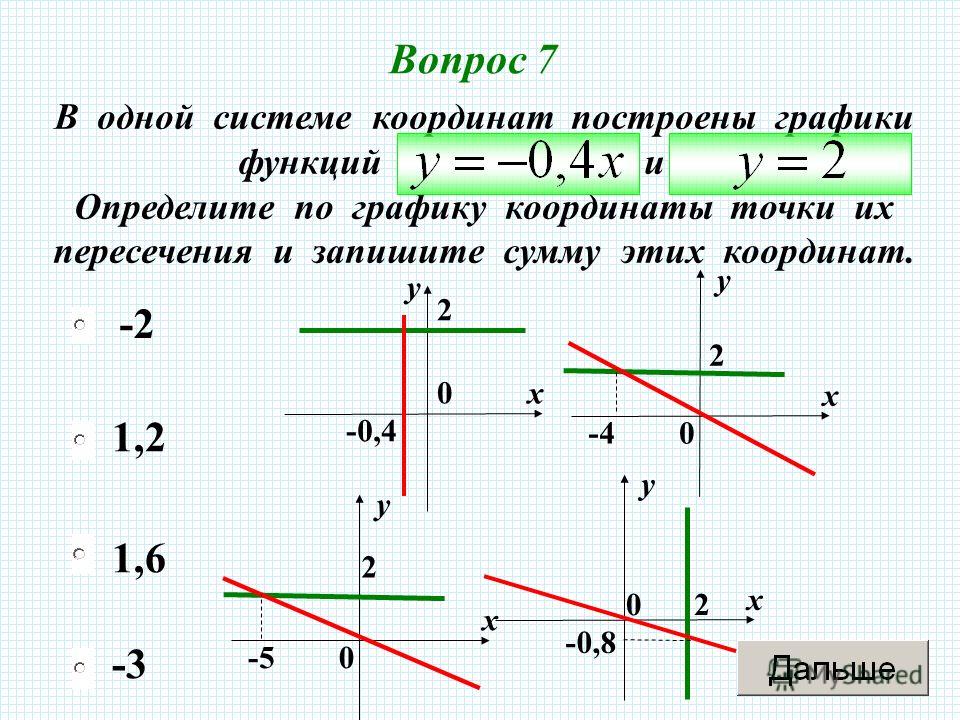 А вообще это только с техникой
А вообще это только с техникой
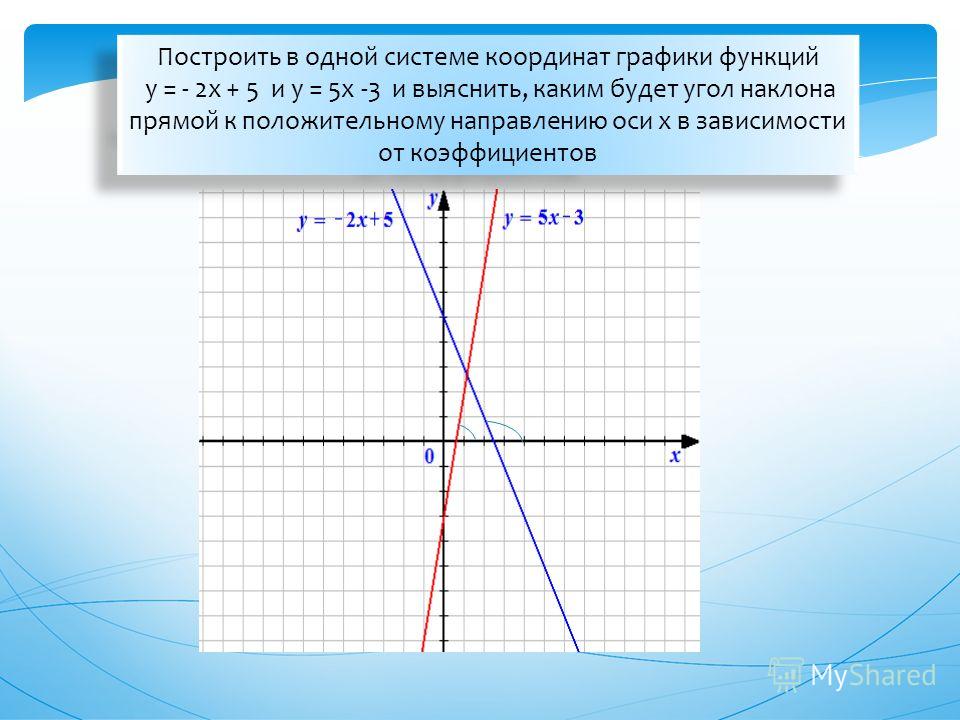 е. x неотрицательно
е. x неотрицательно