Построить вектор b a: Сложение и вычитание векторов. Умножение вектора на число — урок. Геометрия, 10 класс.

Координаты и векторы — презентация онлайн

Похожие презентации:

Векторы в пространстве

Координаты вектора

Векторы в пространстве

Векторы в пространстве

Векторы на плоскости и в пространстве. Основные понятия

Понятие вектора в пространстве

Векторы. Понятие вектора

Векторы в пространстве

Векторы в пространстве

Векторы в пространстве

B1
A1
Тема 5.
C1
D1
Координаты
и векторы
B
A
C
D
AC1 AB AD AA1

2. Тема 5. Координаты и векторы

I. Определение вектора.
Основные понятия, связанные с векторами.

3. Понятие вектора

Отрезок, для которого указано, какой из
его концов считается началом,
а какой – концом, называется вектором.
АВ
А
В
n

4. Нулевой вектор

Любая точка на плоскости может
рассматриваться как вектор.
Такой вектор называется нулевым.
М
ММ = 0

5. Длина вектора

Длиной ненулевого вектора АВ
называется длина отрезка АВ.
В
а
А
АВ = а
0
0 = 0
ДЛИНОЙ или МОДУЛЕМ ненулевого вектора
называется длина отрезка АВ
АВ
АВ
АВ
А
a
C
a
F
0 0
CD 5
АВ 6
EF 2,5
a 13
MM 0
b 4,5
c 3
E
D
B
M
a
b
c
Как и в плоскости, в пространстве ВЕКТОР определяется как
B
направленный отрезок:
A
Точка А – начало вектора, В – конец вектора. Записывают:
AB
или
a.
Обычную точку в пространстве мы также можем считать вектором, у которого
начало совпадает с конечной точкой. Такой вектор называется нулевым и
обозначается: 0 или AA .
0
A
Длина отрезка, изображающего вектор, называется модулем (или абсолютной
величиной) вектора, т.е.
AB AB åä.î ò ð. .
Естественно, что
B
AA 0.
Векторы AB и BA являются
противоположными. Очевидно, что:
AB BA .
A

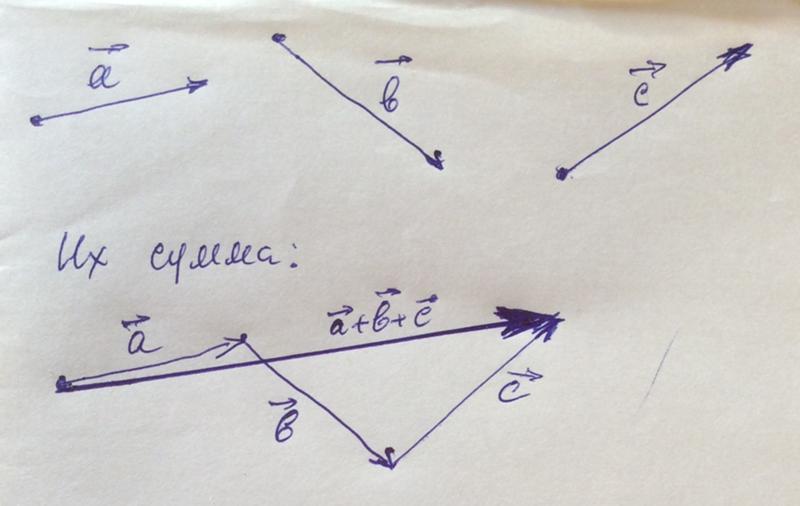
9. Коллинеарность векторов

Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых.
q
р
r

10. Сонаправленные векторы

Два коллинеарных вектора
называются сонаправленными,
если у них совпадают направления.
q
р
q↑↑р

11. Противоположно направленные векторы

Два коллинеарных вектора называются
противоположно направленными, если
они не сонаправлены.
а
b
a↑↓b
Два вектора называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых:
m n
Обозначение коллинеарных векторов:
a b, a c, c b.
Коллинеарные векторы, в свою очередь, бывают одинаково направленными (или
соноправленными) и противоположно направленными. В нашем случае:
a ↑↑ c
– соноправленные векторы,
a ↑↓ b , c ↑↓ b
– противоположно
направленные векторы.
Два вектора называются равными, если: 1) они соноправлены; и 2) их модули
равны, т.е.
a b a ↑↑ b è a b
a
b
От произвольной точки пространства можно отложить единственный вектор,
равный данному:
N
a
a MN
M
Три вектора называются компланарными, если они лежат в одной плоскости:
b
a
c
Углом между векторами называется угол между их направлениями:
a
b
a,b
Величина угла между векторами может изменятся от 00 до 1800. Подумайте, когда:
а) a,b 0 и б) a,b 1800 ?
0
Ответ: а)
a ↑↑ b ;
б)
a ↑↓ b
.

15. Тема 5. Координаты и векторы

II. Действия с векторами
ОТКЛАДЫВАЕНИЕ ВЕКТОРА
ОТ ДАННОЙ ТОЧКИ
a
А
вектор
a отложен
от точки А
https://youtu.be/DlLM97OvqsA
от любой точки М можно отложить вектор, равный
данному вектору a , и при том только один
a ненулевой
a нулевой
MM
А
M
a
В
N
M
N/
р
MN MN / AB
Векторы можно складывать – в результате получается вектор. При сложении двух
векторов применяются
Правило треугольника:
a b
a
b
a b
O
a
F
b
При сложении трех и более векторов применяют правило многоугольника:
b
a
b
c
e
d
d
a
c
e
a b c d e
Обратим внимание, что при сложении соноправленных векторов получается
вектор, соноправленный с данными и его модуль равен сумме модулей слагаемых
векторов:
a
a
b
b
a b a b
a b
При сложении противоположно направленных векторов получается вектор,
соноправленный с вектором, имеющим бóльшую длину и его модуль равен …
(подумайте, чему?):
a
a
b
b
a b
a b b a
b a
Также можно найти разность двух векторов – в результате получается вектор. При
вычитании двух векторов применяется видоизмененное правило треугольника –
вначале оба вектора строятся с общей начальной точкой, затем соединяются
концы этих векторов с выбором направления к «уменьшаемому» вектору:
b
a
a b
Или: т.к. a b a b
, то можно вначале построить вектор, противоположный
вектору b , а затем оба вектора сложить по правилу треугольника.
a
–
b
a b

21. Задача 1.

Даны векторы
a и b . Построить вектор a b
b
a
a OA
b OB
А
OB BA OA
a
В
О
b
b BA a
BA a b
Сложение векторов, как и сложение чисел подчиняется законам:
1)
a b b a
2)
a b c a b c – сочетательный закон сложения;
– переместительный закон сложения;
a 0 a ;
4) a a 0 .
3)
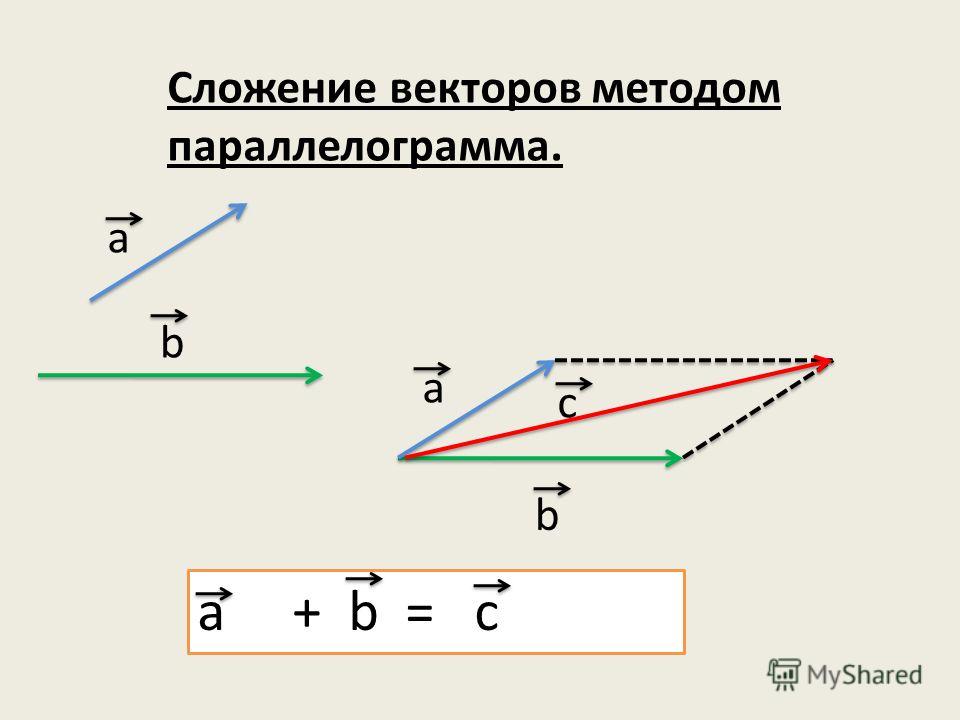
Следующее действие с векторами – умножение вектора на число k. В результате
этого действия получается вектор, причем:
1) если k>0, то
2) если k<0, то
k a ↑↑ a
k a ↑↓ a
ka k · a ;
и ka k · a ;
и
3) если k=0, то 0 ·a 0 .
a
8
a
3
0·a
3a
2a
4
a
3
И еще одно действие с векторами – умножение двух векторов. В школьном курсе
геометрии изучается скалярное произведение векторов. В результате этого
действия (в отличии от предыдущих действий с векторами) получается число,
равное произведению модулей двух данных векторов на косинус угла между этими
векторами, т.е.
a·b a · b ·cos a,b.
Геометрически скалярное произведение векторов можно понимать как площадь
параллелограмма (или противоположная ей величина), стороны которого
образуются одним из данных векторов и вектором, перпендикулярным второму с
таким же модулем:
S a ·b’ ·sin 900 a ·b ·cos a·b;
S a ·b’ ·sin 900 a ·b ·cos a·b.
ò .å. a·b S
a
900
b’
b b’
b’
– острый угол
a
b
900
– тупой угол
b
Задача 2.
Упростить выражение:
Решение:
Первый распределительный закон позволяет нам раскрыть скобки.
А переместительное свойство сложения векторов – привести подобные.
ЗАДАЧА 3:
Точка С – середина отрезка АВ, а О – произвольная
точка плоскости. Доказать, что
1
OC OA OB
2
B
С
+
OC OA AC
OC OB BC
2 OC OA OB AC BC
A
AC BC 0
2 OC OA OB
О
OC
1
OA OB
2
ЗАДАЧА 4:
Доказать, что прямая, проведенная через середины
оснований трапеции, проходит через точку
пересечения продолжений боковых сторон
О
B
A
OBC
OAD
М
— по первому признаку
OA OD
k
OB OC
С
OB OA
OC OD
OA k OB
OD k OC
1
OB OC
2
1
ON OA OD
2
1
ON k OB OC k OM
2
D
N
ON и OM
OM
— коллинеарны
D
Задача 5
Дано: АВСD — тетраэдр
AB = AD = DC = BC = DD = AC
M ∈ АB, AM = MB
N ∈ AD, AN = ND
P ∈ СD, CP = PD
Q ∈ BС, BQ = QC
Задание:
а) выписать пары равных векторов
б) определить вид четырехугольника MNHQ
Решение:
P
N
A
C
Q
M
B
б) NP ∥ АС, QM ∥ АС
MN ∥ DB, QP ∥ DB
MN = DB = PN = QM,
DB ⏊ AC ⇒ MN ⏊ NP ⇒
⇒ MNPQ — квадрат
Задача 6
Упростить выражение:
Решение:
— Заменим в выражении
на сумму.
— Для этого заменим
отрицательные векторы
на противоположные.
Вектор – ВС = вектор СВ,
вектор – РМ = вектор МР.
Вектор – АР = вектор РА.
Вектор АС + вектором СВ =
вектор АВ.
Векторы МР + РА = вектор
МА.
Затем, складывая векторы АВ и ВМ,
получаем вектор АМ.
В итоге сумма векторов АМ и МА дают нулевой
вектор. Выражение упрощено.

English     Русский Правила

Векторы в пространстве — презентация онлайн

Похожие презентации:

Векторы в пространстве. (11 класс)

Векторы в пространстве. (10-11 класс)

Векторы в пространстве

Векторы в пространстве

Векторы в пространстве

Векторы на плоскости и в пространстве. Основные понятия

Векторы

Векторы в пространстве

Координаты и векторы

Векторы в пространстве

B1
A1
ТЕМА:
D1
Векторы в
пространстве.
Записать
конспект с
презентации
C1
B
A
C
D
AC1 AB AD AA1
I.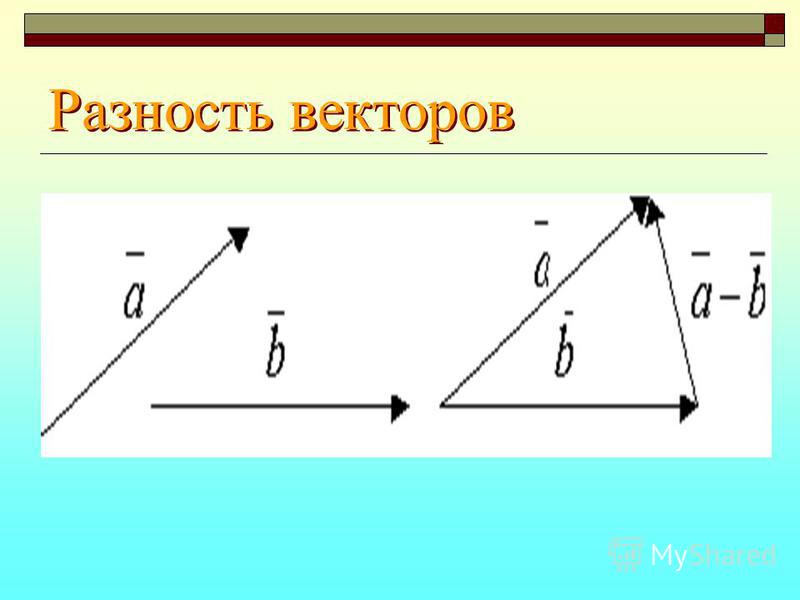 Определение вектора. Основные понятия, связанные с векторами.
Как и в плоскости, в пространстве вектор определяется как направленный
отрезок:
B
A
Точка А – начало вектора, В – конец вектора. Записывают:
AB
или
a.
Обычную точку в пространстве мы также можем считать вектором, у которого

начало совпадает с конечной точкой. Такой вектор называется нулевым и
обозначается: 0 или AA .
0
A
Длина отрезка, изображающего вектор, называется модулем (или абсолютной
величиной) вектора, т.е.
AB AB åä.î ò ð. .
Естественно, что
B
AA 0.
Векторы AB и BA являются
противоположными. Очевидно, что:
AB BA .
A
Два вектора называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых:
Коллинеарные векторы, в свою очередь, бывают одинаково направленными (или
соноправленными) и противоположно направленными. В нашем случае:
a ↑↑ c
– соноправленные векторы,
a ↑↓ b , c ↑↓ b
– противоположно
направленные векторы.
Два вектора называются равными, если: 1) они соноправлены; и 2) их модули
равны, т.е.
a b a ↑↑ b è a b
a
b
От произвольной точки пространства можно отложить единственный вектор,
равный данному:
N
a
a MN
M
Три вектора называются компланарными, если они лежат в одной плоскости:
b
a
c
Углом между векторами называется угол между их направлениями:
a
b
a,b
Величина угла между векторами может изменятся от 00 до 1800. Подумайте, когда:
а) a,b 0 и б) a,b 1800 ?
0
Ответ: а)
a ↑↑ b ;
б)
a ↑↓ b
.
II. Действия с векторами.
Векторы можно складывать – в результате получается вектор. При сложении двух
векторов применяются правила треугольника или параллелограмма:
1) При применении правила треугольника один из векторов откладывают от конца
другого, т.е. MK KF MF :
a b
a
b
2) При применении правила параллелограмма оба вектора откладывают из общей
начальной точки, т. 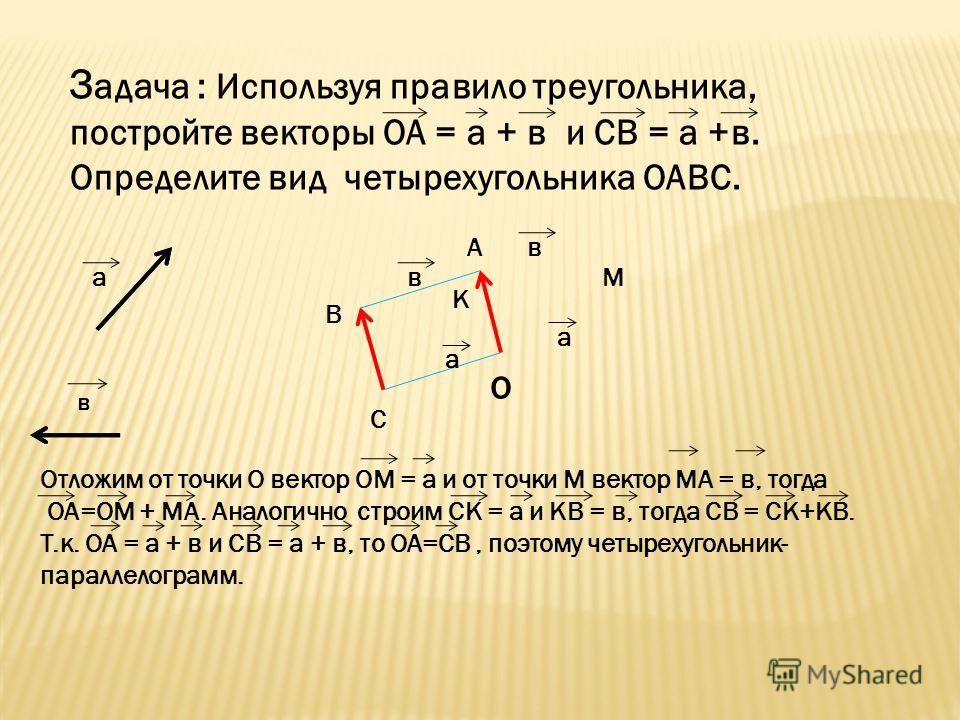е. MK MN MF , где F – вершина параллелограмма,
противоположная общей начальной точке векторов.
a b
a
b
При сложении трех и более векторов применяют правило многоугольника:
b
a
b
c
e
d
d
a
c
e
a b c d e
Обратим внимание, что при сложении соноправленных векторов получается
вектор, соноправленный с данными и его модуль равен сумме модулей слагаемых
векторов:
a
a
b
b
a b a b
a b
При сложении противоположно направленных векторов получается вектор,
соноправленный с вектором, имеющим бóльшую длину и его модуль равен …
(подумайте, чему?):
a
a
b
b
a b
a b b a
b a
Также можно найти разность двух векторов – в результате получается вектор. При
вычитании двух векторов применяется видоизмененное правило треугольника –
вначале оба вектора строятся с общей начальной точкой, затем соединяются
концы этих векторов с выбором направления к «уменьшаемому» вектору:
b
a
a b
Или: т. к. a b a b
, то можно вначале построить вектор, противоположный
вектору b , а затем оба вектора сложить по правилу треугольника.
a
–
b
a b
Сложение векторов, как и сложение чисел подчиняется законам:
1)
a b b a
2)
a b c a b c – сочетательный закон сложения;
– переместительный закон сложения;
a 0 a ;
4) a a 0 .
3)
Следующее действие с векторами – умножение вектора на число k. В результате
этого действия получается вектор, причем:
1) если k>0, то
2) если k<0, то
k a ↑↑ a
k a ↑↓ a
ka k · a ;
и ka k · a ;
и
3) если k=0, то 0 ·a 0 .
a
8
a
3
0·a
3a
2a
4
a
3

English     Русский Правила

Вычисление вектора ab из векторов a и b.

спросил 6 лет, 8 месяцев назад

Изменено 1 год, 7 месяцев назад

Просмотрено 69 тысяч раз

$\begingroup$

Итак, у меня есть вектор $a =( 2 ,2 )$ и вектор $b =( 0, 1 )$.
Как сказал мне мой учитель, $ab = (-2, -1 )$.

$ab = b-a = (0, 1) — (2, 2) = (0-2, 1-2) = (-2, -1)$
$ab = a-b = (2,2) — ( 0 ,1 ) = ( 2-0,2-1 ) = ( 2 ,1 )$

Вроде то же самое, но отрицательные знаки исчезли.

Почему я должен вычесть b из a, чтобы получить ab? Почему не а-б или а+б?

• векторов

$\endgroup$

5

$\begingroup$

Они связаны тем, что $$\mathbf a- \mathbf b = -(\mathbf b- \mathbf a)$$

Разница в направлении. Как правило, вектор от начальной точки до конечной точки равен $$(\textrm{конечная точка})-(\textrm{начальная точка})$$

$\endgroup$

$\begingroup$

Правильно $\;b-a\;$ для вектора направления $\;\vec{ab}\;$. Вычитание $\;a-b\;$ дает противоположный вектор направления, а именно $\;\vec {ба}\;$

$\endgroup$

$\begingroup$

(Вектор AB) = (Вектор B) — (Вектор A)

Подумайте об этом логически, когда у вас есть уравнение 10-2, вы получаете 8 (положительное значение) Однако, если вы сделаете от 2 до 10, вы получите ту же величину 8, но в противоположном направлении -8.

Используйте это, чтобы понять векторы, так как точка вектора AB движется от A к B, вы хотите знать, движется ли она в положительном или отрицательном направлении.

Если B имел большее значение позиции, чем A, то, очевидно, он двигался в положительное направление для достижения этого большего значения, и поэтому B — A (больше — меньше) должно быть положительным. Если бы он имел меньшее значение, чем A, то он двигался бы в отрицательном направлении, и поэтому значение B — A было бы отрицательным (меньше — больше).

И в действительности вы вычитаете векторы OB — OA (O является точкой отсчета), так что разница между этими векторами есть смещение.

Я очень надеюсь, что помог ответить на ваш вопрос.

🙂

$\endgroup$

$\begingroup$

Я знаю, что опаздываю с ответом. Кроме того, у меня не так много знаний по математике. Но я постараюсь упростить. Пожалуйста, не воздерживайтесь от комментариев, если я понял это ужасно или немного ошибся.

Теперь для упрощения давайте сначала представим вещи в одном измерении. Это числовая линия. Теперь у нас есть 2 точки на числовой прямой a и b.

b может быть либо в положительном направлении, т.е. вправо от a, либо в отрицательном направлении, т.е. влево от a.

Итак, чтобы найти направление от a к b, т.е. ab, мы вычтем a из b, т.е. b — a. Таким образом, если b больше, чем a (т.е. в положительном направлении), мы получим положительный ответ, или если b меньше, чем a (т.е. в отрицательном направлении), мы получим отрицательный ответ.

Теперь, когда мы переходим в 2D, та же логика применяется для определения направления, поэтому

ab = b — a т.е. направление от a к b.

и ба = а — б т.е. направление от b к a.

Также важно понимать, что направление от a к b и от b к a — разные значения.

Надеюсь, это поможет.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Начальная буква ba шаблон дизайна логотипа здания векторное изображение

Начальная буква ba шаблон дизайна логотипа здания векторное изображение

1. лицензионные векторы
2. логотип векторов

ЛицензияПодробнее

Стандарт Вы можете использовать вектор в личных и коммерческих целях. Расширенный Вы можете использовать вектор на предметах для перепродажи и печати по требованию.

Тип лицензии определяет, как вы можете использовать этот образ.

	Станд.	Экспл.
Печатный / редакционный
Графический дизайн
Веб-дизайн
Социальные сети
Редактировать и изменять
Многопользовательский
Предметы перепродажи
Печать по требованию

Владение Учить больше

Эксклюзивный Если вы хотите купить исключительно этот вектор, отправьте художнику запрос ниже:

Хотите, чтобы это векторное изображение было только у вас? Эксклюзивный выкуп обеспечивает все права этого вектора.

Мы удалим этот вектор из нашей библиотеки, а художник прекратит продажу работ.

Способы покупкиСравнить

Плата за изображение $ 14,99 Кредиты $ 1,00 Подписка $ 0,69

Оплатить стандартные лицензии можно тремя способами. Цены $ долларов США.

Оплата с помощью	Цена изображения
Плата за изображение $ 14,99 Одноразовый платеж
Предоплаченные кредиты $ 1 Загружайте изображения по запросу (1 кредит = 1 доллар США). Минимальная покупка 30р.
План подписки От 69 центов Выберите месячный план. Неиспользованные загрузки автоматически переносятся на следующий месяц.

Способы покупкиСравнить

Плата за изображение $ 39,99 Кредиты $ 30,00

Существует два способа оплаты расширенных лицензий. Цены $ $ .

Оплата с помощью	Стоимость изображения
Плата за изображение $ 39,99 Оплата разовая, регистрация не требуется.
Предоплаченные кредиты $ 30 Загружайте изображения по запросу (1 кредит = 1 доллар США).

Оплата

Плата за изображение $ 499

Дополнительные услугиПодробнее

Настроить изображение Доступно только с оплатой за изображение $ 85,00

Нравится изображение, но нужны лишь некоторые модификации? Пусть наши талантливые художники сделают всю работу за вас!

Мы свяжем вас с дизайнером, который сможет внести изменения и отправить вам изображение в выбранном вами формате.

Примеры

• Изменить текст
• Изменить цвета
• Изменить размер до новых размеров
• Включить логотип или символ
• Добавьте название своей компании или компании

Включенные файлы

Подробности загрузки.