Постройка графиков онлайн: Построение графика функции онлайн

Содержание

Построение графиков онлайн | Онлайн калькулятор

Сервис позволяет строить графики функций в прямоугольной системе координат на заданном интервале значений. В одной координатной плоскости можно построить сразу несколько графиков функций.
Чтобы построить график функции необходимо задать область построения графика (для переменной x и функции y) и ввести значение зависимости функции от аргумента. Возможно одновременное построение нескольких графиков, для этого необходимо разделять функции через точку с запятой. Графики будут построены на одной координатной плоскости и для наглядности будут отличаться цветом.

Справочная информация по синтаксису математических операций, спискам поддерживаемых функций и констант расположена внизу страницы.

Как вводить функции

Обозначение	Описание
+	Сложение
—	Вычитание
*	Умножение
/	Деление
( )	Группирующие символ
x^n или p(x,n)	Возведение x в степень n
exp(x)	Экспоненциальная функция, т. е. возведение e в степень x
root(x,n)	Корень n-степени из x
sqr(x) или sqrt(x)	Квадратный корень из x
cbr(x) или cbrt(x)	Кубический корень из x
logn(x,a)	Логарифм x по основанию a
ln(x)	Натуральный логарифм x, т.е. логарифм x по основанию e
lb(x)	Логарифм x по основанию 2
lg(x)	Логарифм x по основанию 10
sin(x)	Синус от x
cos(x)	Косинус от x
tan(x)	Тангенс от x
cotan(x)	Котангенс от x
sec(x)	Секанс от x
csc(x)	Косеканс от x
asin(x)	Арксинус от x
acos(x)	Арккосинус от x
atan(x)	Арктангенс от x
acot(x)	Арккотангенс от x
asec(x)	Арксеканс от x
acsc(x)	Арккосеканс от x
sinh(x)	Гиперболический синус от x
cosh(x )	Гиперболический косинус от x
tanh(x)	Гиперболический тангенс от x
coth(x)	Гиперболический котангенс от x
sech(x)	Гиперболический секанс от x
csch(x)	Гиперболический косеканс от x
asinh(x)	Гиперболический арксинус от x
acosh(x)	Гиперболический арккосинус от x
atanh(x)	Гиперболический арктангенс от x
acoth(x)	Гиперболический арккотангенс от x
asech(x)	Гиперболический арксеканс от x
acsch(x)	Гиперболический арккосеканс от x
gaussd(x,m,n)	Нормальное распределение (распределение Гаусса) со средним значением m и стандартным отклонением n
min(n1,n2)	Возвращает наименьшее из двух значений
max(n1,n2)	Возвращает наибольшее из двух значений
round(x)	Классическое округление x до целого числа
floor(n1,n2)	Округление x вниз до ближайшего целого числа
ceil(n1,n2)	Округление x вверх до ближайшего целого числа
abs(x)	Модуль x
rand	Случайное число от 0 до 1
sgn(x)	Сигнум x. Возвращает 1, если x>0 Возвращает 0, если x=0 Возвращает -1, если x<0
e	Число Эйлера: 2.7182818284…
Phi	Золотое отношение: 1.6180339887…
pi	Число Пи: 3.1415926535…

Select rating12345

Рейтинг: 5 (Голосов 2)

Сообщить об ошибке

Вам помог этот калькулятор?

Предложения и пожелания пишите на [email protected]

Поделитесь этим калькулятором на форуме или в сети!

Это помогает делать новые калькуляторы.

НЕТ

Смотрите также

Графические построения	Математический анализ	Решение интегралов	Решение неравенств	Решение уравнений
Решение функций	Решение комплексных чисел	Производные функции	Решение логарифмов	Решение прогрессии

Построение графиков функций онлайн Справка

Онлайн рисование графиков

Этот сервис создан в помощь школьникам и студентам в изучении математики (алгебры и геометрии) и физики и предназначен для онлайн построения графиков функций (обычных и параметрических) и графиков по точкам (графиков по значениям), а также графиков функций в полярной системе координат.

Просто введите формулу функции в поле «Графики:» и нажмите кнопку «Построить».

Почитайте в cправкe, как правильно вводить формулы функций.

Загляните в раздел примеров, наверняка, там есть графики функций, похожие на то, что нужно Вам, останется только слегка откорректировать готовые формулы функций.

Дополнительно на нашем сайте вы можете воспользоваться калькулятором матриц, с помощью которого можно производить различные преобразования и действия с матрицами онлайн.

Этот сервис создан в помощь школьникам и студентам в изучении математики алгебры и геометрии и физики и предназначен для онлайн построения графиков функций обычных и параметрических и графиков по точкам графиков по значениям, а также графиков функций в полярной системе координат.

Yotx. ru

07.02.2018 3:35:35

2018-02-07 03:35:35

Источники:

Http://yotx. ru/

Построение графиков онлайн » /> » /> .keyword { color: red; }

Онлайн рисование графиков

Построение графиков онлайн с помощью нашего сервиса является простой задачей.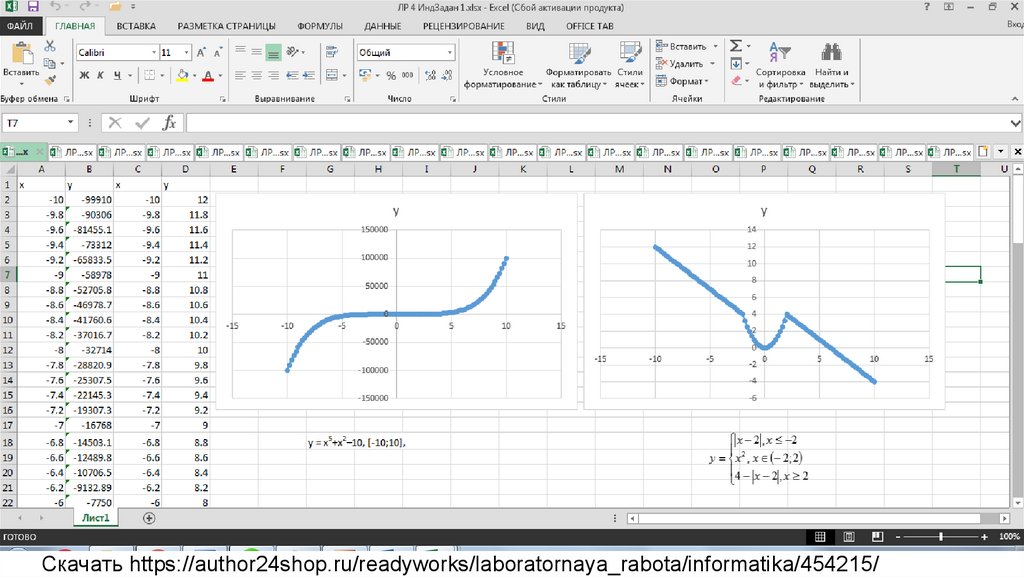 2/16=1) Возможность сохранять графики и получать на них ссылку, которая становится доступной для всех в интернете Управление масштабом, цветом линий Возможность построения графиков по точкам, использование констант Построение одновременно нескольких графиков функций Построение графиков в полярной системе координат (используйте r и θ(\theta) )

С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.

Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos. Для ввода функций воспользуйтесь левой колонкой. 2/16=1) Возможность сохранять графики и получать на них ссылку, которая становится доступной для всех в интернете Управление масштабом, цветом линий Возможность построения графиков по точкам, использование констант Построение одновременно нескольких графиков функций Построение графиков в полярной системе координат (используйте r и θ(\theta) )

Преимущества построения графиков онлайн.

Matematikam. ru

15.11.2018 14:32:47

2018-11-15 14:32:47

Источники:

Https://matematikam. ru/calculate-online/grafik. php

Графики/диаграммы онлайн » /> » /> .keyword { color: red; }

Онлайн рисование графиков

YequalX. com — сайт для построения графиков/диаграмм онлайн. Выберите вид диаграммы (линейная, круговая, столбчатая, полосовая, линии, области), заполните данные таблицы графика, и диаграмма готова! Диаграмму можно скачать в удобном вам формате или получить ссылку на страницу вашего графика. Вы можете также использовать онлайн-конструктор графиков на нашем сайте, чтобы скачать график (png/jpeg/и др.) и вставить его в excel, word и другие программы на вашем компьютере. Построить диаграмму онлайн очень просто! Читайте подробнее о том, как создать диаграмму онлайн здесь. Также вы можете посмотреть примеры диаграмм, чтобы на их основе создать необходимый вам график.

Построить диаграмму онлайн очень просто.

Yequalx. com

16.04.2020 0:04:15

2020-04-16 00:04:15

Источники:

Https://yequalx.

com/ru/

Построить график функции х3 х2 х 2. Построение графиков онлайн

Разделы: Математика

Тема: “Построение графика квадратной функции, содержащей модуль”.
(На примере графика функции у = х 2 — 6x + 3.)

Цель.

Исследовать расположение графика функции на координатной плоскости в зависимости от модуля.
Развить навыки построения графика функции, содержащей модуль.

Ход урока.

1. Этап актуализации знаний.

а) Проверка домашнего задания.

Пример 1. Построить график функции у = х 2 — 6х + 3. Найти нули функции.

Решение.

2. Координаты вершины параболы: х= — b/2а = — (-6)/2=3, у(3) = 9 – 18 + 3 = — 6, А(3; -6).

4. Нули функции: у(х) = 0, х 2 — 6х + 3 = 0, D = 36 — 4·3 = 36 – 12 = 24, D>0,

x 1,2 = (6 ± )/2 = 3 ± ; В(3 — ;0), С(3 + ;0).

График на рис.1.

Алгоритм построения графика квадратной функции.

1. Определить направление “ветвей” параболы.

2. Вычислить координаты вершины параболы.

3. Записать уравнение оси симметрии.

4. Вычислить несколько точек.

б) Рассмотрим построение графиков линейных функций, содержащих модуль:

1. у = |х|. График функции на рисунке 2.

2.у = |х| + 1. График функции на рисунке 3.

3. у = |х + 1|. График функции рисунке 4.

Вывод.

1. График функции у = |х| + 1 получается из графика функции у = |х| параллельным переносом на вектор {0;1}.

2. График функции у = |х + 1| получается из графика функции у = |х| параллельным переносом на вектор {-1;0}.

2.Опирационно-исполнительная часть.

Этап исследовательской работы. Работа в группах.

Группа 1. Построить графики функций:

а) у = х 2 — 6|x| + 3,

б) у = |х 2 — 6х + 3|.

Решение.

1.Построить график функции у = х 2 -6х+3.

2. Отобразить его симметрично относительно оси Оу.

График на рисунке 5.

б) 1. Построить график функции у = х 2 — 6х + 3.

2. Отобразить его симметрично относительно оси Ох.

График функции на рисунке 6.

Вывод.

1. График функции у = f(|x|) получается из графика функции у = f(x), отображением относительно оси Оу.

2. График функции у = |f(x)| получается из графика функции у = f(x), отображением относительно оси Ох.

Группа 2.Построить графики функций:

а) у = |x 2 — 6|x| + 3|;
б) y = |x 2 — 6x + 3| — 3.

Решение.

1. График функции у = х 2 + 6x + 3 отображаем относительно оси Оу, получается график функции у = х 2 — 6|x| + 3.

2. Полученный график отображаем симметрично относительно оси Ох.

График функции на рисунке 7.

Вывод.

График функции y = |f (|x|)| получается из графика функции у = f(х), последовательным отображением относительно осей координат.

1. График функции у = х 2 — 6х + 3 отображаем относительно оси Ох.

2. Полученный график переносим на вектор {0;-3}.

График функции на рисунке 8.

Вывод. График функции у = |f(x)| + a получается из графика функции у = |f(x)| параллельным переносом на вектор {0,a}.

Группа 3.Построить график функции:

а) у = |x|(х — 6) + 3; б) у = х|x — 6| + 3.

Решение.

а) у = |x| (x — 6) + 3, имеем совокупность систем:

Строим график функции у = -х 2 + 6x + 3 при х

График функции на рисунке 9.

б) у = х |х — 6| + 3, имеем совокупность систем:

Строим график функции у = — х 2 + 6х + 3 при х 6.

2. Координаты вершины параболы: х = — b/2a = 3, у(3) =1 2, А(3;12).

3. Уравнение оси симметрии: х = 3.

4. Несколько точек: у(2) = 11, у(1) = 3; у(-1) = — 4.

Строим график функции у = х 2 — 6х + 3 при х = 7 у(7) = 10.

График на рис.10.

Вывод. При решении данной группы уравнений необходимо рассматривать нули модулей, содержащихся в каждом из уравнений. Затем строить график функции на каждом из полученных промежутков.

(При построении графиков данных функций каждая группа исследовала влияние модуля на вид графика функции и сделала соответствующие заключения.)

Получили сводную таблицу для графиков функций, содержащих модуль.

Таблица построения графиков функций, содержащих модуль.

Группа 4.

Построить график функции:

а) у = х 2 — 5x + |x — 3|;
б) у = |x 2 — 5x| + x — 3.

Решение.

а) у = х 2 — 5х + |х — 3|, переходим к совокупности систем:

Строим график функции у = х 2 -6х + 3 при х 3,
затем график функции у = х 2 — 4х — 3 при х > 3 по точкам у(4) = -3, у(5) = 2, у(6) = 9.

График функции на рисунке 11.

б) у = |х 2 — 5х| + х — 3, переходим к совокупности систем:

Строим каждый график на соответствующем интервале.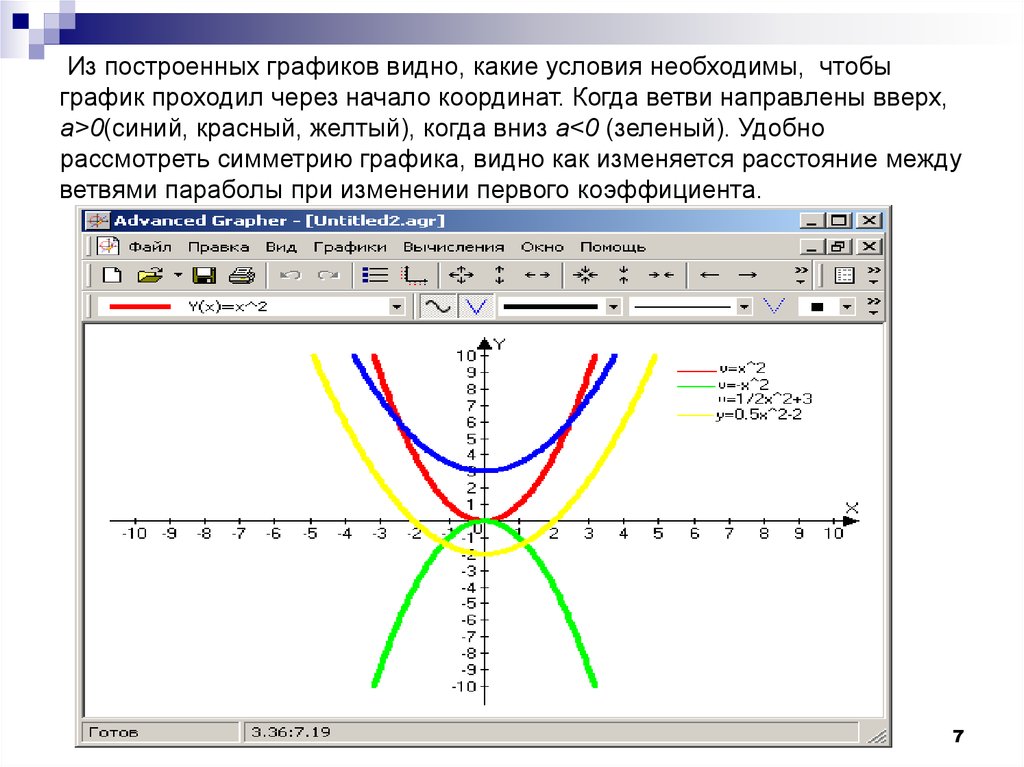

График функции на рисунке 12.

Вывод.

Выяснили влияние модуля в каждом слагаемом на вид графика.

Самостоятельная работа.

Построить график функции:

а) у = |х 2 — 5х + |x — 3||,
б) у= ||x 2 — 5x| + х — 3|.

Решение.

Предыдущие графики отображаем относительно оси Ох.

Группа.5

Построить график функции: у =| х — 2| (|x| — 3) — 3.

Решение.

Рассмотрим нули двух модулей: x = 0, х – 2 = 0. Получим интервалы постоянного знака.

Имеем совокупность систем уравнений:

Строим график на каждом из интервалов.

График на рисунке 15.

Вывод. Два модуля в предложенных уравнениях существенно усложнили построение общего графика, состоящего из трех отдельных графиков.

Учащиеся записывали выступления каждой из групп, записывали выводы, участвовали в самостоятельной работе.

3.

Задание на дом.

Построить графики функций с различным расположением модуля:

1. у = х 2 + 4х + 2;

2. у = — х 2 + 6х — 4.

4. Рефлексивно – оценочный этап.

1.Оценки за урок складываются из отметок:

а) за работу в группе;
б) за самостоятельную работу.

2. Какой момент был наиболее интересен на уроке?

3. Трудное ли домашнее задание?

Построить функцию

Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos . Для ввода функций воспользуйтесь левой колонкой. Вводить можно вручную либо с помощью виртуальной клавиатуры внизу окна. Для увеличения окна с графиком можно скрыть как левую колонку, так и виртуальную клавиатуру.

Преимущества построения графиков онлайн

Визуальное отображение вводимых функций
Построение очень сложных графиков
Построение графиков, заданных неявно (например эллипс x^2/9+y^2/16=1)
Возможность сохранять графики и получать на них ссылку, которая становится доступной для всех в интернете
Управление масштабом, цветом линий
Возможность построения графиков по точкам, использование констант
Построение одновременно нескольких графиков функций
Построение графиков в полярной системе координат (используйте r и θ(\theta))

С нами легко в режиме онлайн строить графики различной сложности. 2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.

Квадратичная функция

Рис 1. Общий вид параболы

Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.

Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).

Основные свойства квадратичной функции

1. При х =0, у=0, и у>0 при х0

2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.

3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }

Заработок в Интернете

Исследование и построение графиков функции

Похожие презентации:

Исследование функций и построение графиков

Исследование функции и построение графика

Исследование функции. Построение графиков

Исследование функции и построение графиков

Схема исследования функции и построение графика

Схема исследования функций и построение графиков

Исследование функций и построение графиков с помощью производной

Исследование функции и построение графика

Исследование функции и построение ее графика

1. Исследование и построение графиков функции

{ интервалы монотонного возрастания и убывания функции — выпуклость функции на промежутке — точки перегиба асимптоты — построение графика функции }
Интервалы монотонного возрастания и убывания функции определяются
знаком производной.

Если производная f | ( x )
положительна на интервале, то
функция f ( x ) возрастает на нем.
x 0 , f 0 lim
x 0
f
f !( x ) 0
x
Если производная f | ( x ) принимает
отрицательные значения на
интервале, то функция f ( x ) на
нем убывает.
Функция f(x) , определенная и непрерывная в промежутке ( a; b ), называется
выпуклой (выпуклой вниз), если для любых точек x1 и x2 из ( a; b ), x1 не
равно x2 , выполняется неравенство:
f ( l1 x1 l2 x2 ) l1f ( x1 ) l2f ( x2 )
каковы бы не были положительные числа l1 и l2 , дающие в сумме единицу.
При f ( l1 x1 l2 x2 ) l1f ( x1 ) l2f ( x2 )
функция f(x) называется вогнутой
y
(выпуклой вверх).
f( x )
x1 x 2
f ( x1 ) f ( x 2 )
f(
)
2
2
f ( x2 )
f ( x1 )
(
a
x1
x2
)
b
x
f ( x ) ( f ( x1 )
f ( x 2 ) f ( x1 )
( x x1 )) 0
( x 2 x1 )
f ( x ) f ( x1 ) f ( x 2 ) f ( x1 )
0
x x1
( x 2 x1 )
f ( x1 ) f ( c ) 0
|
|
x x1
f | ( x1 ) f | ( c )
0
x1 c
Функция f(x) называется вогнутой
(выпуклой вверх), если f || ( x ) 0
f | ( x1 ) f | ( c )
lim
f || ( c ) 0
x1 c
x1 c
y
Функция f(x) называется выпуклой
(выпуклой вниз), если f || ( x ) 0
c ( x1 , x2 )
f ( x ) Y ( x )
f( x )
f ( x2 )
f ( x1 )
0
x1
x
x2
Теорема.

Для выпуклости (вогнутости) функции y = f(x) в промежутке (a,b)
необходимо и достаточно, чтобы здесь выполнялось неравенство
f || ( x ) 0 ( f || ( x ) 0 ) .
Точку M(x0 ;f(x0)) кривой y = f(x) называют её точкой перегиба, если она
отделяет участок графика, где он выпуклый, от участка, где график
функции f(x) вогнут.
В точке перегиба вторая производная функции обращается в ноль.
Достаточным условием существования точки перегиба является смена
знака f || ( x ) при переходе через неё.
f || ( x0 ) 0 f ( x )
y
f || ( x0 ) 0
f || ( x0 ) 0
x
x0
Прямая x = a является вертикальной асимптотой графика функции y = f(x) ,
если хотя бы один из пределов lim f ( x ) или lim f ( x ) равен или .
x a
x a
Прямая y = kx + b является наклонной асимптотой графика функции f(x)
при x , если f(x) представима в виде f ( x ) kx b a( x ) , где
a(x) есть бесконечно малая при x функция.
f( x )
Вертикальная асимптота
lim f ( x )
x a
a(x)
y
a(x)
a(x)
f( x )
y kx b
f( x )
x
x
b lim ( f ( x ) kx )
k lim
x
lim f ( x )
x a
0
x
Для построения рекомендуется следующая последовательность действий.

• Найти множество определения функции, области непрерывности, точки разрыва.
• При построении графика учитывать такие свойства, как четность, нечетность,
периодичность.
• Найти асимптоты графика функции.
• Найти точки пересечения графика с осями координат.
• Найти первую и, если нужно, вторую производную функции. Найти точки в которых
первая и вторая производные либо не существуют, либо обращаются в нуль.
• Составить таблицу изменения знака функции, первой и второй производных.
Определить промежутки возрастания и убывания функции, выпуклости и
вогнутости функции, найти точки экстремума и точки перегиба, вычислить
значения функции в этих точках.
• Окончательно вычертить график функции.
x3
Исследуем и строим график функции y 2
. Функция нечетная.
x 1
Найти множество определения функции, области непрерывности, точки разрыва:
x 2 1 0 D : x 1 D : x ( ; 1 )
y
x3
lim 2
x 1 x
1
x3
lim 2
x 1 x
1
x3
lim 2
x 1 x
1
( 1 ; )
Точки разрыва: x 1 x 1
— второго рода
2
x3
lim 2
x 1 x
1
( 1 ; 1 )
1
-2
-1
0
1
-1
-2
x
2
x3
y 2
x 1
Найти нули функции, наклонные (горизонтальные) асимптоты.

x3
y 2
x 1
y
y
x x x x( x 1 ) x
x
x
x2 1
x2 1
x 2 1
3
2
x3
y( 0 ) 2
0
x
0
x 1
y kx b
f( x )
x3
k lim
lim
1
2
x
x x ( x
x
1 )
x3
b lim ( f ( x ) kx ) lim 2
x
x
x x
1
x
lim 2
0
x x
1
y x
2
1
-2
-1
0
-1
-2
1
2
x
x3
lim 2
x x
1
Найти первую производную функции. Найти точки в которых первая
производная либо не существует, либо обращается в нуль. Найти точки
экстремума.
|
y
x 3 3x 2( x 2 1 ) x 3( 2x )
2
2
2
2
x
1
(
x
1
)
x 3x
x ( x 3 )
( x 2 1 )2 ( x 1 )2( x 1 )2
4
2
2
2
y ( 1 )
x 2( x 2 3 )
|
y (x)
0
( x 1 )2( x 1 )2
x 2 ( x 2 3 ) 0 x1 ,2 0 , x3 ,4 3
y| 0
y| 0
|
1
-1.72
-2
|
|
y| 0 y| 0 y| 0 y 0 y 0
-1
1.

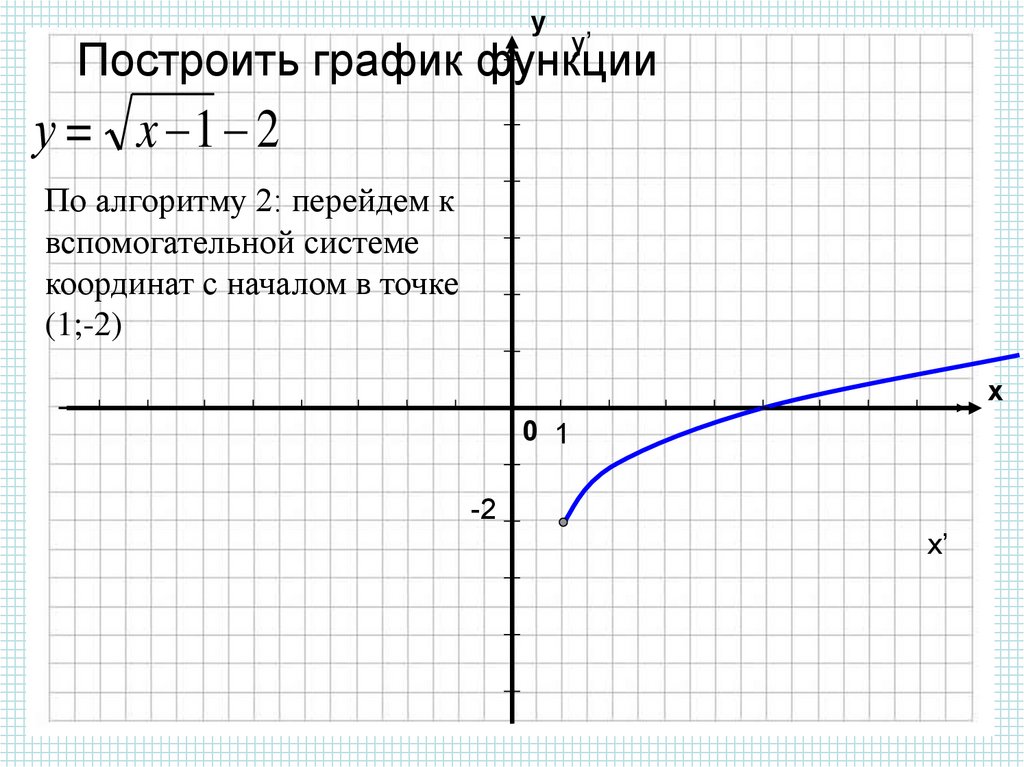72
0
-1
-2
1
x3
y 2
x 1
2
y( 0 ) 0
y( 3 )
x
3 3
2
Найти вторую производную функции. Найти точки в которых вторая
производная либо не существует, либо обращается в нуль. Найти
промежутки выпуклости, точки перегиба.
y
4
2 |
3
x 3x
2 x 6x
y (x) 2
2
2
3
( x 1 )
( x 1 )
2 x( x 2 3 )
||
y
( 1 )
( x 1 )3( x 1 )3
-1.72
||
x ( x 2 3 ) 0 x1 0 , x3 ,4 i 3 -2
y ( x 1 ) 0
y ( 1 x 0 ) 0
y || ( 0 x 1 ) 0
y || ( x 1 ) 0
||
||
-1
2
1
1.72
0
-1
-2
1
2
x3
y 2
x 1
x
y
Построить график функции
x3
y 2
x 1
2
1
-2 -1
0
-1
-2
1
2
x

English Русский Правила

Построение графиков в Excel. Практическая работа

Житкова Ольга Алексеевна, учитель информатики
org/Person»> Лебо Александра Ивановна, учитель информатики

Разделы: Информатика

Цель работы:

научиться строить графики в Excel;
развить самостоятельность;
развить навыки мыслительной деятельности, включая каждого учащегося в учебно – познавательный процесс и создавая условия для работы каждого в индивидуальном темпе;

Оборудование:

ПЭВМ, сеть, проектор;
опорный конспект, план практической работы, варианты для самостоятельной работы учащихся.

Этапы	План урока + опорный конспект	Средства обучения
I	Подготовительный. Постановка учебных задач. Устное разъяснение порядка работы на уроке, тема урока.	—
II	Повторение. Фронтальный опрос изученного материала. Вопросы: предназначение Excel: Расчеты по формулам Графики и диаграммы путь к папке, где сохранить работу.	проектор
III	Объяснение нового материала и подготовка к практической работе: объяснение построения графиков в Excel; работа с проектором. Показать, как и что должно получиться; Раздача вариантов работы.	Проектор, раздаточный материал
IV	Выполнение проектной практической работы: сохранение работы в папку «ГРАФИКИ» под своими идентификаторами; помощь ученикам.	Компьютер
V	Итоги: демонстрация работ учащимися на проекторе и оценка за работы; определение лучшей работы; подведение итогов.	Проектор, раздаточный материал, компьютер

Опорный конспект

Построение совмещенных графиков в Microsoft Office Excel -2007.

Для построения графиков функций Y(X) в Microsoft Office Excel используется тип диаграммы Точечная:

Для этого требуется два ряда значений: Х и Y значения, которые должны быть соответственно расположены в левом и правом столбцах.
Можно совместить построение нескольких графиков. Такая возможность используется для графического решения систем уравнений с двумя переменными, при проведении сравнения анализа значений y при одних и тех же значениях x.

ПРИМЕР.
(Используется при объяснении материала через проектор.)
Построить графики функций y1= x ² и y2= x ³ на интервале [- 3 ; 3] с шагом 0,5.
Алгоритм выполнения задания:
1. Заполнить таблицу значений:

2. Выделить таблицу и указать тип диаграммы Точечная.
3. Выбрать формат точечной диаграммы с гладкими кривыми.
4. В Макете указать название диаграммы «Графики», дать название осей: X и Y

5. Должен получиться график:

P.S. В версии 97-2003 для получения графика, представленного на рисунке надо провести редактирование.

Раздаточный материал

Варианты

ВАРИАНТ 1
Построить графики функций y1= x ²-1, y2= x ²+1 иy=К·(y1/ y2)на интервале [- 3 ; 3] с шагом 0,3.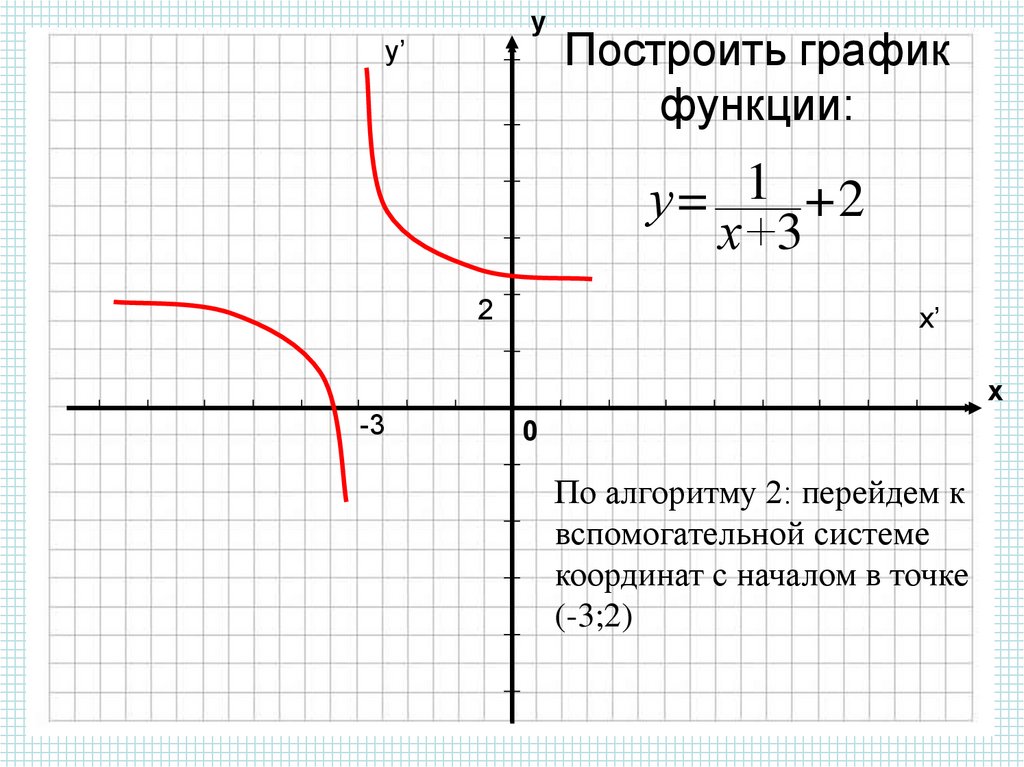

ВАРИАНТ 2
Построить графики функций y1= и y2= 2^х на интервале [- 3 ; 3] с шагом 0,5.

ВАРИАНТ 3
Построить графики функций y1= , y2=на интервале [- 0,5 ; 9] с шагом 0,5.

ВАРИАНТ 4
Построить графики функций y1=, y2= на интервале [- 5 ; -0,5] с шагом 0,5.

ВАРИАНТ 5
Построить графики функций y1= , y2=на интервале [0,5 ; 5] с шагом 0,5.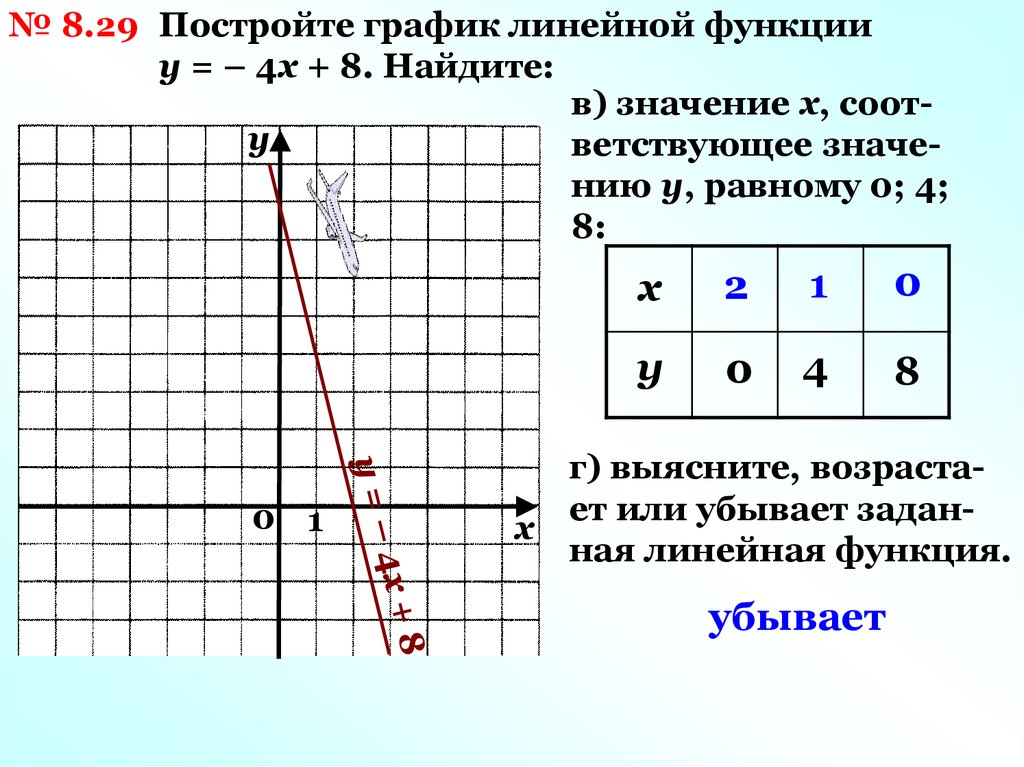

26.02.2009

Применение производной к построению графиков функции

Репетиторы ❯ Математика ❯ Применение производной к построению графиков функции

Автор: Валентин В., онлайн репетитор по математике

●

14.11.2011

●

Раздел: Математика

Если на некотором промежутке график функции представляет собой непрерывную линию, иными словами, такую линию, которую можно провести без карандаша от листа бумаги, то такая функция называется непрерывной на этом промежутке.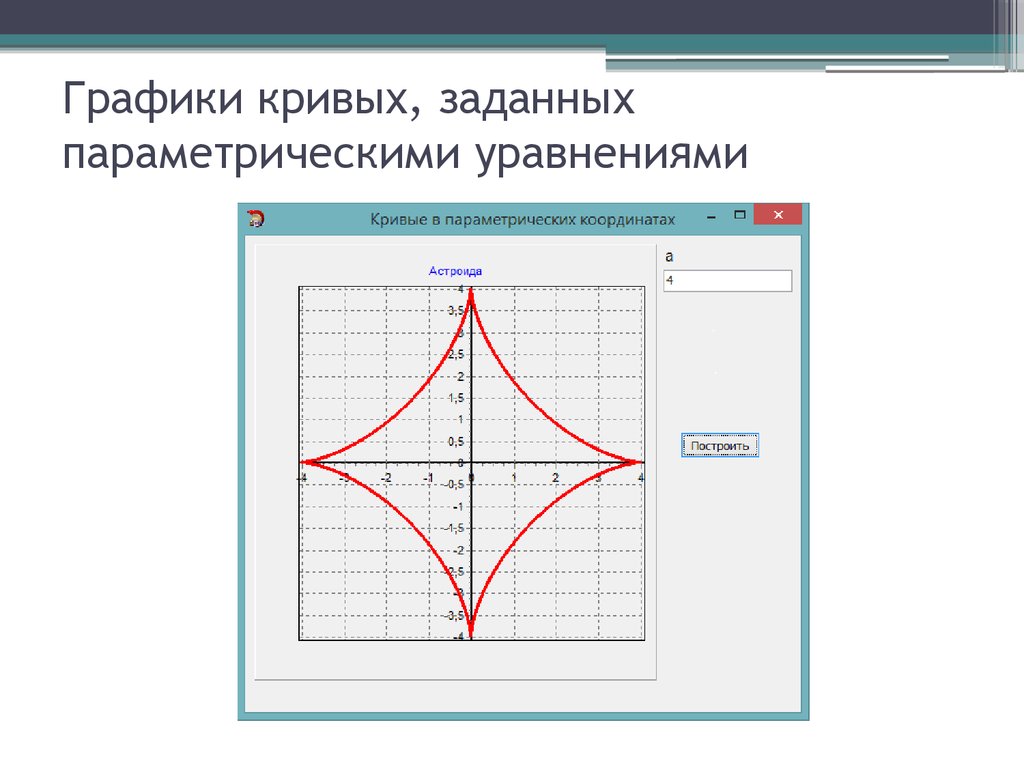 Существуют также функции, которые непрерывными не являются. В качестве примера рассмотрим график функции, которая на промежутках [a; c] и [с; b] непрерывна, но в точке
х = с разрывна и поэтому на всем отрезке [a; b] не является непрерывной. Все функции, изучаемые нами в школьном курсе математики, – это функции непрерывные на каждом промежутке, на котором они определены.
Отметим, что если на некотором промежутке функция имеет производную, то на этом промежутке она непрерывна.
Обратное утверждение является неверным. Функция, которая непрерывна на промежутке, может не иметь производной в некоторых точках этого промежутка. Например, функция
у = |log ₂ x| непрерывна на промежутке х > 0, но в точке х = 1 не имеет производной, в силу того что в этой точке график функции касательной не имеет.
Рассмотрим построение графиков с помощью производной.
Задача 1.
Построить график функции f(x) = x³ – 2x² + x.
Решение.
1) Эта функция определена при всех х € R.
2) Найдем промежутки монотонности рассматриваемой функции и ее точки экстремума с помощью производной. Производная равна f ‘(x) = 3x² – 4x + 1. Найдем стационарные точки:
3x² – 4x + 1 = 0, откуда х₁ = 1/3, х₂ = 1.
Для определения знака производной разложим квадратные трехчлен 3x² – 4x + 1 на множители:
f ‘(x) = 3(х – 1/3)(х – 1). Следовательно, на промежутках х < 1/3 и х > 1 производная положительна; значит, функция возрастает на этих промежутках.
Производная отрицательна при 1/3 < х < 1; следовательно, функция убывает на этом интервале.
Точка х₁ = 1/3 является точкой максимума, так как справа от этой точки функция убывает, а слева – возрастает. В этой точке значение функции равно f (1/3) = (1/3)³ – 2(1/3)² + 1/3 = 4/27.
Точкой минимума является точка х₂ = 1, так как слева от этой точки функция убывает, а справа возрастает; ее значение в этой точке минимума равняется f (1) = 0.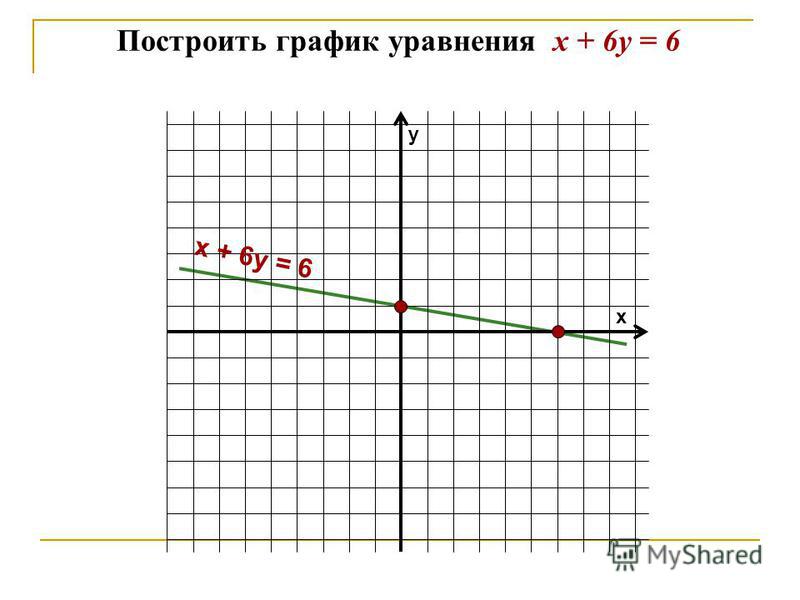
3) При построение графика обычно находят точки пересечения графика с осями координат. Так как f(0) = 0, то график проходит через начало координат. Решая уравнение f(0) = 0, находим точки пересечения графика с осью абсцисс:
x³ – 2x² + x = 0, х(x²– 2х + 1) = 0, х(х – 1) ²= 0, откуда х = 0, х = 1.
4) Для более точного построение графика найдем значения функции еще в двух точках: f(-1/2) = -9/8, f(2) = 2.
5) Используя результаты исследования (пункты 1 – 4), строим график функции у = x³ – 2x² + x.
Для построения графика функции обычно сначала исследуют свойства этой функции с помощью ее производной по схеме, аналогичной схеме при решении задачи 1.
Таким образом, при исследовании свойств функции необходимо найти:
1) область ее определения;
2) производную;
3) стационарные точки;
4) промежутки возрастания и убывания;
5) точки экстремума и значения функции в этих точках.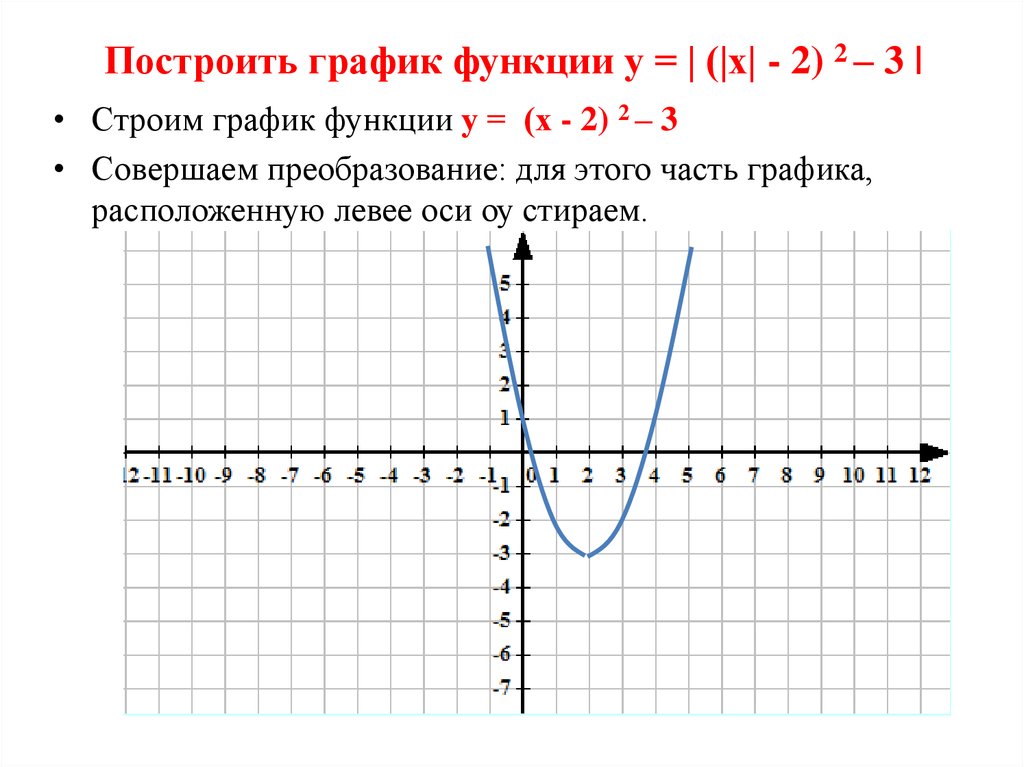
Результаты исследования удобно записывать в виде таблицы. Затем, используя таблицу, строят график функции. Для более точного построения графика обычно находят точки его пересечения с осями координат и – при необходимости – еще несколько точек графика.
Если же мы сталкиваемся с четной или нечетной функцией, то для построения ее графика достаточно исследовать свойства и построить ее график при х > 0, а затем отразить его симметрично относительно оси ординат (начала координат). Например, анализируя функцию f(x) = х + 4/х, мы приходим к выводу о том, что данная функция нечетная: f(-x) = -х + 4/(-х) = -(х + 4/х) = -f(x). Выполнив все пункты плана, строим график функции при х > 0, а график этой функции при х < 0 получаем посредством симметричного отражения графика при х > 0 относительно начала координат.
Для краткости решения задач на построение графиков функции большую часть рассуждений проводят устно.
Также отметим, что при решении некоторых задач мы можем столкнуться с необходимостью исследования функции не на всей области определения, а только на некотором промежутке, например, если нужно построить график, скажем, функции f(x) = 1 + 2x² – x⁴ на отрезке [-1; 2].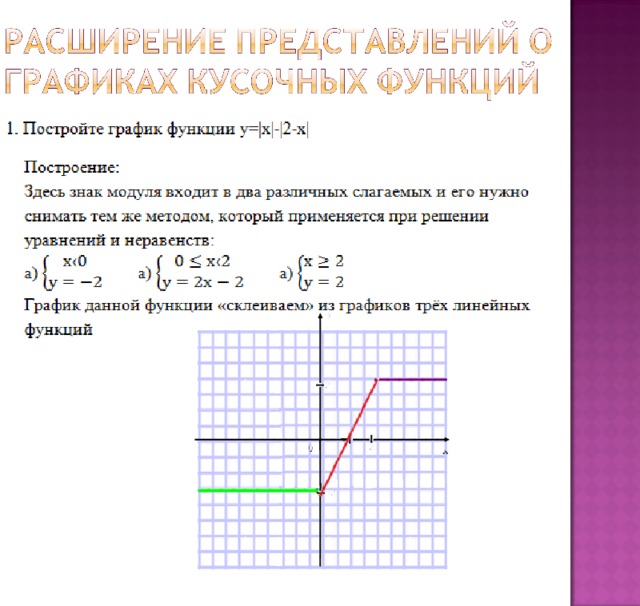
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос

Математика

Курсы по математике 10 класс

Математика

Курсы по математике 9 класс

Математика

Математика 11 класс

Математика

Курсы по геометрии 7 класс

Математика

Курсы по алгебре 7 класс

Математика

Алгебра 8 класс

Математика

Курсы по геометрии 8 класс

Французский язык

Курсы французского языка для начинающих

Генератор диаграмм стеблей и листьев
Использование калькулятора
Создавайте в режиме онлайн диаграмму стеблей и листьев или диаграмму ствола и вычисляйте базовую описательную статистику для выборочного набора данных с 4 или более значениями и до 2500 значений, положительных и отрицательных. Введите значения, разделенные запятыми, например 31, 26, 20, 28, 13, 10, 18, 13.
Вы также можете копировать и вставлять строки точек данных из документов, таких как электронные таблицы Excel или текстовые документы, с запятыми или без них в поле ввода. форматы, указанные в таблице ниже.
Примечания :
Не обрабатывает десятичные дроби. Если вам нужно работать с десятичными дробями, вы можете умножить все свои значения на коэффициент 10 и вычислить на их основе. Вам просто нужно будет правильно интерпретировать результаты.
Дополнительные описательные статистические значения см. Калькулятор описательной статистики.
Ниже приведены образцы стеблей и листьев, а также расчетные статистические значения.
Образец стебля и листа с разделенными стеблями
Набор данных:
42, 14, 22, 16, 2, 15, 8, 27, 6, 15, 19, 48, 4, 31, 26, 20, 28 , 13, 10, 18, 13, 15, 48, 16, 15, 5, 18, 16, 28, 11, 0, 27, 28, 5, 40, 21, 18, 7, 12, 6, 40, 12 , 2, 20, 35, 3, 16, 13, 8, 15, 7, 65, 65, 25, 15, 21, 12, 12, 35, 30, 14, 35, 20, 35, 7, 35
Участок стебля и листьев:
0 2 2 3 4
5 5 6 6 7 7 7 8 8
1
0 1 2 2 2 2 3 3 3 4 4
5 5 5 5 5 5 5 5 5 5 5 5 5
1
6 6 6 6 8 8 8 9
2
0 0 0 1 1 2
2
5 6 7 7 8 8 8
3
5 5 5 5 5
4
0 0 2
Основные статусы и расчеты, используемые в этот Калькулятор
Минимум
Упорядочивание набора данных {x ₁ ≤ x ₂ ≤ x ₃ ≤ .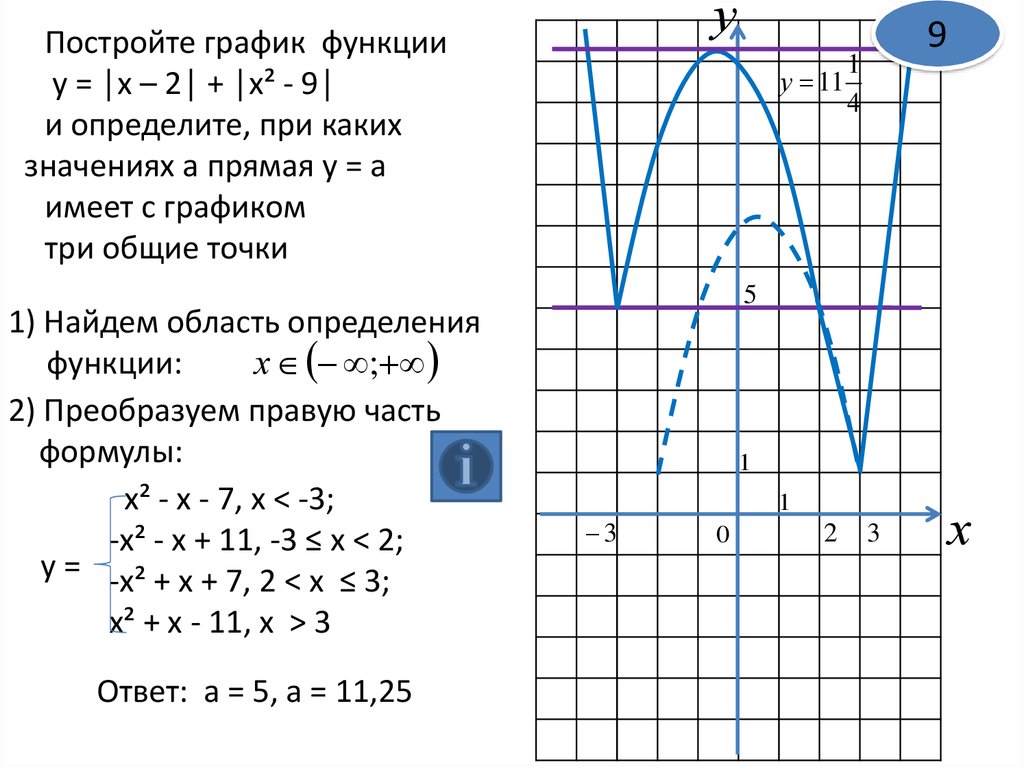 {n} \] 9{n}x_i}{n} \]
Медиана
Упорядочивание набора данных {x ₁ ≤ x ₂ ≤ x ₃ ≤ … ≤ x _n } от меньшего к большему значению, медиана — это числовое значение, отделяющее верхнюю половину упорядоченных выборочных данных из нижней половины. Если n нечетно, медиана является центральным значением. Если n равно четному, медиана является средним значением двух центральных значений.
Если n нечетно, медианой является значение в позиции p, где
9{2}}{n — 1} \]

Допустимо Разделитель
Форматы данных
Столбец (новые строки)
42
54
65
47
59
40
53
42, 54, 65, 47, 59, 40, 53
Разделенные запятыми (CSV)
42,
54,
65, г.
47, г.
59, г.
40, г.
53, г.
или
42, 54, 65, 47, 59, 40, 53
42, 54, 65, 47, 59, 40, 53
Пробелы
42 54
65 47
59 40
53
или
42 54 65 47 59 40 53
42, 54, 65, 47, 59, 40, 53
Смешанные разделители
42
54 65, 47,59,
40 53
42, 54, 65, 47, 59, 40, 53
Сюжет | Онлайн MATLAB Graphing — обмен файлами
0012
Вы будете видеть обновления в ленте отслеживаемого контента
Вы можете получать электронные письма, в зависимости от ваших предпочтений в общении
версия 1. 6.0.0 (312 КБ) от Крис
Опубликуйте свои рисунки MATLAB в Интернете с помощью одной строки кода.
https://github.com/plotly/plotly_matlab
3,4 тыс. загрузок За все время: 3 357″ data-original-title=»Загрузки» aria-describedby=»popover506129″>
Обновлено 8 марта 2022 г.
Из GitHub
Посмотреть историю версий
Версии, использующие ветку GitHub по умолчанию, не могут быть загружены.
8 марта 2022 г. 1.6.0.0
Обновление изображения
18 августа 2015 г. 1.5.0.0
Ссылка на репозиторий GitHub.
27 июня 2013 г. 1.4.0.0
Исправлена ошибка при регистрации API
26 июня 2013 г. 1.2.0.0
Добавлена контактная информация.
18 июня 2013 г. 1.1.0.0
Обновленные документы
18 июня 2013 г. 1.0.0.0
Посмотреть лицензию на GitHub
Обзор
Функции
Отзывы (5)
Обсуждения (10)
Plotly (https://plot.ly/) — это графическая онлайн-платформа, которая позволяет легко создавать и публиковать интерактивные рисунки качества публикации. Этот пакет преобразует ваши рисунки MATLAB в онлайн-графики Plotly с помощью одной строки кода:
«`
[X, Y, Z] = пики;
контур(X,Y,Z,20)
fig2plotly()
«`
Этот код создает этот график в вашем браузере: https://plot. ly/~demos/1574
Подробнее см. в официальной документации по адресу https://plot.ly/MATLAB.
Цитировать как
Крис (2022). Сюжетно | Онлайн-графики MATLAB (https://github.com/plotly/plotly_matlab), GitHub. Проверено 29 сентября 2022 г. .
Совместимость версий MATLAB
Created with Р2013а
Совместимость с любой версией
Совместимость с платформами
Windows macOS Linux
Категории
МАТЛАБ > Графика > Печать и сохранение >
Метки Добавить теги
Панель аннотаций сторонних производителей, цвет, сбор данных, экспорт данных, импорт графики, экспорт графики, импорт графики, графический интерфейс, инструменты графического интерфейса, тепловая карта, гистограмма, латекс, pdf, график, инструменты для совместного использования RGB, подграфик, текст, набор инструментов, утилиты, утилита, визуализация, веб
Благодарности
Вдохновленный: Программа для нанесения слов на график или рисунок
Охота за сокровищами сообщества
Найдите сокровища в MATLAB Central и узнайте, как сообщество может вам помочь!
На охоту!
Чтобы просмотреть или сообщить о проблемах в этом дополнении GitHub, посетите репозиторий GitHub .
Выберите сеть Сайт
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и посмотреть местные события и предложения. На основе ваше местоположение, мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Европа
Обратитесь в местный офис
Научный графический калькулятор онлайн — 100% бесплатный и простой в использовании
Что такое график?
График представляет собой двухмерную диаграмму, которая представляет функциональную связь между любыми двумя величинами, переменными или числами. График можно построить, начертив:

Линия
Кривая
Серия стержней
Серия точек

Все эти формы рисунка, представляющие отношения между любыми двумя величинами. Вкратце это говорит о том, как влияет на одну величину изменение другой величины, которая зависит от первой или связана с ней. График также называется графиком, который показывает, как одна переменная изменяется относительно другой. При построении графика любой переменной с помощью нашего графического онлайн-калькулятора сначала необходимо решить, какая переменная является независимой, а какая зависимой.
Оси и квадранты графика
На графике есть две оси.
Горизонтальная или ось X
Это горизонтальная ось или ось x, и на этой оси представлены независимые переменные.
Вертикальная или ось Y
Это вертикальная ось или ось Y, где представлены зависимые переменные.
Каждый график имеет четыре квадранта, в которых представлены положительные и отрицательные значения.

Графический калькулятор TI 83 (VS) Графический калькулятор TI 84 (VS) Графический калькулятор TI 89:
Графический калькулятор ti 83 специально разработан для учащихся средних и старших классов. Он работает как естественная помощь, которая предлагает отличную поддержку для всех математических курсов, начиная от предварительной алгебры и заканчивая исчислением и статистикой, а также курсами AP или Advanced Placement.

Когда дело доходит до графического калькулятора ti84, говорят, что это действительно самый быстрый инструмент для графических вычислений. Да, этот эффективный и надежный инструмент был разработан для замены TI-83. Он поставляется с удивительными функциями, которые помогают учащимся хорошо успевать по математике и естественным наукам, а также помогают решать задачи линейной алгебры.

Что ж, здесь мы собираемся рассказать вам о графическом калькуляторе ti 89 — еще одном инструменте, который также предназначен для математических курсов, начиная от средней школы и заканчивая колледжем. Оптимистичные исследования показывают, что этот инструмент работает в значительной степени, поскольку он значительно упрощает решение задач для инженерных курсов и математики.

Что ж, вернемся к сути. Компания texas Instruments предоставила серию эффективных калькуляторов с графическим дисплеем, которые способны строить графики, решать математические уравнения и даже выполнять другие задачи с переменными. Тем не менее, специалисты онлайн-калькулятора предоставили эффективный графический онлайн-калькулятор, который выполняет простые вычисления в течение нескольких секунд, и это может быть альтернатива ti 83, 84 и 89.калькулятор серий.

Зачем вам может понадобиться графический калькулятор?
Это учебное пособие, специально разработанное для учащихся и учителей и помогающее понять концепции математики и естественных наук. Учащиеся получают доказанные академические преимущества при использовании графического калькулятора ti 84 и т. д. Оптимистические исследования показывают, что калькулятор ti помогает улучшить математические навыки учащихся и их отношение к математике. Дальнейшие исследования показывают, что техасские инструменты или ти-графический калькулятор повышают уровень успеваемости учащихся.
Некоторые студенты колледжей/университетов не имеют ни малейшего представления о том, насколько полезен научный калькулятор на уроках математики. Да, эти удобные инструменты рекомендуются для занятий математикой, начиная с начальной алгебры, а приложениям высшего образования, которые включают физику, исчисление или данные, часто требуется онлайн-калькулятор ti 84 или другой.
Кроме того, нет необходимости вкладывать средства в покупку научного графического инструмента; Вы можете построить график онлайн с помощью нашего графического калькулятора. Да, приведенный выше онлайн-калькулятор графического отображения может легко использоваться инженерами, экспертами, студентами и преподавателями в основных и профессиональных целях.
Графики в повседневной жизни:
Бухгалтеры, менеджеры по продажам и многие другие используют графики для передачи или представления информации о финансах, целях, которые необходимо достичь, или целях, которые уже достигнуты. График — это визуальная иллюстрация всех этих вещей. В домах графики можно использовать для планирования месячного бюджета, вы можете оценить с помощью графика, где вы тратите больше и где вы должны потратить больше. График может быстро представить данные, факты и цифры в виде диаграммы, что сделает вашу жизнь проще. Вышеупомянутый калькулятор является бесплатным инструментом, который используется от дома до офиса. Бизнесмены также используют графики для оценки своих прибылей и убытков.
Графический калькулятор
Построение графика по уравнению или даже по заданным числам — непростая процедура. Это включает в себя множество сложных вычислений, чтобы получить значение, которое будет отображаться на графике. Это инструмент, который может рисовать для вас графики, решать сложные уравнения. Вам нужно указать значения в заданных полях, и наш инструмент построения графиков предоставит вам готовый график из заданных вами переменных.

Этот бесплатный виджет — чудо-инструмент для учащихся и даже учителей. Они используются в математике, особенно в алгебре, исчислении, где вам нужно решить уравнение, а затем построить графики соответствующих переменных. Инструмент значительно облегчил жизнь студентов и сэкономил время, поскольку они получают график всего за несколько секунд. Единственное, что им нужно сделать, это ввести значения и скопировать график, который наш инструмент для построения графиков сделал из заданных вами значений.

В настоящее время каждый хочет сэкономить время, выполняя работу быстро с использованием передовых технологий. Никто не хочет тратить лишнее время на свою работу, которую можно легко сделать с помощью продвижения. А построение графиков из рисунков — одна из самых сложных задач для студентов, поэтому для облегчения работы студентов мы предоставляем простой и быстрый инструмент для построения графиков, который вы можете увидеть в верхней части этого поста. Они могут использовать его, чтобы сэкономить свое время и выполнить свою работу за минимальное время с гораздо меньшими усилиями и размышлениями. Этот калькулятор позволяет получить точные графики.
Как пользоваться графическим калькулятором онлайн-калькулятором?
Многие графические онлайн-калькуляторы не бесплатны, а бесплатные не предназначены для построения хороших или точных графиков. Наш сайт уникален в этом случае, он предоставит вам лучший бесплатный инструмент для построения графиков, который можно использовать бесплатно в любое время и без ограничений по количеству записей или результатов, что означает, что вы можете использовать его столько раз, сколько хотите для получения графиков.
Вы должны ввести значение, которое вы хотите построить на графике в указанном выше поле
Вы можете добавить несколько значений; вам просто нужно щелкнуть знак «Плюс», чтобы добавить несколько значений
Кроме того, вы можете изучить параметры настроения, т.е. параметры DEG, RAD, GRAD и Gridlines, т.е. НОРМАЛЬНОЕ, МЕНЬШЕ и ВЫКЛ, нажав кнопку настройки
После того, как вы ввели значение, выбрали параметры Mood и Gridlines, затем нажмите кнопку отправки, чтобы получить желаемый график
На рынках вы найдете множество портативных графических калькуляторов, которые имеют множество функций, но стоят дорого, и вам приходилось брать это устройство с собой всякий раз, когда вам нужно было построить график определенных переменных. Брать с собой устройство может быть обременительно. Почти у каждого в этом веке есть мобильный телефон и круглосуточный доступ к Интернету, поэтому использование этого онлайн-инструмента для построения графиков более удобно, поскольку у вас всегда есть мобильный телефон с собой, вы можете просто войти на сайт calculate-online.net и начать использовать. наш бесплатный графический инструмент. Если у вас есть возможность использовать ручной инструмент, зачем использовать большое портативное устройство?

Учителя также используют графические калькуляторы, чтобы учащиеся лучше понимали. Это также экономит его/ее время, и учитель может отображать множество графических данных на графиках за меньшее время. Тогда, если бы ей пришлось сначала решить уравнение, а не отображать данные на графике, ей/ему потребовалось бы время всего класса, чтобы решить и построить один график. Учащимся также трудно понять так много деталей за короткое время. Итак, используйте наш графический калькулятор для графического отображения ваших данных, что сделает их более понятными, а также уменьшит нагрузку на ум учащихся при решении задач, а затем построении графиков.
Преимущества использования онлайн-калькулятора графиков
Да, этот инструмент лучше всего подходит для всех, кто хочет строить графики или решать уравнения с помощью графиков. Его могут использовать учащиеся и учителя, чтобы ускорить работу, требующую построения графиков. Его может использовать любой, неважно, слаб ли он в математике или имеет небольшое представление о дробях, переменных или алгебре. Эти студенты могут воспользоваться нашим калькулятором для решения сложных уравнений и построения графиков. Если человек не может решить или построить график, это не вопрос низкой самооценки. Используя технологии, они могут быть уверены в себе, что они также могут изучать сложные предметы и решать сложные проблемы. Введите необходимые переменные или цифры и подождите несколько секунд, и вы получите нужный график перед вашими глазами всего за несколько секунд.
Калькулятор графических функций помогает учащимся лучше понимать математику и естественные науки:
Несомненно, графический калькулятор является эффективным инструментом, с помощью которого учащиеся могут формировать наборы навыков, чтобы лучше работать как в математике, так и в естественных науках. Да, этот инструмент предлагает учащимся эффективно и надежно решить математическую задачу, визуализируя их. Когда учащиеся могут столкнуться с формулами, выражениями и графиками на экране, они могут изучить определенные концепции и даже установить связи, которые ведут к более глубокому пониманию.
Words By Calculator-Online:
Это удобный инструмент, так как вы можете использовать его в любом месте в любое время, просто имея доступ в Интернет. Вы можете использовать его на настольном ПК, на ноутбуке, мобильном телефоне или планшете. Запомните наш сайт, и мы потратим несколько секунд и сделаем вашу работу в кратчайшие сроки. Этот графический калькулятор — фантастический инструмент, помогающий людям в их сложной работе. Мы гарантируем вам, что вы не найдете в Интернете лучшего и точного графического калькулятора, чем наш.
PlotDigitizer — извлечение данных из графического изображения онлайн
Plotdigitizer — онлайн-инструмент для извлечения данных, который позволяет пользователям извлекать данные из изображений в числовом формате. Короче говоря, он преобразует ваши визуальные графики в числа. Программное обеспечение поставляется с множеством полезных и экономящих время функций.
Запустить приложение Купить сейчас
PlotDigitizer
Множество полезных функций
Благодаря потрясающим функциям извлекайте данные из графиков и диаграмм несколькими щелчками мыши
Несколько графиков
Поддержка нескольких графиков: XY, гистограммы, полярные, троичные, круговые/кольцевые, гистограммы, измерения, карты
Анализ и оценка математических выражений: вы можете вводить 1/4 вместо 0,25 или «пи» вместо 3,14…
Форматы нескольких осей
Работает с линейными и нелинейными шкалами: логарифмическая (натуральная и с основанием 10), дата/время, обратная , широта, долгота
Панель масштабирования
Увеличивает изображение и повышает точность точек данных во время извлечения данных вручную
Форматы файлов изображений
Принимает все распространенные форматы файлов изображений: JPG/JPEG, PNG, GIF, WEPG, BMP, SVG, SVGz
Несколько вариантов экспорта
Экспорт извлеченных данных в несколько форматов: CSV, MS Excel, JSON, MATLAB, Python, Matrix…
Несколько наборов данных
Сохранение, сортировка, извлечение, удаление и управление сотнями наборов данных в PlotDigitizer
UI/UX
Усовершенствованный и усовершенствованный пользовательский интерфейс позволяет пользователям быстро оцифровывать графики и изображения
Редактирование изображений
Редактирование изображения с помощью встроенного редактора изображений: обрезка, поворот, отражение, масштабирование, черная дорожка (удаление линий сетки), и т.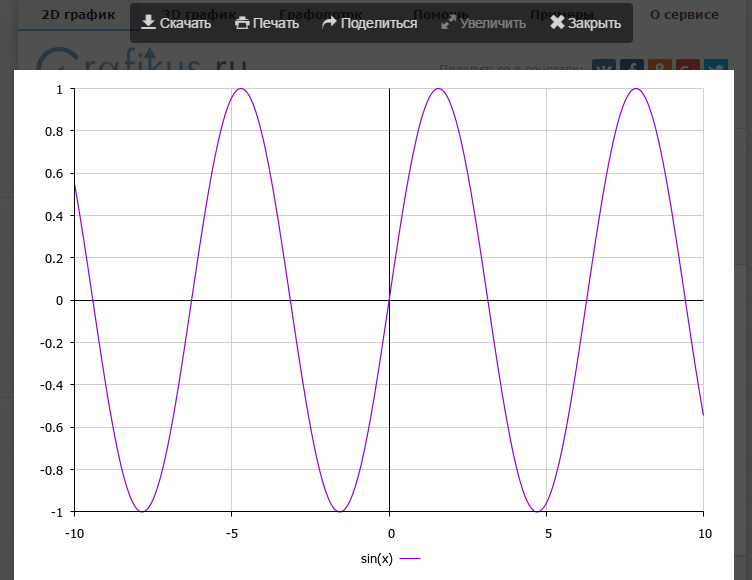 д.
Кросс-платформенный
Доступно для Windows, Mac, Linux и Интернета
Поддержка
Решайте любые технические проблемы с очень быстрым реагированием
AutoTrace Datapoints
Извлечение данных упрощается благодаря мощным алгоритмам, написанным на C++
Автоматическое извлечение данных из вертикальных гистограмм Автоматическое отслеживание кривых из графиков XY Легкое извлечение данных из полярных графиковИзвлечение данных из круговых диаграмм вручную (оцифровка графика) Извлечение из тройных диаграмм Экспорт извлеченных данных в различные форматы: CSV, MS Excel, MatLab, PythonАвтоматическое извлечение данных из гистограммДата/ средство выбора времени для масштаба оси доступно в PlotDigitizer Pro. Автоматическое обнаружение разбросанных точек данных с помощью алгоритмов PlotDigitizer. Использование панели масштабирования PlotDigitizer для повышения точности данных. Использование алгоритма кривой для быстрого извлечения большого количества точек данных.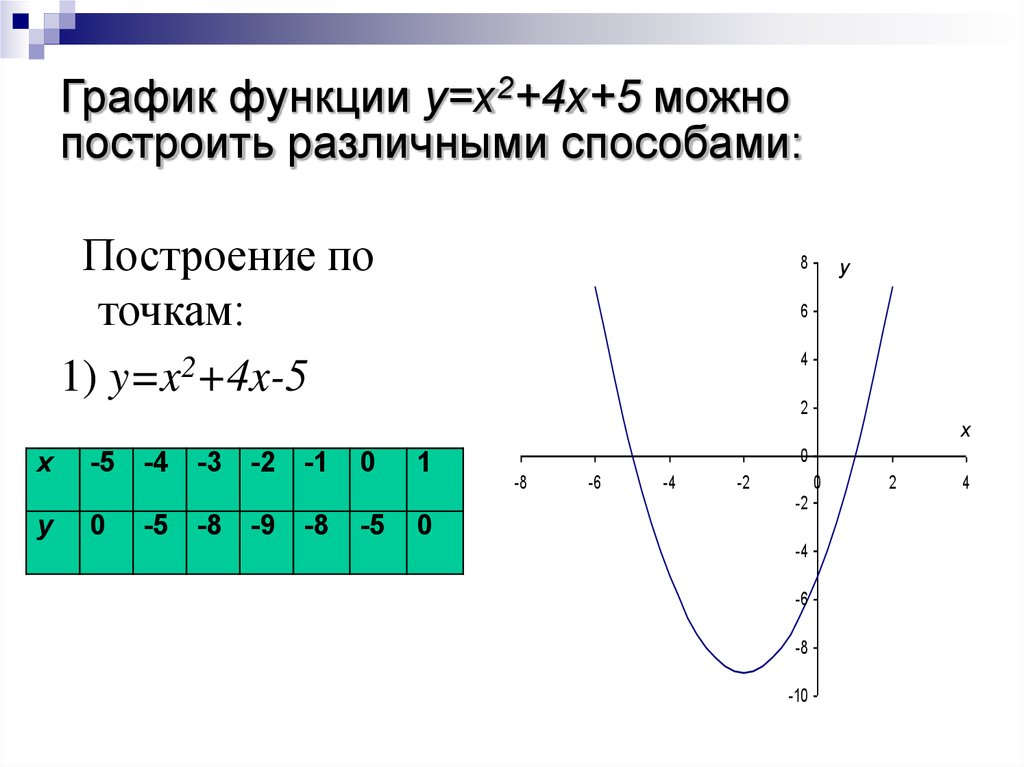
Повышение производительности
Мгновенное автоматическое восстановление исходных числовых данных из графических изображений

Почему Pro?
С PlotDigitizer Pro у вас будет доступ к многочисленным функциям
Функции Бесплатно Про
Платформы Доступно только онлайн
Да
Да
Автономно для Windows, Mac, Linux
№
Да
Типы графиков XY, линейка, столбец, полярная, тройная, круговая/бублик, карты, расстояние
Да
Да
Гистограмма, карты (меркаторские, линейные), измерения (расстояние, угол, площадь)
№
Да
Автотрассировка Алгоритмы автоматического обнаружения: кластер, точки, кривые, полоса, край, центроид, скелет, гистограмма 94
№
Да
Многоосевые весы Линейная, логарифмическая база 10, дата/время
Да
Да
Дата/время (с выбором), логарифмическая база e, обратная величина, широта, долгота
№
Да
Панель масштабирования Панель увеличения (с увеличением по умолчанию)
Да
Да
Панель масштабирования (с настраиваемым увеличением)
№
Да
Форматы файлов изображений JPG/JPEG, PNG, GIF, WEPG, BMP, SVG, SVGz
Да
Да
Автоматическое масштабирование небольших SVG
№
Да
Основные операции Перетаскивание и/или удаление точек данных по одной
Да
Да
Перетаскивание нескольких точек данных, выбор и/или удаление нескольких точек данных одновременно
№
Да
Параметры экспорта Буфер обмена, CSV, MS Excel, список/массив Python, JSON
Да
Да
Пользовательский разделитель, MATLAB, Matrix, HTML, Latex, TSV
№
Да
Сортировка извлеченных значений данных по возрастанию, убыванию или в порядке ближайшего соседа
№
Да
Форматирование извлеченных значений данных до десятичных разрядов, количества цифр или экспоненциального представления
№
Да
Несколько наборов данных Сохранение, хранение и управление сотнями наборов данных
№
Да
Редактирование изображений Обрезка, поворот, отражение, масштабирование вверх/вниз, фильтрация изображения
№
Да
Go Pro Now
Наслаждайтесь полнофункциональным приложением Plotdigitizer — получите пожизненную лицензию за единовременный платеж
Special Limited Time Offer
03
Hours
27
Minutes
35
Seconds
Get 40% Off
LifeTime License
$ 29
$ 49 ~ 40 Скидка %
Единовременный платеж
Продление поддержки и обновлений
Один год
Два года
Без ограничений
Количество лицензий
Купить сейчас
Наши покровители
Нам доверяют тысячи исследователей и инженеров по всему миру

Загрузить сейчас
Загрузите, установите и запустите полнофункциональное приложение в вашей любимой операционной системе
Часто задаваемые вопросы
Краткие ответы на некоторые часто задаваемые вопросы наших пользователей
Что такое PlotDigitizer?
PlotDigitizer — это программное обеспечение для извлечения данных, которое оцифровывает графики и графические изображения. Его встроенная функциональность позволяет пользователям быстро извлекать данные из графиков, графиков и диаграмм.
Как использовать PlotDigitizer или как извлечь данные из графика?
Загрузите изображение графика в PlotDigitizer, выберите тип графика, откалибруйте ось/оси и начните отмечать точки и автоматически генерируемые значения данных точек. Вы также можете экспортировать эти данные в другие форматы. Для получения дополнительной информации прочитайте нашу официальную документацию.
Как получить PlotDigitizer бесплатно?
Онлайн-приложение PlotDigitizer — это бесплатный инструмент, доступный только для онлайн-использования. Инструмент бесплатный и позволяет пользователям извлекать данные из различных графиков, хотя и имеет ограниченные возможности. Для полного доступа к дополнительным функциям, таким как автоматическое отслеживание, хранение наборов данных, вам необходимо приобрести лицензию Pro
Как скачать PlotDigitizer для Windows, Mac или Linux?
PlotDigitizer — кроссплатформенное программное обеспечение.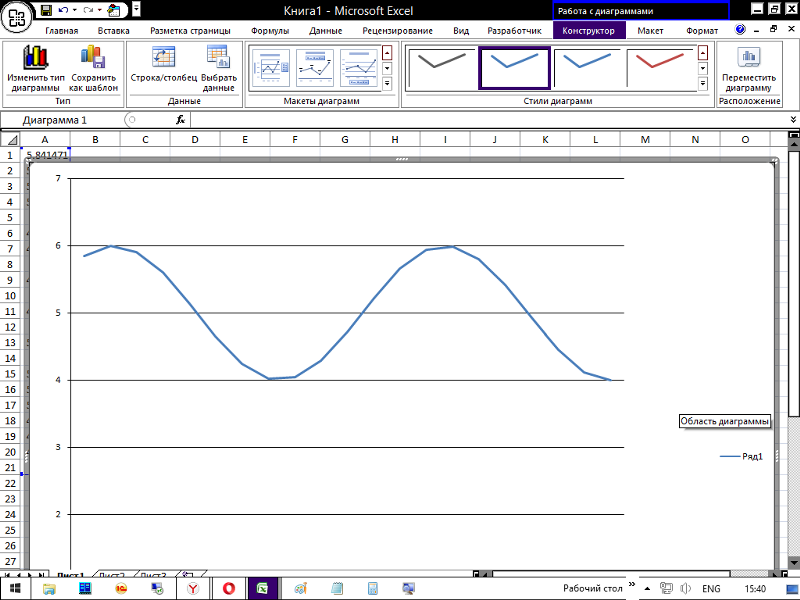 Он доступен для Windows, Mac или Linux.
Как долго действует профессиональная лицензия PlotDigitizer?
Профессиональная лицензия PlotDigitizer для покупной версии действительна бессрочно. Но для будущих обновлений вам придется заплатить дополнительные сборы, если вы хотите обновить.
Для скольких пользователей/устройств действительна профессиональная лицензия PlotDigitizer?
Одна лицензия действительна для одного пользователя для одного устройства одновременно. Однако пользователь может применить ту же лицензию к другому устройству после деактивации с первого устройства.
Могу ли я передать лицензию другим пользователям?
Нет. Лицензия не подлежит передаче, неисключительная и ограниченная. Чтобы узнать больше, перейдите к нашему лицензионному соглашению.
Могу ли я перепродавать программное обеспечение?
Нет. Вы не можете перепродавать программное обеспечение или сублицензировать его. Единственный способ приобрести лицензию — через нас.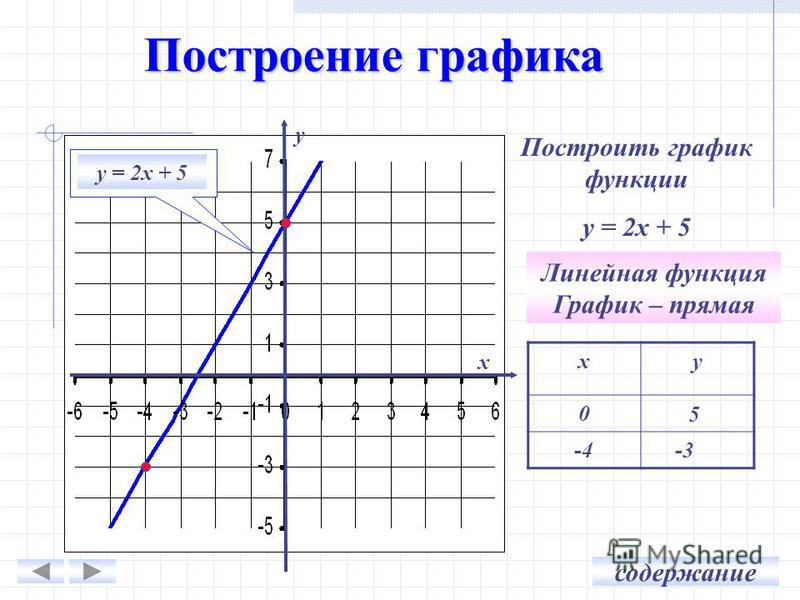
Какова политика возврата?
Мы не предлагаем возврат средств. Пользователи могут использовать онлайн-приложение PlotDigitizer или протестировать загружаемую пробную версию программного обеспечения перед покупкой.

Online Graph Dictionary Learning
Седрик Винсент-Кюаз, Титуан Вайер, Реми Фламари, Марко Корнели, Николя Курти
Материалы 38-й Международной конференции по машинному обучению , PMLR 139:10564-10574, 2021.
Аннотация
Изучение словаря является ключевым инструментом для обучения представлению, которое объясняет данные как линейную комбинацию нескольких основных элементов. Тем не менее, этот анализ не поддается в контексте изучения графов, поскольку графы обычно принадлежат разным метрическим пространствам. Мы заполняем этот пробел, предлагая новый онлайн-подход к обучению по словарю графов, который использует расхождение Громова-Вассерштейна для подгонки данных. В нашей работе графы кодируются через попарные отношения их узлов и моделируются как выпуклая комбинация атомов графа, то есть элементов словаря, оцениваемых благодаря онлайн-стохастическому алгоритму, который работает с набором данных незарегистрированных графов с потенциально разным количеством узлов. Наш подход естественным образом распространяется на помеченные графы и дополняется новой верхней границей, которую можно использовать в качестве быстрой аппроксимации Громова Вассерштейна в пространстве вложений. Мы предоставляем числовые доказательства, демонстрирующие интерес нашего подхода к неконтролируемому встраиванию наборов данных графа, а также к онлайн-оценке и отслеживанию подпространства графа.
Процитировать эту статью
БибТекс
@InProceedings{pmlr-v139-vincent-cuaz21a, title = {Онлайн-обучение графическому словарю}, автор = {Винсент-Куаз, Седрик и Вайер, Титуан и Фламари, Рми и Корнели, Марко и Корти, Николя}, booktitle = {Материалы 38-й Международной конференции по машинному обучению}, страницы = {10564--10574}, год = {2021}, редактор = {Мейла, Марина и Чжан, Тонг}, объем = {139}, серия = {Материалы исследования машинного обучения}, месяц = {18--24 июля}, издатель = {PMLR}, pdf = {http://proceedings. mlr.press/v139/vincent-cuaz21a/vincent-cuaz21a.pdf}, URL = {https://proceedings.mlr.press/v139/vincent-cuaz21a.html}, abstract = {Изучение словаря — это ключевой инструмент для изучения представлений, который объясняет данные как линейную комбинацию нескольких основных элементов. Тем не менее, этот анализ не поддается в контексте изучения графов, поскольку графы обычно принадлежат разным метрическим пространствам. Мы заполняем этот пробел, предлагая новый онлайн-подход к обучению по словарю графов, который использует расхождение Громова-Вассерштейна для подгонки данных. В нашей работе графы кодируются через попарные отношения их узлов и моделируются как выпуклая комбинация атомов графа, то есть элементов словаря, оцениваемых благодаря онлайн-стохастическому алгоритму, который работает с набором данных незарегистрированных графов с потенциально разным количеством узлов. Наш подход естественным образом распространяется на помеченные графы и дополняется новой верхней границей, которую можно использовать в качестве быстрой аппроксимации Громова Вассерштейна в пространстве вложений. Мы предоставляем числовые доказательства, демонстрирующие интерес нашего подхода к неконтролируемому встраиванию наборов данных графа, а также к онлайн-оценке и отслеживанию подпространства графа.} }
Сноска
%0 Документ конференции Онлайн-обучение графическому словарю %T %A Седрик Винсент-Куаз %A Титуан Вайер %A Реми Фламари %A Марко Корнели %A Николя Курти %B Материалы 38-й Международной конференции по машинному обучению %C Материалы исследования машинного обучения %D 2021 %E Марина Мейла %E Тонг Чжан %F pmler-v139-vincent-cuaz21a %I PMLR %P 10564--10574 %U https://proceedings.mlr.press/v139/vincent-cuaz21a.html %V 139 %X Изучение словаря — это ключевой инструмент обучения представлению, который объясняет данные как линейную комбинацию нескольких основных элементов. Тем не менее, этот анализ не поддается в контексте изучения графов, поскольку графы обычно принадлежат разным метрическим пространствам. Мы заполняем этот пробел, предлагая новый онлайн-подход к обучению по словарю графов, который использует расхождение Громова-Вассерштейна для подгонки данных. В нашей работе графы кодируются через попарные отношения их узлов и моделируются как выпуклая комбинация атомов графа, то есть элементов словаря, оцениваемых благодаря онлайн-стохастическому алгоритму, который работает с набором данных незарегистрированных графов с потенциально разным количеством узлов. Наш подход естественным образом распространяется на помеченные графы и дополняется новой верхней границей, которую можно использовать в качестве быстрой аппроксимации Громова Вассерштейна в пространстве вложений. Мы предоставляем числовые доказательства, демонстрирующие интерес нашего подхода к неконтролируемому встраиванию наборов данных графа, а также к онлайн-оценке и отслеживанию подпространства графа.
АПА
Винсент-Куаз, К., Вайер, Т., Фламари, Р., Корнели, М. и Корти, Н. (2021). Онлайн-обучение графическому словарю. Proceedings of the 38th International Conference on Machine Learning , in Proceedings of Machine Learning Research 139:10564-10574 Доступно по адресу https://proceedings.
No related posts.