| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | tan(45) | ||
| 69 | Вычислить | sin(30 град. ) | |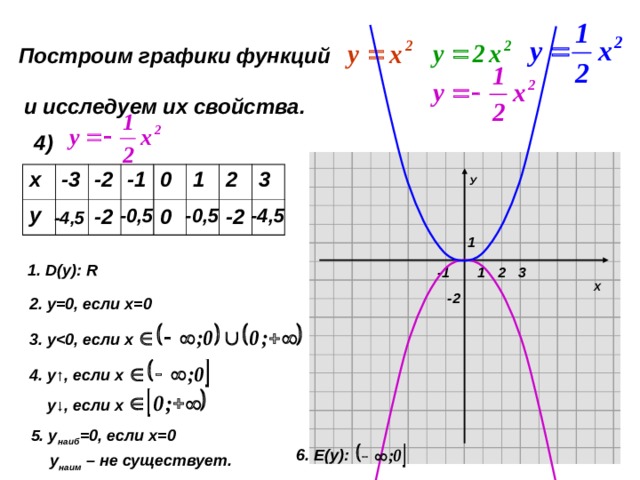
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Y 1 3x 2 график. Как построить график функции. Графический способ построения функции
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
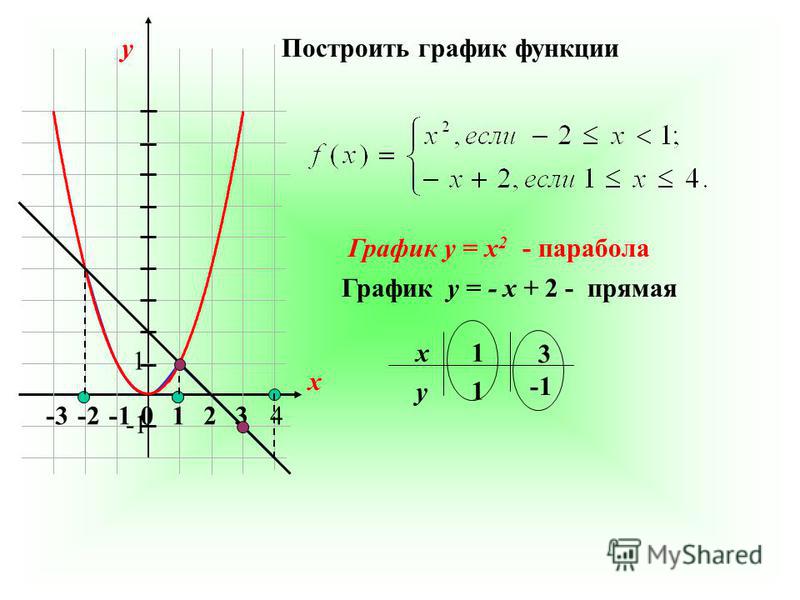
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.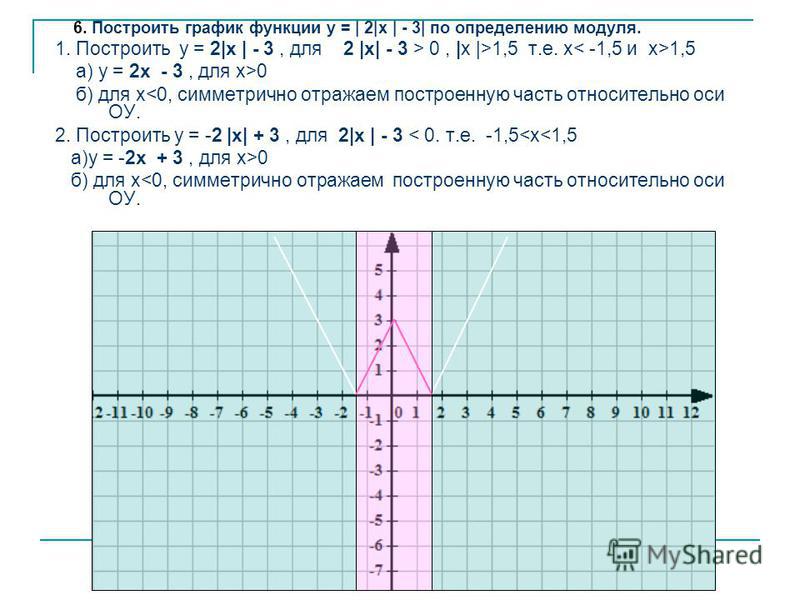
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.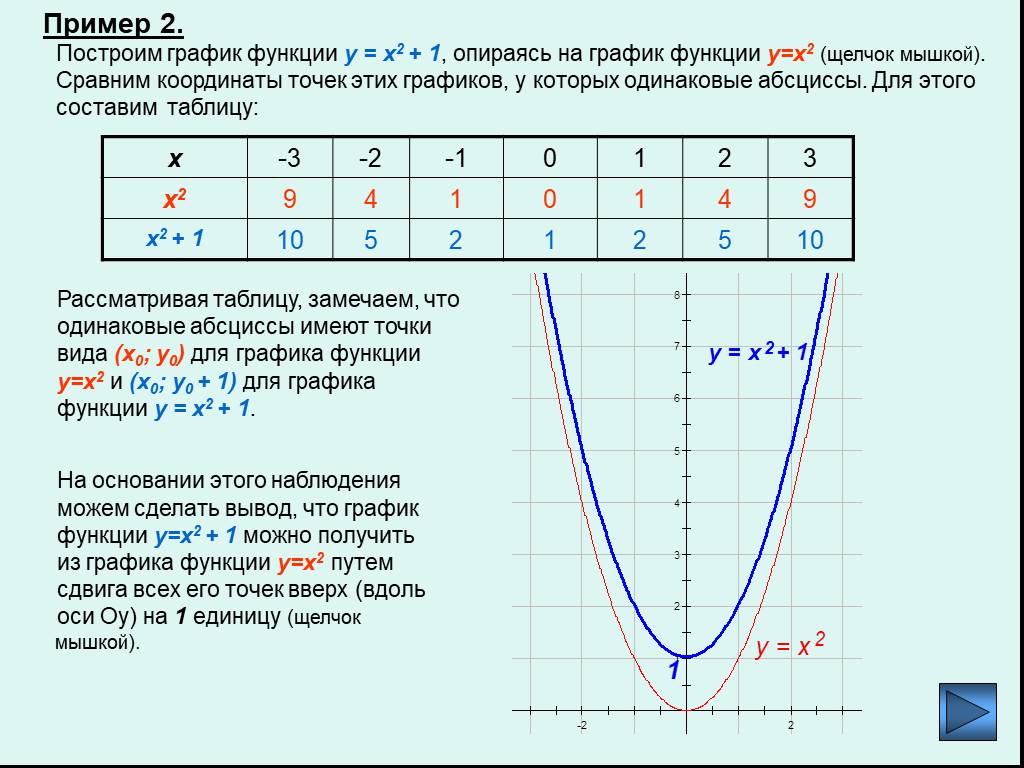
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными.
Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис.
6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x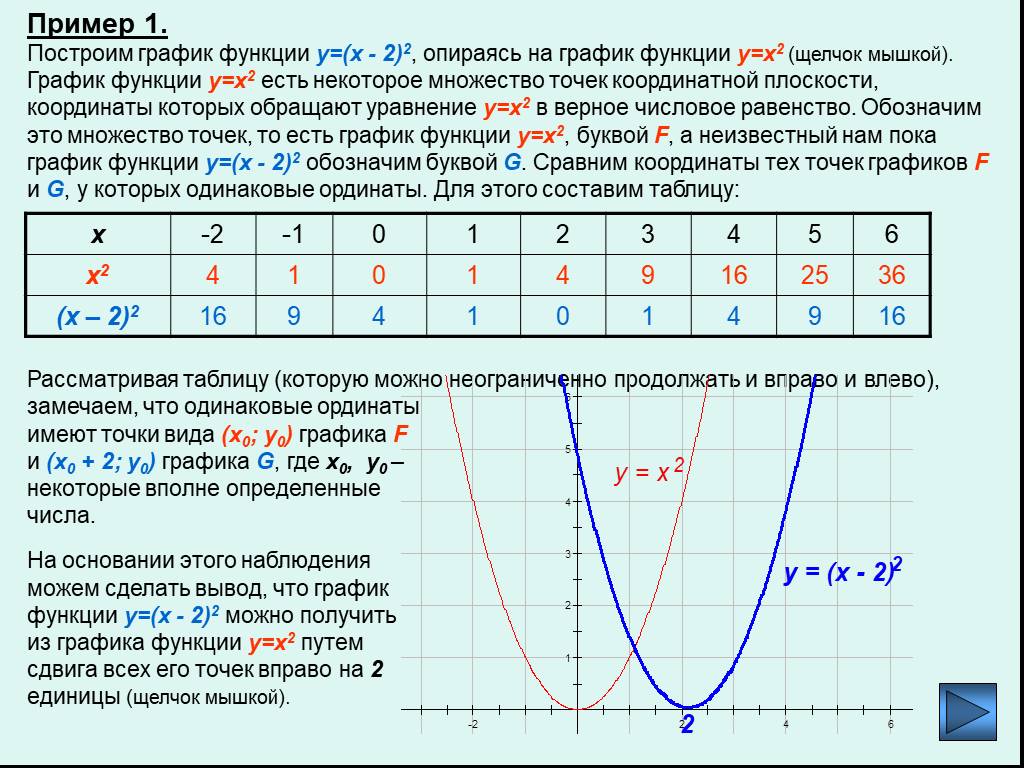 = -3.
3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.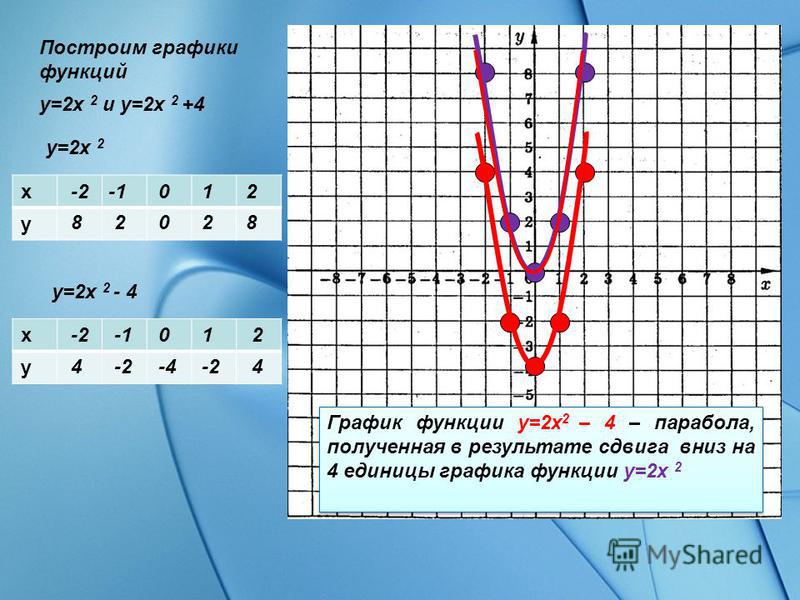
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком.
Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений.
Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Что такое Y-перехват? (Примеры вопросов)
Определение: y — точка пересечения — это точка пересечения графика с осью y .
Другими словами, это значение y , когда \(x=0\).
Y-Intercept Примеры вопросов и часто задаваемые вопросы
Как найти y -intercept:Существует несколько способов найти и — перехват, в зависимости от вашей стартовой информации. Ниже приведены три способа определения точки пересечения и на графике, в таблице или с помощью уравнения:
Сначала определите наклон и точку на графике. Как только это будет сделано, напишите линейное уравнение в форме пересечения наклона ( y = mx + b ). Используя заданную точку ( x, y ) и уклон м , перепишите уравнение, подставив соответствующие значения для x , y и м . Имея эту информацию, решите уравнение для b , чтобы определить точку пересечения y .
Пример: рассмотрим график, содержащий точку (-2, 5), где наклон равен 3. форма.
Используя таблицу или график, определите две показанные точки. Сначала запишите координаты ( x, y ) для каждой точки. Используя эту информацию, найдите подъем и бегите, чтобы определить уклон . Рассчитайте подъем, найдя разницу и координат двух точек. Рассчитайте пробег, найдя разницу в x -координаты этих двух точек. Разделите разницу в координатах и на разницу в координатах x , чтобы найти наклон.
После определения наклона напишите линейное уравнение в форме наклон-отрезок ( y = mx + b ).
Используя один набор координат ( x, y ) и уклон m , перепишите уравнение, подставив соответствующие значения для x , y и m . Затем решите уравнение на 9.0912 b для идентификации y -перехвата.
Y -перехват Пример
Рассмотрим граф, содержащий точки (3, 6) и (-1, -2). Найдите и -перехват.
| \(\frac{rise}{run}=\) | \(\frac{6-(-2)}{3-(-1)}=\frac{8}{4}= 2\) | Начните с расчета подъема и бегите, чтобы найти уклон. Разница и -координат 8 а разница х -координаты равны 4.8 ÷ 4 = 2, поэтому наклон = 2. |
| y = | mx + b | Затем напишите уравнение в форме пересечения наклона. |
| 6 = | (2)(3) + b | Замените переменные y , m и x соответствующими значениями. Выберите одну точку для замены x и y . |
| 6 = | 6 + b | Затем решите одношаговое уравнение для b . |
| 0 = | B | B = 0, поэтому Y -интерцепт -0, |
- Найти Y
- Найти Y
- .
Если у вас уже есть уравнение прямой, решите алгебраически, чтобы найти точку пересечения и . С г. -intercept всегда имеет соответствующее x -значение 0, замените x на 0 в уравнении и решите.
Пример: найти y -пересечение линии \(3x+(-2y)=12\)
Нахождение точки пересечения y в квадратичной функции На показанном графике точка пересечения и равна -3.3(0) + (-2 y ) = 15 = 15 перепишите уравнение, заменив x на 0. 0 + -2 y = 12 Затем решите одношаговое уравнение для y . 
y = -6 y = -6, поэтому точка пересечения y равна -6. Стандартная форма 92+3х+4\).
y = 2(0)2 + 3(0) + 4 Сначала перепишите уравнение, подставив 0 вместо x . y = 0 + 0 + 4 Затем решите одношаговое уравнение для y . y = 4 y = 4, так что Y -интерцепт 4. FAQSPractice
. Часто часто
FAQSPractice
6666666903
.1217
Q
Как найти \(y\)-перехват?
A
Существует несколько способов найти \(y\)-перехват, в зависимости от исходной информации.
Если задано линейное уравнение, решите алгебраически, чтобы найти \(y\)-перехват. Поскольку \(y\)-перехват всегда имеет соответствующее \(x\)-значение \(0\), замените \(x\) на \(0\) в уравнении и найдите \(y\) .На графике точку пересечения \(y\) можно найти, найдя значение \(y\) при \(x=0\). Это точка, в которой график пересекает ось \(y\).
Q
Что такое \(y\)-перехват уравнения?
A
Когда уравнение линии записывается в форме наклон-пересечение \((y=mx+b)\), то пересечение \(y\) является константой, которая представлена переменная \(b\). Например, в линейном уравнении \(y=4x-5\) пересечение \(y\) равно \(-5\).
Q
Где точка пересечения \(y\) на графе?
A
Пересечение \(y\) — это точка пересечения графика прямой с осью \(y\). В показанной координатной плоскости точка пересечения \(y\) равна \(4\), потому что график проходит через \(4\) на оси \(y\).
Q
Почему важен перехват \(y\)?
A
Пересечение \(y\) важно, потому что оно сообщает значение \(y\), когда \(x=0\).
Он обеспечивает отправную точку для линейной функции.Q
Как найти наклон и \(y\)-перехват?
A
На графике точкой пересечения \(y\) является точка пересечения прямой с осью \(y\). Соответствующая координата \(x\) всегда равна \(0\). Уклон находится путем расчета подъема над пробегом. Это делается путем нахождения разницы в \(y\)-координатах и \(x\)-координатах и деления этих разностей.
Когда линейное уравнение записывается в форме наклон-отрезок \((y=mx+b)\), наклон представляется переменной \(m\). Это коэффициент к \(x\) в уравнении. \(y\)-перехват — это константа, представленная переменной \(b\).
Q
Является ли \(b\) \(y\)-перехватом?
A
Когда линейное уравнение записывается в форме наклон-пересечение \((y=mx+b)\), пересечение \(y\) представляется постоянной переменной \(b\) . Например, в уравнении \(y=6x+8\) переменная \(b\) соответствует \(8\).
Это \(y\)-перехват.Q
Что означает перехват \(y\) в реальной жизни?
A
Перехват \(y\) — это значение \(y\), которое соответствует \(x\), когда \(x=0\). В реальной жизни это часто относится к отправной точке, когда что-то измеряется.
Например, рассмотрим изменение численности населения в Соединенных Штатах. В этом сценарии значения \(x\) могут представлять время, измеряемое в годах. \(y\)-значения могут представлять население, измеряемое миллионами человек. Когда \(x=0\), это значение представляет собой начальный год для измерения изменения численности населения. Соответствующее значение \(y\) представляет численность населения в начальный год. Это значение является \(y\)-перехватом.
Практические вопросы
Вопрос №1:
График функции \(y=\frac{1}{2}x+3\) показан ниже. Используйте график, чтобы определить y-пересечение.Пересечение по оси Y = 3
Пересечение по оси Y = 2
Пересечение по оси Y = 4
Пересечение по оси Y = \(\frac{1}{2}\)
Показать ответ
: 0
Правильный ответ: A.
Точка пересечения с осью y — это точка пересечения графика с осью y. Изучая приведенный выше график, обратите внимание, что линия пересекает ось y в точке (0, 3), поэтому 3 — это точка пересечения с осью y.Hide Ответ
Вопрос № 2:
, который переменная представляет собой y-перемещение для квадратного уравнения в стандартной форме:Y = AX 2 + BX + C
Покажите ответь
. :
Правильный ответ: C. В квадратном уравнении переменная c представляет точку пересечения по оси y. Это точка пересечения графика с осью Y.
Скрыть ответ
Вопрос №3:
Без построения графика определите точку пересечения оси Y для функции \(y=-4x+\frac{1}{2}\)\(-\frac{1}{2}\)
2
4
\(\frac{1}{2}\)
Показать ответ
Ответ:
Правильный ответ: D.
- Найти Y
Если задано линейное уравнение, решите алгебраически, чтобы найти \(y\)-перехват. Поскольку \(y\)-перехват всегда имеет соответствующее \(x\)-значение \(0\), замените \(x\) на \(0\) в уравнении и найдите \(y\) .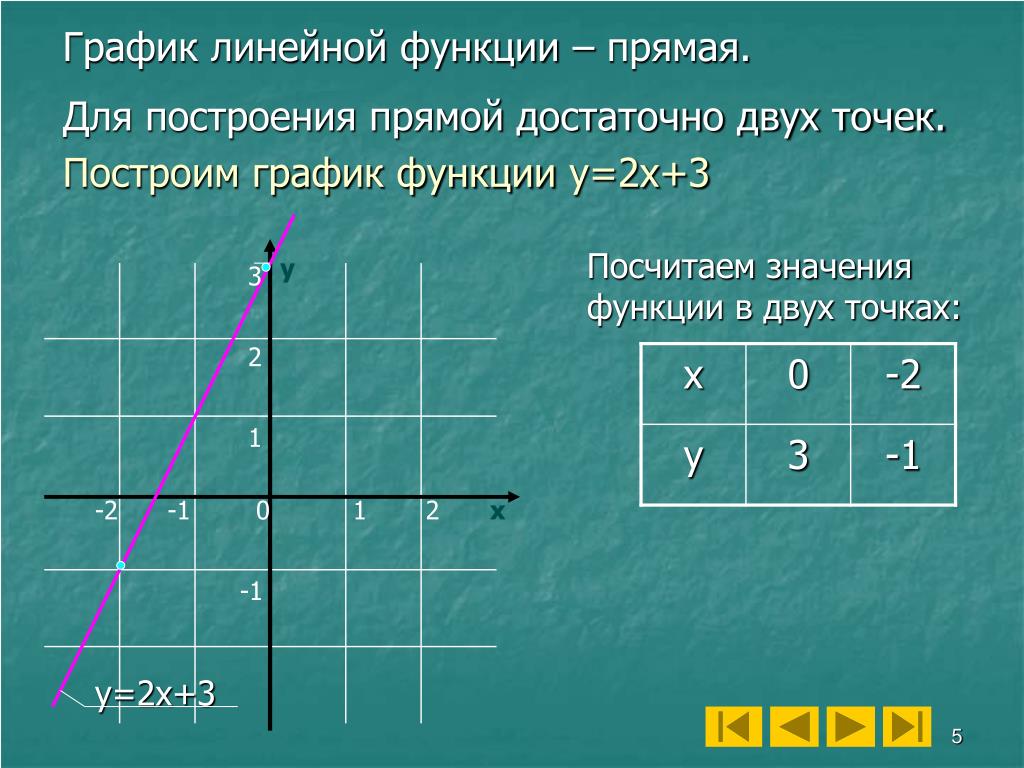
Он обеспечивает отправную точку для линейной функции.
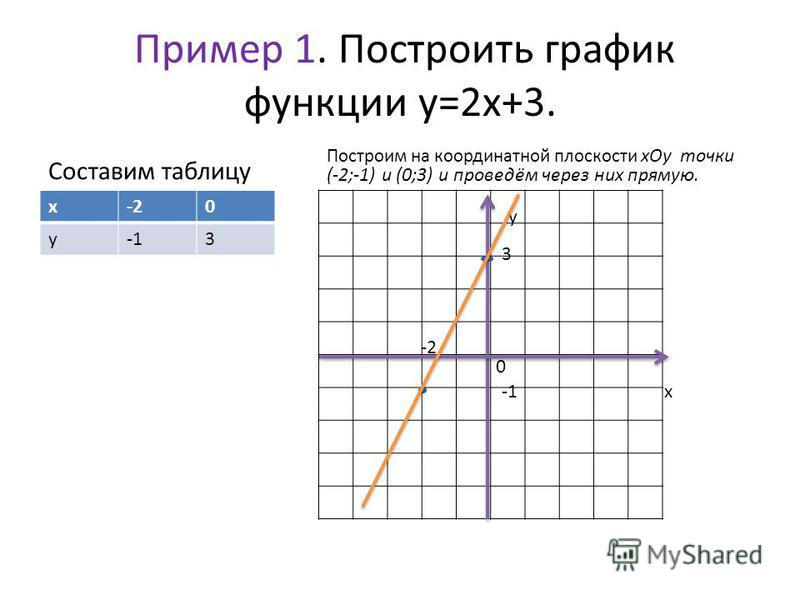Это \(y\)-перехват.
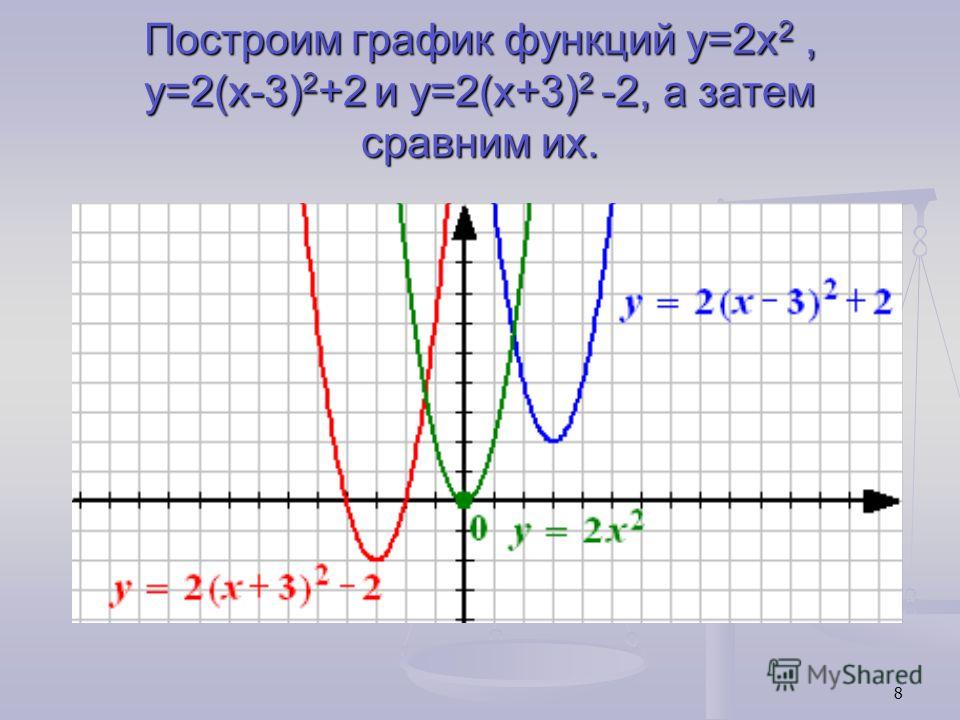Точка пересечения с осью y — это точка пересечения графика с осью y. Изучая приведенный выше график, обратите внимание, что линия пересекает ось y в точке (0, 3), поэтому 3 — это точка пересечения с осью y.