2+n-72)=1/(n+9)Алгебра 8 Мордкович ЗАДАЧНИК 2020
Алгебра 8 Мордкович ЗАДАЧНИК 2020 ответами и решениями. Ознакомительная версия с цитатами из учебника для принятия решения о покупке книги: Алгебра. 8 класс. Учебник для учащихся общеобразовательных организаций. В 2 ч. Ч. 2 / [А. Г. Мордкович и др.]; под ред. А. Г. Мордковича. — перераб. — М.: Мнемозина (новый учебник, года выпуска: 2018-2020). Часть 1-я — теоретический материал (учебник). Часть 2-я — практический материал (задачник).
В учебных целях представлены цитаты из второй части учебника, который содержит практический материал. Подбор и последовательность разноуровневых упражнений и их значительный объём позволяют школьнику освоить предмет, а учителю построить индивидуальную образовательную траекторию обучения для каждого учащегося. Во всех параграфах упражнения сгруппированы по двум блокам. Первый — до черты — содержит задания двух базовых уровней: устные (полу-устные) и задания среднего уровня сложности (слева от номеров таких заданий поставлен специальный значок).
Второй блок — после черты — содержит задания выше среднего уровня и задания повышенной сложности.
Задачи на повторение Упр. 1 — 34 Упр. 35 — 68
ГЛАВА 1. АЛГЕБРАИЧЕСКИЕ ДРОБИ§ 1. Основные понятия. Упр. 1.1 — 1.41
§ 2. Основное свойство алгебраической дроби. Упр. 2.1 — 2.48
§ 3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями. Упр. 3.1 — 3.29
§ 4. Сложение и вычитание алгебраических дробей с разными знаменателями. Упр. 4.1 — 4.23 Упр. 4.24 — 4.56
§ 5. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень. Упр. 5.1 — 5.46
§ 6. Преобразование рациональных выражений. Упр. 6.1 — 6.24
§ 7. Первые представления о рациональных уравнениях. Упр. 7.1 — 7.40
§ 8.
Степень с отрицательным целым показателем. Упр. 8.1 — 8.32
§ 9. Комбинаторные и вероятностные задачи. Дерево вариантов и правило нахождения вероятности. Упр. 9.1 — 9.7
Домашняя контрольная работа № 1 (с решениями)
ГЛАВА 2. ФУНКЦИЯ у = √x. СВОЙСТВА КВАДРАТНОГО КОРНЯ
§ 10. Рациональные числа. Упр. 10.1 — 10.29
§ 11. Понятие квадратного корня из неотрицательного числа. Упр. 11.1 — 11.43
§ 12. Иррациональные числа. Упр. 12.1 — 12.17
§ 13. Множество действительных чисел. Упр. 13.1 — 13.22
§ 14. Функция у = √x, её свойства и график. Упр. 14.1 — 14.32
§ 15. Свойства квадратных корней. Упр. 15.1 — 15.36
§ 16. Преобразование выражений содержащих операцию извлечения квадратного корня. Упр. 16.1 — 16.50 Упр.
2 + bх + с, её свойства и график. Упр. 24.1 — 24.55
§ 25. Графическое решение квадратных уравнений. Упр. 25.1 — 25.24
§ 26. Комбинаторные и вероятностные задачи к главе 3. Упр. 26.1 — 26.7
Домашняя контрольная работа № 3 (с решениями).
ГЛАВА 4. КВАДРАТНЫЕ УРАВНЕНИЯ
§ 27. Основные понятия. Упр. 27.1 — 27.39
§ 28. Формулы корней квадратных уравнений. Упр. 28.1 — 28.48
§ 29. Рациональные уравнения. Упр. 29.1 — 29.28
§ 30. Рациональные уравнения как математические модели реальных ситуаций. Упр. 30.1 — 30.45
§ 31. Ещё одна формула корней квадратного уравнения. Упр. 31.1 — 31.28
§ 32. Теорема Виета и её применения. Упр. 32.1 — 32.55
§ 33. Иррациональные уравнения. Упр. 33.1 — 33.
24
§ 34. Комбинаторные и вероятностные задачи к главе 4. Упр. 34.1 — 34.7
Домашняя контрольная работа № 4 (с решениями).
ГЛАВА 5. НЕРАВЕНСТВА
§ 35. Числовые неравенства. Упр. 35.1 — 35.65
§ 36. Решение линейных неравенств. Упр. 36.1 — 36.37
§ 37. Решение квадратных неравенств. Упр. 37.1 — 37.46
§ 38. Приближённые значения действительных чисел. Упр. 38.1 — 38.11
§ 39. Стандартный вид числа. Упр. 39.1 — 39.19
§ 40. Комбинаторные и вероятностные задачи к главе 5. Упр. 40.1 — 40.7
Домашняя контрольная работа № 5 (с решениями).
ИТОГОВОЕ ПОВТОРЕНИЕ
Вы смотрели: Ознакомительную версию с цитатами из учебника для принятия решения о покупке книги: Алгебра. 8 класс. Учебник для учащихся общеобразовательных организаций.
В 2 ч. Ч. 2 / [А. Г. Мордкович и др.]; под ред. А. Г. Мордковича. — перераб. — М.: Мнемозина (новый учебник, года выпуска: 2018-2020). Алгебра 8 Мордкович ЗАДАЧНИК 2020 ответами и решениями
Просмотров: 995 689
Нарисуйте линию, используя наклон и точку пересечения с осью Y
ПоискЧтобы построить линию, используя ее наклон и y — точку пересечения , нам нужно убедиться, что уравнение линии находится в форме наклона-пересечения,
Из этого формата мы можем легко считать оба значения наклона и y-пересечения. Наклон — это просто коэффициент переменной x, который равен m, а точка пересечения y — это постоянный член b.
Вот небольшая диаграмма, иллюстрирующая эту идею.
Когда эти две части информации будут идентифицированы, мы гарантированно успешно построим уравнение прямой.
- Постройте точку пересечения оси y \left( {0,b} \right) по оси xy. Помните, что эта точка всегда лежит на вертикальной оси y.
- Начиная с точки пересечения y, найдите другую точку, используя наклон. Наклон содержит направление движения от одной точки к другой.
Числитель говорит вам, сколько шагов нужно пройти
- Соедините две точки, образованные пересечением оси Y и наклоном, используя линейку (линейку), чтобы получить график линии.
Примеры построения графика с использованием наклона и точки пересечения с осью Y
Пример 1: Нарисуйте линию ниже с использованием ее наклона и точки с точкой пересечения с осью Y.
Сравните y = mx + b с данным уравнением \large{y = {3 \over 4}x — 2}. Ясно, что мы можем идентифицировать как наклон, так и точку пересечения с осью y. Пересечение по оси y — это просто b = — 2 или \left( {0,2} \right), а наклон \large{m = {3 \over 4}}.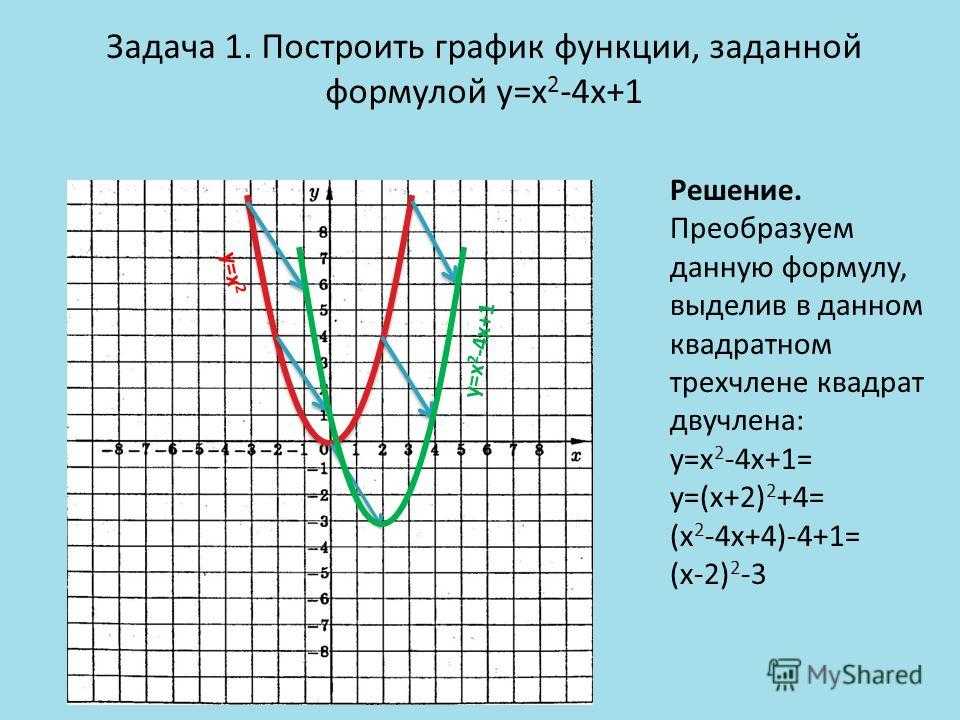
Поскольку наклон положительный, мы ожидаем, что линия будет возрастать, если смотреть слева направо.
- Шаг 1: Давайте построим первую точку, используя информацию, предоставленную нам точкой пересечения по оси y, которая является точкой \left({0, — 2} \right).
- Шаг 2: От точки пересечения y найдите другую точку, используя наклон. Наклон m = {3 \over 4}, значит, мы поднимаемся на 3 единицы вверх и двигаемся вправо на 4 единицы.
- Шаг 3: Соедините две точки, чтобы построить линию.
Пример 2: Постройте линию ниже, используя ее наклон и точку пересечения по оси Y.
Я знаю, что наклон \large{m = {{ — 5} \over 3}}, а точка пересечения по оси y равна b = 3 или \left( {0,3} \right). Поскольку наклон отрицательный, окончательный график линии должен уменьшаться, если смотреть слева направо.
- Шаг 1: Начните с построения точки пересечения по оси y заданного уравнения, равного \left({0,3} \right).
- Шаг 2: Используйте наклон \large{m = {{ — 5} \over 3}}, чтобы найти другую точку, используя точку пересечения с ординатой в качестве точки отсчета. Наклон говорит нам опуститься на 5 единиц вниз, а затем переместиться на 3 единицы вправо.
- Шаг 3: Нарисуйте линию, проходящую через точки.
Вас также могут заинтересовать:
Три способа построения графика
Построение графика с использованием таблицы значений
Построение графика с использованием точек пересечения X и Y
Y=4x+3 — eNotes.com
значок-вопрос Спросите репетитораНачать бесплатную пробную версию
Решите уравнение y=4x+3.
Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяУкажите эту страницу следующим образом:
«Y=4x+3» Редакционная статья eNotes , 24 августа 2012 г.
, https://www.enotes.com/homework-help/solve-y-4x-3-how-do-know-what-number-replace -х-355385.
По состоянию на 6 декабря 2022 г.Чтобы нарисовать уравнение y = 4x + 3 вручную, выберите любые два значения x. Например, x = 1 дает y = 7, а x = 0 дает y = 3. График уравнения представляет собой прямую линию, проведенную между точками (0, 3) и (1, 7)
Утверждено редакцией eNotes
y = 4x + 3 находится в так называемой форме «пересечение наклона» или в форме «y = mx + b», которая является самой простой формой для построения графика. «3» называется «перехватом по оси y» и находится там, где линия пересекает ось y.
Итак, идем в «начало» (0,0) и поднимаемся на три вверх по вертикали. Поставьте там точку. Это одна из точек на линии. Далее мы смотрим на число перед «х». Это «наклон» или «подъем над пробегом». Поскольку у нас нет дроби, мы можем поставить «1» под «4», чтобы получить дробь. Итак, наш наклон равен 4/1. Мы переходим от нашего (0,3) через 1 к 1 и от 4 к 7. Итак, еще одна точка на линии — (1,7). Вам нужно всего две точки, чтобы построить линию, поэтому соедините точки и продолжайте движение по графику в обоих направлениях. Не забудьте стрелки на обоих концах, чтобы указать, что линия продолжается в обоих направлениях до бесконечности.
Утверждено редакцией eNotes
Невозможно решить уравнение y = 4x + 3. Это просто отношение между двумя переменными x и y. Переменная у в 3 раза больше, чем в 4 раза, чем переменная х.
Только если значение одной из переменных фиксировано, другую можно определить так, чтобы они соответствовали заданному критерию.
Утверждено редакцией eNotes
Математика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 ответов педагога
Математика
Последний ответ опубликован 14 ноября 2011 г. в 5:49:28.
Решите для b2:A= 1/2h (b1+b2)
1 Ответ учителя
Математика
Последний ответ опубликован 3 октября 2011 г. в 14:12:01.
Этот предел представляет собой производную некоторой функции f при некотором числе a. укажите это f и a. lim h->0 [(4-й корень из)(16+h)-2]/h a=? ф=?
1 Ответ учителя
Математика
Последний ответ опубликован 17 августа 2010 г.