90 тригонометрических формул
- Файлы
- Абитуриентам и школьникам
- Математика
- Подготовка к экзамену по математике
Математика
6 класс
Алгебра
Геометрия
Для внеклассного чтения
Домашняя работа по математике
-
Задачники по математике для школьников
Математика в начальной школе
Подготовка к экзамену по математике
Школьные математические олимпиады
Шпаргалка
- формат doc
- размер 169 КБ
- добавлен
07 ноября 2011 г.

2011 г.
Содержание:
Основные тригонометрические формулы.
Формулы сложения аргументов.
Формулы двойного угла.
Формулы понижения степени.
Формулы преобразования произведений функций.
Формулы преобразования суммы функций.
Решение простейших тригонометрических уравнений.
Универсальная тригонометрическая подстановка.
Вспомогательный аргумент (метод Юниса).
и др.
Читать онлайн
Смотрите также
- формат djvu
- размер 1.35 МБ
- добавлен 25 сентября 2010 г.
Под редакцией Н. Нечаева и С. Гайсиновича. Наркомпрос РСФСР. Учпедгиз 1935. Содержание: Введение. Определения. Общие замечания. Формулы общего вида. Уравнения «простейшего» вида: sin x=a, cos x=b, tg x=c. Частные случаи «уравнений простешего вида». Уравнение, в котором неизвестное входит в состав аргумента. Двучленные уравнения I степени, содержащие одинаковые функции с численными коэффициентами, равными 1. Общие указания к решению тригонометрич…
Содержание: Введение. Определения. Общие замечания. Формулы общего вида. Уравнения «простейшего» вида: sin x=a, cos x=b, tg x=c. Частные случаи «уравнений простешего вида». Уравнение, в котором неизвестное входит в состав аргумента. Двучленные уравнения I степени, содержащие одинаковые функции с численными коэффициентами, равными 1. Общие указания к решению тригонометрич…
- формат djvu
- размер 450.7 КБ
- добавлен 10 ноября 2010 г.
Тамбов: ТГТУ, 2003. — 104 с. Учебное пособие знакомит учащихся с основными тригонометрическими функциями и их свойствами, также в нем приводятся основные методы решения тригонометрических уравнений. Пособие содержит тесты по тригонометрии.
- формат djvu
- размер 1.49 МБ
- добавлен
19 сентября 2010 г.

Учебник для общеобразовательных учреждений. 4-е изд. — М.: Мнемозина, 2002 — 192 с.: ил. Оглавление. Предисловие для учителя. Рациональные неравенства и их системы. Системы уравнений. Числовые функции. Прогрессии. Элементы теории тригонометрических функций.
Шпаргалка
- формат doc
- размер 1.79 МБ
- добавлен 15 января 2012 г.
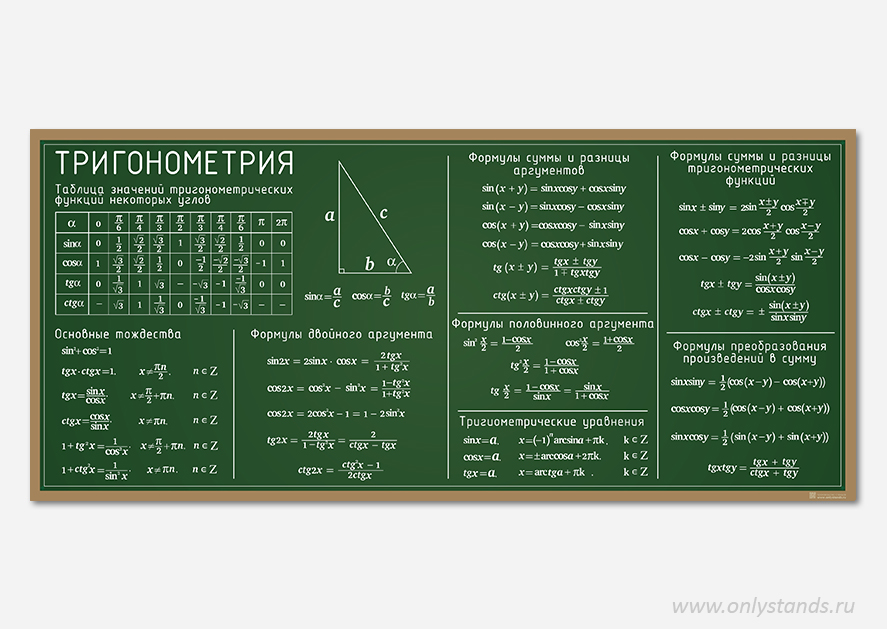
Автор неизвестен. 2011 год. Все формулы на 1 листе в виде таблицы. Степени. Корни. Сокращенное умножение. Квадратный трехчлен. Квадратное уравнение. Формулы Виета. Разложение трехчлена на множители. Логарифмы. основные тождества. Свойства логарифмов. Десятичный логарифм. Натуральный логарифм. Тригонометрия. Основные тождества. Простейшие тригонометрические уравнения. Некоторые значения тригонометрических функций. Формулы приведения. Сумма и разно…
Некоторые значения тригонометрических функций. Формулы приведения. Сумма и разно…
- формат jpg
- размер 12.54 МБ
- добавлен 07 апреля 2011 г.
Сборник формул по математике для школьников. Включает в себя множество формул по алгебре и геометрии, которые могут быть крайне необходимы на экзамене.rn
Шпаргалка
- формат rtf
- размер 480.92 КБ
- добавлен 04 октября 2011 г.
Собраны и размещены все основные и необходимые формулы по школьному курсу математики на нескольких листах. Справочник пригодится ученикам 11-ых классов, сдающим ЕГЭ, и ученикам старших классов. Содержит: тригонометрические формулы(тождества), значения тригонометрических функций, графики степенных, логарифмических и др.
Шпаргалка
- формат doc
- размер 174 КБ
- добавлен 15 января 2012 г.
Автор неизвестен. ТГТУ — г. Тверь. 2011 год. Функции одного и того же угла. Формулы сложения. Формулы двойных, половинных, тройных углов. Преобразование суммы функций в произведение. Преобразование произведения функций. Понижение степени. Формулы, приводящие к виду, удобному для логарифмирования. Значение тригонометрических функций некоторых углов. Простейшие тригонометрические уравнения. Выражения одних тригонометрических функций через другие. Т…
- формат doc
- размер 59.
 41 КБ
41 КБ - добавлен 25 марта 2011 г.
Содержание: Основные тригонометрические тождества. Формулы суммы и разности. Формулы двойного аргумента. Формулы произведений. Формулы сложения. Формулы половинного аргумента. Формулы понижения степени. Решения тригонометрических уравнений. Выражение формул через тангенс. Таблица значения тригонометрических функций основных углов. Формулы приведения тригонометрических функций.
pottee
- формат jpg
- размер 130.37 КБ
- добавлен 27 декабря 2009 г.
Шпаргалка пригодится ученикам 11-ых классов, сдающим ЕГЭ, и ученикам старших классов. Содержит: тригонометрические формулы(тождества), значения тригонометрических функций, графики степенных, логарифмических и др. функций, таблица производных, алгебраическая и геометрическая прогрессии, свойства степеней, корней, логарифмов, уравнение корней и теорема Виета, уравнение касательной, формулы сокращенного умножения, формулы понижения степени, формулы…
функций, таблица производных, алгебраическая и геометрическая прогрессии, свойства степеней, корней, логарифмов, уравнение корней и теорема Виета, уравнение касательной, формулы сокращенного умножения, формулы понижения степени, формулы…
pottee
- формат doc
- размер 13.47 КБ
- добавлен 11 июня 2009 г.
Содержит основные формулы, от сокращённого умножения до тригонометрических формул. Формулы сокращенного умножения и разложения на множители. Формулы сложения. Степени и корни. Формулы двойного аргумента. Формулы половинного аргумента. Стереометрия. Приведенное квадратное Уравнение. Логарифмы. Тригонометрические уравнения. Теорема синусов.
Формулы – Ягубов.РФ
Формулы – Ягубов.РФПОИСК ЗАДАНИЙ |
По математике
По разделам
Раздаточные
- ЕГЭ (ПРОФИЛЬНЫЙ УРОВЕНЬ) по математике: 4644
- ЕГЭ (БАЗОВЫЙ УРОВЕНЬ) по математике: 4645
- ОГЭ (ГИА) по математике: 4646
- Бланки ЕГЭ по математике: 5165
Чтобы скачать материалы от «ФИПИ»,
нажмите сюда!
Алгебра
5-9 КЛАССЫ
- Формулы сокращенного умножения: Ф1
- Свойства квадратных корней и модуля: Ф14
- Линейные и квадратные уравнения: Ф2
- Способы решения систем уравнений: Ф23
- Разложение многочлена на множители: Ф21
- Теория вероятностей и статистика: Ф12
10-11 КЛАССЫ
- Свойства степени и логарифма: Ф6
- Уравнения с корнями, показ.
 и логар.: Ф20
и логар.: Ф20 - Неравенства и числовые промежутки: Ф38
- Метод интервалов и промежутков: Ф22
- Формулы по тригонометрии: Ф8
- Тригонометрическая окружность: Ф28
- Тригонометрические уравнения: Ф9
ГРАФИКИ
- Исследование и построение функции: Ф19
- Преобразование графика функции: Ф25
- Прямая, парабола, гипербола: Ф16
- Корень, степень, логарифм: Ф17
- Тригонометрические функции: Ф18
- Окружность, ромб, перекрёсток: Ф31
Анализ
- Метод рационализации функций: Ф3
- Таблица производных и интегралов: Ф7
- Приложение производной и интеграла: Ф15
- Пределы и числовые ряды: Ф11
Чтобы скачать формулы от «Ягубов.РФ»,
нажмите сюда!
Арифметика
- Умножение/деление и сложение/вычитание: Ф24
- Признаки делимости чисел: Ф5
- Дроби, пропорции и средние величины: Ф13
- Арифметическая и геометрич.
 прогрессии: Ф10
прогрессии: Ф10
Чтобы скачать формулы от «Ягубов.РФ»,
нажмите сюда!
Геометрия
- Углы в планиметрии: Ф34
- Признаки (парал., равен., подоб.): Ф33
- Площади и периметры фигур: Ф29
- Формула Пика: Ф36
- Окружность и её свойства: Ф32
ТРЕУГОЛЬНИКИ
- Виды треугольников и их свойства: Ф37
- Замечательные точки треугольника: Ф35
- Прямоугольный треугольник: Ф26
- Произвольный треугольник: Ф27
ПРОСТРАНСТВО
- Объёмы тел и их свойста: Ф30
- Метод координат в пространстве: Ф4
Чтобы скачать формулы от «Ягубов.РФ»,
нажмите сюда!
Таблицы
- Таблица исходов кубиков и монет: Т20
ЧИСЛА
- Таблица умножения натуральных чисел 9×9: Т1
- Таблица умножения натуральных чисел 20×20: Т2
- Таблица квадратов натуральных чисел от 1 до 99: Т3
- Таблица кубов натуральных чисел от 1 до 99: Т5
- Таблица простых чисел от 2 до 997: Т6
- Таблица степеней натуральных чисел: Т4
- Таблица квадратных корней чисел от 1 до 99: Т8
- Таблица кубических корней чисел от 1 до 99: Т9
- Треугольник Паскаля: Т7
ГЕОМЕТРИЯ
- Таблица взаимно простых троек Пифагора: Т15
- Таблица триад Герона: Т16
- Таблица сторон треугольников с углами 60 и 120: Т17
- Таблица величин правильных многоугольников: Т13
- Таблица целых значений сторон и диагоналей в параллелограмме и параллелепипеде: Т18
- Таблица величин правильных многогранников: Т14
- Таблица целых значений сторон слитых кубов: Т19
ТРИГОНОМЕТРИЯ
- Значения тригонометрических функций: Т10, Т12
- Приведение тригонометрических функций: Т11
Чтобы скачать таблицы от «Ягубов. РФ»,
РФ»,
!
Что такое тригонометрия? Формулы, примеры, приложения, таблицы
Алгебра, геометрия, вероятность, тригонометрия, арифметика и другие области математики относятся к наиболее значимым. С другой стороны, тригонометрия — это подмножество геометрии, связанное со свойствами одной из фигур в геометрии, известной как «треугольник». Хотя тригонометрия и геометрия кажутся связанными, это не одно и то же. Давайте подробно рассмотрим, что такое тригонометрия, в этом посте.
Что такое тригонометрия простыми словами?
Тригонометрия является одной из важнейших областей математики. Термины «Тригонон» и «Метрон», которые означают треугольник и меру соответственно, объединены в тригонометрию. Он изучает взаимосвязь между сторонами и углами прямоугольного треугольника. Таким образом, это облегчает использование формул и тождеств, основанных на этом соотношении, для нахождения меры неизвестных сторон прямоугольного треугольника.
В чем разница между геометрией и тригонометрией?
Изучение различных размеров, форм и качеств пустых пространств определенного количества измерений, таких как 2D или 3D, известно как геометрия. В то же время тригонометрия чрезвычайно важна в современной математике. Тригонометрия в первую очередь связана с изучением треугольников, длин и углов. Он имеет дело с колебаниями и волнами.
В тригонометрии мы прежде всего изучаем отношения между длинами сторон и углами прямоугольного треугольника. Существует шесть тригонометрических соотношений. Синус, косинус и тангенс являются тремя основными, которые складываются вместе с секансом, косекансом и котангенсом.
Для чего используется тригонометрия
Тригонометрия имеет три основные функции: синус, косинус и тангенс. Другие важные тригонометрические функции могут быть получены с использованием этих трех фундаментальных соотношений или функций: котангенса, секанса и косеканса. Это использование составляет основу для всех основных тем тригонометрии. В результате, чтобы понять тригонометрию, мы должны сначала изучить эти функции и их формулы.
В результате, чтобы понять тригонометрию, мы должны сначала изучить эти функции и их формулы.
Три стороны прямоугольного треугольника:
- Сторона, противоположная углу, называется перпендикуляром.
- Прилежащая сторона угла является основанием.
- Гипотенуза против прямого угла.
Тригонометрия использовалась в различных областях на протяжении всей истории, в том числе
- Архитекторы, небесная механика и геодезия — все используют тригонометрию.
- Он применяется в океанографии, сейсмологии, метеорологии, физических науках, астрономии, акустике, навигации, электронике и во многих других областях.
- Сферическая тригонометрия используется для определения местоположения Солнца, Луны и звезд, а также для оценки расстояния между длинными реками, измерения высоты гор и т. д.
- Тригонометрия используется в криминологии для оценки причины столкновения и траектории пули.
- Морские биологи также используют тригонометрию для определения глубины солнечного света, которая запускает фотосинтез водорослей.

- Тригонометрия в авиации используется для расчета направления, в котором пилот может повернуть, чтобы избежать столкновения или сильного ветра.
- Тригонометрия в навигации применяется, когда моряк использует углы для навигации к правильным пунктам назначения.
В большинстве реальных примеров используется тригонометрия.
Мальчик стоит у дерева. «Какая высота дерева?» — удивляется мальчик, высоту дерева легко определить, не измеряя его. Здесь у нас есть прямоугольный треугольник.
Что такое синус в тригонометрии?
Отношение расстояния одной стороны треугольник, противоположный углу к длине гипотенузы треугольника, является синусом одного из углов прямоугольного треугольника (обычно сокращенно «sin»).
Sin θ = Перпендикуляр/Гипотенуза
Что такое Tan в тригонометрии?
Тригонометрическое отношение между соседними и противоположными сторонами прямоугольного треугольника, составляющего этот угол, является тангенсом угла.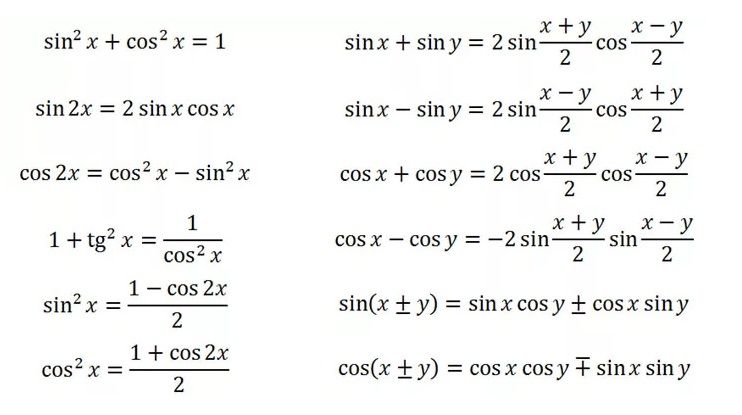
Tan θ = Перпендикуляр/Основание
Важные тригонометрические углы
Тригонометрические углы находятся в прямоугольном треугольнике и могут представлять различные тригонометрические функции. Некоторые углы в тригонометрии включают 0º, 30º, 45º, 60º, 90º. Значения этих углов можно наблюдать непосредственно в тригонометрической таблице. С некоторыми другими жизненно важными углами, такими как 180º, 270º и 360º. Тригонометрический угол выражается через тригонометрические соотношения как
Тригонометрические соотношения
Шесть основных соотношений в тригонометрии помогают установить отношение сторон прямоугольного треугольника к углу.
Sin θ = Перпендикуляр/Гипотенуза
Cos θ = Основание/Гипотенуза
Tan θ = Перпендикуляр/Гипотенуза.
Cot θ = 1/tan θ = основание/перпендикуляр
Sec θ = 1/cos θ = гипотенуза/основание
Cosec θ = 1/sin θ = гипотенуза/перпендикуляр
Что такое формула тригонометрии?
Многие формулы показывают отношения между тригонометрическими отношениями и углами для различных квадрантов тригонометрии. Ниже приведен список основных формул тригонометрии:
Ниже приведен список основных формул тригонометрии:
1. Формулы тригонометрических соотношений
Sin θ = гипотенуза/противоположная сторона
Cos θ = гипотенуза/прилежащая сторона
Tan θ = прилежащая сторона/противоположная сторона
Сек θ = 1/cos θ = Смежная сторона/Гипотенуза
Cosec θ = 1/sin θ = Противоположная сторона/Гипотенуза
θ = sin-1 (Перпендикуляр/Гипотенуза) )
θ = tan-1 (перпендикуляр/основание)
2. Формулы тригонометрии с тождествами Пифагора
cos²θ+sin²θ = 1
1+tan2θ = sec2θ
1+cot2θ = cosec2θ
3. Закон косинуса и Cot2θ в тригонометрии
a/sina = b/sinb = c/sinc
C2 = a2+ b2 – 2ab cos C
a2 = b2 + c2 – 2bc cos A
b2 = a2 + c2 – 2ac cos B
Тригонометрическая таблица
Тригонометрическая таблица состоит из связанных соотношений, таких как синус, косинус, тангенс, косеканс, секанс и котангенс. Этими отношениями являются sin, cos, tan, cosec, sec и cot, и они вычисляют стандартные значения углов. Чтобы узнать больше об этих соотношениях, посмотрите на таблицу тригонометрии ниже.
Чтобы узнать больше об этих соотношениях, посмотрите на таблицу тригонометрии ниже.
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angles (In Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| желтовато-коричневый | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| csc | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Из представленной информации о тригонометрии становится ясно, что работа с углами требует больше математики, чем кажется на первый взгляд. В Acemyhomework мы гордимся тем, что делаем школьную работу легкой и выполнимой задачей для каждого ученика. У нас есть профессиональные писатели, которые доступны круглосуточно, чтобы гарантировать, что вы получите лучшие письменные услуги.
В Acemyhomework мы гордимся тем, что делаем школьную работу легкой и выполнимой задачей для каждого ученика. У нас есть профессиональные писатели, которые доступны круглосуточно, чтобы гарантировать, что вы получите лучшие письменные услуги.
Тригонометрические формулы для 11 класса (скачать PDF)
Тригонометрия Формулы для 11 класса
(скачать в формате PDF)
Тригонометрия – довольно интересный предмет. Вот полезные формулы тригонометрии для математики 11 класса
Базовая формула
$tan(x) = \frac {sin(x)}{cos(x)}$
$cot(x) = \frac { cos(x)}{sin(x)}$
Взаимные тождества:
$cosec(x) = \frac {1}{sin(x)}$
$sec(x) =\frac { 1}{cos(x)}$ 92x $
Тригонометрические отношения общих углов
Мы можем найти значения различного угла тригонометрического соотношения
Формула тригонометрии для комплементарных и дополнительных углов
SIN и COS -функция 9039 4
SIN и COS -функция 9039 4 63
SIN и COS COS -функция 9039 4
. B)=cos(A)cos(B)-sin(A)sin(B)$
B)=cos(A)cos(B)-sin(A)sin(B)$
Функции tan и cot
Если ни один из углов x, y и (x + y) ) является нечетным кратным $\pi /2$
$tan(A+B)=\frac{tan(A)+tan(B)}{1-tan(A)tan(B)}$
$tan(A-B)=\frac{tan(A)-tan(B)}{1+tan(A)tan(B)}$
Если ни один из углов x, y и (x + y) не является кратное $\pi /2$
$cot(A+B)=\frac{cot(A)cot(B)-1}{cot(A)+cot(B)}$
$cot(A-B ) = \ frac {cot (A) раскладушка (B) + 1} {раскладушка (B) — раскладушка (A)} $ 9{2}}x}$
Сумма и разность углов
$cos(A)+cos(B)=2cos\frac{A+B}{2}cos\frac{A-B}{2}$
$cos(A)-cos(B)=-2sin\frac{A+B}{2}sin\frac{A-B}{2}$
$sin(A)+sin(B)=2sin\frac{ A+B}{2}cos\frac{A-B}{2}$
$sin(A)-sin(B)=2cos\frac{A+B}{2}sin\frac{A-B}{2}$
Формула половинного угла
Тождества Пифагора в радикальной форме
Степенные функции редукции
Тригонометрические уравнения Формулы 92 y$
Общее решение дается выражением
$x = n \pi \pm y$, где n — любое целое число
6. Уравнение вида
Уравнение вида
|sin x|=1 , Общее решение дается выражением $x= (2n+1) \frac {\pi}{2}$
|cos x|=1, общее решение дается выражением $x=n \pi$
Некоторые основы Советы по решению вопросы по тригонометрии
(1) Всегда старайтесь свести несколько углов к одному, используя основную формулу. Убедитесь, что все ваши углы одинаковы. Использование $sin(2x)$ и $sin(x)$ сложно, но если вы используете $sin(2x) = 2 sin(x)cos(x)$, остаются $sin(x)$ и $cos( x)$, и теперь все ваши функции совпадают. То же самое касается сложения и вычитания: не пытайтесь работать с $sin(x+y)$ и $sin(x-y)$. Вместо этого используйте $sin(X+Y) = sin(x)cos(y)+cos(x)sin(y)$, чтобы все углы совпали
(2) Преобразование в sin и cos всех элементов задачи по базовой формуле. Я упомянул sin и cos, так как их легко решить. Вы также можете использовать любой другой.
(3)Проверьте все углы на суммы и разности и используйте соответствующие тождества, чтобы удалить их.


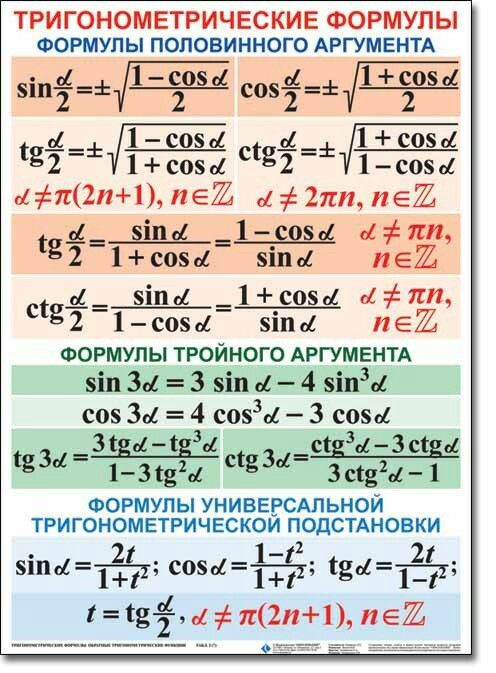
 41 КБ
41 КБ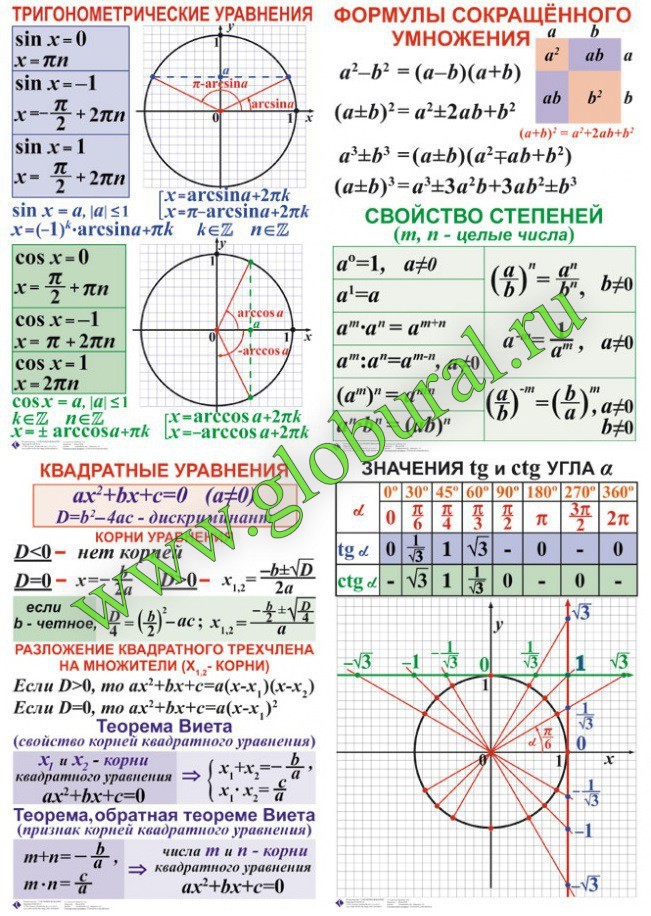 и логар.: Ф20
и логар.: Ф20 прогрессии: Ф10
прогрессии: Ф10