Каталог: gallery -> 646 жүктеу/скачать 53 Kb. Достарыңызбен бөлісу: |
x | y = x2 | (x,y) |
0 | 0 | (0,0) |
1 | 1 | (1,1) |
2 | 4 | (2,4) |
3 | 9 | (3,9) |
-1 | 1 | (-1,1) |
-2 | 4 | (-2,4) |
-3 | 9 | (-3,9) |
X | y=1/x | (x,y) |
1/3 | 3 | (1/3,3) |
1/2 | 2 | (1/2,2) |
1 | 1 | (1 ,1) |
2 | 1/2 | (2,1/2) |
3 | 1/3 | (3,1/3) |
-1/3 | -3 | (-1/3 , -3) |
-1/2 | -2 | (-1/2 , -2) |
-1 | -1 | (-1 , -1) |
-2 | -1/2 | (-2, -1/2) |
-3 | -1/3 | (-3,-1/3) |
| |x| = | x если x ≥ 0, т.e. x — не отрицательно -x если x |
График совпадает с линией y = x для x> 0 и с линией y = -x
для x < 0 .
graph of f(x) = -x
Соединяя эти два графика, мы получаем
график f(x) = |x|
Пример 3. Постройте график
t(x) = (x2— 4)/(x — 2) =
= ((x — 2)(x + 2)/(x — 2)) =
= (x + 2) x ≠ 2
Следовательно, эта функция может быть записана в виде
y = x + 2 x ≠ 2
График h(x)= x2 — 4 Or x — 2
график y = x + 2 x ≠ 2
Пример 4. Постройте график
| g(x) = | 1 если x ≤ 2 x + 2 если x > 2 |
Графики функций с перемещением
— Предположим, что график функции f(x) известен
— Тогда мы можем найти графики
y = f(x) + c
y = f(x) — c
y = f(x + c)
y = f(x — c)
y = f(x) + c — график функции f(x), перемещённый
ВВЕРХ на c значений
y = f(x) — c — график функции f(x), перемещённый
ВНИЗ на c значений
y = f(x + c) — график функции f(x), перемещённый
ВЛЕВО на c значений
y = f(x — c) — график функции f(x), перемещённый
Вправо на c значений
Пример 5. Постройте
Постройте
график y = f(x) = |x — 3| + 2
Переместим график y = |x| на 3 значения ВПРАВО, чтобы получить график
y = |x-3|
Переместим график y = |x — 3| на 2 значения ВВЕРХ, чтобы получить график y = |x — 3| + 2
Пример 8
Постройте график
y = x2 — 4x + 5
Преобразуем заданное уравнение следующим образом, прибавив к обеим частям 4:
y + 4 = (x2 — 4x + 5) + 4 y = (x2 — 4x + 4) + 5 — 4
y = (x — 2)2 + 1
Здесь мы видим, что этот график может быть получен перемещением графика y = x2 вправо на 2 значения, потому что x — 2, и вверх на 1 значение, потому что +1.
y = x2 — 4x + 5
Отражения
(-x, y) есть отражением (x, y) относительно оси y
(x, -y) есть отражением (x, y) относительно оси x
Графики y = f(x) и y = f(-x) являются отражением друг друга относительно оси y
Графики y = f(x) и y = -f(x) являются отражением друг друга относительно оси x
График может быть получен отражением и перемещением:
— Нарисуйте график
— Найдём его отражение относительно оси y, и получим график
— Переместим этот график вправо на 2 значения и получим график
Вот искомый график
Если f(x) умножена на положительною постояную c, то
график f(x) сжимается по вертикали, если 0 < c < 1
график f(x) растягивается по вертикали, если c > 1
Кривая не является графиком y = f(x) для любой функции f
Заключительный урок по теме «Координатная плоскость».
 6-й класс
6-й классТип урока: урок закрепления и применения знаний, умений, навыков.
Цели урока:
Образовательные:
- обобщить ранее изученный материал по построению параллельных и перпендикулярных прямых; координат точек на координатной плоскости; круговых диаграмм;
- научить наглядно представлять информацию в виде столбчатых диаграмм;
- сформировать умения анализировать столбчатые диаграммы;
- показать применение знаний, полученных на уроках математики, на практике.
Развивающие:
- развивать мыслительные операции, посредством наблюдений, сравнений, сопоставлений, обобщений, конкретизацией, сознательного восприятия материала;
- развивать творческий потенциал и самооценку через творческие и тестовые задания;
- развивать умения оперировать ранее полученными знаниями;
- развивать умения планировать свою деятельность.

Воспитательные:
- воспитание познавательного интереса к математике и повышение мотивации к учению по средствам ИКТ;
- воспитание ответственности за выполняемую работу, аккуратности при выполнении работы;
- воспитание наблюдательности, самостоятельности, способности к коллективной и индивидуальной работе.
Ход урока
1. Актуализация знаний— Многие тысячи лет на Земле живет человек, и, по крайней мере, ему были даны два чуда природы: день, освещенный Солнцем, и ночь с ее манящими и загадочными россыпями звезд. Те, кто более пристально изучал перемещение небесных светил и звездных узоров, давно обнаружили строгую ритмичность суточных и сезонных движений. Эти явления были положены в основу различных способов счета времени и ведения календаря – двух необходимых атрибутов любой цивилизации. Занятия астрономией были всегда уважаемы. Математика и позже физика вышли из астрономии, математика – как аппарат для точных расчетов положений звезд, физика – для объяснения неизвестных явлений, обнаруженных при их наблюдении. Так почему бы не вернуться к астрономии хотя бы на одном уроке математики?
Так почему бы не вернуться к астрономии хотя бы на одном уроке математики?
— Вспомните тему прошлого урока?
— Как вы думаете, что мы будем изучать сегодня?
— Как проверить хорошо ли вы освоили данную тему?
— Сегодня у нас необычный урок. Мы проведем урок – путешествие. (Слайд 1)
Презентация
2. Работа на урокеПервое заданиеМатематический диктант. Давайте выясним, на каком виде транспорта мы будем совершать наше путешествие.
(слайд 3)
Координаты точек по порядку перечисляются учителем, учащиеся строят их в системе координат и последовательно соединяют, получается – ракета.
(0;8), (-2;4), (-2;-3), (-3;-5), (-3;-9), (-2;-9), (-2;-7), (-1;-7), (-1;-9), (1;-9), (1;-7), (2;-7), (2;-9), (3;-9), (3;-5), (2;-3), (2;4), (0;8)
Второе заданиеГде применяется система координат? (слайд 4)
В художественной литературе встречаются упоминания о системе координат. В стихотворении К.Симонова «Сын артиллериста» о молодом воспитаннике майора – Лёньке, который корректировал огонь артиллерийской батареи по радио, говорится:
В стихотворении К.Симонова «Сын артиллериста» о молодом воспитаннике майора – Лёньке, который корректировал огонь артиллерийской батареи по радио, говорится:
Третий сигнал по радио:
«Немцы вокруг меня,
Бейте четыре-десять,
Не жалейте огня!»
Майор побледнел, услышав:
«Четыре-десять – как раз
То место, где Лёнька
Должен сидеть сейчас»…
— Какие координаты передавались по радио?
— Где расположена эта точка в координатной плоскости?
Третье заданиеМы «улетаем в космос». (слайд 5 )
Прямо по курсу «Зона метеоритного дождя». (Слайд 6)
Задание 1. Постройте угол МОК, внутри этого угла отметьте точку А.Проведите через точку А прямые перпендикулярные сторонам угла.
Задание 2. Постройте угол АВС. Отметьте внутри угла точку К и проведите через неё прямые параллельные сторонам угла.
3. Физкультминутка
Физкультминутка(Слайд 7)
Четвертое заданиеМы отправляемся дальше в звездную обсерваторию.
У древних греков существовала легенда о созвездиях Большой и Малой Медведиц. Всемогущий бог Зевс решил взять себе в жены прекрасную нимфу Калисто, одну из служанок богини Афродиты, вопреки желанию последней. Чтобы избавить Калисто от преследований богини, Зевс обратил Калисто в Большую медведицу, её любимую собаку – в Малую Медведицу взял их на небо. (Слайд 8)
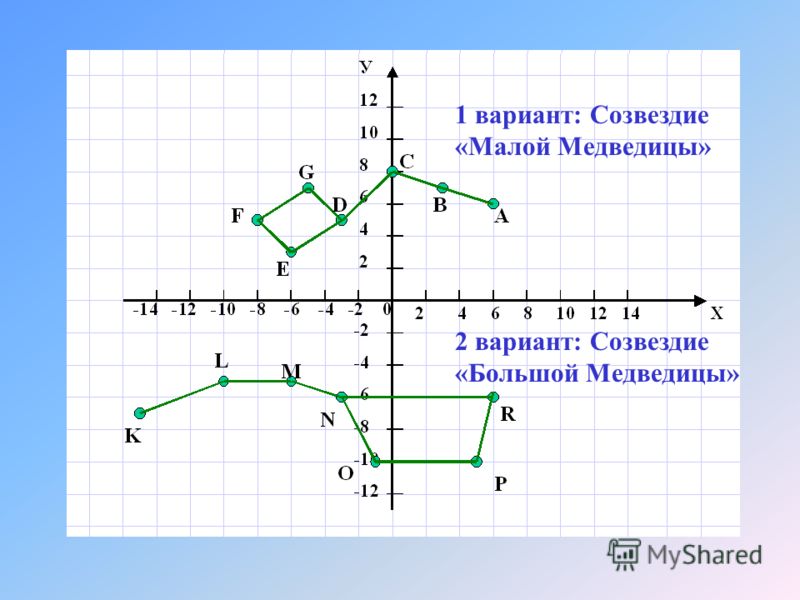
(6;6), (-3;5,5), (-8;5), (0;7,5), (3;7), (-5;7), (-6;3) — созвездие «Малой Медведицы»,
(-15;-7), (-3;-6), (5;-10), (-6;-5,5), (-10; -5), (6;-6), (-1;-10) – созвездие «Большой Медведицы».
Построение выполняется у доски.
Молодцы, ребята.
Историческое созвездие. (Слайд 9)
— Как давно системы координат пронизывают практическую жизнь человека?
Более чем за 100 лет до н. э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.
э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.
Во II веке н.э. знаменитый древнегреческий астроном Клавдий Птолемей уже пользовался долготой и широтой в качестве географических координат. Но эти понятия впервые были систематизированы в 17 веке Рене Декартом. (Слайд 10)
Рене Декарт (1596-1650) — французский философ, естествоиспытатель, математик. Целью Декарта было описание природы при помощи математических законов. Автор координатной плоскости, поэтому ее часто называют декартовой системой координат.
Пятое заданиеМы подлетаем к «Планете внеземной цивилизации». (Слайд 11)
Наша задача – расшифровать неизвестные фигуры, спроектированной инопланетянами и построить их. (Слайд 12)
Название типов звезд | Температура К |
Коричневые карлики | 2500 |
Белые карлики | 7500 |
Красные гиганты | 4000 |
Переменные звёзды | 6250 |
(Слайд 13)
Последним на нашем пути мы встречаем млечный путь с названием «Заморочки».
К сожалению, очень часто наш путь состоит из трудностей, которые надо преодолевать. Я желаю вам успешного преодоления всех «заморочек».
Самостоятельно с последующей проверкой по вариантам на листочках: постройте на координатной плоскости точки по указанным координатам, соедините их последовательно. (Слайд 14)
1. Созвездие Рысь
(4; 4,5), (3; 4), (2,5; 1,5), (0; 0), (-2; 0), (-3; -1), (-3,5; -2)
2. Созвездие Северная Корона
(2; 2), (-1,5; 0), (0,5; -1), (1; -0,5), (2; -0,5), (3; 1,5), (2; 3).
Приложение «Созведия»
4. Итоги урока(Слайд 15)
Я думаю, что вы согласны, у нас получился очень интересный урок, на котором вы показали нам свой багаж знаний, а он не маленький и он будет вам необходим в старших классах, он будет еще пополняться и расширяться. А тема «Координатная плоскость», надеюсь, останется для вас любимой. (Слайд 16)
(Слайд 16)
Выставление оценок.
5. Рефлексия(Слайд 17)
Прикрепи смайлик у тех слов, которые вам больше подходят к окончанию урока.
- Урок полезен, всё понятно.
- Лишь кое-что чуть-чуть неясно.
- Ещё придётся потрудиться.
- Да, трудно всё-таки учиться!
Технологическая карта урока
Задачи с решениями и ответы к упражнениям
Задачи с решениями и ответы к упражнениям
Страница 94 : 1 » « 187
Решите уравнение.
Решение задачи »
Приведите подобные слагаемые: x — 7 + 2х — 5х + 1.
Решение задачи »
Вычислите.
Решение задачи »
Что больше: а или 2а? а или а/2?
Решение задачи »
5/7 некоторого числа равны 7/5 этого числа. Какое это число?
Какое это число?
Решение задачи »
До конца суток осталось 2/3 того времени, которое прошло от начала суток. Который сейчас час?
Решение задачи »
Из пятидесяти звеньев составлена цепь. Найдите длину этой цепи, если просвет каждого звена 16 мм, а толщина 4 мм.
Решение задачи »
Выполните действия.
Решение задачи »
Перечертите рисунок 112 в тетрадь. Проведите через точку К прямую параллельную a; перпендикулярную прямой a.
Решение задачи »
Начертите угол ABC, равный 75°. На стороне ВА отметьте точку M и проведите через нее две прямые, одна из которых параллельна, а другая перпендикулярна стороне BC.
Решение задачи »
В лаборатории стояли 25 столов с ящиками. В одних столах было по 3 ящика, а в других по 4 . Сколько было столов с тремя ящиками и сколько с четырьмя, если общее число всех ящиков равно 91?
Сколько было столов с тремя ящиками и сколько с четырьмя, если общее число всех ящиков равно 91?
Решение задачи »
По норме рабочий должен изготовить 72 детали, а он изготовил 90 деталей. На сколько процентов рабочий выполнил норму и на сколько перевыполнил?
Решение задачи »
На 3/7 земельного участка разбит сад. 3/4 сада занимают яблони. Какую площадь занимают яблони, если площадь земельного участка 1 3/4 га?
Решение задачи »
Найдите значение выражения.
Решение задачи »
По рисунку 115 определите, сколько клеток надо пройти слева направо и сколько снизу вверх, чтобы попасть из точки О в точки М, К, Р и N.
Решение задачи »
Шестиклассники участвовали в спортивной игре. Сначала звено было в точке О. Командир получил приказ: Идите на восток 6 км, а затем на север 4 км . Назовите координаты точки B, в которую должно попасть это звено. Сформулируйте приказы для других звеньев, которые должны попасть из точки О в C, D, E, К, M, N. Назовите их координаты.
Назовите координаты точки B, в которую должно попасть это звено. Сформулируйте приказы для других звеньев, которые должны попасть из точки О в C, D, E, К, M, N. Назовите их координаты.
Решение задачи »
Возьмите географическую карту и назовите широту и долготу городов Москвы, Киева, Алма-Аты.
Решение задачи »
Постройте координатные прямые x и у и отметьте точки А(2; 8), В(3; -4), C(-4; 5), D(-3; -7), E(0; 5), М(0; -4), К(6; 0), Р(-7; 0)
Решение задачи »
Найдите координаты точек A, B, С и D рис. 117
Решение задачи »
У каких точек на координатной плоскости абсцисса равна нулю? У каких точек равна нулю ордината? Какая точка имеет координаты (0; 0)?
Решение задачи »
Где расположены на координатной плоскости точки, абсцисса которых равна 4? А где расположены точки, ордината которых —1?
Решение задачи »
Изобразите на координатной плоскости точки А (-2; -2), B(-1; -1), C(0; 0), D(1; 1), E(2; 2). Проверьте с помощью линейки, лежат ли эти точки на одной прямой и лежит ли на ней M (-5; 5).
Проверьте с помощью линейки, лежат ли эти точки на одной прямой и лежит ли на ней M (-5; 5).
Решение задачи »
Постройте на координатной плоскости четырехугольник ABCD, если А(-10;-2), В(-2;-2), C(-2; -6), D (-10; -6). Является ли он прямоугольником? квадратом? Найдите периметр и площадь этого четырехугольника, если единичный отрезок 1 см. Проведите отрезки AC и BD и найдите координаты точки их пересечения.
Решение задачи »
Постройте треугольник ОВС, где О (0; 0), В (4; 6), C(1;5).
Решение задачи »
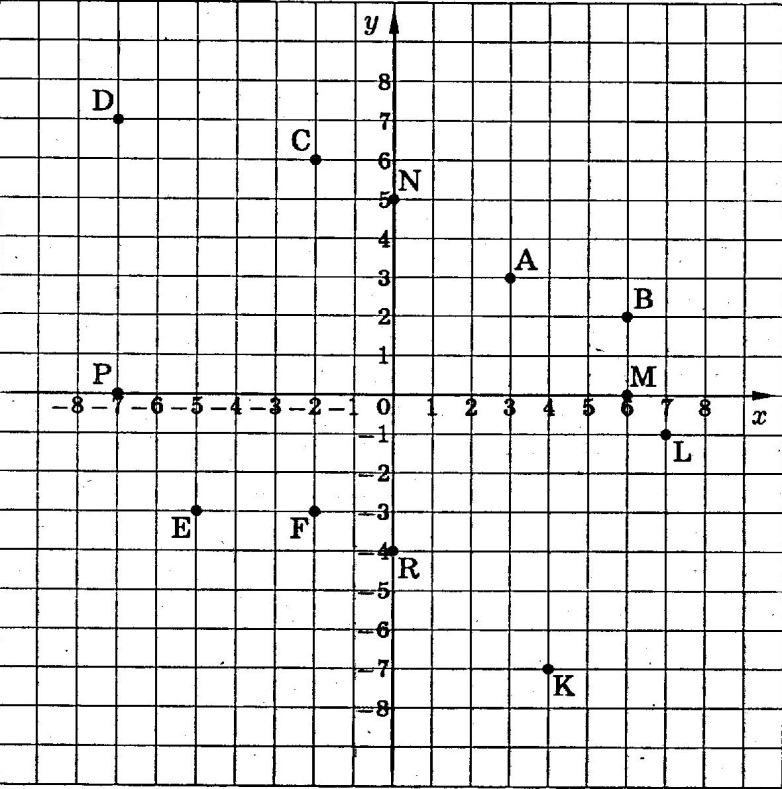
На миллиметровой бумаге отмечены точки A, B, C, D, E, F, К и М. Найдите их координаты.
Решение задачи »
В координатной плоскости проведена линия. Найдите на этой линии точку абсцисса которой равна 2; 1,7; —1,2; ордината которой равна 1,8; 2,1; —1,6; —2,5; —3,2.
Решение задачи »
Даны точки А( 1; 3 ), В(-1; 4 ), C(7; -5 ), D(0; 6 ). Какие из этих точек расположены выше оси абсцисс; левее оси ординат?
Какие из этих точек расположены выше оси абсцисс; левее оси ординат?
Решение задачи »
Вычислите устно -2,8-3,2 :1,2 ·1,6 + 8,5; 1,4-8,2 :3,4 ·0,5 + 0,8
Решение задачи »
Что больше x или х2? х2 или х3
Решение задачи »
Найдите все дроби со знаменателем 15, которые больше 8/9 и меньше 1.
Решение задачи »
Числа 90 и 100 разделили на одно и то же число. В первом случае получили остаток 18, а во втором остаток 4. Найдите делитель.
Решение задачи »
Из корзины взяли 6 яблок, затем треть остатка и еще 6 яблок. После этого в корзине осталась половина первоначального числа. Сколько яблок было в корзине?
Решение задачи »
Попробуйте найти простой способ для вычисления значения выражения: 1/1*2 + 1/2*3 + 1/3*4 + 1/4*5 + 1/5*6 + 1/6*7 + 1/7*8 + 1/8*9 + 1/9*10
Решение задачи »
Начертите какой-нибудь треугольник ABC. Через вершину С проведите прямую l, параллельную стороне AB, и прямую m, перпендикулярную AB.
Через вершину С проведите прямую l, параллельную стороне AB, и прямую m, перпендикулярную AB.
Решение задачи »
Найдите длину окружности, радиус которой 7 см, 0,7 см, 0,14 см, приняв п=22/7
Решение задачи »
Координатная плоскость
Представим себе такую историю…
– Привет, Саша! Мы идём в субботу в кино? Ты купил билеты? – спросил у друга Паша.
– Купил, – ответил Саша. – У нас 5 и 6 места.
– А в каком ряду наши места? – снова задал вопрос Паша. – Ведь в кинотеатре много рядов, и на каждом из них есть и 5, и 6 место.
– Наши места в 3 ряду, – уточнил Саша.
– Вот теперь понятно, – сказал Паша. – Места в зрительном зале кинотеатра всегда задают двумя числами: первое число – номер ряда, второе число – номер кресла в этом ряду. А знать только номер ряда или только номер кресла нам будет мало.
–
Можно сказать, что номер ряда и номер кресла в этом ряду – это наши координаты
в зале, – добавил Саша.
– Саша, а мы ведь на уроках математики не раз встречались с координатами, – сказал Паша.
– Точно. На координатной прямой мы отмечали точку, зная её координату, – вспомнил Саша
– Да. Но положение точки на координатной прямой определяется одной координатой, а расположение наших с тобой мест в зале – двумя, – задумался Паша. – Может, Мудряш поможет нам разобраться в этом.
– Ребята, прежде чем мы с вами поговорим, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.
– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!
–
А сейчас вернёмся к вашему вопросу, – начал Мудряш. – Ребята, вы уже знакомы с
координатной прямой. Это прямая, на которой выбрали начало отсчёта, единичный
отрезок и направление. Вы знаете, как найти точку на ней, если известна
координата этой точки. Например, числу соответствует
единственная точка .
Однако, покупая билеты в кино, вы обратили внимание, чтобы отыскать нужное нам место в зале, недостаточно знать одну координату, то есть только номер ряда или только номер кресла.
Чтобы занять нужное место, нам надо знать и номер кресла, и номер ряда, то есть две координаты.
Подобным образом можно обозначить положение точки на плоскости.
Давайте на плоскости проведём две перпендикулярные координатные прямые таким образом, чтобы их начала отсчёта совпали. Эти прямые называют осями координат. Обозначим точку их пересечения точкой О. Точку О называют началом координат. Горизонтальную ось обозначают буквой и называют осью абсцисс, или осью , а вертикальную ось обозначают буквой и называют осью ординат, или осью .
Ось
и
ось образуют
прямоугольную систему координат. А плоскость, на которой задана система
координат, называют координатной плоскостью.
Обратите внимание, что координатные оси разделяют плоскость на четыре части, которые называют координатными четвертями и нумеруют против часовой стрелки: первая четверть, вторая четверть, третья четверть, четвёртая четверть.
– А давайте отметим на координатной плоскости какую-нибудь точку, – предложили ребята Мудряшу.
– Давайте отметим точку , – начал Мудряш. – Проведём через эту точку прямые, перпендикулярные осям координат. Пересечение с осью обозначим точкой , а с осью – точкой .
Посмотрите, точка на оси имеет координату .
– А точка на оси имеет координату , – помогли Мудряшу ребята.
– Верно, – сказал Мудряш. – Число называют абсциссой точки , число – ординатой точки . Эти числа определяют положение точки на координатной прямой.
–
И их называют координатами точки ?
– задали вопрос мальчишки.
– Да, – ответил Мудряш. – И записывают так: При этом обратите внимание, что абсциссу всегда ставят на первое место, а ординату – на второе.
– А если поменять местами минус и ? – спросили ребята.
– Тогда мы получим другую точку. Например, точку , – объяснил Мудряш. – Отметим эту точку на координатной плоскости.
Для этого на оси находим абсциссу точки . Она равна . Проведём через неё прямую, перпендикулярную оси . Затем на оси находим ординату точки . Она равна минус трём. Проведём через неё прямую, перпендикулярную оси . Точка, в которой пересекаются эти прямые, и есть точка .
– А какие координаты имеет точка О? – поинтересовался Паша.
– Абсцисса и ордината у начала координат равны 0. Записывают это так: .
Ребята, посмотрите на рисунок. Здесь отмечены точка и точка .
–
Точка лежит
на оси ,
а точка лежит
на оси ,
– отметили мальчики.
– И обратите внимание, что у точки ордината равна , а у точки абсцисса равна , – добавил Мудряш. – Запомните! Если точка лежит на оси абсцисс, то её ордината равна , а если точка лежит на оси ординат, то равна её абсцисса.
Теперь отметим на координатной плоскости точку и точку .
– У этих точек абсцисса и ордината – противоположные числа, – заметил Паша.
– Правильно, – сказал Мудряш. – И эти точки симметричны относительно точки О, то есть относительно начала координат. Запомните! Две точки с противоположными абсциссами и ординатами симметричны относительно начала координат.
Отметим на координатной плоскости точку и точку .
– У этих точек абсциссы – противоположные числа, а ординаты равны, – заметили мальчишки.
–
Верно, – сказал Мудряш. – При этом точки и
симметричны
относительно оси .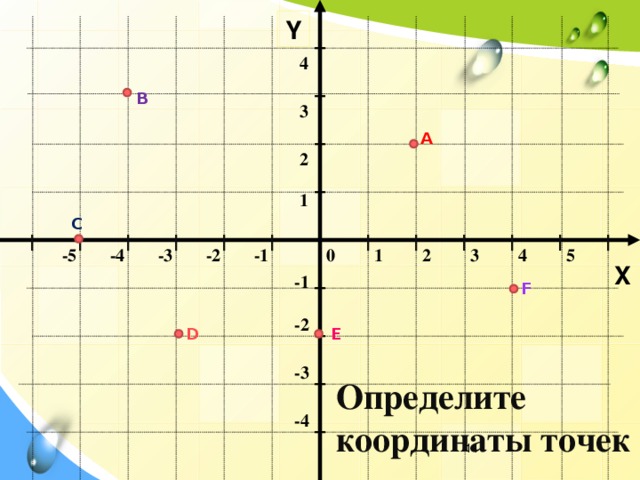 Запомните! Две точки с равными ординатами и противоположными абсциссами
симметричны относительно оси ординат.
Запомните! Две точки с равными ординатами и противоположными абсциссами
симметричны относительно оси ординат.
А теперь давайте отметим точку и точку .
– У этих точек, наоборот, абсциссы равны, а ординаты – противоположные числа, – снова заметили Саша и Паша.
– При этом точки и симметричны относительно оси . Запомните! Две точки с равными абсциссами и противоположными ординатами симметричны относительно оси абсцисс.
Ребята, а сейчас давайте выполним несколько заданий, – предложил Мудряш.
Задание первое: найдите координаты точек , и , изображённых на рисунке.
Решение: найдём
координаты точки .
Для этого проведём через неё прямую, перпендикулярную оси ,
и прямую, перпендикулярную оси .
Видим, что точка пересечения прямой, перпендикулярной оси ,
и оси имеет
координату 3, а значит, абсцисса точки равна
3.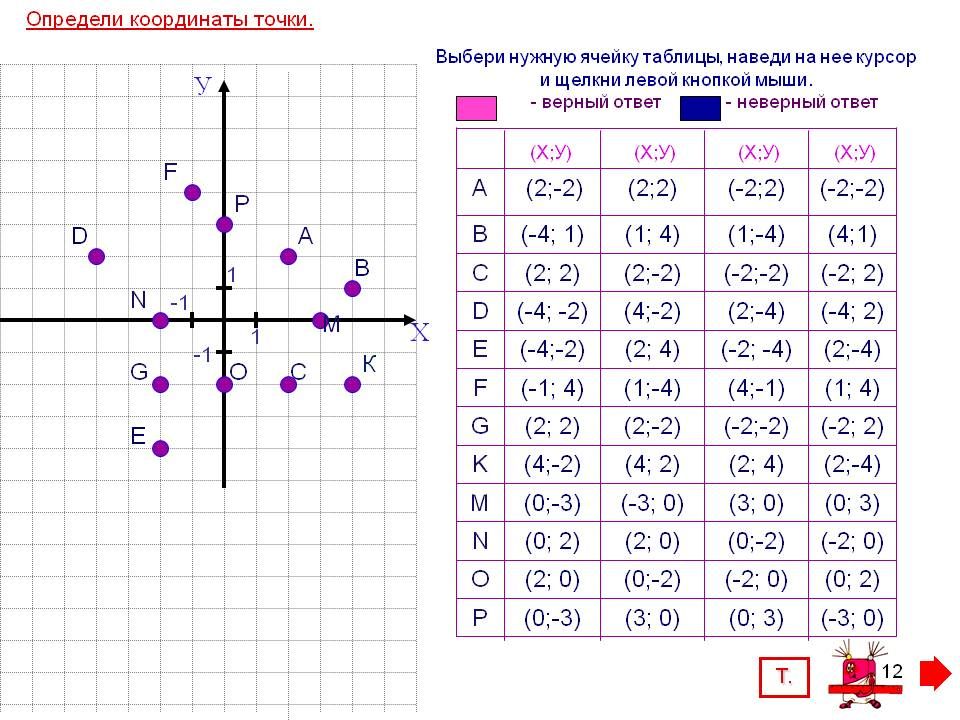 Точка пересечения прямой, перпендикулярной оси ,
и оси имеет
координату 4, а значит, ордината точки равна
4.
Точка пересечения прямой, перпендикулярной оси ,
и оси имеет
координату 4, а значит, ордината точки равна
4.
Найдём координаты точки . Проведём через неё прямую, перпендикулярную оси , и прямую, перпендикулярную оси . Точка пересечения прямой, перпендикулярной оси , и оси имеет координату , а значит, абсцисса точки равна . Точка пересечения прямой, перпендикулярной оси , и оси имеет координату , а значит, ордината точки равна .
И найдём координаты точки . Проведём через неё прямые, перпендикулярные осям координат. Видим, что точка пересечения прямой, перпендикулярной оси , и оси имеет координату , а значит, абсцисса точки равна . Точка пересечения прямой, перпендикулярной оси , и оси имеет координату , а значит, ордината точки равна .
Второе
задание: отметьте на координатной плоскости точки: , , .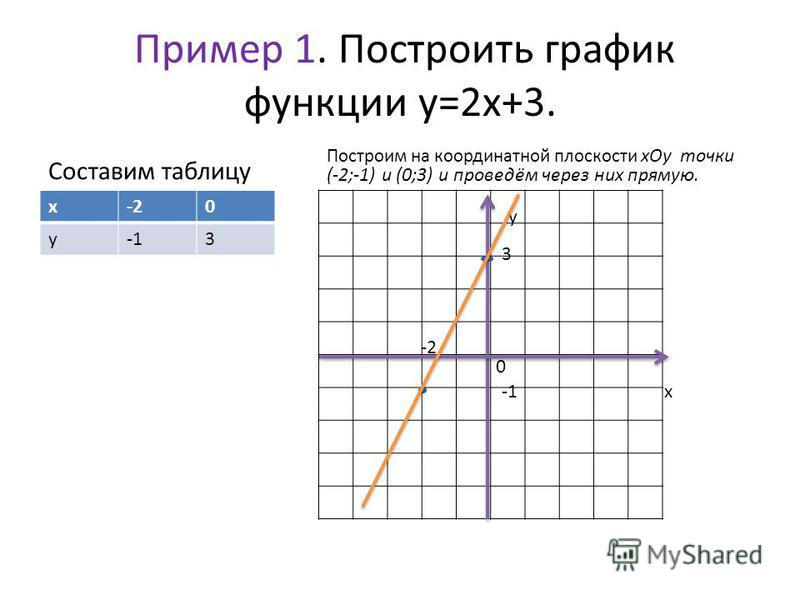
Решение: отметим точку . Абсцисса точки равна . Проведём через неё прямую, перпендикулярную оси . Ордината точки равна . Проведём через неё прямую, перпендикулярную оси . Точка, в которой пересекаются эти прямые, и есть точка .
Теперь отметим точку . Абсцисса точки равна . Проведём через неё прямую, перпендикулярную оси . Ордината точки БЭ – 1. Проведём через неё прямую, перпендикулярную оси . Точка, в которой пересекаются эти прямые, и есть точка .
Осталось отметить точку . Абсцисса этой точки равна , а значит, точка лежит на оси ординат. Ордината этой точки равна .
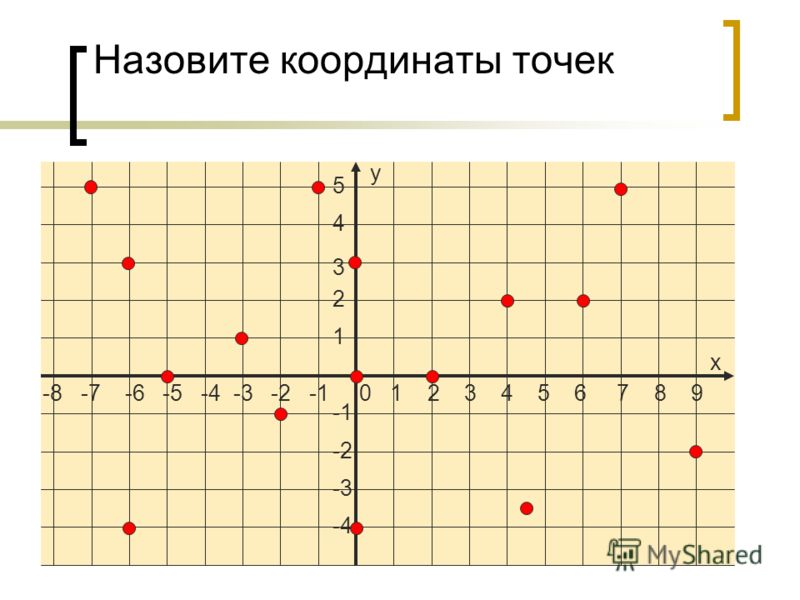
И ещё одно задание: постройте на координатной плоскости отрезки и , если точка , , , . Найдите точку пересечения этих отрезков.
Решение: чтобы
построить отрезки и
,
отметим на координатной плоскости точки ,
,
и
.
Отметим точку . Абсцисса этой точки равна , а значит, точка лежит на оси ординат. Ордината этой точки равна .
Отметим точку . Абсцисса точки равна . Проведём через неё прямую, перпендикулярную оси . Ордината точки равна . Проведём через неё прямую, перпендикулярную оси . Точка, в которой пересекаются эти прямые, и есть точка .
Отметим точку . Ордината этой точки равна , а значит, точка лежит на оси абсцисс. Абсцисса этой точки равна .
Отметим точку . Абсцисса точки равна . Проведём через неё прямую, перпендикулярную оси . Ордината точки ДЭ равна . Проведём через неё прямую, перпендикулярную оси . Точка, в которой пересекаются эти прямые, и есть точка .
Соединим
точки и
,
и
.
Обозначим точку пересечения отрезков и
точкой
.
Найдём координаты этой точки. Для этого проведём через неё прямую,
перпендикулярную оси ,
и прямую, перпендикулярную оси . Видим, что точка пересечения прямой, перпендикулярной оси ,
и оси имеет
на оси координату
,
а значит, абсцисса точки равна
.
Точка пересечения прямой, перпендикулярной оси ,
и оси имеет
на оси координату
,
а значит, ордината точки равна
.
Видим, что точка пересечения прямой, перпендикулярной оси ,
и оси имеет
на оси координату
,
а значит, абсцисса точки равна
.
Точка пересечения прямой, перпендикулярной оси ,
и оси имеет
на оси координату
,
а значит, ордината точки равна
.
Таким образом, отрезки и пересекаются в точке .
Путешествие по системе координат — математика, уроки
Математика 6 класс
Тема: Путешествие вокруг системы координат.
Цель: обобщение, знаний, умений и навыков по теме: «Координатная плоскость»
Отработка навыков построения координат на плоскости, определение координат, координатных углов;
умений достраивать до прямоугольника, до квадрата, симметричные точки в координатной плоскости.
Форма урока: путешествие.
Тип урока: обобщающий.
Кабинет мультимедиа.
Оформление: портрет Р.Декарт, эпиграф к уроку «Будь настойчив как Рене.»
Ход урока:
I. Организационный момент.
II.Устная работа.
Карта путешествия проектируется на экран.
Под музыку учитель сообщает тему урока. Ставит задачу перед учащимися. Разминка. Кросс-опросс.
Закончи мои предложения.
1. Плоскость, на которой задана система координат называется ……
2.Точка пересечения оси ординат и оси абсцисс называется………
3.Координатные прямые называются осями……
4.В первой четверти знаки……
5.Во второй четверти знаки….
6. В третьей четверти знаки….
7. Во четвертой четверти знаки….
8.Если точка лежит на оси ординат, то …..
9. Если точка лежит на оси абсцисс, то …..
10.Начало координат имеет координаты…
11. Точка А(3;4) лежит в …координатном углу.
12. Точка А(-3;0) лежит в …координатном углу.
13. Точка А(-3;-2) лежит в …координатном углу.
14. Точка А(2;-5) лежит в …координатном углу.
15. Точка А(0;4) лежит в …координатном углу.
II. Фронтальный опрос.
Графический диктант.
Организационный момент.
II.Устная работа.
Карта путешествия проектируется на экран.
Под музыку учитель сообщает тему урока. Ставит задачу перед учащимися. Разминка. Кросс-опросс.
Закончи мои предложения.
1. Плоскость, на которой задана система координат называется ……
2.Точка пересечения оси ординат и оси абсцисс называется………
3.Координатные прямые называются осями……
4.В первой четверти знаки……
5.Во второй четверти знаки….
6. В третьей четверти знаки….
7. Во четвертой четверти знаки….
8.Если точка лежит на оси ординат, то …..
9. Если точка лежит на оси абсцисс, то …..
10.Начало координат имеет координаты…
11. Точка А(3;4) лежит в …координатном углу.
12. Точка А(-3;0) лежит в …координатном углу.
13. Точка А(-3;-2) лежит в …координатном углу.
14. Точка А(2;-5) лежит в …координатном углу.
15. Точка А(0;4) лежит в …координатном углу.
II. Фронтальный опрос.
Графический диктант. Определим траекторию полета от Даши Верхоглядкиной.
Даша Верхоглядкина написала некоторые утверждения. Если вы согласны с ее утверждениями, то должны поставить галочку, если вы не согласны.
1.Перпендикулярные прямые образуют при пересечении прямые углы.
2.Если точка лежит на оси ОY, то ее абсцисса равна 0, а ее ордината любое число.
3.ТочкаА(2;5) расположена во II четверти.
4.Точка В(-3;0) расположена выше оси ОX.
5. Плоскость, на которой расположена система координат, называют координатной плоскостью.
6.Точка(4;1)и точка(4;1) симметрична относительно оси ОY.
7.Точка В(-2;-3) лежит в IV координатном углу.
Учитель: В литературе есть упоминание о координатах в стихотворении К.Симонова «Сын артиллериста»
Ученица читает отрывок стихотворения .
Задание 2. Математический диктант.
Мы узнаем название транспорта на котором будем совершать полет.
Постройте последовательно точки на координатной плоскости, затем последовательно соедините, начиная с номера 1 до номера 14
1.
Определим траекторию полета от Даши Верхоглядкиной.
Даша Верхоглядкина написала некоторые утверждения. Если вы согласны с ее утверждениями, то должны поставить галочку, если вы не согласны.
1.Перпендикулярные прямые образуют при пересечении прямые углы.
2.Если точка лежит на оси ОY, то ее абсцисса равна 0, а ее ордината любое число.
3.ТочкаА(2;5) расположена во II четверти.
4.Точка В(-3;0) расположена выше оси ОX.
5. Плоскость, на которой расположена система координат, называют координатной плоскостью.
6.Точка(4;1)и точка(4;1) симметрична относительно оси ОY.
7.Точка В(-2;-3) лежит в IV координатном углу.
Учитель: В литературе есть упоминание о координатах в стихотворении К.Симонова «Сын артиллериста»
Ученица читает отрывок стихотворения .
Задание 2. Математический диктант.
Мы узнаем название транспорта на котором будем совершать полет.
Постройте последовательно точки на координатной плоскости, затем последовательно соедините, начиная с номера 1 до номера 14
1. (-3;0) 5.(-1;7) 9.(1;7) 13.(3;0)
2.(-3;2) 6.(-1;9) 10.(1;5) 14.(0;2)
3.(-3;4) 7.(0;11) 11.(3;4)
4.(-1;5) 8.(1;9) 12.(3;2)
Учитель: Звездное небо. Как это удивительно красиво.
Я расскажу вам легенду.
У древних греков существовал миф о созвездиях Большой и Малой медведицы.
Всемогущий бог Зевс решил взять в жены прекрасную нимфу Калисто, одну из служанок Афродиты, вопреки желанию последней.
Чтобы избавить Калисто от преследований богини, Зевс обратил Калисто в большую Медведицу , ее любимую собаку в Малую медведицу и взял их на небо.
Подготовьте сообщение о созвездиях и изобразите их на координатной плоскости Это будет вашим домашним заданием.
Задание 4. «Метеоритный дождь
В системе координат даны точки каждой группе выписать координаты этих точек.
1 группа красные точки,
2 группа синие точки,
3 группа зеленые точки,
4 группа фиолетовые точки.
(-3;0) 5.(-1;7) 9.(1;7) 13.(3;0)
2.(-3;2) 6.(-1;9) 10.(1;5) 14.(0;2)
3.(-3;4) 7.(0;11) 11.(3;4)
4.(-1;5) 8.(1;9) 12.(3;2)
Учитель: Звездное небо. Как это удивительно красиво.
Я расскажу вам легенду.
У древних греков существовал миф о созвездиях Большой и Малой медведицы.
Всемогущий бог Зевс решил взять в жены прекрасную нимфу Калисто, одну из служанок Афродиты, вопреки желанию последней.
Чтобы избавить Калисто от преследований богини, Зевс обратил Калисто в большую Медведицу , ее любимую собаку в Малую медведицу и взял их на небо.
Подготовьте сообщение о созвездиях и изобразите их на координатной плоскости Это будет вашим домашним заданием.
Задание 4. «Метеоритный дождь
В системе координат даны точки каждой группе выписать координаты этих точек.
1 группа красные точки,
2 группа синие точки,
3 группа зеленые точки,
4 группа фиолетовые точки. Задание 5 «Планета туманности» Распределите следующие точки по координатным углам и осям, не строя их на координатной плоскости.
Занесите их в следующую таблицу.
1 четверть 2 четверть 3 четверть 4 четверть Ось OX Ось OY Начало координат
А(3;4) В(6;8) С(0;5) Д (-8;-6) Р (5;2) Н (4;6) К (6;0) О (0;0) Е (0;-2) М (-5;6) Т(-4;-6) Z (0;-2)
Х (-15;2) L (3;0)
Задание 6. Конструирование.
1 группа.
Построить точки на координатной плоскости.
Постройте точку Д так. Чтобы получился прямоугольник.
А (-4;5)
В (3;5)
С (-4;2)
Д (?;?)
2 группа.
Построить точки на координатной плоскости.
Постройте точку Д так. Чтобы получился прямоугольник.
А (2;4)
В (-2;4)
С (-2;0)
Д (?;?)
3 группа.
Построить точку А (-4;3). Построить для точки А симметричную точки А
1) относительно оси ОХ;
2) относительно оси ОY.
4 группа.
Построить точку А (4;5).
Задание 5 «Планета туманности» Распределите следующие точки по координатным углам и осям, не строя их на координатной плоскости.
Занесите их в следующую таблицу.
1 четверть 2 четверть 3 четверть 4 четверть Ось OX Ось OY Начало координат
А(3;4) В(6;8) С(0;5) Д (-8;-6) Р (5;2) Н (4;6) К (6;0) О (0;0) Е (0;-2) М (-5;6) Т(-4;-6) Z (0;-2)
Х (-15;2) L (3;0)
Задание 6. Конструирование.
1 группа.
Построить точки на координатной плоскости.
Постройте точку Д так. Чтобы получился прямоугольник.
А (-4;5)
В (3;5)
С (-4;2)
Д (?;?)
2 группа.
Построить точки на координатной плоскости.
Постройте точку Д так. Чтобы получился прямоугольник.
А (2;4)
В (-2;4)
С (-2;0)
Д (?;?)
3 группа.
Построить точку А (-4;3). Построить для точки А симметричную точки А
1) относительно оси ОХ;
2) относительно оси ОY.
4 группа.
Построить точку А (4;5). Построить для точки А симметричную точки А
1) относительно оси ОХ
2) относительно оси ОY.
Задание 7. «Из ракеты в конфету» Творческое задание.
Постройте точки по заданным координатам и соедините их последовательно, начиная с первого номера. Затем из ракеты получите конфету, перестановкой наименьшего числа точек.
Задание 9.
Тесты (сборник тестовых заданий по математике 6 класс издательство «Атам?ра 2006 го стр.70 4 задания)
Задания даны на компьютерах. Учащиеся по очереди садятся за тесты, а остальные выполняют карточки по 3 уровням. Каждый ученик получает карточки 3-х уровней. Поэтому каждый имеет возможность выполнить любой уровень.
1 уровень.
1.Отметьте точки на координатной плоскости:
А (2;3) В (4;3) С (-4;2) К (-2;-3) М (0;5) Н (-3;0).
2.Отметить на координатной плоскости точки:
М(6;6) А(-2;2) К(4;1) Р(-2;4).
Проведите прямые МА и КР.
Найдите координаты точек пересечения:
1) прямых МА и КР;
2) 2)прямой МА и осью абсцисс;
3) 3)прямой КР и осью ординат.
Построить для точки А симметричную точки А
1) относительно оси ОХ
2) относительно оси ОY.
Задание 7. «Из ракеты в конфету» Творческое задание.
Постройте точки по заданным координатам и соедините их последовательно, начиная с первого номера. Затем из ракеты получите конфету, перестановкой наименьшего числа точек.
Задание 9.
Тесты (сборник тестовых заданий по математике 6 класс издательство «Атам?ра 2006 го стр.70 4 задания)
Задания даны на компьютерах. Учащиеся по очереди садятся за тесты, а остальные выполняют карточки по 3 уровням. Каждый ученик получает карточки 3-х уровней. Поэтому каждый имеет возможность выполнить любой уровень.
1 уровень.
1.Отметьте точки на координатной плоскости:
А (2;3) В (4;3) С (-4;2) К (-2;-3) М (0;5) Н (-3;0).
2.Отметить на координатной плоскости точки:
М(6;6) А(-2;2) К(4;1) Р(-2;4).
Проведите прямые МА и КР.
Найдите координаты точек пересечения:
1) прямых МА и КР;
2) 2)прямой МА и осью абсцисс;
3) 3)прямой КР и осью ординат. 3.Накоординатной плоскости отметьте точки А (-4;2) В (2;2) С (2;4). Постройте четвертую точку К
Так, чтобы получился квадрат. Определите координаты точки К.
2уровень.
1.Постройте отрезок АВ по координатам А(4;2) В(2;20. Найдите координаты точки, в которой он пересекается с осью абсцисс.
2.На координатной плоскости отметьте точки А(-8;3) В(1;3) С(1;3). Постройте четвертую точку К так, чтобы получился прямоугольник АВСК. Найти длину отрезка АВ.
3.На координатной плоскости отметьте 6 точек, имеющих ординату, равную 1. Запишите координаты этих точек.
Где расположены эти точки?
3уровень.
1.Расположите следующие точки по координатным углам и осям, не строя их на координатной плоскости:
А (1;3), В (6;6),С (-2;3),Д (-8;-6), О (0;0) ,К (6;0),М (-5;6), Т (-4;-2), Н (0;2), Х(-15;2, Р (5;5).
2.Постройте треугольник МРТ, если М(;), Р(-3;0),Т(-3;-3). Замените координаты точек на противоположные, какая фигура получилась сейчас?
3.Отметьте на координатной плоскости все точки, у которых абсцисса и ордината- неположительные числа, и их сумма равна -8.
3.Накоординатной плоскости отметьте точки А (-4;2) В (2;2) С (2;4). Постройте четвертую точку К
Так, чтобы получился квадрат. Определите координаты точки К.
2уровень.
1.Постройте отрезок АВ по координатам А(4;2) В(2;20. Найдите координаты точки, в которой он пересекается с осью абсцисс.
2.На координатной плоскости отметьте точки А(-8;3) В(1;3) С(1;3). Постройте четвертую точку К так, чтобы получился прямоугольник АВСК. Найти длину отрезка АВ.
3.На координатной плоскости отметьте 6 точек, имеющих ординату, равную 1. Запишите координаты этих точек.
Где расположены эти точки?
3уровень.
1.Расположите следующие точки по координатным углам и осям, не строя их на координатной плоскости:
А (1;3), В (6;6),С (-2;3),Д (-8;-6), О (0;0) ,К (6;0),М (-5;6), Т (-4;-2), Н (0;2), Х(-15;2, Р (5;5).
2.Постройте треугольник МРТ, если М(;), Р(-3;0),Т(-3;-3). Замените координаты точек на противоположные, какая фигура получилась сейчас?
3.Отметьте на координатной плоскости все точки, у которых абсцисса и ордината- неположительные числа, и их сумма равна -8. Какую фигуру составляют эти точки?
Учащиеся выполняют задания из любого уровня.
IV Этап домашнего задания. Слайд 8
Творческое задание.
Подготовьте сообщение о созвездиях и изобразите их на координатной плоскости Это будет вашим домашним заданием.
V.Итог урока. Слайд 9Оценки за урок по тестам, за работу в тетрадях.
Учитель: Спасибо за урок! Слайд 10.
Математика 6 класс
«Координатная плоскость»
1 уровень
1. Отметьте точки на координатной плоскости:
А (2;3) В (4;3) С (-4;2) К (-2;-3) М (0;5) Н (-3;0).
2. Отметить на координатной плоскости точки:
М(6;6) А(-2;2) К(4;1) Р(-2;4).
Проведите прямые МА и КР.
Найдите координаты точек пересечения:
4) прямых МА и КР;
5) 2)прямой МА и осью абсцисс;
6) 3)прямой КР и осью ординат.
3. На координатной плоскости отметьте точки А (-4;2) В (2;2) С (2;4). Постройте четвертую точку К так, чтобы получился квадрат. Определите координаты точки К.
Какую фигуру составляют эти точки?
Учащиеся выполняют задания из любого уровня.
IV Этап домашнего задания. Слайд 8
Творческое задание.
Подготовьте сообщение о созвездиях и изобразите их на координатной плоскости Это будет вашим домашним заданием.
V.Итог урока. Слайд 9Оценки за урок по тестам, за работу в тетрадях.
Учитель: Спасибо за урок! Слайд 10.
Математика 6 класс
«Координатная плоскость»
1 уровень
1. Отметьте точки на координатной плоскости:
А (2;3) В (4;3) С (-4;2) К (-2;-3) М (0;5) Н (-3;0).
2. Отметить на координатной плоскости точки:
М(6;6) А(-2;2) К(4;1) Р(-2;4).
Проведите прямые МА и КР.
Найдите координаты точек пересечения:
4) прямых МА и КР;
5) 2)прямой МА и осью абсцисс;
6) 3)прямой КР и осью ординат.
3. На координатной плоскости отметьте точки А (-4;2) В (2;2) С (2;4). Постройте четвертую точку К так, чтобы получился квадрат. Определите координаты точки К. 2 уровень
1. Постройте отрезок АВ по координатам А(4;2) В(2;20. Найдите координаты точки, в которой он пересекается с осью абсцисс.
2. На координатной плоскости отметьте точки А(-8;3) В(1;3) С(1;3). Постройте четвертую точку К так, чтобы получился прямоугольник АВСК. Найти длину отрезка АВ.
3. На координатной плоскости отметьте 6 точек, имеющих ординату, равную 1. Запишите координаты этих точек.
Где расположены эти точки?
3 уровень
1. Расположите следующие точки по координатным углам и осям, не строя их на координатной плоскости:
А (1;3), В (6;6),С (-2;3),Д (-8;-6), О (0;0) ,К (6;0),М (-5;6), Т (-4;-2), Н (0;2), Х(-15;2), Р (5;5).
2. Постройте треугольник МРТ, если М(;), Р(-3;0),Т(-3;-3). Замените координаты точек на противоположные, какая фигура получилась сейчас?
3. Отметьте на координатной плоскости все точки, у которых абсцисса и ордината- неположительные числа, и их сумма равна -8. Какую фигуру составляют эти точки?
Используемая литература:
Учебник «Математика 6 класс»
А.
2 уровень
1. Постройте отрезок АВ по координатам А(4;2) В(2;20. Найдите координаты точки, в которой он пересекается с осью абсцисс.
2. На координатной плоскости отметьте точки А(-8;3) В(1;3) С(1;3). Постройте четвертую точку К так, чтобы получился прямоугольник АВСК. Найти длину отрезка АВ.
3. На координатной плоскости отметьте 6 точек, имеющих ординату, равную 1. Запишите координаты этих точек.
Где расположены эти точки?
3 уровень
1. Расположите следующие точки по координатным углам и осям, не строя их на координатной плоскости:
А (1;3), В (6;6),С (-2;3),Д (-8;-6), О (0;0) ,К (6;0),М (-5;6), Т (-4;-2), Н (0;2), Х(-15;2), Р (5;5).
2. Постройте треугольник МРТ, если М(;), Р(-3;0),Т(-3;-3). Замените координаты точек на противоположные, какая фигура получилась сейчас?
3. Отметьте на координатной плоскости все точки, у которых абсцисса и ордината- неположительные числа, и их сумма равна -8. Какую фигуру составляют эти точки?
Используемая литература:
Учебник «Математика 6 класс»
А. Абылкасымова издательство «Мектеп» 2007, 2013
Тесты (сборник тестовых заданий по математике 6 класс издательство «Атам?ра 2006 го стр.70 (4 задания)
Абылкасымова издательство «Мектеп» 2007, 2013
Тесты (сборник тестовых заданий по математике 6 класс издательство «Атам?ра 2006 го стр.70 (4 задания)
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ
Просмотр содержимого документа
«Путешествие по системе координат »
Математика 6 класс
Тема: Путешествие вокруг системы координат.
Цель: обобщение, знаний, умений и навыков по теме: «Координатная плоскость»
Отработка навыков построения координат на плоскости, определение координат, координатных углов;
умений достраивать до прямоугольника, до квадрата, симметричные точки в координатной плоскости.
Форма урока: путешествие.
Тип урока: обобщающий.
Кабинет мультимедиа.
Оформление: портрет Р.Декарт, эпиграф к уроку «Будь настойчив как Рене.»
Ход урока:
I. Организационный момент.
II.Устная работа.
Карта путешествия проектируется на экран.
Под музыку учитель сообщает тему урока. Ставит задачу перед учащимися.Слайд 2
Разминка. Кросс-опросс.
Закончи мои предложения.
1. Плоскость, на которой задана система координат называется ……
2.Точка пересечения оси ординат и оси абсцисс называется………
3.Координатные прямые называются осями……
4. В первой четверти знаки……
В первой четверти знаки……
5.Во второй четверти знаки….
6. В третьей четверти знаки….
7. Во четвертой четверти знаки….
8.Если точка лежит на оси ординат, то …..
9. Если точка лежит на оси абсцисс, то …..
10.Начало координат имеет координаты…
11. Точка А(3;4) лежит в …координатном углу.
12. Точка А(-3;0) лежит в …координатном углу.
13. Точка А(-3;-2) лежит в …координатном углу.
14. Точка А(2;-5) лежит в …координатном углу.
15. Точка А(0;4) лежит в …координатном углу.
II. Фронтальный опрос.
Графический диктант.
Определим траекторию полета от Даши Верхоглядкиной.
Даша Верхоглядкина написала некоторые утверждения. Если вы согласны с ее утверждениями, то должны поставить галочку, если вы не согласны.
1.Перпендикулярные прямые образуют при пересечении прямые углы.
2.Если точка лежит на оси ОY, то ее абсцисса равна 0, а ее ордината любое число.
3.ТочкаА(2;5) расположена во II четверти.
4.Точка В(-3;0) расположена выше оси ОX.
5. Плоскость, на которой расположена система координат, называют координатной плоскостью.
6.Точка(4;1)и точка(4;1) симметрична относительно оси ОY.
7.Точка В(-2;-3) лежит в IV координатном углу.
Учитель: В литературе есть упоминание о координатах в стихотворении К.Симонова «Сын артиллериста»
Ученица читает отрывок стихотворения .
Задание 2. Математический диктант. Слайд 3
Мы узнаем название транспорта на котором будем совершать полет.
Постройте последовательно точки на координатной плоскости, затем последовательно соедините, начиная с номера 1 до номера 14. Слайд 4
1.(-3;0) 5.(-1;7) 9.(1;7) 13.(3;0)
2.(-3;2) 6.(-1;9) 10.(1;5) 14.(0;2)
3.(-3;4) 7.(0;11) 11.(3;4)
4.(-1;5) 8.(1;9) 12.(3;2)
Учитель: Звездное небо. Как это удивительно красиво.
Я расскажу вам легенду.
У древних греков существовал миф о созвездиях Большой и Малой медведицы.
Всемогущий бог Зевс решил взять в жены прекрасную нимфу Калисто, одну из служанок Афродиты, вопреки желанию последней.
Чтобы избавить Калисто от преследований богини, Зевс обратил Калисто в большую Медведицу , ее любимую собаку в Малую медведицу и взял их на небо.
Подготовьте сообщение о созвездиях и изобразите их на координатной плоскости Это будет вашим домашним заданием.
Задание 4. «Метеоритный дождь» Слайд 5
В системе координат даны точки каждой группе выписать координаты этих точек.
1 группа красные точки,
2 группа синие точки,
3 группа зеленые точки,
4 группа фиолетовые точки.
Задание 5 «Планета туманности» слайд 6
Распределите следующие точки по координатным углам и осям, не строя их на координатной плоскости.
Занесите их в следующую таблицу.
1 четверть | 2 четверть | 3 четверть | 4 четверть | Ось OX | Ось OY | Начало координат |
А(3;4) В(6;8) С(0;5) Д (-8;-6) Р (5;2) Н (4;6) К (6;0) О (0;0) Е (0;-2) М (-5;6) Т(-4;-6) Z (0;-2)
Х (-15;2) L (3;0)
Задание 6.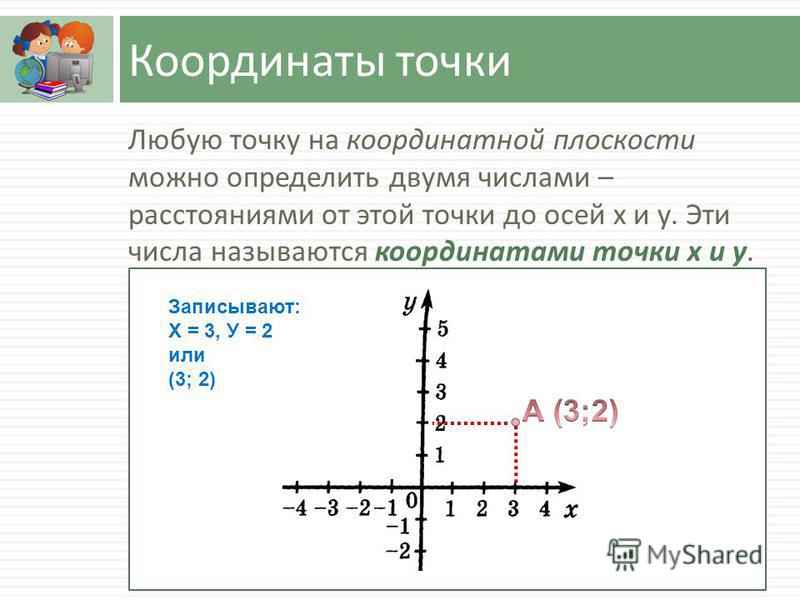 Конструирование.
Конструирование.
1 группа.
Построить точки на координатной плоскости.
Постройте точку Д так. Чтобы получился прямоугольник.
А (-4;5)
В (3;5)
С (-4;2)
Д (?;?)
2 группа.
Построить точки на координатной плоскости.
Постройте точку Д так. Чтобы получился прямоугольник.
А (2;4)
В (-2;4)
С (-2;0)
Д (?;?)
3 группа.
Построить точку А (-4;3). Построить для точки А симметричную точки А
1) относительно оси ОХ;
2) относительно оси ОY.
4 группа.
Построить точку А (4;5). Построить для точки А симметричную точки А
1) относительно оси ОХ
2) относительно оси ОY.
Задание 7. «Из ракеты в конфету» слайд 7
Творческое задание.
Постройте точки по заданным координатам и соедините их последовательно, начиная с первого номера. Затем из ракеты получите конфету, перестановкой наименьшего числа точек.
Задание 9.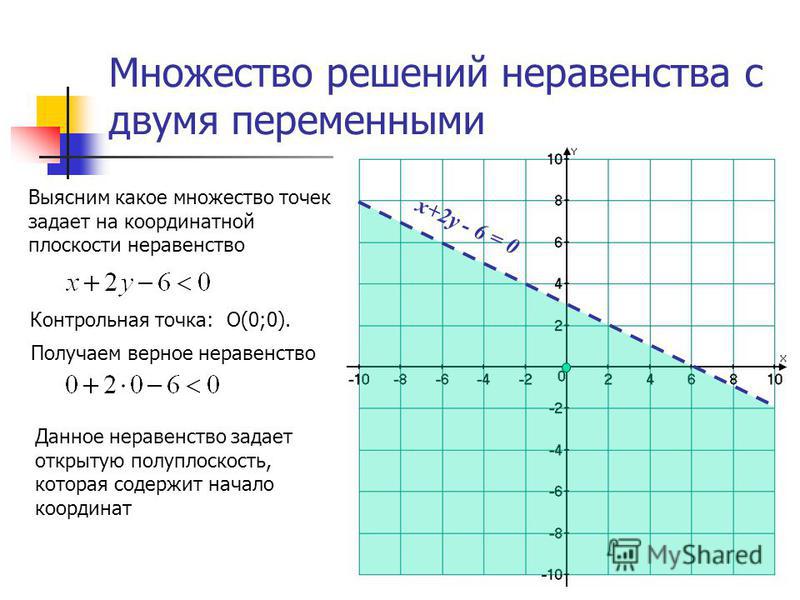
Тесты (сборник тестовых заданий по математике 6 класс издательство «Атамұра 2006 го стр.70 4 задания)
Задания даны на компьютерах. Учащиеся по очереди садятся за тесты, а остальные выполняют карточки по 3 уровням. Каждый ученик получает карточки 3-х уровней. Поэтому каждый имеет возможность выполнить любой уровень.
1 уровень.
1.Отметьте точки на координатной плоскости:
А (2;3) В (4;3) С (-4;2) К (-2;-3) М (0;5) Н (-3;0).
2.Отметить на координатной плоскости точки:
М(6;6) А(-2;2) К(4;1) Р(-2;4).
Проведите прямые МА и КР.
Найдите координаты точек пересечения:
прямых МА и КР;
2)прямой МА и осью абсцисс;
3)прямой КР и осью ординат.
3.Накоординатной плоскости отметьте точки А (-4;2) В (2;2) С (2;4). Постройте четвертую точку К
Так, чтобы получился квадрат. Определите координаты точки К.
2уровень.
1.Постройте отрезок АВ по координатам А(4;2) В(2;20.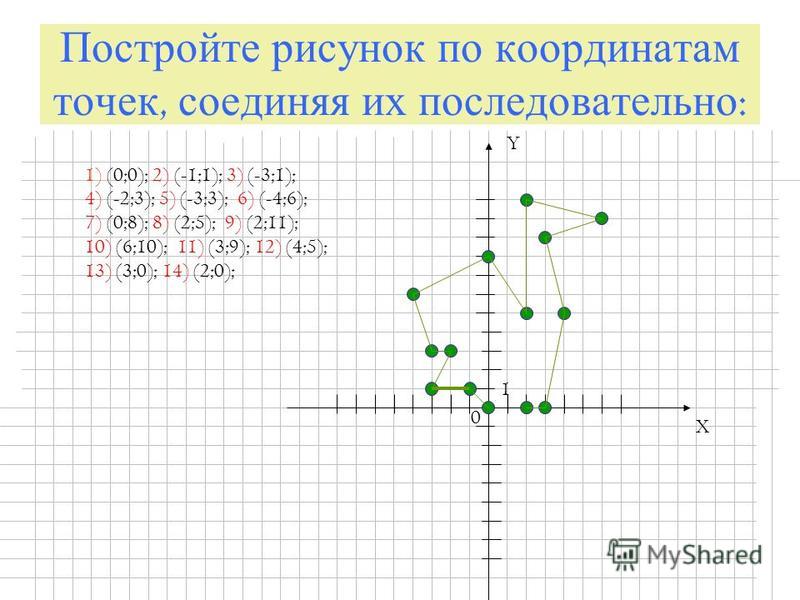 Найдите координаты точки, в которой он пересекается с осью абсцисс.
Найдите координаты точки, в которой он пересекается с осью абсцисс.
2.На координатной плоскости отметьте точки А(-8;3) В(1;3) С(1;3). Постройте четвертую точку К так, чтобы получился прямоугольник АВСК. Найти длину отрезка АВ.
3.На координатной плоскости отметьте 6 точек, имеющих ординату, равную 1. Запишите координаты этих точек.
Где расположены эти точки?
3уровень.
1.Расположите следующие точки по координатным углам и осям, не строя их на координатной плоскости:
А (1;3), В (6;6),С (-2;3),Д (-8;-6), О (0;0) ,К (6;0),М (-5;6), Т (-4;-2), Н (0;2), Х(-15;2, Р (5;5).
2.Постройте треугольник МРТ, если М(;), Р(-3;0),Т(-3;-3). Замените координаты точек на противоположные, какая фигура получилась сейчас?
3.Отметьте на координатной плоскости все точки, у которых абсцисса и ордината- неположительные числа, и их сумма равна -8. Какую фигуру составляют эти точки?
Учащиеся выполняют задания из любого уровня.
IV Этап домашнего задания.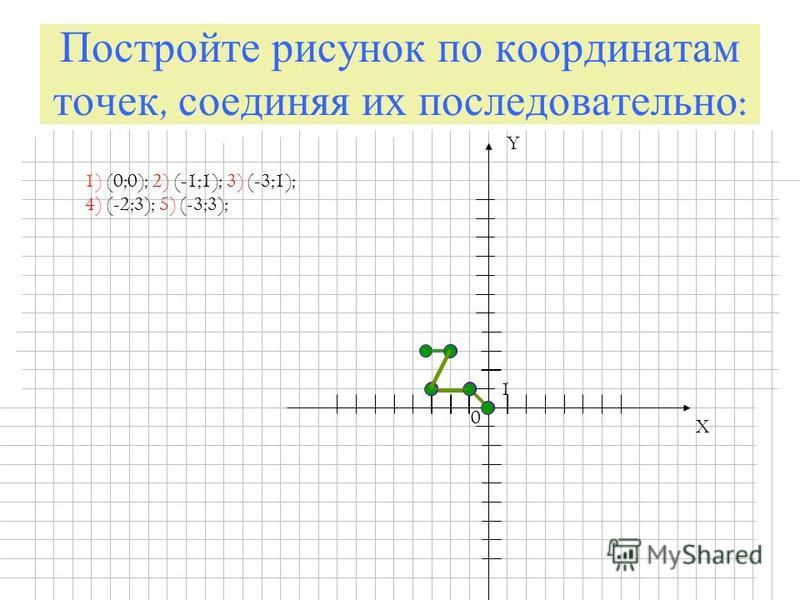 Слайд 8
Слайд 8
Творческое задание.
Подготовьте сообщение о созвездиях и изобразите их на координатной плоскости Это будет вашим домашним заданием.
V.Итог урока. Слайд 9Оценки за урок по тестам, за работу в тетрадях.
Учитель: Спасибо за урок! Слайд 10.
Математика 6 класс
«Координатная плоскость»
1 уровень
1. Отметьте точки на координатной плоскости:
А (2;3) В (4;3) С (-4;2) К (-2;-3) М (0;5) Н (-3;0).
2. Отметить на координатной плоскости точки:
М(6;6) А(-2;2) К(4;1) Р(-2;4).
Проведите прямые МА и КР.
Найдите координаты точек пересечения:
прямых МА и КР;
2)прямой МА и осью абсцисс;
3)прямой КР и осью ординат.
3. На координатной плоскости отметьте точки А (-4;2) В (2;2) С (2;4). Постройте четвертую точку К так, чтобы получился квадрат. Определите координаты точки К.
2 уровень
1. Постройте отрезок АВ по координатам А(4;2) В(2;20. Найдите координаты точки, в которой он пересекается с осью абсцисс.
Постройте отрезок АВ по координатам А(4;2) В(2;20. Найдите координаты точки, в которой он пересекается с осью абсцисс.
2. На координатной плоскости отметьте точки А(-8;3) В(1;3) С(1;3). Постройте четвертую точку К так, чтобы получился прямоугольник АВСК. Найти длину отрезка АВ.
3. На координатной плоскости отметьте 6 точек, имеющих ординату, равную 1. Запишите координаты этих точек.
Где расположены эти точки?
3 уровень
1. Расположите следующие точки по координатным углам и осям, не строя их на координатной плоскости:
А (1;3), В (6;6),С (-2;3),Д (-8;-6), О (0;0) ,К (6;0),М (-5;6), Т (-4;-2), Н (0;2), Х(-15;2), Р (5;5).
2. Постройте треугольник МРТ, если М(;), Р(-3;0),Т(-3;-3). Замените координаты точек на противоположные, какая фигура получилась сейчас?
3. Отметьте на координатной плоскости все точки, у которых абсцисса и ордината- неположительные числа, и их сумма равна -8. Какую фигуру составляют эти точки?
Используемая литература:
Учебник «Математика 6 класс»
А.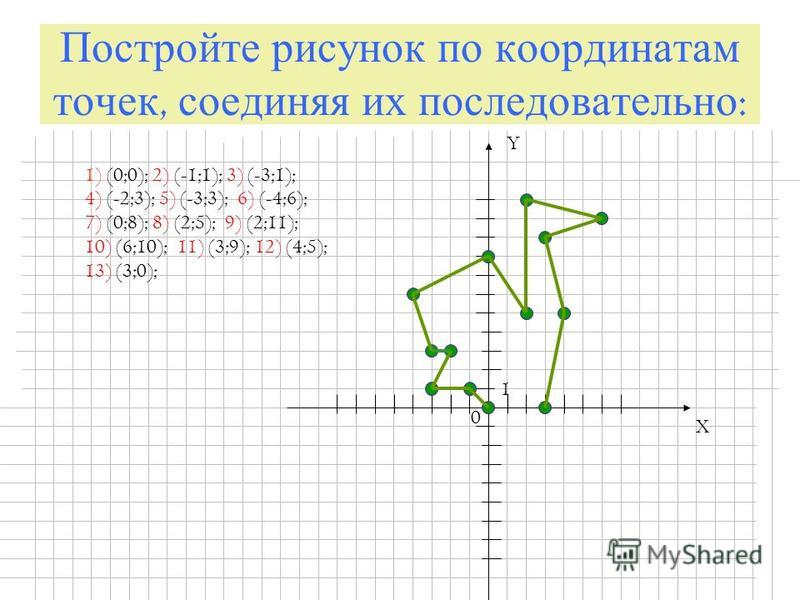 Абылкасымова издательство «Мектеп» 2007, 2013
Абылкасымова издательство «Мектеп» 2007, 2013
Тесты (сборник тестовых заданий по математике 6 класс издательство «Атамұра 2006 го стр.70 (4 задания)
Что такое координатная плоскость? — Факты и примеры определения
Координатная плоскость представляет собой двумерную плоскость, образованную пересечением двух числовых линий. Одна из этих числовых линий представляет собой горизонтальную числовую линию, называемую осью x, а другая числовая линия представляет собой вертикальную числовую линию, называемую осью y. Эти две числовые линии пересекаются друг с другом перпендикулярно и образуют координатную плоскость, которая выглядит так:
Плоскость называется двумерной, потому что в любом месте этой плоскости, куда вы можете приложить палец, для определения местоположения этой точки потребуются две вещи — ее расстояние по оси x и его расстояние по оси y.
Левая и нижняя части плоскости имеют отрицательную ось x и отрицательную ось y для отрицательных целых чисел. Точка, в которой пересекаются числовые линии, называется началом координат.
Точка, в которой пересекаются числовые линии, называется началом координат.
Координатная плоскость — это инструмент, используемый для построения графиков точек, линий и других объектов. Он функционирует как карта, которая следует направлениям от одной точки к другой.
Квадранты: Две числовые линии делят координатную плоскость на 4 области. Эти регионы называются Квадрантами. Квадранты обозначаются римскими цифрами, и каждый из этих квадрантов имеет свои собственные свойства.
Квадрант I: Верхний правый квадрант — это первый квадрант, обозначенный как Квадрант I. В этом квадранте оси x и оси y имеют положительные числа.
Квадрант II: Верхний левый Квадрант — это второй Квадрант, обозначенный как Квадрант II. В этом квадранте ось X имеет отрицательные числа, а ось Y имеет положительные числа.
Квадрант III: Нижний левый Квадрант — это третий Квадрант, обозначенный как Квадрант III. В этом квадранте и ось x, и ось y имеют отрицательные числа.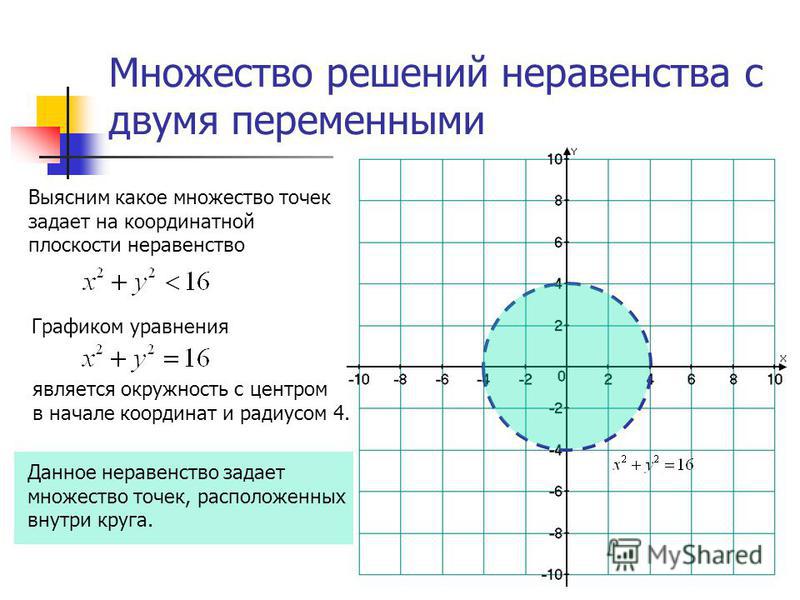
Квадрант IV: Нижний правый Квадрант — это четвертый Квадрант, обозначенный как Квадрант IV. В этом квадранте ось X имеет положительные числа, а ось Y имеет отрицательные числа.
Координата: Каждая точка на координатной плоскости выражается в виде упорядоченной пары (x,y), где x и y — числа, обозначающие положение точки относительно оси x и оси y. оси соответственно.
Если мы хотим передать положение точки A, мы проверим, где она лежит относительно осей x и y соответственно.
Здесь положение A по оси X равно 1 единице, а по оси Y равно 2 единицам, поэтому мы запишем положение A как A(1,2) на координатной плоскости.
Аналогичным образом мы можем найти положение любой точки на координатной плоскости, и она может принимать положительные или отрицательные значения в зависимости от квадранта, в котором она находится. Начало, очевидно; обозначается как (0,0)
Интересные факты
Заключение
Координатная плоскость представляет собой систему построения графиков и описания точек и линий.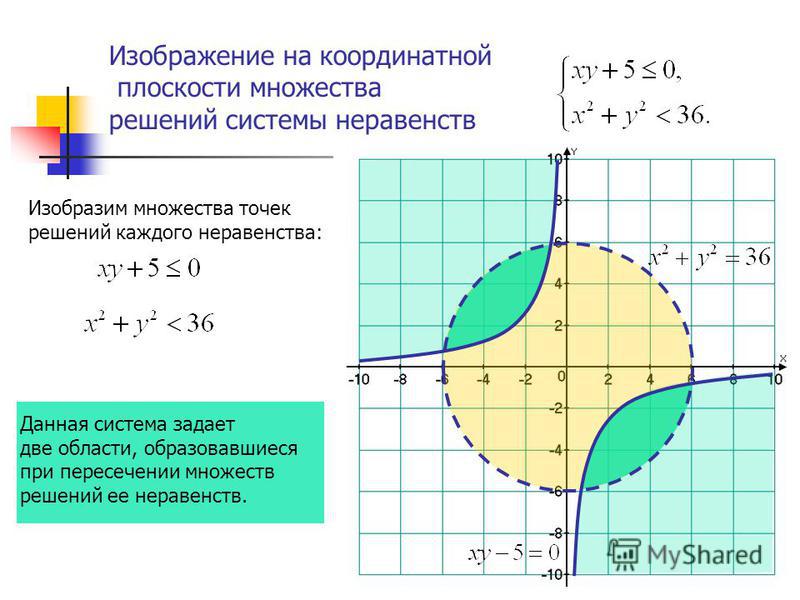 Вертикальная (y) ось и горизонтальная (x) ось составляют координатную плоскость. В координатной плоскости четыре квадранта. Точка, где эти линии соединяются, называется началом координат (0, 0). Перейдите на SplashLearn, чтобы узнать больше о концепциях координатной плоскости.
Вертикальная (y) ось и горизонтальная (x) ось составляют координатную плоскость. В координатной плоскости четыре квадранта. Точка, где эти линии соединяются, называется началом координат (0, 0). Перейдите на SplashLearn, чтобы узнать больше о концепциях координатной плоскости.
Решение: (i) и (iv) лежат на оси y, так как координата x в этих точках равна нулю.
В 3. Вы находитесь в точке (−4, 3). Переместитесь на 5 единиц вправо и на 2 единицы вверх. Напишите координаты точки, куда вы добираетесь.
(1, 5) (–3, 6) (2, 2) (–8, –2) Правильный ответ: (–90, –29) Поскольку точки в третьем квадранте имеют координаты x и y как отрицательные числа. П (2, 5) Q (–2, 4) R (–1, –8) S (4, –2) Правильный ответ: P (2, 5) (0, 1) (1, 0) (1, 1) (4, −3) Правильный ответ: (1, 0) (4, 5) (4, –5) (–4, 5) (–4, –5) Правильный ответ: (–4, 5) Параллельно друг к другу Перпендикулярно друг другу Пересекаются и (0,5) Никакой связи Правильный ответ: Перпендикулярно друг другу |
На координатной плоскости, что является началом координат?
Начало координатной плоскости — это точка в нуле, где две ее оси перпендикулярно пересекают друг друга. Координаты начала координат (0, 0).
Что означает координата?
Координата — это упорядоченная пара значений x и y , которая помогает найти точку на плоскости, обозначенную как (x,y).
Когда пригодится координатная плоскость?
При планировании расстановки различных предметов мебели в помещении создается двухмерная сетка, представляющая комнату. Для этого можно использовать приемлемую единицу измерения. Другой пример: воздушное движение управляется и регулируется с помощью координатной геометрии. Координаты рейса используются для описания его текущего местоположения самолета.
38.3: Интерпретация точек на координатной плоскости
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 40827
Урок
Давайте посмотрим, что могут нам сказать точки на координатной плоскости.
Упражнение \(\PageIndex{1}\): немаркированные точки
Обозначьте каждую точку на координатной плоскости соответствующей буквой и упорядоченной парой.
\(A=(7,-5.5)\qquad B=(-8,4)\qquad C=(3,2)\qquad D=(-3.5,0.2)\)
Упражнение \(\PageIndex{2}\): Баланс счета
График показывает остаток на банковском счете за период 14 дней. Ось, обозначенная \(b\), представляет баланс счета в долларах. Ось с пометкой \(d\) представляет день.
Рисунок \(\PageIndex{2}\): координатная плоскость, горизонтальная ось, d, от 0 до 14 по единицам, вертикальная ось, b, минус от 150 до 400 по пятидесятым. Указывает на (1 запятая 350), (2 запятая 350), (3 запятая 350), (4 запятая 275), (5 запятая 275), (6 запятая минус 50), (7 запятая 110), (8 запятая 110) , (9запятая 110), (10 запятая 110), (11 запятая минус 90), (12 запятая 25), (13 запятая 25).
- Оценка максимального остатка на счете. В какой день это произошло?
- Оценка наименьшего остатка на счете. В какой день это произошло?
- Что точка \((6,-50)\) говорит вам об остатке на счете?
- Как мы можем интерпретировать \(|-50|\) в данном контексте?
Упражнение \(\PageIndex{3}\): Высокие и низкие температуры
Координатная плоскость показывает высокие и низкие температуры в Номе, Аляска, за период в 8 дней. Ось, обозначенная \(T\), представляет температуру в градусах по Фаренгейту. Ось с пометкой \(d\) представляет день.
Рисунок \(\PageIndex{3}\): Координатная плоскость, начало координат O, горизонтальная ось, d, от 0 до 9 по единицам, вертикальная ось, T, минус от 6 до 28 по двойкам. Красные точки на (одна запятая 28), (2 запятая 26), (3 запятая 21), (4 запятая 11), (5 запятая 13), (6 запятая 17), (7 запятая 7), (8 запятая 2) . Синие точки указывают на (1 запятая 28), (2 запятая 20), (3 запятая 11), (4 запятая 3), (5 запятая 10), (6 запятая 7), (7 запятая минус 3), (8 запятая минус 1).
- Какая была самая высокая температура?
- Напишите неравенство для описания высоких температур \(H\) за 8-дневный период.
- Какой была самая низкая низкая температура?
- Напишите неравенство для описания низких температур \(L\) за 8-дневный период.
- В какой день (дни) наблюдалась наибольшая разница между высокими и низкими температурами? Запишите эту разницу.
- В какой день (дни) произошла наименьшая разница между высокой и низкой температурой? Запишите эту разницу.
Готовы ли вы к большему?
Прежде чем решать эту задачу, решите задачу о расстоянии такси на одном из предыдущих уроков.
Точка \((0,3)\) находится в 4 таксопарках от \((-4,3)\) и в 4 таксомоторах от \((2,1)\).
- Найдите как можно больше других точек, которые находятся в 4 единицах такси от и \((-4,3)\) и \((2,1)\).

- Есть ли точки, которые находятся на расстоянии 3 единиц такси от обеих точек?
Резюме
Точки на координатной плоскости могут дать нам информацию о контексте или ситуации. Один из таких контекстов касается денег.
Чтобы открыть банковский счет, мы должны положить на него деньги. Баланс счета – это сумма денег на счете в любой момент времени. Если мы вложим 350 долларов при открытии счета, то остаток на счете будет 350.
Иногда у нас может не быть денег на счете и нам нужно занять деньги в банке. В этом случае баланс счета будет иметь отрицательное значение. Если мы займем 200 долларов, то остаток на счете будет -200.
Координатная сетка может использоваться для отображения как баланса, так и дня или времени для любого баланса. Это позволяет увидеть, как меняется баланс с течением времени или сравнить балансы в разные дни.
Точно так же, если мы нанесем на координатную плоскость данные, такие как изменение температуры во времени, мы сможем увидеть, как температура меняется во времени, или сравнить температуры в разные моменты времени.
Словарь терминов
Определение: квадрант
Координатная плоскость разделена на 4 области, называемые квадрантами. Квадранты нумеруются римскими цифрами, начиная с правого верхнего угла.
Рисунок \(\PageIndex{4}\)Практика
Упражнение \(\PageIndex{4}\)
Высота подводной лодки указана в таблице. Начертите и обозначьте оси координат с соответствующим масштабом и нанесите точки.
| время после полудня (часы) | высота над уровнем моря (метры) |
|---|---|
| \(0\) | \(-567\) |
| \(1\) | \(-892\) |
| \(2\) | \(-1,606\) |
| \(3\) | \(-1,289\) |
| \(4\) | \(-990\) |
| \(5\) | \(-702\) |
| \(6\) | \(-365\) |
Упражнение \(\PageIndex{5}\)
Неравенства \(h>42\) и \(h<60\) представляют требования к высоте для аттракциона в парке развлечений, где \(h\) представляет собой рост человека в дюймах.
Напишите предложение или нарисуйте знак, максимально точно описывающий эти правила.
(из модуля 7.2.1)
Упражнение \(\PageIndex{6}\)
Ось \(x\) представляет количество часов до или после полудня, а ось \(y\) представляет температуру в градусах Цельсия.
Рисунок \(\PageIndex{5}\) 9{\ circ} \ text {C} \). В каком квадранте должна располагаться эта точка?Упражнение \(\PageIndex{7}\)
Решите каждое уравнение.
\(\ begin{array}{lllll}{3a=12}&{\qquad}&{b+3.3=8.9}&{\qquad}&{1=\frac{1}{4}c}\\ {5\frac{1}{2}=d+\frac{1}{4}}&{\qquad}&{2e=6.4}&{}&{}\end{массив}\)
(из модуля 6.1.4)
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Версия лицензии
- 1,3
- Теги

Координаты на плоскости и построение графиков… Пошаговое решение математических задач
7.1 Координаты на плоскости
Пусть PI — плоскость, а X и Y — взаимно перпендикулярные прямые в PI, пересекающиеся в точке точка O. Используя прямые X и Y, мы свяжем пару чисел с каждой точкой на плоскости. Если P это точка, а (a,b) – пара, связанная с P, то a и b – координаты P. Число a – это абцисса или первая координата P. а b – ордината или вторая координата P. Обозначим точку и ее координаты через
П: (а, б).
Координаты P определяются следующим образом. В качестве положительного направления на X выбираем направление от O по X и аналогично выбираем положительное направление для Y. Принято выбирать положительные направления, как показано стрелками на рис. 1. Выбор какой-либо единицы измерения на каждом из две линии, мы отмечаем положительные расстояния в положительном направлении по X и Y и отрицательные расстояния в другом направлении на каждой линии, так что каждая точка на оси находится на направленном расстоянии от начала координат O. См. рис. 2. Пусть k и h – линии на
См. рис. 2. Пусть k и h – линии на
РИСУНОК 1.
РИСУНОК 2.
P, параллельные X и Y соответственно. Тогда h пересекает X в точке на направленном расстоянии {alpha} от точки O, а k пересекает Y в точке на направленном расстоянии b от точки O. Тогда парой координат точки P является (a,b). На рисунке 2 координатной парой P является (3, 3.5).
Линии X и Y вместе с положительными направлениями и единицами измерения называются декартовой системой координат для плоскости. Плоскость, в которой введена система координат, называется плоскостью координат. Линии X и Y являются соответственно горизонтальной и вертикальной осями системы, а их точка пересечения O является началом системы.
Заметим, что оси делят плоскость на четыре части, называемые квадрантами плоскости. Нумерация против часовой стрелки от верхнего правого квадранта представляет собой первый, второй, третий и четвертый квадранты плоскости. У всех точек в первом квадранте обе координаты положительны, во втором — первая координата отрицательна, а вторая положительна и так далее.
Возникает одна простая проблема: найти или нанести на карту точку, координаты которой заданы. Во-вторых, оценить координаты данной точки.
Пример 1. График (-2,4.5) и (3,-7).
Пример 2. Оцените координаты P и Q, указанные ниже.
Используя формулу Пифагора из планиметрии, мы можем получить формулу для расстояния между двумя точками через координаты этих точек. Пусть заданы P: (X 1 ,Y 1 ) и Q: (X 2 ,Y 2 ). Обозначим расстояние между P и Q через d(P,Q). См. рис. 3. По теореме Пифагора 92)
= √ (36+16)
= √52
7.2 Уравнения графики в двух переменных
Рассмотрим уравнение в двух переменных
(1) x-2y = 4
А это уравнение представляет собой пару чисел (a,b), такая что при подстановке x=a,y=b в (1) получается истинное числовое утверждение. Таким образом, (4,0) и (6, 1) являются решениями, а (1, 2) решением не является. Множество решений (1) — это множество всех пар решений.
Множество решений (1) — это множество всех пар решений.
Общую ситуацию мы обозначаем следующим образом. Пусть {Эпсилон}(x,y) обозначает любое выражение в переменных x и y. Тогда решением
(2) {Эпсилон}(x,y)=0
является пара чисел (a,b), такая что подстановка x=a, y=b в (2) приводит к истинному числовое утверждение. Набор решений — это набор всех пар решений.
Поскольку набор решений (2) представляет собой набор пар действительных чисел, мы можем изобразить эти пары как точки на координатной плоскости. Полученная фигура на плоскости называется графиком (2). Для большинства уравнений мы можем точно нанести только конечное число точек, а затем сделать (более или менее) обоснованное предположение относительно других точек.
Пример 1. График x-2y=4.
Сначала составим таблицу, в которой перечислены некоторые пары решений
| x | у | Вычисления |
| -2 | -3 | -2-2y=4so -2y=6,y=-3 |
| -1 | -(5/2) | -1-2y=4, поэтому -2y=5,y=-(5/2) |
| 0 | -2 | |
| 1 | -(3/2) | |
| 2 | -1 | |
| 3 | -(1/2) | |
| 4 | 0 | |
| 5 | 1/2 | |
| 6 | 1 |
Затем нанесите эти точки на координатную плоскость. Эти точки кажутся лежащими на прямой линии, и мы можем разумно предположить, что это так. На самом деле, мы скоро увидим, что они коллинеарны. 92=3, значит, y=+-√3 90 109
Эти точки кажутся лежащими на прямой линии, и мы можем разумно предположить, что это так. На самом деле, мы скоро увидим, что они коллинеарны. 92=3, значит, y=+-√3 90 109
Нанесите эти точки на координатную плоскость. Кажется, что эти точки лежат на окружности с центром (0,0) и радиусом 2. В конце концов мы покажем, что это действительно так.
Давайте посмотрим, как наш решатель генерирует график этого уравнения и подобных уравнений. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров. 92+1.
Построить таблицу пар решений.
| х | г |
| -3 | 10 |
| -2 | 5 |
| -1 | 2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 5 |
| 3 | 10 |
Нанесите эти точки на координатную плоскость и соедините их плавной кривой.
Давайте посмотрим, как наш решатель генерирует график этого уравнения и подобных уравнений. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решить похожую задачуВведите свою задачу
Урок 3 | узоры и координатная плоскость | 5 класс Математика
Цель
Построить координатную плоскость с неединичными интервалами и использовать ее для построения и определения точек.
Общие базовые стандарты
Основные стандарты
Основные стандарты, рассмотренные в этом уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D89505.Г.А.1 — Используйте пару перпендикулярных числовых линий, называемых осями, для определения системы координат, где пересечение линий (начало координат) расположено так, чтобы совпадать с 0 на каждой линии, и заданной точкой на плоскости, расположенной с помощью упорядоченной пары. чисел, называемых его координатами.
 Поймите, что первое число указывает, как далеко нужно пройти от начала координат в направлении одной оси, а второе число указывает, как далеко нужно пройти в направлении второй оси, при условии, что имена двух осей и координаты соответствуют (например, ось x и координата x, ось y и координата y).
Поймите, что первое число указывает, как далеко нужно пройти от начала координат в направлении одной оси, а второе число указывает, как далеко нужно пройти в направлении второй оси, при условии, что имена двух осей и координаты соответствуют (например, ось x и координата x, ось y и координата y).
Основополагающие стандарты
Основные стандарты, рассмотренные в этом уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D89502.MD.B.6
3.NF.A.2
Критерии успеха
Основные концепции, которые учащиеся должны продемонстрировать или понять для достижения цели урока интервал называется масштабом графика.

Советы учителям
Рекомендации учителям по проведению этого урока
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Вы можете изменить этот и следующий урок в зависимости от темпа и готовности учащихся к этим урокам. Эти уроки помогают подготовить учащихся к ответу на вопрос 5 по модульному оцениванию, но, поскольку учащиеся могут построить координатный график со шкалой 1 по обеим осям предоставленной сетки, они не совсем необходимы. Из выпущенных предметов из основных стандартизированных тестов (PARCC, SBAC, NY Regents, MCAS) только один предмет опирается на эти навыки. Таким образом, можно с уверенностью предположить, что это не ожидаемый навык на этом уровне обучения. Если вы решите, что учащиеся не нуждаются в этих навыках, вероятно, будет хорошей идеей оставить время на уроке, чтобы убедиться, что учащиеся имеют глубокое понимание координатной плоскости. Таким образом, вы можете адаптировать их следующим образом:
- Урок 3. Вырежьте задание «Якорь» и посвятите большую часть урока игре «Морской бой» строго на координатной плоскости, где обе оси имеют шкалу 1.

- Урок 4. Измените опорные задачи и набор задач/домашнее задание таким образом, чтобы учащиеся по-прежнему должны были построить координатную плоскость с нуля и нанести на нее различные точки, но ограничить координаты разумным числом, например, 20. Вы можете сосредоточиться на оси не должны превышать самые большие x — и y -координата (например, в одной задаче оси могут быть только до 5, а в другой — до 20).
- Урок 3. Вырежьте задание «Якорь» и посвятите большую часть урока игре «Морской бой» строго на координатной плоскости, где обе оси имеют шкалу 1.
- В то время как работа на уроках 1 и 2 требовала от учащихся внимания к точности нанесения точек и определения местоположения точек в координатной сетке, эта практика требуется еще больше, поскольку учащиеся имеют дело с неинтервальными единицами на уроке 3 (MP .6).
- При выполнении набора задач убедитесь, что учащиеся понимают правила игры «Морской бой». Вы можете решить смоделировать раунд игры, чтобы учащиеся освоились. Вы также можете решить дать учащимся некоторые ограничения на выбранные ими оси, просто чтобы убедиться, что они практикуют недавно приобретенный сегодня навык построения и именования точек на координатной сетке с неединичными интервалами.
 Попросите учащихся сыграть несколько раундов, меняя шкалу по одной или обеим осям с каждым новым раундом.
Попросите учащихся сыграть несколько раундов, меняя шкалу по одной или обеим осям с каждым новым раундом. - В качестве домашнего задания учащиеся будут играть в Морской бой с членом семьи. Отправьте учащихся домой с дополнительной копией набора задач или сеткой.
Учебные материалы
- Маркеры или мелки (по 2 на учащегося) — нужны красный и черный
Fishtank Plus
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Якорные задачи
Задания, предназначенные для обучения критериям успеха урока, и рекомендации, помогающие ученикам понять
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Проблема 1
Хайди и Беатрис пытаются определить местонахождение следующей точки.
Хайди говорит, что точка находится в (2, 18). Беатрис говорит, что точка находится в точке (1, 6). Как Хайди и Беатрис могут быть правы? Объяснять.
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Проблема 2
- Определите координаты всех точек на следующей координатной плоскости.
- Нанесите на координатную плоскость следующие точки:
Точка L : (40, 3) Точка M : $${(10, {1\over2})}$$ }$$
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной проблемы.
Ссылки
EngageNY Mathematics Grade 5 Mathematics > Модуль 6 > Тема A > Урок 3 — Практика беглости
Математика для 5 класса > Модуль 6 > Тема A > Урок 3 общеобразовательной программы штата Нью-Йорк по математике от EngageNY и Great Minds. © 2015 Великие умы. Лицензировано EngageNY Департамента образования штата Нью-Йорк в соответствии с лицензией США CC BY-NC-SA 3. 0. По состоянию на 2 декабря 2016 г., 17:15.
0. По состоянию на 2 декабря 2016 г., 17:15.
Изменено Fishtank Learning, Inc.
Набор задач и домашнее задание
Набор проблем
Домашнее задание
Ключи ответов
Ключи ответов для наборов задач и домашних заданий доступны при наличии подписки Fishtank Plus.
Обсуждение набора задач
- Какой была ваша стратегия при выборе места для размещения вашего флота? Это сработало? Что бы вы сделали по-другому в следующий раз?
- Как вы решили, куда наносить атакующие удары?
- Когда вы попали в корабль противника, как вы планировали свой следующий выстрел?
- Что из того, что сделал ваш оппонент, помогло ему?
- Что можно сделать с координатной плоскостью, чтобы упростить или усложнить игру?
- Как сегодняшняя игра укрепила ваше понимание координатной плоскости?
- Как вы думаете, пары координат действительно используются в бою? Почему или почему нет?
Целевая задача
Задание, которое представляет собой пик мышления урока – мастерство покажет, была ли достигнута цель
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950 Используйте координатную сетку ниже, чтобы ответить на части A и B.
a. Назовите координаты каждой точки.
Точка P : __________
Точка Q : __________
Точка R : __________
б. Нанесите следующие точки на координатную сетку.
Точка S : (15, 3)
Точка T : (2, $$4\tfrac{1}{2}$$)
Ответ учащегося
Создайте бесплатную учетную запись или войдите, чтобы просмотреть ответ учащегося
Дополнительная практика
Контент Fishtank Plus
Задачи Word и упражнения на беглость речи
Доступ к ежедневным занятиям по проблемам гриппа и нашему контенту создан, чтобы помочь учащимся укрепить свои навыки применения и беглости речи.
Предварительный просмотр
Узнать больше
значок/стрелка/вправо/крупная копияУрок 2
значок/стрелка/вправо/крупныйУрок 4
Знакомство с линиями в координатной геометрии
Знакомство с линиями в координатной геометрии — открытый справочник по математикеОткрытый справочник по математике
Главная Контакт О Тематический указатель
Прямой
линии
в координатной геометрии та же идея, что и в обычной геометрии, за исключением того, что они нарисованы на
координатная плоскость
и мы можем сделать больше с ними.
Как определить линию
Рассмотрим линию на рис. 1. Как бы я определил эту конкретную линию? Какую информацию я мог бы дать вам по телефону, чтобы вы могли провести точно такую же линию на своем конце?
Рис. 1. Как определить эту линию?
В координатной геометрии обычно используются три способа:
- Дайте координаты любых двух точек на прямой
- Дайте координаты одной точки на прямой, а наклон линии
- Приведите уравнение, определяющее линию.
Использование двух точек
На рис. 2 линия определяется двумя точками A и B. Указав координаты двух точек,
мы можем провести линию. Никакая другая линия не может проходить через обе эти точки, поэтому определяемая ими линия уникальна.
Я мог бы позвонить вам по телефону и сказать «Проведите линию через (9,9) и (17,4)» и вы сможете восстановить ее идеально на своем конце.
Рис. 2. A, B определяют уникальную строку
Для интерактивной демонстрации линий, определяемых двумя точками, см.
- Линия (координатная геометрия)
- Линейный сегмент (координатная геометрия)
- Луч (координатная геометрия)
Использование одной точки и наклона
Рис. 3. Точка и наклон определяют линию
Другой распространенный метод — дать вам координаты одной точки и наклон линии. На данный момент вы можете думать о наклоне как о направлении линии. Итак, как только вы знаете, что линия проходит через определенную точку и в каком направлении она указывает, вы определили одну уникальную линию.
На рис. 3 мы видим линию, проходящую через точку А в точке (14,23). Мы также видим, что его наклон равен +2 (что означает, что он увеличивается на 2 для каждого пересечения). с этими двумя фактами мы можем установить уникальную линию.
Величину наклона обычно обозначают буквой m.
Для получения дополнительной информации об уклоне и о том, как его определить, см. раздел «Наклон линии».
раздел «Наклон линии».
Уравнение прямой
После того как вы определили линию с помощью метода точка-наклон, вы можете написать алгебраические уравнения, описывающие линию. Применяя алгебраические процессы к этим уравнениям, мы можем решить проблемы, которые в противном случае были бы трудными. Эти и многие другие методы построения графиков описаны в томе по алгебре, но общая идея описана здесь, в Координатной геометрии.
Для описания линии обычно используются два типа уравнений:
- Откос-перехват (самый распространенный). Описано в уравнении линии (наклон-пересечение)
- Точка-наклон. Описано в уравнении линии (точка-наклон).
Обе формы на самом деле являются вариациями одной и той же идеи. В обоих случаях вам нужно знать координаты одной точки и наклон линии.
- В форме пересечения наклона заданная точка всегда находится на оси Y, и вы указываете координату Y этой точки.
(Его координата x всегда равна нулю).

- В форме точка-наклон можно использовать любую точку.
Место, где линия пересекает ось y, называется точкой пересечения и обычно обозначается буквой b. Подробнее об этом см. в разделе Перехват линии.
y = m(x-P x ) + P y
Рис. 4. Точка-наклон
y = mx + b
Рис. 5. Пересечение наклона
Если вы внимательно посмотрите на две формулы, то увидите, что они очень похожи. Если вы возьмете версию точки-наклона на рис. 4 и решите поместить P на ось Y, ее координата x равна нулю, а ее координата y совпадает с точкой пересечения. Если вы замените эти вещи, вы получите формулу пересечения наклона справа на рис. 5.Для чего используются уравнения?
- Вы можете использовать их для построения линии: Возьмите различные значения x, а затем используйте уравнение, чтобы найти соответствующие значения y. Постройте пары, чтобы построить линию.
- Если вы знаете только одну координату точки на линии, вы можете найти другую.

Для получения дополнительной информации
Следующие страницы раскрывают каждое из понятий на этой странице:- Наклон линии
- Перехват строки
- Уравнение прямой (наклон-пересечение)
- Уравнение линии (точка-наклон)
Другие темы по координатной геометрии
- Введение в координатную геометрию
- Координатная плоскость
- Происхождение самолета
- Определение оси
- Координаты точки
- Расстояние между двумя точками
- Знакомство с линиями
в координатной геометрии - Линия (координатная геометрия)
- Луч (координатная геометрия)
- Сегмент (координатная геометрия)
- Теорема о средней точке
- Расстояние от точки до линии
- — Когда линия горизонтальна или вертикальна
- — Использование двух линейных уравнений
- — Использование тригонометрии
- — Использование формулы
- Пересекающиеся линии
- Вписанный прямоугольник (ограничивающая рамка)
- Площадь треугольника (формульный метод)
- Площадь треугольника (метод ящика)
- Центроид треугольника
- Центр треугольника
- Площадь многоугольника
- Алгоритм нахождения площади многоугольника
- Площадь многоугольника (калькулятор)
- Прямоугольник
- Определение и свойства диагоналей
- Площадь и периметр
- Квадрат
- Определение и свойства диагоналей
- Площадь и периметр
- Трапеция
- Определение и свойства, высота, медиана
- Площадь и периметр
- Параллелограмм
- Определение и свойства, высота, диагонали
- Чистая миллиметровка для печати
(C) 2011 Copyright Math Open Reference.
Все права защищены
Координатная плоскость – объяснение и примеры
Координатная плоскость определяется как двумерная плоскость, используемая для определения положения геометрических объектов относительно заданной точки.
Координатная плоскость позволяет выполнять геометрические вычисления. В частности, это позволяет нам сравнивать геометрические объекты, используя заданную точку отсчета.
В этом разделе мы рассмотрим, как наносить точки на координатную плоскость и определять положение заданных точек. Если вы еще этого не сделали, вам следует быстро просмотреть координатную геометрию, чтобы получить максимальную отдачу от этого раздела.
В этом разделе рассматриваются:
- Что такое координатная плоскость?
- Шкала плоскости координат
- Координаты
- Положительная координата Плона
- ОТВЕТСТВЕННАЯ Координата Плана
- .

Координатная плоскость — это система для нанесения точек и других геометрических объектов в двухмерном пространстве. Из всех координатных плоскостей наиболее известной и часто используемой является декартова система координат. Это имя относится к французскому математику Рене Декарту, который первым опубликовал описание самолета. Поскольку в ней используется сетка, эту систему также иногда называют прямоугольными координатами.
Координатная плоскость состоит из двух линий, называемых осями, которые пересекаются под прямым углом. Вертикальная линия называется осью Y, а горизонтальная линия называется осью X. Точка их пересечения называется началом координат.
В определенных ситуациях ось X также известна как «независимая переменная». Точно так же «зависимой переменной» является ось Y.
Координатная плоскость существенно расширяет понятие числовой прямой до двух измерений. Точно так же, как мы можем нанести как положительные, так и отрицательные точки на числовую прямую, мы можем нанести как положительные, так и отрицательные точки на координатную плоскость.

Как и числовая линия, координатная плоскость должна иметь масштаб.
Масштаб координатной плоскости
Координатная плоскость обычно имеет множество горизонтальных и вертикальных линий, которые делают ее похожей на сетку. Эти строки обычно расположены через равные промежутки и отмечены цифрами. Расстояние, представленное пространством между двумя из этих линий, известно как масштаб.
Например, координатная плоскость, показанная ниже слева, имеет масштаб 1, поскольку расстояние между каждой горизонтальной и вертикальной линиями представляет собой расстояние в одну единицу.
Однако в координатной плоскости внизу справа масштаб равен двум, поскольку расстояние между каждой горизонтальной и вертикальной линиями представляет собой расстояние в две единицы.
Координаты
Напомним, что на числовой прямой одного числа достаточно для однозначной идентификации точки. Однако в двумерном пространстве для однозначной идентификации точки необходимы два числа.
 Они называются парами координат и имеют вид (x, y).
Они называются парами координат и имеют вид (x, y).Значение x пары координат представляет положение точки на оси x. Точно так же значение y пары координат представляет положение точки на оси y.
Эти числа непрерывны, поэтому любое положительное или отрицательное число может быть частью пары координат. Например, все точки (-1, -0,1), (2, π) и ( 3 ⁄ 4 , -5) являются парами координат.
При нанесении точек на координатную плоскость люди обычно выбирают масштаб на основе имеющихся у них точек. Как правило, это либо наибольший общий множитель, либо кратное наибольшему общему факту.
Например, предположим, что исследователь должен нанести точки (36, 12) и (48, 72). Шкала 12 была бы наиболее разумной, потому что 12, 36, 48 и 72 кратны 12.
Обратите внимание, однако, что это не всегда возможно. Если координаты включают слишком много чисел без общих множителей или включают иррациональные числа, выбрать масштаб так, чтобы все или большинство точек находились на линиях сетки, будет сложно или невозможно.

Положительная координатная плоскость
На числовой прямой движение вправо считается положительным. Точно так же в координатной плоскости положительным движением является любое движение вверх и любое движение вправо.
Рассмотрим, например, точку A=(1, 2).
Значение x этой пары координат равно 1, а значение y равно 2. Ясно, что оба эти числа положительные. Следовательно, точка будет лежать на одну единицу правее начала координат и на две единицы выше его.
На графике ниже показана нанесенная точка.
Отрицательная координатная плоскость
Движение влево — это отрицательное движение по числовой прямой. Точно так же движение влево и движение вниз отрицательны на координатной плоскости.
Рассмотрим, например, точку B=(-1, -2).
Координата x равна -1, а координата y равна -2. Это означает, что точка находится в положении на одну единицу левее начала координат и на две единицы ниже его, как показано на рисунке.

Также возможно иметь пары координат, которые представляют собой смесь положительных и отрицательных значений. Например, точка C=(-1, 2) имеет отрицательное значение x и положительное значение y. Это означает, что он лежит на одну единицу левее начала координат и на две единицы выше него.
И наоборот, точка D=(1, -2) имеет положительное значение x и отрицательное значение y. Он лежит на одну единицу правее начала координат и на две единицы ниже его.
Все четыре точки нанесены на плоскость ниже.
Квадранты
Оси x и y эффективно делят декартову координатную плоскость на четыре части. Эти разделы называются квадрантами, и у них есть имена.
Первый квадрант, квадрант I, находится справа вверху от начала координат. Все точки в этом квадранте имеют положительные координаты x и y. Поскольку наборы данных часто включают только положительные значения, этот квадрант иногда отображается сам по себе.
Затем квадранты перемещаются вокруг плоскости против часовой стрелки.
 Следующие два — это квадрант II с отрицательными координатами x и положительными координатами y и квадрант III с отрицательными координатами x и y. Эти квадранты находятся в верхнем левом и нижнем правом углу соответственно.
Следующие два — это квадрант II с отрицательными координатами x и положительными координатами y и квадрант III с отрицательными координатами x и y. Эти квадранты находятся в верхнем левом и нижнем правом углу соответственно.Наконец, квадрант IV имеет положительные координаты x и отрицательные координаты y.
Примеры
В этом разделе мы рассмотрим несколько примеров, чтобы узнать больше о координатной плоскости.
Пример 1
Нанесите точки A=(-3, 2) и B=(2, -3). В каких квадрантах находятся точки? Какая связь между этими двумя точками?
Пример 1 Решение
Точка A имеет координату x -3 и координату y 2. Это означает, что она находится на три единицы левее начала координат и на две единицы выше него.
Точка B имеет координату x 3 и координату y -2. Это означает, что он лежит на три единицы правее начала координат и на две единицы ниже его.
Из координатной плоскости видно, что A лежит в квадранте II, а B — в квадранте IV.

Чтобы переместить точку A в точку B, мы должны переместить ее на 6 единиц вправо и на 4 единицы вниз. Это соответствует разнице между значениями x и значениями y координат.
Пример 2
Точка C показана на графике ниже. Если координаты C равны (a+1, 2b), каковы значения a и b?
Пример 2 Решение
Сначала нам нужно найти координаты точки C.
Ясно, что точка лежит на одну единицу левее начала координат и на четыре единицы выше его. Следовательно, его координаты (-1, 4).
Поскольку C имеет координату (-1, 4), а также (a+1, 2b), мы можем установить значения x и y равными друг другу:
-1=a+1
-2=a,
и
2b=4
b=2.
Пример 3
Точка D находится в позиции (4, 2). Каковы координаты точки Е? Подсказка: обратите внимание на масштаб графика.
Пример 3 Решение
Линии сетки на координатной плоскости не обозначены, поэтому мы должны использовать точку D для определения масштаба.

Точка D находится в (4, 2). Он находится на пересечении второй вертикальной линии сетки справа и первой горизонтальной линии сетки над исходной точкой. Таким образом, расстояние между каждой линией сетки равно 2 единицам, а плоскость имеет масштаб 2.
E находится на пересечении третьей горизонтальной линии снизу и третьей вертикальной линии слева от начала координат. Поскольку каждая линия представляет 2 единицы, точка E лежит в (-3×2, -3×2) или (-6, -6).
Пример 4
Парк находится в 2,4 км к югу от мэрии. Дом Яны находится в 2,5 милях к северу и в 1 миле к западу от мэрии. Где дом Яны относительно парка?
Пример 4 Решение
В этом случае было бы полезно нарисовать карту. Пусть парк будет точкой P, а мэрия — точкой C. Дом Яны — точкой J.
Поскольку исходное положение парка и дома Яны относительно мэрии, мы можем использовать мэрию в качестве начала отсчета. нашей карты.
Нам также нужно подобрать весы. Часто имеет смысл выбрать масштаб, который является наибольшим общим множителем координат.


 На координатной плоскости постройте отрезок AB и прямую PК, если A (0; 6), B (5; 1), P (–8; –1), К (4; 5). Запишите координаты точек пересечения прямой PК с построенным отрезком и осями координат.
На координатной плоскости постройте отрезок AB и прямую PК, если A (0; 6), B (5; 1), P (–8; –1), К (4; 5). Запишите координаты точек пересечения прямой PК с построенным отрезком и осями координат.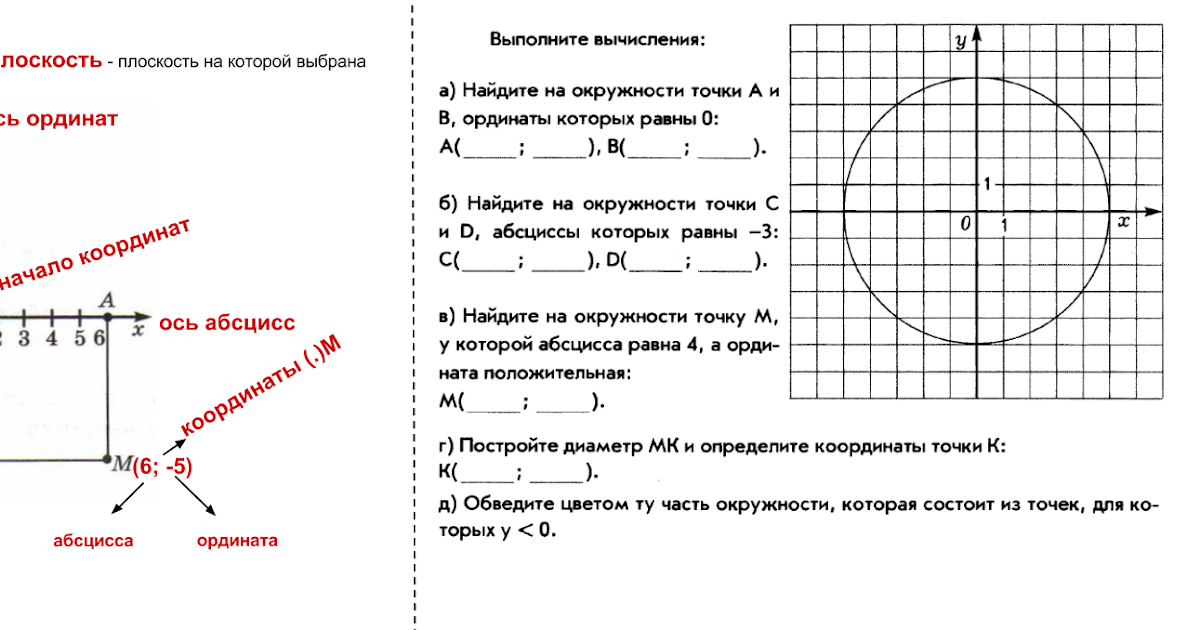

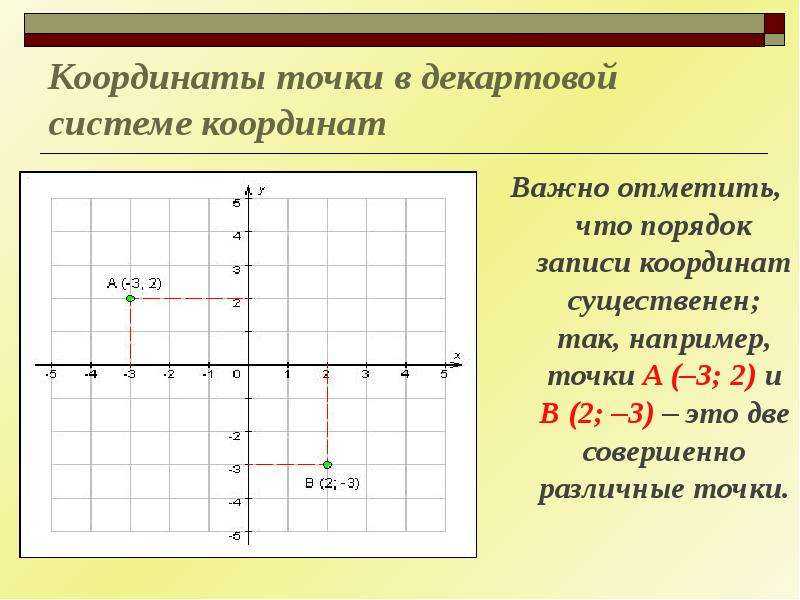 Постройте угол, равный 115. Отметьте внутри этого угла точку N и проведите через нее прямые, параллельные сторонам угла.
Постройте угол, равный 115. Отметьте внутри этого угла точку N и проведите через нее прямые, параллельные сторонам угла.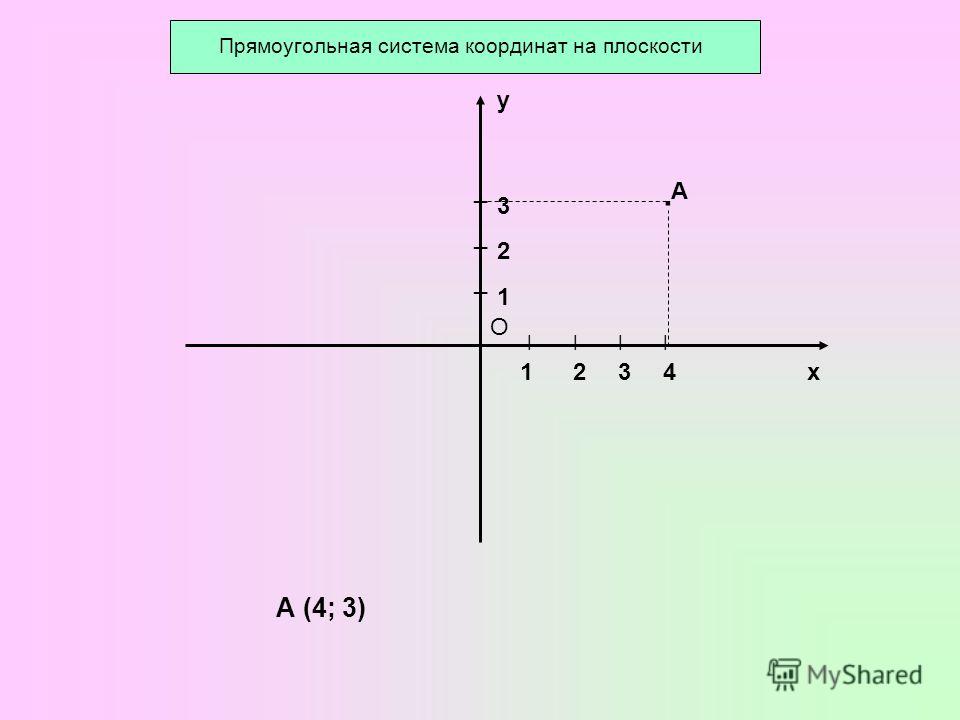 Постройте угол, равный 110. Отметьте внутри этого угла точку
Постройте угол, равный 110. Отметьте внутри этого угла точку 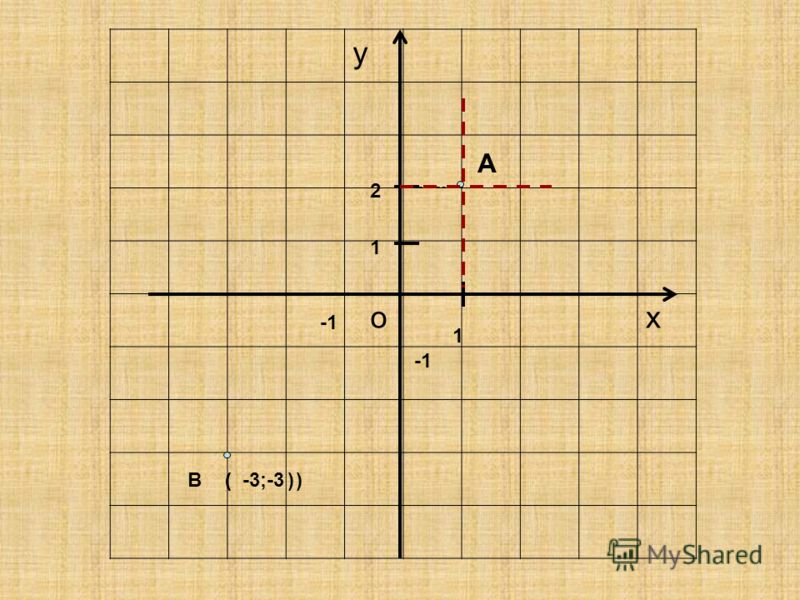

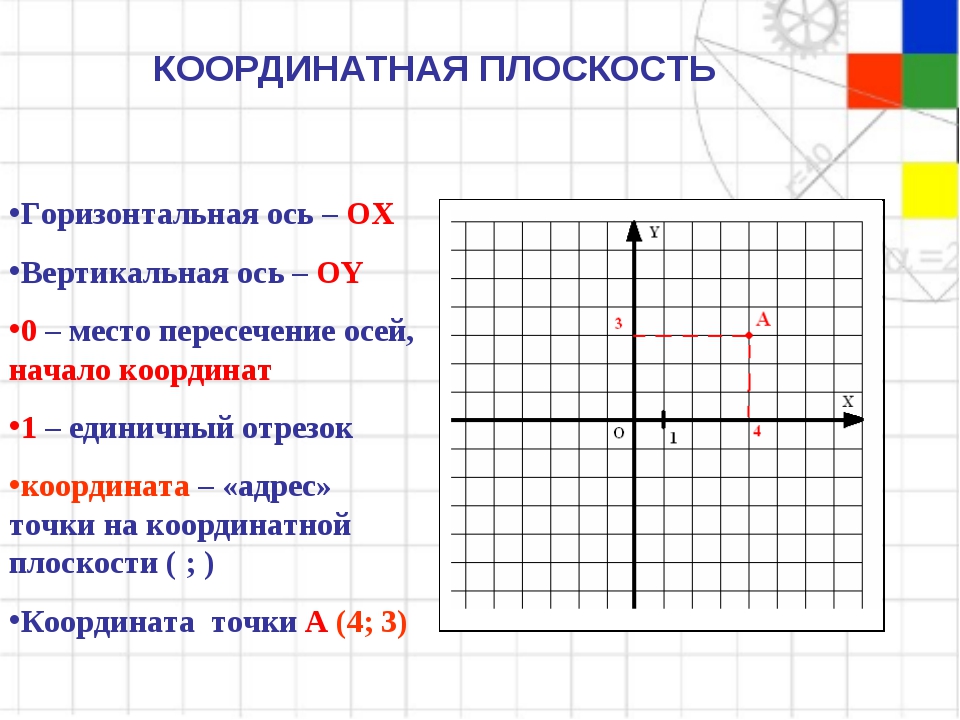
 Постройте график f(x) = |x|
Постройте график f(x) = |x|