П. в. п., имеющая единственный центр симметрии (центр П. в. п.), называется центральной П. в. п.; без центра симметрии или с неопределённым центром – нецентральной поверхностью второго порядка.
Среди П. в. п., содержащих хотя бы одну точку, ограниченными являются лишь эллиптические, все остальные неограниченные. Пересечения П. в. п. с плоскостью являются линиями второго порядка.
Исследование вида П. в. п. может быть проведено (таблицы 1 и 2) без приведения уравнения (*) к канонич. виду с помощью т. н. инвариантов П. в. п., составленных из коэффициентов этого уравнения. Основные инварианты: $$S=a_{11}+a_{22}+a_{33}, \\ T=\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} + \begin{vmatrix} a_{11} & a_{13} \\ a_{31} & a_{33} \end{vmatrix} + \begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix}, \\ \delta=\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{12} & a_{22} & a_{23} \\ a_{13} & a_{23} & a_{33} \end{vmatrix}, \Delta=\begin{vmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{12} & a_{22} & a_{23} & a_{24} \\ a_{13} & a_{23} & a_{33} & a_{34} \\ a_{14} & a_{24} & a_{34} & a_{44} \end{vmatrix}.
| Таблица 1. Классификация поверхностей второго порядка по инвариантам | ||||
| Невырождающиеся поверхности | Вырождающиеся поверхности | |||
| $\Delta \gt 0$ | $\Delta \lt 0$ | $\Delta = 0$ | ||
| Центральные поверхности $\delta \neq 0$ | $\delta S\gt 0, T\gt 0$ | Мнимый эллипсоид | Эллипсоид | Мнимый конус |
| $\delta S \leq 0$ и(или) $T \leq 0$ | Однополостный гиперболоид | Двуполостный гиперболоид | Действительный конус | |
| Нецентральные поверхности $\delta = 0$ | Гиперболический параболоид | Эллиптический параболоид | Цилиндрические и распадающиеся поверхности (см. табл. 2) | |
Таблица 2. Цилиндрические и распадающиеся поверхности второго порядка ($\Delta=0, \delta=0$) Цилиндрические и распадающиеся поверхности второго порядка ($\Delta=0, \delta=0$) | ||||
| $T\gt 0$ | Цилиндрические поверхности $\Delta’ \neq 0$ | Распадающиеся поверхности $\Delta’ = 0$ | ||
| Эллиптический цилиндр | ||||
| Мнимый $\Delta’S \gt 0$ | Действительный $\Delta’S \lt 0$ | |||
| $T\lt 0$ | Гиперболический цилиндр | Пара пересекающихся плоскостей | ||
| $T = 0$ | Параболический цилиндр | Пара мнимых параллельных плоскостей $\Delta» \gt 0$ | Пара совпадающих плоскостей $\Delta» = 0$ | |
| Пара параллельных плоской $\Delta» \lt 0$ | ||||
Их значения не меняются при параллельном переносе и повороте системы координат. Используются также семиинварианты (полуинварианты) $Δ′$ и $\Delta″$, которые являются инвариантами относительно поворота системы координат:$$Δ′=Δ_{11}+Δ_{22}+Δ_{33},$$ где $Δ_{ij}$ – алгебраич. дополнение элемента $a_{ij}$ в $Δ$; $$\Delta»=\begin{vmatrix} a_{11} & a_{14} \\ a_{14} & a_{44} \end{vmatrix} + \begin{vmatrix} a_{22} & a_{24} \\ a_{24} & a_{44} \end{vmatrix} + \begin{vmatrix} a_{33} & a_{34} \\ a_{34} & a_{44} \end{vmatrix}.$$Их значения не меняются при повороте осей координат. Инварианты П. в. п. определяют П. в. п. с точностью до движений евклидова пространства. Любые две нераспадающиеся П. в. п., инварианты которых соответственно равны, эквивалентны по отношению к группе движения пространства, т. е. могут быть совмещены движением.
Используются также семиинварианты (полуинварианты) $Δ′$ и $\Delta″$, которые являются инвариантами относительно поворота системы координат:$$Δ′=Δ_{11}+Δ_{22}+Δ_{33},$$ где $Δ_{ij}$ – алгебраич. дополнение элемента $a_{ij}$ в $Δ$; $$\Delta»=\begin{vmatrix} a_{11} & a_{14} \\ a_{14} & a_{44} \end{vmatrix} + \begin{vmatrix} a_{22} & a_{24} \\ a_{24} & a_{44} \end{vmatrix} + \begin{vmatrix} a_{33} & a_{34} \\ a_{34} & a_{44} \end{vmatrix}.$$Их значения не меняются при повороте осей координат. Инварианты П. в. п. определяют П. в. п. с точностью до движений евклидова пространства. Любые две нераспадающиеся П. в. п., инварианты которых соответственно равны, эквивалентны по отношению к группе движения пространства, т. е. могут быть совмещены движением.
По отношению к более широкой, чем группа движений, группе аффинных преобразований эквивалентными являются П. в. п., канонич. уравнения которых совпадают; имеется 17 аффинно эквивалентных классов, канонич. уравнения которых получаются из уравнений 1–17 при $a=b=c=1$ и $2p=2q=1$.
в. п., канонич. уравнения которых совпадают; имеется 17 аффинно эквивалентных классов, канонич. уравнения которых получаются из уравнений 1–17 при $a=b=c=1$ и $2p=2q=1$.
В проективной геометрии эквивалентными являются П. в. п., которые могут быть переведены друг в друга при проективных преобразованиях (группа которых шире, чем группа аффинных преобразований). Имеется 8 проективно эквивалентных классов, т. е. между некоторыми аффинными классами имеется проективная общность. Это связано с тем, что при проективных преобразованиях исчезает особая роль бесконечно удалённых элементов пространства. Напр., эллипсоид и двуполостный гиперболоид, различные с аффинной точки зрения, принадлежат одному проективному классу поверхностей второго порядка.
П. в. п. впервые представлены уравнениями 2-й степени у Л. Эйлера (1748), совр.
VII. Поверхности второго порядка
§33. Общее уравнение поверхности второго порядка
Определение. Алгебраической поверхностью n-го порядка называется множество точек пространства, имеющее в некоторой аффинной системе координат , в частности, в прямоугольной декартовой системе координат , уравнение вида:
, где — многочлен n-ой степени относительно с действительными коэффициентами.
Можно доказать, что определение поверхности n-го порядка не зависит от выбора системы координат в пространстве, то есть если в какой либо АСК поверхность задаётся уравнением n-ой степени, то и в любой другой АСК она также задаётся уравнением n-ой степени.
Примеры.
Алгебраической поверхностью первого порядка является любая плоскость с общим уравнением , где ;
Алгебраическая поверхность второго порядка имеет уравнение вида: , где хотя бы один из коэффициентов членов второй степени отличен от нуля.

Это уравнение называется общим уравнением поверхности 2-го порядка.
Так же, как и для линии второго порядка на плоскости, можно доказать, что уравнение любой поверхности 2-го порядка с помощью надлежащего выбора системы координат (прямоугольной декартовой) может быть приведено к одному из 17 (семнадцати) простейших видов, которые называются каноническими.
Общую теорию поверхностей второго порядка мы изучать не будем, исследуем свойства этих поверхностей по их каноническим уравнениям.
I. Эллипсоиды
Эллипсоид: .
Мнимый эллипсоид (пустое множество точек): .
II. Гиперболоиды
Однополостный гиперболоид: .
Двуполостный гиперболоид: .
III. Параболоиды
Эллиптический параболоид: .
Гиперболический параболоид: .

IV. Конусы
Конус: .
Мнимый конус (точка O(0,0,0)): .
V. Цилиндры
Эллиптический цилиндр: .
Гиперболический цилиндр: .
Параболический цилиндр: .
Мнимый цилиндр (пустое множество точек):
VI. Пары плоскостей
Пара пересекающихся плоскостей:
Пара мнимых плоскостей, пересекающихся по действительной прямой:
Пара различных параллельных плоскостей:
Пара совпавших плоскостей:
Пара мнимых параллельных плоскостей (пустое множество точек).
 (Изображения поверхностей
2-го порядка смотреть в учебнике геометрии
часть I, глава IX.)
(Изображения поверхностей
2-го порядка смотреть в учебнике геометрии
часть I, глава IX.)
§34. Эллипсоид
Эллипсоид задаётся своим каноническим уравнением:
. (1)
1. Плоскости, оси и центр симметрии
а) Так как переменная z содержится в уравнении (1) лишь во второй степени, то это уравнение не изменится при замене на .
Следовательно, если точка принадлежит эллипсоиду, то ему также принадлежит и точка .
Э ти точки симметричны относительно плоскости , значит и весь эллипсоид симметричен относительно этой плоскости.
Аналогично, эллипсоид симметричен и относительно плоскостей и .
б) Так как уравнение (1) не изменяется при одновременной замене на и на , то эллипсоид симметричен относительно оси .
Аналогично, эллипсоид симметричен и относительно осей и .
в)
Так как уравнение (1) не изменится при
одновременной замене
на
,
на
на
,
то эллипсоид симметричен относительно
начала координат.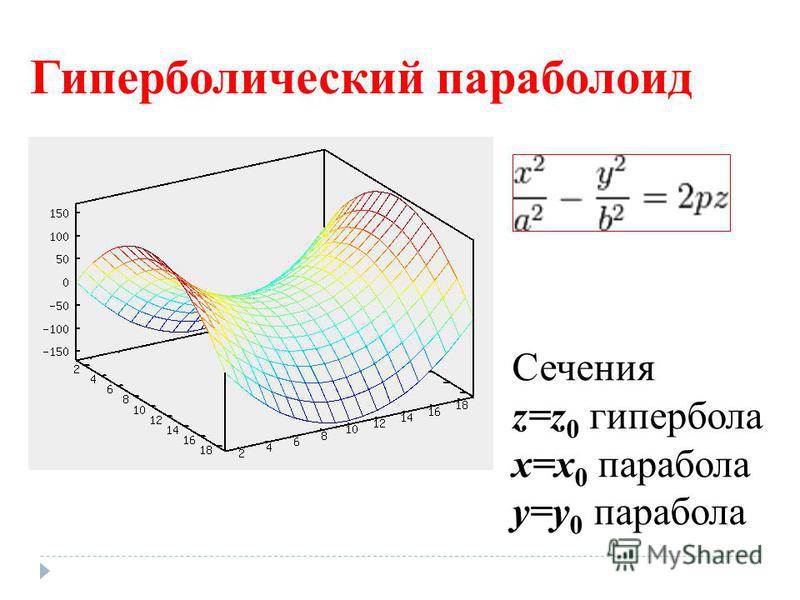
Определение 1. Центр симметрии поверхности второго порядка называется её центром, а её оси симметрии – осями поверхности второго порядка.
Таким образом, эллипсоид с уравнением (1) имеет:
один центр симметрии – начало координат;
три оси симметрии – оси , , и ;
три плоскости симметрии – плоскости , , .
2. Вершины
Определение 2. Вершинами поверхности 2-го порядка называются точки пересечения её с осями.
Найдём вершины эллипсоида с уравнением (1).
или , отсюда .
Точки пересечения эллипсоида с осью обозначим:
и .
Аналогично получим точки пересечения эллипсоида с осью :
и .
И осью :
и .
Итак, эллипсоид имеет шесть вершин. Числа называются комре эллипсоида.
3. Главные сечения
Определение
3. Множество точек (кривая линия), получающиеся
при пересечении некоторой поверхности
(не обязательно 2-го порядка) плоскостью,
называется сечением этой поверхности.
Определение 4. Сечения поверхности 2-го порядка её плоскостями симметрии называются её главными сечениями.
Легко видеть, что все главные сечения эллипсоида есть эллипсы:
Сечение плоскостью :
Сечение плоскостью :
Сечение плоскостью :
4. Сечения плоскостями, параллельными плоскостям симметрии
Рассмотрим сечение эллипсоида с уравнением (1) плоскостью α, параллельной плоскости Оху:
(2)
В зависимости от величины h возможны случаи:
и плоскости α с уравнением z=h эллипсоид не пересекает.
и сечением является либо точка C1(0;0;c), либо точка C2(0;0;-c), то есть, одна из вершин – эллипсоида.
и получаем систему уравнений:
(3)
В уравнении (3) положив: , приходим к уравнению эллипса с полуосями а1 и b1:
. (4)
(4)
Итак, в этом случае в сечении мы получаем эллипс, центр которого лежит на оси Oz в точке D(0;0;h). Легко видеть, что при уменьшении полуоси а1 и b1 возрастают и при h=0 имеем: a1=a, b1=b – сечение является главным.
Аналогично можно показать, что сечение эллипсоида с уравнением (1) плоскостями x=h или y=h является либо эллипсом, либо точкой – соответствующей вершиной эллипсоида, либо пустым множеством.
Заметим дополнительно, что из уравнения (1) следует, что
Поэтому имеем: -a ≤ x ≤ a, -b ≤ y ≤b, -c ≤ z ≤ c. Отсюда следует, что все точки эллипсоида (кроме его вершин) лежат внутри прямоугольного параллелепипеда с измерениями 2a, 2b, 2c. Грани его параллельны координатным плоскостям, а вершины эллипсоида служат центрами симметрии этих граней.
Изобразим теперь эллипсоид, используя проведённые выше исследования его формы.
5. Виды эллипсоидов
Если все полуоси эллипсоида различны: a≠b≠c, то он называется трёхосным.

Если две полуоси эллипсоида равны, например, a=b, то он является поверхностью вращения. Все его сечения, перпендикулярные оси вращения Oz, есть окружности. Эллипсоид называется в этом случае эллипсоидом вращения с осью вращения Oz и имеем каноническое уравнение:
. (5)
Если все три оси эллипсоида равны: a=b=c, то он представляет собой сферу с центром в начале координат радиуса r = a:
. (6)
Следовательно, сфера является частным случаем эллипсоида.
Можно показать, что любой трёхосный эллипсоид с уравнением (1) можно получить из некоторой сферы, например, с уравнением (6), с помощью последовательного сжатия к двум взаимно перпендикулярным плоскостям симметрии этой сферы.
Замечание. Эллипсоид с центром O’(x0;y0;z0)
и полуосями a,
b,
c,
параллельными осям координат, имеем
уравнение: =1.
В частности, сфера радиуса r = a с центром в точке O’(x0;y0;z0) имеем уравнение: +
Поверхности второго порядка
Поверхности второго порядка.
Определение. Поверхности второго порядка – это поверхности, уравнения которых в прямоугольной системе координат являются уравнениями второго порядка.
Цилиндрические поверхности.
Определение. Цилиндрическими поверхностями называются поверхности, образованные линиями, параллельными какой- либо фиксированной прямой.
Рассмотрим
поверхности, в уравнении которых отсутствует составляющая z, т.е.
направляющие параллельны оси Оz. Тип линии на плоскости ХOY (эта линия
называется направляющей поверхности) определяет характер цилиндрической
поверхности. Рассмотрим некоторые частные случаи в зависимости от уравнения
направляющих:
Рассмотрим некоторые частные случаи в зависимости от уравнения
направляющих:
1) — эллиптический цилиндр.
2) — гиперболический цилиндр.
2) x2 = 2py – параболический цилиндр.
Поверхности вращения.
Определение. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращения с осью вращения d.
Если уравнение поверхности в прямоугольной системе координат имеет вид:
F(x2 + y2, z) = 0, то эта поверхность – поверхность вращения с осью вращения Оz.
Аналогично: F(x2 + z2, y) = 0 – поверхность вращения с осью вращения Оу,
F(z2 + y2, x) = 0 – поверхность вращения с осью вращения Ох.
Запишем уравнения поверхностей вращения для некоторых частных случаев:
1) — эллипсоид вращения
2) — однополостный гиперболоид вращения
3) — двуполостный гиперболоид вращения
4) — параболоид вращения
Аналогично могут быть записаны уравнения для
рассмотренных выше поверхностей вращения, если осью вращения являются оси Ох
или Оу.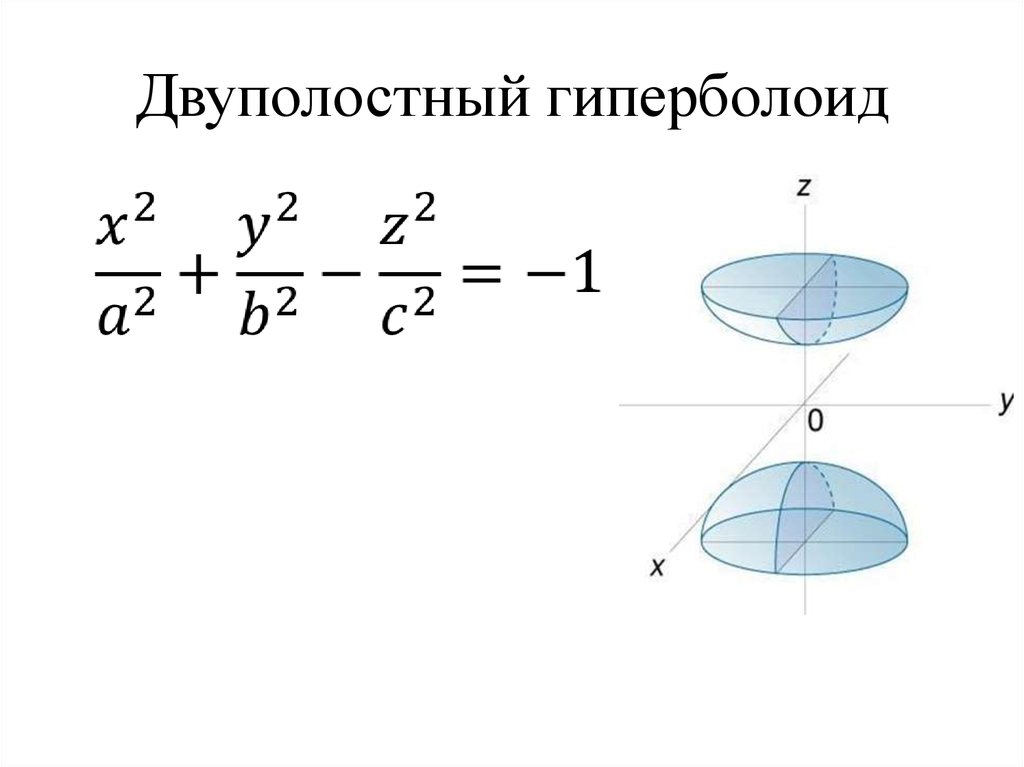
Однако, перечисленные выше поверхности являются всего лишь частными случаями поверхностей второго порядка общего вида, некоторые типы которых рассмотрены ниже:
Сфера:
Трехосный эллипсоид:
В сечении эллипсоида плоскостями, параллельными координатным плоскостям, получаются эллипсы с различными осями.
Однополостный гиперболоид:
Двуполостный гиперболоид:
Эллиптический параболоид:
Гиперболический параболоид:
Конус второго порядка:
Мощный терагерцовый лазер поверхностного излучения с гибридными брэгговскими решетками второго и четвертого порядка -лепестковый пучок дальнего поля.
 Радиационная эффективность может быть увеличена за счет использования изогнутых и чирпированных решеток для инфракрасных диодных лазеров, селекции мод с помощью плазмонов для квантовых каскадных лазеров среднего инфракрасного диапазона (ККЛ) и градиентных фотонных структур для терагерцовых ККЛ. Здесь мы демонстрируем новую схему гибридной решетки, в которой используется суперпозиция брэгговских решеток второго и четвертого порядка, которые возбуждают симметричную моду с гораздо большей радиационной эффективностью. Схема реализована для ККЛ терагерцового диапазона с металлическими волноводами. Пиковая выходная мощность 170 мВт с коэффициентом полезного действия 993 мВт A −1 обнаруживается с устойчивым одномодовым однолепестковым излучением для ККЛ 3,4 ТГц, работающей при 62 K. Схема гибридной решетки, возможно, проще в реализации, чем вышеупомянутые схемы DFB, и может использоваться для увеличения выходной мощности для поверхностно-излучающие РОС-лазеры на любой длине волны.
Радиационная эффективность может быть увеличена за счет использования изогнутых и чирпированных решеток для инфракрасных диодных лазеров, селекции мод с помощью плазмонов для квантовых каскадных лазеров среднего инфракрасного диапазона (ККЛ) и градиентных фотонных структур для терагерцовых ККЛ. Здесь мы демонстрируем новую схему гибридной решетки, в которой используется суперпозиция брэгговских решеток второго и четвертого порядка, которые возбуждают симметричную моду с гораздо большей радиационной эффективностью. Схема реализована для ККЛ терагерцового диапазона с металлическими волноводами. Пиковая выходная мощность 170 мВт с коэффициентом полезного действия 993 мВт A −1 обнаруживается с устойчивым одномодовым однолепестковым излучением для ККЛ 3,4 ТГц, работающей при 62 K. Схема гибридной решетки, возможно, проще в реализации, чем вышеупомянутые схемы DFB, и может использоваться для увеличения выходной мощности для поверхностно-излучающие РОС-лазеры на любой длине волны.
Введение
Мощные полупроводниковые лазеры с поверхностным излучением (SE) 1, 2 имеют значительные преимущества по сравнению со своими аналогами с краевым излучением во многих аспектах, связанных с оптической связью и юстировкой, тестированием и компоновкой, масштабированием мощности с помощью массивов, стабильностью длины волны , невосприимчивость к фасеточным повреждениям среди прочего. Радиационная эффективность SE-лазеров была увеличена за счет использования различных технологий, включая использование изогнутых и чирпированных решеток для инфракрасных диодных лазеров 3, 4 , реализация смещения центральной решетки π для устройств с коротким резонатором 5 , выбор режима с помощью плазмона для квантовых каскадных лазеров среднего инфракрасного диапазона (ККЛ) 6,7,8 , и градиентные фотонные структуры для терагерцовых ККЛ 9 . В ближнем инфракрасном диапазоне такие мощные лазеры в основном реализуются как SE-лазеры с вертикальным резонатором (VCSEL) 10 . Тем не менее, некоторые из самых высоких выходных мощностей одномодовых лазеров были продемонстрированы с решетками РОС второго порядка 3, 4 . Для ККЛ, излучающих на более длинных волнах 11,12,13 , вертикальные резонаторы невозможны из-за поперечной магнитной поляризации межподзонного оптического поля, поэтому для поверхностного излучения используются решетки второго порядка 7, 8, 14 ,15,16,17,18 . Одномодовые ККЛ высокой яркости необходимы в среднем ИК и терагерцовом спектре для применения в химическом и биомолекулярном зондировании и спектроскопии. В среднем ИК-диапазоне для DFB QCL с краевым излучением была продемонстрирована мощность в несколько ватт.0005 19 ; однако для поверхностных (или подложных) ККЛ РОС с решетками второго порядка выходная мощность еще не достигла таких уровней 7, 8, 20 и есть значительные возможности для улучшения. Для терагерцовых ККЛ субволновое ограничение металлических полостей 11 создало новые проблемы для разработки методов РОС.
Тем не менее, некоторые из самых высоких выходных мощностей одномодовых лазеров были продемонстрированы с решетками РОС второго порядка 3, 4 . Для ККЛ, излучающих на более длинных волнах 11,12,13 , вертикальные резонаторы невозможны из-за поперечной магнитной поляризации межподзонного оптического поля, поэтому для поверхностного излучения используются решетки второго порядка 7, 8, 14 ,15,16,17,18 . Одномодовые ККЛ высокой яркости необходимы в среднем ИК и терагерцовом спектре для применения в химическом и биомолекулярном зондировании и спектроскопии. В среднем ИК-диапазоне для DFB QCL с краевым излучением была продемонстрирована мощность в несколько ватт.0005 19 ; однако для поверхностных (или подложных) ККЛ РОС с решетками второго порядка выходная мощность еще не достигла таких уровней 7, 8, 20 и есть значительные возможности для улучшения. Для терагерцовых ККЛ субволновое ограничение металлических полостей 11 создало новые проблемы для разработки методов РОС. Следовательно, было продемонстрировано множество конфигураций DFB 21, 22 . Модификация одномерных решеток второго порядка с градуированной периодичностью привела к предыдущей максимальной выходной мощности 103 мВт при 20 К для одномодовых терагерцовых ККЛ 9 . Совсем недавно аналогичные уровни мощности были реализованы с помощью SE терагерцовых QCL с внешним резонатором 23 , которые предлагают преимущество пучков с малой расходимостью за счет стабильности частоты и специфичности, обеспечиваемых лазерами DFB.
Следовательно, было продемонстрировано множество конфигураций DFB 21, 22 . Модификация одномерных решеток второго порядка с градуированной периодичностью привела к предыдущей максимальной выходной мощности 103 мВт при 20 К для одномодовых терагерцовых ККЛ 9 . Совсем недавно аналогичные уровни мощности были реализованы с помощью SE терагерцовых QCL с внешним резонатором 23 , которые предлагают преимущество пучков с малой расходимостью за счет стабильности частоты и специфичности, обеспечиваемых лазерами DFB.
Здесь мы описываем новую схему повышения эффективности излучения поверхностно-излучающих ККЛ РОС в металлических резонаторах, которая обеспечивает рекордно высокую выходную мощность для одномодовых ККЛ терагерцового диапазона. Реализована рекордно высокая наклонная эффективность, более чем в четыре раза превышающая таковую в исх. 9 , а также значительно выше, чем у терагерцовых ККЛ с одноплазмонными волноводами, недавно достигших выходной мощности ваттного уровня 24, 25 .
Результаты
Концепция
Периодическое возмущение в оптическом волноводе приводит к брэгговской дифракции до нескольких высших порядков, которые можно использовать для соединения встречных волн в волноводе для установления DFB. Следующее уравнение описывает закон сохранения импульса между волновыми векторами падающей направленной волны внутри резонатора k i ≈ 2 π / λ wg = 2 πn eff / λ (where λ wg is the wavelength inside the waveguide, λ is the длина волны в свободном пространстве, а n eff — эффективный показатель распространения) и дифрагированной волны k d , которая может быть снаружи или внутри резонатора под любым углом θ d (как определяется относительно нормали к поверхности). Это также схематически представлено на рис. 1а.
$$n\frac{{2\pi}}{\Lambda} = k_{\rm {i}} + k_{\rm {d}}\,{\mathrm{sin}}(\theta _{ \rm {d}})$$
(1)
здесь Λ — период решетки, 2 π / Λ — волновой вектор решетки, n — целое число ( 6 n 1,2,3…), который определяет порядок дифракции. {(2)}} )\) направлена в направлении, противоположном направленной падающей волне, которая устанавливает DFB. Симметричные (большой радиационный выход) и антисимметричные (малый радиационный выход) резонансные моды устанавливаются на краях фотонной запрещенной зоны из-за РОС. c Концепция гибридной решетки, сочетающая брэгговские решетки второго и четвертого порядка. Решетка второго порядка обеспечивает более сильную DFB и приводит к установлению резонансных оптических мод с такими же фазовыми соотношениями, как и на решетке b . Добавленная решетка четвертого порядка служит для увеличения выхода антисимметричной моды и уменьшения связи симметричной моды. Путем настройки конструктивных параметров любая из этих мод может быть возбуждена в резонаторе РОС-лазера, который имеет большую эффективность излучения по сравнению с возбуждаемой модой для резонатора РОС второго порядка
{(2)}} )\) направлена в направлении, противоположном направленной падающей волне, которая устанавливает DFB. Симметричные (большой радиационный выход) и антисимметричные (малый радиационный выход) резонансные моды устанавливаются на краях фотонной запрещенной зоны из-за РОС. c Концепция гибридной решетки, сочетающая брэгговские решетки второго и четвертого порядка. Решетка второго порядка обеспечивает более сильную DFB и приводит к установлению резонансных оптических мод с такими же фазовыми соотношениями, как и на решетке b . Добавленная решетка четвертого порядка служит для увеличения выхода антисимметричной моды и уменьшения связи симметричной моды. Путем настройки конструктивных параметров любая из этих мод может быть возбуждена в резонаторе РОС-лазера, который имеет большую эффективность излучения по сравнению с возбуждаемой модой для резонатора РОС второго порядка
Изображение полного размера
Далее описывается концепция гибридных решеток РОС второго и четвертого порядка для повышения эффективности излучения КЭ-лазеров. На рисунке 1b показаны обычные решетки второго порядка в оптическом резонаторе, которые используются для реализации нормального излучения широкой поверхности (или подложки) из резонатора, поскольку брэгговская дифракция первого порядка перпендикулярна направлению направленной волны в резонаторе, как по уравнению (1) 1 . Связанная мода 2 или конечно-элементное моделирование периодических структур используются для расчета фотонной зонной структуры. Обычно краевые моды в продольном резонаторе называются симметричными и антисимметричными с высокой и низкой излучательной эффективностью соответственно, где последняя возбуждается для SE DFB-лазера, тем самым ограничивая его выходную мощность. Излучательная эффективность зависит от точной амплитуды и фазы стоячей волны (резонансной моды) по отношению к периодичности решетки. Такое поведение характерно для различных типов волноводов и решеток РОС, а не только для металлических резонаторов, показанных на рис. 1б. На рисунке 1c концептуально показано, как наложение структуры решетки четвертого порядка на существующую решетку второго порядка способствует повышению общей эффективности излучения.
На рисунке 1b показаны обычные решетки второго порядка в оптическом резонаторе, которые используются для реализации нормального излучения широкой поверхности (или подложки) из резонатора, поскольку брэгговская дифракция первого порядка перпендикулярна направлению направленной волны в резонаторе, как по уравнению (1) 1 . Связанная мода 2 или конечно-элементное моделирование периодических структур используются для расчета фотонной зонной структуры. Обычно краевые моды в продольном резонаторе называются симметричными и антисимметричными с высокой и низкой излучательной эффективностью соответственно, где последняя возбуждается для SE DFB-лазера, тем самым ограничивая его выходную мощность. Излучательная эффективность зависит от точной амплитуды и фазы стоячей волны (резонансной моды) по отношению к периодичности решетки. Такое поведение характерно для различных типов волноводов и решеток РОС, а не только для металлических резонаторов, показанных на рис. 1б. На рисунке 1c концептуально показано, как наложение структуры решетки четвертого порядка на существующую решетку второго порядка способствует повышению общей эффективности излучения. Из-за более слабой брэгговской дифракции для обратной связи решетка четвертого порядка существенно не изменяет форму мод краевых мод, что лишь незначительно изменяет распределение электромагнитного поля по длине резонатора, то есть точка максимума Е х немного сместит центр щели и уменьшит эффективность излучения симметричного режима. Массив антенноподобных диполей с противоположными полярностями вводится в каждый период повторения гибридной решетки, что вызывает деструктивную интерференцию для выведенного излучения (отмечено как конкурирующий диполь из DFB 4-го порядка, как показано на рис. 1c), что, в свою очередь, уменьшает выходная эффективность симметричного режима. Однако, поскольку брэгговская дифракция второго порядка происходит в направлении нормали к поверхности, решетка четвертого порядка может быть расположена так, чтобы увеличить радиационные потери для исходной антисимметричной моды РОС-структуры второго порядка. Такая гибридная решетка увеличивает эффективность излучения антисимметричной моды и снижает эффективность излучения симметричной моды, и, следовательно, любая из этих краевых мод может быть возбуждена в соответствии с точной реализацией решетки четвертого порядка.
Из-за более слабой брэгговской дифракции для обратной связи решетка четвертого порядка существенно не изменяет форму мод краевых мод, что лишь незначительно изменяет распределение электромагнитного поля по длине резонатора, то есть точка максимума Е х немного сместит центр щели и уменьшит эффективность излучения симметричного режима. Массив антенноподобных диполей с противоположными полярностями вводится в каждый период повторения гибридной решетки, что вызывает деструктивную интерференцию для выведенного излучения (отмечено как конкурирующий диполь из DFB 4-го порядка, как показано на рис. 1c), что, в свою очередь, уменьшает выходная эффективность симметричного режима. Однако, поскольку брэгговская дифракция второго порядка происходит в направлении нормали к поверхности, решетка четвертого порядка может быть расположена так, чтобы увеличить радиационные потери для исходной антисимметричной моды РОС-структуры второго порядка. Такая гибридная решетка увеличивает эффективность излучения антисимметричной моды и снижает эффективность излучения симметричной моды, и, следовательно, любая из этих краевых мод может быть возбуждена в соответствии с точной реализацией решетки четвертого порядка. В любом случае эффективность излучения увеличивается по сравнению с возбужденной модой для исходной структуры РОС второго порядка. Следует отметить, что дифракция 1-го и 3-го порядка от решеток DFB четвертого порядка потенциально может генерировать ненормальное излучение, поскольку они не преломляются перпендикулярно или параллельно поверхности. Однако возможность такого излучения в таком резонаторе не существует, что можно показать с помощью прямого анализа, основанного на уравнении (1). Для подтверждения этого утверждения также было проведено моделирование методом конечных элементов, которое описано далее в дополнительном примечании 6.
В любом случае эффективность излучения увеличивается по сравнению с возбужденной модой для исходной структуры РОС второго порядка. Следует отметить, что дифракция 1-го и 3-го порядка от решеток DFB четвертого порядка потенциально может генерировать ненормальное излучение, поскольку они не преломляются перпендикулярно или параллельно поверхности. Однако возможность такого излучения в таком резонаторе не существует, что можно показать с помощью прямого анализа, основанного на уравнении (1). Для подтверждения этого утверждения также было проведено моделирование методом конечных элементов, которое описано далее в дополнительном примечании 6.
Реализация гибридной схемы РОС для терагерцовых ККЛ
Чтобы описать конкретную реализацию гибридной схемы РОС для терагерцовых ККЛ с металлическими полостями и сравнение с обычным РОС второго порядка в таких ККЛ 18 , результаты конечных элементов моделирование показано на рис. 2. Показаны радиационные поверхностные потери резонансных мод, их частоты и профили электрического поля для краевых мод для резонаторов конечной длины с решетками, реализованными в верхней металлической оболочке. Утверждается, что значение радиационных потерь само по себе является прямым показателем эффективности выхода из таких полостей РОС. В дополнительном примечании 7 этот аспект эффективности вывода из полости уточняется. Для обычного DFB второго порядка радиационные потери для верхней краевой моды полосы (симметричной в плоскости ( Е х ) поле) значительно больше, чем безызлучательная мода нижнего края полосы (антисимметричная в плоскости ( E x ) поле) 18 . Для сравнения, резонатор с гибридными решетками второго и четвертого порядка значительно увеличивает поверхностные потери для антисимметричной моды нижнего края полосы из-за дополнительного излучения от щели, соответствующей наложенной решетке четвертого порядка. Потери для симметричной моды верхнего края полосы меньше, чем потери для структуры DFB второго порядка. Для смоделированного случая d / Λ на рис. 2, мода верхнего края полосы имеет меньшие потери для гибридной решетки РОС и будет возбуждаться в резонаторе генерации.
Утверждается, что значение радиационных потерь само по себе является прямым показателем эффективности выхода из таких полостей РОС. В дополнительном примечании 7 этот аспект эффективности вывода из полости уточняется. Для обычного DFB второго порядка радиационные потери для верхней краевой моды полосы (симметричной в плоскости ( Е х ) поле) значительно больше, чем безызлучательная мода нижнего края полосы (антисимметричная в плоскости ( E x ) поле) 18 . Для сравнения, резонатор с гибридными решетками второго и четвертого порядка значительно увеличивает поверхностные потери для антисимметричной моды нижнего края полосы из-за дополнительного излучения от щели, соответствующей наложенной решетке четвертого порядка. Потери для симметричной моды верхнего края полосы меньше, чем потери для структуры DFB второго порядка. Для смоделированного случая d / Λ на рис. 2, мода верхнего края полосы имеет меньшие потери для гибридной решетки РОС и будет возбуждаться в резонаторе генерации. Что еще более важно, поверхностные потери возбужденной моды в лазерном резонаторе с гибридной РОС могут быть на порядок больше, чем в резонаторе с РОС второго порядка. Можно отметить, что ширина запрещенной зоны гибридного резонатора РОС имеет красное смещение ~0,08 ТГц в показанном моделировании, что связано с тем, что большая часть затухающих полей распространяется за пределы активной среды, что снижает эффективный показатель распространения n эфф направленных волн.
Что еще более важно, поверхностные потери возбужденной моды в лазерном резонаторе с гибридной РОС могут быть на порядок больше, чем в резонаторе с РОС второго порядка. Можно отметить, что ширина запрещенной зоны гибридного резонатора РОС имеет красное смещение ~0,08 ТГц в показанном моделировании, что связано с тем, что большая часть затухающих полей распространяется за пределы активной среды, что снижает эффективный показатель распространения n эфф направленных волн.
Сравнение гибридной РОС и РОС второго порядка для терагерцовых ККЛ. a Изображение металлического резонатора для ККЛ терагерцового диапазона, в котором щели открыты в верхней металлической оболочке для реализации периодической решетки 18 . Решетка четвертого порядка накладывается со смещением на длину d на исходную решетку второго порядка с периодичностью Λ для реализации структуры гибридной решетки, как на рис. 1c. b Спектр мод для бесконечно широкого резонатора длиной 1,4 мм с решетками РОС ( Λ = 27 мкм, ширина щели ~3 мкм), рассчитанный методом конечно-элементного моделирования. Поверхностные потери на излучение для различных резонансных мод для резонатора с решетками второго порядка показаны красным цветом (тонкие линии), а для резонатора с гибридными решетками ( d / Λ = 3/8) – синим цветом (толстые линии). линии). На вставках показаны профили электрического поля для нижней и верхней крайних мод фотонной зоны соответственно для каждого типа решеток (цветная полоса, показанная на этом рисунке, относится ко всем графикам профилей электрического поля). Радиационные потери эффективно определяются амплитудой и фазой плоскостного электрического поля ( Е х ) в щелях
1c. b Спектр мод для бесконечно широкого резонатора длиной 1,4 мм с решетками РОС ( Λ = 27 мкм, ширина щели ~3 мкм), рассчитанный методом конечно-элементного моделирования. Поверхностные потери на излучение для различных резонансных мод для резонатора с решетками второго порядка показаны красным цветом (тонкие линии), а для резонатора с гибридными решетками ( d / Λ = 3/8) – синим цветом (толстые линии). линии). На вставках показаны профили электрического поля для нижней и верхней крайних мод фотонной зоны соответственно для каждого типа решеток (цветная полоса, показанная на этом рисунке, относится ко всем графикам профилей электрического поля). Радиационные потери эффективно определяются амплитудой и фазой плоскостного электрического поля ( Е х ) в щелях
Полный размер
Для симметричной моды, возбуждаемой в случае гибридной РОС со специфическими к уравнению (1), это относительно низкое значение n eff связано с созданием сильного поля поверхностного плазмон-поляритона (ППП), которое распространяется поверх активной области, как показано на рис. 2b. Напротив, антисимметричная мода имеет большее n eff ~ 3,45, что соответствует большей доле резонансной моды, заключенной внутри активной среды.
2b. Напротив, антисимметричная мода имеет большее n eff ~ 3,45, что соответствует большей доле резонансной моды, заключенной внутри активной среды.
Гибридная решетка DFB обеспечивает гибкость конструкции за счет простого изменения смещения d , при котором реализуется решетка четвертого порядка, как показано на схеме на рис. 2a. Относительные радиационные потери двух краевых мод можно модулировать, регулируя d / Λ , что полезно для проектирования избирательного возбуждения нижней или верхней краевой моды. Это показано на графике расчетных поверхностных потерь краевых мод бесконечно широкого, но конечной длины терагерцового резонатора ККЛ на рис. 3а, где моделирование выполнено с теми же параметрами решетки, что и на рис. 2. определенный диапазон d / Λ потери верхней краевой моды могут быть снижены и, следовательно, такая мода может возбуждаться избирательно. Для экспериментальных результатов, представленных позже, d / Λ = 3/8 было реализовано для выборочного возбуждения моды верхнего края полосы. Обратите внимание, что в этом случае обе моды на краю полосы приводят к однолепестковым лучам в дальней зоне, а обозначения симметричных/антисимметричных теряют значение из-за общей конструктивной интерференции в дальней зоне для обеих мод на границе полосы (дополнительное примечание 2). показывает интуитивное объяснение профиля однолепесткового луча для обеих мод на краю взрыва), при рассмотрении результирующего излучения от каждых 2 Λ длина РОС конструкции. В этом смысле гибридную структуру РОС можно было бы вместо этого просто назвать схемой РОС четвертого порядка, но такой, которая имеет особое требование к своей элементарной ячейке с периодичностью 2 Λ . Мы предпочитаем не использовать эту терминологию, поскольку в этом случае она не дает четкого представления о механизме работы DFB.
Обратите внимание, что в этом случае обе моды на краю полосы приводят к однолепестковым лучам в дальней зоне, а обозначения симметричных/антисимметричных теряют значение из-за общей конструктивной интерференции в дальней зоне для обеих мод на границе полосы (дополнительное примечание 2). показывает интуитивное объяснение профиля однолепесткового луча для обеих мод на краю взрыва), при рассмотрении результирующего излучения от каждых 2 Λ длина РОС конструкции. В этом смысле гибридную структуру РОС можно было бы вместо этого просто назвать схемой РОС четвертого порядка, но такой, которая имеет особое требование к своей элементарной ячейке с периодичностью 2 Λ . Мы предпочитаем не использовать эту терминологию, поскольку в этом случае она не дает четкого представления о механизме работы DFB.
Особенности конструкции и сравнение с двухщелевой структурой РОС второго порядка. a Расчетные поверхностные потери краевых мод для гибридной DFB-структуры, показанной на рис. 2a, в зависимости от д / Λ . Расстояние между апертурами d является конструктивным параметром, который можно использовать для изменения соответствующих потерь, а также ширины запрещенной зоны, которая также отображается на графике. b Поверхностные потери и ширина запрещенной зоны также представлены в зависимости от расстояния между апертурами для двухщелевой структуры РОС второго порядка (т.е. две щели присутствуют в каждом периоде решетки с периодичностью Λ ), которая использовалась для терагерцовых ККЛ ранее 26 . Профили электрического поля вблизи центра полостей для обеих краевых мод построены для случая d / Λ = 0.4 в качестве примера
2a, в зависимости от д / Λ . Расстояние между апертурами d является конструктивным параметром, который можно использовать для изменения соответствующих потерь, а также ширины запрещенной зоны, которая также отображается на графике. b Поверхностные потери и ширина запрещенной зоны также представлены в зависимости от расстояния между апертурами для двухщелевой структуры РОС второго порядка (т.е. две щели присутствуют в каждом периоде решетки с периодичностью Λ ), которая использовалась для терагерцовых ККЛ ранее 26 . Профили электрического поля вблизи центра полостей для обеих краевых мод построены для случая d / Λ = 0.4 в качестве примера
Изображение в полный размер
Учитывая, что представленная здесь гибридная РОС для терагерцовых ККЛ реализуется с двухщелевыми щелями в металлической оболочке в каждом чередующемся периоде длиной Λ , интуитивно заставляет задуматься о том, можно ли также увеличить радиационные потери для РОС второго порядка для таких ККЛ, введя двойные щели в каждом периоде, чтобы избежать нулей радиационного поля E x в одной из двух щелей. Такая структура РОС действительно была экспериментально исследована в работе [1]. 26 . Однако оказывается, что такая РОС-структура также имеет антисимметричную моду для одной из мод края зоны, которая имеет пренебрежимо малую радиационную связь. В этом случае роль симметрии для краевых мод меняется на противоположную, и верхняя краевая мода теперь становится модой с малыми потерями с деструктивной интерференцией для излучательной связи с дальним полем. Поведение поверхностных потерь для двух краевых мод и репрезентативные профили электрического поля для двухщелевой решетки второго порядка показаны на рис. 3b. Этот тип структуры потенциально может быть использован для увеличения выходной мощности, если большой d / Λ был выбран, чтобы сделать фотонную ширину запрещенной зоны большой, чтобы верхние краевые моды находились вне области усиления активной среды. Это действительно была стратегия, использованная в исх. 26 для умеренного увеличения выходной мощности терагерцовых QCL SE DFB.
Такая структура РОС действительно была экспериментально исследована в работе [1]. 26 . Однако оказывается, что такая РОС-структура также имеет антисимметричную моду для одной из мод края зоны, которая имеет пренебрежимо малую радиационную связь. В этом случае роль симметрии для краевых мод меняется на противоположную, и верхняя краевая мода теперь становится модой с малыми потерями с деструктивной интерференцией для излучательной связи с дальним полем. Поведение поверхностных потерь для двух краевых мод и репрезентативные профили электрического поля для двухщелевой решетки второго порядка показаны на рис. 3b. Этот тип структуры потенциально может быть использован для увеличения выходной мощности, если большой d / Λ был выбран, чтобы сделать фотонную ширину запрещенной зоны большой, чтобы верхние краевые моды находились вне области усиления активной среды. Это действительно была стратегия, использованная в исх. 26 для умеренного увеличения выходной мощности терагерцовых QCL SE DFB. Хотя может показаться, что структура с двумя щелями в чем-то похожа на гибридную структуру РОС, последняя существенно отличается по своей функциональности и эффективности для повышения эффективности излучения при поверхностном излучении.
Хотя может показаться, что структура с двумя щелями в чем-то похожа на гибридную структуру РОС, последняя существенно отличается по своей функциональности и эффективности для повышения эффективности излучения при поверхностном излучении.
Экспериментальные результаты
Экспериментальные результаты репрезентативных SE терагерцовых ККЛ, реализованных с гибридными решетками РОС в импульсном режиме работы и установленных внутри охладителя Стирлинга, показаны на рис. 4. Изображение изготовленной и смонтированной ККЛ, полученное на сканирующем электронном микроскопе (СЭМ). чип на рис. 4а показывает несколько ККЛ разного размера, расположенных рядом. Представленные здесь результаты относятся к ККЛ размером 10×200 мкм×1,5 мм. Выбор длины резонатора сделан на основе оценки силы связи РОС и описан в Дополнительных примечаниях 1 и Дополнительных примечаниях 2, где показан смоделированный профиль плотности энергии по длине резонатора для выбранной длины. на дополнительном рисунке 1. Гибридная решетка РОС в виде щелей реализована в верхней металлической оболочке. На рис. 4б показан световой ток ( L – I ) кривые зависимости температуры радиатора, вольтамперная ( I – V ) кривая при 62 K, а также спектры как функция смещения при 62 K. при всех условиях смещения на частоте ~3,39 ТГц и работал до максимальной температуры 105 К. На рисунке 4c показана измеренная диаграмма направленности в дальней зоне, которая является однолепестковой и является характеристикой симметричного возбуждения моды для резонансной моды Структура ДФБ. Полумаксимальное расхождение по всей ширине составляет ~ 5 ° × 25 °, что близко соответствует результату полноволнового конечно-элементного моделирования резонатора РОС, как показано на дополнительном рисунке 1. Наконец, надежность схемы РОС при возбуждении Искомый режим, основанный на литографически заданной периодичности, показан на примере спектров генерации трех разных ККЛ с разными Λ показан на рис.
Гибридная решетка РОС в виде щелей реализована в верхней металлической оболочке. На рис. 4б показан световой ток ( L – I ) кривые зависимости температуры радиатора, вольтамперная ( I – V ) кривая при 62 K, а также спектры как функция смещения при 62 K. при всех условиях смещения на частоте ~3,39 ТГц и работал до максимальной температуры 105 К. На рисунке 4c показана измеренная диаграмма направленности в дальней зоне, которая является однолепестковой и является характеристикой симметричного возбуждения моды для резонансной моды Структура ДФБ. Полумаксимальное расхождение по всей ширине составляет ~ 5 ° × 25 °, что близко соответствует результату полноволнового конечно-элементного моделирования резонатора РОС, как показано на дополнительном рисунке 1. Наконец, надежность схемы РОС при возбуждении Искомый режим, основанный на литографически заданной периодичности, показан на примере спектров генерации трех разных ККЛ с разными Λ показан на рис. 4d. Все ККЛ показали одномодовый режим работы во всем динамическом диапазоне и шкалу частот генерации с Λ с эффективным показателем распространения n eff ~ 3,16 для управляемых мод. Это относительно низкое значение n eff подтверждает, что для этих ККЛ возбуждается верхняя краевая мода, как и было задумано.
4d. Все ККЛ показали одномодовый режим работы во всем динамическом диапазоне и шкалу частот генерации с Λ с эффективным показателем распространения n eff ~ 3,16 для управляемых мод. Это относительно низкое значение n eff подтверждает, что для этих ККЛ возбуждается верхняя краевая мода, как и было задумано.
Экспериментальные результаты. a Изображение, полученное с помощью сканирующего электронного микроскопа изготовленных терагерцовых ККЛ с гибридными решетками РОС, как на рис. 2а. б Вольт-амперные ( I – В ) и спектральные интенсивности (вставка) при различном электрическом смещении при температуре радиатора 62 K и вольтамперные характеристики при различных температурах, измеренные в импульсном режиме работы . Терагерцовая ККЛ имеет размеры 10 мкм × 200 мкм × 1,5 мм, период решетки Λ = 28 мкм и d / Λ = 3/8. c Диаграмма излучения в дальней зоне (оптическая интенсивность), измеренная при температуре 62 K, близкой к пиковому смещению (~405 A см −2 ) на расстоянии 40 мм от ККЛ в направлении нормали к поверхности.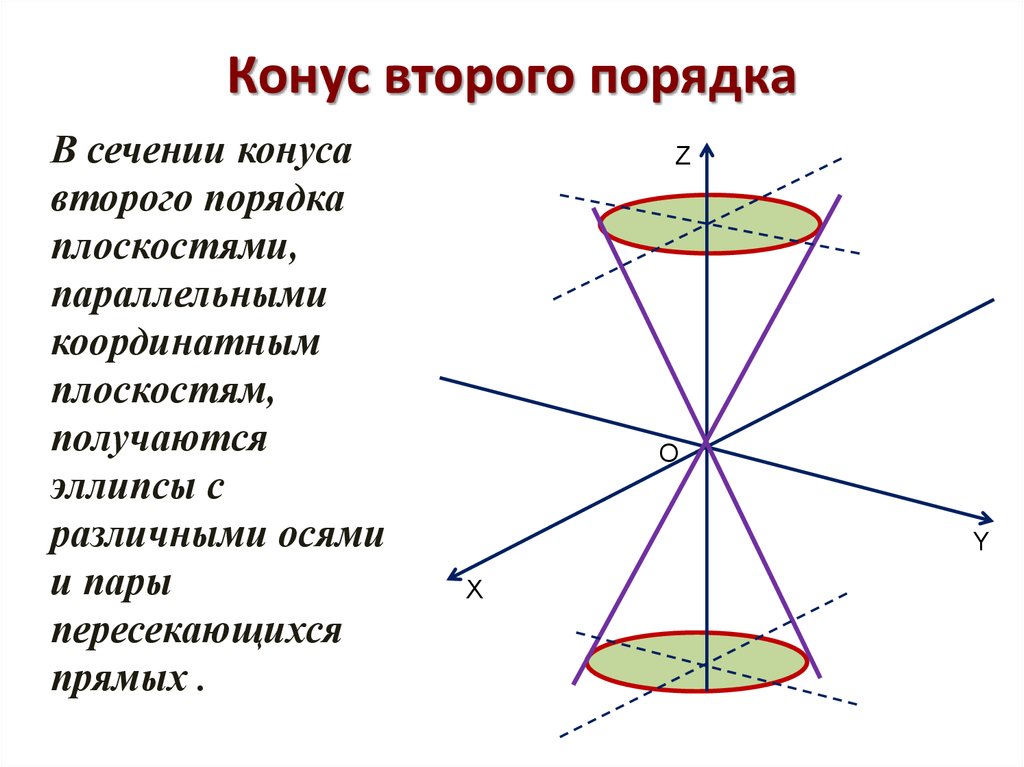 θ х и θ у — углы относительно нормали к поверхности вдоль продольного и поперечного размеров полости ККЛ соответственно. d Спектральные характеристики трех разных ККЛ, расположенных рядом друг с другом на пластине с разными периодами решетки, и d / Λ = 3/8 для каждого ККЛ
θ х и θ у — углы относительно нормали к поверхности вдоль продольного и поперечного размеров полости ККЛ соответственно. d Спектральные характеристики трех разных ККЛ, расположенных рядом друг с другом на пластине с разными периодами решетки, и d / Λ = 3/8 для каждого ККЛ
Изображение в натуральную величину
Основным вкладом этой работы является высокая радиационная эффективность гибридной схемы РОС. Пиковая выходная оптическая мощность 170 ± 3 мВт при 62 K была измерена для QCL, показанного на рис. 4b, что представляет собой мощность, обнаруженную измерителем мощности без каких-либо поправок на несовершенную эффективность сбора и оптические потери из окна криостата. Эффективность настенной розетки этого устройства составляет ~ 0,78%, а эффективность наклона 993 ± 15 мВт A −1 (дифференциальная квантовая эффективность 71 фотон/электрон) оценивается по наклону кривой 62 K L – I с использованием линейной аппроксимации кривой в диапазоне 20−80% диапазона смещения из ККЛ. Дифференциальная и наклонная эффективность на сегодняшний день являются самыми высокими из всех терагерцовых ККЛ, включая ККЛ Фабри – Перо с одноплазмонными волноводами, которые ранее демонстрировали наилучшие излучательные эффективности. Для сравнения, из той же пластины МЛЭ были изготовлены терагерцовые ККЛ с обычными решетками второго порядка. L – I данные одного такого репрезентативного QCL с аналогичными размерами резонатора показаны в дополнительном примечании 3, в котором достигнута пиковая выходная мощность 50 мВт, максимальная рабочая температура 129 K, эффективность сетевой розетки ~ 0,18. % и эффективность наклона ~80 мВт A −1 при 63 K. Хотя пиковые значения выходной мощности нельзя сравнивать, поскольку динамический диапазон генерации выше для обычного устройства DFB второго порядка, эффективность наклона для QCL с гибридный DFB более чем на порядок выше по сравнению с обычным QCL DFB второго порядка, что подтверждает сильное усиление излучения благодаря новому методу DFB.
Дифференциальная и наклонная эффективность на сегодняшний день являются самыми высокими из всех терагерцовых ККЛ, включая ККЛ Фабри – Перо с одноплазмонными волноводами, которые ранее демонстрировали наилучшие излучательные эффективности. Для сравнения, из той же пластины МЛЭ были изготовлены терагерцовые ККЛ с обычными решетками второго порядка. L – I данные одного такого репрезентативного QCL с аналогичными размерами резонатора показаны в дополнительном примечании 3, в котором достигнута пиковая выходная мощность 50 мВт, максимальная рабочая температура 129 K, эффективность сетевой розетки ~ 0,18. % и эффективность наклона ~80 мВт A −1 при 63 K. Хотя пиковые значения выходной мощности нельзя сравнивать, поскольку динамический диапазон генерации выше для обычного устройства DFB второго порядка, эффективность наклона для QCL с гибридный DFB более чем на порядок выше по сравнению с обычным QCL DFB второго порядка, что подтверждает сильное усиление излучения благодаря новому методу DFB. Однако следует отметить, что сравнение выходной мощности гибридного DFB с обычным DFB второго порядка не отражает в действительности улучшение эффективности вывода из-за того, что любое изменение граничного условия вблизи концов полостей приведет к значительно влияют на потери излучения обычного DFB второго порядка 18 . Поэтому данные L – I из ККЛ Фабри – Перо с размерами 10 мкм × 150 мкм × 1,5 мм также показаны в дополнительном примечании 4 для сравнения, которое показывает, что максимальная рабочая температура этой активной среды составляет 137 °С. K. Температурные характеристики этой активной среды относительно скромны по сравнению с современными ККЛ терагерцового диапазона, и, следовательно, ожидается значительное увеличение мощностных характеристик с более эффективной активной средой, которая может обеспечить больший динамический диапазон в генерации с высокой температурное исполнение. Чтобы еще больше раскрыть высокую производительность этого гибридного механизма РОС второго и четвертого порядка, сравнение этой схемы с градиентной фотонной структурой 9 , основанный на численном моделировании, представлен в дополнительном примечании 5.
Однако следует отметить, что сравнение выходной мощности гибридного DFB с обычным DFB второго порядка не отражает в действительности улучшение эффективности вывода из-за того, что любое изменение граничного условия вблизи концов полостей приведет к значительно влияют на потери излучения обычного DFB второго порядка 18 . Поэтому данные L – I из ККЛ Фабри – Перо с размерами 10 мкм × 150 мкм × 1,5 мм также показаны в дополнительном примечании 4 для сравнения, которое показывает, что максимальная рабочая температура этой активной среды составляет 137 °С. K. Температурные характеристики этой активной среды относительно скромны по сравнению с современными ККЛ терагерцового диапазона, и, следовательно, ожидается значительное увеличение мощностных характеристик с более эффективной активной средой, которая может обеспечить больший динамический диапазон в генерации с высокой температурное исполнение. Чтобы еще больше раскрыть высокую производительность этого гибридного механизма РОС второго и четвертого порядка, сравнение этой схемы с градиентной фотонной структурой 9 , основанный на численном моделировании, представлен в дополнительном примечании 5.
Обсуждение
В заключение, здесь мы описали новый метод РОС для значительного повышения эффективности излучения твердотельных лазеров с поверхностным излучением на основе широко используемого второго заказать брэгговские решетки. Показана гибридная РОС-решетка второго и четвертого порядков как эффективный способ возбуждения симметричной излучательной моды с большим радиационным выходом в однолепестковом пучке, который также проще в реализации по сравнению с существующими модификациями РОС второго порядка. решетки в литературе. Гибридная схема DFB реализована для терагерцовых QCL для реализации одномодового QCL с самой высокой на сегодняшний день выходной оптической мощностью (170 мВт). Рекордно высокая эффективность наклона (993 мВт A -1 ) и дифференциальная квантовая эффективность (71 фотон на электрон) также экспериментально продемонстрированы по сравнению со всеми ранее описанными в литературе терагерцовыми ККЛ (включая многомодовые ККЛ Фабри – Перо). Эти значения предполагают, что радиационная эффективность, реализованная для ККЛ, составляет примерно одну треть от максимально теоретически возможной при отсутствии каких-либо механизмов потерь. В принципе, гибридный метод РОС также должен быть применим к полупроводниковым лазерам в ближнем и среднем инфракрасном диапазоне для увеличения выходной мощности одномодовых лазеров с поверхностным излучением на этих длинах волн.
Эти значения предполагают, что радиационная эффективность, реализованная для ККЛ, составляет примерно одну треть от максимально теоретически возможной при отсутствии каких-либо механизмов потерь. В принципе, гибридный метод РОС также должен быть применим к полупроводниковым лазерам в ближнем и среднем инфракрасном диапазоне для увеличения выходной мощности одномодовых лазеров с поверхностным излучением на этих длинах волн.
Методы
Конечно-элементное моделирование
Все расчеты проводились с помощью COMSOL Multiphysics 4.4. Модуль электромагнитных волн, частотная область (ewfd) из каталога Optics был использован для расчета собственных мод различных типов лазерных структур DFB, показанных в этой статье. Чтобы получить точную информацию о потерях излучения, активная область моделируется как без потерь, а металл моделируется как идеальный электрический проводник, высоколегированный контактный слой, служащий поглощающими границами резонатора, реализуется с использованием комплексной диэлектрической проницаемости, вычисленной с использованием Модель Друде и идеально согласованный слой для поглощения граничных эхо-сигналов были приняты для покрытия всех границ. Конкретные детали моделирования как для 2D-, так и для 3D-моделирования такие же, как и в ссылке. 27 , и в этом случае расчетные потери представляют собой сумму потерь на поглощающих границах, а также из-за излучения (выходной связи). Анализируя собственные частоты и соответствующие им потери излучения, можно оценить частоту генерации, а также диаграммы направленности луча в дальней зоне.
Конкретные детали моделирования как для 2D-, так и для 3D-моделирования такие же, как и в ссылке. 27 , и в этом случае расчетные потери представляют собой сумму потерь на поглощающих границах, а также из-за излучения (выходной связи). Анализируя собственные частоты и соответствующие им потери излучения, можно оценить частоту генерации, а также диаграммы направленности луча в дальней зоне.
Материалы
Активная среда ТГц-ККЛ основана на трехямной резонансно-фононной конструкции с GaAs/Al 57/18,5/31/9/28,5/16,5 (начиная с барьера инжектора), где толщина выражена в монослоях (ML, 1 ML = 2,825 Å), и был выращен методом молекулярно-лучевой эпитаксии с 221 каскадным периодом, что приводит к общей толщине 10 мкм. Конструкция аналогична конструкции трехлуночных QCL в 28, 29 с небольшими изменениями для достижения пикового усиления, сосредоточенного вокруг частоты 3,3 ТГц. Сверхрешетка ККЛ имеет среднее легирование n 5,7e15 см −3 и окружена высоколегированными контактными слоями GaAs толщиной 0,1 мкм и 0,05 мкм, легированными на уровне 5e18 см −3 по обе стороны от сверхрешетки. Слой Al 0,50 Ga 0,50 толщиной 200 нм был выращен как слой, препятствующий травлению, предшествующий всей стопке.
Слой Al 0,50 Ga 0,50 толщиной 200 нм был выращен как слой, препятствующий травлению, предшествующий всей стопке.
Изготовление устройств
Металлические волноводы на основе Cu–Cu были изготовлены с использованием стандартной технологии термокомпрессионного соединения пластин. После приклеивания пластин и удаления подложки была использована литография с положительным резистом для селективного вытравливания высоколегированного слоя GaAs толщиной 0,1 мкм почти во всех местах, где может существовать верхняя металлическая оболочка на отдельных полостях, с помощью H 2 SO 4 :H 2 O 2 :H 2 O травитель в концентрации 1:8:80. Слой высоколегированного GaAs шириной 10 мкм под верхней металлической оболочкой был оставлен невытравленным в областях, близких как к продольной, так и к боковой граням, и служит продольной и поперечной поглощающей границей для обеспечения возбуждения желаемой моды как генерации с наименьшими потерями.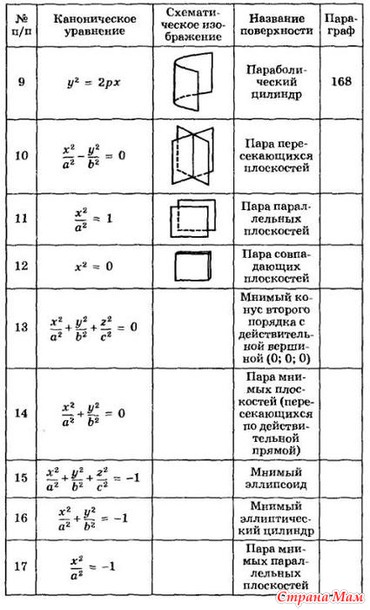 режим, как описано в ref. 27 . Последовательность Ti/Cu/Au была нанесена в виде верхних (20/200/100 нм) металлических слоев, в которых была реализована литография с обращением изображения для формирования металлических решеток. Полости гребня DFB затем обрабатывали влажным травлением с использованием H 9.0057 2 SO 4 :H 2 O 2 :H 2 O травитель в концентрации 1:8:80. Контакт Ti/Cu/Au (20/250/100 нм) также использовался в качестве контакта с обратной стороной для окончательно изготовленных чипов QCL для облегчения пайки. Перед нанесением тыльной стороны пластины подложка была механически отполирована до толщины 250 мкм для улучшения теплоотвода.
режим, как описано в ref. 27 . Последовательность Ti/Cu/Au была нанесена в виде верхних (20/200/100 нм) металлических слоев, в которых была реализована литография с обращением изображения для формирования металлических решеток. Полости гребня DFB затем обрабатывали влажным травлением с использованием H 9.0057 2 SO 4 :H 2 O 2 :H 2 O травитель в концентрации 1:8:80. Контакт Ti/Cu/Au (20/250/100 нм) также использовался в качестве контакта с обратной стороной для окончательно изготовленных чипов QCL для облегчения пайки. Перед нанесением тыльной стороны пластины подложка была механически отполирована до толщины 250 мкм для улучшения теплоотвода.
Экспериментальная характеристика
Во время измерений световой ток-напряжение импульс длительностью 300 нс с циклом сигнала 100 кГц (рабочий цикл 3,0 %) был выбран для управления устройствами, представленными в этой статье, на холодном каскаде Стирлинга. -кулер (работает при ~62 К). В тех же условиях абсолютная мощность была откалибрована с использованием измерителя мощности на термобатарее (номер модели: Scientech AC2500 с AC25H), как сообщается, без каких-либо поправок к обнаруженному сигналу. В этом процессе не использовалась никакая фокусирующая оптика, кроме окна из полиэтилена высокой плотности на криорефрижераторе. Представленные спектры были измерены с использованием инфракрасного спектрометра с преобразованием Фурье (BRUKER; VERTEX 70 v) при работе устройств на частоте 100 кГц с длительностью импульса 300 нс (рабочий цикл 3,0 %). Диаграммы луча в дальней зоне измерялись с помощью пироэлектрического детектора, установленного на 2D моторизованном сканирующем столике, который располагался на расстоянии 40 см от лазеров DFB, с максимальным углом сканирования ± 26,5° в обоих направлениях. Устройства работали вблизи пиковой мощности на частоте 100 кГц с длительностью импульса 300 нс и с электронной модуляцией последовательностями импульсов на частоте 1000 Гц (рабочий цикл 1,5 %).
В тех же условиях абсолютная мощность была откалибрована с использованием измерителя мощности на термобатарее (номер модели: Scientech AC2500 с AC25H), как сообщается, без каких-либо поправок к обнаруженному сигналу. В этом процессе не использовалась никакая фокусирующая оптика, кроме окна из полиэтилена высокой плотности на криорефрижераторе. Представленные спектры были измерены с использованием инфракрасного спектрометра с преобразованием Фурье (BRUKER; VERTEX 70 v) при работе устройств на частоте 100 кГц с длительностью импульса 300 нс (рабочий цикл 3,0 %). Диаграммы луча в дальней зоне измерялись с помощью пироэлектрического детектора, установленного на 2D моторизованном сканирующем столике, который располагался на расстоянии 40 см от лазеров DFB, с максимальным углом сканирования ± 26,5° в обоих направлениях. Устройства работали вблизи пиковой мощности на частоте 100 кГц с длительностью импульса 300 нс и с электронной модуляцией последовательностями импульсов на частоте 1000 Гц (рабочий цикл 1,5 %).
Доступность данных
Все соответствующие данные, относящиеся к численному моделированию, результаты экспериментов будут сохранены у Сушила Кумара в Университете Лихай, наборы данных доступны через соответствующего автора.
История изменений
14 мая 2018 г.
Первоначальная PDF-версия этой статьи содержала ошибку в уравнении 1. В знаменателе отсутствовало « Λ ». Это было исправлено в PDF-версии статьи. HTML-версия была правильной с момента публикации.
Ссылки
Казаринов Р. и Генри К. Лазеры с распределенной обратной связью второго порядка с выбором режима, обеспечиваемым радиационными потерями первого порядка. IEEE J. Quantum Electron. 22 , 144 (1985).
ОБЪЯВЛЕНИЕ Статья Google ученый
Нолл Р. Дж. и Макомбер С. Х. Анализ решетчатых лазеров с поверхностным излучением.
 IEEE J. Quantum Electron. 26 , 456 (1990).
IEEE J. Quantum Electron. 26 , 456 (1990).ОБЪЯВЛЕНИЕ Статья КАС Google ученый
Макомбер, С. Х. и др. Лазеры и массивы РОС с поверхностным излучением с изогнутой решеткой. Проц. SPIE 3001 , 42 (1997).
ОБЪЯВЛЕНИЕ Статья КАС Google ученый
Канскар, М. и др. Высокояркий 975-нм поверхностно-излучающий лазер с распределенной обратной связью и массивы. Проц. SPIE 7686 , 76860J (2010 г.).
Артикул КАС Google ученый
Li, S., Witjaksono, G., Macomber, S. & Botez, D. Анализ лазеров с распределенной обратной связью второго порядка с поверхностным излучением и фазовым сдвигом центральной решетки. IEEE J. Сел. Верхний. Квантовый электрон. 9 , 1153–1165 (2003).

Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Sigler, C. et al. Проектирование мощных однолепестковых квантово-каскадных лазеров с излучающей поверхностью решетки за счет плазмонно-усиленного поглощения антисимметричных мод. Заяв. физ. лат. 104 , 131108 (2014).
ОБЪЯВЛЕНИЕ Статья КАС Google ученый
Boyle, C. et al. Мощный квантово-каскадный лазер с поверхностным излучением, работающий в режиме симметричной решетки. Заяв. физ. лат. 108 , 121107 (2016).
ОБЪЯВЛЕНИЕ Статья КАС Google ученый
Wu, D. H. & Razeghi, M. Мощный квантово-каскадный кольцевой лазер с малой расходимостью, излучающий подложку, в непрерывном режиме. АПЛ Матер. 5 , 035505 (2017).
ОБЪЯВЛЕНИЕ Статья КАС Google ученый
«>Чжоу Д. и др. Прогресс в области мощных высокоярких VCSEL и приложений. Проц. SPIE 9381 , 93810B (2015).
Google ученый
Williams, B.S. Терагерцовые квантово-каскадные лазеры. Нац. Фотон. 1 , 517–525 (2007).
ОБЪЯВЛЕНИЕ Статья КАС Google ученый
Яо, Ю., Хоффман, А.Дж. и Гмахл, К.Ф. Квантовые каскадные лазеры среднего инфракрасного диапазона. Нац. Фотон. 6 , 432 (2012).
ОБЪЯВЛЕНИЕ Статья КАС Google ученый
«>Хофстеттер, Д., Файст, Дж., Бек, М. и Остерле, У. Лазеры с поверхностным излучением 10,1 мкм с квантовым каскадом и распределенной обратной связью. Заяв. физ. лат. 75 , 3769 (1999).
ОБЪЯВЛЕНИЕ Статья КАС Google ученый
Schrenk, W. et al. Квантово-каскадные лазеры с распределенной обратной связью с поверхностным излучением. Заявл. физ. лат. 77 , 2086 (2000).
ОБЪЯВЛЕНИЕ Статья КАС Google ученый
Демишел, О. и др. Поверхностные плазмонные фотонные структуры в терагерцовых квантово-каскадных лазерах.
 Опц. Экспресс 14 , 5335 (2006).
Опц. Экспресс 14 , 5335 (2006).ОБЪЯВЛЕНИЕ Статья пабмед Google ученый
Fan, J. A. et al. Квантово-каскадный лазер поверхностного излучения терагерцового диапазона с двойным металлическим волноводом. Опц. Экспресс 14 , 11672 (2006).
ОБЪЯВЛЕНИЕ Статья пабмед КАС Google ученый
Кумар, С. и др. Терагерцовые квантово-каскадные лазеры с поверхностным излучением и распределенной обратной связью в волноводах металл-металл. Опц. Экспресс 15 , 113 (2007).
ОБЪЯВЛЕНИЕ Статья пабмед КАС Google ученый
Lu, Q.Y., Bai, Y., Bandyopadhyay, N., Slivken, S. & Razeghi, M. 2,4 Вт при комнатной температуре, непрерывная работа квантово-каскадных лазеров с распределенной обратной связью.
 Заявл. физ. лат. 98 , 181106 (2011).
Заявл. физ. лат. 98 , 181106 (2011).ОБЪЯВЛЕНИЕ Статья КАС Google ученый
Лю, К.-В. и другие. Связанные гребенчатые волноводные квантово-каскадные массивы dfb, излучающие подложку. Фотон IEEE. Технол. лат. 29 , 213 (2017).
ОБЪЯВЛЕНИЕ Статья КАС Google ученый
Sirtori, C., Barbieri, S. & Collombelli, R. Волновая инженерия с квантовыми каскадными лазерами ТГц. Нац. Фотон 7 , 691 (2013).
ОБЪЯВЛЕНИЕ Статья КАС Google ученый
Лян Г., Лю Т. и Ван К. Дж. Последние разработки терагерцовых квантовых каскадных лазеров. IEEE J. Сел. Верхний. Квантовый электрон. 23 , 1200118 (2017).
Google ученый
«>Brandstetter, M. et al. Мощные терагерцовые квантово-каскадные лазеры с симметричными активными областями, связанными с пластинами. Заяв. физ. лат. 103 , 171113 (2013 г.).
ОБЪЯВЛЕНИЕ Статья КАС Google ученый
Ли, Л. и др. Многоваттные высокомощные квантовые каскадные лазеры терагерцового диапазона. Электрон. лат. 53 , 799 (2017).
Артикул КАС Google ученый
Малер, Л. и др. Мощное поверхностное излучение терагерцовых лазеров с распределенной обратной связью с двухщелевой элементарной ячейкой. Заяв. физ.
 лат. 96 , 1 (2010).
лат. 96 , 1 (2010).ОБЪЯВЛЕНИЕ Статья КАС Google ученый
Ву, К., Ханал, С., Рено, Дж. Л. и Кумар, С. Терагерцовый плазмонный лазер, излучающий сверхузким лучом. Optica 3 , 734 (2016).
Артикул КАС Google ученый
Кумар, С., Ху, К. и Рено, Дж. Л. 186 K работа терагерцовых квантово-каскадных лазеров на основе диагональной конструкции. Заяв. физ. лат. 94 , 131105 (2009 г.).
ОБЪЯВЛЕНИЕ Статья КАС Google ученый
Fathololoumi, S. et al. Терагерцовые квантовые каскадные лазеры, работающие до ~200 K, с оптимизированной силой генератора и улучшенным инжекционным туннелированием. Опц. Экспресс 20 , 3866 (2012).
ОБЪЯВЛЕНИЕ Статья пабмед КАС Google ученый
Сюй, Г. и др. Эффективное извлечение мощности в полупроводниковых лазерах с поверхностным излучением с использованием градиентных фотонных гетероструктур. Нац. Комм. 3 , 952 (2012).
Артикул КАС Google ученый
Витиелло М.С., Скалари Г., Уильямс Б. и Натале П.Д. Квантовые каскадные лазеры: 20 лет испытаний. Опц. Экспресс 23 , 5167 (2015).
ОБЪЯВЛЕНИЕ Статья пабмед КАС Google ученый
Сюй Л. и др. Метаповерхностный квантово-каскадный лазер с электрически переключаемой поляризацией. Optica 4 , 468 (2017).
Артикул КАС Google ученый
Скачать ссылки
Благодарности
Эта работа поддерживается Национальным научным фондом США в рамках грантов: ECCS 1351142, ECCS 1609168 и CMMI 1437168. Частично она была выполнена в Центре интегрированных нанотехнологий, Научного пользовательского центра, работающего для Министерства энергетики США (DOE) Office of Science. Sandia National Laboratories — это многопрофильная лаборатория, управляемая и управляемая National Technology and Engineering Solutions of Sandia, LLC., дочерней компанией Honeywell International, Inc., для Национального управления ядерной безопасности Министерства энергетики США по контракту DE-NA-0003525. .
Частично она была выполнена в Центре интегрированных нанотехнологий, Научного пользовательского центра, работающего для Министерства энергетики США (DOE) Office of Science. Sandia National Laboratories — это многопрофильная лаборатория, управляемая и управляемая National Technology and Engineering Solutions of Sandia, LLC., дочерней компанией Honeywell International, Inc., для Национального управления ядерной безопасности Министерства энергетики США по контракту DE-NA-0003525. .
Информация о авторе
Авторы и принадлежности
Департамент электрической и компьютерной инженерии, Университет Лихай, Вифлеем, Пенсильвания, 18015, США
Юань Джин, Лян Гао, Джи Чен, Чонгзао Ву и Сушиль Камар
49449449494494949494944944944944949445944594459445944594459595959595949н. Sandia National Laboratories, Center of Integrated Nanotechnologies, MS 1303, Albuquerque, NM, 87185, USA
John L. Reno
Авторы
- Yuan Jin
Посмотреть публикации авторов
Вы также можете искать этого автора в PubMed Google Scholar
- Liang Gao
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Ji Chen
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Chongzhao Wu
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- John L.
 Reno
RenoПросмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Sushil Kumar
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Contributions
S.K. придумал оригинальную идею гибридной решетки и руководил проектом. YJ развил идею с помощью анализа и моделирования, а также методов практической реализации. YJ и CW выполнили численное моделирование. Л.Г. и YJ изготовили устройства. Ю.Дж., Дж.К. и Л.Г. разработал экспериментальную установку и провел измерения. Дж.Л.Р. был ответственен за рост материала QCL методом молекулярно-лучевой эпитаксии. С.К. и YJ написали рукопись с участием всех других авторов.
Авторы переписки
Переписка с Юань Джин или Сушил Кумар.
Заявление об этике
Конкурирующие интересы
Авторы не заявляют об отсутствии конкурирующих интересов.
Дополнительная информация
Примечание издателя: Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Электронный дополнительный материал
Дополнительная информация (PDF 2087 kb)
Файл рецензирования (PDF 213 КБ)
Права и разрешения
Открытый доступ носителя или формата, при условии, что вы укажете первоначальных авторов и источник, предоставите ссылку на лицензию Creative Commons и укажите, были ли внесены изменения. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons для статьи, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.
Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.
Перепечатка и разрешения
Об этой статье
Дополнительная литература
Высокоэффективные полупроводниковые лазеры с поверхностным излучением, использующие квазикристаллические фотонные модели с распределенной обратной связью
- Симоне Биаско
- Андреа Чаватти
- Мириам С. Витиелло
Свет: наука и приложения (2020)
Перестраиваемые по частоте непрерывные случайные лазеры на терагерцовых частотах
- Симоне Биаско
- Харви Э.
 Бир
Бир - Мириам С. Витиелло
Свет: наука и приложения (2019)
Фотонные проволочные лазеры с фазовой синхронизацией за счет π-связи
- Али Халатпур
- Джон Л. Рино
- Цин Ху
Природа Фотоника (2019)
Комментарии
Отправляя комментарий, вы соглашаетесь соблюдать наши Условия и Правила сообщества. Если вы обнаружите что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неприемлемое.
Если вы обнаружите что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неприемлемое.
7.1 Линейные уравнения второго порядка. Расчет, том 3
Цели обучения
- 7.1.1 Знать однородные и неоднородные линейные дифференциальные уравнения.
- 7.1.2 Определить характеристическое уравнение однородного линейного уравнения.
- 7.1.3 Используйте корни характеристического уравнения, чтобы найти решение однородного линейного уравнения.
- 7.1.4 Решение начальных и краевых задач с линейными дифференциальными уравнениями.
При работе с дифференциальными уравнениями обычно цель состоит в том, чтобы найти решение. Другими словами, мы хотим найти функцию (или функции), удовлетворяющую дифференциальному уравнению. Техника, которую мы используем для нахождения этих решений, различается в зависимости от формы дифференциального уравнения, с которым мы работаем. Дифференциальные уравнения второго порядка имеют несколько важных характеристик, которые могут помочь нам определить, какой метод решения использовать. В этом разделе мы рассмотрим некоторые из этих характеристик и связанную с ними терминологию.
В этом разделе мы рассмотрим некоторые из этих характеристик и связанную с ними терминологию.
Однородные линейные уравнения
Рассмотрим дифференциальное уравнение второго порядка
xy″+2x2y′+5x3y=0.xy″+2x2y′+5x3y=0.
Обратите внимание, что и и их производные появляются в относительно простой форме. Они умножаются на функции x , но сами не возводятся ни в какие степени и не перемножаются вместе. Как обсуждалось во Введении в дифференциальные уравнения, уравнения первого порядка с подобными характеристиками называются линейными. То же самое относится и к уравнениям второго порядка. Также обратите внимание, что все члены в этом дифференциальном уравнении включают либо и или один из его производных. Нет условий, связанных только с функциями x . Такие уравнения, в которых каждый член содержит y или одну из его производных, называются однородными.
Не все дифференциальные уравнения однородны. Рассмотрим дифференциальное уравнение
xy″+2x2y′+5x3y=x2.xy″+2x2y′+5x3y=x2.
Член x2x2 справа от знака равенства не содержит y или любых его производных. Следовательно, это дифференциальное уравнение неоднородно.
Определение
Дифференциальное уравнение второго порядка является линейным, если его можно записать в виде
a2(x)y″+a1(x)y′+a0(x)y=r(x),a2(x)y ″+a1(x)y′+a0(x)y=r(x),
(7.1)
где a2(x),a2(x),a1(x),a1(x),a0( x),a0(x) и r(x)r(x) — вещественные функции, а a2(x)a2(x) не тождественно равен нулю. Если r(x)≡0r(x)≡0, другими словами, если r(x)=0r(x)=0 для каждого значения x , уравнение называется однородным линейным уравнением. Если r(x)≠0r(x)≠0 для некоторого значения x,x, уравнение называется неоднородным линейным уравнением.
СМИ
Посетите этот веб-сайт, чтобы узнать больше о линейных дифференциальных уравнениях второго порядка.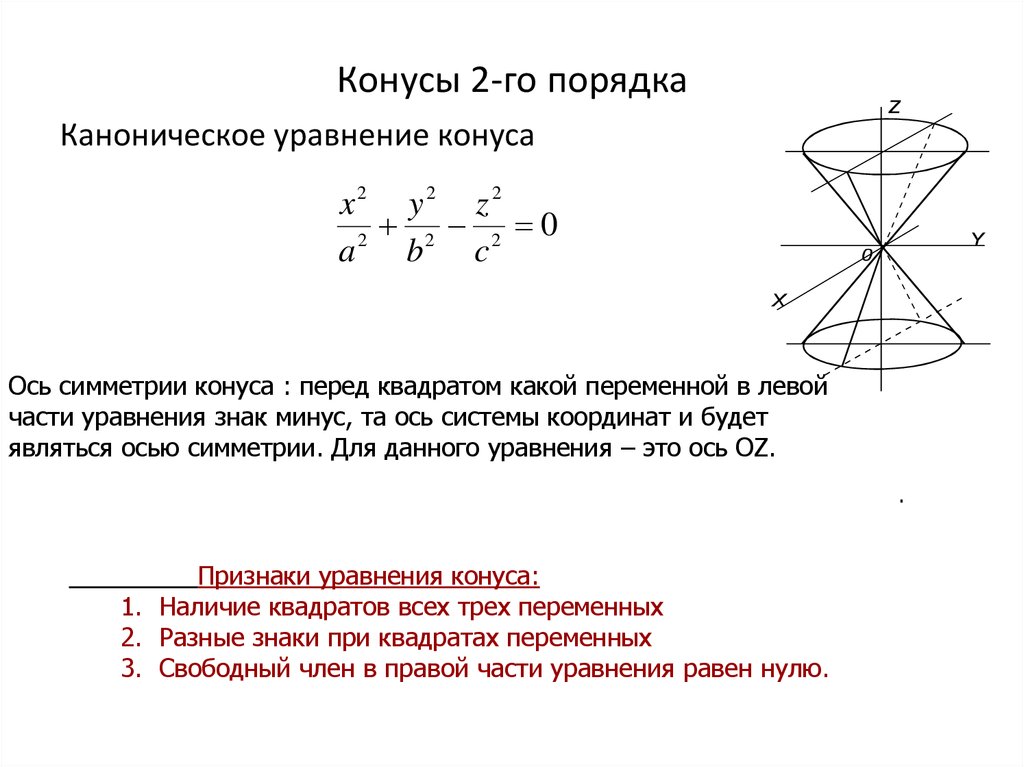
В линейных дифференциальных уравнениях yy и его производные можно возводить только в первую степень, и их нельзя умножать друг на друга. Члены, включающие y2y2 или y′y′, делают уравнение нелинейным. Функции yy и его производные, такие как sinysiny или ey′,ey′, аналогичным образом запрещены в линейных дифференциальных уравнениях.
Обратите внимание, что уравнения не всегда могут быть представлены в стандартной форме (форма, показанная в определении). Может быть полезно переписать их в такой форме, чтобы решить, являются ли они линейными или линейное уравнение однородным.
Пример 7.1
Классификация уравнений второго порядка
Классифицируйте каждое из следующих уравнений как линейное или нелинейное. Если уравнение линейное, определите далее, является ли оно однородным или неоднородным.
- у″+3x4y′+x2y2=x3y″+3x4y′+x2y2=x3
- (sinx)y″+(cosx)y′+3y=0(sinx)y″+(cosx)y′+3y=0
- 4t2x″+3txx′+4x=04t2x″+3txx′+4x=0
- 5y″+y=4x55y″+y=4×5
- (cosx)y″−siny′+(sinx)y−cosx=0(cosx)y″−siny′+(sinx)y−cosx=0
- 8ty″−6t2y′+4ty−3t2=08ty″−6t2y′+4ty−3t2=0
- sin(x2)y″−(cosx)y′+x2y=y′−3sin(x2)y″−(cosx)y′+x2y=y′−3
- y″+5xy′−3y=cosyy″+5xy′−3y=cosy
Решение
- Это уравнение нелинейно из-за члена y2y2.

- Это уравнение является линейным. Не существует члена, включающего степень или функцию от y, y, а все коэффициенты являются функциями от x.x. Уравнение уже записано в стандартной форме, а r(x)r(x) тождественно равно нулю, поэтому уравнение однородно.
- Это уравнение нелинейное. Обратите внимание, что в этом случае x — это зависимая переменная, а t — независимая переменная. Второй член включает произведение xx и x′,x′, поэтому уравнение нелинейно.
- Это уравнение является линейным. Поскольку r(x)=4×5,r(x)=4×5, уравнение неоднородно.
- Это уравнение нелинейно из-за члена siny′siny′.
- Это уравнение является линейным. Переписав его в стандартной форме, мы получим
8t2y″−6t2y′+4ty=3t2.8t2y″−6t2y′+4ty=3t2.
Имея стандартную форму уравнения, мы видим, что r(t)=3t2,r(t)=3t2, поэтому уравнение неоднородно. - Это уравнение выглядит как линейное, но для уверенности мы должны переписать его в стандартной форме.
 Получаем
Получаемsin(x2)y″−(cosx+1)y′+x2y=−3.sin(x2)y″−(cosx+1)y′+x2y=−3.
Это уравнение действительно линейное. При r(x)=−3,r(x)=−3 он неоднороден. - Это уравнение нелинейно из-за косикозиального члена.
СМИ
Посетите этот веб-сайт, на котором обсуждаются дифференциальные уравнения второго порядка.
Контрольно-пропускной пункт 7.1
Классифицируйте каждое из следующих уравнений как линейное или нелинейное. Если уравнение линейное, определите далее, является ли оно однородным или неоднородным.
- (у″)2−y′+8x3y=0(y″)2−y′+8x3y=0
- (sint)y″+cost−3ty′=0(sint)y″+cost−3ty′=0
Далее в этом разделе мы познакомимся с некоторыми методами решения определенных типов дифференциальных уравнений. Однако прежде чем мы перейдем к этому, давайте почувствуем, как ведут себя решения линейных дифференциальных уравнений. Во многих случаях решение дифференциальных уравнений зависит от обоснованных предположений о том, как может выглядеть решение.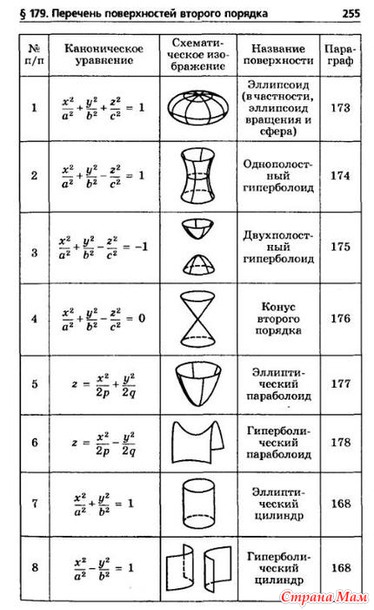 Будет полезно знать, как ведут себя различные типы решений.
Будет полезно знать, как ведут себя различные типы решений.
Пример 7.2
Проверка решения
Рассмотрим линейное однородное дифференциальное уравнение
x2y″−xy′−3y=0,x2y″−xy′−3y=0.
Глядя на это уравнение, обратите внимание, что функции коэффициентов являются многочленами, причем более высокие степени xx связаны с производными более высокого порядка от y.y. Покажите, что y=x3y=x3 является решением этого дифференциального уравнения.
Решение
Пусть y=x3.y=x3. Тогда y′=3x2y′=3×2 и y″=6x.y″=6x. Подставляя в дифференциальное уравнение, видим, что
x2y″−xy′−3y=x2(6x)−x(3×2)−3(x3)=6×3−3×3−3×3=0,x2y″−xy′−3y=x2(6x)−x(3×2) −3(x3)=6×3−3×3−3×3=0.
Контрольно-пропускной пункт 7.2
Показать, что y=2x2y=2×2 является решением дифференциального уравнения
12x2y″−xy′+y=0,12x2y″−xy′+y=0.
Хотя простое нахождение любого решения дифференциального уравнения важно, математики и инженеры часто хотят выйти за рамки поиска одного решения дифференциального уравнения и найти все решений дифференциального уравнения. Другими словами, мы хотим найти общее решение . Как и в случае с дифференциальными уравнениями первого порядка, общее решение (или семейство решений) дает все множество решений дифференциального уравнения. Важное различие между уравнениями первого и второго порядка заключается в том, что в случае уравнений второго порядка нам обычно нужно найти два разных решения уравнения, чтобы найти общее решение. Если мы находим два решения, то любая линейная комбинация этих решений также является решением. Сформулируем этот факт в виде следующей теоремы.
Другими словами, мы хотим найти общее решение . Как и в случае с дифференциальными уравнениями первого порядка, общее решение (или семейство решений) дает все множество решений дифференциального уравнения. Важное различие между уравнениями первого и второго порядка заключается в том, что в случае уравнений второго порядка нам обычно нужно найти два разных решения уравнения, чтобы найти общее решение. Если мы находим два решения, то любая линейная комбинация этих решений также является решением. Сформулируем этот факт в виде следующей теоремы.
Теорема 7.1
Принцип суперпозиции
Если y1(x)y1(x) и y2(x)y2(x) являются решениями линейного однородного дифференциального уравнения, то функция
y(x)=c1y1(x)+c2y2(x),y (x)=c1y1(x)+c2y2(x),
, где c1c1 и c2c2 — константы, также является решением.
Доказательство этой теоремы о принципе суперпозиции оставлено в качестве упражнения.
Пример 7.
 3
3Проверка принципа суперпозиции
Рассмотрим дифференциальное уравнение
y″−4y′−5y=0.y″−4y′−5y=0.
Учитывая, что e-xe-x и e5xe5x являются решениями этого дифференциального уравнения, покажите, что 4e-x+e5x4e-x+e5x является решением.
Решение
Имеем
y(x)=4e−x+e5x,soy′(x)=−4e−x+5e5xandy″(x)=4e−x+25e5x.y(x)=4e−x+e5x, soy'(x)=-4e-x+5e5xandy»(x)=4e-x+25e5x.
Тогда
y″−4y′−5y=(4e−x+25e5x)−4(−4e−x+5e5x)−5(4e−x+e5x)=4e−x+25e5x+16e−x− 20e5x−20e−x−5e5x=0.y″−4y′−5y=(4e−x+25e5x)−4(−4e−x+5e5x)−5(4e−x+e5x)=4e−x+25e5x +16e-x-20e5x-20e-x-5e5x=0.
Таким образом, y(x)=4e−x+e5xy(x)=4e−x+e5x является решением.
Контрольно-пропускной пункт 7.3
Рассмотрим дифференциальное уравнение
y″+5y′+6y=0.y″+5y′+6y=0.
Учитывая, что e-2xe-2x и e-3xe-3x являются решениями этого дифференциального уравнения, покажите, что 3e-2x+6e-3x3e-2x+6e-3x является решением.
К сожалению, чтобы найти общее решение дифференциального уравнения второго порядка, недостаточно найти любые два решения, а затем объединить их. Рассмотрим дифференциальное уравнение
х″+7x′+12x=0.x″+7x′+12x=0.
Оба e-3te-3t и 2e-3t2e-3t являются решениями (отметьте это). Однако x(t)=c1e−3t+c2(2e−3t)x(t)=c1e−3t+c2(2e−3t) — это , а не общее решение. Это выражение не учитывает все решения дифференциального уравнения. В частности, он не учитывает функцию e−4t,e−4t, которая также является решением дифференциального уравнения.
Оказывается, чтобы найти общее решение дифференциального уравнения второго порядка, нужно найти два линейно независимых решения. Мы определяем эту терминологию здесь.
Определение
Набор функций f1(x),f2(x),…,fn(x)f1(x),f2(x),…,fn(x) называется линейно зависимым, если существуют константы c1, c2,…cn,c1,c2,…cn, не все нули, такие, что c1f1(x)+c2f2(x)+⋯+cnfn(x)=0c1f1(x)+c2f2(x)+⋯+cnfn(x )=0 для всех x на интересующем интервале. Набор функций, который не является линейно зависимым, называется линейно независимым.
Набор функций, который не является линейно зависимым, называется линейно независимым.
В этой главе мы обычно проверяем наборы только из двух функций на линейную независимость, что позволяет нам упростить это определение. С практической точки зрения мы видим, что две функции линейно зависимы, если одна из них тождественно равна нулю или если они постоянно кратны друг другу.
Сначала покажем, что если функции удовлетворяют приведенным ранее условиям, то они линейно зависимы. Если одна из функций тождественно равна нулю, скажем, f2(x)≡0f2(x)≡0, то выбираем c1=0c1=0 и c2=1,c2=1, и выполняется условие линейной зависимости. Если, с другой стороны, ни f1(x)f1(x), ни f2(x)f2(x) тождественно равны нулю, но f1(x)=Cf2(x)f1(x)=Cf2(x) для некоторого постоянные C,C, затем выбирают c1=1Cc1=1C и c2=−1,c2=−1, и снова условие выполняется.
Далее мы показываем, что если две функции линейно зависимы, то либо одна из них тождественно равна нулю, либо они постоянно кратны друг другу. Предположим, что f1(x)f1(x) и f2(x)f2(x) линейно независимы. Тогда существуют константы c1c1 и c2,c2, отличные от нуля, такие, что
Предположим, что f1(x)f1(x) и f2(x)f2(x) линейно независимы. Тогда существуют константы c1c1 и c2,c2, отличные от нуля, такие, что
c1f1(x)+c2f2(x)=0c1f1(x)+c2f2(x)=0
для всех x на интересующем интервале. Тогда
c1f1(x)=−c2f2(x).c1f1(x)=−c2f2(x).
Теперь, поскольку мы заявили, что c1c1 и c2c2 не могут быть равны нулю, предположим, что c2≠0.c2≠0. Тогда возможны два случая: либо c1=0c1=0, либо c1≠0.c1≠0. Если c1=0,c1=0, то
0=-c2f2(x)0=f2(x),0=-c2f2(x)0=f2(x),
, поэтому одна из функций тождественно равна нулю. Теперь предположим, что c1≠0.c1≠0. Тогда
f1(x)=(−c2c1)f2(x)f1(x)=(−c2c1)f2(x)
и мы видим, что функции постоянно кратны друг другу.
Теорема 7.2
Линейная зависимость двух функций
Две функции, f1(x)f1(x) и f2(x),f2(x), называются линейно зависимыми, если одна из них тождественно равна нулю или если f1(x)=Cf2(x)f1 (x)=Cf2(x) для некоторой константы C и для всех x на интересующем интервале. Функции, которые не являются линейно зависимыми, называются линейно независимыми .
Функции, которые не являются линейно зависимыми, называются линейно независимыми .
Пример 7.4
Проверка на линейную зависимость
Определите, являются ли следующие пары функций линейно зависимыми или линейно независимыми.
- f1(x)=x2,f1(x)=x2,f2(x)=5x2f2(x)=5×2
- f1(x)=sinx,f1(x)=sinx,f2(x)=cosxf2(x)=cosx
- f1(x)=e3x,f1(x)=e3x,f2(x)=e−3xf2(x)=e−3x
- f1(x)=3x,f1(x)=3x,f2(x)=3x+1f2(x)=3x+1
Решение
- f2(x)=5f1(x),f2(x)=5f1(x), поэтому функции линейно зависимы.
- Не существует константы C такой, что f1(x)=Cf2(x),f1(x)=Cf2(x), поэтому функции линейно независимы.
- Не существует константы C такой, что f1(x)=Cf2(x),f1(x)=Cf2(x), поэтому функции линейно независимы. Пусть вас не смущает тот факт, что показатели степени постоянно кратны друг другу.
 С двумя экспоненциальными функциями, если показатели степени не равны, функции линейно независимы.
С двумя экспоненциальными функциями, если показатели степени не равны, функции линейно независимы. - Не существует константы C такой, что f1(x)=Cf2(x),f1(x)=Cf2(x), поэтому функции линейно независимы.
Контрольно-пропускной пункт 7.4
Определите, являются ли следующие пары функций линейно зависимыми или линейно независимыми: f1(x)=ex,f1(x)=ex,f2(x)=3e3x.f2(x)=3e3x.
Если мы можем найти два линейно независимых решения дифференциального уравнения второго порядка, то мы можем объединить их, чтобы найти общее решение. Этот результат формально сформулирован в следующей теореме.
Теорема 7.3
Общее решение однородного уравнения
Если y1(x)y1(x) и y2(x)y2(x) являются линейно независимыми решениями линейного однородного дифференциального уравнения второго порядка, то общее решение имеет вид
y(x)= c1y1(x)+c2y2(x),y(x)=c1y1(x)+c2y2(x),
, где c1c1 и c2c2 — константы.
Когда мы говорим, что семейство функций является общим решением дифференциального уравнения, мы имеем в виду, что (1) каждое выражение этой формы является решением и (2) каждое решение дифференциального уравнения может быть записано в такой форме, что делает эта теорема чрезвычайно мощная. Если мы можем найти два линейно независимых решения дифференциального уравнения, мы фактически нашли всех решений дифференциального уравнения — весьма примечательное утверждение. Доказательство этой теоремы выходит за рамки этого текста.
Пример 7,5
Написание общего решения
Если y1(t)=e3ty1(t)=e3t и y2(t)=e−3ty2(t)=e−3t являются решениями y″−9y=0,y″−9y =0, каково общее решение?
Решение
Обратите внимание, что y1y1 и y2y2 не являются постоянными кратными друг другу, поэтому они линейно независимы. Тогда общее решение дифференциального уравнения имеет вид y(t)=c1e3t+c2e−3t. y(t)=c1e3t+c2e−3t.
y(t)=c1e3t+c2e−3t.
Контрольно-пропускной пункт 7,5
Если y1(x)=e3xy1(x)=e3x и y2(x)=xe3xy2(x)=xe3x являются решениями y″−6y′+9y=0,y″−6y′+9y=0, то что это общее решение?
Уравнения второго порядка с постоянными коэффициентами
Теперь, когда мы лучше разобрались с линейными дифференциальными уравнениями, мы сосредоточимся на решении уравнений второго порядка вида
.ау″+by′+cy=0,ay″+by′+cy=0,
(7.2)
, где a,a,b,b и cc — константы.
Поскольку все коэффициенты являются константами, решения, вероятно, будут функциями, производные которых постоянно кратны самим себе. Нам нужно, чтобы все члены сокращались, и если при взятии производной вводится член, который не является постоянным кратным исходной функции, трудно увидеть, как этот член сокращается. Экспоненциальные функции имеют производные, которые постоянно кратны исходной функции, поэтому давайте посмотрим, что произойдет, когда мы попытаемся найти решение в форме y(x)=eλx,y(x)=eλx, где λλ (строчная греческая буква лямбда) какая-то постоянная.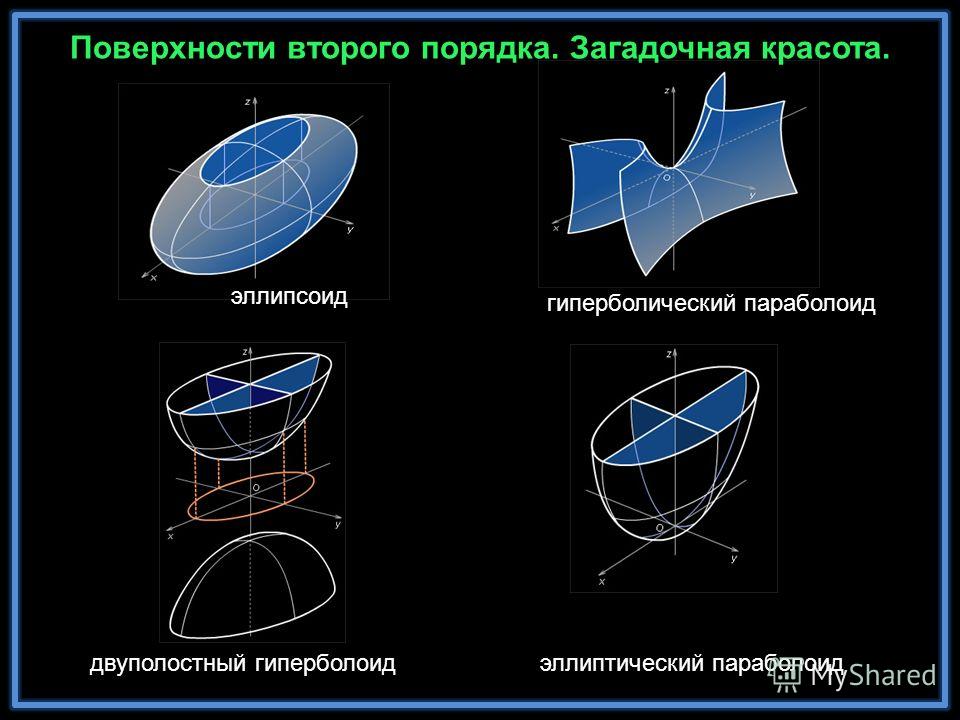
Если y(x)=eλx,y(x)=eλx, то y′(x)=λeλxy′(x)=λeλx и y″=λ2eλx.y″=λ2eλx. Подставляя эти выражения в уравнение 7.1, мы получаем
eλx(aλ2+bλ+c).
Поскольку eλxeλx никогда не равно нулю, это выражение может быть равно нулю для всех x , только если
aλ2+bλ+c=0.aλ2+bλ+c=0.
Мы называем это характеристическим уравнением дифференциального уравнения.
Определение
Характеристическое уравнение дифференциального уравнения ay″+by′+cy=0ay″+by′+cy=0 имеет вид aλ2+bλ+c=0.aλ2+bλ+c=0.
Характеристическое уравнение очень важно при поиске решений дифференциальных уравнений этой формы. Мы можем решить характеристическое уравнение либо с помощью факторизации, либо с помощью квадратичной формулы
λ=−b±b2−4ac2a.λ=−b±b2−4ac2a.
Это дает три случая. Характеристическое уравнение имеет (1) различные вещественные корни; (2) единственный повторяющийся действительный корень; или (3) комплексно-сопряженные корни. Рассмотрим каждый из этих случаев отдельно.
Рассмотрим каждый из этих случаев отдельно.
Различные действительные корни
Если характеристическое уравнение имеет различные действительные корни λ1λ1 и λ2,λ2, то eλ1xeλ1x и eλ2xeλ2x являются линейно независимыми решениями примера 7.1, и общее решение дается выражением
y(x)=c1eλ1x+c2eλ2x,y(x)=c1eλ1x+c2eλ2x,
, где c1c1 и c2c2 — константы.
Например, дифференциальное уравнение y″+9y′+14y=0y″+9y′+14y=0 имеет соответствующее характеристическое уравнение λ2+9λ+14=0,λ2+9λ+14=0. Это приводит к (λ+2)(λ+7)=0, (λ+2)(λ+7)=0, что имеет корни λ1=−2λ1=−2 и λ2=−7.λ2=−7. Следовательно, общее решение этого дифференциального уравнения есть
y(x)=c1e-2x+c2e-7x.y(x)=c1e-2x+c2e-7x.
Одиночный повторный реальный корень
Все немного сложнее, если характеристическое уравнение имеет повторяющийся действительный корень, λ.λ. В этом случае мы знаем, что eλxeλx является решением уравнения 7.1, но это только одно решение, и нам нужны два линейно независимых решения, чтобы определить общее решение. У нас может возникнуть соблазн попробовать функцию вида keλx,keλx, где k — некоторая константа, но она не будет линейно независимой от eλx.eλx. Поэтому попробуем xeλxxeλx в качестве второго решения. Во-первых, заметим, что по квадратичной формуле
У нас может возникнуть соблазн попробовать функцию вида keλx,keλx, где k — некоторая константа, но она не будет линейно независимой от eλx.eλx. Поэтому попробуем xeλxxeλx в качестве второго решения. Во-первых, заметим, что по квадратичной формуле
λ=−b±b2−4ac2a.λ=−b±b2−4ac2a.
Но λλ является повторяющимся корнем, поэтому b2−4ac=0b2−4ac=0 и λ=−b2a.λ=−b2a. Таким образом, если y=xeλx,y=xeλx, имеем
y′=eλx+λxeλxandy″=2λeλx+λ2xeλx.y′=eλx+λxeλxandy″=2λeλx+λ2xeλx.
Подставляя эти выражения в уравнение 7.1, мы видим, что
ay″+by′+cy=a(2λeλx+λ2xeλx)+b(eλx+λxeλx)+cxeλx=xeλx(aλ2+bλ+c)+eλx(2aλ+b)=xeλx(0)+eλx(2a( −b2a)+b)=0+eλx(0)=0.ay″+by′+cy=a(2λeλx+λ2xeλx)+b(eλx+λxeλx)+cxeλx=xeλx(aλ2+bλ+c)+eλx (2aλ+b)=xeλx(0)+eλx(2a(−b2a)+b)=0+eλx(0)=0.
Это показывает, что xeλxxeλx является решением уравнения 7.1. Поскольку eλxeλx и xeλxxeλx линейно независимы, когда характеристическое уравнение имеет повторяющийся корень λ,λ, общее решение уравнения 7. 1 дается выражением
1 дается выражением
y(x)=c1eλx+c2xeλx,y(x)=c1eλx+c2xeλx,
, где c1c1 и c2c2 — константы.
Например, дифференциальное уравнение y″+12y′+36y=0y″+12y′+36y=0 имеет соответствующее характеристическое уравнение λ2+12λ+36=0,λ2+12λ+36=0. Это приводит к (λ+6)2=0, (λ+6)2=0, что имеет повторяющийся корень λ=−6.λ=−6. Следовательно, общее решение этого дифференциального уравнения есть
y(x)=c1e-6x+c2xe-6x.y(x)=c1e-6x+c2xe-6x.
Комплексно-сопряженные корни
Третий случай, который мы должны рассмотреть, это когда b2−4ac<0.b2−4ac<0. В этом случае, когда мы применяем квадратную формулу, мы берем квадратный корень из отрицательного числа. Мы должны использовать мнимое число i=−1i=−1, чтобы найти корни, которые принимают форму λ1=α+βiλ1=α+βi и λ2=α−βi.λ2=α−βi. Комплексное число α+βiα+βi называется сопряженным числом числа α−βi.α−βi. Таким образом, мы видим, что при b2−4ac<0,b2−4ac<0 корни нашего характеристического уравнения всегда комплексно сопряжены.
Это создает нам небольшую проблему. Если мы будем следовать тому же процессу, который мы использовали для различных действительных корней, — используя корни характеристического уравнения в качестве коэффициентов в показателях показательных функций, — мы получим функции e(α+βi)xe(α+βi)x и e( α−βi)xe(α−βi)x в качестве наших решений. Однако есть проблемы с этим подходом. Во-первых, эти функции принимают комплексные (мнимые) значения, и полное обсуждение таких функций выходит за рамки данного текста. Во-вторых, даже если бы нам было удобно работать с комплексными функциями, в этом курсе мы не рассматриваем идею производной для таких функций. Итак, если возможно, мы хотели бы найти два линейно независимых действительных решений дифференциального уравнения. В целях этого развития мы собираемся манипулировать и дифференцировать функции e(α+βi)xe(α+βi)x и e(α−βi)xe(α−βi)x, как если бы они были функциями с действительным значением . Для этих конкретных функций этот подход допустим математически, но имейте в виду, что существуют другие случаи, когда функции комплексного значения не подчиняются тем же правилам, что и функции вещественного значения. Тем из вас, кто заинтересован в более подробном обсуждении функций комплексного значения, следует обратиться к тексту по комплексному анализу.
Тем из вас, кто заинтересован в более подробном обсуждении функций комплексного значения, следует обратиться к тексту по комплексному анализу.
Исходя из корней α±βiα±βi характеристического уравнения, функции e(α+βi)xe(α+βi)x и e(α−βi)xe(α−βi)x являются линейно независимыми решениями уравнения дифференциальное уравнение. и общее решение дано
y(x)=c1e(α+βi)x+c2e(α−βi)x.y(x)=c1e(α+βi)x+c2e(α−βi)x.
Используя разумный выбор для c1c1 и c2,c2, а также немного алгебраических манипуляций, мы можем найти два линейно независимых решения уравнения 7.1 с действительными значениями и выразить наше общее решение в этих терминах.
Ранее мы встречались с экспоненциальными функциями со сложными показателями. Одним из ключевых инструментов, которые мы использовали для выражения этих экспоненциальных функций через синусы и косинусы, была формула Эйлера, которая говорит нам, что
eiθ=cosθ+isinθeiθ=cosθ+isinθ
для всех действительных чисел θ.θ.
Возвращаясь к общему решению, имеем
.
y(x)=c1e(α+βi)x+c2e(α−βi)x=c1eαxeβix+c2eαxe−βix=eαx(c1eβix+c2e−βix).y(x)=c1e(α+βi)x+ c2e(α−βi)x=c1eαxeβix+c2eαxe−βix=eαx(c1eβix+c2e−βix).
Применяя формулу Эйлера вместе с тождествами cos(-x)=cosxcos(-x)=cosx и sin(-x)=-sinx,sin(-x)=-sinx, получаем
y(x)=eαx[c1(cosβx+isinβx)+c2(cos(−βx)+isin(−βx))]=eαx[(c1+c2)cosβx+(c1−c2)isinβx].y(x )=eαx[c1(cosβx+isinβx)+c2(cos(−βx)+isin(−βx))]=eαx[(c1+c2)cosβx+(c1−c2)isinβx].
Теперь, если мы выберем c1=c2=12,c1=c2=12, второй член равен нулю, и мы получим
y(x)=eαxcosβxy(x)=eαxcosβx
как действительное решение уравнения 7.1. Точно так же, если мы выберем c1=−i2c1=−i2 и c2=i2,c2=i2, первый член равен нулю, и мы получим
y(x)=eαxsinβxy(x)=eαxsinβx
в качестве второго, линейно независимого, действительного решения уравнения 7.1.
Исходя из этого, мы видим, что если характеристическое уравнение имеет комплексно-сопряженные корни α±βi,α±βi, то общее решение уравнения 7.1 дается выражением
y(x)=c1eαxcosβx+c2eαxsinβx=eαx(c1cosβx+c2sinβx),y(x)=c1eαxcosβx+c2eαxsinβx=eαx(c1cosβx+c2sinβx),
, где c1c1 и c2c2 — константы.
Например, дифференциальному уравнению y″−2y′+5y=0y″−2y′+5y=0 соответствует характеристическое уравнение λ2−2λ+5=0,λ2−2λ+5=0. По квадратичной формуле корни характеристического уравнения равны 1±2i.1±2i. Следовательно, общее решение этого дифференциального уравнения есть
y(x)=ex(c1cos2x+c2sin2x).y(x)=ex(c1cos2x+c2sin2x).
Сводка результатов
Мы можем решить линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами, найдя корни связанного характеристического уравнения. Форма общего решения меняется в зависимости от того, имеет ли характеристическое уравнение различные действительные корни; одиночный, повторяющийся действительный корень; или комплексно-сопряженные корни. Эти три случая приведены в Таблице 7.1.
| Корни характеристического уравнения | Общее решение дифференциального уравнения |
|---|---|
| Различные действительные корни, λ1λ1 и λ2λ2 | y(x)=c1eλ1x+c2eλ2xy(x)=c1eλ1x+c2eλ2x |
| Повторяющийся действительный корень, λλ | y(x)=c1eλx+c2xeλxy(x)=c1eλx+c2xeλx |
| Комплексно-сопряженные корни α±βiα±βi | y(x)=eαx(c1cosβx+c2sinβx)y(x)=eαx(c1cosβx+c2sinβx) |
Стол
7. 1
Краткое изложение случаев характеристического уравнения
1
Краткое изложение случаев характеристического уравнения
Стратегия решения проблем
Стратегия решения задач: использование характеристического уравнения для решения дифференциальных уравнений второго порядка с постоянными коэффициентами
- Запишите дифференциальное уравнение в виде ay″+by′+cy=0.ay″+by′+cy=0.
- Найдите соответствующее характеристическое уравнение aλ2+bλ+c=0.aλ2+bλ+c=0.
- Либо факторизируйте характеристическое уравнение, либо используйте квадратную формулу, чтобы найти корни.
- Определите форму общего решения на основе того, имеет ли характеристическое уравнение различные действительные корни; одиночный, повторяющийся действительный корень; или комплексно-сопряженные корни.
Пример 7.6
Решение уравнений второго порядка с постоянными коэффициентами
Найдите общее решение следующих дифференциальных уравнений. Дайте свои ответы как функции от x .
Дайте свои ответы как функции от x .
- у″+3y′−4y=0y″+3y′−4y=0
- y″+6y′+13y=0y″+6y′+13y=0
- y″+2y′+y=0y″+2y′+y=0
- y″−5y′=0y″−5y′=0
- г″−16y=0y″−16y=0
- г″+16г=0г″+16г=0
Решение
Обратите внимание, что все эти уравнения уже даны в стандартной форме (шаг 1).
- Характеристическое уравнение имеет вид λ2+3λ−4=0λ2+3λ−4=0 (шаг 2). Это приводит к (λ+4)(λ−1)=0, (λ+4)(λ−1)=0, поэтому корнями характеристического уравнения являются λ1=−4λ1=−4 и λ2=1λ2=1 (шаг 3). Тогда общее решение дифференциального уравнения имеет вид
y(x)=c1e−4x+c2ex(шаг 4).y(x)=c1e−4x+c2ex(шаг 4).
- Характеристическое уравнение имеет вид λ2+6λ+13=0λ2+6λ+13=0 (шаг 2). Применяя квадратную формулу, мы видим, что это уравнение имеет комплексно-сопряженные корни −3±2i−3±2i (шаг 3). Тогда общее решение дифференциального уравнения равно
y(t)=e−3t(c1cos2t+c2sin2t)(этап 4).
 y(t)=e−3t(c1cos2t+c2sin2t)(этап 4).
y(t)=e−3t(c1cos2t+c2sin2t)(этап 4). - Характеристическое уравнение имеет вид λ2+2λ+1=0λ2+2λ+1=0 (шаг 2). Это приводит к (λ+1)2=0, (λ+1)2=0, поэтому характеристическое уравнение имеет повторяющийся действительный корень λ=−1λ=−1 (шаг 3). Тогда общее решение дифференциального уравнения имеет вид
y(t)=c1e-t+c2te-t(шаг 4).y(t)=c1e-t+c2te-t(шаг 4).
- Характеристическое уравнение имеет вид λ2−5λλ2−5λ (шаг 2). Это приводит к λ(λ−5)=0,λ(λ−5)=0, поэтому корнями характеристического уравнения являются λ1=0λ1=0 и λ2=5λ2=5 (шаг 3). Обратите внимание, что e0x=e0=1,e0x=e0=1, поэтому наше первое решение — просто константа. Тогда общее решение дифференциального уравнения равно
y(x)=c1+c2e5x(шаг 4).y(x)=c1+c2e5x(шаг 4).
- Характеристическое уравнение имеет вид λ2−16=0λ2−16=0 (шаг 2). Это приводит к (λ+4)(λ−4)=0, (λ+4)(λ−4)=0, поэтому корнями характеристического уравнения являются λ1=4λ1=4 и λ2=−4λ2=−4 (шаг 3). Тогда общее решение дифференциального уравнения имеет вид
y(x)=c1e4x+c2e−4x(шаг 4).
 y(x)=c1e4x+c2e−4x(шаг 4).
y(x)=c1e4x+c2e−4x(шаг 4). - Характеристическое уравнение: λ2+16=0λ2+16=0 (шаг 2). Оно имеет комплексно-сопряженные корни ±4i±4i (шаг 3). Обратите внимание, что e0x=e0=1,e0x=e0=1, поэтому экспоненциальный член в нашем решении является просто константой. Тогда общее решение дифференциального уравнения равно
y(t)=c1cos4t+c2sin4t(этап 4).y(t)=c1cos4t+c2sin4t(этап 4).
Контрольно-пропускной пункт 7.6
Найдите общее решение следующих дифференциальных уравнений:
- y″−2y′+10y=0y″−2y′+10y=0
- y″+14y′+49y=0y″+14y′+49y=0
Начальные задачи и краевые задачи
До сих пор мы находили общие решения дифференциальных уравнений. Однако дифференциальные уравнения часто используются для описания физических систем, и человек, изучающий эту физическую систему, обычно знает что-то о состоянии этой системы в один или несколько моментов времени. Например, если дифференциальное уравнение с постоянными коэффициентами описывает, насколько сжат амортизатор мотоцикла, мы можем знать, что гонщик неподвижно сидит на своем мотоцикле в начале гонки, момент времени t=t0. t=t0. Это означает, что система находится в равновесии, поэтому y(t0)=0,y(t0)=0, а сжатие амортизатора не меняется, поэтому y′(t0)=0.y′(t0)=0 . Имея эти два начальных условия и общее решение дифференциального уравнения, мы можем найти конкретное решение дифференциального уравнения, удовлетворяющее обоим начальным условиям. Этот процесс известен как решение задачи с начальным значением . (Вспомните, что мы обсуждали начальные задачи во Введении в дифференциальные уравнения.) Обратите внимание, что уравнения второго порядка имеют две произвольные константы в общем решении, и поэтому нам нужны два начальных условия, чтобы найти решение начальной задачи.
t=t0. Это означает, что система находится в равновесии, поэтому y(t0)=0,y(t0)=0, а сжатие амортизатора не меняется, поэтому y′(t0)=0.y′(t0)=0 . Имея эти два начальных условия и общее решение дифференциального уравнения, мы можем найти конкретное решение дифференциального уравнения, удовлетворяющее обоим начальным условиям. Этот процесс известен как решение задачи с начальным значением . (Вспомните, что мы обсуждали начальные задачи во Введении в дифференциальные уравнения.) Обратите внимание, что уравнения второго порядка имеют две произвольные константы в общем решении, и поэтому нам нужны два начальных условия, чтобы найти решение начальной задачи.
Иногда мы знаем состояние системы в два разных момента времени. Например, мы можем знать y(t0)=y0y(t0)=y0 и y(t1)=y1.y(t1)=y1. Эти условия называются граничными условиями, а нахождение решения дифференциального уравнения, удовлетворяющего граничным условиям, называется решением краевой задачи.
Математики, ученые и инженеры заинтересованы в понимании условий, при которых начальная или краевая задача имеет единственное решение. Хотя полное рассмотрение этой темы выходит за рамки этого текста, полезно знать, что в контексте уравнений второго порядка с постоянными коэффициентами задачи с начальными значениями гарантированно имеют единственное решение, пока два заданы начальные условия. Однако краевые задачи ведут себя не так хорошо. Даже когда известны два граничных условия, мы можем столкнуться с краевыми задачами с единственными решениями, множеством решений или вообще без решения.
Пример 7.7
Решение начальной задачи
Решите следующую начальную задачу: y″+3y′−4y=0,y″+3y′−4y=0,y(0)=1,y(0)= 1,y′(0)=−9.y′(0)=−9.
Решение
Мы уже решили это дифференциальное уравнение в примере 7.6а. и нашел общее решение:
y(x)=c1e−4x+c2ex.y(x)=c1e−4x+c2ex.
Тогда
y′(x)=−4c1e−4x+c2ex. y′(x)=−4c1e−4x+c2ex.
y′(x)=−4c1e−4x+c2ex.
Когда x=0,x=0, мы имеем y(0)=c1+c2y(0)=c1+c2 и y′(0)=−4c1+c2.y′(0)=−4c1+c2 . Применяя начальные условия, имеем
c1+c2=1-4c1+c2=-9.c1+c2=1-4c1+c2=-9.
Тогда c1=1−c2.c1=1−c2. Подставляя это выражение во второе уравнение, мы видим, что
−4(1−c2)+c2=−9−4+4c2+c2=−95c2=−5c2=−1,−4(1−c2)+c2 =−9−4+4c2+c2=−95c2=−5c2=−1.
Итак, c1=2c1=2 и решение задачи с начальными значениями равно
y(x)=2e−4x−ex.y(x)=2e−4x−ex.
Контрольно-пропускной пункт 7.7
Решить начальную задачу y″−3y′−10y=0,y″−3y′−10y=0,y(0)=0,y(0)=0,y′(0)=7. у'(0)=7.
Пример 7,8
Решение задачи с начальными значениями и построение графика решения
Решите следующую задачу с начальными значениями и начертите решение:
y″+6y′+13y=0,y(0)=0,y′(0) =2y″+6y′+13y=0,y(0)=0,y′(0)=2
Решение
Мы уже решили это дифференциальное уравнение в примере 7. 6б. и нашел общее решение:
6б. и нашел общее решение:
y(x)=e−3x(c1cos2x+c2sin2x).y(x)=e−3x(c1cos2x+c2sin2x).
Тогда
y′(x)=e−3x(−2c1sin2x+2c2cos2x)−3e−3x(c1cos2x+c2sin2x).y′(x)=e−3x(−2c1sin2x+2c2cos2x)−3e−3x( c1cos2x+c2sin2x).
Когда x=0,x=0, имеем y(0)=c1y(0)=c1 и y′(0)=2c2−3c1.y′(0)=2c2−3c1. Применяя начальные условия, получаем
c1=0−3c1+2c2=2.c1=0−3c1+2c2=2.
Таким образом, c1=0,c1=0,c2=1,c2=1, и решение задачи с начальными значениями показано на следующем графике.
y=e-3xsin2x.y=e-3xsin2x.
Контрольно-пропускной пункт 7,8
Решите следующую задачу с начальными значениями и нарисуйте решение: y″−2y′+10y=0,y(0)=2,y′(0)=−1y″−2y′+10y=0,y( 0)=2,y′(0)=−1
Пример 7,9
Задача с начальными значениями Представление системы пружина-масса
Следующая задача с начальными значениями моделирует положение объекта с массой, прикрепленной к пружине. Пружинно-массовые системы подробно рассматриваются в приложениях. Решение дифференциального уравнения дает положение массы относительно нейтрального (равновесного) положения (в метрах) в любой момент времени. (Обратите внимание, что для систем пружинных масс этого типа принято определять направление вниз как положительное.)
Решение дифференциального уравнения дает положение массы относительно нейтрального (равновесного) положения (в метрах) в любой момент времени. (Обратите внимание, что для систем пружинных масс этого типа принято определять направление вниз как положительное.)
y″+2y′+y=0,y(0)=1,y′(0)=0y″+2y′+y=0,y(0)=1,y′(0)=0
Решите задачу с начальными значениями и нарисуйте решение. Каково положение массы в момент времени t=2t=2 сек? С какой скоростью движется груз в момент времени t=1t=1 сек? В каком направлении?
Решение
В примере 7.6c. мы нашли общее решение этого дифференциального уравнения как
y(t)=c1e-t+c2te-t.y(t)=c1e-t+c2te-t.
Тогда
y′(t)=−c1e−t+c2(−te−t+e−t).y′(t)=−c1e−t+c2(−te−t+e−t) .
При t=0,t=0 имеем y(0)=c1y(0)=c1 и y′(0)=−c1+c2.y′(0)=−c1+c2. Применяя начальные условия, получаем
c1=1−c1+c2=0.c1=1−c1+c2=0.
Таким образом, c1=1,c1=1,c2=1,c2=1, и решение начальной задачи равно
y(t)=e−t+te−t. y(t)=e−t + тэ-т.
y(t)=e−t + тэ-т.
Это решение представлено на следующем графике. В момент времени t=2,t=2 масса находится в положении y(2)=e−2+2e−2=3e−2≈0,406y(2)=e−2+2e−2=3e−2≈ 0,406 м ниже равновесия.
Чтобы вычислить скорость в момент времени t=1,t=1, нам нужно найти производную. Имеем y(t)=e−t+te−t,y(t)=e−t+te−t, поэтому
y'(t)=-e-t+e-t-te-t=-te-t.y'(t)=-e-t+e-t-te-t=-te-t.
Тогда y′(1)=−e−1≈−0,3679.y′(1)=−e−1≈−0,3679. В момент времени t=1,t=1 масса движется вверх со скоростью 0,3679 м/сек.
Контрольно-пропускной пункт 7,9
Предположим, что следующая начальная задача моделирует положение (в футах) массы в системе пружина-масса в любой момент времени. Решите задачу с начальным значением и нарисуйте решение. Каково положение массы в момент времени t=0,3t=0,3 сек? С какой скоростью он движется в момент времени t=0,1t=0,1 с? В каком направлении?
y″+14y′+49y=0,y(0)=0,y′(0)=1y″+14y′+49y=0,y(0)=0,y′(0)=1
Пример 7.10
Решение краевой задачи
В примере 7. 6f. мы решили дифференциальное уравнение y″+16y=0y″+16y=0 и нашли общее решение: y(t)=c1cos4t+c2sin4t.y(t)=c1cos4t+c2sin4t. Если возможно, решите краевую задачу при следующих граничных условиях:
6f. мы решили дифференциальное уравнение y″+16y=0y″+16y=0 и нашли общее решение: y(t)=c1cos4t+c2sin4t.y(t)=c1cos4t+c2sin4t. Если возможно, решите краевую задачу при следующих граничных условиях:
- y(0)=0,y(0)=0,y(π4)=0y(π4)=0
- у(0)=1,у(0)=1,у(π8)=0у(π8)=0
- у(π8)=0,у(π8)=0,у(3π8)=2у(3π8)=2
Решение
Имеем
y(x)=c1cos4t+c2sin4t.y(x)=c1cos4t+c2sin4t.
- Применяя приведенное здесь первое граничное условие, мы получаем y(0)=c1=0.y(0)=c1=0. Таким образом, решение имеет вид y(t)=c2sin4t.y(t)=c2sin4t. Однако, когда мы применяем второе граничное условие, мы получаем y(π4)=c2sin(4(π4))=c2sinπ=0y(π4)=c2sin(4(π4))=c2sinπ=0 для всех значений c2.c2 . Граничных условий недостаточно для определения значения c2,c2, поэтому эта краевая задача имеет бесконечно много решений. Таким образом, y(t)=c2sin4ty(t)=c2sin4t является решением для любого значения c2.c2.
- Применяя первое граничное условие, данное здесь, мы получаем y(0)=c1=1.
 y(0)=c1=1. Применение второго граничного условия дает y(π8)=c2=0,y(π8)=c2=0, поэтому c2=0.c2=0. В этом случае у нас есть единственное решение: y(t)=cos4t.y(t)=cos4t.
y(0)=c1=1. Применение второго граничного условия дает y(π8)=c2=0,y(π8)=c2=0, поэтому c2=0.c2=0. В этом случае у нас есть единственное решение: y(t)=cos4t.y(t)=cos4t. - Применяя первое граничное условие, данное здесь, мы получаем y(π8)=c2=0.y(π8)=c2=0. Однако применение второго граничного условия дает y(3π8)=−c2=2,y(3π8)=−c2=2, поэтому c2=−2.c2=−2. У нас не может быть c2=0=−2,c2=0=−2, поэтому эта краевая задача не имеет решения.
Раздел 7.1 Упражнения
Классифицируйте каждое из следующих уравнений как линейное или нелинейное. Если уравнение линейное, определить, является ли оно однородным или неоднородным.
1.
x3y″+(x−1)y′−8y=0x3y″+(x−1)y′−8y=0
2.
(1+y2)y″+xy′−3y=cosx(1+y2)y″+xy′−3y=cosx
3.
ху″+eyy′=xxy″+eyy′=x
4.
у″+4xy′−8xy=5×2+1y″+4xy′−8xy=5×2+1
5.
y″+(sinx)y′−xy=4yy″+(sinx)y′−xy=4y
6.
y″+(x+3y)y′=0y″+(x+3y)y′=0
Для каждой из следующих задач проверьте, что заданная функция является решением дифференциального уравнения. Используйте графическую утилиту для построения графиков конкретных решений для нескольких значений c 1 и c 2 . Что общего в решениях?
7.
[T] y″+2y′−3y=0;y″+2y′−3y=0;y(x)=c1ex+c2e−3xy(x)=c1ex+c2e−3x
8.
[T] x2y″−2y−3×2+1=0;x2y″−2y−3×2+1=0;y(x)=c1x2+c2x−1+x2ln(x)+12y(x)= c1x2+c2x−1+x2ln(x)+12
9.
[T] y″+14y′+49y=0;y″+14y′+49y=0;y(x)=c1e−7x+c2xe−7xy(x)=c1e−7x+c2xe−7x
10.
[T] 6y″−49y′+8y=0;6y″−49y′+8y=0;y(x)=c1ex/6+c2e8xy(x)=c1ex/6+c2e8x
Найти общее решение линейного дифференциального уравнения.
11.
у″−3y′−10y=0y″−3y′−10y=0
12.
у″−7y′+12y=0y″−7y′+12y=0
13.
y″+4y′+4y=0y″+4y′+4y=0
14.
4y″−12y′+9y=04y″−12y′+9y=0
15.
2y″−3y′−5y=02y″−3y′−5y=0
16.
3y″−14y′+8y=03y″−14y′+8y=0
17.
y″+y′+y=0y″+y′+y=0
18.
5y″+2y′+4y=05y″+2y′+4y=0
19.
у″−121y=0y″−121y=0
20.
8y″+14y′−15y=08y″+14y′−15y=0
21.
у″+81у=0у″+81у=0
22.
y″−y′+11y=0y″−y′+11y=0
23.
2г″=02г″=0
24.
у″−6y′+9y=0y″−6y′+9y=0
25.
3y″−2y′−7y=03y″−2y′−7y=0
26.
4y″−10y′=04y″−10y′=0
27.
36d2ydx2+12dydx+y=036d2ydx2+12dydx+y=0
28.
25d2ydx2−80dydx+64y=025d2ydx2−80dydx+64y=0
29.
d2ydx2-9dydx=0d2ydx2-9dydx=0
30.
4d2ydx2+8y=04d2ydx2+8y=0
Решить задачу с начальным значением.
31.
y″+5y′+6y=0,y(0)=0,y′(0)=−2y″+5y′+6y=0,y(0)=0,y′(0)=−2
32.
y″+2y′−8y=0,y(0)=5,y′(0)=4y″+2y′−8y=0,y(0)=5,y′(0)=4
33.
y″+4y=0,y(0)=3,y′(0)=10y″+4y=0,y(0)=3,y′(0)=10
34.
y″−18y′+81y=0,y(0)=1,y′(0)=5y″−18y′+81y=0,y(0)=1,y′(0)=5
35.
y″−y′−30y=0,y(0)=1,y′(0)=−16y″−y′−30y=0,y(0)=1,y′(0)=−16
36.
4y″+4y′−8y=0,y(0)=2,y′(0)=14y″+4y′−8y=0,y(0)=2,y′(0)=1
37.
25y″+10y′+y=0,y(0)=2,y′(0)=125y″+10y′+y=0,y(0)=2,y′(0)=1
38.
y″+y=0,y(π)=1,y′(π)=−5y″+y=0,y(π)=1,y′(π)=−5
Решите краевую задачу, если это возможно.
39.
y″+y′−42y=0,y(0)=0,y(1)=2y″+y′−42y=0,y(0)=0,y(1)=2
40.
9y″+y=0,y(3π2)=6,y(0)=−89y″+y=0,y(3π2)=6,y(0)=−8
41.
y″+10y′+34y=0,y(0)=6,y(π)=2y″+10y′+34y=0,y(0)=6,y(π)=2
42.
y″+7y′−60y=0,y(0)=4,y(2)=0y″+7y′−60y=0,y(0)=4,y(2)=0
43.
y″−4y′+4y=0,y(0)=2,y(1)=−1y″−4y′+4y=0,y(0)=2,y(1)=−1
44.
y″−5y′=0,y(0)=3,y(−1)=2y″−5y′=0,y(0)=3,y(−1)=2
45.
y″+9y=0,y(0)=4,y(π3)=−4y″+9у=0,у(0)=4,у(π3)=-4
46.
4y″+25y=0,y(0)=2,y(2π)=−24y″+25y=0,y(0)=2,y(2π)=−2
47.
Найдите дифференциальное уравнение с общим решением y=c1ex/5+c2e−4x.y=c1ex/5+c2e−4x.
48.
Найдите дифференциальное уравнение с общим решением y=c1ex+c2e-4x/3.y=c1ex+c2e-4x/3.
Для каждого из следующих дифференциальных уравнений:
- Решить задачу с начальным значением.
- [T] Используйте графическую утилиту для построения графика конкретного решения.
49.
y″+64y=0;y(0)=3,y′(0)=16y″+64y=0;y(0)=3,y′(0)=16
50.
y″−2y′+10y=0y(0)=1,y′(0)=13y″−2y′+10y=0y(0)=1,y′(0)=13
51.
y″+5y′+15y=0y(0)=−2,y′(0)=7y″+5y′+15y=0y(0)=−2,y′(0)=7
52.
(Принцип суперпозиции) Докажите, что если y1(x)y1(x) и y2(x)y2(x) являются решениями линейного однородного дифференциального уравнения, то y″+p(x)y′+q(x) y=0,y″+p(x)y′+q(x)y=0, то функция y(x)=c1y1(x)+c2y2(x),y(x)=c1y1(x)+ c2y2(x), где c1c1 и c2c2 — константы, также является решением.
53.
Докажите, что если a, b, и c положительные константы, то все решения линейного дифференциального уравнения второго порядка ay″+by′+cy=0ay″+by′+cy=0 стремятся к нулю при равенстве х→∞.х→∞. ( Подсказка: Рассмотрим три случая: два различных корня, повторяющиеся действительные корни и комплексно-сопряженные корни.)
Прочный чехол BlackBelt™ 2-й степени для Surface™ Pro | Прочный чехол для планшета и iPad | Прочный чехол Surface
Прочный чехол BlackBelt™ 2-й степени для Surface™ Pro | Прочный чехол для планшета и iPad | Прочный корпус | Кенсингтон Перейти к содержанию Перейти к нижнему колонтитулу Чтобы просмотреть контент, относящийся к вашему местоположению, вернитесь в страну или регион, соответствующие вашему местоположению.
Перейти на сайт моей страны
Аксессуары
Значок шевронаХарактеристики
Значок шевронаРазработан исключительно для Surface Pro
Создан в сотрудничестве с Microsoft для исключительного качества, формы, подгонки и функциональности.
Армейская защита от падений и протирания
Готов ко всему, этот чехол соответствует стандарту MIL-STD-810H Method 504.3 «Загрязнение жидкостями» и испытаниям на падение MIL-STD-810G.
Тросовый замок Совместимость
Может закрываться кенсингтонским ключом или кодовым замком — от изобретателей компьютерных тросовых замков.
Саморегулирующийся наручный ремешок
Наручный ремешок обеспечивает надежный захват во время использования и убирается, когда он не используется, позволяя устройству лежать ровно и устойчиво.
Отверстие для подставки
Позволяет полностью использовать встроенную подставку Surface.
Держатель ручки и шнурок
Удобно закрепляет и хранит ручку Surface.
Держатель клавиатуры и ремешок TypeCover
Защищает клавиатуру во время использования и обеспечивает ее защиту и чистоту.
Правительственные/TAA-совместимые
Для использования в учреждениях и организациях федерального правительства США.
Разработанный специально для Surface Pro прочный чехол BlackBelt™ 2-й степени для Surface™ Pro — это идеальный чехол для защиты вашего Surface Pro. Он имеет защиту от падений военного уровня, совместимость с тросовым замком и двухлетнюю гарантию. Другие функции включают в себя саморегулирующийся ремешок, который позволяет устройству лежать ровно, держатель ручки и троса, открывающуюся подставку, держатель клавиатуры, ремешок TypeCover и соответствие требованиям TAA.
- *Несовместимо с Surface Pro 8
- Разработан специально для Surface Pro и создан в сотрудничестве с Microsoft для обеспечения исключительного качества, формы, посадки и функциональности.
- Готов ко всему, этот корпус соответствует стандарту MIL-STD-810H Method 504.3 «Загрязнение жидкостями» и испытанию на падение MIL-STD-810G.
- Совместим с тросовым замком, поэтому устройство и корпус можно защитить с помощью кенсингтонского замка или кодового замка — от изобретателей компьютерных тросовых замков.
- Саморегулирующийся наручный ремешок обеспечивает надежный захват во время использования и убирается, когда он не используется, позволяя устройству лежать ровно и устойчиво.
- Открытие подставки позволяет полностью использовать встроенную подставку Surface.

- Держатель для пера и ремешок удобно фиксируют и хранят ручку Surface.
- Держатель клавиатуры и ремешок TypeCover защищают клавиатуру во время использования и помогают защитить ее и сохранить в чистоте.
- Соответствует требованиям правительства/TAA, для использования в учреждениях и организациях федерального правительства США.
Технические характеристики изделия
Значок шевронаСоответствует ТАА
Да
сертифицирован для
Предназначен для Microsoft Surface
Цвет
Черный
Гарантия
2 года
Совместимость устройств
Surface Pro 7, Surface Pro 6, Surface Pro 5, Surface Pro 4, Surface Pro 7+
Устройство чтения смарт-карт (CAC)
№
Военный стандарт
Испытание на падение MIL-STD-810G, метод MIL-STD-810H 504.



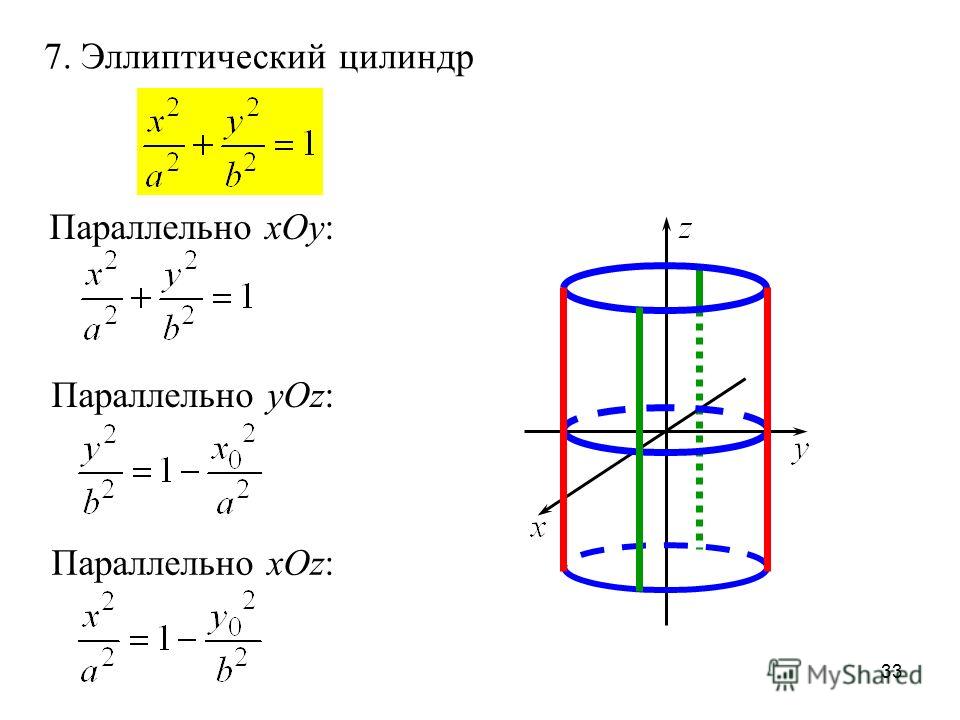
 (Изображения поверхностей
2-го порядка смотреть в учебнике геометрии
часть I, глава IX.)
(Изображения поверхностей
2-го порядка смотреть в учебнике геометрии
часть I, глава IX.)
 IEEE J. Quantum Electron. 26 , 456 (1990).
IEEE J. Quantum Electron. 26 , 456 (1990).
 Опц. Экспресс 14 , 5335 (2006).
Опц. Экспресс 14 , 5335 (2006). Заявл. физ. лат. 98 , 181106 (2011).
Заявл. физ. лат. 98 , 181106 (2011). лат. 96 , 1 (2010).
лат. 96 , 1 (2010).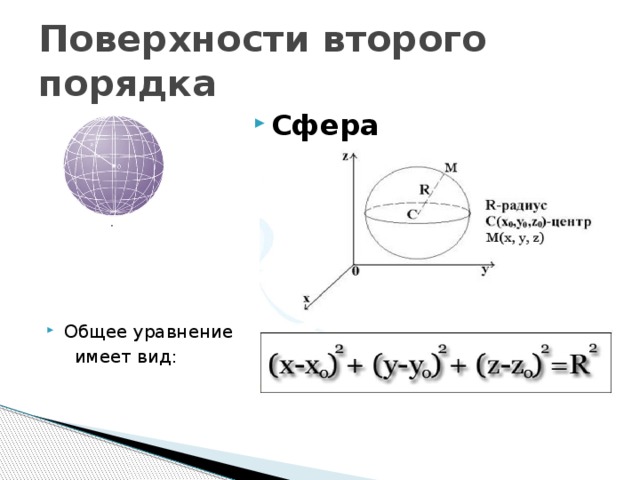 Reno
Reno Бир
Бир
 Получаем
Получаем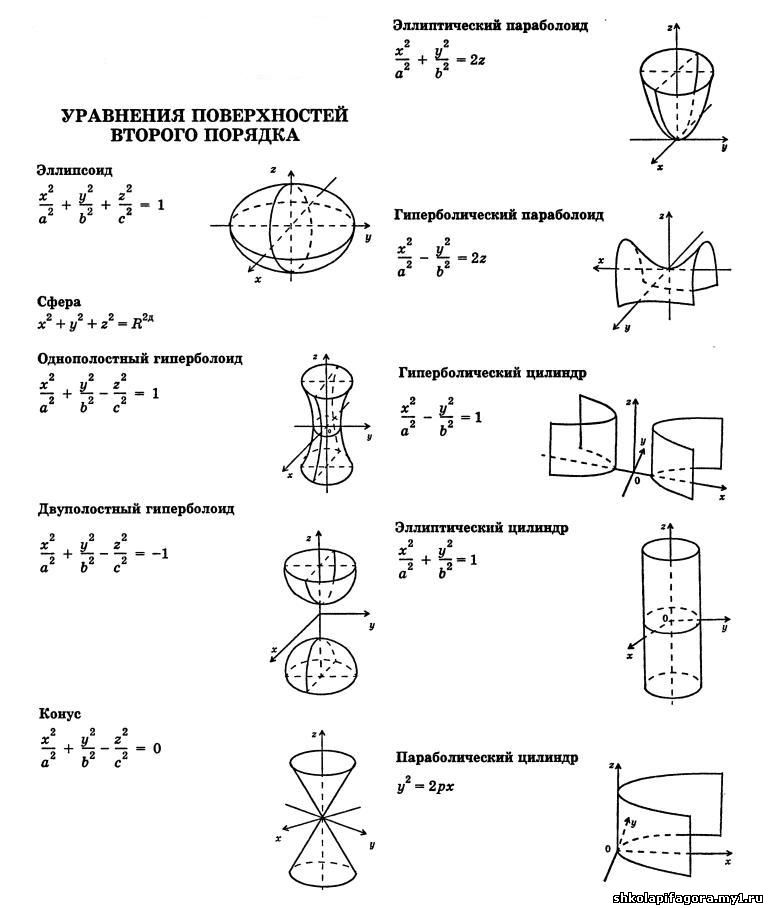 С двумя экспоненциальными функциями, если показатели степени не равны, функции линейно независимы.
С двумя экспоненциальными функциями, если показатели степени не равны, функции линейно независимы.