Sin в кубе cos в кубе если
Автор Сфера закона На чтение 12 мин Просмотров 4 Опубликовано
Содержание
- Формулы понижения степени в тригонометрии
- Формулы понижения степени, их доказательство
- Примеры применения формул понижения степени
- Тригонометрические формулы. Их вывод
Формулы понижения степени в тригонометрии
Тригонометрические формулы обладают рядом свойств, одно из которых это применение формул понижения степени. Они способствуют упрощению выражений при помощи уменьшения степени.
Формулы понижения работают по принципу выражения степени синуса и косинуса через синус и косинус первой степени, но кратного угла. При упрощении формула становится удобной для вычислений, причем повышается кратность угла от α до n α .
Формулы понижения степени, их доказательство
Ниже приводится таблица формул понижения степени со 2 по 4 для sin и cos угла. После ознакомления с ними зададим общую формулу для всех степеней.
После ознакомления с ними зададим общую формулу для всех степеней.
sin 2 α = 1 — cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 = 3 · sin α — sin 3 α 4 sin 4 = 3 — 4 · cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 · cos 2 α + cos 4 α 8
Данные формулы предназначены для понижения степени.
Существует формулы двойного угла у косинуса и синуса, из которых и следуют формулы понижения степени cos 2 α = 1 — 2 · sin 2 α и cos 2 α = 2 · cos 2 α — 1 . Равенства разрешаются относительно квадрата синуса и косинуса, которые предоставляются как sin 2 α = 1 — cos 2 α 2 и cos 2 α = 1 + cos 2 α 2 .
Формулы понижения степеней тригонометрических функций перекликаются с формулами синуса и косинуса половинного угла.
Имеет место применение формулы тройного угла sin 3 α = 3 · sin α — 4 · sin 3 α и cos 3 α = — 3 · cos α + 4 · cos 3 α .
Если решать равенство относительно синуса и косинуса в кубе, получим формулы понижения степеней для синуса и косинуса:
sin 3 α = 3 — 4 · cos 2 α + cos 4 α 8 и cos 3 α = 3 · cos α + cos 3 α 4 .
Формулы четвертой степени тригонометрических функций выглядят так: sin 4 α = 3 — 4 · cos 2 α + cos 4 α 8 и cos 4 α = 3 + 4 · cos 2 α + cos 4 α 8 .
Чтобы понизить степени эти выражений, можно действовать в 2 этапа, то есть дважды понижать, тогда это выглядит таким образом:
sin 4 α = ( sin 2 α ) 2 = ( 1 — cos 2 α 2 ) 2 = 1 — 2 · cos 2 α + cos 2 2 α 4 = = 1 — 2 · cos 2 α + 1 + cos 4 α 2 4 = 3 — 4 · cos 2 α + cos 4 α 8 ; cos 4 α = ( cos 2 α ) 2 = ( 1 + cos 2 α 2 ) 2 = 1 + 2 · cos 2 α + cos 2 2 α 4 = = = 1 + 2 · cos 2 α + 1 + cos 4 α 2 4 = 3 + 4 · cos 2 α + cos 4 α 8
Методом подстановки мы упростили сложное выражение. Для того, чтобы записать общий вид формул понижения степени разделим их на с наличием четных и нечетных показателей. Четные показатели, где n = 2 , 4 , 6 … , выражение имеет вид sin n α = C n 2 n 2 n + 1 2 n — 1 · ∑ ( — 1 ) n 2 — k k = 0 n 2 — 1 · C k n · cos ( ( n — 2 · k ) α ) и cos n α = C n 2 n 2 n + 1 2 n — 1 ∑ ( — 1 ) n 2 — k k = 0 n 2 — 1 · C k n · cos ( ( n — 2 · k ) α ) .
Нечетные показатели, где n = 3 , 5 , 7 …, выражение имеет вид
sin n α = 1 2 n — 1 · ∑ ( — 1 ) n — 1 2 — k k = 0 n — 1 2 · C k n · cos ( ( n — 2 · k ) α ) и cos n α = 1 2 n — 1 ∑ ( — 1 ) n — 1 2 — k k = 0 n — 1 2 · C k n · cos ( ( n — 2 · k ) α ) .
C p q = p ! q ! · ( p — q ) ! — это число сочетаний из p элементов по q .
Формулы понижения степени общего вида используются на любого выражения с высокой степенью для его упрощения. Рассмотрим пример для понижения кубического синуса. Третья степень нечетная, значит воспользуемся формулой sin n α = 1 2 n — 1 · ∑ ( — 1 ) n — 2 2 — k k = 0 n — 1 2 — k · C k n · sin ( ( n — 2 · k ) α ) где значение n присвоим 3 . Подставляя n = 3 в выражение, получим
sin 3 α = 1 2 3 — 1 · ∑ ( — 1 ) 3 — 1 2 — k k = 0 3 — 1 2 — k · C k 3 · sin ( ( 3 — 2 · k ) α ) = = 1 4 · ∑ ( — 1 ) 1 — k k = 0 1 · C k 3 · sin ( ( 3 — 2 · k ) α ) = = 1 4 · ( ( — 1 ) 1 — 0 · C 0 3 · sin ( ( 3 — 2 · 0 ) α ) + ( 1 ) 1 — 1 · C 1 3 · sin ( ( 3 — 2 · 1 ) α ) ) = = 1 4 · ( ( — 1 ) 1 · 3 ! 0 ! · 3 ! · sin 3 α + ( — 1 ) 0 · 3 ! 1 ! · ( 3 — 1 ) ! · sin α ) = = 1 4 · ( — sin 3 α + 3 · sin α ) = 3 · sin α — sin 3 α 4
Примеры применения формул понижения степени
Чтобы закрепить материал, необходимо детально разобрать его на примерах с использованием формулы понижения степени. Таким образом будет понятен принцип решения, подстановка и весь алгоритм.
Таким образом будет понятен принцип решения, подстановка и весь алгоритм.
Справедлива ли формула вида cos 4 α = 3 + 4 · cos 2 α + cos 4 α 8 при α = α 6 .
Для того, чтобы данная формула прошла проверку на возможность понижения степени с заданным значением угла α , необходимо посчитать левую и правую стороны. По условию имеем, что α = π 6 , тогда 2 α = π 3 , следовательно 4 α = 2 π 3 .
По таблице тригонометрических функций имеем, что cos α = cos π 6 = 3 2 , тогда cos 2 α = cos π 3 = 1 2 .
Для подробного уяснения необходимо проштудировать статью значения синуса, косинуса, тангенса и котангенса. Подставляя в формулу, получим cos 4 α = ( cos π 6 ) 4 = ( 3 2 ) 4 = 9 16 и 3 + 4 cos 2 α + cos 4 α 8 = 3 + 4 cos π 3 + cos 2 π 3 8 = 3 + 4 · 1 2 + ( — 1 2 ) 8 = 9 16
Отсюда видим, что левая и правая части равенства верны при α = π 6 , значит, выражение справедливо при значении заданного угла. Если угол отличен от α , формула понижения степени одинаково применима. 2\, \alpha>\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end\]
2\, \alpha>\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end\]
\(\blacktriangleright\) Формула вспомогательного аргумента: \[\begin\hline \text\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin4\right)>\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin6\right)>\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin3\right)>\\\\ \hline \text\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt\cdot \sin, \ \ \cos\phi=\dfrac a>, \ \sin\phi=\dfrac b>\\\\ \hline \end\]
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
\(\blacktriangleright\) Вывод формулы косинуса разности углов \(\cos=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
Рассмотрим тригонометрическую окружность и на ней углы \(\alpha\) и \(\beta\) . Пусть этим углам соответствуют точки \(A\) и \(B\) соответственно. 2\alpha=\dfrac2\)
2\alpha=\dfrac2\)
Заметим, что в данных формулах степень синуса/косинуса равна \(2\) в левой части, а в правой части степень косинуса равна \(1\) .
\(\blacktriangleright\) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
Получим: \(\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)\)
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
3) Сложим формулы синуса суммы и синуса разности двух углов:
\(\blacktriangleright\) Вывод формул суммы/разности функций:
Обозначим \(\alpha+\beta=x, \alpha-\beta=y\) . Тогда: \(\alpha=\dfrac2, \ \beta=\dfrac2\) . Подставим эти значения в предыдущие три формулы:
Получили формулу суммы косинусов.
Получили формулу разности косинусов.
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
Аналогично выводится формула суммы котангенсов.
Таким образом, можно утверждать, что существует такой угол \(\phi\) , для которого, например, \(\cos \phi=a_1, \ \sin \phi=b_1\) . Тогда наше выражение примет вид:
\(\sqrt\,\big(\cos \phi \sin x+\sin \phi\cos x\big)=\sqrt\,\sin (x+\phi)\) (по формуле синуса суммы двух углов)
Значит, формула выглядит следующим образом: \[\,\sin (x+\phi),>> \quad \text \cos \phi=\dfrac a>\] Заметим, что мы могли бы, например, принять за \(\cos \phi=b_1, \ \sin \phi=a_1\) и тогда формула выглядела бы как \[a\sin x+b\cos x=\sqrt\,\cos (x-\phi)\]
\(\blacktriangleright\) Рассмотрим некоторые частные случаи формул вспомогательного угла:
\(a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1\sin x\pm\dfrac1\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac4\right)\)
\(b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac6\right)\)
\(c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac2\cos x\right)=2\,\sin\left(x\pm\dfrac3\right)\)
Источник
Не получается спроецировать (куб, угол между прямой и плоск) : Геометрия
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| reformator |
| ||
11/12/11 |
| ||
| |||
| svv |
| |||
23/07/08 |
| |||
| ||||
| Someone |
| |||
23/07/05 |
| |||
| ||||
| Cute |
| ||
23/05/09 |
| ||
| |||
| reformator |
| ||
11/12/11 |
| ||
| |||
| Cute |
| ||
23/05/09 |
| ||
| |||
| reformator |
| ||
11/12/11 |
| ||
| |||
| Cute |
| ||
23/05/09 |
| ||
| |||
| reformator |
| ||
11/12/11 |
| ||
| |||
| Cute |
| ||
23/05/09 |
| ||
| |||
| vvvv |
| |||
19/09/08 |
| |||
| ||||
| Cute |
| ||
23/05/09 |
| ||
| |||
| reformator |
| ||
11/12/11 |
| ||
| |||
| Cute |
| ||
23/05/09 |
| ||
| |||
| reformator |
| ||
11/12/11 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 15 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
В кубе ABCDA1B1C1D1 найдите угол между
Получи беслпатные курсы подготовки к ЕГЭ и ОГЭ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2014-02-17
Перед вами очередная статья с параллелепипедами. Представленные задания просты, вычислений никаких нет или их минимум. Рассматриваются кубы и прямоугольные параллелепипеды. Важно грамотно выполнить построения и знать элементарные свойства. Например, в данных заданиях используются:
Представленные задания просты, вычислений никаких нет или их минимум. Рассматриваются кубы и прямоугольные параллелепипеды. Важно грамотно выполнить построения и знать элементарные свойства. Например, в данных заданиях используются:
1. В равностороннем треугольнике все его углы равны 60 градусам.
2. Диагонали граней куба равны.
3. Диагонали прямоугольника равны и точкой пересечения делятся пополам.
4. Необходимо понимание понятия — скрещивающиеся прямые.
Напомню какая призма является правильной.
Правильная призма – это призма основания которой — правильные многоугольники, боковые рёбра расположены под прямым углом к основаниям. Например, правильная треугольная призма – это прямая призма, основания которой равносторонние треугольники.
Правильная четырёхугольная призма – это прямая призма, основания которой являются квадратами. Понятно, что такая призма является прямоугольным параллелепипедом.
Правильная шестиугольная призма – это прямая призма, основания которой являются правильными шестиугольниками. Рассмотрим задачи:
Рассмотрим задачи:
315130. В кубе ABCDA1B1C1D1 точка К — середина ребра АA1, точка L — середина ребра A1B1, точка M — середина ребра A1D1. Найдите угол MLK. Ответ дайте в градусах.
Построим куб, обозначим его вершины и точки K, M и L.
Так как данные точки являются серединами ребёр, то отрезки KM, ML, KL будут равны между собой. Это означает, что треугольник KML равносторонний. Известно, что в равностороннем треугольнике его углы равны по 60 градусов. Таким образом, угол MLK равен 600.
Ответ: 60
316554. В кубе ABCDA1B1C1D1 найдите угол между прямыми АD1 и B1D1. Ответ дайте в градусах.
Построим куб, обозначим вершины и данные отрезки, также построим отрезок АВ1.
Отрезки АD1, B1D1 и АD1 являются диагоналями граней куба, то есть все они равны, значит треугольник АD1B1 является равносторонним. Известно, что в равностороннем треугольнике его углы равны по 60 градусов.
Известно, что в равностороннем треугольнике его углы равны по 60 градусов.
Таким образом, угол между прямыми АD1 и B1D1 равен 600.
Ответ: 60
318474. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер AB = 8, AD = 6, AA1 = 21. Найдите синус угла между прямыми CD и A1C1.
Построим отрезки CD и A1C1:
В данной задаче имеем скрещивающиеся прямые, то есть сами они не имеют общей точки пересечения. Но этот угол между скрещивающимся прямыми определяется. Как?
Простыми словами: если вы мысленно представите в пространстве две непараллельные прямые, то всегда существует такой перпендикуляр, который их соединяет. Так вот, если мы параллельным переносом сдвинем одну прямую к другой по этому перпендикуляру до пересечения этих прямых, то полученный между ними угол и будет тем самым искомым углом.
В кубах и параллелепипедах, где прямые проходят через рёбра и диагонали такие углы определить несложно. А вот в части С присутствуют задания со скрещивающимися прямыми на порядок сложнее.
Вернёмся к нашей задаче.
Мысленно сдвинем отрезок CD вдоль перпендикуляра СC1 до пересечения с прямой A1C1. Получается, что необходимо найти синус угла между A1C1 и C1D1. Это мы можем сделать воспользовавшись определением синуса в прямоугольном треугольнике А1C1D1. Найдём:
По определению синуса:
Ответ: 0,6
318475. В правильной четырёхугольной призме ABCDA1B1C1D1 известно, что AC1 = 2BC. Найдите острый угол между диагоналями BD1 и CA1. Ответ дайте в градусах.
Построим правильную четырёхугольную призму, обозначим вершины, построим диагонали BD1 и CA1:
Сразу отметим, что диагонали BD1 и CA1 являются диагоналями прямоугольника A1BCD1, то есть они равны между собой и равны диагонали AC1 (так как призма правильная четырехугольная).
Известно, что диагонали прямоугольника равны и точкой пересечения делятся пополам, то есть:
A1С = D1B
A1O = ОС и D1O = ОB
A1O = ОС = D1O = ОB
В условии сказано, что AC1 = 2BC, значит имеем BD1 = CA1 = 2BC. На основании изложенного можем сделать вывод о том, что:
BO = ОС = BC и A1O = ОD1 = A1D1
то есть треугольники BОС и A1OD1 равносторонние.
Таким образом, угол острый между диагоналями равен 600.
Ответ: 60
В данных заданиях используется теорема Пифагора, для нахождения углов необходимо владеть понятиями синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике.
245359. Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3.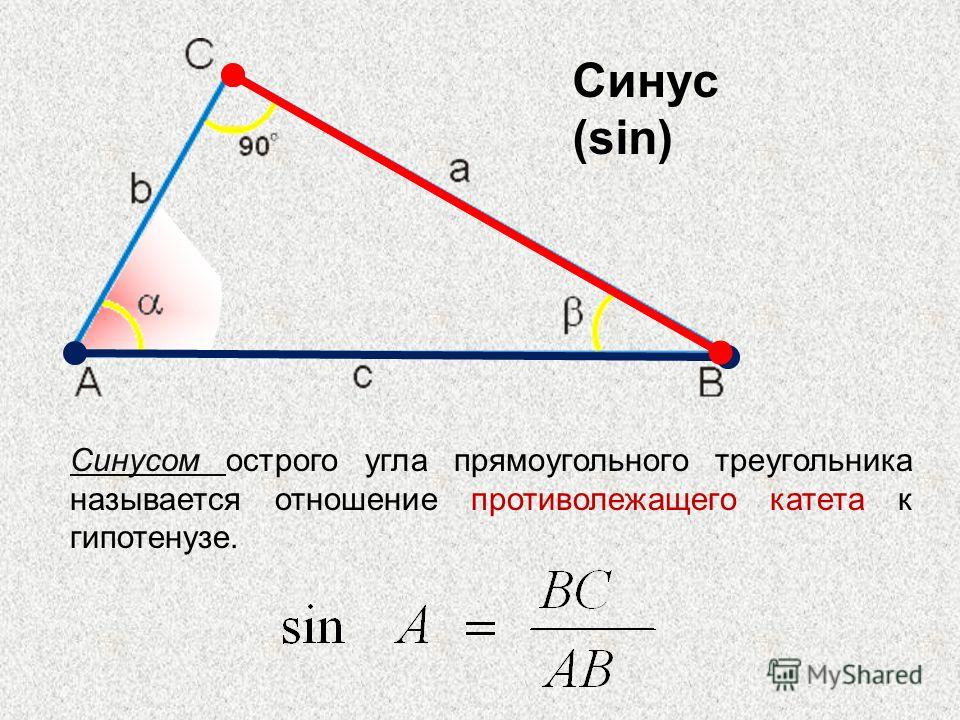
Посмотреть решение
245360. Найдите расстояние между вершинами A и D1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3.
Посмотреть решение
245361. Найдите угол ABD1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3. Ответ дайте в градусах.
Посмотреть решение
245362. Найдите угол C1BC прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 4. Ответ дайте в градусах.
Посмотреть решение
245363. Найдите угол DBD1 прямоугольного параллелепипеда, для которого AB = 4, AD = 3, AA1 = 5. Ответ дайте в градусах.
Посмотреть решение
284357. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BD1 = 3, CD = 2, AD = 2. Найдите длину ребра AA1.
Посмотреть решение
284363. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что DD1 = 1, CD = 2, AD = 2. Найдите длину диагонали CA1.
Посмотреть решение
На этом всё. Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Стереометрия ПРИЗМЫ | ЕГЭ-№2
Подготовка к ОГЭ по математике. Полный курс!
Полный Видеокурс по РУССКОМУ ЯЗЫКУ!
ПРЕМИУМ-КУРС по математике на 100 баллов!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Quiet Sine 3, серия подписки, том. я | zakè
Quiet Sine 3, Subscription Series Vol. я | заке | Заке Дрон Записи $root.artistsMenu.setActiveLabelMemberBand(id)»>••• $root. artistsMenu.setActiveLabelMemberBand(id)»>свернуть
artistsMenu.setActiveLabelMemberBand(id)»>свернутьпо заке
исключительно для подписчиков
поддерживается
Ричард Осборн
Ричард Осборн Красивая, веселая мелодия.
Калеб Пепера
Калеб Пепера Мгновенная ню-классика. Фантастика.
Кристофер Эллис
Кристофер Эллис
Заке снова расширяет границы, открывая новые горизонты чистой эмбиентной красоты :—-)
Билл Браски
смеющийся человек7743
Альтернойз
Рамона
Дэвид Коул
Райан Руппе
Рэндалл
мат. Ом
Ом
скотобойняlive
Джон Маккефри
Фетафанк
ЛасточкаСолнечный свет
Буб
Муравей Рэйфокс
.тишина
Dark Sines / Тейлор Проффит
Франсуа
Космо
хозяйка
Шон Уайлд
Безымянный / Безликий
Ринчен Чоэсанг
Ханс Венеман
Марио1984
DriftDiffusion (CA)
водосбор
DJ Мистер Бен
Шон П. Уилбур
Уилбур
Cripes OnFriday
идиот_транспортное средство
Коллектив Ицамна
вентолин
Скотт Мур
маслозавод
Аполлон1967
Дж Харман
Марк Маккуитти
dae5id-j
си охотник
рыцарьd68
FX
Крис77550
нормальный бластер
Бенджамин Доран
Фелипе номер
Тайлер Квайринг
Микки
меси
Майкл Качмер
топ
Фредерик Ки Смит, доктор философии.
Мишель Тэкабери
Дэвид Гэллоуэй
Олд Гогги
Кир Икслор
AzureAzure
Кристофер Линдсей
ПетертеГантер
Джон Шеффер
Джей Гленн Тейлор
подробнее…
теги
теги
окружающий атмосферный дрон дрон эмбиент музыка для медитации СШАоколо
Заке Дрон Записи
Самостоятельные работы + совместные проекты.
- ссылкаtr.ee
- Прошлое внутри настоящего
- juno.
 co.uk
co.uk - dunkrecords.com
- Записи Azure Vista
Рекомендации
контакт / помощь
Связаться с Zakè Drone Recordings
Потоковая передача и
Справка по загрузке
Активировать код
Пожаловаться на этот альбом или аккаунт
Zakè Drone Recordings рекомендует:
Если вам нравится Quiet Sine 3, Subscription Series Vol. Я, вам также может понравиться:
Bandcamp Daily — ваш путеводитель по миру Bandcamp
На Bandcamp Radio
С бразильской легендой Джойс на ее утерянном LP вместе с восходящей Аримой Эдеррой
слушать сейчас- войти
- условия использования
- конфиденциальность
- политика авторского права
- переключиться на мобильный вид
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктический(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар(60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | желтовато-коричневый (пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | соз(210) | |
| 52 | Найти точное значение | сек (60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-(квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 шт.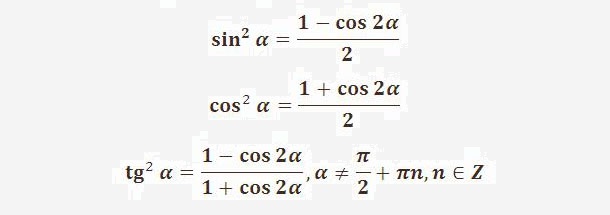 )/4 )/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан( квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | желтовато-коричневый ((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Вариабельные поли(А)-последовательности SINE 3′: обширный класс генетических маркеров в геноме свиньи
. 1993;4(8):429-34.
1993;4(8):429-34.
дои: 10.1007/BF00296816.
Х Эллегрен 1
принадлежность
- 1 Факультет разведения и генетики животных, Шведский университет сельскохозяйственных наук, Уппсала.
- PMID: 8397020
- DOI: 10.1007/BF00296816
Х Эллегрен. Геном Мамм. 1993.
. 1993;4(8):429-34.
дои: 10. 1007/BF00296816.
1007/BF00296816.
Автор
Х Эллегрен 1
принадлежность
- 1 Факультет разведения и генетики животных, Шведский университет сельскохозяйственных наук, Уппсала.
- PMID: 8397020
- DOI: 10.1007/BF00296816
Абстрактный
Предыдущие исследования ДНК человека показали, что 3′-поли(А)-тракты элементов Alu могут проявлять значительный генетический полиморфизм. Чтобы выяснить, применим ли этот тип маркера в целом к геномам млекопитающих, я проанализировал свиные SINE. Скрининг базы данных выявил 17 последовательностей свиней со значительной гомологией с ранее идентифицированным SINE свиньи. Появление в базе данных предполагает частоту SINE, равную одной копии на каждые 12 т.п.о. ДНК свиньи. Все SINE содержали 3′-поли(А) тракт со средним числом 12 непрерывных аденинов. Повторяющиеся области анализировали на полиморфизм с помощью локус-специфической ПЦР-амплификации. Вариации длины аллелей (от двух до пяти аллелей среди 10 свиней) были обнаружены в 8 из 10 исследованных локусов, в большинстве случаев, вероятно, из-за различного количества повторенных остатков аденина. Выявлена положительная связь между длиной повтора и степенью полиморфизма. Стабильное менделевское наследование было задокументировано в 200 мейозах в каждом из четырех локусов. Высокая геномная частота SINE подразумевает, что потенциально информативный маркер может быть обнаружен рядом с любым геном или в любом космидном клоне. Эти SINE 3′-поли(А)-полиморфизмы, названные SINEVA [вариабельные поли(А) SINE], таким образом, обеспечивают богатый и полезный класс генетических маркеров в геномах млекопитающих.
Скрининг базы данных выявил 17 последовательностей свиней со значительной гомологией с ранее идентифицированным SINE свиньи. Появление в базе данных предполагает частоту SINE, равную одной копии на каждые 12 т.п.о. ДНК свиньи. Все SINE содержали 3′-поли(А) тракт со средним числом 12 непрерывных аденинов. Повторяющиеся области анализировали на полиморфизм с помощью локус-специфической ПЦР-амплификации. Вариации длины аллелей (от двух до пяти аллелей среди 10 свиней) были обнаружены в 8 из 10 исследованных локусов, в большинстве случаев, вероятно, из-за различного количества повторенных остатков аденина. Выявлена положительная связь между длиной повтора и степенью полиморфизма. Стабильное менделевское наследование было задокументировано в 200 мейозах в каждом из четырех локусов. Высокая геномная частота SINE подразумевает, что потенциально информативный маркер может быть обнаружен рядом с любым геном или в любом космидном клоне. Эти SINE 3′-поли(А)-полиморфизмы, названные SINEVA [вариабельные поли(А) SINE], таким образом, обеспечивают богатый и полезный класс генетических маркеров в геномах млекопитающих.
Похожие статьи
Полидеоксиаденилатный тракт повторяющихся элементов Alu полиморфен в геноме человека.
Economou EP, Bergen AW, Warren AC, Antonarakis SE. Эконому Е.П. и др. Proc Natl Acad Sci U S A. 1990 Apr; 87(8):2951-4. doi: 10.1073/pnas.87.8.2951. Proc Natl Acad Sci U S A. 1990. PMID: 2326257 Бесплатная статья ЧВК.
SINEs свиней: характеристика и использование в видоспецифичной амплификации.
Френген Э., Томсен П., Кристенсен Т., Кран С., Миллер Р., Дэвис В. Френген Э. и соавт. Геномика. 1991 авг; 10 (4): 949-56. doi: 10.1016/0888-7543(91)
-г. Геномика. 1991. PMID: 1916826
Многочисленные мононуклеотидные повторы (A)n.
 (T)n в геноме свиньи: картирование сцепления свиных локусов APOB, FSA, ALOX12, PEPN и RLN.
(T)n в геноме свиньи: картирование сцепления свиных локусов APOB, FSA, ALOX12, PEPN и RLN.Эллегрен Х. Эллегрен Х. Аним Жене. 1993 окт; 24 (5): 367-72. doi: 10.1111/j.1365-2052.1993.tb00342.x. Аним Жене. 1993. PMID: 71
Характеристика полиморфных микросателлитных локусов свиней.
Коппитерс В., Ван де Веге А., Пилман Л., Депикер А., Ван Зеверен А., Буке Ю. Коппитерс В. и соавт. Аним Жене. 1993 июнь; 24 (3): 163-70. дои: 10.1111/j.1365-2052.1993.tb00281.x. Аним Жене. 1993. PMID: 8103299
Инсерционный мутагенез мобильными элементами в геноме млекопитающих.
Амариглио Н., Рехави Г. Амариглио Н. и др. Энвайрон Мол Мутаген. 1993;21(3):212-8. doi: 10.1002/em.2850210303.
 Энвайрон Мол Мутаген. 1993.
PMID: 8385004
Обзор.
Энвайрон Мол Мутаген. 1993.
PMID: 8385004
Обзор.
Посмотреть все похожие статьи
Цитируется
Полиморфизм SINEVA и картирование гена гликопротеина 1, ассоциированного с беременностью крупного рогатого скота.
Мартин-Бурриэль И., Элдуке К., Оста Р., Лоран П., Барендсе В., Сарагоса П. Мартин-Бурриэль I и др. Геном Мамм. 1998 февраль;9(2):179-80. doi: 10.1007/s003359
0. Геном Мамм. 1998. PMID: 9457691 Аннотация недоступна.Цитогенетическая карта домашней свиньи.
Йерле М., Лахбиб-Мансайс Ю., Пинтон П., Робик А., Гуро А., Милан Д., Геллин Дж. Йерле М. и др. Геном Мамм. 1997 авг; 8 (8): 592-607. doi: 10.1007/s003359
2.
 Геном Мамм. 1997.
PMID: 9250869
Аннотация недоступна.
Геном Мамм. 1997.
PMID: 9250869
Аннотация недоступна.Характеристика микросателлитов свиной хромосомы 13, отсортированной потоком.
Дэвис В., Хойхайм Б., Чапут Б., Арчибальд А.Л., Фрелат Г. Дэвис В. и соавт. Геном Мамм. 1994 ноябрь; 5 (11): 707-11. дои: 10.1007/BF00426077. Геном Мамм. 1994. PMID: 7873881
Использование повторяющихся последовательностей с вкраплениями свиней в генотипировании, опосредованном ПЦР.
Миллер младший. Миллер Дж.Р. Геном Мамм. 1994 окт; 5 (10): 629-32. дои: 10.1007/BF00411458. Геном Мамм. 1994. PMID: 7849399
Карта связей свиньи (Sus scrofa), составленная консорциумом PiGMaP.

Archibald AL, Haley CS, Brown JF, Couperwhite S, McQueen HA, Nicholson D, Coppieters W, Van de Weghe A, Stratil A, Winterø AK, et al. Арчибальд А.Л. и др. Геном Мамм. 1995 март; 6(3):157-75. дои: 10.1007/BF00293008. Геном Мамм. 1995. PMID: 7749223
Просмотреть все статьи «Цитируется по»
использованная литература
- Нуклеиновые Кислоты Res. 1992 25 января; 20 (2): 211-5 — пабмед
- Дж. Херед. 1993 г., июль-август; 84 (4): 259–62. — пабмед
- Геномика.

- Геномика.

 02.2012, 00:09
02.2012, 00:09 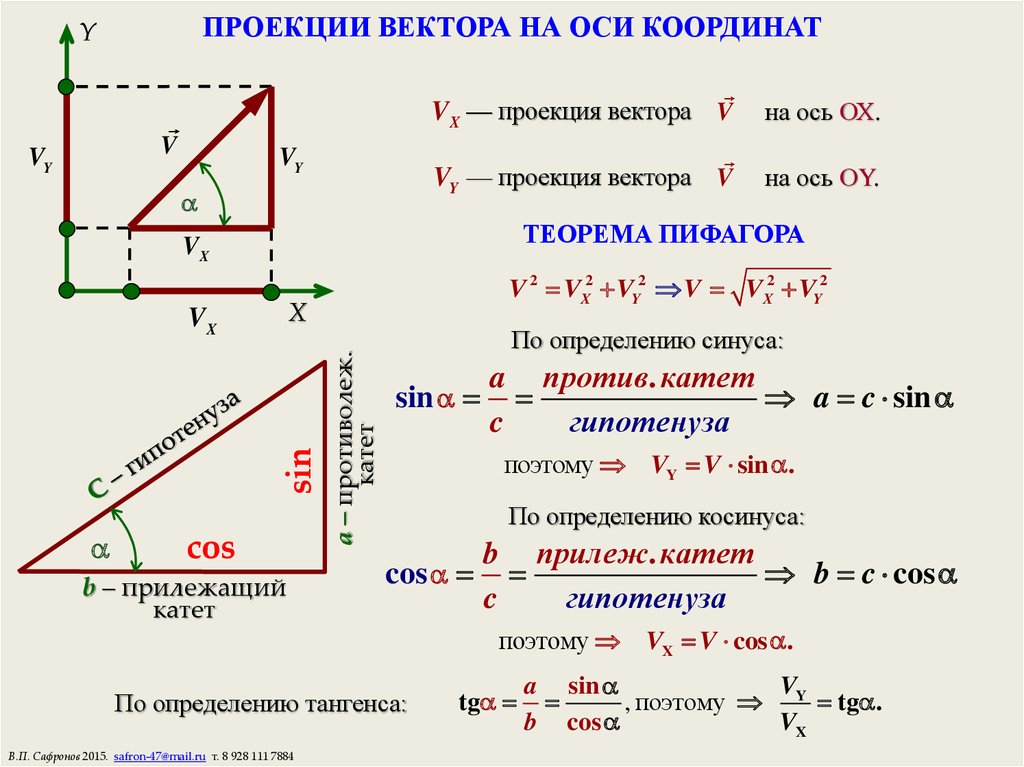 02.2012, 00:12 —
02.2012, 00:12 —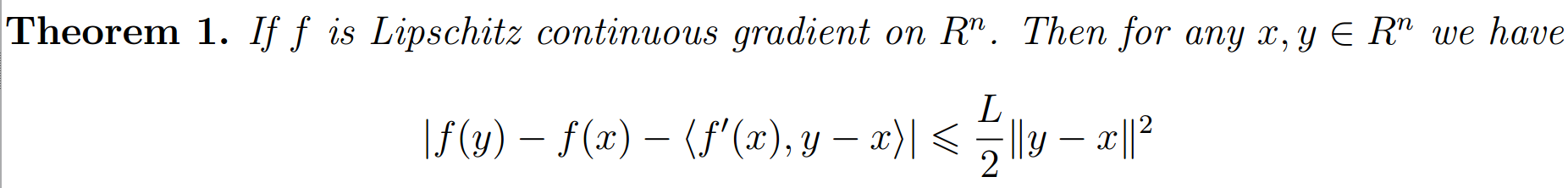 Найти проекцию точки — значит найти координаты этой проекции. Это в общем случае могут быть малосимпатичные, ничем не примечательные числа.
Найти проекцию точки — значит найти координаты этой проекции. Это в общем случае могут быть малосимпатичные, ничем не примечательные числа.
 что диагональ куба перпендикулярна плоскости .
что диагональ куба перпендикулярна плоскости . 02.2012, 04:39
02.2012, 04:39  Тогда прямая — нормаль к плоскости, проходящая через эту точку, задается параметрическим уравнением , или в координатах
Тогда прямая — нормаль к плоскости, проходящая через эту точку, задается параметрическим уравнением , или в координатах .)
.)

 02.2012, 05:48
02.2012, 05:48  02.2012, 05:51
02.2012, 05:51  02.2012, 06:07
02.2012, 06:07  02.2012, 13:16
02.2012, 13:16  02.2012, 13:59
02.2012, 13:59  02.2012, 15:34
02.2012, 15:34  ..
.. 02.2012, 19:25
02.2012, 19:25  02.2012, 20:53
02.2012, 20:53 
 co.uk
co.uk (T)n в геноме свиньи: картирование сцепления свиных локусов APOB, FSA, ALOX12, PEPN и RLN.
(T)n в геноме свиньи: картирование сцепления свиных локусов APOB, FSA, ALOX12, PEPN и RLN. Энвайрон Мол Мутаген. 1993.
PMID: 8385004
Обзор.
Энвайрон Мол Мутаген. 1993.
PMID: 8385004
Обзор. Геном Мамм. 1997.
PMID: 9250869
Аннотация недоступна.
Геном Мамм. 1997.
PMID: 9250869
Аннотация недоступна.
