Отношение 5 к 3: Что такое отношение чисел | Математика

2

6 класс. Математика. Отношения и пропорции — Отношения и пропорции

Комментарии преподавателя

У на­ту­раль­ных чисел есть раз­ное при­ме­не­ние:

1. Обо­зна­чать ко­ли­че­ство. Пять яблок. Три ав­то­мо­би­ля.

2. За­да­вать по­ря­док. Пятый дом идет после тре­тье­го, но рань­ше де­вя­то­го.

3. Да­вать имя. Номер на фут­бол­ке спортс­ме­на, номер те­ле­фо­на – это ана­лог имени.

Точно так же и дробь имеет раз­ное на­зна­че­ние.

1.  Обо­зна­чать ко­ли­че­ство. Пол-лит­ра мо­ло­ка, чет­верть часа, две трети пути.

2. Срав­ни­вать два числа. Брату 5 лет, а сест­ре 3 года. Брат стар­ше в  раза. Эта дробь не обо­зна­ча­ет ни­ка­ко­го ко­ли­че­ства. Она срав­ни­ва­ет одно число с дру­гим. Такое срав­не­ние на­зы­ва­ет­ся от­но­ше­ни­ем. Во сколь­ко раз одно число боль­ше дру­го­го (или мень­ше).

Рас­смот­рим такую си­ту­а­цию. Ху­дож­ник, глядя на дом, на­ри­со­вал его на бу­ма­ге. Мы по­ни­ма­ем, что это тот самый дом. Но ведь на бу­ма­ге он во много раз мень­ше. Что же оста­лось неиз­мен­ным? Без из­ме­не­ния оста­лось от­но­ше­ние вы­со­ты дома к его ши­рине. То есть, если у ре­аль­но­го дома вы­со­та в три раза боль­ше ши­ри­ны, то и на кар­тин­ке то же самое. Если у дома вы­со­та 15 мет­ров, а ши­ри­на 5 мет­ров, то на кар­тин­ке вы­со­та и ши­ри­на могут быть 15 и 5 см, или 30 и 10 см, но не могут быть 10 и 5, иначе изоб­ра­жен­ный дом будет не похож на на­сто­я­щий (см. Рис. 1).

Рис. 1. От­но­ше­ния сто­рон дома

Если раз­де­лить вы­со­ту на ши­ри­ну дома, то мы по­лу­чим их от­но­ше­ние.

От­но­ше­ние везде было оди­на­ко­вым.

От­но­ше­ние может рас­смат­ри­вать­ся не толь­ко для двух, но и для лю­бо­го ко­ли­че­ства ве­ли­чин.

Ло­те­рей­ный билет стоил 100 руб­лей. Маша внес­ла 10 руб­лей, Петя – 20 руб­лей, Вася – 30 руб­лей и Вика – 40 руб­лей.

Всего 100 руб­лей. Билет вы­иг­рал. Вы­иг­рыш 1000 руб­лей. Как спра­вед­ли­во раз­де­лить вы­иг­рыш?

Спра­вед­ли­во будет раз­де­лить в таком же от­но­ше­нии. За­пи­шем от­но­ше­ния взно­сов.

10:20:30:40

В таком от­но­ше­нии у нас раз­де­ле­но 100 руб­лей.

По­нят­но, что, чтобы в таком же от­но­ше­нии раз­де­лить 1000 руб­лей, нужно все уве­ли­чить в 10 раз.

100:200:300:400

Это и будет спра­вед­ли­вым.

В слу­чае от­но­ше­ния двух чисел можно ис­поль­зо­вать и двое­то­чие, и дроб­ную черту:

В слу­чае трех и более чисел ис­поль­зу­ем толь­ко двое­то­чие:

1:2:3

Обыч­но от­но­ше­ние двух чисел ис­поль­зу­ют в двух слу­ча­ях:

1. От­но­ше­ние двух раз­лич­ных ве­ли­чин

От­но­ше­ние вы­со­ты дома к его ши­рине.

От­но­ше­ние роста или воз­рас­та двух че­ло­век.

2. От­но­ше­ние ча­стей или части и це­ло­го

Вы­со­та ос­нов­ной части дома 5 мет­ров, крыши – 3 метра (см.

Рис. 2).

Рис. 2. От­но­ше­ние ча­стей или части це­ло­го на при­ме­ре дома

Можем за­пи­сать раз­лич­ные от­но­ше­ния ча­стей или ча­стей и це­ло­го.

Крыша к ос­нов­ной части: 3:5

Крыша ко всему дому: 3:8

Ос­нов­ная часть ко всему дому: 5:8

Масса слона – 5 т, масса кита – 80 т. Найти от­но­ше­ние их масс.

Чтобы найти от­но­ше­ние, нужно одну ве­ли­чи­ну раз­де­лить на дру­гую. От­но­ше­ние массы слона к массе кита со­став­ля­ет 5:80. В прин­ци­пе, за­да­ча уже ре­ше­на. Но это от­но­ше­ние можно упро­стить. Раз­де­лим обе части на 5. По­лу­чим от­но­ше­ние 1:16.

То же самое можно за­пи­сать в виде дроби.

Можно было по­сту­пить на­о­бо­рот: раз­де­лить массу кита на массу слона.

1:16 – от­но­ше­ние массы слона к массе кита

16:1 – от­но­ше­ние массы кита к массе слона

Такие от­но­ше­ния на­зы­ва­ют вза­им­но-об­рат­ны­ми.

Оба от­но­ше­ния по­ка­зы­ва­ют нам одно и то же. Кит в 16 раз тя­же­лее слона.

Ответ:1:16, 16:1.

Весь путь со­став­ля­ет 30 км. Прой­де­но 6 км.

Ка­ко­во от­но­ше­ние прой­ден­но­го пути ко всему пути; к остав­ше­му­ся? (См. Рис. 3.)

Рис. 3. Ил­лю­стра­ция к за­да­че 2

Раз­де­лим прой­ден­ный путь на весь путь.

От­но­ше­ние 1:5. Это озна­ча­ет, что прой­ден­ный путь в 5 раз мень­ше всего пути. Чаще мы в такой си­ту­а­ции го­во­рим, что прой­ден­ный путь со­став­ля­ет  от всего пути, и ис­поль­зу­ем дробь.

От­но­ше­ние прой­ден­но­го пути к остав­ше­му­ся го­во­рит нам, что оста­лось в 4 раза боль­ше, чем прой­де­но.

Ответ: , .

Сколь­ко про­цен­тов со­став­ля­ет 3 ми­ну­ты от 1 часа?

За­да­чи на про­цен­ты тоже яв­ля­ют­ся за­да­ча­ми на от­но­ше­ние двух ве­ли­чин.

Най­дем от­но­ше­ние 3 минут к часу.

Пе­ре­ве­дем часы в ми­ну­ты, чтобы у нас были оди­на­ко­вые еди­ни­цы из­ме­ре­ния (см. Рис. 4).

Рис. 4. Ил­лю­стра­ция к за­да­че 3

3 мин : 60 мин

Так как еди­ни­цы из­ме­ре­ния оди­на­ко­вые, то раз­ли­чие толь­ко в ко­ли­че­стве, зна­чит, можно рас­смот­реть толь­ко от­но­ше­ние чисел.

3 : 60

Со­кра­тим на 3. По­лу­ча­ем:

1 : 20 или 

Мы можем ска­зать, что 3 мин от­но­сят­ся к 1 ч, как 1 : 20.

Или: 1 час в 20 раз боль­ше, чем 3 мин.

Или: 3 ми­ну­ты со­став­ля­ет  от часа.

Так как в усло­вии про­си­ли дать ответ в про­цен­тах, то надо дробь  пе­ре­ве­сти в про­цен­ты. Про­цен­ты – это сотые. Пе­ре­ве­дем нашу дробь в сотые. До­мно­жим чис­ли­тель и зна­ме­на­тель на 5. По­лу­чим .

Три ми­ну­ты – это 5 % часа

Ответ: 5 %.

 

Не обя­за­тель­но знать, чему равны две ве­ли­чи­ны, чтобы найти их от­но­ше­ние.

В самом деле, если прой­де­на  пути, то ка­ко­во от­но­ше­ние прой­ден­но­го пути к остав­ше­му­ся?

Прой­де­на , оста­лась . Остав­ший­ся путь в два раза боль­ше.

То есть от­но­ше­ние прой­ден­но­го к остав­ше­му­ся равно 1:2.

Тех­ни­че­ски это по­лу­чить не слож­но.

Раз­де­лим  на .

Де­ле­ние на дробь рав­но­силь­но умно­же­нию на об­рат­ную (пе­ре­вер­ну­тую) дробь.

После со­кра­ще­ния по­лу­ча­ем  или от­но­ше­ние 1:2.

Итак, под­ве­дем итог.

• Чтобы найти от­но­ше­ние двух ве­ли­чин, нужно одну раз­де­лить на дру­гую. Это можно за­пи­сать с по­мо­щью знака де­ле­ния или дроб­ной черты.

От­но­ше­ние  к :

• Ве­ли­чи­ны долж­ны быть вы­ра­же­ны в одних еди­ни­цах

• Ве­ли­чи­ны сами могут быть дро­бя­ми или про­цен­та­ми

Пропорция

Слово «про­пор­ция» про­ис­хо­дит от ла­тин­ско­го корня и озна­ча­ет «со­раз­мер­ность». Люди часто ис­поль­зу­ют его в по­все­днев­ной жизни. Го­во­рят, на­при­мер, о про­пор­ци­ях че­ло­ве­че­ско­го тела или о про­пор­ци­ях в ку­ли­на­рии. Се­год­ня мы узна­ем, что вкла­ды­ва­ют в это слово ма­те­ма­ти­ки.

Рас­смот­рим два от­но­ше­ния. Мы пом­ним, что от­но­ше­ние – это част­ное двух чисел.

За­ме­тим, что и в пер­вом и во вто­ром слу­чае зна­че­ние част­но­го равно трем. Перед нами два рав­ных от­но­ше­ния. За­пи­шем ра­вен­ство.

Пят­на­дцать так от­но­сит­ся к пяти, как два­дцать че­ты­ре к вось­ми. Такое ра­вен­ство и на­зы­ва­ют про­пор­ци­ей. Ино­гда это ра­вен­ство за­пи­сы­ва­ют в виде ра­вен­ства обык­но­вен­ных дро­бей.

Сфор­му­ли­ру­ем опре­де­ле­ние:

 ра­вен­ство двух от­но­ше­ний на­зы­ва­ют про­пор­ци­ей.

С по­мо­щью букв про­пор­цию можно за­пи­сать:

От­но­ше­ние aкbравно от­но­ше­нию cк d. Ино­гда про­пор­цию чи­та­ют по-дру­го­му: «aтак от­но­сит­сякb, как cот­но­сит­сяк d». Участ­ву­ю­щие в про­пор­ции числа на­зы­ва­ют чле­на­ми про­пор­ции. Счи­та­ют, что все члены от­лич­ны от нуля.

Числа aи dна­зы­ва­ют край­ним чле­на­ми про­пор­ции, а числа bиc– сред­ни­ми чле­на­ми. Дей­стви­тель­но, в пер­вом ва­ри­ан­те за­пи­си числа bиcна­хо­дят­ся по­се­ре­дине,

а числа aи dс краю.

В рас­смот­рен­ной ранее про­пор­ции най­дем про­из­ве­де­ние ее сред­них и край­них чле­нов.

За­ме­тим, что два по­лу­чен­ных про­из­ве­де­ния равны.

Сфор­му­ли­ру­ем ос­нов­ное свой­ство про­пор­ции в общем виде.

В вер­ной про­пор­ции про­из­ве­де­ние край­них чле­нов равно про­из­ве­де­нию сред­них.

Верно и об­рат­ное утвер­жде­ние.

Если про­из­ве­де­ние край­них чле­нов равно про­из­ве­де­нию сред­них чле­нов про­пор­ции, то про­пор­цияверна.

Най­дем неиз­вест­ный член про­пор­ции, то есть решим про­пор­цию.

Числа 0,5 и 13 – это край­ние члены; числа aи 2 – это сред­ние члены. Вос­поль­зу­ем­ся ос­нов­ным свой­ством про­пор­ции.

Решим про­пор­цию.

Ис­поль­зуя ос­нов­ное свой­ство про­пор­ции, по­лу­чим:

Чтобы из­ба­вить­ся от де­ся­тич­ной дроби в зна­ме­на­те­ле, умно­жим и чис­ли­тель, и зна­ме­на­тель дроби на 10. Со­кра­тим по­лу­чен­ную дробь на 4, а затем еще раз на 4.

 

Х = 60.

Про­ве­рить яв­ля­ют­ся ли дан­ные про­пор­ции вер­ны­ми:

В этом за­да­нии нужно про­ве­рить, дей­стви­тель­но ли вы­пол­ня­ет­ся ра­вен­ство между от­но­ше­ни­я­ми.

Ре­ше­ние

Най­дем про­из­ве­де­ние сред­них и про­из­ве­де­ние край­них чле­нов для каж­дой про­пор­ции. Если по­лу­чен­ные про­из­ве­де­ния равны, то про­пор­ция верна. В про­тив­ном же слу­чае, про­пор­ция яв­ля­ет­ся невер­ной.

вер­ная про­пор­ция, т. к. 

 невер­ная про­пор­ция, т. к. 

Если в вер­ной про­пор­ции по­ме­нять ме­ста­ми сред­ние или край­ние члены, то по­лу­чив­ше­е­ся новые про­пор­ции тоже верны.

Это так по­то­му, что при такой пе­ре­ста­нов­ке про­из­ве­де­ние край­них и сред­них чле­нов не из­ме­ня­ет­ся.

Раз­бе­рем при­мер. Из дан­ной про­пор­ции  по­лу­чить две новые, пе­ре­ста­вив край­ние и сред­ние члены. Сна­ча­ла пе­ре­ста­вим сред­ние члены (рис. 1).

Рис. 1. Пе­ре­ста­нов­ка сред­них чле­нов

Дей­стви­тель­но, про­из­ве­де­ние сред­них и край­них не из­ме­ни­лось, зна­чит, по­лу­чен­ная про­пор­ция верна. Пе­ре­ста­вим край­ние члены (рис. 2).

Рис. 2. Пе­ре­ста­нов­ка край­них чле­нов

И в этом слу­чае про­из­ве­де­ние сред­них и край­них не из­ме­ни­лось. Мы по­лу­чи­ли вер­ную про­пор­цию.

 

источник видео — http://www.youtube.com/watch?v=Uf-9a-0aPNY

источник видео — http://www.youtube.com/watch?v=kvlkxI4CKh5

источник видео — http://www.youtube.com/watch?v=N4Ah2hIvx9s

источник видео — http://www.youtube.com/watch?v=xAMeoTTcKVw

источник видео — http://www.youtube.com/watch?v=GP7392STr3o

источник презентации — http://ppt4web.ru/matematika/matematika-klass-otnoshenija.html

источник презентации — http://ppt4web.ru/matematika/proporcija5.html

источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/otnosheniya-i-proporcii/otnosheniya?seconds=0&chapter_id=341

источник конспекта — http://interneturok. ru/ru/school/matematika/6-klass/otnosheniya-i-proporcii/proportsii-2

Что такое соотношение 3 5? – Обзоры Вики

3 из 5. Отношение меньшего числа к большему, части к целому. Это иллюстрирует 3 из 5: отношение части, 3, к целому, 5. Часть три пятых всего. (Здесь «часть» относится ко всему, что меньше целого.)

Точно так же, как вы вычисляете соотношение? Разделите данные A на данные B, чтобы найти свое соотношение. В приведенном выше примере 5/10 = 0.5. Умножьте на 100, если хотите процент. Если вы хотите получить соотношение в процентах, умножьте ответ на 100.

Как разделить соотношение на троих? Правила деления количества на три заданных соотношения объясняются ниже вместе с примерами различных типов. Первый доля = X / (X + Y + Z) × K, Вторая часть = Y/(X + Y + Z) × K, Третья часть = Z/(X + Y + Z) × K.

Как найти эквивалентное отношение 3 5? Данные соотношения 3: 5 и 15: 25 равны. Потому что, когда вы разделите соотношение 15: 25 на 5 и в числителе, и в знаменателе, можно получить первое соотношение 3: 5. Точно так же, когда вы умножаете первое соотношение 3: 5 на 5, можно получить соотношение 15: 25.

Во-вторых, каково эквивалентное соотношение для 2 5? Ответ: Дроби, равные 2/5, равны 4/10, 6/15, 8/20 и т. Д.

Какова дробь 3 5?

Таблица преобразования десятичных и дробных чисел

Доля	Эквивалентные дроби	Десятичная дробь
3/5	6/10	.6
4/5	8/10	.8
1/6	2/12	.166
5/6	10/12	.833

то Что из следующего эквивалентно 3 5? Ответ: дроби, равные 3/5, 6/10, 9/15, 12/20и др. Эквивалентные дроби имеют одинаковое значение в сокращенном виде. Пояснение: Эквивалентные дроби можно записать, умножив или разделив числитель и знаменатель на одно и то же число.

Чему равен числитель дроби 3 5? Оставьте дробь в виде соотношения, 3:5 = Числитель: 30Ты Вы можете видеть, что для изменения знаменателя с 5 на 30 вам нужно умножить 5 на 6, поэтому числитель дроби, которую вам нужно найти, также должен быть умножен на 6.

Какие три дроби эквивалентны 3 5?

Таблица преобразования десятичных и дробных чисел

Доля	Эквивалентные дроби
3/5	6/10	9/15
4/5	8/10	12/15
1/6	2/12	3/18
5/6	10/12	15/18

Как вы работаете 3/5 в виде десятичной дроби? Чтобы преобразовать любую дробь в десятичную форму, достаточно разделить ее числитель на знаменатель. Здесь дробь 3/5, что означает, что нам нужно выполнить 3 ÷ 5. Это дает ответ как 0.6. Итак, 3/5 в десятичном виде равно 0.6.

Какое соотношение 2 и 3?

2 + 3 = 5. Наше соотношение 2:3 содержит всего 5 частей.

Как разделить 3 на 5 разделить на? Чтобы преобразовать любую дробь в десятичную форму, достаточно разделить ее числитель на знаменатель. Здесь дробь 3/5, что означает, что нам нужно выполнить 3 ÷ 5. Это дает ответ как 0.6. Итак, 3/5 в десятичном виде равно 0.6.

Что такое 5 и 3/5 как неправильная дробь?

Сначала преобразуйте смешанное число 535 5 3 5 в неправильную дробь, умножив знаменатель (5) на целую часть (5) и добавив числитель (3), чтобы получить новый числитель. Поместите новый числитель (28) над старым знаменателем (5).

Что такое 3/5 в целом числе?

3/5 = 0.6.

Как найти 3/5 числа? Вы можете либо умножить число на 3, а затем делить на 4 или разделите число на 4, а затем умножьте его на 3. Например, 3/4 x 20 = 3 x (20/4) = 3 x 5 = 15.

Что такое 3/5 в десятичной системе счисления? Ответ: 3/5 в виде десятичной дроби 0.6.

Чему равна дробь 3/5, имеющая числитель 24?

Ответ: Эквивалентная дробь 3/5, имеющая числитель 24, равна 40.

Чему равна дробь 3 на 5 со знаменателем 20? Найдите эквивалентную дробь 3/5 со знаменателем 20. Пусть искомая дробь равна х/20. Следовательно, искомая дробь 12/20.

Как записать 3/5 в виде эквивалентной дроби?

Ответ: Дроби, эквивалентные 3/5, равны 6/10, 9/15, 12/20 и т.д. Эквивалентные дроби имеют одинаковое значение в сокращенном виде. Объяснение: Эквивалентные дроби можно записать, умножив или разделив числитель и знаменатель на одно и то же число.

Чему равно 3 разделить на 5 в виде дроби? Ответ: Значение 3, деленное на 5 как дробь, равно 3 / 5.

Какая дробь не равна 3 на 5?

Ответ: д.

15/24 не является эквивалентной дробью 3/5.

Как рассчитать 3/5 в процентах? Ответ: 3/5 выражается как 60% в процентном отношении.

Преобразуем дробь 3/5 в проценты. Объяснение: Давайте изменим дробь 3/5 на эквивалентную дробь со знаменателем, равным 100. Теперь 60/100 выражается как 60% в процентах.

Какое соотношение эквивалентно 4 5?

Ответ: Дроби, эквивалентные 4/5, равны 8/10, 12/15,16/20 и т.д. Равные дроби имеют одинаковое значение в сокращенной форме. Объяснение: Равные дроби можно записать, умножив или разделив числитель и знаменатель на одно и то же число.

Какое соотношение сторон 4 5? Так, например, соотношение сторон, записанное как 4:5, имеет значение 4/5 = 0.8 .
…
Каковы допустимые диапазоны соотношения сторон в Instagram?

	Диапазон соотношения сторон	Диапазон соотношения сторон в виде числовых значений
Фотографии	Между 4: 5 и 1.91: 1	Между 0.8 и 1.91
Видео	Между 4: 5 и 16: 9	Между 0.8 и 1.78

Что такое соотношение 1 к 5?

Это соотношение. Сообщает вам взаимосвязь между двумя величинами, т.е. одна часть чего-то на каждые 5 частей другого. Так может быть 1 жидкость 5 лимонада с XNUMX жидкостью XNUMX пива.

Упрощение коэффициентов

Базовый калькулятор

Упрощение коэффициентов

введите целые числа, десятичные дроби или дроби

Термин A

:

Термин B

Ответ:

5 : 3 1/8 = 8 : 5

---

Решение:

---

Изменить значения на целые числа.

Преобразование любых смешанных чисел в дроби.

Преобразование 3 1/8

3 1/8 = 25/8

Теперь у нас есть:

5 : 3 1/8 = 5 : 25/8

Преобразование целого числа 5 с 1 в знаменателе.

Тогда имеем:

5 : 3 1/8 = 5/1 : 25/8

Преобразование дробей в целые числа путем удаления знаменателей.

Наши две дроби имеют разные знаменатели, поэтому мы находим наименьший общий знаменатель и при необходимости переписываем наши дроби с общим знаменателем

LCD(5/1, 25/8) = 8

Теперь у нас есть: 3 1/8 = 40/8 : 25/8

Наши две дроби теперь имеют одинаковые знаменатели, поэтому мы можем умножить обе на 8, чтобы исключить знаменатели.

Тогда мы имеем:

5 : 3 1/8 = 40 : 25

Попробуйте еще уменьшить отношение с помощью наибольшего общего множителя (НОД).

GCF 40 и 25 равен 5

Разделите оба члена на GCF, 5:
40 ÷ 5 = 8
25 ÷ 5 = 5

Отношение 40 : 25 можно привести к наименьшему выражению, разделив оба члена по GCF = 5 :

40 : 25 = 8 : 5

Следовательно:

5 : 3 1/8 = 8 : 5

Как этот калькулятор может быть лучше?

Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.

Получить виджет для этого калькулятора

© Calculator Soup

Поделитесь этим калькулятором и страницей

Калькулятор Используйте

Используйте этот калькулятор для упрощения отношений формы A : B. A или B могут быть целыми числами, целыми числами, десятичными числами, дробями или смешанными числами. Они могут быть разных типов, например, одна дробная и одна десятичная. Значения отношения могут быть положительными или отрицательными.

Этот калькулятор упрощает соотношения, преобразуя все значения в целые числа, а затем уменьшая целые числа до наименьших членов с использованием наибольшего общего множителя (НОД). Полное решение показывает всю работу и шаги, чтобы получить соотношение в простейшей форме.

Что такое коэффициент?

Отношение — это сравнение значений двух чисел. Отношение А : В читается как «А к В» и описывает относительную пропорцию двух сумм.

Как упростить отношение A : B, когда A и B являются целыми числами

• Перечислите факторы A
• Перечислите факторы B
• Найдите наибольший общий делитель A и B, GCF(A, B)
• Разделить А и В на GCF
• Используйте целые числа, чтобы переписать соотношение в простейшей форме

Если GCF = 1, то отношение уже имеет простейшую форму.

Как упростить отношение A : B, если A и B не являются целыми числами, в этом порядке

• Если A или B смешанные числа преобразовать смешанные числа в неправильные дроби
• Если A или B являются десятичными числами, умножьте оба значения на один и тот же коэффициент 10, что удалит все десятичные разряды
• Если одно значение представляет собой дробь, а другое — целое число, уменьшите дробь до целого числа, если можете, или превратите целое число в дробь, придав ему знаменатель, равный 1.
• Если и A, и B являются дробями и имеют одинаковые знаменатели, умножьте обе дроби на знаменатель, чтобы исключить его, и у вас останется два целых числа
• Если и A, и B являются дробями и имеют разные знаменатели, найдите LCD(A, B) и переписать дроби с LCD в знаменателе. Умножьте обе дроби на знаменатель, чтобы исключить его, и у вас останется два целых числа.
• Если и A, и B целые числа, Найдите наибольший общий делитель A и B, GCF(A, B) и разделить A и B на GCF

Пример: Упростите отношение 6 : 10

• Делители 6: 1, 2, 3, 6
• Делители 10: 1, 2, 5, 10
• Тогда наибольший общий делитель 6 и 10 равен 2
• Разделите оба члена на 2
• 6 ÷ 2 = 3
• 10 ÷ 2 = 5
• Перепишите соотношение, используя результаты. Упрощенное соотношение 3 : 5.
• 6 : 10 = 3 : 5 в простейшей форме

Пример: Упростите соотношение 8 : 36

• Делители 8: 1, 2, 4, 8
• Делители числа 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
• Наибольший общий делитель чисел 8 и 36 равен 4
• Разделить оба слагаемых на 4
• 8 ÷ 4 = 2
• 36 ÷ 4 = 9
• Перепишите соотношение, используя результаты. Упрощенное соотношение 2 : 9.
• 8 : 36 = 2 : 9 в простейшей форме

Пример: Упростите соотношение 3 : 8

• Коэффициенты 3 равны 1, 3
• Делители 8: 1, 2, 4, 8
• Наибольший общий делитель чисел 3 и 8 равен 1
• Разделить оба члена на 1
• 3 ÷ 1 = 3
• 8 ÷ 1 = 8
• Перепишите соотношение, используя результаты. Соотношение 3 : 8 уже упрощено.

Можно сделать вывод, что если наибольший общий делитель равен 1, то отношение уже имеет простейшую форму.

Связанные калькуляторы

Чтобы сравнить несколько коэффициентов, см. Калькулятор соотношения.

Чтобы преобразовать дробь в сокращенную дробь или смешанное число, используйте наш Калькулятор упрощенных дробей.

 

Подписаться на калькуляторSoup:

Калькулятор эквивалентного коэффициента

| iCalculator™

Эквивалентные отношения или равные отношения — это два отношения, которые выражают то же отношение между числами, которое мы рассмотрели в нашем руководстве по увеличению коэффициентов. Формула соотношения и руководство по соотношению приведены под калькулятором соотношения. Вы можете использовать этот калькулятор эквивалентных соотношений для решения проблем с соотношениями и/или пропорциями путем сравнения отношения с эквивалентным отношением тех же пропорций, где числитель и знаменатель представляют собой прямое произведение умножаемого значения (m _х ).

Ищете другой тип калькулятора коэффициентов или учебник? Воспользуйтесь приведенными ниже быстрыми ссылками, чтобы получить доступ к другим калькуляторам отношений

Сложить отношения Вычесть отношения Умножить отношения Разделить отношения Упростить отношения Эквивалентные отношения Преобразовать отношения Объяснение отношений

Из нашего набора калькуляторов отношений этот калькулятор отношений имеет следующие функции:

После использования эквивалента Калькулятор отношений, другие пользователи сочли полезными эти калькуляторы отношений:

Как рассчитать эквивалентные отношения

Как мы уже упоминали ранее, эквивалентные отношения представляют собой два отношения, которые выражают одно и то же отношение между числами . Калькулятор эквивалентного отношения предоставляет таблицу эквивалентных отношений, которые имеют одинаковые отношения друг с другом и непосредственно с отношением, которое вы вводите в калькулятор. Вскоре мы рассмотрим, как рассчитать эквивалентные коэффициенты, сначала давайте посмотрим, как использовать бесплатный онлайн-калькулятор эквивалентных коэффициентов:

1. Введите соотношение в калькулятор эквивалентных соотношений, например, вы можете ввести 7:25
2. Выберите количество эквивалентных соотношений, которые вы хотели бы видеть в таблице результатов
3. Калькулятор эквивалентного отношения рассчитает, как вы введите и создайте список эквивалентных соотношений в таблице под калькулятором
4. [Необязательно] Распечатайте или отправьте по электронной почте Таблицу эквивалентных соотношений для последующего использования

Как мы видим, использование калькулятора эквивалентных соотношений — это быстрый и простой способ рассчитать эквивалентные отношения. Это полезно для быстрой математики, но вы можете рассчитать эквивалентное отношение вручную. Очень важно понимать математическую формулу и расчеты, особенно математику соотношений, поскольку соотношения используются в значительном количестве бизнес-расчетов, финансовых расчетов и общих повседневных расчетов, например: миль в час, ваш ИМТ, сумма денег, которую вы доля или сладости, которыми вы делитесь с друзьями, все это хорошие примеры отношений. Если вы все еще работаете над арифметикой в ​​уме и ручным расчетом коэффициента, мы предлагаем вам сначала ввести коэффициент в калькулятор, чтобы увидеть результаты, а затем выполнить математические вычисления вручную, используя формулу эквивалентного коэффициента. Таким образом, вы сможете проверить свои ответы и укрепить свою уверенность.

Как вручную рассчитать эквивалентные соотношения

При расчете эквивалентных соотношений важно понимать, что математически вы выражаете одно и то же отношение, просто в разных количествах. например, если у вас есть 10 сладостей, которыми можно поделиться с 4 друзьями, это то же самое, что и 5 сладостей, которыми можно поделиться с 2 друзьями в соотношении. Хотя количества различаются, соотношение числителя и знаменателя одинаково (в данном случае оба можно разделить на 2). Важно помнить, что эквивалент буквально означает равенство, поэтому вы рассчитываете одно и то же соотношение, выраженное в разных величинах. Это может быть достигнуто только путем умножения деления.

Поскольку коэффициенты эквивалентности имеют одинаковое значение, технически не существует формулы коэффициента эквивалентности, но следующая формула коэффициента эквивалентности поможет вам в математических вычислениях вручную.

Формула эквивалентного отношения

Ранее мы рассмотрели числитель и знаменатель в Калькуляторе дробей, если вы не знакомы с числителем и знаменателем или просто хотите освежить свою память, пожалуйста, просмотрите эту статью и вспомогательный калькулятор, прежде чем продолжить.

N: D = N ^A : D ^A

, где

• N = Число
• D = Denominator
• D = DENOMINATO можно увидеть, что, умножая и числитель, и знаменатель на одну и ту же сумму (а), мы сохраняем соотношение со всеми эквивалентными отношениями и нашим начальным соотношением, с которого мы начали расчет

  More Good Ratio Calculators

  Если вы обнаружили калькулятор эквивалентного соотношения, вы, вероятно, обнаружите, что калькуляторы по отношению к следующему соотношению калькуляторы

• Калькулятор эквивалентного соотношения
• . Калькулятор
• Калькулятор золотого сечения

Что такое соотношение?

Отношение — это прямое сравнение одного числа с другим. Калькулятор соотношений пытается определить отношение, которое сравнивается между этими двумя числами

Где используются расчеты коэффициентов?

Соотношения используются везде, от приготовления пищи по вашим любимым рецептам до строительства жилья, вот некоторые распространенные применения соотношений в повседневной жизни:

• Механика: все гаечные ключи отмечены соответствующими соотношениями, которые соответствуют гайкам, которые они используют. поместиться.
• Предприятия и бухгалтеры: используют коэффициенты для прогнозирования и финансового контроля (коэффициент расходов, коэффициент оборачиваемости, коэффициент долга, коэффициент активов, коэффициент цен, коэффициент прибыли и т. д.)
• Еда: правильная диета имеет правильное соотношение групп продуктов питания (одна из пяти групп в день является общепринятым соотношением, с которым мы все знакомы).
• Веб-разработчики/специалисты по поисковой оптимизации: эти технические ребята живут и дышат отношениями, от показателей отказов до времени на сайте, новых посетителей и вернувшиеся посетители, пропорции управляют их жизнью.0121

Как рассчитать отношения

При расчете эквивалентных отношений вы должны умножить или разделить оба числа в соотношении. Это удерживает оба числа в прямой зависимости друг от друга. Таким образом, отношение 2/3 имеет эквивалентное отношение 4/6: в этом расчете отношения мы просто умножили и 2, и 3 на 2.

Как найти отношение

Все математические ресурсы GRE

13 Диагностические тесты 452 практических теста Вопрос дня Карточки Учитесь по концепции

← Предыдущая 1 2 Следующая →

GRE Math Help » Арифметика » Фракции » Пропорция / Отношение / Скорость » Как найти соотношение

1 : 1

2 : 3

3 : 4

1 : 3

В комнате 28 учеников. Соотношение мальчиков и девочек не может быть ни одним из вышеперечисленных.

Возможные ответы:

3 : 4

2 : 3

1 : 3

1 : 1

Правильный ответ:

2 : 3

Объяснение:

При выборе соотношений для двух переменных (мальчики и девочки) две части соотношения должны в сумме составлять коэффициент общего числа учащихся. Множители числа 28 включают 14, 7, 4 и 2. (1 + 1 = 2 ), (2 + 3 = 5 ), (3 + 4 = 7 ) и (1 + 3 = 4 ). 5 является единственным нефактором и не может быть отношением мальчиков к девочкам, что делает 2 : 3 правильным ответом.

Сообщить об ошибке

Для All Sweets Bakery ежедневное соотношение продаж хлеба и пирожных составляет 5:2. Если во вторник пекарня продает на 12 буханок хлеба больше, чем ежедневно продает 40 буханок, то сколько пирожных было продано во вторник? (округлить до ближайшего целого числа)

Возможные ответы:

Правильный ответ:

Объяснение:

Поскольку ежедневно продается 40 буханок хлеба, а соотношение хлеба и пирожных составляет 5:2, то пирожные продаются ежедневно.

Таким же образом используя отношение, мы можем найти дополнительное количество проданных тортов:

  тортов с приближением.

Таким образом, общее количество тортов, проданных во вторник, равно тортам.

Сообщить об ошибке

Вы готовите торт, для которого по объему требуется в три раза больше муки, чем сахара, в два раза больше сахара, чем молока, в восемь раз больше молока, чем разрыхлителя и в два раза больше разрыхлителя, чем соли. Если вы начнете с чайной ложки соли, сколько чашек муки вам понадобится (в одной чашке 48 чайных ложек)?

Возможные ответы:

Правильный ответ:

Пояснение:

На одну чайную ложку соли требуется 2 чайные ложки разрыхлителя, что требует 16 чайных ложек молока и 32 чайных ложек сахара. На 32 чайные ложки сахара требуется 96 чайных ложек муки, что равняется двум чашкам муки.

Сообщить об ошибке

В пекарне есть 3 печенья на каждые 2 кекса и 6 пирожных на каждые 5 печенек. Каково соотношение капкейков и выпечки?

Возможные ответы:

Правильный ответ:

Объяснение:

Во-первых, вы должны установить заданные соотношения: 3 печенья: 2 кекса и 5 печенья: 6 пирожных. Затем вы находите общее кратное печенья (то есть 15) и конвертируете отношения в 15 печений: 10 кексов и 15 печений: 18 пирожных. Поскольку оба соотношения теперь имеют 15 печений, вы можете сделать вывод, что соотношение кексов и выпечки составляет 10:18 или 5:9..

Сообщить об ошибке

Соотношение учащихся мужского и женского пола в классе составляет 13 к 19. Если в классе 224 человека, включая одного учителя, одного администратора и тридцать оценщиков, сколько человек в классе студенты мужского пола?

Возможные ответы:

80

114

91

78

133

Правильный ответ:

78

Объяснение:

Начните с устранения людей в классе, которые не являются учениками. Вычитая 1 учителя, 1 администратора и 30 оценщиков, остается 192 ученика.

Нам также необходимо определить соотношение студентов мужского пола к общему количеству студентов на основе информации, содержащейся в вопросе. Из каждых тридцати двух студентов тринадцать мужчин.

Теперь мы можем составить пропорцию и найти количество студентов мужского пола.

Сообщить об ошибке

Если длину прямоугольника увеличить на 50 %, а ширину уменьшить на 20 %, каково отношение площади нового прямоугольника к площади исходного прямоугольника?

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала выберите исходную длину и ширину. Для простоты вы можете выбрать длину 1 и ширину 1, что даст площадь 1. Если мы увеличим длину на 50% и уменьшим ширину на 20%, то размеры нового прямоугольника будут be , что дало бы ему площадь 1,2. Таким образом, отношение нового прямоугольника к исходному прямоугольнику равно 6:5

Сообщить об ошибке

В группе A 3500 человек, в группе B 5000 человек:

Тип автомобиля	% в Группе А Кто владеет	% в Группе B Кто владеет
Мотоцикл	4	9
Седан	35	25
Минивэн	22	15
Фургон	9	12
Купе	3	6

Каково отношение количества людей в группе А с мотоциклами и фургонами к общему количеству людей в обеих группах с мотоциклами и фургонами?

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала найдите общее количество владельцев мотоциклов и фургонов каждой группы отдельно:

Группа A:

Группа B:

Теперь у нас есть отношение, которое должно быть: 3

3

2

 

Сообщить об ошибке

Десерт готовится из 2 частей торта и 3 частей глазури. Торт содержит 4 части сахара, 5 частей молока и 11 частей других ингредиентов. Глазурь содержит 3 части сахара, 2 части молока и 15 частей других ингредиентов. Какая величина больше?

Количество A: Части сахара в десерте

Количество B: Части молока в десерте

Возможные ответы:

На основе предоставленной информации невозможно определить взаимосвязь.

Количество A больше.

Количество B больше.

Обе величины равны.

Правильный ответ:

Количество A больше.

Объяснение:

Количество A: Чтобы определить части сахара в десерте, мы используем следующий процесс. Давайте сначала выясним количество сахара в торте. Это 4/20. Далее найдите количество сахара в глазури: 3/20. Затем нам нужно учесть количество торта и глазури в десерте. Используя тот факт, что есть 2 части торта и 3 части глазури, мы можем сказать, что 2/5 части десерта — это торт, а 3/5 — глазурь.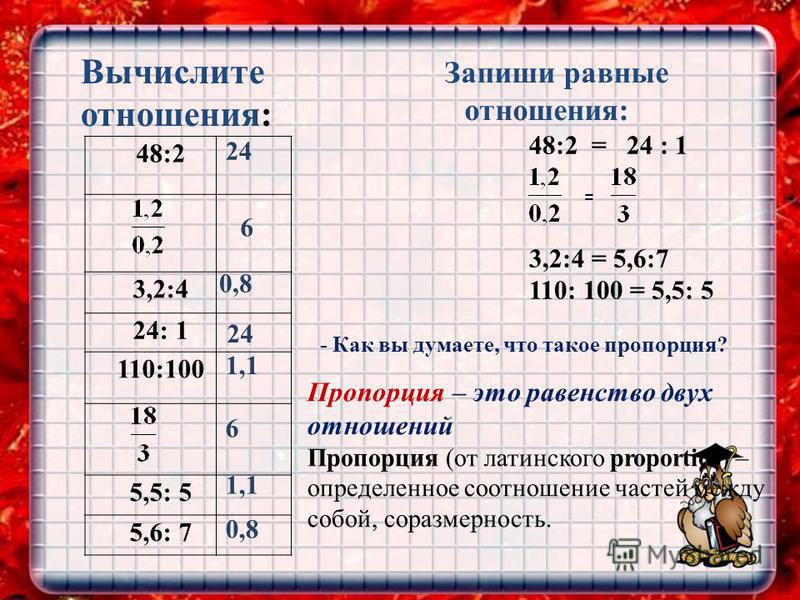 Объединив эту информацию с количеством сахара как в торте, так и в глазури, мы получим: 2/5 * 4/20 + 3/5 * 3/20 = 17/100. Итак, в десерте 17 частей сахара.

Количество B: Используйте тот же метод, чтобы найти количество молока: 2/5 * 5/20 + 3/5 * 2/20 = 16/100. Итак, в десерте 16 частей молока. Таким образом, количество А больше.

Сообщить об ошибке

Отношение числа финансовых работников, оставшихся на той же должности от 2 до 9 лет, к числу строителей, оставшихся на той же должности от 0 до 4 лет, ближе всего к следующее?

Возможные ответы:

Правильный ответ:

Объяснение:

Для этой задачи нам нужно найти количество сотрудников, подпадающих под описанные категории, имея в виду, что для этого необходимо разместить несколько частей круговой диаграммы. Затем мы можем представить их в пропорции:

Для части финансовой индустрии «от 2 до 9 лет» включите

(0,2 + 0,18)(12 000 000) = 4 560 000 рабочих.

No related posts.