Поверхности второго порядка онлайн: Построить поверхность второго порядка

Содержание

Поверхности второго порядка — презентация онлайн

1. §17. Поверхности второго порядка

Поверхностью второго порядка называется геометрическое
место точек в пространстве, декартовы координаты которых
удовлетворяют уравнению
F(x,y,z) = 0, где F(x,y,z) –
многочлен степени 2.
в общем случае уравнение поверхности 2-го порядка имеет
вид:
a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz+2a10x+2a20y+2a30z+a00=0 .
Поверхности второго порядка делятся на
1) вырожденные
и
2) невырожденные
Вырожденные поверхности второго порядка это плоскости и
точки, которые задаются уравнением второй степени. Если
уравнению второго порядка не удовлетворяет ни одна точка
пространства, то тоже говорят, что уравнение определяет
вырожденную поверхность (мнимую поверхность второго
порядка).
Невырожденными
поверхности
второго
порядка
подразделяются на пять типов.

2. 1. Эллипсоид

ОПРЕДЕЛЕНИЕ. Эллипсоидом называется геометрическое
место точек пространства, координаты которых в
некоторой декартовой системе координат удовлетворяют
уравнению
x2 y2 z 2
(1)
2 2 1,
2
a
b
c
где a, b, c – положительные константы.

Система координат, в которой эллипсоид имеет уравнение (1)
называется его канонической системой координат, а
уравнение (1) – каноническим уравнением эллипсоида.
z
C2
A1
B1
x
A2
B2
y
C1
Величины a, b и c называются полуосями эллипсоида.
Если все они различны, то эллипсоид называется трехостным.
Если две из трех полуосей равны, эллипсоид является
поверхностью вращения.
Он получается в результате
вращения эллипса вокруг одной из своих осей.
Эллипсоид, у которого все три полуоси равны, называют
сферой.
Каноническое уравнение сферы принято записывать в виде
x2 + y2 + z2 = r2 ,
где r – величина полуосей, которая называется радиусом
сферы.
С геометрической точки зрения, сфера – геометрическое место
точек пространства, равноудаленных (на расстояние r) от
некоторой фиксированной точки (называемой центром). В
канонической системе координат сферы, центр – начало
координат.

5.

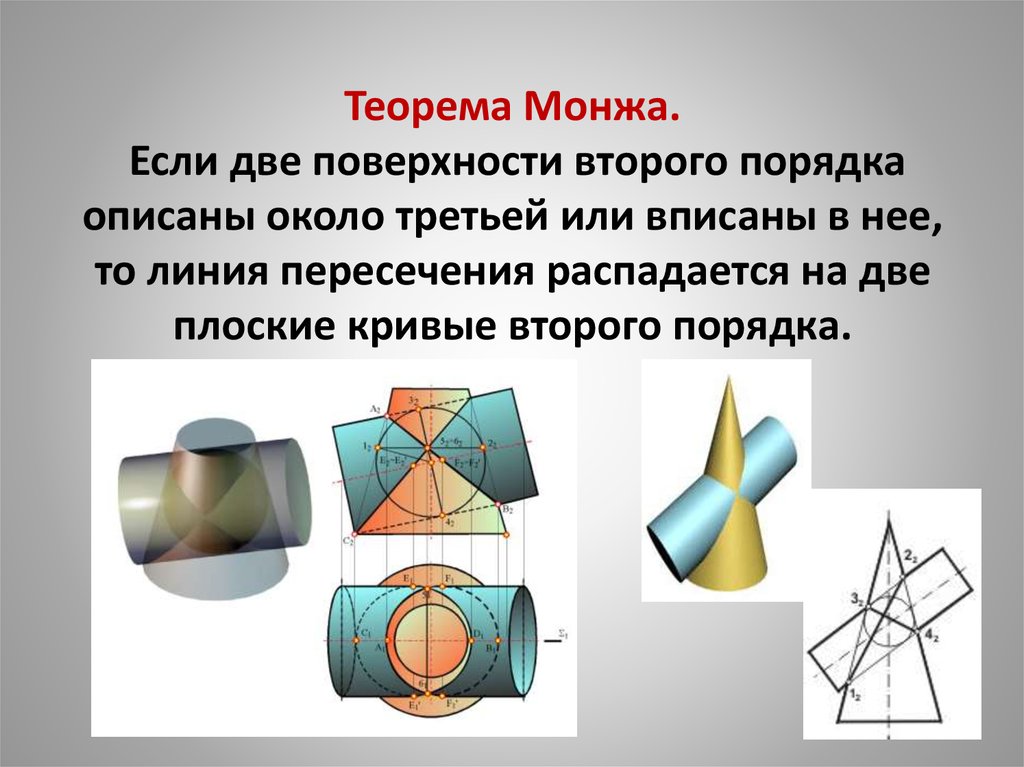2. ГиперболоидыОПРЕДЕЛЕНИЕ. Однополостным гиперболоидом называется
геометрическое место точек пространства, координаты
которых в некоторой декартовой системе координат
удовлетворяют уравнению
x2 y 2 z 2
(2)
2 2 1 ,
2
a
b
c
где a, b, c – положительные константы.
Система координат, в которой однополостный гиперболоид
имеет уравнение (2) называется его канонической системой
координат, а уравнение (2) – каноническим уравнением
однополостного гиперболоида.
Величины a, b и c называются
полуосями
однополостного
гиперболоида.
Если
a=b,
то
однополосный
гиперболоид
является
поверхностью вращения.
Он
получается в результате вращения
гиперболы
y2 z2
2 1
2
b
c
вокруг своей мнимой оси.
z
a
x
b
y
Замечание. Уравнения
x2 y 2 z 2
x2 y 2 z 2
2 2 1 и 2 2 2 1
2
a
b
c
a
b
c
тоже определяют однополостные
гиперболоиды, но они «вытянуты»
вдоль оси Oy и Ox соответственно.

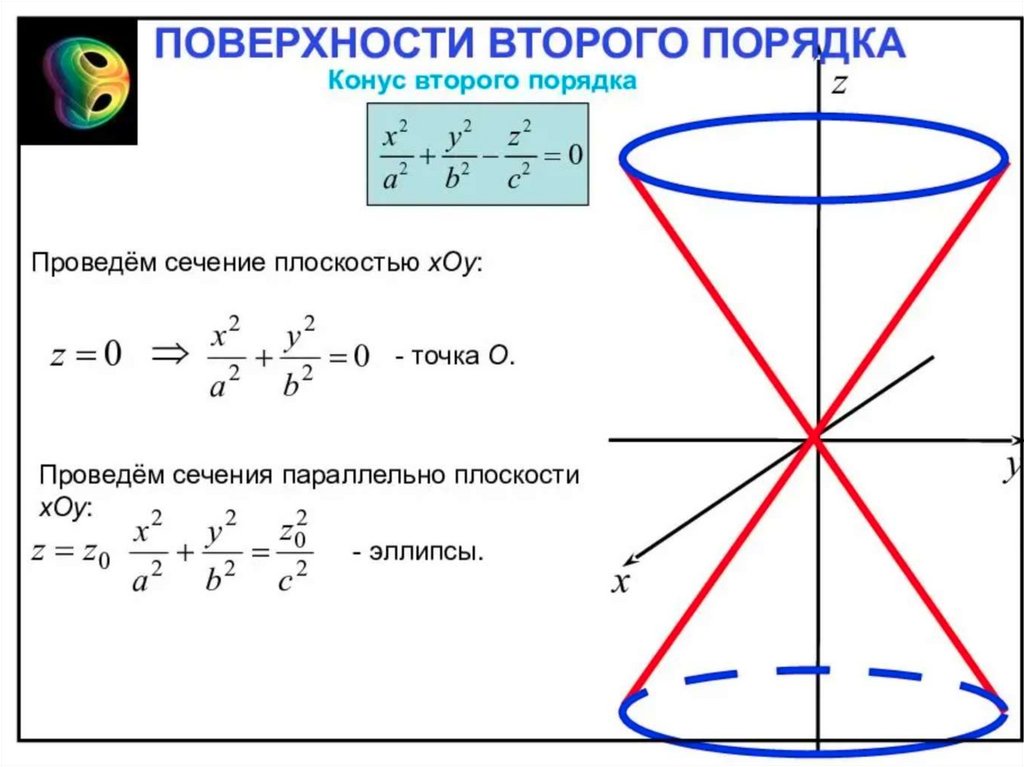
ОПРЕДЕЛЕНИЕ. Двуполостным гиперболоидом называется
геометрическое место точек пространства, координаты
которых в некоторой декартовой системе координат
удовлетворяют уравнению
x2 y 2 z 2
(3)
2 2 1 ,
2
a
b
c
где a, b, c – положительные константы.
Система координат, в которой двуполостный гиперболоид имеет
уравнение (3) называется его канонической системой
координат, а уравнение (3) – каноническим уравнением
двуполостного гиперболоида.
z
c
y
x
Величины a, b и c называются
полуосями
двуполостного
гиперболоида.
Если
a=b,
то
двуполостный
гиперболоид
является
поверхностью вращения.
Он
получается в результате вращения
гиперболы
y2 z2
2 2 1
b
c
вокруг своей действительной оси.
Замечание. Уравнения
x2 y 2 z 2
x2 y 2 z 2
2 2 1 и 2 2 2 1
2
a
b
c
a
b
c
тоже определяют двуполостные
гиперболоиды, но они «вытянуты»
вдоль оси Oy и Ox соответственно.

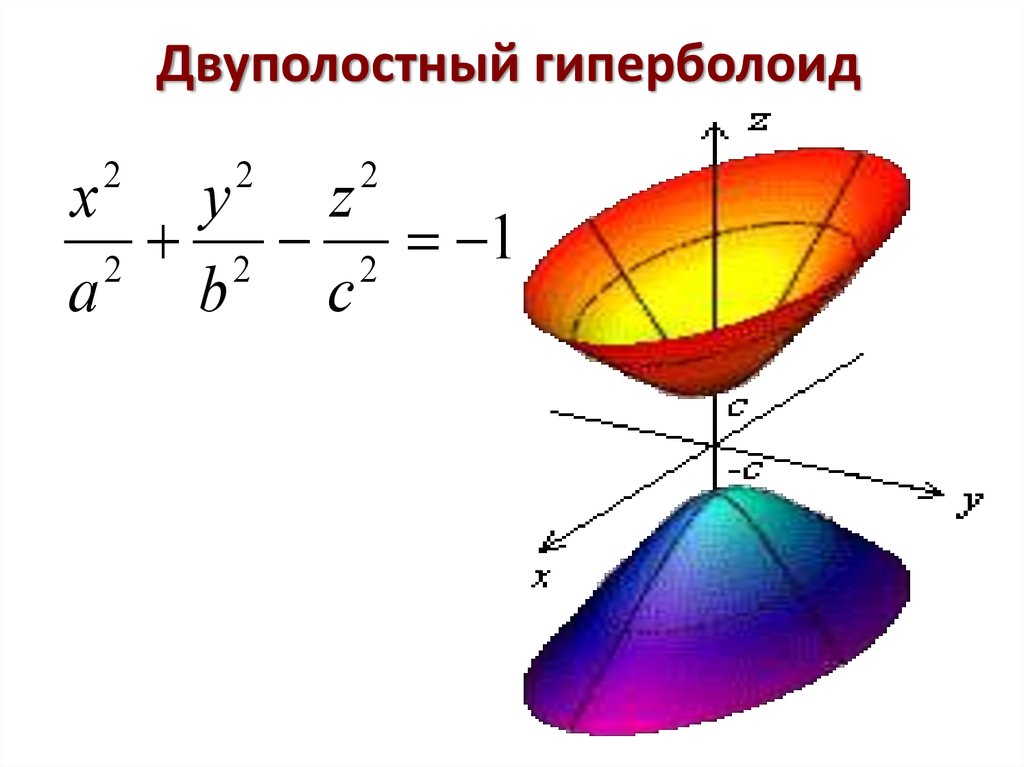
9. 3. Конус

ОПРЕДЕЛЕНИЕ. Конусом называется геометрическое место
точек пространства, координаты которых в некоторой
декартовой системе координат удовлетворяют уравнению
x2 y 2 z 2
(4)
2 2 0,
2
a
b
c
где a, b, c – положительные константы.
Система координат, в которой конус имеет уравнение (4)
называется его канонической системой координат, а
уравнение (4) – каноническим уравнением конуса.
z
Величины a, b и c называются
полуосями
конуса.
Центр
симметрии
O называется
вершиной конуса.
Если a=b, то конус является
поверхностью вращения.
Он
получается
в
результате
вращения прямой
y
x
c
z y
вокруг оси Oz . b
Замечание. Уравнения
x2 y 2 z 2
x2 y 2 z 2
2 2 0 и 2 2 2 0
2
a
b
c
a
b
c
тоже определяют конусы, но они
«вытянуты» вдоль оси Oy и Ox
соответственно.

11. 4. Параболоиды

ОПРЕДЕЛЕНИЕ.

Эллиптическим параболоидом называется
геометрическое место точек пространства, координаты
которых в некоторой декартовой системе координат
удовлетворяют уравнению
x2 y 2
(5)
2 2z ,
2
a
b
где a, b – положительные константы.
Система координат, в которой эллиптический параболоид имеет
уравнение (5) называется его канонической системой
координат, а уравнение (5) – каноническим уравнением
эллиптического параболоида.
Величины a и b называются
z
параметрами параболоида. Точка O
называется вершиной параболоида.
Если a=b, то параболоид является
поверхностью вращения.
Он
получается в результате вращения
параболы y 2 2b 2 z вокруг оси Oz.
x2 y 2
Замечания: 1) Уравнение 2 2 2 z
a
b
тоже
определяет
эллиптический
параболоид, но «развернутый» вниз.
y
2) Уравнения
2
2
x
z
y2 z2
2 2 y и 2 2 2 x
2
a
c
b
c
x
определяют эллиптические параболоиды,
с осями симметрии
Oy
и
Ox
соответственно.

Эллиптический параболоид это поверхность, которая получается
при движении одной параболы вдоль другой (вершина
параболы скользит по параболе, оси подвижной и неподвижной
параболы параллельны, ветви направлены в одну сторону).
ОПРЕДЕЛЕНИЕ. Гиперболическим параболоидом называется
геометрическое место точек пространства, координаты
которых в некоторой декартовой системе координат
удовлетворяют уравнению
x2 y 2
(6)
2 2z ,
2
a
b
где a, b – положительные константы.
Система координат, в которой гиперболический параболоид
имеет уравнение (6) называется его канонической системой
координат, а уравнение (6) – каноническим уравнением
гиперболического параболоида.
z
Величины a и b называются
параметрами параболоида.
Замечания: 1) Уравнение
x2 y 2
2 2 z
2
a
b
тоже определяет параболоид,
но «развернутый» вниз.
2) Уравнения
z 2 x2
y2 z2
2 2 y и 2 2 2 x
2
b
c
y c a
определяют
параболоиды,
x
«вытянутые» вдоль осей Oz
и Oy соответственно.

Гиперболический параболоид это поверхность, которая
получается при движении одной параболы вдоль другой
(вершина параболы скользит по параболе, оси подвижной и
неподвижной параболы параллельны, ветви направлены в
разные стороны).

15. 5. Цилиндры

ОПРЕДЕЛЕНИЕ.
Цилиндрической
поверхностью
(цилиндром) называется поверхность, которую описывает
прямая
(называемая
образующей),
перемещающаяся
параллельно самой себе вдоль некоторой кривой (называемой
направляющей) .
Цилиндры называют по виду направляющей: круговые,
эллиптические, параболические, гиперболические.
z
z
y
x
y
x
Цилиндр в некоторой декартовой системе координат задается
уравнением, в которое не входит одна из координат. Кривая,
которую определяет это уравнение в соответствующей
координатной плоскости, является направляющей цилиндра;
а образующая – параллельна оси отсутствующей
координаты.

Поверхности вращения, цилиндрические и канонические поверхности

Автор: Елена 0 6733

Рассмотрим поверхности, которые задаются уравнением второго порядка. Это цилиндрические поверхности, канонические и поверхности вращения.

Помощь в написании работы

О чем статья

Цилиндрическая поверхность

Цилиндрическая поверхность – это поверхность, которая образована прямыми, – образующими, параллельными заданной прямой и они пересекают данную кривую линию – направляющую (см. рис. 1).

Рис. 1

В общем случае уравнение цилиндрической поверхности записывается .

В отдельных случаях, когда образующие цилиндрические поверхности параллельны одной из координатных осей, тогда у уравнения цилиндрической поверхности есть только две переменные. Причём, образующие цилиндрические поверхности параллельны той координатной оси, переменная которой в уравнении отсутствует:

– цилиндрическая поверхность с образующими ;

– цилиндрическая поверхность с образующими .

Канонические поверхности

Канонические поверхности – это поверхности, которые образованы прямыми, образующими конуса, и которые проходят через данную точку – вершину конуса, – и пересекают данную кривую линию – направляющую конуса.

Допустим, – эллиптический конус (см. рис. 2), ось – ось симметрии, вершина в точке за направляющую можно взять линию – эллипс в плоскости .

Рис. 2

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Поверхности вращения

Пусть в плоскости задана линия уравнением . Чтобы получить поверхность вращения линии вокруг, например, оси необходимо вместо переменной поставить в уравнение выражение . Уравнение описывает поверхность вращения линии вокруг оси (см. рис. 3).

Рис. 3

Поверхности второго порядка и их уравнения

Рассмотрим поверхности второго порядка и какие у них уравнения, которые считаются основными для решения задач:

1. Сфера – :

2. Эллипсоид – :

3. Однополостный гиперболоид – :

4. Двуполостный гиперболоид – :

5.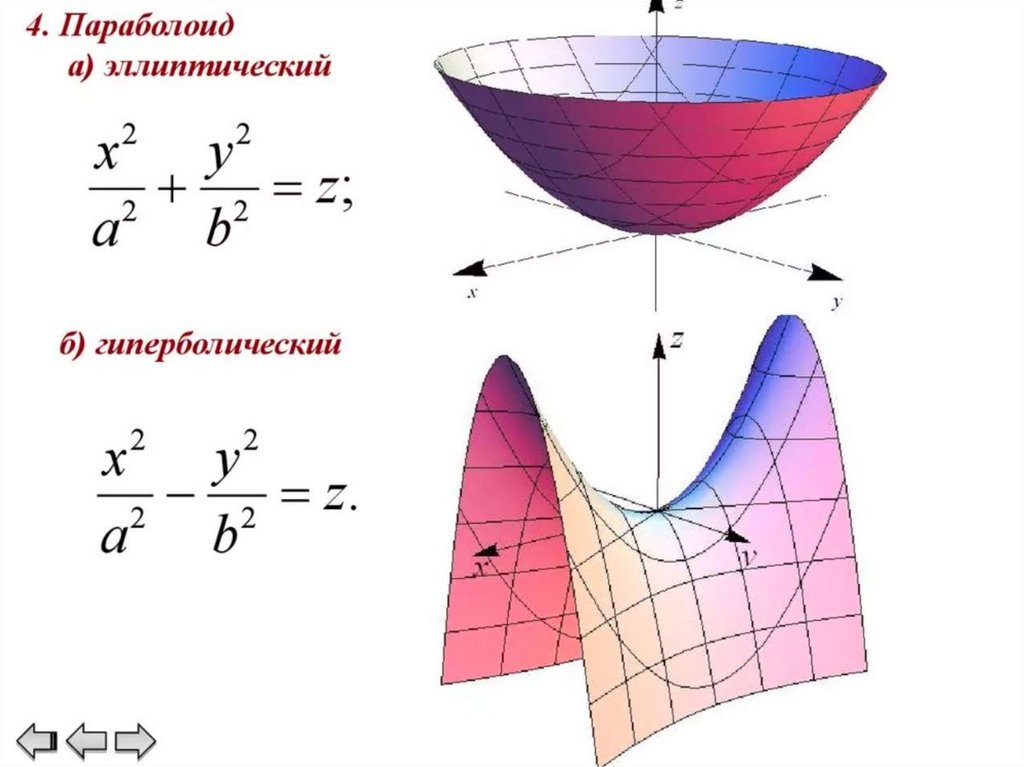 Гиперболический параболоид – :

6. Конус – :

7. Эллиптический параболоид –

Примеры решения задач

Пример 1

Задача

Составить уравнение цилиндрической поверхности, у которой направляющая лежит в плоскости и имеет уравнение , а образующие параллельны вектору .

Решение

Согласно условию задачи и тогда, по формуле у уравнения данной цилиндрической поверхности будет такой вид:

В итоге получается:

Ответ

Уравнение цилиндрической поверхности имеет такой вид:

Пример 2

Задача

Определить вид поверхности .

Решение

Необходимо данное уравнение привести к соответствующему виду:

Это уравнение в пространстве определяет эллиптическую цилиндрическую поверхность с направляющей в плоскости и образующими, параллельными оси .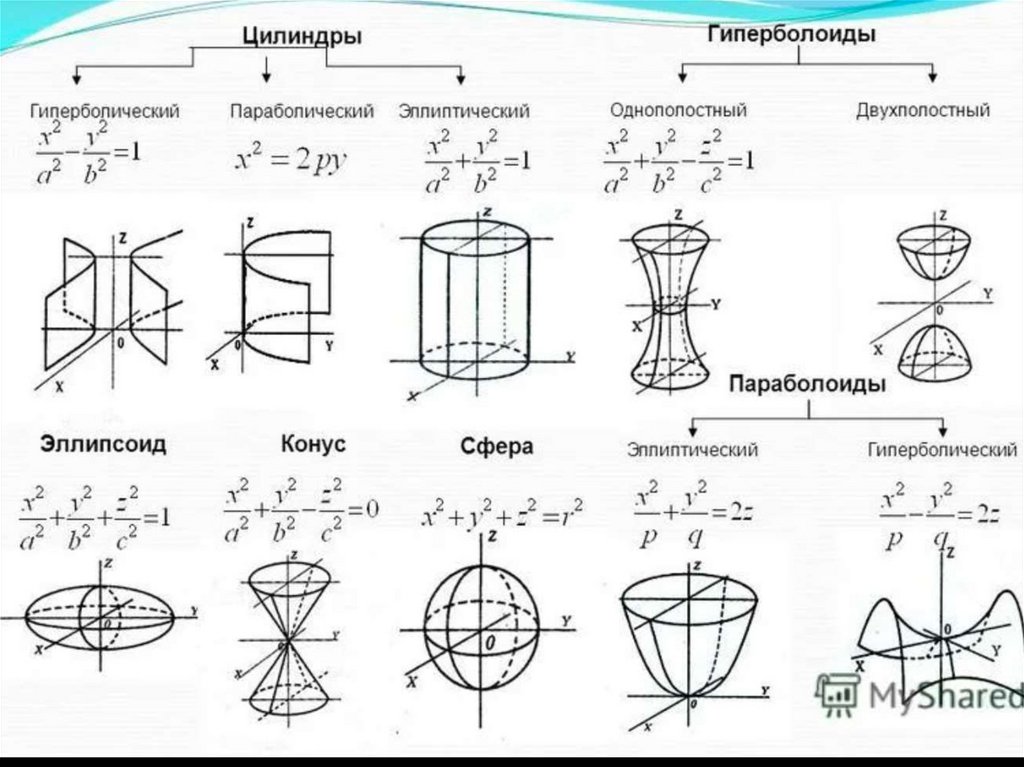

Ответ

Уравнение определяет эллиптическую цилиндрическую поверхность.

Пример 3

Задача

Составить уравнение конической поверхности с вершиной в точке , и направляющей.

Решение

У данной конической поверхности такое уравнение:

После определённых преобразований у нас получается:

Ответ

Уравнение конической поверхности – .

Как видите, в любой задаче большую роль играют формулы, которые необходимо применять во время решения. Только тогда вы достигнете хороших результатов.

Средняя оценка 5 / 5. Количество оценок: 1

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

6733

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Полезно

Помощь в написании работы

Исчисление III — Квадратичные поверхности

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. 3}\)) и хотя они иногда используются довольно интенсивно в классе исчисления есть много других поверхностей, которые также используются довольно регулярно, поэтому нам нужно взглянуть на них. 92}}} = 1\]

Вот эскиз типичного эллипсоида.

Если $a = b = c$, то у нас будет сфера.

Обратите внимание, что мы дали уравнение только для эллипсоида с центром в начале координат. Ясно, что эллипсоиды не обязательно должны быть центрированы в начале координат. Однако, чтобы немного упростить обсуждение в этом разделе, мы решили сосредоточиться на поверхностях, которые так или иначе «центрированы» в начале координат.

Конус

Вот общее уравнение конуса. 92}}}\]

Вот эскиз типичного конуса.

Обратите внимание, хотя мы и назвали это конусом, он больше похож на форму песочных часов, чем на то, что большинство назвало бы конусом. Конечно, верхняя и нижняя части песочных часов на самом деле представляют собой конусы, как мы обычно их себе представляем.
Возникает вопрос: а что, если нам действительно нужна только верхняя или нижняя часть (, т. е. , конус в традиционном смысле)? На это достаточно легко ответить. Все, что нам нужно сделать, это решить данное уравнение для $z$ следующим образом, 92}} \) всегда будет отрицательным и поэтому будет уравнением только нижней части «конуса» выше.
Также обратите внимание, что это уравнение конуса, который раскрывается вдоль оси $z$. Чтобы получить уравнение конуса, раскрывающегося по одной из других осей, все, что нам нужно сделать, это немного изменить уравнение. Это относится и к остальным поверхностям, которые мы рассмотрим в этом разделе.

В случае конуса переменная, стоящая сама по себе по одну сторону от знака равенства, будет определять ось, вдоль которой раскрывается конус. Например, конус, который раскрывается вдоль оси $x$, будет иметь уравнение 92}\]
Вот эскиз типичного цилиндра с эллипсным поперечным сечением.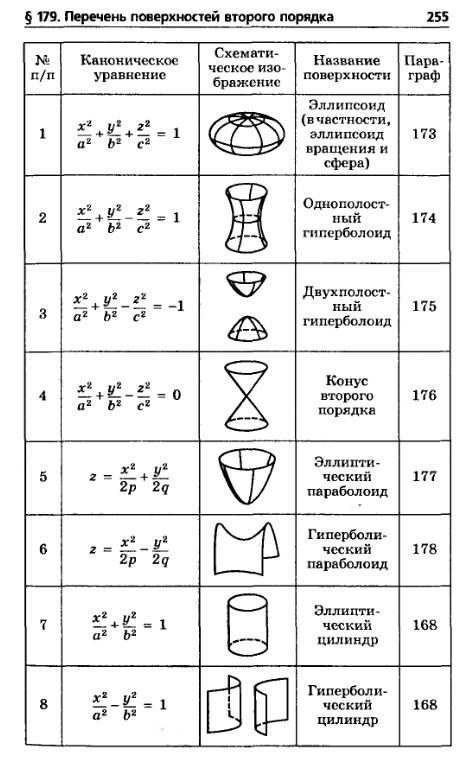 2}}} = 1\] 92}}} = 1\]
Вот эскиз типичного гиперболоида из двух листов.
Переменная с положительным значением перед ней задает ось, вдоль которой центрируется график.
Обратите внимание, что единственная разница между гиперболоидом одного листа и гиперболоидом двух листов заключается в знаках перед переменными. Это прямо противоположные знаки.
Также обратите внимание, что так же, как мы могли бы сделать с конусами, если мы решим уравнение для $z$, положительная часть даст уравнение для верхней части этого, а отрицательная часть даст уравнение для нижней части этот. 92}}} = \frac{z}{c}\]

Как и в случае с цилиндрами, он имеет поперечное сечение в виде эллипса, а если $a = b$, то он будет иметь поперечное сечение в виде круга. Когда мы будем иметь дело с ними, мы, как правило, будем иметь дело с теми, у которых круг вместо поперечного сечения.
Вот эскиз типичного эллиптического параболоида.
В этом случае переменная, не возведенная в квадрат, определяет ось, на которой раскрывается параболоид.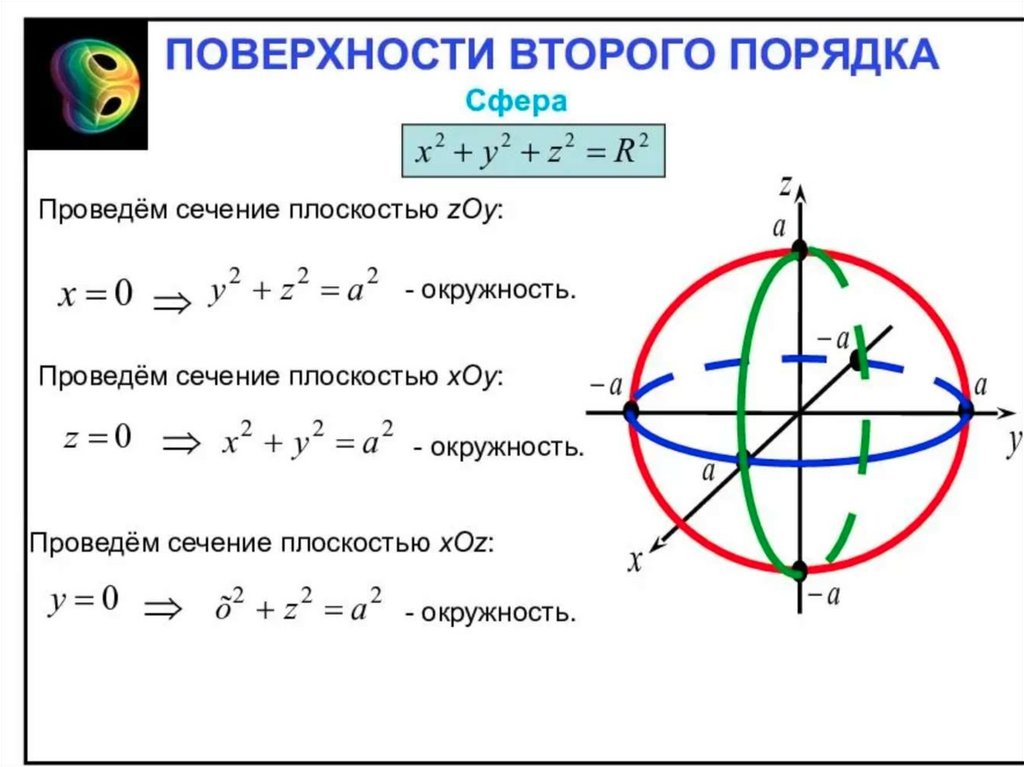 Кроме того, знак $с$ будет определять направление открытия параболоида. Если $с$ положительное, то оно открывается вверх, а если $с$ отрицательное, то открывается вниз. 92}}} = \frac{z}{c}\]
Вот эскиз типичного гиперболического параболоида.
Эти графики имеют неопределенную седловидную форму, и, как и в случае с эллиптическим параболоидом, знак $c$ будет определять направление, в котором поверхность «раскрывается». График выше показан для положительного $c$.

При использовании обоих типов параболоидов, описанных выше, обратите внимание, что поверхность можно легко перемещать вверх или вниз, добавляя/вычитая константу с левой стороны.
92} + 6\]
— это эллиптический параболоид, который открывается вниз (будьте осторожны, «-» стоит на $x$ и $y$ вместо $z$) и начинается в $z = 6$ вместо $z = 0$.
Вот несколько быстрых набросков этой поверхности.
Обратите внимание, что здесь мы дали две формы эскиза. 2 — 1 =0$.
Кривые степени два попадают в четыре (невырожденные) категории и известны как «конические сечения», поскольку каждый из кругов, эллипсов, парабол и гипербол может быть реализован как пересечение конуса с плоскостью. Модель VI 5 демонстрирует, как можно найти эллипс, параболу или гиперболу путем пересечения плоскостей с конусом. К сожалению, в нем отсутствуют две части, поэтому показаны только гипербола и парабола. Чтобы узнать больше о конических сечениях и о том, как они возникают в повседневной жизни, см. интересную статью Джилл Бриттон. 92} = \pm 1$$Если правая часть положительна, мы получаем гиперболоид «из одного листа», а для отрицательного случая мы получаем гиперболоид «из двух листов». Как и прежде, частный случай, когда $a = b$, дает «круговой гиперболоид». Гиперболоиды одного листа представляют собой линейчатые поверхности, как показано на этом рисунке. Интересно отметить, что хотя некоторые квадрики не являются линейчатыми поверхностями в этом контексте, все квадрики являются линейчатыми поверхностями, если рассматривать их в проективном пространстве.

Вырожденные квадратичные поверхности включают (эллиптические и круговые) конусы, (эллиптические, круговые, параболические и гиперболические) цилиндры. Конусы можно получить, применяя предельный процесс к гиперболоидам, уводя $a, b, c$ в бесконечность, и они также являются линейчатыми поверхностями. 92$, через них проходит единственная коника. Однако указание пяти точек — не очень практичный способ определения коники (следующая конструкция намного сложнее, чем решение полинома степени 2), как бы изящно ни выглядели такие конструкции. Эллипс однозначно определяется его большой и малой осями и может быть построен вручную с помощью булавок и веревки.

Эллипсоид, как и эллипс, определяется своими осями. Однако у эллипсоида есть три главные оси, показанные здесь красным. Знание пересечения между эллипсоидом и любыми тремя плоскостями однозначно определяет эллипсоид, и фактически любое такое пересечение с плоскостью является эллипсом (или окружностью, что является частным случаем эллипса).

No related posts.