10. Определение правой тройки векторов. Векторное произведение векторов, его свойства, геометрический смысл.
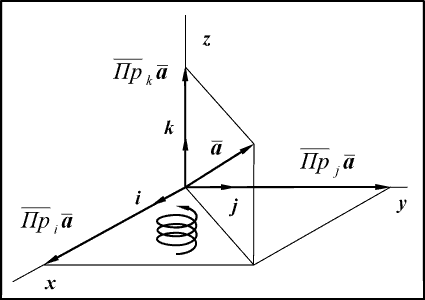
Тройка векторов ,иназывается правой, еслинаправлен так, что из его конца кратчайший поворот откпроисходит против часовой стрелки.
Векторным произведением вектора на векторназывается третий векторкоторый обладает следующими свойствами:
Его длина равна
Вектор перпендикулярен к плоскости, в которой лежат вектораи
Вектор направлен так, что поворот от векторак векторуосуществляется против часовой стрелки, если смотреть из конца вектора(тройка векторов,и– правая).
Основные свойства векторного произведения:
1) Векторное произведение равно нулю, если векторыиколлинеарны или какой-либо из перемножаемых векторов является нулевым.
2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный
Геометрический
смысл векторного произведения: модуль
векторного произведения векторов
численно равен площади параллелограмма,
построенного на этих векторах как на
сторонах.
11. Смешанное произведение 3-х векторов, его свойства. Геометрический смысл. Вычисление в координатах. Необходимое и достаточное условие компланарности 3-х векторов.
Смешанным произведением векторов ,,называется число, равное (*)*= (,,)
Модуль смешанного произведения векторов ,,равен объёму параллелепипеда, построенного на векторах,,.
Свойства:
1) (*)*=*(*)
2) (,,) = (,,) = (,) = — (,,) = … циклически меняем
3) ,,– компланарны (,,) = 0
4) ,,– правая (,,) > 0
, ,– левая (,,) < 0
5) (1+2,,) = (1,,) + (2,,) (α*,,) = α(,,)
Вычисление в координатах:
Необходимое и достаточное условие компланарности 3-х векторов :
Аналитическая геометрия
12. Виды уравнений прямой на плоскости. Расстояние от точки до прямой.
Виды:
1) Общее уравнение прямой: Ax + By + C = 0
2) Уравнение прямой в отрезках:
3) Уравнение прямой с угловым коэффициентом: y = kx + b
4) Каноническое уравнение прямой на плоскости:
5) Параметрические уравнения прямой на плоскости:
6)
Нормальное уравнение прямой: p— длина перпендикуляра,
опущенного из начала координат на
прямую, β- угол наклона этого перпендикуляра к
осиO.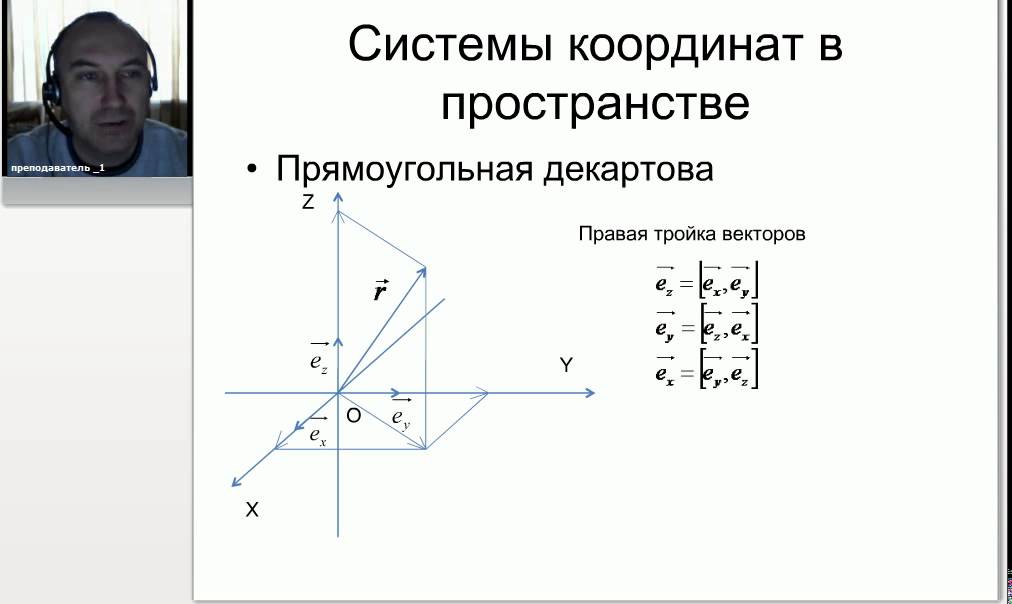
Расстояние точки A(x1, y1) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле:
13. Взаимное расположение двух прямых на плоскости, угол между прямыми.
Если прямые изаданы общими уравнениямии,
тогда угол между ними находится по формуле:
–условие перпендикулярности прямых и.
— прямые совпадают.
14. Виды уравнений плоскости. Расстояние от точки до плоскости.
Виды уравнений плоскости:
1) Общее: Ax + By + Cz + D = 0
2) В отрезках:
3) Нормальное:
Пусть плоскость задана уравнениемAx + By + Cz + D = 0 и дана точка . Тогда расстояниеp от точки Moдо плоскости определяется по формуле
15.
1) Две плоскости не имеют общих точек, и , в таком случае, они называются параллельными
2) Две плоскости имеют хотя бы одну общую точку, и в таком случае они называются пересекающимися.
Пусть наши плоскости изаданы уравнениями:
: :
Косинус угла между плоскостями находится по такой формуле:
1) Плоскости параллельны:
2) Плоскости совпадают, если выполняются следующие условия:
a2*x0 + b2*y0 + c2*z0 + d2 = 0
существует точка M0(x0,y0,z0), принадлежащая плоскости П1
4. О векторном произведении двух векторов
4. О векторном произведении двух векторов
Предпошлём определению векторного произведения двух векторов ряд необходимых в дальнейшем понятий.
Три некомпланарных вектора будем называть упорядоченной тройкой векторов, если указано, какой из них является первым, какой — вторым и какой — третьим.
Записывая упорядоченную тройку векторов, мы будем располагать эти векторы в порядке их следования. Так, запись означает, что первым элементом тройки является вектор , вторым — вектор и третьим — вектор . Таким образом, и — две различные упорядоченные тройки векторов.
В дальнейшем мы будем рассматривать только упорядоченные тройки векторов, поэтому слово «упорядоченная» будем опускать и говорить просто «тройка векторов».
Определение. Тройка некомпланарных векторов называется правой, если выполнено одно из следующих трёх условий.
1. Eсли после приведения всех трёх векторов к общему началу кратчайший поворот от к мы видим из конца вектора совершающимся против часовой стрелки (рис. 264, а).
2. Ecли, находясь внутри трёхгранного угла, определяемого приведёнными к общему началу векторами , , , мы видим поворот от к и от него к совершающимся против часовой стрелки (рис. 264, б).
264, б).
Рис. 264
3. Ecли, будучи приведёнными к общему началу, векторы , и располагаются так, как могут быть расположены большой (), указательный () и средний () пальцы правой руки (рис. 264, в).
Вы можете легко проверить эквивалентность условий один, два и три.
Если кратчайший поворот от к упомянутый в условиях 1 и 2, мы видим из конца вектора совершающимся по часовой стрелке (рис. 265, а, б), то тройка некомпланарных векторов называется левой; также тройка некомпланарных векторов называется левой, если, будучи приведёнными к общему началу, векторы , и располагаются так, как могут быть расположены большой (), указательный () и средний () пальцы левой руки (рис. 265, в). Вы можете легко убедиться в эквивалентности всех трёх определений левой тройки некомпланарных векторов.
Заметим, что для компланарных векторов понятие правой (левой) тройки смысла не имеет.
Если две тройки векторов обе — правые (обе — левые), то говорят, что эти тройки имеют одинаковую ориентацию (тройки одной ориентации).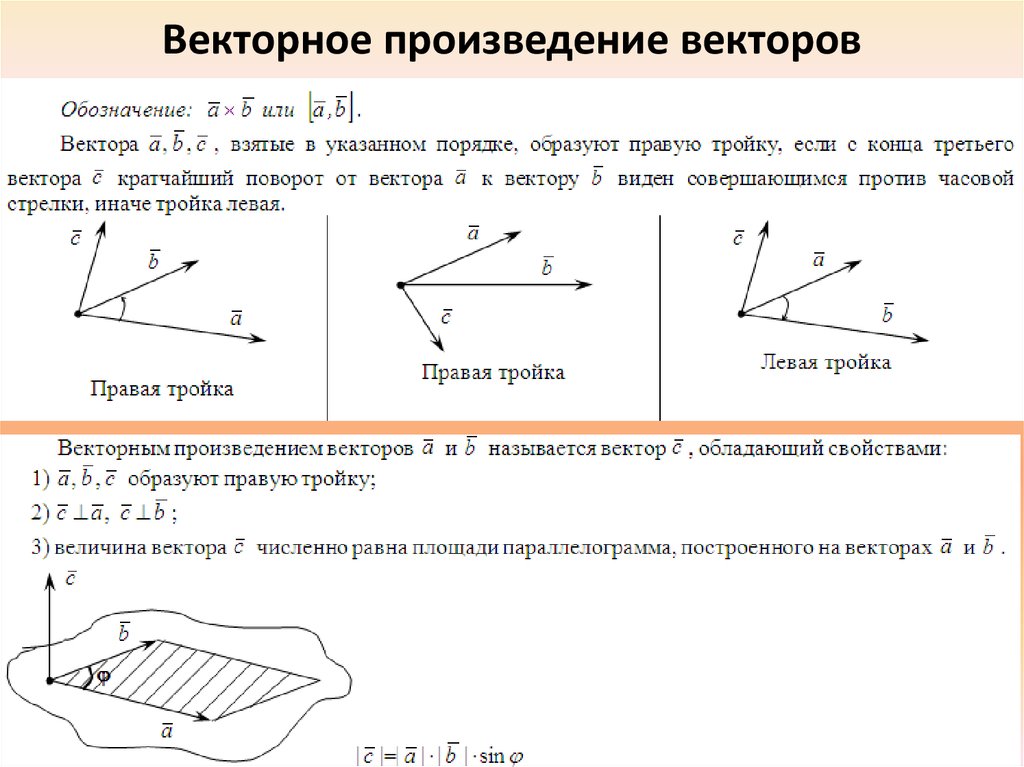 Если же из двух троек векторов одна — правая, а другая — левая, то говорят, что эти тройки имеют противоположную ориентацию (тройки противоположной ориентации). Например, тройки векторов и имеют одинаковую ориентацию, а тройки и — тройки противоположной ориентации (убедитесь в этом с помощью рисунка).
Если же из двух троек векторов одна — правая, а другая — левая, то говорят, что эти тройки имеют противоположную ориентацию (тройки противоположной ориентации). Например, тройки векторов и имеют одинаковую ориентацию, а тройки и — тройки противоположной ориентации (убедитесь в этом с помощью рисунка).
Рис. 265
Из трёх векторов , , можно составить лишь следующие шесть троек: , , , , , . Вы можете убедиться, что если первые три тройки — правые, то остальные три тройки — левые.
Заметим, что тройка векторов , , декартова прямоугольного базиса (ортонормированного репера) трёхмерного векторного пространства является правой, если кратчайший поворот от к наблюдается из конца вектора против часовой стрелки, и является левой, если кратчайший поворот от к наблюдается из конца вектора по часовой стрелке. В нашем учебнике тройка векторов , , предполагается правой.
Теперь введём определение векторного произведения двух векторов.
Определение. Если ненулевые векторы и неколлинеарны, то векторным произведением вектора на вектор называется такой третий вектор , обозначаемый символом × и определяемый следующими тремя условиями: 1) модуль вектора равен произведению модулей векторов и на синус угла ϕ между ними, т. е.
е.
| | = | × | = | |•| |•sin ϕ;(*)
2) вектор перпендикулярен каждому из векторов и ; 3) вектор направлен так, что тройка векторов является правой (рис. 266).
Рис. 266
Рис. 267
Если векторы и коллинеарны, то по определению их векторное произведение полагают равным (нуль-вектору).
Свойства векторного произведения
1. Длина вектора, равного векторному произведению неколлинеарных векторов и , численно равна площади параллелограмма, построенного на приведённых к общему началу векторах и , как на сторонах (рис. 267).
Справедливость этого утверждения основана на том, что площадь параллелограмма равна произведению длин его смежных сторон и синуса угла между ними, что, в свою очередь, следует непосредственно из условия (*): | | = | × | = | |•| | sin ϕ в определении векторного произведения векторов и .
2. × = –( × ) (свойство антиперестановочности сомножителей).
Рис. 268
Для доказательства этого свойства обозначим: = × , = × . Если || , то = = и свойство доказано. Если векторы и неколлинеарны (рис. 268), то: 1) | | = | |; 2) векторы = × и = × коллинеарны, так как каждый из них перпендикулярен плоскости, определяемой векторами и , приведёнными к общему началу. Тогда либо = , либо = –. Если бы имело место = , то обе тройки векторов и были бы правыми, что невозможно, так как эти тройки противоположной ориентации. Значит, остаётся = –, а это означает: × = – ( × ), что и требовалось доказать. ▼
Если || , то = = и свойство доказано. Если векторы и неколлинеарны (рис. 268), то: 1) | | = | |; 2) векторы = × и = × коллинеарны, так как каждый из них перпендикулярен плоскости, определяемой векторами и , приведёнными к общему началу. Тогда либо = , либо = –. Если бы имело место = , то обе тройки векторов и были бы правыми, что невозможно, так как эти тройки противоположной ориентации. Значит, остаётся = –, а это означает: × = – ( × ), что и требовалось доказать. ▼
3. (m•) × = m•( × ) (сочетательное свойство относительно числового (скалярного) множителя).
Для доказательства этого свойства обозначим = (m•) × и = m•( × ) и рассмотрим случаи.
а) Если векторы и коллинеарны, то, вследствие коллинеарности векторов m• и , векторы m• и также коллинеарны. Тогда на основании определения векторного произведения имеем: (m•) × = и m•( × ) = , т. е.
= (m•) × = m•( × ) = .
б) Если m = 0, то m• = и тогда = (m•) × = × = (вектор коллинеарен любому вектору). Обозначим × = , тогда m•( × ) = 0• = . Опять получили:
Обозначим × = , тогда m•( × ) = 0• = . Опять получили:
р = (m•) × = m•( × ) = .
в) Если векторы и неколлинеарны и m ≠ 0, то неколлинеарны и векторы m• и . Обозначим: α = ∠ (; ), β = ∠ (m; ). Тогда
| | = | (m) |•| | sin β = | m |•| |•| | sin β;
| | = | m |•| × | = | m |•| |•| |•sin α.
Учитывая, что α = β при m > 0 (рис. 269, а) и α + β = π при m < 0 (рис. 269, б), приходим к выводу, что sin β = sin α. Это означает, что и при m > 0, и при m < 0 длины векторов и равны.
Осталось доказать, что векторы и коллинеарны и сонаправлены.
Рис. 269
Коллинеарность этих векторов следует из того, что если вектор перпендикулярен плоскости, которой компланарны векторы и (рис. 269, в), то этот вектор перпендикулярен и плоскости, которой компланарны векторы m и , так как m || . Но этой плоскости перпендикулярен и вектор . Значит, || .
И, наконец, докажем, что ⇈ . Если m > 0, то m• ⇈ , значит, ( × ) ⇈ (m•) × . А так как m•( × ) ⇈ ( × ) при m > 0, то m•( × ) ⇈ (m•) × , т. е. ⇈ . Если m < 0, то m• ⇅ , значит, ( × ) ⇅ (m•) × . А так как m•( × ) ⇅ ⇅ ( × ) при m < 0, то m•( × ) ⇈ (m•) × , т. е. ⇈ .
е. ⇈ . Если m < 0, то m• ⇅ , значит, ( × ) ⇅ (m•) × . А так как m•( × ) ⇅ ⇅ ( × ) при m < 0, то m•( × ) ⇈ (m•) × , т. е. ⇈ .
Таким образом, и при m > 0, и при m < 0 имеем | | = | | и ⇈ . Это означает: = , т. е. (m•) × = m•( × ), что и требовалось доказать. ▼
4. ( + ) × = × + × (свойство распределительности векторного произведения относительно сложения векторов).
Преждe чeм доказывать этo свойство векторного произведения векторов, рассмотрим следующий интересный и полезный в дальнейшем геометрический факт.
Пусть неколлинеарные векторы и приведены к общему началу O: = , = , ∠ (; ) = ϕ; α — плоскость, проходящая через точку O перпендикулярно вектору (рис. 270).
Рис. 270
Спроектируем ортогонально вектор на плоскость α и полученный вектор повернём в плоскости α вокруг точки О на угол 90° так, чтобы этот поворот наблюдался из конца вектора происходящим по часовой стрелке. Получим вектор , для которого: a) | | = | | = | |•sin ϕ; б) ⟂ , ⟂ ; в) векторы , , образуют правую тройку. Умножив, далее, вектор на число, равное модулю вектора , получим такой вектор , что | | = | |•| | = | |•| |•sin ϕ. Так как, кроме того, ⇈ , то — правая тройка векторов и ⟂ , ⟂ . Это означает, что вектор равен векторному произведению векторов и , т. е. = × .
Умножив, далее, вектор на число, равное модулю вектора , получим такой вектор , что | | = | |•| | = | |•| |•sin ϕ. Так как, кроме того, ⇈ , то — правая тройка векторов и ⟂ , ⟂ . Это означает, что вектор равен векторному произведению векторов и , т. е. = × .
Докажем теперь свойство ( + ) × = × + × векторного произведения векторов, для чего отложим векторы = , = , = , = = + от точки О и ортогонально спроектируем их на плоскость δ, перпендикулярную вектору . При этом параллелограмм ОАРВ проектируется в такой параллелограмм O1A1P1B1 (рис. 271), что для векторов = , = , = , являющихся ортогональными проекциями соответственно векторов , , , выполняется: + = и | | = | |•sin α, | | = | |•sin β, | | = | |•sin γ, гдe α = ∠ (; ), β = ∠ (; ), γ = ∠ (; ).
Рис. 271
Далее рассмотрим такой поворот пространства вокруг прямой O1C на угол 90°, при котором индуцируемый в плоскости δ поворот вокруг точки О наблюдается из точки C совершающимся по часовой стрелке. Этот поворот отображает параллелограмм O1A1P1B1 на параллелограмм O1A2P2B2, а каждый из векторов , , — на перпендикулярный ему и равный по модулю соответственно вектор , , . Умножив каждый из этих векторов на | |, получим соответственно такие векторы = , = , = , что:
Этот поворот отображает параллелограмм O1A1P1B1 на параллелограмм O1A2P2B2, а каждый из векторов , , — на перпендикулярный ему и равный по модулю соответственно вектор , , . Умножив каждый из этих векторов на | |, получим соответственно такие векторы = , = , = , что:
1) | | = | |•| | = | |•| | = (| |•sin α)•| | = | |•| |•sin α;
аналогично, | | = | |•| |•sin β; | | = | |•| |•sin γ;
2) ⟂ , ⟂ ; ⟂ , ⟂ ; ⟂ , ⟂ ;
3) тройки векторов , и правые.
Это означает, что = × , = × и = × = ( + ) × . Так как в параллелограмме O1A3P3B3 вектор = + , то получаем ( + ) × = × + × , что и требовалось доказать. ▼
5. Для любого вектора справедливо × = , так как любой вектор коллинеарен сам с собой.
Выражение векторного произведения в декартовых координатах
Векторное произведение × двух векторов и есть вектор, координаты которого нужно уметь находить, если известны координаты векторов сомножителей и .
Предварительно найдём все возможные векторные произведения базисных векторов , , .
Рис. 272
Из определения векторного произведения, учитывая, что векторы , , попарно взаимно перпендикулярны (рис. 272) и являются единичными, имеем:
× = , × = , × = ,(**)
× = –, × = –, × = –.
Теперь найдём координаты векторного произведения × векторов и , заданных в декартовом прямоугольном базисе (; ; ) своими координатами: (x1; y1; z1), (x2; y2; z2) или в виде разложения по базисным векторам , , :
= x1 + y1 + z1, = x2 + y2 + z2.
Принимая во внимание свойства векторного произведения векторов, используя соотношения (**) и учитывая, что тройка базисных векторов является правой, находим:
× = (x1 + y1 + z1) × (x2 + y2 + z2) = (x1x2)•( × ) +
+ (x1y2)•( × ) + (x1z2)•( × ) + (y1x2)•( × ) + (y1y2)•( × ) +
+ (y1z2)•( × ) + (z1x2)•( × ) + (z1y2)•( × ) +
+ (z1z2)•( × ) = (x1x2)• + (x1y2)• + (x1z2)•(–) +
+ (y1x2)•(–) + (y1y2)• + (y1z2)• + (z1x2)• + (z1y2)•(–) + + (z1z2)• = (y1z2 – y2z1)• + (z1x2 – x1z2)• + (x1y2 – x2y1)•.
Таким образом, векторное произведение × = векторов (x1; y1; z1) и (x2; y2; z2) имеет координаты:
× = (y1z2 – y2z1; z1x2 – x1z2; x1y2 – x2y1).
Таблица составленная из четырёх чисел a, b, с и d, называется квадратной матрицей второго порядка. Числа а, b, с и d называются элементами матрицы, при этом числа a и b называются элементами первой строки, числа с и d — элементами второй строки; числа a и c — элементами первого столбца, числа b и d — элементами второго столбца; числа a и d — элементами главной диагонали матрицы.
Определение. Число a•d – b•c называется определителем (или детерминантом) матрицы и обозначается так: .
Из определения видно, что определитель матрицы равен разности произведений чисел a и d главной диагонали и чисел b и c второй диагонали определителя, т. е.
= a•d – b•c.
Например, = 3•(–2) – 1•(– 4) = –2.
Тогда координатами X = y1z2 – y2z1, Y = z1x2 – x1z2, Z = x1y2 – x2y1 векторного произведения × = (X; Y; Z) векторов (x1; y1; z1) и (x2; y2; z2) являются определители второго порядка, составленные из координат векторов — сомножителей. Действительно,
Действительно,
X = y1z2 – y2z1 = ; Y = z1x2 – x1z2 = ;
Z = x1y2 – x2y1 = .
Таким образом,
× =
или в виде разложения по базису имеем:
× = = • + • + •.
ЗАДАЧА. Найдём, например, площадь параллелограмма, построенного на приведённых к общему началу векторах = 2 + 3 – 5 и = – 2 + 4, как на сторонах.
Решение. Так как площадь S параллелограмма, построенного на векторах и , как на сторонах, равна модулю векторного произведения × , то найдём | × |.
Имеем:
× = • + • + • =
= (3•4 – (– 2)•(–5))• + ((–5)•1 – 4•2)• +
+ (2•(–2) – 1•3)• = 2 – 13 – 7,
откуда | × | = = Значит, искомая площадь S параллелограмма равна
В высшей школе вы подробнее познакомитесь с векторным произведением и его приложениями в естественных науках. Кроме того, вам расскажут и о смешанном произведении () = (•)• векторов , и , его свойствах и приложениях.
Самостоятельно решите следующие задачи.
1. Найдите площадь треугольника с вершинами А(1; 1; 1), В(2; 3; 4), С(4; 3; 2). (Ответ: )
(Ответ: )
2. На векторах (4; 6; 2) и (–2; 2; 4) построен треугольник. Найдите его площадь и высоты.
S = 18,75; h2 = h3 = ; h4 =
3. Найдите площадь параллелограмма, построенного на векторах + 3 и 3 + , если | | = | | = 1, ∠ (; ) = 30°. (Ответ: 4.)
4. Дан треугольник АВС площади S. Докажите, что площадь треугольника, сторонами которого являются медианы данного треугольника, равна S.
Путаница с векторным тройным произведением
спросил
Изменено 4 года, 6 месяцев назад
Просмотрено 1к раз
$\begingroup$
Вопрос простой. Скажем, у меня есть два вектора $\mathbf{a}$ и $\mathbf{b}$, и я хочу упростить произведение $(\mathbf{a} \times \mathbf{b}) \times \mathbf{b} $.
Однако это векторное произведение абсолютно перпендикулярно к $\mathbf{b}$, поэтому оно не должно иметь компонент на $\mathbf{b}$. Я понял, что $\mathbf{a}$ и $\mathbf{b}$ могут быть не ортогональны, но я не могу продолжить с этого момента, чтобы оправдать наличие $\mathbf{b}$.
Может ли кто-нибудь объяснить это простыми словами, почему там $\mathbf{b}$?
- векторы
- перекрестное произведение
$\endgroup$
1$\begingroup$
Если $a$ и $b$ ортогональны друг другу, то вы правы в том, что $(a\times b)\times b$ должно быть скаляром $a$. В противном случае вы можете нарисовать картинку и увидеть, что $(a\times b)\times b$ — это вектор в плоскости, натянутый на $a$ и $b$ и ортогональный вектору $b$. Но так как $a$ и $b$ не ортогональны, необходимо, чтобы $a$ и $b$ записали $(a\times b)\times b$ как линейную комбинацию $a$ и $b$.
Но так как $a$ и $b$ не ортогональны, необходимо, чтобы $a$ и $b$ записали $(a\times b)\times b$ как линейную комбинацию $a$ и $b$.
$\endgroup$
$\begingroup$
Запишем более систематически. Учитывая равенство $$ (a \times b) \times b = -(b\cdot b)a + (b \cdot a) b, $$ вы правильно утверждаете, что левая сторона должна быть перпендикулярна $b$. Теперь давайте проверим, перпендикулярна ли правая сторона $b$: $$ \text{RHS}\cdot b = -\left( (b\cdot b)a + (b \cdot a) b \right) \cdot b = — (b \cdot b)(a \cdot b) + ( b \cdot a)(b \cdot b) = 0. $$ Как видите, правая часть также перпендикулярна $b$, и противоречия нет.
Ваше замешательство связано с предположением, что существование $b$ в правой части не позволяет ей быть перпендикулярной к $b$. Это не всегда правильно, если только $a$ и $b$ не перпендикулярны. Но, как видите, в данном конкретном случае $a\cdot b$ будет равно нулю, а $\text{RHS}=-(b \cdot b)a$. Итак, все еще нет противоречия.
Итак, все еще нет противоречия.
$\endgroup$
2
$\begingroup$
92}\vec{b}$$$\endgroup$
$\begingroup$
Пока $a$ и $b$ линейно независимы, они охватывают плоскость $P$, и $a\times b$ перпендикулярно $P$. Но $(а\раз б)\раз б$ перпендикулярна $a\times b$, поэтому в является плоскостью $P$. То есть, $(a\times b)\times b=\mu a+\nu b$ для некоторых $\mu$ и $\nu$. Так появляется $b$.
Чтобы подтвердить, что $\mu=-b\cdot b$ и $\nu=a\cdot b$, нужно всего лишь
нужно доказать, что $c=-(b\cdot b)a+(a\cdot b)b$ имеет одинаковые скалярные произведения
с $a$ и $b$, которые имеют $(a\times b)\times b$. Но $$c\cdot b
=-(b\cdot b)(a\cdot b)+(a\cdot b)(b\cdot b)=0$$, что хорошо
поскольку $(a\times b)\times b$ ортогонален $b$. 2t.$$
Действительно, тогда $c=(a\times b)\times b$.
2t.$$
Действительно, тогда $c=(a\times b)\times b$.
$\endgroup$
$\begingroup$
$\frac{(a\cdot b)\,b}{b\cdot b}$ — проекция $a$ на направление $b$.
$\frac{a\times b}{|b|}$ — это проекция $a$ на плоскость, перпендикулярную $b$, с последующим поворотом $\frac\pi2$ вокруг направления $b$. Поскольку $\frac{a\times b}{|b|}$ перпендикулярно $b$, векторное произведение с $\frac{b}{|b|}$ просто поворачивает его еще на $\frac\pi2$ вокруг направление $b$. То есть $-\frac{(a\times b)\times b}{b\cdot b}$ — это проекция $a$ на плоскость, перпендикулярную $b$.
Сложение этих двух ортогональных проекций дает $$ \frac{(a\cdot b)\,b}{b\cdot b}-\frac{(a\times b)\times b}{b\cdot b}=a\tag1 $$ Решение для $(a\times b)\times b$ дает $$ (a\times b)\times b=(a\cdot b)\,b-(b\cdot b)\,a\tag2 $$
Хотя кажется, что компонент $b$ находится в правой части $(2)$, все, что $(a\cdot b)\,b$ служит для того, чтобы отменить часть $(b\cdot b)\,a$, которая находится в направлении $b$. Обратите внимание, что
$$
((a\cdot b)\,b-(b\cdot b)\,a)\cdot b=0\tag3
$$
Таким образом, компоненты в направлении $b$ действительно нет.
Обратите внимание, что
$$
((a\cdot b)\,b-(b\cdot b)\,a)\cdot b=0\tag3
$$
Таким образом, компоненты в направлении $b$ действительно нет.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Скалярное тройное произведение | Суперпроф
В этой статье мы обсудим, как вычислить скалярное тройное произведение векторов. Но прежде чем двигаться дальше, давайте сначала определим вектор.
Вектор — это величина, которая изображается как по величине, так и по направлению. Мы представляем векторы с помощью алфавитов со стрелкой вправо вверху, которая показывает их направление. Например, , и являются представлениями векторов.
Скалярное тройное произведение векторов
Скалярное тройное произведение также известно как смешанный продукт . Скалярное тройное произведение трех векторов , и математически обозначается как и равно скалярному произведению первого вектора на векторное произведение двух других векторов и . Он называется скалярным произведением, потому что, как и скалярное произведение, скалярное тройное произведение дает одно число.
Мы можем математически обозначить это произведение как:
Перекрестное произведение этих векторов равно определителю. Строки этого определителя равны координатам векторов относительно ортонормированного базиса.
Свойства тройного произведения
Свойства тройного произведения приведены ниже:
- Если порядок множителей круговой, тройное произведение остается неизменным. Например,
- Однако тройное произведение меняет знаки, если множители переставлены. Например,
- Если три вектора линейно зависят друг от друга, то тройное произведение равно нулю.
Лучшие репетиторы по математике
Let’s Go
Пример 1
Найдите скалярное тройное произведение следующих векторов:
Решение
Математически Скалярное тройное продукт представлен в виде:
Сначала мы будем собирать продукт, используя, используя использование, используя. определитель. Координаты этих векторов будут элементами определителя.
Вычислим определитель по формуле нахождения определителя матрицы 3х3 так:
Теперь мы рассчитаем точечный продукт и подобно этим:
Пример 2
Найдите скалярную тройную продукт следующих векторов:
Раствор
Математическая математическая произведение представлено как:
Сначала мы вычислим произведение с помощью определителя. Координаты этих векторов будут элементами определителя.
Мы вычислим определитель, используя формулу нахождения определителя матрицы 3×3 следующим образом:
Теперь мы вычислим скалярное произведение и следующим образом:
2
Найдите скалярное тройное произведение следующих векторов:
Решение
Математически тройное скалярное произведение представляется как:
Сначала мы вычислим произведение с помощью определителя. Координаты этих векторов будут элементами определителя.
Мы вычислим определитель, используя формулу нахождения определителя матрицы 3×3 следующим образом:
Теперь мы вычислим скалярное произведение и следующим образом:
Найти еще здесь на Суперпроф.
Пример 4
Найдите скалярное тройное произведение следующих векторов:
Решение
Математически тройное скалярное произведение представляется как:
Сначала мы вычислим произведение с помощью определителя. Координаты этих векторов будут элементами определителя.
Мы вычислим определитель, используя формулу нахождения определителя матрицы 3×3 следующим образом:
Теперь мы вычислим скалярное произведение и следующим образом:
Пример 2
Найдите скалярное тройное произведение следующих векторов:
Решение
Математически скалярное тройное произведение представляется как:
Сначала мы вычислим произведение с помощью определителя.
