Правила деление и умножение: Порядок действий в Математике

Каково правило умножения и деления? – Обзоры Вики

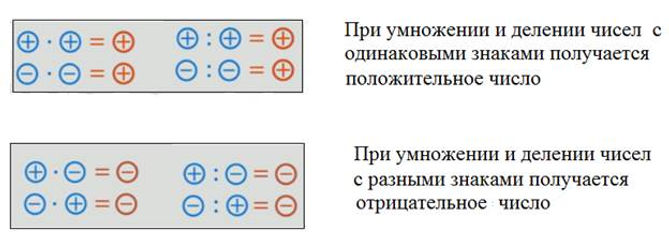
Поскольку деление является обратным умножению, правила деления такие же, как и правила умножения. Поэтому при умножении и делении положительных и отрицательных чисел помните следующее: Если знаки одинаковый ответ положительный, если знаки разные ответ отрицательный.

Вы сначала делите или умножаете? Все выражения должны быть упрощены в этом порядке. Единственным исключением является то, что умножение и деление могут выполняться одновременно. вам разрешено делить, прежде чем вы умножаете, и то же самое касается сложения и вычитания. Однако умножение и деление ДОЛЖНЫ предшествовать сложению и вычитанию.

Дополнительно Что такое правило MDAS в математике? MDAS означает Умножение, деление, сложение и вычитание. Это часть Порядка операций, набора правил, определяющих последовательность упрощения математических операций. Он используется, когда выражение или уравнение имеют более одной операции.

Что такое правило Бодмаса? Правило Бодмаса соответствует порядку аббревиатуры БОДМАС, т.е. B – скобки, O – порядок степеней или корней, D – деление, M – умножение, A – сложение и S – вычитание.. Правило BODMAS гласит, что математические выражения с несколькими операторами необходимо решать слева направо в порядке BODMAS.

Что правильно MDAS или DMAS?

Это не MDAS. На самом деле это DMAS, что означает деление, умножение, сложение и вычитание. В математике это правило соблюдается, что означает, что в уравнении или задаче порядок упрощения будет в указанном выше формате.

Что на первом месте: сложить или умножить? Порядок операций говорит вам выполнить умножение перед сложением. Затем добавьте. Упростите 20 – 16 ÷ 4. Порядок операций говорит вам выполнить деление перед вычитанием.

Что означает N в математике? Натуральные числа, подсчет чисел. Буква (N) — это символ, используемый для обозначения натуральных чисел. Натуральные числа также известны как счетные числа, и они начинаются с цифры 1 и продолжаются до бесконечности (никогда не заканчиваются), что обозначается тремя точками (…).

Как решить Бодмас?

Согласно правилу BODMAS, в данном математическом выражении, содержащем комбинацию знаков: скобки ((), {},, -), умножение, из, сложение, вычитание, деление, мы должны сначала решить или упростить скобки затем of (степени и корни и т. д.), of, затем деление, умножение, сложение и вычитание…

Также Что такое правило Бодмаса для детей? Правило BODMAS является аббревиатурой от помочь детям запомнить порядок действий в вычислениях. Операции — это просто разные вещи, которые мы можем делать с числами в математике. Это означает «скобки, порядок, деление, умножение, сложение, вычитание». ‘

Верно ли правило Бодмаса?

Его буквы обозначают скобки, порядок (значение полномочий), деление, умножение, сложение, вычитание. … Он не содержит скобок, степеней, деления или умножения, поэтому мы будем следовать BODMAS и делать сложение с последующим вычитанием: это ошибочно. Правильное значение 3.

Как вы решаете MDAS и Pemdas?

Как рассчитывается MDAS?

MDAS = Умножение, деление, сложение и вычитание.

Какие четыре математических правила? Четыре правила математики: сложение, вычитание, умножение и деление. На следующих веб-страницах вы можете узнать, как это сделать вручную (без калькулятора), а также другую важную информацию о порядке приоритета этих операций.

Каковы четыре правила умножения? Каковы правила умножения?

• Любое число, умноженное на ноль, всегда равно нулю. …
• Любое число, умноженное на единицу, всегда является одним и тем же числом. …
• Добавьте ноль к исходному числу при умножении на 10. …
• Порядок факторов не влияет на произведение. …
• Произведения всегда положительны при умножении чисел с одинаковыми знаками.

Каков правильный порядок математических операций?

Порядок операций — это правило, указывающее правильную последовательность шагов для вычисления математического выражения. Мы можем запомнить порядок с помощью PEMDAS: Круглые скобки, экспоненты, умножение и деление (слева направо), сложение и вычитание (слева направо).

Является ли ноль действительным числом? На самом деле реальные числа — это практически любые числа, которые только можно придумать. … Действительные числа могут быть положительными или отрицательными, и включить число ноль. Их называют действительными числами, потому что они не являются мнимыми, а это другая система чисел.

Что такое домен Z?

Z-домен комплексная область, также известная как комплексная частотная область, состоящий из реальной оси (ось x) и мнимой оси (ось y). Сигнал обычно определяется как последовательность действительных или комплексных чисел, которая затем преобразуется в Z-область в процессе преобразования z.

Является ли ноль целым числом? Целые числа — это числа 0, 1, 2, 3, 4 и т. д. (натуральные числа и нуль). Отрицательные числа не считаются «целыми числами». Все натуральные числа являются целыми числами, но не все целые числа являются натуральными числами, так как ноль — это целое число, но не натуральное число.

Как вы делаете бодмы без скобок?

Если скобок нет, начните решение от «порядка» или «из‘ с последующим делением или умножением (то, что идет первым слева направо), затем сложением или вычитанием (то, что идет первым слева направо).

Какую скобку вы решите в первую очередь?

Согласно правилу BODMAS, если выражение содержит скобки ((), {}, []) мы должны сначала решить или упростить скобку, за которой следует «порядок» (что означает степени и корни и т. д.), затем деление, умножение, сложение и вычитание слева направо.

Когда Бодмасу обучали в школах? Этот принцип преподавался в моих школах в 1958 когда я учился в эквиваленте 6-го класса (5-й класс для читателей из США). Это было настолько базовым, что предполагалось знание для уровня O, который был получен в 11-м классе.

В какой стране используется Бодмас?

Наиболее распространенный в Великобритания, Пакистан, Индия, Бангладеш и Австралия и в некоторых других англоязычных странах это BODMAS, означающее скобки, порядок, деление/умножение, сложение/вычитание или скобки, деление/умножение, сложение/вычитание. Нигерия и некоторые другие страны Западной Африки также используют BODMAS.

Пемдас и Бодмас — одно и то же?

PEMDAS и BODMAS абсолютно идентичны; это разные названия одного и того же набора правил. В BODMAS вы не всегда делаете «деление перед умножением», а в PEMDAS вы не всегда делаете «умножение перед делением».

Кто открыл умножение? Четыре тысячи лет назад, вавилоняне изобрел умножение. В прошлом месяце математики усовершенствовали его. 18 марта два исследователя описали самый быстрый из когда-либо обнаруженных методов умножения двух очень больших чисел.

Умножение и деление дробей

МКОУ «Ортатюбинская СОШ» Абубекерова Секерхан Мавлидиновна

ПРАКТИКА Методическая разработка урока

Учитель Абубекерова С.М Класс 6

Тема урока: «Умножение и деление дробей»

Тип урока: закрепление изученного материала

Цель урока: повторить и закрепить знания и умения, связанные с правилами умножения и деления дробей и применением их для решения задач, выявить наиболее слабо понятые вопросы данной темы для их дальнейшей коррекции.

Образовательные задачи урока:

• Закрепить в ходе урока правила умножения и деления обыкновенных дробей.

• Продолжить формирование общеучебных умений, умение выполнять самопроверку.

Развивающие задачи урока:

• Развитие самостоятельности мышления.

• Развитие критического мышления;

• Развитие памяти и наблюдательности учащихся.

• Развитие и обогащение речи учащихся.

• Развитие познавательного интереса к предмету.

• развитие внимания, логического мышления,

Воспитательные задачи урока:

• Воспитывать интерес учащихся к математике.

• воспитание личностных качеств: человечности, дружелюбия, солидарности;

• воспитание чувства дисциплинированности, коллективизма, целеустремленности;

• воспитание у обучающихся наблюдательности; умения находить и исправлять корректно свои и чужие ошибки.

Оборудование:

презентация к уроку, рабочий лист ,мультимедийное оборудование

Структура урока:

1. Организационный момент.

2. Постановка целей урока.

3. Актуализация знаний и умений учащихся.

4. Самостоятельная работа.

5. Групповая работа

6. Домашнее задание.

7. Итог урока. Рефлексия.

1.Начинается урок,

Он пойдет ребятам впрок,

Постарайтесь все понять,

Учитесь тайны открывать,

Ответы полные давать,

Чтоб за работу получать

Только лишь оценку «пять»!

Чтобы узнать тему урока разгадайте ребусы

Какая тема нашего урока ? «Умножение и деление дробей»

https://forms.yandex.ru/u/636ba8065d2a060622ad0dd8/ тест на умножение и деление дробей

блиц опрос

— как умножить дробь на натуральное число

— правило умножения обыкновенных дробей

Правило умножения смешанных чисел

Правило деления обыкновенных дробей

«Человек есть дробь

Числитель – это сравнительно с другими – достоинство человека,

Знаменатель – оценка человеком самого себя.

Увеличить своего числителя – свои достоинства , не во власти человека, но всякий может уменьшить своего знаменателя –свое мнение о самом себе» ( ****)

Кто автор этих слов мы узнаем решив уравнения

1 ) Х + х = 2) 3) х + х =

4) : к= 1 :2 5) у : 1 =2 * 6) у — у =

7) к + к -3= 8) ( х — ) * =

1	2	3	4	5	6	7	8
Х=	Х=8	Х=3	К=5	у=1	У=6	К=3	Х=1
й	о	т	с	л	о	Т	Л

Теперь отправляемся в путешествие . У вас путевые листы

Путевой лист Ф.И_______________Путешествие «Умножение и деление дробей»

Задание 1 Чтобы путешествие прошло успешно , необходимо узнать сколько оборотов сделает колесо на расстоянии 480км, если длина окружности колеса равна

Длина окружности колеса
Оборот колеса

	Задание 2 Сколько времени нужно человеку, чтобы, выйдя из автобуса, пересечь дорогу со скоростью 1 м/с? Длина автобуса 9 м. Ширина проезжей части дороги 8 м. расстояние от автобусной остановки до пешеходного перехода 21 м

Задание 3 Реши уравнение и ты узнаешь допустимую скорость автомобиля км/ч , в населенных пунктах	4*( 3х — 9 ) = 920	х = 21
Задание 4 Если автомобиль едет со скоростью V км/ч , то его тормозной путь в метрах можно приближенно вычислить по формуле S =2 + 2 (тормозной путь автомобиля –это расстояние которое он проезжает после того, как водитель нажал на тормоз) определите тормозной путь автомобиля, двигающегося по городу с допустимой скоростью
за два дня 260 км 1 день ? 6/7 пути 2 день ?	Задание 5 За два дня турист проехал 260 км Путь, пройденный в первый день, составлял 6/7 пути, пройденного во второй день. Сколько километров прошел турист в каждый из этих дней?
	Красный –совсем непонятно Желтый – надо повторить еще раз Зеленый –все легко и просто

ПРАВИЛО	ОБРАЗЕЦ	ЗАДАНИЯ
Деление числителя и знаменателя дроби на общий делитель (на одно и то же число) называется  сокращением дроби.	1.Пример. Сократим дробь ==. 2. Пример. Сократить дробь 1.Способ: ======== 2. Способ: НОД (24,432) =24 == 3.Способ. Сократить дробь Суть в том, что число, на которое разделили числитель и знаменатель хранят в уме. В нашем случае, числитель и знаменатель делят на 4 — это число и будем хранить в уме	Сократить дроби: а) = б = в)= г)= = е) = ж) =

ПРАВИЛО	ОБРАЗЕЦ	ЗАДАНИЯ
Сотая часть числа — 1% это 1/100 часть Десятая часть числа -10% 1ц= 100 кг 1 кг= 1% центнера 1 м =100см 1 см = 1% метра	Запишите в виде десятичной дроби 20% это 20/100 = 0,20 = 0,2 Запишите в виде процента дробь 4/25 = 4:25=0,16= 16% или 4/25 = 8/ 50= 16/100=0,16 1 кг=1000 г. Для вычисления части от 1000 г нужно просто найти отношение данной массы к 1000. 500 г : 1000 г = 1/2, то есть 500 г составляет одну вторую часть от одного кг	Запишите в виде десятичной дроби 74%= 3%= 12% Запишите в виде процента дробь 0,7= 0,12= = Какая часть кг составляет 260 г= 13г= 90г=

ПРАВИЛО	ОБРАЗЕЦ	ЗАДАНИЯ
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число и записать в числитель, а знаменатель оставить без изменения. Чтобы умножить дробь на дробь надо: 1.Числители перемножить и записать в числитель. 2.Знаменатели перемножить и записать в знаменатель.	Пример №1. 3 = = * 3 = = Пример №2 * = =	№1. а) * 2 = б) *5 = в) *14= г) 25 * = №2. а) * = б) * = в) * = г) * =

Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй Чтобы разделить дробь на число, нужно это число умножить на знаменатель и записать в знаменатель Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.

Пример №1. : = * = = 2 Пример №2 : 6 = = Пример №3. 7: = 7 * = =

а) : = б) : = в) : = г) : = д) : = е) : = №2 а) : 2= б) : 3= в) : 2= №3 а)8 : = б) 15 : = в) 21 : =

правил умножения целых чисел | умножение и деление целых чисел

Содержание

В арифметике сложение, вычитание, умножение и деление являются четырьмя основными операциями, используемыми при решении задач. Если вы знаете и соблюдаете основные правила целых чисел при умножении и делении, процесс решения задач становится гладким и легким.

Умножение и деление целых чисел

Умножение и деление есть не что иное, как многократное сложение и вычитание чисел соответственно. Вы можете выполнять умножение и деление, используя многократное сложение или вычитание целых чисел и применяя их правила к целым числам.

Но процесс многократного сложения или вычитания долгий и трудоемкий. Как и в случае сложения или вычитания целых чисел, для умножения и деления целых чисел также существуют определенные правила.

Умножение целых чисел

Умножение можно рассматривать как многократное сложение (накопление). Существуют определенные правила умножения целых чисел.

Правила умножения целых чисел:

• Умножение двух положительных чисел
• Умножение двух отрицательных чисел
• Умножение положительного числа на отрицательное число

Теперь, что касается результата умножения двух целых чисел, может произойти любое из следующих событий:

• Произведение двух целых чисел с одинаковыми знаками всегда будет положительным. Это означает, что
  • произведение двух целых положительных чисел положительно
  • произведение двух отрицательных чисел положительно
• Произведение двух целых чисел с разными знаками всегда будет отрицательным. Произведение положительного числа на отрицательное число (целые числа с разными знаками) всегда будет отрицательным.

Примечание: Произведение двух целых чисел всегда является целым числом.

Приведенные выше правила умножения целых чисел можно обобщить как

.

Тип чисел	Результат	Пример
Положительный $\times$ Положительный	Положительный $\left(+\right)$	$3 \times 7 = 21$
Отрицательный $\times$ Отрицательный	Положительный $\left( right)$	$\left(-3 \right) \times \left(-7 \right) = 21$
Положительное $\times$ Отрицательное	Отрицательное $\left(- \right)$	$3 \times \left(-7 \right) = -21$
Отрицательное $\times$ Положительное	Отрицательное $\left(- \right)$	$\left(-3 \right) \times 7 = -21$

Примечание: В случае умножения целых чисел просто умножайте числа без знака.

Получив произведение, поставьте знак в соответствии с правилом умножения, приведенным в таблице выше.

шагов умножения целых чисел

Следующие шаги выполняются при умножении двух целых чисел:

Шаг 1: Определите абсолютное значение чисел.

Шаг 2: Найдите произведение абсолютных значений.

Шаг 3: После получения продукта определите знак числа в соответствии с правилами или условиями.

Примечание: Абсолютное значение целого числа, представляет собой целое число без знака.

Например,

• абсолютное значение $-12$ равно 12$ 
• абсолютное значение $+12$ равно 12$

Деление целых чисел

Как умножение есть многократное сложение (накопление), так и деление есть многократное вычитание (распределение) чисел. Следовательно, деление целых чисел можно рассматривать как операцию, противоположную операции умножения. Тем не менее, правила деления целых чисел такие же, как и правила умножения.

Примечание: Результат двух целых чисел не всегда является целым числом.

• Когда остаток равен 0, результатом является целое число.
• Если остаток не равен 0, результат не является целым числом.

Правила деления

• Результат двух положительных целых чисел всегда будет положительным.
• Результат двух отрицательных целых чисел всегда будет положительным.
• Результат положительного целого числа и отрицательного целого числа всегда будет отрицательным.

Type of  Numbers	Result	Example
Positive $\div$ Positive	Positive $\left(+ \right)$	$15 \div 3 = 5$
Отрицательное $\div$ Отрицательное	Положительное $\left(+\right)$	$\left(-15 \right) \div \left(-3 \right) = 5$
Положительный $\div$ Отрицательный	Отрицательный $\left(- \right)$	$15 \div \left(-3 \right) = -5$
Отрицательное $\div$ Положительное	Отрицательное $\left(- \right)$	$\left(-15 \right) \div 3 = -5$

Как и в случае умножения, разделите целые числа без знака, затем присвойте знак по правилу, указанному в таблице выше.

шагов в делении целых чисел

Следующие шаги выполняются при умножении двух целых чисел:

Шаг 1: Определите абсолютное значение чисел.

Шаг 2: Найдите произведение абсолютных значений.

Шаг 3: После получения продукта определите знак числа в соответствии с правилами или условиями.

Примечание: Абсолютное значение целого числа, представляет собой целое число без знака.

Например,

• абсолютное значение $-12$ равно 12$ 
• абсолютное значение $+12$ равно 12$

Известные математические соревнования для детей

Умножение и деление целых чисел с помощью числовой строки

Как обсуждалось ранее, умножение и деление — это многократное сложение и вычитание чисел. Вы можете выполнять умножение и деление, используя правила сложения и вычитания, используя числовую прямую.

Умножение целых чисел с помощью числовой строки

Чтобы выполнить умножение на числовой прямой, мы начинаем с нуля $\left(0 \right)$ и двигаемся к правой стороне числовой строки заданное количество раз.

Рассмотрим пример. Умножьте $2 \times 4$ с помощью числовой прямой.

Начиная с нуля, на числовой прямой образуются четыре группы равных интервалов по $2$. Таким образом мы достигнем 8.

Следующая числовая строка показывает $2 \times 4 = 8$.

Начать с 0Переместить 2 шагаПовторить 4 раза

Умножение положительных чисел в числовой строке

При умножении двух или более положительных чисел существует простое правило, которое следует за простым умножением. Поскольку это умножение, мы будем двигаться к правой стороне числовой прямой. Давайте решим $3 \times 5$.

Начиная с нуля, на числовой прямой образуются пять групп равных интервалов по $3$. Таким образом, мы достигнем $15$.

Следующая числовая строка показывает $3 \times 5 = 15$.

Начать с 0Переместить 3 шагаПовторить 5 раз

Умножение отрицательных чисел в числовой строке

При умножении более двух отрицательных чисел используйте правило четного-нечетного: 

• Подсчитайте количество отрицательных знаков.
• если количество отрицаний четное, результат положительный
• если количество отрицаний нечетное, результат отрицательный

Примечание:

• Числа, которые входят в таблицу умножения $2$, называются четными числами, такими как $2, 4, 6, 8, 10, 12, …$
• Числа, которые не входят в таблицу умножения 2, называются нечетными числами, например как $1, 3, 5, 7, 9, 11, …$
• Каждое натуральное число является либо четным, либо нечетным числом.

Рассмотрим пример $-4 \times 4$.

Число отрицательных знаков равно $1$, что нечетно. Таким образом, результат будет отрицательным (и будет лежать слева от $0$(ноль)).

Начиная с нуля, в левой части числовой прямой формируются четыре группы равных интервалов по $4$. Таким образом, мы достигнем $-16$.

Начать с 0Переместить 4 шагаПовторить 4 раза Типы систем координат

Деление на числовой прямой

Как упоминалось выше, деление есть не что иное, как многократное вычитание. Воспользуемся этим фактом и поймем представление операции деления на числовой прямой.

Предположим, что число $x$ делится на $y$.

Поскольку операцию деления можно выполнять как повторное вычитание, поэтому мы будем выполнять операцию вычитания, двигаясь влево по числовой строке.

Давайте разберемся с шагами деления на числовой прямой.

Шаг 1: Нарисуйте числовую прямую, начертите числа, кратные $y$, начиная с $0$, и отметьте делимое $x$ на числовой прямой. Мы возьмем $x$ в качестве эталона.

Шаг 2: Начиная с $x$, мы продолжаем вычитать группы по $y$ единиц, пока не достигнем числа $0$. Каждый раз, когда мы делаем вычитание, мы перемещаемся на y единиц влево от $x$, пока не достигнем $0$. Альтернативный метод сделать это, начиная с $0$ в качестве контрольной точки, мы можем двигаться вправо группами по $y$ единиц, пока не достигнем числа $x$.

Шаг 3: Количество шагов на $y$ единиц, на которые мы продвинулись влево от $x$, чтобы достичь $0$, или количество шагов на $y$ единиц, на которые мы продвинулись вправо от $0$ для достижения $x$ даст нам частное.

Давайте рассмотрим пример деления 12$ на 6$, чтобы понять представление деления на числовой прямой.

Давайте выполним действия, описанные выше, чтобы выполнить деление $12 \div 6$.

Начните с 0

Чтобы выполнить $12\div 6$, мы построим числовую прямую и нанесем первые несколько кратных $6$, начиная с $0$, включая дивиденд $12$.

Первые несколько кратных 6

Обведите дивиденд $12$.

Обведи 12

Начиная с $12$, сдвинься влево на $6$ единиц и продолжай повторять эти движения по $6$ единиц, пока не достигнешь $0$.

Move from 12 to 0

Количество ходов, сделанных для достижения $0$ с $14$, будет частным. Как мы видим, нам пришлось переместиться на $2$ прыжков, чтобы достичь $0$.

Следовательно, частное равно $2$.

Деление отрицательных чисел на числовой строке

Теперь мы рассмотрим представление деления отрицательных чисел на числовой прямой. Шаги, чтобы показать деление, будут очень похожи на те, что обсуждались в предыдущем разделе. Возьмем два случая с примерами.

Случай I: отрицательное число разделить на положительное число

Пример: $\left(-12 \right) \div 3$

Согласно правилам работы с целыми числами, при делении отрицательного числа на положительное число или наоборот всегда получается отрицательное число.

Начните с 0

Мы наносим отрицательные числа, кратные $3$, на числовую прямую, начиная с $0$ и по крайней мере до $-12$, поскольку дивиденд равен $-12$.

Отрицательные кратные 3

Обведите делимое $-12$.

Окружить -12

Начиная с $-12$, сместитесь вправо на $3$ единиц и продолжайте повторять эти движения по $3$ единиц, пока не достигнете $0$.

Переход от -12 к 0

Мы видим, что всего было сделано $4$ прыжков, каждый из которых состоит из $3$ единиц, чтобы достичь $-12$.

Так как скачки сделаны влево от $0$ на числовой прямой, следовательно, результат равен $-4$.

Следовательно, $\left(-12 \right) \div 3 = -4$.

Случай II: Отрицательное число разделить на отрицательное число

Пример: $\влево(-15\вправо) \div \влево(-3 \вправо)$

В соответствии с правилами целочисленной операции, когда отрицательное число делится на отрицательное число, результатом всегда является положительное число.

Начните с 0

Мы наносим положительные множители от $3$ по крайней мере до $15$, как показано на диаграмме.

Первые несколько кратных 3

Обведите дивиденд $15$.

Обведи 15

Начиная с $15$, сдвинься влево на $3$ единиц и продолжай повторять эти движения по $3$ единиц, пока не достигнешь $0$.

Переход от 15 к 0

Мы видим, что для достижения 0 было сделано всего $5$ прыжков, каждый из которых состоит из $3$ единиц. 

Следовательно, $\left(-15\right) \div \left(-3 \right) = 5$.

Деление на числовой прямой с остатком

При делении чисел мы часто сталкиваемся с ситуациями, когда делимое не делится на делитель полностью. Это происходит, когда делимое не кратно делителю или делитель не является множителем делимого.

При возникновении такой ситуации мы получаем ненулевой остаток.

Теперь мы поймем, как представить деление на числовой прямой с остатками на примере.

Разделим число $12$ на $5$ и представим его на числовой прямой.

Начните с 0

Поскольку делитель равен $5$, мы начинаем создавать группы из $5$ единиц и начинаем двигаться вправо от $0$, начиная с $0$, чтобы достичь числа $12$.

Первые несколько кратных 5

Обведите дивиденд $17$.

Обведите 17

Начните создавать группы по 5$ с 0$.

Переходим от 0 к 17

Мы видим, что первая группа от 0$ до 5$, вторая группа от 5$ до 10$ и третья группа от 10$ до 15$. Таким образом, у нас есть три группы по $5$ от $0$ до $15$.

Обратите внимание, что для третьей группы нам нужно как минимум на 5$ больше единиц, но у нас есть только на 2$ больше единиц от 15$ до 17$.

Следовательно, мы можем сказать, что остаток равен $2$, так как эти $2$ единицы не образуют группу из $5$.

Следовательно, частное равно $3$, так как есть три группы по $5$, а остаток равен $2$.

Следовательно, мы можем представить это деление как $17 \div 5 =$ Частное равно $2$, а остаток равен $5$.

Ключевые выводы

• Если знаки разные, то ответ отрицательный.
• Если знаки одинаковые, ответ положительный.

Практические задачи

1. $\влево(+8\вправо)\раз\влево(-1\вправо)$
2. $\влево(+4\вправо) \раз\влево(+6\вправо)$
3. $\left(-3 \right) \times \left(-7 \right)$
4. $\left(-9 \right) \times \left(-2 \right)$
5. $\left( -11 \вправо) \раз \влево(+5 \вправо)$
6. $\влево(+12 \вправо) \раз \влево(0 \вправо)$
7. $\влево(-20 \вправо) \раз \left(-4 \right)$
8. $\left(-15 \right) \times \left(+13 \right)$
9. $\left(-20 \right) \times \left(-5 \ вправо)$
10. $\влево(-9\вправо) \раз \влево(+4\вправо)$
11. $\влево(+3\вправо) \раз \влево(-6 \вправо)$
12. $\влево(+11\вправо)\раз\влево(0\вправо)$
13. $\влево(-7\вправо) \раз\влево(-4\вправо)$
14. $\влево(- 9 \right) \times \left(+8 \right)$
15. $0 \div \left(-8 \right)$
16. $\left(+9 \right) \div \left(-3 \right) $
17. $\left(-11 \right) \div \left(-6 \right)$
18. $\left(-12 \right) \div \left(-3 \right)$
19. $\left (-25 \right) \div \left(+5 \right)$
20. $\left(+45 \right) \div \left(-3 \right)$
21. $\left(-24 \right) \дел\влево(-4\вправо)$
22. $\left(-78 \right) \div \left(13 \right)$
23. $\left(30 \right) \div \left(-10 \right)$
24. $\left(+14 \right) \div \left(-2 \right)$
25. $\left(-16 \right) \div \left(-8 \right)$
26. $\left(-48 \right) \div \ влево(+6\вправо)$
27. $\влево(4\вправо) \дел\влево(2\вправо)$
28. $0 \дел\влево(6\вправо)$

Рекомендуемое чтение

• Сложение и вычитание целых чисел
• Как решать радикальные уравнения?
• Что использовать — HCF или LCM?

Вам также может понравиться

Как решать линейные уравнения с матрицами (с методом и примерами)

Содержание Как решать линейные уравнения с матрицамиУсловие непротиворечивости

Читать далее

Правило Крамера – определение, формулы и примеры

Содержание Что такое правило Крамера?Формула правила КрамераПравило Крамера 2 x

Читать далее

Карточки по математике для печати бесплатно – скачать PDF

Карточки по математике являются ценным пособием для учащихся всех возрастов и

Читать далее

Правила умножения и деления для детей

Добро пожаловать в первый набор для обучения математике Kids Academy ! Эта статья призвана помочь вам в постепенном обучении детей умножению и делению. Он представляет уроки в соответствии со сложностью уроков. Он стремится воспитать склонных к математике учащихся, представляя им сценарии из реальной жизни, увлекательные занятия и эффективные рабочие листы для 1-го класса. Он состоит из следующих статей, которые помогут вам познакомить детей с этой темой, Умножение и деление :

• Умножение однозначных чисел ;
• Умножение двузначного числа на однозначное ;
• Решение текстовых задач на умножение ;
• Разделение чисел ;
• Решение словесных задач с участием отдела .

 Первая статья, Умножение однозначных чисел , создана для того, чтобы дети изучили концепцию умножения на базовом уровне и вооружили их фундаментальными знаниями, прежде чем переходить к теме гораздо более высокого уровня. Благодаря этому они узнают, что такое множимое, множитель и произведение. Чтобы дать вам обзор, множимое — это то, что умножается, тогда как множитель — это тот, который умножает множимое.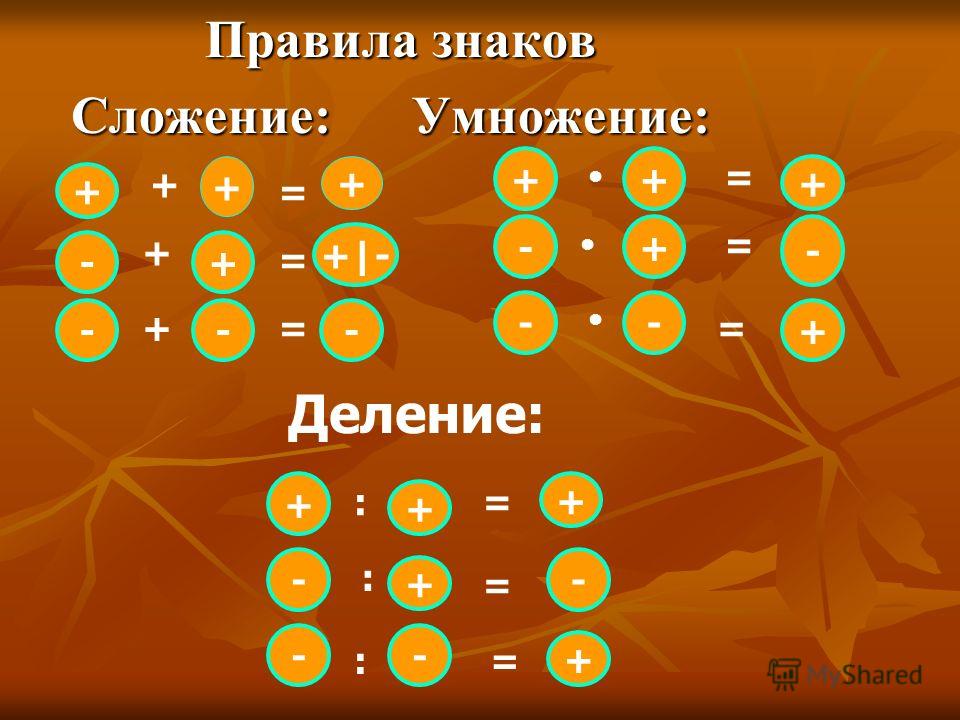 Конечный результат умножения множимого и множителя называется произведением . Мы начинаем с умножения однозначных чисел, так как это увеличит шансы детей приобрести навык, необходимый для продолжения умножения двузначных чисел. Вот несколько примеров занятий, которые помогут вашим детям изучить эту тему:

Щелкайте по рабочим листам, чтобы заполнить их онлайн!

Вторая статья, Умножение двузначного числа на однозначное число , предназначена для учащихся, которые уже знакомы с умножением однозначных чисел и теперь готовы принять более высокий уровень сложности. Двузначные числа имеют разрядные значения единиц и десятков. Эти значения мест определяют, какое из них должно быть умножено первым на однозначный множитель. Умножение двузначного числа на однозначное требует внимания ваших детей, так как процесс немного требует другого набора шагов. Ниже приведены некоторые из заданий, которые ваши дети могут выполнить, чтобы закрепить усвоение понятий, которым их обучают:

Adsense-контейнер

Нажмите на рабочие листы, чтобы заполнить их онлайн!

Третья статья, Решение словесных задач на умножение , предназначена для измерения понимания вашими детьми процесса умножения и того, как он применяется в практической жизни. Словесные задачи содержат определенные ситуации, требующие решения математических процессов. Решение текстовых задач на умножение стоит попрактиковать, так как дети будут использовать этот процесс в своей повседневной жизни, например, покупая в столовой или копя на что-то. Взгляните на некоторые учебные листы, которые помогут вашим детям лучше учиться:

Щелкайте по рабочим листам, чтобы заполнить их онлайн!

Четвертая статья, Разделение чисел , составлена ​​таким образом, чтобы дети познакомились с концепцией деления. Это также позволяет им ознакомиться с такими понятиями, как делимое, делитель и частное. Напомним, делимое — это то, что делится, а делитель — это число, используемое для деления делимого . Результат процесса называется частным. Деление чисел полезно для ваших детей, поскольку вы показываете им ценность обмена и искусство разделения чего-то вроде своего времени на определенные слоты. Вот краткий обзор некоторых занятий, которые помогут детям научиться делению:

Щелкайте по рабочим листам, чтобы заполнить их онлайн!

Пятая статья, Решение текстовых задач с участием отдела , предназначена для того, чтобы дети могли использовать то, что они узнали в предыдущей статье. Словесные задачи позволяют детям выяснить ответы, выполняя необходимые действия. Решение текстовых задач на деление — отличная практика, которая оттачивает математические навыки детей, которые можно использовать во многих вычислениях, с которыми они сталкиваются в повседневной жизни, начиная с простой задачи, такой как деление пачки конфет так, чтобы у каждого была равная доля до сложная задача, такая как разделение периода времени для различных видов деятельности. Рассмотрите эти примеры заданий, чтобы ваши дети получили возможность повысить свои навыки в решении текстовых задач, требующих процесса деления:

Щелкайте по рабочим листам, чтобы заполнить их онлайн!

Подводя итог, этот набор для обучения тщательно спланирован, чтобы обучать ваших детей в более естественном, но увлекательном темпе. От знакомства с умножением и решения задач с его использованием до обучения делению и решения связанных с ним задач — детей не заставляют немедленно углубляться в них, а они проходят через процессы так, как им хотелось бы, с вашей непоколебимой поддержкой.