Презентация «Правильные многогранники»
#Учебно-методические материалы #Презентация #Среднее профессиональное образование
Правильные многогранники Презентация подготовлена :Смирнов Влад, гр.КЭ-9 Преподаватель:Лаврова Н.Н.
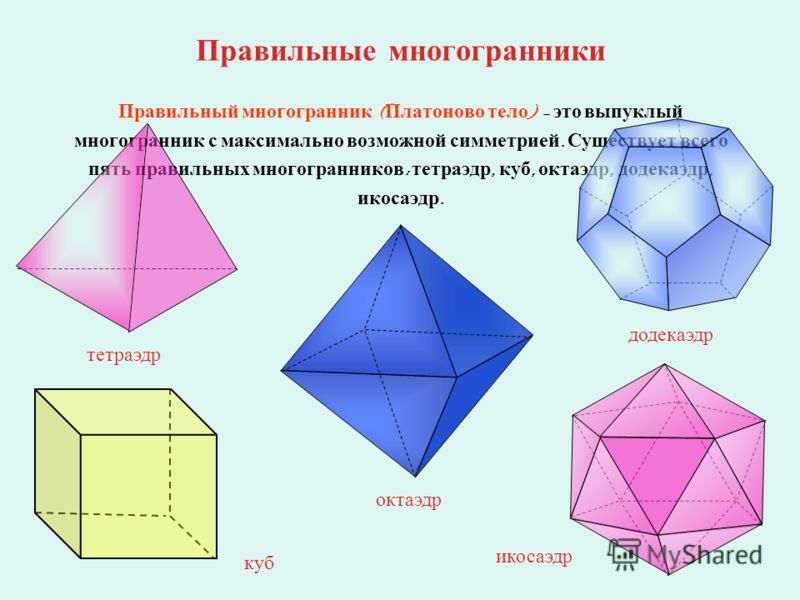
Что такое правильный многогранник? Правильный многогранник или плато́ново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.
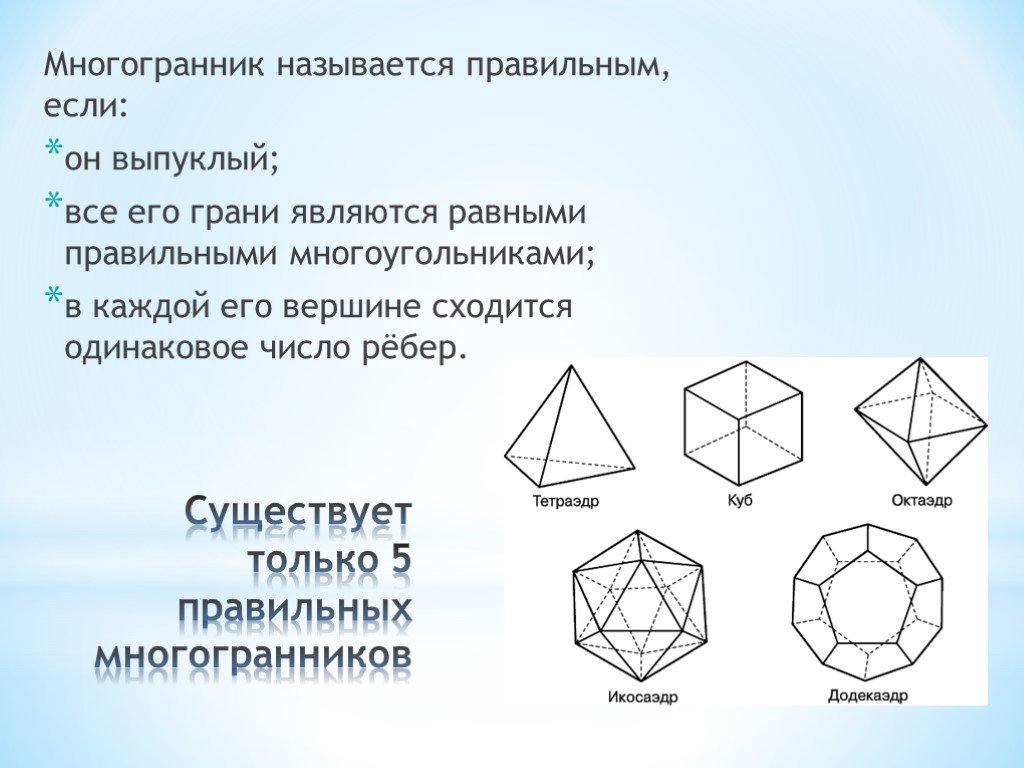
Определение Многогранник называется правильным, если: он выпуклый; все его грани являются равными правильными многоугольниками; в каждой его вершине сходится одинаковое число рёбер.
Виды правильных многогранников В трёхмерном евклидовом пространстве существует всего пять правильных многогранников: Название каждого многогранника происходит от греческого названия количества его граней и слова «грань».
Простейшим среди многогранников является тетраэдр (четырёхгранник – от греческого «тетра», т.
Куб, или гексаэдр (шестигранник – от греческого «гекса», т.е. шесть) – самый общеизвестный и широко используемый многогранник. Все шесть его граней – квадраты, сходящиеся по два вдоль каждого ребра и по три в каждой вершине.
Октаэдр (восьмигранник – от греческого «окта», т.е. восемь), составленный из восьми правильных треугольников, его противоположные грани лежат в параллельных плоскостях.
Иоганн Кеплер (1571-1630) в своём этюде «О снежинке» высказал такое замечание: «Среди правильных тел самое первое, начало и родитель остальных – куб, а его, если позволительно так сказать, супруга – октаэдр, ибо у октаэдра столько углов, сколько у куба граней».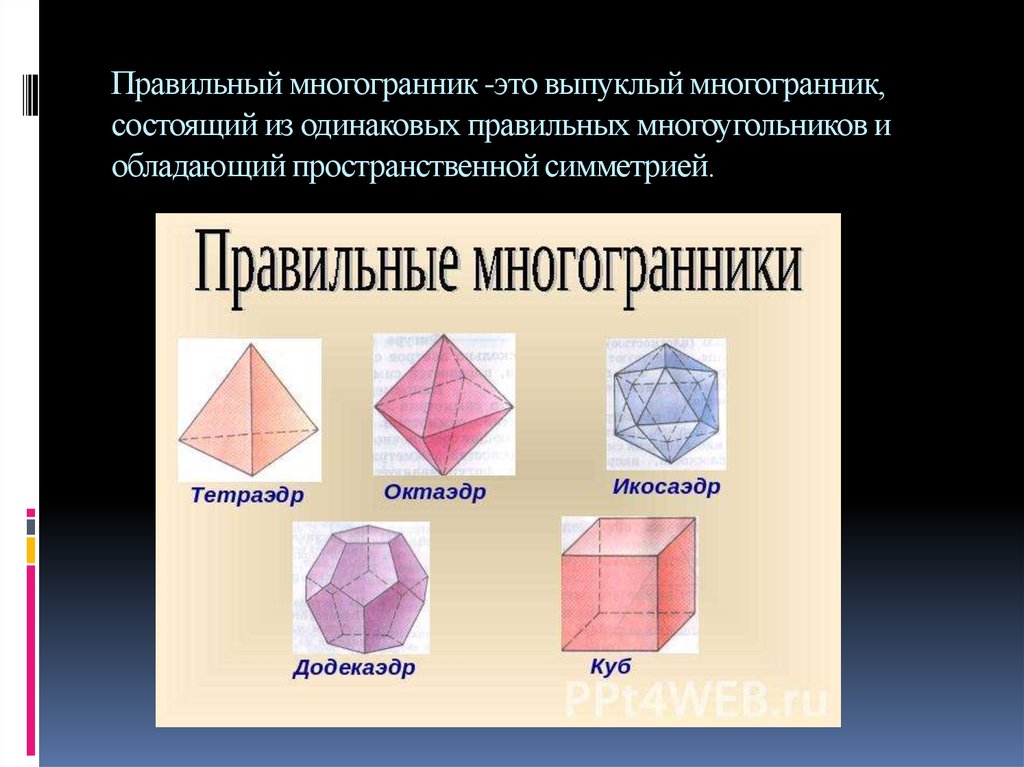
Икосаэдр (двадцатигранник – от греческого «икос», т.е. двадцать), составленный из двадцати правильных треугольников. Икосаэдр – одно из пяти тел, по простоте следующее за тетраэдром и октаэдром. Их объединяет то обстоятельство, что гранями каждого являются равносторонние треугольники.
И загадочный додекаэдр (двенадцатигранник – от греческого «додека», т.е. двенадцать), составленный из двенадцати правильных пятиугольников. В известном смысле додекаэдр представляет наибольшую привлекательность среди тел, соперничая с икосаэдром, который почти ему не уступает (а быть может, в чём-то и превосходит).
Философ Платон и четыре стихии природы Подробно описал свойства правильных многогранников древнегреческий учёный, философ-идеалист Платон (428 –348 до н.э.), в учении которого они играли важную роль. Поэтому эти многогранники носят название «платоновых тел». ПЛАТОН
Платон являлся основателем школы, названной «Академией» по имени местности вблизи Афин, где он постоянно встречался со своими учениками. Сам Платон не был математиком, но он придавал ей исключительно важное значение. При входе в основанную им Академию была надпись следующего содержания: «Пусть сюда не входит тот, кто не знает геометрии …». Одному из желающих поступить в его школу для изучения философии, но не имеющему знаний по геометрии, Платон сказал: «Уйди прочь! У тебя нет орудия для изучения философии …».
Платон связал с этими телами формы атомов основных стихий природы. Какими соображениями при этом он руководствовался?
Сам Платон не был математиком, но он придавал ей исключительно важное значение. При входе в основанную им Академию была надпись следующего содержания: «Пусть сюда не входит тот, кто не знает геометрии …». Одному из желающих поступить в его школу для изучения философии, но не имеющему знаний по геометрии, Платон сказал: «Уйди прочь! У тебя нет орудия для изучения философии …».
Платон связал с этими телами формы атомов основных стихий природы. Какими соображениями при этом он руководствовался?
Итак, правильных многогранников Платон знал пять, а число стихий (огонь, воздух, вода и земля) было ровно четыре. Следовательно, из пяти многогранников надо выбрать четыре, которые можно было бы сопоставить со стихиями. Платон считал, что некоторые элементы правильных многогранников могут перейти друг в друга. Преобразование одних многогранников в другие могли быть осуществлены путем перестройки их внутренней структуры. Но для этого в данных телах нужно было найти такие структурные элементы, которые были бы для них общими.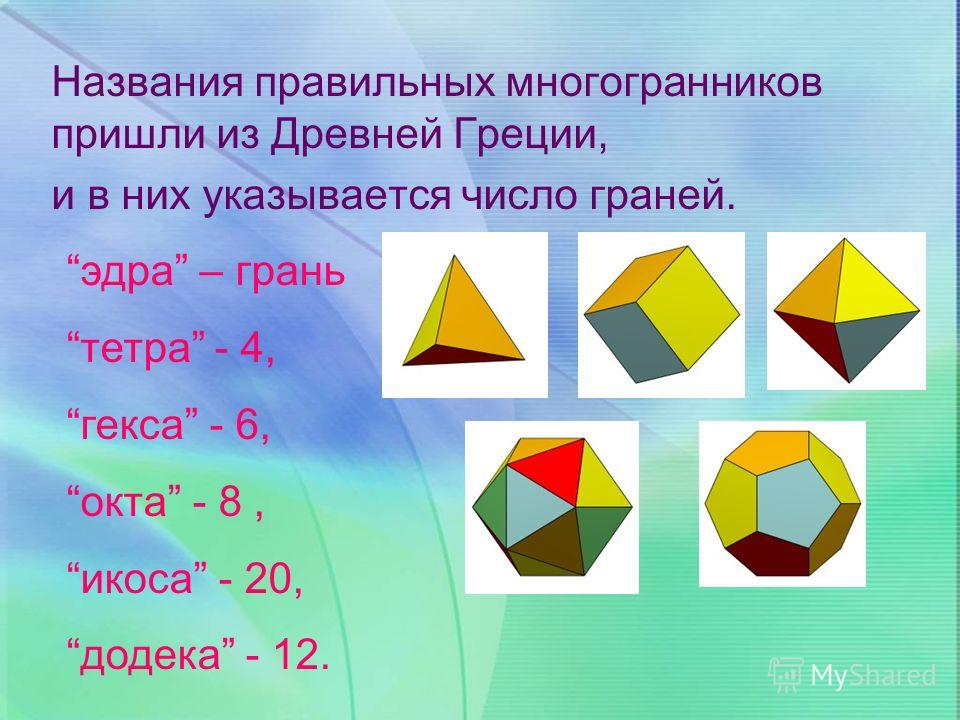
Из внешнего вида правильных многогранников следует, что грани трех многогранников – тетраэдра, октаэдра, икосаэдра – имеют форму равностороннего треугольника. Два оставшихся многогранника – куб и додекаэдр – построены: первый – из квадратов, а второй – из правильных пятиугольников, поэтому они не могут преобразовываться ни друг в друга, ни в рассмотренные три тела.
Итак, тетраэдр символизировал огонь, т.к. его вершина устремлена вверх. Куб или гексаэдр символизировал – землю, как самый «устойчивый». Октаэдр символизирует воздух, как самый «воздушный». Икосаэдр символизирует – воду, т.к. он самый «обтекаемый». И всей вселенной была приписана форма додекаэдра, т. е. мы живём внутри небесного свода.
Комбинаторные свойства
Эйлером была выведена формула, связывающая число вершин (В), граней (Г) и рёбер (Р) любого выпуклого многогранника простым соотношением: В + Г = Р + 2.
Отношение количества вершин правильного многогранника к количеству рёбер одной его грани равно отношению количества граней этого же многогранника к количеству рёбер, выходящих из одной его вершины. У тетраэдра это отношение равно 4:3, у гексаэдра и октаэдра — 2:1, а у додекаэдра и икосаэдра — 4:1.
Правильный многогранник может быть комбинаторно описан символом Шлефли {p, q}, где: p — число рёбер в каждой грани; q — число рёбер, сходящихся в каждой вершине.
У тетраэдра это отношение равно 4:3, у гексаэдра и октаэдра — 2:1, а у додекаэдра и икосаэдра — 4:1.
Правильный многогранник может быть комбинаторно описан символом Шлефли {p, q}, где: p — число рёбер в каждой грани; q — число рёбер, сходящихся в каждой вершине.
Теорема Эйлера
Многогранники в архитектуре Использовать многогранники в архитектуре люди стали очень давно, еще до новой эры. И по мере роста строительного мастерства в мире появлялись новые шедевры, основанные на сложных геометрических фигурах. Национальная библиотека — одна из них.
Национальная библиотека — одна из них.
Многогранники в архитектуре Современный стеклянный вход в Лувр, который появился во дворе ренессансного дворца 20 лет назад и до сих пор остается спорным новоделом — это тоже многогранник, пирамида.
Многогранники в архитектуре
Усеченная пирамида пользуется популярностью у современных архитекторов. Например, в Индианополисе (США) в 1972 году закончили строительство офисного комплекса из трех зданий, который так и назвали — The Pyramids.
Многогранники в архитектуре А это парк развлечений Футуроскоп под Парижем (Франция)
Развёртки правильных многогранников Одним из способов изготовления правильных многогранников является способ с использованием так называемых развёрток. Если модель поверхности многогранника изготовлена из гибкого нерастяжимого материала (бумаги, тонкого картона и т. п.), то эту модель можно разрезать по нескольким рёбрам и развернуть так, что она превратится в модель некоторого многоугольника. Этот многоугольник называют развёрткой поверхности многогранника.
Гармония правильных многогранников / Этюды // Математические этюды
Гармония правильных многогранников / Этюды // Математические этюдыМатематические этюды
К списку
Правильные многогранники интересовали многих великих учёных. И этот интерес выходил далеко за пределы математики.
Платон (427 до н.э. — 347 до н.э.) рассматривал их как основу строения Вселенной,
Кеплер (1571—1630) пытался связать правильные многогранники с движением планет Солнечной системы (которых в его время было известно пять).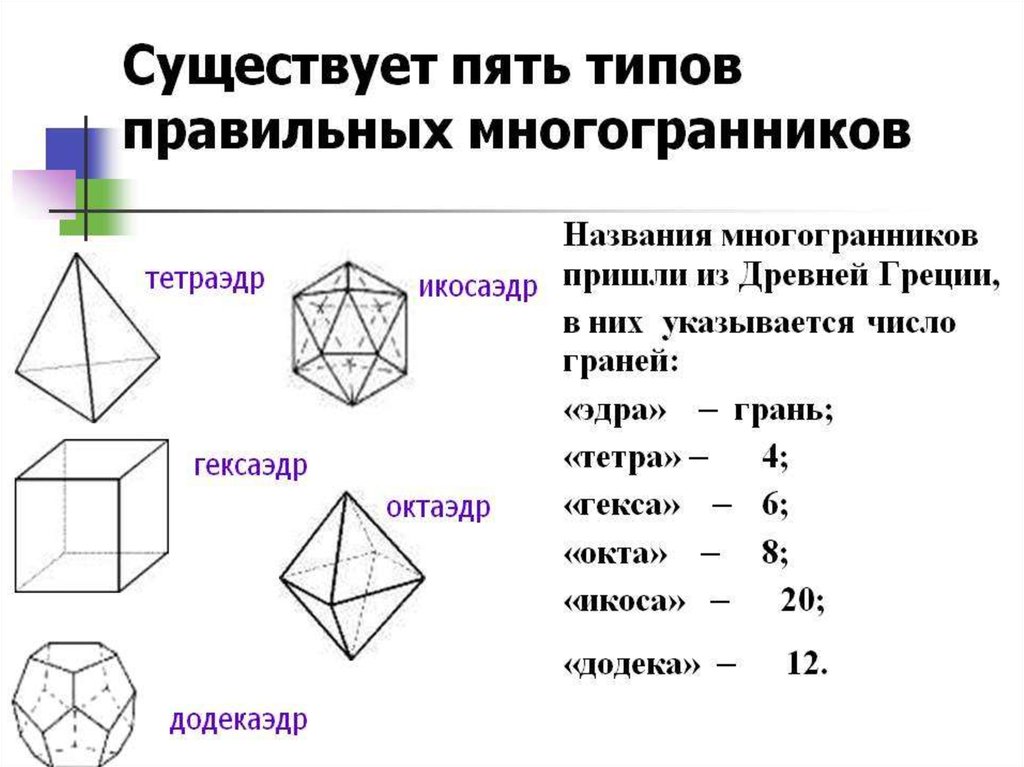
Правильным многогранником называется многогранник, все грани которого суть правильные многоугольники, все плоские углы которого равны между собой и двугранные углы которого равны между собой. (Плоскими углами многогранника называются углы многоугольников-граней, двугранными углами многогранника называются углы между гранями, имеющими общее ребро.)
Заметим, что из этого определения автоматически следует выпуклость правильного многогранника, которая в некоторых книгах включается в определение.
В трёхмерном пространстве существует ровно пять правильных многогранников: тетраэдр, октаэдр, куб (гексаэдр), икосаэдр, додекаэдр. То, что других правильных многогранников не существует,
было доказано Евклидом (около 300 г.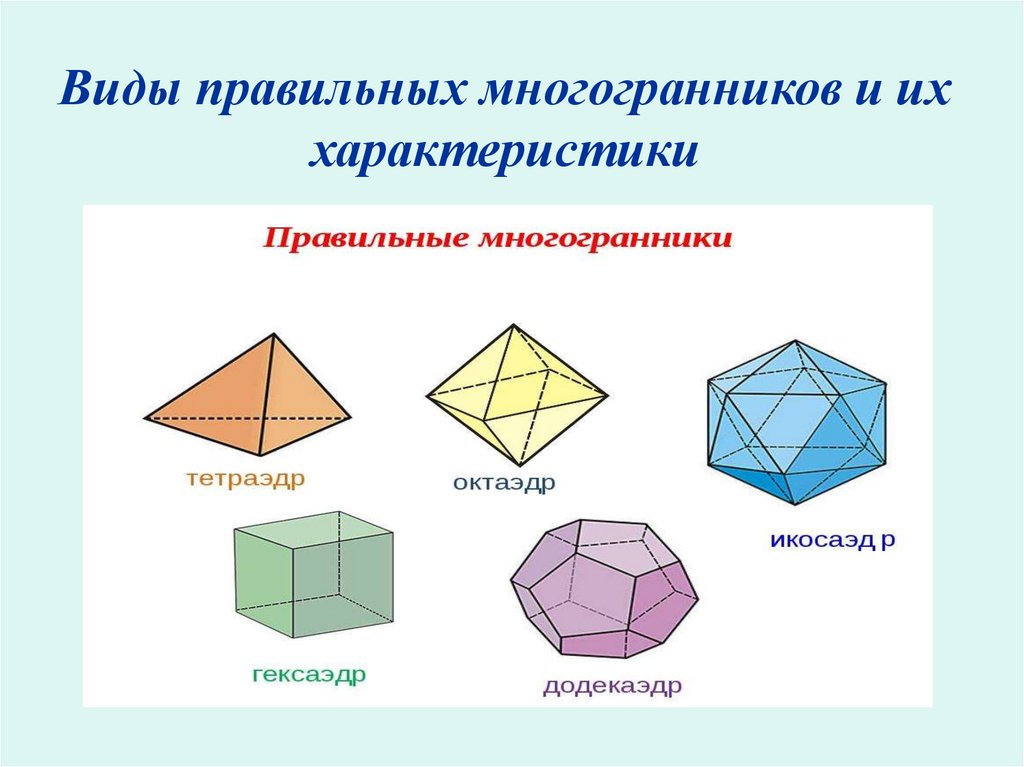 \circ$.
\circ$.
Возьмём в серединах граней тетраэдра по точке и соединим их между собой отрезками. Эти отрезки равны по длине и образуют равносторонние треугольники. Точки являются вершинами, отрезки — рёбрами, а треугольники — гранями ещё одного тетраэдра.
Аналогичное построение применимо и в более общем случае. Рассмотрим произвольный выпуклый многогранник и возьмём точки в серединах его граней. Соединим между собой точки соседних граней отрезками. Тогда точки являются вершинами, отрезки — рёбрами, а многоугольники, которые ограничивают эти отрезки, гранями ещё одного выпуклого многогранника. Этот многогранник называется двойственными к исходному.
Как было показано выше, двойственным к тетраэдру является тетраэдр.
Увеличим размер тетраэдра, вершинами которого являются середины граней исходного тетраэдра, до размеров последнего. Восемь вершин так расположенных тетраэдров являются вершинами куба.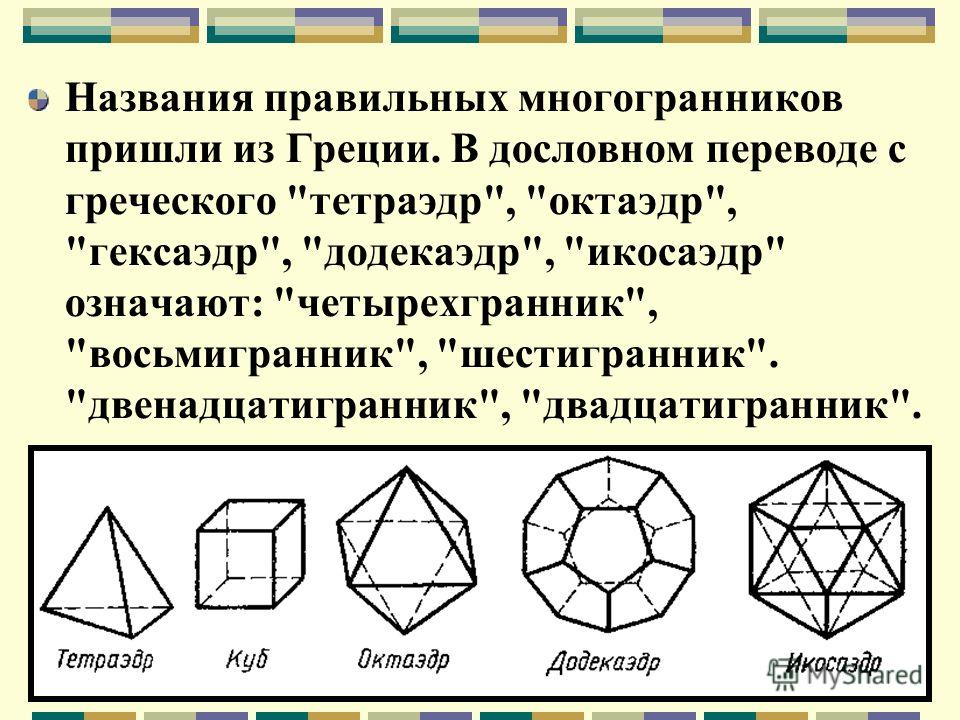 \circ$.
\circ$.
Отметим середины граней октаэдра и перейдём к двойственному к октаэдру многограннику. Это — куб или гексаэдр (от греч. εξά — шесть). У куба грани являются квадратами. Он имеет 6 граней, 8 вершин, 12 рёбер. Плоские углы куба равны $\pi/2$, двугранные углы также равны $\pi/2$.
Если взять точки на серединах граней куба и рассмотреть двойственный к нему многогранник, то можно убедиться, что им снова будет октаэдр. Верно и более общее утверждение: если для выпуклого многогранника построить двойственный, а затем двойственный к двойственному, то им будет исходный многогранник (с точностью до подобия).
Возьмём на рёбрах октаэдра по точке, с тем условием, чтобы каждая делила ребро в соотношении $1:(\sqrt5+1)/2$ (золотое сечение) и при этом точки,
принадлежащие одной грани, являлись вершинами правильного треугольника. Полученные 12 точек являются вершинами ещё одного правильного многогранника — икосаэдра (от греч. \circ$.
\circ$.
Взяв середины граней додекаэдра, и перейдя к двойственному ему многограннику, получим снова икосаэдр. Итак, икосаэдр и додекаэдр двойственны друг другу. Это ещё раз иллюстрирует тот факт, что двойственным к двойственному будет исходный многогранник.
Заметим, что при переходе к двойственному многограннику, вершины исходного многогранника соответствуют граням двойственного, рёбра — рёбрам двойственного, а грани — вершинам двойственного многогранника. Если у икосаэдра 20 граней, значит у двойственного ему додекаэдра 20 вершин и у них одинаковое число рёбер, если у куба 8 вершин, то у двойственного ему октаэдра 8 граней.
Существуют различные способы вписывания правильных многогранников друг в друга, приводящие ко многим замечательным конструкциям. Интересные и красивые многогранники получаются также при объединении и пересечении правильных многогранников.
В додекаэдр впишем куб так, чтобы все 8 вершин куба совпадали с вершинами додекаэдра.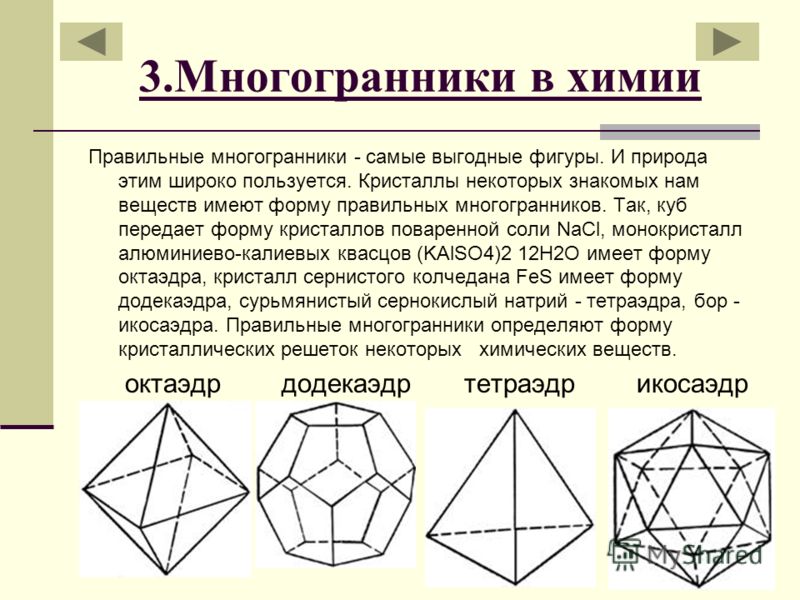 Вокруг додекаэдра опишем икосаэдр
так, чтобы его вершины оказались в серединах граней икосаэдра. Вокруг икосаэдра опишем октаэдр, так, чтобы вершины икосаэдра лежали на рёбрах октаэдра.
Наконец, вокруг октаэдра опишем тетраэдр так, чтобы вершины октаэдра попали на середины рёбер тетраэдра.
Вокруг додекаэдра опишем икосаэдр
так, чтобы его вершины оказались в серединах граней икосаэдра. Вокруг икосаэдра опишем октаэдр, так, чтобы вершины икосаэдра лежали на рёбрах октаэдра.
Наконец, вокруг октаэдра опишем тетраэдр так, чтобы вершины октаэдра попали на середины рёбер тетраэдра.
Такую конструкцию из кусочков сломанных деревянных лыжных палок сделал ещё ребёнком будущий великий математик XX века В. И. Арнольд. Владимир Игоревич хранил её долгие годы, а затем отдал в лабораторию популяризации и пропаганды математики Математического института им. В. А. Стеклова.
Литература
Кокстер Г. С. М. Введение в геометрию. — М. : Наука, 1966.
Адамар Ж. Элементарная геометрия. — Часть 2. Стереометрия. — М. : Просвещение, 1951.
Евклид. Начала Евклида. Книги XXI—XXV. — М.—Л.: ГИТТЛ, 1950.
Другие этюды раздела «Внешняя геометрия многогранников»
Тени Увеличение объёма выпуклых многогранников Удивительные объёмы многогранников Кусочно гладкое вложение многогранника Изгибаемые многогранникиМатематические этюды
 Геометрические свойства Геометрические свойства Правильные многогранники обобщают понятие правильного многоугольника на три измерения. Правильный многогранник – это многогранник с конгруэнтными гранями и одинаковыми вершинами. Есть только пять выпуклых правильных многогранников, и они известны под общим названием платоновых тел, показанных ниже. Слева вверху это правильный тетраэдр (четыре грани), куб (шесть), октаэдр (восемь), додекаэдр (двенадцать) и икосаэдр (двадцать). Нас будет интересовать вычисление объема и площади поверхности этих твердых тел. Ситуация сильно отличается от правильных многоугольников, потому что Платоновых тел всего пять, поэтому мы будем рассматривать каждое из них отдельно. Обозначения немного более громоздкие, но мы всегда будем использовать одни и те же переменные. Пусть n обозначает количество граней многогранника. Пусть s будет длиной ребра, S n общая площадь поверхности, V n объем, r расстояние от центра многогранника до вершины и a расстояние от центра многогранника до центра одного из его лица. Площадь поверхности многогранника просто , где каждая грань многогранника имеет k сторон. Как площадь правильного многоугольника можно найти, разбив его на конгруэнтные треугольники, так и объем правильного многогранника можно найти, разбив его на n конгруэнтных пирамид, где каждая грань многогранника является основанием одна пирамида и ребра пирамид являются отрезками прямых от центра многогранника к вершинам. Объем многогранника равен сумме объемов составляющих его пирамид (и объема пирамиды высотой ч и площадь основания А равна ч · А /3):
(Обратите внимание на сходство этого уравнения с аналогичным уравнением для площади правильного многоугольника: число измерений. Для куба, В 6 = с 3 и S 6 = 6 с 2 . Апофема a = s / 2. Чтобы найти радиус r , мы образуем отрезок от центра куба до вершины, а другой от центра куба до центра грани, касающейся этой вершина. По теореме Пифагора так Площадь поверхности правильного тетраэдра равна Отрезок, проведенный из вершины к середине противоположной стороны, имеет длину h , высоту тетраэдра. Этот отрезок образует прямоугольный треугольник с длиной стороны и отрезком, проведенным от середины базового треугольника к вершине этого треугольника. По теореме Пифагора так Таким образом, объем Правильный октаэдр имеет площадь поверхности Мы находим объем правильного октаэдра, разрезая его на две квадратные пирамиды (имеющие общее основание). Таким образом, ч = с / √2, а объем равен Площадь поверхности правильного икосаэдра составляет Мы вычисляем объем правильного икосаэдра, находя апофему a и, наконец, применяя (1). В поперечном сечении справа два ребра длиной s лежат напротив друг друга на икосаэдре и образуют прямоугольник с диагоналями (длиной d ) из двух правильных пятиугольников. Эти пятиугольники имеют длину стороны s и могут рассматриваться как двумерная «граница» икосаэдра, если смотреть на него. (На рисунке эти два пятиугольника лежат в плоскостях, перпендикулярных странице.) Четыре отрезка длиной х являются высотами треугольных граней икосаэдра. Снова воспользуемся теоремой Пифагора, получив два уравнения: Имеем d = (1 + √5) s / 2 и h = √3 s / 2, поэтому удаление r и нахождение a дает По уравнению (1) объем икосаэдра равен Правильный додекаэдр имеет общую площадь поверхности Нам понадобится больше изобретательности, чтобы найти объем додекаэдра, поскольку геометрия не так проста. (На диаграммах слева x = ( c s ) / 2.) Объединение этих уравнений дает Решаем для высоты h найти или ч = с /2. Тогда объем додекаэдра равен | |||||||||||||||||||||||||
 Сдвоенные многогранники Сдвоенные многогранники В следующей таблице указано количество V вершин, количество E ребер и количество F граней в каждом из пяти Платоновых тел. Как многогранники, эти значения удовлетворяют формуле Эйлера V E + F = 2.
Тетраэдр сам себе дуален. В правильном октаэдре каждая вершина соединена со всеми остальными вершинами, кроме одной. Снова вершины спарены, и есть 3 внутренние диагонали, которые пересекаются в центре октаэдра. Додекаэдр и икосаэдр немного сложнее. Додекаэдр имеет 20 вершин. Число способов выбрать среди них две вершины равно , поэтому число отрезков, соединяющих две различные вершины, равно 190. Правильный икосаэдр имеет 12 вершин и, следовательно, отрезки, соединяющие каждую пару. Треугольные грани не дают диагоналей, но 30 из них являются ребрами. Следовательно, икосаэдр имеет 36 внутренних диагоналей. |
геометрия — Я слышал, что правильных многогранников 48. То, что Ян Мисали называет правильными многогранниками, есть ли еще?
При сделанных вами предположениях на самом деле существует бесконечно много других правильных многогранников. Возьмем любые рациональные $m$, $n$ с $m, n>2$ и $$(m-2)(n-2)<4.$$. Оказывается, можно создать конфигурацию из $\{m \}$ многоугольники вокруг вершины, создавая вершинную фигуру $\{n\}$. Вот пример с $m=n=\frac{5}{2}$ с выделенной пентаграммой:
Эта конфигурация всегда будет иметь описанную сферу. Таким образом, мы можем однозначно повторить эту конструкцию в каждой из новых вершин, которые мы создаем счетно бесконечно много раз, на каждом шаге сохраняя описанную сферу, и мы либо получим Платоново тело, либо тело Кеплера-Пуансо после конечного числа шагов. или получить правильный апейроэдр $\{m,n\}$.
или получить правильный апейроэдр $\{m,n\}$.
В действительности многогранники, рассматриваемые Макмалленом и Шульте, исключают такую конструкцию. Упомянутые вами правила верны, но неполны. Самое основное правило — это, конечно, основное правило, определяющее многогранники:
- Правильный многогранник, конечно же, должен удовлетворять свойствам многогранника. То есть каждое ребро должно быть смежным ровно с двумя вершинами и ровно с двумя гранями.
Макмаллен и Шульте затем добавляют ограничения, о которых вы уже упоминали:
Правильный многогранник должен быть вложен в трехмерное евклидово пространство.
Правильный многогранник должен быть связным, что означает, что каждые две вершины соединены путем ребер.
Никакие две вершины, ребра или грани правильного многогранника не могут занимать одно и то же положение в пространстве.
Конечно, эти ограничения часто являются теми же неявными ограничениями, которые используются для описания всех многогранников.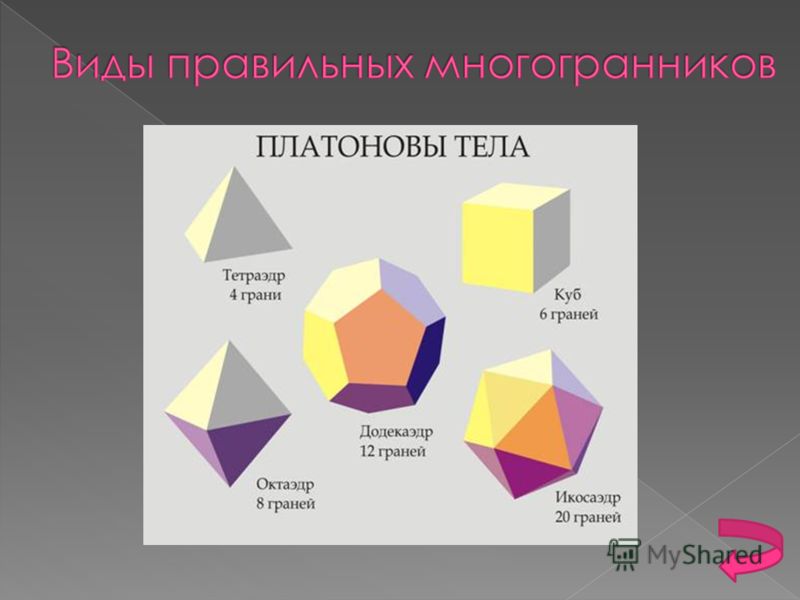 Мы еще не дошли до определения регулярности. Это стандартное определение, которое мы добавляем в качестве дополнительного правила:
Мы еще не дошли до определения регулярности. Это стандартное определение, которое мы добавляем в качестве дополнительного правила:
- Правильный многогранник должен быть транзитивным по флагу.
Флаг — это просто набор граней, ребер и вершин, инцидентных друг другу. Транзитивность флага означает, что для любых двух флагов существует симметрия многогранника (вращение, отражение, перенос или скользящее отражение), которая переводит первый во второй, сохраняя при этом общую форму многогранника.
Можно убедиться, что $\{m,n\}$ апейроэдры, о которых я упоминал ранее, действительно удовлетворяют требованиям 1–5. Однако Макмаллен и Шульте предъявляют еще одно требование, чтобы сузить набор правильных многогранников до 48.
- Группа симметрии правильного многогранника должна быть дискретной.
Для наших целей группа симметрии фигуры есть не что иное, как множество всех симметрий этой фигуры. Группа симметрии называется дискретной, если она имеет наименьшее ненулевое вращение и сдвиг.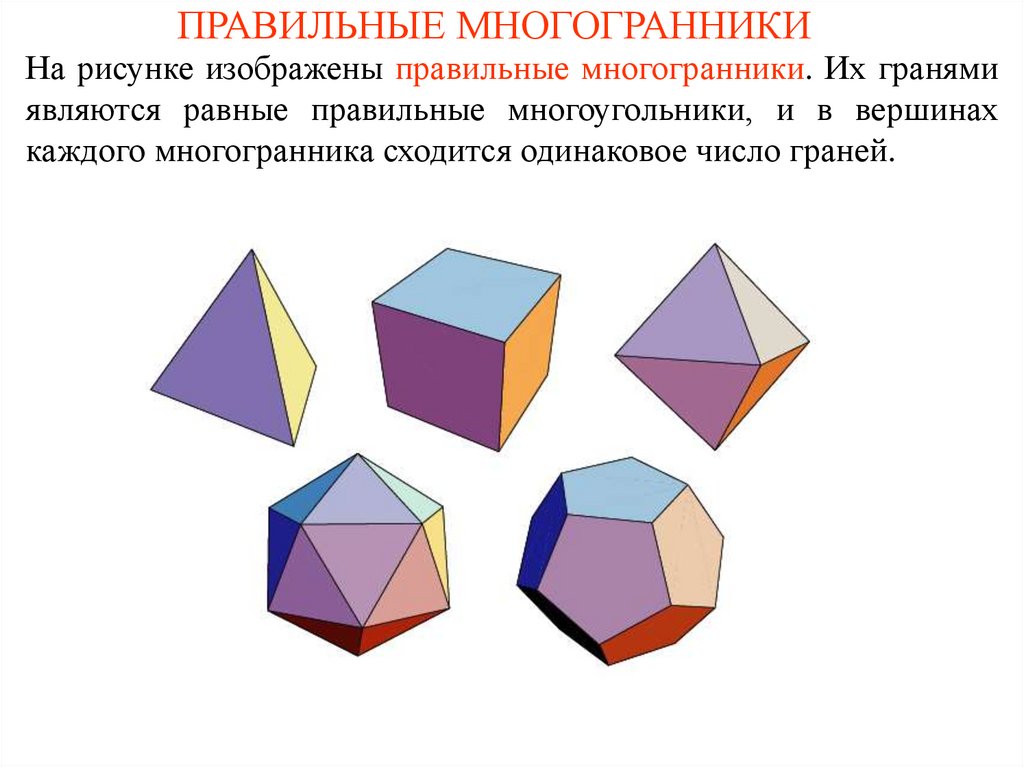

 Определения радиуса r и апофемы a имеют смысл, поскольку они являются радиусами описанной сферы и вписанной сферы соответственно. Пусть А к ( с ) — площадь правильного многоугольника с k сторонами и длиной стороны s .
Определения радиуса r и апофемы a имеют смысл, поскольку они являются радиусами описанной сферы и вписанной сферы соответственно. Пусть А к ( с ) — площадь правильного многоугольника с k сторонами и длиной стороны s .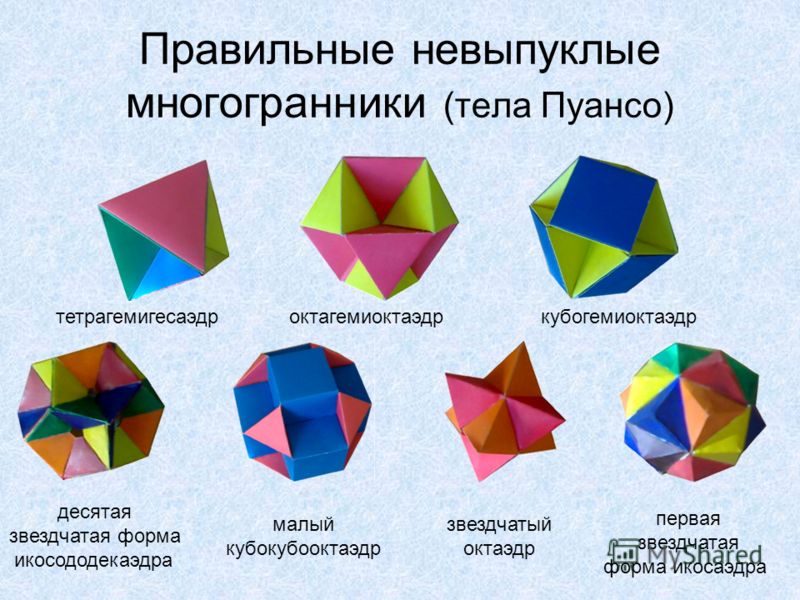 ) В то время как довольно просто найти объем первых трех Платоновых тел, не разбивая их на пирамиды, вычислить объем икосаэдра намного проще, разбив его.
) В то время как довольно просто найти объем первых трех Платоновых тел, не разбивая их на пирамиды, вычислить объем икосаэдра намного проще, разбив его. Если ч высота каждой из этих пирамид, то по теореме Пифагора имеем
Если ч высота каждой из этих пирамид, то по теореме Пифагора имеем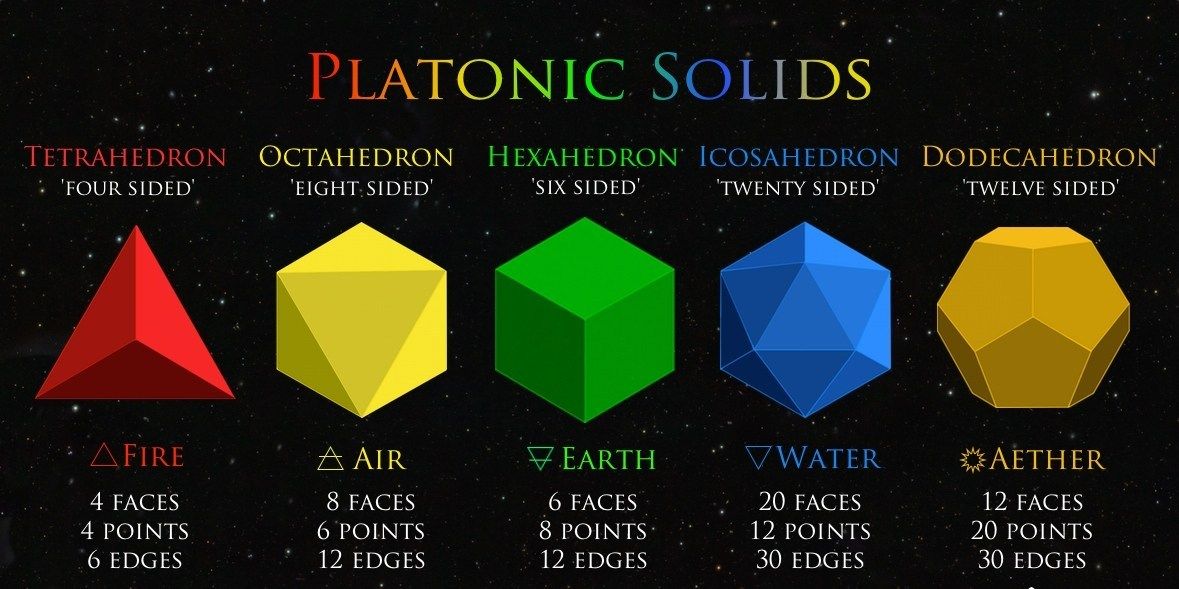 Однако есть более простой способ, чем найти апофему. Мы можем разбить додекаэдр на куб со стороной c = (1 + √5) s / 2 и шесть пирамидоподобных тел, как показано. Затем мы находим объем каждой пирамиды, что можно сделать, рассматривая среднюю часть как треугольную призму, а концевые части вместе как настоящую пирамиду, как показано ниже. Но сначала нам понадобятся два соотношения, включающие наклонную высоту l сторон трапеции и перпендикулярную высоту h тел. Они исходят из теоремы Пифагора:
Однако есть более простой способ, чем найти апофему. Мы можем разбить додекаэдр на куб со стороной c = (1 + √5) s / 2 и шесть пирамидоподобных тел, как показано. Затем мы находим объем каждой пирамиды, что можно сделать, рассматривая среднюю часть как треугольную призму, а концевые части вместе как настоящую пирамиду, как показано ниже. Но сначала нам понадобятся два соотношения, включающие наклонную высоту l сторон трапеции и перпендикулярную высоту h тел. Они исходят из теоремы Пифагора: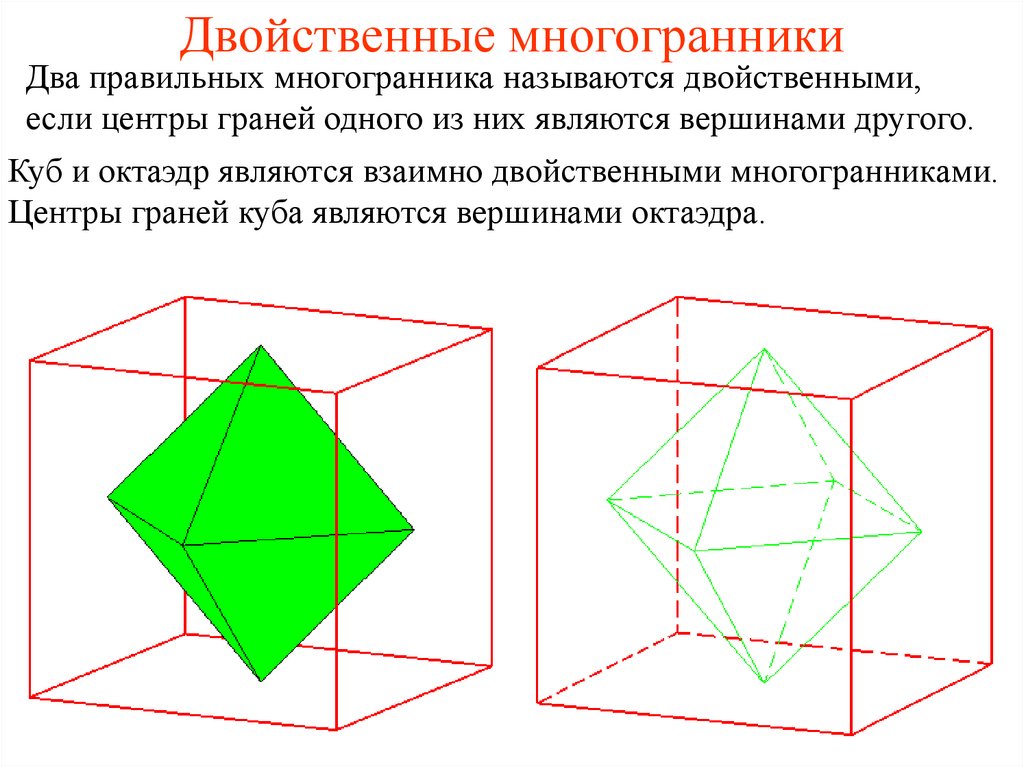 Двойственным правильному октаэдру является куб, а двойственным кубу — правильный октаэдр. Додекаэдр и икосаэдр двойственны. Многогранники, двойственные друг другу, имеют свои V и F 9Значения 0016 поменялись местами в таблице выше.
Двойственным правильному октаэдру является куб, а двойственным кубу — правильный октаэдр. Додекаэдр и икосаэдр двойственны. Многогранники, двойственные друг другу, имеют свои V и F 9Значения 0016 поменялись местами в таблице выше. Из них 30 являются ребрами додекаэдра, а дополнительные 5 · 12 = 60 лежат на гранях додекаэдра . Это оставляет 100 внутренних диагоналей.
Из них 30 являются ребрами додекаэдра, а дополнительные 5 · 12 = 60 лежат на гранях додекаэдра . Это оставляет 100 внутренних диагоналей.