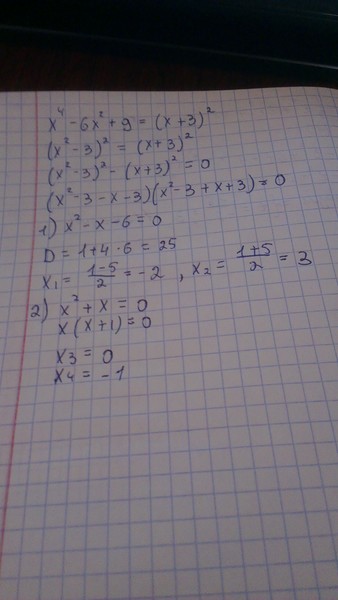x=\frac{-50±\sqrt{2500-4\left(-1\right)\left(-y-225\right)}}{2\left(-1\right)}
Возведите 50 в квадрат.
x=\frac{-50±\sqrt{2500+4\left(-y-225\right)}}{2\left(-1\right)}
Умножьте -4 на -1.
x=\frac{-50±\sqrt{2500-4y-900}}{2\left(-1\right)}
Умножьте 4 на -225-y.
x=\frac{-50±\sqrt{1600-4y}}{2\left(-1\right)}
Прибавьте 2500 к -900-4y.
x=\frac{-50±2\sqrt{400-y}}{2\left(-1\right)}
Извлеките квадратный корень из 1600-4y.
x=\frac{-50±2\sqrt{400-y}}{-2}
Умножьте 2 на -1.
x=\frac{2\sqrt{400-y}-50}{-2}
Решите уравнение x=\frac{-50±2\sqrt{400-y}}{-2} при условии, что ± — плюс. Прибавьте -50 к 2\sqrt{400-y}.
x=-\sqrt{400-y}+25
Разделите -50+2\sqrt{400-y} на -2.
x=\frac{-2\sqrt{400-y}-50}{-2}
Решите уравнение x=\frac{-50±2\sqrt{400-y}}{-2} при условии, что ± — минус. Вычтите 2\sqrt{400-y} из -50.
x=\sqrt{400-y}+25
Разделите -50-2\sqrt{400-y} на -2.
x=-\sqrt{400-y}+25 x=\sqrt{400-y}+25
Уравнение решено.
{2}+2 x-3}
«Применение операторов графики для построения графиков элементарных функций и приближённого решения уравнений»
Предмет Информатика и информационные технологии
Тема «Применение операторов графики для построения
графиков элементарных функций и приближённого решения уравнений»
Разработка учителя МОУ УСОШ №5 с углублённым изучением отдельных предметов Горбиной
Елены Анатольевны
Место: Тема входит в раздел «Графические возможности языка программирования».
Тип уроков – комбинированный – включает как усвоение нового материала в виде лекции с элементами беседы, так и формирование умений и навыков в виде практической работы за компьютерами.
Цели и задачи:
1. образовательные:
· усвоить принцип построения точечного графика;
· получить навыки построения точечного графика элементарной функции с помощью известных операторов графики;
· закрепить навыки вывода текстовой информации в графическом режиме;
· закрепить навыки написания арифметических выражений на языке QBASIC;
· сформировать умение использовать построенный график для решения алгебраических уравнений;
·
укрепить
межпредметные связи информатики с алгеброй и геометрией.
2. развивающие:
· выработать умение применять знания, полученные на информатике при изучении других предметов;
· развить умение делать выводы, самостоятельно проводить исследования и принимать решения.
3. воспитательные:
· сформировать у учащихся представление о компьютере, как о средстве помогающем решать трудоёмкие задачи и экономящем время для творческой работы.
Программно-методическое обеспечение:
— персональные компьютеры для каждого ученика;
— система программирования QBASIC.
Урок 1
Тема: «Построение графиков элементарных функций»
Ход урока:
1. Организационный момент.
Приветствие. Тема урока. Цели урока. (1 мин)
2. Актуальность знаний. (2 мин)
При
изучении математики очень часто возникает необходимость в построении графиков
функций.
Это занимает большую часть времени на уроке. Частично уменьшить затраты
времени может помочь компьютер, который обладает замечательным качеством –
способностью воспроизводить графическое изображение на экране монитора. Трудно
переоценить методическую значимость машинной графики. Вычерченный машиной
график, помимо наглядности и точности, даёт наиболее эффективные возможности
обнаружения и исправления ошибок по сравнению с другими формами представления
знаний. Кроме того, беря на себя трудоемкую часть работы, компьютер освобождает
время для исследовательской творческой работы, появляется возможность делать
самостоятельные выводы, работая с большим объемом изучаемого материала.
- Изучение нового материала.
1) Построение эскиза. (20 мин)
Для построения графика будем
использовать графический режим №12, разрешение которого 640 точек по
горизонтали и 480 точек по вертикали. При построении обращаем внимание на то,
что начало координат экрана находится в левом верхнем углу экрана, а ось ОY экрана направлена вниз.
Обращаем внимание на то, что мы строим точечный график, а значит нужно
1. вычислить значение функции у при определённом значении х,
2. перевести значения x и y в координаты точки на экране xt и yt,
3. изобразить точку с этими координатами (оператор PSET),
4. увеличить значение х на небольшую величину dx и повторить всё c пункта1.
Вводим условные обозначения:
а, b – границы диапазона изменения аргумента х;
ymin, ymax – границы диапазона изменения функции у;
mx, my – масштабные коэффициенты по осям ОХ и ОY – определяют количество точек экрана на единичное значение аргумента и функции
n – количество точек графика;
dx – шаг изменения аргумента
x, y – значения аргумента и соответствующее ему значение функции;
xt, yt – координаты точки графика на экране;
xt = x · mx + 320
yt = – y · my + 240
2) Физкультминутка – упражнения для глаз, спины и шеи.
(2 мин)
3) Написание программы. (20 мин)
‘Предварительные вычисления
a = –10 : b = 10
ymin = –10 : ymax = 10
mx = 640 / (b – a)
my = 480 / abs(ymax – ymin)
n = 3000 : dx = (b – a) / n
‘Построение системы координат с сеткой
SCREEN 12
FOR x = 0 TO 640 STEP mx ‘вертикальная разметка
LINE (x, 0) – (x, 480), 8
NEXT x
LINE (320, 0) – (320, 460), 10 ‘вертикальная ось
LINE (320, 0) – (325, 5), 10 ‘стрелка на вертикальной оси
LINE (320, 0) – (315, 5), 10
LOCATE 1, 42: PRINT «y»
FOR y = 0 TO 480 STEP my ‘горизонтальная разметка
LINE (0, y) – (640, y), 8 ‘самостоятельно на ПК
NEXT y
LINE (0, 240) – (630, 240), 10
LINE (630, 240) – (625, 245), 10
LINE (630, 240) – (625, 235), 10
LOCATE 17, 78: PRINT «x»
LOCATE 17, 42: PRINT «0»
‘Построение точечного графика
FOR x = a TO b STEP dx
y = x ^ 2 ‘Построение параболы
xt = x * mx + 320
yt = – y * my + 240
PSET (xt, yt), 12
NEXT x
END
Урок 2
4) Набор, отладка и
сохранение программы.
(18 мин)
Ученики набирают программу в индивидуальном темпе, добавляя пропущенную часть с горизонтальной разметкой. Построение графика будет происходить прямо на глазах у учащихся. После окончания построения необходимо обратить внимание учащихся на правильность построения – парабола должна проходить через точки (1;1), (–1;1), (2;4) и (–2;4).
5) Физкультминутка – упражнения для глаз, спины и шеи. (2 мин)
6) Работа с программой. (25 мин)
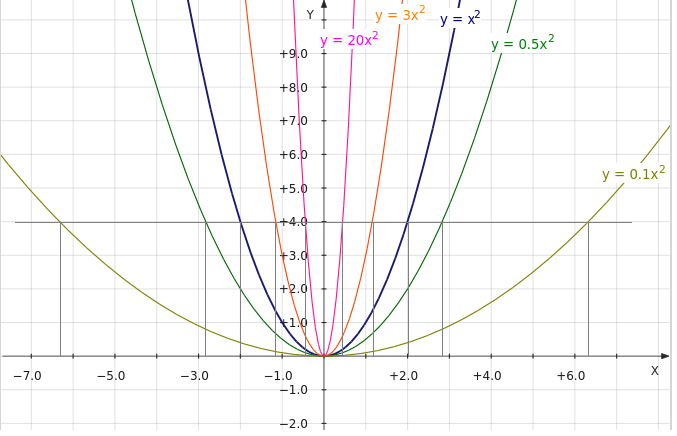
Учащимся предлагаются карточки для проведения индивидуальной практической работы. Для построения графиков других функций необходимо в цикле построения графика записать новую формулу. Каждый построенный график анализируется и демонстрируется учителю.
Ответы:
1) 2) 3)
4) 5) 6)
7) 8) 9)
10) 11) 12)
Урок 3
Тема: «Приближённое решение уравнений с использованием графика функции»
Ход урока:
- Организационный момент.
Приветствие. Тема урока. Цели урока. (1 мин)
- Изучение нового материала. (15 мин)
Построенный график функции может быть использован для приближённого решения уравнений вида f(x)=0. Корни этого уравнения являются точками пересечения графика функции y=f(x) с осью ОХ.
Пример. Решить уравнение х2 – 5х + 4= 0, используя программу построения графиков функций.
На интерактивной доске запускается программа построения графиков и строится график функции у = х2 – 5х + 4.
Отмечаем две точки пересечения графика с осью ОХ: (1;0) и (4;0). Значит, уравнение х2 – 5х + 4= 0 имеет два корня х1 = 1 и х2 = 4.
3. Физкультминутка – упражнения для глаз, спины и шеи.
(2 мин)
- Работа с программой. (27 мин)
Учащимся предлагаются карточки для проведения индивидуальной практической работы. Каждое решённое уравнение оформляется в рабочей тетради в виде схематического эскиза графика и решения. Правильность решения контролируется учителем.
Ответы:
1) х = -1 2) х1 = -2; х2 = 2
3) х1=0;х2=1 4) нет решений
5) х = 2 6) х1=-2; х2=2
7) х1= -1; х2 = 1 8) х1= -2; х2 = 1
Урок 4
Тема: «Приближённое решение уравнений с использованием графика функции»
Ход урока:
- Организационный момент.
Приветствие. Тема урока. Цели урока. (1 мин)
- Изучение нового материала. (25 мин)
Построенный график функции может быть использован для приближённого решения уравнений вида f1(x) = f2(x). Корни этого уравнения являются точками пересечения графиков функций y = f1(x) и у = f2(x).
Пример. Решить уравнение , используя программу построения графиков функций.
Чтобы найти решения этого уравнения можно построить графики двух функций y1 = и , а затем найти точки пересечения графиков.
Для того чтобы построить два графика в одной системе координат можно воспользоваться двумя способами:
Способ 1.
Добавить в программу второй цикл для построения графика, в котором изменить функцию и цвет точек. Получим:
‘Построение первого точечного графика
FOR x = a TO b STEP dx
y = (7 * x + 4) / (x^2 + 5)
xt = x * mx + 320
yt = – y * my + 240
PSET (xt, yt), 12
NEXT x
‘Построение второго точечного графика
FOR x = a TO b STEP dx
y = 0.
2 – 5 * x
+ 9.5
xt = x * mx + 320
yt = – y * my + 240
yt1 = – y * my + 240
PSET (xt, yt), 12
PSET (xt, yt1), 14
NEXT x
Отмечаем две точки пересечения графиков друг с другом: (2;2) и (6;1). Значит, уравнение имеет два корня х1 = 2 и х2 = 6.
3. Физкультминутка – упражнения для глаз, спины и шеи. (2 мин)
- Работа с программой. (17 мин)
Учащимся предлагаются карточки для проведения индивидуальной практической работы. Каждое решённое уравнение оформляется в рабочей тетради в виде схематического эскиза графика и решения. Правильность решения контролируется учителем.
1) х1=-2; х2 =3 2) х=1
3) х1=-4; х2=-1; х3=1; х4=4 4)х=2
5) х1=-2; х2 = 1 6) х1=-3; х2=1
КОНТРОЛЬНАЯ РАБОТА
1 вариант
1.
Наберите программу построения
точечных графиков элементарных функций.
2. Постройте график функции y = | |x2 – 2х | – 8| на экране и перенесите его в тетрадь.
3. Решите уравнение | |x2 – 2x | – 8| = 0, используя построенный график
4. Решите уравнение 4 |x| – х3 = 2x + 7.
2 вариант
1. Наберите программу построения точечных графиков элементарных функций.
2. Постройте график функции y = | |0,5x2 – 5 | – 3| на экране и перенесите его в тетрадь.
3. Решите уравнение | |0,5x2 – 5 | — 3| = 0, используя построенный график.
4.
Решите уравнение 4 – 2x
= х3 – 4 |x|.
3 – 4 * ABS(X), а затем найти точки пересечения графиков.
Отмечаем одну точку пересечения графиков друг с другом: (2;0). Значит, уравнение имеет один корень х= 2.
Для оценивания этой контрольной работы предлагается следующая схема, которая сообщается учащимся до начала работы. Правильно набранная работающая программа (правильность работы должна быть самостоятельно проверена учащимися с помощью известной функции, например у=х или у=х2) и выполненное в тетради задание №2 оцениваются оценкой «удовлетворительно». Задания №1 + №2 + №3 – оценкой «хорошо», все задания – оценкой «отлично».
Приложение 1.
Изучение темы «Применение операторов графики для построения графиков элементарных функций и приближённого решения уравнений» на языке Visual Basic.
1.
На форме размещаются два
инструмента Picture1, Command1.
Вывод графика осуществляется в Picture1. Отличие состоит в том, что не надо вводить масштабные коэффициенты. С помощью оператора Picture1.Scale (a, ymax)-(b, ymin) создаётся нормальная система координат с нулем в центре Picture1. В скобках указываются координаты двух противоположных углов системы координат. В нашем случае (-10,10) и (10,-10). Благодаря такой системе координат нет необходимости пересчитывать значения X и Y в координаты экрана.
2. Создаём процедуру для командной кнопки:
Private Sub Command1_Click()
a = -10: b = 10: ymin = -10: ymax = 10 : n = 3000: dx = (b — a) / n
‘Задание масштаба
Picture1.Scale (a, ymax)-(b, ymin)
‘Вертикальная разметка
For I = a To b
Picture1.Line (I, ymin)-(I, ymax), vbGreen
Picture1.PSet (I, 0) : Picture1.Print I ‘Числа на оси
Next I
‘Горизонтальная разметка
For I = ymin To ymax
Picture1.
2 — 7
Picture1.PSet (X, Y)
Next X
End Sub
3. В результате получается:
Приложение 2.
Раздаточный материал
КОНТРОЛЬНАЯ РАБОТА
Тема «Применение операторов графики для построения графиков элементарных функций и приближённого решения уравнений»
1 вариант
1. Наберите программу построения точечных графиков элементарных функций.
2.
Постройте график функции y = | |x2 – 2х | – 8| на экране и перенесите его в тетрадь.
3. Решите уравнение | |x2 – 2x | – 8| = 0, используя построенный график
4. Решите уравнение 4 |x| – х3 = 2x + 7.
КОНТРОЛЬНАЯ РАБОТА
Тема «Применение операторов графики для построения графиков элементарных функций и приближённого решения уравнений»
2 вариант
1. Наберите программу построения точечных графиков элементарных функций.
2. Постройте график функции y = | |0,5x2 – 5 | – 3| на экране и перенесите его в тетрадь.
3. Решите уравнение | |0,5x2 – 5 | — 3| = 0, используя построенный график.
4.
Решите уравнение 4 – 2x
= х3 – 4 |x|.
x=\frac{-\left(-240\right)±\sqrt{57600-4\times 19\times 625}}{2\times 19}
Квадрат -240.
x=\frac{-\left(-240\right)±\sqrt{57600-76\times 625}}{2\times 19}
Умножить -4 на 19.
x=\frac{- \left(-240\right)±\sqrt{57600-47500}}{2\times 19}
Умножить -76 на 625.
x=\frac{-\left(-240\right)±\sqrt {10100}}{2\times 19}
Добавьте 57600 к -47500.
x=\frac{-\left(-240\right)±10\sqrt{101}}{2\times 19}
Извлеките квадратный корень из 10100.
x=\frac{240±10\sqrt{101}}{2\times 19}
Противоположность -240 равна 240.
x=\frac{240 ±10\sqrt{101}}{38}
Умножить 2 раза на 19.
x=\frac{10\sqrt{101}+240}{38}
Теперь решите уравнение x=\frac{240± 10\sqrt{101}}{38}, когда ± плюс. Добавьте 240 к 10\sqrt{101}.
x=\frac{5\sqrt{101}+120}{19}
Разделите 240+10\sqrt{101} на 38.
x=\frac{240-10\sqrt{101}}{ 38}
92 = \frac{2525}{361} u = \pm\sqrt{\frac{2525}{361}} = \pm \frac{\sqrt{2525}}{19}Упростите выражение, умножив -1 с обеих сторон и извлеките квадратный корень, чтобы получить значение неизвестной переменной u
r =\frac{120}{19} — \frac{\sqrt{2525}}{19} = 3,671 s = \frac{120} {19} + \frac{\sqrt{2525}}{19} = 8,960
Факторы r и s являются решениями квадратного уравнения.