Правило на умножение: Порядок действий в Математике

Умножение целых чисел, правила, примеры, как умножать не целые числа, произведение двух чисел

В этом материале мы покажем, как правильно выполнять умножение целых чисел. Начнем, как всегда, с основных понятий и обозначений и выясним, какой смысл вкладывается в умножение двух целых чисел. Затем сформулируем правила, по которым перемножают целые положительные и целые отрицательные числа, а также числа, имеющие разные знаки. Как всегда, нашу мысль будем пояснять наглядными примерами решений задач. Далее рассмотрим те случаи, когда один из множителей нулевой или равен единице, посмотрим, как можно проверить верность результата, полученного после умножения, а в конце объясним, как правильно перемножать 3, 4 и большее количество целых чисел.

Основные определения при умножении целых чисел

При умножении целых чисел используются те же термины и знаки, о которых мы говорили ранее в статье об умножении натуральных чисел. У нас есть два множителя, которые являются целыми числами, результат, называемый произведением, и знак умножения в виде точки, звездочки или знака «x» (в целях единообразия в дальнейшем будем использовать точку).

Если обозначить множители и произведение буквами a, b и c, то действие умножения можем записать в виде равенства a·b=c. Само числовое выражение a·b тоже называется произведением. Произведение двух целых чисел также является целым числом.

В чем состоит смысл умножения целых чисел?

До этого мы уже объясняли смысл умножения на примере натуральных чисел. Произведение натуральных чисел a и b представляет собой сумму b слагаемых, каждое из которых равно a.

Целые положительные числа – это натуральные числа, поэтому смысл действия умножения для них точно такой же. В буквенном виде его также можно представить как

(значения a и b – целые положительные числа).

В принципе, этот смысл распространяется на все произведения, где одно слагаемое целое и положительное. Второе при этом также должно быть целым, однако оно может быть отрицательным или даже равным нулю. Так, схема умножения числа -3 на 5 будет выглядеть как (−3)·5=(−3)+(−3)+(−3)+(−3)+(−3).

Если вторым множителем является единица, то результат умножения – это сумма одного слагаемого, которое равно другому множителю.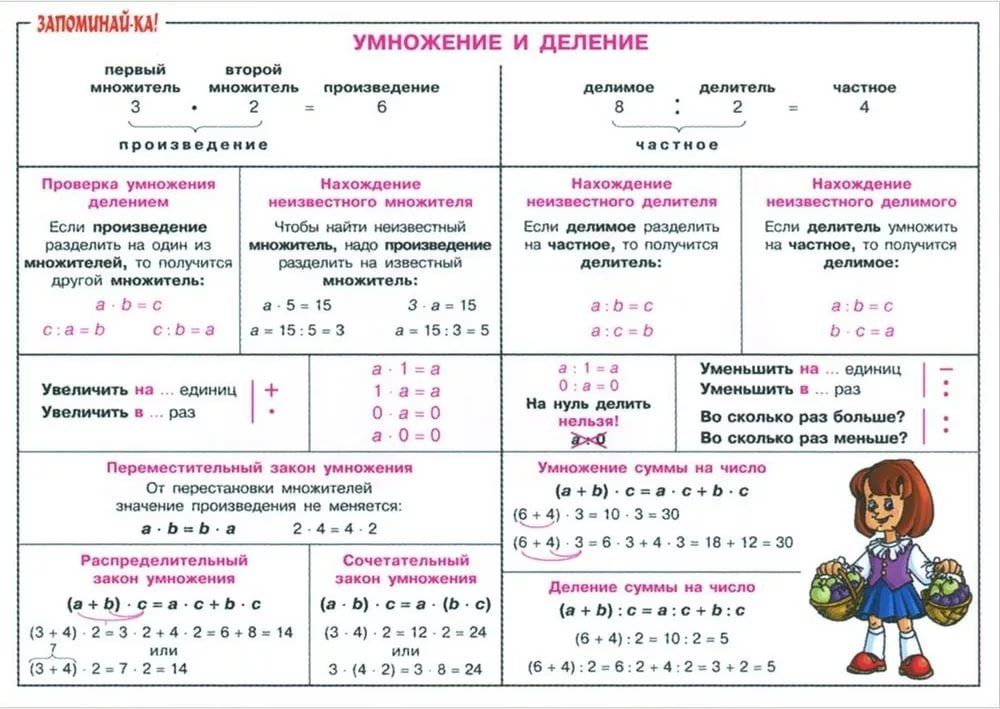 Это можно записать как a·1=a. Результат умножения целого числа на единицу есть само это число.

А как быть в случае, если одно из множителей нулевое? Получается, что в ответе будет сумма из 0 слагаемых. Очевидно, что это будет 0. Запишем, что a·0=0 для любого целого a. Умножение целого числа на ноль дает в результате ноль.

В случае с отрицательными числами общий смысл действия умножения сформулировать достаточно сложно. Примем это действие как данность и подчеркнем, что правила умножения в таком случае должны сохранять справедливыми свойства умножения для целых положительных чисел. В частности, такое числовое выражение должно обладать переместительным и сочетательным свойствами.

Основные правила, применяемые при умножении целых чисел

Можно выполнить умножение исходя из того, что оно по сути представляет собой сложение одинаковых слагаемых. Но, как мы уже отмечали, это долгий и трудный процесс, если таких слагаемых у нас много. А если одним из множителей является отрицательное число, то воспользоваться этим способом мы не можем. Поэтому нам надо вывести особые правила для умножения целых чисел. Сформулируем и запишем их.

Как умножать одно целое положительное число на другое

Целые положительные числа относятся к натуральным, поэтому правила умножения натуральных чисел распространяются и на них. В итоге мы, разумеется, получим целый положительный результат, т.е. натуральное число. Разберем конкретные примеры.

Пример 1

Подсчитайте, сколько будет 9 умножить на 7.

Решение

Обратимся к таблице умножения и возьмем из нее готовый результат.

Получим: 9·7=63.

Ответ: 63.

Пример 2

Сколько будет 127 умножить на 5?

Решение

Представим первый из множителей как сумму разрядных слагаемых, т.е. 100+20+7.

Теперь последовательно умножим слагаемые на данное число: 127·5=(100+20+7)·5=100·5+20·5+7·5.

Заканчиваем вычисление: 100·5+20·5+7·5=500+100+35=600+35=635.

Ответ: 635.

Чтобы перемножать многозначные числа, удобно пользоваться методом подсчета в столбик.

Пример 3

Условие: умножьте 712 на 92.

Решение: запишем множители в столбик и вычислим результат.

Ответ: 65 504.

Как правильно перемножить целые числа, имеющие разные знаки

Для того чтобы вывести правило для такого случая, приведем пример.

Итак, нам надо вычислить произведение числа -5 на 3. Вспомним смысл умножения и запишем: (−5)·3=(−5)+(−5)+(−5)=−15. Если учесть переместительное свойство, то должно быть верным и (−5)·3=3·(−5). Очевидно, что модуль числа, полученного в результате, соответствует произведению данных множителей. Таким образом, произведение двух чисел с разными знаками есть число отрицательное.

Определение 1

Чтобы умножить одно отрицательное число на одно положительное, надо перемножить между собой модули этих чисел и поставить перед результатом минус.

Разберем несколько примеров, подтверждающих это правило.

Пример 4

Умножьте 7 на -14.

Решение

Запишем отдельно модули исходных множителей. Получим 7 и 14. Подсчитаем, чему будет равно их произведение: 7·14=98. Все, что нам нужно сделать дальше, – это поставить знак минуса перед полученным числом.

Ответ: 7·(−14)=−98.

Пример 5

Подсчитайте, сколько будет (−36)·29.

Решение

Согласно правилу умножения чисел с разными знаками, нам нужно начать с умножения модулей. Считаем: 36·29=1 044. Здесь удобно будет воспользоваться методом умножения в столбик. Нам осталось поставить минус перед результатом и записать готовый ответ.

Ответ: (−36)·29=−1 044.

В последней части параграфа мы попробуем доказать, что равенство a·(−b)=−(a·b) справедливо (a и b здесь – любые целые числа). Правило умножения целых чисел с разными знаками, которое мы записали выше, является частным случаем этого равенства.

Задача сводится к тому, что нам надо доказать, что значениями выражений a·(−b) и a·b будут противоположные числа. Для этого вычислим сумму a·(−b)+a·b. Она будет равна 0. Учитывая распределительное свойство умножения целых чисел относительно сложения,  справедливым будет a·(−b)+a·b=a·((−b)+b). Сумма (−b)+b –это ноль, потому что это сумма противоположных чисел, в итоге получается, что a·((−b)+b)=a·0. Итоговое произведение равно 0, согласно свойству умножения целого числа на 0. Получается, что a·(−b)+a·b=0, значит, a·(−b) и a·b являются противоположными числами. Отсюда вытекает справедливость равенства a·(−b)=−(a·b). Таким же образом можно показать, что (−a)·b=−(a·b).

Как перемножить целые отрицательные числа

Для получения этого правила нам понадобится равенство (−a)·(−b)=a·b. Ниже мы приведем его доказательство.

Перед этим мы писали, почему a·(−b)=−(a·b) и (−a)·b=−(a·b), следовательно, мы можем записать цепочку равенств (−a)·(−b)=−(a·(−b))=−(−(a·b)).

У  нас получилось выражение −(−(a·b)), которое идентично a·b в силу определения противоположных чисел. Таким образом, (−a)·(−b)=a·b.

Теперь мы можем перейти к формулировке правила умножения целых отрицательных чисел.

Определение 2

Чтобы найти произведение целых отрицательных чисел, нам надо вычислить произведение их модулей.

Из правила ясно, что результат умножения двух отрицательных свойств есть число положительное.

Посмотрим, как применить это правило на практике.

Пример 6

Умножьте (−34)·(−2).

Решение

Воспользуемся правилом и просто перемножим между собой модули: -34=34 и -2=2.

Весь ход решения можно записать как (−34)·(−2)=34·2=68.

Ответ: 68.

Пример 7

Умножьте −1 041 на -538.

Решение

Вычисляем модули и перемножаем их столбиком.

 

Ответ: (−1 041)·(−538)=560 058.  

Как умножить целое число на единицу

Мы уже упоминали, что если мы умножим на единицу любое целое число, то результат будет равен этому же числу, то есть a·1=a. Так как числовое выражение с умножением обладает переместительным свойством, то a·1=1·a тоже должно быть верным. Получается, что 1·a=a. Выведем основное правило и запомним его:

Определение 3

Если умножить два целых числа, одно из которых равно 1, то результат будет равен второму числу.

К примеру, 58·1=58, 1·0=0 и 1·(−602)=−602. Как видно, от значения второго множителя результат не зависит: произведение −53 и 1 – это −53, а результат умножения 1 и отрицательного целого числа −989 981 – это  −989 981.

Как умножить целое число на нуль

Умножение любого целого числа на нуль дает нам в итоге нулевой результат, т.е. a·0=0. С учетом переместительного свойства умножения мы получим, что 0·a=0 тоже будет верно. Запомним:

Определение 4

Если умножить два целых числа, одно из которых равно 0, то результат тоже будет равен 0. Умножение нуля на нуль в итоге также дает нуль.

Так, произведение 678 на 0 – это 0; произведение -45 на нуль – тоже нуль; (−90 7789)·0=0.

Обратное утверждение тоже будет верным: если произведение двух чисел равно нулю, то один или оба множителя тоже равны нулю.

Как проверить результат умножения целых чисел

Для проверки точности результата умножения нам потребуется вспомнить действие деления. Нужно разделить итоговый результат на один из множителей. Если в итоге мы получим второй множитель, то мы все посчитали правильно. Если же результат будет отличен от значения другого множителя, значит, расчет ошибочен и его нужно переделать.

Посмотрим на примерах, как правильно проверить результат умножения целых чисел.

Пример 8

После умножения 21 на -5 получилось -115. Проверьте, верен ли результат.

Решение

Для проверки нам надо разделить произведение на любой множитель. Возьмем -5. Делимое и делитель у нас отрицательные, значит, в итоге мы получим частное от деления их модулей: (−115):(−5)=115:5 (посмотрите статью о том, как делить целые отрицательные числа).

В итоге мы получим 23, хотя второй множитель в исходных данных равен 21. Значит, вычисления были ошибочными.

Ответ: результат деления неверен.

Пример 9

Умножьте -17 на -67 и проверьте точность результата.

Решение

Вспоминаем, как правильно умножать целые отрицательные числа. Считаем: (−17)·(−67)=17·67=1 139. Теперь переходим к проверке. Для этого делим столбиком результат на любой множитель, например, на -67.

Согласно правилам деления чисел с разными знаками, сначала мы проводим подсчеты с их модулями:

Теперь перед результатом мы должны поставить минус.

У нас получилось -17, что соответствует первоначальному условию. Значит, мы все сделали правильно.

Ответ: (−17)·(−67)=1 139. 

Как перемножить три целых числа и более

Зная, что числовое выражение с умножением имеет сочетательное свойство, мы можем точно подсчитать произведение 3,4, 5 и большего количества множителей. А благодаря остальным свойствам можно сказать, что результат произведения не будет определяться положением множителей в примере и способом расстановки скобок. Ранее мы уже приводили обоснования этих утверждений в случае с натуральными числами. Для примера с целыми множителями эти правила работают таким же образом.

Посмотрим на конкретный пример.

Пример 10

Найдите произведение 5-ти множителей: 5, −12, 1, −2 и 15.

Решение

Заменим соседние множители их произведением и запишем, что

 5·(−12)·1·(−2)·15=(−60)·1·(−2)·15=(−60)·(−2)·15=120·15=1 800

С расстановкой скобок можно записать так: (((5·(−12))·1)·(−2))·15. Это позволит нам делать вычисления быстрее и проще.

Можно было переставить множители и по-другому: 1·5·(−12)·(−2)·15, в таком случае скобки надо было расставить так: ((1·5)·(−12))·((−2)·15)=(5·(−12))·((−2)·15)=(−60)·(−30)=1 800.

Мы видим, что результат будет одинаков вне зависимости от метода расстановки скобок и последовательности вычислений.

Ответ: 1800. 

Если хоть один из множителей в примере был бы нулевым, то подсчет не имел бы смысла. Мы сразу могли бы сказать, что результат будет равен 0. Это не зависит от значения других множителей, они могли бы быть любыми.

Обратное утверждение также будет справедливо: если произведение нескольких множителей равно 0, то один из этих множителей будет нулевым.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

определение и примеры • BUOM

Автор: редакционная команда Indeed

29 апреля 2021 г.

Умножение является одним из четырех основных арифметических действий, наряду с сложением, вычитанием и делением. Люди во многих отраслях ежедневно используют умножение. Способность быстро и точно умножать цифры может помочь вам решать проблемы на работе, выполнять сложные вычисления или даже продвигаться по службе. В этой статье мы обсудим умножение, его использование, правила и место в математическом порядке операций.

Что такое умножение?

Умножение — это математический процесс, при котором число многократно складывается с самим собой определенное количество раз. Например, вы можете выразить задачу умножения 10 x 3 как 10 + 10 + 10, так как у вас есть три группы по 10. В каждом выражении умножения есть множители и произведение. Факторы — это числа, которые вы перемножаете, чтобы получить произведение. Множитель может быть либо множителем, либо множителем. Множимое представляет количество объектов в каждой группе, а множитель — это общее количество групп, которые вы умножаете.

Определение того, какое число является множителем или множителем, может быть полезно в текстовых задачах, но не влияет на произведение. В приведенном выше примере произведение равно 30 независимо от того, является ли множитель 10 или 3. Если вы хорошо разбираетесь в процессах умственного умножения, подобных этим, вы можете улучшить свои навыки счета как в профессиональных, так и в личных ситуациях, связанных с решением проблем.

Каковы правила умножения?

Как и другие основные арифметические операции, умножение подчиняется определенным правилам. Вы можете использовать следующие правила для быстрого умножения чисел:

• Любое число, умноженное на ноль, всегда равно нулю. Множитель — это количество раз, которое появляется множимое. Следовательно, если множимое встречается 0 раз, оно не существует.

• Любое число, умноженное на единицу, всегда является одним и тем же числом. Подобно правилу нуля, если число встречается только один раз, оно не меняется. Например, в задаче 4 x 1 произведение всегда равно четырем.

• Добавляйте ноль к исходному числу при умножении на 10. Этот ярлык позволяет быстро решать выражения, содержащие 10. Например, чтобы решить 34 x 10, просто добавьте ноль в конце 34, чтобы получить ответ 340. Это правило применяется ко всем числам, кратным 10, включая 100, 1000 и т. д.

• Порядок факторов не влияет на произведение. Переключение ролей множителя и множимого приводит к тому же ответу. Например, наличие трех групп по пять апельсинов дает 15 апельсинов, то же самое происходит и с пятью группами по три апельсина.

• Произведения всегда положительны при умножении чисел с одинаковыми знаками. Следовательно, в выражении -2 x -4 произведение будет положительной восьмеркой. То же самое верно, когда множители положительны два и положительны четыре.

• Произведения всегда отрицательны при умножении чисел с разными знаками. Это означает, что при умножении отрицательного числа на положительное число результат будет отрицательным.

Какое место в порядке операций занимает умножение?

В математике порядок операций относится к последовательности шагов, которые необходимо выполнить для упрощения математического выражения, включающего сочетание всех четырех математических операций. Широко распространенным мнемоническим приемом для запоминания порядка операций является аббревиатура PEMDAS, которая означает «круглые скобки, показатели степени, умножение и деление, сложение и вычитание». Порядок операций группирует умножение с делением и сложение с вычитанием, когда вы решаете математическое выражение слева направо, завершая любое умножение и деление, которое вы видите, перед решением сложения и вычитания.

Например, в выражении 8 ÷ 2 + 3 x 4 вы должны сначала обратиться к элементам умножения и деления. Поскольку вы выполняете операцию слева, а деление появляется первым, разделите 8 и два, чтобы получить четыре. Затем выполните операцию умножения 3 x 4 = 12. Последний шаг — 4 + 12, что равно 16.

В каких отраслях используются правила умножения?

Основные математические операции, такие как умножение, являются одними из самых важных функциональных навыков. Большинство профессий, связанных с финансами, бухгалтерским учетом или бухгалтерией, могут полагаться на умножение для ведения точных деловых записей. Умножение также может применяться к личному планированию, составлению графиков и составлению бюджета. Рассмотрим следующие отрасли, которые полагаются на умножение для выполнения важных задач:

• Архитектура: Архитекторы используют умножение для планирования проектов зданий и рисования чертежей, что делает умножение необходимым для определения площади комнаты.

• Бизнес: Владельцы бизнеса, скорее всего, будут использовать умножение для определения оценок ежемесячных накладных расходов или цен на продукты. Сотрудники крупных компаний могут использовать умножение для расчета общей стоимости проекта.

• Кулинарное искусство: с помощью умножения пекарь может определить, сколько муки ему нужно, чтобы испечь 100 буханок хлеба, а повар может умножить количество ингредиентов, необходимых для удвоения порции супа.

• Инженерия: Арифметические операции, включая умножение, являются неотъемлемой частью всех областей техники. Инженер-строитель, например, часто использует умножение для определения количества материалов, необходимых при проектировании и строительстве структурных элементов, таких как мосты и дороги.

• Розничная торговля: менеджеры и продавцы используют розничную математику, включая умножение, для проведения транзакций, расчета прибыли и выполнения других расчетов продаж.

Советы по улучшению навыков умножения

Если вы хотите улучшить свои навыки умножения, рассмотрите следующие варианты:

Запомните таблицу умножения

Таблица умножения, или таблица умножения, представляет собой список, в котором показаны произведения множителей, обычно от 1 до 12. Таблицу умножения обычно изучают и применяют в начале обучения, однако она может быть эффективным инструментом для постоянной практики. и развитие вашей способности быстро размножаться. Запоминая произведения малых чисел, вы легко сможете при необходимости вспомнить произведения общих множителей.

Изучите приемы умножения

Есть несколько приемов умножения, которые можно использовать для быстрого и простого решения выражений умножения. Известный трюк связан с числом девять. Например, чтобы решить выражение 4 х 9, вытяните перед собой обе руки и загните безымянный палец слева. Слева от согнутого пальца должно быть три пальца, а справа шесть пальцев. Вместе получается число 36, что является ответом на пример задачи. Эта стратегия работает для множителей до 10.

Практика ежедневно

Постоянная практика может научить ваш мозг быстро вспоминать знания. Когда вы сталкиваетесь с выражениями умножения, попробуйте найти произведение без калькулятора. Вместо этого используйте карандаш и бумагу, чтобы решить задачу, или попробуйте вычислить, используя ментальную арифметику. Такая последовательная практика может помочь вам укрепить свои навыки умножения и способность быстро решать задачи.

Применяйте примеры из реальной жизни

Помните о том, как умножение вписывается в вашу повседневную жизнь. Например, когда вы идете в магазин или ресторан, тренируйте свои навыки, умножая денежные значения или удваивая и утраивая рецепты, которые вы готовите. Кроме того, потренируйтесь мысленно визуализировать выражения умножения, чтобы улучшить свой подход к быстрому решению задач. Например, если вы заказываете в ресторане три газированных напитка по 1,99 доллара за штуку, визуализируйте транзакцию в виде письменного выражения.

Правило умножения в вероятности

Горячая математика

Если А и Б два независимые события в вероятность опыта, то вероятность того, что оба события произойдут одновременно, равна:

п ( А и Б ) знак равно п ( А ) ⋅ п ( Б )

В случае зависимые события , вероятность того, что оба события произойдут одновременно, равна:

п ( А и Б ) знак равно п ( А ) ⋅ п ( Б | А )

(Обозначение п ( Б | А ) означает «вероятность Б , При условии А случилось. «)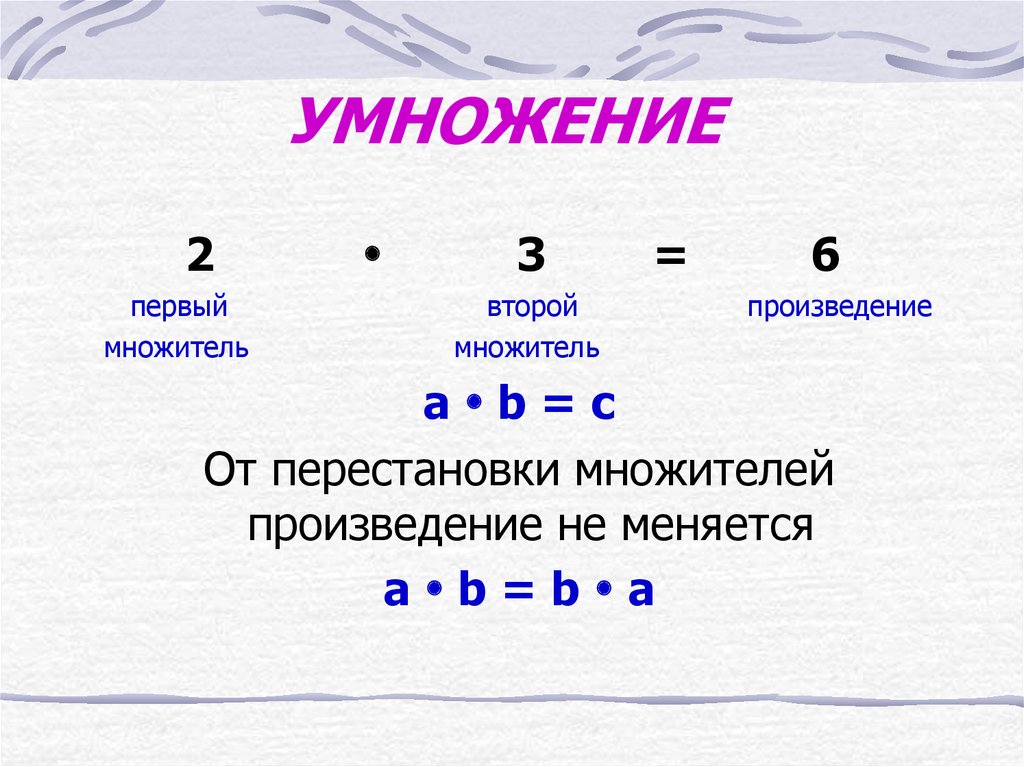

Пример 1:

У вас есть ковбойская шляпа, цилиндр и индонезийская шляпа под названием сонгкок. У вас также есть четыре рубашки: белая, черная, зеленая и розовая. Если вы выберете одну шляпу и одну рубашку наугад, какова вероятность того, что вы выберете сонгкок и черную рубашку?

Эти два события являются независимыми событиями; выбор шляпы не влияет на выбор рубашки.

Есть три разных шляпы, поэтому вероятность выбора сонгкока равна 1 3 . Есть четыре разных рубашки, поэтому вероятность выбора черной рубашки равна 1 4 .

Итак, по правилу умножения:

п ( сонгок и черная рубашка ) знак равно 1 3 ⋅ 1 4 знак равно 1 12

Пример 2:

Предположим, вы достаете из стандартной колоды две карты одну за другой, не заменяя первую карту. Какова вероятность того, что первая карта туз пик, а вторая карта черва?

Два события являются зависимыми событиями, поскольку первая карта не заменяется.

В колоде есть только один туз пик 52 открытки. Так:

п ( 1 ул. карта туз пик ) знак равно 1 52

Если туз клеток вытащен первым, то есть 51 карт, оставшихся в колоде, из которых 13 это сердца:

п ( 2 й карта – сердце | 1 ул. карта — туз пик ) знак равно 13 51

Итак, по правилу умножения вероятности имеем:

п ( туз пик, затем черва ) знак равно 1 52 ⋅ 13 51 знак равно 13 4 ⋅ 13 ⋅ 51 знак равно 1 204

Преалгебра: правила математики: умножение

Числа и счет|Арифметика|Дроби и десятичные дроби| Преалгебра |Карта сайта

Это математика, поэтому вы привыкаете к идее правил. Математика заключается в использовании логики , правил и организации, чтобы вы могли получать один и тот же ответ каждый раз, когда решаете задачу. Если бы правила изменились, 1 + 1 не всегда равнялось бы 2. Это было бы слишком запутанно.

Если вы изучали науку, вы знаете о законы . Есть закон всемирного тяготения и есть законы движения в физике. В математике тоже есть законы. Они устанавливают правила, которые всегда позволяют вам делать определенные вещи. Вы уже использовали три из этих законов на дополнительных страницах. Вы помните, как вы могли переставлять номера или группировать номера, когда мы добавляли? Мы можем это сделать, потому что есть законы, которые говорят, что это нормально, и математика будет продолжать работать правильно. Вы получаете много одинаковых правил в умножении.

Когда вы переставляете числа, вы используете Коммутативный закон умножения . Слово коммутация может показаться большим, но оно просто означает переставить. Если хотите, можете назвать это законом умножения перегруппировки. Закон позволяет нам перемещать все множители в любой задаче на умножение.

Пример:
1 * 95 * 1345 * 2 * 15 * 7 = ?
• Этот макет выглядит немного странно.
1 * 2 * 7 * 15 * 95 * 1345 = ?
• Когда он переставлен, немного легче представить умножение чисел.

Нельзя просто так что-то переставить. Вам все еще нужно обратить внимание на скобки и другие операции . Но для умножения вы можете изменить порядок значений, как хотите. Если бы вы были математиком, вы бы использовали буквы, называемые переменными , чтобы записать идею. В математике мы используем буквы для обозначения любого числа, которое хотим. Вы узнаете больше о переменных в алгебре, но знайте, что «а» и «b» могут быть любыми числами, которые вы себе представляете. Официальное описание коммутативного закона…

а * б = б * а

Порядок не имеет значения при взгляде на операцию умножения.

Теперь вы знаете, что можно переставлять числа при умножении. Вы также можете сгруппировать их. Вы уже делали это во многих своих проблемах.

Пример:
1 * 5 * 9 * 6 * 5 * 4 =?
• Переставьте значения и сгруппируйте их…
(1*9) * (5*5) * (6*4) = ?

Математики знают, что группировка полезна, поэтому они придумали закон: Ассоциативный закон умножения . Закон смотрит на то, как числа могут ассоциироваться друг с другом при умножении. У вас может быть группа из двух и группа из трех человек. Закон позволяет вам разбивать группы и перемещать вещи.

(1*2*75) * (3*4*25) = (1*2*3*4) * (75*25) = (1*2) * (3*4) * (75*25) )

Видите, как мы только что передвинули скобки? Настраиваем новые группы факторов. Как и прежде, это работает только с операцией умножения. Вам нужно обратить внимание на круглые скобки и другие операции, такие как вычитание или деление. Вы также должны заметить, что мы можем сгруппировать любое количество факторов.