«Замечательные пределы. Анализ определения математической функции», Математика, химия, физика
- Выдержка
- Другие работы
- Помощь в написании
Замечательные пределы. Анализ определения математической функции (реферат, курсовая, диплом, контрольная)
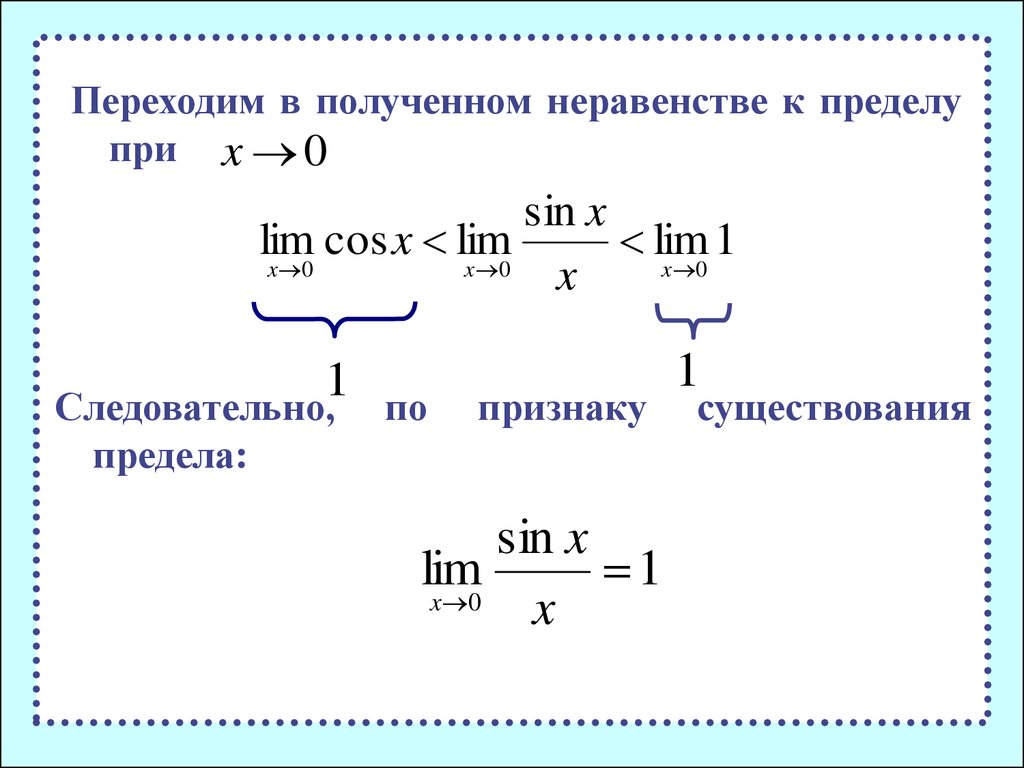
1. Первый замечательный предел.
.
2. Второй замечательный предел.
.
где иррациональное число, как и представимое «бесконечной» десятичной дробью. С точностью до второго десятичного знака .
3. Третий замечательный предел.
.
Здесь используется, так называемый, натуральный логарифм, то есть логарифм, основанием которого является только что введенное число e. Следует заметить, что в высшей математике чаще всего используют именно эти логарифмы.
4. Четвертый замечательный предел.
.
Здесь вводится новая показательная функция с основанием e, чаще всего называемая экспонентой.
Непрерывность функции в точке и на интервале
Введем несколько определений непрерывной функции в точке.
Определение 1. Функция называется непрерывной в точке, если предел этой функции при, стремящемся к, равен значению функции в этой точке, то есть .
Определение 2. Функция непрерывна в точке, если.
.
Поскольку оба определения предела функции эквивалентны, эти два определения непрерывной функции также следуют одно из другого.
Определение 3. Предел приращения функции стремится к нулю при стремлении к нулю приращения ее аргумента. Пусть приращение аргумента, то есть число, на которое изменилось значение аргумента. Приращение может быть как положительным, так и отрицательным. Обозначим приращение функции, то есть ее изменение в результате приращения аргумента. Если, то. При этом называют исходным значением функции, а наращенным ее значением. Приращение функции также может быть как положительным, так и отрицательным числом. Аналитическая форма записи третьего определения непрерывности .
Покажем, что это определение следует из первого, а следовательно, и из второго, используя свойство пределов.
.
Значение предела равно, что следует из первого определения непрерывности функции,, так как не зависит от. Итак,.
.
Определение 4. Функция непрерывна в точке a, если.
.
Справедливость этого определения следует из того, что предел функции существует, если левый предел равен правому, но если это так, то четвертое определение эквивалентно первому.
Определение 5. Функция называется непрерывной в некоторой области, если она непрерывна в каждой точке этой области.
Непрерывную в некоторой области функцию можно изобразить, не отрывая карандаша от бумаги.
Свойства непрерывных функций
- 1. Сумма непрерывных в некоторой области функций непрерывна в этой области.
- 2. Произведение непрерывных функций — есть функция непрерывная.
- 3. Частное непрерывных функций — есть функция непрерывная, кроме точек, в которых ее знаменатель обращается в нуль.
4. Непрерывная функция от непрерывной функции — есть функция непрерывная (непрерывность сложной функции). Например, функции и непрерывны всей на числовой оси, следовательно, сложная функция (функция сложного аргумента) — непрерывна при всех значениях x.
Например, функции и непрерывны всей на числовой оси, следовательно, сложная функция (функция сложного аргумента) — непрерывна при всех значениях x.
Очевидно, элементарные функции непрерывны в области существования.
Точки разрыва функции
Точки, в которых нарушается непрерывность функции, называются точками разрыва, или особыми точками. В этих точках происходит разрыв графика функции.
Разрывы бывают конечными (разрыв первого рода), если левый и правый пределы функции конечны, но не равны, то есть.
Разрывы бесконечны (разрыв второго рода), если левый, или правый, или оба предела равны .
Устранимые разрывы имеют место, когда левый и правый пределы конечны и равны, но функция в предельной точке не существует. Разрыв устраняется введением новой функции, совпадающей с прежней во всех точках области, кроме особой точки, но являющейся непрерывной и в точке, где первая функция имеет особенность. Например, дана функция. Очевидно, она непрерывна на всей числовой оси, кроме точки, поскольку в этой точке происходит не допускаемое в математике деление на 0. Введем функцию.
Введем функцию.
[24, «https://bakalavr-info.ru»].
Эта функция совпадает с функцией при всех, но является определенной и в точке 0, более того, она непрерывна везде, в том числе и в точке 0, что следует из первого замечательного предела.
Замечание. Непрерывность функции нескольких переменных определяется аналогично, первое определение, например, принимает вид.
.
Следует при этом отметить, что для функции многих переменных могут существовать не только точки разрыва (особые точки), но и линии, поверхности разрыва.
Примеры.
1. Функция.
имеет точку разрыва 0.
2. Функция.
существует во всех точках плоскости, кроме прямой.
.
эта прямая является линией разрыва функции.
3. У функции.
поверхностью разрыва является сфера.
.
4. Функция.
имеет особую точку .
Непрерывность составных функций
Рассмотрим функцию, заданную следующим образом.
.
Поскольку функции, (прямые), (парабола) непрерывны на всей числовой оси, а следовательно, и на указанных интервалах, заданная функция может иметь разрывы только в точках стыковки указанных функций, то есть при и. Исследуем поведение функции в окрестности каждой из этих точек, используя определение непрерывности функции с использованием левого и правого ее пределов. Функция непрерывна при, если выполняется условие.
Исследуем поведение функции в окрестности каждой из этих точек, используя определение непрерывности функции с использованием левого и правого ее пределов. Функция непрерывна при, если выполняется условие.
.
Проверим его.
.
Проверим функцию при .
.
Условие непрерывности в этой точке не выполняется, функция имеет конечный разрыв. График.
Показать весь текстЗаполнить форму текущей работой
Рефераты по математике.Второй замечательный предел.
?Previous Entry | Next Entry
Реферат по математикестудента 1 курса факультета управления:»Менеджмент»
Кулагина Максима.
Второй замечательный предел.
Доказательство второго замечательного предела:
Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:
Рассмотрим два случая:
1. Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где — это целая часть x.
- Отсюда следует: , поэтому
- .
- Если , то . Поэтому, согласно пределу , имеем:
- .
- По признаку (о пределе промежуточной функции) существования пределов .
2. Пусть . Сделаем подстановку , тогда
- .
Следствия
- для ,
Разберем несколько примеров нахождения предела по второму замечательному пределу способным описанием решения.
Примеры:
Вычислить предел
Решение.
Подставляем бесконечность:
Пришли к неопределенности единица в степени бесконечность.Сделаем замену переменных. ПустьЕсли , то Исходный предел после замены примет вид:
Ответ:
Пример.
Вычислить предел
Решение.
Подставляем бесконечность:
Пришли к неопределенности единица в степени бесконечность, которая указывает на применение второго замечательного предела. Выделим целую часть в основании показательно степенной функции:
Тогда предел запишется в виде:
Сделаем замену переменных. Пусть
Если , то
Исходный предел после замены примет вид:
В преобразованиях были использованы свойства степени и свойства пределов.
Ответ:
Пример.
Вычислить предел
Решение.
Преобразуем функцию, чтобы применить второй замечательный предел:
Сейчас домножим показатель на и разделим на это же выражение, затем используем свойства степени:
Так как показатели степени числителя и знаменателя дроби одинаковые (они равны 6), то предел этой дроби на бесконечности равен отношению коэффициентов при старших степенях :
Если произвести замену , то получим второй замечательный предел в чистом виде, следовательно,
Ответ:
Ссылки:http://ru.
 wikipedia.org/wiki/%C7%E0%EC%E5%F7%E0%F2%E5%EB%FC%ED%FB%E5_%EF%F0%E5%E4%E5%EB%FB
wikipedia.org/wiki/%C7%E0%EC%E5%F7%E0%F2%E5%EB%FC%ED%FB%E5_%EF%F0%E5%E4%E5%EB%FBhttp://www.cleverstudents.ru/the_second_remarkable_limit.html
| November 2013 | ||||||
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- Андрей Чуприна : (no subject) [+0]
Powered by LiveJournal.com
Произведите хорошее первое впечатление: 6 советов по написанию хорошего реферата
Реферат, возможно, самый важный раздел вашей рукописи по нескольким причинам. Во-первых, реферат — это первый раздел, который читают редакторы журнала при принятии решения о том, отправлять ли вашу рукопись на рецензию. Точно так же, как только ваша работа будет опубликована, читатели просматривают ее в первую очередь; во многих случаях это единственный раздел рукописи, который они когда-либо будут читать. Отчасти это связано с тем, что большинство литературных баз данных индексируют только рефераты, а доступ к полнотекстовым статьям часто ограничен.
Во-первых, реферат — это первый раздел, который читают редакторы журнала при принятии решения о том, отправлять ли вашу рукопись на рецензию. Точно так же, как только ваша работа будет опубликована, читатели просматривают ее в первую очередь; во многих случаях это единственный раздел рукописи, который они когда-либо будут читать. Отчасти это связано с тем, что большинство литературных баз данных индексируют только рефераты, а доступ к полнотекстовым статьям часто ограничен.
Таким образом, реферат становится инструментом для краткого изложения результатов вашего исследования и выделения его наиболее важных аспектов. В следующей статье описывается, как написать отличный реферат, который привлечет максимальное внимание к вашему исследованию.
1. Сначала напишите статью
Некоторые авторы скажут вам, что вы должны написать реферат, как только ваше исследование будет завершено. Однако вполне вероятно, что ваш проект растянулся на месяцы или даже годы; таким образом, полная картина того, чего вы достигли, может быть не свежа в вашем сознании.
Если вам трудно понять, с чего начать, просмотрите свою статью и выделите наиболее важные предложения в каждом разделе (введение, методы, результаты и обсуждение/выводы). Затем используйте эти предложения в качестве плана для написания аннотации. На этом этапе также важно проверить руководство по стилю вашего целевого журнала, чтобы изучить его абстрактные принципы. Например, некоторые журналы требуют структурированного реферата с отдельными разделами, а большинство журналов налагают строгие ограничения на количество слов.
Первый раздел вашего резюме — очень ценная недвижимость. Эти 1-3 предложения должны проинформировать читателя о том, почему вы предприняли это исследование.
Например, «Важность эпистаза — неаддитивных взаимодействий между аллелями — в формировании приспособленности популяции долгое время была спорной темой, частично сдерживаемой отсутствием эмпирических данных». 1 — отличный пример вводного предложения. в котором одновременно указывается основная тема (роль эпистаза в формировании приспособленности популяции) и описывается проблема (отсутствие эмпирических данных в этой области). Таким образом, он сразу привлекает внимание читателя. Следующее предложение может продолжаться, чтобы описать, какой информации не хватает в этой области, или что предприняли предыдущие исследователи, чтобы попытаться решить проблему.
1 — отличный пример вводного предложения. в котором одновременно указывается основная тема (роль эпистаза в формировании приспособленности популяции) и описывается проблема (отсутствие эмпирических данных в этой области). Таким образом, он сразу привлекает внимание читателя. Следующее предложение может продолжаться, чтобы описать, какой информации не хватает в этой области, или что предприняли предыдущие исследователи, чтобы попытаться решить проблему.
Такие заявления могут естественным образом привести к утверждению о том, как ваше исследование уникально решает проблему. Использование вводных фраз, таких как «Здесь мы стремились…» или «Здесь мы демонстрируем, что…», указывает читателю, что вы формулируете цель или цель своей работы.
Служба редактирования рефератов AJE специально разработана, чтобы помочь вам отшлифовать реферат и уложиться в ограничения по количеству слов.
3. Кратко опишите свою методологию
Раздел «Методы» вашего резюме — это ваша возможность подытожить основной план вашего исследования. Чрезмерная детализация не нужна; тем не менее, вы должны кратко указать основные используемые методы. Тезисы в биологических или клинических областях должны упоминать организм, клеточную линию или изучаемую популяцию. Для статей по экологии место исследования часто является важной частью информации. В документах, описывающих клинические испытания, следует указывать размер выборки, группы пациентов, дозировки и продолжительность исследования. В следующем примере вся эта информация четко и кратко представлена в одном предложении: «Сто последовательных добровольных стационарных пациентов мужского пола в состоянии умеренно тяжелой, неосложненной алкогольной абстиненции при скрининге были рандомизированы для получения либо лоразепама (8 мг/день), либо хлордиазепоксида ( 80 мг/день) с титрованием дозы до нуля по схеме с фиксированной дозой в течение 8 дней лечения». 2
Чрезмерная детализация не нужна; тем не менее, вы должны кратко указать основные используемые методы. Тезисы в биологических или клинических областях должны упоминать организм, клеточную линию или изучаемую популяцию. Для статей по экологии место исследования часто является важной частью информации. В документах, описывающих клинические испытания, следует указывать размер выборки, группы пациентов, дозировки и продолжительность исследования. В следующем примере вся эта информация четко и кратко представлена в одном предложении: «Сто последовательных добровольных стационарных пациентов мужского пола в состоянии умеренно тяжелой, неосложненной алкогольной абстиненции при скрининге были рандомизированы для получения либо лоразепама (8 мг/день), либо хлордиазепоксида ( 80 мг/день) с титрованием дозы до нуля по схеме с фиксированной дозой в течение 8 дней лечения». 2
4. Четко опишите наиболее важные результаты вашего исследования
Точно так же, как реферат может быть самой важной частью вашей статьи, подраздел результатов, вероятно, является самой важной частью вашего реферата. Это связано с тем, что основная причина, по которой люди читают ваш реферат, заключается в том, чтобы узнать о ваших выводах. Таким образом, подраздел результатов должен быть самой длинной частью вашего резюме, и вы должны постараться максимально увеличить количество деталей, которые вы включите в него.
Это связано с тем, что основная причина, по которой люди читают ваш реферат, заключается в том, чтобы узнать о ваших выводах. Таким образом, подраздел результатов должен быть самой длинной частью вашего резюме, и вы должны постараться максимально увеличить количество деталей, которые вы включите в него.
Например, такие утверждения, как «существенные различия в массе тела наблюдались между животными в группах А и В», малоинформативны. Вместо этого рассмотрите возможность более конкретных утверждений, таких как «средняя потеря массы тела у животных в группе А была больше, чем у животных в группе В (20,4 ± 0,3 г против 8,4 ± 0,6 г; p < 0,01)». Обратите внимание, что p-значение фактически показывает, что разница была значительной; таким образом, слово «значительный» больше не требуется.
Последние 1-2 предложения вашего резюме должны быть посвящены общей идее вашего исследования: вашим выводам. Хороший способ начать этот раздел — с таких фраз, как «Наше исследование показало, что…» или «В целом, мы пришли к выводу, что…». Затем изложите свой основной вывод как можно короче. Если у вас есть другие интересные вторичные находки, их тоже можно упомянуть. Наконец, рассмотрите возможность включения предложения, в котором говорится о теоретических или практических последствиях вашей работы и/или описывается, как ваша работа продвинула область. Это поможет читателям более четко понять важность ваших выводов.
Затем изложите свой основной вывод как можно короче. Если у вас есть другие интересные вторичные находки, их тоже можно упомянуть. Наконец, рассмотрите возможность включения предложения, в котором говорится о теоретических или практических последствиях вашей работы и/или описывается, как ваша работа продвинула область. Это поможет читателям более четко понять важность ваших выводов.
Как упоминалось ранее, многие читатели, не имеющие доступа к полному тексту вашей рукописи, будут читать только ваше резюме, а без доступа к вашим данным им придется принимать ваши выводы за чистую монету. По этой причине очень важно не преувеличивать свои выводы в реферате, чтобы не вводить читателей в заблуждение.
6. Чего следует избегать в реферате
Реферат должен быть кратким изложением вашего исследования; как таковой, он обычно имеет строгое ограничение на количество слов. Объединение всех наиболее важных аспектов вашей работы в абзац из 250 или менее слов может оказаться непростой задачей. Однако знание того, чего следует избегать при написании аннотации, может немного облегчить работу.
Однако знание того, чего следует избегать при написании аннотации, может немного облегчить работу.
Например, реферат не должен содержать:
- Длинную справочную информацию (читатели просматривают реферат, чтобы узнать о вашей текущей работе, а не о предыдущей работе других исследователей)
- Цитаты
- Подробная информация о рутинных лабораторных процедурах
- Подробная информация об используемых статистических методах или программном обеспечении (если это не является предметом вашего исследования)
- Неопределенные аббревиатуры или акронимы (большинство журналов предоставляют список общих аббревиатур/акронимов, которые не нуждаются в определении; некоторые журналы не разрешают использовать аббревиатуры/акронимы в реферате)
- Результаты или интерпретации, которые не обсуждаются в тексте
После того, как вы заполнили реферат, важно убедиться, что вся информация, которую вы здесь включили, согласуется с информацией в основной части вашей статьи.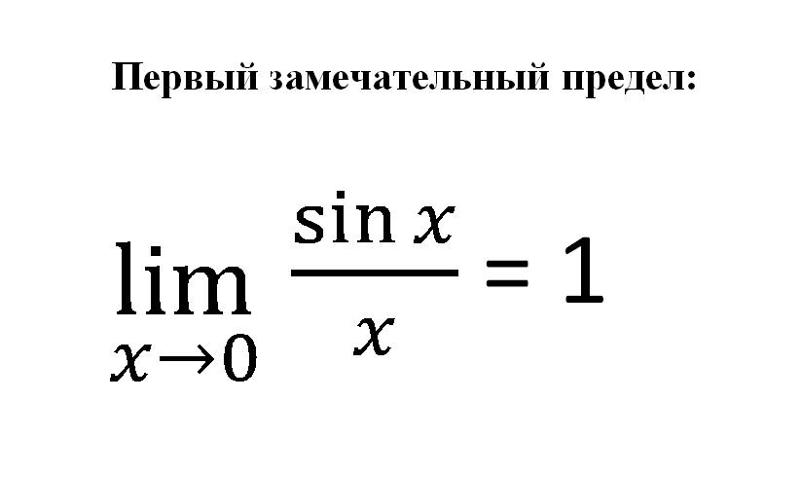 После столь долгой работы над ним иногда может быть трудно объективно оценить, понятен ли ваш реферат, особенно потому, что вы, вероятно, хорошо знакомы с соглашениями в вашей дисциплине.
После столь долгой работы над ним иногда может быть трудно объективно оценить, понятен ли ваш реферат, особенно потому, что вы, вероятно, хорошо знакомы с соглашениями в вашей дисциплине.
Подумайте о том, чтобы дать свой реферат коллеге, работающему в другой дисциплине, и попросить его или ее прочитать его. Спросите своего коллегу, понятно ли исследование, основываясь только на аннотации. Это может помочь вам определить, какие области реферата потребуют пересмотра, либо для уточнения вашего смысла, либо для лучшего выделения ваших основных выводов.
Другие моменты, которые следует учитывать
Определите ключевые термины
Ключевые фразы важны для того, чтобы ваш реферат, а также полный текст статьи был найден. Включите ключевые слова, найденные в вашей журнальной статье, чтобы поисковая система могла их обнаружить.
Рассмотрим тип реферата
Тип реферата полностью зависит от публикаций. Обязательно изучите конкретные рекомендации, прежде чем писать реферат.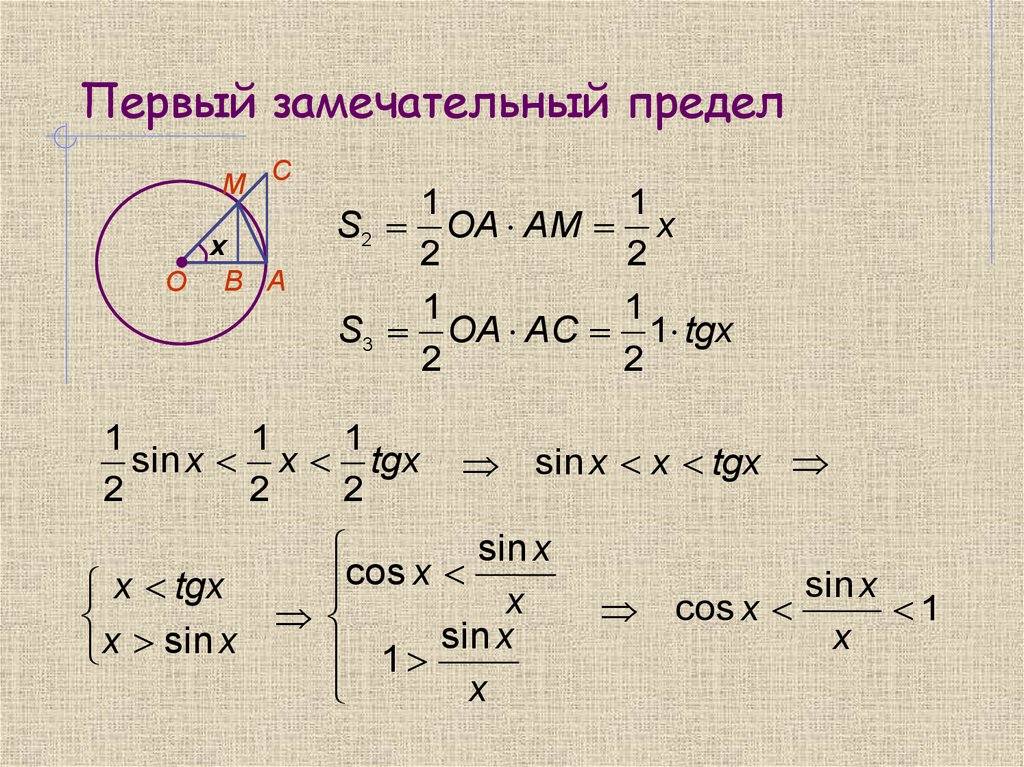 Ниже приведены описания двух разных абстрактных типов: описательных и информативных.
Ниже приведены описания двух разных абстрактных типов: описательных и информативных.
Описательная аннотация
Описательная аннотация больше похожа на план. Описательные аннотации обычно представляют собой краткие изложения вашей основной мысли и выводов. Как правило, это один абзац объемом около 100 слов.
Информационная аннотация
Информационная аннотация содержит больше деталей, чем описательная аннотация. Хорошая информативная аннотация действует как подробное изложение основного вывода. Это выходит за рамки описательной аннотации, чтобы рассказать больше всей истории.
Источники:
- 1: Генетическая несовместимость широко распространена внутри видов.
- 2: Рандомизированное двойное слепое сравнение лоразепама и хлордиазепоксида у пациентов с неосложненной алкогольной абстиненцией.
Поделись с коллегами
функций — Предел как функционал.
 .?
.?спросил
В любом случае, вот что вы можете сделать. Позволять \начать{выравнивать} S:=\{f:\Bbb{R}\to\Bbb{C}\,|\,\text{для каждого $a\in \Bbb{R}$, $\lim\limits_{x\to a }f(x)$ существует в $\Bbb{C}$}\} \end{выравнивание}
Теперь мы можем определить «ограничивающую» операцию как $L:\Bbb{R}\times S\to \Bbb{C}$ как
\начать{выравнивать}
L (а, е): = \ lim_ {х \ к а} е (х). \end{выравнивание}
Итак, конечно, область определения $L$ является векторным пространством и отображается в поле, так что вы можете назвать это функционалом (хотя это не линейный функционал, только для фиксированного $a$ $L(a, \cdot)$ линейный). Если вы хотите поговорить об ограничениях в $\infty$, все может стать сложнее, поскольку домен больше не будет векторным пространством, поэтому я думаю, вы не можете называть их функционалом в обычном смысле этого слова.
\end{выравнивание}
Итак, конечно, область определения $L$ является векторным пространством и отображается в поле, так что вы можете назвать это функционалом (хотя это не линейный функционал, только для фиксированного $a$ $L(a, \cdot)$ линейный). Если вы хотите поговорить об ограничениях в $\infty$, все может стать сложнее, поскольку домен больше не будет векторным пространством, поэтому я думаю, вы не можете называть их функционалом в обычном смысле этого слова.
Также обратите внимание, что иногда термин «функциональный» означает «непрерывное линейное отображение из (топологического/нормированного) векторного пространства в поле ($\Bbb{R}$ или $\Bbb{C}$)». Итак, если вы хотите говорить о преемственности, вы, конечно, должны оснастить $S$ топологией, вы, конечно, можете это сделать, но на данный момент я не вижу в этом смысла. Терминология может сбивать с толку и не всегда стандартизирована; всегда нужно обращаться к контекстуальным подсказкам, для которых предназначено значение.
Как видите, определение $L$ в полной общности несколько неуместно; это не значит, что бесполезно думать об этом таким образом. Есть некоторые проблемы, когда просмотр «базового ванильного» объекта с более абстрактной точки зрения приводит к более быстрым решениям (иногда это просто простое перефразирование, которое позволяет нам вызывать больше силовых теорем, например, из функционального анализа) … хотя я не могу подумайте о каких-нибудь супер убедительных примерах, которые приходят мне в голову.
$\endgroup$
6
$\begingroup$
Почему бы и нет? Существует множество примеров, в которых старые понятия можно рассматривать как функционалы или операторы из некоторого абстрактного пространства в другое абстрактное пространство или действительные числа. И действительно, сейчас это кажется нам очевидным, но это так именно потому, что мы привыкли к точке зрения функционального анализа, где естественно рассматривать функции именно как точки этого пространства; однако это была великая революция в анализе.
Единственное, что нужно проверить, это то, что определение правильно определено . Так как производная определяется как оператор, который каждой функции (с некоторой регулярностью) ставит в соответствие другую функцию (ее производную), то оператор можно определить следующим образом:
$$L : \mathbb{\overline{R}} \times V \rightarrow \mathbb{\overline{R}}$$ определяется следующим образом (обратите внимание, что мы позволяем ему принимать значения в расширенной вещественной строке, поскольку мы хотим разрешить случаи $+\infty $ и $ — \infty$):
$$ L (y, f) := \lim_{x \rightarrow y}f(x)$$
Теперь, чтобы иметь корректно определенный оператор $L$, нам нужно, чтобы предел был уникальным, и это не проблема в реальной линии, поскольку реальная линия является хаусдорфовым пространством. Тем не менее, мы должны быть уверены, что предел существует, иначе каково было бы действительное число, которое дает нам оператор $L$ в случае, когда мы рассматриваем точку $(\infty, sin(x))$? Это будет:
$$ L (\infty, sin(x)) := \lim_{x \rightarrow \infty}\sin(x)$$ которого не существует!
Решил эту проблему, нет ограничения в просмотре лимита оператором. n f(k)$» «$f(k)$» — это выражение с одной свободной переменной $k$, 9n$» является функцией, так как она связывает переменную $k$. То же самое и с кванторами: в «$∀x ∃y (Q(x,y))$» «$∀x$» заведомо не является
n f(k)$» «$f(k)$» — это выражение с одной свободной переменной $k$, 9n$» является функцией, так как она связывает переменную $k$. То же самое и с кванторами: в «$∀x ∃y (Q(x,y))$» «$∀x$» заведомо не является
Таким образом, если вы хотите рассматривать операцию ограничения как абстрактный математический объект, вам необходимо овеществить соответствующие выражения и синтаксическую структуру. но я покажу вам, как сделать это для суммирования, чтобы сделать лежащую в основе концепцию более ясной.Овеществление просто означает уловить «сущность» концепции с помощью объекта.nf(k)$. Но эта проблема сопоставления свободных переменных не появляется в овеществленных частях. Это обычно происходит при овеществлении большинства математических обозначений, включая квантификаторы, суммы/произведения, пределы и так далее.
Кроме того, если вы хотите формализовать рассуждения об ограничениях чистым алгебраическим способом, а также иметь возможность алгебраически работать с неопределенными пределами, то лучший подход — расширить возможные предельные значения, включив в них какое-то сигнальное значение, скажем, $null$ , а затем определим $L(f,x)$ как предел $f$ в $x$, если он существует, но $null$ в противном случае, для любой функции $f : D→ℂ$ с $x∈D⊆ℂ $.
