Площадь правильного треугольника. Радиус описанной окружности равностороннего треугольника. Сумма длин двух сторон треугольника.
- Альфашкола
- Статьи
- 10 фактов о треугольнике
Треугольник рассматривается как фундаментальная форма геометрии, которая может быть многоугольником, состоящим из трех углов и трех сторон, которые являются отрезками линии. Треугольники классифицируются на основе двух критериев, которые задаются относительной длиной их сторон и их внутренними углами. Существуют различные типы треугольников. В этой статье Альфа-школа расскажет вам \(10\) фактов о треугольниках.
Факт 1: В треугольнике внешний угол рассматривается как линейная пара к внутреннему углу, а сумма трех внешних углов любых треугольников равна \(360°\) градусам.
Факт 5: если только две стороны у треугольника равны, то мы называем его равнобедренным треугольником.
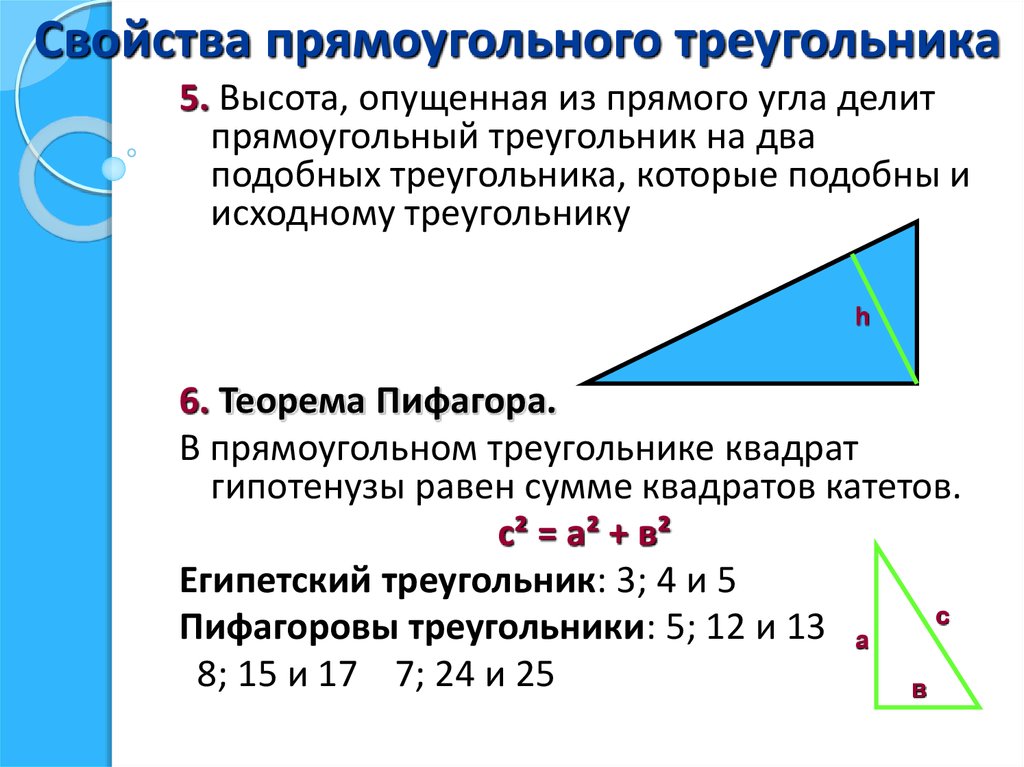
Факт 6: прямоугольный треугольником называется треугольником, если сумма квадратов смежных стороны равна квадрату гипотенузы, \(c-\)гипотенуза.
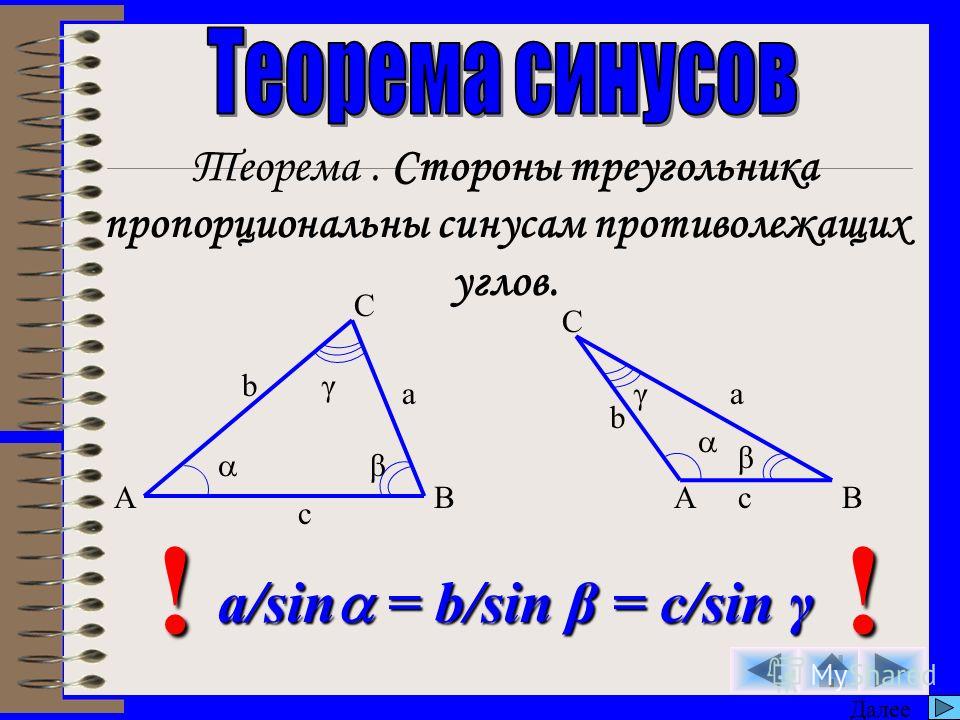
Факт 7: радиус описанной окружности равностороннего треугольника \(R\) :
\(\frac{a√3}{3}\) или \(\frac{a}{√3}\)
Факт 8: радиус вписанной окружности равностороннего треугольника \(r\) :
Факт 9: когда треугольник имеет один из своих углов, измеряющих более \(90°\) градусов, треугольник называется тупым треугольником.
Факт 10: внутренние углы треугольника всегда равны \(180°\) градусам.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Полина Андреевна Галямова
Репетитор по математике
Стаж (лет)
Образование:
ФГБОУ ВО
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5-11 классов. Подготовка к ОГЭ, ЕГЭ. Меня зовут Полина Андреевна и я преподаватель математики, алгебры, геометрии и среды программирования Scratch! Обожаю математику, но эта любовь далась большим трудом и усилиями! Математика подвластна всем! Я познакомлю Вас с прекрасным миром математической науки и научу плыть в потоке знаний строго по течению реки!))
Подготовка к ОГЭ, ЕГЭ. Меня зовут Полина Андреевна и я преподаватель математики, алгебры, геометрии и среды программирования Scratch! Обожаю математику, но эта любовь далась большим трудом и усилиями! Математика подвластна всем! Я познакомлю Вас с прекрасным миром математической науки и научу плыть в потоке знаний строго по течению реки!))
Лиля Алексеевна Шевченко
Репетитор по математике
Стаж (лет)
Образование:
Армавирский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-9 классы.
Надежда Даниловна Кондрашова
Репетитор по математике
Стаж (лет)
Образование:
Западно-Казахстанский государственный университет им.А.С. Пушкина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5 -11 классов по русскому языку. Доброжелательное отношение, создание позитивной эмоциональной атмосферы на занятиях, эффективная отработка материала обеспечивают самые высокие результаты. Стараюсь привить любовь к предмету «Русский язык» у ребенка, использую индивидуальный подход, подбираю материал в зависимости от способностей ребёнка. Приветствую в учениках ответственное отношение, дисциплинированность и стремление учиться.
Стараюсь привить любовь к предмету «Русский язык» у ребенка, использую индивидуальный подход, подбираю материал в зависимости от способностей ребёнка. Приветствую в учениках ответственное отношение, дисциплинированность и стремление учиться.
Похожие статьи
- Жизни математиков (часть 2)
- Как найти делитель?
- Уравнения с десятичными дробями
- Как решать показательно-степенные уравнения
- Задачи с прикладным содержанием (вариант 4)
- Обзор стильных и недорогих смарт-часов
- Если ребенок хочет зарабатывать: идеи и советы для родителей, как помочь подростку
- Плюсы и минусы группового обучения + пара игр на сближение участников
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Треугольник и виды треугольников, свойства сторон и углов треугольника
Главная » Геометрия » Треугольник — определение и основные свойства и виды треугольника
Что такое треугольник знают дети уже в самом младшем возрасте, они умеют находить треугольник среди множества геометрических фигур. Но вот уже в школе по геометрии проходят треугольник и надо не просто узнавать треугольник, но и дать определение этому понятию.
Но вот уже в школе по геометрии проходят треугольник и надо не просто узнавать треугольник, но и дать определение этому понятию.
Содержание
Определение треугольника
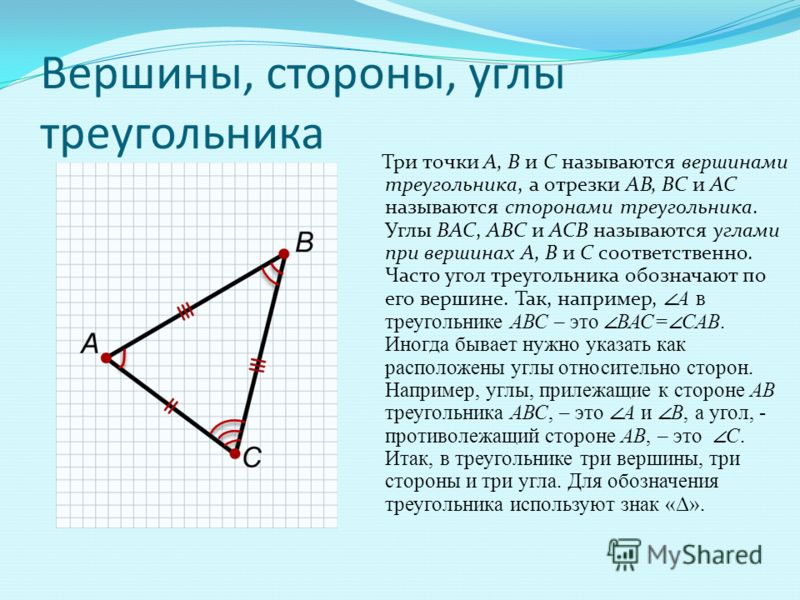
Треугольник — это геометрическая фигура, окруженная тремя отрезками прямой (конечные точки каждых двух смежных отрезков соединены или перекрываются), называется треугольником. Точки пересечения отрезков называются вершинами треугольника, а сами отрезки между двумя соседними вершинами треугольника называются сторонами треугольника.
Посмотрите на треугольник на рисунке.
У него три вершины — , , и три стороны , и . У каждого треугольника есть имя — это имя образовано вершинами треугольника. Наш треугольник зовут ([а-бэ-цэ]). А треугольник на вот этом рисунке
будут звать ([эм-эн-ка]).
По правилам математической грамотности треугольник, как и любой другой многоугольник, следует называть, начиная с левого нижнего угла и называя все вершины по часовой стрелке.
В треугольнике можно провести особенные стороны — высоту, медиану и биссектрису. Начнем с высоты треугольника.
Высота треугольника
В каждом треугольнике можно провести три высоты. Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противолежащую этой вершине сторону.
Например, в треугольнике , высотой будет отрезок .
А теперь проведем из каждой вершины по высоте — получим три высоты — больше провести высот нельзя.
В этом треугольнике три высоты , , .
Про биссектрисы и медианы поговорим в других статьях. Сейчас же давайте с вами рассмотрим каким бывает треугольник.
Виды треугольника
Виды треугольника могут быть по углам и по сторонам. То есть в первом случае вид треугольника зависит от того, какие в этом треугольнике углы, а во втором случае — какие в этом треугольнике стороны.
Виды треугольников по углам
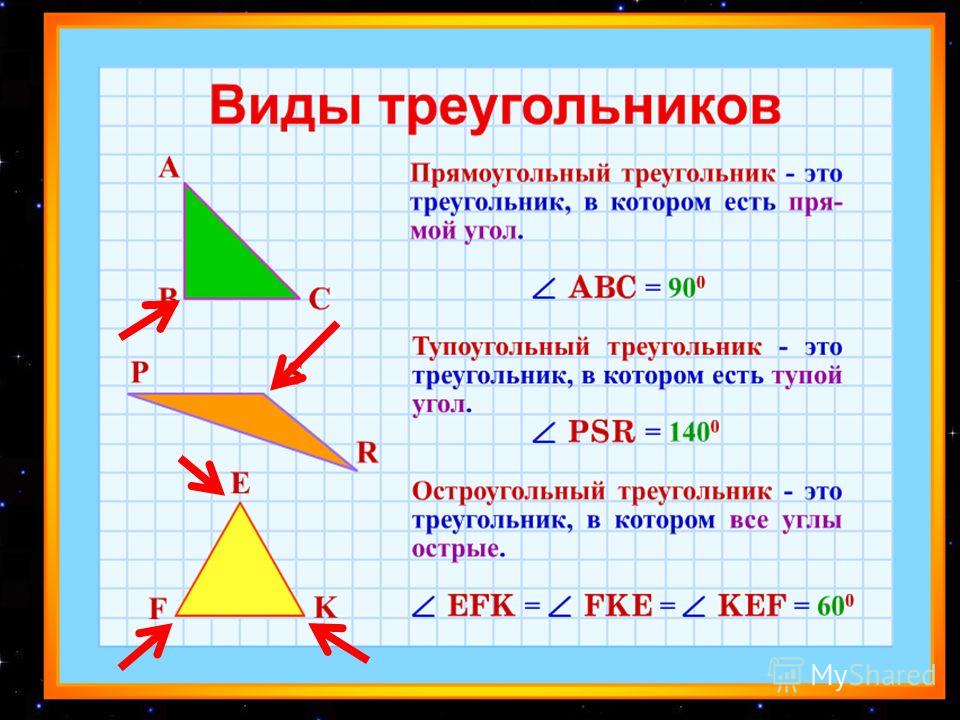
В зависимости от того, все ли углы в треугольнике острые или есть тупой угол или угол, равный , треугольник бывает остроугольным, тупоугольным или прямоугольным.
Посмотрите на рисунки — перед вами три основных вида треугольника:
Виды треугольников по сторонам
Если у треугольника все стороны равны, то такой треугольник называют равносторонним или правильным. Если у треугольника равны только две стороны, то такой треугольник называют равнобедренным.
На рисунке показаны равносторонний и равнобедренный треугольники.
Свойства сторон треугольника
Треугольник имеет важные свойства и характеристики.
Устойчивость — это важное свойство треугольника, оно вам еще пригодится в курсе физики. Но вначале мы с ним знакомимся на уроках геометрии.
Треугольник устойчив на любой своей стороне — то есть чтобы вывести его из состояния равновесия надо приложить силу.
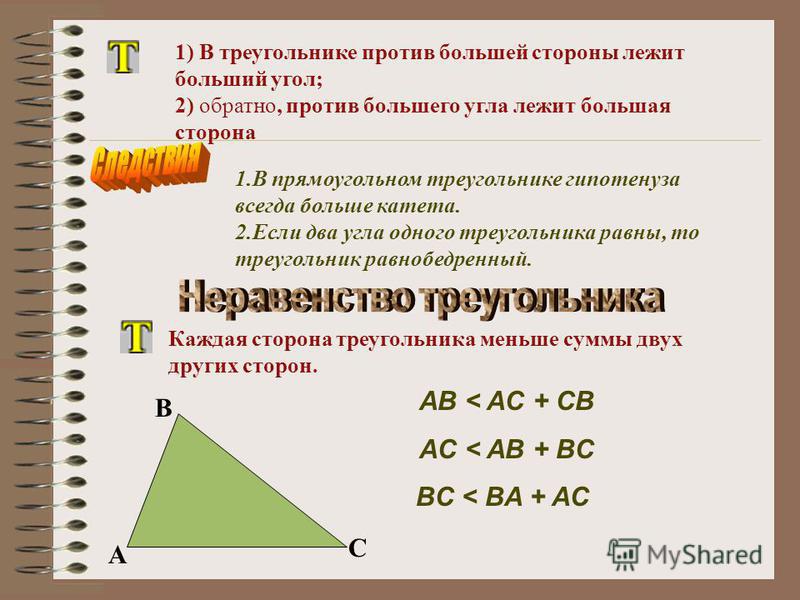
Свойства сторон: разница между любыми двумя сторонами треугольника меньше, чем третья сторона, а также любая сторона треугольника меньше, чем сумма двух других сторон.
То есть: .
Например, пусть наш треугольник имеет длины двух сторон , а см. В каком диапазоне будет размер третьей стороны треугольника?
Решение: согласно свойству сторон треугольника, получим:
, или .
Таким образом, третья сторона треугольника может быть в диапазоне от 4 до 10 см. Или в целых числах ее длина может быть 5, 6, 7, 8 или 9 см.
Правило существования треугольника
Используя свойство сторон треугольника мы можем определить существует ли треугольник с определенными сторонами.
Для проверки сложите длины самых коротких сторон и если сумма их больше длины самой большой стороны, тогда треугольник существует.
Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?
Решение: проверим по свойству сторон треугольника: складываем две самые короткие стороны 3 и 7 см: 3+7=10, а 10<15, то есть треугольник не получится.
А вот такие длины сторон 5 см, 7 см и 6 см вполне могут образовать треугольник: складываем 5+6=11 и 11>7 — треугольник с такими длинами сторон существует.
Свойство углов в треугольнике
Сумма всех углов в треугольнике равна .
Согласно этому свойству мы всегда можем, зная два угла в треугольнике, найти его третий угол. В прямоугольном треугольнике сумма двух острых углов всегда равна .
Например, пусть известно, что в треугольнике , , , нужно найти .
Решение.
Так как сумма углов в треугольнике равна , то находим:
.
Ответ: .
Элементы композиции
Многие школьники спрашивают — а зачем нам знать про треугольник, как это может пригодиться в обычной жизни? Треугольник — простая фигура из которой можно составить более сложные. Это используется во многих сферах жизни, например, вы можете эргономично убирать в своей комнате, или красиво выкладывать бутерброды. Например, из двух равных треугольников можно составить параллелограмм.
А из двух равных прямоугольных треугольником — прямоугольник или квадрат. Два треугольника могут образовать трапецию, так как на рисунке. А вот какую фигурку можно смоделировать для программируемой игры — она вся сделана из треугольников:
Мы, рассмотрели самые важные свойства треугольника, и в дальнейшем изучим еще больше разных интересных свойств, закономерностей. Несмотря на свою простоту, треугольник таит в себе много загадок и открытий.
Несмотря на свою простоту, треугольник таит в себе много загадок и открытий.
Какими могут быть стороны треугольника — свойства и вычисления
Одной из фигур, которая часто встречается в геометрических задачах у школьников, является треугольник. Какими могут быть стороны его, зависит от соотношения длин отрезков, из которых составлен этот многоугольник. В общем случае задачи с использованием рассматриваемой фигуры являются простыми и предполагают использование известных формул для их решения.
Содержание
- Многоугольник с тремя сторонами
- Типы фигуры
- Два основных свойства
- Вопрос вырождения
- Теорема косинусов
- Решение задач
Многоугольник с тремя сторонами
Прежде чем рассматривать задачу о том, как проверить, существует ли треугольник, следует подробно изучить эту фигуру. Согласно общепринятому определению, любой замкнутый многоугольник на плоскости, который состоит из трех отрезков, пересекающихся своими концами друг с другом, является треугольником. Эта фигура имеет две группы образующих ее элементов:
Эта фигура имеет две группы образующих ее элементов:
- стороны;
- вершины.
Сторонами являются три отрезка, длины которых могут быть либо известны по условию задачи, либо их предстоит рассчитать. Касательно вершин следует сказать, что у любого рассматриваемого многоугольника их три. Каждую принято обозначать одной латинской буквой, например, A, B, C и так далее. Поскольку два отрезка пересекаются в вершине, то они образуют некоторый угол. Их у фигуры три, поэтому становится понятным, откуда происходит название «треугольник».
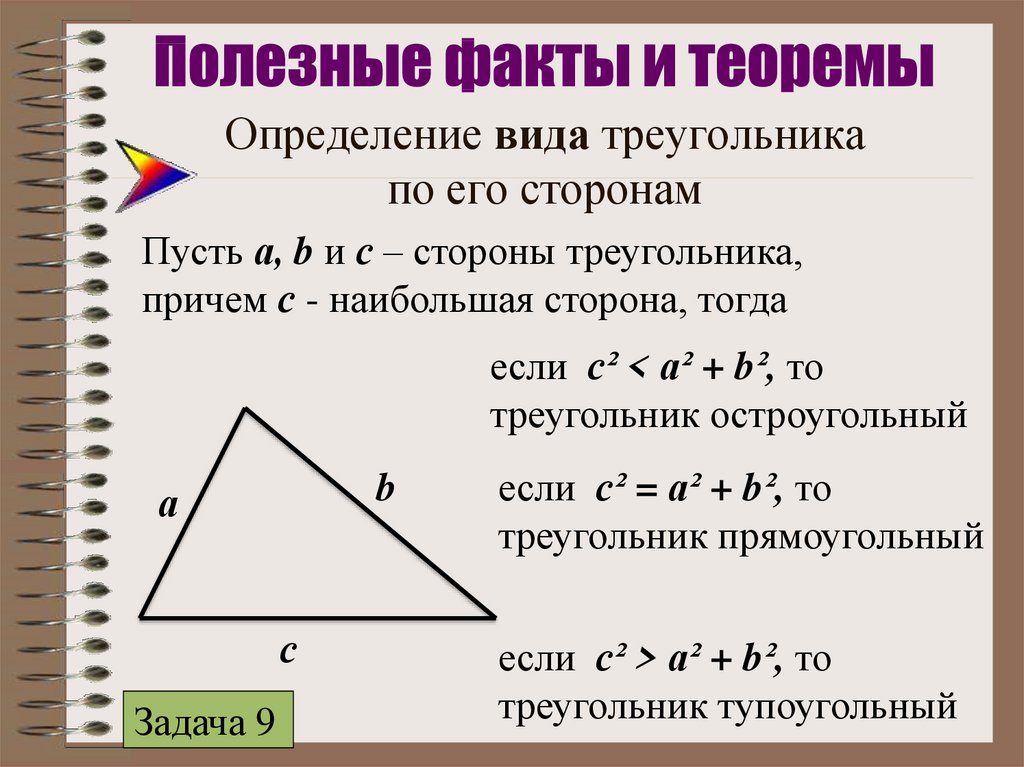
Типы фигуры
Их классификация является достаточно развитой. В ее основу положены принципы взаимоотношения длин сторон друг с другом, а также численные значения углов. В общем случае в геометрии рассматривают следующие типы треугольников:
 Все ее углы также являются одинаковыми, каждый из них составляет 60 °. Специальные отрезки в таком треугольнике (медиана, биссектриса, медиатриса или серединный перпендикуляр и высота) совпадают друг с другом независимо от того, через какую сторону или угол они проходят.
Все ее углы также являются одинаковыми, каждый из них составляет 60 °. Специальные отрезки в таком треугольнике (медиана, биссектриса, медиатриса или серединный перпендикуляр и высота) совпадают друг с другом независимо от того, через какую сторону или угол они проходят. Оставшиеся отрезки называются катетами. Они могут быть как одинаковыми, так и иметь разную длину.
Оставшиеся отрезки называются катетами. Они могут быть как одинаковыми, так и иметь разную длину.Два основных свойства
В некоторых геометрических задачах можно встретить проблемы, которые формулируются так: можно ли построить треугольник со сторонами a, b, c, если известны их длины. Либо другой тип задач, которые предполагают знание некоторых сторон и углов, и требуют определить возможность существования такой фигуры.
Ответ на все эти проблемы заключается всего в одном слове: либо «да» и такой треугольник действительно существует, либо «нет» и из заданных элементов его построить не представляется возможным.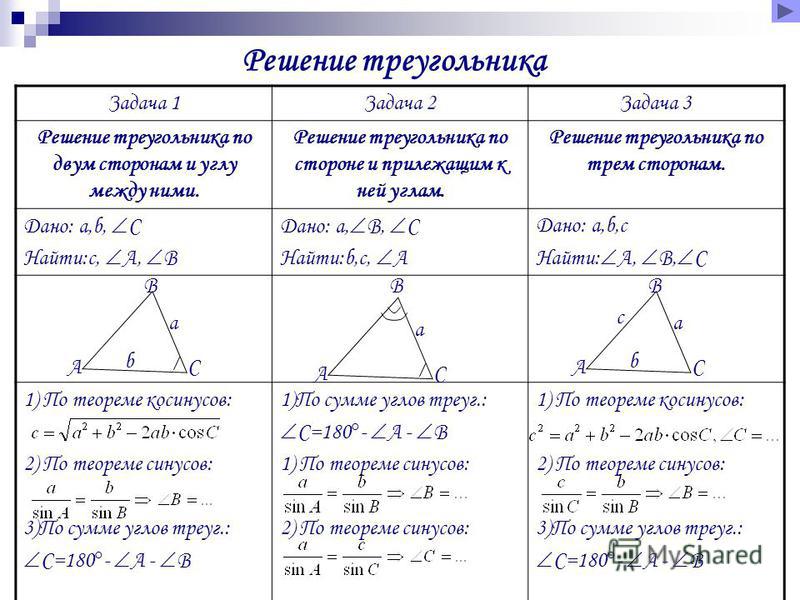 Разобраться со всеми этими задачами поможет знание двух главных свойств, которые всегда справедливы для треугольников любых типов:
Разобраться со всеми этими задачами поможет знание двух главных свойств, которые всегда справедливы для треугольников любых типов:
Оба свойства с успехом можно и необходимо применять, чтобы проверить или узнать возможность существования того или иного треугольника.
Важно понимать, что невыполнение любого из свойств говорит о невозможности построения рассматриваемой фигуры.
Вопрос вырождения
В свете изучения возможности существования треугольников важно рассмотреть вопрос их вырождения. В математике придумали универсальную формулу, которая позволяет оценить качество треугольника. Она имеет вид:
CT = (a+b-c)*(b+c-a)*(c+a-b)/(a*b*c).
Каждый из трех множителей числителя является положительным числом, что следует из главного свойства треугольников. Величина качества CT является положительной и лежит в пределах значений 0 и 1. Возможны следующие случаи:
Теорема косинусов
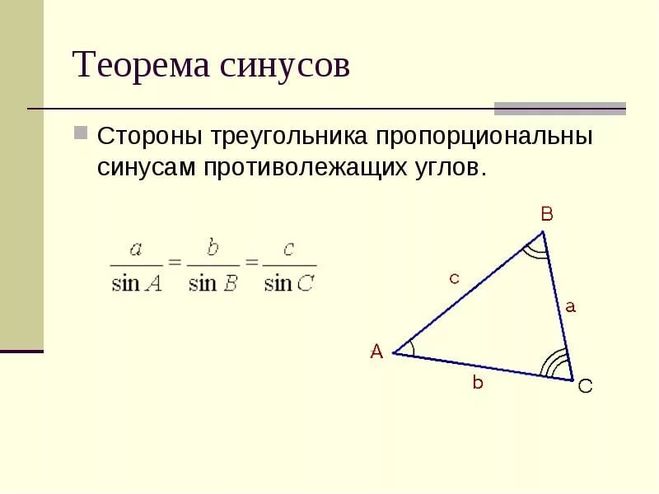
Чтобы решать задачи на треугольники, недостаточно знать лишь главные их свойства. Последние позволяют лишь дать качественный, но не количественный ответ. Теорем и формул для рассматриваемых многоугольников известно много (синусов, Пифагора, медиан, Герона и др.). Однако, теорема косинусов является одной из основополагающих, поскольку позволяет по двум сторонам и углу определить значение длины третьей стороны (справедливости ради следует отметить, что теорема синусов является не менее важной, поскольку она по двум углам и стороне позволяет вычислить неизвестные стороны).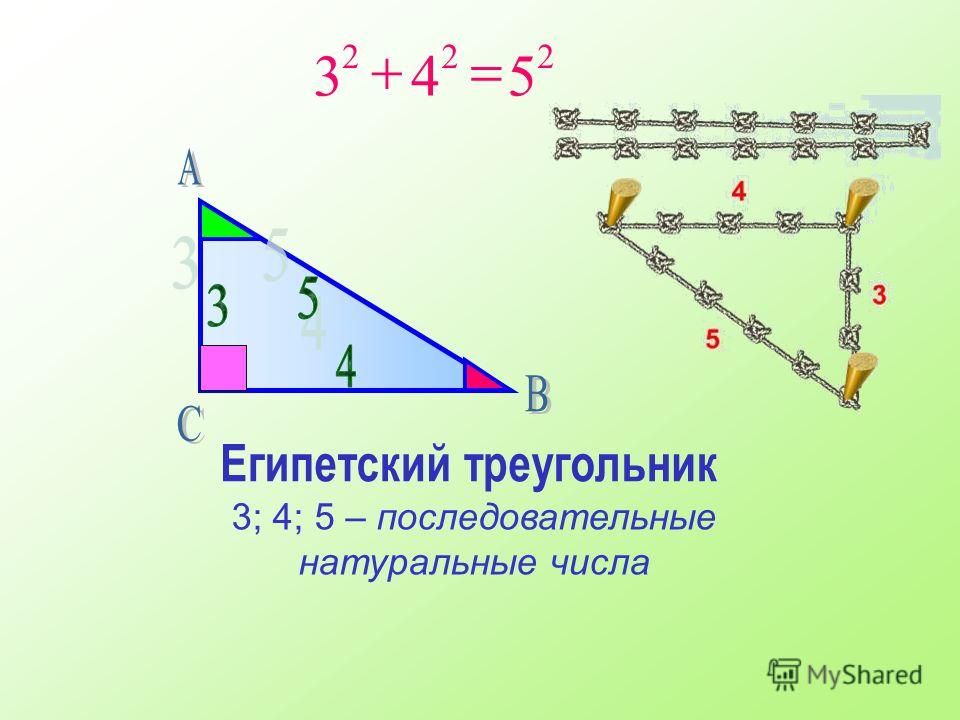
Соответствующее выражение имеет следующий вид:
c 2 = a 2 + b 2 — 2*a*b*cos (α).
Здесь a, b, c — длины сторон фигуры, α — угол между a и b. Нетрудно догадаться, что это выражение является обобщение пифагоровой теоремы для треугольника с прямым углом.
По сути, записанное равенство заключает в себе второе главное свойство треугольников. Действительно, значение угла α может изменяться от 0 ° до 180 °. При этом тригонометрическая функция cos пробегает значения от 1 до -1. Для всех них длина одного отрезка будет меньше суммы двух других. Лишь для значений -1 и +1 получается равенство, что свидетельствует о полном вырождении треугольника в отрезок.
Решение задач
Для закрепления полученных знаний полезно привести пару примеров решения типичных геометрических задач с треугольниками, в которых нужно будет либо дать качественный ответ, либо получить некоторое количественное значение.
Первая задача требует получить качественный ответ. Пусть имеется треугольник со сторонами 1, 2, 4. Существует ли такая фигура, требуется выяснить.
Для решения этой проблемы абсолютно неважно измеряются стороны в метрах, в сантиметрах, в дюймах или в других величинах. Важно лишь взаимоотношение между ними. Для каждой из длин отрезков следует проверить свойство существования рассматриваемой фигуры. Если получится хотя бы одна ложь, то треугольник построить нельзя:
- 1<2+4 — правда;
- 2<1+4 — правда;
- 4<1+2 — ложь.
Таким образом, не существует треугольник со сторонами 1−2-4. Длин сторон 1 и 2 недостаточно даже для построения абсолютно вырожденной фигуры. Следует отметить, что является необязательным проверка всех трех неравенств, если встретилась «ложь», то есть уже по одному неравенству можно сказать о невозможности начертить фигуру.
Вторая задача требует дать не только качественный ответ, но и получить количественные характеристики фигуры.
Нужно узнать, возможно ли построить треугольник со сторонами 3, 4 и 6, и, если да, то какой должен быть угол между сторонами с длинами 3 и 4.
Сначала следует проверить существующие неравенства:
- 3<4+6 — правда;
- 4<3+6 — правда;
- 6<3+4 — правда.
Все три неравенства являются истинными (править их не нужно), значит, треугольник со сторонами 3, 4 и 6 можно построить. Для определения значения угла между отрезками 3 и 4 следует применить формулу косинусов. Пусть a=3, b=4, c=6, тогда:
α = arccos ((a 2 + b 2 — c 2 )/(2*a*b)) = arccos ((3 2 + 4 2 — 6 2 )/(2*3*4)) ≈ 51,38 °.
Таким образом, для определения возможности существования того или иного треугольника на плоскости необходимо проверить тот факт, что каждая из его сторон имеет меньшую длину, чем сумма двух других отрезков. Теорема косинусов является удобным инструментом для определения количественных характеристик рассматриваемого типа фигур.
Предыдущая
ГеометрияПлощадь треугольника через радиус описанной окружности — формулы и примеры определения
Следующая
ГеометрияСредняя линия трапеции — свойства, теоремы и задачи
Как найти центральный угол
Обновлено 16 мая 2018 г.
Автор: Элиза Хансен
Представьте, что вы стоите посреди совершенно круглой арены. Вы смотрите на толпу по бокам арены и замечаете своего лучшего друга на одном месте и своего учителя математики в средней школе через пару секций. Какое расстояние между ними и вами? Какое расстояние вам придется пройти, чтобы добраться от места вашего друга до места вашего учителя? Каковы меры углов между вами? Все эти вопросы связаны с центральными углами.
Центральный угол — это угол, который образуется при проведении двух радиусов из центра круга к его краям. В этом примере два радиуса — это две линии вашего обзора от вас в центре арены к вашему другу и ваша линия обзора к вашему учителю. Угол, который образуется между этими двумя линиями, является центральным углом. Это угол, ближайший к центру окружности.
В этом примере два радиуса — это две линии вашего обзора от вас в центре арены к вашему другу и ваша линия обзора к вашему учителю. Угол, который образуется между этими двумя линиями, является центральным углом. Это угол, ближайший к центру окружности.
Ваш друг и ваш учитель сидят вдоль окружности или по краям круга. Путь вдоль арены, который их соединяет, равен 9.0009 дуга .
Найдите центральный угол по длине дуги и окружности
Есть несколько уравнений, которые можно использовать для нахождения центрального угла. Иногда вы получите длину дуги , расстояние по окружности между двумя точками. (В примере это расстояние, которое вам придется пройти по арене, чтобы добраться от друга до учителя.) Соотношение между центральным углом и длиной дуги:
(длина дуги) ÷ длина окружности = (центральный угол ) ÷ 360°
Центральный угол указывается в градусах.
Эта формула имеет смысл, если подумать. Длина дуги от общей длины окружности (окружности) равна той же пропорции, что и угол дуги от общего угла окружности (360 градусов).
Чтобы эффективно использовать это уравнение, вам нужно знать длину окружности. Но вы также можете использовать эту формулу, чтобы найти длину дуги, если вы знаете центральный угол и длину окружности. Или, если у вас есть длина дуги и центральный угол, вы можете найти длину окружности!
Найдите центральный угол по длине и радиусу дуги
Вы также можете использовать радиус окружности и длину дуги, чтобы найти центральный угол. Назовите меру центрального угла θ. Тогда:
θ = s ÷ r , где s — длина дуги, а r — радиус. θ измеряется в радианах.
Опять же, вы можете изменить это уравнение в зависимости от имеющейся у вас информации. Длину дуги можно найти по радиусу и центральному углу. Или вы можете найти радиус, если у вас есть центральный угол и длина дуги.
Или вы можете найти радиус, если у вас есть центральный угол и длина дуги.
Если вам нужна длина дуги, уравнение выглядит так:
s = θ * r , где s — длина дуги, r — радиус, а θ — центральный угол в радианах.
Теорема о центральном угле
Давайте добавим поворот к вашему примеру, когда вы находитесь на арене со своим соседом и учителем. Теперь на арене появился третий человек, которого вы знаете: ваш ближайший сосед. И еще: они за вами. Вы должны обернуться, чтобы увидеть их.
Ваш сосед находится примерно через арену от вашего друга и вашего учителя. С точки зрения вашего соседа есть угол, образованный их линией взгляда на друга и их линией взгляда на учителя. Это называется вписанный угол. Вписанный угол — это угол, образованный тремя точками на окружности.
Теорема о центральном угле объясняет соотношение между величиной центрального угла, образованного вами, и вписанного угла, образованного вашим соседом. Центральный угол Теорема утверждает, что центральный угол вдвое больше вписанного угла . (Это предполагает, что вы используете одни и те же конечные точки. Вы оба смотрите на учителя и друга, а не на кого-то другого).
Центральный угол Теорема утверждает, что центральный угол вдвое больше вписанного угла . (Это предполагает, что вы используете одни и те же конечные точки. Вы оба смотрите на учителя и друга, а не на кого-то другого).
Вот еще один способ написать это. Назовем место вашего друга A, место вашего учителя B и место вашего соседа C. Вы, в центре, можете быть O.
Итак, для трех точек A, B и C по окружности круга и точки O на центральный угол ∠AOC вдвое больше вписанного угла ∠ABC.
То есть ∠AOC = 2∠ABC.
В этом есть смысл. Вы ближе к другу и учителю, поэтому для вас они смотрят дальше друг от друга (под большим углом). Вашему соседу с другой стороны стадиона они кажутся намного ближе друг к другу (меньший угол).
Исключение из теоремы о центральном угле
А теперь давайте сдвинем ситуацию вверх. Ваш сосед на дальнем конце арены начинает двигаться! Они по-прежнему видят друга и учителя, но линии и углы продолжают смещаться по мере движения соседа. Угадайте, что: пока сосед остается за пределами дуги между другом и соседом, теорема о центральном угле остается верной!
Угадайте, что: пока сосед остается за пределами дуги между другом и соседом, теорема о центральном угле остается верной!
Но что происходит, когда сосед перемещается между другом и учителем? Теперь ваш сосед находится внутри малой дуги , относительно небольшого расстояния между другом и учителем по сравнению с большим расстоянием вокруг остальной части арены. Тогда вы получите исключение из теоремы о центральном угле.
Исключение из теоремы о центральном угле утверждает, что, когда соседняя точка C находится внутри малой дуги, вписанный угол является дополнением половины центрального угла. (Помните, что угол и его дополнение добавить к 180 градусам.)
Итак: вписанный угол = 180 — (центральный угол ÷ 2)
Или: ∠ABC = 180 — (∠AOC ÷ 2) 9 Math
3
Visual В справочнике есть инструмент для визуализации теоремы о центральном угле и ее исключений.
 Вы можете перетаскивать «соседей» во все разные части круга и наблюдать, как меняются углы. Попробуйте, если вам нужна визуальная или дополнительная практика!
Вы можете перетаскивать «соседей» во все разные части круга и наблюдать, как меняются углы. Попробуйте, если вам нужна визуальная или дополнительная практика!Как найти длину стороны остроугольного/тупоугольного треугольника
Все математические ресурсы SAT
16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
SAT Math Help » Геометрия » Плоская геометрия » Треугольники » Остроугольные/тупоугольные треугольники » Как найти длину стороны остроугольного/тупоугольного треугольника
Треугольник имеет стороны длины 8, 13 и L . Что из следующего не может быть равно L ?
Возможные ответы:
6
15
7
4
Правильный ответ:
4
Пояснение:
Сумма длин двух сторон треугольника не может быть меньше длины третьей стороны.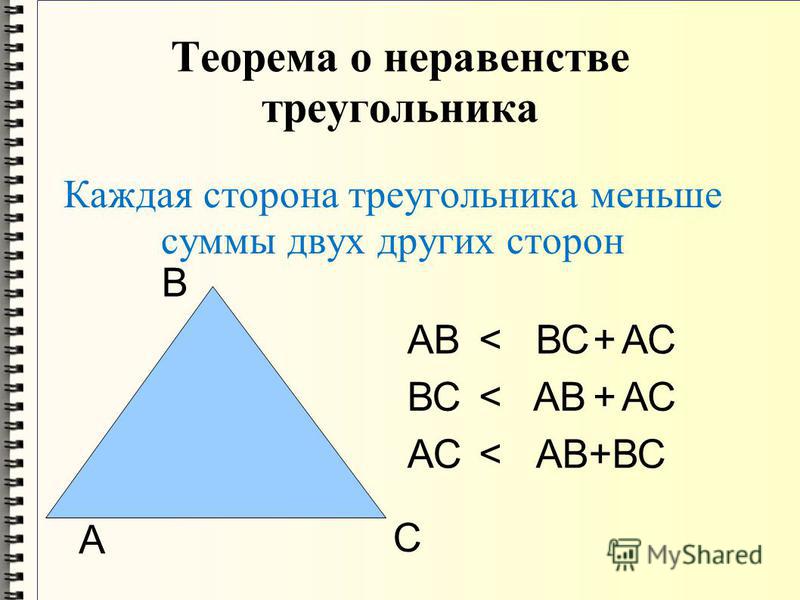 8 + 4 = 12, что меньше 13.
8 + 4 = 12, что меньше 13.
Сообщить об ошибке
Две стороны треугольника равны 20 и 32. Какая из следующих сторон НЕ МОЖЕТ быть третьей стороной этого треугольника.
Возможные ответы:
10
17
13
15
20
Правильный ответ:
10
Пояснение:
Помните теорему о неравенстве треугольников, которая гласит, что сумма любых двух сторон треугольника должна быть больше третьей стороны. Следовательно, правильный ответ — 10, потому что сумма 10 и 20 не будет больше третьей стороны 32.
Сообщить об ошибке
Длина сторон треугольника равна 5, 7 и x. Что из следующего НЕ может быть значением x?
Возможные ответы:
11
7
3
5
13
Правильный ответ:
13
Объяснение:
Сумма длин любых двух сторон треугольника должна превышать длину третьей стороны; следовательно, 5+7 > x, что невозможно, если x = 13.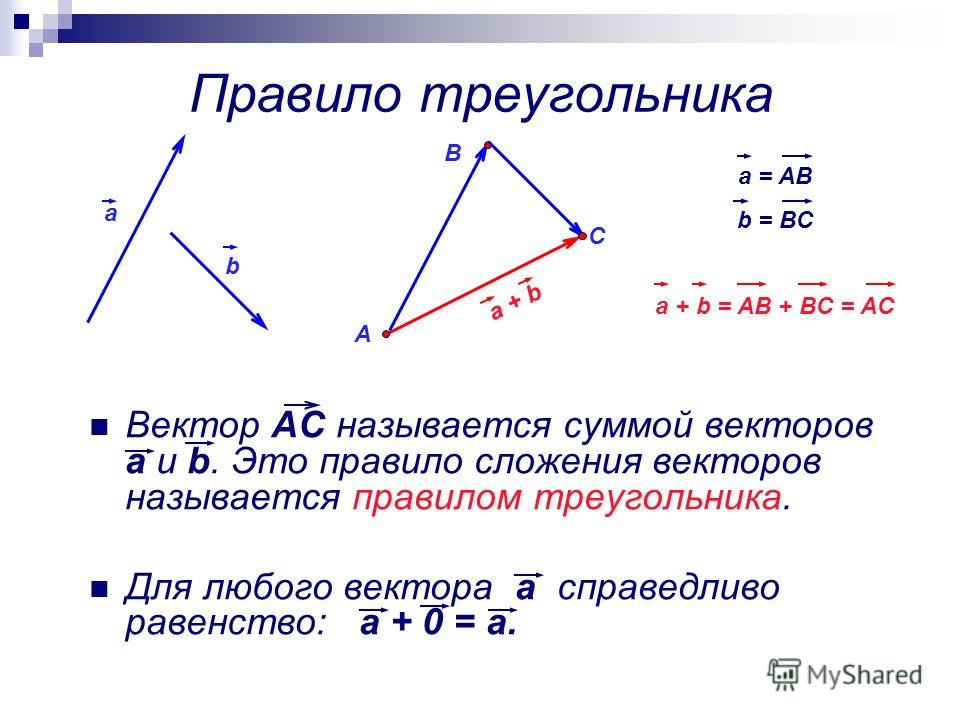
Сообщить об ошибке
Длины двух сторон треугольника равны 9 и 7. Что из следующего может быть длиной третьей стороны?
Возможные ответы:
2
1
12
17
16
Правильный ответ:
12
Пояснение:
Обозначим третью сторону x. Согласно теореме о неравенстве треугольника, сумма любых двух сторон треугольника должна быть больше двух других сторон. Таким образом, все следующее должно быть верно:
x + 7 > 9
x + 9 > 7
7 + 9 > x
Мы можем решить эти три неравенства, чтобы определить возможные значения x.
x + 7 > 9
Вычтите 7 с обеих сторон.
x > 2
Теперь мы можем посмотреть на x + 9 > 7. Вычитая 9 с обеих сторон, мы получаем
x > –2
Наконец, 7 + 9 > x, что означает, что 16 > x.
Следовательно, x должен быть больше 2, больше –2, но также и меньше 16.
Ответ: 12.
Сообщить об ошибке
Длины треугольника равны 8, 12 и x. Какое из следующих неравенств показывает все возможные значения x?
Возможные ответы:
4 4 ≤ x ≤ 20 4 ≤ x ≤12 4 8 <12 Правильный ответ: 4 < х < 20 Пояснение: Согласно теореме о неравенстве треугольника сумма любых двух сторон треугольника должна быть больше (не больше или равна) оставшейся стороны. Таким образом, все следующие неравенства должны выполняться: х + 8 > 12 х + 12 > 8 8 + 12 > х Решим каждое неравенство. x + 8 > 12 Вычтите 8 с обеих сторон. x > 4 Далее давайте посмотрим на неравенство x + 12 > 8 x + 12 > 8 Вычтите 12 из обеих частей. x > –4 Наконец, 8 + 12 > x, что означает x < 20. Это означает, что x должно быть меньше двадцати, но больше 4 и больше –4. Поскольку любое число больше 4 также больше –4, мы можем исключить неравенство x > –4. Подводя итог, x должен быть больше 4 и меньше 20. Мы можем записать это как 4 < x < 20. Ответ: 4 < x < 20. Сообщить об ошибке Если 2 стороны длины треугольника равны 8 и 14, какова возможная длина третьей стороны? Возможные ответы: Недостаточно информации 20 4 6 22 0 Правильный ответ:0003 Объяснение: Сумма длин двух сторон треугольника должна быть больше, но не равна длине третьей стороны. Далее, третья сторона должна быть длиннее, чем разница между большей и меньшей из двух других сторон; следовательно, 20 — единственный возможный ответ. Сообщить об ошибке Длина стороны AB равна 15, а длина стороны AC равна 5. Какова наименьшая возможная целочисленная длина стороны BC? Возможные ответы: 10 17 11 13 Правильный ответ: 11 Пояснение: Правило — длина одной стороны треугольника должна быть больше разности и меньше суммы длин двух других сторон. Заданные длины двух сторон равны 15 и 5. Длина третьей стороны должна быть больше 15-5 или 10 и меньше 15+5 или 20. Вопрос спрашивает, какова наименьшая возможная целочисленная длина BC, которая должна быть равна 11 Сообщить об ошибке Две стороны треугольника имеют длины 4 и 7. Что из следующего представляет набор всех возможных длин треугольника третья сторона, х? Возможные ответы: 4 4 3 2 3 Правильный ответ: 0010 3 < х < 11 Объяснение: Набор возможных длин: 7-4 < x < 7+4 или 3 < X < 11. Сообщить об ошибке Если две стороны треугольника имеют длины 8 и 10, какая длина третьей стороны НЕ будет? Возможные ответы: 8 19 5 14 10 Правильный ответ: 19 Объяснение: Согласно теореме о неравенстве треугольника, сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. Поскольку 10 + 8 равно 18, единственная невозможная длина вариантов ответа — 19. Сообщить об ошибке Дано с и . Какой из следующих может быть правильным порядком длин сторон треугольника? I) II) III) Возможные ответы: Только II. Только II или III. Только я. Только III. Только I или II. Правильный ответ: Только II. Пояснение: В треугольнике даны два угла неравной величины, сторона, лежащая напротив большего угла, длиннее стороны, противоположной другому углу. Поэтому мы стремимся найти отношение между мерами углов. , и меры внутренних углов общей суммы треугольника, поэтому С тех пор , и аналогично, , , и , , и , , и , и длины их противоположных сторон имеют одинаковый ранг: . Правильный ответ: только (II) может быть правдой. Сообщить об ошибке ← Предыдущая 1 2 Следующая → Уведомление об авторских правах 16 диагностических тестов
660 практических тестов
Вопрос дня
Карточки
Учитесь по концепции Автор: Ханна Памула, кандидат наук Отзыв от Bogna Szyk Последнее обновление: 05 ноября 2021 г. 45 45 90 Калькулятор треугольника — это специальный инструмент для решения этого специального прямоугольного треугольника. Узнайте, каковы стороны, гипотенуза, площадь и периметр вашей фигуры, а также узнайте о формуле треугольника 45 45 90, соотношениях и правилах. Если вы хотите узнать больше о других популярных прямоугольных треугольниках, ознакомьтесь с этим инструментом треугольника 30 60 90 и калькулятором для специальных прямоугольных треугольников. Если вам интересно, как найти формулу для гипотенузы треугольника 45 45 90, вы попали по адресу. Хорошо, выглядит просто, но откуда это взялось? Есть несколько методов доказательства этого уравнения, самые популярные из них: Поскольку вы знаете длину одной ноги a , вы знаете и длину другой ноги, так как они обе равны. Найдите гипотенузу по теореме Пифагора: Вы заметили, что треугольник 45 45 90 — это половина квадрата, разрезанная по диагонали квадрата? Если вы слышали о тригонометрии, вы могли бы использовать свойства синуса и косинуса. Для этого особого угла 45° оба они равны √2/2. Итак: Чтобы найти площадь такого треугольника, используйте основную формулу площади треугольника: Чтобы вычислить периметр , просто сложите все 45 45 90 сторон треугольника: Катеты такого треугольника равны, гипотенуза вычисляется сразу из уравнения Треугольники (квадраты). Красный это 45 45 9Треугольник с углом 0 градусов Самое главное правило состоит в том, что в этом треугольнике один угол прямой, а два других угла равны 45°. Отсюда следует, что две стороны — катеты — равны по длине и гипотенуза легко вычисляется. Другими интересными свойствами треугольников 45 45 90 являются: В треугольнике 45 45 90 соотношения равны: Взгляните на этот реальный пример, чтобы понять правила треугольника 45 45 90. Предположим, мы хотим решить равнобедренный треугольник по набору треугольников. Помните, что каждый раз вы можете изменить отображаемые единицы измерения, просто нажав на название единицы измерения. Также не забывайте, что наш калькулятор является гибким инструментом — если вы знаете только площадь, гипотенузу или даже периметр, он может рассчитать и остальные параметры.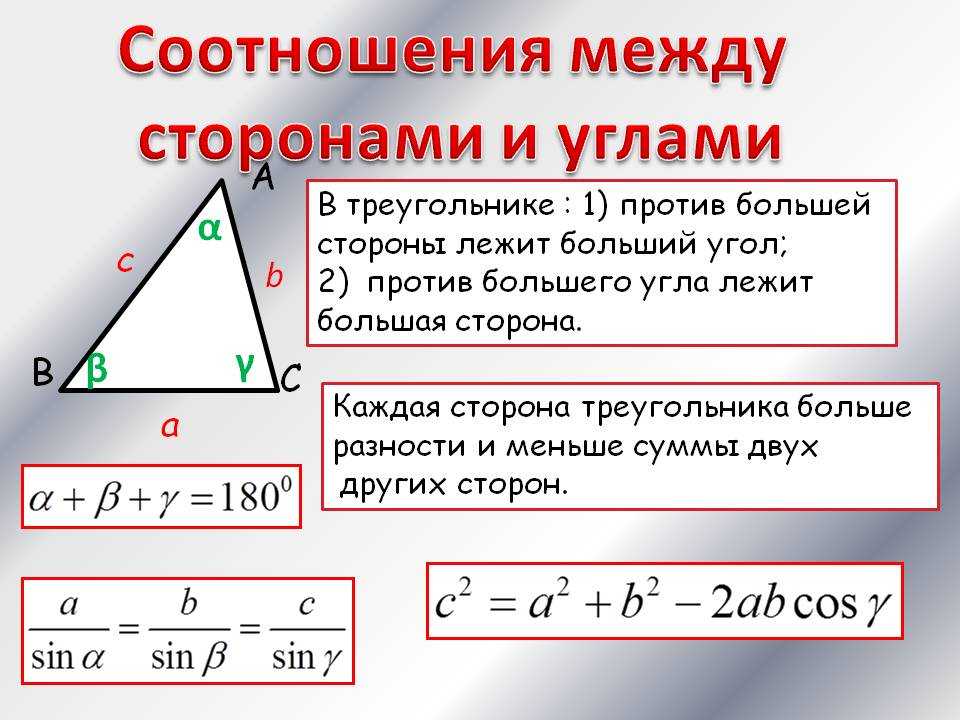
Все математические ресурсы SAT
45 45 90 Треугольник.
 Калькулятор | Формула
Калькулятор | Формула Как решить треугольник 45 45 90? Формула треугольника 45 45 90
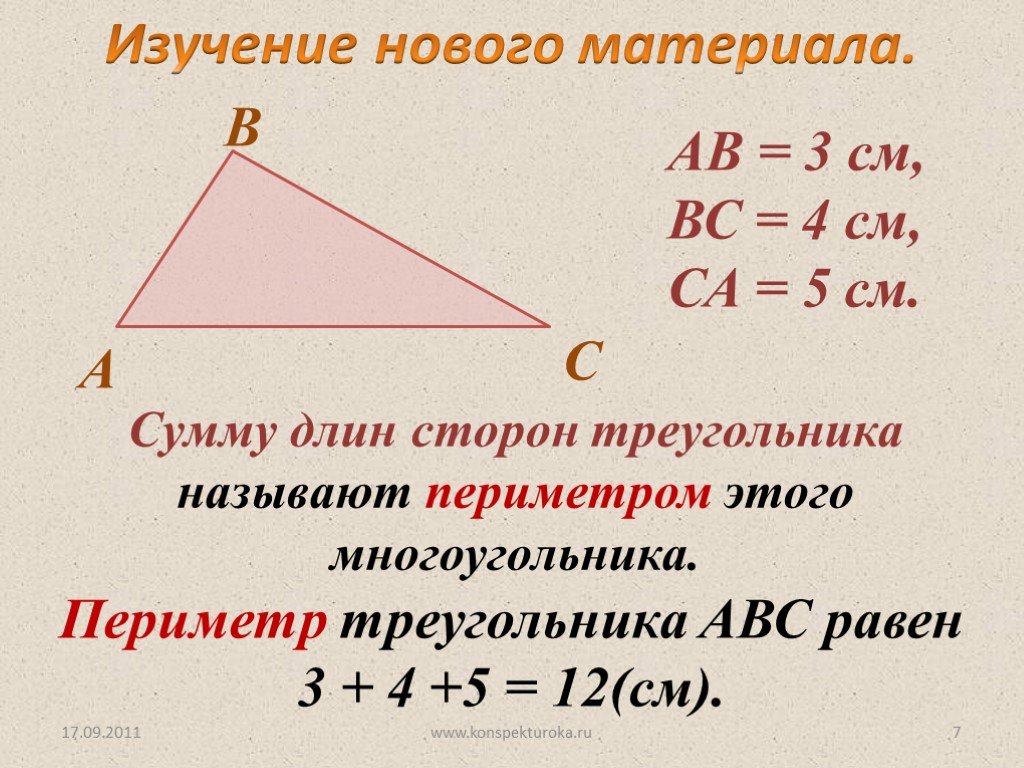
Если катет треугольника равен a , то: a² + b² = c² => a² + a² = c² поэтому с = √(2а²) = а√2 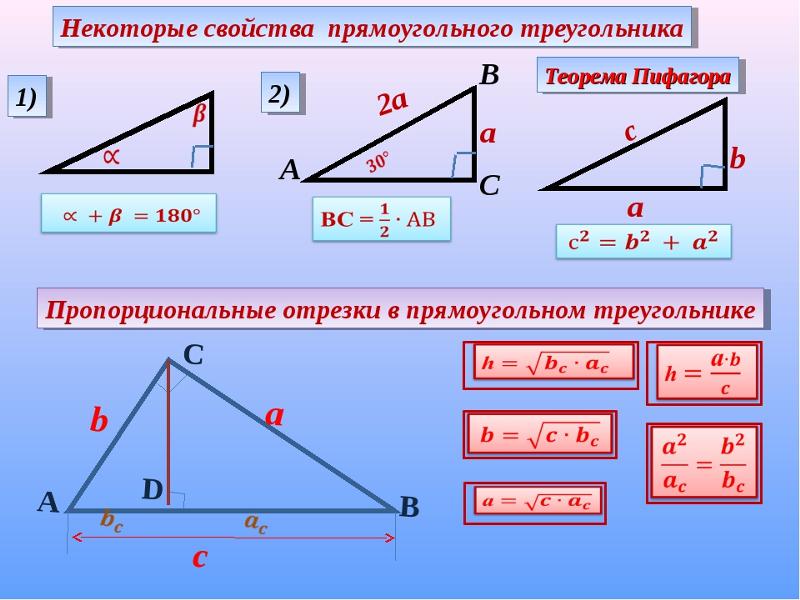
a√2 . В нашем случае эта диагональ равна гипотенузе. Это было быстро! 905:30
a/c = √2/2 , поэтому c = a√2 площадь = основание * высота / 2 . В нашем случае одна нога является основанием, а другая высотой, так как между ними прямой угол. Значит площадь 45 45 90 треугольников: `площадь = a² / 2`
периметр = a + b + c = a + a + a√2 = a(2 + √2) 45 45 90 стороны треугольника
c = a√2 .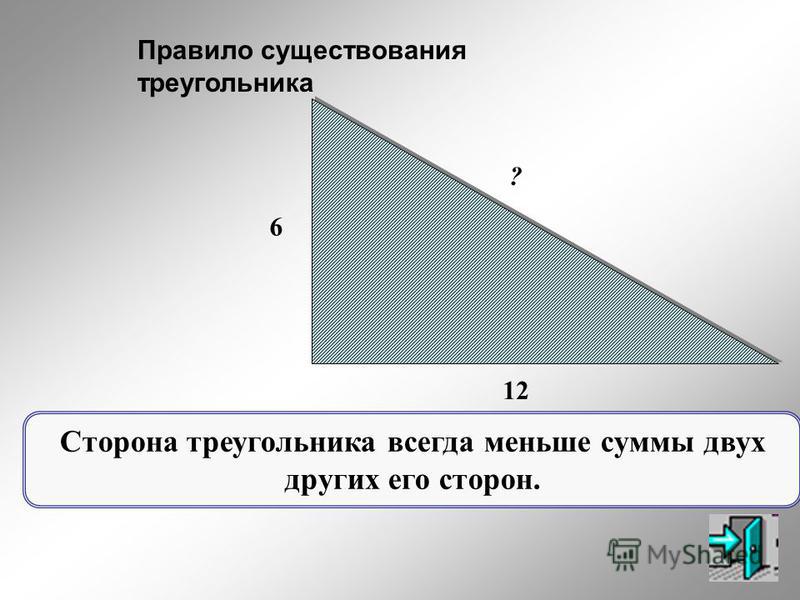 Если задано значение гипотенузы, длина стороны будет равна
Если задано значение гипотенузы, длина стороны будет равна a = c√2/2 . 45 45 90 правила и свойства треугольника
Соотношение треугольника 45 45 90
Как решить треугольник 45 45 90: пример
9 дюймов * √2 = 12,73 дюймов 9 дюймов * 9 дюймов / 2 = 40,5 дюймов² 9 дюймов + 9 дюймов + 9 дюймов * √2 = 30,73 дюйма 

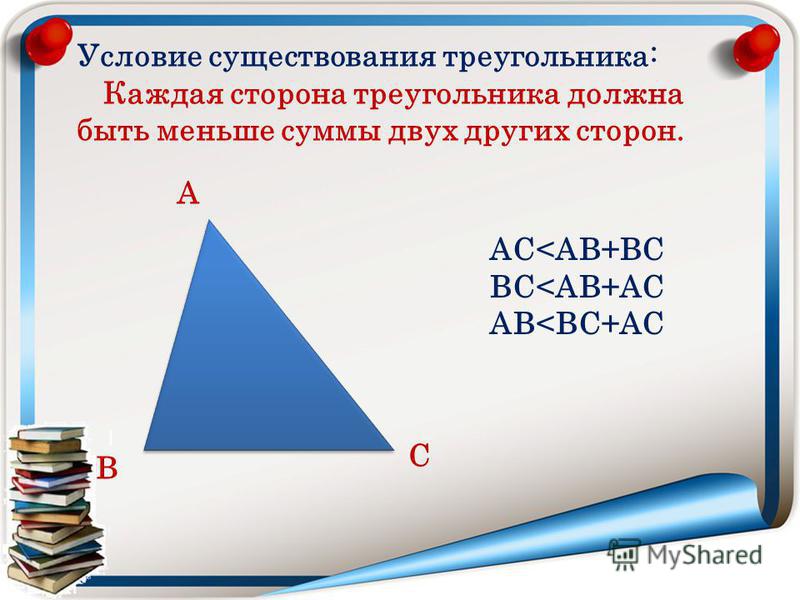 То есть: .
То есть: .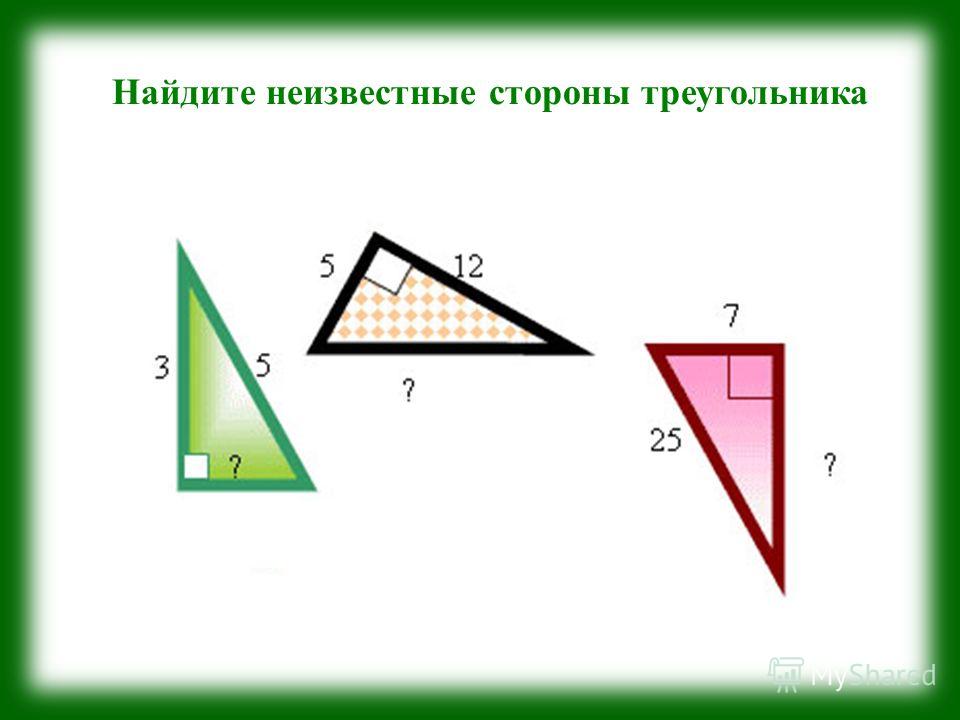 Важно понимать, что невыполнение любого из свойств говорит о невозможности построения рассматриваемой фигуры.
Важно понимать, что невыполнение любого из свойств говорит о невозможности построения рассматриваемой фигуры.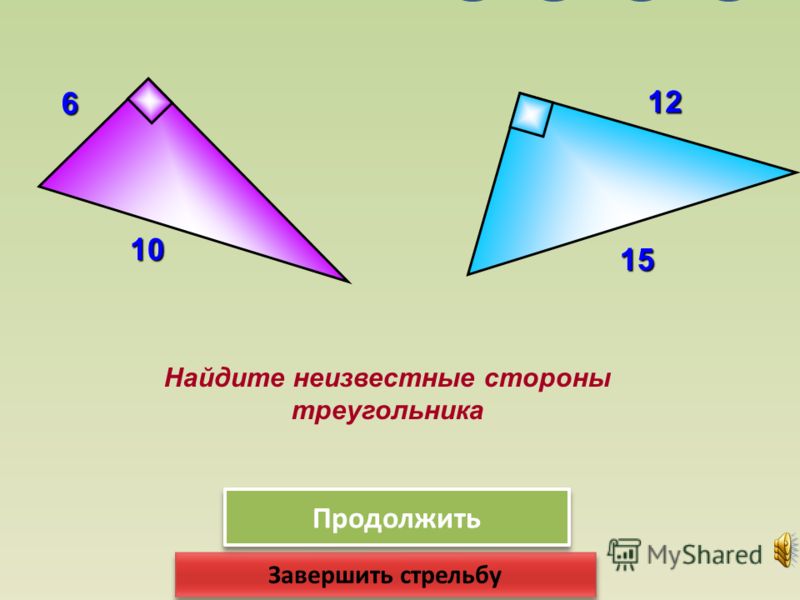 Нужно узнать, возможно ли построить треугольник со сторонами 3, 4 и 6, и, если да, то какой должен быть угол между сторонами с длинами 3 и 4.
Нужно узнать, возможно ли построить треугольник со сторонами 3, 4 и 6, и, если да, то какой должен быть угол между сторонами с длинами 3 и 4.