Правило треугольника сложение и вычитание векторов: Правило треугольника — урок. Геометрия, 9 класс.

Сложение и вычитание векторов — презентация онлайн

Похожие презентации:

Сложение и вычитание векторов

Сложение и вычитание векторов. Законы сложения

Сложение и вычитание векторов

Сложение и вычитание векторов

Сложение и вычитание векторов

Сложение и вычитание векторов

Сложение векторов. Правило треугольника

Векторы в пространстве. (10-11 класс)

Векторы в пространстве

Векторы на плоскости и в пространстве. Основные понятия

Какая запись является верной?
В
450
С
А
AВ > BC;
AВ > BC
AC = BC ;
AC = BC
Назовите
Назовите
коллинеарные
векторысонаправленные векторы
Назовитеравные
коллинеарные
противоположнонаправленные векторы
A
B
C
D
N
M
R
E
S
F
Q
V
T
Y
U
I
O
P
X
G
H
J
K
L
Z
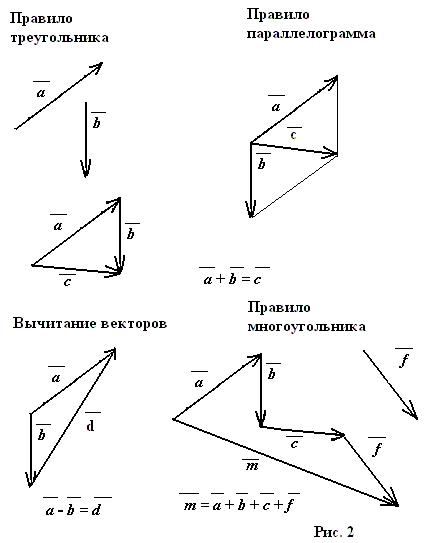
Сложение векторов. Правило треугольника.
АВ + ВС = АС
С
!
a+b
b
А
a

b
a
В
Для любого нулевого вектора
справедливо равенство
a+0=a
!
Докажем, что если при сложении векторов точку А
заменить другой точкой А1, то полученный вектор А1С1
будет равен АС. Рассмотрим случай.
a
b
В
b
a
С
А
В1
a
А1
АВВ1А1 –
параллелограмм
ВСС1В1 –
параллелограмм
АСС1А1 –
параллелограмм
b
С1
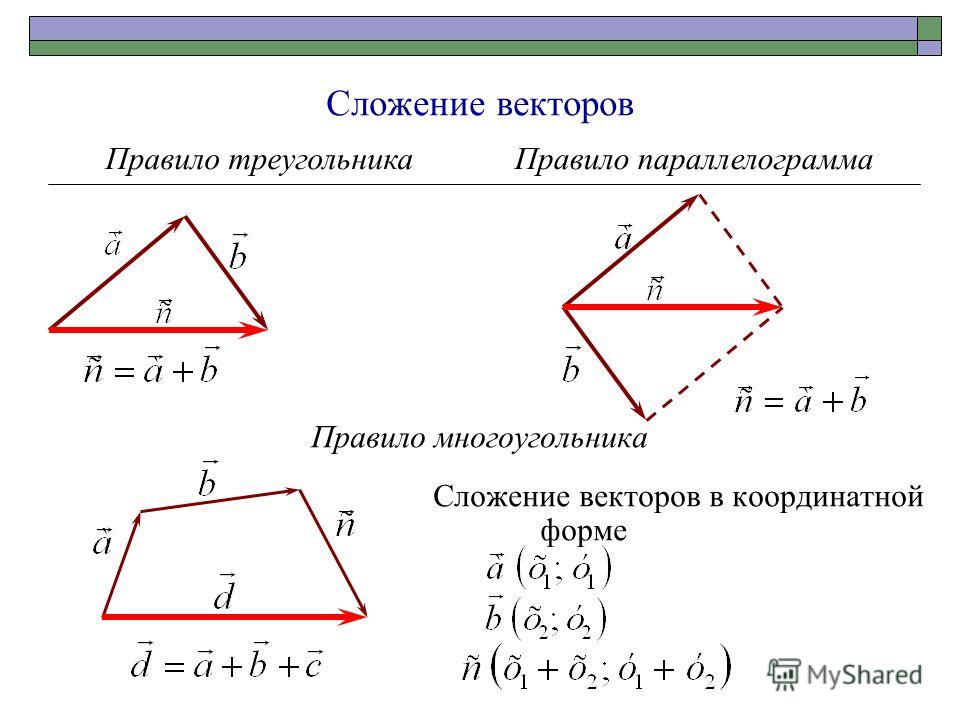
Правило треугольника.
АВ + ВС = АС
АS + SС =
АО + ОР = АР
NM + ML = NL
MN + NR = MR
RP + PR = RR = 0
MK + KM = MM = 0
ZK + KZ =
MK + OM = OM + MK
DE + KD = KD + DE =
= OK
АС
ZZ = 0
= KE
Правило треугольника.
АС = АВ + ВС
из ОВN
ON = OB + ВN
OB = ON + NВ
из ASR
AS = AR + RS
RA = RS + SA
из XKH
XH = XK + KH
KX = KH + HX
из АMD
MD = MA + AD
AD = AM + MD
из FPO
OP = OF + FP
FO = FP + PO
По правилу треугольника складываются и
коллинеарные векторы, хотя при их сложении
треугольника и не получается
b
a+b
a
b
a
b
a+b
a
f
c
c+ f
Законы сложения векторов
Теорема
Для любых векторов
1
2
a, b, c
a+b=b+a
справедливы равенства:
!
переместительный закон
(a + b) + c = a + (b + c)
сочетательный закон
!
Докажем свойство 1
Рассмотрим случай, когда векторы
a и b не коллинеарны.
В
b
b
a+b
А
a
a
D
из АВС
из АDС
b +a
АD + DС = a + b
АС = АВ + ВС =
АС =
C
При доказательстве свойства 10 мы обосновали
правило параллелограмма сложения неколлинеарных
векторов.
Чтобы применить
правило
параллелограмма,
надо отложить
векторы от одной
точки, как стрелки
часов.
11
12
1
10
2
3
9
4
8
7
6
5
Сложение векторов. Правило параллелограмма.
11
10
12
a
8
a
b
2
a+b
b
9
1
3
4
7
6
5
Докажем свойство 2
b
a
В
b
C
c
c
a
D
А
(a + b)+c
АC
= (АВ + ВС) + CD = АС + CD = АD
a + (b+c)
BD
= АВ + (ВС + CD) = АB + BD = АD
Сложение векторов.
Правило многоугольника.
АВ + ВС + СD + DO = АO
n
m
a
m
c
c
a
n
Правило многоугольника можно сформулировать также
следующим образом: если А1, А2, …, Аn – произвольные
точки плоскости, то А1А2 + А2А3 + … + Аn-1An = А1An
А6
А7
А1
А4
А5
А3
А2
!
Если начало первого вектора совпадает с концом
последнего вектора, то сумма данных векторов равна
1
2
3
4
5
нулевому вектору.
a +a +a +a +a
=0
a3
a3
a5
a2
a4
a4
a1
a2
a1
a5
a1 называется противоположным
вектору a, если векторы a и a1 имеют равные
Вектор
длины и противоположно направлены.
a1
a
А
-b
a1
-b, противоположный вектору b
Вектор
b
a = a1 ; a
А
Вектор ВА, противоположный
вектору АВ
ВА = – АВ
В
В
a + (-a) = 0
№ 766 На рисунке изображены векторы
a, b, c, d
ХУ. Представьте вектор ХУ в виде суммы остальных или им
противоположных векторов.
–b
–a
c
Х
d
–a–b+c+d=
ХУ
У
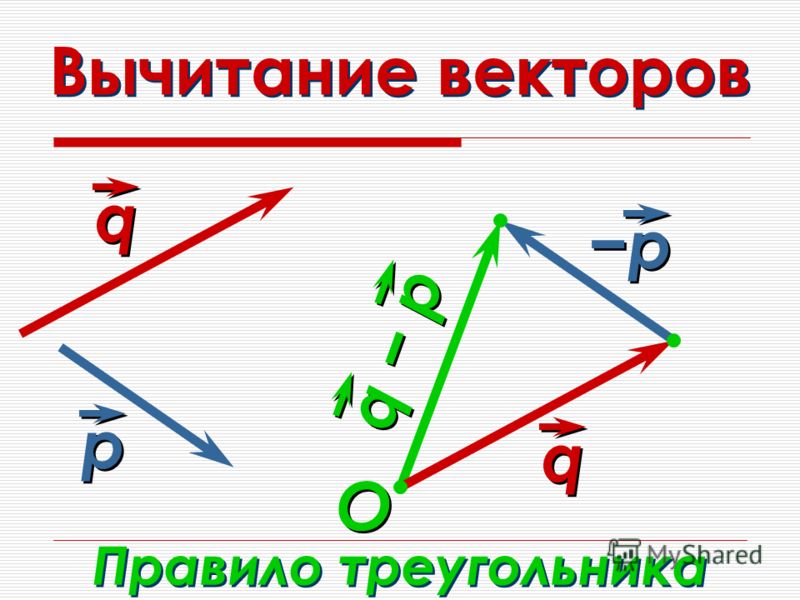
Вычитание векторов.
a – b = a +(–b)
-b
b
-b
a
a
a- b
Вычитание векторов.
MF — SF =
MF + FS = MS
RO — RM = RO + MR = MR + RO = MO
MD — SD =
MD + DS = MS
RO — AO = RO + OA = RA
RO — RO = RO + OR = RR = 0
— OS — ST =
SO + TS = TS + SO = TO
№ 768 Точки М и N – середины сторон АВ и АС
треугольника АВС. Выразите векторы ВМ, NC, MN, BN
через векторы
a = АМ
и
b = АN
В
М
a
ВМ =
-a
NC =
b
из AMN
MN = MA + AN =
А
b
N
С
-a + b
из ABN
BN = BA + AN =
-a-a + b
Найдите
АВ + AD – DC – OD
ABCD — прямоугольник
B
C
5
О
А
(
4
)
3
D
= АС – DC – OD = АС + CD + DO = АО
1
АО 5 2,5
2
АВ + ВС =
АS + SС =
АО + ОР =
NM + ML =
MN + NR =
RP + PR =
MK + KM =
ZK + KZ =
MK + OM =
DE + KD =
из ОВN
из ASR
из XKH
из АMD
из FPO
AS =
из ОВN
из ASR
RA =
XH =
из XKH
KX =
ON =
MD =
OP =
из АMD
из FPO
OB =
AD =
FO =

English     Русский Правила

Сложение и вычитание векторов

Материал урока.

Вспомним, как мы вводили понятие суммы двух векторов в планиметрии.

Сначала мы рассматривали такой пример.

Под действием воздушных масс воздушный шар сначала двигался из точки А в точку B, а затем из точки B переместился в точку C.

Каждое из этих двух перемещений можно представить в виде вектора.  и .

Но можно ведь сказать, что в результате воздушный шар из точки А попал в точку C. И это перемещение задает вектор .

Так как перемещение из точки А в C складывается из перемещений из точки А в B и из B в C, то можно записать, что вектор .

Этот пример подводит нас к понятию суммы двух векторов.

Рассмотрим два ненулевых вектора:  и .

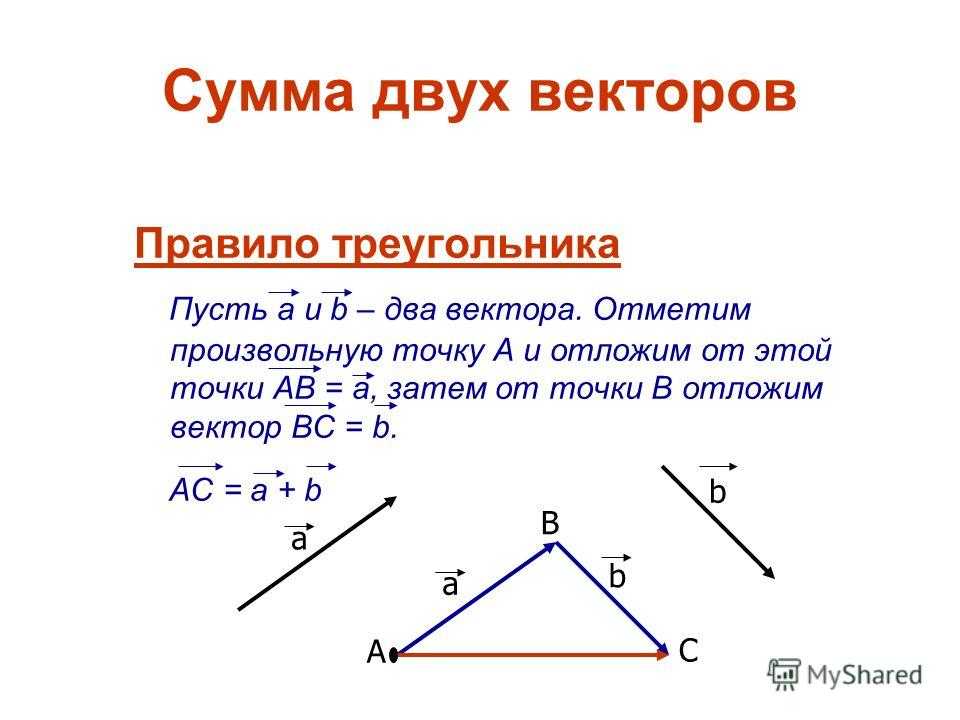
Отметим произвольную точку А и отложим от неё вектор , равный вектору . Далее от точки B отложим вектор , равный вектору .

Можем изобразить вектор , который называется суммой векторов  и .

Данное правило сложения векторов в пространстве, так же, как и в планиметрии, будем называть правилом треугольника.

Нужно отметить, что сумма векторов  и  не зависит от выбора точки А, от которой будет отложен вектор .

Докажем это.

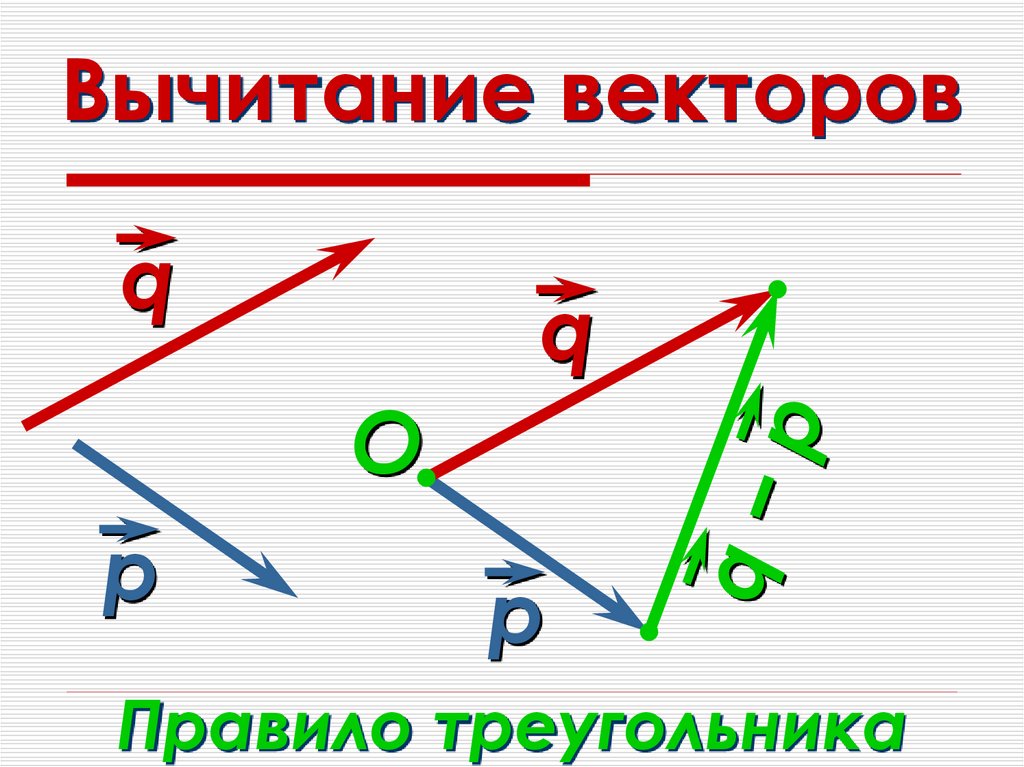
Найдём сумму векторов  и , но начнём откладывать их от некоторой точки А₁.

Нам необходимо доказать, что полученный вектор  равен вектору .

Из построений очевидно, что векторы  и  равны. А значит, они сонаправлены и равны по длине. То есть стороны AB и A₁B₁ четырёхугольника ABB₁A₁ параллельны и равны. И этот четырёхугольник является параллелограммом.

 

Стороны AA

1 и  BB₁ данного параллелограмма также равны и параллельны. Тогда получаем, равны векторы  и .

Аналогично, из равенства векторов  и  следует, что четырёхугольник BCC₁B₁ также является параллелограммом.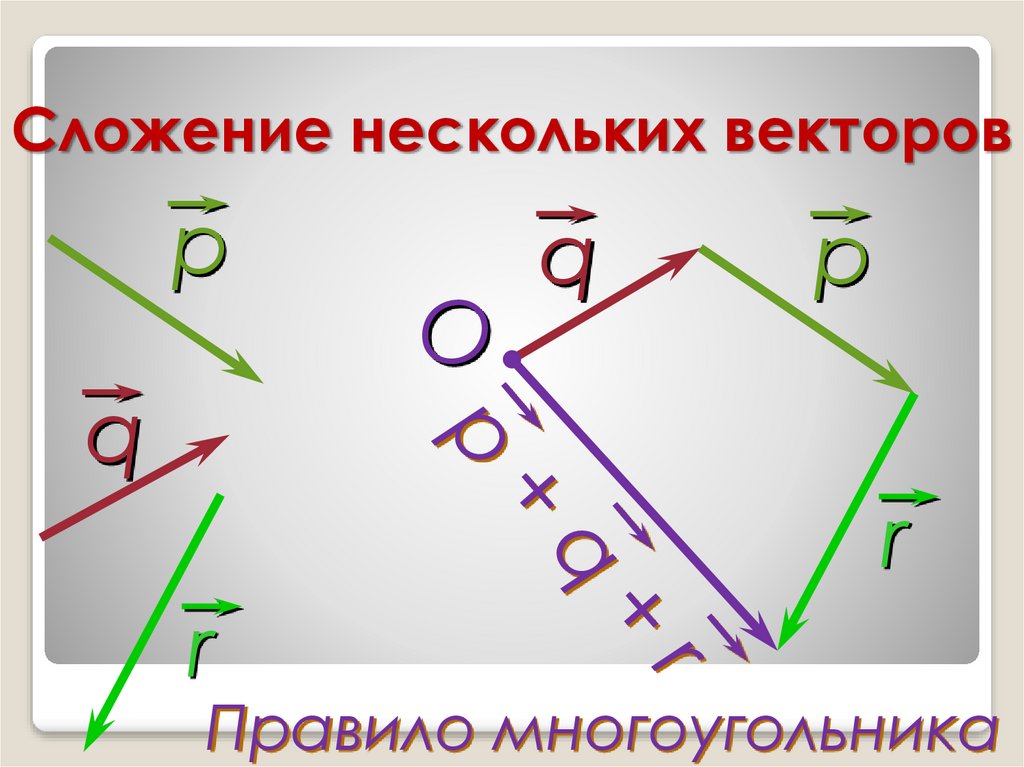 А значит, равны векторы  и .

Из полученных равенств получаем, что равны векторы  и .

Поэтому четырёхугольник AA₁C₁C — параллелограмм. Его стороны AC и A₁C₁ параллельны и равны. А значит, равны векторы  и .

Что и требовалось доказать.

Итак, в точности так же, как и на плоскости, мы ввели правило треугольника сложения двух векторов в пространстве. И доказали, что сумма векторов  и  не зависит от выбора точки А, от которой будет отложен вектор .

Для любых трёх точек пространства А, B и C правило треугольника можно сформулировать так: сумма векторов  и  равна вектору .

То есть даже не строя вектор суммы можно его найти. Если конец вектора, являющегося первым слагаемым, совпадаем с началом вектора, являющегося вторым слагаемым, то началом вектора суммы является начало первого вектора, а концом — конец второго вектора.

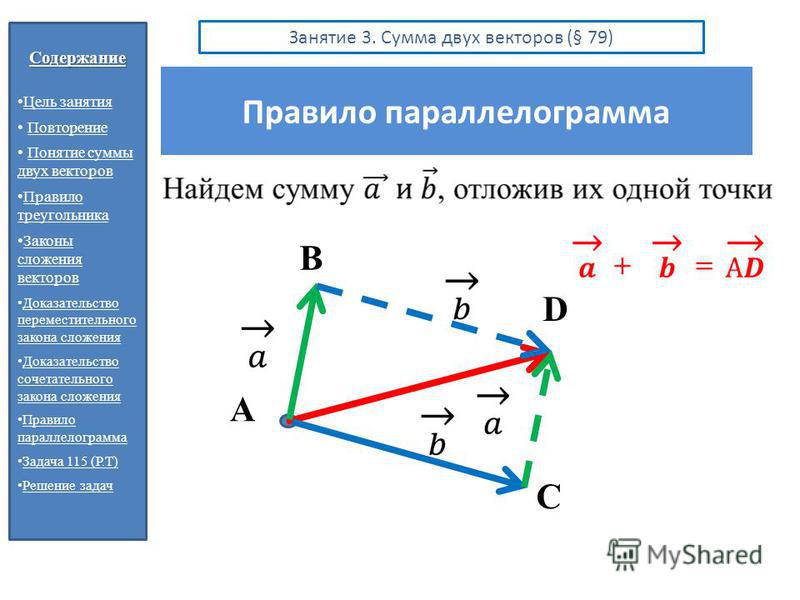
Так же для сложения двух векторов можно применять правило параллелограмма, которое мы уже формулировали в планиметрии. Вспомним его. От произвольной точки А отложим векторы  и , равные векторам  и соответственно.

Теперь на этих векторах построим параллелограмм ABCD. Вектор  является вектором суммы векторов  и .

Для любых векторов ,  и  действуют

переместительный и сочетательный законы сложения векторов.

Эти законы мы уже записывали и доказывали для векторов на плоскости.

Выполним задание.

На экране изображён параллелепипед ABCDA₁B₁C₁D₁.

Требуется назвать векторы, начало и конец которых совпадают с вершинами параллелепипеда, и которые равны соответствующей сумме векторов.

Первой рассмотрим сумму векторов  и

Чтобы сложить векторы по правилу треугольника, они должны быть отложены друг за другом, а чтобы воспользоваться правилом параллелограмма, они должны быть отложены от одной точки.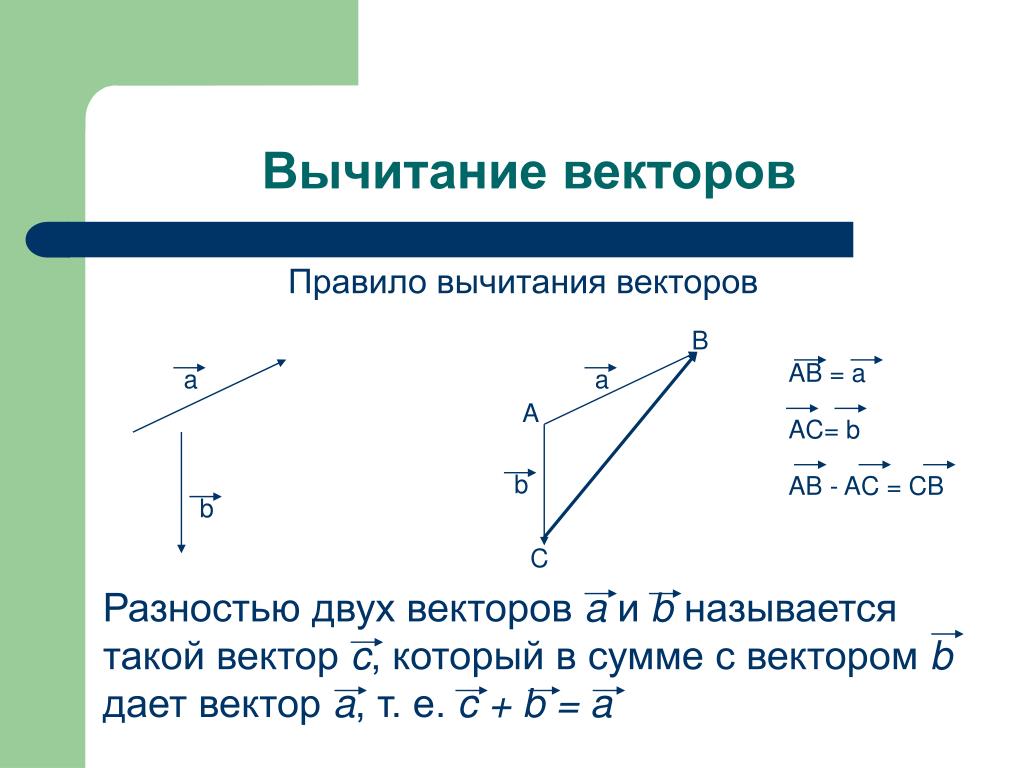

Данные векторы не подходят ни к одному правилу.

Но здесь нам поможет знание о том, что от любой точки пространства можно отложить вектор равный данному, и притом только один.

Так как перед нами параллелепипед и все его грани являются параллелограммами, то можно сказать, что есть вектор, который отложен от точки А и равен вектору  Напомним, что равными называются сонаправленные векторы, длины которых равны.

Вектор Ведь эти векторы лежат на противоположных сторонах параллелограмма, которые равны и параллельны.

От данной нам суммы перейдём к сумме векторов  и . Они отложены от одной точки, поэтому воспользуемся правилом параллелограмма. Если построить параллелограмм на этих векторах, то мы получим грань ABCD.

Диагональ AC и будет вектором суммы данных векторов.

Следующей рассмотрим сумму векторов  и .

Они уже отложены от одной точки, и на этих векторах можно построить параллелограмм ABC₁D₁.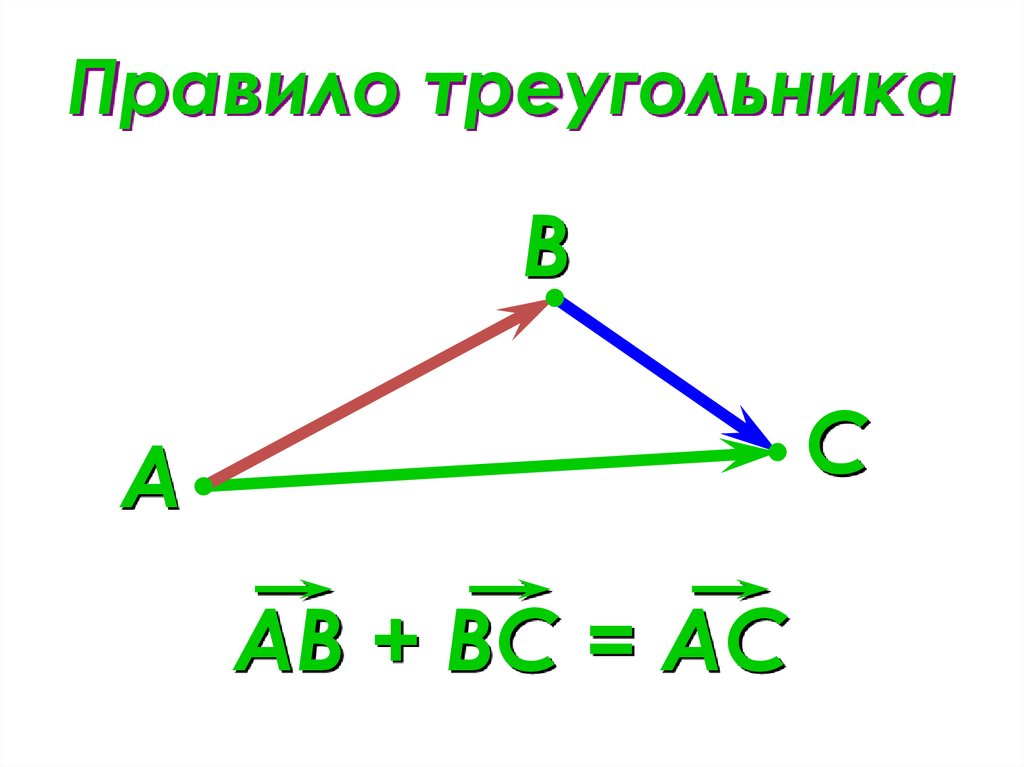 Диагональ AC₁ и будет являться вектором суммы.

Далее рассмотрим сумму векторов  и .

Вектор равен вектору . И перейдя к сумме векторов  и , не трудно заметить, что они отложены друг за другом, и именно поэтому можно применить правило треугольника. Вектор  — искомый.

Обратите внимание, пользуясь переместительным законом, можно записать, что сумма векторов  и ,  равна сумме векторов ,  и . Тогда по правилу треугольника сложения векторов для трёх произвольных точек пространства, можно сразу записать вектор суммы — . Так мы получили тот же вектор.

Теперь рассмотрим сумму векторов  и . Вектор  равен вектору . Векторы полученной суммы отложены друг за другом, поэтому вектором их суммы будет вектор .

Последней рассмотрим сумму векторов  и . Видим, что конец первого вектора в сумме совпадает с началом второго вектора.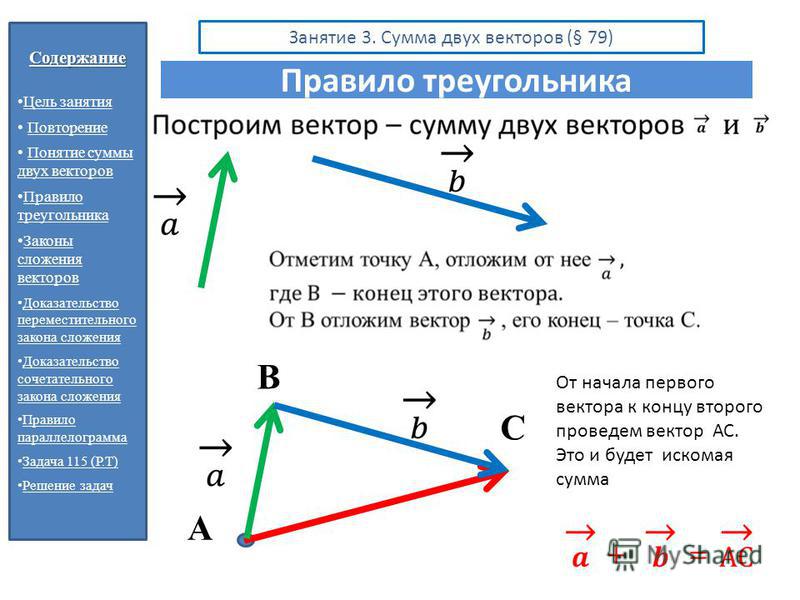 Тогда можно сразу сказать, что вектором суммы является вектор . Этот же результат мы получим, пользуясь рисунком.

Далее поговорим о разности векторов  и . Это такой вектор, сумма которого с вектором  равна вектору .

Проиллюстрируем это определение для данных векторов  и .

Итак, вектор должен являться суммой векторов  и . Тогда, отложив вектор  от начала вектора , мы без труда проведём вектор  из конца вектора  к концу вектора .

 

Действительно,  плюс  равно . А значит, вектор  равен разности векторов  и .

Таким образом, можно откладывать векторы уменьшаемое и вычитаемое от одной точки, а вектором разности будет являться вектор, направленный из конца вектора вычитаемого к концу вектора уменьшаемого.

Вы помните, что векторы называются противоположными, если их длины равны, а направления противоположны

Так вот если в данной иллюстрации у вектора  сменить направление, то есть заменить его на «», то мы получим, что вектор  равен разности векторов  и , а также, по правилу треугольника, сумме векторов  и «».

Так мы получили два способа построения вектора разности.

Рассмотрим тот же параллелепипед, что и в предыдущей задаче.

Нужно назвать векторы, начало и конец которых совпадают с вершинами параллелепипеда, и которые равны соответствующей разности векторов.

Найдём вектор разности векторов  и .

Они отложены от одной точки, поэтому вектором разности будет являться вектор, направленный из конца вектора-вычитаемого  к концу вектора-уменьшаемого . Так получаем вектор .

Применим второй способ построения вектора разности.

Нам известно, что разность векторов можно представить в виде суммы вектора уменьшаемого и вектора, противоположного вектору вычитаемому. Вектором противоположным вектору  является вектор . По правилу треугольника сложения двух векторов мы также получим вектор .

Далее рассмотрим разность векторов  и .

Они отложены от одной точки. и поэтому вектор разности будет направлен из конца вектора-вычитаемого  к концу вектора-уменьшаемого . Таким образом мы получим вектор .

Последней рассмотрим разность векторов  и . Вектор  заменим равным ему вектором . А разностью векторов  и  будет вектор . В результате и разность векторов  и  равна вектору .

Подведём итоги нашего урока.

В точности так же, как и на плоскости, на этом уроке мы с вами сформулировали правило треугольника и правило параллелограмма сложения двух векторов в пространстве, а также записали переместительный и сочетательный законы сложения векторов.

Убедившись в том, что разность векторов  и  равна сумме вектора  и вектора, противоположного вектору , мы получили два способа построения вектора разности двух векторов.

Так мы рассмотрели сложение и вычитание векторов в пространстве.

Урок 22: Сложение и вычитание векторов

Во многих вопросах вам будет предложено сложить два или более векторов.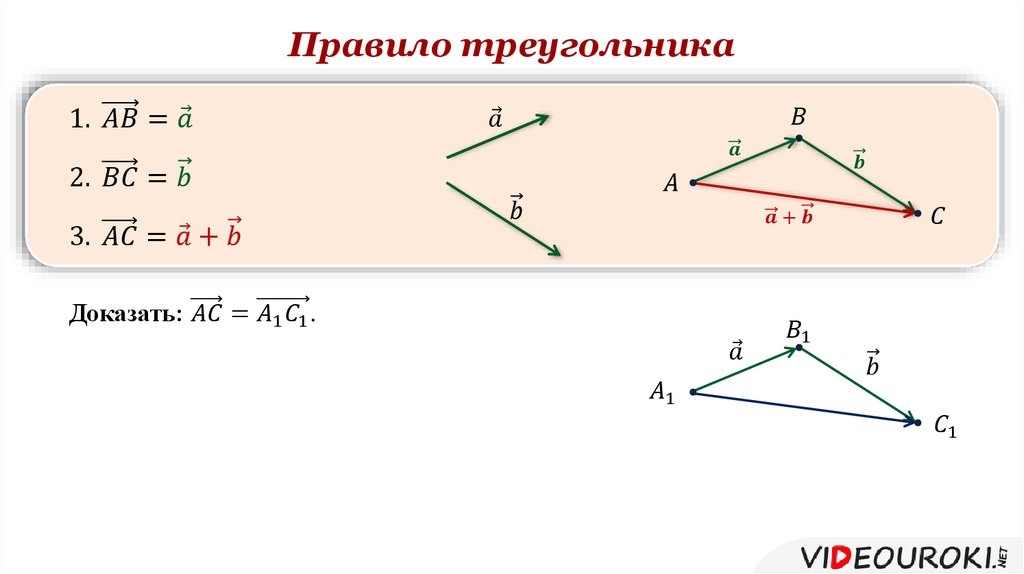

• Ваша первая реакция может состоять в том, чтобы просто взять два числа и сложить их (как если бы вы сложили 3 + 2 = 5).
• Вы абсолютно точно можете , а не сделать это!!! Вы должны помнить, что векторы большую часть времени будут указывать в разных направлениях под странными углами. Вы должны «сложить» их с помощью тригонометрии и указать направление в конце.

Сложение A + B

Давайте рассмотрим очень простой пример сложения векторов. Пока у нас даже не будет никаких чисел, мы просто нарисуем векторы с именами A и B.

Рисунок 1

Если бы вас попросили сложить A и B, вам нужно было бы сначала расположить их в виде диаграммы, показывающей A + B.

• Вы можете брать и перемещать векторы, пока они остаются одного размера и указывают в одном направлении.
• Добавляемые векторы всегда должны соприкасаться головой к хвосту.
• Вы должны быть в состоянии начать с конца первого вектора и следовать направлениям стрелок, пока не доберетесь до начала последнего.
  • Я часто предлагаю людям смотреть на это как на игру в Pac Man (я знаю, я стар!), и что Pac Man может двигаться только в направлении, указанном стрелками.

Если мы будем следовать этим правилам и начертим A + B, мы должны получить что-то похожее на это…

Рис. следуйте за ним до головы.

Я также нарисовал равнодействующую (помните ее из прошлого урока?), которая касается хвост к хвосту и голова к голове. Результирующее действительно равно тому, чему равны A + B.

Добавление B + A

Удивительный вопрос теперь должен звучать так: «Получите ли вы тот же ответ, если вы добавите B + A?»

• Быстрый ответ: «Да!» так как вы можете добавлять векторы в любом порядке и получать тот же ответ.
• В математике с обычными скучными старыми числами вы определенно можете сказать A + B = B + A… неважно, в каком порядке вы складываете числа.
  • Это называется коммутативным свойством.
• Диаграмма будет выглядеть немного по-другому, но результат будет таким же, как и выше в Рисунок 2 . Взгляните на Рисунок 3 ниже, который показывает это.

Рисунок 3

• Здесь показано B + A, потому что мы начинаем с B, который указывает на A, и продолжается до конца.
• Даже если мы проследим от хвоста равнодействующей (B + A) к ее голове, мы все равно придем к тому же месту в конце.

Это означает, что вы можете добавлять векторы в любом порядке. Вы можете измерить другой угол, чем кто-то другой, поскольку ваша диаграмма отличается, и вы собираетесь использовать другие точки отсчета.

• Это как в прошлом уроке, где мы видели, что [N30°E] — это то же самое, что сказать [E60°N].

Вычесть A — B

Здесь все становится немного интереснее.

• Здесь нам нужно помнить, что в физике отрицательный знак просто означает «в противоположном направлении».
• Мы можем взять A — B и просто заменить его на A + -B
• Знак «минус» у B просто означает, что нам нужно взять исходный вектор B и направить его точно в противоположном направлении (на 180° от того места, где он указывает прямо сейчас).
• Затем мы просто добавим их, как мы это делали на предыдущих диаграммах (соприкасаясь, конечно, лицом к хвосту!)

Рисунок 4

Вы можете видеть, что результат, который мы получаем, отличается от показанного в Рисунок 2 и 3 .

• Также будьте осторожны, вычитание не коммутативно (это просто означает, что A — B ≠ B — A).

Решение прямоугольных (90°) треугольников

Большинство треугольников, с которыми вы будете иметь дело, будут прямоугольными.

• Если они есть, просто используйте свою обычную триггерную систему (SOH CAH TOA) и пифагоров (c ² = a ² + b ² ).
• Обычно вам нужно думать о физике, когда вы настраиваете свою диаграмму (так, чтобы все указывало в лоб и все такое), а затем переключаетесь на решение этой задачи, как в любой математической задаче на триггер.s

Пример 1: Автомобиль проезжает 10 км [E], а затем 7 км [N]. Определить его водоизмещение.

Сначала нарисуйте правильную схему:

Обратите внимание, как это показывает, что векторы добавляются в правильном порядке в соответствии с вопросом.

• 10 км [E] показаны впереди 7 км [N]. Начните с хвоста красной стрелки и следуйте по пути, по которому она вас ведет.
• Если вы добавите к ним 7 км [N], а затем 10 км [E], вы все равно получите тот же окончательный ответ, только с другим углом из-за другой точки отсчета.

Это определенно прямоугольный треугольник, поэтому просто используйте c ² = a ² + b ² , чтобы узнать величину ( размер ) равнодействующей.

• Попробуйте сами и посмотрите, получите ли вы около 12.21 (здесь я не слишком осторожен с моими раскопками!)

Угол, который мы должны измерить, находится в левом нижнем углу.

Как подсказка, вам, вероятно, следует использовать загар, чтобы определить этот угол. Использование sin или cos потребует использования только что вычисленного результата. Если вы ошибетесь в результате, вы также ошибетесь в своем угле.

• Традиционно вы измеряете от начала равнодействующей до ее хвоста.
• Это также дает нам хорошую опорную линию, так как мы сможем сказать, на сколько градусов к северу от востока мы находимся.
• Попробуйте подсчитать и посмотрите, получилось ли около 35°.

Добавление треугольников, которые не являются прямыми углами

Если треугольник не является прямым углом, у вас есть два варианта:

1. Используйте закон косинусов или закон синусов, чтобы выяснить это.
   Это метод « сложных вычислений, если вы еще не сделали этого много в математике «. Если вы не знакомы с ними, нажмите здесь, чтобы посмотреть короткое видео, в котором я рассказываю вам об основах их использования.
2. Разбейте его на горизонтальные и вертикальные компоненты, затем используйте базовый триггер.
   Это требует больше вычислений, но каждое вычисление меньше. Подробнее об этом после того, как мы рассмотрим следующий урок… а пока просто держите это в голове.

Определение, формула, правила и примеры

Возможно, мы этого не осознаем, но каждый день мы что-то добавляем. Мы делаем это, когда идем в продуктовый магазин, чтобы купить что-то, мы делаем это, когда добавляем ингредиенты в еду во время приготовления пищи и даже когда играем с друзьями. Это часть нашей повседневной жизни, и ее также можно применять к более сложным вещам, таким как векторы.

В этой статье мы узнаем о векторах и различных способах добавления векторов.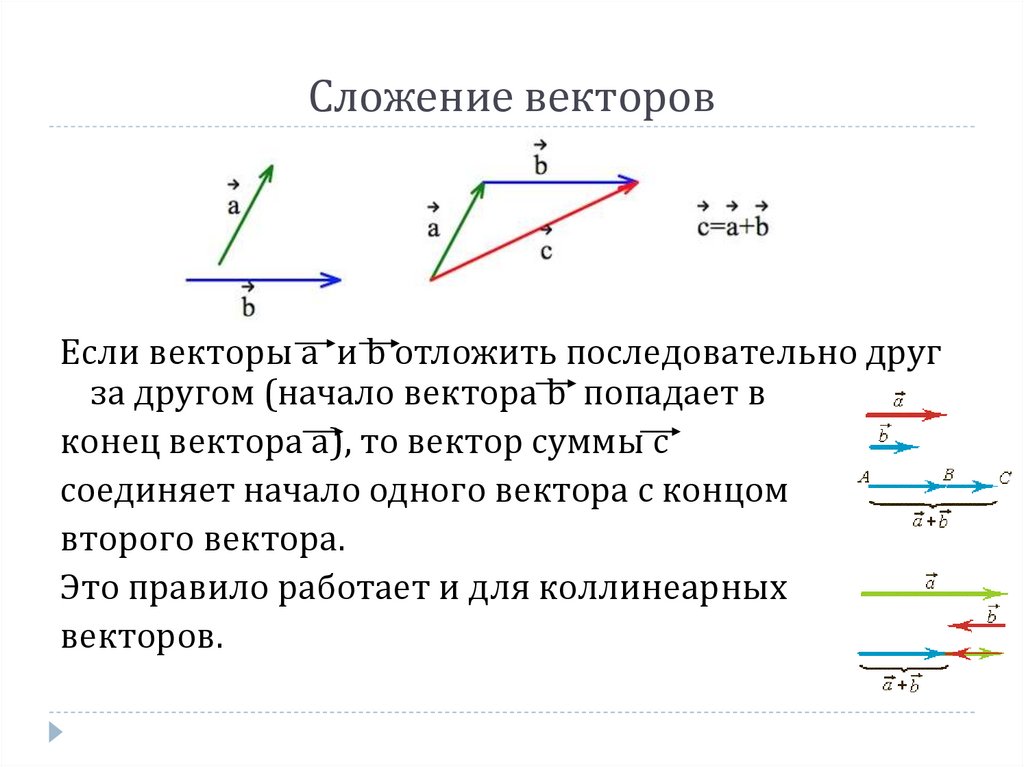

Определение сложения векторов

Добавление векторов можно определить как процедуру добавления двух или более векторов.

Вектор, образованный сложением векторов, называется результирующим вектором и обычно обозначается как r⇀ . Способ добавления этих векторов может различаться в зависимости от того, заданы ли они в виде точек или в геометрическом представлении. Хотя сложение можно выполнить с помощью математики для точек, практично использовать закон параллелограмма, когда они представлены геометрически.

Формула векторного сложения

Предположим, что A и B являются точками на плоскости с их координатами, заданными как A=(a1,a2) и B=(b1,b2) соответственно. Тогда формула сложения векторов для A⇀+B⇀ может быть записана как:

A⇀+B⇀=(a1+b1,a2+b2)

Свойства сложения векторов

Коммутативность : Изменение порядка векторов не меняет сумму. A+B=B+A

Ассоциативность: Изменение группировки дополнений не меняет сумму.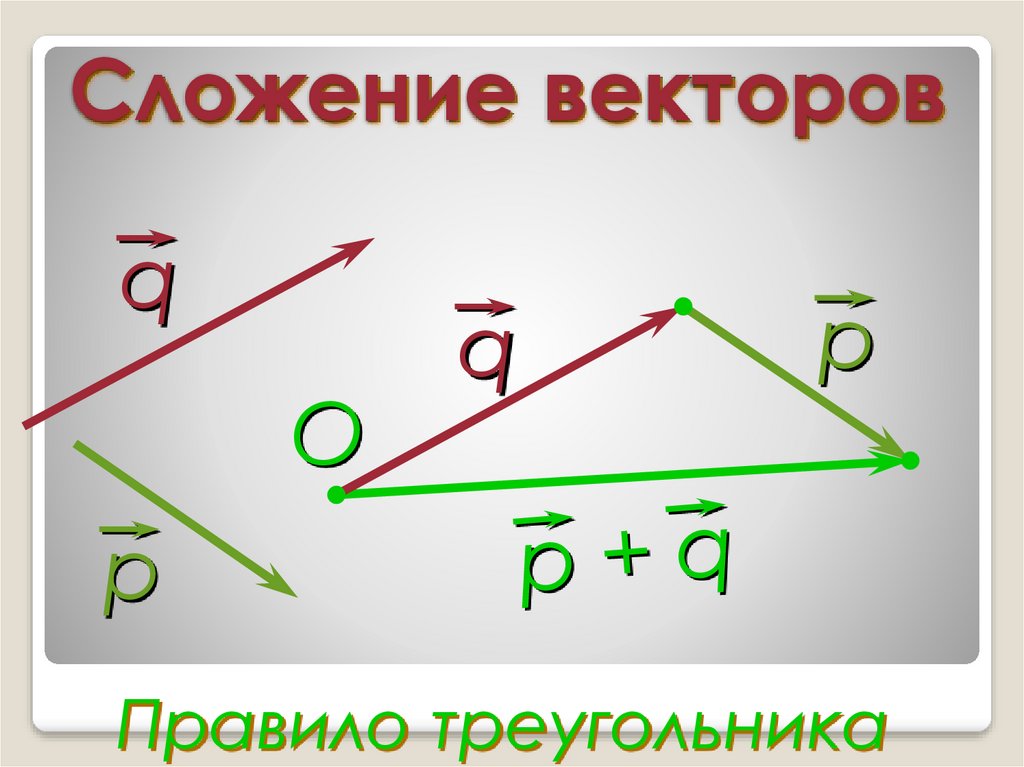 А+(В+С)=(А+В)+С

Нулевой элемент: Добавление точки с нулем равно точке. Если нулевой элемент равен O=(0,0), то A+O=A

Обратный аддитив: Если точка A есть A=(a1,a2), то ее обратный равен -A=(- а1,-а2). Когда эти векторы складываются, в результате получается ноль.

A+(-A)=(a1,a2)+(-a1,-a2)=(a1-a1,a2-a2)=(0,0)

Графическое сложение векторов

Как сложение векторов будет выполняться графически? Ниже приведены различные методы.

Треугольный закон сложения векторов

Треугольный закон сложения векторов. Он также известен как метод «голова к хвосту» , потому что головы и хвосты задействованных векторов помещаются друг на друга при попытке найти их сумму. На рисунке ниже показано, как выглядят голова и хвост вектора.

Рис.1 Показ головы и хвоста вектора

Давайте посмотрим, как используется этот закон. Рассмотрим векторы A и B ниже.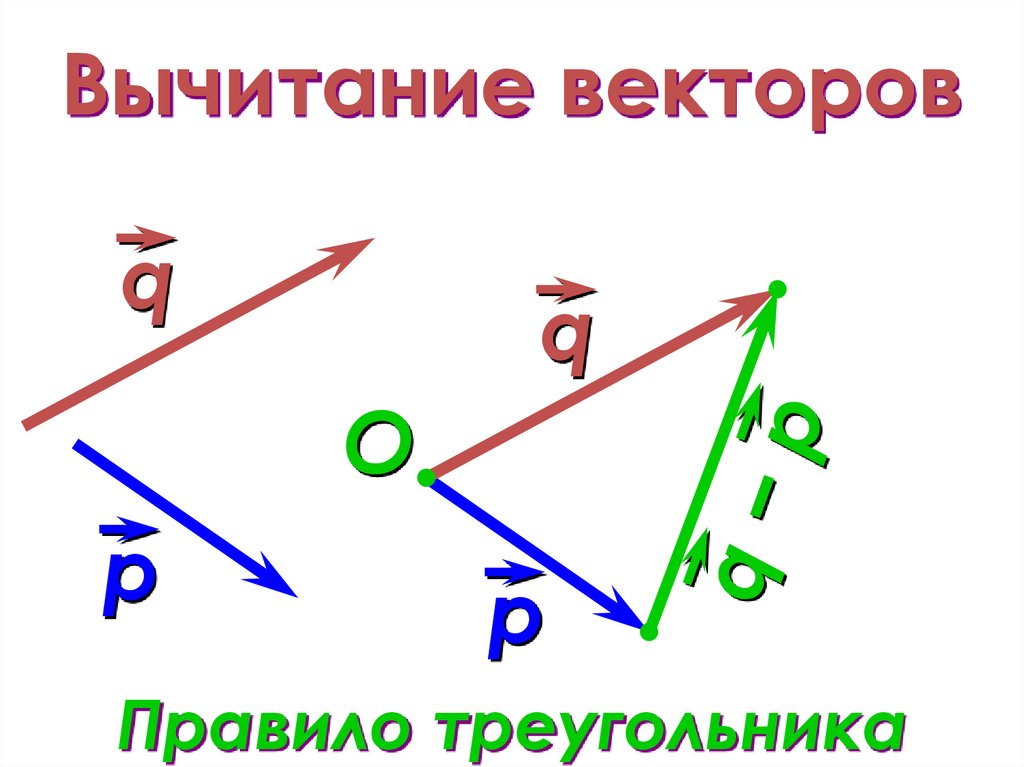

Рис.2 Два вектора A и B

Чтобы сложить два вектора прямым методом, выполните следующие действия.

1. Поместите конец второго вектора на начало первого вектора.
2. Чтобы найти сумму, нарисуйте результирующий вектор, чтобы соединить конец первого вектора с головой второго вектора.

Рис.3 Сложение двух векторов

На рисунке выше A⇀+B⇀=C⇀.

Если есть третий вектор, вы продолжаете размещать хвост третьего вектора на голове второго вектора. Результирующий вектор будет нарисован так, чтобы соединить хвост первого вектора с головой второго вектора.

Вектор можно перемещать вдоль своей плоскости до тех пор, пока длина/направление не меняются.

Закон сложения векторов в виде параллелограмма

Согласно закону параллелограмма, если два вектора можно представить как две смежные стороны, исходящие из общей вершины, а затем дополнить их так, как если бы они образовывали параллелограмм, то результирующий вектор можно найти из диагонали этого параллелограмма.

Чтобы найти u→+w→:

1. Сложите хвосты векторов вместе

2. Завершите параллелограмм, нарисовав две параллельные стороны.

3. После завершения параллелограмма нарисуйте диагональ, начинающуюся с вершины исходных векторов, как показано на рисунке ниже.

Рис.4. Сложение двух векторов

Закон параллелограмма также можно использовать, когда заданы векторы, определенные как координаты.

Для точек A=(2,3) и B=(1,3) сумму можно найти по закону параллелограмма, показанному на рис. 2.

Вычитание вектора

Чтобы понять вычитание, нужно сначала понять, что такое отрицательное значение вектора. Допустим, есть вектор A. Отрицательное значение этого вектора определяется как -A. Отрицательный вектор вектора А имеет ту же величину, что и вектор А, однако они направлены в противоположные стороны.

Рис. 6 Разница между вектором A и отрицательным значением вектора A

Закон параллелограмма для векторного вычитания

Чтобы найти u→-w→, его следует представить как u→+(-w→).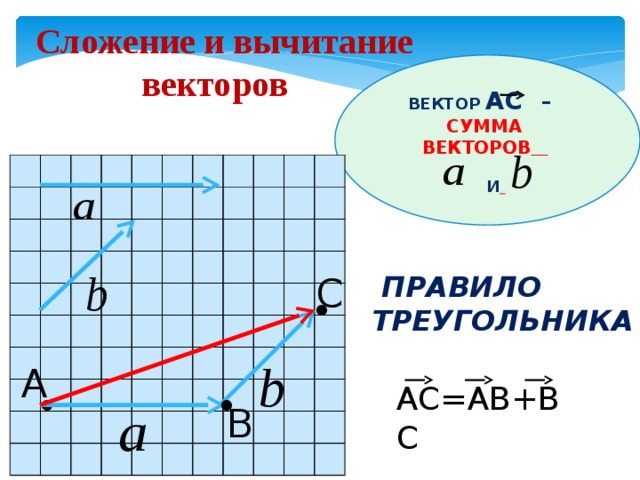 Имея это в виду, мы получаем цифру ниже:

Рис.7 Закон параллелограмма для вычитания векторов

Примеры сложения векторов

Рассмотрим несколько примеров.

Если A=(2,4) и B=(-2,5) — две векторные точки, какова сумма векторов?

Ответ.

Формула сложения векторов:

A+B=(a1+b1,a2+b2)

Приведены баллы A=(2,4) и B=(-2,5)

From набрано очков:

a1=2a2=4b1=-2b2=5

Подставив в формулу сложения векторов, получим:

A+B=(2+(-2),4+5)=(0,9)

Если A=(1,7) и B=(5,-7) — две точки вектора, найдите сумма векторов.

Ответ.

Полученные баллы:

A=(1,7)B=(5,-7)

Формула сложения векторов:

A+B=(a1+b1,a2+b2)

Из точек имеем:

a1=1a2=7b1=5b2=-7

Применяя формулу сложения векторов:

A+B=(1+5,7+(-7))=(6,0)

Возьмем другой пример.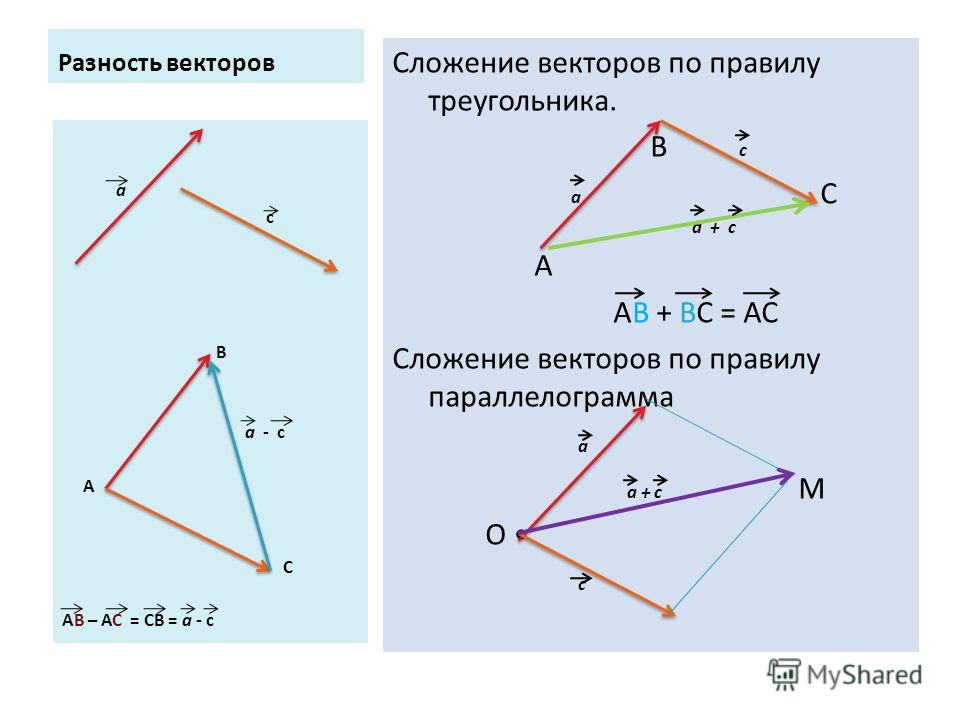

Игрушечная машинка переместилась на 10 см на восток и на 24 см на север. Используя закон треугольника, найдите результирующий вектор двух векторов.

Ответ.

У нас есть два вектора величиной 10 см и 24 см. Назовем их A и B.

A→=10смB→=24см

Направление A→ — это восток, а направление B→ — север. Таким образом, мы имеем:

Рис. 8

Обратите внимание, что хвост второго вектора расположен на голове первого вектора, как и говорит закон. Чтобы найти результирующий вектор, мы завершим треугольник, нарисовав линию, соединяющую хвост первого вектора с головой второго вектора, а затем добавим обе величины.

Обозначим результирующий вектор C.

Рис. 9

Результирующий вектор:

C→=10см+24см=34см

Возьмем другой пример.

Рассмотрим векторы A→=5см в восточном направлении, B→=4см в северном направлении и C→=7см в восточном направлении. Используя правило треугольника, найдите результирующий вектор.

Ответы.

Во-первых, нам нужно нарисовать векторы в соответствии с их направлениями. При этом имейте в виду, что хвост одного вектора должен располагаться над головой другого вектора.

Рис. 10

Как видно из рисунка выше, хвост второго вектора помещается на голову первого вектора, а хвост третьего вектора — на голову второго вектора.

Результирующий вектор будет суммой величин всех векторов.

Рис. 11

Чтобы найти результирующий вектор, была проведена линия, соединяющая хвост первого вектора с головой третьего вектора. результирующий вектор:

C→=5см+4см+7см=16см

Рис. 12

Используя рисунок выше, найдите векторы A→+B→,B→+C→, A→-B→ и B→-C→ по закону параллелограмма.

Решение

• Чтобы найти A→+B→, можно применить закон параллелограмма, как показано на рисунке. Диагональ параллелограмма представляет собой сумму векторов, как на рисунке ниже.

  No related posts.