Векторы — что это, определение и ответ
ОСНОВНЫЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
Вектор – отрезок, у которого есть начало и конец, то есть указано его направление.
Вектор обозначается через точки начала и конца вектора, например \(\overrightarrow{АВ}\) (первая буква – начало вектора, вторая – конец) или, если мы хотим обозначить вектор без указания точек, пишем просто \(\overrightarrow{a}\).
Точка тоже может быть вектором, в таком случае вектор называют нулевым, т.к. его началом и концом является одна и та же точка. Обозначаем нулевой вектор как, например, \(\overrightarrow{\text{MM}}\) или \(\overrightarrow{0}\).
Длина или модуль вектора – это длина отрезка (как если бы у него не было направления).
Длина вектора \(\overrightarrow{АВ}\) обозначается как \(\left| \overrightarrow{АВ} \right|\), длина вектора \(\overrightarrow{a}\ \)как \(\left| \overrightarrow{a} \right|\), а длина нулевого вектора всегда равна нулю:
\(\left| \overrightarrow{АВ} \right| = 7\)
\(\left| \overrightarrow{a} \right| = 3\)
\(\left| \overrightarrow{\text{MM}} \right| = \left| \overrightarrow{0} \right| = 0\)
РАСПОЛОЖЕНИЕ ВЕКТОРОВ
Коллинеарные векторы – это векторы, которые лежат на параллельных прямых или на одной прямой. Нулевой вектор коллинеарен любому вектору.
Нулевой вектор коллинеарен любому вектору.
Сонаправленные векторы – это коллинеарные векторы, которые направлены в одну сторону.
Обозначается как \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) (вектор \(\overrightarrow{a}\) сонаправлен вектору \(\overrightarrow{b}\))
Противоположно направленные векторы – это коллинеарные векторы, которые направлены в противоположные стороны.
Обозначаются как \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}\) (вектор \(\overrightarrow{a}\) противоположно напрвлен вектору \(\overrightarrow{b}\))
Равные векторы – это сонаправленные векторы, у которых равны длины, т.е. у них одинаковые и направление, и длина.
Например:
\(\overrightarrow{АВ}\) и \(\overrightarrow{a}\) – коллинеарны, при этом противоположно направлены, т.к. лежат параллельных прямых и направлены в разные стороны:
\(\overrightarrow{АВ} \uparrow \downarrow \overrightarrow{a}\)
\(\overrightarrow{\text{CD}}\) и \(\overrightarrow{b}\) – коллинеарны, при этом сонаправлены, т.
 к. лежат параллельных прямых и направлены в одну сторону:
к. лежат параллельных прямых и направлены в одну сторону:
\(\overrightarrow{\text{CD}} \upuparrows \overrightarrow{b}\)
\(\overrightarrow{\text{CD}}\) и \(\overrightarrow{b}\) – равны, т.к. сонаправлены (из п.2) и равны по модулю:
\(\left. \ \frac{\overrightarrow{\text{CD}} \upuparrows \overrightarrow{b}}{\overrightarrow{\left| \text{CD} \right|} = 5 = \left| \overrightarrow{b} \right|} \right\} \Longrightarrow \overrightarrow{\text{CD}} = \overrightarrow{b}\)
\(\overrightarrow{М}\) коллинеарен всем векторам, и может являться им как сонаправленным, так и противоположно направленным, т.к. \(\overrightarrow{М} = \overrightarrow{0}\).
СВОЙСТВА НЕНУЛЕВЫХ КОЛЛИНЕАРНЫХ ВЕКТОРОВ:
\(\left. \ \frac{\overrightarrow{a} \upuparrows \overrightarrow{b}}{\overrightarrow{b} \upuparrows c} \right\} \Longrightarrow \overrightarrow{a} \upuparrows \overrightarrow{c}\)
Если \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) и \(\overrightarrow{b} \upuparrows c\), то \(\overrightarrow{a} \upuparrows \overrightarrow{c}\)
\(\left.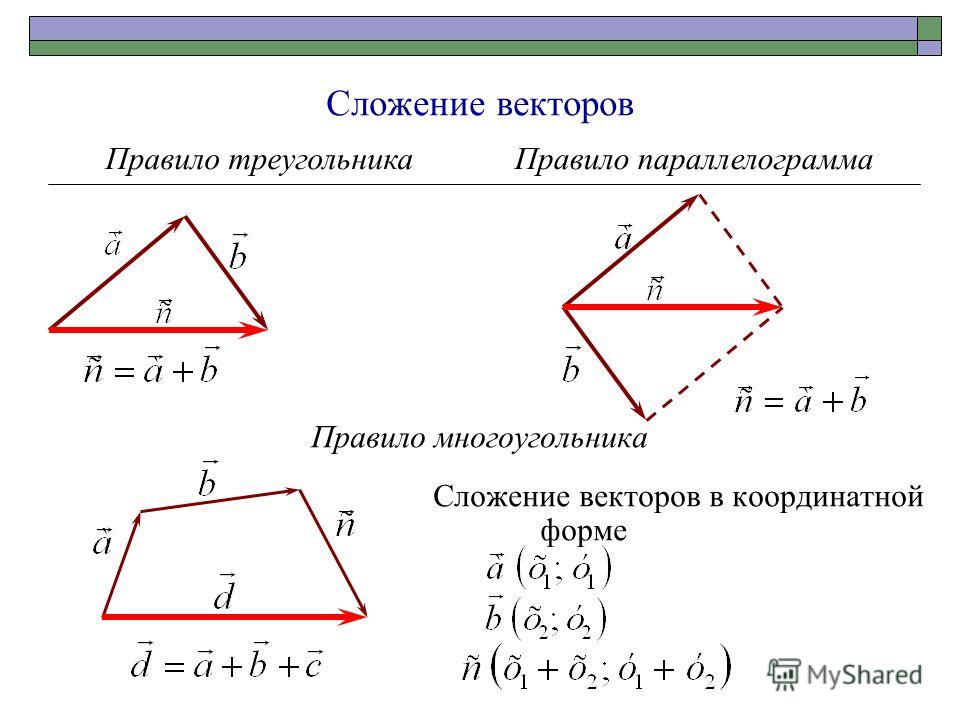 \ \frac{\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}}{\overrightarrow{b} \uparrow \downarrow c} \right\} \Longrightarrow \overrightarrow{a} \upuparrows \overrightarrow{c}\)
\ \frac{\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}}{\overrightarrow{b} \uparrow \downarrow c} \right\} \Longrightarrow \overrightarrow{a} \upuparrows \overrightarrow{c}\)
Если \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}\) и \(\overrightarrow{b} \uparrow \downarrow c\), то \(\overrightarrow{a} \upuparrows \overrightarrow{c}\)
\(\left. \ \frac{\overrightarrow{a} \upuparrows \overrightarrow{b}}{\overrightarrow{a} \uparrow \downarrow \overrightarrow{c}} \right\} \Longrightarrow \overrightarrow{b} \uparrow \downarrow \overrightarrow{c}\)
Если \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) и \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{c}\), то \(\overrightarrow{b} \uparrow \downarrow \overrightarrow{c}\)
ОТКЛАДЫВАЕНИЕ ВЕКТОРА ОТ ТОЧКИ:
Говорят, что вектор отложен от точки, если она является его началом. Например, \(\overrightarrow{АВ}\) отложен от точки А, \(\left| \text{CD} \right|\) отложен от точки С и так далее.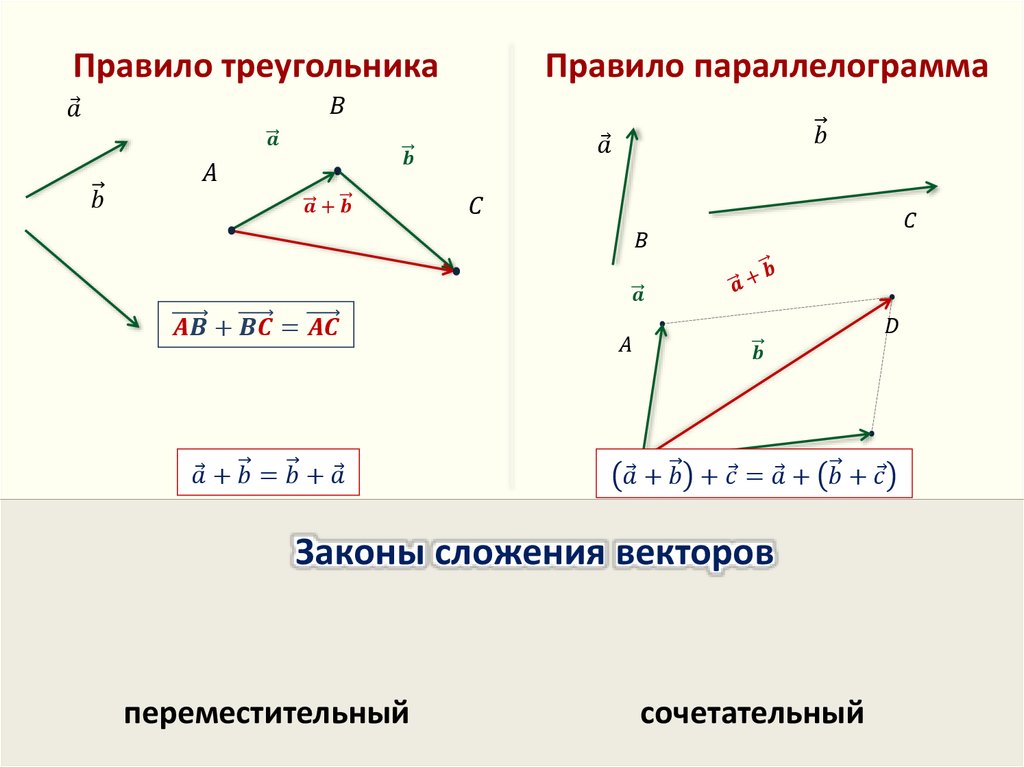 Можно откладывать абсолютно любые векторы абсолютно из любых точек. Это описывается следующим правилом:
Можно откладывать абсолютно любые векторы абсолютно из любых точек. Это описывается следующим правилом:
От любой точки можно отложить вектор, равный данному и при том только один.
Например, возьмем точку М и два вектора \(\overrightarrow{a}\) и \(\overrightarrow{b}\). Мы можем отложить от точки М вектора, равные \(\overrightarrow{a}\) и \(\overrightarrow{b}\) всего один раз. Делается это параллельным переносом:
Таким образом \(\overrightarrow{a} = \overrightarrow{a’}\), и \(\overrightarrow{b} = \overrightarrow{b’}\), при этом \(\overrightarrow{a’}\ и\ \overrightarrow{b’}\) отложены от точки М.
СЛОЖЕНИЕ ВЕКТОРОВ:
При сложении векторов нужно учитывать их направления, поэтому проще всего складывать вектора визуально. Существуют два самых простых способа сложить два вектора – это правило треугольника и правило параллелограмма.
ПРАВИЛО ТРЕУГОЛЬНИКА
Если нужно найти сумму двух векторов, по правилу треугольника нужно:
Параллельным переносом перенести начало одного вектора в конец другого.

Пусть эти векторы будут сторонами треугольника, тогда третья его сторона – их сумма.
Обозначить направление получившегося вектора суммы – от начала первого вектора в конец второго (стрелка к стрелке).
Пример №1:
Найдите сумму векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) по правилу треугольника:
Перенесем вектор \(\overrightarrow{b}\) так, чтобы он начинался там, где заканчивается вектор \(\overrightarrow{a}\).
Соединим эти векторы в треугольник, третьей стороной которой будет вектор \(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}\).
Направление вектора \(\overrightarrow{c}\) будет идти от начала \(\overrightarrow{a}\) до конца \(\overrightarrow{b}\) (стрелка к стрелке)
ПРАВИЛО ПАРАЛЛЕЛОГРАММА:
Если нужно найти сумму двух векторов, по правилу параллелограмма нужно:
Параллельным переносом перенести начала этих векторов в одну точку.

Пусть эти векторы будут сторонами параллелограмма, тогда диагональ этого параллелограмма – их сумма.
Обозначить направление получившегося вектора суммы – от начала векторов в противоположный конец параллелограмма (по диагонали).
Пример №2:
Найдите сумму векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) по правилу параллелограмма:
Перенесем оба вектора параллельным переносом так, чтобы они начинались из одной точки.
Представим, что они являются сторонами параллелограмма.
Диагональ этого параллелограмма, которая начинается в точке начала векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) – это вектор \(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}\).
СВОЙСТВА СЛОЖЕНИЯ ВЕКТОРОВ:
Переместительное свойство:
\(\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}\)
Сочетательное свойство:
\((\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c})\)
СЛОЖЕНИЕ НЕСКОЛЬКИХ ВЕКТОРОВ:
Чтобы сложить несколько векторов, нужно ставить их друг за другом, сохраняя их направление (используя параллельный перенос), тогда их суммой будет являться вектор, начала которого – это начало первого вектора, а конец – конец последнего вектора (как в правиле треугольника).
Пример №3:
Найдите сумму векторов \(\overrightarrow{a}\), \(\overrightarrow{b}\), \(\overrightarrow{c}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\):
Поставим эти векторы как бы по порядку сохраняя их длину и направление. По переместительному свойству неважно, в каком порядке мы будем располагать вектора. Соединим их, например, в таком порядке — \(\overrightarrow{d}\), \(\overrightarrow{e}\), \(\overrightarrow{b}\), \(\overrightarrow{c}\), \(\overrightarrow{a}\).
Проведем вектор их суммы от начала первого вектора в конец второго:
ВЫЧИТАНИЕ ВЕКТОРОВ:
Вычесть вектор – это то же самое, что прибавить отрицательный вектор:
\(\overrightarrow{a}\ –\ \overrightarrow{b} = \overrightarrow{a} + (–\overrightarrow{b})\)
То есть и при вычитании можно использовать правила сложения.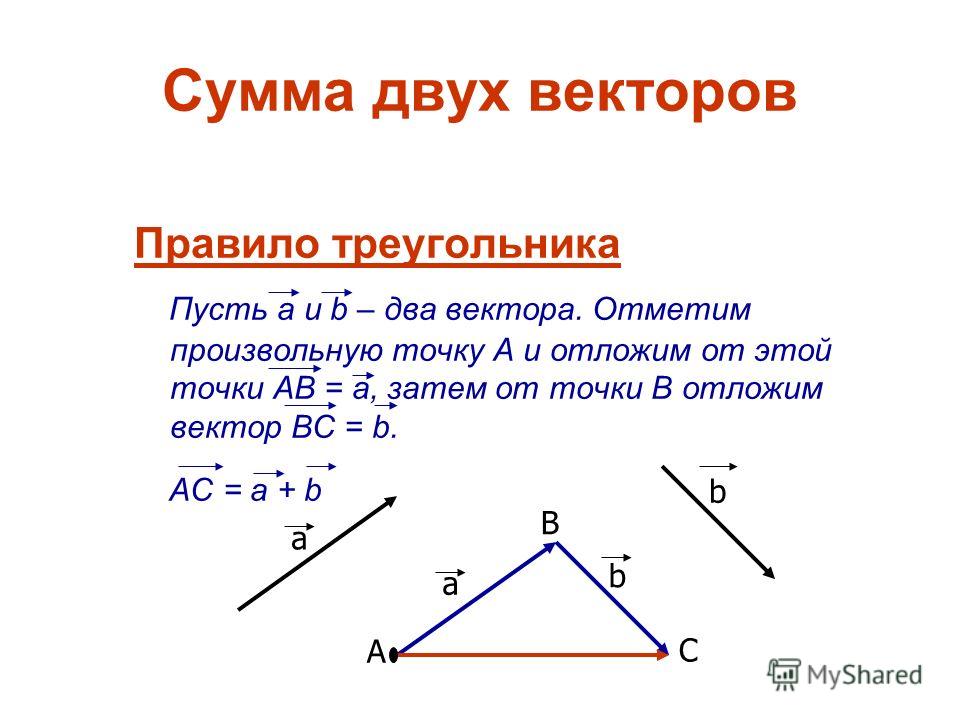 Главное – найти противоположный вектор.
Главное – найти противоположный вектор.
Само словосочетание «противоположный вектор» говорит о том, что такие вектора направлены в разные стороны.
Значит вычесть вектор – значит прибавить вектор с противоположным ему направлением.
Мы можем проверить это свойство алгебраически. Мы знаем, что противоположные числа в сумме дают 0:
\(a + (–a) = a\ –\ a = 0\)
Тогда и сумма противоположных векторов дадут 0 (т.е. если мы «пойдем» от начала до конца \(\overrightarrow{a}\) и обратно по –\(\overrightarrow{a}\), то мы вернемся снова в начало \(\overrightarrow{a}\)):
Значит и для векторов справедливо это свойство:
\(\overrightarrow{a}\ + (–\ \overrightarrow{a}) = 0\)
Пример №4:
Найдите \(\overrightarrow{f} = \overrightarrow{a}\ –\ \overrightarrow{b} + \overrightarrow{c}\ –\ \overrightarrow{d}\ –\ \overrightarrow{e}\), если
Можем использовать сложение векторов, если мы найдем отрицательные векторы.
 В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие:
В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие:
Теперь сложим все векторы, учитывая отрицательные:
ПРОИЗВЕДЕНИЕ ВЕКТОРА И ЧИСЛА:
Произведением ненулевого вектора и числа является вектор, коллинеарный данному, длина которого равна произведению длины данного вектора и числа:
\(k \bullet \overrightarrow{a} = \overrightarrow{\text{ka}}\)
где k – это число, при этом:
\(\overrightarrow{a} \upuparrows \overrightarrow{\text{ka}}\) при \(k > 0\)
\(\overrightarrow{a} \uparrow \downarrow \overrightarrow{\text{ka}}\) при \(k < 0\)
Произведением любого вектора на ноль является нулевой вектор.
Пример №5:
Найдите 5\(\overrightarrow{a}\) и –2\(\overrightarrow{a}\) , если:
1. Также можно представить произведение вектора и числа как сложение этого вектора несколько раз:
Также можно представить произведение вектора и числа как сложение этого вектора несколько раз:
\(5\overrightarrow{a} = \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a}\):
\(5\overrightarrow{a} \upuparrows \overrightarrow{a}\), т.к 5 > 0
2. Аналогично поступим и с отрицательным числом, только теперь уже складываем противоположные векторы:
\(–2\overrightarrow{a} \uparrow \downarrow \overrightarrow{a}\), т.к –2 < 0
СВОЙСТВА ПРОИЗВЕДЕНИЯ ВЕКТОРА И ЧИСЛА:
Сочетательное свойство:
\(kl \bullet \overrightarrow{a} = k(l\overrightarrow{a}) \)
Распределительный закон:
\(\overrightarrow{a}(k + l) = k\overrightarrow{a} + l\overrightarrow{a}\)
и
\(k(\overrightarrow{a} + \overrightarrow{b}) = k\overrightarrow{a} + k\overrightarrow{b}\)
ПРИМЕНЕНИЕ ВЕКТОРОВ К РЕШЕНИЮ ЗАДАЧ:
Используя векторы и связанные с ними свойства можно решать различные геометрические задачи.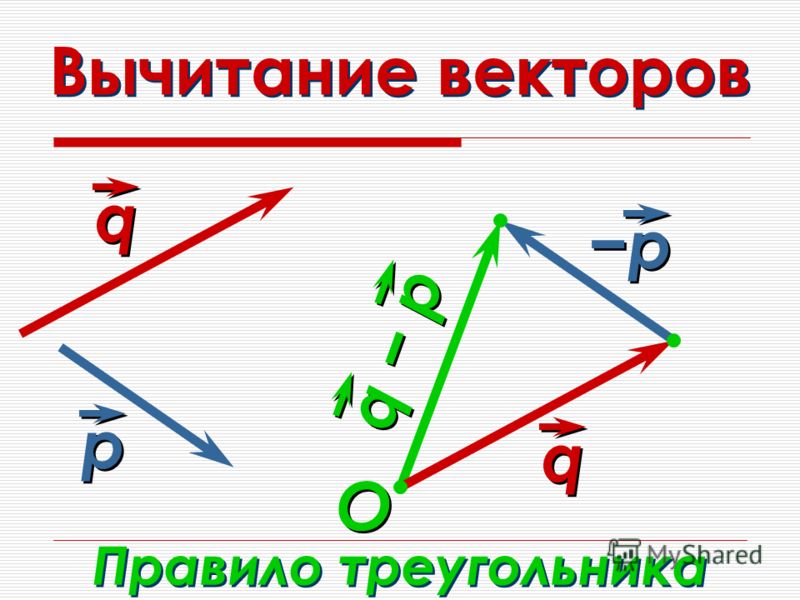
Пример №6:
Точка С – середина отрезка АВ, О – произвольная точка на плоскости. Докажите, что
\(ОС = \frac{1}{2}(АО + ОВ)\)
По правилу треугольника:
\(\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{АС}\)
\(\overrightarrow{ОС} = \overrightarrow{ОВ} + \overrightarrow{ВС}\)
Сложим два этих выражения, получим:
\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + \overrightarrow{АС} + \overrightarrow{ВС}\)
При этом \(\overrightarrow{АС}\) и \(\overrightarrow{ВС}\) – противоположные векторы, т.к. равны по модулю (точка С середина АВ), и имеют противоположное направление, значит:
\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + \overrightarrow{АС} + \overrightarrow{ВС}\)
\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + 0\)
\(ОС = \frac{1}{2}(АО + ОВ)\)
Что и требовалось доказать.
Пример №7:
ABCD – трапеция. Точки M и N середины оснований BC и AD соответственно. Точка О – точка пересечения прямых AB и CD. Докажите, что О, M и N лежат на одной прямой.
Треугольники OAD и OBC подобны по двум углам:
\(\left. \ \frac{\angle\text{OBC} = \angle OAD\ как\ соответствующие\ углы}{\angle O\ — \ общий} \right\}\Delta\text{OAD}\sim\text{ΔOBC}\)
\(\frac{\text{OA}}{\text{OB}} = \frac{\text{OD}}{\text{OC}} = k\)
При этом соответствующие стороны коллинеарны, значит можем выразить их как произведение числа и вектора:
\(\overrightarrow{\text{OA}} \upuparrows \overrightarrow{\text{OB}} \Longrightarrow \overrightarrow{\text{OA}} = k\overrightarrow{\text{OB}}\)
\(\overrightarrow{\text{OD}} \upuparrows \overrightarrow{\text{OC}} \Longrightarrow \overrightarrow{\text{OD}} = k\overrightarrow{\text{OC}}\)
В данной задаче можем выразить \(\overrightarrow{\text{OM}}\) и \(\overrightarrow{ON}\) как
\(\overrightarrow{\text{OM}} = \frac{1}{2}\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)\)
\(\overrightarrow{\text{ON}} = \frac{1}{2}(\overrightarrow{\text{OA}} + \overrightarrow{\text{OD}})\)
т. к. М – середина BC, а N – середина AD (аналогично вектору \(\overrightarrow{\text{OC}}\) из Примера №6).
к. М – середина BC, а N – середина AD (аналогично вектору \(\overrightarrow{\text{OC}}\) из Примера №6).
Соединим выразим вектор \(\overrightarrow{\text{ON}}\) через \(\overrightarrow{\text{OA}}\) и \(\overrightarrow{\text{OD}}\) из пункта 3:
\(\overrightarrow{\text{ON}} = \frac{1}{2}\left( \overrightarrow{\text{OA}} + \overrightarrow{\text{OD}} \right)\)
\(\overrightarrow{\text{ON}} = \frac{1}{2}\left( k\overrightarrow{\text{OB}} + k\overrightarrow{\text{OC}} \right)\)
\(\overrightarrow{\text{ON}} = \frac{1}{2}k\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)\)
\(\overrightarrow{\text{ON}} = k(\frac{1}{2}\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)) = k\overrightarrow{\text{OM}}\)
Если вектор \(\overrightarrow{\text{ON}}\) можно представить как произведение числа k с вектором \(\overrightarrow{\text{OM}}\), значит \(\overrightarrow{\text{ON}}\) и \(\overrightarrow{\text{OM}}\) коллинеарны, а значит лежат на одной прямой (они не могут быть параллельны, т.
 к. уже пересекаются в точке О).
к. уже пересекаются в точке О).
Что и требовалось доказать.
8 класс. Геометрия. Векторы. Сложение и вычитание векторов. — Сложение и вычитание векторов.
Комментарии преподавателяСложение и вычитание векторов
На предыдущем уроке мы определили понятие вектора, сказали, какие векторы называются равными, коллинеарными, сонаправленными и противонаправленными.
Теперь пусть задано два вектора – вектора и . Найдем сумму этих двух векторов . Для этого отложим из некоторой точки А вектор . Из точки В отложим вектор . Тогда вектор называют суммой заданных векторов: (см. Рис. 1).
Рис. 1
Данное определение можно объяснить так: пусть был задан груз, и сначала на него подействовала сила – он переместился из точки А в точку В, после этого подействовала сила – груз переместился из точки В в точку С. Но в результате действия двух этих сил груз переместился из точки А в точку С.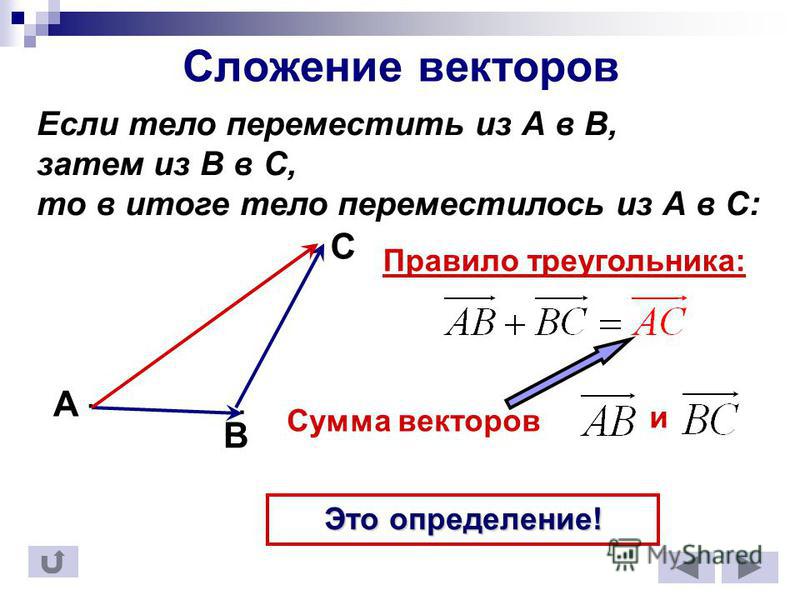
Таким образом, мы получили определение суммы двух векторов – правило треугольника.
Правило треугольника
Для того чтобы получить сумму двух векторов, нужно из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго – это и будет сумма двух векторов.
Можно провести аналогию с числами. Мы ввели понятие числа, научились складывать числа, определили законы сложения и так далее. Теперь мы ввели понятие вектора, научились находить равные вектора, складывать вектора. Теперь нужно определить законы сложения.
Законы сложения векторов
Для любых векторов , и справедливы следующие равенства:
– переместительный закон.
Доказательство: отложим из точки сначала вектор , получаем точку В, из нее откладываем вектор , получаем точку С и вектор .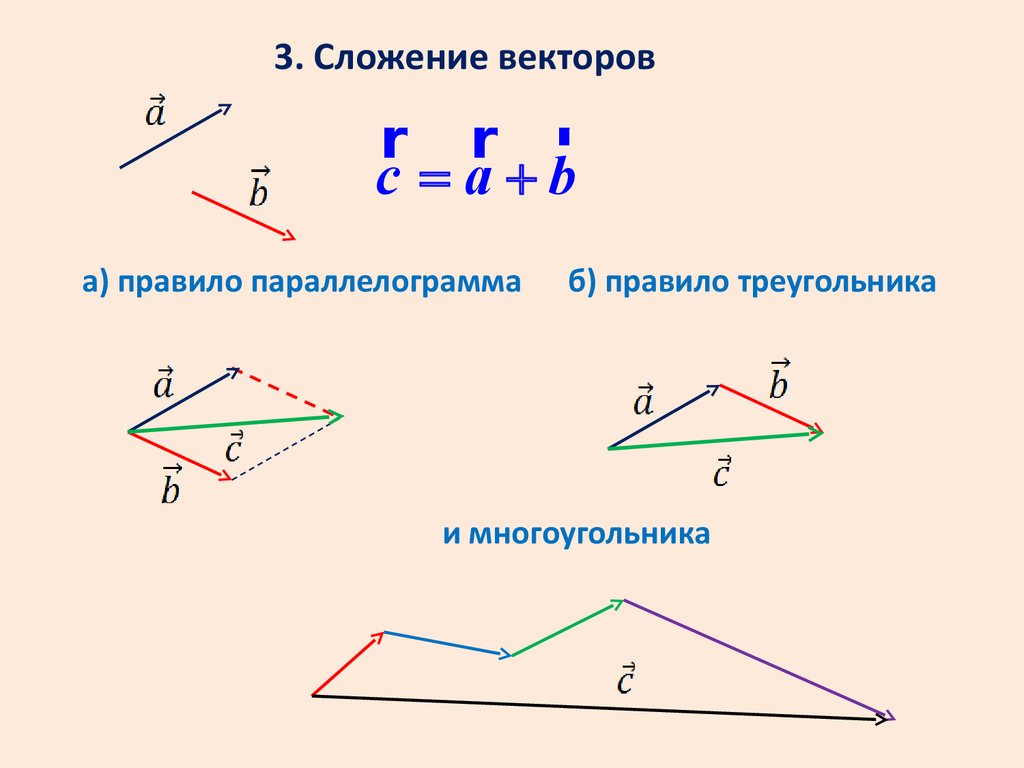
Теперь отложим из точки А сначала вектор получим точку В, из нее отложим вектор, получим точку С и вектор .
Чтобы доказать равенство полученных векторов, выполним оба построения из одной точки и получим таким образом правило параллелограмма (см. Рис. 2).
Рис. 2
Откладываем из точки А вектор и вектор . Из точки В откладываем вектор , вектора и равны, а значит, стороны ВС и АВ1 четырехугольника АВСВ1 параллельны. Аналогично параллельны и стороны АВ и В1С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма. , таким образом, мы доказали переместительный
Рис. 3
закон сложения векторов и получили правило параллелограмма (см. Рис. 3).
Правило параллелограмма
Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти два вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, и будет суммой заданных векторов.
Диагональ параллелограмма, исходящая из начальной точки, и будет суммой заданных векторов.
– сочетательный закон;
Из произвольной точки А отложим вектор , прибавим к нему вектор , получим их сумму . К этой сумме прибавим вектор , получим результат (см. Рис. 4).
Рис. 4
В правой части выражения мы сначала получили сумму векторов , после прибавили ее к вектору и получили результат: (см. Рис. 5).
Таким образом, мы доказали сочетательный закон сложения векторов.
Рис. 5
Правило многоугольника
Чтобы сложить несколько векторов, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее; когда все векторы отложены, соединив начальную точку с концом последнего вектора, получим сумму нескольких векторов (см. Рис. 6).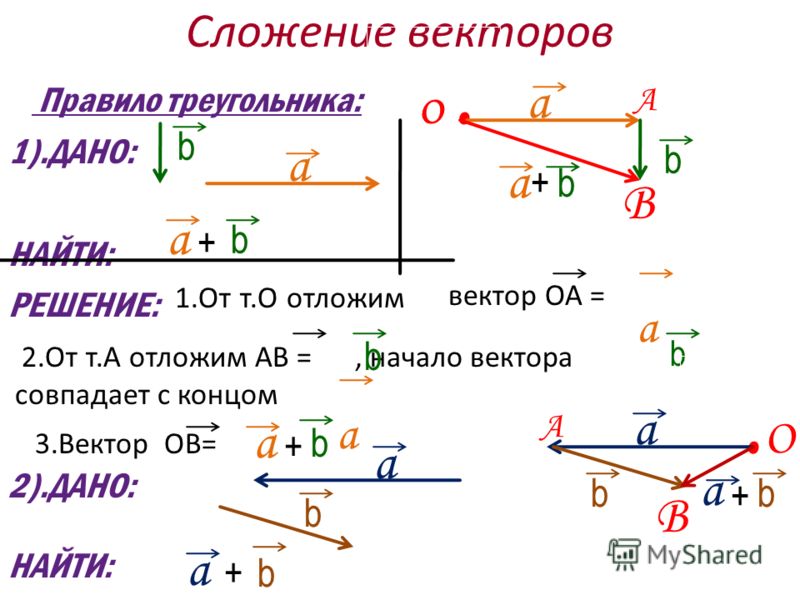
Рис. 6
По аналогии с действительными числами после того, как мы научились их складывать, нужна обратная операция – вычитание.
Пусть задано два вектора – векторы и . Найдем разность этих двух векторов .
Определение
Разностью двух векторов и называют такой третий вектор, сумма которого с вектором равна вектору .
Если задан вектор , то можно построить противоположный ему вектор , который будет равен по длине, но противонаправлен. Сумма противоположных векторов всегда есть нулевой вектор: . Таким образом, .
Отложим из произвольной точки вектор , из его конца отложим вектор , получим в результате вектор (см. Рис. 7).
Рис. 7
Рассмотрим вычитание векторов на параллелограмме. Из точки А отложим векторы и . Из точек В и D отложим векторв и соответственно. Диагональ АС – это сумма векторов и : .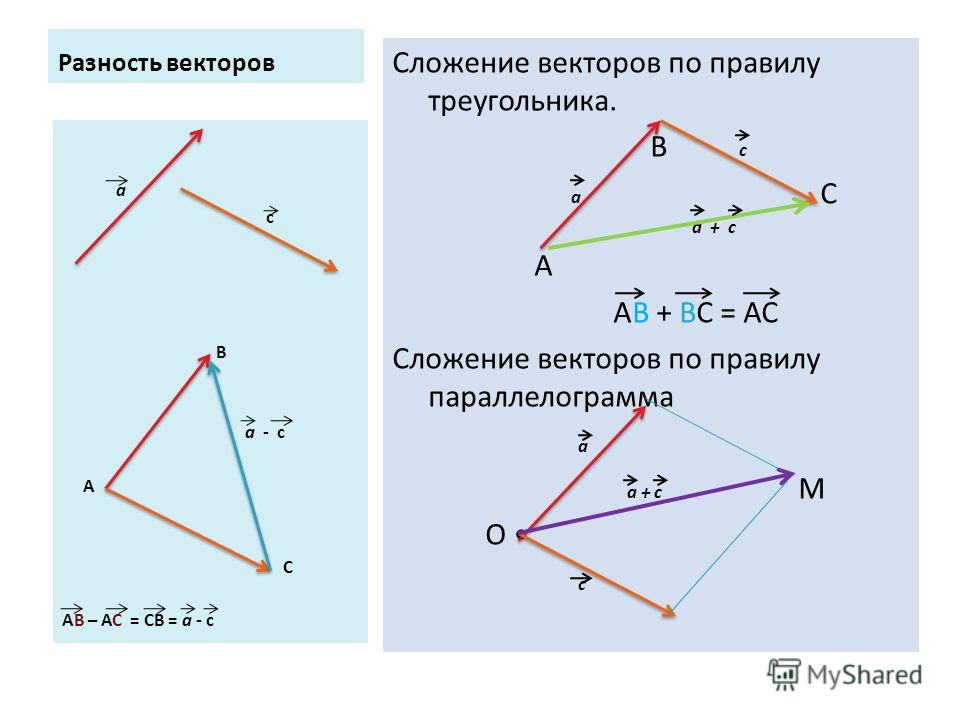 Но в параллелограмме есть еще вторая диагональ – BD. Прибавим к вектору вектор , получим вектор (см. Рис. 8).
Но в параллелограмме есть еще вторая диагональ – BD. Прибавим к вектору вектор , получим вектор (см. Рис. 8).
Рис. 8
Итак, на данном уроке мы вывели правила сложения и вычитания векторов при помощи треугольника и параллелограмма, сформулировали законы сложения векторов.
ИСТЧНИК
http://interneturok.ru/ru/school/geometry/8-klass/vektory/slozhenie-i-vychitanie-vektorov
http://www.youtube.com/watch?v=r8icqcsv5AQ
http://metodbook.ru/index.php/matematika/9-testy-po-geometrii-9-klass/4-test-po-geometrii-9-klass-tema-slozhenie-i-vychitanie-vektorov-variant-1.html
http://gdz-matem.ru/8class/25-9.2-slozhenie-i-vychitanie-vektorov.html
http://www.lenbaza.ru/baza/pict/111.jpg
Треугольник, параллелограмм и многоугольник Закон векторов
В этой статье мы обсудим сложение векторов как концепцию. Сложение векторов преподается с использованием закона треугольника и закона параллелограмма в дополнение к коммутативным и ассоциативным особенностям сложения векторов.
Треугольный закон сложения векторов
Если два вектора представлены двумя сторонами треугольника по величине и направлению, взятыми в одном порядке, то третья сторона этого треугольника представляет (по величине и направлению) равнодействующую векторов.
Треугольный закон сложения векторов — это математическая формула, описывающая, как векторы складываются в треугольник.
Перемещение из точки A в точку B представлено вектором AB, который может быть записан в следующем виде: мальчик путешествует из точки A в точку B и затем из точки B в точку C. Какова общая сумма вызванного им смещения из точки А в точку С?
Это смещение обеспечивается вектором AC, где AC — вектор ускорения.
АС = АВ + ВС.
В сложении векторов это известно как закон сложения векторов треугольника.
Если у вас есть два вектора a и b, вы должны разместить их таким образом, чтобы начальная точка одного вектора совпадала с конечной точкой другого вектора, чтобы сложить их вместе. Это показано на рис. 2 (i) и (ii) ниже, соответственно:
Это показано на рис. 2 (i) и (ii) ниже, соответственно:
На рис. 2 (ii) показано, что вектор b был перемещен без изменения его величины или направления, так что его начальная точка совпадает с конечной точкой вектора a. Это помогает в формировании треугольника ABC, а третья сторона AC дает нам сумму двух векторов a и b соответственно. В результате на основании рис. 2 (ii) мы можем записать
AB + BC = AC
Ведь теперь мы знаем, что AC = – CA. В результате приведенного выше уравнения мы имеем
AB + BC = -CA
Альтернативно, AB + BC + CA = 0,
Альтернативно, AA = 0,
Кроме того, это нулевой вектор, поскольку начальная и конечная точки совпадают, как показано на рис. следующую диаграмму:
Теперь, как показано на рис. 4 ниже, давайте построим вектор BC ‘, величина которого такая же, как у вектора BC, но чье направление противоположно направлению вектора ДО Н.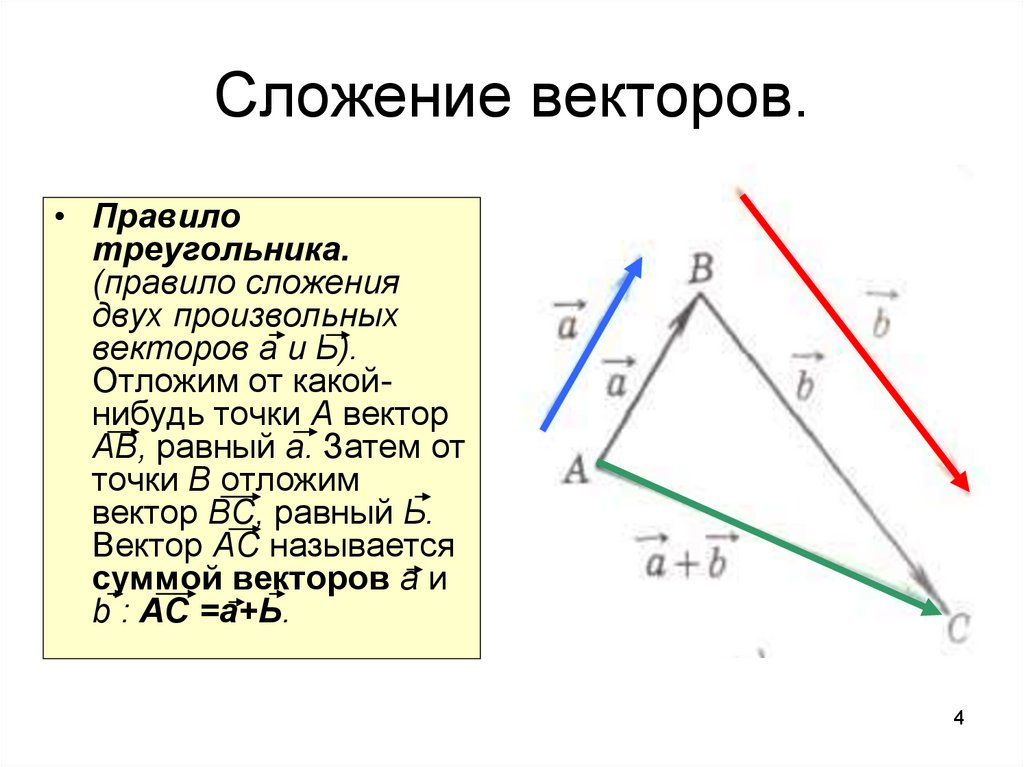 Э. Или
Э. Или
до н.э. =– до н.э.
Поэтому, когда мы используем закон сложения векторов треугольника, мы получаем
AC′ = AB + BC′ = AB + (– BC′) = a – b.
Разница между векторами a и b представлена вектором AC′.
Закон сложения векторов параллелограмма
Закон сложения векторов параллелограмма гласит, что если два вектора представлены двумя смежными сторонами параллелограмма по направлению и величине, то равнодействующая этих векторов представлена (по величине и направлению) Диагональ параллелограмма начинается в той же точке, что и два исходных вектора.
Закон сложения векторов в виде параллелограмма — это математическая формула, описывающая, как векторы складываются в параллелограмм.
Теперь давайте рассмотрим немного более сложную проблему. Рассмотрим сценарий лодки, плывущей по реке с одного берега на другой в направлении, перпендикулярном течению реки. На эту лодку действуют два вектора скорости:
На эту лодку действуют два вектора скорости:
Скорость лодки определяется мощностью двигателя.
Скорость течения реки измеряется в метрах в секунду.
Когда эти две скорости воздействуют на лодку одновременно, лодка начинает двигаться с другой скоростью. Изучите, как мы можем вычислить результирующую скорость лодки, и посмотрите, что у нас получится.
Чтобы найти решение, рассмотрим два приведенных ниже вектора a и b, которые являются двумя соседними сторонами параллелограмма с точки зрения их размера и направления, как показано на диаграмме ниже.
Они представлены по размеру и направлению диагональю параллелограмма, проходящей через их общую точку, которая представляет их сумму, a + b. В векторном сложении это известно как параллелограммный закон сложения векторов.
Пожалуйста, имейте в виду, что закон треугольника позволяет нам вывести из рис. 5 следующее:
5 следующее:
OA +AC = OC.
В качестве альтернативы, OA + OB OC… из-за того, что AC=OB
В результате можно сделать вывод, что правила сложения векторов треугольника и параллелограмма аналогичны друг другу по функциональности.
Изображение, показывающее закон сложения векторов полигонов тогда их равнодействующая может быть представлена по величине и направлению замыкающей стороной многоугольника, взятого в обратном порядке.
Заключение
Если два вектора представлены двумя сторонами треугольника по величине и направлению, взятыми в одном порядке, то третья сторона этого треугольника представляет (по величине и направлению) равнодействующую векторов. Треугольный закон сложения векторов — это математическая формула, описывающая, как векторы складываются в треугольник. Закон сложения векторов параллелограмма гласит, что если два вектора представлены двумя соседними сторонами параллелограмма по направлению и величине, то равнодействующая этих векторов представлена (по величине и направлению) диагональю параллелограмма, начинающейся в той же точке.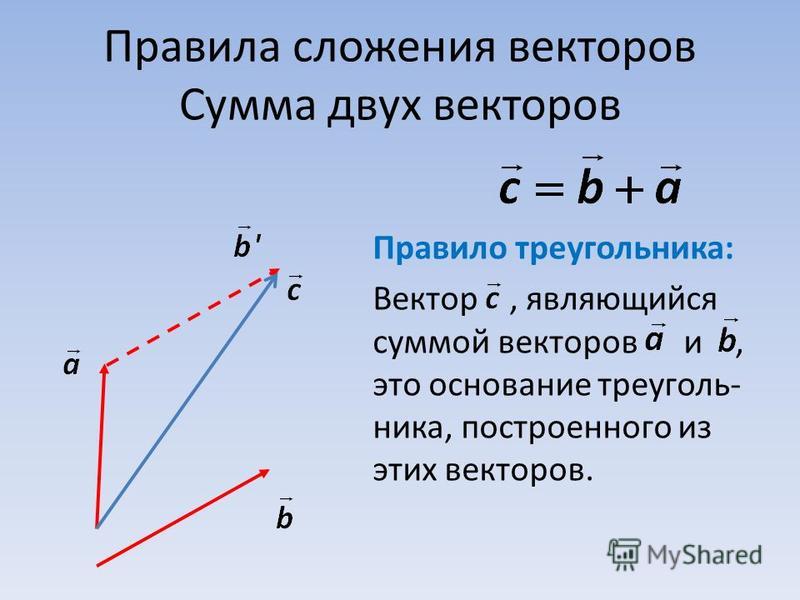 как два исходных вектора. Перемещение из точки А в точку В изображается вектором АВ. Закон сложения векторов параллелограмма — это математическая формула, описывающая, как векторы складываются в параллелограмм. Утверждается, что если множество векторов можно представить по величине и направлению сторонами многоугольника, взятыми в том же порядке, то их равнодействующая может быть представлена по величине и направлению замыкающей стороной многоугольника, взятого в обратном порядке. .
как два исходных вектора. Перемещение из точки А в точку В изображается вектором АВ. Закон сложения векторов параллелограмма — это математическая формула, описывающая, как векторы складываются в параллелограмм. Утверждается, что если множество векторов можно представить по величине и направлению сторонами многоугольника, взятыми в том же порядке, то их равнодействующая может быть представлена по величине и направлению замыкающей стороной многоугольника, взятого в обратном порядке. .
сил — Как и почему работает закон сложения векторов?
Задать вопрос
спросил
Изменено 2 года, 9 месяцев назад
Просмотрено 355 раз
$\begingroup$
Наш учитель объяснил нам сложение векторов. Он объяснил нам треугольный закон векторного сложения.
Он объяснил нам треугольный закон векторного сложения.
У меня два вопроса:
Он сказал, что вектор $\vec{R}$ является результирующим вектором, что означает, что вместо того, чтобы проходить через $\vec{A}$ и $\vec{B}$, мы мог бы напрямую пройти через $\vec{R}$. Я не очень понимаю это, и, очевидно, это легко понять интуитивно, когда речь идет о смещении. Но включение сил и других векторных величин в это изображение действительно трудно понять. Так как же работает закон треугольника для сложения сил?
Правило объединения «голова-конец» сбивает с толку и выглядит как уловка для запоминания. Итак, если существует треугольный закон сложения векторов, то зачем нужен параллелограммный закон сложения векторов, когда оба говорят о сложении сущностей с направлениями и величинами?
Кроме того, как можно понять сложение векторов силы, используя закон параллелограмма (я полагаю, что ответ на этот вопрос будет получен, когда будет дан ответ на первый вопрос)?
Редактировать: я здесь новичок, поэтому не знаю, как добавлять изображения к вопросу. Также, пожалуйста, не отвечайте на этот вопрос математически, пожалуйста, отвечайте таким образом, чтобы сложения векторов имели смысл интуитивно и их было легко представить.
Также, пожалуйста, не отвечайте на этот вопрос математически, пожалуйста, отвечайте таким образом, чтобы сложения векторов имели смысл интуитивно и их было легко представить.
- силы
- векторы
- геометрия
- линейная алгебра
- перемещение
$\endgroup$
2
$\begingroup$
Как вы сказали, это легко понять, когда речь идет о смещении.
Тогда вам нужно только признать, что вектор смещения является одним и тем же вектором, где бы он ни появлялся на плоскости.
(это также показывает закон параллелограмма. Он не отличается от закона треугольника, просто другой способ его осмысления).
Итак, чтобы применить это к силам и другим векторным величинам, вам нужно только признать, что не имеет значения, где вы поместите векторы на диаграмме.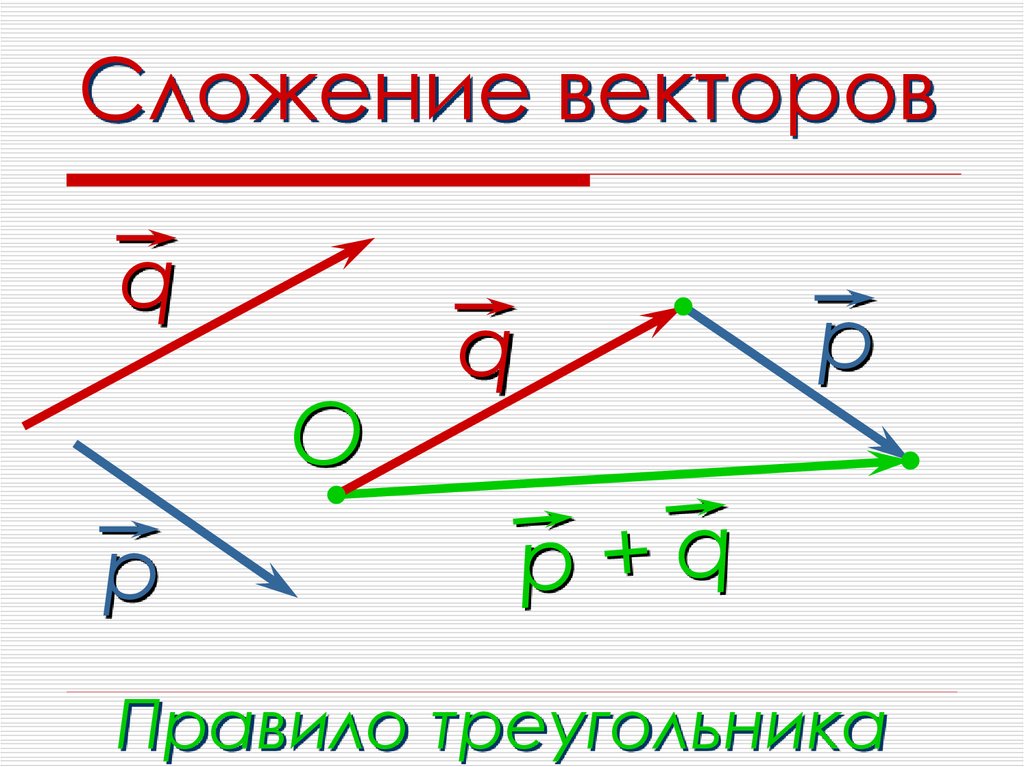

 к. лежат параллельных прямых и направлены в одну сторону:
к. лежат параллельных прямых и направлены в одну сторону:

 В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие:
В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие: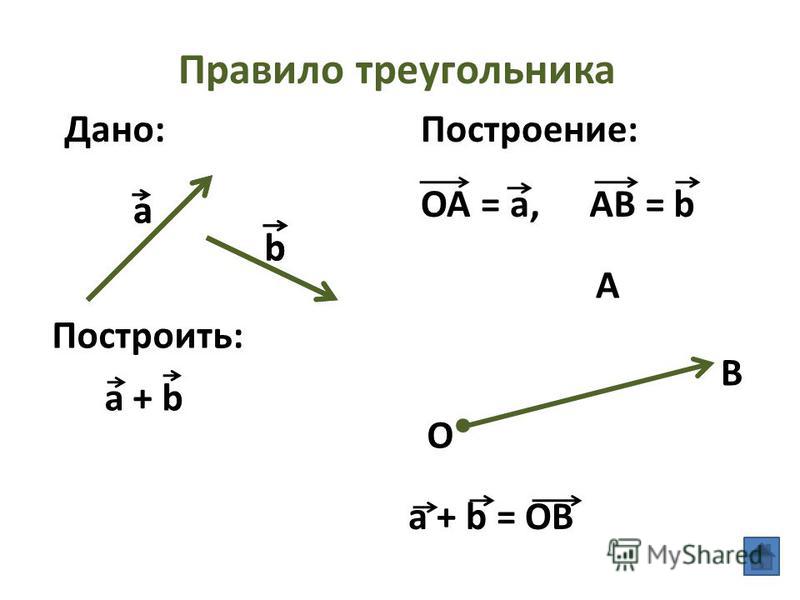 к. уже пересекаются в точке О).
к. уже пересекаются в точке О).