Производная, Геометрический смысл производной | univer-nn.ru
Перед прочтением информации на текущей странице советуем посмотреть видео о производной и её геометрическом смысле
Также смотрите пример вычисления производной в точке
Касательной к линии l в точке М0 называется прямая М0Т — предельное положение секущей М0М, когда точка М стремится к М0 вдоль данной линии (т.
Производной функции у = f{x) в точке x0 называется предел отношения приращения этой функции к приращению аргумента, когда последнее стремится к нулю. Производную функции у = f{x) в точке х0 в контрольных по математике и учебниках обозначают символом f'(x0). Следовательно, по определению
Термин «производная» (а также «вторая производная») ввел Ж. Лагранж (1797), к тому же он дал обозначения y’, f’(x), f”(x) (1770,1779). Обозначение dy/dx впервые встречается у Лейбница (1675).
Геометрический смысл производной
Производная функции y = f(х) при х = xо равна угловому коэффициенту касательной к графику данной функции в точке Мо(хо, f(xо)), т. е.

Уравнение касательной к линии у = f(x) в точке Мо(хо, уо ) принимает вид
Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если f(x0) не равно 0, то уравнение нормали к линии у = f(x) в точке Мо(хо, уо) запишется так:
Физический смысл производной
Если x = f(t) — закон прямолинейного движения точки, то x’ = f’(t) — скорость этого движения в момент времени t. Быстрота протекания физических, химических и других процессов выражается с помощью производной.
Если отношение dy/dх при х->х0 имеет предел справа (или слева), то он называется производной справа (соответственно производной слева).
Очевидно, функция f{x) определенная в некоторой окрестности точки х0, имеет производную f’{x) тогда и только тогда, когда односторонние производные существуют и равны между собой.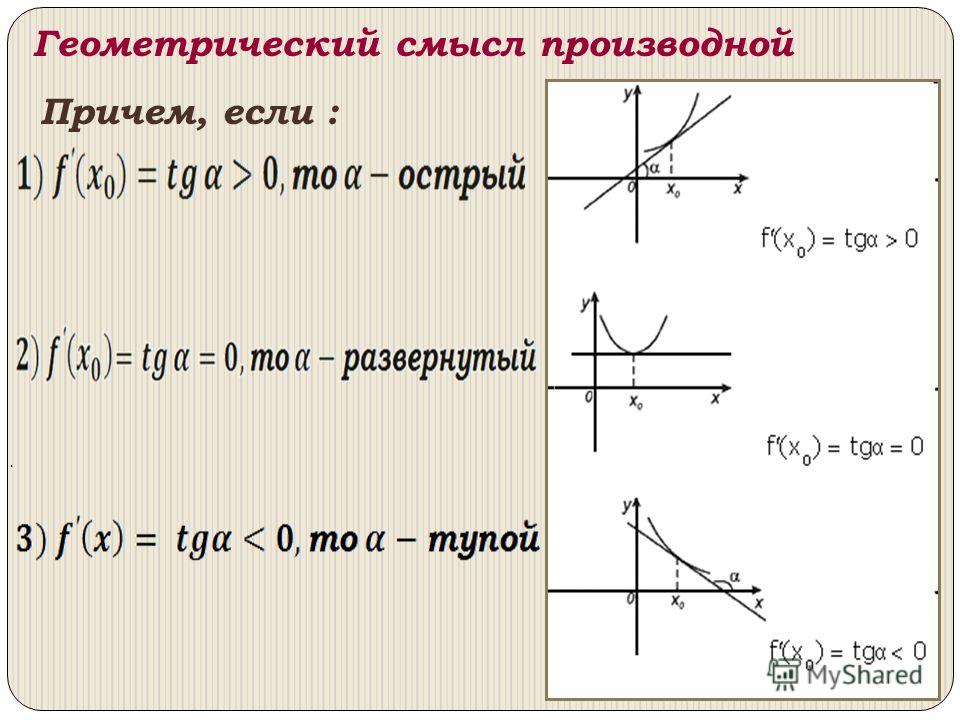
Геометрическое истолкование производной как углового коэффициента касательной к графику распространяется и на этот случай: касательная в данном случае параллельна оси Оу.
Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке данного промежутка, называется дифференцируемой в этом промежутке. Если промежуток является замкнутым, то на концах его имеются односторонние производные.
Операция нахождения производной называется дифференцированием
.Применение производной для исследования функций на монотонность и экстремумы 10 класс онлайн-подготовка на Ростелеком
Напоминание «Понятие производной »
Рассмотрим график функции (Рис. 1).
Рис. 1. График функции
Функция описывает некий реальный процесс, например поход на прогулку, – это расстояние от дома, – фиксированный момент времени.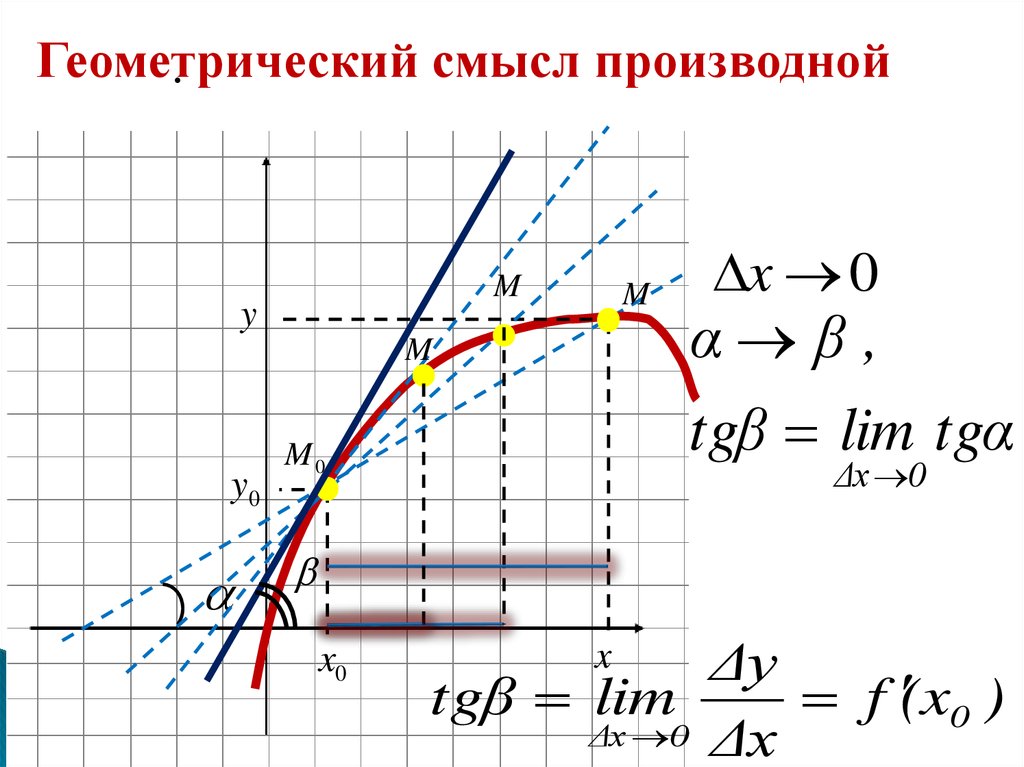 В этот момент времени расстояние от дома было (Рис. 2).
В этот момент времени расстояние от дома было (Рис. 2).
Рис. 2. Значение
По прошествии времени – приращение аргумента. Получился момент времени . В этот момент времени расстояние от дома равнялось (Рис. 3):
Рис. 3. Приращение аргумента , значение
Имеем знаменитый треугольник (Рис. 4). Здесь – приращение аргумента, – приращение функции, а тангенс это отношение , то есть за время пройдено расстояние . – это средняя скорость, но если , то и числитель и знаменатель стремятся к нулю. И если эта дробь стремится к некоторому числу, то это число и называется производной данной функции в данной точке. Она обозначается так:
Это определение производной (Рис. 4). Теперь нужно понять, каков смысл производной.
– это мгновенная скорость в данной точке.
Если в этой точке провести касательную, которая имеет угол наклона , то производная в этой точке есть тангенс угла наклона касательной. .
Рис. 4. Определение производной
Итак, нам надо исследовать функцию, рассмотрим инструменты, имеющиеся у нас.
Из соотношения имеем:
– это физический и геометрический смысл производной.
Определение «Монотонные функции»
Монотонно возрастающая функция – это функция, у которой большему значению аргумента соответствует большее значение функции.
Монотонно убывающая функция – это функция, у которой большему значению аргумента соответствует меньшее значение функции.
Связь производной и промежутков монотонности функции
Если , то знак приращения и знак производной в точке совпадает со знаком . То есть если производная в этой точке больше нуля, то и понятно, что функция в окрестности этой точки будет возрастать. А если производная меньше нуля, значит, и понятно, что в окрестности этой точки функция будет убывать.
Далее, производная в точке есть тангенс угла наклона касательной (Рис. 5). Касательная описывается линейной функцией. В окрестности точки кривая и линейная функция почти совпадают. Если угол наклона острый, тангенс будет положительным, угловой коэффициент – величина положительная, и линейная функция возрастает, а значит, в окрестности этой точки и сама функция возрастает:
Если угол наклона острый, тангенс будет положительным, угловой коэффициент – величина положительная, и линейная функция возрастает, а значит, в окрестности этой точки и сама функция возрастает:
И наоборот, если линейная функция убывает, угол тупой, тангенс – величина отрицательная, значит, линейная функция убывает, а с ней убывает функция .
Рис. 5. Угол наклона касательной в точке
Так события развиваются в окрестностях точки . Эти события подчиняются геометрическому смыслу производной (ее физическому смыслу, соотношению ).
Исследование промежутков монотонности функции с помощью производной
Рассмотрим функцию и ее поведение на всей ОДЗ (Рис. 6). Предположим, что это график исследуемой функции.
Рис. 6. График функции
Есть точка . Касательная наклонена под острым углом (Рис. 7). Значит, в точке функция возрастает.
Рис. 7. Угол наклона касательной в точке
В точке касательная параллельна оси , значит точка – точка экстремума.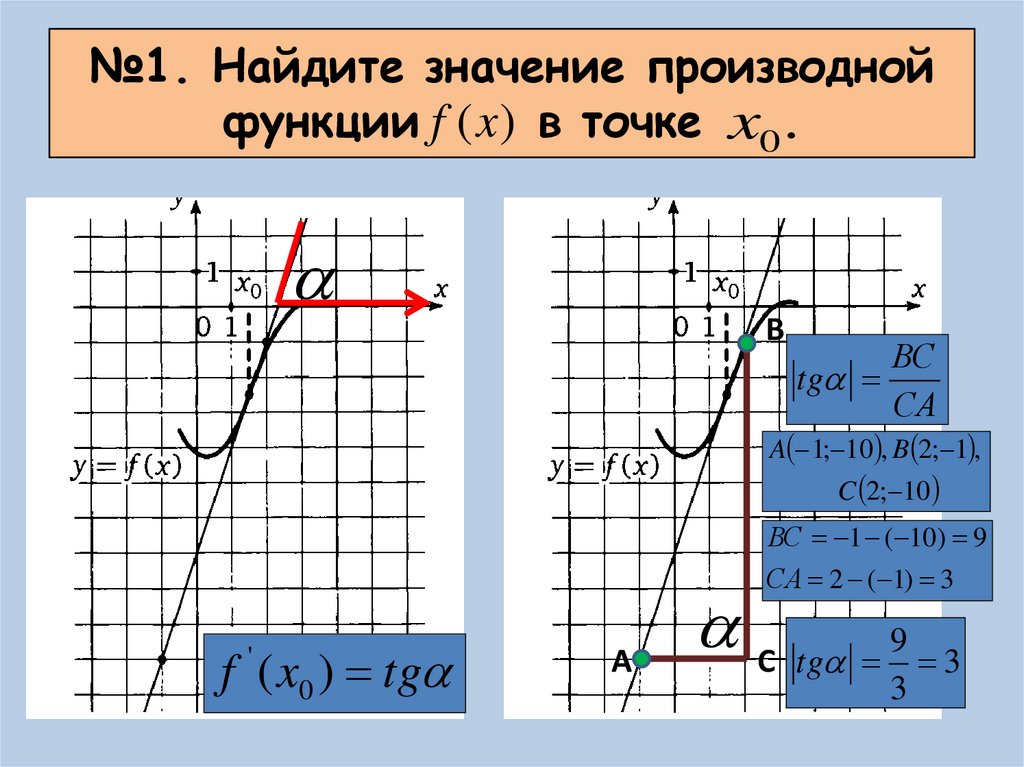 Об этом мы поговорим отдельно.
Об этом мы поговорим отдельно.
Рис. 8. – точка экстремума
В точке угол наклона касательной будет тупым, тангенс будет величиной отрицательной, значит, производная отрицательная и функция здесь убывает (Рис. 9).
Рис. 9. Угол наклона касательной в точке
И, наконец, в точке производная равно нулю и дальше функция возрастает (Рис. 10).
Рис. 10. Угол наклона касательной в точке – точке экстремума
Выясняется, что функция возрастает на интервалах, где производная больше нуля:
Если же значение производной отрицательное, то функция убывает:
Вся ОДЗ состоит из отдельных точек, значит, надо выделить те интервалы, на которых производная меньше нуля, на которых производная больше нуля, и они определят те участки ОДЗ, на которых функция либо возрастает, либо убывает. Этот же вывод мы получим, рассматривая соотношение . На тех областях, на которых производная меньше нуля, функция убывает. Соответственно, на тех областях ОДЗ, где производная больше нуля, функция возрастает.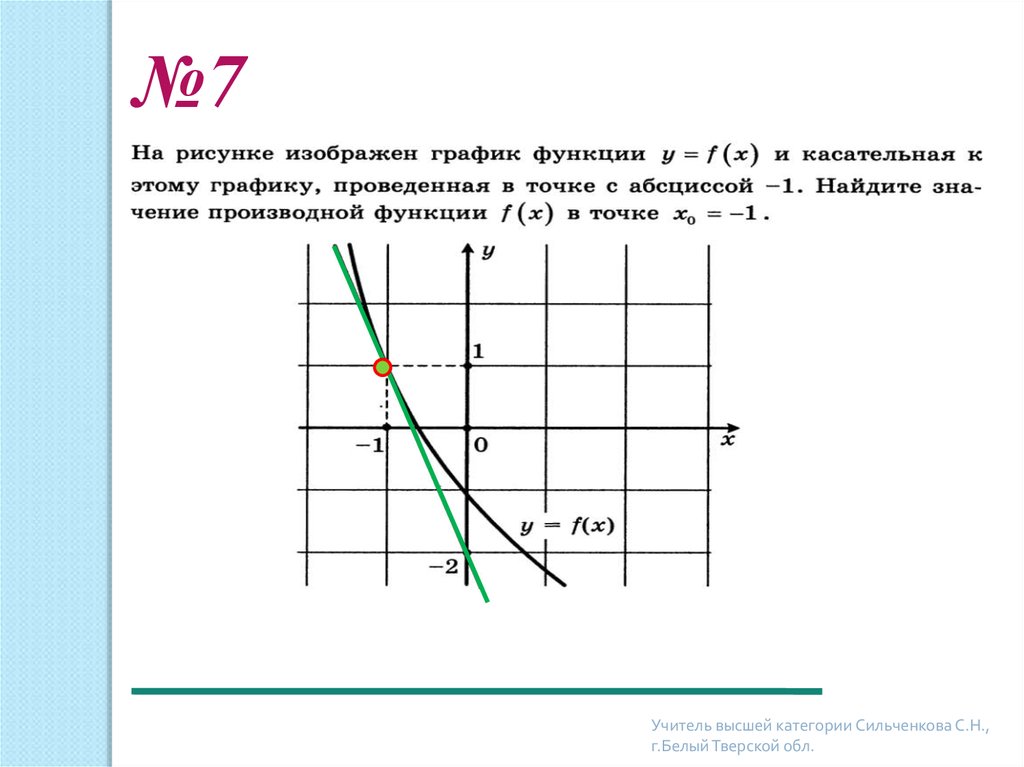
Теперь мы готовы написать, где убывает, а где возрастает (Рис. 11) данная нам функция:
при
Рис. 11. Промежутки возрастания функции
Теперь выясним, где данная функция убывает (Рис. 12):
при
Рис. 12. Промежутки убывания функции
Тонкий момент: включать ли значения в точках ?
не включаем, потому что в них производная равна нулю, а мы рассматриваем тот случай, когда производная меньше нуля. Но функция убывает, когда принадлежит отрезку .
При этом эти точки включены также в интервалы, когда функция возрастает.
Приходим к важному выводу: интервалы знакопостоянства являются интервалами монотонности .
Цель урока: научиться находить промежутки возрастания и убывания функции с помощью производной. Выясняется, что надо найти производную, выделить ее интервалы знакопостоянства и тем самым мы узнаем, где эта функция монотонно убывает и где она монотонно возрастает.
Далее нас интересуют точки экстремумов функции. Мы рассмотрели случаи, когда производная меньше нуля, когда она больше нуля, также важный случай, когда производная равна нулю.
Мы рассмотрели случаи, когда производная меньше нуля, когда она больше нуля, также важный случай, когда производная равна нулю.
Вспомним, что такое точка максимума и точка минимума функции.
Рис. 13. Точки экстремумов функции
Рассмотрим рисунок (Рис 13). Точка – точка максимума функции (max), если существует окрестность точки , для которой , то есть если значение функции в этой точке больше, чем значение функции в любой точке ее окрестности.
Аналогичное определение для точки минимума. Точка – точка минимума функции (min), если существует окрестность точки , для которой , то есть если значение функции в этой точке меньше, чем значение функции в любой точке ее окрестности.
При поиске наибольшего и наименьшего значения функции на всей ОДЗ, то есть ее глобальных экстремумов, следует понимать, что они могут не совпадать с ее локальными экстремумами, точками, где производная меняет знак.
Пример локального и глобального экстремума
Рассмотрим функцию (Рис.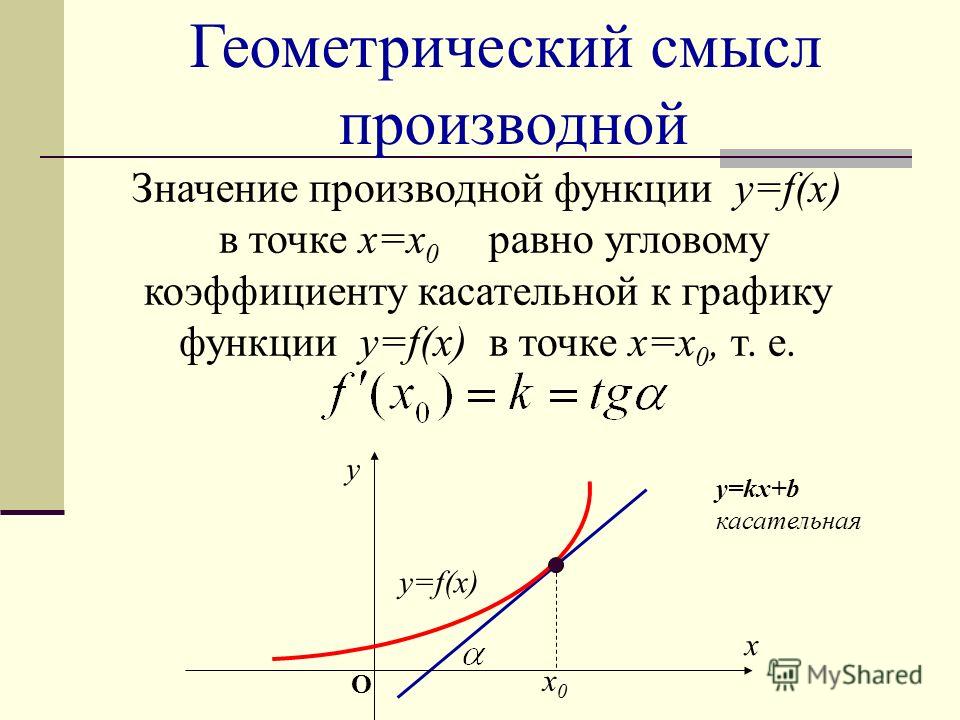 14).
14).
Здесь точка – точка локального максимума. Функция здесь равна нулю.
Точка – точка глобального максимума, в них функция равняется 24.
Рис. 14. График функции
На данном уроке, когда говорится об экстремумах, подразумеваются локальные экстремумы.
Как узнать, где точка максимума, а где точка минимума, подскажет производная. Вернемся к точке . На рисунке наглядно показано, что до этой точки функция возрастает, производная , а после этой точки функция убывает, производная . А значение производной в точке : . Мы получили достаточный признак максимума: производная равна нулю и при этом знак производной меняется с плюса на минус при переходе аргумента через точку .
Рассмотрим точку . Производная в этой точке . Но является ли данная точка точкой экстремума? Производная слева от этой точки отрицательна, касательная наклонена под тупым углом. Производная справа положительная, значит, производная меняет знак с минуса на плюс при переходе через точку , значит, точка – точка минимума.
Итак, мы рассмотрели точку минимума и точку максимума и достаточный признак точки минимума и точки максимума.
Как узнать, является ли точка точкой минимума или точкой максимума? Нужно взять производную и приравнять ее к нулю. Тогда мы найдем точки , и т. д. Это внутренние точки области определения, в которых производная равна нулю.
Критическая точка функции – это внутренняя точка области определения, в которой производная равна нулю или не существует. То есть точки и – критические точки.
– т. max.
– т. min.
Но так происходит не всегда.
Точка перегиба
Рассмотрим следующую функцию (Рис. 15):
Рис. 15. Иллюстрация точки перегиба
Производная в точке равна нулю: , касательная параллельна оси . Является ли она точкой экстремума? Нет. Почему? Потому что до точки производная положительна, функция возрастает (Рис. 16):
Рис. 16. Возрастание функции до точки перегиба
После этой точки производная также положительна (Рис. 17):
17):
Рис. 17. Возрастание функции после точки перегиба
Функция возрастает и слева, и справа от точки, значит, не является точкой экстремума.
Лемма Ферма
Если функция имеет производную и в точке имеет экстремум, то значение производной в этой точке равно 0.
Это необходимый мощный признак, из него мы выясняем, какие точки нам нужны для исследования. Все остальные отметаем.
Еще раз подчеркнем, что нам иллюстрирует данный рисунок: равенство нулю – это лишь необходимый признак экстремума, но не достаточный.
Точка перегиба, локальный характер точек экстремума
Рассмотрим в качестве примера функцию, график которой изображен на рисунке (Рис. 18).
Рис. 18. График функции с несколькими локальными экстремумами
– точкаминимума, – точкамаксимума, – такжеточкаминимума.
– точкаминимума, значит, существует некая окрестность, где значение функции является наименьшим, но существует также вторая точка минимума.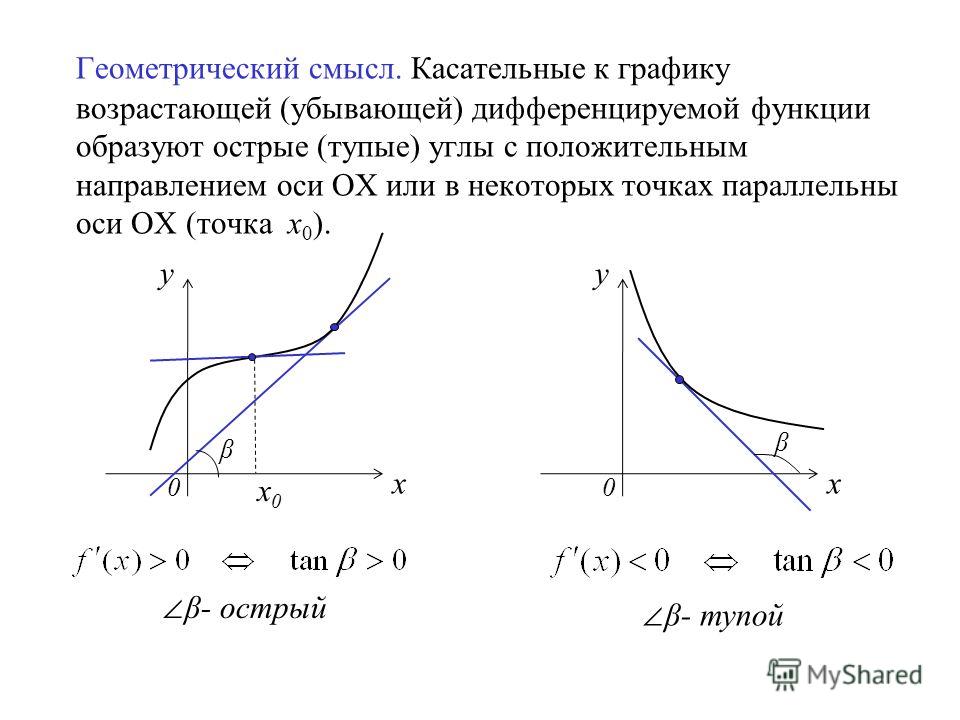
таким образом, глобально, наименьшим значением функции на всей ОДЗ является значение функции в точке .
– точкамаксимума, но наибольшего значения данной функции не существует, потому что есть точки, в которых значение функции значительно больше, чем в точке .
Таким образом, данным рисунком мы подчеркиваем локальный характер точек экстремума. Можем записать:
То есть значение функции в точке меньше либо равно значению функции в любой другой точке ОДЗ.
Алгоритм
Мы знаем, как по знаку производной найти интервалы монотонного возрастания или убывания функции, знаем, каким образом определить точки максимума и точки минимума функции. Пусть теперь есть задача исследовать функцию на экстремумы и на монотонность с помощью производной.
Алгоритм таков:
1. Найти .
2. Выделить интервалы знакопостоянства . Они определят интервалы монотонности .
3. Найти критические точки (внутренние точки ОДЗ, в которых или не существует).
4. Выделить из критических точек и концов отрезка точки экстремума и исследовать их.
Задача
Найти интервалы монотонности и точки экстремума функции (Рис. 19) с помощью .
Найдем производную:
(Рис. 19)
Приравниваем ее к нулю и находим единственное решение:
– единственная критическая точка.
На рисунке в нижней части изображен график производной.
Рис. 19. Графики функций и
На интервале левее производная отрицательна (Рис. 20), функция убывает (Рис. 21).
|
Рис. 20. Левый интервал производной |
Рис. 21. Левый интервал функции |
На интервале правее производная положительна (Рис. 22), функция возрастает (Рис. 23).
|
Рис. 22. Правый интервал производной |
Рис. |
Ответ:
1. при
2.
3. – т. min.
Итак, мы решили задачу, исследовали функцию с помощью производной, но мы знали свойства этой функции, знали, где она возрастает, где убывает, и знали точку экстремума.
Видим, что результаты, которые получены с помощью производной, совпадают с результатами, найденными ранее.
Подведение итогов
Итак, мы рассмотрели и узнали, каким образом с помощью производной исследовать функцию, а именно найти ее интервалы монотонного возрастания, убывания и точки экстремума.
Список литературы
- «Алгебра и начало анализа 10–11» Алимов Ш.А., Колягин Ю.М. и др.
- Колмогоров А.Н. «Алгебра и начала математического анализа»
- Алгебра, 9 класс. Задачник (Л.И. Звавич, А.Р. Рязановский, П.В. Семенов) – 2008.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Interneturok.
 ru (Источник).
ru (Источник). - Interneturok.ru (Источник).
- Interneturok.ru (Источник).
- Interneturok.ru (Источник).
Домашнее задание
- Исследовать следующие функции:
исчисление — Производная функции является уравнением касательной?
Производная — это мгновенная скорость изменения функции $f(x)$, обычно обозначаемая как $f'(x)$ или $\frac{d}{dx}\begin{pmatrix}f(x)\end {pmatrix}$. Что на самом деле означает мгновенная скорость изменения? Скорость изменения линии — это ее наклон. Наклон линии можно рассчитать, используя две точки на линии: $(x_1,f(x_1))$ и $(x_2,f(x_2))$. Вы, наверное, знаете формулу:
$$\frac{f(x_2)-f(x_1)}{x_2-x_1}.$$
Теперь попробуйте найти скорость изменения чего-то другого, кроме линии. Если вы используете приведенную выше формулу, вы будете вычислять только среднюю скорость изменения функции за этот интервал $[x_1,x_2]$. Это связано с тем, что поведение этой нелинейной функции может резко меняться в течение интервала. Например, если средняя скорость изменения положительна на интервале $[x_1,x_2]$, ничто не мешает функции быстро возрастать до $y>f(x_2)$, а затем уменьшаться до $f(x_2)$ как $x$ приближается к $x_2$ (это просто пример того, как может вести себя нелинейная функция).
Это связано с тем, что поведение этой нелинейной функции может резко меняться в течение интервала. Например, если средняя скорость изменения положительна на интервале $[x_1,x_2]$, ничто не мешает функции быстро возрастать до $y>f(x_2)$, а затем уменьшаться до $f(x_2)$ как $x$ приближается к $x_2$ (это просто пример того, как может вести себя нелинейная функция).
Таким образом, учитывая, что наклон ломается для кривой, отличной от прямой, может быть полезно рассчитать скорость изменения другим способом. Поэтому используется производная. Это мгновенная скорость изменения, потому что она вычисляет наклон, когда точки $x_1$ и $x_2$ становятся произвольно близкими друг к другу. Это приводит к определению предела
$$f'(x)=lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{(x+\Delta x)- x}=lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$$
Легко видеть, что вы берете среднюю скорость изменения между точками $(x,f(x))$ и $(x+\Delta x,f(x+ \Delta x))$ и стремитесь к $\Delta x$ к нулю, чтобы рассчитать мгновенную скорость изменения.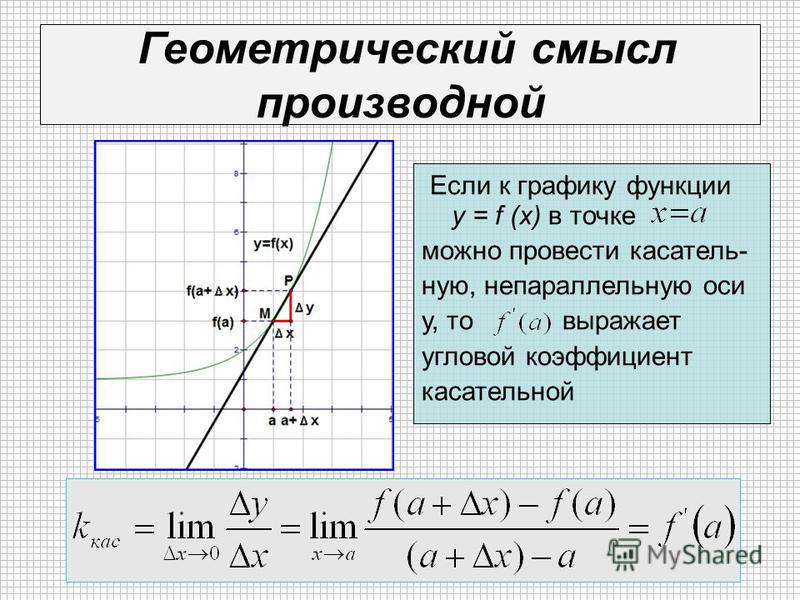 Вы можете свободно думать об этом как о «наклоне» кривой в этой точке.
Вы можете свободно думать об этом как о «наклоне» кривой в этой точке.
Взгляните на это изображение, чтобы увидеть, как вы переходите от так называемой секущей к касательной, когда $\Delta x$ обращается в нуль:
http://www.google.com/imgres?imgurl=http%3A %2F%2Fdj1hlxw0wr920.cloudfront.net% 2Fuserfiles% 2Fwyzfiles% 2F7fd0a10d-1edf-487a-9d2a-4e52d68d181d.gif & imgrefurl = http% 3A% 2F% 2Fwww. mvITD9NKPbtmDM%3A&zoom=1&docid=gyQmTOqjs3b9vM&ei=6RSsU4qjFofi8gHswoGACQ&tbm=isch&client=safari&ved=0CGAQMygnMCc&iact=rc&uact=3&dur=639&page=3&start=25&ndsp=16
x$ и т. д.
Теперь, учитывая, что вы можете думать о производной в точке как о «наклоне» кривой в этой точке, вы можете вычислить уравнение линии, касательной к кривой в этой точке. Предположим, у нас есть кривая $f(x)$, и мы хотим найти уравнение касательной в точке $x=a$. Напомним, что для вычисления уравнения прямой нам нужен наклон и точка. Используя производную от $f$, мы получаем всю необходимую информацию.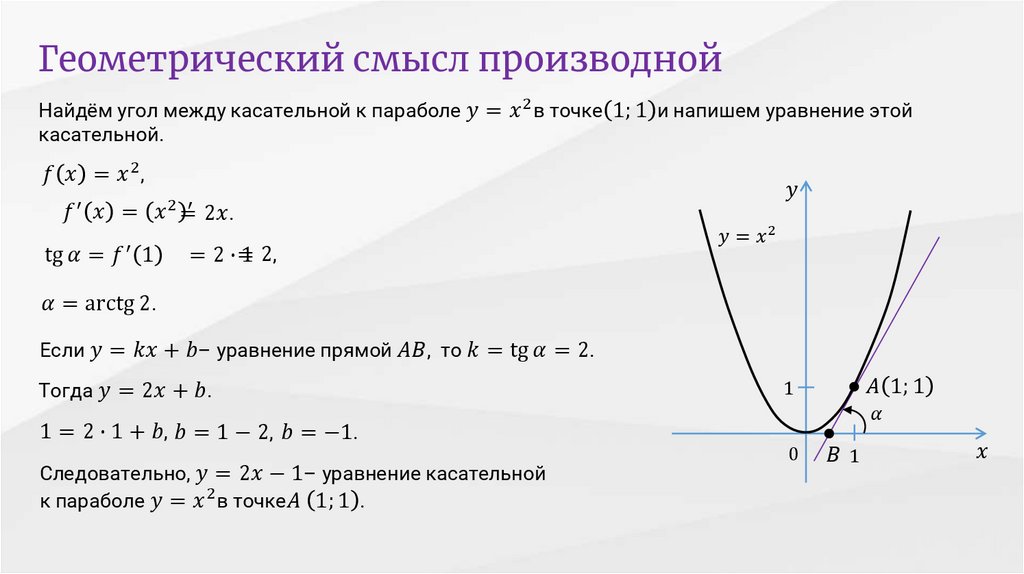 Чтобы найти наклон кривой в точке или наклон линии, касательной к этой точке, мы находим $f'(a)$, производную, оцениваемую в $a$. Затем мы просто вычисляем $f(a)$, чтобы получить нашу точку $(a,f(a))$. Теперь мы находим касательную как
Чтобы найти наклон кривой в точке или наклон линии, касательной к этой точке, мы находим $f'(a)$, производную, оцениваемую в $a$. Затем мы просто вычисляем $f(a)$, чтобы получить нашу точку $(a,f(a))$. Теперь мы находим касательную как
$$y-f(a)=f'(a)(x-a)$$
, так как это стандартное определение линии.
Все это в одном измерении, но его можно расширить в $n$-мерное пространство.
исчисление— Как производные могут представлять касательные?
- Формула, определяющая функцию производной, сама по себе не является уравнением касательной; эта формула дает вам для каждой касательной (одной касательной для каждой точки $(x, f(x))$ графика $f$) наклон этой линии. И наклон номер .
Суть здесь в том, что производная функция — это функция, которая возвращает числа в качестве выходных данных (не прямых, не касательных). Одно и только одно число далеко от каждого допустимого входа $x$.
- Чтобы понять это, вспомним, что для всех точек $(x, f(x))$ графика (таких, что в этой точке есть касательная к графику) эта касательная будет иметь вид:
$$y = mx + b$$.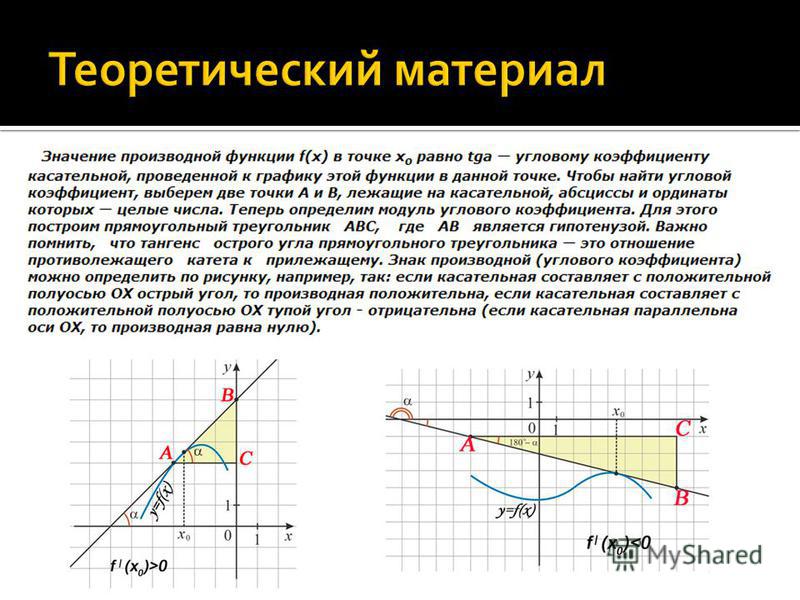
Число $m$ равно 93$ функция).
Итак, для каждого входа $x$, производная дает на выходе число $m$ (то есть наклон) касательной к графику в точке $( x, f(x) )$.
Прелесть в том, что, хотя касательные будут (обычно) иметь разный наклон, хотя выходы функции $f'(x)$ будут разными для разных значений $x$ ( входы), мы часто можем найти правило, определяющее постоянное числовое отношение между значением $x$ и соответствующим наклоном 92$ $=$ $2\х$.
Примечание : это число, которое отправляется обратно в качестве вывода, формально определяется как предел, а именно предел , когда $h$ приближается к $0$ , отношения
$\frac {f (x+h) — f(x)} { (x+h) — x}$ = $\frac{change- in-y}{change-in-x}$
Это показывает, что наклон касательной оказывается идентичным мгновенной скорости роста исходной функции $f$ в точке $( x, f(x))$.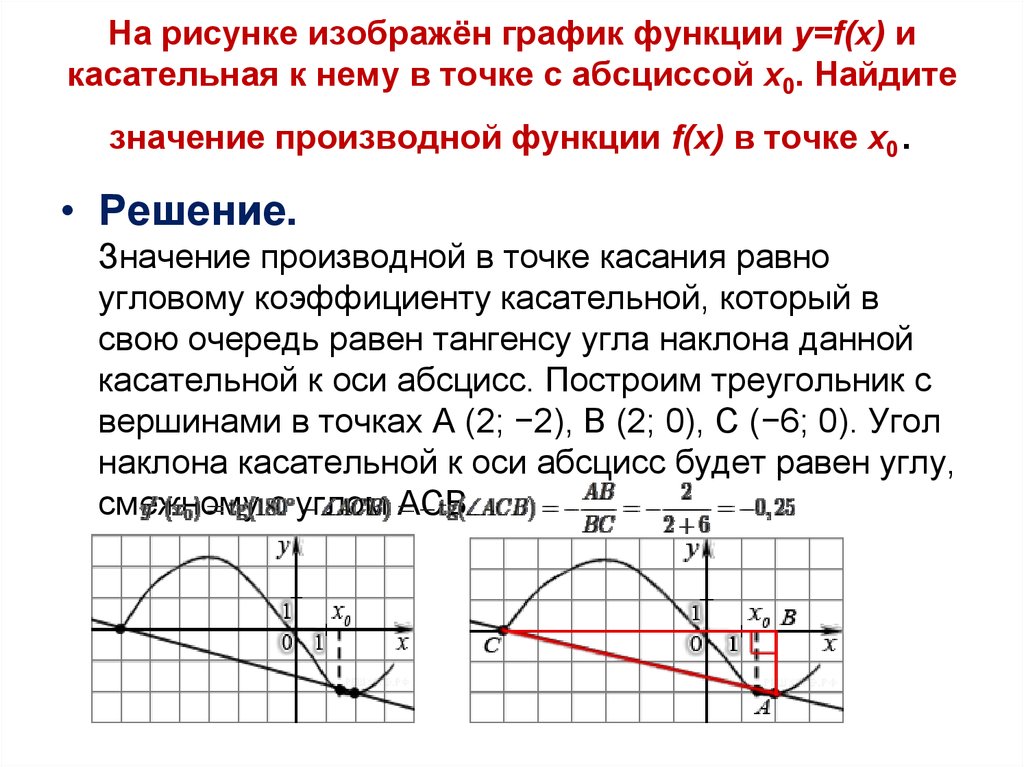

 23. Правый интервал функции
23. Правый интервал функции