Вычитание векторов. Правило вычитания векторов. Геометрия вычитание векторов.
- Альфашкола
- Статьи
- Правила вычитания векторов
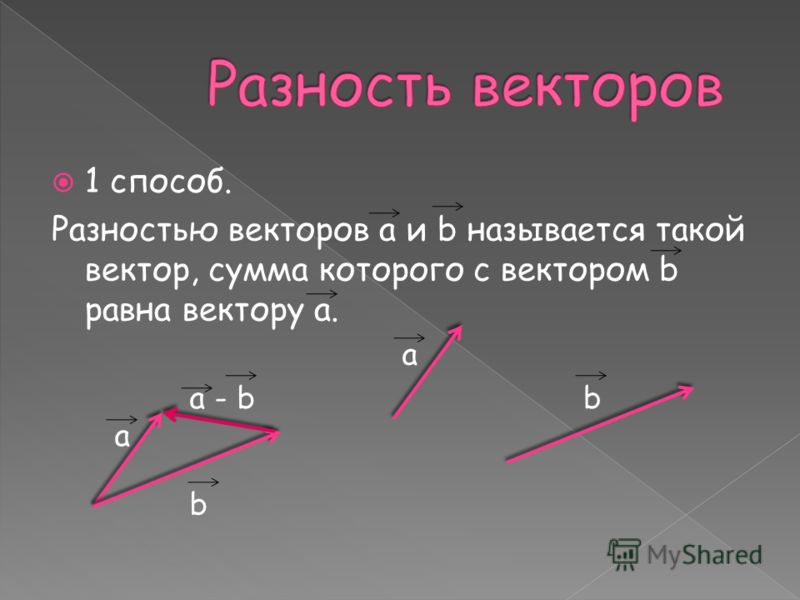
В этой статье мы узнаем как вычесть вектора. Вектор — это величина, имеющая величину размер и направление. Вычитание вектора равносильно добавлению вектора с отрицательным знаком. Разность векторов \(\overline{a}\) и \(\overline{-b}\) равна сумме \(\overline{a}\) и \(\overline{-b}\):
Перемещение векторов
Наша задача — найти способ четко и последовательно представлять векторы. Графически это просто: поскольку мы можем перемещать вектор в любом месте, давайте всегда будем располагать «хвост» вектора в начале координатной плоскости. Теперь, когда хвост вектора помещен в конец другого вектора (помните, мы можем перемещать вектор в любом месте, пока мы сохраняем его направление и длину). Проводим от начала вектора \(\overline{b}\) (вычитаемого вектора) вектор \(\overline{c}\) к началу вектора \(\overline{a}\) (уменьшаемого вектора) получаем разость вектор \(\overline{c}\) :
Теперь, когда хвост вектора помещен в конец другого вектора (помните, мы можем перемещать вектор в любом месте, пока мы сохраняем его направление и длину). Проводим от начала вектора \(\overline{b}\) (вычитаемого вектора) вектор \(\overline{c}\) к началу вектора \(\overline{a}\) (уменьшаемого вектора) получаем разость вектор \(\overline{c}\) :
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Надежда Геннадьевна Зубкова
Репетитор по математике
Стаж (лет)
Образование:
Астраханский педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов по русскому языку и литературе. Подготовка к ОГЭ.
Люблю свой предмет за то, что знание языка делает детей грамотными. Больше предпочитаю традиционную систему обучения. Использую игровые формы, тесты, презентации. Люблю объяснять правила легко и просто с помощью схем и таблиц. Вторая специальность «Изобразительное искусство», поэтому также могу научить Вас рисовать, Также прошла курсы по специальности «Русский язык как иностранный».
Подготовка к ОГЭ.
Люблю свой предмет за то, что знание языка делает детей грамотными. Больше предпочитаю традиционную систему обучения. Использую игровые формы, тесты, презентации. Люблю объяснять правила легко и просто с помощью схем и таблиц. Вторая специальность «Изобразительное искусство», поэтому также могу научить Вас рисовать, Также прошла курсы по специальности «Русский язык как иностранный».
Анна Александровна Журавлева
Репетитор по математике
Стаж (лет)
Образование:
Белорусский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии 7 – 11 классы. Удивительный мир химии не только сложен и загадочен, но и невероятно прекрасен. Вместе мы сможем разобраться даже в самых сложных формулах и задачах! Цель моих занятий – помочь понять предмет, показать логичность и простоту трудных задач. Ведь зачастую интерес пропадает, когда непонятно. А непонимание может развить страх.
Удивительный мир химии не только сложен и загадочен, но и невероятно прекрасен. Вместе мы сможем разобраться даже в самых сложных формулах и задачах! Цель моих занятий – помочь понять предмет, показать логичность и простоту трудных задач. Ведь зачастую интерес пропадает, когда непонятно. А непонимание может развить страх.
Елена Анатольевна Вьюгина
Репетитор по математике
Стаж (лет)
Образование:
БГПУ им.М.Танка
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-6 классов. Люблю математику за её красоту и элегантность. «Математика — это музыка в цифрах.» При обучении всегда провожу параллели с примерами из жизни.
Люблю математику за её красоту и элегантность. «Математика — это музыка в цифрах.» При обучении всегда провожу параллели с примерами из жизни.
Похожие статьи
- Стадии подготовки к экзамену по математике
- Расстояние между точками на координатной прямой
- Как решать показательные уравнения?
- ЕГЭ по математике, профильный уровень. Уравнения
- Как найти точку пересечения плоскости и прямой
- Остаться или уйти после 9 класса: преимущества и недостатки каждого решения
- Основы финансовой грамотности подросткам от психолога
- Как перестать программировать детей на бедность?
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
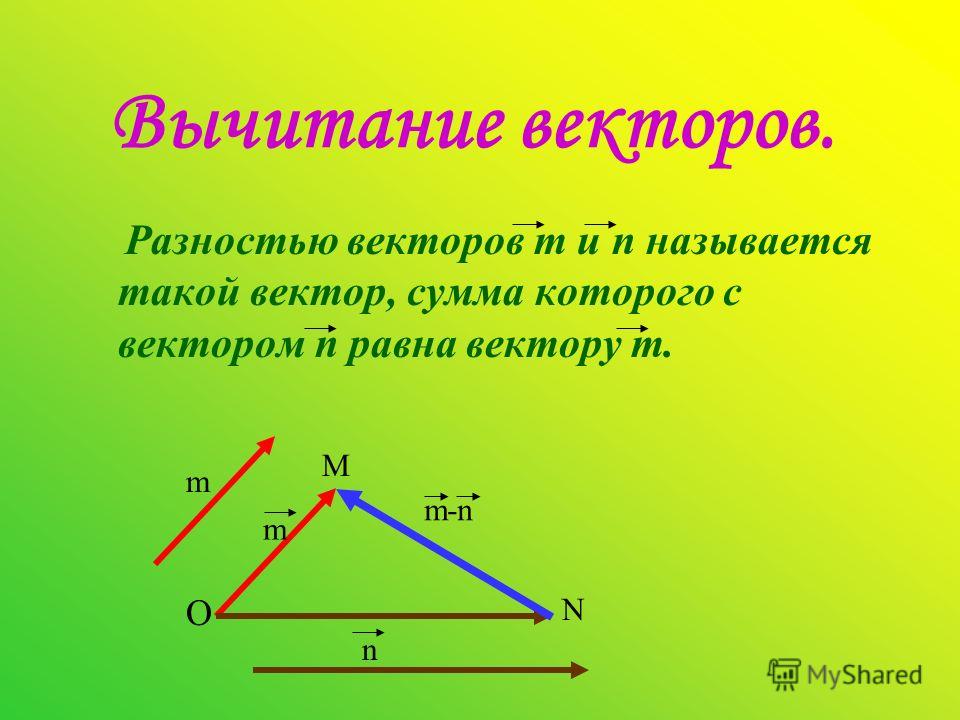
Вычитание векторов.
 Как найти разность векторов
Как найти разность векторовОткладывание вектора от данной точки
Для того, чтобы ввести разность векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.
Определение 1
Если точка $A$ начала какого-либо вектора $\overrightarrow{a}$, то говорят, что вектор $\overrightarrow{a}$ отложен от точки $A$ (рис. 1).
Рисунок 1. $\overrightarrow{a}$ отложенный от точки $A$
Введем следующую теорему:
Теорема 1
От любой точки $K$ можно отложить вектор $\overrightarrow{a}$ и притом только один.
Доказательство.
Существование: Здесь нужно рассмотреть два случая:
Вектор $\overrightarrow{a}$ — нулевой.
В этом случае, очевидно, что искомый вектор — вектор $\overrightarrow{KK}$.
Вектор $\overrightarrow{a}$ — ненулевой.
Обозначим точкой $A$ — начало вектора $\overrightarrow{a}$, а точкой $B$ — конец вектора $\overrightarrow{a}$.
 Проведем через точку $K$ прямую $b$ параллельную вектору $\overrightarrow{a}$. Отложим на этой прямой отрезки $\left|KL\right|=|AB|$ и $\left|KM\right|=|AB|$. Рассмотрим векторы $\overrightarrow{KL}$ и $\overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $\overrightarrow{a}$ (рис. 2)
Проведем через точку $K$ прямую $b$ параллельную вектору $\overrightarrow{a}$. Отложим на этой прямой отрезки $\left|KL\right|=|AB|$ и $\left|KM\right|=|AB|$. Рассмотрим векторы $\overrightarrow{KL}$ и $\overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $\overrightarrow{a}$ (рис. 2)
Рисунок 2. Иллюстрация теоремы 1
Единственность: единственность сразу следует из построения, проведенного в пункте «существование».
Теорема доказана.
Вычитание векторов. Правило первое
Пусть нам даны векторы $\overrightarrow{a}$ и $\overrightarrow{b}$.
Определение 2
Разностью двух векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ называется такой вектор $\overrightarrow{c}$, который при сложении с вектором $\overrightarrow{b}$ дает вектор $\overrightarrow{a}$, то есть
\[\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{a}\]
Обозначение: $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{c}$.
Построение разности двух векторов рассмотрим с помощью задачи.
Пример 1
Пусть даны векторы $\overrightarrow{a}$ и $\overrightarrow{b}$. Построить вектор $\overrightarrow{a}-\overrightarrow{b}$.
Решение.
Построим произвольную точку $O$ и отложим от нее векторы $\overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OB}=\overrightarrow{b}$. Соединив точку $B$ с точкой $A$, получим вектор $\overrightarrow{BA}$ (рис. 3).
Рисунок 3. Разность двух векторов
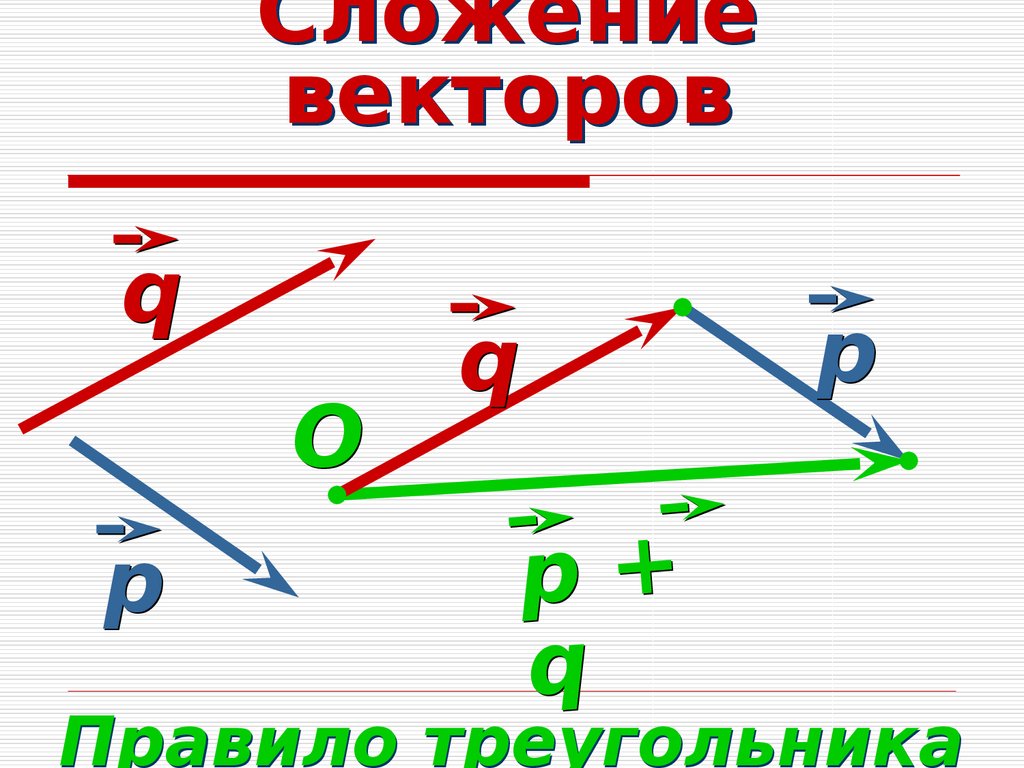
По правилу треугольника для построения суммы двух векторов видим, что
То есть
\[\overrightarrow{b}+\overrightarrow{BA}=\overrightarrow{a}\]
Из определения 2, получаем, что
\[\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{BA}\]
Ответ: $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{BA}$.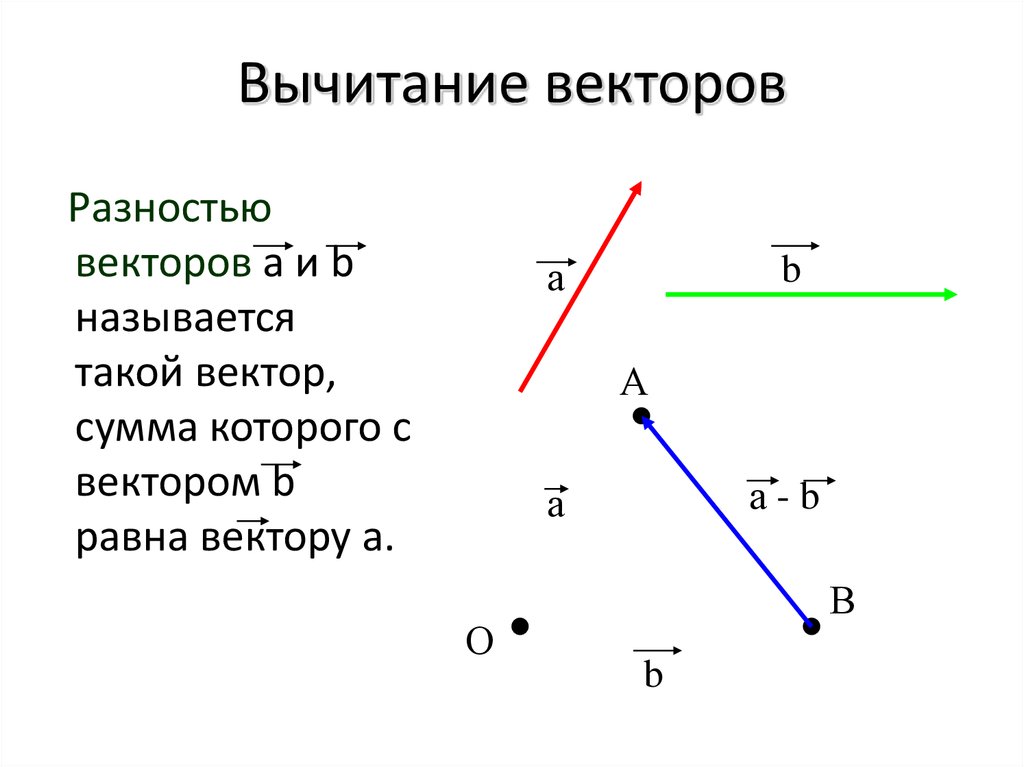
Из этой задачи получаем следующее правило для нахождения разности двух векторов. Чтобы найти разность $\overrightarrow{a}-\overrightarrow{b}$ нужно от произвольной точки $O$ отложить векторы $\overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OB}=\overrightarrow{b}$ и соединить конец второго вектор с концом первого вектора.
Вычитание векторов. Правило второе
Вспомним следующее необходимое нам понятие.
Определение 3
Вектор $\overrightarrow{a_1}$ называется произвольным для вектора $\overrightarrow{a}$, если эти векторы противоположно направлены и имеют равную длину.
Обозначение: Вектор $(-\overrightarrow{a})$ противоположный для вектора $\overrightarrow{a}$.
Для того чтобы ввести второе правило для разности двух векторов, нам необходимо в начале ввести и доказать следующую теорему.
Теорема 2
Для любых двух векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ справедливо следующее равенство:
\[\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})\]
Доказательство.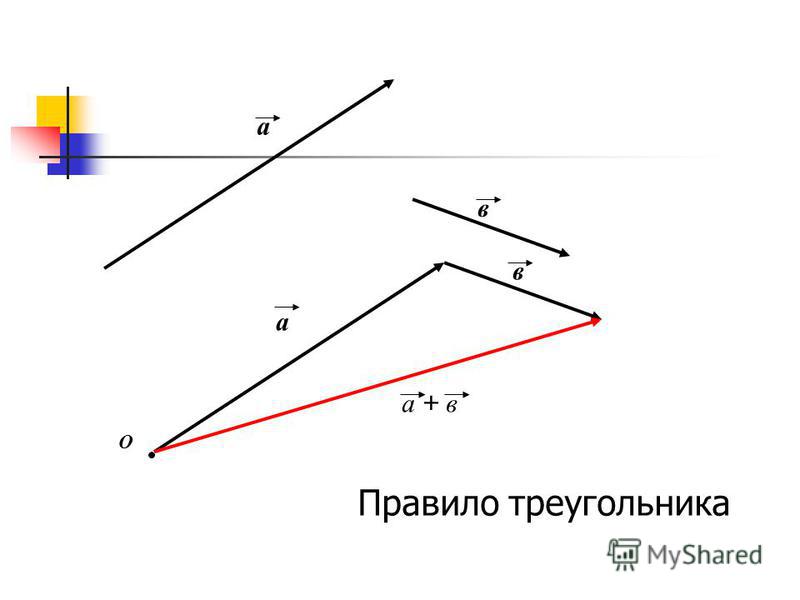
По определению 2, имеем
Прибавим к обеим частям вектор $\left(-\overrightarrow{b}\right)$, получим
Так как векторы $\overrightarrow{b}$ и $\left(-\overrightarrow{b}\right)$ противоположны, то $\overrightarrow{b}+\left(-\overrightarrow{b}\right)=\overrightarrow{0}$. Имеем
Теорема доказана.
Из этой теоремы получаем следующее правило для разности двух векторов: Чтобы найти разность $\overrightarrow{a}-\overrightarrow{b}$ нужно от произвольной точки $O$ отложить вектор $\overrightarrow{OA}=\overrightarrow{a}$, затем от полученной точки $A$ отложить вектор $\overrightarrow{AB}=-\overrightarrow{b}$ и соединить начало первого вектора с концом второго вектора.
Пример задачи на понятие разности векторов
Пример 2
Пусть дан параллелограмм $ADCD$, диагонали которого пересекаются в точке $O$. $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{AD}=\overrightarrow{b}$ (рис. 4). Выразить через векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ следующие векторы:
а) $\overrightarrow{DC}+\overrightarrow{CB}$
б) $\overrightarrow{BO}-\overrightarrow{OC}$
Рисунок 4. Параллелограмм
Параллелограмм
Решение.
а) Произведем сложение по правилу треугольника, получим
\[\overrightarrow{DC}+\overrightarrow{CB}=\overrightarrow{DB}\]
Из первого правила разности двух векторов, получаем
\[\overrightarrow{DB}=\overrightarrow{a}-\overrightarrow{b}\]
б) Так как $\overrightarrow{OC}=\overrightarrow{AO}$, получим
\[\overrightarrow{BO}-\overrightarrow{OC}=\overrightarrow{BO}-\overrightarrow{AO}\]
По теореме 2, имеем
\[\overrightarrow{BO}-\overrightarrow{AO}=\overrightarrow{BO}+\left(-\overrightarrow{AO}\right)=\overrightarrow{BO}+\overrightarrow{OA}\]
Используя правило треугольника, окончательно имеем
\[\overrightarrow{BO}+\overrightarrow{OA}=\overrightarrow{BA}=-\overrightarrow{AB}=-\overrightarrow{a}\]
Геометрия Сложение и вычитание векторов
Материалы к уроку
Конспект урока
3. Сложение и вычитание векторов
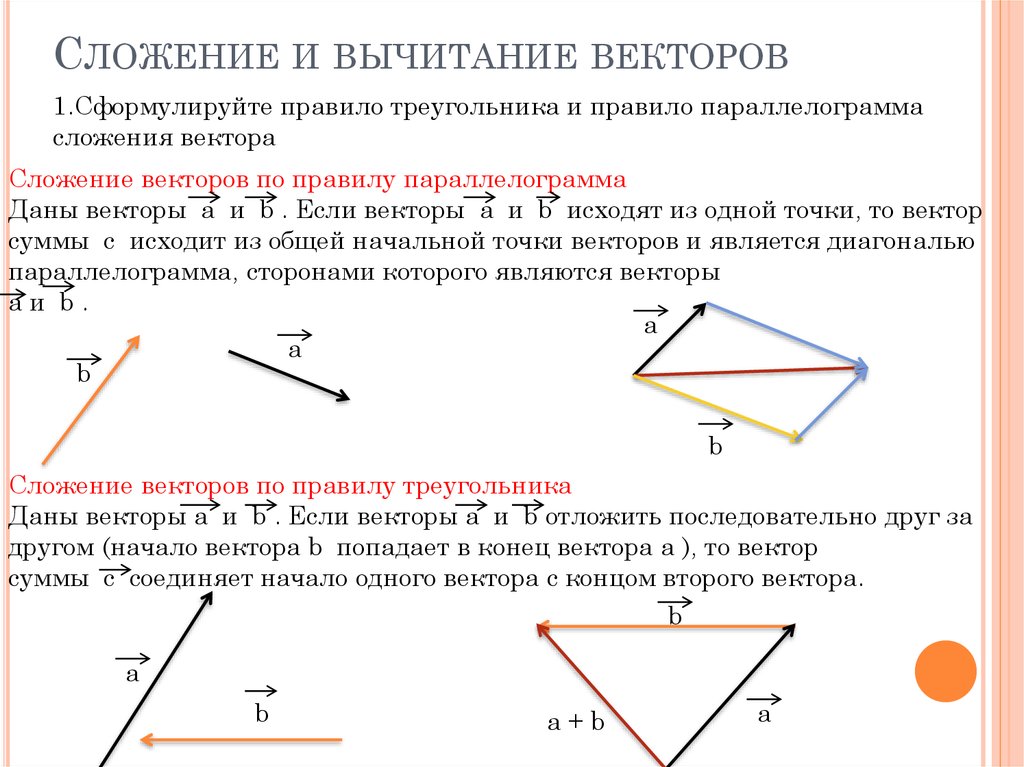
Сложение и вычитание векторов
|
Введем правило сложения двух векторов. Пусть нам даны два неколлинеарных вектора a и b. Отложим от произвольной точки пространства А вектор АВ, равный вектору а. Затем от точки В отложим вектор ВС, равный вектору b. Вектор АС называется суммой векторов а и b. Нужно отметить, что сумма векторов не зависит от выбора точки А. Это правило сложения векторов называется правилом треугольника. |
Текст Сложение двух векторов Рисунок двух неколлинеарных векторов, треугольник, две стороны параллельны данным векторам
|
|
При сложении неколлинеарных векторов можно воспользоваться правилом параллелограмма. Пусть даны векторы а и b. От произвольной точки А отложим векторы АВ и АС, равные соответственно а и b. |
Текст Правило треугольника Рисунок параллелепипеда
|
|
Решим задачу №327 под буквой а. На рисунке изображен параллелепипед ABCDA1B1C1D1.Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов AB и A1D1 . Воспользуемся правилом параллелограмма. К вектору АВ прибавим вектор АD, равный вектору A1D1. Суммой этих векторов будет диагональ основания параллелепипеда, то есть вектор АС. |
Текст №327(а) Рисунок параллелепипеда
По правилу параллелограмма , |
|
Напомним свойства сложения векторов, так как они ни чем не отличаются от свойств сложения векторов в планиметрии: Для любых трех векторов а, бэ и це, выполняются равенства 1) переместительный закон 2) сочетательный закон |
|
|
Введем определение противоположных векторов. Два вектора называются противоположными, если их длины равны и они противоположно направлены Вектор минус а противоположен вектору а
Вектор DF противоположен вектору FD, и равен минус вектор FD
|
Противоположные векторы
Если и – противоположные, то | |=| |, .
и – противоположные, = – |
|
Определим вычитание векторов
|
Текст Вычитание векторов Разностью векторов a и b называется такой вектор, сумма которого с вектором b равна вектору a.
|
|
Разность можно найти как сумму вектора с противоположным вектором вектору . |
|
|
Существует правило для трех точек.
Любой вектор можно представить как разность двух векторов, проведенных из одной точки. Добавляем третью точку (любую) и задаем разность из вектора, проведенного из этой точки в конец данного вектора минус вектор, проведенный в начало. |
Текст Правило трех точек
Рисунок разности векторов
(по ходу правила строить сначала вектор ВК затем вектор АК и АВ) |
|
Решим задачу №332 На рисунке изображен параллелепипед ABCDA1B1C1D1 Представьте векторы АВ1 и DK в виде разности двух векторов, начала и концы которых совпадают с отмеченными на рисунке точками.
|
Текст Задача №332 Рисунок параллелепипеда
|
|
Решение. Рассмотрим вектор АВ1 и воспользуемся правилом трех точек. Третьей точкой удобно взять точку А1. Вектор, проведенный в конец то есть в точку В1 будет А1В1 и в начало точку А – вектор А1А. Получаем АВ1 равно А1В1 минус А1А. |
Текст Задача №332 Решение. Рисунок прежний
|
|
Выполним это же задание для вектора DK. Здесь третьей точкой удобно взять точку D1. Вектор в конец — D1K, в начало — D1D. Получим вектор DK равен D1K минус D1D. |
Текст Задача №332
|
Комментарий, было упущено свойства сложения векторов, и определение противоположного вектора.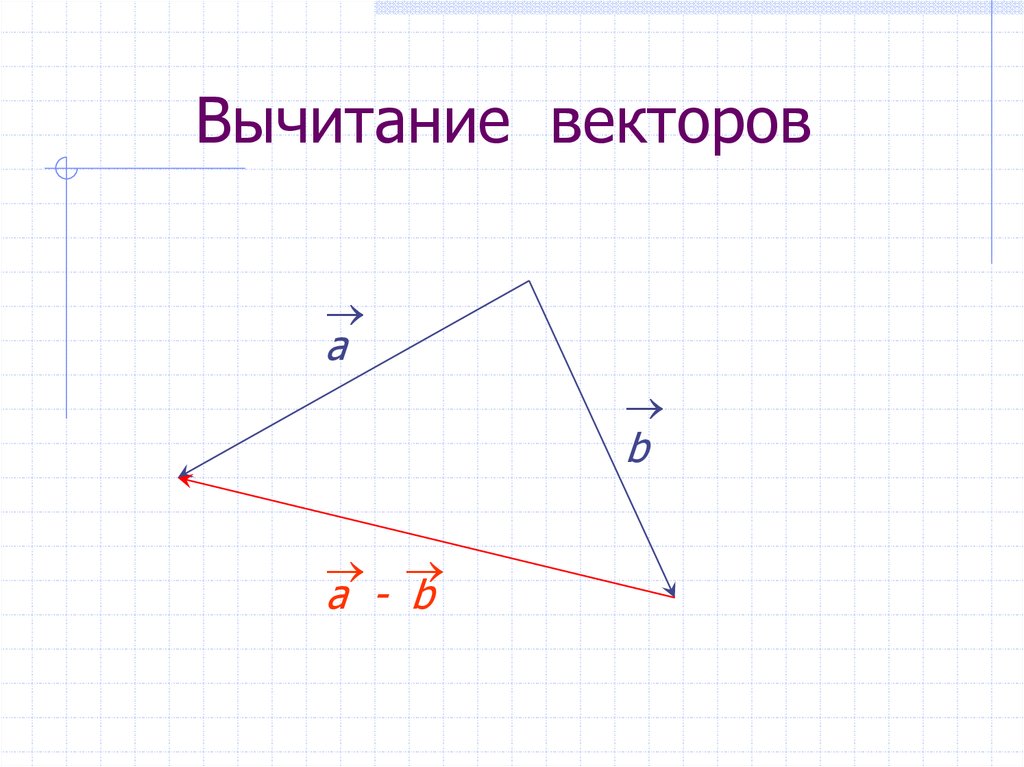
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов… Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре… Динамика и детерминанты показателей газоанализа юных спортсменов в восстановительном периоде после лабораторных нагрузок до отказа. Интересное: Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
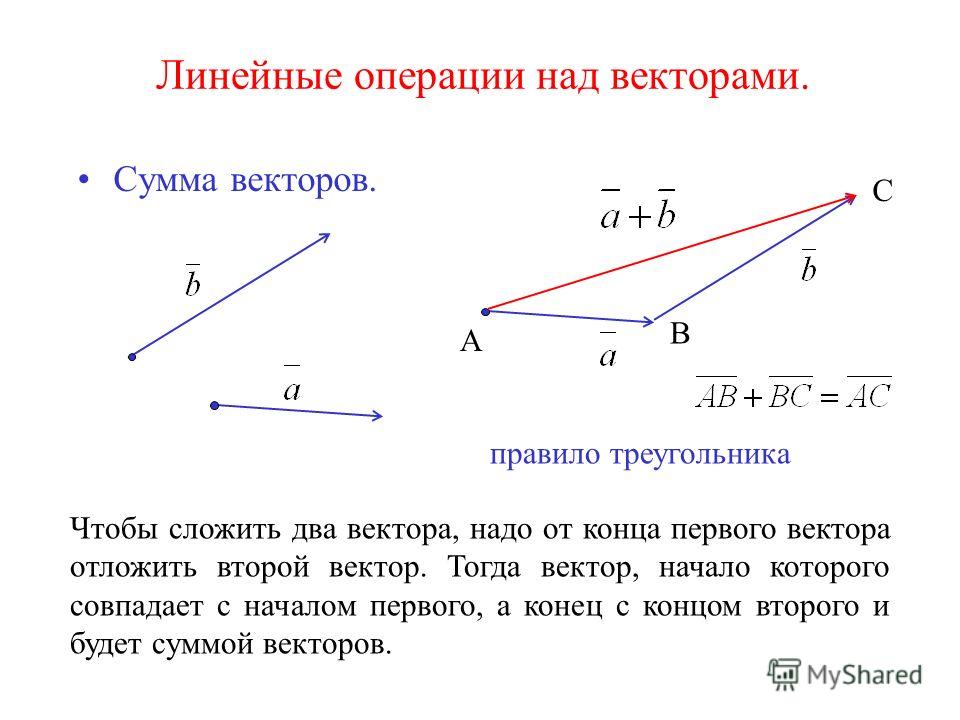
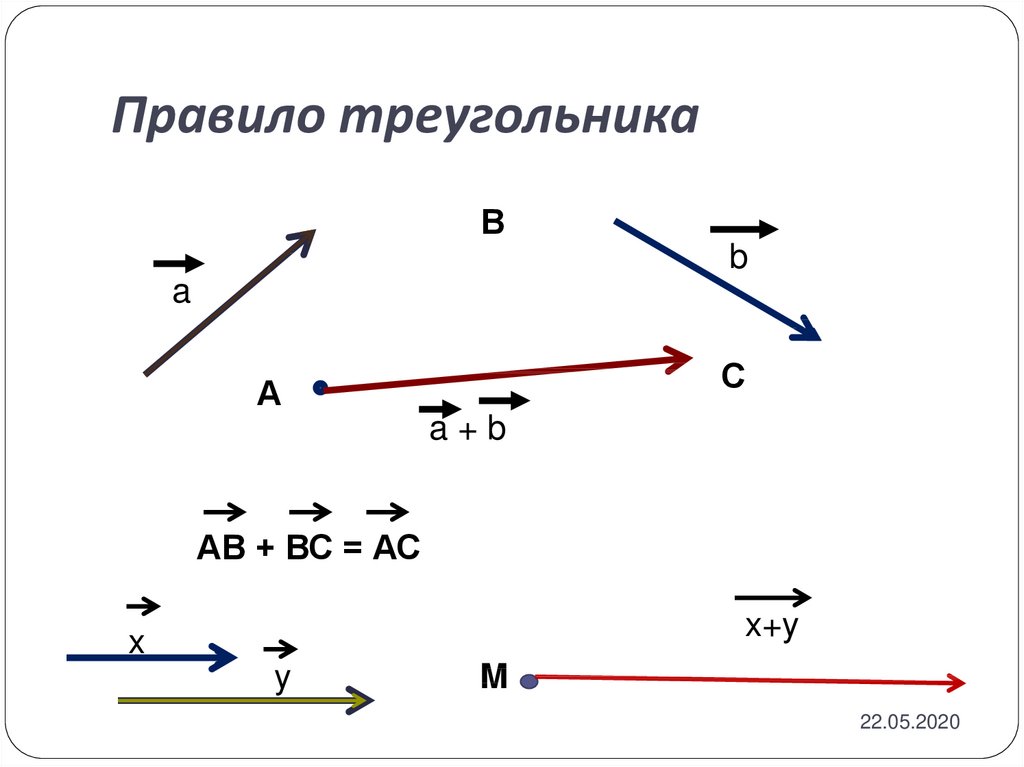
⇐ ПредыдущаяСтр 2 из 11Следующая ⇒ Линейными операциями над векторами называется сложение, вычитание векторов и умножение вектора на число. Результатом сложения векторов является их сумма. Сумма векторов и обозначается . Существует два правила сложения двух векторов: правило треугольника и правило параллелограмма. Правило треугольника Чтобы сложить векторы и , надо взять произвольную точку и от нее отложить последовательно сначала вектор , затем вектор . Вектор, начало которого совпадает с началом вектора (т.е. первого вектора), а конец – с концом вектора (т.е. второго вектора), есть искомая сумма. На рис. 4 .
По правилу треугольника можно складывать любые векторы. Коротко правило треугольника можно записать так: для любых трех точек А,В и С . Правило параллелограмма Чтобы сложить векторы и , надо привести их к общему началу, т.
По правилу параллелограмма можно складывать тольконеколлинеарные векторы. Свойства сложения векторов: 10. . 20. . 30. . 40. . Суммой трех векторов и называется вектор . Учитывая свойство 40, скобки можно опустить и обозначать сумму в виде . Суммой nвекторовназывается вектор и обозначается так: . При построении суммы n векторов пользуются правилом многоугольника. Правило многоугольника Чтобы найти сумму nвекторов, надо взять произвольную точку и отложить от нее последовательно эти векторы. Разностью векторов и называется такой вектор , что . Разность – это результат вычитания векторов. Разность векторов и обозначается так: . Правило построения разности двух векторов Чтобы построить разность векторов и , надо привести их к общему началу. Тогда вектор, начало которого совпадает с концом второго вектора (т.е. вектора ), а конец – с концом первого (т.е. ), есть искомая разность .
На рис. 6 .
По правилу треугольника , откуда получаем краткую запись правила нахождения разности векторов: . Умножение вектора на число Рассмотрим еще одну линейную операцию над векторами – умножение вектора на число. Результатом этой операции является произведение вектора на число. Произведением вектора на действительное число a называется вектор , обозначаемый через и удовлетворяющий двум условиям: 1) его длина ; 2) если a 0, то ; если <0, то . Алгоритм построения произведения вектора числоa таков. Берем произвольную точку М. Проводим луч ,сонаправленный с вектором , если a 0, и противоположно направленный с вектором , если <0. На луче от начала М откладываем отрезок MP, длина которого в раз больше длины вектора .Вектор — искомый вектор . Продемонстрируем этот алгоритм на конкретном примере. Построим вектор , если — данный вектор. Возьмем произвольную точку А. Так как <0, то проводим луч (рис. 7). На луче строим такую точку С, что .
⇐ Предыдущая12345678910Следующая ⇒ Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… |
Правила сложение векторов по физике
Тестирование онлайн
Вектор
Вектор – это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало – точка. Модуль вектора (абсолютная величина) – длина этого направленного отрезка.
Конец вектора совпадает со стрелкой, начало – точка. Модуль вектора (абсолютная величина) – длина этого направленного отрезка.
Если начало вектора совпадает с его концом, получим нулевой вектор.
Два вектора являются равными, если их длина одинаковая и они имеют одинаковое направление. Они совмещаются при переносе.
На рисунке только вектор a равен вектору b. Вектор c им не равен, так как направлен в противоположную сторону
Вектор -c – это вектор c, но противоположного направления. Тогда
Проекция вектора
Проекция вектора на ось имеет положительное значение в том случае, когда направление вектора совпадает с направлением оси. Отрицательное значение – в противоположном случае.
Спроецируем вектор перемещения на ось Ox и на ось Oy. Для того, чтобы получить проекцию необходимо из координаты конца вектора отнять координату начала. На ось ОХ: sx=x-x, на ось ОУ: sy=y-y.
Частные случаи, когда проекция на ось Ox или Oy нулевая.
Сумма составляющих вектора по осям равна данному вектору, т.е.
Сложение векторов
Правило параллелограмма: диагональ параллелограмма – сумма двух векторов с общим началом.
Правило треугольника: от конца первого вектора отложить второй вектор, тогда их суммой будет вектор, начало которого совпадает с началом первого вектора, а конец с концом второго вектора.
Рассмотрим правила на примерах.
Вычитание векторов
Вычитание векторов – это сумма положительного и отрицательного вектора.
Упражнения
Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть численно равной одному из составляющих векторов?
Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть меньше меньшего из составляющих векторов?
Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .
Существование: Имеем два следующих случая:
Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .
Из данного выше построения сразу же будет следовать единственность данного вектора.
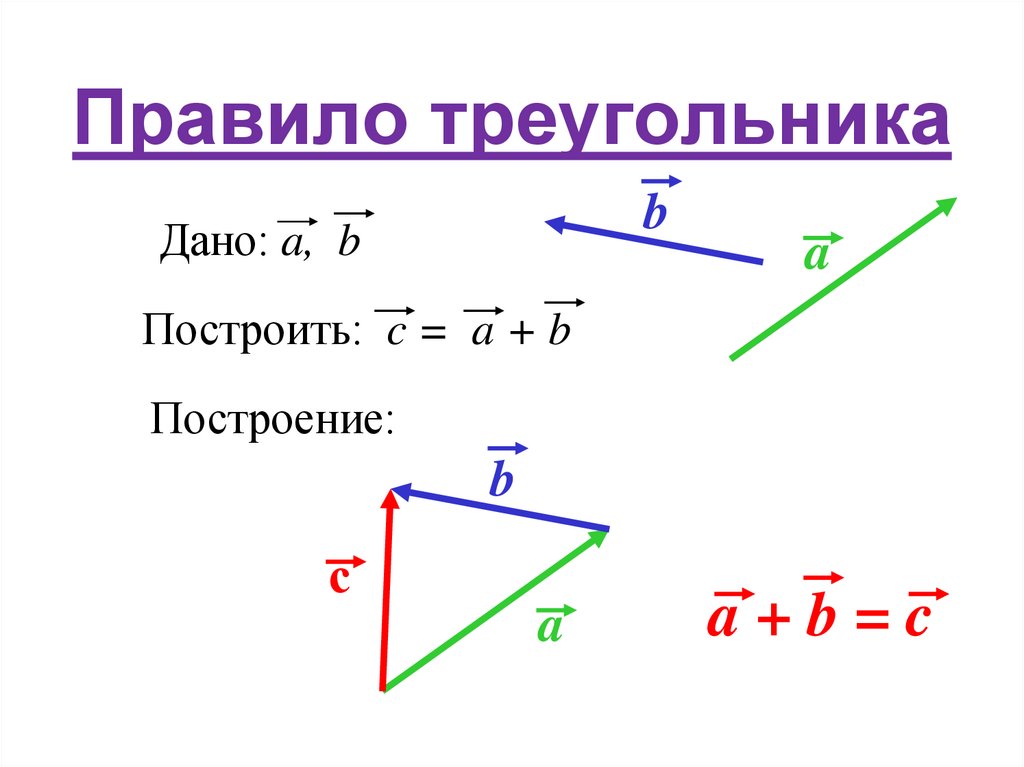
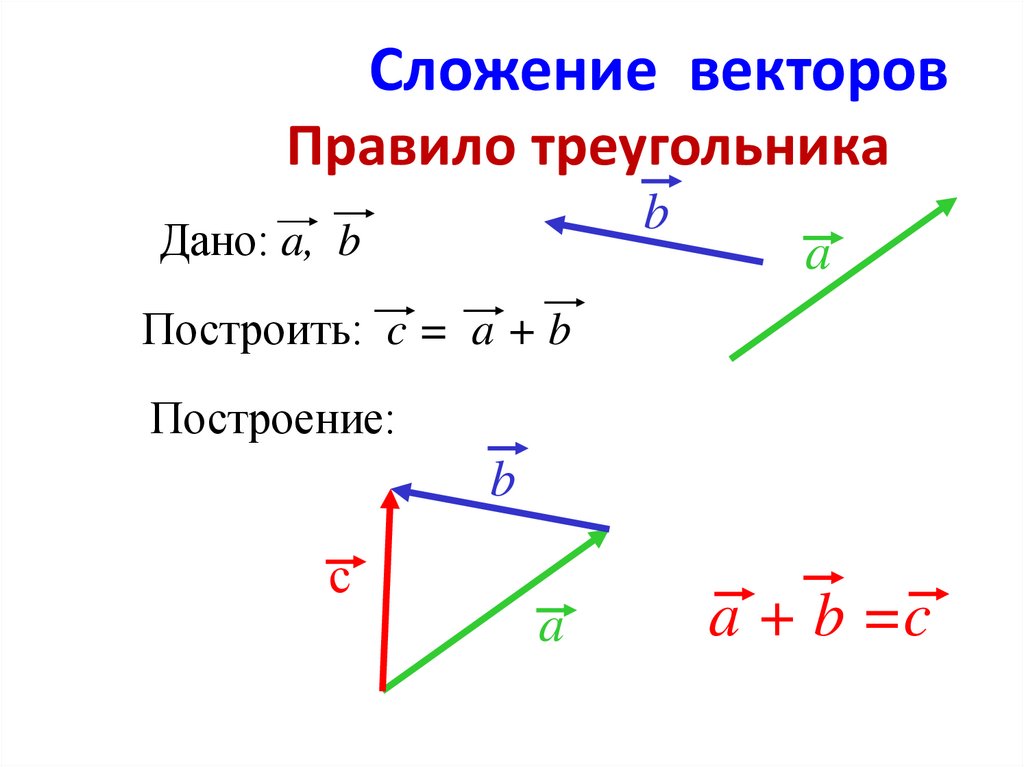
Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + >
ight) )
Отметим несколько свойств сложения двух векторов:
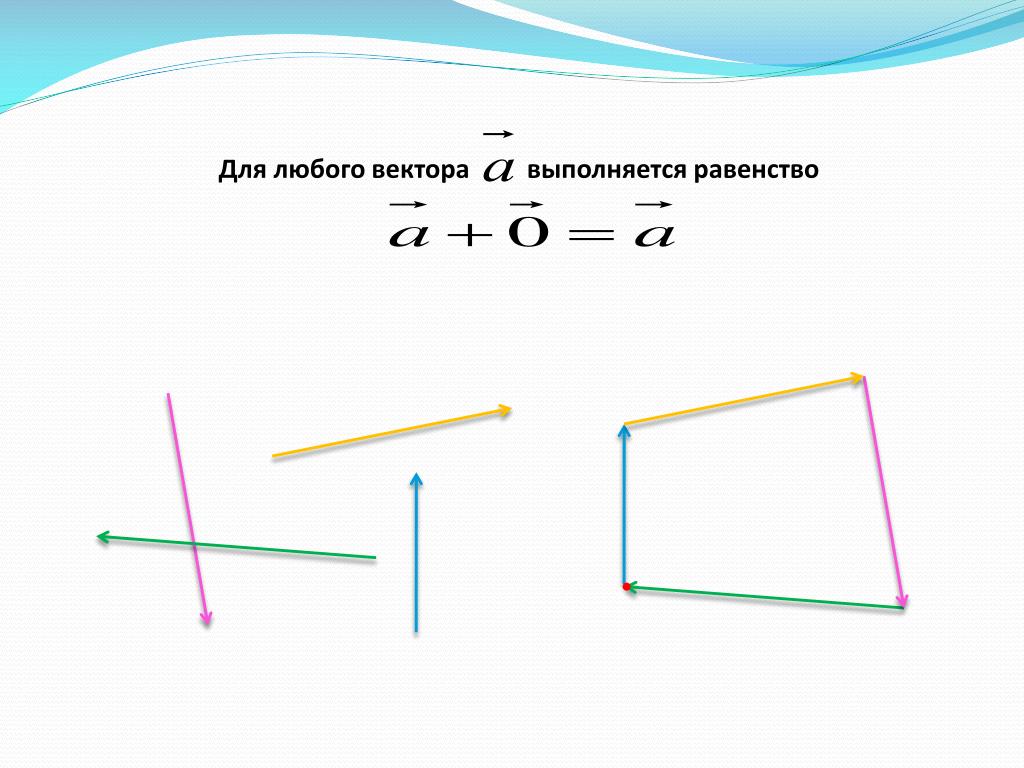
Для произвольного вектора ( overrightarrow ) выполняется равенство
Для произвольных точек ( A, B и C ) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов.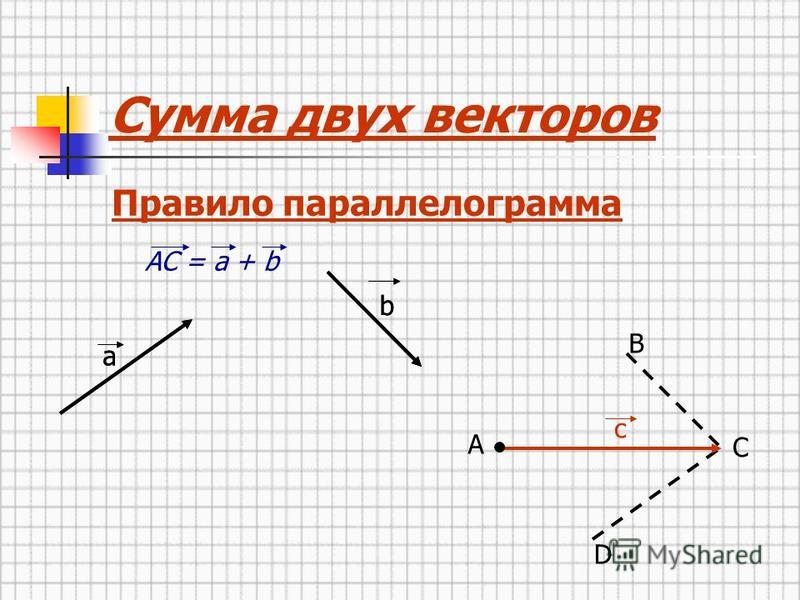 Тогда оно будет носить название правила многоугольника.
Тогда оно будет носить название правила многоугольника.
Разность векторов. Вычитание векторов
Разность двух одинаковых векторов равна нулевому вектору :
( vec – vec = vec <0>)
Длина нулевого вектора равна нулю:
( left| vec <0>
ight| = 0 )
Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec – vec = left( <– , – , – >
ight) )
Умножение вектора на число
Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .
Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:
Длина вектора ( overrightarrow ) равна ( left|overrightarrow
ight|=left|k
ight||overrightarrow| ) ;
Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )
Обозначение: ( overrightarrow=koverrightarrow ) .
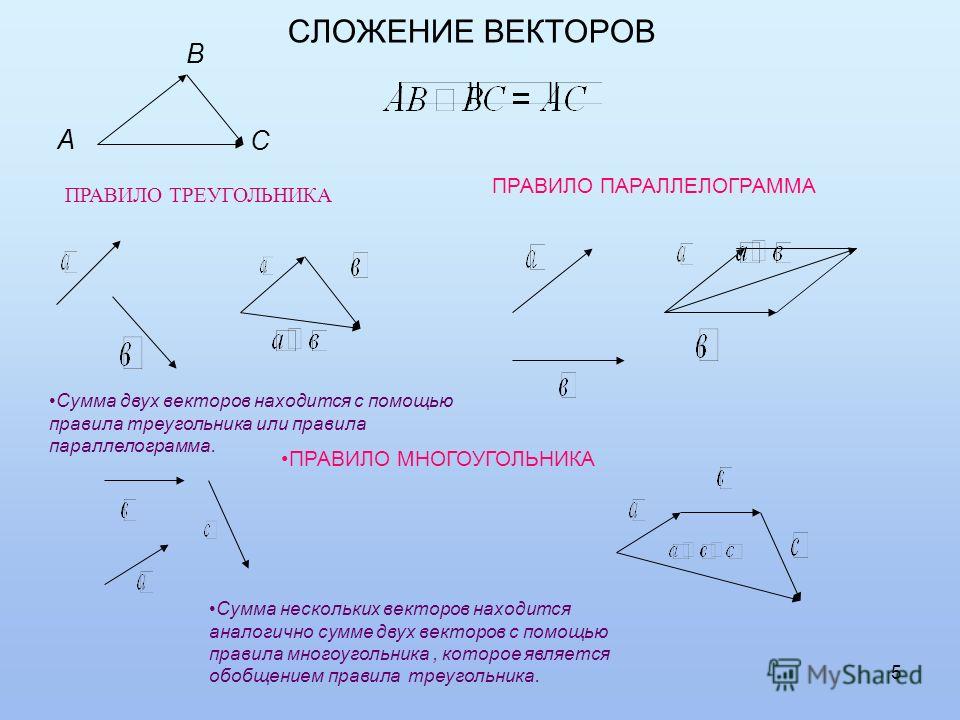
Векторы можно складывать способом параллелограмма и способом многоугольника.
Сложение векторов способом параллелограмма: сумма двух векторов а и Ъ, направленных под углом а (рис. 1.1, а), равна диагонали параллелограмма, сторонами которого являются складываемые векторы (т. е. векторы складываются геометрически).
С помощью символов эта операция записывается так: а + Ь = с.
При сложении этих векторов можно пользоваться правилом «треугольника». В этом случае к концу одного вектора приставляют начало второго (порядок сложения векторов не существен), тогда их суммой будет вектор с, начало которого совпадает с началом первого вектора, а конец — с концом второго вектора (рис. 1.2, б).
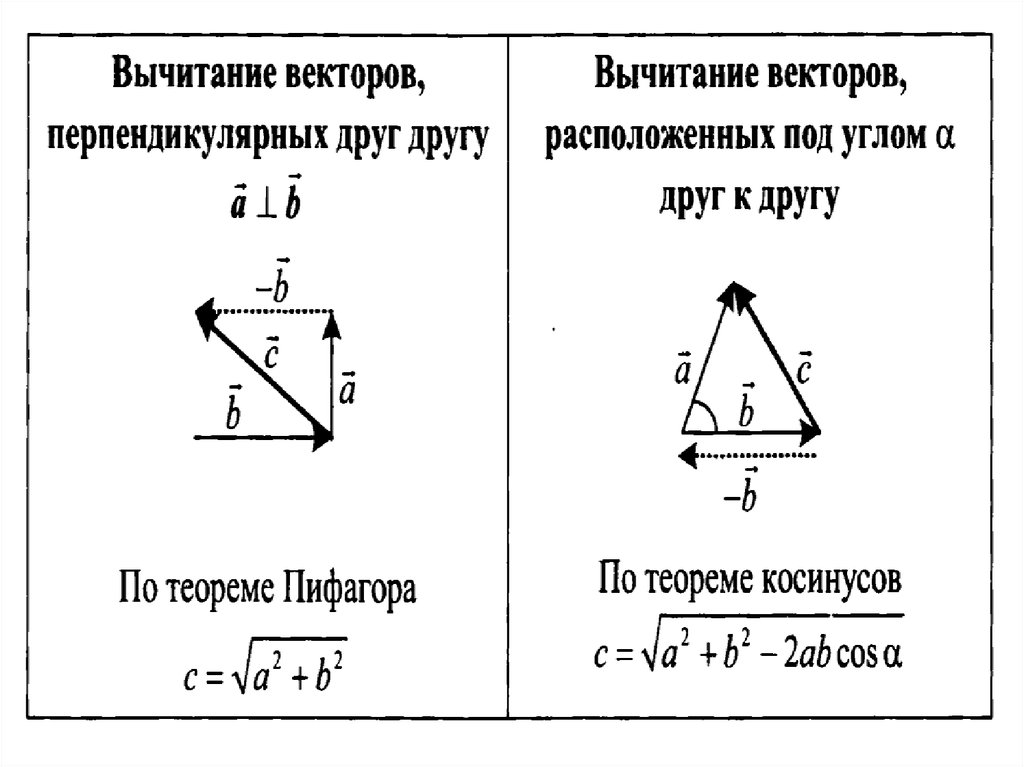
Длину вектора суммы (его модуль) определяют по теореме косинусов (рис. 1.2):
А= tJo 2 +b 2 -2abcos(180-a) = %/a 2 +b 2 + 2abcosa,
где a — угол между векторами а и Б.
Сложение векторов способом многоугольника (чаще применяется при сложении трех и более векторов): к концу первого вектора а приставляют начало второго Б, к концу второго — начало третьего сит. д., тогда результирующий вектор ё представляет собой направленный отрезок, начало которого совпадает с началом первого вектора, а конец — с концом последне-
д., тогда результирующий вектор ё представляет собой направленный отрезок, начало которого совпадает с началом первого вектора, а конец — с концом последне-
го d (рис. 1.3). Результирующий вектор ё не зависит от последовательности, в котором складываются заданные векторы.
Вычитание векторов — действие, обратное сложению векторов. Действительно, разность векторов а и Б можно представить как с = а -Ь = а + (-Б), т. е. для нахождения вектора разности необходимо сложить два вектора d и -Б, где -Б — противоположный вектор (рис. 1.4, а).
Другое правило вычитания векторов: чтобы произвести вычитание векторов а и Б (рис. 1.4, б), нужно совместить их начала и провести результирующий вектор с = а – Б из конца вычитаемого вектора – Б в конец уменьшаемого вектора а.
Сложение и вычитание векторов
Сумма векторов
Пусть даны два вектора а = \(\overrightarrow{OA}\) и b = \(\overrightarrow{OB}\) (рис.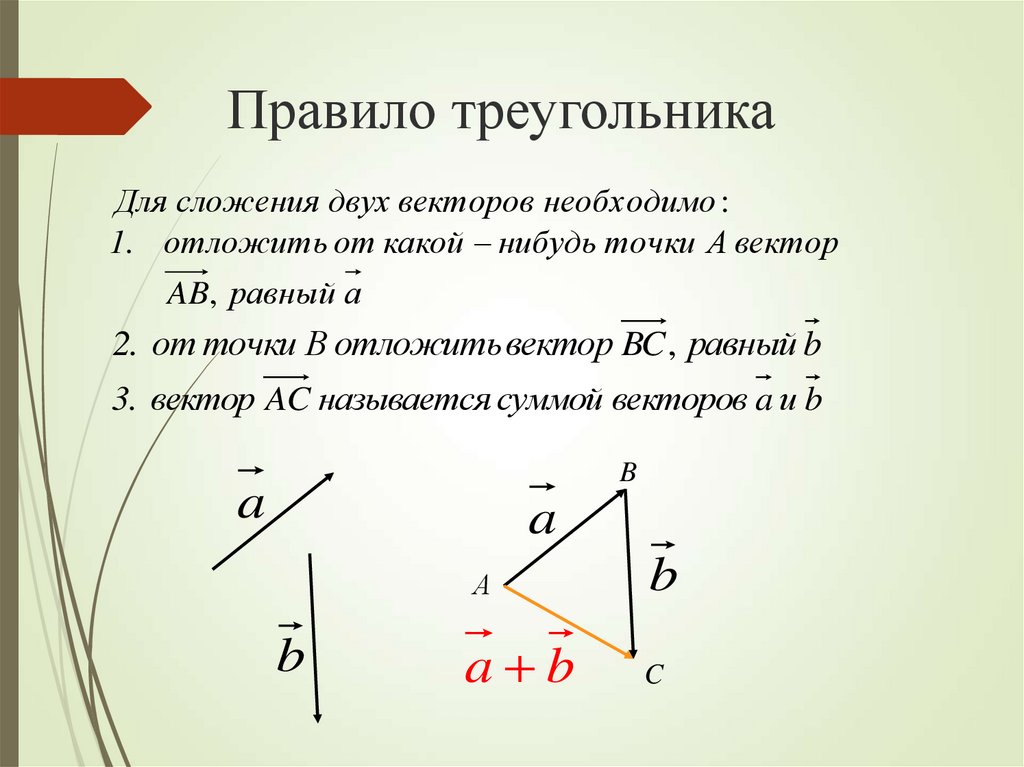 5).
5).
От точки А отложим отрезок АС такой, что \(\overrightarrow{AC}\) = b. Тогда, вектор с = \(\overrightarrow{OC}\) называется суммой векторов а и b и
обозначается а + b.
Таким образом, \(\overrightarrow{OA}\) + \(\overrightarrow{AC}\) = \(\overrightarrow{OC}\). Это равенство называют
правилом треугольника сложения двух векторов.
Oчевидно, что это правило справедливо и в том случае, когда точки О, А и В лежат на одной прямой (рис. 6, 7). В частности, а + 0 = а.
Сложение векторов обладает следующими свойствами:
1. Свойство коммутативности (перестановочности): для любых векторов а и b
а + b = b + а. (1)
2. Свойство ассоциативности (сочетательности): для любых векторов а, b и с
(а + b) + с = а + (b + с).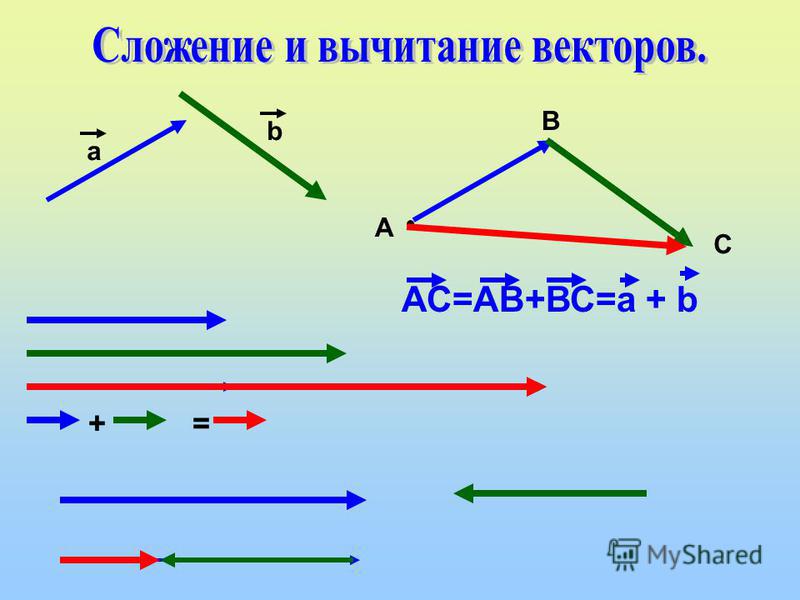 (2)
(2)
1. Пусть a = \(\overrightarrow{OA}\), b = \(\overrightarrow{OB}\). Рассмотрим случай, когда точки О, А и В не лежат на одной прямой. На отрезках ОА и ОВ построим параллелограмм OACB (рис. 8).
Тогда |ОА| = |ВС|, (ОА) || (ВС) и |ОВ| = |АС|, (ОВ) || (АС), как противоположные стороны параллелограмма. Следовательно,
а = \(\overrightarrow{OA}\)= \(\overrightarrow{BC}\), b = \(\overrightarrow{OB}\) = \(\overrightarrow{AC}\),
и поэтому
а + b = \(\overrightarrow{OA}\)+ \(\overrightarrow{AC}\) = \(\overrightarrow{OC}\),
b + а = \(\overrightarrow{OB}\) + \(\overrightarrow{BC}\) = \(\overrightarrow{OC}\),
что и доказывает равенство (1).
Для случая, когда точки О, А, В лежат на одной прямой, доказательство можно провести самостоятельно.
2. От некоторой точки О отложим вектор \(\overrightarrow{OA}\) = а, от точки А отложим вектор \(\overrightarrow{AB}\) = b и, наконец, от точки В отложим вектор \(\overrightarrow{BC}\) = с (рис. 9, 10).
9, 10).
Соединим точки О и С отрезком ОС. Тогда, с одной стороны (см. рис. 9),
(а + b) + с = (\(\overrightarrow{OA}\) + \(\overrightarrow{AB}\)) + \(\overrightarrow{BC}\) =
\(\overrightarrow{OB}\) + \(\overrightarrow{BC}\)= \(\overrightarrow{OC}\)
и, с другой стороны (см. рис. 10),
а + (b + с) = \(\overrightarrow{OA}\) + (\(\overrightarrow{AB}\)+ \(\overrightarrow{BC}\)) = \(\overrightarrow{OA}\) + \(\overrightarrow{AC}\) = \(\overrightarrow{OC}\),
что и доказывает равенство (2).
Из риc. 8 видно, что сумма векторов а = \(\overrightarrow{OA}\) и b = \(\overrightarrow{OB}\) равна направленной диагонали \(\overrightarrow{OC}\) параллелограмма OACB, построенного на отрезках ОА и ОВ, т.е.
\(\overrightarrow{OA}\) + \(\overrightarrow{OB}\) = \(\overrightarrow{OC}\).
Это равенство называется правилом параллелограмма сложения двух векторов.
Так как сложение векторов ассоциативно, то сумма трех и большего числа векторов записывается без скобок. Например, вместо (а + b) + с или а + ( b + с ) пишут а + b + с.
Если требуется найти сумму трех или большего числа векторов, то применяют так называемое правило многоугольника. Оно состоит в следующем.
Пусть даны векторы а, b, с, d и требуется найти их сумму.
Выберем некоторую точку О (рис. 11) и построим отрезок ОА такой, что \(\overrightarrow{OA}\) = а,
затем построим отрезок АВ такой, что \(\overrightarrow{AB}\) = b, и т. д.
Построение продолжается до тех пор, пока не будут исчерпаны все векторы-слагаемые. Направленный отрезок \(\overrightarrow{OD}\), замыкающий полученную ломаную, будет равен сумме данных векторов.
Противоположные векторы. Вычитание векторов.
Любые два вектора, сумма которых равна нулевому вектору, называются противоположными.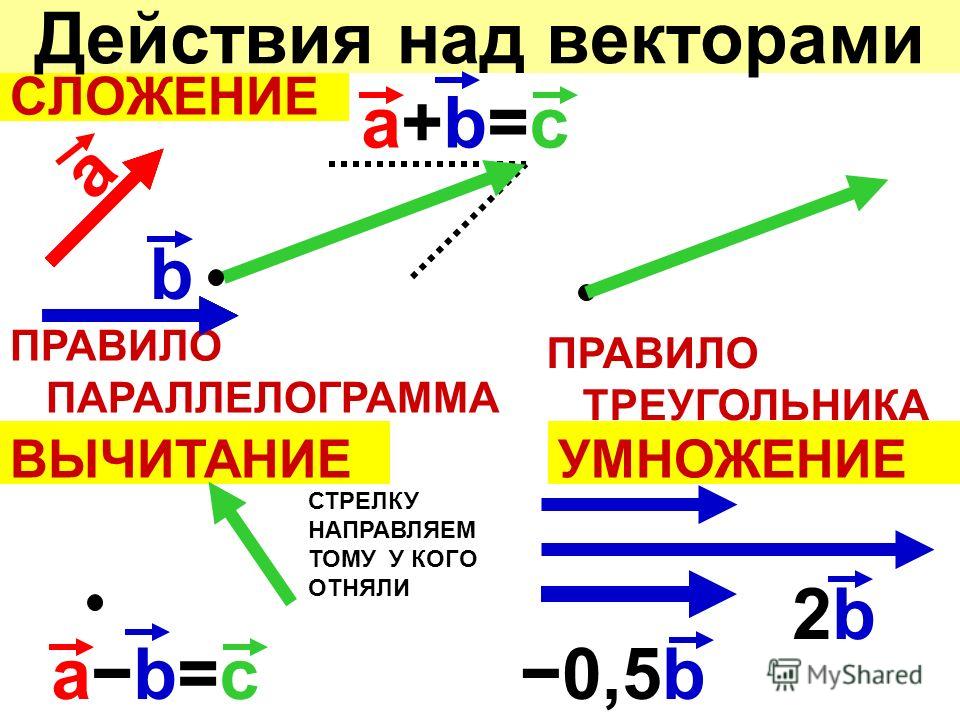 Вектор, протипоположный вектору а, обозначается — а. Следовательно, по определению
Вектор, протипоположный вектору а, обозначается — а. Следовательно, по определению
а + (- а) = 0.
Из определения следует, что если а = \(\overrightarrow{AB}\), то — а = \(\overrightarrow{BA}\), т. е. противоположные векторы имеют одинаковую длину и противоположные направления.
Например, если ABCD — параллелограмм, то векторы \(\overrightarrow{AB}\) и \(\overrightarrow{CD}\) противоположные (рис. 15). Векторы \(\overrightarrow{AD}\) и \(\overrightarrow{CB}\) тоже противоположные.
Для любых двух векторов а и b вектор с = а + (- b) называется разностью векторов а и b и обозначается а — b. Таким образом, по определению
а — b = а + (- b).
Если а = \(\overrightarrow{OA}\) и b = \(\overrightarrow{OB}\) (рис.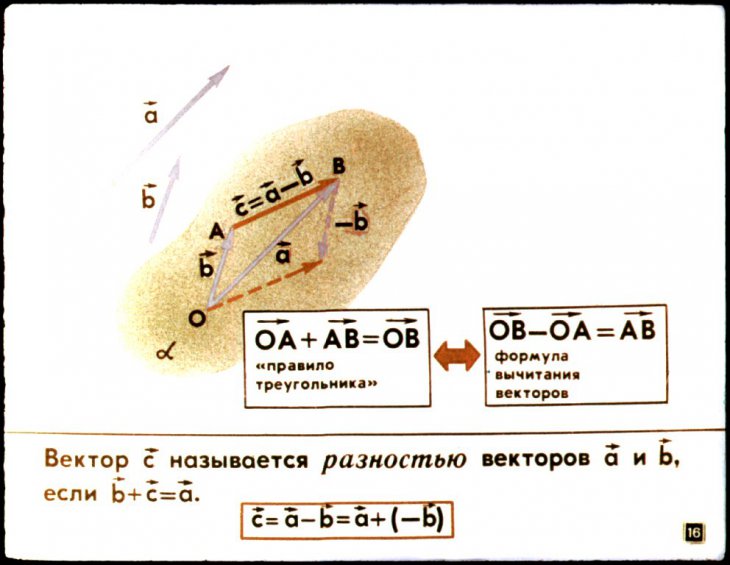 16), то
16), то
а — b = \(\overrightarrow{OA}\) — \(\overrightarrow{OB}\) = \(\overrightarrow{OA}\) + \(\overrightarrow{BO}\) = \(\overrightarrow{BO}\)+ \(\overrightarrow{OA}\) = \(\overrightarrow{BA}\).
Следовательно,
\(\overrightarrow{OA}\) — \(\overrightarrow{OB}\) = \(\overrightarrow{BA}\) (1)
Из рисунка видно, что \(\overrightarrow{BA}\) — это направленная диагональ параллелограмма ОАСВ, построенного на отрезках ОА и ОВ. Другая диагональ \(\overrightarrow{OC}\) изображает сумму векторов \(\overrightarrow{OA}\) и \(\overrightarrow{OB}\).
Нетрудно заметить, что формулу (1) можно применять, не прибегая к чертежу: для этого достаточно внимательно проследить за порядком расположения букв в записи данных и искомого векторов. Так, например,
$$ \overrightarrow{PQ} — \overrightarrow{PN} = \overrightarrow{NQ}\;\; (2)$$
векторное вычитание — примеры | Как вычитать векторы?
Мы можем выполнять вычитание векторов точно так же, как мы делаем вычитание скаляров.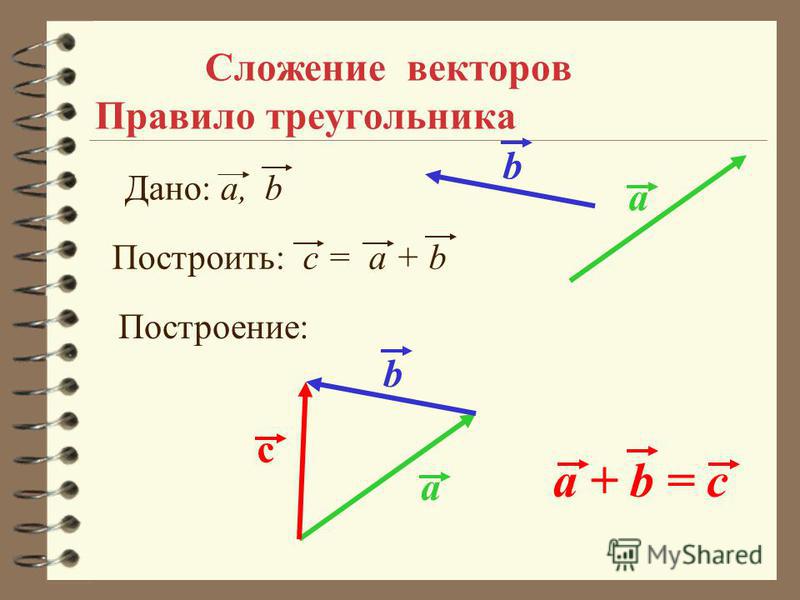 Мы вычитаем соответствующие компоненты векторов при вычитании векторов. Графическую интерпретацию вычитания векторов можно понять, используя закон параллелограмма и закон сложения треугольника.
Мы вычитаем соответствующие компоненты векторов при вычитании векторов. Графическую интерпретацию вычитания векторов можно понять, используя закон параллелограмма и закон сложения треугольника.
Давайте узнаем больше о вычитании векторов вместе с геометрической интерпретацией и примерами.
| 1. | Что такое векторное вычитание? |
| 2. | Вычитание векторов по закону параллелограмма |
| 3. | Вычитание векторов по закону треугольника |
| 4. | Как вычитать векторы? |
| 5. | Свойства векторного вычитания |
| 6. | Часто задаваемые вопросы о векторном вычитании |
Что такое векторное вычитание?
Вычитание вектора из двух векторов a и b представляется как a — b , и это не что иное, как сложение отрицательного значения вектора b с вектором a . т. е. a — b = a + (- b ). Таким образом, вычитание векторов включает в себя сложение векторов и отрицание вектора. Результат векторного вычитания снова является вектором. Ниже приведены правила вычитания векторов:
т. е. a — b = a + (- b ). Таким образом, вычитание векторов включает в себя сложение векторов и отрицание вектора. Результат векторного вычитания снова является вектором. Ниже приведены правила вычитания векторов:
- Следует выполнять только между двумя векторами (не между одним вектором и одним скаляром).
- Оба вектора в вычитании должны представлять одну и ту же физическую величину.
Давайте разберемся, как вычитать векторы графически в следующих разделах.
Вычитание векторов по закону параллелограмма
Предположим, что a и b — два вектора. Как можно графически интерпретировать вычитание этих векторов? То есть какой смысл мы придаем а — б ? Для начала отметим, что a — b будет вектором, который при добавлении к b должен вернуть a . то есть,
то есть,
( A — B ) + B = A
Но как мы определили вектор A — B , дали Vectors A и B , дали Vectors A и B ? На следующем рисунке показаны векторы a и b (мы нарисовали их совпадающими).
Используя закон сложения векторов параллелограмма, мы можем определить вектор следующим образом. Мы интерпретируем a — b как a + (- b ), то есть векторную сумму a и — b . Теперь мы обращаем вектор b , а затем складываем a и — b , используя закон параллелограмма:0051 a и − b .
Вычитание векторов по закону треугольника
Теперь мы интерпретируем вычитание векторов, используя треугольный закон сложения векторов.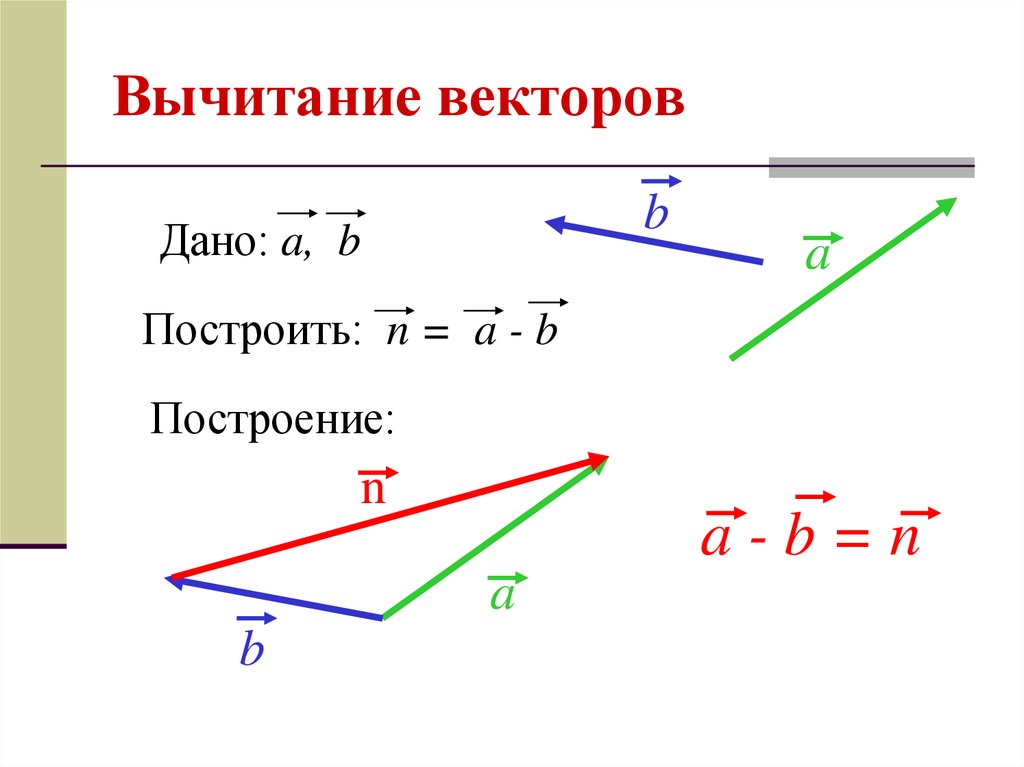 Обозначим вектор, проведенный из конечной точки b в конечную точку a , через c .
Обозначим вектор, проведенный из конечной точки b в конечную точку a , через c .
Обратите внимание, что b + c = a . Таким образом, c = a — b . Другими словами, вектор a — b — это вектор, проведенный от вершины b к вершине a (если a и b совпадают с начальными).
Обратите внимание, что оба описанных выше способа (с использованием закона параллелограмма и закона треугольника) дают нам один и тот же вектор для a — b . Это становится яснее из рисунка ниже:
Вектор PT получается сложением a и − b по закону параллелограмма. Вектор RQ получается путем рисования вектора от вершины b до вершины — a .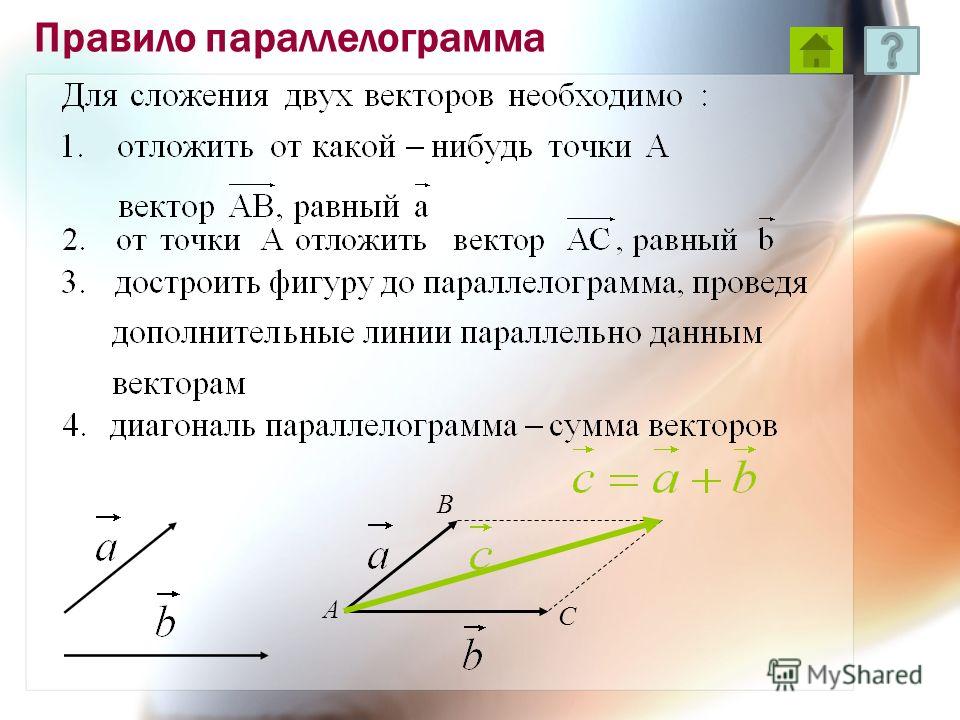 Ясно, что оба вектора одинаковы (поскольку их величины и направления одинаковы).
Ясно, что оба вектора одинаковы (поскольку их величины и направления одинаковы).
Как вычитать векторы?
Вот несколько способов вычитания векторов:
- Чтобы вычесть два вектора a и b графически (т. кончик b до наконечника a .
- Мы можем добавить — b (отрицательное значение вектора b , полученное путем умножения b на -1) к a , чтобы выполнить вычитание вектора a — b . то есть a — b = a + ( -b ).
- Если векторы находятся в компонентной форме, мы можем просто вычесть их соответствующие компоненты в порядке вычитания векторов.
Вот пример.
Пример: Если a = <4, -2, 3> и b = <1, -2, 5>, то найдите a — b .
Решение:
а — б = <4, -2, 3> — <1, -2, 5>
= <4 - 1, -2 - (-2), 3 - 5>
= <3, 0, -2>
Следовательно, a — b = <3, 0, -2>.
Свойства векторного вычитания
Вот некоторые важные свойства векторного вычитания.
- Любой вектор, вычтенный из самого себя, дает нулевой вектор. то есть a — a = 0 для любого вектора a .
- Вычитание векторов НЕ является коммутативным. т. е. a — b не обязательно равно b — a.
- Вычитание векторов НЕ является ассоциативным. т. е. ( a — b ) — c не обязательно должен быть равен a — ( b — c ).
- ( a — b ) · ( a + b ) = | и | 2 — | б | 2 .

- ( а — б ) · ( а — б ) = | а — б | 2 = | и | 2 + | б | 2 — 2 а · б .
☛ Связанные темы:
- Типы векторов
- Калькулятор добавления векторов
- Калькулятор векторного вычитания
- Угол между векторами
Часто задаваемые вопросы о векторном вычитании
Что означает векторное вычитание?
Векторное вычитание двух векторов a и b — это просто сложение векторов a и -b . т. е. a — b = a + (- b ). Чтобы найти — b , мы должны умножить каждый компонент вектора b на -1.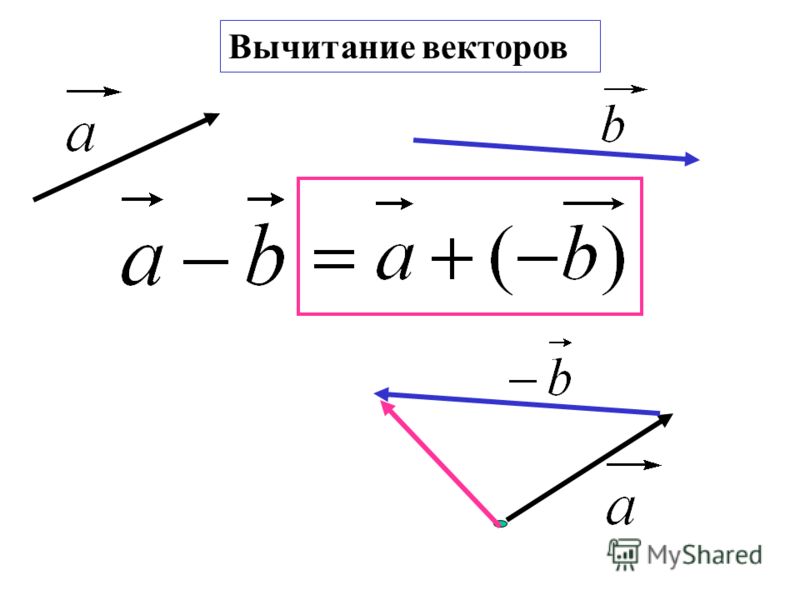
Как вычитать векторы?
- Чтобы вычесть вектор b из другого вектора a , просто сделайте их совпадающими по началу и затем нарисуйте вектор от вершины b до вершины a .
- Чтобы вычесть вектор b из другого вектора a , когда их компоненты заданы, просто вычтите каждый компонент b из соответствующего компонента a .
Как найти разность векторов графически?
Чтобы найти разность векторов двух векторов a и b графически:
- Нарисуйте оба вектора, чтобы начать с одной и той же начальной точки.
- Нарисуйте вектор разности a — b от наконечника b до наконечника a .
Как вычитать векторы в компонентной форме?
Если два вектора a =  то есть a — b =
то есть a — b =
Что такое параллелограммный закон вычитания векторов?
Закон вычитания параллелограмма гласит: «Если два вектора a и -b начинаются из точки P и являются двумя смежными сторонами параллелограмма, то их сумма, равная a + (- b ) (который также может быть записан как a — b ) — это вектор, который представляет собой диагональ параллелограмма, начинающегося с P».
Что такое треугольный закон вычитания векторов?
Треугольный закон вычитания векторов гласит: «Чтобы найти разность a — b двух векторов a и b (которые совпадают по началу), просто начертите вектор от хвоста b к хвост и «.
Вычитание векторов – объяснение и примеры
Существует много параллелей между скалярами и векторами, и вычитание векторов не является исключением. В частности, векторное вычитание:
В частности, векторное вычитание:
«Сложение вектора с отрицательным значением другого вектора».
Из приведенного выше определения ясно, что вычитание векторов означает просто сложение отрицательных векторов. Поэтому перед изучением вычитания векторов важно просмотреть отрицательные векторы.
Как известно, отрицательный вектор получается умножением заданного вектора на -1. Это меняет направление вектора.
Допустим, — это вектор, указывающий слева направо. Умножение вектора A на -1 дает нам -A, , что является отрицательным вектором A. Хотя величины двух векторов A и – A останутся прежними, отрицательный вектор – A будет направлен справа налево.
В этой теме мы обсудим следующие аспекты вычитания векторов:
- Как вычитать векторы
- Вычитание векторов графически
Как вычитать векторы
Мы знаем, что два вектора, A и B, можно сложить вместе, используя сложение векторов, и результирующий вектор можно записать как R = A + B .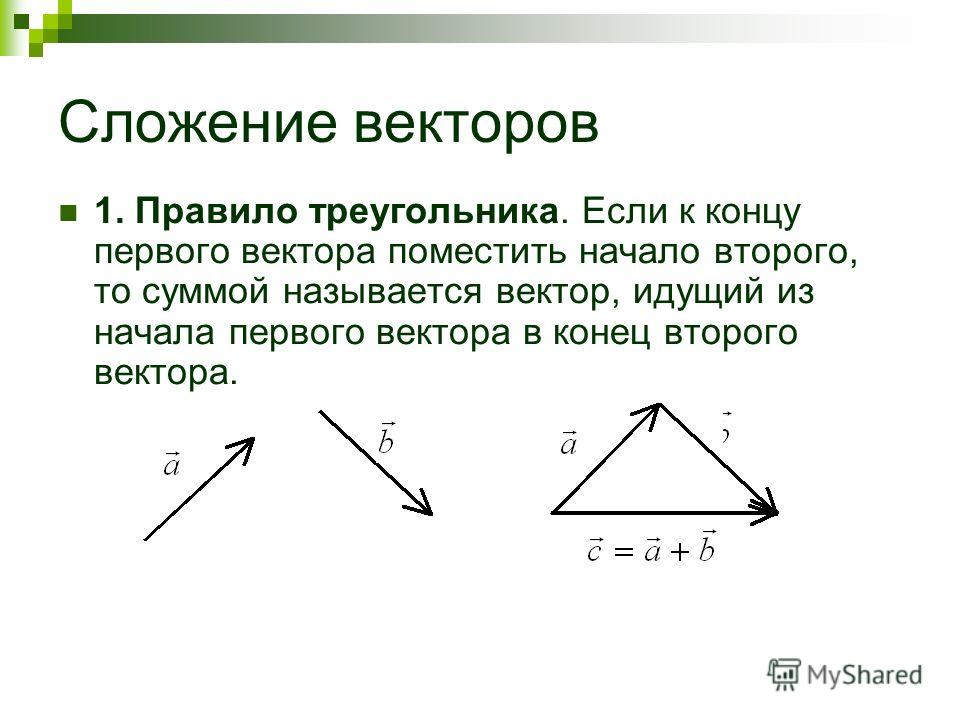 Точно так же, если мы хотим вычесть два вектора, A и B математически выражается как:
Точно так же, если мы хотим вычесть два вектора, A и B математически выражается как:
R = A – B
Альтернативно как: )
Таким образом, вычитание двух векторов аналогично сложению вектора A и отрицательного вектора B (т. е. В ). Векторы B и – B будут иметь одинаковую величину, но направление -B’ s будет противоположно вектору B.
Вычитание векторов также работает, когда два вектора даны в компонентной форме. или как векторы-столбцы. Если A = (ax1, ay1) и B = (bx1, by1), то разница между ними составляет: результирующего вектора R можно выразить как:
Rx = ax1 – bx1
и
Ry = ay1 – by1.
Таким образом, результирующий вектор можно вычислить, просто вычислив разность соответствующих горизонтальных и вертикальных составляющих двух исходных векторов.
Графическое вычитание векторов
Графически правило «голова к хвосту», используемое при сложении векторов, может быть адаптировано для вычитания векторов. Например, рассмотрим два вектора P и Q , как показано на изображении ниже. Обратите внимание, что вектор – Q получается изменением направления Q.
Затем мы складываем векторы P и – Q , используя прямое правило:
Сначала рисуем вектор P, , а затем поместите вектор – Q так, чтобы его хвост соединился с головой вектора P . Теперь, чтобы найти сумму P и – Q , начертите результирующий вектор R так, чтобы он соединял хвост вектора P в начало вектора — Q как показано на изображении ниже.
Математически результирующий вектор может быть выражен следующим образом: шаг решения с использованием различных методов, как обсуждалось выше.
Пример 1
Графически вычтите заданные векторы A и B, показанные на изображении ниже, используя метод «голова к хвосту».
Решение
Сначала нарисуем отрицательную сторону вектора B , поменяв его направление на противоположное, то есть -B . Далее складываем векторы A и – B , применяя метод «голова к хвосту».
Сначала мы размещаем заданные векторы A и – B так, чтобы хвост вектора -B соединился с головой вектора A , как показано на рисунке ниже. Далее, чтобы найти их сумму, рисуем результирующий вектор R так, чтобы он соединял хвост вектора A с началом вектора – B . Математически, результирующее может быть выражено как:
R = A + (- B )
Пример 2
Указанные два вектора AB = (3, 2) и BC AB = (3, 2) и BC AB = (3, 2) и BC AB = (3, 2) и B.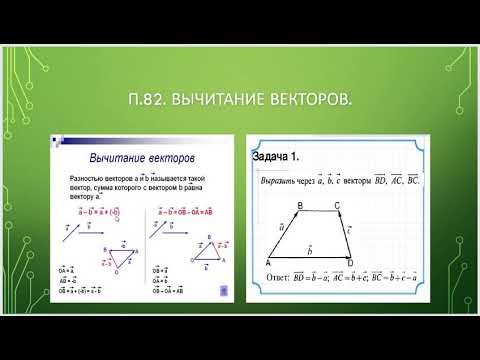 . = (2, 2), алгебраически вычтите два вектора. Затем определите величину и угол результирующего вектора, заданного как:
. = (2, 2), алгебраически вычтите два вектора. Затем определите величину и угол результирующего вектора, заданного как:
S = AB + ( — до н.э. )
Решение
Сначала определите отрицательный вектор BC на размножение на -1:
-Bc . -2, -2).
Далее, чтобы найти результирующий вектор S, Мы добавляем векторы AB и- до н.э. следующим образом:
S = AB + (- до н.э. , 2) + (-2, -2) 92
| С | = √ 1
| С | = 1 единица
Угол результирующего вектора S можно найти следующим образом:
φ = TAN -1 (0)
φ = 0 градусов
Пример 3
Учитывая два вектора S = 10 м, φ = 30 градусов и T = 20m, φ = 60 M, φ = 30 градусов и T = 20m, φ = 60 M, φ = 30 градусов и T = 20m, φ = 60 м.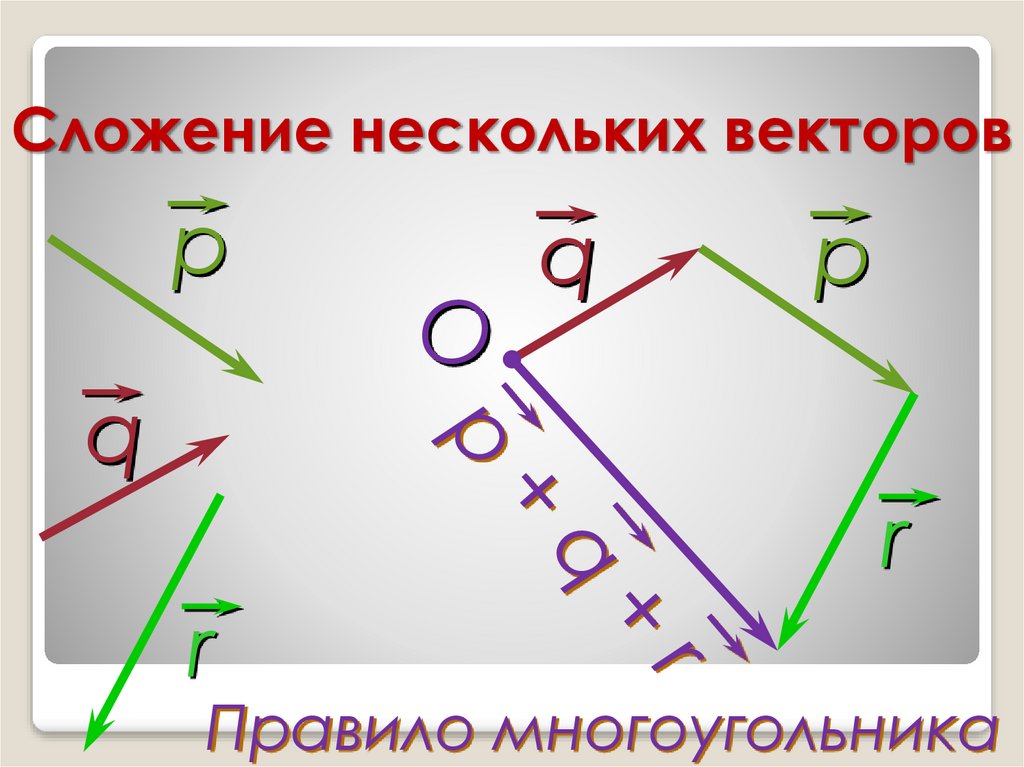 градусов. Вычтите два вектора, затем вычислите величину и угол результирующего вектора, используя метод компонентов.
градусов. Вычтите два вектора, затем вычислите величину и угол результирующего вектора, используя метод компонентов.
Решение
LET R Будьте результирующим вектором, равным сумме данных векторов S и — T. . (- T )
Чтобы использовать компонентный метод, мы сначала разобьем заданные векторы на их соответствующие горизонтальную и вертикальную составляющие:
Sx = S Cos Φ
Sx = 10 Cos 30 Примерно)
Аналогично, для вертикального компонента:
SY = S SIN φ
SY = 10 SIN 30
SY = 5 M
Далее мы вычисляем компоненты вектора T:
TX = T COS φ
TY = T SIN φ
Где,
TX = 20 COS 60
TX = 10M
TY = 20 SIN 60
TY = 17,320 (приблизительно)
мы можем вычислить вектор разности, вычислив разность отдельных компонентов x и y S and – T vector as:
Rx = Sx + ( -Tx )
Rx = 8.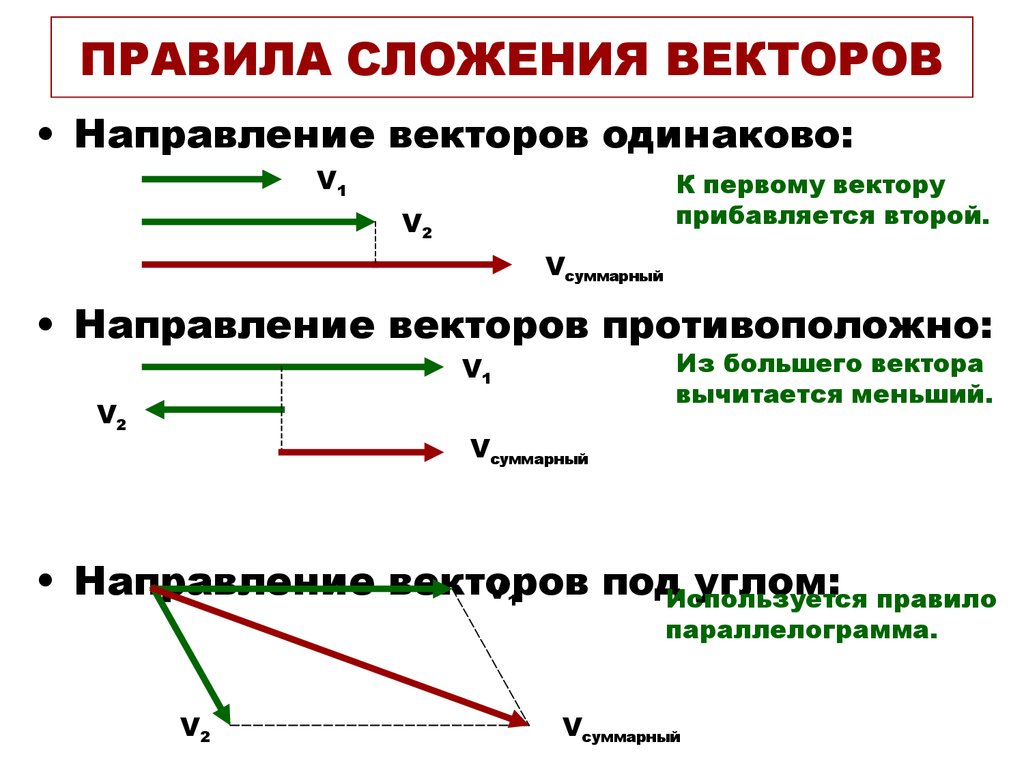 660 + (-10)
660 + (-10)
Rx = -1.34 m
RY = SY + ( -TY )
RY = 5 + (-17,32)
RY = -12,32 M
ВЕКТОР R может быть выраженным COLANDAIN WACER. :
R = (-1,34, -12,32).
92|Р| = 12,392 M
φ = TAN -1 ( RY / RX )
φ = TAN -1 (-12,32 / -1,34)
φ = 83,79 DEGEEES (-12,32 / -1,34)
φ = 83,79 DEGEEES (-12,32 / -1,34)
φ = 83,79. , результирующий вектор суммы может быть выражен как:
R = 12,392 м, Φ = 83,79 градуса
Пример 4
Определить результирующий вектор суммы для двух векторов ) и – В = (2,-1).
Решение
Данные векторы уже находятся в своих составных формах, поэтому сначала определяем их углы.
для вектора A:
φ = TAN -1 ( AY / AX )
φ = TAN -1 (-1 / -5)
a = 11,309999.309 (-1 / -5)
a = 11,309999.309 (-1 / -5)
a = 11,309999999.309 (-1 / -5)
a = 11.309.309.309 (-1 / -5)
9000 2 9037 -1 (-1 / -5).Для вектора – B:
Φ = tan -1 ( By / Bx )
Φ = tan -1 (-1/2)
φ = -26,56 градусов
Далее мы находим результирующий вектор, добавив отдельные компоненты:
S = A + ( — B )
SX = AX + ( — SX = AX + ( — — = AX + ( — — = AX + ( — — = .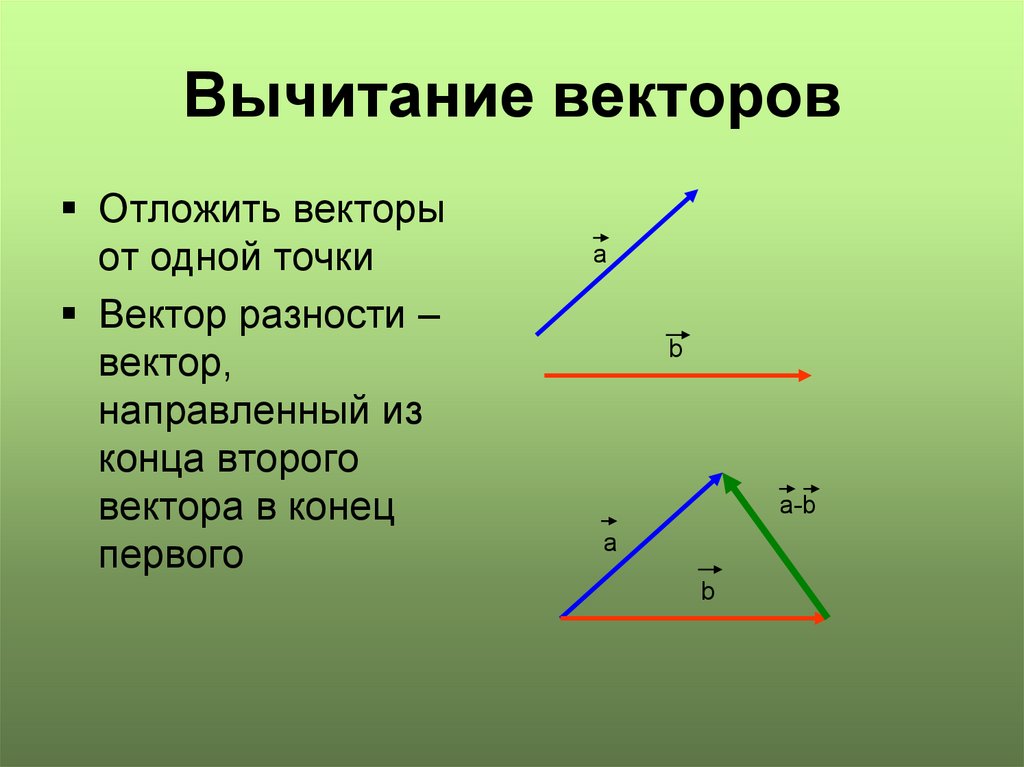 BX )
BX )
SX = -5 + 2
SX = -3
SY = AY + ( -BY )
SY = -1 -1 )
SY = -1 -1 )
SY = -1 -1 )
SY = -1 -1 )
SY = -1 -1 )
SY = -1 -1 )
. Sy = -2
Результирующий вектор 92
|С| = 3,605 единиц
φ = TAN -1 ( SY / SX )
φ = TAN -1 (-2 / -3)
φ = 33,69 DEGREES
Таким Суммарный вектор может быть выражен как:
S = 3,605 единиц, Φ = 33,69 градуса
Пример 5
Учитывая три вектора ,-4), и Y = (2,6), определяют вектор Z = A – X – Y .
Раствор
Z = A – X – Y
Z = (-20, -1) – 900 1 2 Z – 90 0 1 = (-20-5-2, -1+4-6)
Z = (-27 , -3)
Практические вопросы- Даны два вектора V = (2, 052 ) и С = (3, -2), определить А = В – С . Затем определите величину и угол результирующего вектора A .
- Имея два вектора G = (5, 5) и – H = (4, -10), определите их сумму, используя правило «голова к хвосту». Затем определите модуль и угол результирующего вектора P = G – H .
- Рассмотрим вектор OA, , где O = (-1, 3) и A = (5,2), и вектор UV, , где U = (1, -2) и V = (-2, 2).
 Вычтите два вектора, затем задайте величину и угол результирующего вектора S .
Вычтите два вектора, затем задайте величину и угол результирующего вектора S . M = 10 м прямо на восток и N = 15 м прямо на север. Вычтите два вектора, а затем задайте величину и угол результирующего вектора.
- Имея два вектора A = (10, 2, 5) и M = (5, 0, -4 ), определить вектор B = M – А .
Ответы
- Результирующий вектор A равен A = (-1, 7), модуль A равен | А | = 7,079 единиц (приблизительно), а угол Φ = -81,86 градуса.
- Результирующий вектор P равен: P = (9, -5), величина P равна | Р | = 10,30 ед. (приблизительно), а угол Φ = -29,05 градуса.
- Векторов OA = (6, -1) и – UV = (3, -4), результирующий вектор S равен S = (9, -5), модуль S равен | С | = 10,30 ед.
 (приблизительно), а угол Φ = -29,05 градуса.
(приблизительно), а угол Φ = -29,05 градуса. - Результат двух векторов:
R = M + (- N )
|R| = 18,027 м (Приблизительно)
А угол равен:
Φ = tan -1 (15/10)
Φ = 56,30 градуса
Таким образом, результирующий вектор R равен R = 18,027 м , Φ = 56,30 градуса на северо-восток.
B = M — A
B = (10, 2, 5)-(5, 0, -4)
B = (10-5, 2- 0, 5+4)
B = (5, 2, 9)
Треугольный и параллелограммный закон сложения, векторное вычитание
Намрата Дас
Мастер по подготовке к экзаменам | Обновлено 15 июня 2022 г.
Вектор известен как количество, которое имеет оба; величина и направление, но не положение. Например; скорость и ускорение. В геометрии вектор — это направленный отрезок линии, длина которого равна величине вектора и со стрелкой, указывающей направление. Обычно вектор представлен стрелкой, направление которой аналогично направлению величины, а длина пропорциональна величине величины. Кроме того, векторные величины обычно представляются масштабированными векторными диаграммами. Векторная диаграмма обозначает вектор смещения. Здесь мы узнаем больше о векторных формулах, законе сложения треугольников и параллелограммов и обсудим несколько важных вопросов.
Читайте также: Строка уравнения
Содержание
|
Ключевые термины: Скаляр, Тройка, Произведение, Векторы, величина этого вектора, Точечное и перекрестное произведение, Результирующая, векторные формулы.
Что такое векторная формула?
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Как упоминалось выше, вектор в основном представлен стрелкой, направление которой совпадает с направлением величины, а длина прямо пропорциональна ее величине. На векторной диаграмме будет изображен вектор смещения:
- Математическое представление физических величин: величина и направление называются векторами.
- Векторы складываются геометрически, а не алгебраически,
- Их результирующая должна вычисляться независимо,
- Величина этого вектора задается как |ab| или |а|. Он представляет собой длину вектора и с помощью теоремы Пифагора
- Вектор любой физической величины представляется в виде прямой линии со стрелкой, длина прямой линии обозначает величину вектора, а стрелка указывает его направление.

- Для лучшего понимания, вектор — это сила, приложенная к объекту, поскольку сила и направление приложенной силы влияют на ее действие на объект.
Вектор
Проверить еще: Угол между линией и плоскостью
Треугольный закон сложения закон. Если оба вектора сил a и вектор b действуют в одном направлении, то их результирующий вектор r будет суммой двух векторов.
Треугольный закон добавления
Формула для треугольного закона о добавлении: вектор (r = A + B)
Прочтите далее: Трехмерная Геометрия
.
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Если две силы представлены векторами a и векторами b смежными сторонами параллелограмма, то результат будет представлен диагональю параллелограмма, проведенной из той же точки.
Параллелограммный закон сложения
Формула для параллелограмма как закона сложения: вектор (r = a + b)
Полигональный закон вектора
Вопросы для примеров]
Когда количество векторов представлено в виде величины и направления, тогда их результирующая представляется так, что замыкающая сторона многоугольника берется в противоположном направлении,
Формула: ab + bc +cd + de = ae .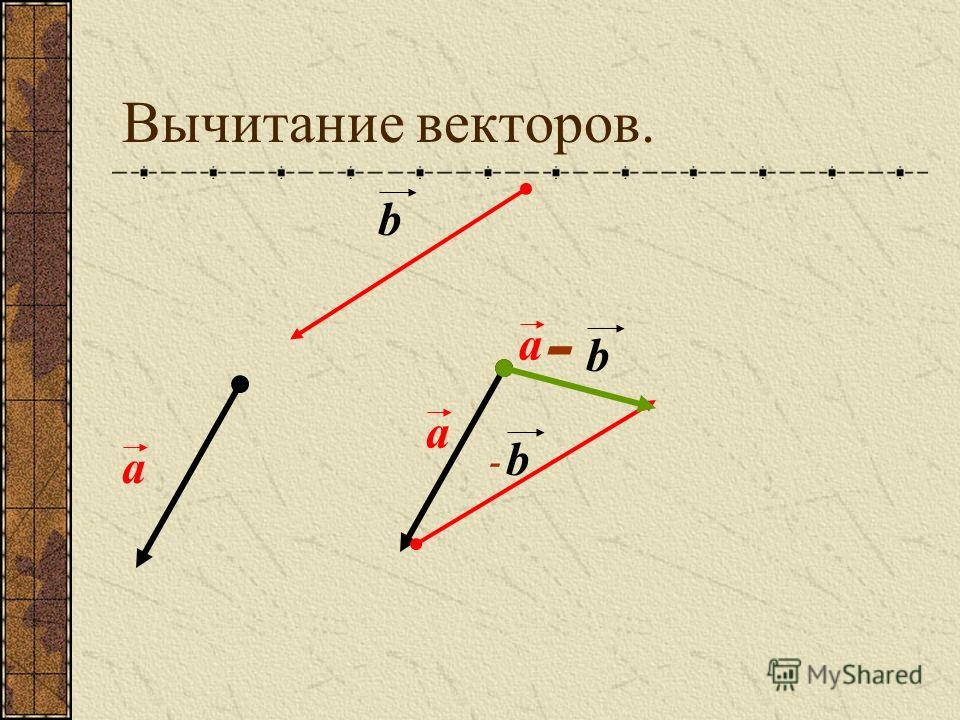 Ae = закрытая сторона
Ae = закрытая сторона
Also Read: Angle Between Two Planes
Types of Vectors
[Click Here for Sample Questions]
Vectors are of various types:
- Zero vector or null vector- When the величина вектора равна нулю, или мы можем сказать, что начальная и конечная точки этого вектора совпадают, тогда говорят, что вектор является нулевым вектором. Нулевые векторы не имеют определенного направления.
Нулевой вектор или нулевой вектор
Например: ab — это отрезок, координаты точки a совпадают с координатами точки b. Таким образом, вектор обозначается как 0.
- Единичный вектор- Когда величина вектора составляет одну единицу длины, тогда говорят, что вектор является Единичным вектором . Но два вектора не могут быть равны, так как они имеют разные направления.

Например: если p является вектором, имеющим величину p и имеющую величину, равную 1.
Ознакомьтесь с важными примечаниями для Типы векторов
- Вектор положения- Когда вектор обозначает положение точки относительно ее начала, тогда говорят, что вектор является вектором положения.
Вектор положения
- Совместно начальные векторы- Когда два или более векторов имеют одну и ту же начальную точку, то говорят, что вектор является начальным вектором. Например, два вектора, ab и ac, называются ко-начальными векторами, потому что они имеют одну и ту же начальную точку a.
- Подобные и разные векторы- Говорят, что векторы, имеющие одинаковые направления, являются подобными векторами, тогда как векторы, имеющие противоположные направления, называются непохожими векторами.
- Копланарные векторы- Три или более вектора, лежащие в одной плоскости , известны как копланарные векторы.

- Коллинеарные векторы- Векторы, которые также известны как параллельные векторы, представляют собой векторы, лежащие на одной линии относительно их величины и направления.
- Равные векторы- Два вектора называются равными, если они имеют одинаковое направление и величину, даже если они имеют разные начальные точки.
- Векторы смещения- Вектор ab представляет собой вектор смещения, если точка смещена из положения a в положение b.
- Отрицательные векторы- Отрицательные векторы — это векторы, точки которых лежат в направлении, противоположном положительному направлению.
- Евклидов вектор- Любой геометрический объект, имеющий как величину, так и направление, называется евклидовым вектором.
Подробнее:
Математические операции с вектором
[Нажмите здесь, чтобы просмотреть примеры вопросов] в соответствии с этим законом складываются два вектора, которые представлены двумя сторонами треугольника с одинаковой величиной и направлением, а третья сторона дает результирующий вектор сложения. Сумма векторов получается путем размещения этих головы к хвосту.
Сумма векторов получается путем размещения этих головы к хвосту.
- Вычитание вектора-
Вычитание вектора означает Сложение векторов с отрицательным значением другого вектора,
Например: есть два вектора q и r. Если вектор «q» нужно вычесть из вектора «r», то следует найти отрицательное значение вектора «q» и добавить его к вектору «r» по закону треугольника. Вычитание векторов не коммутативно
Значит формула лежит здесь: r — q = r + (-q).
Проверьте важные примечания для Разница между скалярными и векторными величинами
- Умножение векторов-
Это относится к технике умножения двух или более векторов друг на друга. При перемножении двух произвольных векторов величина числа отличается, но скалярное произведение аналогично.
формула- a*b = ll a ll ll b ll sin \(\Theta\) n
| Ll a ll | = | Length of vector a |
| Ll b ll | = | Length of vector b |
| \(\Theta\) | = | Угол между a и b |
| N | = | Единичный вектор, перпендикулярный плоскости, содержащей a и b такая же, как у величины, и длина которой прямо пропорциональна ее величине.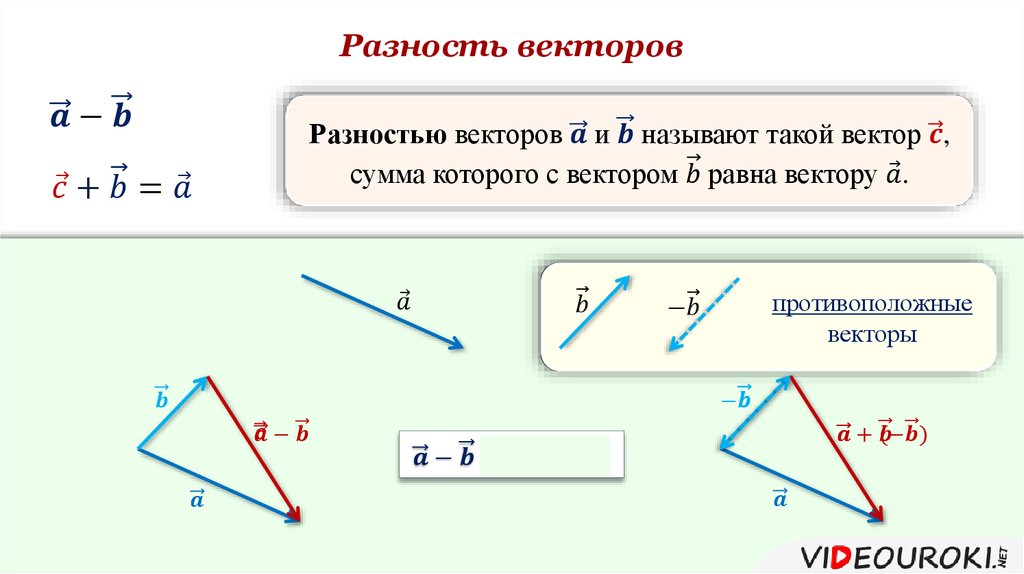 На векторной диаграмме будет изображен вектор смещения. На векторной диаграмме будет изображен вектор смещения.Подробнее: Примеры вопросов Вопросы: Укажите вектор для каждого из следующих: (3 балла) Ответ:
{1 -2, -3 – (-7), -5 -0} = {-1, 4, -5}
Следует отметить, что единственная разница между первыми двумя состоит в том, что все знаки противоположны. Эта разница существенна, поскольку именно эта разница означает, что два вектора указывают в противоположных направлениях.
Вопрос: Если ABCDEF правильный шестиугольник, то вектор AD + вектор EB + вектор FC равен. (3 балла) Ответ: Правильный ответ D. Вопрос: Если ABCDEF правильный шестиугольник, то каково значение вектора (AD + EB + FC)? (2 балла) Ответ:
У нас есть, Вопросы: Пять сил, представленных вектором (AB, AC, AD) в векторе AE A правильного шестиугольника ABCDEF. Ответ: Это обязательный ответ. Вопрос: Если вектор (a, b, c, d) — это векторы положения точек A, B, C, D, такие, что никакие три из них не лежат на одной прямой, и вектор (a + b + c = b + d) , тогда a, b, c, d равно: (4 балла) С. параллелограмм. Умножение приведенного выше уравнения на ½ \(\frac{1}{2}(\overrightarrow{a}+\overrightarrow{c}) = \frac{1}{2}(\overrightarrow{b}+ \overrightarrow{d})\) Следовательно, вектор положения средней точки BD = Вектор положения средней точки AC. Следовательно, диагонали делят друг друга пополам и данная фигура ABCD является параллелограммом. Вопрос: Если векторы (a, b, c) являются тремя ненулевыми векторами, никакие два из которых не лежат на одной прямой, а векторы (a + b) лежат на одной прямой с вектором c, а векторы (b + c) коллинеарны вектору (а), тогда векторы (а, b, с): (4 балла) Ответ: 90 b3 As 90 ) коллинеарна вектору c, \(\следовательно \overrightarrow{a} + \overrightarrow{b} = \lambda \overrightarrow{c}. Как векторы ( b + c) коллинеарно вектору (a) \(\следовательно \overrightarrow{b} + \overrightarrow{c} = \mu \overrightarrow{a}……..(ii)\) Добавление вектора c к обеим частям уравнения (i) \(\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} = \lambda \overrightarrow{c} + \overrightarrow{c}\ ) \(\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} = \overrightarrow{c}(\lambda + 1)……..(iii)\) Добавление вектор a в обе части уравнения (iii) \(\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} = \mu \overrightarrow{a} + \overrightarrow{a}\) \(\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} = \overrightarrow{a}(\mu + 1)……..(iv)\) Приравнивание Правая часть уравнений (iii) и (iv), \(\overrightarrow{c}(\lambda + 1) = \overrightarrow{a}(\mu + 1)\) Поскольку a не коллинеарно c , \(\следовательно \lambda + 1 = \mu + 1 = 0\) \(\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} = \text 0 \text {{От уравнение (iv)}}\) \(\следовательно \overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} = 0 \) Сложение векторов и вычитание векторов: концепции, 2+MockTests Мы охватываем все о Сложение векторов и вычитание векторов , закон треугольника, закон параллелограмма и закон сложения векторов многоугольника, примеры, пробные тесты, важные часто задаваемые вопросы. Мы также обсудим Разрешение векторов, Прямоугольные компоненты трехмерных векторов и Графическое сложение и вычитание векторов . Содержание Что такое сложение векторов | Правила сложения векторов | Сложение векторов в физике Векторы имеют как величину, так и направление. Величину можно добавить, используя правила алгебры, но не направление. Итак, для сложения векторов используются правила геометрии. Существуют определенные законы для нахождения суммы заданных векторов, когда они наклонены под определенным углом.
Государственный треугольный закон сложения векторов | сформулируйте и объясните треугольный закон сложения векторов Что такое треугольный закон сложения векторов? Если два ненулевых вектора {вектор A & вектор B } представлены двумя сторонами треугольника, взятыми в одном порядке, то результирующий {вектор R } дан замыкающей стороной треугольника в обратном порядке. Другими словами, : Если конец одного вектора поместить в начало или конец стрелки другого, их сумма или результирующий вектор R вычерчены из хвоста конца первого к головному концу другого. то есть \vec{R}=\vec{A}+\vec{B} \Rightarrow, потому что \Rightarrow\vec{OB}=\overrightarrow{OA}+\vec{AB} 1. Величина результирующий вектор В треугольнике ABN (из рис. ниже) Треугольный закон сложения векторов cos\theta=\frac{AN}{AB}=\frac{AN}{B}\Rightarrow AN=Bcos\theta sin\theta=\ frac{BN}{AB}=\frac{BN}{B}\Rightarrow BN=Bsin\theta cosθ = AB/AN = B/AN ⇒ AN = Bcos42 90 ⇒ R =∣ R ∣=∣ A + B ∣=✓( A 2 + B 2 +2 ABcosθ ) Now in Right angle triangle OBN , we have OB 2 =ON 2 +BN 2 2. If vector R makes an angle α with vector A , then in △ OBN, Parallelogram law of vectors additionГосударственный параллелограммный закон сложения векторов | Что такое параллелограммный закон сложения векторов ? Если два ненулевых вектора {вектор A & вектор B } представлены двумя смежными сторонами параллелограмма, то результирующий {вектор R } задается диагональю параллелограмм, проходящий через точку пересечения двух векторов. 1. Величина результирующего вектора: 9{2}+2ABcos\theta} 2. Направление результирующих векторов: Если множество ненулевых векторов представлено (n – 1) сторонами n-стороннего многоугольника, взятого в том же порядке, то результирующая дается замыканием сторона n -я сторона многоугольника взятая в обратном порядке . Результат двух векторов Если угол между векторами A и результирующий вектор R равно α тогда Особые условия:0003 1. Когда оба вектора находятся в Тот же направление / Параллель , т.е. θ = 0 Тогда COSθ = COS0 = 1 9051 COSθ = COS0 = 1 92 COSO = COS0 = 1 92 . 0=0 Now we have the resultan t, R= ✓(A 2 + B 2 + 2ABcosθ)=✓(A 2 + B 2 + 2ABcos0 )=✓(А 2 + В 2 + 2АВ)= А+В and the angle between vectors A & R will be, tanα = Bsinθ /( A + Bcosθ ) = 0 i. т.е. R max =| А + В | max = A+B ⇒ Таким образом, максимальное значение равнодействующей двух векторов равно сумме их модулей. 2. Когда оба вектора находятся в противоположном направлении / Антипараллель , т.е. θ = 180 Тогда COSθ = COS180 = -1 COSθ = COS180 = -1 Now we have the resultan t, R= ✓(A 2 + B 2 + 2ABcosθ)=✓(A 2 + B 2 + 2ABcos180 )=✓(А 2 + В 2 – 2АВ)= А-В и Угол Между векторами A и R будет , TANα = , TANα = 1, . т.е. R мин =| А + В | мин = A-B ⇒ Таким образом, минимальное значение равнодействующей двух векторов равно разности их модулей. 3. When both vectors are at the Perpendicular direction , i.e. θ = 90 then⇒ cosθ = cos90 = 0 & sinθ = sin 90=1 Теперь у нас есть результирующий, R = ✓ (A 2 + B 2 + 2ABCOS θ ) = ✓ (A 2 + B 2 + 2ABCOS90) = œ 2 + 2ABCOS90) = œ 2 + 2ABCOS90) = œ 2 + 2ABCOS90) = 2 + B 2 + 2ABCOS90) = 2 + B 2 + 2ABCOS90) = 2 + B 2 + 2ABCOS90) = 2 + B 2 . + B 2 ) и угол между векторами A и R будет, TANα = BSINθ /( A + BSINθ /B /B /.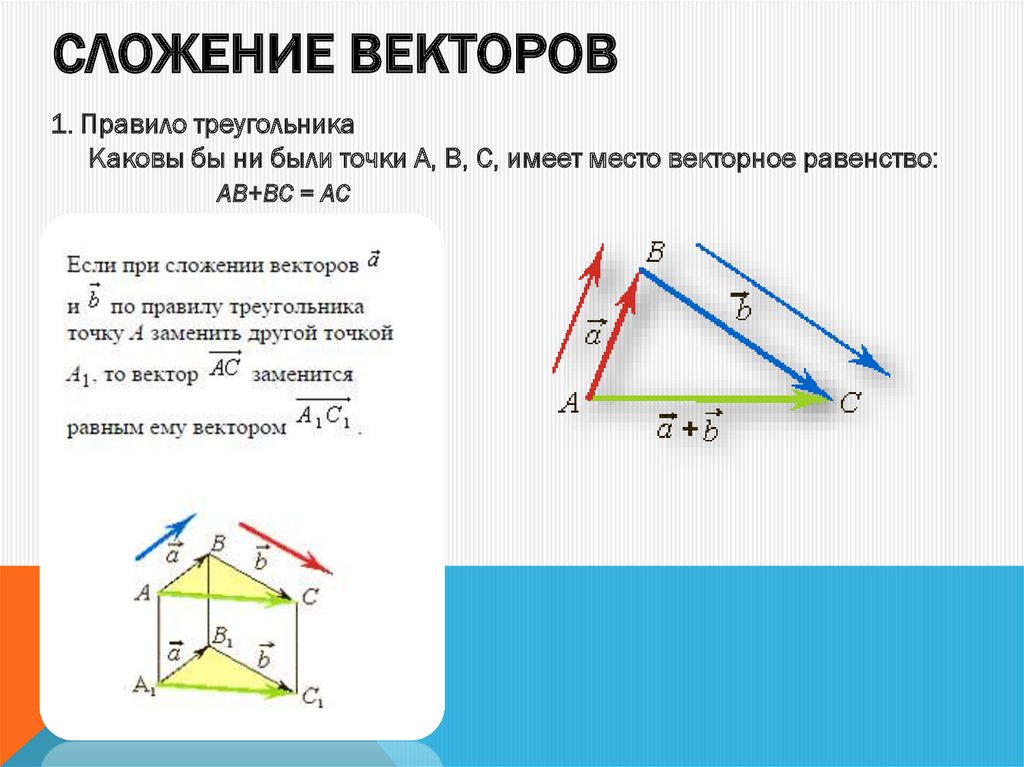 Минимальное количество векторов неравной величины, результант которых может быть равен нулю, равно трем. Минимальное количество векторов неравной величины, результант которых может быть равен нулю, равно трем.5. Минимальное количество векторов , равное величине, равнодействующая которых может быть равна нулю, равно двум. Свойства дополнения из Вектор1. Коммутативный закон: Добавление вектора содержит коммутативный закон, т. е. \vec{a}+\vec{b}= \vec{b}+\vec{a} что означает, что порядок добавления векторов не влияет на результат. 2. Ассоциативный закон: Добавление вектора сохраняет ассоциативный закон, т. е. (\vec{a}+\vec{b}) +\vec{c}=\vec{a}+(\ vec{b}+\vec{c}) , что означает, что сумма трех векторов a, B и c не зависит от порядка их добавления. 92 + 2ABcos(180-\theta)} мы знаем, что cos (180− θ )= sin θ , поэтому результат вектора R вычитания векторовИ угол между векторами A и R равно α 2 определяется как tan\alpha_{2}=\frac{Bsin\theta}{A-Bcos\theta} Разрешение вектора Разложение векторов на прямоугольные компоненты 900 компоненты трехмерных векторов
Проверьте свое понимание Векторы сложения и вычитания (на основе теории)
Примечание:
1 / 21 1. Прямоугольные компоненты не могут иметь величину ................, отличную от величины самого вектора. Меньше Б. Равно С. Большой Д. Ничего из этого 2 / 21 2. Сколько максимальное количество компонентов может быть у вектора? Один Б. Два С. Д. Бесконечный 3 / 21 3. Вектор смещения неподвижного тела принимает вид
А. единичный вектор B. Нулевой вектор C. а и б оба Д. Ничего из этого 4 / 21 4. Какой должен быть угол между ними, чтобы равнодействующая двух векторов была максимальной А. 0° Б. 60° С. 90° Д. 5 / 21 5. Выберите правильное уравнение для сложения векторов a и b А. Р=а+б Б. R=а-б С. R=б-а Д. ничего из этого 6 / 21 6. Единичный вектор обычно представляет А. Величина Б. Направление C. Оба вышеперечисленных Д. Ничего из этого 7 / 21 7. A + B = C тогда A. Векторы, A+B+C=0 B. Векторы, A+B+C≠00 C. Векторы, A+B-C=0 Д. Ничего из этого 8 / 21 8. Всегда ли можно сложить любые два вектора? А. Да Б. Нет 9 / 21 9. Выберите правильное уравнение для векторов a и b А. Р=а+б Б. С. R=б-а Д. ничего из этого 10 / 21 10. Вектор положения начала координат становится А. Нулевой вектор Б. единичный вектор C. Ноль и единичный вектор Д. Ничего из этого 11 / 21 11. Выберите правильное уравнение для векторов a и b А. Р=а+б Б. R=а-б С. Д. Р=б-а 12 / 21 12. Минимальное количество коллинеарных векторов, результант которых может быть равен нулю, равно Один Б. Два С. Три Д. Четыре 13 / 21 13. Сколько может быть минимальное количество компонент вектора? Один Б. Два С. Три Д. Бесконечный 14 / 21 14. А. 0° Б. 60° С. 90° Д. 180° 15 / 21 15. равнодействующая двух векторов неравной величины никогда не может быть a.. А. Нулевой вектор Б. единичный вектор C. Правильный вектор Д. Ничего из этого 16 / 21 16. Выберите правильный вариант для векторов a и b А. Б. R=а-б С. R=б-а Д. ничего из этого 17 / 21 17. Выберите правильное уравнение
А. Р=а+б Б. R=а-б С. R=б-а Г. Р=б+а 18 / 21 18. Минимальное количество некомпланерных векторов, результант которых может быть равен нулю, равно Один Б. Два С. Д. Четыре 19 / 21 19. Вектор может иметь в пространстве только ......... прямоугольные компоненты. А. ноль Б. два С. три Д. ∞ 20 / 21 20. Вектор может иметь только ......... прямоугольные компоненты на плоскости. Один Б. два С. ноль Д. ∞ 21 / 21 21. Один Б. Два С. Три Д. Четыре Пожалуйста, заполните поля нижеМы отправляем вам ваши результаты со всеми вопросами и ответами по электронной почте, поэтому, пожалуйста, введите действительный адрес электронной почты в поле ниже. ИмяЭлектронная почта Ваш результат: Средний балл: 67% Векторы сложения и вычитания (числовые)
Примечание:
1 / 21 1. Какой вектор нужно прибавить к двум векторам х - 2х + 2k̂ и 2х + х - k̂, так, чтобы результирующий был единичным вектором вдоль оси x А. 2î + ĵ - к̂ Б. -2î + ĵ - к̂ C. 2î - ĵ + k̂ D. 2î - ĵ - к̂ 2 / 21 2. Какой должен быть угол между равнодействующей двух векторов А. 0° Б. С. 90° Д. 180° 3 / 21 3. Две силы, каждая из которых имеет величину F, имеют равнодействующую той же величины F. Угол между двумя силами равен А. 45° Б. 90° С. 120° Д. 180° 4 / 21 4. На тело действуют следующие наборы трех сил. Результат которого не может быть равен нулю А. 10, 10, 10 Б. 10, 10, 20 С. Д. 10, 20, 40 5 / 21 5. Равнодействующая двух векторов A и B перпендикулярна вектору A и его модуль равен половине модуля вектора B . Угол между А и В это А. 120° Б. 150° С. 180° Д. нет 6 / 21 6. Если частица движется из точки P (2,3,5) в точку Q (3,4,5). Его вектор смещения равен А. î + ĵ + 10k̂ Б. С. î + ĵ D. î + ĵ - к̂ 7 / 21 7. Значение суммы двух векторов a и b с θ так как угол между ними равен
А. 1 БИ 2 С. 3 Д. 4 8 / 21 8. Если векторы | А - В | =| А | =| B |, угол между векторами A и B равен А. Б. 120° С. 90° Д. 0° 9 / 21 9. Векторная проекция вектора (3î +4 k̂) на ось Y равна А. 5 Б. 3 С. 4 Д. ноль 10 / 21 10. Если сумма двух единичных векторов является единичным вектором, то величина разности равна А. ✓(2) Б. ✓(3) С. Д. ✓(5) 11 / 21 11. Сила 5 Н действует на частицу в направлении, составляющем угол 60° с вертикалью. Его вертикальная составляющая равна А. 10н. Б. 3н С. 5Н Д. 2,5Н 12 / 21 12. Пусть угол между двумя ненулевыми векторами A и B равен 120°, а результирующий вектор равен C , тогда
А. БИ 2 С. 3 Д. 4 13 / 21 13. Максимальная и минимальная величины равнодействующей двух векторов величин P и Q относятся как 3 : 1. Какое из следующих соотношений верно А. Р = 2Q Б. Р = Q С. PQ = 1 Д. ничего из этого 14 /21 14. Если вектор A , B и C Lie в одной плоскости и A + B = C Затем A. B. Векторы, A+B+C≠00 C. Векторы, A+B-C=0 Д. Ничего из этого 15 / 21 15. Если векторы | А + В | =| А | =| B |, угол между векторами A и B равен А. 60° Б. 90° С. 120° Д. 180° 16 / 21 16. Пять равных сил по 10 Н приложены в одной точке и все лежат в одной плоскости. А. ноль Б. 10н С. 20н. Д. 10✓(2)С 17 / 21 17. Имеются два вектора силы, один 5 Н, а другой 12 Н, под каким углом сложить два вектора, чтобы получить результирующий вектор 17 Н, 7 Н и 13 Н соответственно А. 0°, 180° и 90° Б. 0°, 90° и 180° С. 0°, 90° и 90° Г. 180°, 0° и 90° 18 / 21 18. А. 0° Б. 60° С. 90° Д. 180° 19 / 21 19. На частицу действуют одновременно две силы, равные 4 Н и 3 Н. Суммарная сила, действующая на частицу, равна А. 1 Н Б. 5 Н С. 7 Н D. Между 1 Н и 7 Н 20 / 21 20. Силы F1 и F2 действуют на точечную массу в двух взаимно перпендикулярных направлениях.
А. 1 БИ 2 С. 3 Д. 4 21 / 21 21. Равнодействующая векторов P и Q перпендикулярны P. Какой угол между P и Q A. cos⁻¹(P/Q) B. cos⁻¹(-P/Q) C. sin⁻¹(P/Q) D. sin⁻¹(-P/Q) Пожалуйста, заполните поля ниже Мы отправляем вам ваши результаты со всеми вопросами и ответами по электронной почте, поэтому, пожалуйста, введите действительный адрес электронной почты в поле ниже. ИмяЭлектронная почта Ваш результат: Средний балл: 62% Часто задаваемые вопросы
|


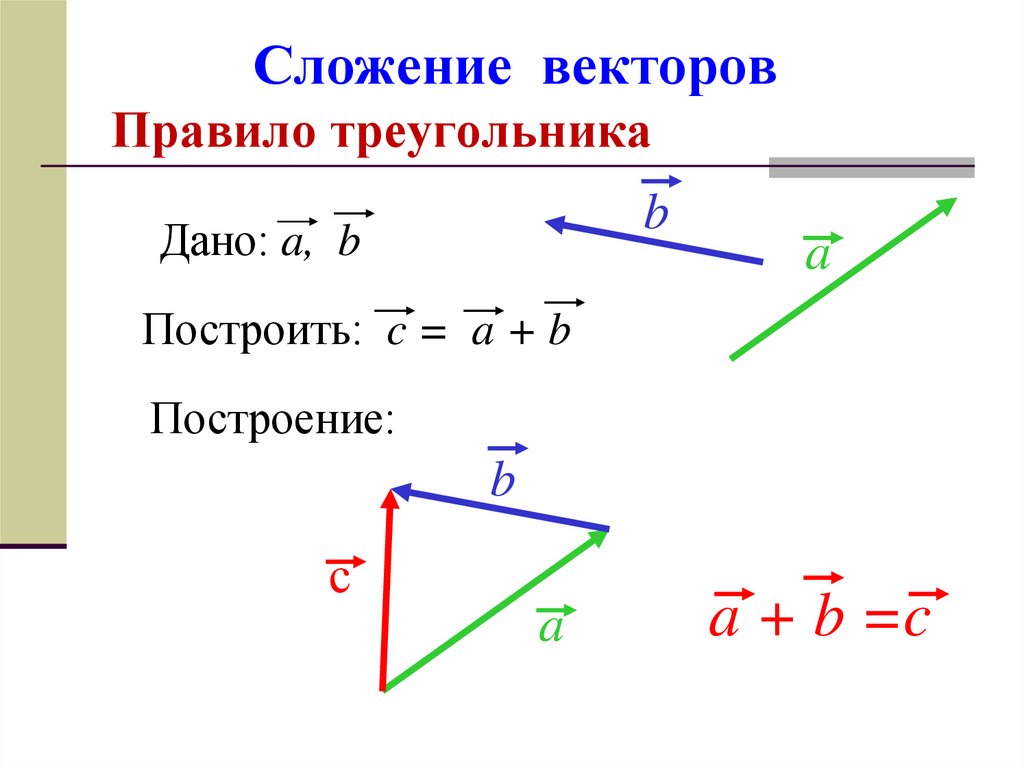 Достроим до параллелограмма, проведя дополнительные линии, параллельно данным векторам. Вектор AD являющийся диагональю параллелограмма, выходящий из точки А есть сумма векторов а и b.
Достроим до параллелограмма, проведя дополнительные линии, параллельно данным векторам. Вектор AD являющийся диагональю параллелограмма, выходящий из точки А есть сумма векторов а и b.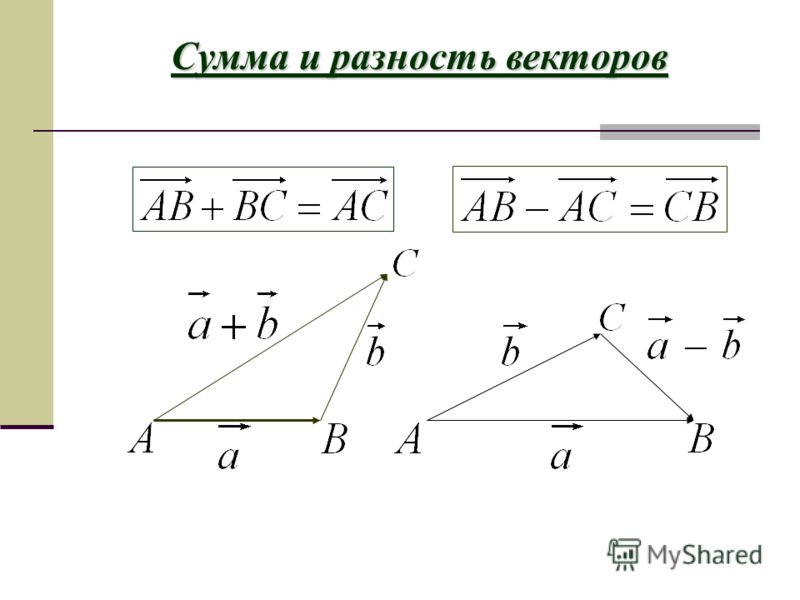
 ..
..
 е. взять произвольную точку А, построить такие точки В и С, что и , и достроить полученную фигуру до параллелограмма . Вектор — искомая сумма (рис. 5).
е. взять произвольную точку А, построить такие точки В и С, что и , и достроить полученную фигуру до параллелограмма . Вектор — искомая сумма (рис. 5). Вектор, начало которого совпадает с началом первого вектора, а конец – с концом последнего (n-го вектора), есть искомая сумма.
Вектор, начало которого совпадает с началом первого вектора, а конец – с концом последнего (n-го вектора), есть искомая сумма.
 Тогда — искомый вектор.
Тогда — искомый вектор.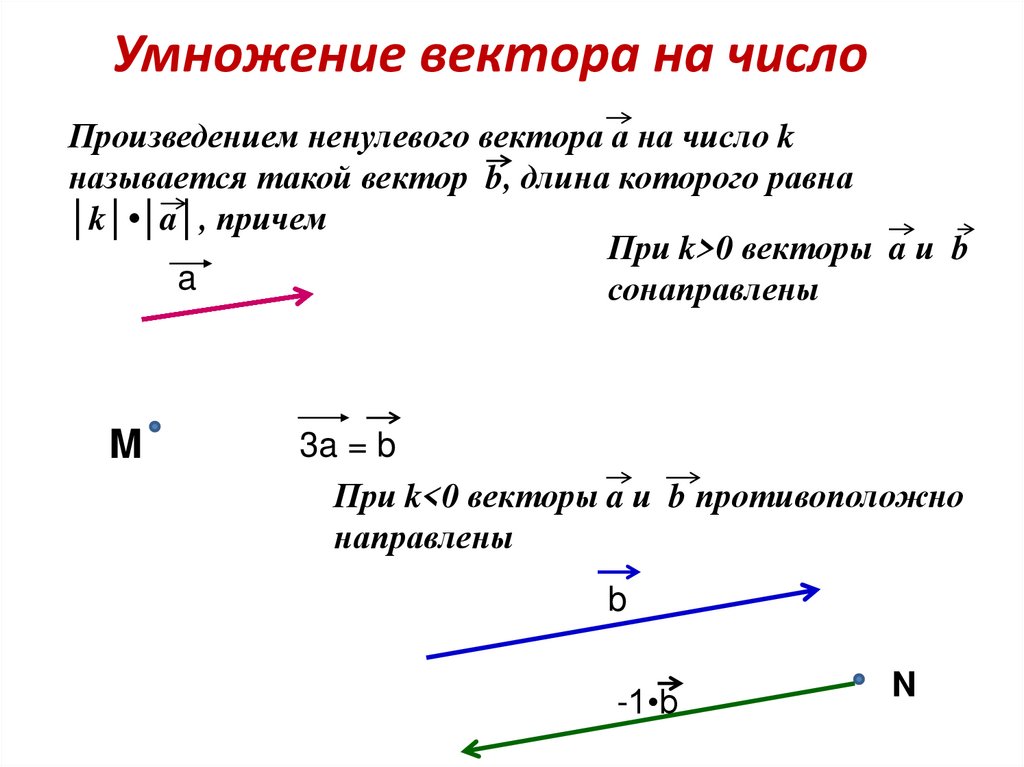
 Вычтите два вектора, затем задайте величину и угол результирующего вектора S .
Вычтите два вектора, затем задайте величину и угол результирующего вектора S .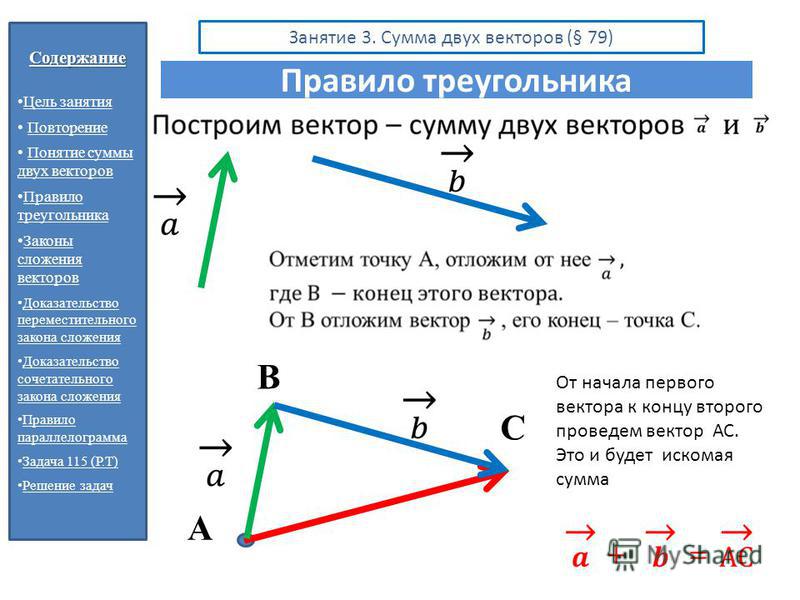 (приблизительно), а угол Φ = -29,05 градуса.
(приблизительно), а угол Φ = -29,05 градуса. 0052
0052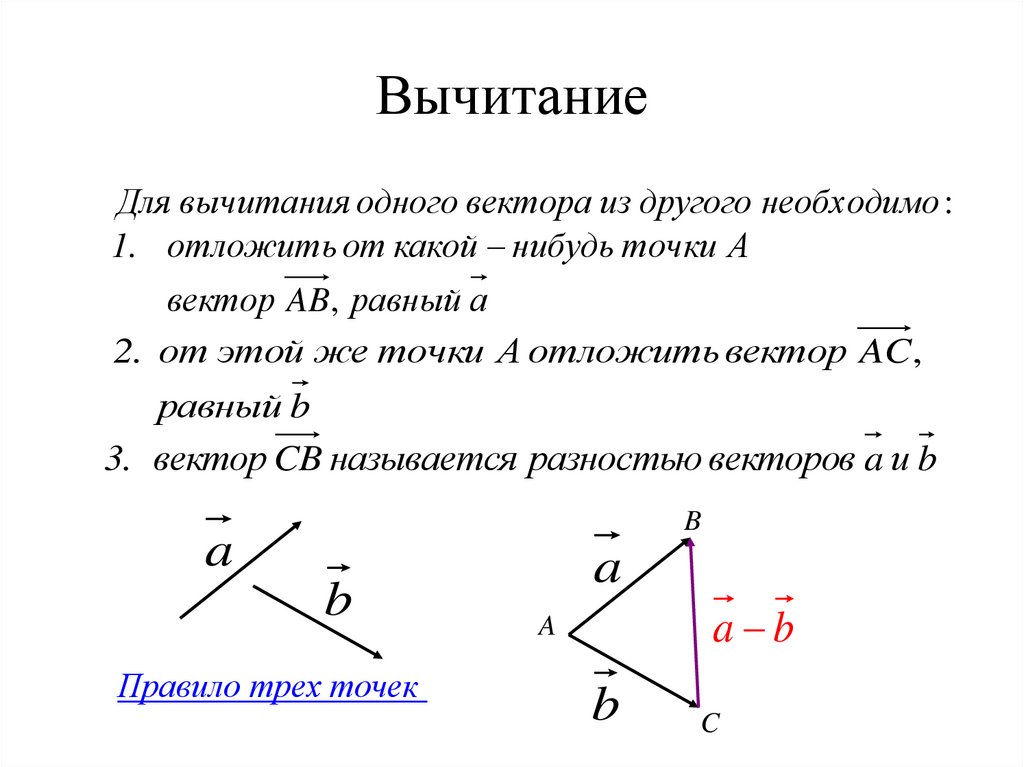


 Докажите, что их результатом является сила, представленная 6 вектором АО, где О — центр шестиугольника. (3 балла)
Докажите, что их результатом является сила, представленная 6 вектором АО, где О — центр шестиугольника. (3 балла)  …….(i)\)
…….(i)\)

 Direction of the Resultant vectors:
Direction of the Resultant vectors: 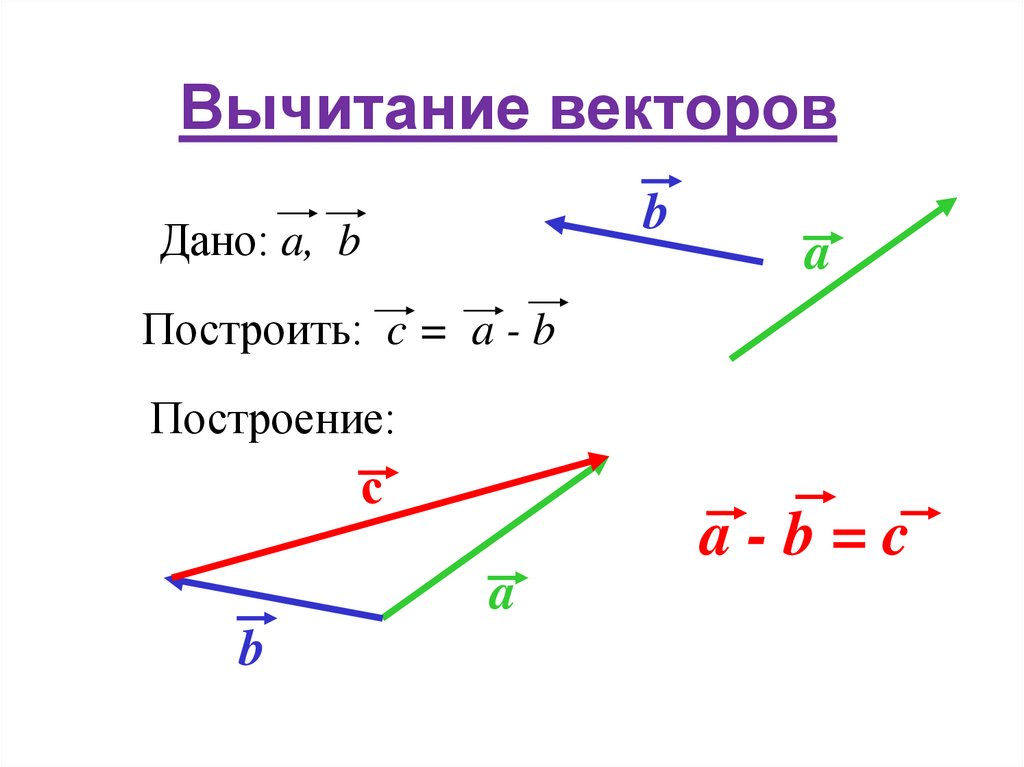 т.е.
т.е.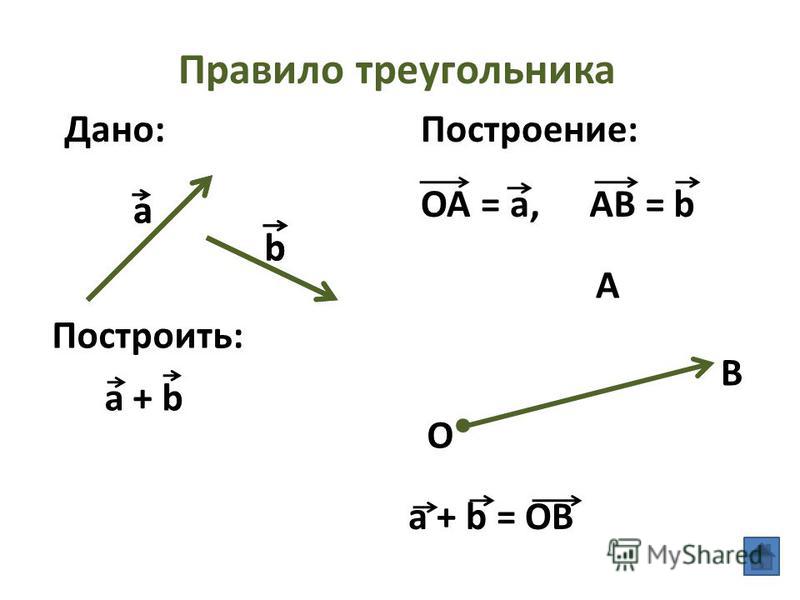 e. α = 0
e. α = 0 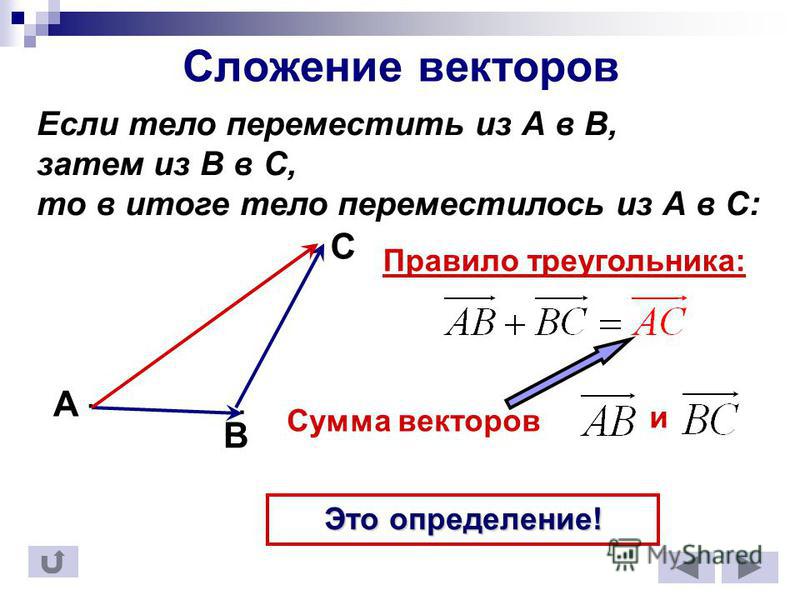 т.е. α = 0 или 180
т.е. α = 0 или 180 
 î – 3х – 2к̂
î – 3х – 2к̂ Если векторы А и B be respectively equal to (3 î – 4 ĵ + 5 k̂ ) and (2 î + 3 ĵ – 4 k̂ ), получаем величину вектора A + B и A – B .
Если векторы А и B be respectively equal to (3 î – 4 ĵ + 5 k̂ ) and (2 î + 3 ĵ – 4 k̂ ), получаем величину вектора A + B и A – B .
 Сила представлена как 2 х + 3 х +6k. Какова величина силы?
Сила представлена как 2 х + 3 х +6k. Какова величина силы?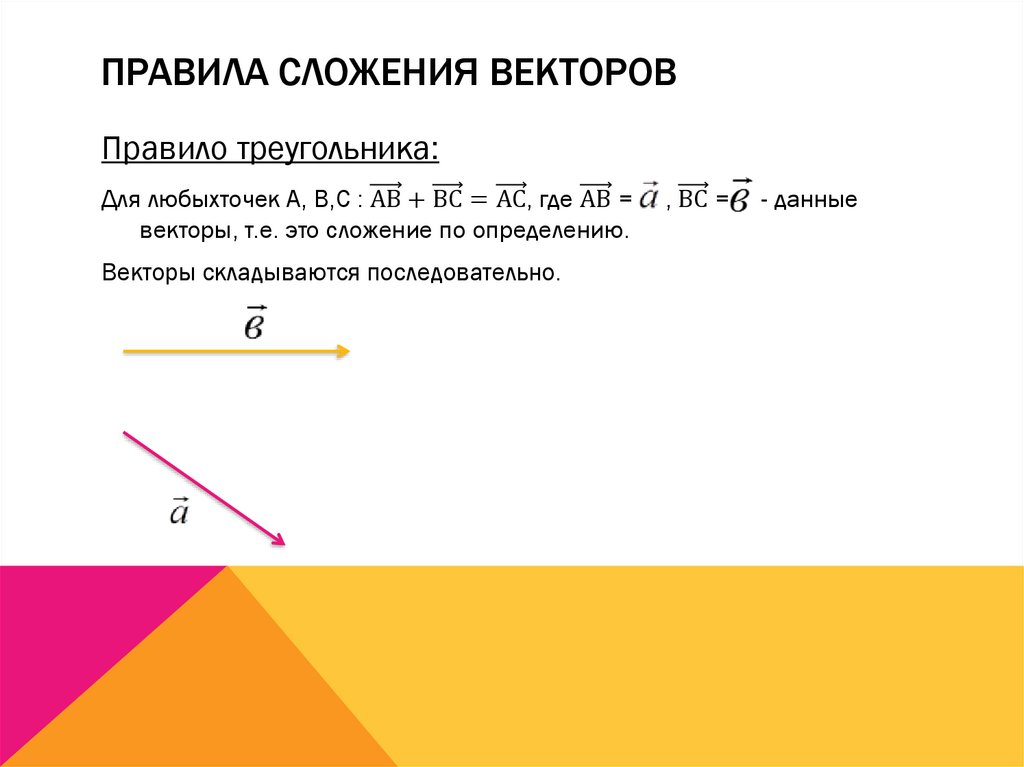 1 ✓ (3)
1 ✓ (3) 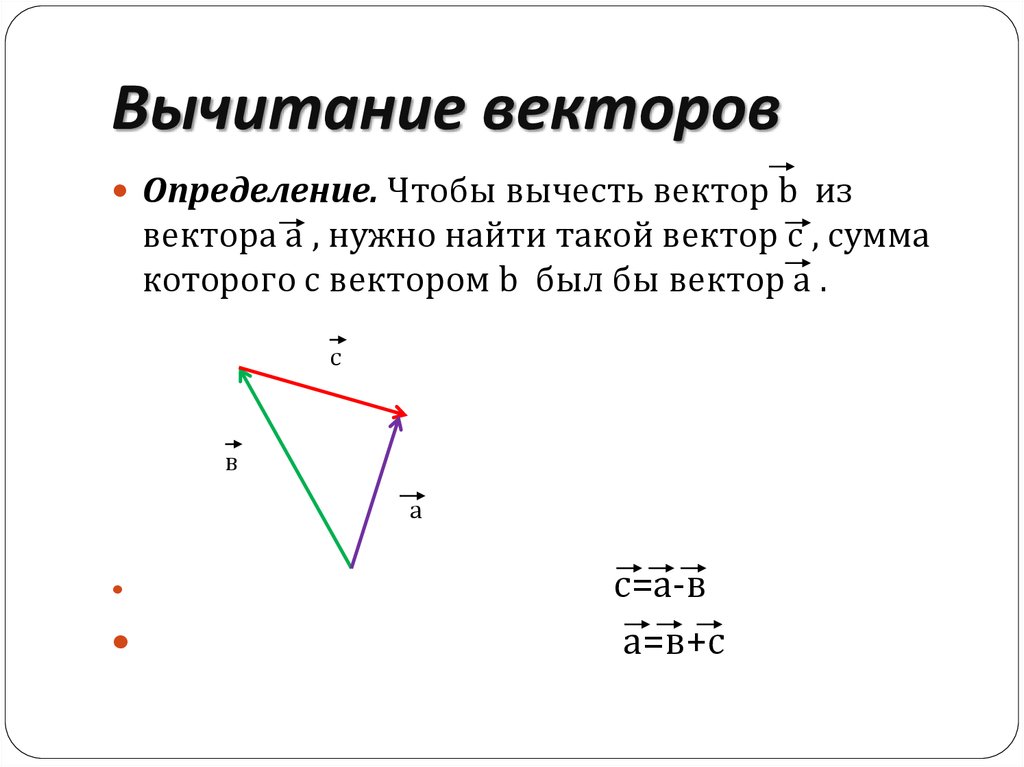 Также A, B и C могут иметь следующие значения.
Также A, B и C могут иметь следующие значения.
 Три
Три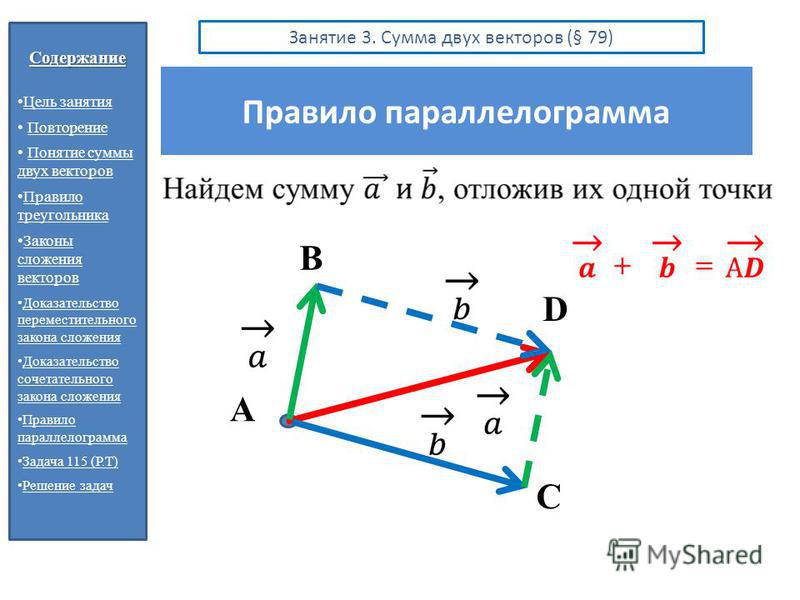 180°
180° Если вектор A , B и C лежат в одной плоскости и
Если вектор A , B и C лежат в одной плоскости и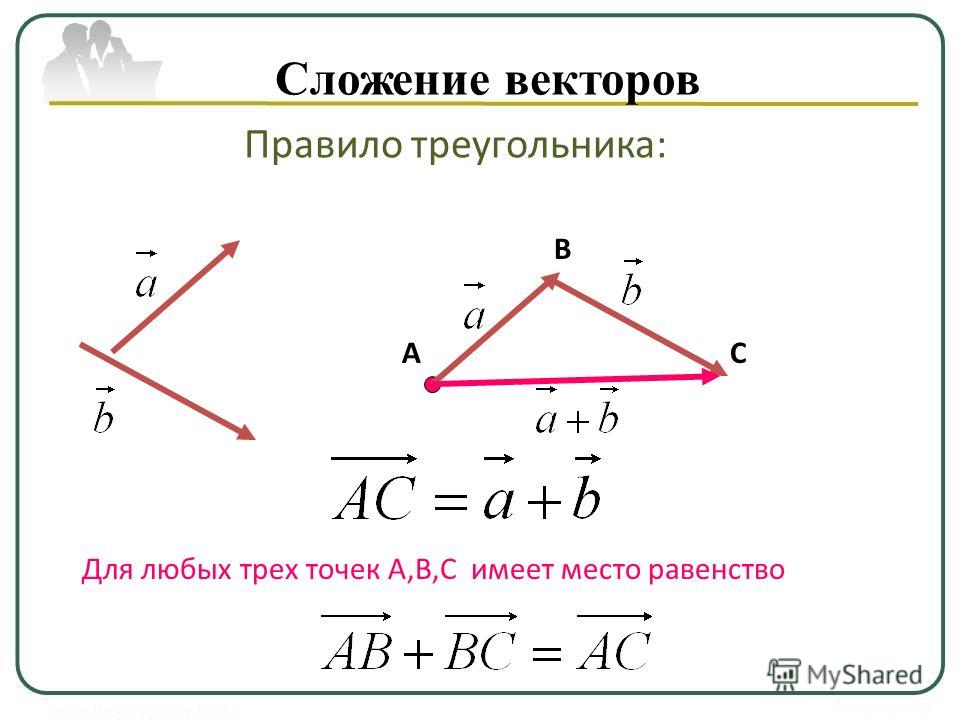 R=а-б
R=а-б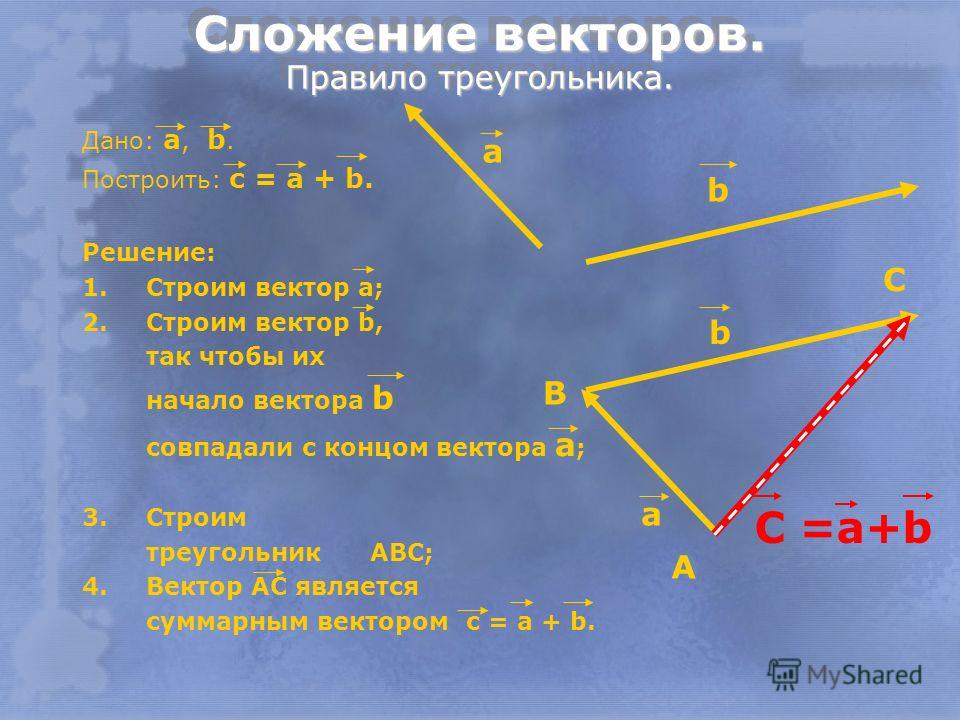 R=b+a
R=b+a Чтобы равнодействующая двух векторов была минимальной, какой должен быть угол между ними
Чтобы равнодействующая двух векторов была минимальной, какой должен быть угол между ними  Р=а+б
Р=а+б Три
Три Минимальное количество копланарных векторов, результант которых может быть равен нулю, равно
Минимальное количество копланарных векторов, результант которых может быть равен нулю, равно 
 60°
60° 10, 20, 23
10, 20, 23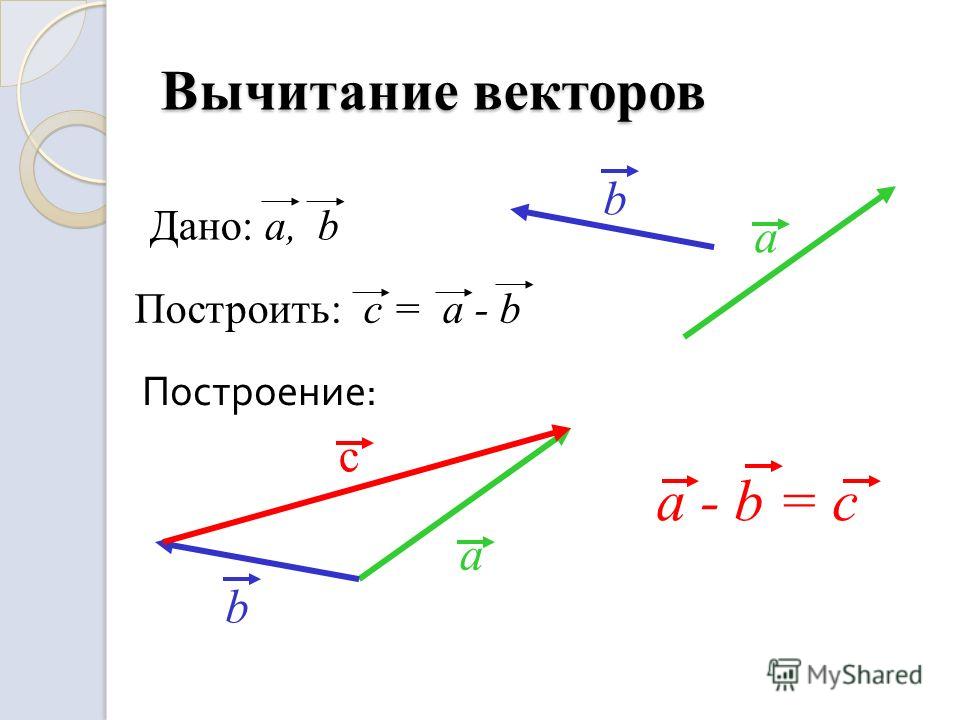 î +3х + 5к̂
î +3х + 5к̂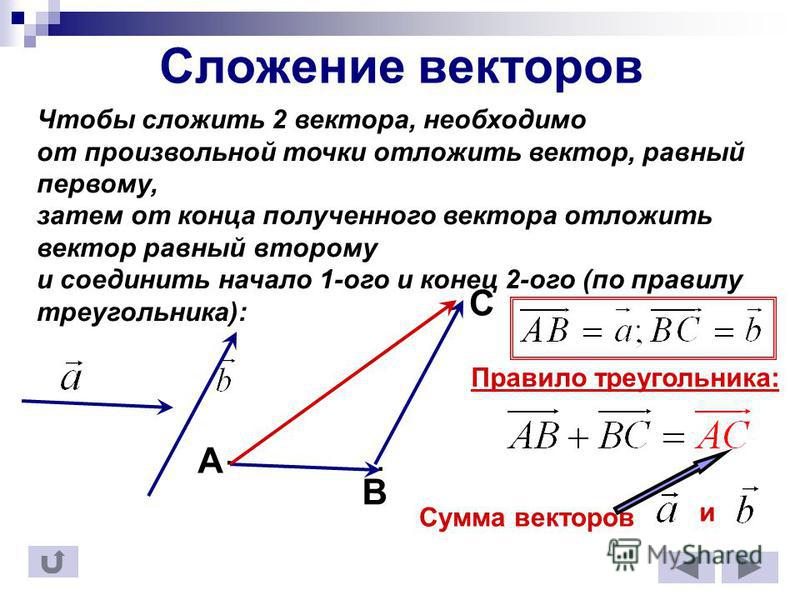 60°
60°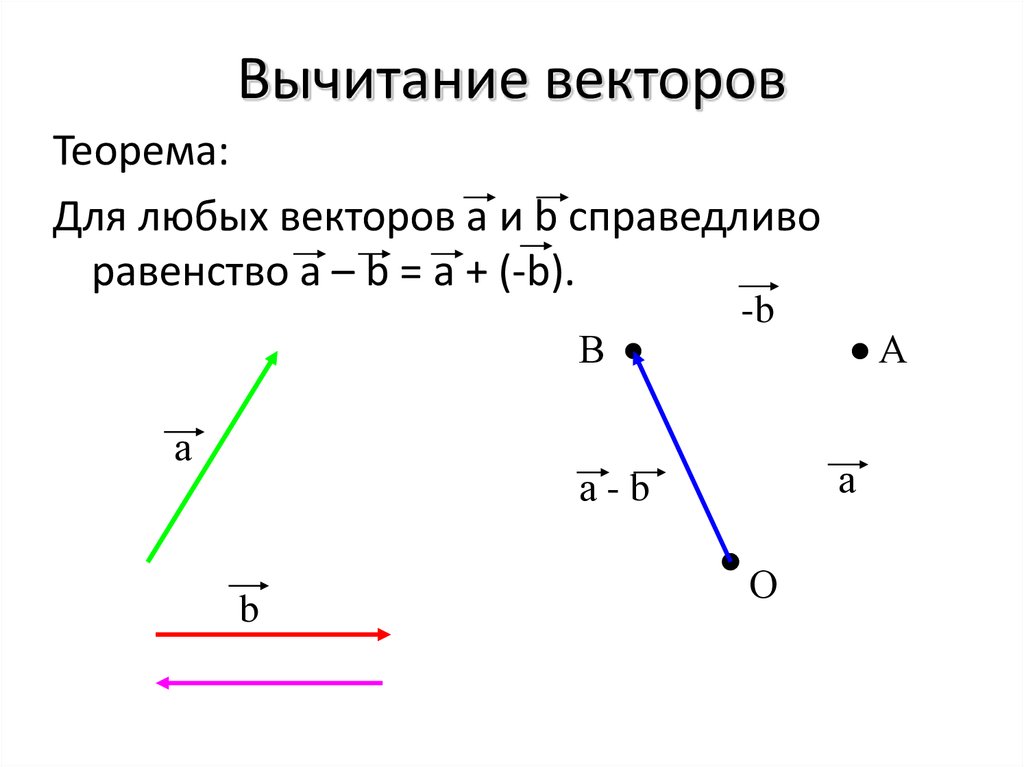 1/✓(2)
1/✓(2) 1
1 Векторы, A+B+C=0
Векторы, A+B+C=0 Если углы между ними равны, результирующая сила будет
Если углы между ними равны, результирующая сила будет  Какой должен быть угол между ними, чтобы равнодействующая двух векторов была максимальной
Какой должен быть угол между ними, чтобы равнодействующая двух векторов была максимальной  Результирующая сила, действующая на точечную массу, будет равна
Результирующая сила, действующая на точечную массу, будет равна 

 Но применим ассоциативный закон.
Но применим ассоциативный закон. 
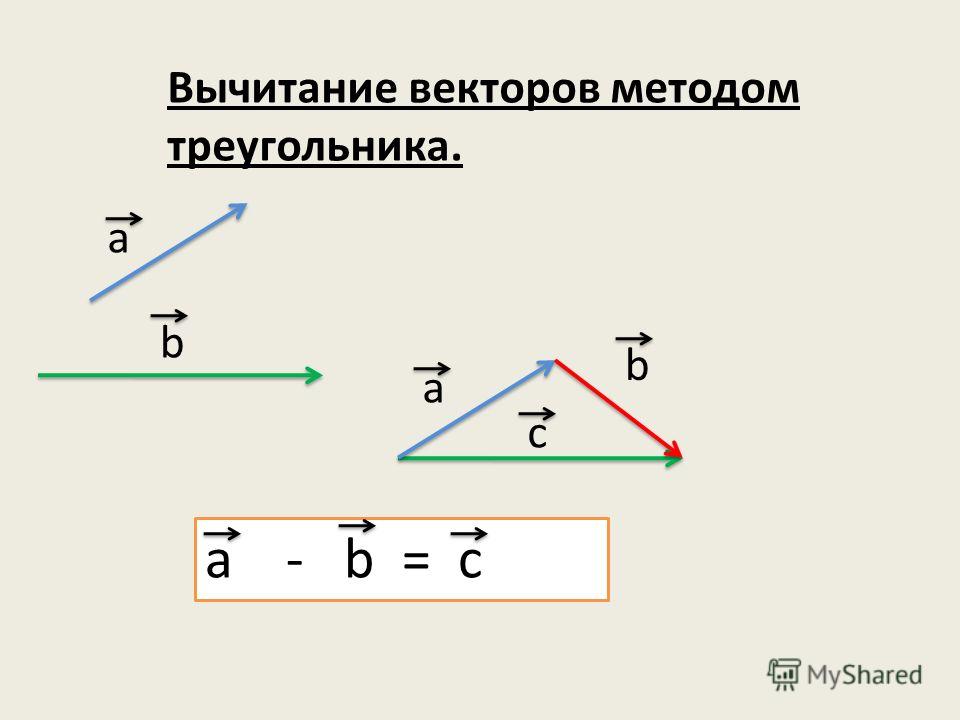
 Разница между двумя векторами или вычитание векторов соответствует правилам сложения векторов. Для двух векторов и операция может быть записана как . Пример показан на рис. 2.8.
Разница между двумя векторами или вычитание векторов соответствует правилам сложения векторов. Для двух векторов и операция может быть записана как . Пример показан на рис. 2.8. Например . Пример показан ниже:
Например . Пример показан ниже:
 Из закона косинуса,
Из закона косинуса,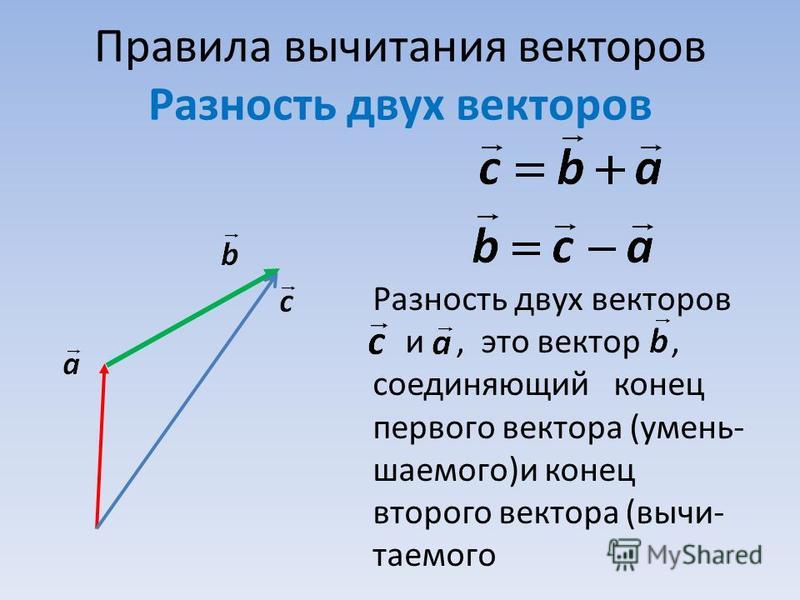 Чтобы вычесть B из A, направление B сначала меняется на противоположное. Затем он добавляется к A. Результат A и –B дает A–B, который сам является вектором, имеющим определенную величину и направление. Она показана третьей стороной треугольника по закону треугольника. Вектор A–B показан на рисунке ниже.
Чтобы вычесть B из A, направление B сначала меняется на противоположное. Затем он добавляется к A. Результат A и –B дает A–B, который сам является вектором, имеющим определенную величину и направление. Она показана третьей стороной треугольника по закону треугольника. Вектор A–B показан на рисунке ниже. Вектор единичной длины называется единичным вектором. Векторы положения обозначают положение или расположение точки в трехмерном пространстве. Векторы с одинаковой начальной точкой называются ко-начальными векторами. Векторы с одинаковым направлением называются похожими векторами, а векторы с противоположным направлением называются непохожими векторами. Векторы, лежащие на одной или параллельных прямых, называются копланарными векторами. Векторы с одинаковыми величинами и направлением называются равными векторами. Вычитание векторов можно выполнять многими методами. Двумя наиболее важными из них являются следующие:
Вектор единичной длины называется единичным вектором. Векторы положения обозначают положение или расположение точки в трехмерном пространстве. Векторы с одинаковой начальной точкой называются ко-начальными векторами. Векторы с одинаковым направлением называются похожими векторами, а векторы с противоположным направлением называются непохожими векторами. Векторы, лежащие на одной или параллельных прямых, называются копланарными векторами. Векторы с одинаковыми величинами и направлением называются равными векторами. Вычитание векторов можно выполнять многими методами. Двумя наиболее важными из них являются следующие: 
 Значение a–b также показано в соответствии с законом треугольника. Мы можем легко заметить, что величина a+b больше, чем величина a–b. Другими словами, сумма двух векторов больше, чем разность двух векторов по величине. Если мы возьмем угол между двумя векторами, равными 90 градусов, параллелограмм становится прямоугольником, и все диагонали становятся равными по длине. Одна диагональ представляет a+b, а другая диагональ представляет a–b. Они оба равны. Отсюда мы видим, что сумма двух векторов становится равной разности двух векторов по модулю. Далее можно заметить, что a+b становится меньше, чем a–b, если мы возьмем угол между двумя заданными векторами, который меньше 90 градусов.
Значение a–b также показано в соответствии с законом треугольника. Мы можем легко заметить, что величина a+b больше, чем величина a–b. Другими словами, сумма двух векторов больше, чем разность двух векторов по величине. Если мы возьмем угол между двумя векторами, равными 90 градусов, параллелограмм становится прямоугольником, и все диагонали становятся равными по длине. Одна диагональ представляет a+b, а другая диагональ представляет a–b. Они оба равны. Отсюда мы видим, что сумма двух векторов становится равной разности двух векторов по модулю. Далее можно заметить, что a+b становится меньше, чем a–b, если мы возьмем угол между двумя заданными векторами, который меньше 90 градусов.