Правило векторного умножения векторов: формула, как найти по координатам, примеры решения

формула, как найти по координатам, примеры решения

Содержание:

• Что такое произведение векторов
• Основные типы перемножения векторов
  • Скалярное
  • Векторное
  • Смешанное умножение векторов
• Произведение векторов, примеры и решения

Содержание

• Что такое произведение векторов
• Основные типы перемножения векторов
  • Скалярное
  • Векторное
  • Смешанное умножение векторов
• Произведение векторов, примеры и решения

Что такое произведение векторов

Определение

Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.

Это одна из основных операций над векторами в векторной алгебре. Вектор, в отличие от обычного отрезка, имеет не только длину, но и направление в пространстве.

Основные типы перемножения векторов

В математике есть два основных вида умножения векторов: скалярное и векторное. Результатом первого является число, результатом второго — вектор. Оба произведения применяются к двум векторам. Также выделяют смешанное произведение векторов, которое является комбинацией двух вышеописанных. Оно применяется, когда необходимо узнать результат умножения трех векторов.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Скалярное

Определение

Скалярным произведением двух векторов называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними.

Длина вектора является его модулем.

Записывается скалярное произведение двумя способами: \( (\overline a,\;\overline b) \) или \( \overline a\cdot\overline b.\)

Алгебраические свойства скалярного произведения

1. Перестановочность. Произведение не меняется от перемены мест множителей: \(\overline a\cdot\overline b=\overline b\cdot\overline a.\)
2. Сочетательность относительно числа. Умножение одного из векторов на число равносильно умножению обоих векторов на это число: \((\lambda\overline a)\cdot\overline b=\lambda(\overline a\cdot\overline b)(\lambda\overline a)\cdot(\mu\overline b)=(\lambda\mu)(\overline a\cdot\overline b).\)
3. Распределительный закон. Скалярное произведение суммы двух векторов на третий равносильно сумме скалярных произведений этих векторов на третий вектор: \((\overline a+\overline b)\cdot\overline c=\overline a\cdot\overline c+\overline b\cdot\overline c.\)

Примечание

Таким образом, при выполнении алгебраических действий, связанных со скалярным произведением, с векторами можно обращаться как с числами. \circ\)), то их скалярное произведение будет равняться нулю.

Если координаты перемножаемых векторов известны, то их скалярное произведение будет равняться сумме произведений соответствующих координат:\( \overline a\cdot\overline b=a_x\cdot b_x+a_y\cdot b_y+a_z\cdot b_z.\)

Геометрический смысл

Скалярное произведение двух векторов равно произведению модуля одного из них на проекцию второго вектора на первый.

\(\overline a\cdot\overline b=\left|\overline a\right|\cdot пр_\overline a\overline b=\overline{\left|b\right|}\cdot пр_\overline b\overline a\)

\(пр_\overline b\overline a=\frac{\overline a\cdot\overline b}{\left|\overline b\right|}\)

Физический смысл

Скалярное произведение применяется для расчета работы, выполняемой при перемещении материальной точки вдоль вектора \(\overline s\) под действием силы \(\overline F\), приложенной под некоторым углом \(\varphi.\)

 

Рисунок 1. Физический смысл скалярного произведения

Силу \(\overline F\) необходимо разложить на ортогональные компоненты \(\overline{F_1}\) и \(\overline{F_2}. \) Тогда \(\overline{F_1}\) будет являться проекцией силы \(\overline F\) на вектор \(\overline s:\)

\(\left|\overline{F_1}\right|=\left|\overline F\right|\cdot\cos\left(\varphi\right).\)

В свою очередь, работа A вычисляется по формуле:

\(A=\left|\overline{F_1}\right|\cdot\left|\overline S\right|.\)

Соединив данные формулы получим:

\(A=\left|\overline F\right|\cdot\left|\overline S\right|\cdot\cos\left(\varphi\right),\)

что является скалярным произведением векторов \(\overline F\) и \(\overline s:\)

\(A=\overline F\cdot\overline S.\)

Векторное

Определение

Векторным произведением векторов \overline a и \overline b называют перпендикулярный им вектор \overline c из правой тройки, модуль которого равняется произведению модулей векторов \overline a и \overline b на синус угла между ними.

Упорядоченная тройка некомпланарных векторов называется правой, если с конца третьего вектора кратчайший поворот от первого ко второму совершается против часовой стрелки. В противном случае такая тройка называется левой.

Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Векторное произведение может выражаться в записи двумя способами: \(\overline a\times\overline b\) и \(\lbrack\overline a,\overline b\rbrack.\)

Алгебраические свойства

1. Антиперестановочность. В отличие от скалярного произведения, в векторном при перемене мест множителей знак меняется на противоположный: \(\overline a\times\overline b=-(\overline b\times\overline a)\)
2. Сочетательность относительно числа. Как и в случае со скалярным умножением, произведение числа на один из векторов равняется произведению его на другой или на оба вектора: \((\lambda\overline a)\times\overline b=\overline a\times(\lambda\overline b)=\lambda(\overline a\times\overline b).\)
3. Распределительный закон. Векторное произведение суммы двух векторов на третий равносильно сумме векторных произведений этих векторов на третий вектор: \((\overline a+\overline b)\times\overline c=\overline a\times\overline c+\overline b\times\overline c. \)

Из этого следует, что при выполнении алгебраических действий, связанных с векторным произведением, скобки можно раскрывать так же, как при работе с числами, с поправкой на правило антиперестановочности.

Геометрические свойства

1. Если вектора \(\overline a\) и \(\overline b\) параллельны, то их векторное произведение равняется нулю.
2. Векторное произведение векторов с известными координатами выражается в матричном виде: \(\overline a\times\overline b=\begin{vmatrix}i&j&k\\a_x&a_y&a_z\\b_x&b_y&b_z\end{vmatrix}=\left(\begin{vmatrix}a_y&a_z\\b_y&b_z\end{vmatrix};\;-\begin{vmatrix}a_x&a_z\\b_x&b_z\end{vmatrix};\;\begin{vmatrix}a_x&a_y\\b_x&b_y\end{vmatrix}\right).\)

Геометрический смысл

Модуль векторного произведения двух векторов равняется площади параллелограмма, сторонами которого являются эти вектора.

 

Рисунок 2. Геометрический смысл векторного произведения

Из определения векторного умножения следует, что модуль полученного вектора равняется произведению модулей исходных векторов на синус угла между ними:

\(\left|\overline c\right|=\left|\overline a\right|\cdot\left|\overline b\right|\cdot\sin\left(\varphi\right)\)

Площадь параллелограмма вычисляется так:

\(S=\left|\overline a\right|\cdot h, где h=\left|\overline b\right|\cdot\sin\left(\varphi\right). \)

Таким образом, получаем:

\(S=\left|\overline a\right|\cdot\left|\overline b\right|\cdot\sin\left(\varphi\right)=\left|\overline a\times\overline b\right|\)

Отсюда следует формула для площади треугольника:

\(S_\bigtriangleup=\frac12\left|\overline a\times\overline b\right|\)

Физический смысл

В физике векторное произведение применяется для расчета момента силы, приложенной к одной точке относительно другой:

\(\overline M=\overline{AB}\times\overline F\)

Смешанное умножение векторов

Фактически, смешанное произведение векторов представляется как скалярное умножение одного вектора на векторное произведение двух других. Результатом смешанного произведения является число.

Свойства смешанного умножения

1. \((\overline a\times\overline b)\cdot\overline c=\overline a\cdot(\overline b\times\overline c)=\overline a\cdot\overline b\cdot\overline c.\)
2. Если \(\overline a\cdot\overline b\cdot\overline c\) больше нуля, тройка векторов — правая.
3. Если\( \overline a\cdot\overline b\cdot\overline c\) меньше нуля, тройка векторов — левая.
4. Если вектора \(\overline a, \overline b\) и \(\overline c\) компланарны, то их смешанное произведение равняется нулю.

Геометрический смысл

Если вектора \overline a, \overline b и \overline c не компланарны, то их смешанное произведение равно объему параллелепипеда, построенного на этих векторах. Число будет положительным, если тройка векторов правая, и отрицательным, если тройка левая.

\(V_{пар.}=\overline a\cdot\overline b\cdot\overline c\)

Следствием этого является формула нахождения объема пирамиды:

\(V_{пир.}=\frac16\left(\overline a\cdot\overline b\cdot\overline c\right)\)

Произведение векторов, примеры и решения

Задача №1

Даны вектора \(\overline a=(-1,\;0,\;3) и \overline b=(2,\;-3,\;1).\)

Найти их скалярное произведение.

Решение

Возьмем формулу скалярного произведения для векторов с известными координатами:

\(\overline a\cdot\overline b=a_x\cdot b_x+a_y\cdot b_y+a_z\cdot b_z\) и подставим имеющиеся значения:

\(\overline a\cdot\overline b=(-1)\cdot2+0\cdot(-3)+3\cdot1=1\)

Задача №2

Найти площадь треугольника с известными координатами угловых точек

 

Координаты точек: \(A(-1,\;2,\;3), B(0,\;-2,\;1), C(1,\;2,\;1)\)

Решение

Для решения этой простейшей задачи из геометрии воспользуемся следствием геометрического смысла векторного произведения:

\(S_\bigtriangleup=\frac12\left|\overline a\times\overline b\right|\)

В данном случае треугольник построен на векторах\( \overline{AB}\) и \(\overline{AC}\). Чтобы рассчитать их координаты, необходимо вычесть из координат конечной точки координаты начальной:

\(\overline{AB}=(0-(-1),\;(-2)-2,\;1-3)=(1,\;-4,\;-2)\)

\(\overline{AC}=(1-(-1),\;2-2,\;1-3)=(2,\;0,\;-2)\)

Векторное произведение векторов с известными координатами выполняется в матричном виде:

\(\overline a\times\overline b=\begin{vmatrix}i&j&k\\a_x&a_y&a_z\\b_x&b_y&b_z\end{vmatrix}=\left(\begin{vmatrix}a_y&a_z\\b_y&b_z\end{vmatrix};\;-\begin{vmatrix}a_x&a_z\\b_x&b_z\end{vmatrix};\;\begin{vmatrix}a_x&a_y\\b_x&b_y\end{vmatrix}\right)\)

Подставляем значения векторов\( \overline{AB}\) и \(\overline{AC}\) в матрицу и производим вычисления:

\(\overline{AB}\times\overline{AC}=\begin{vmatrix}i&j&k\\1&-4&-2\\2&0&-2\end{vmatrix}=\left(i\begin{vmatrix}-4&-2\\0&-2\end{vmatrix};\;-j\begin{vmatrix}1&-2\\2&-2\end{vmatrix};\;k\begin{vmatrix}1&-4\\2&0\end{vmatrix}\right)=8i-2j+8k\)

Подставляем полученное значение в формулу вычисления площади треугольника, учитывая, что в ней фигурирует модуль произведения:

\(S_\bigtriangleup=\frac12\left|\overline{AB}\times\overline{AC}\right|=\frac12\sqrt{8^2+{(-2)}^2+8^2}=\sqrt{132}=11. 49\)

Насколько полезной была для вас статья?

Рейтинг: 4.20 (Голосов: 10)

Поиск по содержимому

Векторное произведение векторов.

Векторное произведение векторов.

Навигация по странице:

• Определение векторного произведения векторов
• Формулы вычисления векторного произведения векторов
• Свойства векторного произведения векторов
• Примеры задач на вычисления векторного произведения векторов

Онлайн калькулятор. Векторное произведение векторов.

Упражнения на тему векторное произведение векторов.

Определение. Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c (рис. 1).

рис. 1

Формулы вычисления векторного произведения векторов

Векторное произведение двух векторов a = {a_x; a_y; a_z} и b = {b_x; b_y; b_z} в декартовой системе координат — это вектор, значение которого можно вычислить, используя следующие формулы:

a × b = ijka_xa_ya_zb_xb_yb_z = i (a_yb_z — a_zb_y) — j (a_xb_z — a_zb_x) + k (a_xb_y — a_yb_x)

a × b = {a_yb_z — a_zb_y; a_zb_x — a_xb_z; a_xb_y — a_yb_x}

Свойства векторного произведения векторов

• Геометрический смысл векторного произведения.

  Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах:

  S_парал = [a × b]

• Геометрический смысл векторного произведения.

  Площадь треугольника построенного на векторах a и b равна половине модуля векторного произведения этих векторов:

  SΔ =	1	|a × b|
  	2

• Векторное произведения двух не нулевых векторов a и b равно нулю тогда и только тогда, когда вектора коллинеарны.

• Вектор c, равный векторному произведению не нулевых векторов a и b, перпендикулярен этим векторам.

• a × b = -b × a

• (k a) × b = a × (k b) = k (a × b)

• (a + b) × c = a × c + b × c

Примеры задач на вычисления векторного произведения векторов

Пример 1. Найти векторное произведение векторов a = {1; 2; 3} и b = {2; 1; -2}.

Решение:

a × b =	i	j	k	=
	1	2	3
	2	1	-2

= i(2 · (-2) — 3 · 1) — j(1 · (-2) — 2 · 3) + k(1 · 1 — 2 · 2) =

= i(-4 — 3) — j(-2 — 6) + k(1 — 4) = -7i + 8j — 3k = {-7; 8; -3}

Пример 2. Найти площадь треугольника образованного векторами a = {-1; 2; -2} и b = {2; 1; -1}.

Решение: Найдем векторное произведение этих векторов:

a × b =	i	j	k	=
	-1	2	-2
	2	1	-1

= i(2 · (-1) — (-2) · 1) — j((-1) · (-1) — (-2) · 2) + k((-1) · 1 — 2 · 2) =

= i(-2 + 2) — j(1 + 4) + k(-1 — 4) = -5j — 5k = {0; -5; -5}

Из свойств векторного произведения:

SΔ =

12

|a × b| =

12

√0² + 5² + 5² =

12

√25 + 25 =

12

√50 =

5√22

= 2. 5√2

Ответ: SΔ = 2.5√2.

Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису

Онлайн калькуляторы с векторами

Онлайн упражнения с векторами на плоскости

Онлайн упражнения с векторами в пространстве

Умножение векторов — определение, формула, примеры

Умножение векторов бывает двух типов. Вектор имеет как величину, так и направление, и, исходя из этого, двумя способами умножения векторов являются скалярное произведение двух векторов и перекрестное произведение двух векторов. Скалярное произведение двух векторов также называется скалярным произведением, поскольку результирующее значение является скалярной величиной. Перекрестное произведение называется векторным произведением, так как в результате получается вектор, перпендикулярный этим двум векторам.

Давайте узнаем о двух умножениях векторов, рабочем правиле, свойствах, использовании, примерах этого умножения векторов.

1.	Как сделать умножение векторов?
2.	Рабочее правило умножения векторов
3.	Свойства умножения векторов
4.	Применение умножения векторов
5.	Примеры умножения векторов
6.	Практические вопросы по умножению векторов
7.	Часто задаваемые вопросы об умножении векторов

Как сделать умножение векторов?

Вектор имеет как величину, так и направление. Мы можем умножать два или более векторов на скалярное произведение и перекрестное произведение. Давайте разберемся подробнее о каждом умножении векторов.

Скалярное произведение

Скалярное произведение векторов также называется скалярным произведением векторов. Результат скалярного произведения векторов является скалярным значением. Скалярное произведение векторов равно произведению величин двух векторов и косинуса угла между двумя векторами. Результат скалярного произведения двух векторов лежит в одной плоскости двух векторов. Скалярный продукт может быть положительным действительным числом или отрицательным действительным числом.

Пусть a и b — два ненулевых вектора, а θ — угол между векторами. Тогда скалярное произведение или скалярное произведение обозначается буквой a.b, которая определяется как:

\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ .

Здесь \(|\overrightarrow a|\) — величина \(\overrightarrow a\), \(|\overrightarrow b|\) — величина \(\overrightarrow b\), а θ — величина угол между ними.

Перекрестное произведение

Перекрестное произведение также называется векторным произведением. Перекрестное произведение — это форма умножения векторов, выполняемая между двумя векторами разной природы или вида. Когда два вектора перемножаются друг с другом, и умножение также является векторной величиной, то результирующий вектор называется перекрестным произведением двух векторов или векторным произведением. Результирующий вектор перпендикулярен плоскости, содержащей два заданных вектора.

Понять это можно на примере: если у нас есть два вектора, лежащих в плоскости X-Y, то их векторное произведение даст результирующий вектор в направлении оси Z, которая перпендикулярна плоскости XY. Символ × используется между исходными векторами. Умножение векторов или перекрестное произведение двух векторов показано следующим образом.

\(\overrightarrow{a} \times \overrightarrow{b} = \overrightarrow{c}\)

Здесь \(\overrightarrow{a}\) и \(\overrightarrow{b}\) — два вектора, и \(\overrightarrow{c}\) — результирующий вектор. Пусть θ — угол, образованный между \(\overrightarrow{a}\) и \(\overrightarrow{b}\), а \(\hat n\) — единичный вектор, перпендикулярный плоскости, содержащей обе \(\overrightarrow{a }\) и \(\overrightarrow{b}\). Перекрестное произведение двух векторов определяется следующей формулой:

\(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\)

Рабочее правило умножения векторов

Рабочее правило умножения векторов, которое включает скалярное произведение и векторное произведение, можно понять из приведенных ниже предложений.

Скалярное произведение

Для скалярного умножения векторов два вектора выражаются через единичные векторы i, j, k вдоль осей x, y, z, затем скалярное произведение получается следующим образом:

Если \(\overrightarrow a = a_1\hat i + b_1 \hat j + c_1 \hat k\) и \(\overrightarrow b = a_2 \hat i + b_2 \hat j + c_2\hat k\), то

\(\overrightarrow a. \overrightarrow b\) = \((a_1 \hat i + b_1 \hat j + c_1 \hat k)(a_2 \hat i + b_2 \hat j + c_2 \hat k)\)

= \((a_1a_2) (\hat i. \hat i) + (a_1b_2) (\hat i.\hat j)+ (a_1c_2) (\hat i. \hat k) + \\(b_1a_2) ( \hat j. \hat i) + (b_1b_2)(\hat j. \hat j) + (b_1c_2 (\hat j. \hat k) + \\(c_1a_2)(\hat k. \hat i) + ( c_1b_2)(\шляпа k.\шляпа j) + (c_1c_2)(\шляпа k.\шляпа k)\)

\(\overrightarrow a. \overrightarrow b\) = \(a_1a_2 + b_1b_2+ c_1c_2\)

Перекрестное произведение

Предположим, что \(\overrightarrow{a}\) и \(\overrightarrow{b}\ ) — два вектора, такие, что \(\overrightarrow{a}\)= \(a_1\hat i+b_1 \hat j+c_1 \hat k\) и \(\overrightarrow{b}\) = \(a_2 \ шляпа i+b_2 \ шляпа j+c_2 \ шляпа k\), то с помощью определителей мы могли бы найти векторное произведение векторов, используя следующую матричную запись.

Перемножение векторов также представляется с помощью формулы перекрестного произведения как:

\(\overrightarrow{a} \times \overrightarrow{b} = \hat i (b_1c_2-b_2c_1) — \hat j (a_1c_2-a_2c_1) + \hat k (a_1b_2-a_2b_1)\)

Примечание: \ ( \hat i, \hat j, \text{ и } \hat k \) — единичные векторы в направлении оси x, оси y и оси z соответственно.

Свойства умножения векторов

Скалярное произведение единичного вектора изучается путем взятия единичных векторов \(\hat i\) вдоль оси x, \(\hat j\) вдоль оси y и \(\hat k\) по оси Z соответственно. Скалярное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и скалярное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их скалярное произведение равно 1. А угол между двумя перпендикулярными векторами равен 90º, а их скалярное произведение равно 0.

• \(\hat i.\hat i\) = \(\hat j.\hat j\) = \(\hat k.\hat k\)= 1
• \(\шляпа i.\шляпа j\) = \(\шляпа j.\шляпа k\) = \(\шляпа k.\шляпа i\)= 0

Перекрестное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и перекрестное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их векторное произведение равно 0. А угол между двумя перпендикулярными векторами равен 90º, и их векторное произведение дает вектор, который перпендикулярен двум заданным векторам.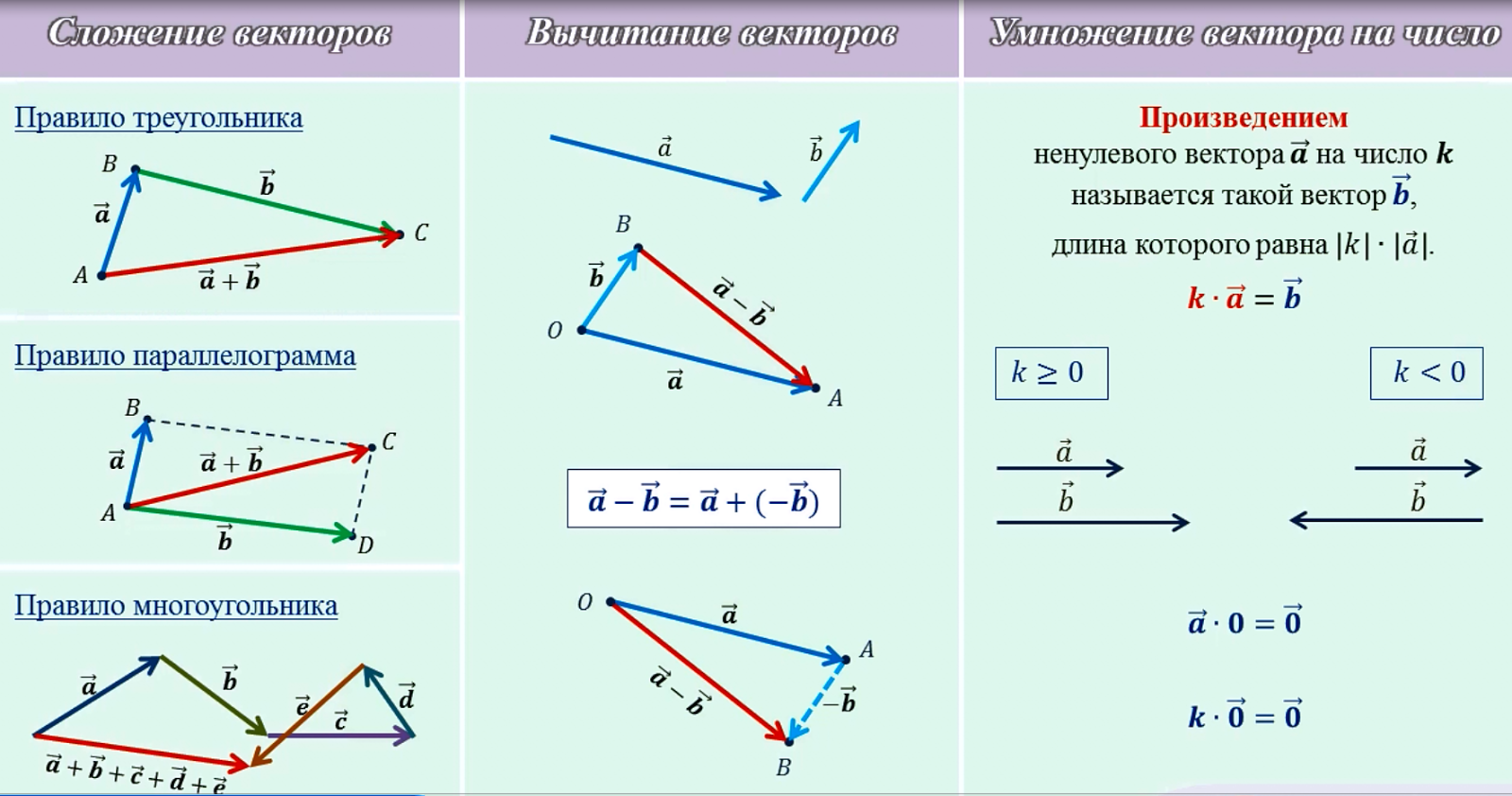

• \(\overrightarrow{i}\times \overrightarrow{i} =\overrightarrow{j}\times \overrightarrow{j} = \overrightarrow{k}\times \overrightarrow{k} = 0\)

Перекрестное произведение двух векторов следует циклическому порядку, как показано на изображении ниже. Перекрестное произведение двух векторов в циклической последовательности дает третий вектор в последовательности.

• \(\overrightarrow{i}\times \overrightarrow{j} = \overrightarrow{k}; \overrightarrow{j}\times \overrightarrow{k}= \overrightarrow{i}; \overrightarrow{k} \times \overrightarrow{i} = \overrightarrow{j}\)
• \(\overrightarrow{j}\times \overrightarrow{i} = \overrightarrow{-k}; \overrightarrow{k}\times \overrightarrow{j}= \overrightarrow{-i}; \overrightarrow{i}\times \overrightarrow{k} = \overrightarrow{-j}\)

Свойства умножения векторов помогают получить детальное представление об умножении векторов, а также выполнять многочисленные вычисления с использованием векторов. Здесь перечислены несколько важных свойств умножения векторов.

1. Перекрестное произведение двух векторов определяется формулой \( \overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta)\).
2. Скалярное произведение двух векторов определяется формулой \( \overrightarrow{a} . \overrightarrow{b} = |a| |b| \cos(\theta)\).
3. Скалярное произведение двух векторов подчиняется свойству коммутативности. \(\vec a. \vec b = \vec b. \vec a \)
4. Перекрестное произведение двух векторов не соответствует свойству коммутативности. \( \vec a \times \vec b\neq \vec b \times \vec a \)
5. Антикоммутативное свойство: \(\overrightarrow{a} \times \overrightarrow{b} = — \overrightarrow{b} \times \overrightarrow{a}\)
6. Распределительное свойство: \(\overrightarrow{a} \times (\overrightarrow{b} + \overrightarrow{c}) = (\overrightarrow{a}\times \overrightarrow{b} )+ (\overrightarrow{a}\times \overrightarrow{с})\)
7. Перемножение нулевого вектора: \(\overrightarrow{a}\times \overrightarrow{0} = \overrightarrow{0}\)
8. Перемножение вектора с самим собой: \(\overrightarrow{a}\times \overrightarrow{a} = \overrightarrow{0}\)
9. Умножить на скалярную величину: \(c(\overrightarrow{a}\times \overrightarrow{b}) = c\overrightarrow{a}\times \overrightarrow{b} = \overrightarrow{a}\times c\overrightarrow{ б}\)
10. Скалярное произведение двух векторов является скаляром и лежит в плоскости двух векторов.
11. Перекрестное произведение двух векторов — это вектор, который перпендикулярен плоскости, содержащей эти два вектора.

Применение умножения векторов

Ниже приведены некоторые из важных применений умножения векторов. Давайте разберемся с каждым из этих применений в следующих параграфах.

• Проекция вектора
• Угол между двумя векторами
• Продукт тройного креста
• Площадь параллелограмма
• Объем параллелепипеда

Проекция вектора

Скалярное произведение полезно для нахождения компонента одного вектора в направлении другого. Проекция вектора одного вектора на другой вектор — это длина тени данного вектора на другой вектор. Он получается путем умножения величины данных векторов на косеканс угла между двумя векторами. Результатом формулы векторной проекции является скалярное значение.

Здесь \(\overrightarrow a\) и \(\overrightarrow b\) — два вектора, а θ — угол между двумя векторами. 2}}\)

Тройное перекрестное произведение

Перекрестное произведение вектора на произведение двух других векторов представляет собой тройное перекрестное произведение векторов. Результатом тройного перекрестного произведения является вектор. Равнодействующий вектора тройного пересечения лежит в плоскости данных трех векторов. Если a, b и c — векторы, то векторное тройное произведение этих векторов будет иметь вид:

\((\overrightarrow{a}\times \overrightarrow{b}) \times \overrightarrow{c} = (\overrightarrow{a}\cdot \overrightarrow{c})\overrightarrow{b} -(\overrightarrow{b}\cdot \overrightarrow{c}) \overrightarrow{a}\)

Площадь параллелограмма

Две смежные стороны параллелограмма могут быть представлены векторами \(\overrightarrow a\) и \(\overrightarrow b\). Площадь параллелограмма равна произведению основания и высоты параллелограмма. Рассмотрим основание параллелограмма как \(|\overrightarrow a|\), а высоту параллелограмма как \(|\overrightarrow b|\)sin θ.

Здесь Основание = \(|\overrightarrow a|\), Высота = \(|\overrightarrow b|\)sin θ, а Площадь параллелограмма = Основание x Высота

Площадь параллелограмма = \(|\overrightarrow a|.|\overrightarrow b|\)sin θ = \(\overrightarrow a \times \overrightarrow b \)

Объем параллелепипеда

Параллелепипед равен шести двусторонняя фигура, каждая из сторон которой является параллелограммом. Здесь параллелограммы противоположных сторон одинаковы. Объем V параллелепипеда можно получить со стороны ребер a, b, c. Объем параллелепипеда можно получить из произведения площади основания на высоту параллелепипеда. Площадь основания параллелепипеда равна |b x c| а высота параллелепипеда равна |a|. Формула расчета объема параллелепипеда выглядит следующим образом.

V = a.(b x c)

Связанные темы

Следующие темы помогают лучше понять умножение векторов.

• Коллинеарные векторы
• Векторы
• Типы векторов
• Добавление векторов
• Перекрестное произведение двух векторов

Часто задаваемые вопросы по умножению векторов

Что такое скалярное умножение векторов?

Скалярное умножение векторов также называется скалярным произведением двух векторов и имеет два определения. Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. a.b = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного умножения векторов является скалярным значением.

Как вычислить скалярное произведение векторов?

Скалярное умножение векторов можно вычислить в три простых шага. Сначала найдите величину двух векторов a и b, т.е. |a| и |б|. Во-вторых, найдите косеканс угла θ между двумя векторами. Наконец, возьмите произведение величины двух векторов и косеканса угла между двумя векторами, чтобы получить скалярное произведение двух векторов. (a.b = |a|.|b|.Cosθ). Также проверьте калькулятор скалярного произведения, чтобы легко найти векторное скалярное произведение.

Почему скалярное произведение называется скалярным умножением векторов?

Скалярное произведение называется скалярным умножением векторов, поскольку все отдельные составляющие ответа являются скалярными величинами. В a.b = |a|.|b|.Cosθ, |a|, |b| и Cosθ — скалярные значения. Следовательно, скалярное произведение также называют скалярным умножением векторов.

Почему мы используем косинус в скалярном умножении векторов?

Чтобы найти скалярное произведение векторов, нам нужно, чтобы два вектора a, b были направлены в одном направлении. Поскольку векторы a и b расположены под углом друг к другу, значение acosθ является компонентом вектора a в направлении вектора b. Следовательно, мы находим cosθ в скалярном произведении или скалярном умножении двух векторов.

Что такое векторное умножение векторов?

Перемножение двух векторов при умножении приводит к третьему вектору, перпендикулярному двум исходным векторам. Величина результирующего вектора определяется площадью параллелограмма между ними, а его направление можно определить по правилу большого пальца правой руки. a × b = c, где c — перекрестное произведение или векторное произведение двух векторов a и b.

Что такое скалярное умножение и векторное умножение векторов?

Векторы можно умножать двумя разными способами: точечным произведением и перекрестным произведением. Результаты обоих этих умножений векторов различны. Скалярное умножение векторов или скалярное произведение дает в результате скалярную величину, тогда как векторное умножение векторов или перекрестное произведение дает векторную величину. Векторное произведение двух векторов задается как: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\) и формула скалярного произведения двух векторов задается как: \(\overrightarrow{a}. \overrightarrow{b} = |a| |b| \cos(\theta)\).

В чем разница между скалярным умножением и векторным умножением векторов?

При умножении векторов скалярное умножение векторов или скалярное произведение исходных векторов дает скалярную величину, тогда как векторное умножение двух векторов или перекрестное произведение двух векторов дает векторную величину. Скалярное произведение — это произведение величины векторов на косинус угла между ними. а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ.

Что такое правило большого пальца правой руки для перекрестного произведения векторов?

Правило правой руки для векторного произведения двух векторов помогает определить направление результирующего вектора. Если мы направим правую руку в направлении первой стрелки, а пальцы согнем в направлении второй, то наш большой палец окажется в направлении векторного произведения двух векторов. Правило большого пальца правой руки дает формулу векторного произведения для нахождения направления результирующего вектора.

Перекрестное произведение

Вектор имеет величину (длину) и направление :

Два вектора могут быть умножены на с использованием « Cross Product » (также см. Скалярный продукт)

Перекрестное произведение a × b двух векторов равно другому вектору , который находится под прямым углом к ​​обоим:

И все это происходит в 3-х измерениях!

Величина (длина) векторного произведения равна площади параллелограмма с векторами a и b для сторон:

Посмотрите, как он меняется под разными углами:

Перекрестное произведение ( синий ) равно:

• нулевая длина, когда векторы a и b указывают в одном или противоположном направлении
• достигает максимальной длины, когда векторы a и b расположены под прямым углом

И он может указывать то в одну, то в другую сторону!

Так как же нам его рассчитать?

Расчет

Мы можем вычислить векторное произведение следующим образом:

а × б = | и | | б | sin(θ) n

• | и | является величиной (длиной) вектора a
• | б | — величина (длина) вектора б
• θ — угол между a и b
• n — единичный вектор под прямым углом к ​​ a и b

Итак, длина равна: длина a умножить на длину b умножить на синус угла между a и b ,

Затем мы умножаем на вектор n , чтобы получить правильную девятку. 0281 в направлении (под прямым углом к ​​ a и b ).

 

ИЛИ мы можем вычислить это так:

Когда a и b начинаются в исходной точке (0,0,0), перекрестное произведение заканчивается на:

• c _x = a _y b _z − a _z b _y
• в _у = а _z б _x − a _x b _z
• c _z = a _x b _y − a _y b _x

Пример: перекрестное произведение

a = (2,3,4) и b = (5,6,7)

• c _x = a _y b _z − a 9 0422 г б _у = 3×7 — 4×6 = -3
• с _у = а _z б _х — а _х б _г = 4×5 — 2×7 = 6
• c _z = a _x b _y − a _y b _x = 2×6 − 3×5 = −3

Ответ: a × b = (−3,6,−3)

 

В каком направлении?

Перекрестное произведение может указывать в совершенно противоположном направлении и по-прежнему находиться под прямым углом к ​​двум другим векторам, поэтому мы имеем:

«Правило правой руки»

Правой рукой укажите указательным пальцем вдоль вектора a , и укажите средним пальцем вдоль вектора b : перекрестное произведение идет в направлении большого пальца.