Определенного интеграла формулы: Определённые интегралы — урок. Алгебра, 11 класс.

Вычисление определенного интеграла. Формула Ньютона-Лейбница

Решение прикладных задач сводится к вычислению интеграла, но не всегда это возможно сделать точно. Иногда необходимо знать значение определенного интеграла с некоторой степенью точности, к примеру, до тысячной.

Существуют задачи, когда следовало бы найти приближенное значение определенного интеграла с необходимой точностью, тогда применяют численное интегрирование такое, как метод Симпосна, трапеций, прямоугольников. Не все случаи позволяют вычислить его с определенной точностью.

Данная статья рассматривает применение формулы Ньютона-Лейбница. Это необходимо для точного вычисления определенного интеграла. Будут приведены подробные примеры, рассмотрены замены переменной в определенном интеграле и найдем значения определенного интеграла при интегрировании по частям.

Формула Ньютона-Лейбница

Определение 1

Когда функция y=y(x) является непрерывной из отрезка [a; b] ,а F(x) является одной из первообразных функции этого отрезка, тогда формула Ньютона-Лейбница считается справедливой. Запишем ее так ∫abf(x)dx=F(b)-F(a).

Данную формулу считают основной формулой интегрального исчисления.

Чтобы произвести доказательство этой формулы, необходимо использовать понятие интеграла с имеющимся переменным верхним пределом.

Когда функция y=f(x) непрерывна из отрезка [a; b], тогда значение аргумента x∈a; b, а интеграл имеет вид ∫axf(t)dt и считается функцией верхнего предела. Необходимо принять обозначение функции примет вид ∫axf(t)dt=Φ(x), она является непрерывной, причем для нее справедливо неравенство вида ∫axf(t)dt’=Φ'(x)=f(x).

Зафиксируем, что приращении функции Φ(x) соответствует приращению аргумента ∆x, необходимо воспользоваться пятым основным свойством определенного интеграла и получим

Φ(x+∆x)-Φx=∫ax+∆xf(t)dt-∫axf(t)dt==∫ax+∆xf(t)dt=f(c)·x+∆x-x=f(c)·∆x

где значение c∈x; x+∆x.

Зафиксируем равенство в виде Φ(x+∆x)-Φ(x)∆x=f(c).  По определению производной функции необходимо переходить к пределу при ∆x→0, тогда получаем формулу вида Φ'(x)=f(x). Получаем, что Φ(x) является одной из первообразных для функции вида y=f(x), расположенной на [a; b]. Иначе выражение можно записать

F(x)=Φ(x)+C=∫axf(t)dt+C, где значение C является постоянной.

Произведем вычисление F(a) с использованием первого свойства определенного интеграла. Тогда получаем, что

F(a)=Φ(a)+C=∫aaf(t)dt+C=0+C=C, отсюда получаем, что C=F(a). Результат применим при вычислении F(b) и получим:

F(b)=Φ(b)+C=∫abf(t)dt+C=∫abf(t)dt+F(a), иначе говоря, F(b)=∫abf(t)dt+F(a). Равенство доказывает формулу Ньютона-Лейбница ∫abf(x)dx+F(b)-F(a).

Приращение функции принимаем как Fxab=F(b)-F(a). С помощью обозначения формулу Ньютона-Лейбница принимает вид ∫abf(x)dx=Fxab=F(b)-F(a).

Чтобы применить формулу, обязательно необходимо знать одну из первообразных y=F(x) подынтегральной функции y=f(x) из отрезка [a; b] , произвести вычисление приращения первообразной из этого отрезка. Рассмотрим несколько примером вычисления, используя формулу Ньютона-Лейбница.

Пример 1

Произвести вычисление определенного интеграла ∫13x2dx по формуле Ньютона-Лейбница.

Решение

Рассмотрим, что подынтегральная функция вида y=x2 является непрерывной из отрезка [1;3], тогда и интегрируема на этом отрезке. По таблице неопределенных интегралов видим, что  функция y=x2 имеет множество первообразных для всех действительных значений x, значит, x∈1; 3 запишется как F(x)=∫x2dx=x33+C. Необходимо взять первообразную с С=0, тогда получаем, что F(x)=x33.

Воспользуемся формулой Ньютона-Лейбница и получим, что вычисление определенного интеграла примет вид ∫13x2dx=x3313=333-133=263.

Ответ: ∫13x2dx=263

Пример 2

Произвести вычисление определенного интеграла ∫-12x·ex2+1dx по формуле Ньютона-Лейбница.

Решение

Заданная функция непрерывна из отрезка [-1;2], значит, на нем интегрируема. Необходимо найти значение неопределенного интеграла ∫x·ex2+1dx при помощи метода подведения под знак дифференциала , тогда получаем ∫x·ex2+1dx=12∫ex2+1d(x2+1)=12ex2+1+C.

Отсюда имеем множество первообразных функции y=x·ex2+1, которые действительны для всех x, x∈-1; 2.

Необходимо взять первообразную при С=0 и применить формулу Ньютона-Лейбница. Тогда получим выражение вида

∫-12x·ex2+1dx=12ex2+1-12==12e22+1-12e(-1)2+1=12e(-1)2+1=12e2(e3-1)

Ответ: ∫-12x·ex2+1dx=12e2(e3-1)

Пример 3

Произвести вычисление интегралов ∫-4-124×3+2x2dx и ∫-114×3+2x2dx.

Решение

Отрезок -4; -12 говорит о том, что функция, находящаяся под знаком интеграла, является непрерывной, значит, она интегрируема. Отсюда найдем множество первообразных функции y=4×3+2×2. Получаем, что

∫4×3+2x2dx=4∫xdx+2∫x-2dx=2×2-2x+C

Необходимо взять первообразную F(x)=2×2-2x, тогда, применив формулу Ньютона-Лейбница, получаем интеграл, который вычисляем:

∫-4-124×3+2x2dx=2×2-2x-4-12=2-122-2-12-2-42-2-4=12+4-32-12=-28

Производим переход к вычислению второго интеграла.

Из отрезка [-1;1] имеем, что подынтегральная функция считается неограниченной, потому как limx→04×3+2×2=+∞, тогда отсюда следует, что необходимым условием интегрируемости  из отрезка. Тогда F(x)=2×2-2x не является первообразной для y=4×3+2×2из отрезка [-1;1], так как точка O принадлежит отрезку, но не входит в область определения. Значит, что имеется определенный интеграл Римана и Ньютона-Лейбница для функции y=4×3+2×2 из отрезка [-1;1].

Ответ: ∫-4-124×3+2x2dx=-28, имеется определенный интеграл Римана и Ньютона-Лейбница для функции y=4×3+2×2 из отрезка [-1;1].

Перед использованием формулы Ньютона-Лейбница нужно точно знать о существовании определенного интеграла.

Замена переменной в определенном интеграле

Когда функция y=f(x) является определенной и непрерывной из отрезка [a;b], тогда имеющееся множество [a;b] считается областью значений функции x=g(z), определенной на отрезке α; β с имеющейся непрерывной производной, где g(α)=a и gβ=b, отсюда получаем, что ∫abf(x)dx=∫αβf(g(z))·g'(z)dz.

Данную формулу применяют тогда, когда нужно вычислять интеграл ∫abf(x)dx, где неопределенный интеграл имеет вид ∫f(x)dx, вычисляем при помощи метода подстановки.

Пример 4

Произвести вычисление определенного интеграла вида ∫9181x2x-9dx.

Решение

Подынтегральная функция считается непрерывной на отрезке интегрирования, значит определенный интеграл имеет место на существование. Дадим обозначение, что 2x-9=z⇒x=g(z)=z2+92. Значение х=9, значит, что z=2·9-9=9=3, а при х=18 получаем, что z=2·18-9=27=33, тогда gα=g(3)=9, gβ=g33=18. При подстановке полученных значений в формулу ∫abf(x)dx=∫αβf(g(z))·g'(z)dz получаем, что

∫9181x2x-9dx=∫3331z2+92·z·z2+92’dz==∫3331z2+92·z·zdz=∫3332z2+9dz

По таблице неопределенных интегралов имеем, что одна из первообразных функции 2z2+9 принимает значение 23arctgz3. Тогда при применении формулы Ньютона-Лейбница получаем, что

∫3332z2+9dz=23arctgz3333=23arctg333-23arctg33=23arctg3-arctg 1=23π3-π4=π18

Нахождение можно было производить, не используя формулу ∫abf(x)dx=∫αβf(g(z))·g'(z)dz.

Если при методе замены использовать интеграл вида ∫1x2x-9dx, то можно прийти к результату ∫1x2x-9dx=23arctg2x-93+C.

Отсюда произведем вычисления по формуле Ньютона-Лейбница и вычислим определенный интеграл. Получаем, что

∫9182z2+9dz=23arctgz3918==23arctg2·18-93-arctg2·9-93==23arctg3-arctg 1=23π3-π4=π18

Результаты совпали.

Ответ: ∫9182x2x-9dx=π18

Интегрирование по частям при вычислении определенного интеграла

Если на отрезке [a;b] определены и непрерывны функции u(x) и v(x), тогда их производные первого порядка v'(x)·u(x) являются интегрируемыми, таким образом из этого отрезка для интегрируемой функции u'(x)·v(x) равенство ∫abv'(x)·u(x)dx=(u(x)·v(x))ab-∫abu'(x)·v(x)dx справедливо.

Формулу можно использовать тогда, необходимо вычислять интеграл ∫abf(x)dx, причем ∫f(x)dx необходимо было искать его при помощи интегрирования по частям.

Пример 5

Произвести вычисление определенного интеграла ∫-π23π2x·sinx3+π6dx.

Решение

Функция x·sinx3+π6 интегрируема на отрезке -π2; 3π2, значит она непрерывна.

Пусть u(x)=х, тогда d(v(x))=v'(x)dx=sinx3+π6dx, причем d(u(x))=u'(x)dx=dx, а v(x)=-3cosπ3+π6. Из формулы ∫abv'(x)·u(x)dx=(u(x)·v(x))ab-∫abu'(x)·v(x)dx получим, что

∫-π23π2x·sinx3+π6dx=-3x·cosx3+π6-π23π2-∫-π23π2-3cosx3+π6dx==-3·3π2·cosπ2+π6—3·-π2·cos-π6+π6+9sinx3+π6-π23π2=9π4-3π2+9sinπ2+π6-sin-π6+π6=9π4-3π2+932=3π4+932

Решение примера можно выполнить другим образом.

Найти множество первообразных функции x·sinx3+π6 при помощи интегрирования по частям с применением формулы Ньютона-Лейбница:

∫x·sinxx3+π6dx=u=x, dv=sinx3+π6dx⇒du=dx, v=-3cosx3+π6==-3cosx3+π6+3∫cosx3+π6dx==-3xcosx3+π6+9sinx3+π6+C⇒∫-π23π2x·sinx3+π6dx=-3cosx3+π6+9sincosx3+π6—3·-π2·cos-π6+π6+9sin-π6+π6==9π4+932-3π2-0=3π4+932

Ответ: ∫x·sinxx3+π6dx=3π4+932

Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Справочник по математике

Элементы математического анализа

Интегралы

Определенный интеграл как площадь криволинейной трапеции

Производная от определенного интеграла по верхнему пределу

Теорема Ньютона — Лейбница

Примеры решения задач

Определенный интеграл как площадь криволинейной трапеции

      Рассмотрим на плоскости прямоугольную систему координат   Oty ,   ось абсцисс которой в данном разделе будем обозначать   Ot ,   а не   Ox   (рис. 1).

Рис.1

      Пусть   y = f (t)   – непрерывная на отрезке   [a, b]  функция, принимающая только положительные значения.

      Определение 1. Фигуру, ограниченную графиком функции   y = f (t)   сверху, отрезком   [a, b]   снизу, а справа и слева отрезками прямых   t = a   и   t = b   (рис. 2), называют криволинейной трапецией.

Рис.2

      Определение 2. Число, равное площади криволинейной трапеции, изображенной на рисунке 2, называют определенным интегралом от функции   f (t)   в пределах от   a   до   b   и обозначают

(1)

      Формула (1) читается так: «Интеграл от   a   до   b   от функции   f (t)   по   dt»

      Определение 3. В формуле (1) функцию   f (t)   называют подынтегральной функцией, переменную   t   называют переменной интегрирования, отрезок   [a, b]  называют отрезком интегрирования, число   b   называют верхним пределом интегрирования, а число   a   – нижним пределом интегрирования.

Производная от определенного интеграла по верхнему пределу

      Если обозначить   S (x)   площадь криволинейной трапеции, ограниченной с боков отрезками прямых   t = a   и   t = x   (рис. 3),

Рис.3

то будет справедлива формула

(2)

      Теорема 1. Производная от определенного интеграла по верхнему пределу интегрирования равна значению подынтегральной функции в верхнем пределе интегрирования.

      Другими словами, справедлива формула

      Доказательство. Из формулы (2) следует, что

(3)

где через  Δx   обозначено приращение аргумента   x   (рис. 4)

Рис.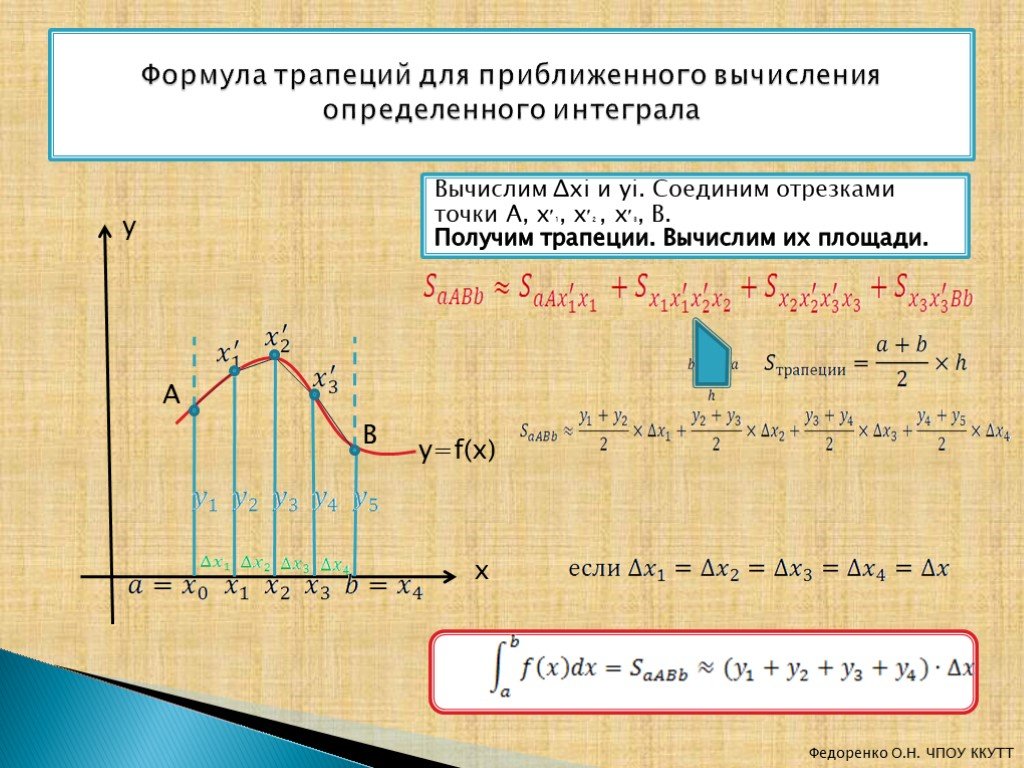 4

      Из формул (3) и (2) получаем, что

(4)

где через  ΔS  обозначено приращение функции   S (x),   соответствующее приращению аргумента   Δx   (рис. 5)

Рис.5

      Если ввести обозначения

(см. раздел «Наибольшее и наименьшее значение функции на отрезке»), то можно заметить, что выполнено неравенство

(5)

смысл которого заключается в том, что площадь криволинейной трапеции, изображенной на рисунке 5, не может быть меньше, чем площадь прямоугольника с основанием  Δx  и высотой   m,   и не может быть больше, чем площадь прямоугольника с основанием  Δx   и высотой   M.

      Из неравенства (5) следует, что

откуда, переходя к пределу при  Δx → 0,   получаем

      В силу непрерывности функции   y = f (t)   выполнено равенство

      По определению производной функции   S (x)   имеем

(6)

что и завершает доказательство теоремы 1.

      Следствие 1. Функция   S (x)   является первообразной подынтегральной функции   f (x)  .

Теорема Ньютона — Лейбница

      Теорема Ньютона-Лейбница. Если   F (x)   – любая первообразная функции   f (x),   то справедливо равенство

(7)

      Доказательство. Поскольку   S (x)   и   F (x)   – две первообразных функции   f (x),   то существует такое число   c,  что выполнено равенство

S (x) = F (x) + c

(8)

      Воспользовавшись равенством (8), из формулы (2) получаем, что

(9)

      Подставив в формулу (9) значение   x =  a,  получаем равенство

(10)

      Заметим, что

(11)

поскольку площадь криволинейной трапеции, «схлопнувшейся» в отрезок, лежащий на прямой   t = a,   равна   0 .

      Из формул (10) и (11) следует, что

c = – F (a) ,

и формула (9) принимает вид

,

что и завершает доказательство теоремы Ньютона-Лейбница.

      Замечание 1. Формулу (7) часто записывают в виде

(12)

и называют формулой Ньютона-Лейбница.

      Замечание 2. Для правой части формулы Ньютона-Лейбница часто используют обозначение

      Замечание 3. Формулу Ньютона-Лейбница (12) можно записывать, как с переменной интегрирования   t ,   так и с любой другой переменной интегрирования, например,   x :

      Замечание 4.Все определения и теоремы остаются справедливыми не только в случае положительных непрерывных функций   f (x),   но и для гораздо более широкого класса функций, имеющих произвольные знаки и интегрируемых по Риману, однако этот материал уже выходит за рамки школьного курса математики.

Примеры решения задач

      Задача 1. Найти площадь фигуры, ограниченной линиями

y = e ^{– x},     y = 0,     x = 0,     x = ln 3.

      Решение. Рассматриваемая фигура является криволинейной трапеции (рис. 6)

Рис.6

      Найдем площадь этой криволинейной трапеции:

      Ответ.

      Задача 2. График функции   y = f (x)   изображен на рисунке 7.

Рис.7

Вычислить интеграл

(13)

      Решение. Интеграл (13) равен площади криволинейной трапеции, ограниченной сверху графиком функции   y = f (x),   ограниченной снизу осью абсцисс   Ox   и ограниченной с боков отрезками прямых   x = 2   и   x = 9.   Криволинейная трапеция состоит из квадрата, раскрашенного на рисунке 7 розовым цветом, и трапеции, раскрашенной на рисунке 7 зеленым цветом. Площадь квадрата равна   9,   а площадь трапеции равна   20.   Таким образом, интеграл (13) равен   29.

      Ответ.   29.

      Задача 3. Вычислить определенный интеграл

(14)

      Решение. Поскольку одной из первообразных подынтегральной функции интеграла (14) является функция

то в соответствии с формулой Ньютона-Лейбница получаем

      Ответ.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

определенных интегралов | Brilliant Math & Science Wiki

Содержание

• Определение
• Характеристики
• Различные типы интегралов
• Методы интеграции
• Смотрите также

Первоначальное определение, данное Бернхардом Риманом, выражает площадь как комбинацию бесконечного множества вертикально ориентированных прямоугольников. Этот метод известен как сумма Римана. Одним из преимуществ этого определения является то, что оно визуально интуитивно понятно.

По мере того, как прямоугольники становятся тоньше, общая площадь прямоугольников приближается к значению интеграла. 9b f(x) \, dx.\]

Пределы равны \(a\) и \(b\), подынтегральная функция равна \(f(x)\), а дифференциал равен \(dx\). пределы интегрирования дают информацию о том, где происходит интегрирование, а интервал интегрирования представляет собой интервал \([a, \, b]\), определяемый этими пределами. Подынтегральная функция дает информацию о форме области и представляет высоту каждого прямоугольника в сумме Римана. Дифференциал дает информацию о том, какую переменную использует подынтегральная функция, и представляет ширину каждого прямоугольника в сумме Римана. 9b f(x) \, dx = F(b) — F(a).\]

Это переводит язык интегрирования из чего-то чисто геометрического в структурированную алгебраическую конструкцию, которой можно манипулировать различными способами.

Будучи одним из основных инструментов исчисления, интегралы обладают большим количеством свойств, вытекающих из геометрии координатной плоскости, определения функционала и связи между интегралами и производными. Интегралы также имеют алгебраическую интерпретацию, которая позволяет использовать очень полезные методы, такие как \(u\)-подстановка, которые необходимы для многих типов интегральных вычислений (и в доказательствах многих свойств ниже!). 92} \, dt.\]

Поверхностный интеграл подобен линейному интегралу, но для двойных интегралов. Интегралы могут быть вложены друг в друга для интегрирования по нескольким измерениям (например, с поверхностью).

Существуют также методы интегрирования по комплексным числам и более экзотическим числовым полям. Теория меры расширяет понятие интервала интегрирования на любое множество, удовлетворяющее набору параметров. Он также предоставляет способ определения методов интегрирования, отличных от предложенного Риманом, которые позволяют интегрировать более обобщенные наборы (например, векторные пространства функций). 92} \, dx\]

нельзя оценить без численных методов.

Существует множество численных методов аппроксимации интегралов с любой степенью точности, но их эффективность полностью зависит от рассматриваемой функции и интервала. Когда это возможно, всегда предпочтительнее точный расчет.

Частичные суммы Римана, правило трапеций и правило Симпсона стремятся обеспечить геометрическую аппроксимацию рассматриваемой области. Другие подходы, такие как использование формулы Чебышева, стремятся смоделировать рассматриваемую функцию (по крайней мере, в соответствующем интервале) с функциями, которые легче интегрировать.

Нахождение хороших приближений для определенных интегралов является одной из основных целей численного анализа.

• Антипроизводные
• Основная теорема исчисления
• Интеграция
• Интеграционные хитрости
• Суммы Римана

Цитировать как: Определенные интегралы. Brilliant.org . Извлекаются из https://brilliant.org/wiki/definite-integrals/

Определенные интегралы: что это такое и как их вычислить

В этой статье

1. Определение определенных интегралов

2. Определенные интегралы и неопределенные интегралы

3. Как вычислять определенные интегралы

4. Свойства определенных интегралов и ключевых уравнений

5. 3 практических упражнения и решения

Определение определенных интегралов 9{b} f(x)dx = A∫ab​f(x)dx=A

В этих обозначениях изогнутый знак интеграла ∫\int∫ указывает на операцию взятия интеграла. Остальная часть этого обозначения состоит из трех частей:

• Подынтегральная функция f(x)f(x)f(x)

• Интегральные границы aaa и bbb, где aaa — нижняя граница, а bbb — верхняя граница. Их также называют лимитами.

• Дифференциал dxdxdx, который говорит нам, что мы интегрируем fff по переменной xxx. 9{b} f(x)dx∫ab​f(x)dx примерно так:

  Определенные интегралы и неопределенные интегралы

  Прежде чем мы узнаем, как именно решать определенные интегралы, важно понять разницу между определенными и неопределенными интегралами.

  Определенные интегралы находят площадь между кривой функции и осью x на определенном интервале, а неопределенные интегралы находят первообразную функции. Нахождение неопределенного интеграла и нахождение определенного интеграла — это операции, которые выводят разные вещи.

  Вычисление неопределенного интеграла принимает одну функцию и выводит другую функцию: первообразную функцию f (x) f (x) f (x), обозначаемую как F (x) F (x) F (x).

  Эта выходная функция сопровождается произвольной константой C и не включает нижние и верхние границы. Напротив, при вычислении определенного интеграла всегда выводится действительное число, представляющее площадь под кривой на определенном интервале. Вы можете увидеть разницу в их обозначениях ниже:

  Учитывая f(x)f(x)f(x), неопределенный интеграл отвечает на вопрос: «Какая функция при дифференцировании дает нам f(x)f(x)f(x)?» Неопределенный интеграл дает нам семейство функций FFF, так как этому вопросу удовлетворяет бесконечное число функций. Таким образом, неопределенный интеграл дает нам «неопределенный» ответ. Определенный интеграл дает нам действительное число — уникальный «определенный» ответ.

  Вы можете узнать больше о разнице с этим образцом урока по неопределенным интегралам одного из наших преподавателей доктора Ханны Фрай. 9b_a = F(b) — F(a)∫ab​f(x)dx=[F(x)]ab​=F(b)−F(a).

  Это означает, что для нахождения определенного интеграла функции на отрезке [a, b] мы просто берем разность между неопределенным интегралом функции, вычисленной при aaa, и неопределенным интегралом функции, вычисленной при bbb.

  Этот процесс можно разбить на четыре этапа:

  1. Найдите неопределенный интеграл F(x)F(x)F(x). Вы можете использовать правила интегрирования, которые вы изучили с неопределенными интегралами, чтобы помочь с этой частью.

  2. Найдите F(b)F(b)F(b). Это можно найти, подставив верхнюю границу bbb в неопределенный интеграл, найденный на шаге 1.

  3. Найдите F(а)F(а)F(а).

     No related posts.