Правило знаков при сложении и вычитании: Сложение Чисел с Разными Знаками

Содержание

Каковы правила вычитания целых чисел? – Обзоры Вики

Чтобы вычесть два целых числа, перепишите выражение вычитания как первое число плюс противоположное второму числу. Некоторые примеры показаны ниже. Чтобы вычесть два целых числа, прибавьте противоположное второму целому числу к первому целому числу. Символически это можно записать как a – b = a + (-b).

Итак, каковы правила сложения и вычитания отрицательных чисел? При сложении или вычитании отрицательных чисел может быть полезно использовать числовую прямую.
…
Сложение и вычитание

Чтобы складывать и вычитать числа, всегда начинайте отсчет с нуля.
При сложении положительных чисел считайте вправо.
При вычитании положительных чисел считайте влево.

Каковы 3 правила вычитания целых чисел? Целочисленное вычитание

Во-первых, сохраните первое число (известное как уменьшаемое).
Во-вторых, измените операцию с вычитания на сложение.
В-третьих, получите знак, противоположный второму числу (известное как вычитаемое).
Наконец, приступайте к регулярному сложению целых чисел.

Как заменить сложение на вычитание? Оставьте первое число точно таким же.

Измените знак вычитания на знак сложения.
Измените знак последнего числа на противоположный. Если число было положительным, измените его на отрицательное ИЛИ, если оно было отрицательным, измените его на положительное.

Как складывать и вычитать положительные и отрицательные целые числа?

Каковы правила сложения и вычитания положительных и отрицательных чисел? Сложение: разные знаки, вычитание чисел

Если вы складываете положительные и отрицательные числа вместе, из большего числа вычесть меньшее и поставить знак из большего числа.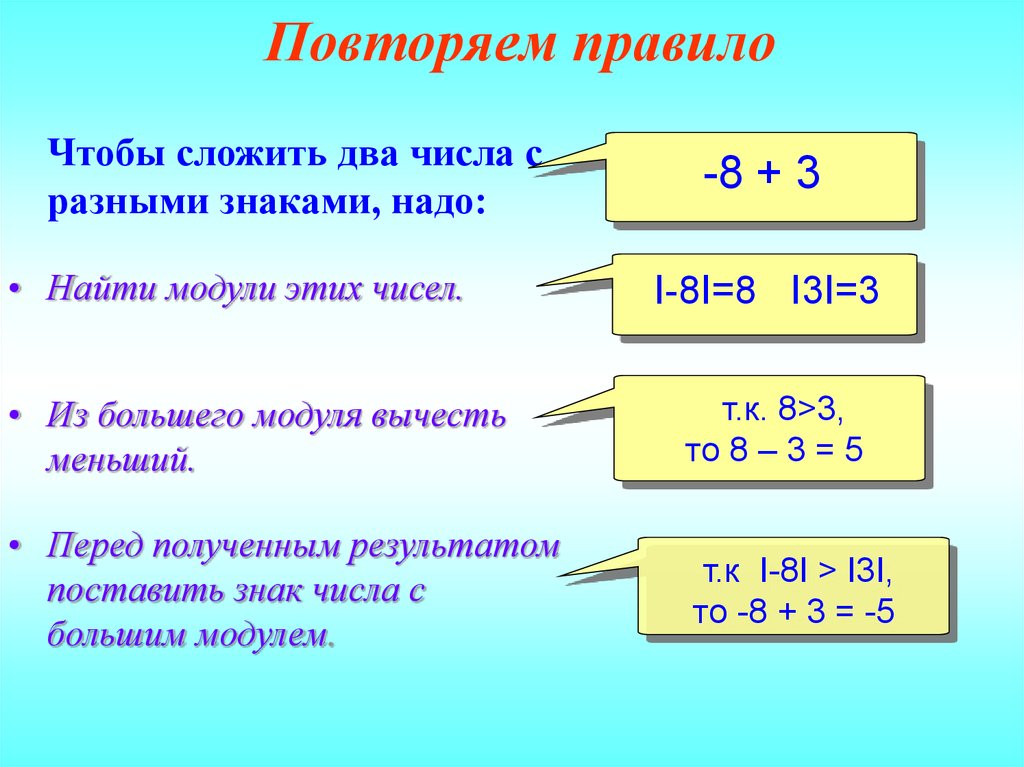

Как работает сложение и вычитание целых чисел?

Чтобы добавить целые числа с одинаковым знаком, сохраните тот же знак и добавьте абсолютное значение каждого числа. Чтобы сложить целые числа с разными знаками, сохраните знак числа с наибольшим абсолютным значением и вычтите наименьшее абсолютное значение из наибольшего. Вычесть целое число, добавив его противоположность.

Также Что означает KCC в математике? Сохранить изменения КСС золото

Это означает СОХРАНЯТЬ первое число таким же. ЗАМЕНИТЕ вычитание на сложение. Затем ИЗМЕНИТЕ знак второго числа.

Как вычитать целые числа с разными знаками?

Чтобы вычесть два целых числа с разными знаками, мы сложите абсолютные значения и прикрепите к ответу знак минут. Вычитание целых чисел производится изменением знака вычитаемого. После этого, если оба числа одного знака, то складываем абсолютные значения и присоединяем общий знак.

Каково правило вычитания рациональных чисел? Правила вычитания

Оставьте первое число таким же, меняет знак вычитания на знак сложения и меняет второе число на противоположное. Не забывайте находить общий знаменатель при сложении или вычитании дробей.

Как вы складываете и вычитаете?

Как поэтапно вычитать целые числа?

Почему вы добавляете, когда вычитаете отрицательное число? Вычитание числа равносильно добавлению его противоположности. Итак, вычитание положительного числа похоже на добавление отрицательного; вы двигаетесь влево по числовой прямой. Вычитание отрицательного числа похоже на добавление положительного; ты двигаться вправо по числовой прямой.

Каковы три правила сложения и вычитания целых чисел? Чтобы добавить целые числа с одинаковым знаком, сохраните тот же знак и добавьте абсолютное значение каждого числа. Чтобы сложить целые числа с разными знаками, сохраните знак числа с наибольшим абсолютным значением и вычтите наименьшее абсолютное значение из наибольшего. Вычтите целое число, добавив его противоположное.

Каковы четыре правила целых чисел?

ПРАВИЛО 1: Произведение положительного целого числа на отрицательное число отрицательно.. ПРАВИЛО 2: произведение двух натуральных чисел положительно. ПРАВИЛО 3: произведение двух отрицательных целых чисел положительно. ПРАВИЛО 1: Частное положительного целого числа и отрицательного целого числа отрицательно.

Как узнать, когда прибавлять или вычитать в алгебре?

Чтобы добавить два или более одночленов, похожих на термы, добавьте коэффициенты; сохраните переменные и показатели у переменных одинаковыми. Чтобы вычесть два или более одночленов, похожих на термы, вычесть коэффициенты; сохраните переменные и показатели у переменных одинаковыми.

Как сложение и вычитание целых чисел связано с сложением и вычитанием рациональных чисел?

Сложение целых чисел требует сложения или вычитания их абсолютных значений и понимания знака суммы. Вычитание числа равносильно добавлению этого числа. аддитивное обратное число. … Деление рациональных чисел аналогично делению целых чисел.

Что означает вычитание целых чисел?

Целые числа — это положительные и отрицательные числа. С математической точки зрения, вычитание означает сложение противоположного. Обращайте внимание на свои знаки при вычитании целых чисел, а когда вы застряли, думайте о числах с точки зрения наличия или долга денег!

Сложение и вычитание десятичных дробей

Тема: Сложение и вычитание десятичных дробей

Чтобы научиться правильно выполнять сложение десятичных дробей, достаточно выучить правило, состоящее всего из трех слов.

Три слова такие: запятая под запитой. Это самое важное, что следует помнить при сложении десятичных дробей. Складывая десятичные дроби, мы записываем их так, чтобы запятые в слагаемых находились строго одна под другой. Если после запятой в одном слагаемом цифр меньше, чем в другом, можно недостающие цифры дополнить нулями (а можно и не делать этого). В остальном сложение десятичных дробей практически ничем не отличается от сложения натуральных чисел — темы, которую проходили еще в начальной школе.

Запомните!

Если исходные десятичные дроби имеют разное количество знаков (цифр) после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.

Итак, ещё раз коротко основные правила сложения:

уравниваем количество знаков после запятой;
записываем десятичные дроби друг под другом так, чтобы запятые были друг под другом;
выполняем сложение десятичных дробей, не обращая внимания на запятые, по правилам сложения в столбик натуральных чисел;
ставим в ответ запятую под запятыми.

Рассмотрим на примерах, как происходит сложение десятичных дробей.

Чтобы сложить 5,7 и 6,8, записываем их запятая под запятой. Затем складываем цифры по разрядам и в полученном ответе сносим запятую все по тому же правилу — запятая под запятой.

При сложении 2,256 и 0,74 числа записываем так, чтобы запятая находилась под запятой. Поскольку во втором числе после запятой два знака, а в первом — три, недостающий один знак в конце второго числа дополняем нулем (но его можно и не писать). После этого складываем числа, не обращая внимания на запятую (то есть к 2256 прибавляем 740). В результате сносим запятую (ровно под запятой слагаемых).

Как обычно, сложение десятичных дробей начинаем с их записи таким образом, чтобы запятая стояла точно под запятой. Первым удобнее записать число, у которого количество цифр после запятой больше. Чтобы уравнять количество знаков после запятой в обоих слагаемых, во втором третьей цифрой после запятой записываем нуль. Складываем 52462 и 4980, не обращая внимания на запятую. В ответе сносим запятую под запятой.

Чтобы сложить десятичные дроби, записываем их «запятая под запятой». Складываем 4821 и 3179, не обращая внимания на запятую. После этого сносим запятую под запятой. Поскольку в десятичной дроби после запятой нули на конце не пишут, окончательный ответ 8.

Чтобы к натуральному числу прибавить десятичную дробь, можно в записи натурального числа в конце приписать запятую и столько нулей, сколько нужно (в данном примере — три). Затем складываем 35000 и 3146 и сносим запятую.

Сложение начинаем с записи десятичных дробей по правилу «запятая под запятой». Затем недостающий знак после запятой у числа 8,3 дополняем нулем. Складываем 374 и 830. В ответ сносим запятую под запятой.

Как и сложение, вычитание десятичных дробей зависит от правильной записи чисел.

Правило вычитания десятичных дробей

1) ЗАПЯТАЯ ПОД ЗАПЯТОЙ!

Эта часть правила самая важная. При вычитании десятичных дробей их следует записать так, чтобы запятые уменьшаемого и вычитаемого находились строго одна под другой.

2) Уравниваем количество цифр после запятой. Для этого в том числе, где количество цифр после запятой меньше, дописываем после запятой в конце нули.

3) Вычитаем числа, не обращая внимания на запятую.

4) Сносим запятую под запятыми.

Чтобы найти разность десятичных дробей 9,7 и 3,5, запишем их так, чтобы запятые в обоих числах находились строго одна под другой. Затем вычитаем, не обращая внимания на запятую. В полученном результате запятую сносим, то есть записываем под запятыми уменьшаемого и вычитаемого:

9,7-3,5=6,2.

Чтобы из одной десятичной дроби вычесть другую, надо записать их так, чтобы запятые располагались точно одна под другой. Так как у 23,45 после запятой две цифры, а у 1,5 — только одна, дописываем в 1,5 нуль. После этого ведем вычитания, не обращая внимания на запятую. В результат сносим запятую под запятыми:

23,45 — 1,5=21,95.

Вычитание десятичных дробей начинаем с их записи так, чтобы запятые были расположены ровно одна под одной. В первом числе после запятой одна цифра, во втором — три, поэтому на место недостающих двух цифр в первом числе записываем нули. Затем вычитаем числа, не обращая внимания на запятую. В полученном результате сносим запятую под запятыми:

63,5-8,921=54,579.

Задания для самостоятельного решения:

1. Вычислите:

а) 10,3 – 8,17; б) 9,432 – 8,32; в) 7,3 + 0,865;

г) 4,1 – 2,74; д) 2,031 – 1,05; е) 3,6 + 0,55

2. Выполните сложение:

1,08 + 5,1 + 0,988 =

3. Решите уравнение:

х +3,72 = 8

4. Вычислите выражение:

12,36 + ((11,31 + 0,03) — 1,38) — 3, 04 =

5. Решите задачу:

В первый день магазин продал 87,5 кг сахара, а во второй – на 9,85 кг больше. Сколько килограммов сахара продал магазин за два дня?

Купить

Узнайте, как складывать и вычитать числа со знаком — предварительная алгебра

В этом видео мы изучим правила и концепции сложения и вычитания чисел со знаком. Числа со знаком означают положительные и отрицательные числа. После того, как вы закончите этот урок, просмотрите все наши уроки Pre-Algebra и Algebra 1 и попрактикуйтесь в решении задач.

Правила сложения и вычитания чисел со знаком

Сложение Как Знаки: сложите числа вместе и сохраните знак

Добавление В отличие от Знаков: Найдите разницу и сохраните знак большего числа

Вычитание Чисел со знаком: Сохранить – Изменить – Изменить

Примеры сложения

Цифры

Пример 1

Сначала нам нужно взглянуть на знаки.

При добавлении действительных чисел с одинаковым знаком нам просто нужно сложить два числа вместе и сохранить знак.

Следовательно,

Пример 2

-9 – 11

Для вычитания разных знаков просто следуйте формуле: сохранить-изменить-изменить.

Сначала неделю сохраняем

Затем меняем знак следующего числа с отрицательного на положительный

Наконец, меняем знак последнего числа с положительного 11 на отрицательное 11.

Следовательно,

Используя правило сложения одинаковых знаков, просто нужно сложить два числа вместе и сохранить знак.

Теперь у нас есть:

Стенограмма видеоурока

В этом уроке мы обсудим, как складывать и вычитать числа со знаком. Это сложение и вычитание положительных и отрицательных чисел.

Теперь давайте складывать и вычитать числа со знаком.

Давайте начнем с добавления одинаковых чисел. Это может быть самым простым.

Нарисуем числовую линию.

Начнем с классического примера.

Это сложение двух положительных чисел.

Давайте докажем, правда ли это.

Начнем с добавления еще трех.

В числовой строке мы получаем .

Давайте посмотрим, сложим ли мы вместе отрицательные числа.

Итак, давайте начнем и добавим еще.

В числовой строке мы получаем .

Теперь добавим

, так что мы начнем с и добавим .

Мы получаем в числовой строке.

Теперь давайте разберемся с этим.

Если мы добавим два числа с одинаковыми знаками, нам просто нужно сложить числа вместе и сохранить знак, положительный или отрицательный.

Другой пример:

Поскольку два числа имеют один и тот же знак, мы просто складываем их вместе и сохраняем отрицательный знак.

Теперь давайте пройдемся по добавлению непохожих знаков.

Проведем еще одну числовую линию.

Начнем с

Теперь давайте добавим . Итак, двигаемся влево.

Но если мы сделаем

Начнем с того, что добавим . Двигаемся вправо.

В числовой строке мы заканчиваем .

Давайте сделаем .

Итак, давайте начнем с в числовой строке и добавим . Мы получаем .

Посмотрим, что это за шаблон.

Когда знаки разные, находим разницу между числами.

Итак, разница между и . И оно отрицательное, потому что большее число отрицательное.

В разность двух чисел составляет . А так как большее число отрицательное, то и ответ отрицательный.

Здесь в , так как они имеют разные знаки, мы должны найти разницу, и ответ положительный, потому что большее число положительное. Итак, ответ.

Давайте сделаем еще один пример без числовой строки.

Здесь мы находим разницу между и которая есть . Большее число положительно, поэтому наш ответ также положительный.

Складывая разные знаки, находим разность и сохраняем знак большего числа.

Давайте рассмотрим вычитание чисел со знаком.

Нарисуем числовую линию.

Имеем , в числовой строке получаем .

Попробуем другой.

, мы начинаем и вычитаем влево. Здесь мы заканчиваем с .

Что, если у нас есть , начнем с и уберем. В числовом ряду получаем .

Давайте сначала посмотрим на логику.

Допустим у вас есть и мы забрали.

Это хорошо. Может быть, вы были должны кому-то, и вы взяли его. Ты больше никому не должен. Человек сказал: «Забудь об этом».

Это все равно, что иметь следующий, потому что за него не нужно платить.

Итак, мы увеличили до .

Далее, допустим, у вас есть, потому что вы должны людям.

Потом как-нибудь потратишь еще . Может быть, вы заняли эту сумму.

Итак, теперь вы должны . У вас на самом деле есть.

Вот, ты уже минус, но потратил еще немного. Так что у вас еще больше негатива.

То же самое с третьим примером.

Вы уже на месте, но потратьте еще . Так что теперь вы полностью должны.

Вы также можете запомнить эту формулу:

сохранить-изменить-изменить

Здесь мы сохраняем первое число, затем меняем второй знак, а также меняем третий знак.

Взгляните на это:

Давайте попробуем следующее

Просто следуйте формуле: постоянное изменение-изменение.

Сохраните первое число, затем измените знак следующего числа с отрицательного на положительный, а затем измените знак последнего числа с положительного на отрицательный.

Помните правило добавления похожих знаков? Нам просто нужно сложить два числа вместе и сохранить знак.

Итак, наш окончательный ответ.

Давайте сделаем третий пример.

Опять же, мы будем делать изменения-изменения-изменения.

Сохраните первое число, измените отрицательный знак на положительный, а затем измените положительный знак на отрицательный в последнем числе.

Позвольте мне показать вам еще один пример.

У нас есть

Это не так уж и плохо. Оба числа положительные. Но мы должны ожидать, что ответ будет отрицательным, поскольку мы вычитаем больше, чем имеем.

Давайте решим это с помощью команды «сохраняй-изменяй-изменяй».

Сохранить первое число , изменить следующий знак с отрицательного на положительный, а затем изменить положительный знак последнего числа на отрицательный.

Теперь у нас есть

Напомним, что когда мы вычитаем числа со знаком, мы можем использовать функцию Keep-Change-Change, чтобы сделать это задачей сложения, и мы просто будем использовать наши правила при добавлении чисел со знаком. Вот как складывать и вычитать числа со знаком.

Сложение и вычитание чисел со знаком

Навыки
в н
А Л Г Е Б Р А

Содержание | Дом

«Добавление» отрицательного числа

Термины наименования

Правила «добавления» терминов

Ноль

Вычитание отрицательного числа

Добавление ряда терминов

Отмена

МЫ ДОЛЖНЫ ПРИДАТЬ АЛГЕБРАИЧЕСКИЙ СМЫСЛ «прибавлению» отрицательного числа:

8 + (-2).

Теперь, когда мы добавляем положительное число, мы получаем больше. Следовательно, когда мы «добавляем» отрицательное число, мы должны получить меньше. Это значит вычесть.

8 + (−2) = 8 − 2 = 6.

Алгебраически, вот правило:

a + (− b ) = a − b

Обратите внимание, что мы используем круглые скобки,

a + (- b ), чтобы отделить знак операции + от алгебраического знака — . Было бы дурным тоном писать a + − b .
Мы собираемся научиться добавлять числа со знаком. Но сначала мы должны научиться называть термины.
Термины наименования
Применяя это правило—
a + (− b ) = a − b
— теперь мы можем назвать члены любой суммы.
Вот сумма четырех слагаемых:
1 + (-2) + 3 + (-4).
Условия равны 1, −2, 3 и −4.
Но по правилу скобки можно убрать:
1 + (−2) + 3 + (−4) = 1 – 2 + 3 – 4.
Мы говорим, что сумма справа имеет те же четыре члена:
1, −2, 3 и −4.
Другими словами, мы включаем знак вычитания как часть названия термина.
1 − 2 + 3 − 4
1 и 3 — положительные члены. −2 и −4 — отрицательные члены.
Когда термин появляется без знака впереди — а именно первый термин, 1 — мы должны понимать, что он положительный. 1 = +1.
Опять же, с положительными числами мы обычно не пишем алгебраический знак + .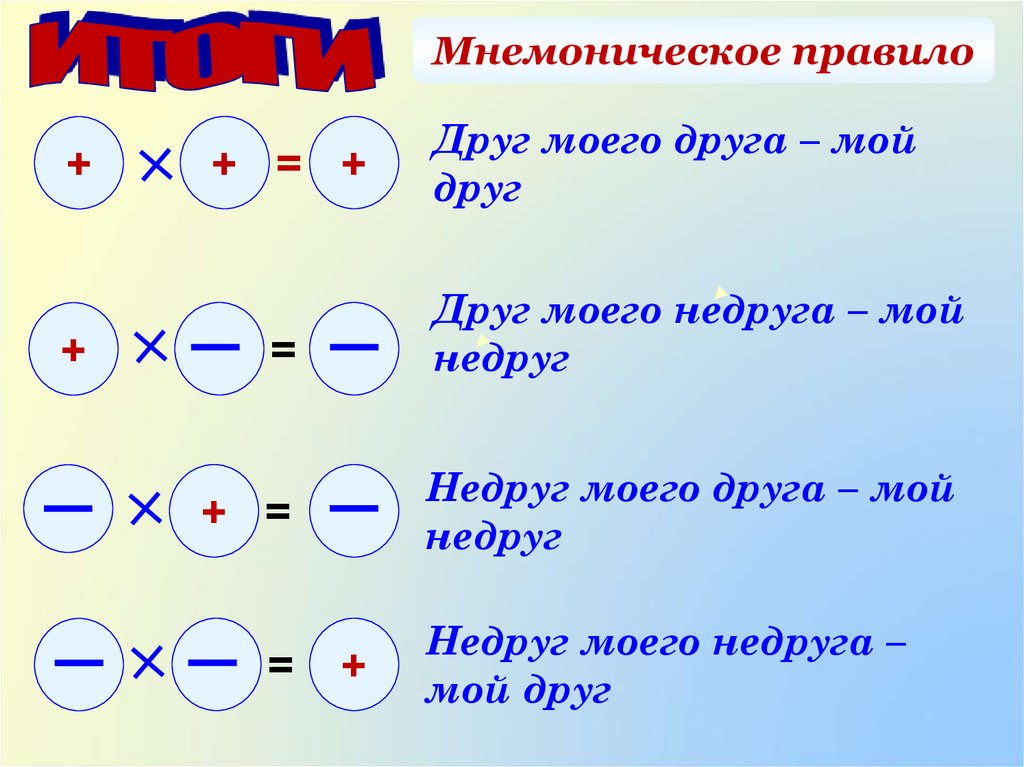 (Урок 2.)
Задача 1.   Назовите каждый термин.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
а) 3 + (-4) + 5 + (-6). 3, −4, 5, −6.

б) 3 — 4 + 5 — 6. 3, -4, 5, -6.

в) −2 − 5. −2, −5. г) − а − б + в − г . − a , − b , c , − d .
Правила «добавления» терминов
В алгебре мы говорим о «сложении», даже несмотря на то, что есть знаки «минус». Поняв это, мы можем теперь сформулировать правила «добавления» терминов.
1) Если термины имеют тот же знак, добавляют их абсолютные значения и сохраняют тот же знак.
2 + 3 = 5. -2 + (-3) = -5. -2 — 3 = -5.
2) Если члены имеют знака напротив , вычесть меньшее по модулю из большего и сохранить знак большего.
2 + (-3) = -1. -2 + 3 = 1,
В конце концов, алгебра имитирует арифметику, и эти правила легко обосновать, рассматривая приход и расход денег. Например, если вы берете взаймы 10 долларов, а затем возвращаете 4 доллара, мы выражаем это алгебраически как 9.0005
-10 + 4 = -6.
Теперь вы должны 6 долларов.
Или, если вы проиграете 6 долларов, а затем выиграете 8 долларов,
-6 + 8 = 2,
Теперь вы впереди $2.
Проблема 2.   Вы занимаете 5 долларов у Сандры, а затем занимаете еще 10 долларов. Выразите это алгебраически.
−5 − 10 = −15.
Примечание: Опять же, в алгебре мы говорим, что мы «добавляем» члены, даже если есть знаки вычитания. И мы называем сами термины — и ответ — «суммой». Другими словами, мы всегда говорим о сумме терминов.
Задача 3. Добавить по правилам добавления терминов.
а) 6 + 2 = 8. б) −6 + (−2) = −8.

в) -6 — 2 = -8. г) −4 − 1 = −5.

д) −6 + 2 = −4. е) 6 + (−2) = 4,

ж) 2 + (-6) = -4. ч) -2 + 6  = 4.
Проблема 4.   Добавьте эти термины.
а) 8 + (−3) = 5 б) −8 + 3 = −5 в) -8 + (-3) = -11

г) -8 — 3 = -11 д) 2 + (- 5) = -3 е) −2 + (− 5) = −7

ж) −2 − 5 = −7 ч) 8 + (− 11) = −3 и) -7 + (- 6) = -13

к) 9 + (− 2) = 7 к) −9− 2 = −11 л) -9 + (- 2) = -11

м) 6 + (- 10) = -4 п) -6 — 10 = -16 п) −6 + 10 = 4

р) −9+ 9 = 0 с) −9 − 9 = −18 г) 9 + 9 = 18
Ноль
Вот основное правило для 0:

а + 0 = 0 + а = а
Добавление 0 к любому термину не меняет его .
Задача 5.
а) 0 + 6 = 6 б) 0 + (-6) = -6

в) 0 − 6 = −6 г) −6 + 0 = −6
Вычитание отрицательного числа
Какой смысл мы можем сделать из
2 — (-5) ?
«2 вычесть минус 5.»
Назовем термины. Первый член равен 2. Второй член равен −(−5), поскольку мы включаем знак минус как часть имени термина. Но
-(-5) = +5.
Урок 2. Следовательно,
2 − (−5) = 2 + 5

= 7.
Вот правило:
а — (- б ) = а + б
Любая проблема, что выглядит вот так—
а — (- б )
— переписать так, чтобы это выглядело так:
а + б .
Это единственная форма, которую студент должен переписать.
(Пожалуйста, не зачеркивайте. Перепишите. Если вы зачеркнете, вы не сможете прочитать исходную задачу.)
Еще раз обратите внимание, что мы используем круглые скобки: a − (− b ), чтобы
отделить знак операции − от алгебраического знака − .
Примеры. 10 − (−3) = 10 + 3 = 13.

−10 − (−3) = −10 + 3 = −7.
Первый номер a не меняется. Посмотрите на правило. Замените только -(-3) на + 3.
Задача 6.   Переписать без скобок и вычислить.
а) 7 — (- 4) = 7 + 4 = 11 б) 1 — (- 9) = 1 + 9 = 10

в) 8 — (- 5) = 8 + 5 = 13 г) -8 — (- 5) = -8 + 5 = -3

д) -5 — (- 7) = -5 + 7 = 2 е) 2 — (- 10) = 2 + 10 = 12

ж) -9 — (- 8) = -9 + 8 = -1 ч) -20 — (- 1) = -20 + 1 = -19

i) 4 — (-4) = 4 + 4 = 8 к) −4 − (−4) = −4 + 4 = 0
Задача 7. Обзор.
а) 8 + (− 2) = 6 б) 8 — (- 2) = 10

в) -8 + (- 2) = -10 г) −8 − 2 = −10

д) 12 − 20 = −8 е) −12 − 20 = −32

ж) −12 + (− 20) = −32 ч) −12 − (− 20) = 8

i) 6 + (- 10) = -4 к) -5 — 9 = -14

к) −30 − (− 6) = −24 л) 4 − 28 = −24

м) 0 − 9 = −9 п) 0 + 9 = 9

о) 9 + (− 9) = 0 р) −1 − 9 = −10
Задача 8.    Вычислите − x , когда x = −4.
− x = −(−4) = 4,
Задача 9. Вычислить x − y при
а) х = 5, у = -2. 5 — (-2) = 5 + 2 = 7
б) х = -5, у = -2. −5 − (−2) = −5 + 2 = −3
Добавление ряда терминов
Рассмотрим следующую серию терминов:
1 – 3 + 5 – 6 + 9 – 2
Мы могли бы, конечно, добавить их в том порядке, в котором они появляются:
«1 — 3 = -2. -2 + 5 = 3. 3 — 6 = -3.» И так далее.
Или мы могли бы добавить положительные и отрицательные термины отдельно:
1 − 3 + 5 − 6 + 9 − 2 = 15 − 11

= 4.
Опять же, порядок терминов не имеет значения. И этот метод обычно более искусный.
Задача 10.    Добавьте каждую серию.
а) 2 – 3 + 4 – 5 = 2 + 4 — 3 — 5 = 6 — 8 = -2.
б) 8 — 10 — 4 + 12 — 5 = 8 + 12 — 10 — 4 — 5 = 20 — 19 = 1,
в) -3 + 5 — 6 — 4 + 8 = -13 + 13 = 0,
Отмена
Когда сумма чисел равна 0, мы можем «отменить» их.
Пример 1.     5 − 2 + 3 − 5
5 + (−5) = 0. Следовательно, мы можем их отменить, то есть проигнорировать. У нас осталось -2 + 3 = 1,
Пример 2.     8 − 10 + 5 − 3 + 2
8 − 10 = −2, что мы можем сократить на +2. У нас осталось
5 — 3 = 2.
Или 8 + 2 = 10, что мы могли бы сократить на -10. порядок терминов никогда не имеет значения
Задача 11.   Добавить каждую серию. Отмените, если это возможно.
а) 2 — 6 + 4 — 2 + 3 + 5 — 4 = (2 — 2) + (4 — 4) — 6 + (3 + 5) = 2,
б) 12 — 3 — 7 + 10 — 5 — 12 = (12 — 12) — 3 — 7 + 10 — 5 = -5.
в) 7 — 17 + 2 — 4 + 15 + 2 = 5
г) -10 + 6 — 3 + 4 + 2 — 5 + 3 = −3
Задача 12.    Перепишите без скобок:
а + (- б ) = а − б

а — (- б ) = а + б
Пример 3.   Перепишите без скобок, затем вычислите:
2 + (- 3) — (- 4) + 5 + (- 6).
Решение . Мы удалим скобки в соответствии с предыдущей задачей.
2 + (- 3) — (- 4) + 5 + (- 6)

= 2 — 3 + 4 + 5 — 6.
Теперь 2 + 4 отменяется на -6. У нас осталось
−3 + 5 = 2,
Задача 13.   Перепиши без скобок, а потом посчитай.
а) −1 − (− 2) + (− 3) − 4 + 5 = -1 + 2 — 3 — 4 + 5 = -1
б) 8 — (- 2) + (-3) — (- 4) — 7 = 4
в) −10 − (− 8) + (− 3) − 1 + (− 8) = -14
Задача 14.
No related posts.