Векторное произведение 2 векторов: 9.6. Векторное произведение векторов

– модуль вектора численно равен площади плоскости параллелограмма, построенного на векторах и ;

3).вектор направлен в ту сторону, от которого поворот от к на наименьший угол осуществляется против часовой стрелки.

Рис. 1

Алгебраические свойства векторного произведения

Давайте рассмотрим свойства векторного произведения.

Если    – произвольные векторы, а – произвольные число, тогда:

1. x = x . (Векторное произведение антикоммутативно).
2. x = x = x .(Векторное произведение обладает сочетательным свойством относительно скалярного множителя).
3. x = x + x .
4. x = ||, , . (Два ненулевых вектора коллинеарны только тогда, когда их векторное произведение равно нулевому вектору).

Таблица векторного умножения ортов

x = , x = ;

x = , x = ;

x = , x = .

x = x = x = .

Рис. 2

Векторное произведение одноимённых ортов равняется . При самом коротком повороте от одного орта к другому против часовой стрелки получаем третий орт, а по часовой стрелке – третий орт со знаком .

Формулы векторного произведения в координатной форме

Формулы векторного произведения в координатной форме получаем с учётом таблицы векторного произведения ортов:

x = x = x x x =

x – x + x x =

Примеры нахождения векторного произведения

Чтобы закрепить материал, рассмотрим на примерах, как найти векторное произведение векторов.

Пример 1

Найти векторное произведение векторов = и = . Построить в системе координат векторы и = x .

Решение:

Обратите внимание, что определитель (1) удобнее вычислять, если применить теорему про разложение за элементами первой строки:

= x = = – + =

Теперь построим векторы по их координатам.

Рис. 3

Из рисунка видно, что положение найденного вектора отвечает определению векторного произведения x .

Пример 2

Найти площадь треугольника , если .

Решение:

Сначала находим векторы:

и и их векторное произведение:

x = = .

Длина полученного вектора по определению численно равняется площади параллелограмма, построенного на данных векторах и поэтому:

пар = x = = .

А площадь треугольника составляет половину найденной площади, то есть:

тр. = пар = x x ,

Средняя оценка 0 / 5. Количество оценок: 0

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

7109

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Не отобразилась форма расчета стоимости? Переходи по ссылке

5.2. Векторное произведение двух векторов.

Определение векторного произведения.

Определение. Векторным произведением двух векторов иназывается вектор, удовлетворяющий следующим условиям:

а) вектор перпендикулярен плоскости векторов ии направлен так, что тройка векторов,,правая;

б) длина вектора численно равна площади

Рис. 2.19 параллелограмма, построенного на векторах и, т.е., где- угол между векторамии(рис. 2.19).

Очевидно, что ,,,,,.

Пример 11. Проверить справедливость равенства .

Решение. ,,

.

Метод Жуковского.

Рассмотрим метод Жуковского построения вектора .

Пусть угол между векторами иравен.

Векторы иприложим к общему началу(рис. 2.20). Через точкуперпендикулярно векторупроведем плоскость. Из конца вектораопустим перпендикуляр на плоскость. Точку пересечения этого перпендикуляра и плоскости обозначим через. Проведем в плоскостивектори построим вектор.

Рис. 2.20 Покажем, что вектор.

а) Из построения следует, что вектор перпендикулярен векторам,, и векторы,,образуют правую тройку.

б) .

Из а) и б) следует, что .

Если проекцию вектора на плоскостьобозначить через, то

.

Свойства векторного произведения.

Векторное произведение двух векторов обладает следующими свойствами:

1) (векторное произведение

антикоммутативно, т.е. при перестановке сомножителей направление вектора меняется на противоположное, при этом его модуль остаётся неизменным).

Это свойство следует из определения векторного произведения. Если тройка векторов правая, то тройка- левая.

2) (ассоциативный закон). Это свойство легко доказывается из определения векторного произведения.

3) (дистрибутивный закон.) ►.◄

4) . Это свойство следует из определения векторного произведения, а именно из того, что модуль векторного произведения равен площади параллелограмма, построенного на векторахи. Это свойство дает возможность записать в удобной форме параллельность двух векторов.

Например, означает, что векторколлинеарен биссектрисе первого координатного угла.

Векторное произведение в координатной форме.

Пользуясь свойствами векторного произведения и равенствами ,,,,,, вычислим

=

=

, т.

е. или.

Применение векторного произведения.

Векторное произведение векторов иприменяется:

для нахождения площади параллелограмма, построенного на векторах и;

для нахождения площади треугольника, построенного на векторах и;

для нахождения синуса угла между векторами и;

для нахождения вектора, перпендикулярного векторам и.

1) Площадь параллелограмма, построенного на векторахи, может быть вычислена по формуле, где- угол между векторамии.

Замечание. Если и, тои. Отсюда следует, чтомодуль определителя второго порядка численно равен площади параллелограмма, построенного на векторах и.

2) Площадь треугольника, построенного на векторахи, равна половине площади параллелограмма, построенного на этих же векторах, т.е., где- угол между векторамии.

3) Синус угла между векторами иможет быть вычислен по формуле.

4) Вектор перпендикулярен векторуи вектору.

Замечание. Векторное произведение может быть использовано при решении системы линейных однородных уравнений вида Если векторыинеколлинеарны, тоявляется решением исходной системы.

►Действительно, из системы уравнений следует, что вектор перпендикулярен векторами, а, следовательно,.◄

● Пример 12. Дано: ,,,,.

Найти площадь параллелограмма, построенного на векторах и.

Найти синус угла между векторамии.

Решение. Площадь параллелограмма, построенного на векторах иравнамодулю векторного произведения векторов и, т.е…=.

.

Ответ: ,.

● Пример 13. Дано: ,,,,.

Найти значение параметра , при котором векторыиколлинеарны.

Решение.

Первый способ. Так как векторы иколлинеарны, то их векторное произведение равно нулю.=0, а так как, тои.

Второй способ. Векторы исоставляют базис системы векторов,,и. В базисеи. Так как векторыиколлинеарны, то, откуда●

● Пример 14. Найти координаты вектора , длина которого равна 15, зная, что он перпендикулярен осии векторуи образует острый угол с осью.

Решение. и, поэтому.

, откуда

Так как вектор образует острый угол с осью, то вторая его координата положительна, тогдаи●

● Пример 15. Найти площадь параллелограмма , если известны координаты трёх его вершин,и.

Решение. .,,,.

● Пример 16. ,,- вершины треугольника. Найти недостающую координатуточки. если площадь треугольникаравна 3.

Решение. Площадь равна половине площади параллелограмма, построенного на векторахи, т.е..

, ,., откуда16,и.

Ответ: или.

● Пример 17. Решить систему

Решение. Из уравнений системы следует, что вектор перпендикулярен векторами. Тогда- решение данной системы. ●

Объяснение урока: перекрестное произведение в 2D

В этом объяснении мы узнаем, как найти перекрестное произведение двух векторов в координатной плоскости.

Существует два способа перемножения векторов. Возможно, вы уже знакомы с скалярным произведением, также называемым скалярным произведением. Это произведение приводит к скалярной величине , которая задается произведением величины обоих векторов, умноженные на косинус угла между два вектора. Что касается перекрестного произведения, то это произведение векторов что приводит к вектор .

Определение: перекрестное произведение

перекрестное произведение двух векторов ⃑𝐴 и ⃑𝐵 это вектор, перпендикулярный плоскости, содержащей ⃑𝐴 и ⃑𝐵 и величина которого определяется выражением ‖‖⃑𝐴×⃑𝐵‖‖=‖‖⃑𝐴‖‖‖‖⃑𝐵‖‖|𝜃|,sin где 𝜃 — угол между ⃑𝐴 и ⃑𝐵.

Из определения перекрестного произведения мы находим, что перекрестное произведение двух параллельные (или коллинеарные) векторы равны нулю, так как синус угла между ними (0 или 180∘) равно нулю. Примечание что никакая плоскость не может быть определена двумя коллинеарными векторами, поэтому непротиворечиво, что ⃑𝐴×⃑𝐵=0 если ⃑𝐴 и ⃑𝐵 коллинеарны.

Из приведенного выше определения следует, что перекрестное произведение любых двух неколлинеарных векторы в координатной плоскости с ⃑𝑖 и ⃑𝑗 как единичный вектор параллелен ⃑𝑘, где ⃑𝑘 — единичный вектор, перпендикулярный плоскости, содержащей ⃑𝑖 и ⃑𝑗, как показано на диаграмме.

Рассмотрим два вектора ⃑𝐴 и ⃑𝐵 в координатной плоскости.

Вектор ⃑𝐴 образует угол 𝜃 с ⃑𝑖 и вектором ⃑𝐵 образует угол 𝜃. Угол 𝜃 между ⃑𝐴 и ⃑𝐵 это поэтому 𝜃−𝜃, поэтому имеем sinsin𝜃=(𝜃−𝜃). Используя тригонометрическое тождество вычитания sinsincoscossin(𝜃−𝜃)=𝜃𝜃−𝜃𝜃, находим, что sinsincoscossin𝜃=𝜃𝜃−𝜃𝜃.

Составим матрицу с компонентами в терминах 𝜃 и 𝜃 из ⃑𝐴 в первом ряду и те, ⃑𝐵 во втором ряду ‖‖⃑𝐴‖‖𝜃‖‖⃑𝐴‖‖𝜃‖‖⃑𝐵‖‖𝜃‖‖⃑𝐵‖‖𝜃коссинкоссин и вычислить его определитель. Напомним, что определитель Матрица 2 × 2 определяется выражением |||𝑎𝑏𝑐𝑑|||=𝑎𝑑−𝑏𝑐.

Отсюда получаем, что ||||| ‖⃑𝐴⃑𝐴⃑𝐴𝜃𝜃𝜃⃑𝐴⃑𝐴𝜃𝜃𝜃𝜃𝜃⃑𝐵⃑𝐵) ‖‖‖⃑𝐵⃑𝐵⃑𝐵⃑𝐵𝜃𝜃𝜃𝜃 = ‖⃑𝐴⃑𝐴⃑𝐴‖‖⃑𝐵⃑𝐵⃑𝐵‖ 𝜃𝜃 — 𝜃𝜃) = ‖⃑𝐴⃑𝐴‖‖⃑𝐵⃑𝐵𝜃𝜃⃑𝐵⃑𝐵‖ поскольку sincoscossinsin𝜃𝜃−𝜃𝜃=𝜃.

Если мы объединим это с тем фактом, что ⃑𝐴×⃑𝐵 является вектором, параллельным ⃑𝑘, мы можем написать следующее определение векторного произведения двух векторов в координатная плоскость с ⃑𝑖 и ⃑𝑗 как единичные векторы.

Определение: перекрестное произведение двух векторов в координатной плоскости

Для двух векторов ⃑𝐴=𝐴⃑𝑖+𝐴⃑𝑗 и ⃑𝐵=𝐵⃑𝑖+𝐵⃑𝑗 в координатной плоскости с ⃑𝑖 и ⃑𝑗 как единичные векторы, перекрестное произведение ⃑𝐴 и ⃑𝐵 равно ⃑𝐴 × ⃑𝐵 = ||| 𝐴𝐴𝐵𝐵 ||| ⃑𝑘 = 𝐴𝐵 — 𝐵𝐴⃑𝑘 = ⃑𝐴⃑𝐴⃑𝐴⃑𝐴‖‖⃑𝐵⃑𝐵, sin где 𝜃 — угол между ⃑𝐴 и ⃑𝐵, а векторы ⃑𝑖, ⃑𝑗 и ⃑𝑘 фундаментальные единичные векторы вдоль 𝑥-, 𝑦- и 𝑧-осей соответственно, как показано на диаграмме.

Проиллюстрируем это определение векторного произведения на первом примере.

Пример 1. Поиск недостающего компонента по векторному произведению двух двумерных векторов

Если ⃑𝐴=3⃑𝑖−5⃑𝑗, ⃑𝐵=𝑚⃑𝑖+5⃑𝑗, и ⃑𝐴×⃑𝐵=50⃑𝑘, найдите значение 𝑚.

Ответ

Так как ⃑𝐴=3⃑𝑖−5⃑𝑗, то 𝐴=3 и 𝐴=−5; и как ⃑𝐵=𝑚⃑𝑖+5⃑𝑗, у нас есть 𝐵=𝑚 и 𝐵=5.

Кроме того, мы знаем, что ⃑𝐴×⃑𝐵=|||𝐴𝐴𝐵𝐵|||⃑𝑘=50⃑𝑘.

Отсюда ||3−5𝑚5||=503×5−(−5)𝑚=5015+5𝑚=505𝑚=50−15𝑚=7.

Давайте попрактикуемся в вычислении векторного произведения двух векторов, задав еще один вопрос о сложении векторов.

Пример 2. Вычисление перекрестного произведения двух двумерных векторов

Учитывая, что ⃑𝐶=6⃑𝑖+6⃑𝑗, определить ⃑𝐶+⃑𝐴×⃑𝐵.

Ответ

Сначала вычислим ⃑𝐶+⃑𝐴: ⃑𝐶+⃑𝐴=7⃑𝑖+2⃑𝑗+6⃑𝑖+6⃑𝑗=13⃑𝑖+8⃑𝑗.

Отсюда получаем, что 𝑥- и 𝑦-компоненты из ⃑𝐶+⃑𝐴 равны (𝐶+𝐴)=13 и (𝐶+𝐴)=8. Кроме того, из ⃑𝐵=−⃑𝑖+2⃑𝑗, мы знаем, что 𝐵=−1 и 𝐵=2.

Теперь мы можем вычислить ⃑𝐶+⃑𝐴×⃑𝐵 как ⃑𝐶+⃑𝐴×⃑𝐵=|||(𝐶+𝐴)(𝐶+𝐴)𝐵𝐵|||⃑𝑘=||138−12||⃑𝑘=(13×2−(−1)×8)⃑𝑘= 34⃑𝑘.

В предыдущем примере мы можем задаться вопросом, является ли векторное произведение дистрибутивным, то есть имеем ли мы ⃑𝐶+⃑𝐴×⃑𝐵=⃑𝐶×⃑𝐵+⃑𝐴×⃑𝐵?

В этом легко убедиться, если более внимательно посмотреть на определитель, который мы использовали для рассчитать ⃑𝐶+⃑𝐴×⃑𝐵: |||(𝐶+𝐴)(𝐶+𝐴)𝐵𝐵|||=(𝐶+𝐴)𝐵−𝐵(𝐶+𝐴). 

Правило сложения векторов: (𝐶 +𝐴)=𝐶+𝐴 и (𝐶+𝐴)=𝐶+𝐴; следовательно, ||| (𝐶+𝐴) (𝐶+𝐴) 𝐵𝐵 ||| = 𝐶𝐵+𝐴𝐵 — 𝐵𝐶 = 𝐶𝐵 — 𝐵𝐶+𝐴𝐵- = ||| 𝐶𝐶𝐵𝐵 |||+||| 𝐴𝐴𝐵𝐵 |||.

Отсюда следует, что ⃑𝐶+⃑𝐴×⃑𝐵=⃑𝐶×⃑𝐵+⃑𝐴×⃑𝐵; перекрестное произведение поэтому дистрибутив .

Свойство: Распределимость перекрестного произведения

Перекрестное произведение является распределительным: ⃑𝐶+⃑𝐴×⃑𝐵=⃑𝐶×⃑𝐵+⃑𝐴×⃑𝐵.

Теперь мы воспользуемся нашими знаниями о том, как вычисляются перекрестные произведения, чтобы найти неизвестный вектор по результатам его перекрестного произведения с двумя известными векторами.

Пример 3. Нахождение вектора по его перекрестному произведению с двумя известными векторами

Если ⃑𝐴=−⃑𝑖−2⃑𝑗, ⃑𝐵=−4⃑𝑖−4⃑𝑗, ⃑𝐴×⃑𝐶=−3⃑𝑘, и ⃑𝐶×⃑𝐵=4⃑𝑘, найти ⃑𝐶.

Ответ

Выделим компоненты ⃑𝐴 и ⃑𝐵 из их выражений через ⃑𝑖 и ⃑𝑗: 𝐴=−1 и 𝐴=−2, и 𝐵=-4 и 𝐵=-4.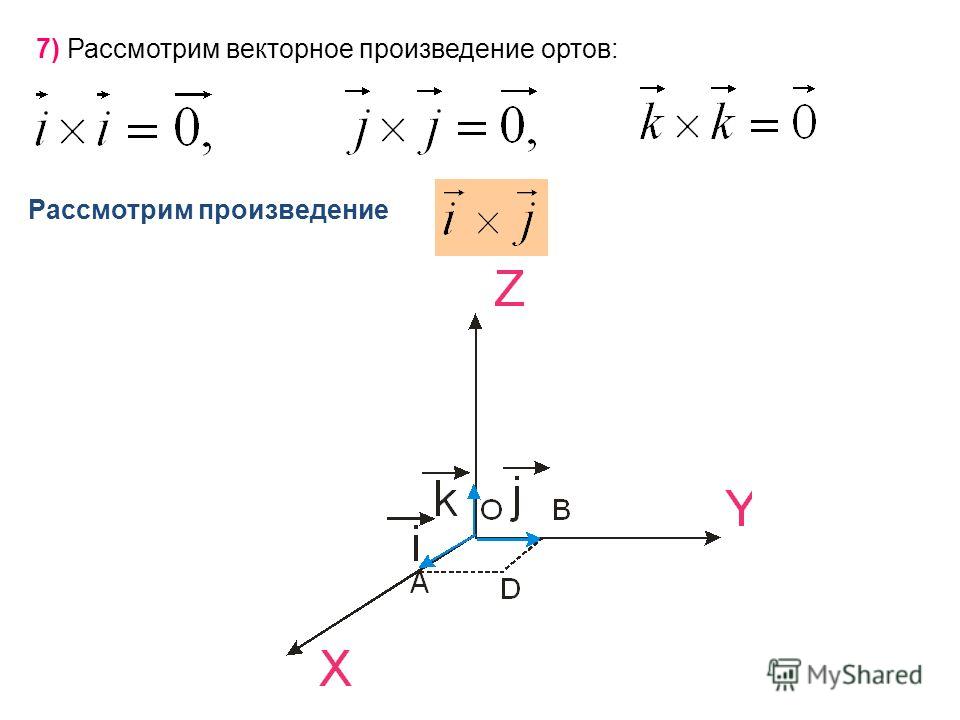

Теперь мы можем записать их перекрестные произведения с ⃑𝐶 как ⃑𝐴 × ⃑𝐶 = ||| 𝐴𝐴𝐶𝐶 ||| ⃑𝑘 = −3⃑𝑘, ⃑𝐶 × ⃑𝐵 = ||| 𝐶𝐶𝐵𝐵 ||| ⃑𝑘 = 4⃑𝑘. и

Следовательно, у нас есть

|||−1−2𝐶𝐶|||⃑𝑘=−3⃑𝑘,−1×𝐶−𝐶×(−2)=−3,−𝐶+2𝐶=−3,

( 1)

и

|||𝐶𝐶−4−4|||⃑𝑘=4⃑𝑘,−4𝐶−(−4)𝐶=4,−4𝐶+4𝐶=4.

(2) 90

Теперь у нас есть два линейных уравнения с двумя неизвестными (𝐶 и 𝐶).

Из уравнения (1) находим, что 𝐶=2𝐶+3. Подстановка этого выражения для 𝐶 в уравнение (2) дает −4𝐶+4⋅(2𝐶+3)=4−4𝐶+8𝐶+12=44𝐶=4−12𝐶=−2.

Замена 𝐶=−2 на 𝐶=2𝐶+3, получаем, что 𝐶=−1.

Следовательно, имеем ⃑𝐶=−2⃑𝑖−⃑𝑗.

Теперь найдем векторное произведение двух векторов, компоненты которых не заданы явно, но определены с помощью определенных точек в прямоугольнике.

Пример 4. Нахождение векторного произведения двух векторов в прямоугольнике

𝐴𝐵𝐶𝐷 — прямоугольник, где ⃑𝐾 — единичный вектор, перпендикулярный его плоскости.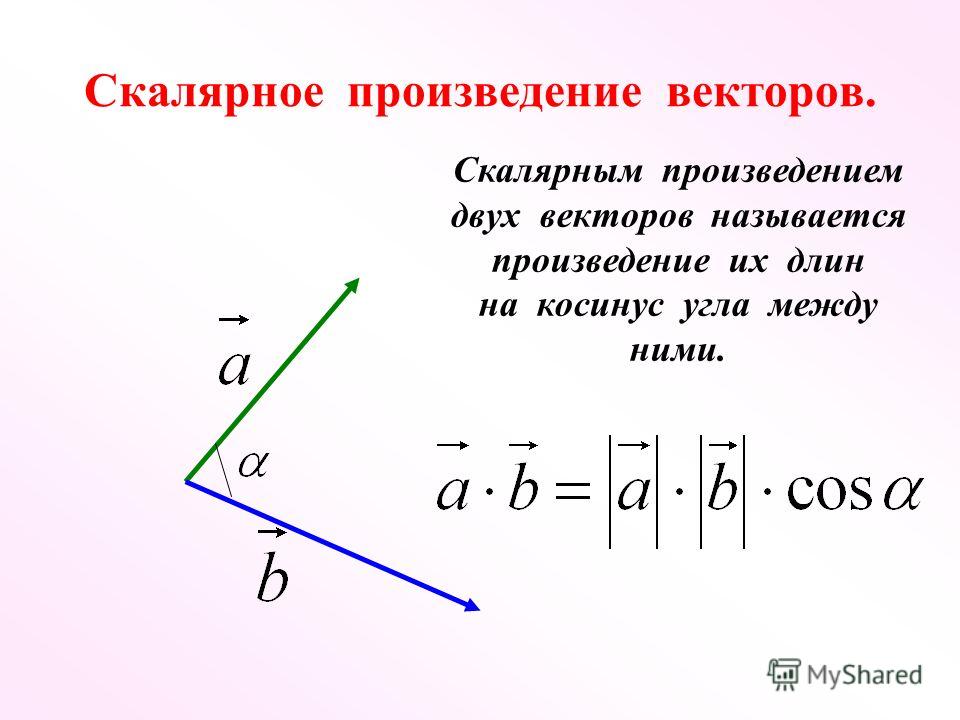 Находить 𝐶𝑀×𝐶𝐵.

Ответ

Чтобы найти 𝐶𝑀×𝐶𝐵, у нас есть две возможности. Либо мы находим компоненты обоих векторов, например, в координате плоскость с началом координат 𝐶, ⃑𝑖=𝐶𝐵‖‖𝐶𝐵‖‖, и ⃑𝑗=𝐶𝐷‖‖𝐶𝐷‖‖, или применяем 𝐶𝑀×𝐶𝐵=‖‖𝐶𝑀‖‖‖‖𝐶𝐵‖‖𝜃⃑𝐶sin, где 𝜃 — угол между 𝐶𝑀 и 𝐶𝐵 и ⃑𝐾 есть единичный вектор, перпендикулярный плоскости прямоугольника. Этот второй метод подразумевает, что мы должны найти величину обоих векторов и sin𝜃.

Первый метод

В координатной плоскости имеем 𝐶(0,0), 𝐵(44,0), и 𝑀(22,16,5). Отсюда получаем, что 𝐶𝑀=(22,16,5) и 𝐶𝐵=(44,0).

Перекрестное произведение 𝐶𝑀 и 𝐶𝐵 равно 𝐶𝑀×𝐶𝐵=||2216,5440||⃑𝐾, поскольку ⃑𝐾 — единичный вектор, перпендикулярный плоскости прямоугольника. 𝐶𝑀×𝐶𝐵=(22×0−44×16,5)⃑𝐾=−726⃑𝐾.

Второй метод

Величина 𝐶𝐵 — это просто длина 𝐶𝐵, значит 44 см.

Точка 𝑀 — середина диагоналей прямоугольника, поэтому 𝐶𝑀=12𝐶𝐴 и 𝐶𝐴=√𝐴𝐵+𝐵𝐶 (применив теорему Пифагора в прямоугольном треугольнике 𝐴𝐵𝐶). Следовательно, 𝐶𝑀=12√33+44.

Синус угла между 𝐶𝑀 и 𝐶𝐵 дается −𝐴𝐵𝐴𝐶=−33√33+44. Знак минус обусловлен тем, что угол от 𝐶𝑀 до 𝐶𝐵 идет по часовой стрелке (отрицательный угол), и sinsin(−𝜃)=−𝜃, или, для людей, работающих только с позитивом углов (против часовой стрелки), то 360−∠𝐵𝐶𝐴∘, и sinsin(360−𝜃)=−𝜃∘.

Теперь мы можем написать 𝐶𝑀×𝐶𝐵=‖‖𝐶𝑀‖‖‖‖𝐶𝐵‖‖𝜃⃑𝐾=12√33+44×44×−33√44×−33√4×44‖−3−2 ⃑𝐾=−726⃑𝐾sin

Используя второй метод для решения последнего примера, мы видим важность порядок векторов в векторном произведении, потому что их коммутация означает, что меняется знак угла, или что он меняется с 𝜃 на 360−𝜃∘, когда один использует только положительные углы. Эффект заключается в том, что синус меняет знак. Это значит, что ⃑𝐴×⃑𝐵=−⃑𝐵×⃑𝐴.

Мы говорим, что векторное произведение антикоммутативно .

Свойство: Антикоммутативность перекрестного произведения

Перекрестное произведение является антикоммутативным: ⃑𝐴×⃑𝐵=−⃑𝐵×⃑𝐴.

Давайте теперь посмотрим на геометрический смысл величины векторного произведения. Для двух векторов ⃑𝐴 и ⃑𝐵 величина их векторного произведения это ‖‖⃑𝐴×⃑𝐵‖‖=‖‖⃑𝐴‖‖‖‖⃑𝐵‖‖|𝜃|грех.

Поскольку нас здесь интересует абсолютное значение sin𝜃, нам не нужно беспокоиться, если угол от ⃑𝐴 до ⃑𝐵 или от ⃑𝐵 до ⃑𝐴.

Если мы мысленно поместим диаграмму в единичный круг, мы немедленно посмотрите, что такое ‖‖⃑𝐵‖‖|𝜃|грех.

Мы видим, что ‖‖⃑𝐵‖‖|𝜃|=𝑂𝑌sin.

В геометрическом контексте 𝑂𝑌 — высота параллелограмма. охватывает ⃑𝐴 и ⃑𝐵. Следовательно, ‖‖⃑𝐴‖‖‖‖⃑𝐵‖‖|𝜃|sin площадь параллелограмма 𝑂𝐴𝐶𝐵.

Площадь треугольника 𝑂𝐴𝐵 вдвое меньше площади 𝑂𝐴𝐶𝐵. Отсюда следует, что площадь треугольника 𝐴𝐵𝐶 равна половине величины векторного произведения двух из трех векторов, составляющих его стороны, то есть площадь𝐴𝐵𝐶=12‖‖𝐴𝐵×𝐴𝐶‖‖=12‖‖𝐵𝐴×𝐵𝐶‖‖=12‖‖𝐶𝐵×𝐶𝐴. ‖‖‖𝐶𝐵×𝐶‖‖.

Поскольку нас здесь интересует величина векторного произведения, порядок векторов и их направления (𝐴𝐵 или 𝐵𝐴) на самом деле не имеют значения. Однако здесь мы решили написать векторы, начинающиеся с одной из вершин треугольника, чтобы помочь визуализировать параллелограмм, натянутый на эти два вектора, и треугольник как половину параллелограмма.

Давайте воспользуемся значением перекрестного произведения в геометрическом контексте с последним примером.

Пример 5. Нахождение площади треугольника по трем его вершинам

Найдите площадь треугольника 𝐴𝐵𝐶, где 𝐴(−8,−9), 𝐵(−7,−8) и 𝐶(9,−2).

Ответ

Величина векторного произведения двух векторов равна площади параллелограмм, натянутый на них. Площадь треугольника 𝐴𝐵𝐶 равна на половину площади параллелограмма, натянутого двумя векторами, определяемыми его вершинами: площадь𝐴𝐵𝐶=12‖‖𝐴𝐵×𝐴𝐶‖‖=12‖‖𝐵𝐴×𝐵𝐶‖‖=12‖‖𝐶𝐵×𝐶𝐴.‖‖‖𝐶𝐵×𝐶‖‖.

Следовательно, здесь нам нужно выбрать только одну вершину, например 𝐶, и найдите компоненты двух векторов из этой точки, 𝐶𝐵 и 𝐶𝐴: 𝐶𝐵=(−7−9,−8−(−2))=(−16,−6),𝐶𝐴=(−8−9,−9−(−2))=(−17,−7).

Следовательно, площадь квадратов𝐴𝐵𝐶=12‖‖𝐶𝐵×𝐶𝐴‖‖=12||||−16−6−17−7||||=12|−16×(−7)−(−17)× (−6)|=12|112−102|=5.

Поскольку конкретные единицы длины координатной плоскости не указаны, мы пишем «квадратные единицы», чтобы показать, что мы вычислили площадь.

Ключевые точки

• Для двух векторов координатная плоскость 𝑂, ⃑𝑖, ⃑𝑗, перекрестное произведение ⃑𝐴 и ⃑𝐵 равно ⃑𝐴 × ⃑𝐵 = ||| 𝐴𝐴𝐵𝐵 ||| ⃑𝑘 = 𝐴𝐵 — 𝐵𝐴⃑𝑘 = ⃑𝐴⃑𝐴⃑𝐴⃑𝐴‖‖⃑𝐵⃑𝐵, sin где 𝜃 — угол между ⃑𝐴 и ⃑𝐵, а векторы ⃑𝑖, ⃑𝑗 и ⃑𝑘 являются перпендикулярными единичными векторами.
• Перекрестный продукт дистрибутив : ⃑𝐴+⃑𝐵×⃑𝐶=⃑𝐴×⃑𝐶+⃑𝐵×⃑𝐶.
• Перекрестное произведение антикоммутативное : ⃑𝐴×⃑𝐵=−⃑𝐵×⃑𝐴.
• Перекрестное произведение двух коллинеарных векторов равно нулю, поэтому ⃑𝐴×⃑𝐴=0.
• Площадь параллелограмма, натянутого на ⃑𝐴 и ⃑𝐵, равна ‖‖⃑𝐴×⃑𝐵‖‖. Отсюда следует, что площадь треугольника с ⃑𝐴 и ⃑𝐵 определяющее две его стороны, равно 12‖‖⃑𝐴×⃑𝐵‖‖.

93\) — вектор, перпендикулярный к обоим a и b . Если a и b являются массивами векторов, то векторы определяются последней осью a и b по умолчанию, и эти оси может иметь размеры 2 или 3. Если размер a или b равен 2 предполагается, что третья компонента входного вектора равна нулю, а перекрестный продукт рассчитывается соответственно. В случаях, когда оба входных вектора имеют размерность 2, возвращается z-компонент векторного произведения.

Параметры:

a array_like

Компоненты первого вектора(ов).

b array_like

Компоненты второго вектора(ов).

axisa int, необязательный

Ось a , которая определяет вектор(ы). По умолчанию последняя ось.

axisb int, опционально

Ось b , определяющая вектор(ы). По умолчанию последняя ось.

axisc int, необязательный

Ось c , содержащая вектор(ы) векторного произведения. Игнорируется, если оба входных вектора имеют размерность 2, так как возврат является скалярным. По умолчанию последняя ось.

ось int, опционально

Если определено, ось a , b и c , которая определяет вектор(ы) и перекрестный продукт (ы). Переопределяет ось a , ось b и ось c .

Возвраты:

c ndarray

Векторное перекрестное произведение.

Повышение:

ValueError

Когда размерность вектора(ов) в a и/или b не равно 2 или 3.

См. также

внутренний

Внутренний продукт

внешний

Внешний продукт.

ix_

Создание индексных массивов.

Примечания

Новое в версии 1.9.0.

Поддерживает полную трансляцию входов.

Примеры

Векторное перекрестное произведение.

 >>> х = [1, 2, 3]
>>> у = [4, 5, 6]
>>> нп.кросс(х, у)
массив([-3, 6, -3])
 

Один вектор размерностью 2.

 >>> х = [1, 2]
>>> у = [4, 5, 6]
>>> нп.кросс(х, у)
массив([12, -6, -3])
 

Эквивалент:

 >>> х = [1, 2, 0]
>>> у = [4, 5, 6]
>>> нп.кросс(х, у)
массив([12, -6, -3])
 

Оба вектора размерностью 2.

 >>> х = [1,2]
>>> у = [4,5]
>>> нп.кросс(х, у)
массив(-3)
 

Множественные векторные векторные произведения. Обратите внимание, что направление креста вектор произведения определяется правилом правой руки .