Предел по базе – как понять, вычислить, подробное объяснение с решением

alexxlab / / Разное

Содержание

Предел вдоль фильтра Википедия

Предел вдоль фильтра (предел по базису фильтра, предел по базе) — обобщение понятия предела.

Содержание

  • 1 Определение фильтра
  • 2 Определение предела
    • 2.1 Предел числовой функции
    • 2.2 Предел функции со значениями в метрическом пространстве
    • 2.3 Предел функции со значениями в топологическом пространстве
  • 3 Примеры
    • 3.1 Обычный предел
    • 3.2 Односторонние пределы
    • 3.3 Пределы на бесконечности
    • 3.4 Предел последовательности
    • 3.5 Интеграл Римана
  • 4 Литература

Определение фильтра[ | ]

Основная статья: Фильтр (математика)

Пусть дано множество X.{\displaystyle X.} Непустая система B{\displaystyle {\mathfrak {B}}} подмножеств множества X{\displaystyle X} называется базисом фильтра (базой) множества X{\displaystyle X}, если

  • для любого B∈B{\displaystyle B\in {\mathfrak {B}}} выполнено B≠∅;{\displaystyle B\neq \varnothing ;}
  • для любых B1,B2∈B{\displaystyle B_{1},B_{2}\in {\mathfrak {B}}} существует B3∈B{\displaystyle B_{3}\in {\mathfrak {B}}} такое, что B3⊂B1∩B2.{\displaystyle B_{3}\subset B_{1}\cap B_{2}.}

Определение предела[ | ]

Везде далее B{\displaystyle {\mathfrak {B}}} — базис фильтра (база) множества X{\displaystyle X}.

Предел числов

ru-wiki.ru

Предел вдоль фильтра Википедия

Предел вдоль фильтра (предел по базису фильтра, предел по базе) — обобщение понятия предела.

Определение фильтра

Пусть дано множество X.{\displaystyle X.} Непустая система B{\displaystyle {\mathfrak {B}}} подмножеств множества X{\displaystyle X} называется базисом фильтра (базой) множества X{\displaystyle X}, если

Определение предела

Везде далее B{\displaystyle {\mathfrak {B}}} — базис фильтра (база) множества X{\displaystyle X}.

Предел числовой функции

Пусть f:X→R{\displaystyle f:X\to \mathbb {R} }. Число A∈R{\displaystyle A\in \mathbb {R} } называется пределом функции f{\displaystyle f} по базе B,{\displaystyle {\mathfrak {B}},} если

для любого ε>0{\displaystyle \varepsilon >0} существует B∈B{\displaystyle B\in {\mathfrak {B}}} такое, что для всех x∈B{\displaystyle x\in B} выполнено неравенство |f(x)−A|<ε.{\displaystyle |f(x)-A|<\varepsilon .}

Обозначение предела по базе: limBf(x)=A.{\displaystyle \lim \limits _{\mathfrak {B}}f(x)=A.}

Предел функции со значениями в метрическом пространстве

Пусть (M,ρ){\displaystyle (M,\rho )} — метрическое пространство и f:X→M{\displaystyle f:X\to M}. Точка a∈M{\displaystyle a\in M} называется пределом функции f{\displaystyle f} по базе B,{\displaystyle {\mathfrak {B}},} если

для любого ε>0{\displaystyle \varepsilon >0} существует B∈B{\displaystyle B\in {\mathfrak {B}}} такое, что для всех x∈B{\displaystyle x\in B} выполнено неравенство ρ(f(x),a)<ε.{\displaystyle \rho (f(x),a)<\varepsilon .}

Обозначение: limBf(x)=a.{\displaystyle \lim \limits _{\mathfrak {B}}f(x)=a.}

Предел функции со значениями в топологическом пространстве

Пусть (M,T){\displaystyle (M,{\mathcal {T}})} — топологическое пространство и f:X→M{\displaystyle f\colon X\to M}. Точка a∈M{\displaystyle a\in M} называется пределом функции f{\displaystyle f} по базе B,{\displaystyle {\mathfrak {B}},} если

для любой окрестности V{\displaystyle V} точки a{\displaystyle a} существует B∈B{\displaystyle B\in {\mathfrak {B}}} такое, что f(B)⊂V{\displaystyle f(B)\subset V}, то есть для всех x∈B{\displaystyle x\in B} выполняется включение f(x)∈V{\displaystyle f(x)\in V}.

Обозначение: limBf(x)=a.{\displaystyle \lim \limits _{\mathfrak {B}}f(x)=a.}

Замечание. Последнее «равенство» корректно использовать лишь в случаях, когда пространство (M,T){\displaystyle (M,{\mathcal {T}})} — хаусдорфово. Пределом функции со значениями в нехаусдорфовом пространстве могут быть сразу несколько различных точек (и, таким образом, нарушается теорема о единственности предела).

Примеры

Обычный предел

Пусть (X,T){\displaystyle (X,{\mathcal {T}})} — топологическое пространство, и M⊂X.{\displaystyle M\subset X.} Пусть a∈M′.{\displaystyle a\in M’.} Тогда система множеств

B={M∩U˙≡M∩U∖{a}∣a∈U∈T}{\displaystyle {\mathfrak {B}}=\left\{M\cap {\dot {U}}\equiv M\cap U\setminus \{a\}\mid a\in U\in {\mathcal {T}}\right\}}

является базисом фильтра множества M{\displaystyle M} и обозначается M∋x→a{\displaystyle M\ni x\to a} или просто x→a.{\displaystyle x\to a.} Предел функции по базе x→a{\displaystyle x\to a} множества M{\displaystyle M} называется пределом функции в точке a{\displaystyle a} и обозначается записью limx→af(x){\displaystyle \lim \limits _{x\to a}f(x)}.

Односторонние пределы

  • Пусть M⊂R,{\displaystyle M\subset \mathbb {R} ,} и a∈(M∩(a,∞))′.{\displaystyle a\in {\bigl (}M\cap (a,\infty ){\bigr )}’.} Тогда система множеств
B={(a,a+δ)∩M∣δ>0}{\displaystyle {\mathfrak {B}}=\{(a,a+\delta )\cap M\mid \delta >0\}}

является базисом фильтра и обозначается x→a+{\displaystyle x\to a+} или x→a+0.{\displaystyle x\to a+0.} Предел limx→a+f(x){\displaystyle \lim \limits _{x\to a+}f(x)} называется правосторонним пределом функции f{\displaystyle f} при x{\displaystyle x} стремящемся к a.{\displaystyle a.}

  • Пусть M⊂R,{\displaystyle M\subset \mathbb {R} ,} и a∈(M∩(−∞,a))′.{\displaystyle a\in {\bigl (}M\cap (-\infty ,a){\bigr )}’.} Тогда система множеств
B={(a−δ,a)∩M∣δ>0}{\displaystyle {\mathfrak {B}}=\{(a-\delta ,a)\cap M\mid \delta >0\}}

является базисом фильтра и обозначается x→a−{\displaystyle x\to a-} или x→a−0.{\displaystyle x\to a-0.} Предел limx→a−f(x){\displaystyle \lim \limits _{x\to a-}f(x)} называется левосторонним пределом функции f{\displaystyle f} при x{\displaystyle x} стремящемся к a.{\displaystyle a.}

Пределы на бесконечности

  • Пусть M⊂R,{\displaystyle M\subset \mathbb {R} ,} и supM=∞.{\displaystyle \sup M=\infty .} Тогда система множеств
B={M∩(T,∞)∣T∈R}.{\displaystyle {\mathfrak {B}}=\{M\cap (T,\infty )\mid T\in \mathbb {R} \}.}

является базисом фильтра и обозначается x→∞{\displaystyle x\to \infty } или x→+∞.{\displaystyle x\to +\infty .} Предел limx→∞f(x){\displaystyle \lim \limits _{x\to \infty }f(x)} называется пределом функции f{\displaystyle f} при x{\displaystyle x} стремящемся к бесконечности.

  • Пусть M⊂R,{\displaystyle M\subset \mathbb {R} ,} и infM=−∞.{\displaystyle \inf M=-\infty .} Тогда система множеств
B={M∩(−∞,T)∣T∈R}.{\displaystyle {\mathfrak {B}}=\{M\cap (-\infty ,T)\mid T\in \mathbb {R} \}.}

является базисом фильтра и обозначается x→−∞.{\displaystyle x\to -\infty .} Предел limx→−∞f(x){\displaystyle \lim \limits _{x\to -\infty }f(x)} называется пределом функции f{\displaystyle f} при x{\displaystyle x} стремящемся к минус-бесконечности.

Предел последовательности

Система множеств B={Bn}n=1∞,{\displaystyle {\mathfrak {B}}=\{B_{n}\}_{n=1}^{\infty },} где

Bn={n,n+1,n+2,…}n∈N,{\displaystyle B_{n}=\{n,n+1,n+2,\ldots \}\quad n\in \mathbb {N} ,}

является базисом фильтра и обозначается n→∞.{\displaystyle n\to \infty .} Функция n∈N↦fn∈R{\displaystyle n\in \mathbb {N} \mapsto f_{n}\in \mathbb {R} } называется числовой последовательностью, а предел limn→∞fn{\displaystyle \lim \limits _{n\to \infty }f_{n}} пределом этой последовательности.

Интеграл Римана

Пусть f:[a,b]⊂R→R.{\displaystyle f\colon [a,b]\subset \mathbb {R} \to \mathbb {R} .} Назовём размеченным разбиением отрезка [a,b]{\displaystyle [a,b]} коллекцию точек T={a=x0<x1<⋯<xn−1<xn=b,xn−1⩽ξn⩽xnn∈N}.{\displaystyle T=\{a=x_{0}<x_{1}<\cdots <x_{n-1}<x_{n}=b,\;x_{n-1}\leqslant \xi _{n}\leqslant x_{n}\;n\in \mathbb {N} \}.} Назовём диаметром разбиения T{\displaystyle T} число d(T)=maxi∈{1,…,n}(xi−xi−1).{\displaystyle d(T)=\max \limits _{i\in \{1,\ldots ,n\}}(x_{i}-x_{i-1}).} Тогда система множеств

B={T∣d(T)<δ,δ>0}{\displaystyle {\mathfrak {B}}=\{T\mid d(T)<\delta ,\delta >0\}}

является базисом фильтра в пространстве T{\displaystyle {\mathfrak {T}}} всех размеченных разбиений [a,b].{\displaystyle [a,b].} Определим функцию Sf:T→R{\displaystyle S_{f}:{\mathfrak {T}}\to \mathbb {R} } равенством

Sf(T)=∑i=1nf(ξi)(xi−xi−1)T∈T.{\displaystyle S_{f}(T)=\sum \limits _{i=1}^{n}f(\xi _{i})(x_{i}-x_{i-1})\quad T\in {\mathfrak {T}}.}

Тогда предел limBSf(T){\displaystyle \lim \limits _{\mathfrak {B}}S_{f}(T)} называется интегралом Римана функции f{\displaystyle f} на отрезке [a,b].{\displaystyle [a,b].}

Литература

  • Кудрявцев Л. Д. Курс математического анализа (в двух томах), — М.: Высшая школа, т. II — 584 с. — 1981.

wikiredia.ru

Предел вдоль фильтра — Википедия

Предел вдоль фильтра (предел по базису фильтра, предел по базе) — обобщение понятия предела.

Определение фильтра

Пусть дано множество X.{\displaystyle X.} Непустая система B{\displaystyle {\mathfrak {B}}} подмножеств множества X{\displaystyle X} называется базисом фильтра (базой) множества X{\displaystyle X}, если

Определение предела

Везде далее B{\displaystyle {\mathfrak {B}}} — базис фильтра (база) множества X{\displaystyle X}.

Предел числовой функции

Пусть f:X→R{\displaystyle f:X\to \mathbb {R} }. Число A∈R{\displaystyle A\in \mathbb {R} } называется пределом функции f{\displaystyle f} по базе B,{\displaystyle {\mathfrak {B}},} если

для любого ε>0{\displaystyle \varepsilon >0} существует B∈B{\displaystyle B\in {\mathfrak {B}}} такое, что для всех x∈B{\displaystyle x\in B} выполнено неравенство |f(x)−A|<ε.{\displaystyle |f(x)-A|<\varepsilon .}

Обозначение предела по базе: limBf(x)=A.{\displaystyle \lim \limits _{\mathfrak {B}}f(x)=A.}

Предел функции со значениями в метрическом пространстве

Пусть (M,ρ){\displaystyle (M,\rho )} — метрическое пространство и f:X→M{\displaystyle f:X\to M}. Точка a∈M{\displaystyle a\in M} называется пределом функции f{\displaystyle f} по базе B,{\displaystyle {\mathfrak {B}},} если

для любого ε>0{\displaystyle \varepsilon >0} существует B∈B{\displaystyle B\in {\mathfrak {B}}} такое, что для всех x∈B{\displaystyle x\in B} выполнено неравенство ρ(f(x),a)<ε.{\displaystyle \rho (f(x),a)<\varepsilon .}

Обозначение: limBf(x)=a.{\displaystyle \lim \limits _{\mathfrak {B}}f(x)=a.}

Предел функции со значениями в топологическом пространстве

Пусть (M,T){\displaystyle (M,{\mathcal {T}})} — топологическое пространство и f:X→M{\displaystyle f\colon X\to M}. Точка a∈M{\displaystyle a\in M} называется пределом функции f{\displaystyle f} по базе B,{\displaystyle {\mathfrak {B}},} если

для любой окрестности V{\displaystyle V} точки a{\displaystyle a} существует B∈B{\displaystyle B\in {\mathfrak {B}}} такое, что f(B)⊂V{\displaystyle f(B)\subset V}, то есть для всех x∈B{\displaystyle x\in B} выполняется включение f(x)∈V{\displaystyle f(x)\in V}.

Обозначение: limBf(x)=a.{\displaystyle \lim \limits _{\mathfrak {B}}f(x)=a.}

Замечание. Последнее «равенство» корректно использовать лишь в случаях, когда пространство (M,T){\displaystyle (M,{\mathcal {T}})} — хаусдорфово. Пределом функции со значениями в нехаусдорфовом пространстве могут быть сразу несколько различных точек (и, таким образом, нарушается теорема о единственности предела).

Примеры

Обычный предел

Пусть (X,T){\displaystyle (X,{\mathcal {T}})} — топологическое пространство, и M⊂X.{\displaystyle M\subset X.} Пусть a∈M′.{\displaystyle a\in M’.} Тогда система множеств

B={M∩U˙≡M∩U∖{a}∣a∈U∈T}{\displaystyle {\mathfrak {B}}=\left\{M\cap {\dot {U}}\equiv M\cap U\setminus \{a\}\mid a\in U\in {\mathcal {T}}\right\}}

является базисом фильтра множества M{\displaystyle M} и обозначается M∋x→a{\displaystyle M\ni x\to a} или просто x→a.{\displaystyle x\to a.} Предел функции по базе x→a{\displaystyle x\to a} множества M{\displaystyle M} называется пределом функции в точке a{\displaystyle a} и обозначается записью limx→af(x){\displaystyle \lim \limits _{x\to a}f(x)}.

Односторонние пределы

  • Пусть M⊂R,{\displaystyle M\subset \mathbb {R} ,} и a∈(M∩(a,∞))′.{\displaystyle a\in {\bigl (}M\cap (a,\infty ){\bigr )}’.} Тогда система множеств
B={(a,a+δ)∩M∣δ>0}{\displaystyle {\mathfrak {B}}=\{(a,a+\delta )\cap M\mid \delta >0\}}

является базисом фильтра и обозначается x→a+{\displaystyle x\to a+} или x→a+0.{\displaystyle x\to a+0.} Предел limx→a+f(x){\displaystyle \lim \limits _{x\to a+}f(x)} называется правосторонним пределом функции f{\displaystyle f} при x{\displaystyle x} стремящемся к a.{\displaystyle a.}

  • Пусть M⊂R,{\displaystyle M\subset \mathbb {R} ,} и a∈(M∩(−∞,a))′.{\displaystyle a\in {\bigl (}M\cap (-\infty ,a){\bigr )}’.} Тогда система множеств
B={(a−δ,a)∩M∣δ>0}{\displaystyle {\mathfrak {B}}=\{(a-\delta ,a)\cap M\mid \delta >0\}}

является базисом фильтра и обозначается x→a−{\displaystyle x\to a-} или x→a−0.{\displaystyle x\to a-0.} Предел limx→a−f(x){\displaystyle \lim \limits _{x\to a-}f(x)} называется левосторонним пределом функции f{\displaystyle f} при x{\displaystyle x} стремящемся к a.{\displaystyle a.}

Пределы на бесконечности

  • Пусть M⊂R,{\displaystyle M\subset \mathbb {R} ,} и supM=∞.{\displaystyle \sup M=\infty .} Тогда система множеств
B={M∩(T,∞)∣T∈R}.{\displaystyle {\mathfrak {B}}=\{M\cap (T,\infty )\mid T\in \mathbb {R} \}.}

является базисом фильтра и обозначается x→∞{\displaystyle x\to \infty } или x→+∞.{\displaystyle x\to +\infty .} Предел limx→∞f(x){\displaystyle \lim \limits _{x\to \infty }f(x)} называется пределом функции f{\displaystyle f} при x{\displaystyle x} стремящемся к бесконечности.

  • Пусть M⊂R,{\displaystyle M\subset \mathbb {R} ,} и infM=−∞.{\displaystyle \inf M=-\infty .} Тогда система множеств
B={M∩(−∞,T)∣T∈R}.{\displaystyle {\mathfrak {B}}=\{M\cap (-\infty ,T)\mid T\in \mathbb {R} \}.}

является базисом фильтра и обозначается x→−∞.{\displaystyle x\to -\infty .} Предел limx→−∞f(x){\displaystyle \lim \limits _{x\to -\infty }f(x)} называется пределом функции f{\displaystyle f} при x{\displaystyle x} стремящемся к минус-бесконечности.

Предел последовательности

Система множеств B={Bn}n=1∞,{\displaystyle {\mathfrak {B}}=\{B_{n}\}_{n=1}^{\infty },} где

Bn={n,n+1,n+2,…}n∈N,{\displaystyle B_{n}=\{n,n+1,n+2,\ldots \}\quad n\in \mathbb {N} ,}

является базисом фильтра и обозначается n→∞.{\displaystyle n\to \infty .} Функция n∈N↦fn∈R{\displaystyle n\in \mathbb {N} \mapsto f_{n}\in \mathbb {R} } называется числовой последовательностью, а предел limn→∞fn{\displaystyle \lim \limits _{n\to \infty }f_{n}} пределом этой последовательности.

Интеграл Римана

Пусть f:[a,b]⊂R→R.{\displaystyle f\colon [a,b]\subset \mathbb {R} \to \mathbb {R} .} Назовём размеченным разбиением отрезка [a,b]{\displaystyle [a,b]} коллекцию точек T={a=x0<x1<⋯<xn−1<xn=b,xn−1⩽ξn⩽xnn∈N}.{\displaystyle T=\{a=x_{0}<x_{1}<\cdots <x_{n-1}<x_{n}=b,\;x_{n-1}\leqslant \xi _{n}\leqslant x_{n}\;n\in \mathbb {N} \}.} Назовём диаметром разбиения T{\displaystyle T} число d(T)=maxi∈{1,…,n}(xi−xi−1).{\displaystyle d(T)=\max \limits _{i\in \{1,\ldots ,n\}}(x_{i}-x_{i-1}).} Тогда система множеств

B={T∣d(T)<δ,δ>0}{\displaystyle {\mathfrak {B}}=\{T\mid d(T)<\delta ,\delta >0\}}

является базисом фильтра в пространстве T{\displaystyle {\mathfrak {T}}} всех размеченных разбиений [a,b].{\displaystyle [a,b].} Определим функцию Sf:T→R{\displaystyle S_{f}:{\mathfrak {T}}\to \mathbb {R} } равенством

Sf(T)=∑i=1nf(ξi)(xi−xi−1)T∈T.{\displaystyle S_{f}(T)=\sum \limits _{i=1}^{n}f(\xi _{i})(x_{i}-x_{i-1})\quad T\in {\mathfrak {T}}.}

Тогда предел limBSf(T){\displaystyle \lim \limits _{\mathfrak {B}}S_{f}(T)} называется интегралом Римана функции f{\displaystyle f} на отрезке [a,b].{\displaystyle [a,b].}

Литература

  • Кудрявцев Л. Д. Курс математического анализа (в двух томах), — М.: Высшая школа, т. II — 584 с. — 1981.

wikipedia.green

Предел вдоль фильтра — WiKi

Везде далее B{\displaystyle {\mathfrak {B}}}  — базис фильтра (база) множества X{\displaystyle X} .

Предел числовой функции

Пусть f:X→R{\displaystyle f:X\to \mathbb {R} } . Число A∈R{\displaystyle A\in \mathbb {R} }  называется пределом функции f{\displaystyle f}  по базе B,{\displaystyle {\mathfrak {B}},}  если

для любого ε>0{\displaystyle \varepsilon >0}  существует B∈B{\displaystyle B\in {\mathfrak {B}}}  такое, что для всех x∈B{\displaystyle x\in B}  выполнено неравенство |f(x)−A|<ε.{\displaystyle |f(x)-A|<\varepsilon .} 

Обозначение предела по базе: limBf(x)=A.{\displaystyle \lim \limits _{\mathfrak {B}}f(x)=A.} 

Предел функции со значениями в метрическом пространстве

Пусть (M,ρ){\displaystyle (M,\rho )}  — метрическое пространство и f:X→M{\displaystyle f:X\to M} . Точка a∈M{\displaystyle a\in M}  называется пределом функции f{\displaystyle f}  по базе B,{\displaystyle {\mathfrak {B}},}  если

для любого ε>0{\displaystyle \varepsilon >0}  существует B∈B{\displaystyle B\in {\mathfrak {B}}}  такое, что для всех x∈B{\displaystyle x\in B}  выполнено неравенство ρ(f(x),a)<ε.{\displaystyle \rho (f(x),a)<\varepsilon .} 

Обозначение: limBf(x)=a.{\displaystyle \lim \limits _{\mathfrak {B}}f(x)=a.} 

Предел функции со значениями в топологическом пространстве

Пусть (M,T){\displaystyle (M,{\mathcal {T}})}  — топологическое пространство и f:X→M{\displaystyle f\colon X\to M} . Точка a∈M{\displaystyle a\in M}  называется пределом функции f{\displaystyle f}  по базе B,{\displaystyle {\mathfrak {B}},}  если

для любой окрестности V{\displaystyle V}  точки a{\displaystyle a}  существует B∈B{\displaystyle B\in {\mathfrak {B}}}  такое, что f(B)⊂V{\displaystyle f(B)\subset V} , то есть для всех x∈B{\displaystyle x\in B}  выполняется включение f(x)∈V{\displaystyle f(x)\in V} .

Обозначение: limBf(x)=a.{\displaystyle \lim \limits _{\mathfrak {B}}f(x)=a.} 

Замечание. Последнее «равенство» корректно использовать лишь в случаях, когда пространство (M,T){\displaystyle (M,{\mathcal {T}})}  — хаусдорфово. Пределом функции со значениями в нехаусдорфовом пространстве могут быть сразу несколько различных точек (и, таким образом, нарушается теорема о единственности предела).

Обычный предел

Пусть (X,T){\displaystyle (X,{\mathcal {T}})}  — топологическое пространство, и M⊂X.{\displaystyle M\subset X.}  Пусть a∈M′.{\displaystyle a\in M’.}  Тогда система множеств

B={M∩U˙≡M∩U∖{a}∣a∈U∈T}{\displaystyle {\mathfrak {B}}=\left\{M\cap {\dot {U}}\equiv M\cap U\setminus \{a\}\mid a\in U\in {\mathcal {T}}\right\}} 

является базисом фильтра множества M{\displaystyle M}  и обозначается M∋x→a{\displaystyle M\ni x\to a}  или просто x→a.{\displaystyle x\to a.}  Предел функции по базе x→a{\displaystyle x\to a}  множества M{\displaystyle M}  называется пределом функции в точке a{\displaystyle a}  и обозначается записью limx→af(x){\displaystyle \lim \limits _{x\to a}f(x)} .

Односторонние пределы

  • Пусть M⊂R,{\displaystyle M\subset \mathbb {R} ,}  и a∈(M∩(a,∞))′.{\displaystyle a\in {\bigl (}M\cap (a,\infty ){\bigr )}’.}  Тогда система множеств
B={(a,a+δ)∩M∣δ>0}{\displaystyle {\mathfrak {B}}=\{(a,a+\delta )\cap M\mid \delta >0\}} 

является базисом фильтра и обозначается x→a+{\displaystyle x\to a+}  или x→a+0.{\displaystyle x\to a+0.}  Предел limx→a+f(x){\displaystyle \lim \limits _{x\to a+}f(x)}  называется правосторонним пределом функции f{\displaystyle f}  при x{\displaystyle x}  стремящемся к a.{\displaystyle a.} 

  • Пусть M⊂R,{\displaystyle M\subset \mathbb {R} ,}  и a∈(M∩(−∞,a))′.{\displaystyle a\in {\bigl (}M\cap (-\infty ,a){\bigr )}’.}  Тогда система множеств
B={(a−δ,a)∩M∣δ>0}{\displaystyle {\mathfrak {B}}=\{(a-\delta ,a)\cap M\mid \delta >0\}} 

является базисом фильтра и обозначается x→a−{\displaystyle x\to a-}  или x→a−0.{\displaystyle x\to a-0.}  Предел limx→a−f(x){\displaystyle \lim \limits _{x\to a-}f(x)}  называется левосторонним пределом функции f{\displaystyle f}  при x{\displaystyle x}  стремящемся к a.{\displaystyle a.} 

Пределы на бесконечности

  • Пусть M⊂R,{\displaystyle M\subset \mathbb {R} ,}  и supM=∞.{\displaystyle \sup M=\infty .}  Тогда система множеств
B={M∩(T,∞)∣T∈R}.{\displaystyle {\mathfrak {B}}=\{M\cap (T,\infty )\mid T\in \mathbb {R} \}.} 

является базисом фильтра и обозначается x→∞{\displaystyle x\to \infty }  или x→+∞.{\displaystyle x\to +\infty .}  Предел limx→∞f(x){\displaystyle \lim \limits _{x\to \infty }f(x)}  называется пределом функции f{\displaystyle f}  при x{\displaystyle x}  стремящемся к бесконечности.

  • Пусть M⊂R,{\displaystyle M\subset \mathbb {R} ,}  и infM=−∞.{\displaystyle \inf M=-\infty .}  Тогда система множеств
B={M∩(−∞,T)∣T∈R}.{\displaystyle {\mathfrak {B}}=\{M\cap (-\infty ,T)\mid T\in \mathbb {R} \}.} 

является базисом фильтра и обозначается x→−∞.{\displaystyle x\to -\infty .}  Предел limx→−∞f(x){\displaystyle \lim \limits _{x\to -\infty }f(x)}  называется пределом функции f{\displaystyle f}  при x{\displaystyle x}  стремящемся к минус-бесконечности.

Предел последовательности

Система множеств B={Bn}n=1∞,{\displaystyle {\mathfrak {B}}=\{B_{n}\}_{n=1}^{\infty },}  где

Bn={n,n+1,n+2,…}n∈N,{\displaystyle B_{n}=\{n,n+1,n+2,\ldots \}\quad n\in \mathbb {N} ,} 

является базисом фильтра и обозначается n→∞.{\displaystyle n\to \infty .}  Функция n∈N↦fn∈R{\displaystyle n\in \mathbb {N} \mapsto f_{n}\in \mathbb {R} }  называется числовой последовательностью, а предел limn→∞fn{\displaystyle \lim \limits _{n\to \infty }f_{n}}  пределом этой последовательности.

Интеграл Римана

Пусть f:[a,b]⊂R→R.{\displaystyle f\colon [a,b]\subset \mathbb {R} \to \mathbb {R} .}  Назовём размеченным разбиением отрезка [a,b]{\displaystyle [a,b]}  коллекцию точек T={a=x0<x1<⋯<xn−1<xn=b,xn−1⩽ξn⩽xnn∈N}.{\displaystyle T=\{a=x_{0}<x_{1}<\cdots <x_{n-1}<x_{n}=b,\;x_{n-1}\leqslant \xi _{n}\leqslant x_{n}\;n\in \mathbb {N} \}.}  Назовём диаметром разбиения T{\displaystyle T}  число d(T)=maxi∈{1,…,n}(xi−xi−1).{\displaystyle d(T)=\max \limits _{i\in \{1,\ldots ,n\}}(x_{i}-x_{i-1}).}  Тогда система множеств

B={T∣d(T)<δ,δ>0}{\displaystyle {\mathfrak {B}}=\{T\mid d(T)<\delta ,\delta >0\}} 

является базисом фильтра в пространстве T{\displaystyle {\mathfrak {T}}}  всех размеченных разбиений [a,b].{\displaystyle [a,b].}  Определим функцию Sf:T→R{\displaystyle S_{f}:{\mathfrak {T}}\to \mathbb {R} }  равенством

Sf(T)=∑i=1nf(ξi)(xi−xi−1)T∈T.{\displaystyle S_{f}(T)=\sum \limits _{i=1}^{n}f(\xi _{i})(x_{i}-x_{i-1})\quad T\in {\mathfrak {T}}.} 

Тогда предел limBSf(T){\displaystyle \lim \limits _{\mathfrak {B}}S_{f}(T)}  называется интегралом Римана функции f{\displaystyle f}  на отрезке [a,b].{\displaystyle [a,b].} 

ru-wiki.org

Предел вдоль фильтра — Википедия

Предел вдоль фильтра (предел по базису фильтра, предел по базе) — обобщение понятия предела.

Содержание

  • 1 Определение фильтра
  • 2 Определение предела
    • 2.1 Предел числовой функции
    • 2.2 Предел функции со значениями в метрическом пространстве
    • 2.3 Предел функции со значениями в топологическом пространстве
  • 3 Примеры
    • 3.1 Обычный предел
    • 3.2 Односторонние пределы
    • 3.3 Пределы на бесконечности
    • 3.4 Предел последовательности
    • 3.5 Интеграл Римана
  • 4 Литература

Определение фильтра[ | ]

Основная статья: Фильтр (математика)

Пусть дано множество X.{\displaystyle X.} Непустая система B{\displaystyle {\mathfrak {B}}} подмножеств множества X{\displaystyle X} называется базисом фильтра (базой) множества X{\displaystyle X}, если

  • для любого B∈B{\displaystyle B\in {\mathfrak {B}}} выполнено B≠∅;{\displaystyle B\neq \varnothing ;}
  • для любых B1,B2∈B{\displaystyle B_{1},B_{2}\in {\mathfrak {B}}} существует B3∈B{\displaystyle B_{3}\in {\mathfrak {B}}} такое, что B3⊂B1∩B2.{\displaystyle B_{3}\subset B_{1}\cap B_{2}.}

Определение предела[ | ]

Везде далее B{\displaystyle {\mathfrak {B}}} — базис фильтра (база) множества X{\displaystyle X}.

Предел числовой функции[ | ]

Пусть f:X→R{\displaystyle f:X\to \mathbb {R} }. Число A∈R{\displaystyle A\in \mathbb {R} } называется пределом функции f{\displaystyle f} по базе B,{\displaystyle {\mathfrak {B}},} если

для любого

encyclopaedia.bid

Раздел 1. ОпределЕнный интеграл § Основная задача интегрального исчисления – нахождение площади криволинейной трапеции

П

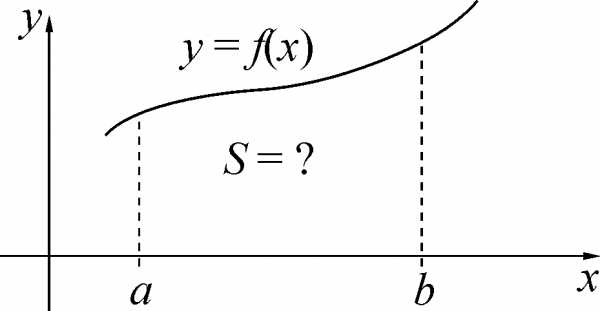
остановка задачи:Найти площадь фигуры, ограниченной снизу замкнутым промежутком оси абсциссI = [a,b] (y= 0), слева – вертикальной прямойx =a, справа – вертикальной прямойx=bи сверху – дугой графика функцииy=f (x). Такая фигура называется криволинейной трапецией опирающейся на промежутокI .

Несколько слов о понятии площади. Студенты с большим трудом и невнятно формулируют понятие площади. И не мудрено. В программе школьного образования не формулируется понятие площади, и оно остается чисто интуитивным. На самом деле площадь это некоторая функция 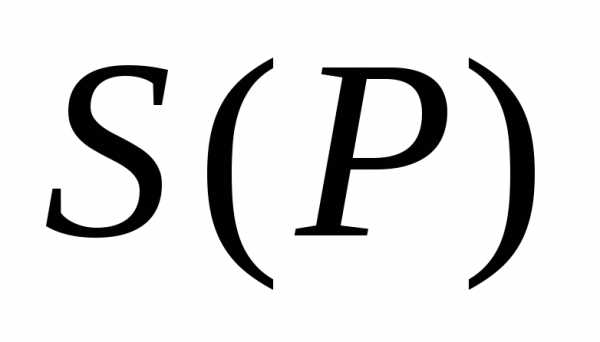, заданная на геометрических объектах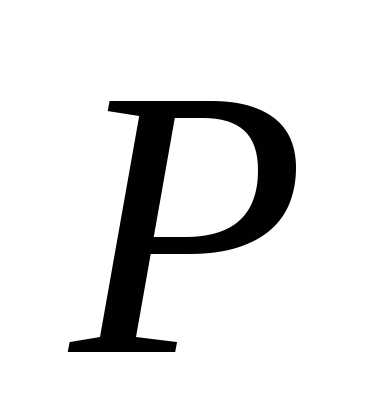и такая, что1)и 2).

Теперь займемся решением поставленной задачи. Для этого поступим следующим образом:

А.Разобьём промежутокIнаnчастей, не обязательно равных по длине, точками:

, и обозначим

– промежутки разбиения. Величинуназовем диаметром промежутка разбиения, а величину– мерой промежутка разбиения.

При этом: 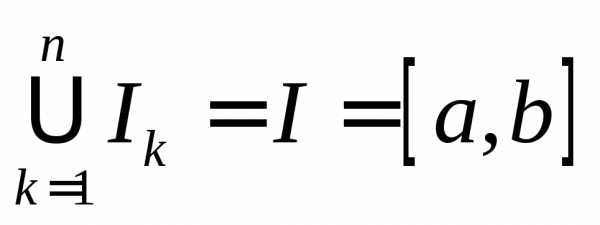и

. Для интервала понятие меры и диаметра не отличаются. Для произвольного множества самое большое из расстояний между элементами множеств, конечно, не всегда не совпадает с суммарной длиной интервалов, его составляющих.

Пусть 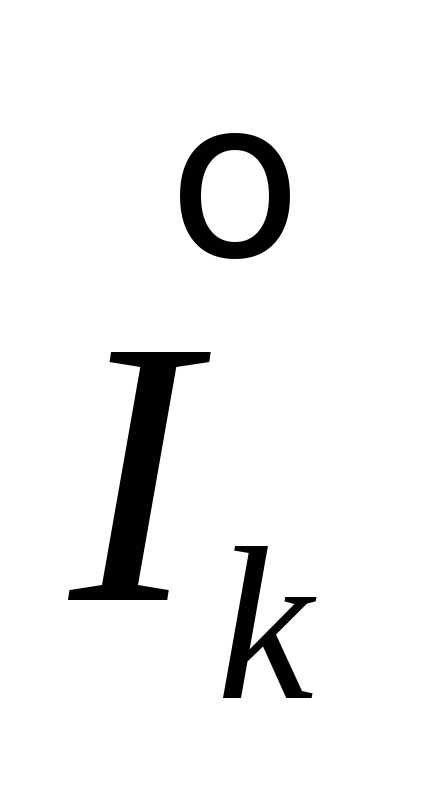– внутренность промежутка разбиения: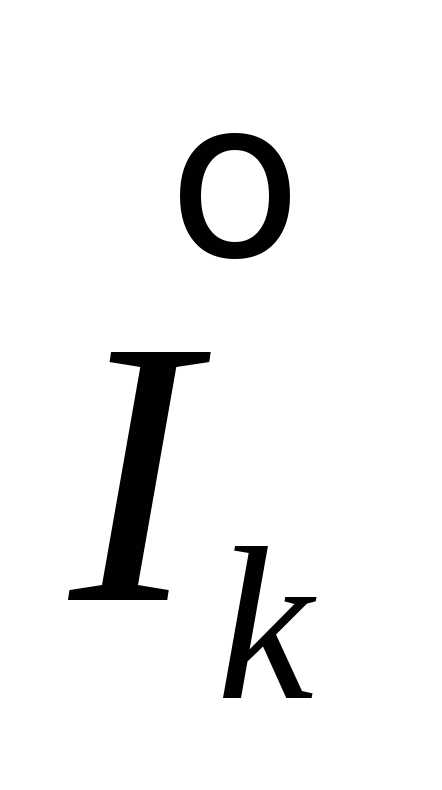=(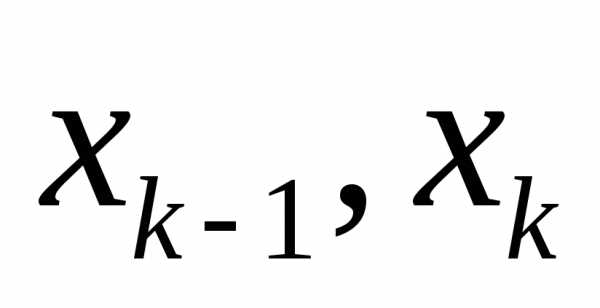) т.е.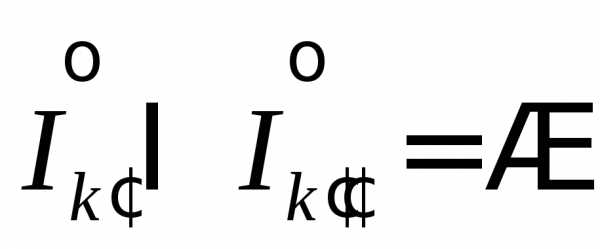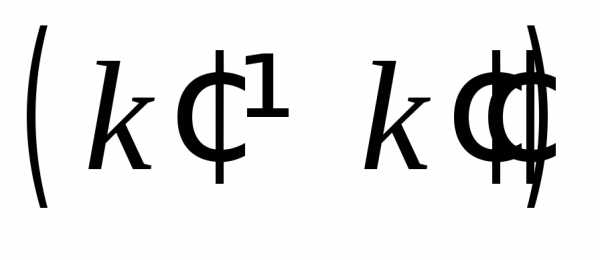. При этом говорят: Задано разбиениеР =промежуткаI= [a,b], а величинаназывается параметром разбиенияР.

Б.Теперь для каждого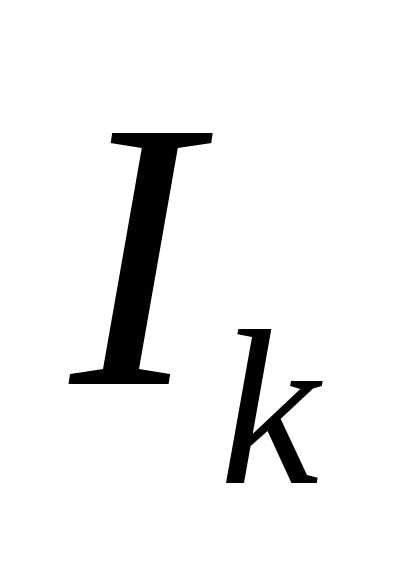выберем точки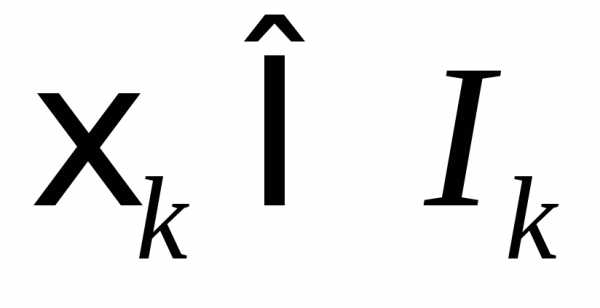т.е..

П

олучаемразбиение с отмеченными точками.

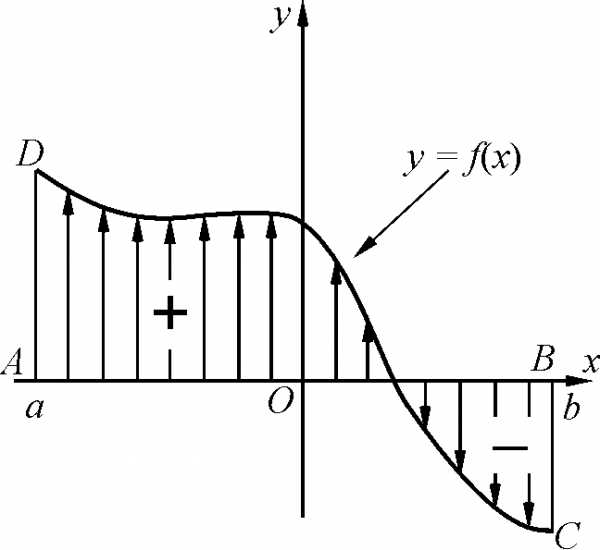
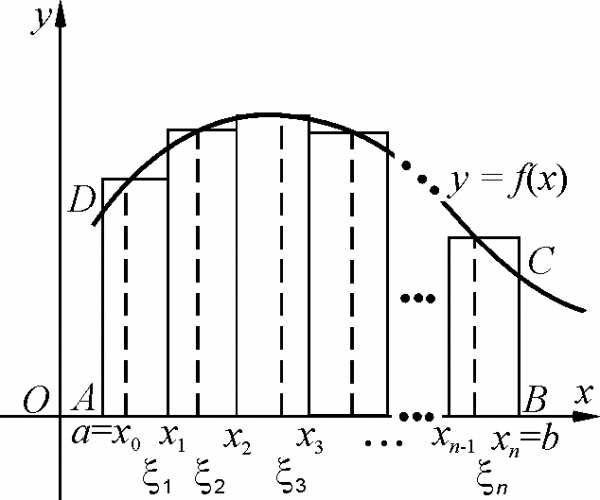
В.Построим сумму площадей образовавшихся прямоугольников:, и перейдем к пределу при параметре разбиения, стремящемся к нулю. Если такой предел существует, то он называется определенным интегралом от функции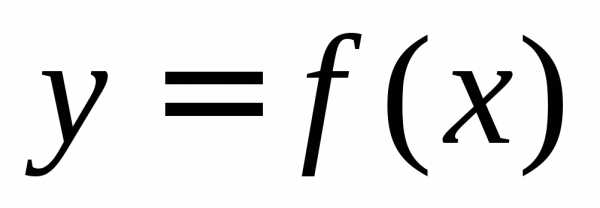по промежуткуи для неотрицательной функции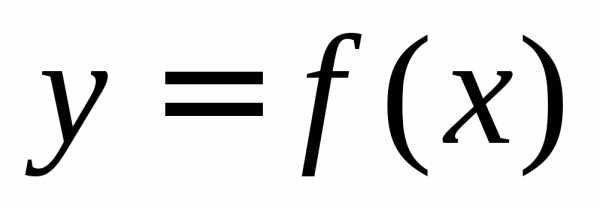является площадью криволинейной трапеции.

.

Если функция является знакопеременной то определенный интеграл это, вообще говоря, не площадь а ориентированная площадь, когда считается, что фигуры лежащие выше оси абсцисс имеют положительную площадь, а фигуры лежащие ниже оси абсцисс имеют отрицательную площадь.

§ Свойства разбиений

Говорят, что разбиение Рмельче чем разбиение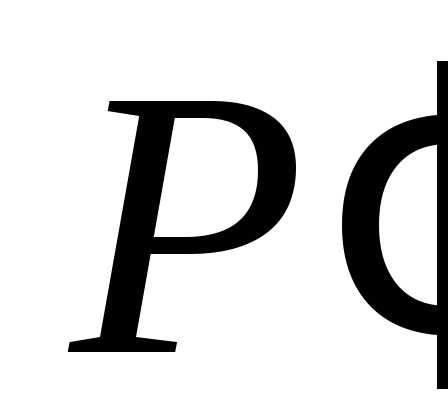(иликрупнееР), (илиРследует за) и записывают, если все точки разбиениясодержатся среди точек разбиенияР. Отметим три важных свойства отношения «крупнее – мельче» для разбиений:

а)существуют разбиения со сколь угодным малым параметром:

I= [a,b]. Выбирая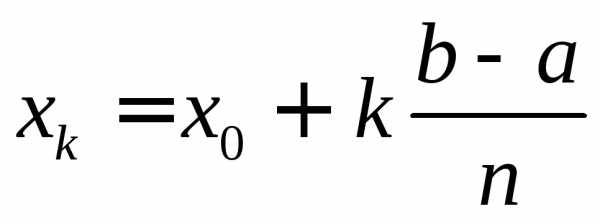;k= 0,1,2,…,n. Тогда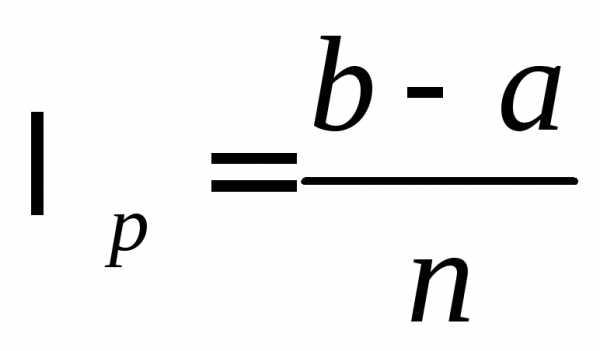и выбирая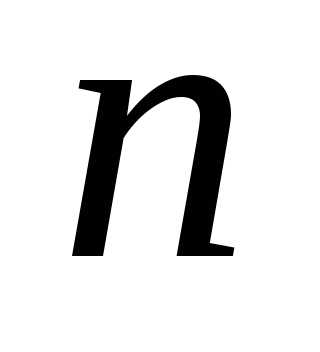достаточно большим, можно сделать параметр разбиения сколь угодно малым.

б)для двух любых разбиений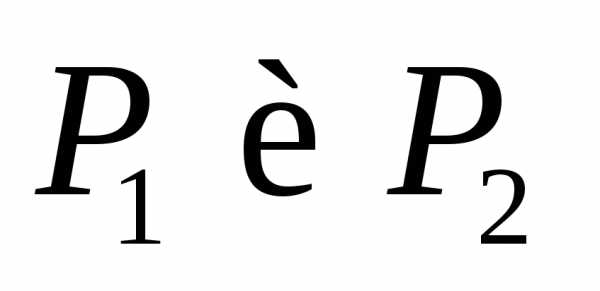существует третье разбиение, следующее за любым из них:

с) транзитивность отношения «крупнее – мельче»:

и, что то же самоеP1P2P2P3P1P3.

§ Определение определённого интеграла на языке . Предел по базе

Def:ВеличинаI(f ) называется определённым интегралом от функцииf на промежутке [a,b]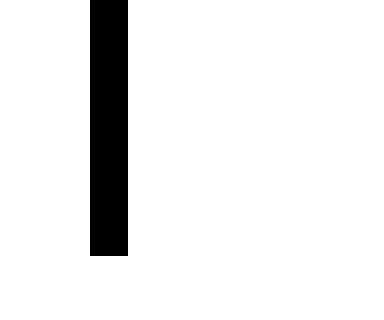D(f), если:.

Def:Если в множествеX задана системаB подмножествBмножестваXтакая, что:

а) BBB; б)B1,B2BB3BB3B1∩B2,

то говорят, что в множестве Xзадана база.

Примеры.

1˚. Множество открытых окрестностей точкиа образуют базу. Обозначим эту базуP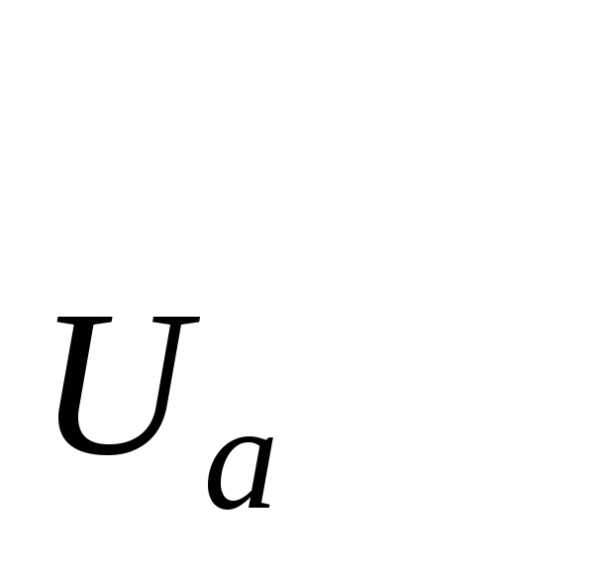

.

2˚. Множество открытых проколотых окрестностей точкиа образуют базу (P).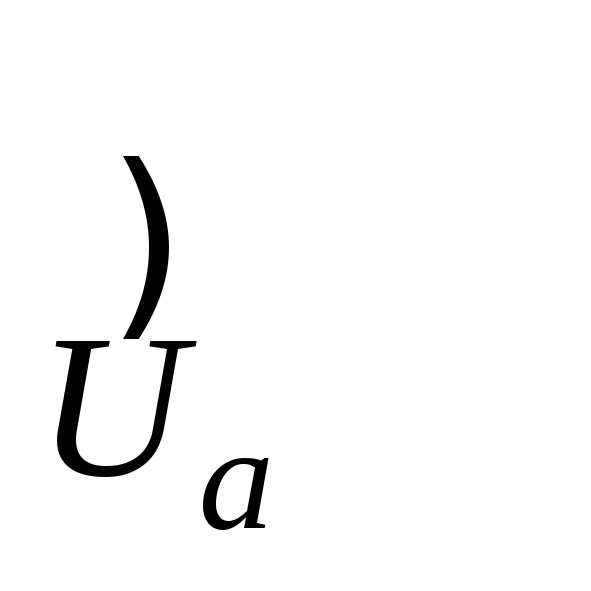

3˚. Множество открытых окрестностей точкиа на плоскости образуют базу(P).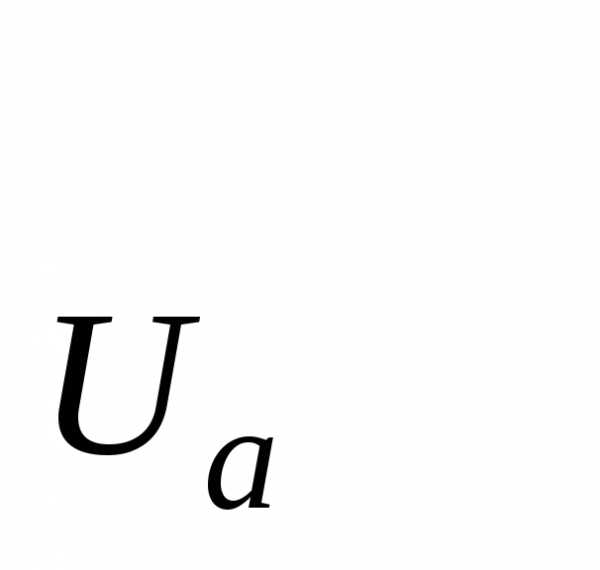

4˚. Множество открытых проколотых окрестностей точкиа на плоскости образуют базу(P).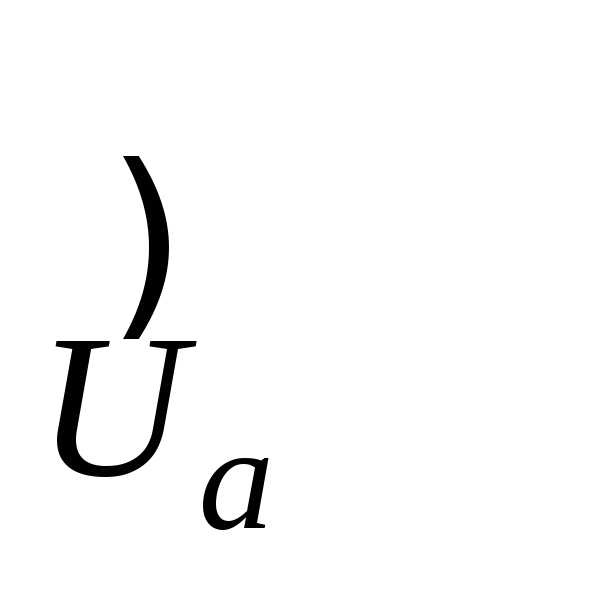

5˚. Множество всех разбиений промежутка [a,b] образуют базу (P)..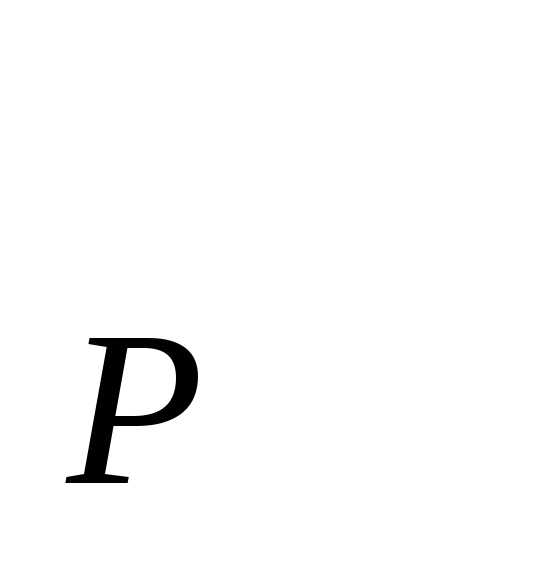

6˚. Множество всех разбиений промежутка [a,b] с параметром разбиенияP<образуют базу.

7˚. Множество всех разбиений промежутка [a,b] с отмеченными точками образуют базу.

6˚. Множество всех разбиений промежутка [a,b] с отмеченными точками с параметром разбиенияP<образуют базу. Последние три базы обозначают базуP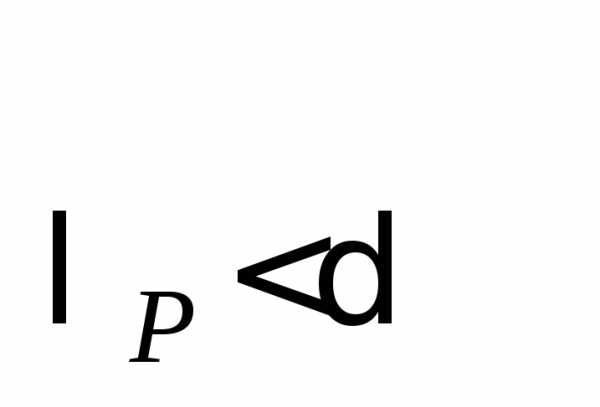или.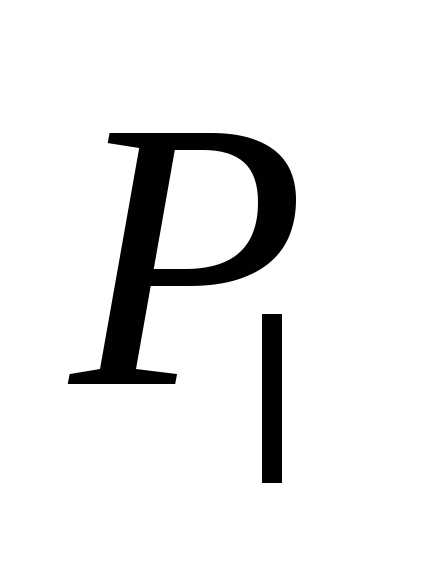

Def:. Пределом функцииf(x) по базе Bназывается числоА, такое, что:

. и тогда определение определенного интеграла может быть записано через предел по базе разбиений с отмеченными точками с параметром разбиенияP<:.

studfiles.net

Предел функции по Зоричу и по Бурбаки. : Анализ-I

Все цитаты из Зорича взяты из четвертого издания 2002 года и упомянутая книга Бурбаки это «Общая топология основные структуры» издания 1968 года.

В учебнике Зорича на странице 126 дается определение предела функции в точке по множеству. Вот это определение: «Число А называется пределом функции f: Е–> при x, стремящемся по множеству Е к точке а (предельной для Е), если для любой окрестности точки А найдётся проколотая окрестность точки а в множестве Е, образ которой при отображении f: Е–> содержится в заданной окрестности точки А.»

К этому определению надо добавить, что под окрестностью понимается открытая окрестность. (Что, как известно, бывает не всегда).

Через 22 страницы Зорич справедливо пишет, что от проколотых окрестностей фактически были использованы только два свойства и отправляясь от этих двух свойств дает определение базы в множестве.

Базой множества Х он называет любую совокупность непустых подмножеств Х, такую, что в пересечении любых двух подмножеств из этой совокупности «содержится некоторый элемент из той же совокупности». Далее Зорич отмечает, что «термин «база» есть краткое обозначение того, что в математике называется «базисом фильтра»». Упоминает Картана, ссылается на Бурбаки и дает определение предела функции по базе. Вот это определение (страница 150):

Пусть f: Х–> функция на множестве Х; ß – база в Х. Число называется пределом функции f: Х–> по базе ß, если для любой окрестности V(А) точки А найдётся элемент B базы ß, образ которого f(В) содержится в окрестности V(А).

Конечно, опять все окрестности открытые множества и образ окрестности f(В) должен быть открыт (хорошо бы это доказать). И теперь то «чему так долго предисловье».

Ради чего страдали? У Бурбаки предел функции (отображения) по базе области определения это точка у множества значений, такая, что её фильтр окрестностей имеет образ фильтра базы области определения как базу (открытых ли окрестностей?).
У меня ощущение, что я где-то наврал (Где?). Но смысл, во-первых в том, что под «х стремится к а» понимается некая база области определения (как и у Зорича), а во-вторых под пределом функции (отображения) по этой базе, точка множества значений, база фильтра окрестностей которой содержит образ базы области определения (и сама тоже является базой фильтра окрестностей точки у).

dxdy.ru

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *