Предел по базе: Предел функции по Зоричу и по Бурбаки. : Анализ-I

Предел функции в точке : Помогите решить / разобраться (М)

Someone Someone в сообщении #1392259 писал(а): project15 в сообщении #1392245 писал(а): Элемент Что такое ? Если это множество действительных с добавленными «бесконечными» элементами, то отдаёте ли Вы себе отчёт, что в математическом анализе используются два различных способа добавления «бесконечных» элементов, и что оба надо определить? Вы отметили, что Someone в сообщении #1392233 писал(а): Однако удобно ввести обобщающие понятия окрестности и проколотой окрестности… и я исходил из того, что эти понятия уже есть и можно ими пользоваться. Someone в сообщении #1392259 писал(а): project15 в сообщении #1392245 писал(а): Посчитал, что слово «целочисленного аргумента» — своеобразный исторический устоявшийся оборот (в учебниках Куранта и Фихтенгольца, если мне не изменяет память, именно так). Насчёт «исторически устоявшегося оборота» Вы заблуждаетесь, потому что математики отличают натуральные числа от целых. Нету такого «исторически устоявшегося оборота». У Фихтенгольца точно говорится о натуральных числах (глава первая, § 1, пункт 22). Куранта я не читал, но очень сильно сомневаюсь, что он путает целые числа с натуральными. Курант Бермант На счет Фихтенгольца, видимо, был не прав. Я для себя уяснил, что если есть возможность сказать точно и не прибегать к формулировке, допускающей двусмысленное трактование, то лучше так и сделать. Вы мне ясно дали понять, что такая терминология не является общепринятой. Но тем не менее, такой оборот в старых книжках иногда встречается. Someone в сообщении #1392259 писал(а): Проблема в том, что натуральные числа должны быть определены до целых, целые — до рациональных, а рациональные — до действительных, поэтому, если Вы будете считать, что , у Вас получится порочный круг. Другое дело, что числовые системы , и допускают изоморфизмы на подмножества . Я писал выше, что вещественные числа у нас уже есть. Расшифрую, что я под этим подразумевал. Мы определили аксиомами Пеано. Построили из системы и . Построение числовых систем — это точно не задача матанализа (возможно, одна из задач алгебры и теории чисел). Оно должно осуществляться до всего того, что изучается в матанализе. Далее мы определили вещественные числа аксиоматически. Рассмотрели несколько моделей этой системы аксиом. Доказали категоричность этой системы аксиом. Выделили в подмножество (которое само является алгебраической структурой), изоморфное тем объектам, которые определяются аксиомами Пеано и назвали элементы этого подмножества натуральными числами (для единообразия, как обычно. зачем создавать новый термин, если можно обойтись старым). Сделали то же самое с и . И только после всего этого выдохнули и сказали, что «теперь вещественные числа у нас есть». Вещественные числа будет не лишним немного поисследовать: доказать эквивалентность 5-6 формулировок непрерывности, доказать существование и единственность арифметического корня -ой степени произвольного положительного числа, вывести свойства неравенств (включая те свойства, которые относятся к арифметическим корням и степеням с натуральными показателями) и т.д. При таком подходе никакого порочного круга и никаких проблем с областью определения последовательности я не наблюдаю. Someone в сообщении #1392259 писал(а): Если Вы с целью единообразия рассматриваете натуральный ряд как подмножество множества действительных чисел, то условие «функция определена в проколотой окрестности предельной точки» будет нарушено, и у Вас будет два варианта выхода: либо дать для последовательности отдельное определение предела, что убивает вашу идею на корню, либо «для единообразия» определять предел функции, заданной на произвольном подмножестве множества действительных чисел. Про то, что натуральный ряд — подмножество множества действительных чисел, написал выше. А вот далее непонятно. Почему условие «функция определена в проколотой окрестности предельной точки» будет нарушено? Бесконечно удаленные предельные точки и точки прикосновения, а так же общее понятие проколотой окрестности мы определили, с натуральными числами и областью определения последовательности тоже никаких проблем нету. Не понимаю этот момент. Someone в сообщении #1392259 писал(а): и у Вас будет два варианта выхода: либо дать для последовательности отдельное определение предела, что убивает вашу идею на корню, либо «для единообразия» определять предел функции, заданной на произвольном подмножестве множества действительных чисел. Но этот вариант (не думайте, что его никто не пробовал) требует усложнения самого определения, а также формулировок и доказательств теорем, в первую очередь — свойств пределов. А это крайне нежелательно, поскольку речь идёт об обучении начинающих, а им и так трудно разобраться с этим понятием. Да, последовательность отдельно я определять не хочу (из соображений единообразия, как вы точно отметили). Меня больше заинтересовала ваша фраза «либо «для единообразия» определять предел функции, заданной на произвольном подмножестве множества действительных чисел.» А разве во всех курсах матанализа не делают ровно это? Разве предел функции в точке определяется только для каких-то частных видов функций, а не для любых функций вида ? Я всегда считал, что предел функции в точке применим к абсолютно любым функциям вида и никаких ограничений на функции тут нету (понятно, что точка, в которой рассматривается предел, должна быть предельной для ). Someone в сообщении #1392259 писал(а): И, наконец, должен отметить, что идея учить специалистов, как им излагать математический анализ, при вашем понимании вопроса выглядит крайне самонадеянной. Я Вам категорически не советую этим заниматься, поскольку ничего хорошего из этого не выйдет. Я очень ценю Ваши содержательные комментарии и то, что Вы тратите свое время, помогая мне, но, пожалуйста, не приписывайте мне те действия и намерения, которые не имеют места быть. Я прямо написал в вышестоящем посте project15 в сообщении #1392217 писал(а): Все вышеперечисленное я делаю исключительно для себя исходя из своего чувства эстетики и видения этого предмета. Никого не призываю относиться к матанализу так же. Я ни в коем разе не пытаюсь никого учить. Странно, что у Вас возникло подобное представление в свете того, что свои намерения я предельно ясно изложил в этой цитате.

Решение высшей математики онлайн

‹— Назад

Заметим, что во всех определениях предыдущего пункта ключевым оказывалось определение набора тех множеств, в которые последовательно, при своём изменении в соответствии с рассматриваемым условием, попадает переменное ( или ), от которого зависит изменяющаяся величина ( или ). В случае условия эти множества имеют вид ; в случае  — вид ; в случае  — вид .

Назовём их окончаниями базы предела при данном условии, а полный набор таких окончаний — базой предела. Базу предела будем обозначать так же, как само условие, а именно, , , и т. п. Таким образом,

Итак, база предела — это набор окончаний, которые должны удовлетворять таким свойствам: все они непусты и если и  — два разных окончания (одной и той же базы), то база должна содержать третье окончание , которое содержится в каждом из первых двух: .

Нетрудно видеть, что в рассмотренных выше трёх примерах баз, действительно, все окончания — непустые множества и пересечение двух окончаний совпадает с одним из них (с меньшим) и, тем самым, можно взять равным этому меньшему окончанию. Получили, что рассмотренные наборы множеств действительно являются базами.

Произвольную базу будем обозначать , а её окончания — буквой , быть может, снабжённой индексами. Если , причём , то окончание будем называть более далёким, чем окончание . Например, для базы окончание более далёкое, чем , если ; для базы окончание является тем более далёким, чем меньше число .

Теперь дадим определение предела по заданной базе .

        Определение 2.4   Пусть  — некоторая база и функция определена во всех точках некоторого окончания базы (и, значит, определена во всех точках более далёких окончаний ). Число называется пределом функции по базе (или при базе ) и обозначается

если

для любого (сколь угодно малого) числа найдётся такое окончание базы , что при всех выполняется неравенство

Тот факт, что , записывают ещё в виде

    

Нетрудно заметить, что в случае баз , и это общее определение предела, при соответствующей подстановке вида окончаний этих баз, означает ровно то же самое, что приведённые выше, в предыдущем разделе, частные определения пределов.

Геометрический смысл данного определения предела таков: на плоскости , на которой нарисован график функции , проведём горизонтальную полосу ширины вокруг горизонтальной прямой . Тот факт, что , означает, что найдётся достаточно далёкое окончание базы , на котором график функции целиком лежит в этой полосе. При уменьшении ширины полосы окончание, возможно, придётся брать более далёким, но, всё равно, и в любую более узкую полосу умещается график на достаточно далёком окончании.

Рис.2.8.График функции, имеющей предел, умещается в любую узкую полосу на достаточно далёком окончании

        Пример 2.4   Постоянная величина, то есть функция, значения которой не зависят от аргумента , имеет предел, равный этой постоянной, при любой (допустимой для данного множества аргументов ) базе .

Действительно, пусть при всех из некоторого окончания базы . Тогда при любом, сколь угодно малом и любом

Это и означает, что .

(Неудивительно: ведь график постоянной — это горизонтальная прямая линия; тем самым, этот график целиком умещается в горизонтальную полосу любой, сколь угодно малой ширины.)     

Выгода от введения общего определения предела по базе заключается в том, что теперь, чтобы дать определение предела при некотором новом условии, нам достаточно лишь указать ту базу (набор окончаний), которая этому условию соответствует. Кроме того, весьма многие свойства пределов окажутся общими для пределов по любой базе, и устанавливать эти свойства можно будет исходя из общего определения; было бы слишком расточительно доказывать каждое из общих свойств для каждой новой базы отдельно.

Приведём несколько примеров широко используемых в математическом анализе баз.

        Определение 2.5   Правосторонний предел функции. Рассмотрим базу , окончаниями которой служат интервалы, примыкающие справа к точке , то есть интервалы вида , где . Легко видеть, что все такие интервалы действительно образуют базу. Предел функции по этой базе называется пределом функции при , стремящемся к справа. База обозначается также или , а предел по этой базе обозначается так: .

Рис.2.9.Предел справа

Оказываясь во все более далёких окончаниях базы, то есть в интервалах с уменьшающимися значениями , точка приближается к точке , оставаясь справа от неё. Это объясняет название предела, вычисляемого по данной базе.     

        Упражнение 2.2   Запишите с помощью неравенств, содержащих и , данное выше определение в развёрнутом виде.    

Аналогично определяется предел функции при , стремящемся к слева.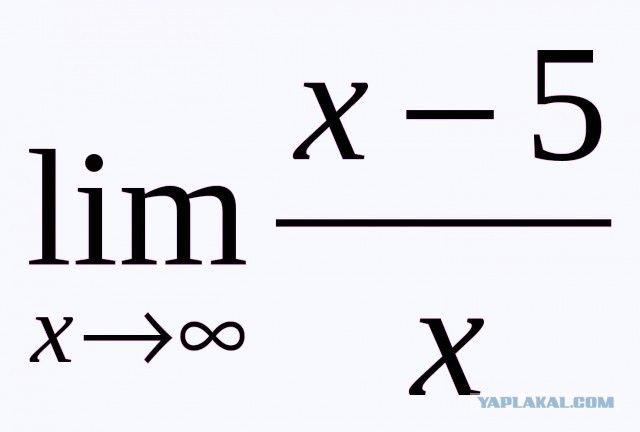 Для этого достаточно указать, какие множества являются окончаниями базы этого предела.

        Определение 2.6   Левосторонний предел. База состоит из интервалов , , примыкающих к точке слева.

Рис.2.10.Предел слева

База обозначается также . Предел по этой базе называется пределом функции при , стремящемся к слева и обозначается так: .    

Левосторонний и правосторонний пределы функции называются односторонними пределами этой функции при . Чтобы подчеркнуть отличие от односторонних пределов, предел называют двусторонним пределом.

        Теорема 2.1   Если функция имеет оба односторонних предела при и эти пределы равны одному и тому же числу , то существует двусторонний предел , который также равен ; ноаборот, если существует двусторонний предел , то существуют оба односторонних предела и оба они равны числу .

Рис.2.11.Пределы справа и слева совпадают с двусторонним пределом

        Доказательство.     Пусть фиксировано некоторое число . Так как , то существует такое окончание базы , при из которого выполняется неравенство . Так как , то существует такое окончание базы , при из которого также выполняется неравенство . Рассмотрим теперь меньшее из чисел и и обозначим его . Тогда при и при , то есть на объединении этих двух интервалов , выполняется неравенство . Однако такое объединение интервалов — это окончание базы . Тем самым при любом мы предъявили окончание базы двустороннего предела, такое что при всех из этого окончания верно неравенство . По определению это и означает, что .

Обратно, если существует , то при всех из некоторого двустороннего окончания базы и, следовательно, из каждой из двух половинок (окончания базы ) и (окончания базы ) выполнено неравенство . Это и означает, что и .     

        Определение 2.7   Через (или ) обозначим базу, окончаниями которой служат объединения двух лучей , где . При увеличении получаем всё более далёкие окончания, уходящие в бесконечность в обе стороны. Предел по такой базе обозначается или .     

Введённый этим определением двусторонний (при ) предел уже не имеет такого «наглядного смысла», как, например, пределы при , . Действительно, как представить себе, что переменная «уходит бесконечно далеко» сразу и направо, в , и налево, в ? Тем не менее, понятие базы позволяет вычислять такой предел с не большими усилиями, чем пределы при условиях, имеющих «наглядное представление».

        Упражнение 2.3   Покажите, пользуясь последним определением, что предел функции, рассмотренной в примере 2.3, при равен 3. Найдите окончание базы , на котором при данном выполняется неравенство .    

        Упражнение 2.4   Сформулируйте и докажите теорему о связи односторонних (при и ) и двустороннего (при ) пределов, аналогичную теореме 2.1.    

В дальнейшем при изучении высшей математики нам понадобятся и гораздо более экзотические базы пределов, в которых представить себе, что именно и к чему стремится, совсем нелегко. Например, при введении определённых интегралов они будут получаться как пределы некоторых величин (интегральных сумм), зависящих от сложного параметра, называемого размеченным разбиением, при некоторой базе, называемой измельчением размеченного разбиения. Тем не менее, и случай таких сложных пределов будет отлично укладываться в общую схему предела по базе, и нам не понадобится доказывать каких-то дополнительных теорем о свойствах таких пределов.

Для того, чтобы нагляднее представлять себе обсуждаемые общие результаты, читатель должен выбрать какую-либо конкретную базу (рекомендуем или какой-либо из односторонних пределов) и наглядно представлять себе, что означает общий результат применительно к выбранной конкретной базе.

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Предел последовательности и предел функции по коши.

Строгое определение предела функции

Доказывая свойства предела функции, мы убедились, что от проколотых окрестностей, в которых были определены наши функции и которые возникали в процессе доказательств, кроме свойств указанных во введении к предыдущему пункту 2, действительно ничего не потребовалось. Это обстоятельство служит оправданием для выделения следующего математического объекта.

а. База; определение и основные примеры

Определение 11. Совокупность В подмножеств множества X будем называть базой в множестве X, если выполнены два условия:

Иными словами, элементы совокупности В суть непустые множества и в пересечении любых двух из них содержится некоторый элемент из той же совокупности.

Укажем некоторые наиболее употребительные в анализе базы.

Если то вместо пишут и говорят, что х стремится к а справа или со стороны больших значений (соответственно, слева или со стороны меньших значений). При принята краткая запись вместо

Запись будет употребляться вместо Она означает, что а; стремится по множеству Е к а, оставаясь больше (меньше), чем а.

то вместо пишут и говорят, что х стремится к плюс бесконечности (соответственно, к минус бесконечности).

Запись будет употребляться вместо

При вместо мы (если это не ведет к недоразумению) будем, как это принято в теории предела последовательности, писать

Заметим, что все перечисленные базы обладают той особенностью, что пересечение любых двух элементов базы само является элементом этой базы, а не только содержит некоторый элемент базы. С другими базами мы встретимся при изучении функций, заданных не на числовой оси.

Отметим также, что используемый здесь термин «база» есть краткое обозначение того, что в математике называется «базисом фильтра», а введенный ниже предел по базе есть наиболее существенная для анализа часть созданного современным французским математиком А. Картаном понятия предела по фильтру

b. Предел функции по базе

Определение 12. Пусть — функция на множестве X; В — база в X. Число называется пределом функции по базе В, если для любой окрестности точки А найдется элемент базы, образ которого содержится в окрестности

Если А — предел функции по базе В, то пишут

Повторим определение предела по базе в логической символике:

Поскольку мы сейчас рассматриваем функции с числовыми значениями, полезно иметь в виду и следующую форму этого основного определения:

В этой формулировке вместо произвольной окрестности V (А) берется симметричная (относительно точки А) окрестность (е-окрестность). Эквивалентность этих определений для вещественнозначных функций вытекает из того, что, как уже говорилось, в любой окрестности точки содержится некоторая симметричная окрестность этой же точки (проведите доказательство полностью!).

Мы дали общее определение предела функции по базе. Выше были рассмотрены примеры наиболее употребительных в анализе баз. В конкретной задаче, где появляется та или иная из этих баз, необходимо уметь расшифровать общее определение и записать его для конкретной базы.

Рассматривая примеры баз, мы, в частности, ввели понятие окрестности бесконечности. Если использовать это понятие, то в соответствии с общим определением предела разумно принять следующие соглашения:

или, что то же самое,

Обычно под подразумевают малую величину. В приведенных определениях это, разумеется, не так. В соответствии с принятыми соглашениями, например, можем записать

Для того чтобы можно было считать доказанными и в общем случае предела по произвольной базе все те теоремы о пределах, которые мы доказали в пункте 2 для специальной базы , необходимо дать соответствующие определения: финально постоянной, финально ограниченной и бесконечно малой при данной базе функций.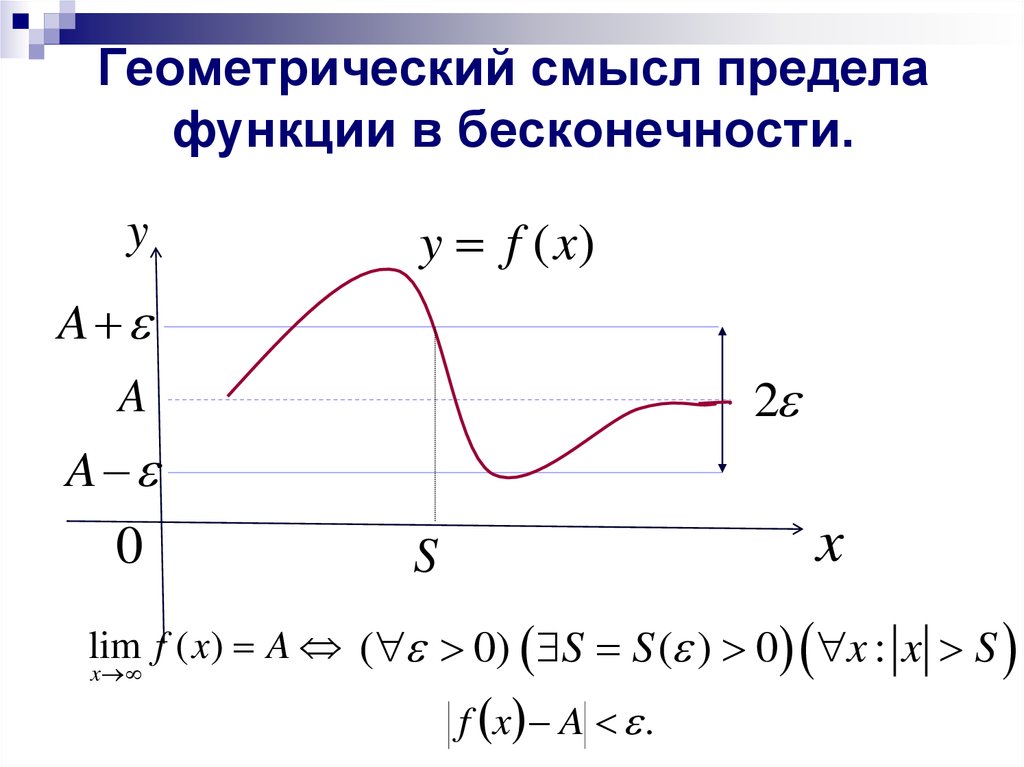

Определение 13. Функция называется финально постоянной при базе В, если существуют число и такой элемент базы, в любой точке которого

В данный же момент основная польза от сделанного наблюдения и введенного в связи с ним понятия базы состоит в том, что они избавляют нас от проверок и формальных доказательств теорем о пределах для каждого конкретного вида предельных переходов или, в нашей нынешней терминологии, для каждого конкретного вида баз.

Для того чтобы окончательно освоиться с понятием предела по произвольной базе, доказательства дальнейших свойств предела функции мы проведем в общем виде.

Постоянное число а называется пределом последовательности {x n }, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения x n , у которых n>N, удовлетворяют неравенству

|x n — a|

Записывают это следующим образом: или x n → a.

Неравенство (6.1) равносильно двойному неравенству

a- ε

которое означает, что точки x n , начиная с некоторого номера n>N, лежат внутри интервала (a- ε, a+ ε), т. е. попадают в какую угодно малую ε-окрестность точки а .

Последовательность, имеющая предел, называется сходящейся , в противном случае — расходящейся .

Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции x n = f(n) целочисленного аргумента n .

Пусть дана функция f(x) и пусть a — предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a . Точка a может принадлежать множеству D(f), а может и не принадлежать ему.

Определение 1. Постоянное число А называется предел функции f(x) при x→ a, если для всякой последовательности {x n } значений аргумента, стремящейся к а , соответствующие им последовательности {f(x n)} имеют один и тот же предел А.

Это определение называют определением предел функции по Гейне, или “на языке последовательностей ”.

Определение 2 . Постоянное число А называется предел функции f(x) при x→ a, если, задав произвольное как угодно малое положительное число ε , можно найти такое δ >0 (зависящее от ε ), что для всех x , лежащих в ε-окрестности числа а , т.е. для x , удовлетворяющих неравенству
0

Это определение называют определением предел функции по Коши, или “на языке ε — δ “.

Определения 1 и 2 равносильны. Если функция f(x) при x → a имеет предел , равный А, это записывается в виде

. (6.3)

В том случае, если последовательность {f(x n)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а , то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:

Переменная величина (т.е. последовательность или функция), предел которой равен нулю, называется бесконечно малой величиной.

Переменная величина, предел которой равен бесконечности, называется бесконечно большой величиной .

Чтобы найти предел на практике пользуются следующими теоремами.

Теорема 1 . Если существует каждый предел

(6.4)

(6.5)

(6.6)

Замечание . Выражения вида 0/0, ∞/∞, ∞-∞ , 0*∞ , — являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и найти предел такого вида носит название “раскрытие неопределенностей”.

Теорема 2. (6.7)

т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности, ;

(6.8)

(6.9)

Теорема 3.

(6.10)

(6.11)

где e » 2.7 — основание натурального логарифма. Формулы (6.10) и (6.11) носят название первый замечательного предело и второй замечательный предел.

Используются на практике и следствия формулы (6.11):

(6.12)

(6.13)

(6.14)

в частности предел,

Eсли x → a и при этом x > a, то пишут x →a + 0.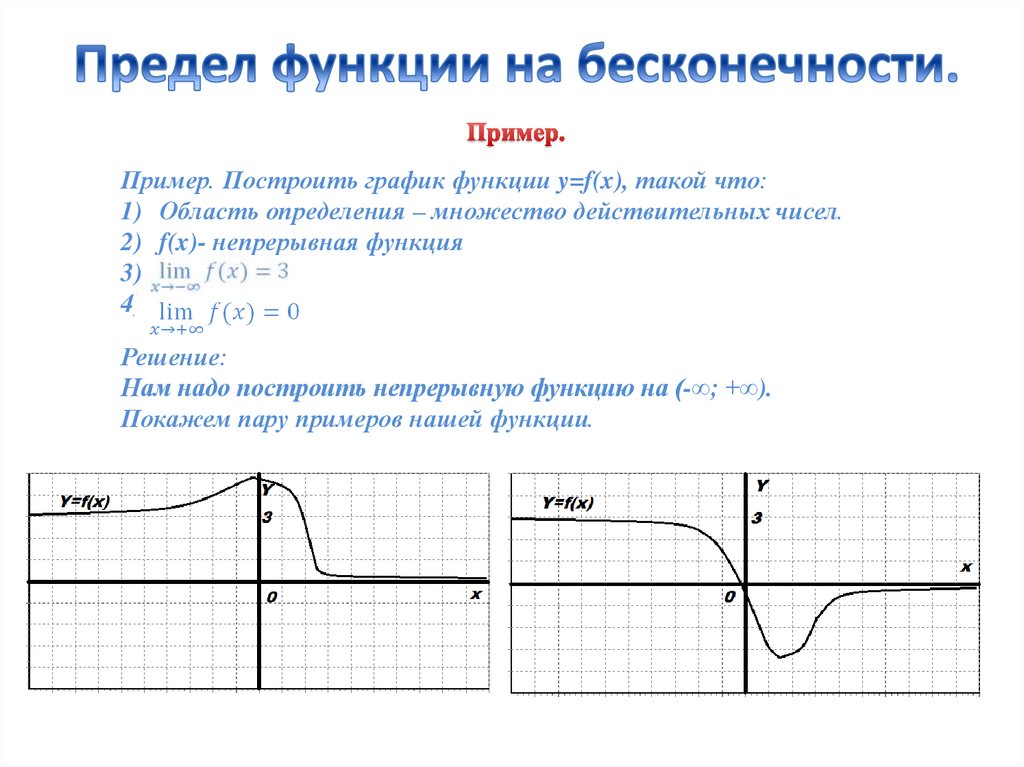 Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→ a и при этом x и называются соответственно предел справа и предел слева функции f(x) в точке а . Чтобы существовал предел функции f(x) при x→ a необходимо и достаточно, чтобы . Функция f(x) называется непрерывной в точке x 0 , если предел

. (6.15)

Условие (6.15) можно переписать в виде:

,

то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.

Если равенство (6.15) нарушено, то говорят, что при x = x o функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множество R , кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(x o)= f(0) не определено, поэтому в точке x o = 0 функция имеет разрыв.

Функция f(x) называется непрерывной справа в точке x o , если предел

,

и непрерывной слева в точке x o, если предел

.

Непрерывность функции в точке x o равносильна ее непрерывности в этой точке одновременно и справа и слева.

Для того, чтобы функция была непрерывна в точке x o , например, справа, необходимо, во-первых, чтобы существовал конечный предел , а во-вторых, чтобы этот предел был равен f(x o). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.

1. Если предел существует и не равен f(x o), то говорят, что функция f(x) в точке x o имеет разрыв первого рода, или скачок .

2. Если предел равен +∞ или -∞ или не существует, то говорят, что в точке x o функция имеет разрыв второго рода .

Например, функция y = ctg x при x → +0 имеет предел, равный +∞ , значит, в точке x=0 она имеет разрыв второго рода.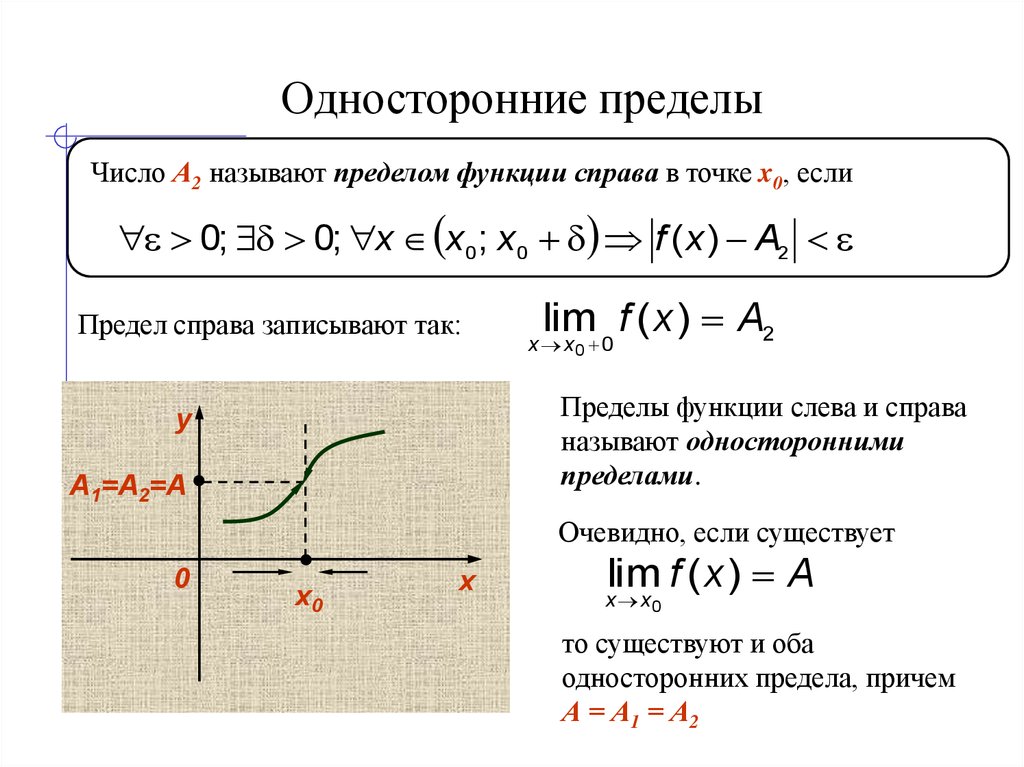 Функция y = E(x) (целая часть от x ) в точках с целыми абсциссами имеет разрывы первого рода, или скачки.

Функция, непрерывная в каждой точке промежутка , называется непрерывной в . Непрерывная функция изображается сплошной кривой.

Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п.

Рассмотрим пример Я. И. Перельмана , дающий интерпретацию числа e в задаче о сложных процентах. Число e есть предел . В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 × 1,5 = 150, а еще через полгода — в 150 × 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 × (1 +1/3) 3 » 237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:

100 × (1 +1/10) 10 » 259 (ден. ед.),

100 × (1+1/100) 100 » 270 (ден. ед.),

100 × (1+1/1000) 1000 » 271 (ден. ед.).

При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что предел

Пример 3. 1. Пользуясь определением предела числовой последовательности, доказать, что последовательность x n =(n-1)/n имеет предел, равный 1.

Решение. Нам надо доказать, что, какое бы ε > 0 мы ни взяли, для него найдется натуральное число N, такое, что для всех n N имеет место неравенство |x n -1|

Возьмем любое e > 0. Так как ; x n -1 =(n+1)/n — 1= 1/n, то для отыскания N достаточно решить неравенство 1/n1/ e и, следовательно, за N можно принять целую часть от 1/ e , N = E(1/ e ). Мы тем самым доказали, что предел .

Пример 3 .2 . Найти предел последовательности, заданной общим членом .

Решение. Применим теорему предел суммы и найдем предел каждого слагаемого. При n → ∞ числитель и знаменатель каждого слагаемого стремится к бесконечности, и мы не можем непосредственно применить теорему предел частного. Поэтому сначала преобразуем x n , разделив числитель и знаменатель первого слагаемого на n 2 , а второго на n . Затем, применяя теорему предел частного и предел суммы, найдем:

.

Пример 3.3 . . Найти .

Решение. .

Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.

Пример 3 .4 . Найти ().

Решение. Применять теорему предел разности нельзя, поскольку имеем неопределенность вида ∞-∞ . Преобразуем формулу общего члена:

.

Пример 3 .5 . Дана функция f(x)=2 1/x . Доказать, что предел не существует.

Решение. Воспользуемся определением 1 предела функции через последовательность. Возьмем последовательность { x n }, сходящуюся к 0, т.е. Покажем, что величина f(x n)= для разных последовательностей ведет себя по-разному. Пусть x n = 1/n. Очевидно, что , тогда предел Выберем теперь в качестве x n последовательность с общим членом x n = -1/n, также стремящуюся к нулю. Поэтому предел не существует.

Пример 3 . 6 . Доказать, что предел не существует.

Решение. Пусть x 1 , x 2 ,…, x n ,… — последовательность, для которой
. Как ведет себя последовательность {f(x n)} = {sin x n } при различных x n → ∞

Если x n = p n, то sin x n = sin p n = 0 при всех n и предел Если же
x n =2 p n+ p /2, то sin x n = sin(2 p n+ p /2) = sin p /2 = 1 для всех n и следовательно предел . Таким образом, не существует.

Виджет для вычисления пределов on-line

В верхнем окошке вместо sin(x)/x введите функцию, предел которой надо найти. В нижнее окошко введите число, к которому стремится х и нажмите кнопку Calcular, получите искомый предел. А если в окне результата нажмете на Show steps в правом верхнем углу, то получите подробное решение.

Правила ввода функций: sqrt(x)- квадратный корень, cbrt(x) — кубический корень, exp(x) — экспонента, ln(x) — натуральный логарифм, sin(x) — синус, cos(x) — косинус, tan(x) — тангенс, cot(x) — котангенс, arcsin(x) — арксинус, arccos(x) — арккосинус, arctan(x) — арктангенс. возведение в степень, вместо бесконечности Infinity. Пример: функция вводится так sqrt(tan(x/2)).

Пусть функция у=ƒ (х) определена в некоторой окрестности точки х о, кроме, быть может, самой точки х о.

Сформулируем два, эквивалентных между собой, определения предела функции в точке.

Определение 1 (на «языке последовательностей», или по Гейне).

Число А называется пределом функции у=ƒ(х) в топке x 0 (или при х® х о), если для любой последовательности допустимых значений аргумента x n , n є N (x n ¹ x 0), сходящейся к х о последовательность соответствующих значений функции ƒ(х n), n є N, сходится к числу А

В этом случае пишут
или ƒ(х)->А при х→х о. Геометрический смысл предела функции: означает, что для всех точек х, достаточно близких к точке х о, соответствующие значения функции как угодно мало отличаются от числа А.

Определение 2 (на «языке ε», или по Коши).

Число А называется пределом функции в точке х о (или при х→х о), если для любого положительного ε найдется такое положительное число δ, что для все х¹ х о, удовлетворяющих неравенству |х-х о |

Геометрический смысл предела функции:

если для любой ε-окрестности точки А найдется такая δ-окрестность точки х о, что для всех х¹ хо из етой δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε , у=А-ε (см. рис. 110). Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).

Доказать, что

Решение: Возьмем произвольное ε>0, найдем δ=δ(ε)>0 такое, что для всех х, удовлетворяющих неравенству |х-3|

Взяв δ=ε/2, видим, что для всех х, удовлетворяющих неравенству |х-3|3.

16.2. Односторонние пределы

В определении предела функции считается, что х стремится к x 0 любым способом: оставаясь меньшим, чем x 0 (слева от х 0), большим, чем х о (справа от х о), или колеблясь около точки x 0 .

Бывают случаи, когда способ приближения аргумента х к х о существенно влияет на значение придела функции. Поэтому вводят понятия односторонних пределов.

Число А 1 называется пределом функции у=ƒ(х) слева в точке х о, если для любого число ε>0 существует число δ=δ(ε)> 0 такое, что при х є (х 0 -δ;x o), выполняется неравенство |ƒ(х)-А|х 0 -0 или коротко: ƒ(х о- 0)=А 1 (обозначение Дирихле) (см. рис. 111).

Аналогично определяется предел функции справа, запишем его с помощью символов:

Коротко предел справа обозначают ƒ(х о +0)=А.

Пределы функции слева и справа называются односторонними пределами. Очевидно, если существует , то существуют и оба односторонних предела, причем А=А 1 =А 2 .

Справедливо и обратное утверждение: если существуют оба предела ƒ(х 0 -0) и ƒ(х 0 +0) и они равны, то существует предел и А=ƒ(х 0 -0).

Если же А 1 ¹ А 2 , то етот придел не существует.

16.3. Предел функции при х ® ∞

Пусть функция у=ƒ(х) определена в промежутке (-∞;∞). Число А называется пределом функции ƒ(х) при х→∞ , если для любого положительного числа ε существует такое число М=М()>0, что при всех х, удовлетворяющих неравенству |х|>М выполняется неравенство |ƒ(х)-А|

Геометрический смысл этого определения таков: для » ε>0 $ М>0, что при х є(-∞; -М) или х є(М; +∞) соответствующие значения функции ƒ(х) попадают в ε-окрестность точки А, т. е. точки графика лежат в полосе шириной 2ε, ограниченной прямыми у=А+ε и у=А-ε (см. рис. 112).

16.4. Бесконечно большая функция (б.б.ф.)

Функция у=ƒ(х) называется бесконечно большой при х→х 0 , если для любого числа М>0 существует число δ=δ(М)>0, что для всех х, удовлетворяющих неравенству 0М.

Например, функция у=1/(х-2) есть б.б.ф. при х->2.

Если ƒ(х) стремится к бесконечности при х→х о и принимает лишь положительные значения, то пишут

если лишь отрицательные значения, то

Функция у=ƒ(х), заданная на всей числовой прямой, называется бесконечно большой при х→∞, если для любого числа М>0 найдется такое число N=N(M)>0, что при всех х, удовлетворяющих неравенству |х|>N, выполняется неравенство |ƒ(х)|>М. Коротко:

Например, у=2х есть б.б.ф. при х→∞.

Отметим, что если аргумент х, стремясь к бесконечности, принимает лишь натуральные значения, т. е. хєN, то соответствующая б.б.ф. становится бесконечно большой последовательностью. Например, последовательность v n =n 2 +1, n є N, является бесконечно большой последовательностью. Очевидно, всякая б.б.ф. в окрестности точки х о является неограниченной в этой окрестности. Обратное утверждение неверно: неограниченная функция может и не быть б.б.ф. (Например, у=хsinх.)

Однако, если limƒ(х)=А при х→x 0 , где А — конечное число, то функция ƒ(х) ограничена в окрестности точки х о.

Действительно, из определения предела функции следует, что при х→ х 0 выполняется условие |ƒ(х)-А|

Сегодня на уроке мы разберём строгое определение последовательности и строгое определение предела функции , а также научимся решать соответствующие задачи теоретического характера. Статья предназначена, прежде всего, для студентов 1-го курса естественнонаучных и инженерно-технических специальностей, которые начали изучать теорию математического анализа, и столкнулись с трудностями в плане понимания этого раздела высшей математики. Кроме того, материал вполне доступен и учащимся старших классов.

За годы существования сайта я получил недобрый десяток писем примерно такого содержания: «Плохо понимаю математический анализ, что делать?», «Совсем не понимаю матан, думаю бросить учёбу» и т.п. И действительно, именно матан часто прореживает студенческую группу после первой же сессии. Почему так обстоят дела? Потому что предмет немыслимо сложен? Вовсе нет! Теория математического анализа не столь трудна, сколько своеобразна . И её нужно принять и полюбить такой, какая она есть =)

Начнём с самого тяжёлого случая. Первое и главное – не надо бросать учёбу. Поймите правильно, бросить, оно всегда успеется;-) Безусловно, если через год-два от выбранной специальности будет тошнить, тогда да – следует задуматься (а не пороть горячку!) о смене деятельности. Но пока стОит продолжить. И, пожалуйста, забудьте фразу «Ничего не понимаю» – так не бывает, чтобы СОВСЕМ ничего не понимать.

Что делать, если с теорией плохо? Это, кстати, касается не только математического анализа. Если с теорией плохо, то сначала нужно СЕРЬЁЗНО налечь на практику. При этом решаются сразу две стратегические задачи:

– Во-первых, значительная доля теоретических знаний появилась благодаря практике. И поэтому многие люди понимают теорию через… – всё верно! Нет-нет, вы не о том подумали =)

– И, во-вторых, практические навыки с большой вероятностью «вытянут» вас на экзамене, даже если…, но не будем так настраиваться! Всё реально и всё реально «поднять» в достаточно короткие сроки. Математический анализ – это мой любимый раздел высшей математики, и поэтому я просто не мог не протянуть вам ноги руку помощи:

В начале 1-го семестра обычно проходят пределы последовательностей и пределы функций. Не понимаете, что это такое и не знаете, как их решать? Начните со статьи Пределы функций , в которой «на пальцах» рассмотрено само понятие и разобраны простейшие примеры. Далее проработайте другие уроки по теме, в том числе урок о пределах последовательностей , на котором я фактически уже сформулировал строгое определение.

Какие значки помимо знаков неравенств и модуля вы знаете?

– длинная вертикальная палка читается так: «такое, что», «такая, что», «такой, что» либо «такие, что» , в нашем случае, очевидно, речь идёт о номере – поэтому «такой, что»;

– для всех «эн», бОльших чем ;

– знак модуля означает расстояние , т.е. эта запись сообщает нам о том, что расстояние между значениями меньше эпсилон.

Ну как, убийственно сложно? =)

После освоения практики жду вас в следующем параграфе:

И в самом деле, немного порассуждаем – как сформулировать строгое определение последовательности? …Первое, что приходит на ум в свете практического занятия : «предел последовательности – это число, к которому бесконечно близко приближаются члены последовательности».

Хорошо, распишем последовательность :

Нетрудно уловить, что подпоследовательность бесконечно близко приближаются к числу –1, а члены с чётными номерами – к «единице».

А может быть предела два? Но тогда почему у какой-нибудь последовательности их не может быть десять или двадцать? Так можно далеко зайти. В этой связи логично считать, что если у последовательности существует предел, то он единственный .

Примечание : у последовательности нет предела, однако из неё можно выделить две подпоследовательности (см. выше), у каждой из которых существует свой предел.

Таким образом, высказанное выше определение оказывается несостоятельным. Да, оно работает для случаев вроде (чем я не совсем корректно пользовался в упрощённых объяснениях практических примеров) , но сейчас нам нужно отыскать строгое определение.

Попытка вторая: «предел последовательности – это число, к которому приближаются ВСЕ члены последовательности, за исключением, разве что их конечного количества». Вот это уже ближе к истине, но всё равно не совсем точно. Так, например, у последовательности половина членов вовсе не приближается к нулю – они ему просто-напросто равны =) К слову, «мигалка» вообще принимает два фиксированных значения.

Формулировку нетрудно уточнить, но тогда возникает другой вопрос: как записать определение в математических знаках? Научный мир долго бился над этой проблемой, пока ситуацию не разрешил известный маэстро , который, по существу, и оформил классический матанализ во всей его строгости. Коши предложил оперировать окрестностями , чем значительно продвинул теорию.

Рассмотрим некоторую точку и её произвольную -окрестность:

Значение «эпсилон» всегда положительно, и, более того, мы вправе выбрать его самостоятельно . Предположим, что в данной окрестности находится множество членов (не обязательно все) некоторой последовательности . Как записать тот факт, что, например десятый член попал в окрестность? Пусть он находится в правой её части. Тогда расстояние между точками и должно быть меньше «эпсилон»: . Однако если «икс десятое» расположено левее точки «а», то разность будет отрицательна, и поэтому к ней нужно добавить знак модуля : .

Определение : число называется пределом последовательности, если для любой его окрестности (заранее выбранной) существует натуральный номер – ТАКОЙ, что ВСЕ члены последовательности с бОльшими номерами окажутся внутри окрестности:

Или короче: , если

Иными словами, какое бы малое значение «эпсилон» мы ни взяли, рано или поздно «бесконечный хвост» последовательности ПОЛНОСТЬЮ окажется в этой окрестности.

Так, например, «бесконечный хвост» последовательности ПОЛНОСТЬЮ зайдёт в любую сколь угодно малую -окрестность точки . Таким образом, это значение является пределом последовательности по определению. Напоминаю, что последовательность, предел которой равен нулю, называют бесконечно малой .

Следует отметить, что для последовательности уже нельзя сказать «бесконечный хвост зайдёт » – члены с нечётными номерами по факту равны нулю и «никуда не заходят» =) Именно поэтому в определении использован глагол «окажутся». И, разумеется, члены такой последовательности, как тоже «никуда не идут». Кстати, проверьте, будет ли число её пределом.

Теперь покажем, что у последовательности не существует предела. Рассмотрим, например, окрестность точки . Совершенно понятно, что нет такого номера, после которого ВСЕ члены окажутся в данной окрестности – нечётные члены всегда будут «выскакивать» к «минус единице». По аналогичной причине не существует предела и в точке .

Закрепим материал практикой:

Пример 1

Доказать что предел последовательности равен нулю. Указать номер , после которого, все члены последовательности гарантированно окажутся внутри любой сколь угодно малой -окрестности точки .

Примечание : у многих последовательностей искомый натуральный номер зависит от значения – отсюда и обозначение .

Решение : рассмотрим произвольную найдётся ли номер – такой, что ВСЕ члены с бОльшими номерами окажутся внутри этой окрестности:

Чтобы показать существование искомого номера , выразим через .

Так как при любом значении «эн» , то знак модуля можно убрать:

Используем «школьные» действия с неравенствами, которые я повторял на уроках Линейные неравенства и Область определения функции . При этом важным обстоятельством является то, что «эпсилон» и «эн» положительны:

Поскольку слева речь идёт о натуральных номерах, а правая часть в общем случае дробна, то её нужно округлить:

Примечание : иногда для перестраховки справа добавляют единицу, но на самом деле это излишество. Условно говоря, если и мы ослабим результат округлением в меньшую сторону , то ближайший подходящий номер («тройка») всё равно будет удовлетворять первоначальному неравенству.

А теперь смотрим на неравенство и вспоминаем, что изначально мы рассматривали произвольную -окрестность, т.е. «эпсилон» может быть равно любому положительному числу.

Вывод : для любой сколько угодно малой -окрестности точки нашлось значение . Таким образом, число является пределом последовательности по определению. Что и требовалось доказать .

К слову, из полученного результата хорошо просматривается естественная закономерность: чем меньше -окрестность – тем больше номер , после которого ВСЕ члены последовательности окажутся в данной окрестности. Но каким бы малым ни было «эпсилон» – внутри всегда будет «бесконечный хвост», а снаружи – пусть даже большое, однако конечное число членов.

Как впечатления? =) Согласен, что странновато. Но строго! Пожалуйста, перечитайте и осмыслите всё ещё раз.

Рассмотрим аналогичный пример и познакомимся с другими техническими приёмами:

Пример 2

Решение : по определению последовательности нужно доказать, что (проговариваем вслух!!!) .

Рассмотрим произвольную -окрестность точки и проверим, существует ли натуральный номер – такой, что для всех бОльших номеров выполнено неравенство:

Чтобы показать существование такого , нужно выразить «эн» через «эпсилон». Упрощаем выражение под знаком модуля:

Модуль уничтожает знак «минус»:

Знаменатель положителен при любом «эн», следовательно, палки можно убрать:

Перетасовка:

Теперь надо бы извлечь квадратный корень, но загвоздка состоит в том, что при некоторых «эпсилон» правая часть будет отрицательной. Чтобы избежать этой неприятности усилим неравенство модулем:

Почему так можно сделать? Если, условно говоря, окажется, что , то подавно будет выполнено и условие . Модуль может только увеличить разыскиваемый номер , и это нас тоже устроит! Грубо говоря, если подходит сотый, то подойдёт и двухсотый! В соответствии с определением, нужно показать сам факт существования номера (хоть какого-то), после которого все члены последовательности окажутся в -окрестности. Кстати, именно поэтому нам не страшнО финальное округление правой части в бОльшую сторону.

Извлекаем корень:

И округляем результат:

Вывод : т. к. значение «эпсилон» выбиралось произвольно, то для любой сколько угодно малой -окрестности точки нашлось значение , такое, что для всех бОльших номеров выполнено неравенство . Таким образом, по определению. Что и требовалось доказать .

Советую особо разобраться в усилении и ослаблении неравенств – это типичные и очень распространённые приёмы математического анализа. Единственное, нужно следить за корректностью того или иного действия. Так, например, неравенство ни в коем случае нельзя ослаблять , вычитая, скажем, единицу:

Опять же условно: если номер точно подойдёт, то предыдущий может уже и не подойти.

Следующий пример для самостоятельного решения:

Пример 3

Используя определение последовательности, доказать, что

Краткое решение и ответ в конце урока.

Если последовательность бесконечно велика , то определение предела формулируется похожим образом: точка называется пределом последовательности, если для любого, сколь угодно большого числа существует номер , такой, что для всех бОльших номеров , будет выполнено неравенство . Число называют окрестностью точки «плюс бесконечность» :

Иными словами, какое бы большое значение мы ни взяли, «бесконечный хвост» последовательности обязательно зайдёт в -окрестность точки , оставив слева лишь конечное число членов.

Дежурный пример:

И сокращённая запись: , если

Для случая запишите определение самостоятельно. Правильная версия в конце урока.

После того, как вы «набили» руку на практических примерах и разобрались с определением предела последовательности, можно обратиться к литературе по математическому анализу и/или своей тетрадке с лекциями. Рекомендую закачать 1-й том Бохана (попроще – для заочников) и Фихтенгольца (более подробно и обстоятельно) . Из других авторов советую Пискунова, курс которого ориентирован на технические ВУЗы.

Попытайтесь добросовестно изучить теоремы, которые касаются предела последовательности, их доказательства, следствия. Поначалу теория может казаться «мутной», но это нормально – просто нужно привыкнуть. И многие даже войдут во вкус!

Строгое определение предела функции

Начнём с того же самого – как сформулировать данное понятие? Словесное определение предела функции формулируется значительно проще: «число является пределом функции , если при «икс», стремящемся к (и слева, и справа) , соответствующие значения функции стремятся к » (см. чертёж) . Всё вроде бы нормально, но слова словами, смысл смыслом, значок значком, а строгих математических обозначений маловато. И во втором параграфе мы познакомимся с двумя подходами к решению данного вопроса.

Пусть функция определена на некотором промежутке за исключением, возможно, точки . В учебной литературе общепринято считают, что функция там не определена:

Такой выбор подчёркивает суть предела функции : «икс» бесконечно близко приближается к , и соответствующие значения функции – бесконечно близко к . Иными словами, понятие предела подразумевает не «точный заход» в точки, а именно бесконечно близкое приближение , при этом не важно – определена ли функция в точке или нет.

Первое определение предела функции, что неудивительно, формулируется с помощью двух последовательностей. Во-первых, понятия родственные, и, во-вторых, пределы функций обычно изучают после пределов последовательностей.

Рассмотрим последовательность точек (на чертеже отсутствуют) , принадлежащих промежутку и отличных от , которая сходится к . Тогда соответствующие значения функции тоже образуют числовую последовательность, члены которой располагаются на оси ординат.

Предел функции по Гейне для любой последовательности точек (принадлежащих и отличных от ) , которая сходится к точке , соответствующая последовательность значений функции сходится к .

Эдуард Гейне – это немецкий математик. …И не надо тут ничего такого думать, гей в Европе всего лишь один – это Гей-Люссак =)

Второе определение предела соорудил… да-да, вы правы. Но сначала разберёмся в его конструкции. Рассмотрим произвольную -окрестность точки («чёрная» окрестность) . По мотивам предыдущего параграфа, запись означает, что некоторое значение функции находится внутри «эпсилон»-окрестности.

Теперь найдём -окрестность, которая соответствует заданной -окрестности (мысленно проводим чёрные пунктирные линии слева направо и затем сверху вниз) . Обратите внимание, что значение выбирается по длине меньшего отрезка, в данном случае – по длине более короткого левого отрезка. Более того, «малиновую» -окрестность точки можно даже уменьшить, поскольку в нижеследующем определении важен сам факт существования этой окрестности. И, аналогично, запись означает, что некоторое значение находится внутри «дельта»-окрестности.

Предел функции по Коши : число называется пределом функции в точке , если для любой заранее выбранной окрестности (сколь угодно малой) , существует -окрестность точки , ТАКАЯ , что: КАК ТОЛЬКО значения (принадлежащие ) входят в данную окрестность: (красные стрелки) – ТАК СРАЗУ соответствующие значения функции гарантированно зайдут в -окрестность: (синие стрелки) .

Должен предупредить, что в целях бОльшей доходчивости я немного сымпровизировал, поэтому не злоупотребляйте =)

Короткая запись: , если

В чём суть определения? Образно говоря, бесконечно уменьшая -окрестность, мы «сопровождаем» значения функции до своего предела, не оставляя им альтернативы приближаться куда-то ещё. Довольно необычно, но опять же строго! Чтобы как следует проникнуться идеей, перечитайте формулировку ещё раз.

! Внимание : если вам потребуется сформулировать только определение по Гейне или только определение по Коши , пожалуйста, не забывайте о существенном предварительном комментарии: «Рассмотрим функцию , которая определена на некотором промежутке за исключением, возможно, точки » . Я обозначил это единожды в самом начале и каждый раз не повторял.

Согласно соответствующей теореме математического анализа, определения по Гейне и по Коши эквивалентны, однако наиболее известен второй вариант (ещё бы!) , который также называют «предел на языке »:

Пример 4

Используя определение предела, доказать, что

Решение : функция определена на всей числовой прямой кроме точки . Используя определение , докажем существование предела в данной точке.

Примечание : величина «дельта»-окрестности зависит от «эпсилон», отсюда и обозначение

Рассмотрим произвольную -окрестность. Задача состоит в том, чтобы по этому значению проверить, существует ли -окрестность, ТАКАЯ , что из неравенства следует неравенство .

Предполагая, что , преобразуем последнее неравенство:
(разложили квадратный трёхчлен )

Рассмотрим функцию %%f(x)%%, определенную, по крайней мере, в некоторой проколотой окрестности %%\stackrel{\circ}{\text{U}}(a)%% точки %%a \in \overline{\mathbb{R}}%% расширенной числовой прямой.

Понятие предела по Коши

Число %%A \in \mathbb{R}%% называют пределом функции %%f(x)%% в точке %%a \in \mathbb{R}%% (или при %%x%%, стремящемся к %%a \in \mathbb{R}%%), если, каково бы ни было положительное число %%\varepsilon%%, найдется положительное число %%\delta%%, такое, что для всех точек проколотой %%\delta%%-окрестности точки %%a%% значения функции принадлежат %%\varepsilon%%-окрестности точки %%A%%, или

$$ A = \lim\limits_{x \to a}{f(x)} \Leftrightarrow \forall\varepsilon > 0 ~\exists \delta > 0 \big(x \in \stackrel{\circ}{\text{U}}_\delta(a) \Rightarrow f(x) \in \text{U}_\varepsilon (A) \big) $$

Это определение называется определением на языке %%\varepsilon%% и %%\delta%%, предложено французским математиком Огюстеном Коши и используется с начала XIX века по настоящее время, поскольку обладает необходимой математической строгостью и точностью. — (a)%% с окрестностями %%\text{U}_\varepsilon (A), \text{U}_\varepsilon (\infty), \text{U}_\varepsilon (+\infty), \text{U}_\varepsilon (-\infty)%%, получим 24 определения предела по Коши.

Геометрический смысл

Геометрический смысл предела функции

Выясним, в чем заключается геометрический смысл предела функции в точке. Построим график функции %%y = f(x)%% и отметим на нем точки %%x = a%% и %%y = A%%.

Предел функции %%y = f(x)%% в точке %%x \to a%% существует и равен A, если для любой %%\varepsilon%%-окрестности точки %%A%% можно указать такую %%\delta%%-окрестность точки %%a%%, что для любого %%x%% из этой %%\delta%%-окрестности значение %%f(x)%% будет находиться в %%\varepsilon%%-окрестности точки %%A%%.

Отметим, что по определению предела функции по Коши для существования предела при %%x \to a%% не важно, какое значение принимает функция в самой точке %%a%%. Можно привести примеры, когда функция не определена при %%x = a%% или принимает значение, отличное от %%A%%. Тем не менее предел может быть равен %%A%%.

Определение предела по Гейне

Элемент %%A \in \overline{\mathbb{R}}%% называется пределом функции %%f(x)%% при %% x \to a, a \in \overline{\mathbb{R}}%%, если для любой последовательности %%\{x_n\} \to a%% из области определения, последовательность соответствующих значений %%\big\{f(x_n)\big\}%% стремится к %%A%%.

Определение предела по Гейне удобно использовать, когда возникают сомнения в существовании предела функции в данной точке. Если можно построить хотя бы одну последовательность %%\{x_n\}%% с пределом в точке %%a%% такую, что последовательность %%\big\{f(x_n)\big\}%% не имеет предела, то можно сделать вывод о том, что функция %%f(x)%% не имеет предела в этой точке. Если для двух различных последовательностей %%\{x»_n\}%% и %%\{x»»_n\}%%, имеющих одинаковый предел %%a%%, последовательности %%\big\{f(x»_n)\big\}%% и %%\big\{f(x»»_n)\big\}%% имеют различные пределы, то в этом случае также не существует предел функции %%f(x)%%. n n\pi\right)} \equiv 0%% и %%\lim\big\{f(x_n)\big\} = 0%%.

Затем возьмем сходящуюся к той же точке последовательность $$ x»_n = \left\{ \frac{2}{(4n + 1)\pi} \right\}, $$

для которой %%\lim{x»_n} = +0%%, %%f(x»_n) = \sin{\big((4n + 1)\pi/2\big)} \equiv 1%% и %%\lim\big\{f(x»_n)\big\} = 1%%. Аналогично для последовательности $$ x»»_n = \left\{-\frac{2}{(4n + 1)\pi} \right\}, $$

также сходящейся к точке %%x = 0%%, %%\lim\big\{f(x»»_n)\big\} = -1%%.

Все три последовательности дали разные результаты, что противоречит условию определения по Гейне, т.е. данная функция не имеет предела в точке %%x = 0%%.

Теорема

Определение предела по Коши и по Гейне эквивалентны.

Налогооблагаемая база заработной платы Определение

Что такое налогооблагаемая база заработной платы?

Налогооблагаемая база заработной платы — это максимальная сумма заработанного дохода, с которой работники должны платить налоги на социальное обеспечение. Как правило, валовая заработная плата работника будет равна налогооблагаемой базе заработной платы. Как правило, этим расчетом занимается работодатель и удерживает правильную сумму налогов с каждой зарплаты работника; тем не менее, работник по-прежнему несет ответственность за ежегодное указание налога в своей налоговой декларации. Налогооблагаемая база заработной платы также известна как база заработной платы социального обеспечения.

Ключевые выводы

• Налогооблагаемая база заработной платы — это максимальная сумма заработанного дохода, с которой работники должны платить налоги на социальное обеспечение.
• Налогооблагаемая база заработной платы также известна как база заработной платы социального обеспечения.
• В 2022 году максимальная сумма дохода, с которой налогоплательщики должны платить налог на социальное обеспечение, составляет 147 000 долларов США.
• Что касается налога на социальное обеспечение, то половину налога платит работодатель, а половину — работник.
• Некоторые агентства штата по безработице используют налогооблагаемую базу заработной платы для расчета налогов по безработице.

Понимание налогооблагаемой базы заработной платы

Ставка налога на социальное обеспечение составляет 12,4%. Половину налога, который составляет 6,2%, платит работодатель, а работник несет ответственность за уплату другой половины. Однако налог на социальное обеспечение применяется к доходам только до определенного предела. Заработная плата, оклады и бонусы, превышающие установленную максимальную сумму заработка, не подлежат налогообложению. Лимит корректируется ежегодно в зависимости от изменения индекса средней заработной платы по стране.

$147 000

Налогооблагаемая база заработной платы на 2022 год — максимальная сумма дохода, облагаемого налогом на социальное обеспечение.

Рассмотрим работника, Роба, который зарабатывает 85 000 долларов валового дохода и имеет 6,2% налога на социальное обеспечение, удерживаемого из его заработной платы. Федеральное правительство, по сути, получит от Роба 6,2% x 85 000 долларов = 5 270 долларов, чтобы помочь финансировать пенсионные пособия и пособия по инвалидности для пенсионеров. В некоторых случаях работник получает заработную плату, которая может быть классифицирована как превышение заработной платы. Избыточную заработную плату можно вычесть из валового дохода, чтобы налогооблагаемая база заработной платы была ниже валового дохода.

Например, предположим, что другая сотрудница, Сью, получает валовой доход в размере 175 000 долларов. Ставка налога на социальное обеспечение будет применяться только до налогооблагаемой базы заработной платы в размере 147 000 долларов США, что меньше ее валового дохода. Таким образом, Сью заплатит 6,2% x 147 000 долларов = 9 114 долларов в качестве своего взноса на счет социального обеспечения страны для пенсионеров и инвалидов.

Обратите внимание, что, хотя налог на социальное обеспечение применяется до налогооблагаемой базы заработной платы, налог Medicare в размере 2,9% не имеет такого ограничения; применяется на 100% дохода.

Налог на социальное обеспечение и налог на Medicare вместе известны как налоги на Федеральный закон о страховых взносах (FICA). 7,65% валового дохода, которые работник выплачивает им, указаны как налоги FICA в их платежной ведомости и в их годовой форме W-2.

Налог на пособие по безработице

Налогооблагаемая база заработной платы чаще всего используется в отношении налогов на социальное обеспечение, хотя она может применяться к любому подоходному налогу. Например, некоторые государственные агентства по безработице используют налогооблагаемую базу заработной платы для расчета налогов по безработице. Это налогооблагаемая база заработной платы для расчета государственного страхования по безработице в 2021 году:

• Alaska: $43,600
• California: $7,000
• Florida: $7,000
• Kentucky: $11,100
• New York: $11,800
• Ohio: $9,000
• Pennsylvania: $10,000
• Wyoming: $27,300
• Nevada: $33,400

У Американской ассоциации расчета заработной платы есть список налогооблагаемой базы заработной платы по страхованию от безработицы для всех штатов.

Как и налогооблагаемая база заработной платы для социального обеспечения, база налога на безработицу увеличивается каждый год или, в некоторых случаях, каждые несколько лет.

Освобождение от налогооблагаемой базы заработной платы

Даже если они включены в зарплату, некоторые распространенные виды компенсации полностью или в определенных пределах освобождаются от налогооблагаемой базы заработной платы. Они включают:

• Выплаты партнерам товарищества
• Заработная плата инвалидов
• Компенсационные выплаты работникам
• Компенсации, выплачиваемые несовершеннолетним членам семьи
• Страхование жизни
• Командировочные расходы
• Помощь в уходе за иждивенцами, образование, услуги планирования выхода на пенсию
• Выплаты некоторым лицам, не являющимся работниками
• Чаевые до 20 долларов в месяц

Закон о налоговых льготах, связанных с COVID, от 2020 г. откладывает срок уплаты доли налога на социальное обеспечение работников с заработной платы за четвертый квартал до периода, начинающегося 1 января 2021 г. и заканчивающегося 31 декабря 2021 г. 2021. Это относится к работникам, чья заработная плата по системе социального обеспечения за двухнедельный период выплаты заработной платы составляла менее 4000 долларов США.

Как указывается налогооблагаемая база заработной платы?

Налогооблагаемая база заработной платы работника ежегодно указывается в его форме W-2 (Отчет о заработной плате и налогах). Работодатели готовят W-2 ежегодно, отправляя копии как в IRS, так и работнику.

В форме 2021 года в поле 3, озаглавленном «Заработная плата по социальному обеспечению», по существу указана ваша налогооблагаемая база заработной платы: в нем указано, какая часть вашего заработка облагалась налогом на социальное обеспечение. В графе 4 указана сумма удержанного налога на социальное обеспечение.

Что делает фонд заработной платы социального обеспечения?

Налоги, взимаемые с заработной платы социального обеспечения, идут на финансирование выплат по социальному обеспечению, которые ежемесячно получают миллионы людей. Самыми известными из них являются пенсионные пособия, выплачиваемые лицам в возрасте 65 лет и старше. По состоянию на июнь 2021 года насчитывалось 46,7 миллиона пенсионеров и еще 2,9 миллиона иждивенцев, получавших в среднем 1555 долларов в месяц.

Около 8,1 миллиона рабочих-инвалидов и 1,4 миллиона их иждивенцев также получают пособия по социальному обеспечению — чеки в среднем составляют 1280 долларов в месяц.

Наконец, оставшиеся в живых умершие пенсионеры или инвалиды имеют право на все или некоторые льготы. В этой группе 5,9 миллиона американцев, которые в совокупности получают 7,3 миллиарда долларов.

Что такое налог FICA?

Сокращенный от Федерального закона о страховых взносах налог FICA – это налог, взимаемый с заработной платы и доходов. Составляя 7,65% от общей заработной платы работника, он фактически состоит из двух отдельных налогов: социального обеспечения (6,2%) и медицинской помощи (1,45%). Работник и работодатель вносят по половине налога FICA, который вычитается из каждой зарплаты.

Как облагаются налогом программы социального обеспечения и Medicare для самозанятых лиц?

Самозанятые лица (независимые подрядчики, индивидуальные предприниматели и т. д.) должны платить обе половины налогов на социальное обеспечение и медицинскую помощь — весь налог FICA в размере 15,3%. Он выплачивается из чистого дохода их бизнеса или суммы их доходов от самостоятельной работы после вычета расходов и убытков. В то время как ставка налога на социальное обеспечение и Medicare такая же, как и для наемных работников, самозанятые могут получить вычет в размере половины суммы в своих налоговых декларациях.

Учитывается ли социальное обеспечение в качестве дохода?

Да, для большинства людей социальное обеспечение считается доходом и, следовательно, облагается подоходным налогом. Точнее, это считается незаработанным доходом. Однако, платите ли вы на самом деле налоги, зависит от вашего общего валового дохода. В 2021 году до 50% дохода социального обеспечения облагается налогом для физических лиц с общим валовым доходом не менее 25 000 долларов США или пар, подающих совместную декларацию с совокупным валовым доходом не менее 32 000 долларов США. До 85% пособий по социальному обеспечению облагаются налогом для лица с совокупным валовым доходом не менее 34 000 долларов США или супружеской пары, подающей совместную декларацию с совокупным валовым доходом не менее 44 000 долларов США. (Эти суммы включают ваши выплаты пособий.)

С какого возраста социальное обеспечение больше не облагается налогом?

Теоретически, когда вы достигнете полного пенсионного возраста (около 66–67 лет, в зависимости от года вашего рождения), ваши пособия по социальному обеспечению могут не облагаться налогом. Но это только в том случае, если они являются вашим единственным источником дохода. В частности, если ваш общий валовой доход составляет 25 000 долларов США или выше (32 000 долларов США, если вы состоите в браке, подающем совместную декларацию), они облагаются налогом по вашей обычной ставке подоходного налога.

Как предел базовой заработной платы влияет на ваше социальное обеспечение

Когда вы работаете и зарабатываете деньги, вы платите налоги Социального обеспечения в пенсионную систему Социального обеспечения. Большинство людей платят налоги со всех доходов, которые они зарабатывают. Пособия по социальному обеспечению, которые вы получаете, затем рассчитываются на основе заработной платы, которую вы заработали и уплатили налоги в течение своей карьеры.

Некоторые люди, однако, не облагаются налогом на каждый доллар, который они зарабатывают, и они не получают кредит на всю свою заработную плату при расчете пособий. Это из-за предела базовой заработной платы.

Базовый предел заработной платы, который также называют налогооблагаемым максимумом, меняется почти каждый год. Важно понимать предел базовой заработной платы, поскольку он определяет как налоги, которые вы платите, так и максимальные пособия по социальному обеспечению, которые вы можете получить. В этом руководстве объясняется, что такое предел базовой заработной платы и как он влияет на ваше социальное обеспечение.

Источник изображения: Getty Images.

Каков предел базовой заработной платы?

Базовый предел заработной платы — это годовой предел суммы заработанного дохода, с которого вы платите налог на социальное обеспечение. Базовый предел заработной платы устанавливается ежегодно и корректируется с учетом изменения индекса средней заработной платы. Эта корректировка обеспечивает соответствие предела базовой заработной платы темпам роста заработной платы.

Базовый предел заработной платы также является годовым пределом суммы вашей заработной платы, которая учитывается при определении ваших пособий по социальному обеспечению. Размер вашего пособия по социальному обеспечению устанавливается на основе формулы, учитывающей средний доход, который вы зарабатывали за 35 лет, когда вы зарабатывали больше всего денег. Но если вы зарабатывали больше базового предела заработной платы, не вся ваша заработная плата учитывается при определении этого среднего показателя.

Если бы этого предела не существовало, то человек, зарабатывающий миллионы долларов в год, получал бы десятки тысяч долларов в месяц в виде пособий по социальному обеспечению.

Какова предельная базовая заработная плата?

Базовый предел заработной платы меняется каждый год. На 2019 год базовый предел заработной платы составляет 132 900 долларов США. Вы можете найти лимит базовой заработной платы за текущий год на веб-сайте Администрации социального обеспечения. В таблице ниже также показан предел базовой заработной платы за последние несколько лет.

Год	Базовый предел заработной платы
2012	110 100 долларов США
2013	113 700 долл. США
2014	117 000 долларов США
2015	118 500 долларов США
2016	118 500 долларов США
2017	127 200 долларов США
2018	128 400 долларов США
2019	132 900 долларов США

Источник таблицы: Администрация социального обеспечения.

Как лимит базовой заработной платы влияет на уплачиваемые вами налоги на социальное обеспечение?

Одна из основных причин, по которой предел базовой заработной платы важен, заключается в том, что он определяет максимальную сумму налогов на социальное обеспечение, которую вы платите. Это потому, что вы облагаетесь налогом только на заработную плату до предела базовой заработной платы.

В настоящее время существует налог на социальное обеспечение в размере 12,4% от заработной платы работника. Работники работодателей платят половину своего налога на социальное обеспечение, а работодатели платят другую половину. Это означает, что работники платят 6,2%, а работодатели — 6,2%.

Из-за предела базовой заработной платы существует максимальная сумма налога на социальное обеспечение, которую работник потенциально может платить каждый год. Поскольку предел базовой заработной платы в 2019 г.составляет 132 900 долларов США, максимальный налог на социальное обеспечение, который платит работник, составляет 8 239,80 долларов США. В приведенной ниже таблице показан максимальный размер налога на социальное обеспечение, подлежащий уплате каждый год, исходя из предела базовой заработной платы за соответствующий год.

Год	Максимальная задолженность по налогу на социальное обеспечение
2012	6 826,20 $
2013	7 049,40 $
2014	7 254,00 $
2015	7 347,00 $
2016	7 347,00 $
2017	7 886,40 $
2018	7 960,80 $
2019	8 239,80 $

Если ваш доход выше, эффективная ставка налога на социальное обеспечение ниже, поскольку вы не платите налоги со всей суммы заработка. Тот, кто зарабатывает 20 000 долларов и платит налог в размере 6,2% от всей своей заработной платы, фактически имеет ставку налога в размере 6,2%. Но тот, кто зарабатывает 300 000 долларов, заплатит максимум 8 239 долларов.0,80 налогов на 2019 год, поэтому его фактическая ставка налога на социальное обеспечение составит около 2,7466% от его общего дохода. Из-за этого многие люди утверждают, что налоги на социальное обеспечение являются регрессивными.

Как лимит базовой заработной платы влияет на налоги на социальное обеспечение, если вы работаете не по найму?

Как упоминалось выше, работодатели платят половину налога на социальное обеспечение в размере 12,4% для работников. Но те, кто работает не по найму, не имеют отдельного работодателя, чтобы покрыть половину своих налогов.

Самозанятые работники должны сами платить весь налог на социальное обеспечение в размере 12,4%. Тем не менее, предел базовой заработной платы по-прежнему применяется к ним, но максимальный налог на социальное обеспечение, который они платят каждый год, выше, поскольку они должны платить всю сумму самостоятельно. В приведенной ниже таблице показан максимальный размер налога на социальное обеспечение, который самозанятое лицо будет платить, исходя из предела базовой заработной платы за последние несколько лет.

Год	Максимальная задолженность по налогу на социальное обеспечение
2012	$13 652,40
2013	14 098,80 $
2014	14 508,00 $
2015	14 694,00 $
2016	14 694,00 $
2017	15 772,80 $
2018	15 921,60 $
2019	$16 479,60

Самозанятым работникам разрешается вычитать половину своего налога на социальное обеспечение. Это уменьшает налогооблагаемый доход на половину суммы уплачиваемых ими налогов на социальное обеспечение, что помогает компенсировать тот факт, что работодатели не берут на себя какую-либо часть стоимости налога.

Medicare не имеет предела базовой заработной платы

Налоги на социальное обеспечение разрешены в соответствии с Законом о федеральных страховых взносах, поэтому они называются налогами FICA. В дополнение к налогу на социальное обеспечение налог Medicare также является частью ваших налогов FICA.

Налоги Medicare идут на оплату страховки, доступной большинству пожилых людей в США после 65 лет. Текущая ставка налога на Medicare составляет 2,9%. Работодатели платят 1,45% налогов Medicare, а сотрудники платят 1,45%. Те, кто работает не по найму, должны сами платить весь налог Medicare в размере 2,9%. С налогом Medicare в размере 1,45% и налогом на социальное обеспечение в размере 6,2% общая ставка налога FICA, которую платит большинство работников, составляет 7,65% от дохода, а общая сумма налогов FICA, которую платит самозанятый работник, равна 15,3% от дохода. Самозанятые работники также могут вычитать половину налогов Medicare из своего дохода.

Medicare, однако, не имеет предела базовой заработной платы. Таким образом, работник с доходом, превышающим базовый предел заработной платы Социального обеспечения, будет платить налог Medicare со своего полного заработанного дохода, но будет платить налог Социального обеспечения только с части дохода. Существует также дополнительный налог Medicare в размере 0,9%, взимаемый с высокооплачиваемых лиц. Этот дополнительный налог применяется ко всей заработной плате свыше 200 000 долларов США для большинства статусов подачи налоговых деклараций: свыше 125 000 долларов США, если супружеская пара подает декларацию отдельно, или более 250 000 долл. США, если женатая подает декларацию совместно.

Как лимит базовой заработной платы влияет на ваши пособия по социальному обеспечению?

Предельная базовая заработная плата также влияет на пособие по социальному обеспечению, которое вы получаете как пенсионер. Это связано с тем, как рассчитываются пособия по социальному обеспечению. Чтобы рассчитать ваше пособие, Управление социального обеспечения:

• Просматривает всю вашу запись о доходах за всю вашу карьеру и корректирует вашу заработную плату за каждый год с учетом роста заработной платы. Индекс средней заработной платы по стране используется для корректировки вашей заработной платы с учетом роста.
• Суммирует вашу самую высокую заработную плату за 35 лет после поправки на рост заработной платы и разделит на 420 (количество месяцев за 35 лет работы), чтобы определить ваш средний индексированный месячный заработок (AIME).
• Предоставляет льготы, равные определенному проценту AIME. Ваши пособия равны 90% AIME до определенного уровня дохода, называемого точкой изгиба, плюс 32% AIME между первой и второй точкой изгиба, плюс 15% AIME выше второй точки изгиба.

Так как вы получаете кредит только на заработную плату, полученную до предела базовой заработной платы, это, очевидно, влияет на вашу среднюю заработную плату. Если ваша заработная плата с поправкой на инфляцию в 2019 году составляла 350 000 долларов США, и все 350 000 долларов США были учтены при определении вашей средней заработной платы, ваша средняя заработная плата, очевидно, была бы намного выше, чем если бы у вас было всего 132,9 доллара США. 00 учитываются в вашем среднем.

Предел базовой заработной платы определяет максимальное пособие по социальному обеспечению

Предел базовой заработной платы играет определяющую роль в максимальном размере пособия по социальному обеспечению, которое может получить получатель. Пенсионер будет получать максимальное пособие по социальному обеспечению только в том случае, если он или она зарабатывает и платит налоги с дохода, равного базовому пределу заработной платы, в течение полных 35 лет.

В приведенной ниже таблице указан максимальный месячный доход пенсионера, подавшего заявку на пособие в 2019 году, в зависимости от пенсионного возраста.

Возраст выхода на пенсию влияет на максимальное пособие, поскольку работники могут претендовать на пособие уже в 62 года, но получат меньшее пособие, если они подадут заявление на социальное обеспечение до достижения возраста, установленного законом как их полный пенсионный возраст. Работники также получают повышенные пособия, если они откладывают подачу заявления на социальное обеспечение после полного пенсионного возраста, до 70 лет, когда пособия больше не увеличиваются. Вы можете узнать больше об этом в нашем руководстве о том, как полный пенсионный возраст влияет на ваш доход социального обеспечения.

Пенсионный возраст	Максимальное ежемесячное пособие при выходе на пенсию в 2019 году
62	2 209 долл. США
65	2 757 долл. США
66	2 861 $
70	3770 долларов США

Источник таблицы: Администрация социального обеспечения.

Большинство людей не используют максимальное количество своих пособий по социальному обеспечению, потому что для этого вам придется зарабатывать столько денег в течение стольких лет. Даже если вы зарабатываете в конце своей карьеры на уровне или выше минимального предела заработной платы, вам необходимо было бы сделать это в начале своей профессиональной жизни, чтобы получать максимальную налогооблагаемую заработную плату за 35 лет.

Как определить, что вы достигли предела базовой заработной платы?

Если вы знаете свой доход за год, вы можете сказать, достигли ли вы предела базовой заработной платы или превышает ли ваш доход этот предел. Просто сравните заработанный вами доход, облагаемый налогом FICA, с пределом базовой заработной платы за год. Если ваш доход в 2018 году составлял 30 000 долларов, вы не достигнете предела базовой заработной платы. Если доход составлял 200 000 долларов, вы выше этого. Вы можете найти пределы базовой заработной платы за каждый год на веб-сайте социального обеспечения, где вы также увидите предел, необходимый для сравнения вашего дохода.

Налоги FICA рассчитываются на основе валовой заработной платы, но вы платите налоги FICA только с дохода, полученного от работы. Вы платите налоги FICA на заработную плату или оклад, а также на прибыль от самозанятости. Вы не платите налоги FICA на взносы работодателя в соответствующие пенсионные планы; компенсация некоторых командировочных расходов; страхование сотрудников; выплаты партнерам; или дистрибутивы S-корпорации. Инвестиционный доход также не облагается налогами FICA. Таким образом, доход из этих источников не учитывается, когда вы определяете, достигли ли вы предела базовой заработной платы, и не учитывается при определении размера вашего пособия по социальному обеспечению.

Вы также можете войти в свою учетную запись Social Security и просмотреть сведения о своих доходах. Посетите SocialSecurity.gov и выберите «Зарегистрироваться/Войти», чтобы создать учетную запись, или войдите в существующую учетную запись. После входа в систему выберите параметр «Просмотреть отчет о доходах», который находится на главной странице.

Источник изображения: Администрация социального обеспечения.

Вы увидите свой заработок за каждый отработанный год. Таблица состоит из трех столбцов и похожа на приведенную ниже, но с включенными доходами за многие годы (при условии, что вы работали не только в 2017 и 2018 годах).

Вы заметите, что есть столбец для налогооблагаемых доходов социального обеспечения, а также для налогооблагаемых доходов Medicare. Если ваш налогооблагаемый заработок по программе Medicare выше, чем ваш налогооблагаемый заработок Social Security, ваш доход превысил базовый предел заработной платы за год. Это означает, что вы не платили налоги на социальное обеспечение со своего полного заработанного дохода, и вы не будете учитывать полную стоимость своей заработной платы при определении среднего дохода, заработанного за всю вашу жизнь. Если ваш налогооблагаемый заработок по программе Medicare и налогооблагаемый заработок по социальному обеспечению совпадают, это означает, что ваш доход был равен или ниже предела базовой заработной платы, и вы уплатили налог на социальное обеспечение со всей заработанной суммы.

В приведенном выше образце таблицы работник заработал ниже минимального предела заработной платы Социального обеспечения в 2017 г., но превысил базовый предел заработной платы Социального обеспечения в 2018 г. Вы увидите эти столбцы для каждого года зарегистрированных доходов, начиная с самого начала. вашей карьеры, поэтому легко определить, на сколько лет вы превысили базовый предел заработной платы.

Что произойдет, если вы достигнете предела базовой заработной платы?

Налоги на социальное обеспечение удерживаются из вашей зарплаты, если вы получаете зарплату от работодателя. Это означает, что налоги, которые вы должны выплатить, вычитаются из вашей зарплаты вашим работодателем до того, как вы получите свою зарплату. Ваш работодатель отправляет деньги, удержанные из вашей зарплаты, вместе с частью налога работодателя на социальное обеспечение, непосредственно в IRS.

Как только ваша зарплата достигнет предела базовой заработной платы, ваш работодатель должен перестать удерживать деньги в счет налогов на социальное обеспечение. Таким образом, если у вас очень высокая зарплата и вы заработали 132 900 долларов за первые шесть месяцев 2019 года, вы достигнете предела базовой заработной платы в первой половине года. Ваш работодатель перестанет удерживать налог на социальное обеспечение из вашей зарплаты до конца года.

Если вы работаете не по найму, вы должны ежеквартально производить расчетные налоговые платежи, включая уплату налога на социальное обеспечение, а также других федеральных налогов и налогов штата. Ознакомьтесь с нашим руководством о том, как рассчитать предполагаемый налог, чтобы узнать больше о том, как это работает и сколько вы должны платить в течение рабочего года.

Что делать, если вы получаете доход из нескольких источников и достигаете предела базовой заработной платы?

Если вы работаете на нескольких работодателей, вы можете достичь предела базовой заработной платы без ведома каждого работодателя.

Допустим, вы зарабатываете 90 000 долларов у одного работодателя и 45 000 долларов у другого в течение первых девяти месяцев года. Совместив ваши две работы, вы превысили предел базовой заработной платы за год, но каждый отдельный работодатель не будет знать, что нужно прекратить удерживать налоги, потому что этот конкретный работодатель еще не выплатил вам доход сверх предела.

Когда это произойдет, вы можете запросить кредит в счет любых налогов, причитающихся за превышение суммы. Если вы не должны платить какие-либо налоги, вы можете запросить возврат избыточной суммы уплаченного вами налога на социальное обеспечение.

Следует ли изменить правила ограничения базовой заработной платы?

Социальное обеспечение сталкивается с нехваткой финансирования, и некоторые эксперты и политики утверждают, что правила, касающиеся предела базовой заработной платы, должны быть изменены, чтобы помочь укрепить программу.

Последний раз Конгресс корректировал правила ограничения базовой заработной платы в 1977. Во время этой последней корректировки политики установили предел базовой заработной платы, чтобы налог FICA взимался с 90% всей заработной платы. Предполагалось, что будущие увеличения предела базовой заработной платы будут увеличиваться ежегодно на основе среднего роста заработной платы.

Тем не менее, рост заработной платы работников с более высокими доходами опережает рост средней заработной платы, а это означает, что заработная плата выше предела заработной платы росла быстрее, чем в среднем. Результатом этого является то, что только около 82% совокупной заработной платы в настоящее время облагаются налогом FICA. Налоговая база социального обеспечения сократилась, что побудило некоторых утверждать, что повышение или отмена предела базовой заработной платы необходимы.

Если базовый предел заработной платы будет повышен или изменен, директивным органам необходимо будет определить, будут ли лица с более высоким доходом учитывать полную сумму налогооблагаемой заработной платы при определении их пенсионных пособий по социальному обеспечению. Это может привести к тому, что лица с более высоким доходом будут получать значительно большие пособия по социальному обеспечению, чем те, которые предусмотрены действующими правилами.

Некоторые законодатели предложили облагать больше заработной платы налогами без предоставления соответствующего увеличения пособий по социальному обеспечению. Это сделает программу пособий по социальному обеспечению более перераспределительной и прогрессивной, но коренным образом изменит характер социального обеспечения как заработанного пособия и потенциально ослабит поддержку программы.

Теперь вы понимаете, как лимит базовой заработной платы влияет на социальное обеспечение

Теперь вы лучше понимаете, как лимит базовой заработной платы влияет на ваше социальное обеспечение. Базовый предел заработной платы определяет максимальную сумму дохода, с которого вы платите налог на социальное обеспечение, и определяет максимальную годовую заработную плату, которая учитывается при определении суммы ваших пособий по социальному обеспечению.

Если вы хотите получать максимально возможное пособие по социальному обеспечению, вам необходимо иметь заработок, равный или превышающий базовый предел заработной платы в течение как минимум 35 лет вашей трудовой жизни. Несмотря на то, что это веха, которую большинство людей не достигают, получение дохода на уровне или выше минимального предела заработной платы в любой момент вашей карьеры увеличит получаемое вами пособие по социальному обеспечению и может стать целью, к которой вы хотите стремиться.

Что такое базовая заработная плата социального обеспечения?

Уплата налога на социальное обеспечение является проверенной временем традицией, если быть точным, с 1937 года. И работодатели, и работники платят налог. Но когда работник попадает в базовую заработную плату социального обеспечения, игра окончена для удержания и внесения налога.

Хотя ставка налога на социальное обеспечение обычно не меняется из года в год, изменяется налогооблагаемая база заработной платы социального обеспечения.

Читайте дальше, чтобы узнать больше о налоге на социальное обеспечение. Узнайте, какова ставка удержания, каков фонд заработной платы и, конечно же, база заработной платы.

Ваш 1-минутный обзор налога на социальное обеспечение

Налог на социальное обеспечение — это налог на заработную плату, который работодатели удерживают из заработной платы работников и вносят соответствующую часть. И налоги на социальное обеспечение, и налоги на Medicare составляют налог на заработную плату, известный как FICA.

Вот краткий обзор налогов на заработную плату и кто что платит:

• Федеральный подоходный налог: работник
• налог FICA: работник и работодатель
• Федеральный налог на безработицу: работодатель
)
• Подоходный налог штата (если применимо): Сотрудник
• Другие налоги штата (если применимо): Сотрудник
• Местный подоходный налог (если применимо): Сотрудник 

Закон о социальном обеспечении, который является законом, который начал программу, был подписан в 1935 году. Социальное обеспечение — это программа социального страхования. Администрация социального обеспечения является федеральным агентством, которое управляет программой.

Ставка налога на социальное обеспечение 

Удерживаемая ставка налога на социальное обеспечение составляет 6,2%. Вы должны удерживать 6,2% от заработной платы каждого работника. Взнос работодателя социального обеспечения также составляет 6,2%.

Допустим, работник получает 1000 долларов за каждую зарплату. Вы должны удержать 62 доллара (1000 долларов X 0,062) из ​​их заработной платы и заплатить дополнительно 62 доллара в качестве налога на социальное обеспечение.

Опять же, как Social Security, так и Medicare составляют налог FICA. Налог на медицинскую помощь составляет 1,45%. Таким образом, налог FICA составляет 7,65% для части работника и 7,65% для части работодателя (6,2% + 1,45%).

Что покрывает заработная плата социального обеспечения?

Налог на социальное обеспечение финансирует ряд вещей, включая пособия для:

• Пенсионеры
• Иждивенцы пенсионеров
• Иждивенцы инвалидов
• Оставшиеся в живых

По данным Управления социального обеспечения, пенсионеры получают среднее ежемесячное пособие по социальному обеспечению в размере 1514 долларов США. Работники-инвалиды получают среднее ежемесячное пособие в размере 1259 долларов.

Налоги на социальное обеспечение также идут на оплату администрирования программы. После выплаты пособий и административных расходов остается излишек. Федеральное правительство занимает оставшиеся деньги из фонда социального обеспечения. Правительство несет ответственность за выплату процентов по заемным средствам.

База заработной платы социального обеспечения 2022

Теперь о хорошем. Лимит удержания социального обеспечения.

Удерживать и вносить налоги социального обеспечения только до тех пор, пока работник не заработает выше базовой заработной платы. Будьте в курсе годовой базовой заработной платы Social Security, поскольку она обычно меняется каждый год.

Базовая заработная плата социального обеспечения на 2022 год составляет 147 000 долларов США.

После того, как работник заработает больше базовой годовой заработной платы, не удерживайте деньги для уплаты налогов на социальное обеспечение. И не вносите ничего другого.

Не все сотрудники будут зарабатывать больше удерживаемого лимита. Если работник не соответствует этой базовой заработной плате, продолжайте удерживать и вносить взносы круглый год.

Максимальный взнос на социальное обеспечение в 2022 году составляет 9 114 долларов (147 000 долларов X 0,062).

Если вы удерживаете более 9 114 долларов США (2022 г.), вы превысили базовую заработную плату и должны возместить расходы своему сотруднику.

Помните, что сумма, которую вы удерживаете за каждого сотрудника, зависит от его заработка.

Patriot’s Payroll избавляет от стресса, связанного с налогами на заработную плату

• Устранение необходимости ручных расчетов
• Попрощайтесь со случайным удержанием сверх базовой заработной платы социального обеспечения
• Наслаждайтесь бесплатной (и дружественной!) поддержкой в ​​США

Попробуйте бесплатно в течение 30 дней

Имеются ли другие налоги в качестве базы заработной платы?

Налог на социальное обеспечение является единственным федеральным налогом, который работники платят с базовой заработной платы.