Предел функции: основные понятия и определения
В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.
Понятие предела
В математике принципиально важным является понятие бесконечности, обозначаемое символом ∞. Его следует понимать как бесконечно большое +∞ или бесконечно малое -∞ число. Когда мы говорим о бесконечности, часто мы имеем в виду сразу оба этих ее смысла, однако запись вида +∞ или -∞ не стоит заменять просто на ∞.
Запись предела функции имеет вид limx→x0f(x). В нижней части мы пишем основной аргумент x, а с помощью стрелочки указываем, к какому именно значению x0 он будет стремиться. Если значение x0 является конкретным действительным числом, то мы имеем дело с пределом функции в точке. Если же значение x0 стремится к бесконечности (не важно, ∞, +∞ или -∞), то следует говорить о пределе функции на бесконечности.
Предел бывает конечным и бесконечным. Если он равен конкретному действительному числу, т.е. limx→x0f(x)=A, то его называют конечным пределом, если же limx→x0f(x)=∞, limx→x0f(x)=+∞ или limx→x0f(x)=-∞, то бесконечным.
Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.
Что такое предел функции
В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.
Определение 1Число A является пределом функции f(x) при x→∞, если последовательность ее значений будет сходиться к A для любой бесконечно большой последовательности аргументов (отрицательной или положительной).
Запись предела функции выглядит так: limx→∞f(x)=A.
Определение 2При x→∞ предел функции f(x) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).
Запись выглядит как limx→∞f(x)=∞.
Пример 1Докажите равенство limx→∞1×2=0 с помощью основного определения предела для x→∞.
Решение
Начнем с записи последовательности значений функции 1×2 для бесконечно большой положительной последовательности значений аргумента x=1, 2, 3,…, n,….
11>14>19>116>…>1n2>…
Мы видим, что значения будут постепенно уменьшаться, стремясь к 0. См. на картинке:
Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.
x=-1, -2, -3,…, -n,…
11>14>19>116>…>1-n2>…
Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:
Ответ: Верность данного в условии равенства подтверждена.
Пример 2Вычислите предел limx→∞e110x.
Решение
Начнем, как и раньше, с записи последовательностей значений f(x)=e110x для бесконечно большой положительной последовательности аргументов.
e110; e410; e910; e1610; e2510;…; e10010;…==1,10; 1,49; 2,45; 4,95; 12,18;…;22026,46;…
Мы видим, что данная последовательность бесконечно положительна, значит, f(x)=limx→+∞e110x=+∞
Переходим к записи значений бесконечно большой отрицательной последовательности, например, x=-1, -4, -9, -16,-25,…, -102,…→-∞.
e-110; e-410; e-910; e-1610; e-2510;…;e-10010;…==0,90; 0,67; 0,40; 0,20; 0,08;…;0,000045;…x=1, 4, 9, 16, 25,…,102 ,…→∞
Поскольку она тоже стремится к нулю, то f(x)=limx→∞1e10x=0.
Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными – отрицательных.
Ответ: limx→∞e110x=+∞, при x→+∞0, при x→-∞.
Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.
Число B является пределом функции f(x) слева при x→a в том случае, когда последовательность ее значений сходится к данному числу при любой последовательности аргументов функции xn, сходящейся к a, если при этом ее значения остаются меньше a (xn<a).
Такой предел на письме обозначается как limx→a-0f(x)=B.
Теперь сформулируем, что такое предел функции справа.
Определение 4Число B является пределом функции f(x) справа при x→a в том случае, когда последовательность ее значений сходится к данному числу при любой последовательности аргументов функции xn, сходящейся к a, если при этом ее значения остаются больше a (xn>a).
Этот предел мы записываем как limx→a+0f(x)=B.
Мы можем найти предел функции f(x) в некоторой точке тогда, когда для нее существуют равные пределы с левой и правой стороны, т.е. limx→af(x)=limx→a-0f(x)=limx→a+0f(x)=B. В случае бесконечности обоих пределов предел функции в исходной точке также будет бесконечен.
Теперь мы разъясним данные определения, записав решение конкретной задачи.
Докажите, что существует конечный предел функции f(x)=16(x-8)2-8 в точке x0=2 и вычислите его значение.
Решение
Для того чтобы решить задачу, нам потребуется вспомнить определение предела функции в точке. Для начала докажем, что у исходной функции имеется предел слева. Запишем последовательность значений фукнции, которая будет сходиться к x0=2, если xn<2:
f(-2); f(0); f(1); f112; f134; f178; f11516;…; f110231024;…==8,667; 2,667; 0,167; -0,958; -1,489; -1,747; -1,874;…; -1,998;…→-2
Поскольку приведенная последовательность сводится к -2, мы можем записать, что limx→2-016x-82-8=-2.
Далее докажем наличие предела справа: запишем аргументы в последовательности, которая будет сходиться к x0=2, если xn>2:
6, 4, 3, 212, 214, 218, 2116,…, 211024,…→2
Значения функции в этой последовательности будут выглядеть так:
f(6); f(4); f(3); f212; f234; f278; f21516;…; f210231024;…==-7,333; -5,333; -3,833; -2,958; -2,489; -2,247;-2,124;.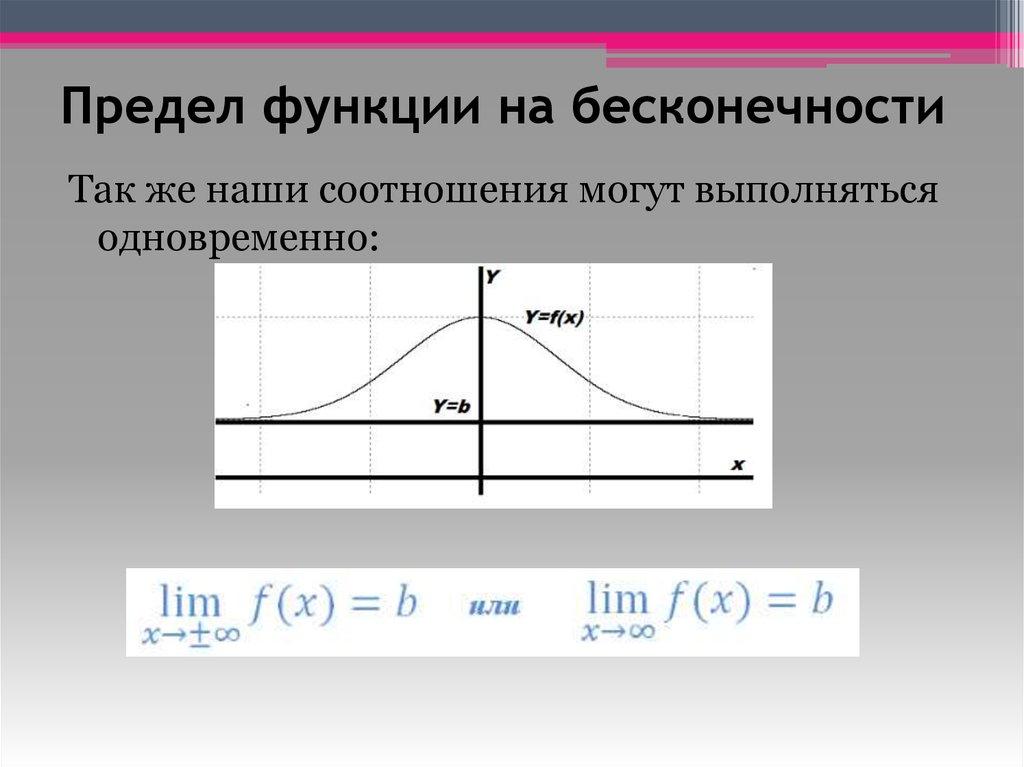
.., -2,001,…→-2
Данная последовательность также сходится к -2, значит, limx→2+016(x-8)2-8=-2.
Мы получили, что пределы с правой и левой стороны у данной функции будут равными, значит, предел функции f(x)=16(x-8)2-8 в точке x0=2 существует, и limx→216(x-8)2-8=-2.
Вы можете увидеть ход решения на иллюстрации (зеленые точки– последовательность значений, сходящаяся к xn<2, синие – к xn>2).
Ответ: Пределы с правой и левой стороны у данной функции будут равными, значит, предел функции существует, и limx→216(x-8)2-8=-2.
Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики.
Навигация по статьям
Предыдущая статья
Метод трапеций
Следующая статья
Интегрирование тригонометрических функций
- Второй замечательный предел
- Основные неопределенности пределов и их раскрытие
- Первый замечательный предел
- Предел показательно степенной функции, примеры нахождения
- Все темы по математике
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Узнать подробнее
Программирование нейронных сетей
Вид работы:
Курсовая работа
Выполнена:
31 мая 2022 г.
Стоимость:
4 800 руб
Заказать такую же работу
Автоматизированое проэктирование Поперечный разрез здания фасад здания
Вид работы:
Практическая работа
Выполнена:
23 мая 2022 г.
Стоимость:
3 000 руб
Заказать такую же работу
Гидравлика и противопожарное водоснабжение
Заказать такую же работу
Управление социльно техническими системами
Вид работы:
Контрольная работа
Выполнена:
13 февраля 2022 г.
Стоимость:
1 900 руб
Заказать такую же работу
Сделать расчеты работу закрепил С пункта по пункт
Вид работы:
Курсовая работа
Выполнена:
8 февраля 2022 г.
Стоимость:
4 800 руб
Заказать такую же работу
Тема в методичке
Вид работы:
Контрольная работа
Выполнена:
28 января 2022 г.
Стоимость:
1 300 руб
Заказать такую же работу
Смотреть все работы по основам программирования
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Пределы в бесконечности: правила, комплекс и график
Вы становитесь больше или приближаетесь к тому, на что смотрите? Перспектива может изменить все! В этой статье вы увидите, что происходит, когда входные данные функции становятся достаточно большими.
Оценка пределов в бесконечности
Знаете ли вы, что существует несколько способов думать о бесконечных пределах и оценивать их? Один из способов — это то, что происходит, когда вы получаете вертикальную асимптоту. Для получения дополнительной информации о таком бесконечном пределе см. разделы «Односторонние пределы» и «Бесконечные пределы».
Другой вид бесконечного предела — это размышления о том, что происходит со значениями функции \(f(x)\), когда \(x\) становится очень большим, и это то, что исследуется здесь с использованием определения, полезных правил и графиков. . Итак, читайте дальше, чтобы узнать, как оценивать пределы на бесконечности!
Определение предела в бесконечности
Помните, что символ \(\infty\) не представляет действительное число. Вместо этого он описывает поведение значений функции, которые становятся все больше и больше, точно так же, как \(-\infty\) описывает поведение функции, которая становится все более и более отрицательной.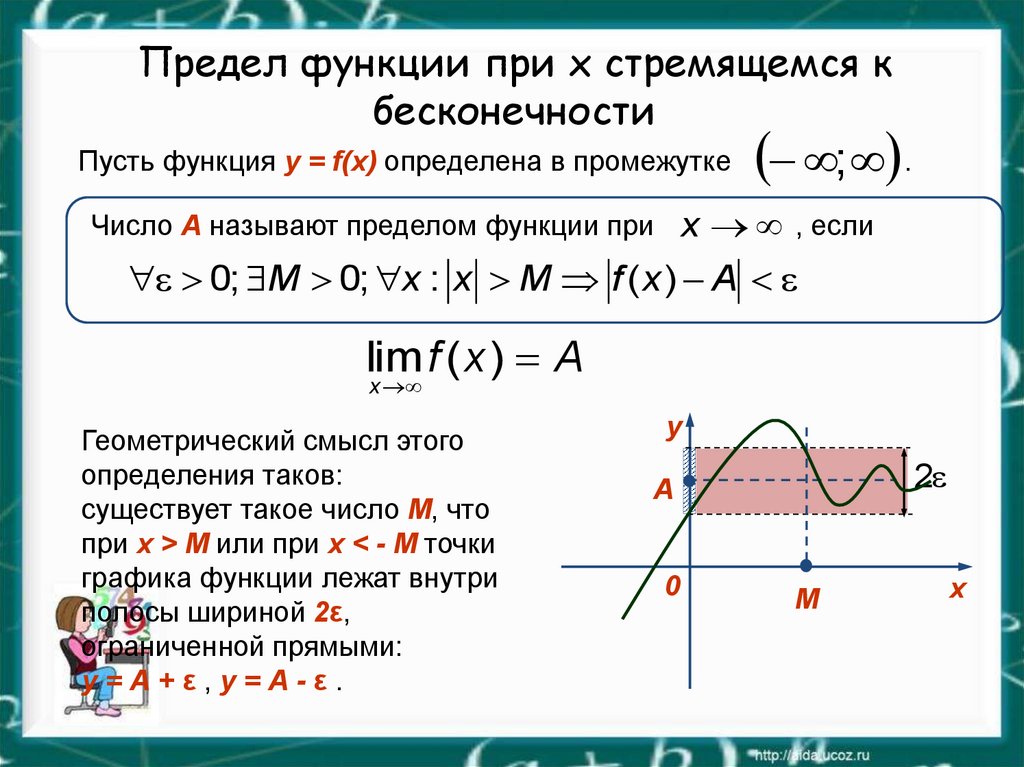
Итак, если вы видите
\[\lim_{x\to\infty}f(x)=L,\]
не думайте, что вы можете использовать \(\infty\) как значение функции! Написание предела таким образом — это просто сокращение, чтобы дать вам лучшее представление о том, что делает функция. Итак, сначала давайте посмотрим на определение, а затем на пример.
Мы говорим, что функция \(f(x)\) имеет предел на бесконечности , если существует действительное число \(L\) такое, что для всех \(\epsilon > 0\) существует \(N >0\) такое, что
\[|f(x)-L|<\epsilon\] 9{-x}+1,\) и решить, существует ли
\[\lim_{x\to\infty}f(x)=L \]
.
Решение
Сначала посмотрим на график функции. Из того, что вы знаете об экспоненциальных функциях (см. Экспоненциальные функции), хорошим кандидатом на предел является \(L=1\). Итак, на том же графике, что и функция, нарисуйте линии \(y=1\), \(y=1-\epsilon\) и \(y=1+\epsilon\). Хотя вы точно не знаете, какое значение имеет \(\epsilon\), вы знаете, что это небольшое положительное число.
График функции для нахождения предела на бесконечности
Итак, вы можете видеть, что для приведенного выше графика, пока \(x>4\) график \(f(x)\) заперт между линиями \ (у=1-\эпсилон\) и \(у=1+\эпсилон\). Но что произойдет, если у вас есть еще меньшее значение \(\epsilon\)?
На приведенном ниже графике есть исходные линии, но теперь есть две дополнительные линии, \(y=1-\epsilon_{1}\) и \(y=1+\epsilon_{1}\), где \(\epsilon_{1}\) — это некоторое число, меньшее, чем \(\epsilon\).
График с меньшим значением эпсилон для нахождения предела на бесконечности
Как видно из графика выше, с этим меньшим значением \(\эпсилон_{1}\) нужно взять \(x>7\ ), чтобы убедиться, что функция находится между \(y=1-\epsilon_{1}\) и \(y=1+\epsilon_{1}.\)
Обычно значение \(N\) вы find будет зависеть как от функции, так и от значения \(\epsilon\), и поскольку вы берете меньшие значения \(\epsilon\), вам потребуется большее значение для \(N\).
9{-x}+1=1.\] Теперь может случиться так, что предел как \(x\to\infty\) не существует.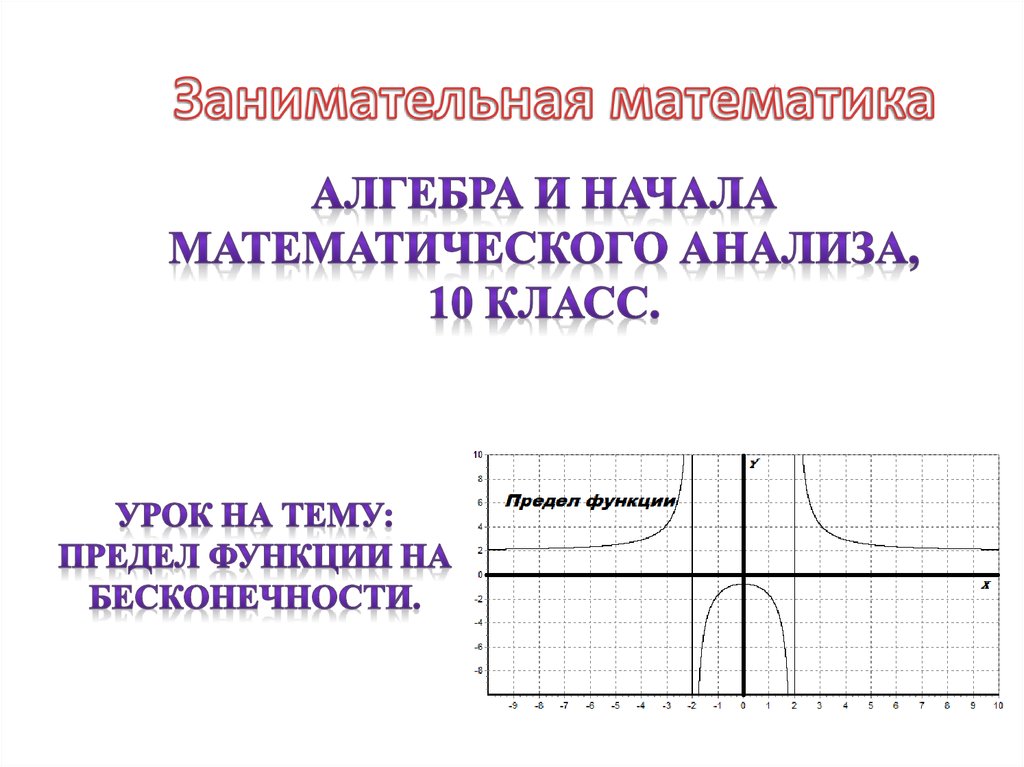
Рассмотрим функцию \(f(x)=\sin x\) . Существует ли
\[\lim_{x\to\infty}f(x)\]
?
Решение
Первое, что вам нужно сделать, если вы хотите найти предел, это выбрать кандидата на значение предела \(L\). Но если вы попытаетесь выбрать одно значение для \(L\), скажем, \(L=1\), вы всегда найдете значения функции для \(f(x)=\sin (x)\), которые превышают \ (\dfrac{1}{2}\) от \(L\), потому что функция синуса колеблется между \(-1\) и \(1\). На самом деле, для любого \(L\), который вы пытаетесь выбрать, колебание синусоидальной функции всегда будет проблемой. Так
\[\lim_{x\to\infty} \sin x\]
не существует.
Иногда при \(x\to \infty\) значения функции продолжают увеличиваться, как в случае с функцией \(f(x)=x\). Так как это происходит со многими функциями, для этого поведения существует специальное определение.
Мы говорим, что функция \(f(x)\) имеет бесконечный предел на бесконечности , и пишем
\[\lim_{x\to\infty}f(x)=\infty,\]
если для всех \(M>0\) существует \(N>0\) такое, что \(f(x)>M\) для всех \(x>N.
\)
Это не то же самое, что сказать, что предел существует или что функция на самом деле «упирается» в бесконечность. Запись
\[\lim_{x\to\infty}f(x)=\infty\]
— это просто сокращение для того, чтобы сказать, что функция становится все больше и больше, когда вы берете \(x\), чтобы стать больше и больше.
Возьмем функцию \(f(x)=\sqrt{x}\) и покажем, что
\[\lim_{x\to\infty}f(x)=\infty.\]
Решение
Чтобы показать, что предел бесконечен, возьмем фиксированное \(M>0\). Вы хотите, чтобы \(x>N\) означало, что \(f(x)>M\), или, другими словами, что \(\sqrt{x}>M\). 92}=M,\]
, и все это верно, потому что вы знаете, что \(N\) и \(M\) положительны. Таким образом, вы показали, что
\[\lim_{x\to\infty}f(x)=\infty.\]
Пределы на отрицательной бесконечности
Подобно пределу на бесконечности, вы можете определить предел на отрицательной бесконечность.
Мы говорим, что функция \(f(x)\) имеет предел на отрицательной бесконечности , если существует действительное число \(L\) такое, что для всех \(\epsilon>0\) существует \( N>0\) такой, что
\[|f(x)-L|<\epsilon\]
для всех \(x<-N\), и мы пишем
\[\lim_{x\to -\infty}=L.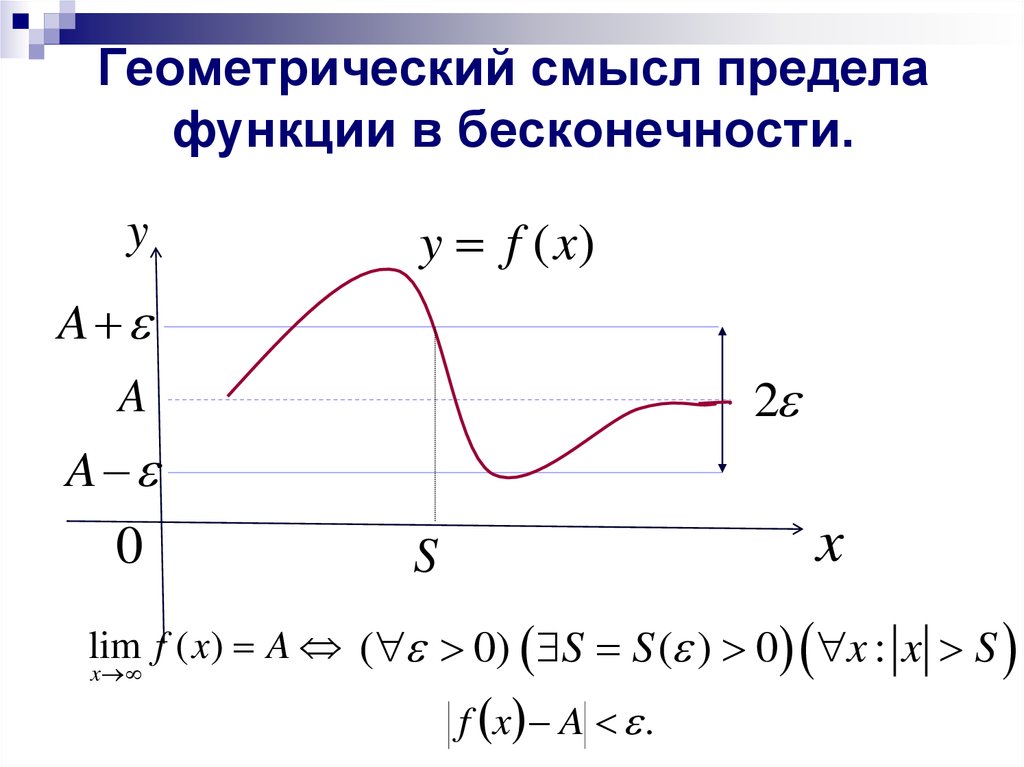
\]
Вы также можете определить функцию, имеющую предел в бесконечности, равный отрицательной бесконечности. Обратите внимание, что это очень похоже на определение выше.
Мы говорим, что функция \(f(x)\) имеет отрицательный бесконечный предел на бесконечности , и пишем
\[\lim_{x\to\infty}f(x)=-\infty, \]
, если для всех \(M>0\) существует \(N>0\) такое, что \(f(x)<-M\) для всех \(x>N.\)
Конечно, то, что вы можете сделать для положительного направления, вы можете сделать и для отрицательного.
Мы говорим, что функция \(f(x)\) имеет бесконечный предел на отрицательной бесконечности , и пишем
\[\lim_{x\to-\infty}f(x)=\infty,\]
если для всех \(M>0\) существует \(N>0\) такое, что \(f(x)>M\) для всех \(x<-N.\)
И, наконец, отрицательный бесконечный предел на отрицательной бесконечности.
Мы говорим, что функция \(f(x)\) имеет отрицательных бесконечный предел на отрицательной бесконечности , и напишите
\[\lim_{x\to -\infty} f(x)=-\infty,\]
, если для всех \(M>0\) существует такое \(N>0\), что \(f(x)<-M\) для всех \(x<-N.
\)
Нахождение бесконечного предела по графу
Иногда бывает очень полезно постройте график функции и посмотрите на таблицу значений при попытке найти бесконечный предел. Это особенно верно, когда у вас может быть не очень хорошее представление о том, как выглядит функция.
С помощью функции
\[f(x)=\frac{1}{x}\sin x,\]
найти
\[\lim_{x\to\infty} f(x).\ ]
Решение
Сначала сделайте график функции и таблицу значений функции. На графике ниже вы можете увидеть точки в таблице, нанесенные на функцию.
Использование графика для нахождения бесконечного предела
Из таблицы и графика видно, что значения функции приближаются к нулю как \(x\to \infty\), но вы можете не быть в этом уверены. Так как это ищет предел в бесконечности, а не график от \(x=0\) вправо, вместо этого начните с большего значения \(x\) для лучшего просмотра.
Начиная с большего значения x для лучшего обзора
Сдвигая окно графика, становится намного легче увидеть, что значения функции приближаются к нулю как \(x\to\infty\).
Теперь вы можете сказать, что
\[\lim_{x\to\infty}f(x)=0.\]
Давайте рассмотрим другой пример.
При поиске предела на бесконечности важно сочетать графики и таблицы. Например, если вы возьмете функцию \(f(x)=\sin x,\), вы можете составить следующую таблицу значений,
| \(x\) | \(\sin x\) |
| \(0\) | \(0\) |
| ) 0\) | |
| \(100 \pi\) | \(0\) |
| \(1000 \pi \) | \(0\) | что предел на бесконечности равен нулю. Однако, если вы нарисуете функцию, вы увидите, что \(f(x)=\sin x\) продолжает колебаться независимо от того, насколько большими вы берете значения \(x\). Таким образом, просто просмотр таблицы может ввести в заблуждение, если вы не будете осторожны в выборе значений \(x\), которые вы в нее введете. Зная, что вы делаете с функцией синуса, вы можете с уверенностью сказать, что \[\lim_{x\to\infty}\sin x\] не существует. Обзор поведения функции синуса см. в разделе Тригонометрические функции. Примеры бесконечных пределовСуществует специальное название для случаев, когда существует предел на бесконечности или предел на отрицательной бесконечности функции. Если \[\lim_{x\to\pm\infty}f(x)=L,\] , где \(L\) — действительное число, то мы говорим, что строка \(y=L \) является горизонтальной асимптотой для \(f(x)\). Вы уже видели примеры функций с горизонтальными асимптотами в исчислении, это просто дает вам точное математическое определение. Давайте посмотрим на пример. 93}.\end{align}\] Используя то, что вы знаете о полиномах, вы можете видеть, что на самом деле эта функция обладает тем свойством, что \[\lim_{x\to\infty}f(x)=5 ,\] и что \[\lim_{x\to-\infty}f(x)=5,\] , поэтому эта функция имеет \(y=5\) в качестве горизонтальной асимптоты. Обзор поведения полиномиальных функций см. в разделе Полиномиальные функции. Правила пределов в бесконечностиПодобно законам пределов, существуют свойства пределов, которые полезно знать, когда вы смотрите на \(x\to\infty\). Предположим, что \(L\), \(M\) и \(k\) — вещественные числа, причем \(f\) и \(g\) — такие функции, что \[\lim_{x \to\pm\infty}f(x)=L\quad \text{and}\quad \lim_{x\to\pm\infty}g(x)=M.\] Тогда верно следующее, Правило суммы. \[\lim_{x\to\pm\infty}(f(x)+g(x))=L+M.\] Правило разницы . \[\lim_{x\to\pm\infty} (f(x)-g(x))=L-M.\] Правило продукта . \[\lim_{x\to\pm\infty}(f(x)\cdot g(x))=L\cdot M.\] Постоянное множественное правило. \[\lim_{x\to\pm \infty}k\cdot f(x)=k\cdot L.\] Частное правило. Если \(M\neq 0\), то \[\lim_{x\to\pm\infty}\frac{f(x)}{g(x)}=\frac{L}{M} .\] Силовое правило. Можете ли вы применить приведенное выше правило частных, чтобы найти \[\lim_{x\to\infty}\dfrac{5x+\sin x}{x}? \] Решение Если вы попытаетесь взять \(f(x)=5x+\sin x\) и \(g(x)=x\), то обе эти функции имеют бесконечный предел на бесконечности , поэтому вы не можете применить правило частного. Вместо этого вы можете сначала сделать небольшую алгебру, \[\begin{align} \frac{5x+\sin x}{x} &=\frac{5x}{x}+\frac{1}{x}\ sin x\\ &=5+\frac{1}{x}\sin x. \конец{выравнивание}\] Если взять \(f(x)=5\) и \(g(x)=\frac{1}{x}\sin x\), то из приведенной выше работы известно, что \[\lim_{ x\to\infty}f(x)=\lim_{x\to\infty}5=5,\] и \[\lim_{x\to\infty}\frac{1}{x} \sin(x)=0,\] , так что вы можете использовать правило суммы, чтобы получить это, \[\begin{align} \lim_{x\to\infty}\frac{5x+\sin x}{ x} &=\lim_{x\to\infty}5+\lim_{x\to\infty}\frac{1}{x}\sin x \\ &=5+0\\ &=5. Так что нет, вы не можете использовать правило частного, но вы можете использовать немного алгебры, а затем правило суммы, чтобы найти предел. Один из наиболее важных результатов о пределах, Теорема сжатия, также верен для пределов на бесконечности. Теорема сжатия для пределов в бесконечности. Предположим, что \[g(x)\le f(x)\le h(x),\] и \[\lim_{x\to\pm\infty}g(x)= \lim_{x\to\pm\infty}h(x)=L,\] затем \[\lim_{x\to\pm\infty}f(x)=L.\] Примечание что на самом деле важно только то, что \(g(x)\le f(x) \le h(x)\) верно для очень больших значений \(x\), если вы пытаетесь найти предел как \(x \to\infty\), или что это верно для очень отрицательных значений, если вы пытаетесь найти предел как \(x\to -\infty.\) 92)+3\sin x-\cos x}{x}=0.\] Пределы тригонометрических функций на бесконечности Вы можете задаться вопросом о пределах тригонометрических функций. В разделах выше есть примеры с функциями синуса и косинуса. Бесконечные пределы — ключевые выводы
|
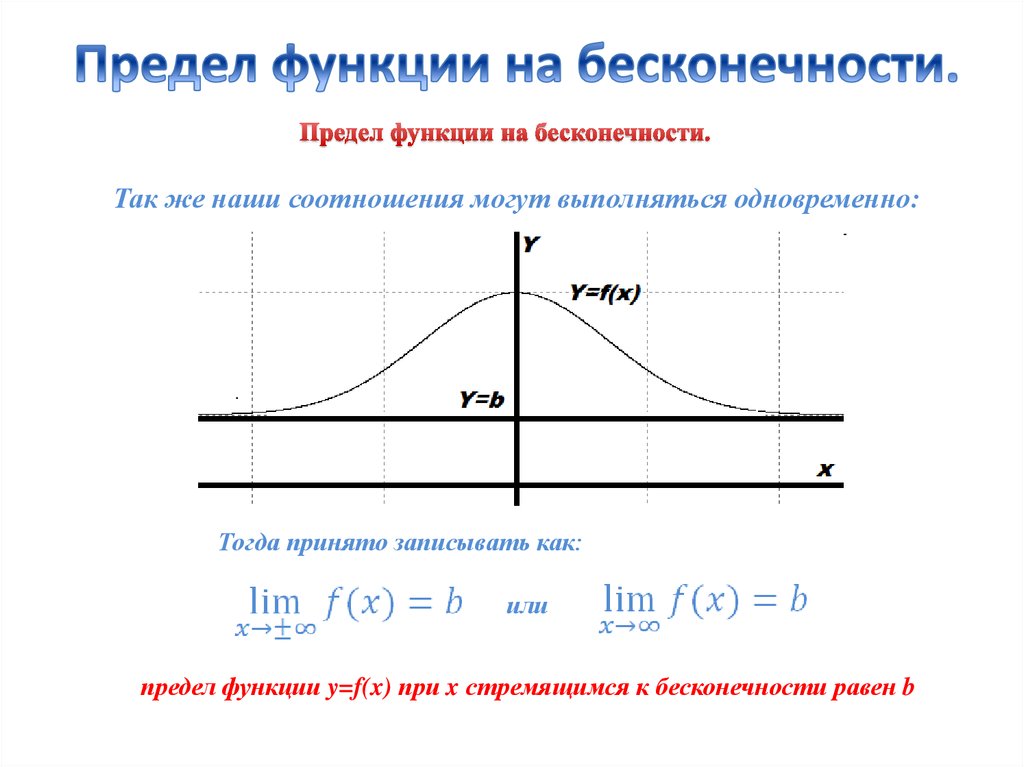
r\) определено для всех \(x>0\), то 9г}\\ &=0. \end{align}\]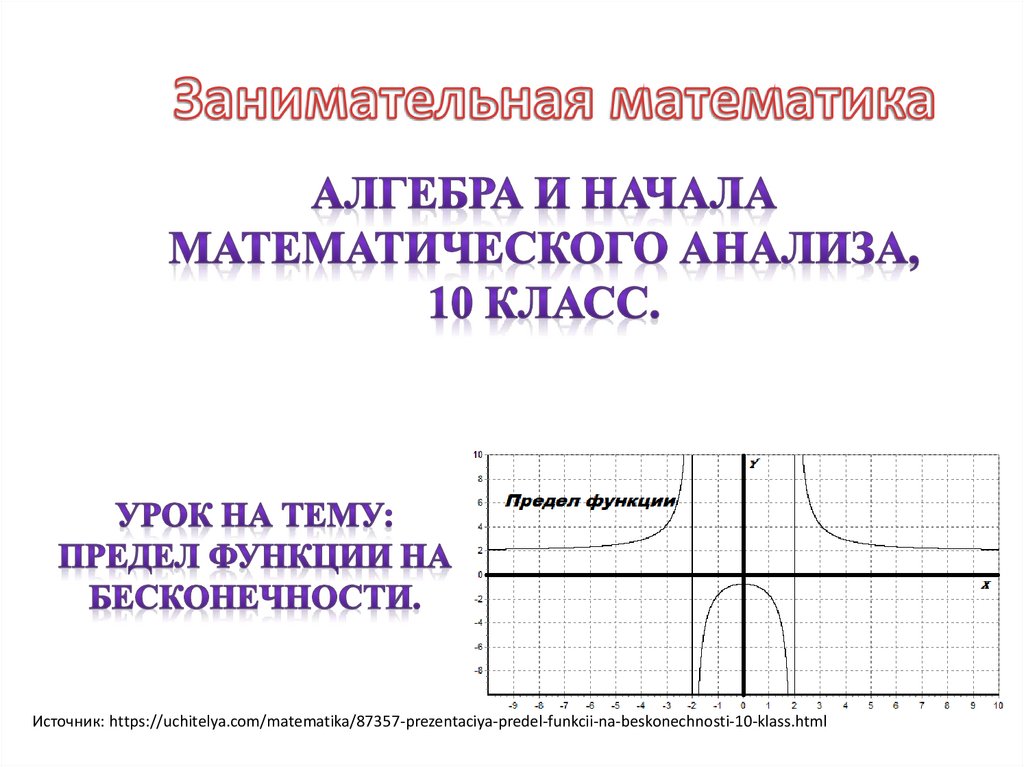
Если \(r,s\in\mathbb{Z}\), где \(s\neq 0\), то
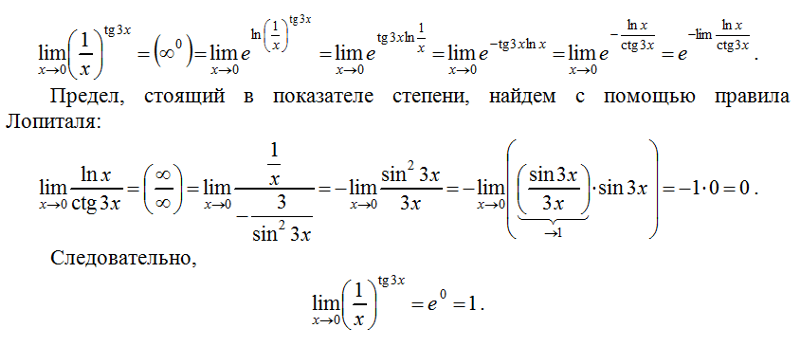\end{align}\]
Те же концепции могут быть применены к любой триггерной функции, обратной триггерной функции или гиперболической триггерной функции. Дополнительные сведения и примеры см. в статьях Тригонометрические функции, Гиперболические функции, Обратные функции и Обратные тригонометрические функции.