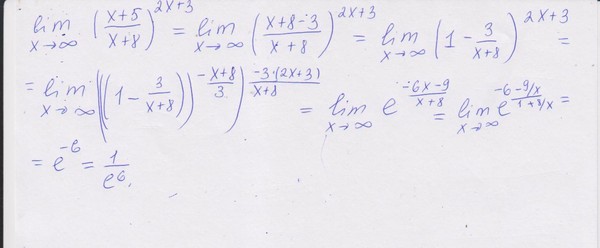39.Косячный!!!Определение предела функции и его свойства.
Определение предела функции. Пусть функция у = f(х) определена в некоторой точке а, кроме, может быть, самой этой точки.
Число b называется пределом функции f(х) при х стремящемся к а, если для любого сколь угодно малого, наперед заданного ε>0 существует такое δ>0, что для всех х таких, что |х-а|<δ выполняется неравенство |f(x) — b|<ε.
x→a
В компактном виде это определение можно записать lim f(x) = b.
(lim – сокращенное слово limit(предел)).
Читается так: предел f(x) при х стремящемся к а равен b.
При отыскании предела мы не учитываем значение функции в самой точке а, оно может быть любым.
1. Предел суммы двух функций равен сумме пределов.
х→а
х→а
х→а
lim (f(x) + φ(x)) = lim f(x) + lim φ(x)
2.
Предел произведения двух функций равен
произведению пределов.
х→а
х→а
х→а
lim [f(x) * φ(x)] = lim f(x) * lim φ(x)
3. Предел произведения числа на функцию равен произведению числа на предел функции.
х→а
х→а
lim С*f(x) = С *lim f(x)
Это свойство можно записать так: постоянный множитель выносится за знак предела.
4. Предел отношения двух функций равен отношению пределов этих функций. (Кроме случая, когда знаменатель стремиться к нулю).
х→а
х→а
х→а
х→а
lim f(x) / φ(x) = lim f(x) / lim φ(x), limφ(х)≠0.
№ 40 Теорема о сущности пределов
Теорема 1. если числовая последовательность Аn монотонна и ограниченна, то она имеет предел . возможны два случая а) последовательность неубывающая и ограничена сверху б) последовательность невозрастающая и ограничена снизу
Теорема 2.
Если в некоторой окрестности точки х
нулевое (или при достаточно больших
значениях х) функция эф от икс заключена
между двумя функциями фи от икс и пси
от икс, имеющих одинаковый предел А при
х ->x0
то функция эф от икс имеет тот же предел
А.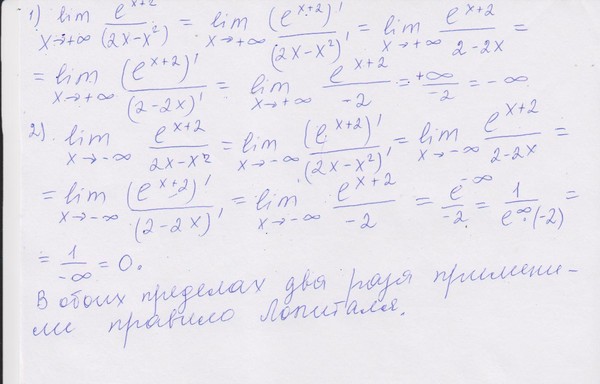
№ 41 Предел функции в бесконечности.
Предел функции в бесконечности. С понятием предела числовой последовательности а n = f(n) тесно связано понятие предела функции у = f(х) в бесконечности. Если в первом случае переменная n, возрастая, принимает лишь целые значения, то во втором случае переменная х , изменяясь, принимает любые значения..
Определение. Число А называется пределом функции у = f(х) при х , стремящимся к бесконечности, если для любого даже сколь угодно малого положительного числа ε > 0 найдется такое положительное число S>0 ( зависящее от ε ; S=S(ε)) , что для всех х, таких, что >S, верно неравенство:
< ε
(6.3)Этот предел функции обозначается limf(x) = A при х -> бесконечности,или f(x)->A при x-> бесконечности. Смысл определения остается тем же, что для предела числовой последовательности: при достаточно больших по модулю значениях х значения функции f(x) как угодно мало отличаются от числа А (по абсолютной величине)
Выясним геометрический
смысл предела функции у = f(х)
в бесконечности.
Неравенство 6.3
< ε равносильно двойному неравенству А-е <f(x)<A+e ,соответствующему расположению части графика в полосе шириной 2е (рис.6.3.)
Итак, число А есть предел функции у=f(x) при x->бесконечности, если для любого e>0
Найдется такое число S>0, что для всех х, таких что >S, соответствующие ординаты графика функции будут заключены в полосе А-е меньше у меньше А+е, какой бы узкой эта полоса не была.
Билет 42 Основные теоремы о пределах
Предположим, что все данные величины (слагаемое, сомножители, делимое и делитель) зависят от одного и того же аргумента х и обладают конечными пределами (при x →a). Обозначим так же некоторые функции y1 = f1(x), y2 = f2(x), …., yn = fn(x). Тогда: Теорема 1Предел суммы неизменного числа слагаемых равен сумме пределов отдельных слагаемых.
Теорема
2Предел
произведения неизменного числа
сомножителей равен произведению их
пределов.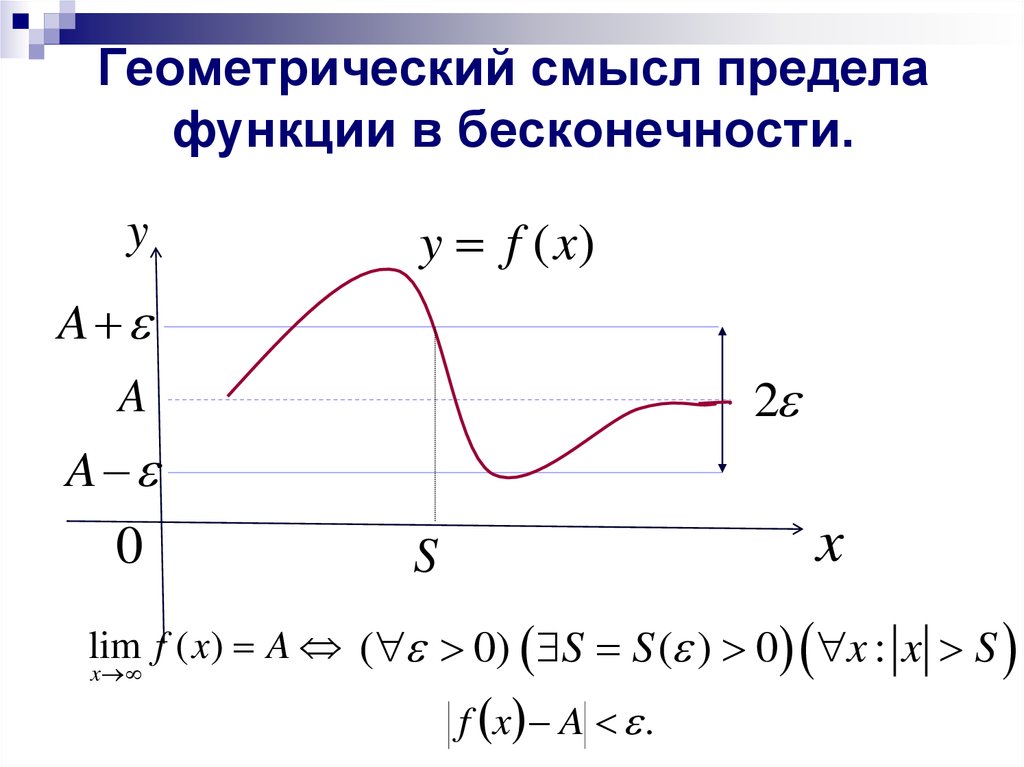
Теорема 3Постоянный множитель можно вынести за знак предела. Теорема 4Предел частного равен частному пределов, если предел делителя не равен нулю.
Например, f(x) = (x2-4)/(x-2) — оба односторонних предела в точке х = 2 равны 4. Но в самой точке х = 2 функция неопределенна и потому разрывна. График этой функции есть прямая y = x+2, с «выколотой» точкой М(2,4). (Точка разрыва второго рода.)Теорема 5. Если функция f(x) имеет конечный предел при ха, то она ограничена вблизи точки х = а. Доказательство. Пусть , т.е. , тогда
или
, т.е.
где М = + А
билет43 теорема о сжатой переменной
теорема о сжатой
переменной. n>N1 Xn³Zn³Yn $ limXn = lim Yn = a (n®¥)
=> $ lim Zn=a (n®¥) Док-во: 1.
из того, что $ lim
Xn=a (n®¥) => n>N2 |Xn-a|a-E => lim Zn=a
(n®¥)Функция y=f(x) наз-ся ограниченной в
данной обл-ти изменения аргумента Х,
если сущ-ет положит число М такое, что
для всех значений Х, принадлежащих
рассматриваемой обл-ти, будет выполн-ся
нер-во |f(x)|£M. Если же такого числа М не
сущ-ет, то f(x) наз-ся неограниченной в
данной обл-ти.
Билет 44 теорема о предельном переходе сложной функции!Теорема о пределе сложной функции.
Пусть существует lim (x->x0) g(x)=y0 и существует lim (y->y0) f(y)=A, и кроме того существует проколотая окрестность точки х0, в которой g(x) <> y0. Тогда существует lim (x->x0) f(g(x)) = lim (y->y0) f(y)=A (точно не знаю правильная та ли это теорема,но по идеи больше ничего не накопать)
№45 1й замечат предел
В этих нер-вах перейдем к переделу
;тогда по т.о сжатой переменной
IV четверть
Чтд.
№46 Второй замечат предел
Докажем что будет выполняться для любого
Док-во:
Пусть ,тогда для любого x ,такой что
Тогда
Пусть
Следствия:
47.
Бесконечно
малые(б.м)и бесконечно большие(б.б)величины.
Отношения порядка (малости) величин. Функция
В(х)наз. Б.м.в при (х) х стремится хо(где
х стрем.к бесконечности),если limB(x)=o(x
стрем. хо).Б.Б.В:функция F(x)
наз.бесконечно большой при х стрем. Хо(x
стрем.к бесконечности),если для каждого
сколь угодно боьшого числа М>0найдется
такое положительное число б(М)>0
(зависящие от М),что для всех х не равно
хо,удовлетворяющих условию (х-хо)<0,будет
верно неравенство F(x)>M.
Отношение порядка б.м.в.:Пусть L1(x)и
L2(x)суть
две б.м.в при х стрем. хо(х стрем. к
бесконечности).Тогда:1)если lim
L2(x)/
lim
L1(x)=0,то
L2(x)наз.б.м.в.высшого
порядка(малости),чем L1(х)и
пишут L2=0(L1)
(х стрем.хо)2)Если lim
L2(x)/L1(x)=А
не равно 0,то L1(x)наз.
Б.м.в. того те порядка(малости),что и
L2(x)и
пишут:L2=0(L1)(x
стрем. хо)
31. Пусть функция у = f(х) определена в некоторой точке а, кроме, может быть, самой этой точки.
Число
b называется пределом функции f(х) при х
стремящемся к а, если для любого сколь
угодно малого, наперед заданного ε>0
существует такое δ>0, что для всех х
таких, что |х-а|<δ выполняется неравенство
|f(x) — b|<ε.
x→a
В компактном виде это определение можно записать lim f(x) = b.
(lim – сокращенное слово limit(предел)).
Читается так: предел f(x) при х стремящемся к а равен b.При отыскании предела мы не учитываем значение функции в самой точке а, оно может быть любым. Функция f(x) называется непрерывной в точке а, если ее предел в этой точке совпадает со значением функции в той же точке, или lim f(x) = f(a).
Все элементарные функции непрерывны в каждой точке, где они определены.Для раскрытия неопределенностей используются так называемые замечательные пределы.
Понимание предела при приближении x к бесконечности
В этой статье
Понимание пределов по мере приближения x к бесконечности
Можно ли вычислить бесконечность?
5 примеров расчета пределов при стремлении x к бесконечности
Практические упражнения
Понимание пределов при приближении x к бесконечности
Знание того, как оценить пределы, идущие к бесконечности, важно для понимания поведения функций, которые приближаются к определенному значению yyy, когда их переменная xxx становится бесконечно большой или малой.
Во-первых, мы должны понять, что такое предел. Предел — это значение, к которому приближается функция, когда переменная xxx приближается к некоторому значению. 93 + 3 = -8 + 3 = -5(-2)3+3=-8+3=-5.
Это простой пример, но мы узнаем, что оценка пределов часто требует от вас использования и других методов, включая замещение, факторинг и радикализацию.
Но что произойдет, если мы хотим оценить предел функции, когда xxx приближается к бесконечно большому или бесконечно малому значению?
В этом случае нам нужно оценить один из следующих двух пределов:
limx→∞f(x)\lim_{x\to\infty} f(x)limx→∞f(x)
limx→−∞f(x)\lim_{x\to-\infty} f(x)limx→−∞f(x)
Можно ли вычислить бесконечность?
Давайте посмотрим, что мы имеем в виду, когда говорим «xxx приближается к бесконечности». Помните, что бесконечность не является конкретной величиной. Скорее, бесконечность — это идея. Мы можем думать о бесконечности как о «безграничном возрастании» или «безгранично убывающем».
Бесконечность — это то, к чему функции могут приблизиться, но никогда не достичь.
Например, рассмотрим функцию f(x)=2x−1xf(x) = \frac{2x-1}{x}f(x)=x2x−1. Взгляните на приведенную ниже таблицу значений функции.
Ясно, что по мере того, как xxx растет без ограничений, yyy стремится к 2, никогда не достигая 2.
Давайте посмотрим на график fff ниже, чтобы увидеть, как это выглядит.
Итак, мы можем сказать, что limx→∞2x−1x=2\lim_{x\to\infty} \frac{2x-1}{x} = 2limx→∞x2x−1=2, так как yyy приближается к 2, когда xxx неограниченно увеличивается. Хотя мы можем представить, что yyy бесконечно приближается к 2 по мере того, как xxx становится все больше и больше в положительном направлении, yyy никогда не достигает 2.
Обратите внимание, что f(x)f(x)f(x) демонстрирует аналогичное поведение по мере того, как xxx становится все меньше и меньше в отрицательном направлении. Таким образом, мы также можем сказать, что limx→−∞2x−1x=2\lim_{x\to-\infty} \frac{2x-1}{x} = 2limx→−∞x2x−1=2 .
Обратите внимание, что на графике этой функции имеется невидимая линия при y=2y = 2y=2. Это называется горизонтальной асимптотой. Обратите внимание, что горизонтальная асимптота имеет то же значение yyy, что и предел f(x)f(x)f(x), когда xxx приближается к ∞\infty∞.
Если limx→∞f(x)=L\lim_{x\to\infty} f(x) = Llimx→∞f(x)=L или limx→−∞f(x)= L\lim_{x\to-\infty} f(x) = Llimx→−∞f(x)=L, мы говорим, что существует горизонтальная асимптота при y=Ly = Ly=L. 92}} =\фракция{3}{1+0} = 3limx→∞x2+53×2=limx→∞x2x2+x25x23x2=1+03=3
Таким образом, предел f(x)f(x)f(x) при приближении xxx к ∞\infty∞ равен 3. Этот пример дает нам полезное правило, которому следует следовать при оценке пределов, приближающихся к бесконечности. Если наибольшая степень числителя совпадает с наибольшей степенью знаменателя, то пределом выражения при стремлении xxx к бесконечности является отношение коэффициентов их членов наивысшей степени.
Например, в этой задаче наивысшая степень числа xxx как в числителе, так и в знаменателе равна x2x^2×2.
2 + 5} = 3limx→∞x2+53×2 = 3. 92}{4x+1} = \inftylimx→∞4x+13×2=∞.
Три вышеприведенных примера дают нам некоторые экономящие время правила для принятия предела, когда xxx приближается к бесконечности для рациональных функций:
Если степень числителя меньше степени знаменателя, то limx→∞f(x)=0\lim_{x\to\infty} f(x) = 0limx→∞f(x)= 0.
Если степень числителя равна степени знаменателя, то limx→∞f(x)\lim_{x\to\infty} f(x)limx→∞f(x) равно отношению коэффициенты членов с наибольшей степенью в числителе и знаменателе. 9x}{2x}limx→∞2xex.
В этом примере и числитель, и знаменатель приближаются к бесконечно большим значениям, оставляя нам неопределенное ∞∞\frac{\infty}{\infty}∞∞. Мы не можем использовать тот же метод, что и раньше, так как числитель не имеет степени ххх. Вместо этого мы будем использовать правило Лопиталя, которое гласит:
. limx→∞f(x)g(x)=limx→∞f'(x)g'(x)\lim_{x\to\infty}\frac{f(x)}{g(x )} = \lim_{x\to\infty}\frac{f'(x)}{g'(x)}limx→∞g(x)f(x)=limx→∞g'(x )f'(х) 9x}{2} = \inftylimx→∞2xex=limx→∞2ex=∞
Правило Лопиталя — отличное правило, которое нужно знать, когда сталкиваешься с неопределенными формами в частных, таких как ∞∞\frac{\infty}{\infty}∞∞ или 00\frac{0}{0}00.
Если вам дан предел, который не находится в форме частного, но имеет другой неопределенный предел, например ∞−∞\infty — \infty∞−∞, его часто можно переписать как частное, чтобы можно было применить правило Лопиталя. .Практические упражнения
Вот несколько упражнений для практики оценки пределов, когда xxx приближается к бесконечности. 96 = \inftylimx→∞14×6+x3−x=limx→∞x6(14+x31−x51=limx→∞x6(14+0−0)=limx→∞14×6=∞
We’ Воспользуемся правилом Лопиталя, потому что у нас неопределенная форма \ln{(x)}}{x} = \lim_{x\to-\infty}\frac{\frac{1}{x}}{1} = 0limx→−∞xln(x)=limx→–∞1×1=0.
Узнайте об отмеченных наградами курсах Outlier For-CreditOutlier (от соучредителя MasterClass) собрал лучших в мире преподавателей, дизайнеров игр и кинематографистов для создания будущего онлайн-колледжа.
Ознакомьтесь с этими родственными курсами:
Исчисление I
Изучите курс
Исчисление I
Математика изменений.
Изучить курс
Введение в статистику
Изучить курс
Введение в статистику
Как данные описывают наш мир.
Изучить курс
Введение в микроэкономику
Изучить курс
Введение в микроэкономику
Почему маленькие решения имеют большое влияние.
Исследуйте курс
Ограничения в бесконечности | Математика
Пределы в бесконечности
Лимиты не ограничиваются реальными числами. Взять предел функции, когда она стремится к положительной бесконечности, $\infty$, или к отрицательной бесконечности, $-\infty$, тоже интересно. Стремится ли эта функция к бесконечности? Или он останавливается на одном значении?
Однако пределы на бесконечности не обязательно должны сходиться к одному значению. Осциллирующие функции, такие как синус и косинус, не сходятся к одному значению и не растут до бесконечности либо в сторону $\infty$, либо в сторону $-\infty$.
Если вам дан предел, который не находится в форме частного, но имеет другой неопределенный предел, например ∞−∞\infty — \infty∞−∞, его часто можно переписать как частное, чтобы можно было применить правило Лопиталя. .
