Функции. Предел функции
10.1Понятие функции
10.1.1Функции и отображения
Мы, наконец, добрались до главного объекта математического анализа — до функций. Слова «функция» и «отображения» в принципе являются синонимами, они обозначают одно и то же математическое понятие, но в зависимости от контекста чаще используют одно или другое. Говоря «функция», мы будем как правило иметь в виду числовую функцию одной переменной, то есть отображение, которое числу ставит в соответствие число. Именно такие функции изучают в школе.
Определение 1. (Числовой) функцией (одной переменной) называется отображение
f:X→R,
где X⊂R — некоторое подмножество множества вещественных чисел. В этом случае X называется областью определения функции. Обозначают также X=:D(f).
Выбранный термин — функция или отображение — также влияет на выбор терминов для
обозначения некоторых связанных понятий. Например, если x — некоторый элемент
области определения, а y=f(x), в терминах отображений x называется
Например, если x — некоторый элемент
области определения, а y=f(x), в терминах отображений x называется
10.1.2Функции и формулы
Функции можно задавать формулами.
Пример 1. Запись f(x)=x2 задаёт функцию, которая любому вещественному числу ставит в соответствие его квадрат, см. рис. 10.1.
Рис. 10.1: Функция y=x2 как отображение: точки с левой оси переходят в точки на правой оси. Стрелочек нужно было бы нарисовать бесконечно много, но тогда ничего нельзя было бы разобрать
Если функция задана формулой, и не сказано ничего специального про её область
определения, считается, что областью определения такой функции является
множество всех чисел, при которых значение формулы может быть вычислено (так
называемая естественная область определения).
Пример 2. Функция g(x)=1×2−1 определена во всех точках, кроме x=1 и x=−1. Её область опредеделения — R∖{−1,1}.
При необходимости можно задать функцию, определенную на каком-то более узком подмножестве. Например, можно рассмотреть функцию g(x)=x2, x≥0. Несмотря на то, что f из примера выше и только что определенная g задаются одной и той же формулой, это разные функции, поскольку у них разные области определения. Можно сказать, что функция g была получена из функции f путём ограничения её на множество [0,+∞). Графиком функции f (см. ниже) является парабола, а функции g — только её правая ветвь. Ограничение обозначается так:
g=f|[0,+∞),
Иногда область определения функции ясна из контекста и смысла входящих в неё
переменных. Например, если x — это размер какой-нибудь популяции, вряд ли он
может быть отрицательным.
Пример 3. Функции можно задавать более сложными выражениями. Например:
f(x)={x2,x>0−x,x≤0
Это пример кусочного задания функции. В зависимости от того, какому условию удовлетворяет значение x, применяется либо одна формула, либо другая.
10.1.3График функции
Один из правильных способов думать про функции — это думать про их графики. По определению, график функции — это множество точек на декартовой плоскости, у которых x-координата равна какому-то значению из области определения функции, а y-координата равна f(x). Формально:
Gr(f):={(x,f(x))∣x∈D(f)}.
Функции можно задавать графиками. Eсли нарисовать произвольную кривую на декартовой плоскости, она будет графиком некоторой функции если и только если с любой вертикальной прямой x=x0 у неё будет не более одной точки пересечения, см. рис. 10.2.
Рис. 10.2: Кривые слева являются графиками функций. Слева сверху функция принимает
значение 6 в точке 2 и значение 5 в точке 3,5. Слева снизу
функция не определена на интервале (4,7). Кривые справа не являются
графиками функций: для некоторых (в частности, отмеченных) вертикальных
прямых у них более одной точки пересечения.
Слева сверху функция принимает
значение 6 в точке 2 и значение 5 в точке 3,5. Слева снизу
функция не определена на интервале (4,7). Кривые справа не являются
графиками функций: для некоторых (в частности, отмеченных) вертикальных
прямых у них более одной точки пересечения.
Если точки пересечения нет, значит, функция не определена в точке x0. Если есть, y-координата точки пересечения задаёт значение функции в точке x0. Если бы нашлась вертикальная прямая с более чем одной точкой пересечения, было бы непонятно, какое значение принимает функция в соответствующей точке.
Как правило, думая о свойствах функции, правильнее всего представлять себе
именно графики, а не, скажем, формулы, которыми эти функции задаются. Однако,
нужно понимать, что любой физически нарисованный график — лишь приближение к
абстрактному математическому графику. Графики как правило сами по себе не могут
использоваться для доказательств утверждений, хотя придумать доказательства без
них часто может быть очень сложно.
Впрочем, бывают функции, графики которых трудно себе представить.
Пример 4. Рассмотрим функцию Дирихле:
D(x)={1,x∈Q;0,x∉Q.
Она принимает значение 1 во всех рациональных точках и 0 во всех иррациональных. Представить себе её график довольно сложно — он не выглядит как привычная нам кривая. Поскольку и рациональные и иррациональные числа всюду плотны, на любом сколь угодно маленьком интервальчике будут как точки, в которых функция принимает значение 0, так и точки, в которых функция принимает значение 1. Получится два таких «дырявых» множества точек, одно лежит на прямой y=0, другое на y=1.
10.1.4Свойства функций
Часть свойств функций очень похожи на аналогичные свойства последовательностей.
Определение 2. Говорят, что функция f ограничена (ограничена сверху, ограничена снизу) на множестве A⊂D(f), если существует такое
C, что для всех x∈A выполняется неравенство |f(x)|<C
(соответственно, f(x)<C, f(x)>C).
В этом определении для краткости сформулированы сразу три определения: из скобок нужно выбирать соответствующие элементы. Если множество A не указано, считается, что A — вся область определения функции.
Пример 5. Функция f(x)=1x не является ограниченной, поскольку выражение 1x может принимать сколь угодно большие значения (для всякого C>0 можно выбрать x=1C+1 и получить |f(x)|=C+1>C). Однако, эта функция ограничена на отрезке [1,2].
Определение 3. Функция f называется возрастающей (убывающей, неубывающей, невозрастающей) на множестве A⊂D(f) если для всех x1,x2∈A, таких, что x2>x1, справедливо неравенство f(x2)>f(x1) (соответственно, f(x2)<f(x1), f(x2)≥f(x1), f(x2)≤f(x1)). Неубывание также называется нестрогим возрастанием, а невозрастание — нестрогим убыванием.
Пример 6. Рассмотрим функцию f(x)=sinx. Она возрастает на отрезке
[−π/2,π/2], убывает на отрезке [π/2,3π/2] и снова возрастает на
отрезке [3π/2,5π/2].
Вопрос 1. Верно ли, что функция f(x)=sinx возрастает на множестве [−π/2,π/2]∪[3π/2,5π/2]?
Верно, об этом же выше написано!
Неверный ответ. Не совсем, написано, что она возрастает на отрезке [−π/2,π/2] и на отрезке [3π/2,5π/2]. Возрастает ли она на их объединении? Проверьте с помощью определения.
Звучит странно, но нет, неверно.
Верный ответ. Именно так! Хотя функция возрастает на каждом из отрезков, она не возрастает на их объединении, поскольку требования определения не выполняются. Например, если x1=π2 и x2=3π/2, обе точки принадлежат объединению, x2>x1 и при этом f(x2)=−1<1=f(x1).
Ограниченностью и монотонностью дело не ограничивается, у функций ещё много разных свойств, которые не встречаются у последовательностей.
Определение 4. Пусть область определения функции f(x) симметрична относительно нуля, то
есть вместе с каждой точкой x содержит и точку (−x).
График чётной функции симметричен относительно оси Oy: вместе с каждой точкой (x,f(x)) он содержит точку (−x,f(x)). График нечётной функции симметричен относительно начала координат: вместе с каждой точкой (x,f(x)) он содержит точку (−x,−f(x)).
Пример 7. Функция sin(x) является нечётной, а cos(x) — чётной. Функция f(x)=xn является чётной при чётных значениях n и нечётной при нечётных (отсюда и название).
10.1.5Экстремумы
Очень часто нам важно уметь отвечать на вопросы вроде «какое максимальное
значение может принимать данная функция» или «как бы так подобрать x, чтобы
f(x) было как можно меньше». Такого типа задачи называются задачами
оптимизации, и вся наша жизнь ими пронизана. Владелец компании хочет
максимизировать её прибыль, сотрудник — свою зарплату, программист — скорость
работы программы, собака — количество вкусняшек, кошка… Ладно, с кошками
непонятно, но они тоже наверняка что-нибудь оптимизируют.
Чтобы иметь возможность формулировать и решать задачи оптимизации нам нужно сформулировать ряд дополнительных понятий.
Определение 5. Говорят, что функция f достигает своего максимального значения в точке x0∈D(f), если для всех x∈D(f) выполняется неравенство f(x0)≥f(x). В этом случае точка x0 называется точкой глобального максимума функции f. Иногда слово «точка» опускается и говорят просто «глобальный максимум», имея в виду точку x0. Также под словами «глобальный максимум» может подразумеваться значение f(x0) или точка (x0,f(x0)) на графике функции. Как правило, из контекста ясно, что имеется в виду.
Определение 6. Ну и наоборот, f достигает своего минимального значения в точаке x0∈D(f), если для всех x∈D(f) выполняется неравенство f(x0)≤f(x). В этом случае точка x0 называется точкой глобального минимума функции f.
Совместно максимумы и минимумы называются экстремумами. То есть экстремум — это максимум или минимум.
Пример 8. У функции может не быть глобальных экстремумов. Например, функция f(x)=x, определенная на интервале (0,1), не имеет ни глобального максимума, ни глобального минимума.
Вопрос 2. А почему?
Узнать ответ
Верный ответ. Докажем от противного. Пусть x0∈(0,1) — точка глобального максимума. Возьмём точку x=(x0+1)/2 — это середина отрезка [x0,1]. Тогда f(x)=x=x0/2+1/2>x0/2+x0/2=x0=f(x0), поскольку 1>x0. Значит, x0 — не точка глобального максимума. Значит, никакого глобального максимума нет. Аналогично можно показать, что нет и глобального минимума.
Пример 9. У функции может быть много глобальных экстремумов. Например, у функции f(x)=cosx бесконечно много глобальных максимумов (все точки вида 2kπ, k — целое) и бесконечного много минимумов (каких?).
Вопрос 3. Может ли глобальный максимум совпадать с глобальным минимумом?
Нет.
Неверный ответ. А вот и нет.
Да.
Верный ответ. Действительно, у функции f(x)=42 бесконечно много глобальных максимумов и все они также являются глобальными минимумами.
Определение 7. Точка x0 называется точкой строгого локального максимума (минимума) если для всех x∈D(f), не совпадающих с x0, выполняется неравенство f(x0)>f(x) (соответственно, f(x0)<f(x)). Иными словами, в определении экстремума мы заменили неравенство на строгое, и ещё добавили условие, что x не совпадает с x0 — если бы мы этого не сделали, никакая точка не могла бы удовлетворять определению.
Вопрос 4. Может ли у функции быть несколько строгих глобальных максимумов?
Нет.
Верный ответ. Действительно, не может: значение функции в каждом из них должно быть строго больше, чем в другом. Так не бывает.
Да.
Неверный ответ. Как же?
Вопрос 5. Может ли у функции быть строгий глобальный максимум, являющийся одновременно строгим глобальным минимумом?
Нет.
Верный ответ. Это почти правда: значение функции в строгом глобальном максимуме должно быть строго больше её значения в строгом глобальном минимуме, и значит это должно быть два разных значения, и значит две разные точки. Но есть одно исключение. Угадаете, какое?
Да.
Верный ответ. Технически, это верно: для любой функции, определённой лишь в одной точке, эта точка является одновременно глобальным максимумом и минимумом. Однако, такие функции не очень интересны — как говорят, это вырожденный пример.
Определение 8. Точка x0∈D(f) называется точкой локального максимума (минимума) функции
f, если существует такой интервал (a,b), содержащий точку x0, что
для всех x∈(a,b)∩D(f) выполняется неравенство f(x0)≥f(x)
(соответственно, f(x0)≤f(x)).
Как видно, определение локального экстремума отличается от определения глобального только требованиями на x. Например, в случае глобального максимума, мы хотим, чтобы f(x0) было не меньше, чем значение f в любой другой точке области определения, а в случае с локальным максимумом f(x0) должно быть не меньше, чем значения f в точках x, близких к x0. Любой глобальный максимум автоматически является локальным, но не всякий локальный максимум обязан быть глобальным.
Рис. 10.3: Точки локального и глобального максимума на графике функции y=f(x).
Перейдём теперь к ключевому понятию курса: пределу функции.
10.2Предел функции
10.2.1Примеры и мотивировка
Начнём как всегда с неформального описания и примеров.
Как бы определение 1. Говорят, что функция y=f(x) имеет предел в точке x=x0, равный b, если
значение этой функции становится сколь угодно близким к числу b если
значение x достаточно близко к x0, но при этом не равно x0.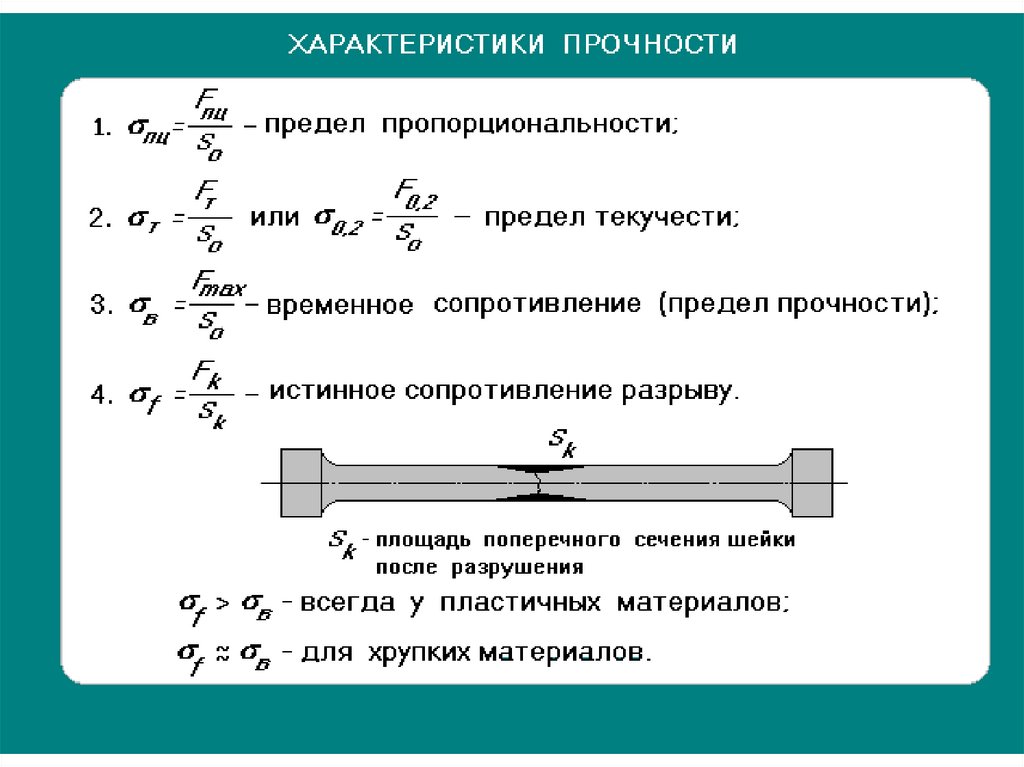
Обозначение:
limx→x0f(x)=b
или
f(x)→b при x→x0.
Рассмотрим несколько примеров.
Пример 10. Пусть f(x)=x2. К чему стремится f(x), если x стремится к 2? Можно посмотреть на график и увидеть, что если мы выибраем значения x, близкие к 2, то соответствующая точка на графике будет близка к точке (2,4).
Рис. 10.4: Предел функции y=x2 при x→2.
Значит, значение f(x) будет близким к 4. Таким образом, предел f при x стремящемся к двум равен четырём:
limx→2×2=4.
Казалось бы, зачем городить такой огород в предыдущем примере — понятно, что
достаточно просто подставить значение x в формулу для функции и получить
ответ. Однако, это не всегда работает. Во-первых, в квазиопределении
предела явно сказано, что мы не можем брать x, равное
x0. Во-вторых, функция может быть не определена в точке x0 — и это не
мешает ей иметь предел в этой точке.
Пример 11. Пусть
f(x)=x2−1x−1.
К чему приближается значение функции когда x приближается к 1? Если попытаться просто подставить значение x=1 в формулу, ничего не получится: знаменатель обнуляется и значение не определено. Однако, можно выбирать близкие значения x, подставлять их в формулу и посмотреть, что получается:
def f(x):
return (x ** 2 - 1) / (x - 1)
print("x\tf(x)")
for x in [1.01, 1.001, 1.0001, 1.00001,
0.99, 0.999, 0.9999, 0.99999]:
print(f"{x}\t{f(x)}")x f(x) 1.01 2.009999999999999 1.001 2.0009999999999177 1.0001 2.0000999999993923 1.00001 2.0000100000008274 0.99 1.990000000000001 0.999 1.9989999999999712 0.9999 1.9998999999994975 0.99999 1.9999899999991726
Из таблички, которую мы видим, можно сделать вывод, что значение f(x) приближается к 2. То же самое можно увидеть на графике.
Рис. 10.5: Функция не определена в точке, но предел у неё есть.
Как это можно было бы доказать?
Заметим, что выражение для f(x) можно упростить. Если разложить числитель на скобки, получится (x−1)(x+1):
f(x)=(x−1)(x+1)(x−1).
Если x≠1, дробь можно сократить на (x−1) и получится выражение (x+1). Если x=1, значение функции не определено. Таким образом, можно сказать, что функция f(x) определена при всех значениях x∈R∖{1}, и на этом множестве задаётся формулой
f(x)=x+1.(10.1)
Поскольку нас интересует, к чему приближается f(x), когда x приближается к 1, но не равен 1 (см. как бы определение 1), нас интересуют только значения функции при x≠1, и значит мы можем смело использовать формулу (10.1). Очевидно, если x приближается к 1, то (x+1) приближается к 2. Таким образом,
limx→1×2−1x−1=2.
Пример 12. Рассмотрим функцию
f(x)={1,x≠2;3,x=2.
Чему равняется её предел при x→2?
В этом примере функция определена в точке x=2 и может возникнуть искушение
подставить x=2 в формулу и сказать, что результат (число 3) и будет ответом. Однако,
это неверно. На самом деле, значение функции в этой точке никак не влияет на
ответ: предел функции при x стремящемся к x0 зависит от значений
функции в точках, близких к x0, но не в самой точке x0.
Однако,
это неверно. На самом деле, значение функции в этой точке никак не влияет на
ответ: предел функции при x стремящемся к x0 зависит от значений
функции в точках, близких к x0, но не в самой точке x0.
Рис. 10.6: Предел функции в точке не равен её значению в этой точке.
Во всех точках, близких к 2, значение функции равно 1. Значит, предел этой функции при x→2 также равен 1:
limx→2f(x)=1.
Пример 13. Рассмотрим функцию
f(x)={x+1,x≤1;x−2,x>1.(10.2)
Что вы можете сказать про её предел при x→1?
Посмотрим на график.
Если x чуть меньше 1, действует верхняя строчка в определении функции и
значение оказывается чуть меньше 2. Однако, если x чуть больше 1,
действует уже нижняя строчка, и значение функции оказывается чуть больше
−1. Никакого одного числа, к которому бы приближалось значение функции,
когда x приближается к 1, нет. Значит, нет и предела.
Значит, нет и предела.
Итак, limx→1f(x) в этом случае не существует.
В этом примере несуществование предела было связано с тем фактом, что при приближении x с разных сторон значение функции приближалось к разным числам. Это не единственный механизм несуществования предела.
Пример 14. Рассмотрим функцию
f(x)=sinπx.
Что вы можете сказать про её предел при x→0? Просто подставить x=0 в формулу нельзя, да и как мы видели это не всегда работает. Попробуем использовать тот же приём, что и в примере 10: подставим в f какие-нибудь значения x, близкие к 0, и посмотрим, что получается.
import numpy as np
def f(x):
return np.sin(np.pi / x)
print(" x\t\t f(x)")
for x in [0.01, 0.001, 0.0001, 0.00001,
-0.01, -0.001, -0.0001, -0.00001]:
print(f"{x: .7f}\t{f(x): .7f}")x f(x) 0.0100000 0.0000000 0.0010000 -0.0000000 0.0001000 -0.0000000 0.0000100 -0.0000000 -0.0100000 -0.0000000 -0.0010000 0.0000000 -0.0001000 0.0000000 -0.0000100 0.0000000
Чему же равен предел? Из таблички может сложиться ощущение, что нулю — во всех наших пробных точках значение функции нулевое. Однако, на самом деле это не так.
Рассмотрим последовательность точек xn=12n+1/2. Очевидно xn→0 при n→∞. Найдём f(xn):
f(xn)=sin⎛⎜⎝π12n+1/2⎞⎟⎠=sin(2nπ+π/2)=1.
Таким образом, существуют сколь угодно близкие к нулю числа, в которых значение функции принимает значение 1. Это значит, что предел никак не может быть равен нулю! На самом деле, предел в этом случае не существует: выбирая разные значения x, близкие к нулю, например, справа (то есть положительные числа), можно получать значения функции, близкие к 1, или к 0, или к −1, или ещё к чему-нибудь. Одного числа, к которому приближалось бы значение функции, не существует.
Упражнение 1. Крайне полезное упражнение — построить график функции y=sinπ/x. Чтобы
понять, как он выглядит, полезно найти все значения x, при которых функция
принимает значения 0, 1 и −1 и отметить соответствуюие точки на графике.
Чтобы
понять, как он выглядит, полезно найти все значения x, при которых функция
принимает значения 0, 1 и −1 и отметить соответствуюие точки на графике.
10.2.2Строгое определение предела
Мы хотим формализовать квазиопределение 1. В нём есть слова «значение функции становится сколь угодно близким». Что это значит? Это значит, что мы можем сделать значения f(x) настолько близкими к числу b, насколько хотим. Но для этого нужно потребовать, чтобы x был достаточно близок к x0 (и при этом не равен x0). С чем-то подобным мы уже сталкивались, когда придумывали понятие предела последовательности. Определение предела функции очень похоже.
Нам понадобится пара вспомогательных определений.
Определение 9. Окрестностью точки x0 называется любой интервал (a,b),
содержащий точку x0, см. рис. 10.8. Проколотой
окрестностью точки x0 назвается окрестность, из которой выкинули
саму точку x0, то есть множество (a,x0)∪(x0,b), где
a<x0<b. Эпсилон-окрестностью (ε-окрестностью)
точки x0 называется интервал (x0−ε,x0+ε). Проколотой
ε-окрестностью точки x0 называется множество
Эпсилон-окрестностью (ε-окрестностью)
точки x0 называется интервал (x0−ε,x0+ε). Проколотой
ε-окрестностью точки x0 называется множество
(x0−ε,x0)∪(x0,x0+ε)=(x0−ε,x0+ε)∖{x0}.
(x0−ε,x0)∪(x0,x0+ε)==(x0−ε,x0+ε)∖{x0}.
Обычно ε-окрестность точки x0 обозначается как Uε(x0), а проколотая ε-окрестность — как ˚Uε(x0).
Рис. 10.8: Различные типы окрестностей: обычная окрестность, проколотая окрестность, ε-окрестность и проколотая ε-окрестность.
Определение 10. Пусть функция f(x) определена в некоторой проколотой окрестности точки x0,
то есть существует такая проколотая окрестность, в которой функция
определена; в самой точке x0 она может быть определена, а может и не
быть. Говорят, что предел функции f(x) в точке x=x0 равен числу b,
если для всякого ε>0 найдётся такое δ>0, что для всех x из
проколотой δ-окрестности точки x0 значения функции лежат в
ε-окрестности точки b, см. рис. 10.9.
рис. 10.9.
Формально: утверждение
limx→x0f(x)=b
по определению означает, что
∀ε>0 ∃δ>0 ∀x∈˚Uδ(x0):f(x)∈Uε(b),
или, с учётом замечания 3:
∀ε>0 ∃δ>0 ∀x∈R:0<|x−x0|<δ⇒|f(x)−b|<ε.
∀ε>0 ∃δ>0 ∀x∈R:0<|x−x0|<δ⇒|f(x)−b|<ε.
Рис. 10.9: Окрестности в определении предела. Заметим, что значение функции в самой точке x0 может не лежать в ε-окрестности точки b или быть вообще не определено, но может и лежать: про него мы ничего не говорим.
Пример. Вернёмся к примеру 10 и докажем, что limx→2×2=4, пользуясь только что сформулированным определением.
Пусть нам дано произвольное ε>0. Мы хотим подобрать такое δ>0, что для всех x из проколотой δ-окрестности точки 2, |x2−4|<ε. Заметим, что
|x2−4|=|(x−2)(x+2)|=|x−2|⋅|x+2|.
Если x лежит в проколотой дельта-окрестности точки 2, значит,
|x−2|<δ. Таким образом мы получили оценку на первый сомножитель: его
можно сделать сколь угодно маленьким подходящим выбором δ. Осталось
оценить второй сомножитель. Поскольку δ мы выбираем сами, на неё можно
накладывать любые условия, какие мы хотим. Пусть δ≤1. (Почему именно
1? На самом деле, подойдёт любое фиксированное число, нужно взять какое-то
конкретное, почему бы и не 1?) Тогда
Таким образом мы получили оценку на первый сомножитель: его
можно сделать сколь угодно маленьким подходящим выбором δ. Осталось
оценить второй сомножитель. Поскольку δ мы выбираем сами, на неё можно
накладывать любые условия, какие мы хотим. Пусть δ≤1. (Почему именно
1? На самом деле, подойдёт любое фиксированное число, нужно взять какое-то
конкретное, почему бы и не 1?) Тогда
−1≤−δ<x−2<δ≤1
или (прибавим ко всем членам число 2):
1<x<3.
В этом случае выражение |x+2| обязательно меньше |3+2|=5: поскольку x>0, выражение под модулем гарантированно положительно и значит его нужно сделать как можно больше, чтобы модуль был как можно больше, и значит нужно брать как можно большее значение x, но x<3. Таким образом, если |x−x0|<δ≤1,
|x2−4|=|x−2|⋅|x+2|<δ⋅5.
Мы хотим, чтобы эта величина была меньше ε. Это будет выполняться, если
потребовать, чтобы δ≤ε/5. Итак, у нас есть два условия на
δ: δ≤1 и δ≤ε/5. Чтобы они оба были
удовлетворены, достаточно взять
Итак, у нас есть два условия на
δ: δ≤1 и δ≤ε/5. Чтобы они оба были
удовлетворены, достаточно взять
δ(ε):=min(ε/5,1).
Проверяем: для всех x∈˚Uδ(2) верно неравенство |x−2|<δ, и значит
|x2−4|<δ⋅5=5ε/5=ε.
Таким образом, выбранная нами δ удовлетворяет определению, и предел действительно равен 4, см. анимацию на рис. 10.10.
Рис. 10.10: Как работает определение предела: хотя значение ε уменьшается, нам каждый раз удаётся подобрать такое значение δ, чтобы все точки графика над проколотой δ-окрестностью точки x0=2 лежали в ε-окрестности точки b=4.
10.3Односторонние пределы
В мире последовательностей всё было просто: последовательность могла иметь
предел при n→∞, и больше никакого. В мире функций всё сложнее. Мало
того, что x может приближаться к различным точкам, и нужно уточнять, к чему
именно он приближается. Он ещё может это делать разными способами.
Рассмотрим функцию f(x), заданную формулой (10.2) (см. пример 13). У неё нет предела в точке x=1, поскольку при приближении по x к точке 1 справа или слева, значение функции f(x) приближается к разным числам (−1 и 2 соответственно). Чтобы сказать это формально, нужно дать определение односторонних пределов.
Определение 11. Пусть функция f(x) определена в правой полуокрестности точки x0, то есть на множестве (x0,x0+δ∗) для некоторого δ∗>0. Говорят, что предел функции f(x) при x стремящемся к x0 справа равен b, если для всякого ε>0 найдётся такая δ>0, что для всех x∈(x0,x0+δ) выполняется неравенство |f(x)−b|<ε.
Определение 12. Пусть функция f(x) определена в левой полуокрестности точки x0, то есть на множестве (x0−δ∗,x0) для некоторого δ∗>0. Говорят, что предел функции f(x) при x стремящемся к x0 слева равен b, если для всякого ε>0 найдётся такая δ>0, что для всех x∈(x0−δ,x0) выполняется неравенство |f(x)−b|<ε.
Записывают:
limx→x+0f(x)=b
для предела справа и
limx→x−0f(x)=b
для предела слева.
Упражнение 2. Докажите, что для функции f(x), заданной формулой (10.2), предел справа равен −1, а предел слева равен 2.
Упражнение 3. Докажите, что если у функции существует предел при x→x0, то пределы при x→x+0 и при x→x−0 также существуют, равны между собой и равны пределу при x→x0. Докажите, что верно и обратное: если оба односторонние пределы существуют и равны между собой, то предел при x→x0 также существует и его значение равно значению односторонних пределов.
10.4Заключение
Функции одной переменной нам всем знакомы со школы. Однако, объект этот не так прост, как может показаться. Чтобы приобрести хорошую интуицию о том, какими бывают функции и какими свойствами они могут обладать, придётся хорошо поработать. И для начала — освоить понятие предела функции в точке, которое мы будем постоянно использовать в будущем.
← Предыдущая глава Следующая глава →
Пределы применимости формулы Эйлера (Лекция №44)
Казалось бы, что полученные в предыдущих параграфах результаты решают задачу проверки сжатого стержня на устойчивость; остается выбрать лишь коэффициент запаса . Однако это далеко не так. Ближайшее же изучение числовых величин, получаемых по формуле Эйлера, показывает, что она дает правильные результаты лишь в известных пределах.
Однако это далеко не так. Ближайшее же изучение числовых величин, получаемых по формуле Эйлера, показывает, что она дает правильные результаты лишь в известных пределах.
На рис.1 приведена зависимость величины критических напряжений, вычисленных при различных значениях гибкости для стали 3, обычно применяемой в металлических конструкциях. Эта зависимость представляется гиперболической кривой, так называемой «гиперболой Эйлеpa»:
При пользовании этой кривой надо вспомнить, что представляемая ею формула получена при помощи интегрирования дифференциального уравнения изогнутой оси, т. е. в предположении, что напряжения в стержне в момент потери устойчивости не превосходят предела пропорциональности.
Рис.1. Гиперболическая зависимость критического напряжения от гибкости стержня
Следовательно, мы не имеем права пользоваться величинами критических напряжений, вычисленных по формуле Эйлера, если они получаются выше этого предела для данного материала. Иначе говоря, формула Эйлера применима лишь при соблюдении условия:
Иначе говоря, формула Эйлера применима лишь при соблюдении условия:
или
Если из этого неравенства выразить гибкость , то условие применимости формул Эйлера получит иной вид:
Подставляя соответствующие значения модуля упругости и предела пропорциональности для данного материала, находим наименьшее значение гибкости, при которой еще можно пользоваться формулой Эйлера. Для стали 3 предел пропорциональности может быть принят равным , поэтому, для стержней из этого материала можно пользоваться формулой Эйлера лишь при гибкости
т. е. большей, чем 100 %
Для стали 5 при формула Эйлера применима при гибкости ; для чугуна при , для сосны при и т. д. Если мы на Рис.1 проведем горизонтальную линию с ординатой, равной , то она рассечет гиперболу Эйлера на две части; пользоваться можно лишь нижней частью графика, относящейся к сравнительно тонким и длинным стержням, потеря устойчивости которых происходит при напряжениях, лежащих не выше предела пропорциональности.
Теоретическое решение, полученное Эйлером, оказалось применимым на практике лишь для очень ограниченной категории стержней, а именно, тонких и длинных, с большой гибкостью. Между тем, в конструкциях очень часто встречаются стержни с малой гибкостью. Попытки использовать формулу Эйлера для вычисления критических напряжений и проверки устойчивости при малых гибкостях вели иногда к весьма серьезным катастрофам, да и опыты над сжатием стержней показывают, что при критических напряжениях, больших предела пропорциональности, действительные критические силы значительно ниже определенных по формуле Эйлера.
Таким образом, надо найти способ вычисления критических напряжений и для тех случаев, когда они превышают предел пропорциональности материалов, например, для стержней из мягкой стали при гибкостях от 0 до 100.
Необходимо сразу же отметить, что в настоящее время важнейшим источником для установления критических напряжений за пределом пропорциональности, т. е. при малых и средних гибкостях, являются результаты экспериментов. Имеются попытки и теоретического решения этой задачи, но они скорее указывают путь к дальнейшим исследованиям, чем дают основания для практических расчетов.
е. при малых и средних гибкостях, являются результаты экспериментов. Имеются попытки и теоретического решения этой задачи, но они скорее указывают путь к дальнейшим исследованиям, чем дают основания для практических расчетов.
Прежде всего надо выделить стержни с малой гибкостью, от 0 примерно до 3040; у них длина сравнительно невелика по отношению к размерам поперечного сечения. Например, для стержня круглого сечения гибкости 20 соответствует отношение длины к диаметру, равное 5. Для таких стержней трудно говорить о явлении потери устойчивости прямолинейной формы всего стержня в целом в том смысле, как это имеет место для тонких и длинных стержней.
Эти короткие стержни будут выходить из строя главным образом за счет того, что напряжения сжатия в них будут достигать предела текучести (при пластичном материале) или предела прочности (при хрупких материалах). Поэтому для коротких стержней, до гибкости примерно 3040, критические напряжения «будут равны, или немного ниже (за счет наблюдающегося все же некоторого искривления оси стержня), соответственно или (сталь), или (чугун, дерево).
Таким образом, мы имеем два предельных случая работы сжатых стержней: короткие стержни, которые теряют грузоподъемность в основном за счет разрушения материала от сжатия, и длинные, для которых потеря грузоподъемности вызывается нарушением устойчивости прямолинейной формы стержня. Количественное изменение соотношения длины и поперечных размеров стержня меняет и весь характер явления разрушения. Общим остается лишь внезапность наступления критического состояния в смысле внезапного резкого возрастания деформаций.
В сжатых стержнях большой гибкости, для которых применима формула Эйлера, после достижения силой Р критического значения обычно наблюдается резкий рост деформаций. До этого момента прогибы, как правило, растут с ростом нагрузки, но остаются незначительными. Теоретически можно было бы ожидать, что до критической силы стержень будет оставаться прямым; однако ряд неизбежных на практике обстоятельств начальная кривизна стержня, некоторый эксцентриситет приложения нагрузки, местные перенапряжения, неоднородность материала вызывают небольшие прогибы и при сжимающих силах, меньших критических. тонких и длинных стержней; они теряют свою прямолинейную форму и разрушаются при явлениях значительного бокового выпучивания. При опытах для них можно отметить наличие ясно выраженной критической силы в «эйлеровом» смысле; критические напряжения получаются выше предела пропорциональности и ниже предела текучести для пластичных и предела прочности для хрупких материалов.
тонких и длинных стержней; они теряют свою прямолинейную форму и разрушаются при явлениях значительного бокового выпучивания. При опытах для них можно отметить наличие ясно выраженной критической силы в «эйлеровом» смысле; критические напряжения получаются выше предела пропорциональности и ниже предела текучести для пластичных и предела прочности для хрупких материалов.
Однако потеря прямолинейной формы и понижение критических напряжений по сравнению с короткими стержнями для этих стержней «средней» гибкости связаны с такими же явлениями нарушения прочности материала, какие вызывают потерю грузоподъемности в коротких стержнях. Здесь комбинируются и влияние длины, понижающее величину критических напряжений, и влияние значительного роста деформаций материала при напряжениях за пределом пропорциональности.
Экспериментальное определение критических сил для сжатых стержней производилось неоднократно как у нас, так и заграницей. Особенно обширный опытный материал собрал проф. Ф. Ясинский, составивший таблицу критических («ломающих») напряжений в. зависимости от гибкости для целого ряда материалов и положивший начало современным методам расчета сжатых стержней на устойчивость.
Ф. Ясинский, составивший таблицу критических («ломающих») напряжений в. зависимости от гибкости для целого ряда материалов и положивший начало современным методам расчета сжатых стержней на устойчивость.
На основании полученного опытного материала можно считать, что при критических напряжениях, меньших предела пропорциональности, все эксперименты подтверждают формулу Эйлера для любого материала.
Для стержней средней и малой гибкости были предложены различные эмпирические формулы, показывающие, что критические напряжения при таких гибкостях меняются по закону, близкому к линейному:
где а и b коэффициенты, зависящие от материала, a гибкость стержня. Для литого железа Ясинский получил: а = 338,7МПа, b = 1,483 МПа. Для стали 3 при гибкостях от = 40 до = 100 коэффициенты а и b могут быть приняты: а = 336 МПа; b = 1,47МПа. Для дерева (сосна): а = 29,3 МПа; b = 0,194 МПа.
Иногда удобны эмпирические формулы, дающие для неупругой области изменение критических напряжений по закону квадратной параболы; к ним относится формула
Здесь при = 0 считают для пластичного и для хрупкого материала; коэффициент а, подобранный из условия плавного сопряжения с гиперболой Эйлера, имеет значение:
для стали с пределом текучести = 280 МПа а = 0,009 МПа
сосны прочности = 30; а = 0,0008 »
чугуна = 420; а = 0,044 »
При наличии приведенных здесь данных может быть построен полный график критических напряжений (в зависимости от гибкости) для любого материала. На Рис.2 приведен такой график для строительной стали с пределом текучести и пределом пропорциональности .
Рис.2. Полный график критических напряжений для строительной стали.
График состоит из трех частей: гиперболы Эйлера при, наклонной прямой при и горизонтальной, или слабо наклонной, прямой при . Подобные же графики можно построить, комбинируя формулу Эйлера с результатами экспериментов, и для других материалов.
Подобные же графики можно построить, комбинируя формулу Эйлера с результатами экспериментов, и для других материалов.
Таким образом, можно считать, что задача определения критических напряжений для стержней любой гибкости решена с достаточной для практических целей точностью.
Проверка сжатых стержней на устойчивость.
Ранее было отмечено, что для сжатых стержней должны быть произведены две проверки:
на прочность
на устойчивость
где
Для установления допускаемого напряжения на устойчивость нам остается теперь выбрать только коэффициент запаса k.
На практике этот коэффициент колеблется для стали в пределах от 1,8 до 3,0. Коэффициент запаса на устойчивость выбирается выше коэффициента запаса на прочность, равного для стали 1,5 1,6.
Это объясняется наличием ряда обстоятельств, неизбежных на практике (начальная кривизна, эксцентриситет действия, нагрузки, неоднородность материала и т. д.) и почти не отражающихся на работе конструкции при других видах деформации (кручение, изгиб, растяжение).
д.) и почти не отражающихся на работе конструкции при других видах деформации (кручение, изгиб, растяжение).
Для сжатых же стержней, ввиду возможности потери устойчивости, эти обстоятельства могут сильно снизить грузоподъемность стержня. Для чугуна коэффициент запаса колеблется от 5,0 до 5,5, для дерева от 2,8 до 3,2.
Чтобы установить связь между допускаемым напряжением на устойчивость [] и допускаемым напряжением на прочность [], возьмем их отношение:
или
Обозначая
получим:
здесь коэффициент уменьшения основного допускаемого напряжения для сжатых стержней.
Имея график зависимости от для данного материала, зная или и выбрав коэффициенты запаса на прочность и на устойчивость , можно составить таблицы значений коэффициента в функции от гибкости. Такие данные приводятся в наших технических условиях на проектирование сооружений; они сведены в таблицу.
Пользуясь этой таблицей, можно произвести подбор сечения сжатого стержня. Так как величина площади сечения зависит от [], а это напряжение в свою очередь через коэффициент связано с гибкостью стержня , т. е. с формой и размерами его сечения, то подбор приходится осуществлять путем последовательных приближений в таком, например, порядке.
Так как величина площади сечения зависит от [], а это напряжение в свою очередь через коэффициент связано с гибкостью стержня , т. е. с формой и размерами его сечения, то подбор приходится осуществлять путем последовательных приближений в таком, например, порядке.
Выбираем форму сечения и задаемся его размерами; вычисляем наименьший радиус инерции и гибкость; находим по таблице коэффициент и вычисляем допускаемое напряжение на устойчивость ; сравниваем действительное напряжение с величиной []; если условие устойчивости
не удовлетворено, или удовлетворено с большим запасом, меняем размеры сечения и повторяем расчет. Конечно, окончательно выбранное сечение должно удовлетворять и условию прочности
В практических расчетах условие устойчивости иногда записывается так:
В левой части представляет собой расчетное (условное) напряжение.
Таблица.
Пример.
Подобрать двутавровое сечение стойки с одним защемленным концом, сжатой силами Р = 400 кН; длина стойки l=1,5 м. Основное допускаемое напряжение (Рис.3).
Основное допускаемое напряжение (Рис.3).
Рис.3. Расчетная схема сжатой стойки.
Так как в условии устойчивости нам не известно ни , ни , одной из этих величин необходимо задаться. Примем для первого приближения . В этом случае необходимая площадь поперечного сечения стержня будет равна
или
По сортаменту выбираем двутавр No 24, b с площадью . Наименьший радиус инерции сечения . Соответствующая гибкость стойки
Коэффициент по интерполяции между значениями его из таблицы для и равен . Расчетным напряжением будет:
Перенапряжение составляет. Подбираем двутавр No 27, а. ; ; наибольшая его гибкость . Так как коэффициент , то расчетное напряжение
Перенапряжение составляет теперь что допустимо.
Пределы применимости формулы Эйлера
Получив
значение критической силы, мы можем
найти и значение критического напряжения
кр,
разделив критическую силу Ркр на площадь сечения:
.
Учитывая, что отношение равно квадрату минимального радиуса инерции поперечного сечения , получим: , где безразмерный коэффициент называемый гибкостью стержня: , (10.6)
П
Рисунок 10.8. Гипербола Эйлера
олученная зависимость (10.5) представляет собой гиперболическую кривую, называемую гиперболой Эйлера.
В качестве примера на рисунке 10.8 приведена гипербола Эйлера для стали марки Ст3, для которой модуль упругости Е = 2,1105 МПа. Из графика видно, что при возрастании гибкости стержня критическое напряжение стремиться к нулю и, наоборот, по мере приближения гибкости к нулю критическое напряжение увеличивается.
Однако вывод формулы Эйлера был построен на предположении, что напряжения в стержне не превышают предела пропорциональности: , откуда предельное значение гибкости: .
Значит
формула Эйлера непригодна для стержней
с гибкостью меньшей пр. Например, для стали марки Ст3 формула
Эйлера становится непригодной, если:
.
Например, для стали марки Ст3 формула
Эйлера становится непригодной, если:
.
То же значение можно получить, рассматривая график гиперболы Эйлера (рис. 10.8).
Потеря устойчивости может происходить и при напряжениях, превышающих предел пропорциональности. Опытным путем было установлено, что для стержней с гибкостью меньше пр действительные критические напряжения ниже критических напряжений, определенных по формуле Эйлера. Поэтому использование формулы Эйлера для стержней, теряющих устойчивость за пределом пропорциональности, не только принципиально неправильно, но и крайне опасно.
Что бы определить значения критических напряжений для стержней с гибкостью меньше пр проводились многочисленные испытания. На основании результатов экспериментальных исследований Ф. Ясинский предложил эмпирическую формулу, показывающую, что критические напряжения при таких гибкостях меняются по закону, близкому к линейному: , г
Рисунок
10. 9
9
де a и b величины, зависящие от материала; их значения приводятся в справочниках.
Например, для стали марки Ст3 значения данных коэффициентов составляют а = 310 МПа; b = 1,14 МПа.
На рис. 10.9 пунктиром показана прямая, уравнение которой соответствует выражению (10.8). Очевидно, что с правой стороны данная прямая ограничивается гиперболой Эйлера.
При некотором значении гибкости (обозначим его 0) величина кр становиться равной предельному напряжению при сжатии: 0 = т для пластичных материалов или 0 = в для хрупких материалов. Стержни, у которых < 0, называют стержни малой гибкости. Их рассчитывают только на прочность.
Таким
образом, для стали марки Ст3 график кр = f()состоит
из трех частей: гиперболы Эйлера при
> 100, наклонной прямой при 60 <
< 100 и горизонтальной прямой при
< 60. Горизонтальная прямая соответствует
пределу текучести.
Горизонтальная прямая соответствует
пределу текучести.
Ранее во всех рассмотренных нами задачах предполагалось, что действующие нагрузки статические, т.е. не изменяющиеся с течением времени. При проектировании машин обычно сталкиваются с деталями, находящимися в неравномерном движении, что приводит к появлению инерционных нагрузок.
Примером статической нагрузки, или статического действия нагрузки, может послужить действие подвешенного на цепи груза. Это действие остается статическим, если груз будет подниматься цепью с постоянной скоростью. Но тот же груз, поднимаемый цепью с ускорением, будет действовать на цепь динамически. Для расчета цепи в данном случае мы должны учесть не только вес груза, но и силу инерции груза.
Д
Рисунок 11.1
ля примера рассмотрим расчет
равномерно вращающегося тонкого кольца
(рис. 11.1, a).Для
расчета примем следующие обозначения: r
средний радиус кольца; F
площадь поперечного сечения;
удельный вес материала;
угловая скорость кольца; g
ускорение силы тяжести.
Рассмотрим бесконечно малый элемент кольца массой dm, вырезанный двумя плоскостями, составляющими центральный угол d (рис. 11.1, б)
Элементарная сила инерции dФ: . Элементарная масса, выраженная через площадь сечения кольца: .
Элементарная сила инерции с учетом (11.2) будет равна: Для определения продольной силы N в поперечном сечении кольца рассмотрим равновесие половины кольца под действием двух продольных сил N и суммы вертикальных составляющих элементарных сил инерций: , откуда . (11.4)
Полагая, что в тонком кольце все волокна растягиваются одинаково, найдем напряжение в сечении кольца: . Определим теперь, на сколько удлинится радиус вращающегося кольца. Относительное удлинение волокон кольца равны: .Из закона Гука: .Откуда . (11.6)
Урок 8. предел функции на бесконечности — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №8. Предел функции на бесконечности.
Предел функции на бесконечности.
Перечень вопросов, рассматриваемых в теме
1)понятие бесконечности;
2) определение предела функции на плюс бесконечности;
2) определение предела функции на минус бесконечности;
3) правила вычисления пределов функции на бесконечности;
4) формулы вычисления предела функции на бесконечности;
5) нахождение горизонтальные, вертикальные, наклонные асимптоты.
Глоссарий по теме
Бесконечность – сколь угодно большое(малое), безграничное число.
Дробно-рациональная функция – это такая алгебраическая дробь, у которой числитель и знаменатель представляют собой многочлены некоторой степени.
Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
– М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Понятие «бесконечность» используется для характеристики безграничных, беспредельных, неисчерпаемых предметов и явлений, в нашем случае характеристика чисел.
Бесконечность – сколь угодно большое(малое), безграничное число.
Если рассмотреть координатную плоскость, то ось абсцисс(ординат) уходит на бесконечность, если ее безгранично продолжать влево или вправо (вниз или вверх).
Теперь давайте перейдем к пределу функции на плюс и минус бесконечности.
Предел функции на плюс бесконечности.
Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч [a; +∞), и пусть прямая y=b является горизонтальной асимптотой графика функции y=f(x), запишем все это на математическом языке:
Предел функции на минус бесконечности.
Посмотрим немного другой случай:
Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч (-∞; a], и пусть прямая y=b является горизонтальной асимптотой графика функции y=f(x), запишем все это на математическом языке:
Предел функции на бесконечности.
Так же наши соотношения могут выполняться одновременно:
Тогда принято записывать как:
Для вычисления предела на бесконечности пользуются несколькими утверждениями.
Основные свойства:
- Для любого натурально числа m справедливо следующее соотношение:
- Если и
а) Предел суммы равен сумме пределов:
б) Предел произведения равен произведению пределов:
в) Предел частного равен частному пределов:
г) Постоянный множитель можно вынести за знак предела:
А теперь давайте перейдем к дробно — рациональной функции.
Дробно-рациональная функция – это такая алгебраическая дробь, у которой числитель и знаменатель представляют собой многочлены некоторой степени.
Дробно-линейная функция представляет собой частный случай дробно-рациональной функции.
Дробно-линейная функция – это такая алгебраическая дробь , у которой числитель и знаменатель представляют собой линейные функции.
Во всякой дробно-линейной функции можно выделить целую часть.
Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность.
x=a уравнение вертикальной асимптоты
y=b уравнение горизонтальной асимптоты
y=kx+b уравнение наклонной асимптоты
Перейдем к практической части.
Примеры и разбор решения заданий тренировочного модуля
Пример1. Вычислить пределы функций:
а)
б)
в)
г)
Пример 2. Построим график функции .
Преобразуем функцию с выделением целой части:
.
Дробно-линейная функция имеет две асимптоты: горизонтальную и вертикальную.
y=2 горизонтальная асимптота
x=1 вертикальная асимптота, т. к.
к.
Точки пересечения графика с осями координат:
при x=0 y=3 , точка (0; 3)
при y=0 x=1,5 , точка (1,5; 0)
Пример 3
Построить график функции .
Преобразуем функцию с выделением целой части
- y=2x наклонная асимптота
x | 0 | 2 |
y | 0 | 4 |
X=0 вертикальная асимптота
функция ни четная, ни нечетная.
- точки пересечения графика с осями координат:
Приy=0
, точка
с осью ординат график функции не пересекается, т.к. эта ось есть асимптота.
y’=0
xкр=1
6) y(1)=3
7) Построим график
Пределы применимости формулы Эйлера
Формула Эйлера применима при работе трения в упругой стадии, когда критическое напряжение меньше предела пропорциональности формула. 2
2
2. Стержень средней гибкости. рассчитывается на прочность и устойчивость
λ=60:100
δр<δкр<δу
Для таких стержней применяется напряжение определяющееся по формуле Яшинского.
δпр=авλ
а и в постоянные для материала.
Для стали а=310МПА, в=1,41МПА
Fкр=δпр*А
3. Стержень малой гибкости Λ=0:60
Рассчитывается только на прочность δкр=δу
δ=F\A≤R
Можно построить график продольных напряжений для стали
РАСЧЕТ НА УСТОЙЧИВОСТЬ
Поскольку стержни рассчитывающиеся на устойчивость находятся под действием сжимающейся силы, условия прочности и условия устойчивости записываются аналогично. Условия прочности на сжатие:
δ=F\A≤R
R=δ0\K
Опасное напряжение для пластичных напряжений равно пределу текучести δ0=δy. Для хрупких материалов опасное напряжение равно пределу прочности
Условие устойчивости
δ=F\A≤Ry
Ry=δy\Ky
Коэффициент (фи) зависит от гибкости стержня и определяется по таблице по λ и материалу стержня.
Условие устойчивости имеет вид:
δ=F\A≤Ry
При расчете на прочность учитывается ослабленное сечение.
30. ПРОВЕРОЧНЫЙ И ПРОЕКТИРОВОЧНЫЙ РАСЧЕТЫ НА УСТОЙЧИВОСТЬ
При проверочном расчете, когда площадь поперечного сечения задана, проверяют условие устойчивости след. образом:
1)определяют минимальный радиус инерции imin =
2)определяют гибкость стойки ʎ=
3)по гибкости и материалу стержня определяют коэф-т φ; ʎ → φ
4)определяется расчетное сопротивление на устойчивость Ry= R* φ
5)проверяется устойчивость
При проектировочном расчете площадь сечения и коэфф-ент продольного изгиба не известны.
Для подбора поперечного сечения одной из величин необходимо задаваться. Обычно φ:
1)принимаем φ=0,5
2)определяем требуемую площадь поперечного сечения т.е. ; A ≥
3) imin = 4) ʎ= 5) ʎ → φ 6) провер. условие устойчивости
7) сравниваем и R. Если расхождение не превышает 5%,то расчет заканчивается,в противном случае задается новое значение .
, и далее расчет повторяется.
31. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ
Если к стержню одновременно приложены продольная сила N и поперечная нагрузки, то возникает продольно-поперечный изгиб.
Изгибающий момент в сечении на расстоянии z можно рассматривать как сумму двух моментов. М= — (Мо+ Nу) , где Мо- изгибающий момент от поперечных нагрузок,
Ny-изгибающий момент от продольной силы.
Запишем диф-ое уравнение изогнутой оси балки
EJy”=M
EJy”=-(Mo+Ny) *
————————
E Jy”+Ny=-Mo
y”+ y= —
=K2
y”+ K2y=-
Решение этого уравнения представляет собой сумму 2 интегралов: интегр. однородного уравнения и частного интеграла неоднород. уравнения. Такая задача имеет сложное решение. Поэтому использ. приближ. метод решения т.е. задается деформация балки или стойки,но таким образом чтобы удовлетвор-сь граничные условия.
При продольном изгибе было установлено,что балка изгибается по синусоидальному закону.
Предположим,что и заданная балка деф-ся по такому же закону.
y=ymax sin z; Проверим выполнение граничных условий.
z=0 → y=0
z=1 → y=0
z=1/2 → y= ymax продиференцир. заданное выражение *
y’= ymax cos
y”= — ymax sin z подставим значение 2-ой производной в выр-ие *
EJ ymax sin z=Mo+Ny
при z= /2 y= EJ ymax = Mo+Nymax обозначение =Fэ – Эйлерова сила
здесь µ=1 Fэ= ymax -Nymax =Мо
ymax= ymax= ymax—полный прогиб от совместного действия поперечных и продольных сил.
Зная максим. прогиб и внутр. силы запишем условия прочности.
σmax= + =
ПРИМЕР: Проверить прочность и устойчивость стойки.
[ №18 Jx=1090 см4 ; ix=7,24 см ; Wx=121 cм3 ; A=20,7 см ; Е=210 Гпа ; R=200Мпа
σmax= + =
Момент инерции и мом. сопротивл. берутся относит. оси перпендикулярной пл-ти действия поперечной нагрузки.
сопротивл. берутся относит. оси перпендикулярной пл-ти действия поперечной нагрузки.
ymax= ; Fэ=
yo = = Fэ=705 кН
ymax = Проверим прочность σmax= 181Мпа
Проверяем на устойчивость плоскость действия попереч. сил
σmax=
ʎ= =110
σmax =109,4Мпа <R
ПРАВИЛА КОНТРОЛЯ КОЛИЧЕСТВА НЕФТИ СЫРОЙ, В ОТНОШЕНИИ КОТОРОЙ МОГУТ ПРИМЕНЯТЬСЯ ОСОБЫЕ ФОРМУЛЫ РАСЧЕТА СТАВОК ВЫВОЗНЫХ ТАМОЖЕННЫХ ПОШЛИН НА НЕФТЬ СЫРУЮ
Утверждены
постановлением Правительства
Российской Федерации
от 29 марта 2013 г. N 277
Список изменяющих документов
(в ред. Постановления Правительства РФ от 25.12.2018 N 1667)
1. Настоящие Правила устанавливают порядок проведения контроля количества нефти сырой, в отношении которой могут применяться особые формулы расчета ставок вывозных таможенных пошлин на нефть сырую (далее — нефть сырая).
2. Контроль количества нефти сырой осуществляется Федеральной таможенной службой.
3. Участник внешнеэкономической деятельности, осуществляющий вывоз нефти сырой из Российской Федерации за пределы таможенной территории Евразийского экономического союза трубопроводным транспортом (далее — заявитель), ежеквартально, не позднее чем за 15 календарных дней до начала квартала, в котором осуществляется вывоз добытой нефти из Российской Федерации, представляет в Министерство энергетики Российской Федерации справку о подтверждении соответствия сведений об экспорте нефти сырой графику транспортировки нефти из Российской Федерации, утвержденному Министерством, по форме, утвержденной Министерством (далее — справка).
(в ред. Постановления Правительства РФ от 25.12.2018 N 1667)
(см. текст в предыдущей редакции)
4. Министерство энергетики Российской Федерации в течение 3 рабочих дней со дня поступления справки проводит проверку сведений, содержащихся в справке, и при достоверности указанных сведений подтверждает ее и направляет заявителю. В случае выявления в ходе проверки недостоверных сведений, содержащихся в справке, Министерство в течение 5 рабочих дней со дня поступления справки направляет заявителю мотивированный отказ в подтверждении справки.
5. Справка (копия справки), подтвержденная Министерством энергетики Российской Федерации, представляется декларантом (таможенным представителем) в таможенный орган, в котором осуществляется таможенное декларирование товаров, для подтверждения заявляемого во временной таможенной декларации количества нефти сырой, планируемого к вывозу трубопроводным транспортом.
6. При вывозе нефти сырой из Российской Федерации за пределы таможенной территории Евразийского экономического союза иными видами транспорта, помимо трубопроводного транспорта, количество нефти сырой заявляется во временной декларации на товары исходя из планового объема вывоза. Для подтверждения планового объема вывоза количества нефти сырой декларант (таможенный представитель) представляет в таможенный орган, в котором осуществляется таможенное декларирование товаров, следующие сведения:
(в ред. Постановления Правительства РФ от 25.12.2018 N 1667)
(см. текст в предыдущей редакции)
а) прогноз добычи нефти сырой в отчетном календарном году согласно утвержденной проектной документации;
б) выписка из государственного баланса запасов полезных ископаемых на дату не ранее чем 1 января года, предшествующего году периода добычи и экспорта нефти сырой, содержащая сведения о физико-химических характеристиках нефти сырой;
в) данные о количестве нефти сырой, добытой на соответствующем месторождении и вывезенной из Российской Федерации за пределы таможенной территории Евразийского экономического союза в предыдущие периоды с применением особых формул расчета ставок вывозных таможенных пошлин на нефть сырую;
(в ред. Постановления Правительства РФ от 25.12.2018 N 1667)
Постановления Правительства РФ от 25.12.2018 N 1667)
(см. текст в предыдущей редакции)
г) плановый объем вывоза нефти сырой иными видами транспорта, помимо трубопроводного транспорта.
7. При подаче декларации (полной декларации) на товары таможенные органы осуществляют контроль количества нефти сырой, вывезенной из Российской Федерации за пределы таможенной территории Евразийского экономического союза, на основании представляемых декларантом (таможенным представителем) в таможенный орган письменного подтверждения факта добычи нефти сырой за отчетный месяц на соответствующем месторождении (с указанием участка недр), выдаваемого в соответствии с Правилами подтверждения факта добычи нефти сырой с вязкостью в пластовых условиях не менее 10000 миллипаскаль-секунд или нефти сырой с особыми физико-химическими характеристиками, добытой в границах географических объектов, указанных в подпункте 4 пункта 5 статьи 3.1 Закона Российской Федерации «О таможенном тарифе», утвержденными постановлением Правительства Российской Федерации от 29 марта 2013 г. N 277 «О порядке подтверждения факта добычи и контроля количества нефти сырой, в отношении которой могут применяться особые формулы расчета ставок вывозных таможенных пошлин на нефть сырую, а также о признании утратившим силу постановления Правительства Российской Федерации от 16 июля 2009 г. N 574», а также актов приема-сдачи нефти сырой и паспортов качества.
N 277 «О порядке подтверждения факта добычи и контроля количества нефти сырой, в отношении которой могут применяться особые формулы расчета ставок вывозных таможенных пошлин на нефть сырую, а также о признании утратившим силу постановления Правительства Российской Федерации от 16 июля 2009 г. N 574», а также актов приема-сдачи нефти сырой и паспортов качества.
(п. 7 в ред. Постановления Правительства РФ от 25.12.2018 N 1667)
(см. текст в предыдущей редакции)
8. Контроль количества нефти сырой, вывозимой различными видами транспорта, осуществляется таможенными органами нарастающим итогом с учетом установленного подпунктом 4 пункта 5 статьи 3.1 Закона Российской Федерации «О таможенном тарифе» предельного количества нефти, добытой на участке недр, за исключением объемов нефти, добытой на новых морских месторождениях углеводородного сырья, которое может быть вывезено из Российской Федерации за пределы таможенной территории Евразийского экономического союза с применением особых формул расчета ставок вывозных таможенных пошлин.
(п. 8 в ред. Постановления Правительства РФ от 25.12.2018 N 1667)
(см. текст в предыдущей редакции)
Формулы пределов и формулы целей
| Ежемесячная техническая подсказка от Тони ХансенаSignUp | Нет отслеживания ! Нет объявлений ! Вот почему эта страница загружается быстро! |
Все товары
Недорогой тестер текучести расплава глазури
Односкоростной лабораторный или студийный смеситель для суспензии 20 лет замены Albany Slip
Обзор красителей для керамики
Контролируете ли вы свой производственный процесс?
Безопасны ли ваши глазури для пищевых продуктов или они выщелачиваются?
Атака на стекло: механизмы коррозионного воздействия
Глазури, массы, ангобы для шаровой мельницы
Связующие для керамических масс
Выявление больших пушек в борьбе с безумием: MgO (G1215U) Изменение нашего взгляда на глазури
Сравнение химии и смешения матриц для создания глазурей из природных материалов
Сконцентрируйтесь на одной хорошей глазури
Конус 6 Рецепт плавающей синей глазури
Медно-красные глазури
Трещины и бактерии: есть ли опасность?
Растрескивание керамических глазурей: устранение причин, а не симптомов
Создание неглазурованного керамического шликера или ангоба
Создание собственной бюджетной глазури
Кристаллические глазури: понимание процесса и материалов
Дефлокулянты: подробный обзор
Демонстрация проблем прилегания глазури к Учащиеся
Диагностика проблемы литья на заводе сантехники
Сушка керамики без трещин
Дублирование шликера Albany
Дублирование AP Green Fireclay
Любительские электрические печи: что нужно знать То, что вам не нужно: Стабильность глазури Raku
Фиксация глазури, которая не остается в суспензии
Составление массы с использованием местных глин
Составление прозрачной глазури, совместимой с хромо-оловянными красителями
Рецептура фарфора
Рецептура глазури из золы и нативных материалов
G1214M Конус 5-7 20×5 Глянцевая базовая глазурь
G1214W Конус 6 Прозрачная базовая глазурь
G1214Z Конус 6 Матовая базовая глазурь
G1916M Конус 52/9016G17A77/02 G12G16-04 Базовая глазурь 904 /10R Base Matte/Glossy Glazes
Получение желаемого цвета глазури: работа с пятнами
Глазурь и телесные пигменты и пятна в производстве керамической плитки
Основы химии глазури — формула, анализ, молярный %, единица приблизительный анализ
Рецепты глазури: создавайте собственные рецепты
Типы глазури, рецептура и применение в производстве плитки
Проверка глазури на выделение токсичных металлов
Высокоглянцевые глазури
Как проводится химический анализ материала Formula Weight
Как найти и протестировать собственные глины
Я всегда делал это так!
Струйное украшение керамической плитки
Безопасна ли ваша обожженная посуда?
Конус для выщелачивания 6 Пример использования глазури
Предельные формулы и целевые формулы
Бюджетные испытания свойств глазури в сыром виде и после обжига
Рецепт отливки из белого талька с низкой огнестойкостью
Изготовление собственного стенда для шаровой мельницы
Изготовление конусов для испытаний глазури
Монопороза или плитка для стен однократного обжига Глины: подробный обзор
Керамика, устойчивая к атмосферным воздействиям на открытом воздухе
Окрашивание глазурью вместо погружения или распыления
Распределение размеров частиц керамических порошков
Фарфоровая плитка, стекловидная плитка
Рационализация противоречивых мнений о пластичности
Рождение шликера Ravenscrag
Переработка лома глины
Снижение температуры обжига глазури с конуса 10 до 6
Простое физическое испытание глины
Одинарное огнеупорное остекление
Растворимые соли в минералах: подробный обзор Работа с трещинами, вызванными обжигом
Рецепты литья керамогранита
Замена корнуоллского камня
Сверхочищенный Terra Sigillata
Химия, физика и производство глазури
Влияние подгонки глазури на прочность обожженной посуды
Четыре уровня просмотра керамической глазури
Процесс изготовления глиняной посуды из майолики
Молитва гончара
Правильный химический состав для конуса 6 MgO Matte
Испытания быть единственным техническим специалистом в Клуб
На этом нытье прекращается: реалистичный взгляд на глиняные тела
Эти немаркированные мешки и ведра
Плитка и мозаика для гончаров
Токсичность огнеупорных кирпичей, используемых в печах
Торговля рецептами глазури
Общие сведения о керамических материалах
Общие сведения о керамических оксидах
Общие сведения о свойствах глазури
Общие сведения о процессе дефлокуляции при шликерном литье
Основные сведения о рецептах шликерного литья терракотовой плитки в Северной Америке
Общие сведения о тепловом расширении керамических глазурей
Нежелательная кристаллизация в конусе 6 глазури
Вулканический пепел
Что определяет температуру обжига глазури?
Что такое крот, проверка крота
Что такое глазурь-дракон?
С чего начать знакомство с глазурью?
Почему глазури из учебников такие сложные
Описание
Химический состав глазури для каждого типа глазури имеет типичный вид, что позволяет нам определить нетипичные. Формулы лимита и цели полезны для нас, если мы будем иметь в виду их правильное использование.
Формулы лимита и цели полезны для нас, если мы будем иметь в виду их правильное использование.
Артикул
Целевые формулы
Я избегаю классификации и классификации глазурей по конкретным категориям. В прошлом я переоценивал химический состав глазури (настольное программное обеспечение Digitalfire Insight много лет полностью фокусировалось на этом). Хотя химия является ключевым фактором в понимании того, почему глазури так воспламеняются, мы не должны упускать из виду их физическое присутствие. Insight-live, преемник настольного Insight, гораздо больше связан с пониманием физики глазурей (например, понимание их текучести, цвета, поверхности, пестроты, формирования кристаллов в зависимости от температуры, графика обжига, нанесения, методов подготовки и выбора материала) и тела, к которым они применяются. Insight-live по-прежнему занимается химией, но менее идеалистично и более реалистично оценивает свое воздействие, помещая его в контекст с физикой. Таким образом, я обнаружил, что термин «предельные формулы» предполагает, что мы лучше понимаем и контролируем химию, чем на самом деле, и что определенные типы глазури имеют узкий химический профиль (чего они чаще всего не делают). Вот почему я предпочитаю термин «целевая формула». В последние годы все больше и больше людей даже не пользуются формулами единства, предпочитая сравнивать глазури с помощью процентного анализа или молярных процентов. Чем больше вы знаете о рецепте, тем больше он не поддается классификации таким образом, физическая часть Insight как раз об этом. Речь идет о понимании тела или глазури с точки зрения тех, о которых вы уже знаете. Когда вы используете физический подход, вы гораздо более склонны к более тщательному тестированию глазури и в большем количестве обстоятельств, и вы менее склонны классифицировать их слишком конкретно.
Вот почему я предпочитаю термин «целевая формула». В последние годы все больше и больше людей даже не пользуются формулами единства, предпочитая сравнивать глазури с помощью процентного анализа или молярных процентов. Чем больше вы знаете о рецепте, тем больше он не поддается классификации таким образом, физическая часть Insight как раз об этом. Речь идет о понимании тела или глазури с точки зрения тех, о которых вы уже знаете. Когда вы используете физический подход, вы гораздо более склонны к более тщательному тестированию глазури и в большем количестве обстоятельств, и вы менее склонны классифицировать их слишком конкретно.
Целевая формула — это формула, которая может произвести определенный эффект. Обратите внимание, я говорю о формулах, а не о рецептах. Это «универсальный язык» глазури. Вы должны рассчитать смесь материалов, необходимых для подачи формулы. Рассмотрим кристаллическую глазурь. Среди прочего, целевая формула должна указывать низкое содержание оксида алюминия, чтобы стимулировать плавление жидкости, чтобы могли расти кристаллы. Точно так же матовые, медно-красные, хромово-оловянно-розовые и многие специальные поверхностные эффекты и цвета имеют «механизмы», которые мы можем изолировать, то есть рационализировать в терминах формулы. В некоторых глазури баланс всей формулы имеет решающее значение для получения эффекта, в других вы можете определить присутствие одного или двух ответственных оксидов. В последнем обычно можно «пересадить» механизм в проверенную базовую глазурь. Для первого часто можно настроить химию основы, а затем пересадить в механизм.
Точно так же матовые, медно-красные, хромово-оловянно-розовые и многие специальные поверхностные эффекты и цвета имеют «механизмы», которые мы можем изолировать, то есть рационализировать в терминах формулы. В некоторых глазури баланс всей формулы имеет решающее значение для получения эффекта, в других вы можете определить присутствие одного или двух ответственных оксидов. В последнем обычно можно «пересадить» механизм в проверенную базовую глазурь. Для первого часто можно настроить химию основы, а затем пересадить в механизм.
Есть соблазн выявить механизмы, захватив существующие рецепты нужного типа (т.е. из Интернета) и изучив их как группу. Однако при таком подходе вывод будет испорчен влиянием «плохих» примеров в исследовательской группе или рецептов, которые производят тот же визуальный эффект, используя другой механизм. Лучший подход — выбрать проверенный рецепт и изучить его формулу в свете того, что написано и что известно об оксидах. Сравнение с более плохими образцами того же типа глазури может затем помочь определить допуски.
Предельные формулы
Когда я говорю о предельных формулах, я имею в виду рекомендации для базовых функциональных глазурей . Мы все хотим, чтобы глазури были надежными, стабильными, предсказуемыми, работали со многими цветами, устойчивы к выщелачиванию, не образовывали пузырей, расползаний и проколов, были прочными, регулируемыми по расширению, имели прозрачность, не расстекловывались и т. д. В Digitalfire мы выступаем за основу: с корректировками, чтобы обеспечить прочную основу для последующих цветных, непрозрачных и пестрых версий. Теоретически невозможно придумать ориентир, который всегда будет обеспечивать все вышеперечисленные свойства для определенного типа глазури. Это связано с тем, что меры, необходимые для достижения этих свойств, часто противоречат друг другу и должны быть сбалансированы и рационализированы. Эта область, безусловно, является таким случаем, ничто не заменит знание оксидов, когда дело доходит до сравнения существующей глазури с предельными или целевыми формулами.
Однако, как люди, нам все равно нужны числа, верно! По общему признанию, предельные формулы оказались ценным сторожевым псом для выявления подозрительных глазурей и объяснения очевидных недостатков стабильности, твердости и других проблем. Тот факт, что мы можем выделить механизм поверхностного характера для типа глазури и воспроизвести его с замечательным успехом, также является свидетельством возможной полезности предельных формул для достижения конкретных функциональных свойств в основных глазурях. Предельные формулы можно найти во многих учебниках, они были разработаны опытными специалистами керамической промышленности как консервативное руководство для хорошо плавящихся и прочных глазурей (однако не обязательно устойчивых к выщелачиванию). Как правило, это не просто «средний рецепт», рассчитанный на основе большого количества рабочих рецептов, каждый диапазон оксидов был рационализирован в свете истории испытаний и производства, а также того, что известно о нем и его взаимодействии с другими. Мы можем только догадываться о мыслительных процессах и проверках, которые необходимы для разработки набора предельных формул. Автор диаграммы должен сбалансировать количество оксидов, принимая во внимание тот факт, что одни повышают твердость, другие ускоряют плавление, противостоят выщелачиванию, матируют поверхность, уменьшают расширение, стабилизируют стекло и т. д. Например, оксид, способствующий повышению твердости глазури, не обязательно способствует химическая стабильность и наоборот (например, CaO). Использование ограничений, по общему признанию, является вопросом доверия и веры. Тем не менее, когда учащиеся смешивают рецепт, формула которого находится на среднем уровне, они имеют высокую вероятность успеха с первого раза.
Мы можем только догадываться о мыслительных процессах и проверках, которые необходимы для разработки набора предельных формул. Автор диаграммы должен сбалансировать количество оксидов, принимая во внимание тот факт, что одни повышают твердость, другие ускоряют плавление, противостоят выщелачиванию, матируют поверхность, уменьшают расширение, стабилизируют стекло и т. д. Например, оксид, способствующий повышению твердости глазури, не обязательно способствует химическая стабильность и наоборот (например, CaO). Использование ограничений, по общему признанию, является вопросом доверия и веры. Тем не менее, когда учащиеся смешивают рецепт, формула которого находится на среднем уровне, они имеют высокую вероятность успеха с первого раза.
Формулы пределов обычно показывают предпочтительные диапазоны для каждого оксида для определенного типа глазури, они говорят нам, какой химический состав является общим для класса глазури. Термин «формула ограничения» имеет тенденцию побуждать к несоблюдению, поэтому мы иногда используем термин «формула предложения». Тем не менее, если у вас есть глазурь, которая не соответствует диапазонам для своего типа, у вас должно быть четкое обоснование и результаты испытаний, подтверждающие это (дополнительную информацию см. в статьях о тестировании глазури).
Тем не менее, если у вас есть глазурь, которая не соответствует диапазонам для своего типа, у вас должно быть четкое обоснование и результаты испытаний, подтверждающие это (дополнительную информацию см. в статьях о тестировании глазури).
Споры о формулах ограничения
Люди из лагеря «керамика без ограничений» отмечают, что ограничения являются ограничительными и произвольными для среднего керамиста, они предназначены для профессионалов, они производят базовые глазури с ограниченным цветовым диапазоном и качеством поверхности, и что можно изготавливать долговечные глазури. которые выходят далеко за пределы. Это правда? Я не видел ни одного из них доказанным. Тем не менее, они предлагают анализ формул существующих глазурей для выявления общности, чтобы лучше понять данный тип глазури, таким образом, в некотором смысле пытаясь создать предельные формулы. Я утверждаю, что среднестатистический человек не имеет опыта или средств тестирования, чтобы выбрать хороших кандидатов для группового анализа, и что наилучший диапазон «функциональных» цветов и качеств поверхности возможен, когда вы придерживаетесь ограничений, предназначенных для того, чтобы сделать глазури функциональными и долговечными. Я также считаю, что формулы пределов лучше всего использовать неопытными людьми в качестве консервативного подхода, пока они не разработают «лицензию» для превышения пределов. Позвольте мне выразить это по-другому: дайте мне любую функциональную глазурь, которая выглядит великолепно, но при этом сумасшедшая, мягкая, поддающаяся выщелачиванию, с пузырями, точечными отверстиями, ненадежная и с которой трудно работать, держу пари, я смогу воспроизвести ее как твердую, устойчивы к выщелачиванию, не сходят с ума, надежны и функциональны. И я готов поспорить, что его формула окажется в типичных пределах для этого типа!
Я также считаю, что формулы пределов лучше всего использовать неопытными людьми в качестве консервативного подхода, пока они не разработают «лицензию» для превышения пределов. Позвольте мне выразить это по-другому: дайте мне любую функциональную глазурь, которая выглядит великолепно, но при этом сумасшедшая, мягкая, поддающаяся выщелачиванию, с пузырями, точечными отверстиями, ненадежная и с которой трудно работать, держу пари, я смогу воспроизвести ее как твердую, устойчивы к выщелачиванию, не сходят с ума, надежны и функциональны. И я готов поспорить, что его формула окажется в типичных пределах для этого типа!
Это правда, что пределы не отражают сложность науки о функциональной глазури. Но до тех пор, пока у нас не будет жизнеспособной альтернативы, отказ от ограничений означает предоставление студенту лицензии на полный отказ. И это происходит. Я вижу учебники, полные глазури, которой не место в функциональной посуде. Новичкам следует придерживаться консервативного подхода. Когда вы смотрите на таблицу предельных значений, представьте себе специалиста по промышленной глазури с многолетним опытом, который проверяет, что работает, а что нет. Стоит ли игнорировать его?
Когда вы смотрите на таблицу предельных значений, представьте себе специалиста по промышленной глазури с многолетним опытом, который проверяет, что работает, а что нет. Стоит ли игнорировать его?
Сравнение и изучение этих таблиц пределов
К сожалению, существует некоторая путаница с таблицами пределов. В следующей таблице сравниваются два набора таблиц предельных значений (для глазурей с низкой, средней и высокой огнестойкостью) и это иллюстрируется. Один из них мы использовали в течение многих лет (традиция британской керамической промышленности), другой — от Green and Cooper. На первый взгляд урок состоит в том, что цифры G&C более остро подчеркивают необходимость достаточного количества кремнезема и глинозема в глазури, особенно при более высоких температурах.
Оксид | Традиционные пределы Великобритании | Границы Green & Cooper | |||||
|---|---|---|---|---|---|---|---|
Конус 04-02 | Конус 3-7 | Конус 8-10 | Конус 04 | Конус 6 | Конус 10 | ||
| СаО | 0,1-0,6 | 0,1-0,7 | 0,35-0,8 | 0-0,3 | 0-0,55 | 0-0,7 | |
| ZnO | -0,20 | -0,25 | -0,3 | 0-0,18 | 0-0,3 | 0-0,36 | |
| ВаО | -0,3 | -0,3 | -0,3 | 0-0,28 | 0-0,4 | 0-0,475 | |
| MgO | -0,3 | -0,3 | -0,4 | 0-0,3 | 0–0,325 | 0-0,34 | |
| КНаО | -0,5 | 0,1-0,5 | 0,1-0,5 | 0-0,525 | 0–0,375 | 0-0,3 | |
| Ли 2 О | -0,2 | н/д | н/д | н/д | |||
| ООО | -0,4 | 0,7 | н/д | н/д | н/д | ||
| Б 2 О 3 | 0,3-1,1 | -0,4 | -0,3 | 0-1,0 | 0–. 35 35 | 0–.225 | |
| Ал 2 О 3 | 0,1-0,4 | 0,2-0,35 | 0,3-0,55 | 0,1-0,45 | 0,275-0,65 | 0,45-0,825 | |
| SiO 2 | 1,5-3,0 | 2,5-3,5 | 3,0-5,0 | 1,375-3,15 | 2,4-4,7 | 3,5-6,4 | |
- Функциональные глазури должны содержать достаточное количество диоксида кремния и оксида алюминия для образования химически стабильного и прочного стекла, а недостаточное их количество является наиболее распространенным источником нестабильности функциональных глазурей.
 Второй набор диаграмм также рекомендует более высокие минимумы для обоих. Отметим также, что, в отличие от других, SiO 9Оксиды 0307 2 и Al 2 O 3 всегда указываются с минимальными количествами, что подчеркивает необходимость адекватных уровней для достижения твердости глазури.
Второй набор диаграмм также рекомендует более высокие минимумы для обоих. Отметим также, что, в отличие от других, SiO 9Оксиды 0307 2 и Al 2 O 3 всегда указываются с минимальными количествами, что подчеркивает необходимость адекватных уровней для достижения твердости глазури. - Обратите внимание, что суммы B 2 O 3 близки к одинаковым, хотя сумма G&C немного более консервативна. Это подчеркивает необходимость минимизировать B 2 O 3 для твердости глазури.
- В диаграммах предельных значений всегда предполагается единица потока. Как упоминалось выше, некоторые технические специалисты предпочитают классифицировать B 2 O 3 как флюс, в то время как другие рассматривают его отдельно, признавая его дополнительную функцию стеклообразователя. В некоторых таблицах предельных значений не указано, являются ли они единицами бора или нет. Обратите внимание, что первый набор из трех вышеприведенных диаграмм имеет 1,1 как максимальное количество B 2 O 3 в конусе 04, это предупреждение о том, что он не должен включать B 2 O 3 в единицу ( поскольку 1,0 будет математическим максимумом).
 Аналогично, второй набор диаграмм показывает предел конуса 04 на уровне 1,0, это также указывает на то, что они не включают B 2 О 3 в единстве.
Аналогично, второй набор диаграмм показывает предел конуса 04 на уровне 1,0, это также указывает на то, что они не включают B 2 О 3 в единстве. - Оксиды двойного назначения, оптимальное плавление: некоторые флюсы интенсивно плавятся при высоких температурах, но не функционируют как флюсы при низких температурах (например, MgO, CaO). Это слабость всего стандарта единства потока. Также подразумеваемым пределом является то, что концентрации более тугоплавких флюсов не превышают тех, которые полностью растворяются, и что для любого количества одного флюса существует оптимальная смесь других сопутствующих флюсов для получения наилучшего расплава. Однако предельные формулы не предназначены для руководства по оптимальному плавлению, они представляют собой диапазон, в пределах которого наиболее вероятно обнаружение оптимальных смесей. Например, в нижней части диапазона температур должна быть более высокая доля щелочей и более низкая доля щелочноземельных металлов.

- Точность: Непонятно, почему в таблице G&C используются значения с точностью до трех знаков после запятой, предельная диаграмма не может быть такой точной.
- Другие отличия в таблицах:
— Более высокие G&C CaO при низкой температуре могут быть признание его функции матирующего агента.
-G&C позволяет больше ZnO, и это кажется необычным, учитывая наш опыт работы с глазурями с высоким содержанием цинка.
— На диаграмме G&C KNaO рассматривается скорее как низкотемпературный поток. Также возможно, что это побуждает читателей разнообразить многие эффективные потоки на высоких скоростях. температурах и низком тепловом расширении.
-Графики G&C позволяют намного выше Al 2 O 3 и SiO 2 . Это подтверждает важность достаточного количества эти оксиды и их большое количество допустимы, если глазурь надлежащим образом проверена на плавление. - Таблицы (особенно G&C) допускают чрезмерное количество BaO.
 Не используйте BaO на функциональных поверхностях. Несмотря на то, что BaO указан в обоих тестах, мы рекомендуем не добавлять его в глазури для пищевых продуктов, если у вас нет возможности проводить испытания на выщелачивание.
Не используйте BaO на функциональных поверхностях. Несмотря на то, что BaO указан в обоих тестах, мы рекомендуем не добавлять его в глазури для пищевых продуктов, если у вас нет возможности проводить испытания на выщелачивание. - Превышение одних пределов не так серьезно, как другие. Например, если бы вы использовали первый набор диаграмм, нетрудно было бы получить избыточное количество Al 2 O 3 в хорошо расплавленной глазури. Это гораздо менее серьезно, чем недоподача, особенно если бора достаточно для его плавления.
- Подходить к некоторым пределам следует с осторожностью. Например, если глазурь находится на нижнем уровне как SiO 2 , так и Al 2 O 3 , то размещение B 2 O 3 на верхнем конце может привести к чрезмерно жидкой глазури.
- Таблицы созданы для конкретных типов глазури. Например, не обращайтесь к ограничениям для свинцовой глазури, если вы используете борсодержащую глазурь.
 Кроме того, глазури, предназначенные для напольной плитки, будут иметь совсем другие ограничения, чем те, которые предназначены для художественных изделий, поскольку формула подчеркивает твердость, долговечность и способность к быстрому возгоранию, последний внешний вид и визуальные эффекты.
Кроме того, глазури, предназначенные для напольной плитки, будут иметь совсем другие ограничения, чем те, которые предназначены для художественных изделий, поскольку формула подчеркивает твердость, долговечность и способность к быстрому возгоранию, последний внешний вид и визуальные эффекты. - Ассортимент оксидов: большее разнообразие флюсов, как правило, само по себе является стимулом для более низких температур плавления. Формулы предельного значения обычно предполагают использование диапазона потоков.
- В диаграммах Великобритании указаны минимальные значения оксидов, а в диаграммах G&C — нет. Например, CaO и KNaO являются достаточно полезными флюсами, поэтому авторы первого набора формул считали, что в каждой глазури должно быть хотя бы их количество.
- Другие осложняющие факторы: Присутствие красителей, герметиков, замутнителей, вариегаторов и т. д. вызывает изменения в расплаве, которые часто сужают пределы для других оксидов. Например, замутнитель сделает расплав более жестким и снизит допустимое количество оксида алюминия.
 Медь может превратить устойчивую к выщелачиванию основу в выщелачиватель.
Медь может превратить устойчивую к выщелачиванию основу в выщелачиватель. - Интерпретация этих диаграмм предполагает некоторое знание эффектов каждого оксида. Например, если количество одного оксида высокое или низкое, это обычно сужает диапазон для других оксидов. Предположим, вы хотите получить прозрачную глазурь без пузырьков и кристаллических облаков. Если высокое содержание CaO, вам также потребуется высокое содержание Al 2 O 3 , чтобы предотвратить его кристаллизацию. Однако высокое содержание Al 2 O 3 сделает расплав более жестким и предотвратит выход пузырьков. Таким образом, для достижения успеха потребуются рационализация и тестирование.
Так стоят ли пределы проблем, связанных с их интерпретацией? Да. Эффективность красителей в рецептах представляет собой аналогию, подтверждающую концепцию предельных формул. Если 2% красителя дают светлый цвет, а 7,5% — самый темный, то зачем ставить 15%? Он тратится впустую, это, вероятно, способствует химической нестабильности. Таким образом, существует подразумеваемый предел в 7,5%. Предельные формулы являются отличным эталоном для глазури для пищевых продуктов, в пределах ограничений не гарантируется долговечность или устойчивость к выщелачиванию, но хорошо расплавленная глазурь, очевидно, является лучшим началом. Кроме того, я считаю, что предельные формулы являются хорошей отправной точкой для объяснения проблемных глазурей, анализ их отклонения от пределов часто указывает на плодотворную стратегию решения проблемы.
Таким образом, существует подразумеваемый предел в 7,5%. Предельные формулы являются отличным эталоном для глазури для пищевых продуктов, в пределах ограничений не гарантируется долговечность или устойчивость к выщелачиванию, но хорошо расплавленная глазурь, очевидно, является лучшим началом. Кроме того, я считаю, что предельные формулы являются хорошей отправной точкой для объяснения проблемных глазурей, анализ их отклонения от пределов часто указывает на плодотворную стратегию решения проблемы.
Этика
Однако формулы ограничения выходят за рамки практичности и фокусируют внимание на вопросах этики и ответственности. Если вы не химик-глазуритель и у вас нет испытательного оборудования, то должны ли вы использовать функциональные и лайнерные глазури, которые бросают вызов этим ограничениям без какого-либо тестирования и четкой рационализации? Я никогда не пекла хлеб, но я уверена, что есть некоторые ограничения, я предполагаю, что 1 чайная ложка дрожжей хороша, а одна чашка — нет. Точно так же, если формула глазури имеет в два раза больше оксида (я вижу это все время с марганцем, барием, литием, флюсами, металлами) или вдвое меньше (т.е. SiO 2 или Al 2 O 3 ) брови должны подняться! Это правда, что «визуальные» или реактивные глазури часто не соответствуют нормам (например, жидкие пестрые глазури часто не содержат глинозема или имеют высокое содержание бора), но никто не ожидает, что они будут безопасными для пищевых продуктов, идеально подходят для глины и будут очень твердыми и невосприимчивыми к огню. устойчивая поверхность либо. Мы также ожидаем, что такие глазури не будут продаваться на рынке функциональных глазурей, где у них быстро развивается амнезия в отношении того, кто они и что они собой представляют.
Точно так же, если формула глазури имеет в два раза больше оксида (я вижу это все время с марганцем, барием, литием, флюсами, металлами) или вдвое меньше (т.е. SiO 2 или Al 2 O 3 ) брови должны подняться! Это правда, что «визуальные» или реактивные глазури часто не соответствуют нормам (например, жидкие пестрые глазури часто не содержат глинозема или имеют высокое содержание бора), но никто не ожидает, что они будут безопасными для пищевых продуктов, идеально подходят для глины и будут очень твердыми и невосприимчивыми к огню. устойчивая поверхность либо. Мы также ожидаем, что такие глазури не будут продаваться на рынке функциональных глазурей, где у них быстро развивается амнезия в отношении того, кто они и что они собой представляют.
Помните, что альтернативой диаграммам ограничений является отсутствие указаний или, что еще хуже, усреднение формул непроверенных рецептов из учебников. Будьте консервативны, когда дело доходит до производства посуды, которая, как ожидают люди, будет долговечной и безопасной для пищевых продуктов.
Таблицы предельных значений для нестабильных глазурей
Многие визуальные эффекты могут быть достигнуты только путем выхода за пределы типичных функциональных формул. Например, матовые глазури должны раздвигать границы, чтобы даже быть матовыми. Поэтому они нетрадиционны в том смысле, что редко хорошо сочетаются без функциональных ограничений. Однако химия глазури также играет роль в понимании нетрадиционных механизмов, а может быть, даже в большей степени. Таким образом, термин «целевая формула» очень подходит для этого.
Сопутствующая информация
Ссылки
| Статьи | Малобюджетное тестирование свойств глазури в сыром виде и после обжига Глазури — это нечто большее, чем их внешний вид. Они обладают и другими физическими свойствами, такими как твердость, тепловое расширение, выщелачиваемость, химический состав, и имеют множество дефектов. Вот несколько простых тестов. |
|---|---|
| Артикул | Недорогой тестер текучести расплава глазури Этот прибор для измерения текучести расплава глазури поможет вам лучше понять ваши глазури и материалы и решить всевозможные проблемы.  |
| Артикул | Создание собственной бюджетной глазури Как превратить склад, полный неиспользованных материалов, в хорошую глазурь, вместо того, чтобы пробовать бесчисленные онлайн-рецепты, которые требуют покупки еще большего количества материалов, которые вам не нужны и не работают. |
| Глоссарий | Формула ограничения Способ установления рекомендаций для каждого оксида в химии для различных типов керамической глазури. Понимание роли каждого оксида и ограничений этого подхода является ключом к эффективному использованию этих рекомендаций. |
Тони Хансен
Расскажите нам, как улучшить эту страницу
Или задайте вопрос, и мы изменим эту страницу, чтобы лучше ответить на него.
Адрес электронной почты
Имя
Субъект
Сообщение
Сообщение Введите это, чтобы доказать, что вы не робот, или Обновить
Оставьте следующее пустым
https://digitalfire.
 com, все права защищены
com, все права защищены Политика конфиденциальности
Формула лимита
| Ежемесячная техническая подсказка от Тони ХансенаSignUp | Нет отслеживания ! Нет объявлений ! Вот почему эта страница загружается быстро! |
Весь глоссарий
200 меш |325 меш |3D-дизайн |3D-принтер |3D-слайсер |3D-печать на глине |3D-печать |Абразионная керамика |Кислотные оксиды |Агломерация |Щелочные |Щелочноземельные |Аморфные | пористость |Шаровая мельница |Бамбуковая глазурь |Основная глазурь |Основное покрытие для окунания глазури |Основные оксиды |Периодический рецепт |Биск |Битовое изображение |Черное выделение сердцевины |Вытекающие цвета |Волдыри |Вздутие |Вспучивание |Костяной фарфор |Борат |Бор синий |Борная фритта |Боросиликат |Разрушающая глазурь |Нанесение глазури кистью |Прокаливание |Расчетное тепловое расширение |Свечение |Выгорание углерода |Глазурь с углеродной ловушкой |Номера CAS |Литье-отсадка |Селадоновая глазурь |Керамика |Керамическое связующее |Керамические наклейки |Керамическая глазурь |Дефекты керамической глазури |Керамика Чернила | Керамический материал | Оксид керамики | Керамический шликер | Керамическая морилка | Керамическая плитка | Керамика | Характеристика | Химический анализ | Цветность | Глина | Глиняное тело | Пористость глиняного тела | Глина для печей и обогревателей | Жесткость глины | Коэффициент теплового расширения |С Нумерация оды |Кулачковая керамика |Коллоид |Краситель |Конус 1 |Конус 5 |Конус 6 |Конусная пластинка |Красная медь |Кордиерит Керамика |Кракл глазурь |Ползание |Крейсинг |Кристобалит |Кристобалит Инверсия |Тигель |Кристаллические глазури |Кристаллизация |Cuerda Seca | Маркировка столовых приборов | Разложение | Дефлокуляция | Деоксилидация | Digitalfire Foresight | Digitalfire Insight | Справочная библиотека Digitalfire | Глазурь с ямочками | Глазурование погружением | Глазурь погружением | Можно мыть в посудомоечной машине | Доломитовый матовый | Дунтинг |Пылепрессование |Фаянс |Высолы |Инкапсулированная морилка |Ангоб |Эвтектика |Быстровоспламеняющиеся глазури |Жировая глазурь |Полевошпатные глазури |Оклеивающий агент |Огнеупорный кирпич |Шаммот |Прочность при обжиге |График обжига |Усадка при обжиге |Пламенные изделия |Вспышка |Флокуляция |Жидкий расплав Глазури |Флюс |Безопасно для пищевых продуктов |Кольцо для ног |Метод формования |Соотношение формул |Вес формулы |Фритта |Фритта |Функциональные |Паспорта безопасности СГС |Стекло и кристаллы |Стеклокерамические глазури |Глазурь пузырьковая s |Химия глазури |Сжатие глазури |Стойкость глазури |Подгонка глазури |Гелеобразование глазури |Нанесение слоев глазури |Смешивание глазури |Рецепты глазури |Усадка глазури |Толщина глазури |Глобально согласованные таблицы данных |Глянцевая глазурь |Green Strength |Grog |Глазурь из бронзы |Ручки | Высокотемпературная глазурь | Горячее прессование | Резное украшение | Промышленная глина | Струйная печать | Остекление только внутри | Insight-Live | Интерфейс | Железная красная глазурь | Изделия из яшмы | Джиггеринг | Каки | Контроллер печи | Обжиг в печи | Дымы печи | Печь система вентиляции |Промывка в печи |Коварский металл |Ламинирование |Выщелачивание |Свинец в керамических глазурях |Твердая кожа |Известь |Формула лимита |Рецепт лимита |Лайнерная глазурь |Лайнерная глазурь |LOI |Низкотемпературная глазурь |Блестящие цвета |Майолика |Мраморность |Материал Замещение | Матовая глазурь | Созревание | Максимальная плотность | МДТ | Механизм | Среднетемпературная глазурь | Текучесть расплава | Температура плавления | Оксиды металлов | Металлические глазури | Микроорганизмы | Безопасно для микроволновой печи | Минеральная фаза | Минералогия | Мокко глазури | Твердость по шкале Мооса | Моль% | Мононуклеоз cottura |Мозаичная плитка |Крапчатая |Кристаллы муллита |Нативная глина |Безоксидная керамика |Масляная глазурь |Огненная глазурь |Замутнитель |Непрозрачность |Посуда |Надглазурь |Окислительный обжиг |Формула оксида |Взаимодействие оксидов |Оксидная система |Ориентация частиц |Частица Распределение по размерам |Размеры частиц |PCE |Проницаемость |Фазовая диаграмма |Фазовое разделение |Физические испытания |Тонкопрокалывание |Глины Plainsman |Гипсовая бита |Гипсовый стол |Пластилин |Пластичность |Выщипывание |Фарфор |Фарфоровый керамогранит |Заливка глазури |Обработка порошка |Осадки |Первичная обработка Глина | Примитивный обжиг | Пропан | Пропеллерный смеситель | Pugmill | Пирокерамика | Пирометрический конус | Инверсия кварца | Раку | Реактивные глазури | Восстановительный обжиг | Восстановительный спекл | Огнеупоры | Огнеупорные керамические покрытия | Репрезентативный образец | Вдыхаемый кристаллический кремнезем | Посуда для ресторанов | Реология | Рутил Глазурь |Соляной обжиг |Сантехника |Скульптура |Вторичная глина |Shino Glazes |Дрожь |Сито |Вибросито |Соотношение диоксида кремния и глинозема |Шелкография |Спекание |Гашение |Шликерное литье |Шликерное литье |Шлам |Обработка шлама |Нанесение суспензии |Замачивание |Растворимые красители |Растворимые соли |Удельный вес |Расщепление |Остекление распылением |Среда окрашивания |Герамита |Stull Chart |Сульфатная пена |Сульфаты |Площадь поверхности |Поверхность Натяжение | Подвеска | Таппер Глина | Тенмоку | Терра Котта | Терра Сигилатта | Испытательная печь | Теоретический материал | Теплопроводность | Термический удар | Термопара | Тиксотропия | Метание | Тони Хансен | Токсичность | Торговля | Прозрачность | Прозрачные глазури | Смешивание трехосной глазури | Окончательный Частицы |Подглазурная обработка |Формула единства |Upwork |Разнообразие |Вязкость |Стекловидность |Витрификация |Летучие вещества |Деформация |Вода в керамике |Водокурение |Растворимость в воде |Расклинивание |Белая посуда |Глазурь из древесной золы |Обжиг древесины |Zero3 |Zero4 |Zeta Potential
Способ установления рекомендаций для каждого оксида в химии для различных типов керамической глазури. Понимание роли каждого оксида и ограничений этого подхода является ключом к эффективному использованию этих рекомендаций.
Понимание роли каждого оксида и ограничений этого подхода является ключом к эффективному использованию этих рекомендаций.
Детали
Термин «предельная формула» исторически обычно относился к усилиям по установлению абсолютных диапазонов для смесей оксидов, которые хорошо плавятся при заданной температуре и не находятся в достаточном избытке, чтобы вызвать дефекты. Эти формулы обычно показывают диапазоны для каждого оксида, обычно используемого в конкретном типе глазури (в отличие от концепции предельного рецепта, который выражает нормальные количества материала, ожидаемые в данном типе продукта).
Многие предпочитают термин «целевая формула». Это связано с тем, что термин «предельная формула» предполагает, что глазури за пределами диапазона не будут работать, а те, что внутри, каким-то образом безопасны. Однако, это не так. Хорошее плавление просто несет с собой гораздо более высокую вероятность того, что глазурь достаточно функциональна и сбалансирована (не содержит чрезмерного количества какого-либо отдельного оксида, который может привести к нестабильности или реакционной способности). Эти лимиты также зависят от количества B 2 O 3 присутствует (если допустимо большее количество, чем допустимо большее количество Al 2 O 3 и SiO 2 ).
Эти лимиты также зависят от количества B 2 O 3 присутствует (если допустимо большее количество, чем допустимо большее количество Al 2 O 3 и SiO 2 ).
Определенные керамические отрасли установили запатентованные ограничения для глазурей, которые они производят (например, сверхнизкое расширение, высокая стойкость к истиранию, устойчивость к росту бактерий, высокая эластичность, определенные цвета, быстрое возгорание). Эти пределы часто являются тщательно охраняемыми секретами и будут значительно отличаться от показанных здесь нормальных диапазонов. Распространенным примером мишени общественного достояния являются кристаллические глазури, они почти не требуют глинозема, намного выше, чем обычные натрий и цинк. Они также требуют специальной обработки при обжиге.
Существует разница между получением оксида из фритты или сырья. Фритты легко выделяют свои оксиды в расплав глазури, что дает им больше времени для непосредственного участия в формировании однородной структуры глазури (это особенно важно, когда материалы имеют высокие температуры плавления). Таким образом, такие оксиды, как BaO, которые потенциально могут выщелачиваться в глазури, если они получены из сырья, могут не выщелачиваться из фритты, особенно при относительно низких уровнях.
Таким образом, такие оксиды, как BaO, которые потенциально могут выщелачиваться в глазури, если они получены из сырья, могут не выщелачиваться из фритты, особенно при относительно низких уровнях.
Однако в основном мы занимаемся созданием глазури для функциональной посуды. Использование термина «целевая формула» вместо «предельная формула» предполагает, что нас больше интересует сравнение новой глазури с той, которую мы уже понимаем (использовали и широко тестировали). Он признает, что оценка пригодности глазури является скорее относительной, чем абсолютной наукой. Это хорошо.
Вот пример типичной предельной формулы для конуса 6 глазури.
CaO — 0-0,55
MgO — 0-0,325
KNaO — 0-0,375
ZnO — 0-0,3
БаО — 0-0,4
В 2 О 3 — 0-0,35
Ал 2 О 3 — 0,285-0,64
SiO 2 — 2,4-4,7
Эти значения относятся к сравнительным числам молекул. Они предназначены для сравнения с глазурью, формула которой унифицирована (флюсы или плавители в сумме дают единицу). На конусе 6 потоки от CaO до BaO. Они уравновешивают Al 2 O 3 (стабилизатор) и SiO 2 (формирователь стекла). B 2 O 3 — это низкотемпературное стекло, которое также действует как флюс.
На конусе 6 потоки от CaO до BaO. Они уравновешивают Al 2 O 3 (стабилизатор) и SiO 2 (формирователь стекла). B 2 O 3 — это низкотемпературное стекло, которое также действует как флюс.
Это предполагает, что содержание CaO (обычно из карбоната кальция или волластонита) может варьироваться от нуля до 0,55. Но на практике почти никогда не встретишь глазури с нулевым содержанием СаО, почти всегда его значительное количество (0,3 и более). В матовой глазури содержание СаО очень часто превышает этот предел.
-MgO (из талька и доломита) менее распространен, чем CaO или KNaO в глазури, он матирует их, когда количество достигает 0,3 и выше. Фактически, шелковисто-матовые глазури, которые очень распространены, часто имеют 0,35 или более.
-KNaO (совокупность K 2 O и Na 2 O из полевых шпатов и фритт) является ключевым плавителем. Как и CaO, он есть почти во всех глазурях. Глазури обжигают до блестящего блеска, когда это выше. Но KNaO имеет высокое тепловое расширение, поэтому ограничивающим фактором является восприимчивость вашего тела к сумасшествию (что, вероятно, поставит его ниже предела, указанного здесь).
Но KNaO имеет высокое тепловое расширение, поэтому ограничивающим фактором является восприимчивость вашего тела к сумасшествию (что, вероятно, поставит его ниже предела, указанного здесь).
-ZnO является вспомогательным плавильным средством, он редко встречается в глазури с медленным обжигом (например, для гончарных изделий), особенно если он получен из оксида цинка. Поскольку другие плавители (особенно бор) имеют гораздо меньше побочных эффектов (например, дефекты глазури, искажения цвета), они почти никогда не достигают этого предела 0,3. Однако в промышленных применениях с быстрым обжигом (обжиг от 1 до 2 часов) его можно допустить, если он получен из фритт, и он будет достигать этого предела.
-BaO требует осторожного обращения из-за токсичности; любая глазурь, которая имеет 0,4 BaO, будет зашкаливать с точки зрения потенциала выщелачивания! Кроме того, единственное время, когда BaO будет находиться на этом высоком уровне, должно быть для специального назначения, нефункциональных, кристально-матовых или синих матовых глазурей. Однако, несмотря на то, что глазурь не используется для функциональной посуды, гончар, изготавливающий посуду, подвергается воздействию высокого уровня бария-сырца. Для функциональных глазурей низкие уровни BaO часто допустимы (например, 0,05–0,1), если химический состав глазури сбалансирован (достаточно SiO 2 и Al 2 O 3 ) и хорошо плавятся (но не кристаллизуются). Промышленность часто использует фритты для получения BaO, очевидно, что они намного безопаснее в использовании.
Однако, несмотря на то, что глазурь не используется для функциональной посуды, гончар, изготавливающий посуду, подвергается воздействию высокого уровня бария-сырца. Для функциональных глазурей низкие уровни BaO часто допустимы (например, 0,05–0,1), если химический состав глазури сбалансирован (достаточно SiO 2 и Al 2 O 3 ) и хорошо плавятся (но не кристаллизуются). Промышленность часто использует фритты для получения BaO, очевидно, что они намного безопаснее в использовании.
-SrO, хотя и не показан, может рассматриваться как BaO (он не токсичен и является обычным вспомогательным флюсом).
-Li 2 O также не показан. Используйте только небольшое количество (например, 0,05), это мощный поток. У него также есть проблемы с токсичностью.
-B 2 O 3 используется почти во всех среднетемпературных глазурях, без него они просто не расплавятся. Верхний предел здесь консервативен, но хорошо плавящаяся глазурь все же может быть достигнута при уровнях ниже этого (например, 0,2). Но если вам нужна глазурь с сильным блеском с красителем и замутнителями или с пестрыми реактивными визуальными эффектами, то, вероятно, потребуется значительно больше, чем 0,35 (удвоение этого количества не является чем-то необычным!). Однако этот предел, вероятно, отражает потребности промышленности, у них есть причины минимизировать использование бора из-за его побочных эффектов (борный синий и расстеклование, микропузырьки, проблемы с долговечностью, трудности с быстрым огнем).
Но если вам нужна глазурь с сильным блеском с красителем и замутнителями или с пестрыми реактивными визуальными эффектами, то, вероятно, потребуется значительно больше, чем 0,35 (удвоение этого количества не является чем-то необычным!). Однако этот предел, вероятно, отражает потребности промышленности, у них есть причины минимизировать использование бора из-за его побочных эффектов (борный синий и расстеклование, микропузырьки, проблемы с долговечностью, трудности с быстрым огнем).
-Al3O 3 требуется для всех глазурей (кроме кристаллических). Он удерживает расплав от стекания с вертикальных поверхностей, стабилизируя его. Он также придает твердость и долговечность. Как правило, вам нужно как можно больше (но если слишком много, блеск будет потерян), и более того, он не расплавится (было бы очень необычно увидеть верхний предел 0,64). Около 0,4 было бы гораздо более типичным.
-SiO 2 составляет основную часть всех глазурей, является стеклообразователем. Чем больше глазури возьмет (и при этом хорошо расплавится), тем лучше. Все его эффекты полезны. Этот верхний предел является консервативным, если больше бора (или вспомогательных флюсов, таких как Li 2 O, ZnO) могут присутствовать больше SiO 2 .
Чем больше глазури возьмет (и при этом хорошо расплавится), тем лучше. Все его эффекты полезны. Этот верхний предел является консервативным, если больше бора (или вспомогательных флюсов, таких как Li 2 O, ZnO) могут присутствовать больше SiO 2 .
— Красители (например, оксиды Fe, Co, Mn, Cu, Cr). Будьте благоразумны. Если 1% кобальта дает ярко-синий цвет, не добавляйте 5%. Если 5% пятна достаточно, не добавляйте 10%. Железо не опасно. Медь может сделать глазурь выщелачиваемой, проверьте это. MnO выделяет дым при обжиге. Кадмий и свинец, очевидно, требуют ноу-хау для безопасного использования.
— Титан и рутил: они обычно добавляются в разнообразные глазури (кристаллизуются и вызывают фазовые переходы). Они эффективны примерно до 5%, выше поверхность обычно становится шероховатой и матовой (сетка из кристаллов). Есть ломовые способы предотвратить это, например, включение значительного количества цинка или лития. Но такие глазури, как известно, привередливы и сложны. Остерегаться.
Остерегаться.
Физические пределы: Хорошо ли плавится глазурь? Можно ли поцарапать его металлом? Выдержит ли он испытание на выщелачивание? сильно кристаллизуется? (сделайте крупным планом камеру и увеличьте ее). В расплавленном стекле полно пузырьков воздуха? Это безумие? Это очевидные вещи, но нет особого смысла возиться с химией, если есть такие очевидные проблемы!
Большинство людей, имеющих большой опыт смешивания и тестирования глазури и наблюдения за их химическим составом, вероятно, рационализируют эти ограничения так же, как это сделано здесь. Как только вы зафиксируете этот план, вам больше никогда не понадобится смотреть на другой лимитный график, это становится вашей второй натурой!
Ниже есть ссылка на длинную статью о лимитах.
Дополнительная информация
A Ограничение формулы единства Сегера
Нажмите на изображение, чтобы увидеть полный размер
Минеральные источники оксидов имеют свои собственные модели плавления, и когда один заменяется другим для получения оксида, вводится другая система со своим относительным химическим составом. Крайним примером этого может быть получение Al 2 O 3 для глазури с использованием прокаленного оксида алюминия вместо каолина. Хотя формула может быть точно такой же, результат обжига будет совершенно другим, потому что очень мало глинозема растворится в расплаве глазури. С другой стороны, можно использовать другую фритту для подачи набора оксидов (при сохранении общего химического состава глазури), и результат обжига будет гораздо более химически предсказуем. Почему? Потому что легко и высвобождают свои оксиды в расплаве.
Крайним примером этого может быть получение Al 2 O 3 для глазури с использованием прокаленного оксида алюминия вместо каолина. Хотя формула может быть точно такой же, результат обжига будет совершенно другим, потому что очень мало глинозема растворится в расплаве глазури. С другой стороны, можно использовать другую фритту для подачи набора оксидов (при сохранении общего химического состава глазури), и результат обжига будет гораздо более химически предсказуем. Почему? Потому что легко и высвобождают свои оксиды в расплаве.
Всегда ли добавление бора увеличивает плавление глазури?
Коснитесь изображения для полного размера
Бор (B 2 O 3 ) похож на кремнезем, но также является флюсом. Frits и Gerstley Borate поставляют его в глазури. В этом тесте я увеличил количество бора с 0,33 до 0,40 (используя химические инструменты в моем аккаунте Insight-live.com). Я был уверен, что это заставит глазурь больше таять и меньше склонна к потрескиванию. Но, как показывают эти тесты GBMF на текучесть расплава (10-граммовые тестовые шарики GBMF, расплавленные на фарфоровой плитке), этого не произошло. Почему? Я предполагаю, что для получения эффекта B 2 O 3 должен быть заменен, молекула за молекулой на SiO 2 (а не просто добавлен в глазурь).
Но, как показывают эти тесты GBMF на текучесть расплава (10-граммовые тестовые шарики GBMF, расплавленные на фарфоровой плитке), этого не произошло. Почему? Я предполагаю, что для получения эффекта B 2 O 3 должен быть заменен, молекула за молекулой на SiO 2 (а не просто добавлен в глазурь).
Предельная или целевая формула глазури. Что это значит?
Нажмите на изображение, чтобы увидеть его в полном размере
Рецепты показывают нам материалы в виде порошка глазури (или суспензии). Формулы перечисляют молекулы оксида и их сравнительные количества в обожженном стекле. Оксиды составляют обожженное стекло. Печь разрушает керамические материалы, чтобы получить их оксиды, выбрасывает углерод, серу и т. д. и создает стекло из остального. Существует прямая зависимость между свойствами обожженной глазури (например, диапазоном плавления, блеском, тепловым расширением, твердостью, долговечностью, цветовой чувствительностью и т. д.) и ее оксидной формулой. Нужно знать 8-10 оксидов (против сотен материалов). Таким образом, с точки зрения формулы материалы являются «источниками оксидов». Хотя есть и другие факторы, помимо чистой химии, которые определяют, как горит глазурь, ни один из них не является столь важным. Insight-live может рассчитать и показать формулу рецепта, это позволяет сравнивать ее бок о бок и с целевой формулой (или другим рецептом, который, как известно, работает по мере необходимости). Целевые формулы открываются с помощью расширенного поиска рецептов, выбора пакета лимитов и нажатия/нажатия кнопки поиска (ищите «целевой рецепт» в интерактивной справке Insight для получения дополнительной информации).
д.) и ее оксидной формулой. Нужно знать 8-10 оксидов (против сотен материалов). Таким образом, с точки зрения формулы материалы являются «источниками оксидов». Хотя есть и другие факторы, помимо чистой химии, которые определяют, как горит глазурь, ни один из них не является столь важным. Insight-live может рассчитать и показать формулу рецепта, это позволяет сравнивать ее бок о бок и с целевой формулой (или другим рецептом, который, как известно, работает по мере необходимости). Целевые формулы открываются с помощью расширенного поиска рецептов, выбора пакета лимитов и нажатия/нажатия кнопки поиска (ищите «целевой рецепт» в интерактивной справке Insight для получения дополнительной информации).
Ссылки
| Статьи | Формулы ограничения и целевые формулы Химические составы глазури для каждого типа глазури имеют типичный вид, что позволяет нам выявить нетипичные. Формулы лимита и цели полезны для нас, если мы будем иметь в виду их правильное использование.  |
|---|---|
| Артикул | С чего начать в понимании глазури? Избавьтесь от зависимости от онлайн-рецептов, которые не работают. Получить контроль. Узнайте, почему глазури так горят. Для чего используется каждый материал. Немного химии. Как создать идеальные свойства погружения и сушки. Будьте наделены полномочиями. Корректируйте рецепты с проблемами, а не с sta |
| Артикул | Создание собственной бюджетной глазури Как превратить склад, полный неиспользованных материалов, в хорошую глазурь, вместо того, чтобы пробовать бесчисленные онлайн-рецепты, которые требуют покупки еще большего количества материалов, которые вам не нужны и не работают. |
| Оксиды | Al2O3 — оксид алюминия, глинозем |
| Оксиды | SiO2 — диоксид кремния, диоксид кремния |
| Оксиды | B2O3 — оксид бора |
| Оксиды | CaO — оксид кальция, кальций |
| Оксиды | CoO — оксид кобальта |
| Оксиды | Cr2O3 — оксид хрома |
| Оксиды | MnO — оксид марганца |
| Оксиды | MnO2 — диоксид марганца |
| Оксиды | Li2O — оксид лития, литий |
| Оксиды | ZnO — оксид цинка |
| Оксиды | BaO — оксид бария, бария |
| Глоссарий | краситель В керамике и гончарных изделиях красители добавляют к глазури в виде оксидов металлов, сырьевых материалов, содержащих оксиды металлов, или в виде промышленных красителей. 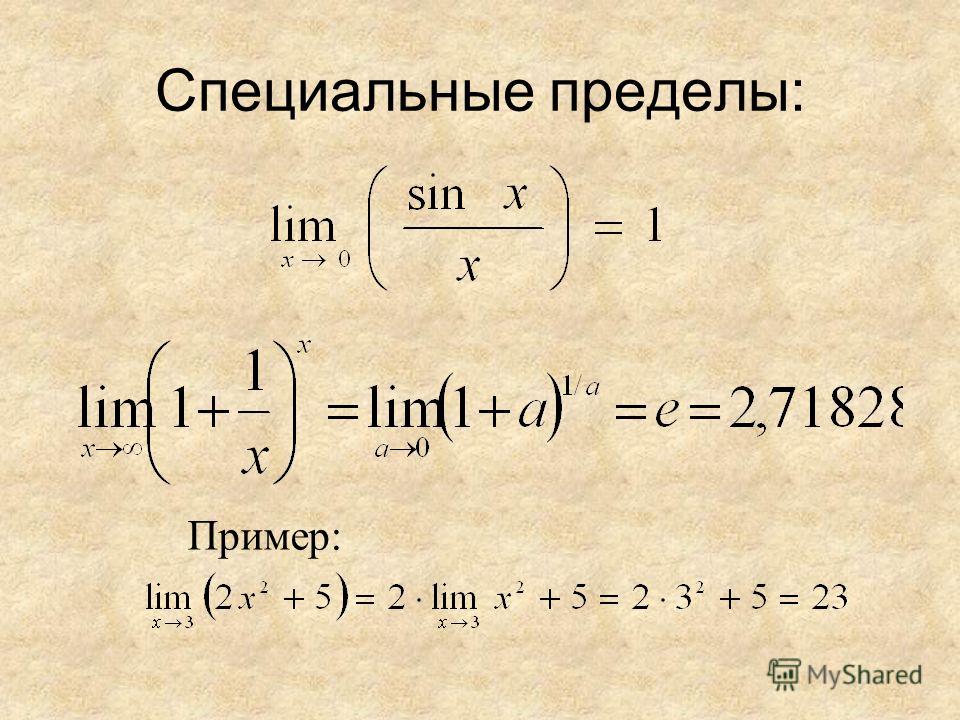 |
| Глоссарий | Флюс Благодаря флюсам мы можем обжигать глиняные тела и глазури в обычных печах, они заставляют глазури плавиться, а тела стекловаться при более низких температурах. |
| Глоссарий | Выщелачивание Керамические глазури могут выделять тяжелые металлы в пищу и напитки. Эта тема не сложна, есть много вещей, которые каждый может сделать, чтобы решить эту проблему |
| Глоссарий | Предельный рецепт Этот термин относится к способности критического мышления, которую гончары и техники могут развить, чтобы распознавать рецепты, имеющие очевидные проблемы и достоинства, просто видя материалы и проценты. |
| Глоссарий | Керамический оксид В химии глазури оксид является основной единицей формул и анализов. Знание того, какие материалы поставляют оксид и как он влияет на обожженное стекло или глазурь, является ключом к контролю.  |
| Глоссарий | Химия глазури Химия глазури — это изучение того, как химический состав оксидов глазури связан с тем, как они обжигаются. Он учитывает цвет, поверхность, твердость, текстуру, температуру плавления, тепловое расширение и т. д. |
| Глоссарий | Глазурь Долговечность Керамические глазури широко различаются по своей устойчивости к износу и выщелачиванию кислотами и щелочами. Основными факторами, определяющими долговечность, являются химический состав глазури и температура обжига. |
| Медиа | Desktop Insight 1B — Превратите полевой шпат в глазурь Научитесь сравнивать целевую формулу с химическим составом полевого шпата. Узнайте, почему она сама по себе не дает хорошей глазури и какие материалы нужно добавить, чтобы получить сбалансированную глазурь. |
| Рецепты | G3806C — Cone 6 Clear Fluid-Melt Clear Base Glaze Базовый рецепт плавящейся глазури, разработанный Тони Хансеном.  С добавками красителей образует реактивные расплавы, которые пестрят и текут. Он более устойчив к растрескиванию, чем другие. С добавками красителей образует реактивные расплавы, которые пестрят и текут. Он более устойчив к растрескиванию, чем другие. |
| Рецепты | G2926B — Cone 6 Белая посуда/Фарфоровая прозрачная глазурь Базовый рецепт прозрачной глазури, созданный Тони Хансеном для Plainsman Clays, обеспечивает высокий глянец и ультрапрозрачность при низкой подвижности расплава. |
| Рецепты | G2934 — Матовая глазурь для конуса 6 Рецепт матовой глазури на основе MgO позволяет получить твердую утилитарную поверхность и обладает очень хорошими рабочими свойствами. Растушуйте глянец, если он слишком матовый. |
| URL-адреса | Немецкий гончар Корнелиус Брейманн исследует предельные формулы, эвтектику В этом видео на Youtube Корнелиус отправит вас в медленное и осознанное путешествие.  Если вы будете придерживаться его, вы обнаружите, как путем тщательного смешивания полевого шпата, карбоната кальция и кремнезема мы можем увидеть, какие соотношения CaO, SiO2 и Al2O3 (и материалов, из которых они получены) дают хорошо плавящуюся высокотемпературную глазурь. Вы увидите, как процесс демонстрирует, где полевой шпат сам по себе не годится для глазури и каким он должен быть. И вы увидите продемонстрированную эвтектику CaO:SiO2:Al2O3. Если вы будете придерживаться его, вы обнаружите, как путем тщательного смешивания полевого шпата, карбоната кальция и кремнезема мы можем увидеть, какие соотношения CaO, SiO2 и Al2O3 (и материалов, из которых они получены) дают хорошо плавящуюся высокотемпературную глазурь. Вы увидите, как процесс демонстрирует, где полевой шпат сам по себе не годится для глазури и каким он должен быть. И вы увидите продемонстрированную эвтектику CaO:SiO2:Al2O3. |
Тони Хансен
Расскажите нам, как улучшить эту страницу
Или задайте вопрос, и мы изменим эту страницу, чтобы лучше ответить на него.
Адрес электронной почты
Имя
Субъект
Сообщение
Сообщение Введите это, чтобы доказать, что вы не робот, или Обновить
Оставьте следующее пустым
https://digitalfire.com, все права защищены
Политика конфиденциальности
Спецификации и ограничения Excel
Спецификации и ограничения рабочих листов и рабочих книг
Особенность | Максимальный предел |
|---|---|
Открытые книги | Ограничен доступной памятью и системными ресурсами |
Общее количество строк и столбцов на листе | 1 048 576 строк по 16 384 столбца |
Ширина столбца | 255 символов |
Высота строки | 409 баллов |
Разрывы страниц | 1026 горизонтальные и вертикальные |
Общее количество символов, которое может содержать ячейка | 32 767 символов |
символов в верхнем или нижнем колонтитуле | 255 |
Максимальное количество переводов строки на ячейку | 253 |
листов в книге | Ограничен доступной памятью (по умолчанию 1 лист) |
Цвета в книге | 16 миллионов цветов (32 бита с полным доступом к 24-битному цветовому спектру) |
Именованные представления в книге | Ограничен доступной памятью |
Уникальные форматы/стили ячеек | 65 490 |
Стили заливки | 256 |
Толщина линии и стили | 256 |
Уникальные типы шрифтов | 1024 глобальных шрифта, доступных для использования; 512 на книгу |
Числовые форматы в рабочей книге | От 200 до 250, в зависимости от установленной языковой версии Excel |
Имена в книге | Ограничен доступной памятью |
Окна в книге | Ограничен доступной памятью |
Гиперссылки на листе | 65 530 |
Стекла в окне | 4 |
Связанные листы | Ограничен доступной памятью |
Сценарии | Ограничен доступной памятью; сводный отчет показывает только первые 251 сценарий |
Изменение ячеек в сценарии | 32 |
Настраиваемые ячейки в Solver | 200 |
Пользовательские функции | Ограничен доступной памятью |
Диапазон увеличения | от 10 до 400 процентов |
Отчеты | Ограничен доступной памятью |
Сортировать ссылки | 64 в одном сорте; неограниченно при использовании последовательных сортировок |
Уровни отмены | 100 |
Поля в форме данных | 32 |
Параметры рабочей книги | 255 параметров на книгу |
Элементы, отображаемые в раскрывающихся списках фильтров | 10 000 |
Несмежные ячейки, которые можно выбрать | 2 147 483 648 ячеек |
Максимальные ограничения на объем памяти и размер файла для рабочих книг модели данных | 32-разрядная среда зависит от 2 гигабайт (ГБ) виртуального адресного пространства, совместно используемого Excel, книгой и надстройками, которые выполняются в одном процессе. 64-битная среда не накладывает жестких ограничений на размер файла. Размер рабочей книги ограничен только доступной памятью и системными ресурсами. Начиная с Excel 2016, функция Large Address Aware позволяет 32-разрядному Excel потреблять в два раза больше памяти, когда пользователи работают в 64-разрядной операционной системе Windows. Дополнительные сведения см. в статье Изменение возможности поддержки больших адресов для Excel. Примечание. Добавление таблиц в модель данных увеличивает размер файла. Если вы не планируете создавать сложные отношения модели данных с использованием множества источников данных и типов данных в своей книге, снимите флажок Добавьте эти данные в поле Модель данных при импорте или создании таблиц, сводных таблиц или подключений к данным. Дополнительные сведения см. в разделе Спецификация и ограничения модели данных. |
ядер процессора | 64 |
Длина имени файла | 218 символов — включая путь к файлу. Например, C:\Username\Documents\FileName.xlsx. |
Расчетные спецификации и ограничения
Особенность | Максимальный предел |
|---|---|
Числовая точность | 15 цифр |
Наименьшее допустимое отрицательное число | -2. |
Наименьшее допустимое положительное число | 2.2251E-308 |
Максимально допустимое положительное число | 9.99999999999999E+307 |
Наибольшее допустимое отрицательное число | -9,99999999999999E+307 |
Наибольшее допустимое положительное число по формуле | 1. | 8623158e+308
Максимально допустимое отрицательное число по формуле | -1,7976 | 8623158e+308
Длина содержания формулы | 8 192 символа |
Внутренняя длина формулы | 16 384 байта |
итераций | 32 767 |
Массивы рабочих листов | Ограничен доступной памятью |
Выбранные диапазоны | 2 048 |
Аргументы в функции | 255 |
Вложенные уровни функций | 64 |
Определенные пользователем категории функций | 255 |
Количество доступных функций рабочего листа | 341 |
Размер стека операндов | 1 024 |
Зависимость между рабочими листами | 64 000 рабочих листов, которые могут ссылаться на другие листы |
Зависимость формулы массива между рабочими листами | Ограничен доступной памятью |
Зависимость от области | Ограничен доступной памятью |
Зависимость области на рабочий лист | Ограничен доступной памятью |
Зависимость от одной ячейки | 4 миллиарда формул, которые могут зависеть от одной ячейки |
Длина содержимого связанной ячейки из закрытых книг | 32 767 |
Самая ранняя дата, разрешенная для расчета | 1 января 1900 г. |
Последняя дата, разрешенная для расчета | 31 декабря 9999 |
Максимальное количество времени, которое можно ввести | 9999:59:59 |
Спецификации и ограничения для графиков
Особенность | Максимальный предел |
|---|---|
Диаграммы, связанные с рабочим листом | Ограничен доступной памятью |
Рабочие листы, на которые ссылается диаграмма | 255 |
Ряд данных в одной диаграмме | 255 |
Точки данных в серии данных для двумерных диаграмм | Ограничен доступной памятью |
Точки данных в серии данных для трехмерных диаграмм | Ограничен доступной памятью |
Точки данных для всех рядов данных на одной диаграмме | Ограничен доступной памятью |
Спецификации и ограничения сводных таблиц и сводных диаграмм
Функция | Максимальный предел |
|---|---|
Отчеты сводной таблицы на листе | Ограничен доступной памятью |
Уникальных элементов на поле | 1 048 576 |
Поля строки или столбца в отчете сводной таблицы | Ограничен доступной памятью |
Фильтры отчетов в отчете сводной таблицы | 256 (может быть ограничено доступной памятью) |
Поля значений в отчете сводной таблицы | 256 |
Формулы вычисляемых элементов в отчете сводной таблицы | Ограничен доступной памятью |
Фильтры отчетов в отчете сводной диаграммы | 256 (может быть ограничен доступной памятью) |
Поля значений в отчете сводной диаграммы | 256 |
Формулы вычисляемых элементов в отчете сводной диаграммы | Ограничен доступной памятью |
Длина имени MDX для элемента сводной таблицы | 32 767 |
Длина строки реляционной сводной таблицы | 32 767 |
Элементы, отображаемые в раскрывающихся списках фильтров | 10 000 |
Книги с включенным параметром «Разрешить изменения более чем одному пользователю.
 ..»
..»Если для книги включен параметр Разрешить изменения более чем одному пользователю… , применяется следующая информация. Доступ к этой настройке осуществляется нажатием кнопки Вкладка «Просмотр » > Совместное использование книги . Обратите внимание, что в более новых версиях Excel кнопка Share Workbook была скрыта. Чтобы отобразить его, щелкните Файл > Параметры > Панель быстрого доступа . Откройте список под Выберите команды из и выберите Все команды . Прокрутите список вниз, пока не увидите Share Workbook (Legacy) . Выберите этот элемент и нажмите Добавить . Нажмите ОК . Кнопка «Поделиться книгой» теперь находится в верхней части окна Excel.
Особенность | Максимальный предел |
|---|---|
Пользователи, которые могут открывать файл одновременно | 256 |
Личные просмотры в книге | Ограничен доступной памятью |
Дней, в течение которых ведется история изменений | 32 767 (по умолчанию 30 дней) |
Рабочие книги, которые можно объединить одновременно | Ограничен доступной памятью |
Ячейки, которые можно выделить | 32 767 |
Цвета, используемые для обозначения изменений, сделанных разными пользователями, когда включено выделение изменений | 32 (каждый пользователь обозначен отдельным цветом; изменения, внесенные текущим пользователем, выделены темно-синим цветом) |
Таблицы Excel в книге | 0 (ноль) Примечание. |
Спецификации и ограничения рабочих листов и рабочих книг
Особенность | Максимальный предел |
|---|---|
Открытые книги | Ограничен доступной памятью и системными ресурсами |
Общее количество строк и столбцов на листе | 1 048 576 строк по 16 384 столбца |
Ширина столбца | 255 символов |
Высота строки | 409 баллов |
Разрывы страниц | 1026 горизонтальные и вертикальные |
Общее количество символов, которое может содержать ячейка | 32 767 символов |
символов в верхнем или нижнем колонтитуле | 255 |
Максимальное количество переводов строки на ячейку | 253 |
листов в книге | Ограничен доступной памятью (по умолчанию 3 листа) |
Цвета в книге | 16 миллионов цветов (32 бита с полным доступом к 24-битному цветовому спектру) |
Именованные представления в книге | Ограничен доступной памятью |
Уникальные форматы/стили ячеек | 65 490 |
Стили заливки | 256 |
Толщина линии и стили | 256 |
Уникальные типы шрифтов | 1024 глобальных шрифта, доступных для использования; 512 на книгу |
Числовые форматы в книге | От 200 до 250, в зависимости от установленной языковой версии Excel |
Имена в книге | Ограничен доступной памятью |
Окна в книге | Ограничен доступной памятью |
Гиперссылки на листе | 65 530 гиперссылок |
Стекла в окне | 4 |
Связанные листы | Ограничен доступной памятью |
Сценарии | Ограничен доступной памятью; сводный отчет показывает только первые 251 сценарий |
Изменение ячеек в сценарии | 32 |
Настраиваемые ячейки в Solver | 200 |
Пользовательские функции | Ограничен доступной памятью |
Диапазон увеличения | от 10 до 400 процентов |
Отчеты | Ограничен доступной памятью |
Сортировать ссылки | 64 в одном сорте; неограниченно при использовании последовательных сортировок |
Уровни отмены | 100 |
Поля в форме данных | 32 |
Параметры рабочей книги | 255 параметров на книгу |
Элементы, отображаемые в раскрывающихся списках фильтров | 10 000 |
Несмежные ячейки, которые можно выбрать | 2 147 483 648 ячеек |
ядер процессора | 64 |
Расчетные спецификации и пределы
Особенность | Максимальный предел |
|---|---|
Точность числа | 15 цифр |
Наименьшее допустимое отрицательное число | -2. |
Наименьшее допустимое положительное число | 2.2251E-308 |
Наибольшее допустимое положительное число | 9.99999999999999E+307 |
Наибольшее допустимое отрицательное число | -9,99999999999999E+307 |
Наибольшее допустимое положительное число по формуле | 1. | 8623158e+308
Наибольшее допустимое отрицательное число по формуле | -1,7976 | 8623158e+308
Длина содержания формулы | 8 192 символа |
Внутренняя длина формулы | 16 384 байта |
итераций | 32 767 |
Массивы рабочих листов | Ограничен доступной памятью |
Выбранные диапазоны | 2 048 |
Аргументы в функции | 255 |
Вложенные уровни функций | 64 |
Определенные пользователем категории функций | 255 |
Количество доступных функций рабочего листа | 341 |
Размер стека операндов | 1 024 |
Зависимость между рабочими листами | 64 000 рабочих листов, которые могут ссылаться на другие листы |
Зависимость формулы массива между рабочими листами | Ограничен доступной памятью |
Зависимость от области | Ограничен доступной памятью |
Зависимость области на рабочий лист | Ограничен доступной памятью |
Зависимость от одной ячейки | 4 миллиарда формул, которые могут зависеть от одной ячейки |
Длина содержимого связанной ячейки из закрытых книг | 32 767 |
Самая ранняя дата, разрешенная для расчета | 1 января 1900 г. |
Последняя дата, разрешенная для расчета | 31 декабря 9999 |
Максимальное количество времени, которое можно ввести | 9999:59:59 |
Спецификации и ограничения для графиков
Особенность | Максимальный предел |
|---|---|
Диаграммы, связанные с рабочим листом | Ограничен доступной памятью |
Рабочие листы, на которые ссылается таблица | 255 |
Ряд данных на одной диаграмме | 255 |
Точки данных в серии данных для двумерных диаграмм | Ограничен доступной памятью |
Точки данных в серии данных для трехмерных диаграмм | Ограничен доступной памятью |
Точки данных для всех рядов данных на одной диаграмме | Ограничен доступной памятью |
Спецификации и ограничения сводных таблиц и сводных диаграмм
Особенность | Максимальный предел |
|---|---|
Отчеты сводной таблицы на листе | Ограничен доступной памятью |
Уникальных элементов на поле | 1 048 576 |
Поля строки или столбца в отчете сводной таблицы | Ограничен доступной памятью |
Фильтры отчетов в отчете сводной таблицы | 256 (может быть ограничено доступной памятью) |
Поля значений в отчете сводной таблицы | 256 |
Формулы вычисляемых элементов в отчете сводной таблицы | Ограничен доступной памятью |
Фильтры отчетов в отчете сводной диаграммы | 256 (может быть ограничено доступной памятью) |
Поля значений в отчете сводной диаграммы | 256 |
Формулы вычисляемых элементов в отчете сводной диаграммы | Ограничен доступной памятью |
Длина имени MDX для элемента сводной таблицы | 32 767 |
Длина строки реляционной сводной таблицы | 32 767 |
Элементы, отображаемые в раскрывающихся списках фильтров | 10 000 |
Книги с включенным параметром «Разрешить изменения более чем одному пользователю.
 ..»
..»Если для книги включен параметр Разрешить изменения более чем одному пользователю… , применяется следующая информация. Этот параметр доступен, если щелкнуть вкладку Review > Share Workbook .
Особенность | Максимальный предел |
|---|---|
Пользователи, которые могут открывать и совместно использовать файл одновременно | 256 |
Личные представления в рабочей книге | Ограничен доступной памятью |
Дней, в течение которых ведется история изменений | 32 767 (по умолчанию 30 дней) |
Рабочие книги, которые можно объединить одновременно | Ограничен доступной памятью |
Ячейки, которые можно выделить в книге | 32 767 |
Цвета, используемые для обозначения изменений, внесенных разными пользователями, когда включено выделение изменений | 32 (каждый пользователь обозначен отдельным цветом; изменения, сделанные текущим пользователем, выделены темно-синим цветом) |
таблиц Excel в книге | 0 (ноль) Примечание. |
Спецификации и ограничения рабочих листов и рабочих книг
Особенность | Максимальный предел |
|---|---|
Открытые книги | Ограничен доступной памятью и системными ресурсами |
Общее количество строк и столбцов на листе | 1 048 576 строк по 16 384 столбца |
Ширина столбца | 255 символов |
Высота строки | 409 баллов |
Разрывы страниц | 1026 горизонтальный и вертикальный |
Общее количество символов, которое может содержать ячейка | 32 767 символов |
Символы в верхнем или нижнем колонтитуле | 255 |
Максимальное количество переводов строки на ячейку | 253 |
листов в книге | Ограничен доступной памятью (по умолчанию 3 листа) |
Цвета в книге | 16 миллионов цветов (32 бита с полным доступом к 24-битному цветовому спектру) |
Именованные представления в книге | Ограничен доступной памятью |
Уникальные форматы/стили ячеек | 65 490 |
Стили заливки | 256 |
Толщина линии и стили | 256 |
Уникальные типы шрифтов | 1024 глобальных шрифта, доступных для использования; 512 на книгу |
Числовые форматы в рабочей книге | От 200 до 250, в зависимости от установленной языковой версии Excel |
Имена в книге | Ограничен доступной памятью |
Окна в книге | Ограничен доступной памятью |
Гиперссылки на листе | 65 530 гиперссылок |
Стекла в окне | 4 |
Связанные листы | Ограничен доступной памятью |
Сценарии | Ограничен доступной памятью; сводный отчет показывает только первые 251 сценарий |
Изменение ячеек в сценарии | 32 |
Настраиваемые ячейки в Solver | 200 |
Пользовательские функции | Ограничен доступной памятью |
Диапазон увеличения | от 10 до 400 процентов |
Отчеты | Ограничен доступной памятью |
Сортировать ссылки | 64 в одном сорте; неограниченно при использовании последовательных сортировок |
Уровни отмены | 100 |
Поля в форме данных | 32 |
Параметры рабочей книги | 255 параметров на книгу |
Фильтр раскрывающихся списков | 10 000 |
Расчетные спецификации и пределы
Особенность | Максимальный предел |
|---|---|
Числовая точность | 15 цифр |
Наименьшее допустимое отрицательное число | -2. |
Наименьшее допустимое положительное число | 2.2251E-308 |
Наибольшее допустимое положительное число | 9.99999999999999E+307 |
Наибольшее допустимое отрицательное число | -9,99999999999999E+307 |
Наибольшее допустимое положительное число по формуле | 1. | 8623158e+308
Наибольшее допустимое отрицательное число по формуле | -1,7976 | 8623158e+308
Длина содержания формулы | 8 192 символа |
Внутренняя длина формулы | 16 384 байта |
Итераций | 32 767 |
Массивы рабочих листов | Ограничен доступной памятью |
Выбранные диапазоны | 2 048 |
Аргументы в функции | 255 |
Вложенные уровни функций | 64 |
Определенные пользователем категории функций | 255 |
Количество доступных функций рабочего листа | 341 |
Размер стека операндов | 1 024 |
Зависимость между рабочими листами | 64 000 рабочих листов, которые могут ссылаться на другие листы |
Зависимость формулы массива между рабочими листами | Ограничен доступной памятью |
Зависимость от области | Ограничен доступной памятью |
Зависимость области на рабочий лист | Ограничен доступной памятью |
Зависимость от одной ячейки | 4 миллиарда формул, которые могут зависеть от одной ячейки |
Длина содержимого связанной ячейки из закрытых книг | 32 767 |
Самая ранняя дата, разрешенная для расчета | 1 января 1900 г. |
Последняя дата, разрешенная для расчета | 31 декабря 9999 |
Максимальное количество времени, которое можно ввести | 9999:59:59 |
Спецификации и ограничения для графиков
Особенность | Максимальный предел |
|---|---|
Диаграммы, связанные с рабочим листом | Ограничен доступной памятью |
Рабочие листы, на которые ссылается диаграмма | 255 |
Ряд данных в одной диаграмме | 255 |
Точки данных в серии данных для двумерных диаграмм | 32 000 |
Точки данных в серии данных для трехмерных диаграмм | 4000 |
Точки данных для всех рядов данных на одной диаграмме | 256 000 |
Спецификации и ограничения сводных таблиц и сводных диаграмм
Особенность | Максимальный предел |
|---|---|
Отчеты сводной таблицы на листе | Ограничен доступной памятью |
Уникальных элементов на поле | 1 048 576 |
Поля строки или столбца в отчете сводной таблицы | Ограничен доступной памятью |
Фильтры отчетов в отчете сводной таблицы | 256 (может быть ограничено доступной памятью) |
Поля значений в отчете сводной таблицы | 256 |
Формулы вычисляемых элементов в отчете сводной таблицы | Ограничен доступной памятью |
Фильтры отчетов в отчете сводной диаграммы | 256 (может быть ограничено доступной памятью) |
Поля значений в отчете сводной диаграммы | 256 |
Формулы вычисляемых элементов в отчете сводной диаграммы | Ограничен доступной памятью |
Длина имени MDX для элемента сводной таблицы | 32 767 |
Длина строки реляционной сводной таблицы | 32 767 |
Книги с включенным параметром «Разрешить изменения более чем одному пользователю.
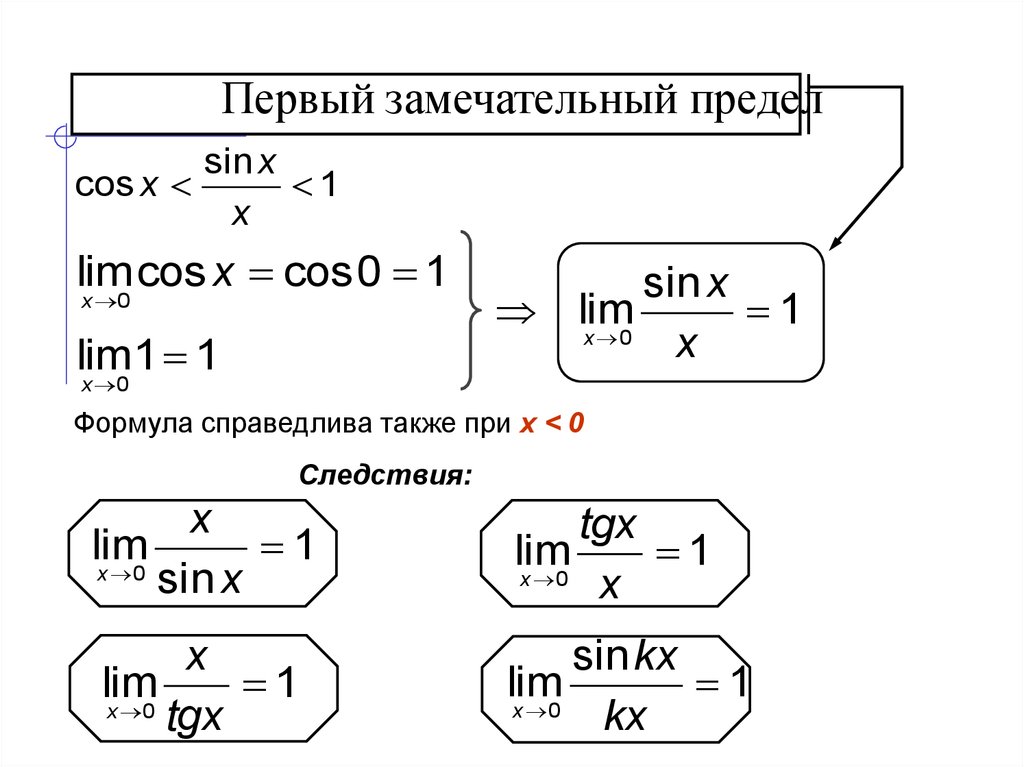 ..»
..»Если для книги включен параметр Разрешить изменения более чем одному пользователю… , применяется следующая информация. Этот параметр включен при использовании общих книг.
Особенность | Максимальный предел |
|---|---|
Пользователи, которые могут одновременно открывать и совместно использовать книгу | 256 |
Личные представления в рабочей книге | Ограничен доступной памятью |
Дней, в течение которых ведется история изменений | 32 767 (по умолчанию 30 дней) |
Рабочие книги, которые можно объединить одновременно | Ограничен доступной памятью |
Ячейки, которые можно выделить | 32 767 |
Цвета, используемые для обозначения изменений, сделанных разными пользователями, когда включено выделение изменений | 32 (каждый пользователь обозначен отдельным цветом; изменения, сделанные текущим пользователем, выделены темно-синим цветом) |
Таблицы Excel в книге | 0 (ноль) Примечание. |
Верх страницы
Типы, свойства, формулы, примеры решения
Пределы — это фундаментальные понятия в математике, которые используются для выяснения состояния частицы в определенном положении, для нахождения начального и конечного положения частицы для определения значений. Он получен из исчисления и доказал свою эффективность как процесс получения выходных данных для заданных пределов. Пределы также используются при анализе характеристик функции вблизи и в конкретной точке.
Содержание
|
Читайте также: Преемственность и дифференциация
Что такое предел?
В математике предел просто дает близкие значения или высокие значения выходных данных. Они необходимы для определения производных, непрерывности и интегралов функций. Он представлен как
lim x->a f(x) = b
равен б.
ЛимитыПредставления различаются в зависимости от типа лимитов. Вот несколько примеров:
Правосторонние пределы: Представлено как
lim 1 +f(x) = 1
19 Левостороннее ограничение: Оно представлено в виде
lim 1 -f(x) = 1
Левая и правая стороны Ограничение Бесконечные пределы: В этом значении f (x) нет предела, и оно может простираться в любую точку плоскости. Он представлен как
Он представлен как
lim x->∞ f(x) = 1
Односторонние бесконечные пределы: Здесь одна сторона f(x) представлена как бесконечность. Они представлены как
LIM 1 +F (x) = ∞ или LIM 1 -F (x) = ∞
-F (x) = ∞ -F (x) = ∞ -F (x) = ∞ -F (x) = ∞ -F (x) = ∞ -F (x) = ∞ свойства и теоремы, связанные с понятием пределов.Правило сумм: Предел суммы двух функций равен сумме пределов их индивидуальных функций.
Lim x->a [f(x) + g(x)] = lim x->a f(x) + lim x->a g(x)
Правило разности: Предел разности двух функций равен разнице пределов их индивидуальных функций.
Lim x->a [f(x) — g(x)] = lim x->a f(x) — lim x->a g(x)
Правило произведения: Предел произведения двух функций равен произведению пределов их индивидуальных функций.
Lim x->a [f(x)*g(x)] = lim x->a f(x)*lim x->a g(x)
Частное правило: Предел частного любых двух функций равен пределу частного обеих функций, когда знаменатель не равен нулю.
Lim x->a f(x)/g(x) = lim x->a f(x)/lim x->a g(x)
Степенное правило: Мощность любой корневой функции указывается как.
Lim x->a √|f(x)| = √lim x->a |f(x)|
Это эффективный подход к устранению корней власти.
Положительные целые числа: Для любых положительных целых чисел n,
Lim x n -a n /x-a = na (n-1)
Теорема сэндвича: )≤ g(x)≤h(x), то для любого действительного числа a, если
lim x->a f(x) = l = lim x->a g(x)
, то
lim x->a g(x) = l
Правило L-больницы: Правило L-больницы позволяет решить функцию, разделив ее на отдельные пределы. Он представлен как
Он представлен как
lim x->a f(x)/g(x) = lim x->a f 1 (x)/g
Формулы предела
Вот некоторые основные формулы предела, приведенные в таблице ниже.
| S.NO | Формула |
|---|---|
| 1 | LIM X-> 0 SIN X = 0 |
| 2 | LIM X-> 0 |
| 0308 COS X = 0 | |
| 3 | LIM X-> 0 SIN X /X = 0 |
| 4 | LIM X-> 0 TAN X /X = 1 |
| 5 5 | LIM X-> 0 1-COS X/X = 0 |
| 6 | LIM X-> 0 SIN -1 X/X = 1 |
| 7 | LIM x->0 tan -1 x/x = 1 |
| 8 | lim x->a sin -1 x = sin -1 a,|a|≤1 |
| 9 | lim x->a cos -1 cos -1 cos A, | a | ≤1 |
| 10 | LIM X-> A TAN -1 x = TAN -1 A, -1 |
76.
 Некоторые формулы логарифмов и экспоненциальных вычислений перечислены ниже.
Некоторые формулы логарифмов и экспоненциальных вычислений перечислены ниже.| S.NO | Формула | |
|---|---|---|
| 1 | LIM X-> 0 E x = 1 | |
| 2 | LIM X-> 0 E X -1/x-> 0 E x -1/x-> 0 E x| -1/-1/x-> 0 E . 1 | |
| 3 | LIM X-> 0 A x -1/x = log E A | |
| 4 | Lim X-> 0 x = 1 | |
| 5 | lim x->∞ (1+1/x) x = E | |
| 6 | LIM x-> 0 (1+x) 1/x = E | |
| 7 | Lim x-> ∞ (1+a/x) x = E A | |
| 8 | LIM x-> ∞ (x+a/x+b) x+c = E (A+B) | 99455 (a+b) | 99 | 9955 (a+b) | 99 40004. | lim x->∞ x n /e x = 0 |
| 10 | lim x->a x a -a x /x x -a a = 1 + loga/(1-loga) |
Вещи, которые нужно помнить В ближайшем пределе, дает просто
значения или высокие значения вывода.Примеры вопросов
Вопросы. Решите lim x->0 (sin x)/x, используя правило L-больницы.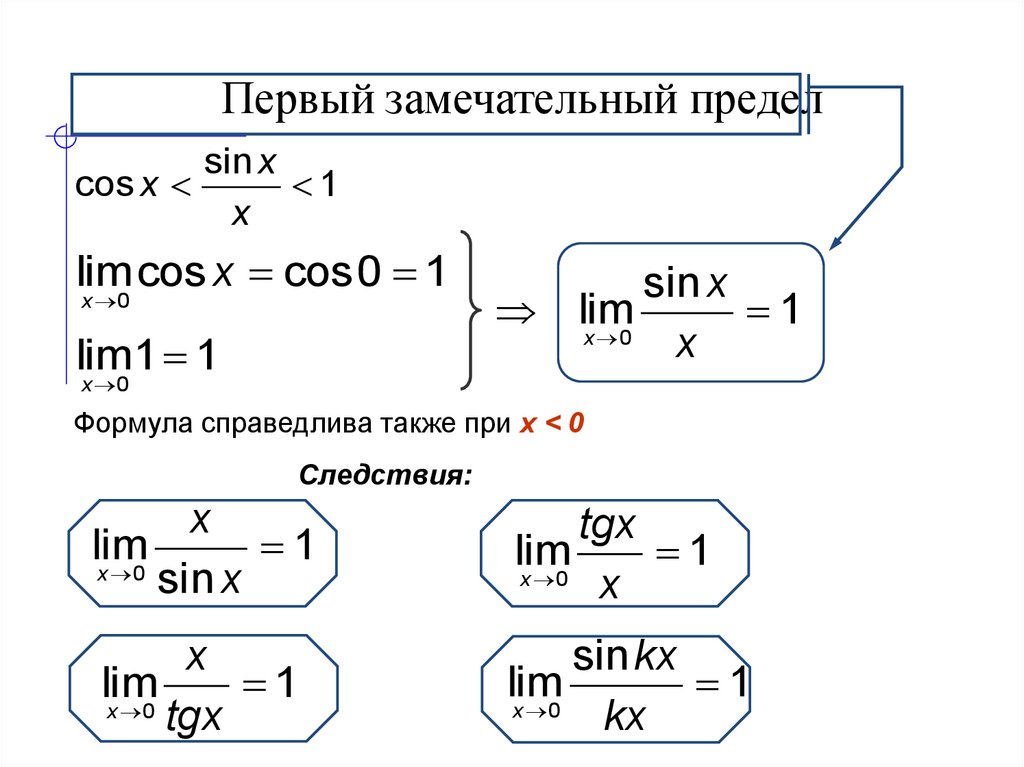 (2 балла)
(2 балла)
Отв. lim x->0 (sin x)/x = 0/0
Используя правило L-больниц,
lim x->0 (sin x)/x = lim x->0 ( cos x)/1
lim x->0 (cos x) = 1 и lim x->0 (1) = 1
lim x->0 (sin x)/x = 1
Вопрос. В чем польза правила L-госпиталя? (2 балла)
Отв. Правило L-госпиталя используется для решения задач, числитель и знаменатель которых становятся равными нулю, путем подстановки пределов в основном для неопределенных задач.
Вопрос. Сформулировать и доказать правило L-Hospitals? (2 балла)
Отв. lim x->0 f(x)/g(x) = lim x->c f(x)-0/g(x)-0
→ lim x->c f(x)-f(c)/g(x)-g(c)
→ lim x->c ((f(x)-f(c)/x-c)/(g(x)-g(c)/x-c
→ lim x->c ((f(x) )-f(c)/x-c)/ lim x->c ((f/g(x)-f/g(c)/x-c)
→ lim x->c f1(c)/ g1(c)
Отсюда доказано
Вопрос Кто разработал идею пределов? исчисление
Вопрос. Могут ли существовать несколько ограничений для одной и той же функции, если не объяснить, почему? (2 балла)
Могут ли существовать несколько ограничений для одной и той же функции, если не объяснить, почему? (2 балла)
Отв. Предел не может иметь несколько функций, потому что ни одна функция не может существовать между двумя разными временными интервалами одновременно.
Вопрос. В каких случаях предела не существует? (2 балла)
Отв.
1)Если на графике есть разрыв при значении x a, то предел не существует
2)Если функция не имеет конечного значения
3) если значение функции стремится к нулю.
Вопрос. Оцените LIM X-> 3 (2x 3 -3X 2 +155 2 +155 2 +155) (2 ). Это может быть записано в виде
= 2lim х->3 (х 3 )- 3lim х->3 (х 2 )+ (1)
= 2(3 3 )- 3(3 2 )+1
2*= 3 *9+1
= 28
Следовательно, значение приведенного выше квадратного уравнения равно 3.
Ques. Вычислить заданный предел lim x->0 (1+cosx) 2 secx (2 балла)
Ответ. Предположим, что y= cosx,
Если x->0 и y->0, то
= Sec x = 1/cos x = 1/y
= lim x->0 (1+cosx) 2 secx
= lim x->0 (1+y) 2 /y
Мы знаем, что из предельных формул Lim x->0 (1+x) 1/x = e
Тогда это можно записать как lim x->0 (1+y) 2/год
=е 2
Воп. Оцените следующий предел lim x-> 0 (e x — e -x ) / cos x (3 балла)
Анс. lim x-> 0 (e x — e -x ) / cos x
= lim x-> 0 (e x — (1/e x )) / sin х
= lim х-> 0 ((е х ) 2 — 1)/е х cos х
= lim х-> 0 5/ 1 ) (е 2 х 1) е х соз х
Теперь умножим числитель на 2x/2x, cos x на (x/x)
= lim x -> 0 (e 2x — 1)(2x/2x)/e x cos x (x/x)
= lim x-> 0 ((e 2x — 1)/2x)(2x/x)/(e x (cos x/x))
= 2lim x-> 0 ((e 2x — 1)/2x)/lim x-> 0 (e x lim x-> 0 (cos x/x))
= 2 (1)/1(1)
= 2
Отсюда значение lim x-> 0 (e x — e -x ) / cos x равно 2.
Вопрос. Вычислить lim x->1 log(x+1) (2 балла)
Ответ. допустим, что x=1 в log(x+1)
= lim x->1 log(x+1)
=log(1+1)
=log2
Вопросы. Вычислить lim x->0 (1+x) 1/3x (2 балла)
Ответ. Это можно записать в виде lim x->0 (1+x) 1/3x
= lim x->0 (1+x) 1/3x
= lim x->0 [(1+x) 1/x ] 1/3
=e 1/3
Отсюда оценка lim x->0 (1+x) 1/3x is e 1/3
Продовольственные магазины установили ограничения на покупку детских смесей в связи с общенациональным дефицитом нехватка, затрагивающая родителей младенцев по всей стране.
Лимиты, которые начались 13 мая, варьируются в зависимости от местоположения в зависимости от лимитов на закупки в рамках программ дополнительного питания для женщин, младенцев и детей на государственном уровне, говорится в заявлении представителей продовольственного магазина во вторник. Магазины за границей привязаны к лимитам покупок в рамках программы WIC-Overseas. Ограничения распространяются на все специальные детские смеси.
Магазины за границей привязаны к лимитам покупок в рамках программы WIC-Overseas. Ограничения распространяются на все специальные детские смеси.
Ограничения аналогичны тем, которые вводятся коммерческими розничными торговцами и военными биржами, говорится в объявлении. По крайней мере, неделей ранее военные биржи установили лимит в пять единиц на покупателя на покупку, и эти лимиты распространяются на все детские смеси.
Запасы детских смесей в зарубежных магазинах составляют около 70% от того, что обычно находится на полках. По словам официальных лиц, складские запасы в США еще ниже, около 50% от нормы.
«Если наличие детских смесей станет проблемой для зарубежных продавцов, агентство при необходимости доставит продукты по воздуху, при условии, что продукты будут в наличии», — сказал Билл Мур, директор и главный исполнительный директор Агентства оборонных продовольственных магазинов.
В зависимости от региона страны запасы детских смесей в коммерческих магазинах на 40-50 процентов ниже нормы, но запасы некоторых наиболее важных специализированных смесей, таких как гипоаллергенные продукты, истощены еще больше.
Дети, не находящиеся на грудном вскармливании, как правило, получают смесь в течение первых 12 месяцев жизни.
«Мы вводим ограничения на покупки из-за повышенного спроса и для того, чтобы у всех был равный доступ к предметам первой необходимости, а также для предотвращения «панических покупок» там, где продукт доступен», — сказал Мур. «Наличие детских смесей во всех наших магазинах сейчас постоянно меняется и меняется с каждым днем. Мы работаем с нашими дистрибьюторами, чтобы увеличить объем поставок этих критически важных продуктов».
В магазинах Европы есть возможность приобрести детское питание у местных производителей. Эти продукты иногда используются для пополнения запасов товаров в США в случае их нехватки. Но официальные лица заявили, что в Тихоокеанском регионе нет утвержденных вариантов детского питания местного производства. Эти магазины зависят от американских дистрибьюторов торгового агентства.
«В наших магазинах мы находимся в том же положении, что и коммерческие розничные торговцы», — сказал Мур. Дистрибьюторы получают ограниченные ассигнования, существенно меньше, чем они заказывают у производителей. Это ограничивает количество смеси, поступающей в магазины.
Дистрибьюторы получают ограниченные ассигнования, существенно меньше, чем они заказывают у производителей. Это ограничивает количество смеси, поступающей в магазины.
В дополнение к фирменным детским смесям в магазинах продаются детские смеси под торговой маркой магазина: Tippy Toes. С февраля продажи рецептуры торговой марки Tippy Toes выросли на 600%, сказал Рене Хантер, вице-президент Spartan Nash Military Division, в более раннем интервью Military Times. Эта компания заключила контракт с агентством по продаже товаров под частными торговыми марками по всему миру. ФАЙЛ
. Завод Abbott Laboratories показан в Стерджисе, штат Мичиган, 23 сентября 2010 г. В середине февраля 2022 г. Abbott объявила об отзыве с завода различных партий трех сухих детских смесей после исследование редких бактериальных инфекций у четырех детей, получивших этот продукт. Двое младенцев умерли. Но нет уверенности, что бактерии произошли от растения; штаммы, обнаруженные на заводе, не соответствовали двум имеющимся образцам от младенцев. (Журнал Брэндона Уотсона/Стерджиса через AP, файл)
(Журнал Брэндона Уотсона/Стерджиса через AP, файл)
В центре нехватки молочных смесей находится единственная фабрика: завод Abbott Nutrition в Стерджисе, штат Мичиган. Завод является крупнейшим в своем роде в США и является источником ведущих брендов молочных смесей, таких как Similac.
В середине февраля компания Abbott объявила об отзыве с завода различных партий трех сухих детских смесей после того, как федеральные чиновники начали расследование редких бактериальных инфекций у четырех детей, которых кормили смесями. Двое младенцев умерли. Но нет уверенности, что бактерии произошли от растения; штаммы, обнаруженные на заводе, не соответствовали двум имеющимся образцам от младенцев.
Компания остановила производство, пока инспекторы Управления по санитарному надзору за качеством пищевых продуктов и медикаментов проводили шестинедельное расследование завода.
Предварительный отчет, опубликованный в марте, обнаружил следы бактерий — cronobacter — на нескольких поверхностях по всему заводу, но не в местах, используемых для изготовления порошка. Заводские записи показали, что с 2019 года компания Abbott восемь раз обнаруживала бактерии в своих продуктах или на объектах. Но пока неясно, как скоро сайт заработает.
Заводские записи показали, что с 2019 года компания Abbott восемь раз обнаруживала бактерии в своих продуктах или на объектах. Но пока неясно, как скоро сайт заработает.
— Ассошиэйтед Пресс способствовало этому отчету.
О Карен Джоуэрс
Карен более 30 лет освещала семьи военнослужащих, качество жизни и проблемы потребителей для Military Times, а также является соавтором главы, посвященной освещению в СМИ семей военнослужащих в книге «План битвы». для поддержки семей военнослужащих». Ранее она работала в газетах Гуама, Норфолка, Джексонвилля, Флорида, и Афин, Джорджия.
Поделиться:
Тэги:
Карен Джоуэрсдетская смесьпромхозыобменыцепочка снабжениядефициттытыв других новостях
смертельный выстрел в Форт-Брэгг десантник под следствием
сержант. 22-летний Николас Антонио Бобо был найден около 23:00. с множественными огнестрельными ранениями за пределами своей квартиры.
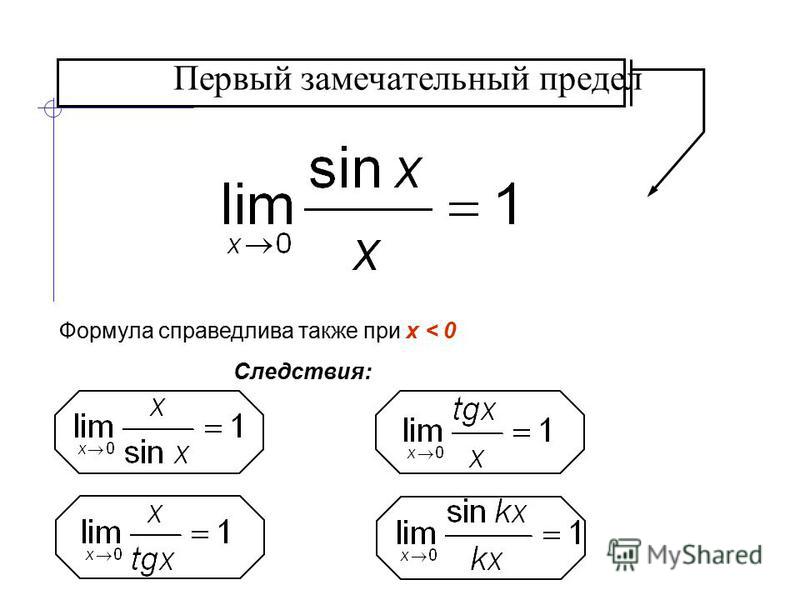
Мужчина погиб после того, как врезался в барьер на военно-морской авиабазе Джексонвилл
Официальные лица NAS в Джексонвилле заявили, что водитель, имя которого не было названо сразу, не имел известной принадлежности к вооруженным силам.
Чиновники и продавцы армейских складов осуждены за мошенничество на торгах
Взятки должностным лицам складов включали модификации старинных автомобилей и билеты Dallas Cowboys.
Республиканцы угрожают судебными исками и бюджетными санкциями за решение об абортах в штате Вирджиния
Департамент заявил, что будет предлагать аборты в случаях изнасилования, инцеста и угроз жизни или здоровью ветеранов.
Дело о вакцине ВВС останется коллективным иском, решение апелляционного суда
Устные прения по апелляционному делу запланированы на 19 октября.
 .
.Загрузить еще
Нехватка детского питания: в каких магазинах действуют ограничения на покупку?
Многие компании, представленные на Money, размещают у нас рекламу. Мнения наши собственные, но компенсация и углубленное исследование
определяют, где и как могут появиться компании. Узнайте больше о том, как мы зарабатываем деньги.
Крупные розничные торговцы, такие как Target и Walgreens, ограничивают покупки американцами детских смесей на фоне продолжающегося дефицита.
По состоянию на 3 апреля 31% самых популярных детских смесей отсутствовали на складе, согласно данным исследовательской компании Datasembly, которая проанализировала около 11 000 магазинов в США.
В нескольких штатах показатели были хуже. Datasembly обнаружил, что Коннектикут, Делавэр, Монтана, Нью-Джерси, Род-Айленд, Техас и Вашингтон столкнулись с острой нехваткой в начале апреля, в результате чего более 40% смесей отсутствовало на складе. В трех городах — Де-Мойне, Миннеаполисе и Сан-Антонио — уровень отсутствия детских смесей превысил 50%.
В трех городах — Де-Мойне, Миннеаполисе и Сан-Антонио — уровень отсутствия детских смесей превысил 50%.
Почему не хватает детских смесей?
Нехватка возникла после отзыва в феврале некоторых порошковых смесей Similac, Alimentum и EleCare, произведенных Abbott Nutrition после четырех жалоб потребителей на возможное бактериальное загрязнение. Отзыв был добровольным; Abbott заявила, что ни один из продуктов, которые она распространяла, не дал положительных результатов на бактерии, указанные в жалобах.
Текущие проблемы с цепочками поставок усложняют производителям замену отозванной продукции, что способствует дефициту по всей стране.
Отозванная формула больше не продается на полках магазинов, но если вы считаете, что приобрели ее ранее, вы можете проверить номер партии продукта на веб-сайте Abbott. Для получения дополнительной информации прочитайте веб-страницу Центров по контролю и профилактике заболеваний о продуктах формулы Abbott, затронутых отзывами.
Детская смесь стала дороже?
Компания Datasembly обнаружила, что цены на молочные смеси остаются относительно стабильными, несмотря на растущий дефицит. Средняя цена всех детских смесей, которые компания отслеживает в январе, составляла 24,37 доллара, и в то время только 3,3% товаров отсутствовали на складе. В марте, когда частота выпуска акций, которых нет в наличии, подскочила почти до 30%, средняя цена немного выросла до 26,21 доллара.
Это не значит, что рост цен не влияет на родителей и опекунов. Рекордно высокий уровень инфляции — недавно установленный на уровне 8,5% в годовом исчислении — означает, что деньги просто не тянутся так далеко, как в прошлом году. Последние данные Бюро статистики труда показывают, что цены на детское питание подскочили почти на 11% в период с марта 2021 года по март 2022 года9.0014
Детская смесь является незаменимым продуктом для миллионов семей. По данным CDC, только 25,6% детей, родившихся в 2017 году в США, находились на исключительно грудном вскармливании до шестимесячного возраста.
Объявления за деньги. Мы можем получить компенсацию, если вы нажмете на это объявление. Объявление
Вы никогда не знаете, когда вы можете оказаться в финансовом затруднении — хорошая новость в том, что у вас есть выбор.
Индивидуальный заем может помочь вам уменьшить потери и вернуться на правильный путь. Нажмите здесь, чтобы изучить варианты!
Подать заявку сегодня
Магазины, ограничивающие покупку детских смесей
Со ссылкой на Совет по детскому питанию Америки, CBS News сообщила на этой неделе, что производители наращивают производство, чтобы справиться с нехваткой смесей. Совет посоветовал родителям хранить дома 10-дневный или двухнедельный запас смеси. По данным CBS News, он предостерег от дальнейшего накопления запасов и рекомендовал родителям покупать смесь только у авторитетных розничных продавцов или непосредственно у производителя.
«Мы надеемся, что по мере роста производства этой весной семьям по всей стране станет легче», — сообщил USA Today Брайан Диттмайер, старший директор по государственной политике Национальной ассоциации WIC, в Instagram. Жить.
Жить.
В то же время некоторые розничные продавцы предлагают детское питание.
Walgreens ввела ограничение в три продукта формулы на транзакцию, как в Интернете, так и в магазине, сославшись на «повышенный спрос и различные проблемы с поставщиками», сообщил Money по электронной почте представитель Walgreens. Target также ограничивает покупку некоторых детских смесей в Интернете.
Walmart подтвердил Money, что в соответствии с запросом Управления по санитарному надзору за качеством пищевых продуктов и медикаментов США он ограничивает количество покупок смесей до пяти на одного покупателя, на одного ребенка в день в большинстве магазинов и в Интернете.
CVS Health и Kroger, как сообщается, также установили ограничения на покупку детских смесей.
Американская академия педиатрии предостерегает от разбавления детской смеси, чтобы сэкономить деньги и продлить срок ее действия. Если вы не можете найти обычную смесь для вашего ребенка, CDC советует обратиться к лечащему врачу вашего ребенка за рекомендациями.
Информационный бюллетень
Все еще изучаете основы личных финансов? Позвольте нам преподать вам основные уроки денег, которые вам НЕОБХОДИМО знать. Получайте полезные советы, советы экспертов и милых животных в свой почтовый ящик каждую неделю.
Нажимая «Зарегистрироваться», я соглашаюсь получать информационные бюллетени и рекламные акции от Money и его партнеров. Я согласен с Условиями использования и Уведомлением о конфиденциальности Money и даю согласие на обработку моей личной информации.
Информационный бюллетень
Подписаться удалось!
Теперь вы будете получать информационный бюллетень Money’s Dollar Scholar по телефону
. Ответьте в любое время, чтобы сообщить нам, что мы можем улучшить. Наслаждаться!
Убедитесь, что мы попали в папку «Входящие», а не в папку «Спам». Мы только что отправили вам приветственное письмо. Иногда почтовые клиенты отправляют наше первое письмо в папку со спамом или рекламными акциями.

 0000000
-0.0010000 0.0000000
-0.0001000 0.0000000
-0.0000100 0.0000000
0000000
-0.0010000 0.0000000
-0.0001000 0.0000000
-0.0000100 0.0000000
 Второй набор диаграмм также рекомендует более высокие минимумы для обоих. Отметим также, что, в отличие от других, SiO 9Оксиды 0307 2 и Al 2 O 3 всегда указываются с минимальными количествами, что подчеркивает необходимость адекватных уровней для достижения твердости глазури.
Второй набор диаграмм также рекомендует более высокие минимумы для обоих. Отметим также, что, в отличие от других, SiO 9Оксиды 0307 2 и Al 2 O 3 всегда указываются с минимальными количествами, что подчеркивает необходимость адекватных уровней для достижения твердости глазури. Аналогично, второй набор диаграмм показывает предел конуса 04 на уровне 1,0, это также указывает на то, что они не включают B 2 О 3 в единстве.
Аналогично, второй набор диаграмм показывает предел конуса 04 на уровне 1,0, это также указывает на то, что они не включают B 2 О 3 в единстве.
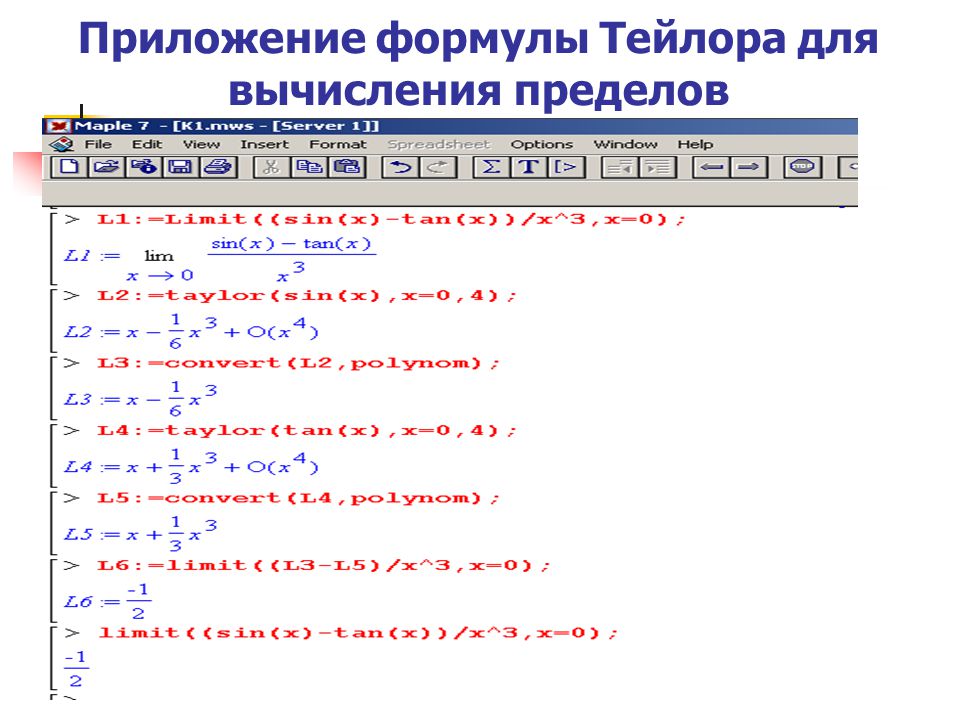 Не используйте BaO на функциональных поверхностях. Несмотря на то, что BaO указан в обоих тестах, мы рекомендуем не добавлять его в глазури для пищевых продуктов, если у вас нет возможности проводить испытания на выщелачивание.
Не используйте BaO на функциональных поверхностях. Несмотря на то, что BaO указан в обоих тестах, мы рекомендуем не добавлять его в глазури для пищевых продуктов, если у вас нет возможности проводить испытания на выщелачивание. Кроме того, глазури, предназначенные для напольной плитки, будут иметь совсем другие ограничения, чем те, которые предназначены для художественных изделий, поскольку формула подчеркивает твердость, долговечность и способность к быстрому возгоранию, последний внешний вид и визуальные эффекты.
Кроме того, глазури, предназначенные для напольной плитки, будут иметь совсем другие ограничения, чем те, которые предназначены для художественных изделий, поскольку формула подчеркивает твердость, долговечность и способность к быстрому возгоранию, последний внешний вид и визуальные эффекты. Медь может превратить устойчивую к выщелачиванию основу в выщелачиватель.
Медь может превратить устойчивую к выщелачиванию основу в выщелачиватель.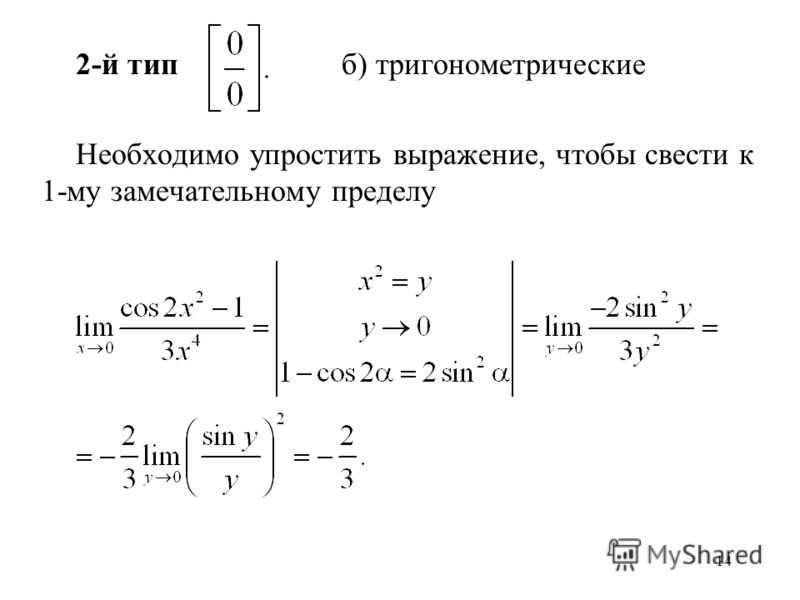 Доля модели данных в адресном пространстве может достигать 500–700 мегабайт (МБ), но может быть меньше, если загружены другие модели данных и надстройки.
Доля модели данных в адресном пространстве может достигать 500–700 мегабайт (МБ), но может быть меньше, если загружены другие модели данных и надстройки.
 2251Е-308
2251Е-308 7976
7976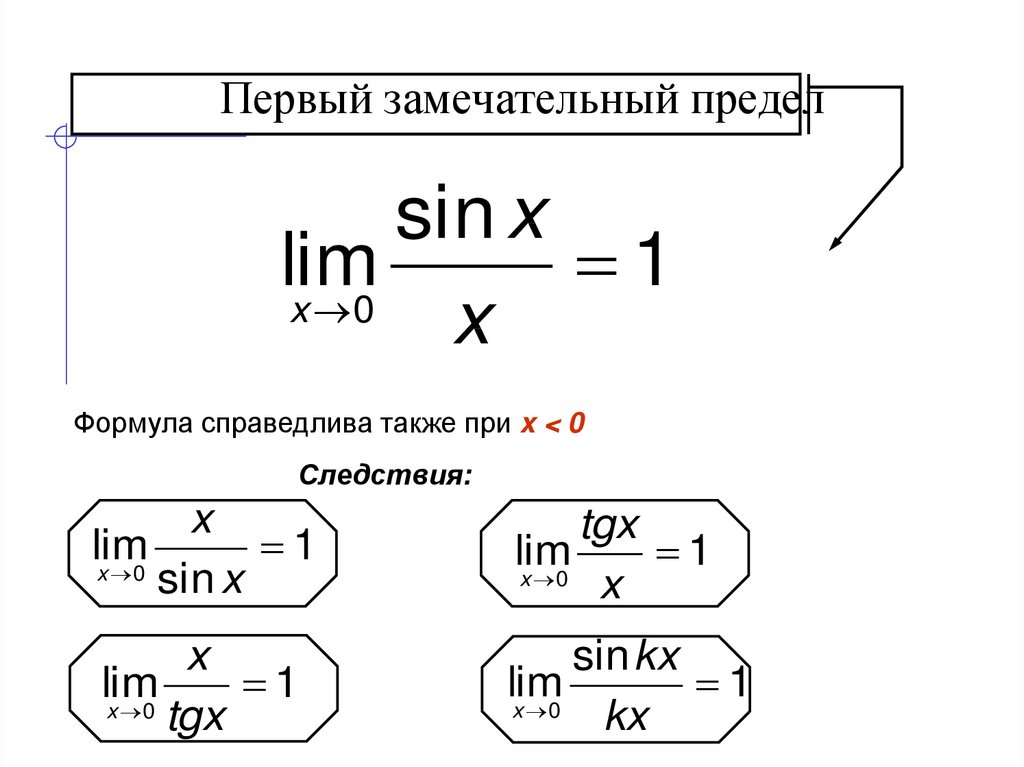 (1 января 1904 г., если используется система дат 1904 г.)
(1 января 1904 г., если используется система дат 1904 г.) В книге, содержащей одну или несколько таблиц Excel, не может быть включен параметр Разрешить изменения более чем одному пользователю… .
В книге, содержащей одну или несколько таблиц Excel, не может быть включен параметр Разрешить изменения более чем одному пользователю… . 2251Е-308
2251Е-308 7976
7976 (1 января 1904 г., если используется система дат 1904 г.)
(1 января 1904 г., если используется система дат 1904 г.) В книге, содержащей одну или несколько таблиц Excel, не может быть включен параметр Разрешить изменения более чем одному пользователю… .
В книге, содержащей одну или несколько таблиц Excel, не может быть включен параметр Разрешить изменения более чем одному пользователю… . 2251Е-308
2251Е-308 7976
7976 (1 января 1904 г., если используется система дат 1904 г.)
(1 января 1904 г., если используется система дат 1904 г.) В книге, содержащей одну или несколько таблиц Excel, не может быть включен параметр Разрешить изменения более чем одному пользователю… .
В книге, содержащей одну или несколько таблиц Excel, не может быть включен параметр Разрешить изменения более чем одному пользователю… . 81
81