Как легко решать сложные задачи — 5 полезных советов от профессора-математика
Валерий Иванович Опойцев — математик, просветитель, профессор МФТИ, всю жизнь занимался наукой и преподаванием. Он издал 16-томник «Лекции по математике»*, а в последние годы создал крупный онлайн-проект «Школа Опойцева», который развивается до сих пор — хотя автора уже нет с нами. Сын ученого Сергей Опойцев выбрал 5 видеоуроков своего отца, которые будут полезны всем.
Если набрать в поисковике запрос «школьная математика», лекции моего отца до сих пор будут на первой-второй странице в выдаче. Мне кажется, все дело в том, что у отца был особый дар: он умел объяснять сложные вещи простым языком. А в своих лекциях доходчиво и доступно разъяснял те разделы математики и физики, которые вызывают наибольшие трудности у школьников и студентов.
«Это [лекции Опойцева] продукт нового поколения. Те же колеса, тот же руль, та же математическая суть — но по-другому» — так он сам описывал свой подход. Мой отец был убеждён, что «в условиях информационного наводнения инструменты вчерашнего дня перестают работать». Сегодня нужно учить иначе.
Мой отец был убеждён, что «в условиях информационного наводнения инструменты вчерашнего дня перестают работать». Сегодня нужно учить иначе.
Сейчас на канале «Школы Опойцева» в YouTube размещено более 270 лекций. Для того чтобы составить представление о методике моего отца, я выбрал пять интересных лекций — они посвящены вопросам преподавания в целом и могут быть интересны и учителям, и школьникам, и их родителям.
1. Преамбула
Некоторые говорят, отмечает Опойцев, что математика — трудный и ненужный предмет. Музыкантам и ветеринарам математика, считается, не нужна. Но математика, полагает Валерий Иванович, — это язык высокого уровня, часть мира. Если исключить математику из багажа знаний, будет потеряна часть Вселенной.
Главная сложность, по мнению Опойцева, в том, что математику учат умом, а не нутром. Но как создать среду, где изучение математики было бы необходимой потребностью? Первое — убрать строгость изложения.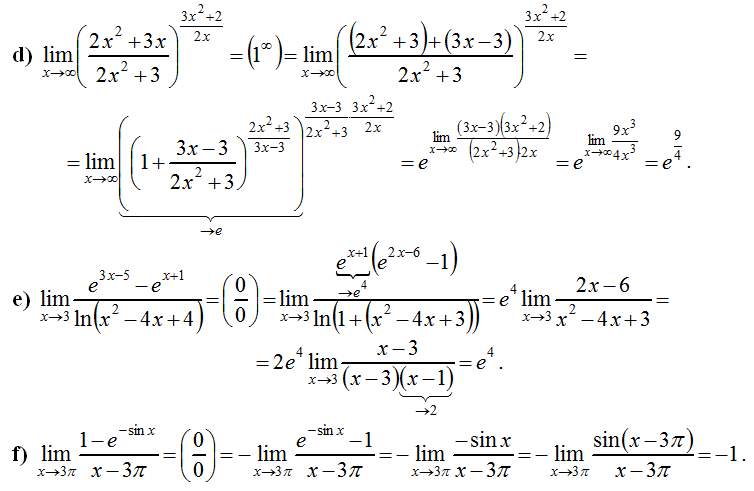 Остальные принципы — в этой лекции.
Остальные принципы — в этой лекции.
2. «Не боги горшки обжигают!»
Этот видеоурок отвечает на часто задаваемые родителями вопросы: почему учебники написаны так, что детям ничего не понятно, и как объяснить материал, чтобы ребенок все же понял.
Профессор рассказывает истории из своего преподавательского опыта и пытается дать ответ на вопрос, почему даже современные учебные пособия перегружены информацией и очень запутанны. По мнению Опойцева, это зачастую происходит потому, что авторы при написании учебников все время думают, как их будет оценивать комиссия при Минобразовании. Именно страх перед комиссией подталкивает авторов вывалить на учеников все темы сразу.
Как переломить этот паттерн? Ответ на этот и другие вопросы Валерий Опойцев дает в этом видео.
3. Опасно ли клиповое мышление?
Изменился мир, изменилось то, как люди потребляют информацию и общаются. Валерий Опойцев считает, что клиповое мышление сейчас не только у школьников, но и у всех людей вокруг. Люди меньше читают толстые книги. В метро сегодня большинство людей листают страницы в социальных сетях или ищут информацию в интернете и лишь у единиц можно увидеть в руках книгу. Стоит ли с этим бороться? Нет. А вот преподавать точные науки с учетом новых вводных — пожалуй.
Валерий Опойцев считает, что клиповое мышление сейчас не только у школьников, но и у всех людей вокруг. Люди меньше читают толстые книги. В метро сегодня большинство людей листают страницы в социальных сетях или ищут информацию в интернете и лишь у единиц можно увидеть в руках книгу. Стоит ли с этим бороться? Нет. А вот преподавать точные науки с учетом новых вводных — пожалуй.
4. Как искать пути решения?
В этом уроке Опойцев размышляет, как правильно решать сложные задачи. «Для решения некоторых задач нужно выйти за пределы стандартного мышления», — говорит он. Стандартные решения — взять длину, умножить на ширину, и получится площадь — тут не работают. На людей находит ступор, они толпятся вокруг стеклянного забора, а решение лежит за его пределами.
Как научиться хитро решать задачи? Рецепт такой: нужно решать их, и решать, и решать. Не надо торопиться и искать сразу подсказку в ответах. Надо думать и думать, и все эти раздумья даром не проходят. Причем это может быть не только решение задач, это могут быть игры в слова и другие головоломки.
Надо думать и думать, и все эти раздумья даром не проходят. Причем это может быть не только решение задач, это могут быть игры в слова и другие головоломки.
5. «Корабли Колумба» в системе образования
В этой лекции Опойцев рассказывает легенду о том, что индейцы не видели кораблей Колумба, когда те приблизились к берегам Америки. Некоторые не верят в это. Но сам Опойцев считает, что это вполне закономерно: люди часто просто не хотят видеть новое и незнакомое, как бы закрываются от этой информации.
Эффект «кораблей Колумба», по мнению Опойцева, довольно часто встречается и в процессе обучения. И при обучении математике в том числе — но и эту ситуацию можно исправить.
* Лекции выпущены под псевдонимом Валерий Босс.
Свойства пределов функций
- Дёмина Светлана Владимировна, учитель математики
Цели урока:
— научиться решать основные типы пределов функций, раскрывать неопределённости;
— совершенствование мыслительных умений учащихся сравнивать, анализировать и обобщать;
— формирование образовательных, коммуникативных и информационных компетентностей для продолжения математического образования в вузах;
— формирование навыков самостоятельной работы, чувства ответственности, познавательного интереса к обучению.
Задачи урока:
— изучить свойства пределов функций;
— отработать навыки применения данных знаний при решении примеров различной сложности, раскрытия неопределённостей;
— отработать навыки самостоятельной работы;
— отработать навыки тестирования в режиме online;
— способствовать развитию алгоритмического мышления учащихся;
— воспитывать уважение к интеллектуальному
труду.
Тип урока: урок изучения и первичного закрепления новых знаний.
Оборудование: персональные ПК (подключены к сети Интернет), МП, раздаточный материал.
Учебник: Алгебра и начала математического анализа. 11 класс: учебник для общеобразовательных учреждений: базовый и профильный уровни / [С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин]. — 10-е изд. – М.:Просвещение, 2011. -464 с.: ил. – (МГУ – школе).
Эпиграф:
“В математике следует помнить не
формулы, а процессы мышления”.
В. П. Ермаков
Ход урока
1. Оргмомент. Постановка цели урока.
2. Актуализация знаний. Подготовка к ЕГЭ. Тестирование on-line на сервисе проверки знаний учащихся http://www.diagtest.ru/ по теме “Основы тригонометрии”. Итог тестирования (Приложение 1).
3. Изучение нового материала.
Мотивирование. На первом курсе университета студенты часто сталкиваются с вопросом как решить предел функции? Решение пределов — это довольно трудный этап математического обучения который сразу встает перед Вами высокой и непробиваемой стеной, поскольку первокурсники еще не научились как следует преодолевать сложные теории. А теория пределов — это серьезная и сложная теория, без четкого понимания которой нельзя полноценно научиться решать задачи по вычислению пределов.
Лекция учителя и первичное закрепление новых знаний. (Приложение 2 – МП, Приложение 3 – раздаточный материал).
а) Свойства пределов:
Закрепление. Устно № 2.15 а), б). (с. 59)
б) Для решения пределов вспомним первый и второй замечательные пределы:
Закрепление. Доказательство (фронтально, с помощью учителя) № 2.16. а), б). (с.59)
Решение (использование подсказки – слайд № 6 ):
— самостоятельно: 1 вариант — № 2. 17г), 2 вариант №
2.17и),
17г), 2 вариант №
2.17и),
— у доски: 2.18 в) с. 59.
Рекомендация: если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
в) раскрытие неопределённостей:
| Неопреде- лённость |
Алгебраические преобразования |
| В числителе и знаменателе
сложные степенные или показательные функции. Для степенных функций – вынести за скобку в числителе и знаменателе х с наибольшим показателем степени; для показательных функций – вынести за
скобку в числителе и знаменателе наиболее быстро
возрастающее слагаемое. После сокращения дроби неопределённость устраняется. Пример №1. . Старшая степень числителя и знаменателя равна 2.
Что принципиально важно в оформлении решения? Во-первых, указываем неопределенность, если она есть. Во-вторых, желательно прервать решение для промежуточных объяснений. Можно использовать знак (*), он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения. В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так:
Закрепление. Пример №2. |
|
Если в числителе и знаменателе
находятся многочлены, и имеется
неопределенности вида , то для ее раскрытия нужно
разложить числитель и знаменатель на множители,
затем сократить и вычислить предел. Для этого
чаще всего нужно решить квадратное уравнение и
(или) использовать формулы сокращенного
умножения. В тригонометрических выражениях
необходимо упростить выражение, чтобы привести к
первому замечательному пределу. Для этого
чаще всего нужно решить квадратное уравнение и
(или) использовать формулы сокращенного
умножения. В тригонометрических выражениях
необходимо упростить выражение, чтобы привести к
первому замечательному пределу.Пример №3. , разложив квадратный трёхчлен на множители и сократив, получим Рекомендация: если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем. Пример №4. |
|
Если функция представляет собой
алгебраическую сумму дробей, то
неопределённость устраняется или приводится к
типу
после приведения дробей к общему знаменателю.
Если функция представляет собой алгебраическую
сумму иррациональных выражений (корней), то
неопределённость устраняется или приводится к
типу
путём домножения и деления функции на одно и то
же (сопряжённое) выражение, приводящее к
формулам сокращённого умножения. |
|
| 1 | Сводится ко второму замечательному пределу (см. пример №4). |
4. Итог урока: “Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию”. Ян Амос Коменский.
Рефлексия. Незаконченные предложения.
(“Микрофон”)
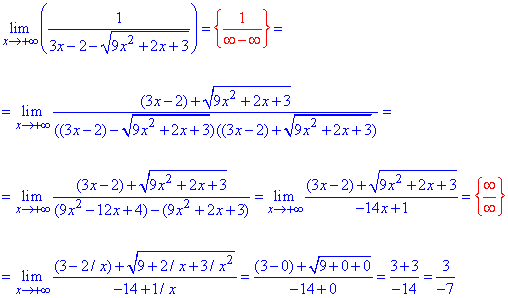
5. Домашнее задание.
- Выполнить работу над ошибками на сервисе проверки знаний по теме “Основы тригонометрии”.
- Для хорошо подготовленных учащихся: рассмотреть пример №4 в приложении № 3 “Раздаточный материал”.
Источники:
www.mathprofi.ru/predely_primery_reshenii.html
http://www.diagtest.ru/
Техника PSDM: как решать сложные проблемы и принимать правильные решения
Решение проблем — главная компетенция человека будущего. Эксперт по развитию лидерства Павел Меринов рассказал, что такое сложные проблемы, как принимать решения и почему обратная связь — важная часть решения проблемы
Об эксперте: Павел Меринов — международный коуч-консультант по оценке и развитию лидерства, фасилитатор по разработке стратегий и инноваций. Доцент НИУ ВШЭ, преподаватель Школы Критического Мышления. Представитель Hogan Assessment Systems (Hogan/ASI) и Development Dimensions International (DDI).
Доцент НИУ ВШЭ, преподаватель Школы Критического Мышления. Представитель Hogan Assessment Systems (Hogan/ASI) и Development Dimensions International (DDI).
Что такое принятие решений и решение проблем
Каждый день мы принимаем сотни решений, которые влияют на нашу жизнь: по разным оценкам только относительно еды их количество доходит до 225 в день. Решения часто оказываются неудачными, нам приходится работать с их последствиями и принимать новые решения. По данным Росстата за 2019 год, в России на 1 000 браков пришлось 653 развода, а за последние 15 лет индустрия сведения татуировок выросла на 440%.
Неэффективные, неуместные, необоснованные решения в бизнесе и управлении встречаются не реже, чем в бытовых ситуациях. Пять лет назад Мировой Экономический Форум в Давосе сделал прогноз, какие компетенции будут определять профессионала будущего в 2020 году. Сейчас это будущее уже наступило. Компетенции, связанные с принятием решений, остаются в ТОП-10 самых важных навыков, а решение сложных проблем занимает лидирующую позицию.
Прогноз 2016 года о самых востребованных навыках будущего — в 2020 году (Фото: World Economic Forum)
Решение проблем и принятие решений часто смешивают или используют как синонимы. Корректно их разделять, при этом рассматривать в одном «семействе» компетенций РППР (PSDM) — Решение Проблем и Принятие Решений (Problem Solving & Decision Making).
К PSDM обычно относят:
- Системное мышление.
- Стратегическое мышление.
- Критический анализ информации.
- Осознанность в принятии решений.
- Взаимодействие со стейкхолдерами.
- Креативный подход к решению проблем.
- Лидерство в условиях неопределенности.
- Стимулирование организационных изменений.
Большинство компаний, которые я консультирую, добавляют хотя бы два-три навыка из этого списка в модели корпоративных компетенций или эталонные профили должности. При этом чем выше управленческая позиция, тем серьезнее требования бизнеса и меняющегося ландшафта к уровню этих компетенций. Здесь есть две новости: хорошая и не очень.
При этом чем выше управленческая позиция, тем серьезнее требования бизнеса и меняющегося ландшафта к уровню этих компетенций. Здесь есть две новости: хорошая и не очень.
Хорошая новость в том, что научные сообщества давно изучают PSDM с разных сторон. Например, Ариэль Рубинштейн развил концепцию Герберта Саймона о нашей ограниченной рациональности и рассмотрел наши решения в русле институциональной экономики и теории игр. Психологи-когнитивисты Дэниел Канеман, лауреат Нобелевской премии по экономике в 2002 году и Амос Тверски описали, как мы ищем «короткие» пути в решении сложных задач, но попадаем в ловушки и предубеждения. А социолог Барри Шварц в книге «Парадокс выбора» объяснил, почему большой выбор затрудняет принятие решений и приводит к ощущению неудовлетворенности.
Новость, которая не очень. Ни исследовательское, ни бизнес-сообщество до сих пор не решили, что именно считать решением: взгляды на природу решений разные, а единого определения — нет.
Как мы принимаем решения
Американский психолог и профессор Джой Пол Гилфорд создал концепцию многомерного интеллекта — модель мышления, основанную на базе конкретных математических измерений, которые он проводил. Гилфорд предложил решать проблемы, чередуя «дивергентное» (расходящееся) и «конвергентное» (сходящееся) мышление. То есть, сосредотачиваться на целях, которые помогают решать проблему на данном этапе: создавать варианты выбора или этот выбор делать.
Именно эта концепция, визуально показанная в виде «двойного алмаза», плотно укоренилась в подходах к управлению инновационными процессами и дизайн-мышлении.
Визуально концепция чередования «режимов мышления» Гилфорда может быть изображена как ромб. Она наглядно показывает, как эффективно решать проблемы
Теперь мы можем дать определения:
Решение проблем — это последовательный творческо-аналитический процесс. Мы анализируем ситуацию, ищем причины проблемы, формулируем ее и придумываем варианты решения.
Принятие решений — выбор, который мы делаем в процессе, что-то предпочитая и от чего-то отказываясь на каждом из ключевых этапов. Мы выбираем факторы, которые будем считать значимыми, а какие — нет, расставляем приоритеты, строим планы.
Получается, что принятие решений — это часть решения сложных проблем. Чем лучше мы определяем и решаем проблемы, выбираем и принимаем решения, тем успешнее сможем справляться с изменениями. Например, разрабатывать новые продукты, проводить стратегические сессии и управлять инновациями.
Что такое сложные проблемы
Посмотрите на две задачи. Подумайте, как бы вы их решили и чем они отличаются.
Задача 1. Мать поручила сыну принести домой ровно 7 л воды с реки. Она дала ему два кувшина емкостью 3 и 5 л. Как мальчик может отмерить точно 7 л воды, используя только два этих кувшина?
Задача 2. Вообразите, что регулярные частные полеты на орбиту Земли стали возможны и сопоставимы по стоимости с среднестатистическим путешествием в другую страну. Подумайте, что делать представителям туристической индустрии на Земле? Запишите мысли, которые придут в голову.
Подумайте, что делать представителям туристической индустрии на Земле? Запишите мысли, которые придут в голову.
Первая задача — это «задачка». У нее есть конкретный правильный ответ, к которому можно прийти через ряд вычислений. Это фрагмент классического Стэнфордского теста Термана на измерение интеллекта «The Measurement of Intelligence» 1916 года. Правильное и быстрое решение подобных задач показывает высокие значения в тестах когнитивных способностей и уже более 100 лет вызывает горячие дискуссии в профессиональном исследовательском сообществе. Однако, даже несмотря на высокие когнитивные способности, люди склонны попадать в ментальные ловушки, принимать решения на основе ошибочных предположений и опираться на стереотипные представления.
Вторая задача — это сложная «проблема». У нее нет единственно правильного решения. Есть большое количество факторов, которые нужно учесть, и условий, которые будут формировать разные сценарии; при этом существенную роль будет играть эмоциональный фон решающего.
В управленческой практике у менеджеров есть все необходимые данные для принятия решений и решения проблем. По данным Гарвардского исследования, 68% руководителей уверены в точности большей части данных, лежащих в основе их бизнес-решений. То есть, когнитивные способности обеспечивают возможность решать проблемы, но качество решений не от них.
Как комплексный подход помогает решать проблемы
Мы живем в VUCA-мире — мире ускоряющихся изменений, в котором компании и целые отрасли трансформируются быстрее, чем раньше. Например, CEO General Motors Мэри Барра считает, что автомобильная индустрия изменится сильнее в последующие пять-десять лет, чем за предыдущие 50 лет. Такой мир становится стрессовым фоном для всех людей и выводит на первый план личностные особенности, которые либо помогают, либо мешают решать сложные проблемы.
Психотерапевт Андрей Курпатов о том, как помочь мозгу обучаться и принимать решения
По личностной характеристике человека можно предсказать, как он будет решать проблемы и принимать решения. Например, экстраверсия отрицательно связана с качеством решений, но положительно влияет на их внедрение в практику. Высокая импульсивность связана с ошибочными решениями, склонностью к рискованному и необдуманному поведению, хотя часто прикрывается ширмой «надо уметь думать на ходу».
Например, экстраверсия отрицательно связана с качеством решений, но положительно влияет на их внедрение в практику. Высокая импульсивность связана с ошибочными решениями, склонностью к рискованному и необдуманному поведению, хотя часто прикрывается ширмой «надо уметь думать на ходу».
Специалист управляет самим собой и задачами, которыми занимается. Чем выше он поднимается по организационной иерархии, тем более комплексные задачи встречает и тем важнее развитые навыки решения сложных проблем. Лидерские и стратегические компетенции становятся важнее предметных. Теперь он управляет «портфелями» проектов, решает трансформационные задачи и повышает стоимость бизнеса в целом. Для этого нужны долгосрочное видение, умение вести переговоры и решать сложные проблемы.
Именно поэтому при исследовании РППР нам требуется комплексный подход, который не ограничен лишь когнитивным аспектом — что человек способен делать, а включает в себя оценку личностных характеристик — к чему человек склонен и поведенческий аспект — что человек умеет делать на практике.
Как научиться решать проблемы
Чтобы решать проблемы с большей удовлетворенностью от результата, нужно выйти за пределы когнитивного аспекта. Доктор Роберт Хоган предлагает учитывать наши реакции на плохие решения, собирать обратную связь, быть открытым для дальнейшего развития и восприимчивым к коучингу (coachability).
Объединяя исследования способностей, личности, творческого решения проблем и организационной эффективности, мы можем «собрать» единый процесс решения сложных проблем.
Процесс решения сложных проблем
Решение сложных проблем — это работа с неопределенностью без единственно правильного ответа. Чтобы развить навык, необходимо практиковаться, разделять этапы решения проблем и задавать правильные вопросы.
Четкое разделение этапов решения проблемы поможет сфокусироваться на главном, сэкономить энергию и ресурсы и управлять решением проблемы как проектом.
При этом на каждом этапе нужно задавать правильные вопросы. Своевременные вопросы повысят точность собственных суждений, помогут развить свое и мышление сотрудников. Вот вопросы для каждого этапа:
Своевременные вопросы повысят точность собственных суждений, помогут развить свое и мышление сотрудников. Вот вопросы для каждого этапа:
Сложная ситуация
- Что именно я знаю о ситуации наверняка?
- Какие я могу сделать предположения?
- Какими данными я могу пренебречь?
Решение правильной проблемы
- Это точно проблема? Где мы проведем границу между особенностями ситуации (человека, продукта или организации) и тем, что мы будем считать проблемой?
- Какому приоритету она противоречит?
- На кого, на что, и как влияет эта проблема?
Правильное решение проблемы
- Достаточно ли альтернатив мы рассмотрели?
- Что будет минимально необходимым решением, что неприемлемым, а что — сверх-задачей?
- Что для нас будет образом хорошего результата?
Реакция на неправильное решение
- Не воспринимаю ли я обратную связь на свое решение «в штыки»? Как я отреагировал на нее?
- Каким был мой вклад в неправильное решение?
- Какую часть обратной связи я считаю полезной для будущих действий?
Если мы хотим максимально реализовать свои способности, использовать склонности и совершенствовать навыки, в общую рамку РППР необходимо включить способность и анализировать, и синтезировать, и генерировать, и выбирать, и работать с обратной связью. Ошибки в решениях невозможно устранить полностью, но с каждой следующей проблемой можно совершенствовать свое мастерство и добиваться лучших результатов.
Ошибки в решениях невозможно устранить полностью, но с каждой следующей проблемой можно совершенствовать свое мастерство и добиваться лучших результатов.
Дюжина рекомендаций по развитию навыков решения проблем и принятия решений
1. Определите проблему, требующую решения. Подумайте:
- какую информацию вам нужно собрать;
- из каких источников ее получить: отраслевые отчеты, эксперты, клиенты;
- что вы будете считать лишней и неподходящей информацией;
- что будет проблемой, а что – нет;
- по каким критериям выбираете возможные решения;
- что будет хорошим результатом.
2. Начинайте с конца. Прежде чем собирать информацию, подумайте, что вы будете делать после решения проблемы. Это поможет сфокусировать усилия и сократить затраты на предварительный анализ и генерацию идей. Если ответ «ничего», возможно, эту проблему не нужно решать в принципе.
3. Ищите «причины причин» имеющихся событий. Обычно настоящая проблема находится глубже на два—три слоя, чем проблемы на поверхности.
Ищите «причины причин» имеющихся событий. Обычно настоящая проблема находится глубже на два—три слоя, чем проблемы на поверхности.
4. Насыщайте свое «фоновое знание» контекста. Оставайтесь в курсе событий своей специализации, регулярно читайте отраслевые публикации, обзоры и дискуссии.
5. Обменивайтесь опытом с коллегами. Обсуждайте подходами к решению проблем с командой, коллегами в компании, отрасли или профессии.
6. Ищите интересные подходы в других областях. Коллекционируйте метафоры решения проблем и аналогии из других профессий.
7. Визуализируйте свои идеи. Неаккуратные закорючки, нарисованные от руки на листке бумаги, или элегантные графики в Excel: визуальное отображение ситуации, проблем и возможных путей решения добавит ясности и разовьет абстрактное мышление.
8. Изучайте разные источники. Знакомьтесь с разными моделями решения проблем, но главное — ставьте себе задачи на экспериментирование. Пробуйте как можно быстрее применить тот или иной подход, чтобы собрать собственный инструментарий.
Пробуйте как можно быстрее применить тот или иной подход, чтобы собрать собственный инструментарий.
9. Наблюдайте за профессиональными аналитиками. Попросите аналитиков описать ключевые этапы их работы. Фиксируйте для себя, как именно они подходят к сбору данных, обработке, анализу и интерпретации данных.
10. Участвуйте в мозговых штурмах. Присоединяйтесь к генерации идей и инициируйте их сами, но убедитесь, что в основе обсуждения лежит настоящая проблема.
11. Ищите возможности, чтобы применить навыки:
- сбора подходящей информации;
- упрощения сложной информации;
- формирования выводов на основе ограниченных данных;
- определения критериев оценки;
- генерации и отбор идей;
- оценки своих личностных характеристик и их влияния на решения.
12. Запросите обратную связь. Попросите людей, с которыми вы работаете, дать обратную связь:
- какую информацию вы обычно принимаете во внимание;
- как точно вы формулируете выводы о ситуации;
- понятно ли вы описываете суть проблемы;
- насколько оригинальные и при этом действенные решения вы обычно предлагаете;
- внимательны ли вы к анализу результатов.

Больше информации и новостей о трендах образования в нашем Telegram-канале. Подписывайтесь.
Исчисление I — Предел
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-2: Предел
В предыдущем разделе мы рассмотрели пару задач, и в обеих задачах у нас была функция (наклон в случае касательной задачи и средняя скорость изменения в задаче о скорости изменения) и мы хотели знать, как эта функция ведет себя в какой-то момент \(x = a\). На данном этапе игры нас больше не волнует, откуда взялись функции, и нас больше не волнует, увидим ли мы их снова в будущем или нет. Все, что нам нужно знать или беспокоиться, это то, что у нас есть эти функции, и мы хотим что-то о них знать.
Чтобы ответить на вопросы в последнем разделе, мы выбираем значения \(x\), которые все ближе и ближе к \(x = a\), и подставляем их в функцию. Мы также убедились, что рассмотрели значения \(x\), которые были как слева, так и справа от \(x = a\). Сделав это, мы посмотрели на нашу таблицу значений функции и увидели, к чему приближаются значения функции по мере того, как \(x\) становилось все ближе и ближе к \(x = a\), и использовали это, чтобы угадать значение, которое нам нужно.
Этот процесс называется 92} + 25}}{{т — 5}} = 15\]
В этих обозначениях мы заметим, что мы всегда даем функцию, с которой работаем, а также значение \(x\) (или \(t\)), к которому мы движемся.
В этом разделе мы собираемся применить интуитивный подход к ограничениям и попытаться понять, что они из себя представляют и что они могут рассказать нам о функции. Имея в виду эту цель, мы пока не собираемся вдаваться в то, как мы на самом деле вычисляем лимиты. Вместо этого мы будем полагаться на то, что мы сделали в предыдущем разделе, а также на другой подход, чтобы угадать значение пределов.
Оба подхода, которые мы собираемся использовать в этом разделе, разработаны, чтобы помочь нам понять, что такое ограничения. Как правило, мы обычно не используем методы, описанные в этом разделе, для вычисления лимитов, и во многих случаях их может быть очень сложно использовать даже для оценки значения лимита, и/или иногда мы будем давать неправильное значение. Мы рассмотрим фактические вычисления пределов в нескольких разделах.
Мы рассмотрим фактические вычисления пределов в нескольких разделах.
Начнем со следующего «определения» лимита.
Определение
Мы говорим, что предел \(f(x)\) равен \(L\), когда \(x\) приближается к \(a\), и записываем это как
\[\ mathop {\lim}\limits_{x \to a} f\left(x \right) = L\]
при условии, что мы можем сделать \(f(x)\) настолько близким к \(L\), насколько мы хотим, для всех \(x\), достаточно близких к \(a\), с обеих сторон, фактически не позволяя \( х\) быть \(а\).
Это не точное определение предела. Если вы хотите увидеть более точное и математическое определение лимита, вам следует обратиться к разделу «Определение лимита» в конце этой главы. Приведенное выше определение является скорее «рабочим». Это определение помогает нам понять, что такое пределы и что они могут рассказать нам о функциях.
Так что же означает это определение? Что ж, давайте предположим, что мы знаем, что предел действительно существует. В соответствии с нашим «рабочим» определением мы можем решить, насколько близко к \(L\) мы хотим сделать \(f(x)\). В качестве аргумента предположим, что мы хотим сделать \(f(x)\) не более чем на 0,001 от \(L\). Это означает, что нам нужен один из следующих
В соответствии с нашим «рабочим» определением мы можем решить, насколько близко к \(L\) мы хотим сделать \(f(x)\). В качестве аргумента предположим, что мы хотим сделать \(f(x)\) не более чем на 0,001 от \(L\). Это означает, что нам нужен один из следующих
\[\ begin{array}{lcl}f\left(x\right) — L <0,001 & \hspace{0,25in} & {\mbox{if}}f\left(x\right){\mbox{ is больше, чем L}}\\ L - f\left( x \right) < 0,001& \hspace{0,25in} & {\mbox{if}}f\left( x \right){\mbox{ меньше L }}\конец{массив}\]
Согласно «рабочему» определению это означает, что если мы получим \(x\) достаточно близко к \(a\), мы можем сделать одно из приведенных выше истинным. Однако на самом деле это говорит немного больше. В нем говорится, что где-то в мире есть значение \(x\), скажем, \(X\), так что для всех \(x\), которые ближе к \(a\), чем \(X \), то одно из приведенных выше утверждений будет верным.
Это довольно важная идея. В мире существует множество функций, которые мы можем сделать максимально близкими к \(L\) для конкретных значений \(x\), близких к \(a\), но будут и другие значения \(x \) ближе к \(a\), которые дают значения функций, далекие от \(L\). Чтобы предел существовал, как только мы получим \(f(x)\) настолько близко к \(L\), насколько мы хотим для некоторого \(x\), тогда он должен будет оставаться в этом близком к \(L\ ) (или приблизиться) для всех значений \(x\), которые ближе к \(a\). Мы увидим пример этого позже в этом разделе.
Чтобы предел существовал, как только мы получим \(f(x)\) настолько близко к \(L\), насколько мы хотим для некоторого \(x\), тогда он должен будет оставаться в этом близком к \(L\ ) (или приблизиться) для всех значений \(x\), которые ближе к \(a\). Мы увидим пример этого позже в этом разделе.
Проще говоря, определение говорит, что по мере того, как \(x\) становится все ближе и ближе к \(x=a\) (конечно, с обеих сторон…), тогда \(f(x)\) должно приближаться все ближе и ближе к \(L\). Или, когда мы движемся к \(x=a\), тогда \(f(x)\) должно двигаться к \(L\).
Важно еще раз отметить, что мы должны смотреть на значения \(x\), которые находятся по обе стороны от \(x=a\). Мы также должны отметить, что нам не разрешено использовать \(x=a\) в определении. Мы часто будем использовать информацию, которую дают нам ограничения, чтобы получить некоторую информацию о том, что происходит прямо в точке \(x=a\), но сам предел не связан с тем, что на самом деле происходит в точке \(x=a\). . Предел связан только с тем, что происходит вокруг точки \(x=a\). Это важное понятие об ограничениях, которые мы должны иметь в виду.
. Предел связан только с тем, что происходит вокруг точки \(x=a\). Это важное понятие об ограничениях, которые мы должны иметь в виду.
Альтернативное обозначение, которое мы иногда будем использовать для обозначения пределов:
\[f(x) \to L\hspace{0,25 дюйма}{\rm{as}}\hspace{0,25in}x \to a\]
Как мы можем использовать это определение, чтобы оценить пределы? Мы делаем именно то, что делали в предыдущем разделе. Мы берем \(x\) по обе стороны от \(x=a\), которые приближаются все ближе и ближе к \(a\), и подставляем их в нашу функцию. Затем мы смотрим, можем ли мы определить, к какому числу приближаются значения функции, и используем это как нашу оценку. 92} — 2x}}\]
Показать решение
Обратите внимание, что мы сказали оценить значение лимита. Опять же, в этом разделе мы не собираемся напрямую вычислять ограничения. Цель этого раздела — дать нам лучшее представление о том, как работают ограничения и что они могут рассказать нам о функции.
Итак, помня об этом, мы собираемся работать почти так же, как в предыдущем разделе. Мы выберем значения \(x\), которые все ближе и ближе к \(x=2\), и подставим эти значения в функцию. Это дает следующую таблицу значений.
| \(х\) | \(ф(х)\) | \(х\) | \(ф(х)\) |
|---|---|---|---|
| 2,5 | 3,4 | 1,5 | 5,0 |
| 2.1 | 3,857142857 | 1,9 | 4.157894737 |
| 2,01 | 3,985074627 | 1,99 | 4.015075377 |
| 2,001 | 3,998500750 | 1,999 | 4.001500750 |
2. 0001 0001 | 3,999850007 | 1,9999 | 4.000150008 |
| 2.00001 | 3,999985000 | 1,99999 | 4.000015000 |
Обратите внимание, что мы удостоверились и выбрали значения \(x\), которые были по обе стороны от \(x = 2\), и что мы подошли очень близко к \(x = 2\), чтобы убедиться, что любые тенденции, которые мы можем наблюдать, на самом деле верны. 92} — 2x}} = 4\]
Давайте еще немного подумаем о том, что здесь происходит. Построим график функции из последнего примера. Ниже показан график функции в интересующем диапазоне \(x\).
Во-первых, обратите внимание на довольно большую открытую точку \(x = 2\). Это должно напомнить нам, что функция (и, следовательно, график) не существует в точке \(x = 2\).
Поскольку мы подставляли значения \(x\) в функцию, мы фактически двигаемся по графику к точке как \(x = 2\). Это показано на графике двумя стрелками на графике, которые движутся к точке.
Это показано на графике двумя стрелками на графике, которые движутся к точке.
Когда мы вычисляем пределы, мы действительно задаемся вопросом, к какому значению \(y\) приближается наш график, когда мы приближаемся к \(x = a\) на нашем графике. Мы НЕ спрашиваем, какое значение \(y\) принимает график в рассматриваемой точке. Другими словами, мы спрашиваем, что делает график вокруг точки \(x = a\). В нашем случае мы можем видеть, что по мере того, как \(x\) приближается к 2 (с обеих сторон), функция приближается к \(y = 4\), хотя сама функция даже не существует в \(x = 2\). ). Поэтому можно сказать, что предел на самом деле равен 4,9.0003
Итак, что мы узнали о пределах? Пределы спрашивают, что функция делает вокруг \(x = a\), и не связаны с тем, что функция на самом деле делает в \(x = a\). Это хорошо, так как многие функции, которые мы будем рассматривать, даже не будут существовать в \(x = a\), как мы видели в нашем последнем примере. 2} — 2x}} & {\mbox{if} }x \ne 2\\ 6 & {\mbox{if}}x = 2\end{массив} \right.\]
2} — 2x}} & {\mbox{if} }x \ne 2\\ 6 & {\mbox{if}}x = 2\end{массив} \right.\]
Показать решение
Прежде всего следует отметить, что это точно такая же функция, как и в первом примере, за исключением того, что мы присвоили ей значение \(x = 2\). Итак, сначала отметим, что
\[г\влево( 2 \вправо) = 6\]
Что касается оценки значения этого лимита, то по сравнению с первым примером ничего не изменилось. Мы могли бы построить таблицу значений, как в первом примере, или быстро взглянуть на график функции. Любой метод даст нам значение предела.
Давайте сначала посмотрим на таблицу значений и посмотрим, что она нам говорит. Обратите внимание, что наличие значения функции в \(x = 2\) не изменит наш выбор для \(x\). Мы выбираем только те значения \(x\), которые приближаются к \(x = 2\), но никогда не берем \(x = 2\). Другими словами, таблица значений, которую мы использовали в первом примере, будет точно такой же таблицей, которую мы будем использовать здесь. Итак, поскольку мы уже сделали это один раз, нет причин переделывать это здесь.
Итак, поскольку мы уже сделали это один раз, нет причин переделывать это здесь.
Из этой таблицы снова видно, что ограничение равно
\[\ mathop {\lim}\limits_{x \to 2} g\left(x\right) = 4\]
Предел НЕ 6! Помните из обсуждения после первого примера, что пределы не заботятся о том, что на самом деле делает функция в рассматриваемый момент. Ограничения касаются только того, что происходит вокруг точки. Поскольку единственное, что мы фактически изменили в функции, это ее поведение при \(x = 2\), это не изменит предел.
Давайте также взглянем на график этой функции, чтобы увидеть, говорит ли он о том же самом.
Опять же, мы можем видеть, что по мере того, как мы приближаемся к \(x = 2\) на нашем графике, функция все еще приближается к значению \(y\), равному 4. Помните, что мы только спрашиваем, что делает функция около \(x = 2\), и нам все равно, что на самом деле делает функция в \(x = 2\). Затем график также поддерживает вывод о том, что предел равен
Затем график также поддерживает вывод о том, что предел равен
. \[\ mathop {\lim}\limits_{x \to 2} g\left(x\right) = 4\]
Давайте еще раз остановимся на этом, просто чтобы убедиться, что мы его поняли. Пределы , а не связаны с тем, что происходит в точке \(x = a\). Пределы касаются только того, что происходит вокруг \(x = a\). Мы продолжаем говорить об этом, но это очень важная концепция ограничений, которую мы всегда должны помнить. Поэтому мы будем использовать любую возможность, чтобы напомнить себе об этой идее.
Поскольку пределы не связаны с тем, что на самом деле происходит в \(x = a\), мы будем иногда сталкиваться с ситуациями, подобными предыдущему примеру, когда предел в точке и значение функции в точке различны. Это не всегда будет происходить, конечно. Бывают случаи, когда значение функции и предел в точке совпадают, и мы в конечном итоге увидим несколько таких примеров. Однако важно не волноваться по поводу вещей, когда функция и предел не принимают одно и то же значение в какой-то точке. Это случается иногда, поэтому нам нужно будет иметь дело с такими случаями, когда они возникают.
Однако важно не волноваться по поводу вещей, когда функция и предел не принимают одно и то же значение в какой-то точке. Это случается иногда, поэтому нам нужно будет иметь дело с такими случаями, когда они возникают.
Давайте рассмотрим еще один пример, чтобы попытаться воплотить эту идею в жизнь.
Пример 3. Оцените значение следующего предела. \[\ mathop {\lim}\limits_{\theta\to 0} \,\frac{{1 — \cos\left(\theta\right)}}{\theta}\]
Показать решение
Во-первых, не волнуйтесь по поводу \(\theta\) в функции. Это просто буква, точно так же, как \(х\) — это буква! Это греческая буква, но это буква, и иногда вам будет предложено иметь дело с греческими буквами, поэтому неплохо начать привыкать к ним на этом этапе.
Теперь также обратите внимание, что если мы подставим \(\theta =0\), то получим деление на ноль, так что на данный момент функция не существует. На самом деле в этой точке мы получаем 0/0, но из-за деления на ноль эта функция не существует в точке \(\theta=0\).
Итак, как и в первом примере, давайте получим таблицу значений и посмотрим, что если мы сможем угадать, к какому значению движется функция.
| \(\ тета \) | \(f\влево(\тета\вправо)\) | \(\тета\) | \(f\влево(\тета\вправо)\) |
|---|---|---|---|
| 1 | 0,45969769 | -1 | -0,45969769 |
| 0,1 | 0,04995835 | -0,1 | -0,04995835 |
| 0,01 | 0,00499996 | -0,01 | -0,00499996 |
| 0,001 | 0,00049999 | -0,001 | -0,00049999 |
Хорошо, похоже, что функция приближается к нулевому значению, когда \(\theta\) приближается к 0, конечно, с обеих сторон.
Следовательно, мы предполагаем, что предел имеет значение
\[\ mathop {\lim}\limits_{\theta\to 0} \,\frac{{1 — \cos\left(\theta\right)}}{\theta} = 0\]
Итак, еще раз, предел имел значение, хотя функция не существовала в интересующей нас точке. что мы собираемся обсудить.
Пример 4. Оцените значение следующего предела. \[\ mathop {\lim}\limits_{t \to 0} \cos\left({\frac{\pi}}{t}} \right)\]
Показать решение
Давайте составим таблицу значений и посмотрим, что происходит с нашей функцией в этом случае.
| \(т\) | \(ф(т)\) | \(т\) | \(ф(т)\) |
|---|---|---|---|
| 1 | -1 | -1 | -1 |
| 0,1 | 1 | -0,1 | 1 |
| 0,01 | 1 | -0,01 | 1 |
| 0,001 | 1 | -0,001 | 1 |
Теперь, если бы нам нужно было угадать предел из этой таблицы, мы бы предположили, что предел равен 1. Однако, если бы мы сделали это предположение, мы бы ошиблись. Рассмотрим любую из следующих оценок функции.
Однако, если бы мы сделали это предположение, мы бы ошиблись. Рассмотрим любую из следующих оценок функции.
\[f\left( {\frac{1}{{2001}}} \right) = — 1\hspace{0,55in}f\left({\frac{2}{{2001}}} \right) = 0 \ hspace {0,5 дюйма} f \ слева ( {\ гидроразрыва {4} {{4001}}} \ справа) = \ гидроразрыва {{\ sqrt 2}} {2} \]
Во всех трех вычислениях функции мы оценили функцию как число меньше 0,001 и получили три совершенно разных числа. Напомним, что определение предела, с которым мы работаем, требует, чтобы функция приближалась к единственному значению (нашему предположению) по мере того, как \(t\) становится все ближе и ближе к рассматриваемой точке. Это не говорит о том, что только некоторые значения функции должны приближаться к догадке. В нем говорится, что все значения функции должны быть все ближе и ближе к нашему предположению.
Чтобы увидеть, что здесь происходит, был бы удобен график функции.
Из этого графика видно, что по мере приближения к \(t = 0\) функция начинает сильно колебаться, и чем ближе к \(t = 0\), тем больше скорость колебаний. Напомним из нашего определения предела, что для того, чтобы предел существовал, функция должна стремиться к одному значению по мере того, как мы приближаемся к рассматриваемой точке.
Эта функция явно не подходит для одного номера, поэтому этот предел не существует !
Последний пример указывает на недостаток простого выбора значений переменной и использования таблицы значений функций для оценки значения предела. Значения переменной, которые мы выбрали в предыдущем примере, были действительными и фактически были значениями, которые выбрали бы многие. На самом деле, это были точно такие же значения, которые мы использовали в предыдущей задаче, и они работали в этой задаче!
При использовании таблицы значений всегда существует вероятность того, что мы выбираем неправильные значения и неправильно угадываем наш лимит. Это то, что мы всегда должны помнить, когда делаем это, чтобы угадать значение ограничений. На самом деле это такая проблема, что после этого раздела мы больше никогда не будем использовать таблицу значений, чтобы угадать значение лимита.
Это то, что мы всегда должны помнить, когда делаем это, чтобы угадать значение ограничений. На самом деле это такая проблема, что после этого раздела мы больше никогда не будем использовать таблицу значений, чтобы угадать значение лимита.
Этот последний пример также показал нам, что ограничения не обязательно должны существовать. До этого момента мы видели только существующие ограничения, но это не всегда так.
Давайте рассмотрим еще один пример в этом разделе.
Пример 5. Оцените значение следующего предела. \[\ mathop {\ lim } \ limit_ {t \ to 0} H \ left ( t \ right) \ hspace {0,25 дюйма} {\ mbox {где}} \ hspace {0,25 дюйма} H \ left ( t \ справа) = \left\{ \begin{array}{ll}0 & {\mbox{if}}t < 0\\ 1 & {\mbox{if}}t \ge 0\end{массив} \right. \]
Показать решение
Эту функцию часто называют функцией Heaviside или step . Мы могли бы использовать таблицу значений для оценки предела, но, вероятно, в этом случае будет так же быстро использовать график, так что давайте сделаем это. Ниже представлен график этой функции.
Мы могли бы использовать таблицу значений для оценки предела, но, вероятно, в этом случае будет так же быстро использовать график, так что давайте сделаем это. Ниже представлен график этой функции.
На графике видно, что если мы приближаемся к \(t = 0\) справа, функция приближается к значению \(y\), равному 1. На самом деле она просто остается на уровне 1, но в терминология, которую мы использовали в этом разделе, приближается к 1…
Кроме того, если мы движемся к \(t = 0\) слева, функция движется к значению \(y\), равному 0.
Согласно нашему определению предела, функция должна двигаться в к одному значению по мере продвижения к \(t = a\) (с обеих сторон). В данном случае этого не происходит, поэтому в этом примере мы также будем говорить, что предела не существует.
Обратите внимание, что предел в этом примере немного отличается от предыдущего примера. В предыдущем примере функция не остановилась на одном числе, когда мы приблизились к \(t = 0\). Однако в этом примере функция сводится к одному числу как \(t = 0\) с обеих сторон. Проблема в том, что число на каждой стороне \(t = 0\) разное. Это идея, которую мы рассмотрим более подробно в следующем разделе.
Проблема в том, что число на каждой стороне \(t = 0\) разное. Это идея, которую мы рассмотрим более подробно в следующем разделе.
Давайте обобщим то, что мы (надеюсь) узнали в этом разделе. В первых трех примерах мы видели, что пределы не заботятся о том, что на самом деле делает функция в рассматриваемой точке. Их интересует только то, что происходит вокруг точки. На самом деле у нас могут быть пределы в \(x = a\), даже если самой функции в этой точке не существует. Точно так же, даже если функция существует в какой-то точке, нет оснований (на данный момент) думать, что предел будет иметь то же значение, что и функция в этой точке. Иногда предел и функция будут иметь одно и то же значение в точке, а иногда они не будут иметь одинакового значения.
Далее, в третьем и четвертом примерах мы увидели основную причину отказа от использования таблицы значений для угадывания значения лимита. В этих примерах мы использовали точно такой же набор значений, однако они работали только в одном из примеров. Использование таблиц значений для угадывания значений лимитов — просто не лучший способ получить значение лимита. Это единственный раздел, в котором мы будем это делать. Таблицы значений всегда должны быть вашим последним выбором при поиске значений пределов.
Использование таблиц значений для угадывания значений лимитов — просто не лучший способ получить значение лимита. Это единственный раздел, в котором мы будем это делать. Таблицы значений всегда должны быть вашим последним выбором при поиске значений пределов.
Последние два примера показали нам, что не все пределы на самом деле существуют. Мы не должны зацикливаться на идее, что ограничения всегда будут существовать. В большинстве курсов по математическому анализу мы работаем с ограничениями, которые почти всегда существуют, поэтому легко начать думать, что ограничения существуют всегда. Ограничения не всегда существуют, поэтому не привыкайте предполагать, что они будут.
Наконец, в четвертом примере мы увидели, что единственный способ справиться с пределом — построить график функции. Иногда это единственный способ, однако этот пример также иллюстрирует недостатки использования графиков. Чтобы использовать график, чтобы угадать значение предела, вы должны иметь возможность набросать график. Для многих функций это не так просто сделать.
Для многих функций это не так просто сделать.
Есть еще один недостаток в использовании графиков. Даже если у вас есть график, он будет полезен только в том случае, если значение \(y\) приближается к целому числу. Если значение \(y\) приближается, скажем, к \(\frac{{ — 15}}{{123}}\), вы никак не сможете угадать это значение по графику, и мы обычно потребуются точные значения для наших пределов.
Таким образом, хотя графики функций иногда могут облегчить вашу жизнь при угадывании значений пределов, они опять же, вероятно, не лучший способ получить значения пределов. Они будут полезны только в том случае, если вы можете получить их в свои руки, а значение лимита является «хорошим» числом.
Тогда возникает естественный вопрос: почему мы вообще говорим об использовании таблиц и/или графиков для оценки пределов, если это не лучший способ? Было несколько причин.
Во-первых, они могут помочь нам лучше понять, что такое ограничения и что они могут нам сказать. Если мы не установим хотя бы пару ограничений таким образом, мы можем не получить достаточно хорошего представления о том, что такое ограничения.
Если мы не установим хотя бы пару ограничений таким образом, мы можем не получить достаточно хорошего представления о том, что такое ограничения.
Вторая причина использования лимитов таким образом — указать на их недостаток, чтобы не возникало соблазна использовать их постоянно!
В конце концов мы поговорим о том, как мы на самом деле делаем лимиты. Однако есть еще одна тема, которую нам нужно обсудить, прежде чем делать это. Поскольку этот раздел уже длился некоторое время, мы поговорим об этом в следующем разделе.
реальный анализ — Как доказать, что мы можем решить пределы путем замены?
Спросил
Изменено 2 года, 5 месяцев назад
Просмотрено 134 раза
4
Новинка! Сохраняйте вопросы или ответы и организуйте свой любимый контент.
Узнать больше.
$\begingroup$
В настоящее время я изучаю анализ, и мой профессор использовал подстановку для решения многих предельных задач, поэтому я хочу знать, при каких обстоятельствах мы можем использовать подстановку и как это доказать. 92$
92$
Вот моя попытка.
Мое понимание предельного решения подстановкой таково, что
$\lim_{x\rightarrow a}u(x)=b\implies\lim_{x\rightarrow a}f(u(x))=\lim_{u \rightarrow b}f(u)$
Доказательство (возможно, неправильное):
Предположим, что $\lim_{x\rightarrow a}u(x)=b$ и $\lim_{x\rightarrow a}f(u( x))=L$
тогда $\forall\epsilon\gt 0 \exists\delta_1$ s.t $0\lt|x-a|\lt\delta_1\implies|f(u(x))-L|\lt\epsilon $
тогда $\forall\delta_1\gt 0 \exists\delta_2$ s.t $0\lt|x-a|\lt\delta_2\implies|u(x)-b|\lt\delta_1$
затем исправить $\delta=\min(\delta_1,\delta_2)$
имеем $\forall\epsilon\gt 0 \exists\delta$ s.t $0\lt|x-a|\lt\delta$ подразумевает $| f(u(x))-L|\lt\epsilon$ и $|u(x)-b|\lt\delta_1$
имеем $\lim_{u\rightarrow b}f(u)=L$
и делаем то же самое для обратного случая, тогда утверждение доказано.
- реальный анализ
- функциональный анализ
- пределы
- анализ
$\endgroup$
5
$\begingroup$
Ваш профессор должен описать вам предельный закон для сложения функций таким же образом, как описываются законы, касающиеся пределов суммы, разности, произведения, частного функций. Такие законы можно использовать для решения типичных задач, не предоставляя каждый раз явное доказательство.
Такие законы можно использовать для решения типичных задач, не предоставляя каждый раз явное доказательство.
Закон предела составных функций гласит:
Ограничение составных функций 92}=\lim_{u\to 0}\frac{\sin u} {u} =1$$ Ожидается, что экзаменатор или читатель поймет правильное значение и использование закона, как описано выше, просто взглянув на эти шаги.
Ваше доказательство пытается доказать обратное действие закона, которое в общем случае неверно. Закон имеет дело с пределом сложной функции как с выводом, а не как с гипотезой.
Закон, изложенный выше в ответе, можно доказать, используя определение предела. Таким образом, начнем с $\epsilon>0$, а затем получим $\delta’>0$, такое что $|g(x) — L|<\epsilon$ всякий раз, когда $0<|x-b|<\delta'$. 9+}\frac{\sin u}{u}$$
, а обоснование состоит в том, что отображение $x\to u$ сюръективно.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.Обучение без ограничений / Об обучении без ограничений
Learning Without Limits
Solving complex problems
Connecting with others Engaging in rigorous learning Owning the learning
Решение сложных задач
В очень раннем возрасте учащиеся узнают основные факты мира математики, например, 2+2=4; 8-3=5 и так далее.Сейчас, когда вы на это смотрите, это может показаться довольно простым.Подумайте, однако, как часто вы, возможно, боролись с одними и теми же цифрами в рамках ежедневного или ежемесячного бюджета или заявки на автокредит. Почему-то цифры не складываются.Разница в том, что эти задачи сложны и открыты, математические факты просты и закрыты. Цель обучения – дать учащимся возможность выявлять и решать проблемы в своей академической работе и в жизни. Это включает в себя решение поставленных перед ними задач (тип решения проблем, о котором мы обычно думаем в школе) и решение новых проблем, которые они определяют сами; создание чего-то нового в качестве решения. В этом случае «способность мыслить» означает, что учащиеся могут решать свои собственные сложные проблемы и творчески работать над этим.
Связь с другими
Каждый день нам напоминают, насколько на самом деле тесен мир.Событие в малоизвестной стране на другом конце света, хорошее или плохое, может оказать глубокое влияние на нашу повседневную жизнь. Цены на продукты могут расти или падать; страхи перед здоровьем становятся безудержными, вспыхивает насилие, начинается движение.
Мы глобальное общество.Чем больше наши дети узнают и узнают о своих сверстниках по всему миру, тем насыщеннее будет их жизнь. Расширяются возможности для студентов общаться друг с другом и со студентами по всему миру, поскольку они погружаются в темы и уроки, представляющие большой интерес. Skype, ePals и блоги друзей со всего мира дают учащимся возможность сравнить опыт из одной страны в другую. В течение последних нескольких лет наши студенты, изучающие ракетостроение, несколько раз в год консультировались со своими наставниками из НАСА посредством телеконференций по проектам, результатам испытаний и спецификациям для будущих испытаний.Строгое обучение
Строгость имеет разное значение для разных людей.
То, что строго для одного студента, может быть совершенно невозможным для другого; или только несколько сложно для еще одного.
Здесь наиболее важны индивидуальные отношения между учителем и учеником.
Работая с вашим ребенком, учитель знает способности вашего ребенка и знает, как лучше всего бросить ему вызов, не оказывая давления. Учащиеся, которые тщательно учатся, в восторге от школы; они заинтересованы в том, что они делают, и чувствуют, что они принадлежат к школа. Они могут показать свое обучение различными способами и тяжелая работа признается и приветствуется, что заставляет их чувствовать себя хорошо школа, что они узнали и о себе.
Владение обучением
Мы никогда не уклонялись от всего, что, по нашему мнению, было необходимо, чтобы помочь нашим ученикам добиться успеха после окончания средней школы.
Мы призываем студентов следовать своим интересам и вдохновению, куда бы они ни вели; будь то строительство ракет, участие в инсценированном судебном процессе или написание романа. Вы, наверное, читали о том, что многие из наших студентов занимаются тем же самым.
Не каждый студент хочет браться за такой большой проект, но все они хотят учиться «наилучшим образом», быть вовлеченными, связанными и глубоко вовлеченными в процесс. В последнее время учителя переписывают планы уроков, чтобы воспользоваться новыми идеями.
Для некоторых это может быть онлайн-обучение, особенно для учащихся старших классов. При этом учителя и ученики могут работать вместе, чтобы разрабатывать вопросы и находить ответы, вместо того, чтобы учителя держали всю информацию и читали лекции.Учащиеся младших классов уже не имеют ограничений в обучении.Для очень маленького ребенка обучение — это процесс, который, кажется, никогда не заканчивается.

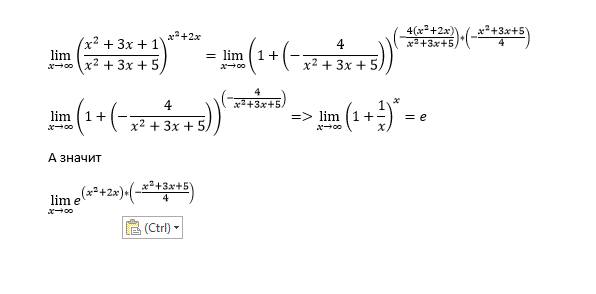


 Событие в малоизвестной стране на другом конце света, хорошее или плохое, может оказать глубокое влияние на нашу повседневную жизнь. Цены на продукты могут расти или падать; страхи перед здоровьем становятся безудержными, вспыхивает насилие, начинается движение.
Событие в малоизвестной стране на другом конце света, хорошее или плохое, может оказать глубокое влияние на нашу повседневную жизнь. Цены на продукты могут расти или падать; страхи перед здоровьем становятся безудержными, вспыхивает насилие, начинается движение.  То, что строго для одного студента, может быть совершенно невозможным для другого; или только несколько сложно для еще одного.
То, что строго для одного студента, может быть совершенно невозможным для другого; или только несколько сложно для еще одного. Мы призываем студентов следовать своим интересам и вдохновению, куда бы они ни вели; будь то строительство ракет, участие в инсценированном судебном процессе или написание романа. Вы, наверное, читали о том, что многие из наших студентов занимаются тем же самым.
Мы призываем студентов следовать своим интересам и вдохновению, куда бы они ни вели; будь то строительство ракет, участие в инсценированном судебном процессе или написание романа. Вы, наверное, читали о том, что многие из наших студентов занимаются тем же самым.