Примеры на сложение и вычитание. 2 класс, первое полугодие.
Примеры на сложение и вычитание. 2 класс, первое полугодие. Задачи по математике 2 класс
MAT-ZADACHI.RU
Математика 2 класс
- Нестандартные задачи
- Математические диктанты
- Примеры
- Логические примеры
- Тесты
- Диагностические работы
Задачи для 2 класса
- Операции
- Обратные операции
- Прямая, луч, отрезок
- Сложение и вычитание двузначных чисел
- Сотня. Счет сотнями.
- Метр
Контрольные работы
- Контрольная работа 1
- Контрольная работа 2
- 1 четверть
- 2 четверть
- Итоговая контрольная работа
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Итоговая контрольная работа
| | Математика 2 класс ->> Примеры Первое полугодиеВторое полугодие |
| 17 + 2 = 19 | 15 + 1 = 16 | 17 — 6 = 13 | 18 — 1 = 17 | 19 — 7 = 12 | 14 + 4 = 18 |
| 11 + 4 = 15 | 18 — 1 = 17 | 16 — 3 = 13 | 11 + 4 = 15 | 19 — 3 = 16 | 15 — 3 = 12 |
| 17 — 4 = 13 | 18 — 7 = 11 | 19 — 8 = 11 | 17 + 2 = 19 | 14 — 3 = 11 | 15 + 2 = 17 |
| 12 + 5 = 17 | 15 + 3 = 18 | 17 — 1 = 16 | 13 + 5 = 18 | 15 + 2 = 17 | 18 — 2 = 20 |
| 19 — 6 = 13 | 16 + 3 = 19 | 11 + 7 = 18 | 15 + 4 = 19 | 12 + 3 = 15 | 11 + 3 = 14 |
| 11 + 5 = 16 | 17 — 5 = 12 | 17 + 2 = 19 | 19 — 3 = 16 | 15 — 4 = 11 | 17 — 3 = 14 |
| 18 — 7 = 11 | 16 + 1 = 17 | 13 — 2 = 11 | 18 — 7 = 11 | 13 + 2 = 15 | 18 + 1 = 19 |
| 14 + 4 = 18 | 17 — 1 = 16 | 15 — 3 = 12 | 16 — 4 = 12 | 15 + 4 = 19 | |
| 16 — 5 = 11 | 13 + 3 = 16 | 15 + 4 = 19 | 12 + 5 = 17 | 17 + 2 = 19 | 13 + 1 = 14 |
| 11 + 6 = 17 | 16 — 4 = 12 | 15 — 4 = 11 | 16 + 3 = 19 | 18 — 7 = 11 | 16 — 2 = 14 |
| 19 — 2 = 17 | 12 + 7 = 19 | 19 — 7 = 12 | 18 + 1 = 19 | 17 + 2 = 19 | 14 + 4 = 18 |
| 18 — 3 = 15 | 19 — 3 = 16 | 14 + 2 = 16 | 11 + 4 = 15 | 16 — 5 = 11 | 18 — 7 = 11 |
| 17 — 4 = 13 | 12 + 6 = 18 | 15 + 2 = 17 | 18 — 6 = 14 | 14 — 3 = 11 | 15 + 4 = 19 |
| 15 + 3 = 18 | 17 — 2 = 19 | 19 — 6 = 13 | 12 + 3 = 15 | 18 — 2 = 16 | 19 — 2 = 17 |
| 13 + 1 = 14 | 11 + 7 = 18 | 18 — 5 = 13 | 17 — 5 = 12 | 17 — 1 = 16 | 11 + 5 = 16 |
| _______________ | _______________ | _______________ | _______________ | _______________ | _______________ |
| 19 — 9 = 10 | 15 — 10 = 5 | 19 — 10 = 9 | 17 — 7 = 10 | 10 + 6 = 16 | 12 — 10 = 2 |
| 17 — 7 = 1= | 16 — 10 = 6 | 10 + 6 = 16 | 13 — 10 = 3 | 12 — 2 = 10 | 17 — 10 = 7 |
| 10 + 1 = 11 | 12 — 2 = 10 | 13 — 3 = 10 | 18 — 8 = 1= | 10 + 6 = 16 | 13 — 10 = 3 |
| 19 — 9 = 10 | 16 — 6 = 10 | 13 — 10 = 3 | 12 — 10 = 2 | 10 + 9 = 19 | 19 — 9 = 10 |
| 10 + 8 = 18 | 15 — 5 = 10 | 18 — 10 = 8 | 10 + 8 = 18 | 15 — 10 = 5 | 17 — 10 = 7 |
| 14 — 10 = 4 | 10 + 9 = 19 | 16 — 10 = 6 | 13 — 10 = 3 | 11 — 10 = 1 | 10 + 7 = 17 |
| 13 — 3 = 10 | 15 — 5 = 10 | 14 — 4 = 10 | 15 — 10 = 5 | 10 + 7 = 17 | 19 — 10 = 9 |
| 10 + 8 = 18 | 16 — 10 = 6 | 15 — 10 = 5 | 10 + 8 = 18 | 17 — 7 = 10 | 10 + 3 = 13 |
| 12 — 10 = 2 | 16 — 6 = 10 | 14 — 4 = 10 | 14 — 4 = 10 | 10 + 7 = 17 | |
| 10 + 1 = 11 | 10 + 4 = 14 | 10 + 5 = 15 | 15 — 10 = 5 | 18 — 8 = 10 | 10 + 5 = 15 |
| 12 — 10 = 2 | 19 — 10 = 9 | 12 — 2 = 10 | 14 — 4 = 4 | 10 + 3 = 13 | 17 — 7 = 10 |
| 10 + 5 = 15 | 14 — 4 = 10 | 19 — 10 = 9 | 10 + 4 = 14 | 10 + 6 = 16 | 19 — 9 = 10 |
| 15 — 5 = 10 | 17 — 7 = 10 | 16 — 6 = 10 | 12 — 2 = 10 | 10 + 5 = 15 | 10 + 7 = 17 |
| 12 — 10 = 2 | 18 — 10 = 8 | 13 — 10 = 3 | 13 — 3 = 10 | 14 — 10 = 4 | 10 + 3 = 13 |
| 18 — 10 = 8 | 12 — 2 = 10 | 10 + 8 = 18 | 10 + 4 = 14 | 11 — 10 = 1 | 10 + 2 = 12 |
| _______________ | _______________ | _______________ | _______________ | _______________ | _______________ |
| 80 — 30 = 50 | 90 + 10 = 100 | 20 + 50 = 70 | 30 + 30 = 60 | 40 — 20 = 60 | |
| 70 — 60 = 10 | 30 + 60 = 90 | 80 — 60 = 20 | 50 — 20 = 30 | 70 — 10 = 60 | 40 + 30 = 70 |
| 100 — 60 = 40 | 20 + 50 = 70 | 40 — 10 = 30 | 90 — 10 = 80 | 80 — 10 = 70 | 70 + 30 = 100 |
| 40 + 20 = 60 | 80 — 50 = 30 | 30 + 50 = 80 | 90 — 20 = 70 | 30 + 10 = 40 | 20 + 20 = 40 |
| 90 — 50 = 40 | 80 — 40 = 40 | 60 — 30 = 30 | 70 — 50 = 20 | 20 + 30 = 50 | 50 — 30 = 20 |
| 33 + 5 = 38 | 78 + 1 = 79 | 37 — 4 = 33 | 23 + 5 = 28 | 25 — 3 = 22 | 44 — 3 = 41 |
| 78 + 1 = 79 | 72 + 3 = 75 | 83 + 6 = 89 | 51 + 4 = 55 | 49 — 5 = 44 | 76 + 2 = 78 |
| 52 + 6 = 58 | 43 + 6 = 49 | 38 — 5 = 33 | 35 — 4 = 31 | 64 — 3 = 61 | 26 — 4 = 22 |
| 54 + 3 = 57 | 67 — 4 = 63 | 35 — 4 = 31 | 22 + 3 = 25 | 47 + 2 = 49 | 28 — 6 = 22 |
| 45 + 3 = 48 | 66 — 2 = 64 | 91 + 2 = 93 | 55 — 3 = 52 | 67 — 2 = 65 | 56 + 3 = 59 |
| 35 + 4 = 39 | 78 + 1 = 79 | 21 + 7 = 28 | 72 + 2 = 74 | 76 + 2 = 78 | 26 + 3 = 29 |
| 34 — 3 = 31 | 64 — 3 = 61 | 43 + 6 = 49 | 75 — 1 = 74 | 64 + 2 = 66 | 54 + 3 = 57 |
| 50 — 9 = 41 | 30 — 8 = 22 | 40 — 7 = 33 | 20 — 7 = 13 | 30 — 2 = 28 | 40 — 2 = 38 |
| 70 — 9 = 81 | 70 — 1 = 69 | 30 — 2 = 28 | 70 — 3 = 67 | 60 — 1 = 59 | 80 — 7 = 73 |
| 90 — 2 = 88 | 70 — 5 = 65 | 90 — 9 = 81 | 50 — 4 = 46 | 30 — 8 = 22 | 80 — 1 = 79 |
| _______________ | _______________ | _______________ | _______________ | _______________ | _______________ |
| 5 + 8 = 13 | 8 + 4 = 12 | 6 + 8 = 14 | 3 + 9 = 12 | 5 + 6 = 11 | 2 + 9 = 11 |
| 5 + 7 = 12 | 3 + 9 = 12 | 5 + 9 = 14 | 5 + 7 = 12 | 9 + 9 = 18 | 5 + 6 = 11 |
| 4 + 7 = 11 | 7 + 5 = 12 | 8 + 4 = 12 | 9 + 2 = 11 | 9 + 5 = 14 | 7 + 6 = 13 |
| 8 + 6 = 14 | 7 + 9 = 16 | 8 + 3 = 11 | 7 + 9 = 16 | 8 + 8 = 16 | 6 + 5 = 11 |
| 3 + 8 = 11 | 5 + 9 = 14 | 4 + 9 = 13 | 7 + 8 = 15 | 3 + 8 = 11 | 6 + 7 = 13 |
| 13 — 4 = 9 | 13 — 9 = 4 | 14 — 9 = 5 | 11 — 3 = 8 | 11 — 2 = 9 | 13 — 5 = 8 |
| 16 — 9 = 7 | 15 — 7 = 8 | 14 — 5 = 9 | 17 — 8 = 9 | 16 — 9 = 7 | 12 — 3 = 9 |
| 13 — 4 = 9 | 15 — 8 = 7 | 12 — 4 = 8 | 15 — 9 = 6 | 16 — 7 = 9 | 13 — 5 = 8 |
| 15 — 7 = 8 | 13 — 9 = 4 | 18 — 9 = 9 | 11 — 9 = 2 | 15 — 6 = 7 | 11 — 3 = 8 |
| 14 — 9 = 5 | 14 — 5 = 9 | 12 — 3 = 9 | 17 — 8 = 9 | 13 — 6 = 7 | 11 — 5 = 6 |
| 8 + 7 = 15 | 6 + 6 = 12 | 12 — 4 = 8 | 17 — 8 = 9 | 14 — 9 = 5 | 13 — 5 = 8 |
| 11 — 2 = 9 | 11 — 92 | 15 — 6 = 9 | 7 + 4 = 11 | 9 + 4 = 13 | 15 — 7 = 8 |
| 8 + 8 = 16 | 8 + 3 = 11 | 6 + 8 = 14 | 7 + 9 = 16 | 11 — 8 = 3 | 13 — 7 = 6 |
| 17 — 8 = 9 | 14 — 8 = 6 | 5 + 6 = 11 | 9 + 9 = 18 | 8 + 8 = 16 | 9 + 2 = 11 |
| 9 + 4 = 13 | 8 + 6 = 14 | 16 — 7 = 9 | 7 + 9 = 16 | 11 — 3 = 8 | 12 — 6 = 6 |
| _______________ | _______________ | _______________ | _______________ | _______________ | _______________ |
Составные задачи
- Задачи на нахождение слагаемого и вычитаемого
- Задачи на нахождение третьего слагаемого
- Задачи на 2 действия
- Задачи на 3 действия
- Задачи на нахождение суммы
Простые задачи
- Простые задачи на умножение
- Задачи на деление по содержанию и на равные части
- Задачи на 1 действие
Примеры по математике на сложение и вычитание в пределах 100
Данный материал подготовлен для учителей начальных классов для улучшения вычислительных навыков до 100 для детей 2 класса. Также примеры на сложение и вычитание до 100 могут использовать родители детей 2-3 классов.
Также примеры на сложение и вычитание до 100 могут использовать родители детей 2-3 классов.
Задания и примеры соответствуют программным требованиям учащихся 2 класса. Ребенок повторит то, что изучал в первом классе, а далее будет отрабатывать сложение и вычитание в пределах 100 за второй класс: примеры на сложение и вычитание в пределах сотни как без перехода через десяток, так и с переходом.
Содержание
- Примеры по математике на сложение и вычитание в пределах ста
- Примеры с переходом через десяток в пределах 20 (повторяем изученное за 1 класс)
- Примеры на сложение и вычитание круглых чисел. Примеры на знание разрядного состава числа.
- Примеры на вычитание из круглого числа однозначного числа без перехода через десяток
- Примеры на сложение и вычитание до 100 (распечатать бесплатно)
Примеры по математике на сложение и вычитание в пределах ста
Примеры с переходом через десяток в пределах 20 (повторяем изученное за 1 класс)
Всего дано 4 варианта примеров для самостоятельной работы школьников 2 -го класса.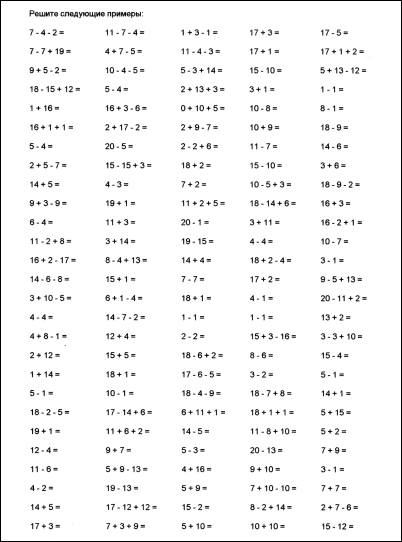
| Первый вариант | Второй вариант |
| 14 – 9 = 9 + 6 = 15 – 6 = 8 + 8 = 16 – 8 = 7 + 5 = 14 – 5 = 8 + 3 = 15 – 7 = 9 + 5 = 16 – 9 = 9 + 9 = 14 – 7 = 7 + 7 = 15 – 9 = 8 + 7 = 16 – 7 = 7 + 6 = 14 – 8 = 9 + 8 = 15 – 8 = 6 + 5 = 17 – 9 = 9 + 4 = 14 – 6 = 7 + 4 = 18 – 9 = 8 + 5 = 17 — 8 = 8 + 4 = | 14 – 8 = 9 + 3 = 15 – 9 = 8 + 5 = 16 — 7 = 7 + 4 = 14 – 6 = 6 + 7 = 15 – 6 = 9 + 9 = 16 – 9 = 8 + 7 = 14 – 5 = 7 + 6 = 15 – 8 = 9 + 2 = 16 – 8 = 8 + 8 = 14 – 7 = 7 + 5 = 15 – 7 = 9 + 4 = 17 – 8 = 8 + 3 = 18 – 9 = 6 + 5 = 14 – 9 = 7 + 7 = 17 – 9 = 9 + 5 = |
| Третий вариант | Четвертый вариант |
| 14 – 7 = 9 + 3 = 15 – 8 = 7 + 4 = 16 – 9 = 8 + 4 = 14 – 8 = 7 + 8 = 15 – 9 = 6 + 5 = 16 – 7 = 9 + 9 = 14 – 6 = 6 + 7 = 15 – 7 = 8 + 6 = 16 – 8 = 9 + 8 = 14 – 5 = 8 + 7 = 15 – 6 = 8 + 5 = 18 – 9 = 9 + 5= 17 – 8 = 7 + 7 = 14 – 9 = 6 + 6 = 17 – 9 = 6 +8 = | 12- 3= 9 + 6 = 13- 5= 8 + 8 = 11- 9= 7 + 6 = 12- 4= 9 + 4 = 12- 5= 8 + 9 = 13- 4= 7 + 9 = 12- 6= 9 + 2= 11- 6= 8 + 8 = 12- 7= 13- 6= 7 + 6= 11- 4= 8 + 7= 13- 8= 6 + 5= 13- 7= 9 + 9= 11- 3= 7 + 5= 13- 9= 8 + 5= 11- 2= |
Примеры на сложение и вычитание круглых чисел.
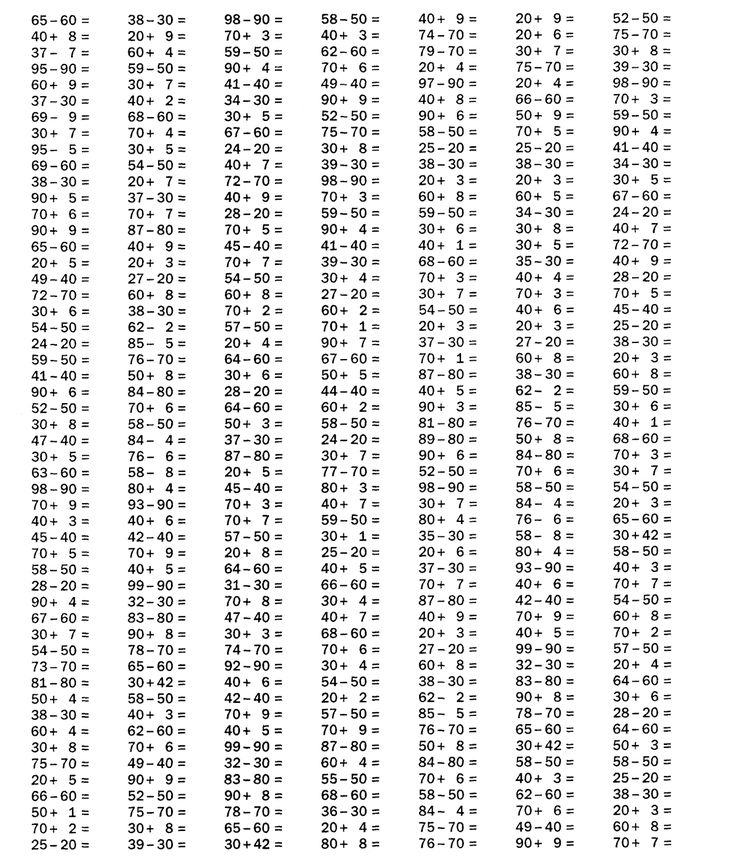 Примеры на знание разрядного состава числа.
Примеры на знание разрядного состава числа.| Первый вариант | Второй вариант |
| 100-70= 40 + 5 = 30+ 40 = 34 — 4 = 28 –20 = 90- 60 = 76 — 6 = 49 –40= 50+30= 20+ 9= 80-60= 60+ 9= 60+20= 97- 7= 65-60= 80+8= 57-50= 35 -5= 70+30= 80+9= 62-60= 74 — 4= 100-90= 31- 30= 69 -9= | 90-60= 70 +3= 40+40= 59-50= 62- 2 = 80-50= 38 -8 = 61-60= 30+30= 80+7 = 70-50= 60+ 6= 50- 40= 30+ 8= 80+10= 30-20= 70+ 3= 67-7= 98-90= 20+70= 60-50= 20+ 9= 40+ 4= 38- 8= 93-90= |
| Третий вариант | Четвертый вариант |
| 80-50= 80+5= 50+40= 98- 8 = 53-50= 60- 50= 30+ 4= 30+20= 57- 7= 28-20= 40 -20= 60+ 7= 50+ 20= 69- 9= 94-90= 90-70= 90+ 3= 60+ 40= 87 – 7= 58-50= 100-30= 20+ 9= 70+30= 91 – 1= 36 -30= | 70-40= 30+9= 70+10= 85- 5= 39-30= 100-80= 50+ 2= 40+30= 65- 5= 78-70= 90-60= 90+ 4= 60+40= 49- 9= 38-30= 50-40= 60+ 9= 62- 2= 95-90= 60-30= 80+ 6= 50+40= 80-40= 70+ 8= 80+20= |
Примеры на вычитание из круглого числа однозначного числа без перехода через десяток
| Первый вариант | Второй вариант |
| 100-5= 50-7= 90-8= 40-4= 60-9= 20-6= 70-4= 80-2= 100-6= 30-3= 70-5= 90-7= 40-6= 60-4= 80-3= 50-9= 30-9= 70-6= 100-7= 50-9= 30-4= 90-6= 40-3= 80-4= 60-8= 70-7= | 30-8= 70-1= 90-9= 40-2= 60-6= 80-8= 50-2= 30-7= 70-9= 90-1= 60-5= 20-7= 30-6= 80-7= 50-5= 70-7= 40-5= 100-3= 80-6= 60-7= 30-5= 90-2= 70-8= 100-2= 80-5= 50-6= |
| Третий вариант | Четвертый вариант |
| 40-4= 80-9= 100-7= 30-9= 70-3= 80-1= 40-6= 20-9= 60-3= 80-2= 50-7= 30-5= 40-2= 70-3= 60-8= 80-3= 50-4= 90-4= 100-8= 70-3= 40-8= 100-9= 80-4= 90-3= 70-5= 60-2= | 100-4= 90-5= 70-9= 100-6= 60-7= 80-7= 50-9= 100-5= 70-8= 80-6= 40-3= 90-6= 100-4= 70-7= 50-8= 30-4= 60-9= 20-8= 80-9= 90-7= 50-6= 60-1= 100-3= 80-5= 50-3= 30-5= |
Примеры на сложение и вычитание до 100 (распечатать бесплатно)
Примеры на сложение и вычитание до 100 — бланк 1Скачать
Примеры на сложение и вычитание до 100 — бланк 2Скачать
Примеры на сложение и вычитание до 100 — бланк 3Скачать
Тренажер Примеры на сложение и вычитание до 100 — Скачать
На нашей страничке мы подготовили несколько вариантов примеров до 100 для 2 класса: примеры на повторение до 20 на повтор после первого класса, шаблоны листов А4 с примерами, чтобы вам было удобнее распечатать.
Также листы с примерами, где нужно вписать правильные ответы в клетки.
- Математика: арифметика, примеры в пределах сотни.
- При знаке плюс необходимо найти сумму.
- При знаке минус нужно найти разность.
Распечатать примеры на сложение и вычитание могут учителя 1 и 2 класса.
Примеры онлайн на сложение и вычитание в пределах 1000
Примеры онлайн на сложение и вычитание в пределах 1000ПримерОнлайн.ru
Генератор примеров по математике 1-3 класс
Онлайн примеры на сложение трёхзначных чисел позволяют вывести большое количество неповторяющихся примеров с трёхзначными числами.
Примеры можно разделить по степени сложности: лёгкие – это примеры без перехода через десяток, сложные – с обязательным переходом, обычные – слагаемые выбираются случайным образом.
| Настройка генератора примеров |
|---|
|
|
|
Образец примеров
320 + 224
222 + 654
352 — 197
758 — 627
139 + 189
980 — 221
507 — 158
877 — 722
731 — 507
537 — 234
794 — 637
554 — 295
876 — 601
845 — 295
290 + 738
805 — 541
291 + 807
576 + 347
229 + 242
812 — 769
461 + 188
519 — 187
221 + 561
216 + 161
440 + 282
263 + 608
981 — 882
215 + 401
489 — 402
947 + 106
821 — 667
592 + 427
171 + 170
488 + 287
439 — 265
269 + 129
568 + 141
426 + 568
934 — 161
356 — 341
247 + 156
654 — 481
409 + 250
264 — 150
769 — 722
655 + 328
119 + 874
816 + 113
981 — 401
822 — 445
176 + 915
234 + 115
563 + 374
750 — 439
793 + 121
571 + 492
973 — 616
626 + 205
127 + 937
789 — 769
650 — 528
809 — 532
634 — 574
921 + 138
686 — 207
465 — 441
416 + 381
244 — 196
624 — 615
154 + 437
970 — 255
411 + 309
835 — 270
389 + 236
363 + 583
379 + 227
428 + 287
748 — 109
535 — 275
586 + 277
807 + 238
203 + 270
689 + 307
557 — 151
504 — 315
705 — 311
306 + 362
202 + 410
798 — 727
671 — 469
640 — 115
970 — 183
251 + 818
581 — 453
433 — 354
569 + 264
509 + 489
879 + 103
425 — 185
112 + 584
455 + 249
942 — 436
985 — 806
957 — 129
694 — 198
459 — 261
885 — 311
535 — 215
607 + 393
413 — 388
976 — 767
630 + 271
349 — 335
219 + 378
503 + 471
986 — 217
598 — 523
229 + 442
882 — 654
817 — 243
389 + 672
395 + 549
971 — 279
459 — 159
575 — 407
864 + 190
715 + 240
979 — 277
668 — 492
297 + 388
565 — 389
981 — 361
234 + 680
132 + 528
814 — 390
131 + 823
131 + 826
824 — 758
827 — 729
788 — 764
272 + 673
459 + 423
728 — 369
939 — 902
730 — 175
648 + 300
530 — 480
630 — 552
214 + 158
374 — 191
155 + 352
797 — 165
195 + 177
292 + 585
555 + 127
721 — 581
598 — 476
459 + 322
942 — 122
900 — 520
775 — 268
674 + 293
640 + 360
559 — 433
625 + 167
931 — 388
571 + 239
686 — 300
832 + 131
586 — 310
659 + 112
224 + 792
168 + 550
880 — 845
623 — 463
678 — 432
345 + 628
926 — 110
810 — 205
249 + 803
696 — 383
705 — 531
442 + 230
915 — 716
941 — 270
692 + 364
708 — 191
366 + 410
813 + 190
283 + 280
163 + 136
121 + 896
507 + 237
949 — 543
122 + 812
248 — 125
346 — 184
613 — 502
535 + 459
614 + 285
110 + 587
439 — 233
681 — 213
511 — 433
336 + 460
511 — 241
575 — 168
232 + 452
788 — 519
426 + 276
524 + 366
669 + 367
187 + 263
134 + 914
818 — 495
407 — 276
472 — 467
385 — 177
279 — 209
517 — 254
618 — 220
244 + 372
106 + 952
872 — 234
358 + 741
434 + 118
447 + 490
814 — 356
261 — 181
660 — 313
918 — 376
955 — 943
451 — 376
951 + 148
211 + 804
530 + 305
481 + 468
878 — 292
203 + 690
522 + 555
231 + 451
524 — 161
593 + 443
383 — 218
155 + 887
147 + 425
717 — 135
361 + 516
591 — 184
841 + 183
957 — 920
876 — 571
759 — 511
630 — 356
993 — 231
795 — 640
616 + 274
505 + 348
813 — 371
470 + 206
341 + 490
432 + 220
458 — 195
927 — 924
997 — 223
885 — 704
875 — 269
702 — 682
964 — 763
392 + 632
722 — 502
862 — 122
873 — 551
269 + 342
797 + 256
521 + 528
482 + 171
917 — 202
672 — 519
575 — 426
726 — 258
534 + 301
426 + 331
587 + 432
248 + 435
766 — 326
666 + 141
770 + 183
175 + 799
251 + 400
928 + 117
469 + 250
421 + 184
938 — 247
352 + 308
570 — 244
346 + 244
789 + 285
633 — 283
599 — 259
573 — 465
229 + 714
294 — 127
765 — 158
980 — 180
469 — 458
460 + 325
230 + 674
211 + 823
851 — 193
744 — 603
401 + 333
571 + 380
740 — 701
918 — 777
458 + 300
686 — 136
475 — 248
425 — 263
790 — 150
850 — 367
574 — 484
745 — 204
499 + 285
217 + 186
969 — 662
588 + 302
216 + 379
335 — 254
207 + 106
376 — 267
738 — 573
291 — 228
588 — 398
519 + 488
819 + 217
882 — 846
881 — 251
483 — 305
248 + 528
378 + 318
632 + 205
566 + 300
232 + 701
322 + 712
959 — 265
627 + 222
768 — 557
102 + 165
254 + 416
542 — 196
281 + 411
925 — 576
515 — 147
817 — 599
309 + 642
949 — 811
834 + 136
286 + 268
565 — 257
192 + 351
191 + 785
278 + 510
675 — 616
168 + 465
546 — 260
419 + 169
830 — 404
408 + 219
130 + 544
467 + 601
528 + 237
104 + 511
397 + 295
274 + 431
453 + 460
744 — 675
604 — 102
384 + 276
842 — 359
609 + 229
224 + 342
633 + 400
185 — 141
700 + 135
495 + 433
927 — 192
415 — 226
979 — 814
708 — 250
397 + 476
277 + 374
797 — 119
684 — 614
759 — 702
604 — 249
661 + 309
435 + 523
906 — 564
222 + 463
901 — 664
646 — 445
121 + 604
342 + 151
730 — 280
540 + 314
703 — 463
477 + 261
510 — 137
886 — 746
279 — 195
843 — 451
988 — 370
284 + 812
913 — 860
291 + 345
821 + 253
608 — 177
386 — 340
412 + 189
659 + 394
897 — 803
129 + 226
778 — 310
995 — 283
567 + 126
512 + 508
503 + 143
596 — 421
323 + 475
223 + 734
365 + 524
593 — 425
581 — 138
408 + 313
654 + 440
163 + 198
980 — 611
208 + 809
297 + 753
103 + 405
900 — 767
828 — 173
121 + 728
349 + 198
760 + 229
678 — 411
309 — 147
649 + 307
121 + 322
489 + 604
553 + 543
736 — 191
844 + 132
476 — 161
146 + 945
145 + 758
554 + 246
356 + 573
214 + 231
321 + 751
639 — 471
500 — 442
556 — 323
151 + 399
715 — 301
879 — 240
280 + 710
484 + 275
419 + 199
528 — 452
694 — 168
781 — 713
535 — 188
261 — 250
578 — 295
400 + 588
957 — 297
860 — 288
364 — 351
514 + 373
171 + 366
741 — 200
977 — 834
913 + 120
812 — 625
790 + 110
988 — 200
207 — 164
338 + 511
372 — 351
185 + 743
132 + 100
162 + 438
613 + 463
184 + 544
957 — 471
208 + 623
Сложение и вычитание со временем
Все основные арифметические ресурсы
6 Диагностические тесты 75 практических тестов Вопрос дня Карточки Learn by Concept
Справка по основам арифметики » Деньги и время » Сложение и вычитание со временем
Джимми начал сдавать контрольную по математике в 11:03 и закончил в 12:29. Сколько минут понадобилось Джимми, чтобы закончить тест?
Сколько минут понадобилось Джимми, чтобы закончить тест?
Возможные ответы:
Правильный ответ:
Пояснение:
Во-первых, нам нужно узнать, сколько времени Джимми понадобилось, чтобы закончить тест.
Вычтите часы, затем вычтите минуты.
Теперь вопрос заключается в том, сколько МИНУТ потребуется Джимми, чтобы закончить тест. Переведите часы в минуты.
Сообщить об ошибке
Пит работал над домашним заданием, и ему потребовалось час и минуты, чтобы закончить. Если он начал свою домашнюю работу в , во сколько он закончил свою домашнюю работу?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы сложить время, нужно сложить часы, а затем сложить минуты.
Поскольку в часе всего 60 минут, у вас не может быть времени, значение которого в минутах больше 60. В этом случае вычтите 60 минут и добавьте еще 1 к часу.
Сообщить об ошибке
Если вы ляжете вздремнуть в , и будете дремать в течение минут, во сколько вы проснетесь?
Возможные ответы:
Правильный ответ:
Объяснение:
Во-первых, нам нужно преобразовать минуты в комбинацию часов и минут. Один час равен минутам, поэтому мы можем переписать минуты следующим образом:
и поскольку
Теперь нам нужно добавить к .
.
Таким образом, вы просыпаетесь от дремоты в .
Сообщить об ошибке
Пожалуйста, выберите лучший ответ на вопрос ниже.
Если Эндрю выходит из дома в час дня и ему требуется ровно два часа и четырнадцать минут, чтобы добраться до своего офиса, а затем еще восемь минут, чтобы добраться до своего стола, в какое время он будет за своим столом?
Возможные ответы:
pm
pm
pm
вечера
вечера
Правильный ответ:
вечера
Объяснение:
Первым шагом в этом процессе является добавление двух часов и четырнадцати минут к pm. Просто сложите их вместе, сначала часы, а затем минуты:
Просто сложите их вместе, сначала часы, а затем минуты:
Часы
Минуты:
Итак, теперь мы знаем, что Эндрю добрался до своего офиса в час дня. Добавьте последние восемь минут, чтобы решить задачу:
.
Час не изменился, поэтому мы знаем, что Андрей пришел к своему рабочему столу в час дня.
Сообщить об ошибке
Мелисса начала играть на фортепиано в 15:34. Она тренировалась до 17:17. Как долго она тренировалась?
Возможные ответы:
2 часа и 17 минут
1 час и 17 минут
2 часа 43 минуты
1 час и 43 минуты
Правильный ответ:
1 час и 43 минуты
Объяснение:
Чтобы вычесть время, вычтите минуты, а затем вычтите часы.
Поскольку у нас не может быть отрицательных минут, прибавьте 60 к минутам и вычтите 1 из часов (60 минут = 1 час).
Сообщить об ошибке
Нейт начал делать домашнюю работу по математике, истории, английскому и французскому языку в . Ему потребовались минуты, чтобы закончить домашнюю работу по математике, минуты, чтобы закончить домашнюю работу по истории, минуты, чтобы закончить домашнюю работу по английскому языку, и минуты, чтобы закончить домашнюю работу по французскому языку. Во сколько Нейт перестал делать домашнее задание?
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала подсчитайте общее количество времени, которое Нейт потратил на выполнение домашнего задания.
Теперь вычтите минуты, пока количество минут не станет меньше, чтобы вычислить, сколько часов и минут потребовалось ему, чтобы сделать домашнее задание.
Поскольку мы вычли дважды, мы знаем, что он выполнил домашнюю работу за несколько часов и минут.
Чтобы узнать, когда он закончил делать домашнее задание, сложите часы, а затем сложите минуты.
Итак, он закончил на
Сообщить об ошибке
Уведомление об авторских правах
Все основные арифметические ресурсы
6 диагностических тестов 75 практических тестов Вопрос дня Карточки Learn by Concept
Статьи по основам математики — макеты
стр. 1
Стр. 2
Стр. 3
Стр. 4
Стр. 5
Стр. Page 14
Page 15
Page 16
Результаты фильтра
153 Результаты
Статьи 144
Статьи (144)Чит -шпаргалка 6
Чит.0005Базовая математика Обучение детей новой математике (K-5) Памятка для чайников
Памятка / Обновлено 04.
 05.2022
05.2022Когда вы тренируете математические навыки со своим ребенком K–5, это может помочь иметь инструмент, чтобы напомнить вам некоторые основы, связанные с сложением, вычитанием, умножением, делением и дробями. В таких случаях может пригодиться эта шпаргалка.
Посмотреть шпаргалку
Базовая математика Базовая математика и предварительная алгебра: 1001 Практические задачи для чайников Шпаргалка
Памятка / Обновлено 27 апреля 2022 г.
Чтобы успешно освоить базовую математику, вам необходимо попрактиковаться в задачах на сложение, вычитание, умножение и деление. Вам также необходимо понимать порядок операций, дроби, десятичные дроби, проценты, отношения, веса и меры и даже немного геометрии. После того, как вы овладеете этими и другими основными математическими понятиями, вы можете приступить к предварительной алгебре, которая включает в себя переменные, выражения и уравнения.

Посмотреть памятку
Базовая математика Техническая математика для чайников Памятка
Памятка / Обновлено 27 апреля 2022 г.
Понимание некоторых основ технической математики может упростить повседневные ситуации, с которыми сталкиваются многие профессионалы и даже непрофессионалы, включая решение текстовых задач, вычисления чаевые, внесите сдачу или сопоставьте американские и метрические измерения.
Посмотреть шпаргалку
Базовая математика Математика на каждый день для чайников Шпаргалка
Шпаргалка / Обновлено 14-04-2022
Повседневная математика пригодится, когда вы имеете дело с финансами, такими как кредитные карты и ипотечные кредиты, и даже помогает, когда вы пытаетесь выяснить, сколько оставить на чаевые.
 Знание некоторых основных математических формул, теоремы Пифагора и более простого способа сложения является ключом к повседневной математике.
Знание некоторых основных математических формул, теоремы Пифагора и более простого способа сложения является ключом к повседневной математике.Посмотреть шпаргалку
Базовая математика Базовая математика и предварительная алгебра Для чайников Шпаргалка
Шпаргалка / Обновлено 21 марта 2022 г.
Небольшое понимание может иметь большое значение для овладения математикой. Некоторые математические понятия поначалу могут показаться сложными, но после того, как вы немного поработаете с ними, вы можете задаться вопросом, из-за чего весь этот шум. В этих статьях вы найдете простые для понимания объяснения и наглядные примеры, которые охватывают основные математические понятия, такие как порядок операций; коммутативные, ассоциативные и дистрибутивные свойства; радикалы, экспоненты и абсолютные значения — которые вы можете помнить (или не помнить) из своих ранних уроков математики и начальной алгебры.
 Вы также найдете удобные и простые для понимания руководства по преобразованию между метрическими и английскими единицами измерения, а также между дробями, процентами и десятичными знаками.
Вы также найдете удобные и простые для понимания руководства по преобразованию между метрическими и английскими единицами измерения, а также между дробями, процентами и десятичными знаками.Посмотреть шпаргалку
Базовая математика Математика для реальной жизни Для чайников Шпаргалка
Шпаргалка / Обновлено 28 февраля 2022 г.
Использование реальной математики может упростить повседневные ситуации. Математика пригодится каждый раз, когда вы отправляетесь в путешествие, ходите по магазинам или занимаетесь домашними делами.
Посмотреть шпаргалку
Основы математики Как рассчитать проценты
Статья / Обновлено 26 августа 2021 г. Не уйти от процентов. Несмотря на то, что в Интернете есть множество процентных калькуляторов, полезно иметь возможность быстро посчитать в уме, чтобы рассчитать проценты без какой-либо цифровой помощи.
 Прежде чем вы сможете рассчитать процент, вы должны точно понимать, что такое процент.
Слово процент происходит от слова процент. Если вы разделите слово «процент» на его корневые слова, вы увидите «процент» и «процент». Цент — это старое европейское слово французского, латинского и итальянского происхождения, означающее «сто». Таким образом, процент переводится непосредственно как «на сотню». Если у вас есть 87 процентов, вы буквально имеете 87 на 100. Если за последние 100 дней снег шел 13 раз, он шел в 13 процентах случаев.
Числа, которые вы будете преобразовывать в проценты, могут быть предоставлены вам в двух различных форматах: десятичном и дробном. Десятичный формат легче вычислить в процентах. Преобразование десятичного числа в проценты так же просто, как умножение его на 100. Чтобы преобразовать 0,87 в проценты, просто умножьте 0,87 на 100.
0,87 × 100 = 87, что дает нам 87 процентов.
Процент часто обозначается символом %. Вы можете представить свой ответ как 87% или 87% — оба варианта приемлемы.
Прежде чем вы сможете рассчитать процент, вы должны точно понимать, что такое процент.
Слово процент происходит от слова процент. Если вы разделите слово «процент» на его корневые слова, вы увидите «процент» и «процент». Цент — это старое европейское слово французского, латинского и итальянского происхождения, означающее «сто». Таким образом, процент переводится непосредственно как «на сотню». Если у вас есть 87 процентов, вы буквально имеете 87 на 100. Если за последние 100 дней снег шел 13 раз, он шел в 13 процентах случаев.
Числа, которые вы будете преобразовывать в проценты, могут быть предоставлены вам в двух различных форматах: десятичном и дробном. Десятичный формат легче вычислить в процентах. Преобразование десятичного числа в проценты так же просто, как умножение его на 100. Чтобы преобразовать 0,87 в проценты, просто умножьте 0,87 на 100.
0,87 × 100 = 87, что дает нам 87 процентов.
Процент часто обозначается символом %. Вы можете представить свой ответ как 87% или 87% — оба варианта приемлемы. Если вам дана дробь, преобразуйте ее в проценты, разделив верхнее число на нижнее. Если вам дано 13/100, вы должны разделить 13 на 100.
13 ÷ 100 = 0,13
Затем выполните описанные выше шаги для преобразования десятичной дроби в проценты.
0,13 × 100 = 13, что дает вам 13%.
Более сложная задача возникает, когда вам нужно узнать процентное соотношение, когда вам даны числа, которые не так точно вписываются в 100.
В большинстве случаев вам будет дан процент от определенного числа. Например, вы можете знать, что 40 процентов вашей зарплаты пойдет на налоги, и вы хотите узнать, сколько это денег. Чтобы вычислить процент определенного числа, вы сначала преобразуете процентное число в десятичное число.
Этот процесс является обратным тому, что вы делали ранее. Вы делите свой процент на 100. Итак, 40 процентов будет 40, деленное на 100.
40 ÷ 100 = 0,40
Получив десятичную версию своего процента, просто умножьте его на заданное число (в данном случае на сумму вашей зарплаты). Если ваша зарплата составляет 750 долларов, вы должны умножить 750 на 0,40.
Если вам дана дробь, преобразуйте ее в проценты, разделив верхнее число на нижнее. Если вам дано 13/100, вы должны разделить 13 на 100.
13 ÷ 100 = 0,13
Затем выполните описанные выше шаги для преобразования десятичной дроби в проценты.
0,13 × 100 = 13, что дает вам 13%.
Более сложная задача возникает, когда вам нужно узнать процентное соотношение, когда вам даны числа, которые не так точно вписываются в 100.
В большинстве случаев вам будет дан процент от определенного числа. Например, вы можете знать, что 40 процентов вашей зарплаты пойдет на налоги, и вы хотите узнать, сколько это денег. Чтобы вычислить процент определенного числа, вы сначала преобразуете процентное число в десятичное число.
Этот процесс является обратным тому, что вы делали ранее. Вы делите свой процент на 100. Итак, 40 процентов будет 40, деленное на 100.
40 ÷ 100 = 0,40
Получив десятичную версию своего процента, просто умножьте его на заданное число (в данном случае на сумму вашей зарплаты). Если ваша зарплата составляет 750 долларов, вы должны умножить 750 на 0,40. 750 × 0,40 = 300
Ваш ответ будет 300. Вы платите 300 долларов в виде налогов.
Давайте попробуем другой пример. Вам нужно откладывать 25 процентов своей зарплаты в течение следующих 6 месяцев, чтобы заплатить за предстоящий отпуск. Если ваша зарплата составляет 1500 долларов, сколько вы должны откладывать?
Начните с преобразования 25 процентов в десятичную дробь.
25 ÷ 100 = 0,25
Теперь умножьте десятичную дробь на сумму вашей зарплаты, или 1500.
1500 × 0,25 = 375
Это означает, что вам нужно откладывать 375 долларов с каждой зарплаты.
750 × 0,40 = 300
Ваш ответ будет 300. Вы платите 300 долларов в виде налогов.
Давайте попробуем другой пример. Вам нужно откладывать 25 процентов своей зарплаты в течение следующих 6 месяцев, чтобы заплатить за предстоящий отпуск. Если ваша зарплата составляет 1500 долларов, сколько вы должны откладывать?
Начните с преобразования 25 процентов в десятичную дробь.
25 ÷ 100 = 0,25
Теперь умножьте десятичную дробь на сумму вашей зарплаты, или 1500.
1500 × 0,25 = 375
Это означает, что вам нужно откладывать 375 долларов с каждой зарплаты.Просмотреть статью
Основы математики Как заимствовать при вычитании
Статья / Обновлено 24 июля 2021 г.
Иногда, когда вы вычитаете большие числа, верхняя цифра в столбце меньше, чем нижняя цифра в этом столбце. В этом случае вам нужно заимствовать из следующего столбца слева. Заем — это двухэтапный процесс: Вычтите 1 из верхнего числа в столбце непосредственно слева.
 Вычеркните число, которое вы берете взаймы, вычтите 1 и напишите ответ над числом, которое вы вычеркнули.
Добавьте 10 к верхнему числу в столбце, в котором вы работали.
Например, предположим, что вы хотите вычесть 386 – 9.4. Первый шаг — вычесть 4 из 6 в столбце единиц, что даст вам 2:
Однако когда вы переходите к столбцу десятков, вы обнаружите, что вам нужно вычесть 8–9. Поскольку 8 меньше 9, вам нужно заимствовать значения из столбца сотен. Сначала зачеркните цифру 3 и замените ее цифрой 2, потому что 3 – 1 = 2:
Затем поместите 1 перед 8, изменив его на 18, потому что 8 + 10 = 18:
Теперь вы можете вычесть в столбце десятков: 18 – 9 = 9:
Последний шаг прост: 2 – 0 = 2:
Следовательно, 386 – 94 = 292.
В некоторых случаях в столбце непосредственно слева может не быть ничего, что можно было бы одолжить. Предположим, например, что вы хотите вычесть 1002 – 39.8. Начиная со столбца единиц, вы обнаружите, что вам нужно вычесть от 2 до 8. Поскольку 2 меньше 8, вам нужно заимствовать из следующего столбца слева.
Вычеркните число, которое вы берете взаймы, вычтите 1 и напишите ответ над числом, которое вы вычеркнули.
Добавьте 10 к верхнему числу в столбце, в котором вы работали.
Например, предположим, что вы хотите вычесть 386 – 9.4. Первый шаг — вычесть 4 из 6 в столбце единиц, что даст вам 2:
Однако когда вы переходите к столбцу десятков, вы обнаружите, что вам нужно вычесть 8–9. Поскольку 8 меньше 9, вам нужно заимствовать значения из столбца сотен. Сначала зачеркните цифру 3 и замените ее цифрой 2, потому что 3 – 1 = 2:
Затем поместите 1 перед 8, изменив его на 18, потому что 8 + 10 = 18:
Теперь вы можете вычесть в столбце десятков: 18 – 9 = 9:
Последний шаг прост: 2 – 0 = 2:
Следовательно, 386 – 94 = 292.
В некоторых случаях в столбце непосредственно слева может не быть ничего, что можно было бы одолжить. Предположим, например, что вы хотите вычесть 1002 – 39.8. Начиная со столбца единиц, вы обнаружите, что вам нужно вычесть от 2 до 8. Поскольку 2 меньше 8, вам нужно заимствовать из следующего столбца слева. Но цифра в колонке десятков — 0, так что вы не можете взять оттуда, потому что шкаф, так сказать, пуст:
Когда заимствование из следующего столбца невозможно, вам нужно заимствовать из ближайшего ненулевого столбца слева.
В этом примере столбец, из которого вам нужно заимствовать, — это столбец тысяч. Сначала зачеркните 1 и замените его на 0. Затем поставьте 1 перед 0 в столбце сотен:
Теперь зачеркните 10 и замените на 9.. Поставьте 1 перед 0 в столбце десятков:
Наконец, вычеркните 10 в столбце десятков и замените его на 9. Затем поставьте 1 перед 2:
Наконец, вы можете начать вычитать в столбце единиц: 12 – 8 = 4:
Затем вычтите в столбце десятков: 9 – 9 = 0:
Затем вычтите в столбце сотен: 9 – 3 = 6:
Поскольку в столбце тысяч ничего не осталось, вам не нужно больше ничего вычитать. Следовательно, 1002 – 398 = 604.
Но цифра в колонке десятков — 0, так что вы не можете взять оттуда, потому что шкаф, так сказать, пуст:
Когда заимствование из следующего столбца невозможно, вам нужно заимствовать из ближайшего ненулевого столбца слева.
В этом примере столбец, из которого вам нужно заимствовать, — это столбец тысяч. Сначала зачеркните 1 и замените его на 0. Затем поставьте 1 перед 0 в столбце сотен:
Теперь зачеркните 10 и замените на 9.. Поставьте 1 перед 0 в столбце десятков:
Наконец, вычеркните 10 в столбце десятков и замените его на 9. Затем поставьте 1 перед 2:
Наконец, вы можете начать вычитать в столбце единиц: 12 – 8 = 4:
Затем вычтите в столбце десятков: 9 – 9 = 0:
Затем вычтите в столбце сотен: 9 – 3 = 6:
Поскольку в столбце тысяч ничего не осталось, вам не нужно больше ничего вычитать. Следовательно, 1002 – 398 = 604.Просмотреть статью
Основы математики Как делить десятичные дроби
Статья / Обновлено 24.
 07.2021
07.2021Деление десятичных дробей похоже на деление целых чисел, за исключением того, что перед началом деления необходимо обработать десятичную точку. Вот как делить десятичные дроби шаг за шагом: Переместите десятичную точку в делителе и делимом. Превратите делитель (число, на которое вы делите) в целое число, переместив десятичную точку до упора вправо. При этом переместите запятую в делимом (числе, которое вы делите) на такое же количество знаков вправо. Поместите десятичную точку в частном (ответе) прямо над тем местом, где десятичная точка теперь появляется в делимом. Разделите как обычно, стараясь правильно выстроить частное, чтобы десятичная точка встала на свое место. Выровняйте каждую цифру частного сразу после последней цифры делимого, используемого в этом цикле. Как и в случае целочисленного деления, иногда десятичное деление не работает равномерно в конце. Однако с десятичными дробями вы никогда не записываете остаток. Вместо этого добавьте достаточно нулей в конце, чтобы округлить частное до определенного числа знаков после запятой.
 Цифра справа от цифры, до которой вы округляете, указывает, нужно ли округлять в большую или меньшую сторону, поэтому вам всегда нужно вычислять деление на один дополнительный разряд.
См. следующую диаграмму:
Чтобы округлить десятичную до
Заполните дивиденд с замыкающими нулями, чтобы
Целое число
Один десятичный знак
Один десятичный знак
Два десятичных знака
Два десятичных знака
Три десятичных знака
Примеры вопросов
Разделите следующее: 90,152 / 0,8 = ?
11.44. Для начала напишите задачу как обычно:
Превратите 0,8 в целое число 8, переместив запятую на одно место вправо. При этом запятую в числе 9,1526 переместите на один разряд вправо. Поставьте запятую в частном прямо над тем местом, где она попадает в 91,25:
Теперь вы готовы разделить. Просто будьте осторожны, чтобы правильно выстроить частное, чтобы десятичная точка встала на свое место.
Разделите следующее: 21,9 / 0,015 = ?
1460. Ставьте задачу как обычно:
Обратите внимание, что к делимому добавлены два завершающих нуля, потому что вам нужно переместить десятичные точки в каждом числе на три позиции вправо.
Цифра справа от цифры, до которой вы округляете, указывает, нужно ли округлять в большую или меньшую сторону, поэтому вам всегда нужно вычислять деление на один дополнительный разряд.
См. следующую диаграмму:
Чтобы округлить десятичную до
Заполните дивиденд с замыкающими нулями, чтобы
Целое число
Один десятичный знак
Один десятичный знак
Два десятичных знака
Два десятичных знака
Три десятичных знака
Примеры вопросов
Разделите следующее: 90,152 / 0,8 = ?
11.44. Для начала напишите задачу как обычно:
Превратите 0,8 в целое число 8, переместив запятую на одно место вправо. При этом запятую в числе 9,1526 переместите на один разряд вправо. Поставьте запятую в частном прямо над тем местом, где она попадает в 91,25:
Теперь вы готовы разделить. Просто будьте осторожны, чтобы правильно выстроить частное, чтобы десятичная точка встала на свое место.
Разделите следующее: 21,9 / 0,015 = ?
1460. Ставьте задачу как обычно:
Обратите внимание, что к делимому добавлены два завершающих нуля, потому что вам нужно переместить десятичные точки в каждом числе на три позиции вправо. Опять же, поместите десятичную точку в частном непосредственно над тем местом, где она теперь появляется в делимом, 21900:
Теперь вы готовы разделить. Аккуратно выровняйте частное, чтобы десятичная точка встала на свое место:
Несмотря на то, что деление получается даже после того, как вы вписываете цифру 6 в частное, вам все равно нужно добавить замещающий ноль, чтобы десятичная точка стояла в правильном месте.
Практические вопросы
Разделите эти два десятичных знака: 9,345 / 0,05 = ?
Решите следующее деление: 3,15 / 0,021 = ?
Выполните следующее десятичное деление, округлив до одного знака после запятой: 6,7/10,1.
Найдите решение, округлив до сотых: 9.13/4.25.
Ниже приведены ответы на практические вопросы:
9,345/0,05 = 186,9. Для начала напишите задачу как обычно:
Превратите делитель (0,05) в целое число, переместив запятую на два знака вправо. При этом переместите запятую в делимом (9,345) на два знака вправо. Поместите десятичную точку в частном непосредственно над тем местом, где она теперь появляется в делимом:
Теперь вы готовы разделить.
Опять же, поместите десятичную точку в частном непосредственно над тем местом, где она теперь появляется в делимом, 21900:
Теперь вы готовы разделить. Аккуратно выровняйте частное, чтобы десятичная точка встала на свое место:
Несмотря на то, что деление получается даже после того, как вы вписываете цифру 6 в частное, вам все равно нужно добавить замещающий ноль, чтобы десятичная точка стояла в правильном месте.
Практические вопросы
Разделите эти два десятичных знака: 9,345 / 0,05 = ?
Решите следующее деление: 3,15 / 0,021 = ?
Выполните следующее десятичное деление, округлив до одного знака после запятой: 6,7/10,1.
Найдите решение, округлив до сотых: 9.13/4.25.
Ниже приведены ответы на практические вопросы:
9,345/0,05 = 186,9. Для начала напишите задачу как обычно:
Превратите делитель (0,05) в целое число, переместив запятую на два знака вправо. При этом переместите запятую в делимом (9,345) на два знака вправо. Поместите десятичную точку в частном непосредственно над тем местом, где она теперь появляется в делимом:
Теперь вы готовы разделить. Будьте осторожны, чтобы правильно выстроить частное, чтобы десятичная точка встала на свое место.
3,15 / 0,021 = 150. Запишите задачу как обычно:
Вам нужно переместить десятичную точку в делителе (0,021) на три знака вправо, поэтому добавьте дополнительный нуль в конце делимого (3,15), чтобы расширить его до трех знаков после запятой:
Теперь вы можете переместить обе десятичные точки на три позиции вправо. Поместите запятую в частном над запятой в делимом:
Разделите, стараясь правильно выстроить частное:
Не забудьте вставить в частное замещающий ноль, чтобы десятичная точка оказалась в правильном месте.
6,7/10,1 = 0,7. Для начала напишите задачу как обычно:
Превратите делитель (10.1) в целое число, переместив запятую на одно место вправо. При этом переместите запятую в делимом (6.7) на один разряд вправо:
В задаче предлагается округлить частное до одного десятичного знака, поэтому заполните делимое нулями в конце до двух знаков после запятой:
Теперь вы готовы разделить:
Округлите частное до одного десятичного знака:
90,13/4,25 = 2,15.
Будьте осторожны, чтобы правильно выстроить частное, чтобы десятичная точка встала на свое место.
3,15 / 0,021 = 150. Запишите задачу как обычно:
Вам нужно переместить десятичную точку в делителе (0,021) на три знака вправо, поэтому добавьте дополнительный нуль в конце делимого (3,15), чтобы расширить его до трех знаков после запятой:
Теперь вы можете переместить обе десятичные точки на три позиции вправо. Поместите запятую в частном над запятой в делимом:
Разделите, стараясь правильно выстроить частное:
Не забудьте вставить в частное замещающий ноль, чтобы десятичная точка оказалась в правильном месте.
6,7/10,1 = 0,7. Для начала напишите задачу как обычно:
Превратите делитель (10.1) в целое число, переместив запятую на одно место вправо. При этом переместите запятую в делимом (6.7) на один разряд вправо:
В задаче предлагается округлить частное до одного десятичного знака, поэтому заполните делимое нулями в конце до двух знаков после запятой:
Теперь вы готовы разделить:
Округлите частное до одного десятичного знака:
90,13/4,25 = 2,15. Сначала напишите задачу как обычно:
Превратите делитель (4.25) в целое число, переместив запятую на два знака вправо. При этом переместите запятую в делимом (9.13) на два знака вправо:
В задаче предлагается округлить частное до сотых, поэтому заполните делимое нулями в конце до трех знаков после запятой:
Теперь разделите, тщательно выстраивая частное:
Округлите частное до сотых:
Сначала напишите задачу как обычно:
Превратите делитель (4.25) в целое число, переместив запятую на два знака вправо. При этом переместите запятую в делимом (9.13) на два знака вправо:
В задаче предлагается округлить частное до сотых, поэтому заполните делимое нулями в конце до трех знаков после запятой:
Теперь разделите, тщательно выстраивая частное:
Округлите частное до сотых:Посмотреть статью
Основы математики Как измерять окружности
Статья / Обновлено 09.07.2021
Центр окружности — это точка, которая находится на одинаковом расстоянии от любой точки самой окружности. Это расстояние называется радиусом окружности, или сокращенно r. И любой отрезок прямой из одной точки окружности через центр в другую точку окружности называется диаметром, или сокращенно d. Диаметр Как видите, диаметр любого круга состоит из одного радиуса плюс еще один радиус, то есть два радиуса (произносится как луч-ди-ай).
 Эта концепция дает вам следующую удобную формулу:
Например, для круга с радиусом 5 миллиметров вы можете вычислить диаметр следующим образом:
Окружность
Поскольку круг имеет особую форму, его периметр (длина его «сторон») имеет особое название: окружность (сокращенно C). Ранние математики приложили немало усилий, чтобы выяснить, как измерить длину окружности. Вот формула, которую они нашли:
Примечание. Поскольку 2 x r совпадает с диаметром, вы также можете записать формулу в виде C = π x d.
Символ π называется пи (произносится как «пирог»). Это просто число, приблизительное значение которого выглядит следующим образом (десятичная часть числа пи продолжается бесконечно, поэтому вы не можете получить точное значение числа пи):
Итак, учитывая окружность с радиусом 5 мм, вы можете вычислить примерную длину окружности:
Площадь круга
В формуле площади (A) круга также используется π:
Вот как использовать эту формулу, чтобы найти приблизительную площадь круга с радиусом 5 мм:
Эта концепция дает вам следующую удобную формулу:
Например, для круга с радиусом 5 миллиметров вы можете вычислить диаметр следующим образом:
Окружность
Поскольку круг имеет особую форму, его периметр (длина его «сторон») имеет особое название: окружность (сокращенно C). Ранние математики приложили немало усилий, чтобы выяснить, как измерить длину окружности. Вот формула, которую они нашли:
Примечание. Поскольку 2 x r совпадает с диаметром, вы также можете записать формулу в виде C = π x d.
Символ π называется пи (произносится как «пирог»). Это просто число, приблизительное значение которого выглядит следующим образом (десятичная часть числа пи продолжается бесконечно, поэтому вы не можете получить точное значение числа пи):
Итак, учитывая окружность с радиусом 5 мм, вы можете вычислить примерную длину окружности:
Площадь круга
В формуле площади (A) круга также используется π:
Вот как использовать эту формулу, чтобы найти приблизительную площадь круга с радиусом 5 мм:Посмотреть статью
14 Стратегии обучения сложению
- Поделиться
- Твит
Стратегии сложения великолепны, потому что они предоставляют вашим учащимся инструменты, которые упрощают и ускоряют вычисления.
Стратегии сложения : Kinder & 1st Class Эти стратегии помогают развить беглость и более глубокое чувство числа. В этом посте рассматриваются основные советы и приемы обучения стратегиям, которые учащиеся 1-го и 2-го классов учатся использовать при решении уравнений на сложение.
Эти стратегии помогают развить беглость и более глубокое чувство числа. В этом посте рассматриваются основные советы и приемы обучения стратегиям, которые учащиеся 1-го и 2-го классов учатся использовать при решении уравнений на сложение.Давайте начнем с краткого обзора стратегий сложения, которые внедряются в детском саду и первом классе. Эти первые две стратегии являются конкретными и манипулятивными.
Этот пост содержит партнерские ссылки Amazon.
1- Счетчики и манипуляции
Здесь большинство наших учеников начинают свои математические приключения. Лучшая часть этой стратегии в том, что ВСЁ может быть противодействием. Счетные чипы легко хранить и дезинфицировать, и они относительно дешевы. Эти милые счетные мишки всегда пользуются успехом. Тем не менее, не чувствуйте себя обязанным покупать что-то необычное. Фасоль, макароны, камешки, крышки от использованных клеевых стержней или крышки от бутылок могут быть фишками.
Загрузите карточки с математическими задачами.
Научите своих учеников записывать уравнения и использовать счетчики для представления каждого слагаемого. Затем они считают их все, чтобы получить сумму. Не забывайте вводить и использовать термины «сложение», «сложение», «сумма» и «уравнение» как можно чаще. Знакомство с этими словами словарного запаса уровня 3 очень важно для наших студентов.
2- Стратегии сложения: подсчет баллов
Подсчет баллов вводится в детском саду, и в течение следующих нескольких лет этот навык совершенствуется. У нас есть отличный пост с видео, которые вы можете использовать в своем классе, чтобы помочь в обучении подсчету оценок. Манипуляции — отличный способ научить подсчету очков. Все, что прямое, можно использовать для отработки подсчета очков. Чтобы научить этому навыку, потренируйтесь преобразовывать однозначные числа стандартной формы в счетные метки, используя всевозможные забавные вещи, которые вы можете найти вокруг себя. Попробуйте палочки для эскимо, ватные палочки, палочки для кренделя или восковые палочки.
 Бумага и карандаш тоже работают, но всегда интересно смешивать вещи, и это будет увлекать ваших учеников при изучении этого важного навыка. Не забудьте модели пропустить счетные метки на 5 с. Имейте в виду, пропуск счета приводит учащихся прямо к умножению.
Бумага и карандаш тоже работают, но всегда интересно смешивать вещи, и это будет увлекать ваших учеников при изучении этого важного навыка. Не забудьте модели пропустить счетные метки на 5 с. Имейте в виду, пропуск счета приводит учащихся прямо к умножению.3- Стратегии сложения: десять фреймов
Причина, по которой мы обучаем наших студентов всем этим стратегиям сложения, заключается в желании развить более устойчивое чувство числа. Десять рамок помогают вашим ученикам визуализировать уравнения и дают им возможность попрактиковаться в субитизации. Десять кадров посвящены пониманию ценности чисел. После ознакомления вашего класса с тем, что такое десятичная рамка и как ее можно использовать , дайте каждому учащемуся свою собственную десятичную рамку для работы. Всей группой или небольшими группами потренируйтесь представлять уравнения с помощью десяти рамок и счетчиков. Моделирование можно выполнить, заполнив десятую рамку по горизонтали, чтобы попрактиковаться в счете на 5 секунд, или заполнив ее вертикально, чтобы попрактиковаться в счете на 2 секунды.
Скачать этот десятый кадр | Загрузить круговые счетчики
Стратегии сложения: 1-й и 2-й класс
4- Подсчет
Числовые линии — прекрасный инструмент для ваших учеников. В первом классе хорошо начинать с помеченных и замкнутых числовых рядов. Научите своих учеников начинать с наибольшего числа и считать вперед.
По мере повышения уровня знаний учащихся в первом и втором классе можно вводить открытые числовые ряды. Обучение открытым числовым рядам может быть сложной задачей, но все дело в моделировании и метапознании. Поскольку открытые числовые ряды — это то, что многие взрослые уже делают в уме, разговор вслух о том, что вы делаете и почему, помогает учащимся понять, как использовать открытые числовые ряды. Студенты должны обладать прочной базой знаний о разрядных значениях, чтобы успешно использовать открытые числовые ряды. Если вы обнаружите, что ваши ученики борются с этим навыком, добавьте в свой блок по математике несколько упражнений с условными значениями.

5- Ноль фактов
В моем классе мы называем ноль «зеркалом». Чтобы ввести ноль фактов, у меня в классе есть овальное зеркало. Когда они смотрят в зеркало, что они видят? Сами себя! Все, что плюс ноль, есть само! Затем мы тренируемся с однозначными числами и становимся глупее, чтобы показать им, что прибавить ноль к чему угодно просто. Мои ученики ОБОЖАЮТ, когда я пишу смешное уравнение вроде 3 452 872 965 + 0= ? и попросите их решить ее.
6- Сложите 10
Будучи взрослыми, многие из нас автоматически складывают 10, чтобы создать более удобные числа для сложения в уме. Набрать 10 — такая мощная стратегия и для наших юных учеников. Второй уровень — это когда сложение действительно повышает уровень сложности, когда вводится сложение с перегруппировкой. Практика составления 10 и, в конечном итоге, запоминание того, какие пары составляют десять, — это навык, к которому они будут прибегать, когда учатся складывать большие числа или складывать вместе 3+ числа.

Обучение этому навыку связано с возможностью попрактиковаться. Десять рамок — отличный способ поработать над созданием 10. Раздайте своим ученикам жетоны двух цветов. Попросите их найти как можно больше способов сделать десять, используя свои жетоны. В тетради по математике для 1-го класса: дополнение есть несколько замечательных интерактивных страниц, над которыми учащиеся могут работать. Веселые песни могут помочь вашим ученикам научиться делать десять! Когда учащиеся станут более опытными, не забудьте смоделировать, как использовать этот навык для решения более сложных уравнений сложения.
7- Двойники
Прежде чем мы перейдем к тому, как работают двойники, давайте сначала разберемся, почему. Механическое заучивание иногда имеет плохую репутацию. Исследования показывают, что, когда учащиеся развивают автоматизм в своих основных математических фактах, они освобождают место в своей рабочей памяти. Проще говоря, когда учащимся не нужно беспокоиться о базовых вычислениях, они лучше справляются с математикой более высокого уровня.
 У студентов не так много оперативной памяти, и использовать ее для сложения 8+8 — пустая трата времени. Запоминание их двойников облегчает когнитивную нагрузку вашего ученика, и это то, что мы ищем! Кроме того, как только их двойники запоминаются, учащиеся могут быстро использовать эти знания для решения почти двойных задач.
У студентов не так много оперативной памяти, и использовать ее для сложения 8+8 — пустая трата времени. Запоминание их двойников облегчает когнитивную нагрузку вашего ученика, и это то, что мы ищем! Кроме того, как только их двойники запоминаются, учащиеся могут быстро использовать эти знания для решения почти двойных задач.Так как же нам обучать двойников? Так же, как сделать 10, много возможностей для практики. В блокноте Addition Note есть действительно забавные интерактивные практические страницы. К ним относятся изображения, удобные для детей, в качестве наглядных пособий. Опять же, песни также являются действительно эффективным методом обучения. Нет ничего более приятного, чем слышать, как ваши дети напевают себе математические факты для развлечения.
8- Почти двойники
Как только ваши ученики зафиксируют двойные факты, переходите к почти двойникам. Это означает удвоение плюс один или два. Как и в случае со счетом 10, научить учащихся решать почти двойные числа — это моделирование.
 При введении концепции напишите уравнения, чтобы ваши ученики могли видеть и говорить вслух все, что вы замечаете и делаете.
При введении концепции напишите уравнения, чтобы ваши ученики могли видеть и говорить вслух все, что вы замечаете и делаете.Например, если вы используете уравнение 6+5, это может звучать так: «Я заметил, что это почти двойное уравнение. Число 6 всего на единицу больше, чем 5. Держу пари, я мог бы использовать свои двойные факты, чтобы решить эту проблему». Нарисуйте числовые связи, чтобы показать, что 6 равно 5+1, а затем продолжите: «Я заметил, что когда я разлагаю 6, я получаю еще 5! О, смотрите, 5+5 это 10, а потом у меня остался только один остаток. Я могу добавить это в моей голове! 10+1 равно 11». Проведите своих учеников через это шаг за шагом несколько раз, а затем попросите их попробовать вместе с вами. Выявление числовых связей очень полезно для многих учащихся.
Если у вас есть ученики, которые все еще борются с трудностями, манипуляции, такие как счетчики, могут быть очень полезными, чтобы добавить больше физического элемента.
9- «Переворачивание фактов» или свойство перестановочности
Свойство перестановочности вводится в начале сложения, а затем возвращается к нему, когда учащиеся изучают умножение.
 Таким образом, это словарный термин, к которому они будут часто возвращаться в течение первых нескольких лет обучения в школе. Называть это «обернуть факты» удобно для детей и помогает учащимся запомнить, что это значит, но не забывайте часто ссылаться на фактическое название свойства. Это пригодится им в третьем классе, когда они будут изучать свойства умножения.
Таким образом, это словарный термин, к которому они будут часто возвращаться в течение первых нескольких лет обучения в школе. Называть это «обернуть факты» удобно для детей и помогает учащимся запомнить, что это значит, но не забывайте часто ссылаться на фактическое название свойства. Это пригодится им в третьем классе, когда они будут изучать свойства умножения.Творческий подход к изучению фактов — отличный способ повысить вовлеченность. Коммутативное свойство помогает вашим учащимся понять значение чисел и, кроме того, перемещение слагаемых не влияет на сумму. Проще всего это сделать, нарисовав схему уравнения сложения для каждого ученика. Используйте пустые клетки для представления слагаемых и оставьте строку для ваших учеников, чтобы написать сумму.
Раздайте прилавки любого вида: пластиковые прилавки, хлопья, фруктовые закуски, лего, слоеные шарики, все, что у вас есть под рукой. Начните с уравнения вроде 5 + 2. Попросите учащихся смоделировать это уравнение, поместив соответствующее количество манипуляций в соответствующее место.
 Затем напишите сумму. Теперь запишите поворот вокруг факта 2 + 5, попросите учащихся смоделировать это новое уравнение, используя свои манипуляции, и напишите сумму. Сумма меняется? Сделайте это несколько раз, используя разные числа. Спросите учащихся, что они замечают. Как переворачивание слагаемых влияет на сумму?
Затем напишите сумму. Теперь запишите поворот вокруг факта 2 + 5, попросите учащихся смоделировать это новое уравнение, используя свои манипуляции, и напишите сумму. Сумма меняется? Сделайте это несколько раз, используя разные числа. Спросите учащихся, что они замечают. Как переворачивание слагаемых влияет на сумму?Стратегии сложения: 2-й и 3-й классы
10- Расширенная форма
Учащиеся практикуются в написании чисел в различных формах: стандартной, расширенной, письменной и с основанием десять в течение первых нескольких лет обучения в классе. Способность разложить число в его расширенную форму показывает, что учащиеся действительно понимают значение чисел, с которыми они работают. У
We Are Teachers есть потрясающая статья о том, почему расширенная форма так важна. Прежде чем использовать расширенную форму в качестве стратегии сложения, убедитесь, что ваши ученики действительно понимают, как разбивать числа на их значения. В этом посте от Teach Junkie есть несколько хороших идей для практики.
 У нас также есть несколько отличных интерактивных страниц блокнота для дополнительного обзора.
У нас также есть несколько отличных интерактивных страниц блокнота для дополнительного обзора.Ваши ученики получили развернутую форму. Как они используют его для решения уравнений сложения? Как только учащиеся начнут складывать двух- и трехзначные числа, они могут использовать расширенную форму для выполнения вычислений в уме. Например, давайте попробуем 64 + 42. Покажите учащимся, как решить эту задачу, используя числовые связи или десятичные блоки. 64 становится 60 + 4, а 42 становится 40 + 2. Старайтесь всегда моделировать свое мышление и произносите все, что делаете, вслух. Это может звучать так: « 64 становится 60+4, потому что 6 стоит в разряде десятков, поэтому его значение равно 60, а 4 — в разряде единиц, поэтому его значение равно 4. ” Привяжите другие стратегии, такие как упоминание о том, что 6 и 4 составляют 10, когда вы мысленно складываете 60 и 40. Для учащихся, которые борются с ментальной арифметикой, рисование или использование физических десятичных кубиков действительно хорошая поддержка.

11- Блоки с основанием 10
Сложение с использованием блоков с основанием 10 начинается в 1-м классе и используется, когда учащиеся изучают перегруппировку. Его также можно использовать в качестве поддержки для старших школьников, которые борются со сложением.
Скачать этот базовый десятичный мат | Скачать печатную версию базы десять блоковУчащиеся могут использовать пластиковые/деревянные или распечатанные бумажные базовые кубики или рисовать их. В 1-м и начале 2-го класса иметь что-то конкретное для использования действительно полезно, но как только они станут более уверенными в рисовании блоков с основанием 10, это будет совершенно нормально.
12- Подсчет пропусков
Нельзя недооценивать важность подсчета пропусков. Иногда кажется, что пропуск счета откладывается на второй план для других «более важных» навыков, но так не должно быть! Подсчет пропусков основан на шаблонах и используется по-разному. Учащиеся используют его, когда считают деньги, определяют время и изучают умножение.
 У Мистера Элементарной Математики есть несколько отличных идей, как попрактиковаться в счете.
У Мистера Элементарной Математики есть несколько отличных идей, как попрактиковаться в счете.Счет в пропуске может быть сложным, но важным навыком, который нужно осваивать в первом, втором и третьем классе. Часто в учебной программе есть несколько уроков по подсчету пропусков, после чего ожидается, что учащиеся усвоят эту концепцию. Если вашим ученикам нужна дополнительная практика с пропуском счета по 5, вы можете получить эту распечатанную форму для подсчета пропусков бесплатно!
Загрузить эту игруОбучая учащихся тому, как использовать пропуск счета в качестве стратегии сложения, начните с открытых числовых рядов. Возьмите уравнение типа 25 + 32 и напишите число 25 в открытой числовой строке. Не забывайте моделировать все мысли вслух. Это может звучать так: «Я заметил, что 25 оканчиваются на 5. Когда число оканчивается на 5, я могу легко пропустить счет на 5 или 10. Теперь я смотрю на 32 и знаю, что в 32 3 десятка. Я собираюсь прыгнуть вперед на десятки. Начните с 25, прыгайте 10, 35, прыгайте 10, 45, прыгайте 10, 55.
 Отлично! Я израсходовал 30 и у меня осталось 2. Я буду прыгать вперед на единицу. Начните с 55, прыжок 1, 56, прыжок 1, 57». Смоделируйте несколько раз со своими учениками, затем позвольте им попробовать это вместе с вами, а затем постепенно отпустите их, когда они начнут чувствовать себя уверенно. Для старших или отличников используйте 3-значные сложения.
Отлично! Я израсходовал 30 и у меня осталось 2. Я буду прыгать вперед на единицу. Начните с 55, прыжок 1, 56, прыжок 1, 57». Смоделируйте несколько раз со своими учениками, затем позвольте им попробовать это вместе с вами, а затем постепенно отпустите их, когда они начнут чувствовать себя уверенно. Для старших или отличников используйте 3-значные сложения.13- Округление или «дружественные числа»
Учащиеся знакомятся с округлением в 3-м классе. В некоторых школах его преподают в начале года, а в некоторых предпочитают откладывать на конец. Проверьте карту своей учебной программы, чтобы узнать, когда она есть в вашем расписании. Если в вашей школе округление проводится в начале года, его можно использовать в качестве дополнительной стратегии в течение всего года.
Вы наверняка слышали, что эту стратегию называют «дружественными числами», потому что именно этому мы учим наших студентов. Они учатся создавать числа, с которыми легче (более дружелюбно) работать в уме.
 Сложение 312+453 в уме может быть трудным, но округление этих чисел до 300 и 450 значительно облегчает работу с ними. Ключом к этому навыку является прочное базовое знание округления. Как только ваши ученики освоят округление, объясните, ПОЧЕМУ эта стратегия. Обычный комментарий, который студенты делают при изучении этой стратегии, звучит так: «Но это неправильный ответ». Технически они верны. Поэтому необходимо помочь им понять, почему и когда используются оценки, если вы хотите, чтобы ваши ученики приняли эту стратегию.
Сложение 312+453 в уме может быть трудным, но округление этих чисел до 300 и 450 значительно облегчает работу с ними. Ключом к этому навыку является прочное базовое знание округления. Как только ваши ученики освоят округление, объясните, ПОЧЕМУ эта стратегия. Обычный комментарий, который студенты делают при изучении этой стратегии, звучит так: «Но это неправильный ответ». Технически они верны. Поэтому необходимо помочь им понять, почему и когда используются оценки, если вы хотите, чтобы ваши ученики приняли эту стратегию.Когда учащиеся поймут, почему они округляют перед сложением, пора практиковаться! Начните с двузначных чисел, таких как 34+29 (становится 30+30), и позвольте им потренироваться давать вам приблизительные ответы. Затем перейдите к трехзначным числам и попросите их округлить до ближайшей сотни 245+682 (становится 200+700). После того, как они овладеют этими двумя навыками, вы можете начать округлять трехзначные числа до ближайших десяти. Для студентов, которые действительно преуспевают, вы можете усилить строгость, дав им уже понятное уравнение, такое как 300 + 600, и попросив их привести примеры того, что могло быть первоначальными «недружественными» числами.

14- Стандартный алгоритм
Во 2 классе вводится перегруппировка, а в 3 классе она пересматривается и совершенствуется. Стандартный алгоритм или, как многие его называют, «старая математика». Обычно стандартный алгоритм преподается после того, как студенты освоят некоторые другие стратегии. Благодаря чувству чисел, полученному во всех предыдущих стратегиях сложения, стандартный алгоритм становится больше направленным на применение того, что они знают, и меньше на запоминание рутины. Вот что такого замечательного в заполнении ящиков с математическими инструментами! К тому времени, как дети начинают перегруппировываться — брать и носить с собой, как это известно нам, старожилам, — они понимают, ПОЧЕМУ они перемещают эти числа в следующую колонку.
Когда дело доходит до обучения стандартному алгоритму, песнопения — отличный способ помочь учащимся запомнить шаги, которые им необходимо выполнить! Попробуйте два из перечисленных ниже способов со своими учениками.
- Дополнение с пением перегруппировки: Десять или больше? Нести рядом.
 Девять или меньше? Пусть отдыхает!
Девять или меньше? Пусть отдыхает! - Вычитание с перегруппировкой чата: Еще сверху? Не нужно останавливаться! Больше на полу? Иди по соседству и возьми еще 10! номера одинаковые? Нулевая игра.
Не забывайте медленно выполнять инструкции. Студентам легко запутаться и в конечном итоге заимствовать и нести в незнакомых местах. Начните с двузначных чисел и переходите к трехзначным числам, когда учащиеся почувствуют себя уверенно и будут готовы к повышенной сложности. Для многих учеников вычитание через нули затруднено. Сохранение этого навыка напоследок может предотвратить разочарование.
Ресурсы для обучения стратегиям сложения
Если вы ищете комплексный пакет с МНОЖЕСТВОМ печатных и цифровых математических ресурсов для ваших учеников, включая десять рамок, счетчики, числовые линии, коврики «часть-часть-целое», ознакомьтесь с Lucky Little Toolkit в нашей библиотеке ресурсов полного доступа. Он загружен невероятными ресурсами для вас и ваших учеников.


 05.2022
05.2022
 Знание некоторых основных математических формул, теоремы Пифагора и более простого способа сложения является ключом к повседневной математике.
Знание некоторых основных математических формул, теоремы Пифагора и более простого способа сложения является ключом к повседневной математике. Вы также найдете удобные и простые для понимания руководства по преобразованию между метрическими и английскими единицами измерения, а также между дробями, процентами и десятичными знаками.
Вы также найдете удобные и простые для понимания руководства по преобразованию между метрическими и английскими единицами измерения, а также между дробями, процентами и десятичными знаками. Прежде чем вы сможете рассчитать процент, вы должны точно понимать, что такое процент.
Слово процент происходит от слова процент. Если вы разделите слово «процент» на его корневые слова, вы увидите «процент» и «процент». Цент — это старое европейское слово французского, латинского и итальянского происхождения, означающее «сто». Таким образом, процент переводится непосредственно как «на сотню». Если у вас есть 87 процентов, вы буквально имеете 87 на 100. Если за последние 100 дней снег шел 13 раз, он шел в 13 процентах случаев.
Числа, которые вы будете преобразовывать в проценты, могут быть предоставлены вам в двух различных форматах: десятичном и дробном. Десятичный формат легче вычислить в процентах. Преобразование десятичного числа в проценты так же просто, как умножение его на 100. Чтобы преобразовать 0,87 в проценты, просто умножьте 0,87 на 100.
0,87 × 100 = 87, что дает нам 87 процентов.
Процент часто обозначается символом %. Вы можете представить свой ответ как 87% или 87% — оба варианта приемлемы.
Прежде чем вы сможете рассчитать процент, вы должны точно понимать, что такое процент.
Слово процент происходит от слова процент. Если вы разделите слово «процент» на его корневые слова, вы увидите «процент» и «процент». Цент — это старое европейское слово французского, латинского и итальянского происхождения, означающее «сто». Таким образом, процент переводится непосредственно как «на сотню». Если у вас есть 87 процентов, вы буквально имеете 87 на 100. Если за последние 100 дней снег шел 13 раз, он шел в 13 процентах случаев.
Числа, которые вы будете преобразовывать в проценты, могут быть предоставлены вам в двух различных форматах: десятичном и дробном. Десятичный формат легче вычислить в процентах. Преобразование десятичного числа в проценты так же просто, как умножение его на 100. Чтобы преобразовать 0,87 в проценты, просто умножьте 0,87 на 100.
0,87 × 100 = 87, что дает нам 87 процентов.
Процент часто обозначается символом %. Вы можете представить свой ответ как 87% или 87% — оба варианта приемлемы. Если вам дана дробь, преобразуйте ее в проценты, разделив верхнее число на нижнее. Если вам дано 13/100, вы должны разделить 13 на 100.
13 ÷ 100 = 0,13
Затем выполните описанные выше шаги для преобразования десятичной дроби в проценты.
0,13 × 100 = 13, что дает вам 13%.
Более сложная задача возникает, когда вам нужно узнать процентное соотношение, когда вам даны числа, которые не так точно вписываются в 100.
В большинстве случаев вам будет дан процент от определенного числа. Например, вы можете знать, что 40 процентов вашей зарплаты пойдет на налоги, и вы хотите узнать, сколько это денег. Чтобы вычислить процент определенного числа, вы сначала преобразуете процентное число в десятичное число.
Этот процесс является обратным тому, что вы делали ранее. Вы делите свой процент на 100. Итак, 40 процентов будет 40, деленное на 100.
40 ÷ 100 = 0,40
Получив десятичную версию своего процента, просто умножьте его на заданное число (в данном случае на сумму вашей зарплаты). Если ваша зарплата составляет 750 долларов, вы должны умножить 750 на 0,40.
Если вам дана дробь, преобразуйте ее в проценты, разделив верхнее число на нижнее. Если вам дано 13/100, вы должны разделить 13 на 100.
13 ÷ 100 = 0,13
Затем выполните описанные выше шаги для преобразования десятичной дроби в проценты.
0,13 × 100 = 13, что дает вам 13%.
Более сложная задача возникает, когда вам нужно узнать процентное соотношение, когда вам даны числа, которые не так точно вписываются в 100.
В большинстве случаев вам будет дан процент от определенного числа. Например, вы можете знать, что 40 процентов вашей зарплаты пойдет на налоги, и вы хотите узнать, сколько это денег. Чтобы вычислить процент определенного числа, вы сначала преобразуете процентное число в десятичное число.
Этот процесс является обратным тому, что вы делали ранее. Вы делите свой процент на 100. Итак, 40 процентов будет 40, деленное на 100.
40 ÷ 100 = 0,40
Получив десятичную версию своего процента, просто умножьте его на заданное число (в данном случае на сумму вашей зарплаты). Если ваша зарплата составляет 750 долларов, вы должны умножить 750 на 0,40. 750 × 0,40 = 300
Ваш ответ будет 300. Вы платите 300 долларов в виде налогов.
Давайте попробуем другой пример. Вам нужно откладывать 25 процентов своей зарплаты в течение следующих 6 месяцев, чтобы заплатить за предстоящий отпуск. Если ваша зарплата составляет 1500 долларов, сколько вы должны откладывать?
Начните с преобразования 25 процентов в десятичную дробь.
25 ÷ 100 = 0,25
Теперь умножьте десятичную дробь на сумму вашей зарплаты, или 1500.
1500 × 0,25 = 375
Это означает, что вам нужно откладывать 375 долларов с каждой зарплаты.
750 × 0,40 = 300
Ваш ответ будет 300. Вы платите 300 долларов в виде налогов.
Давайте попробуем другой пример. Вам нужно откладывать 25 процентов своей зарплаты в течение следующих 6 месяцев, чтобы заплатить за предстоящий отпуск. Если ваша зарплата составляет 1500 долларов, сколько вы должны откладывать?
Начните с преобразования 25 процентов в десятичную дробь.
25 ÷ 100 = 0,25
Теперь умножьте десятичную дробь на сумму вашей зарплаты, или 1500.
1500 × 0,25 = 375
Это означает, что вам нужно откладывать 375 долларов с каждой зарплаты. Вычеркните число, которое вы берете взаймы, вычтите 1 и напишите ответ над числом, которое вы вычеркнули.
Добавьте 10 к верхнему числу в столбце, в котором вы работали.
Например, предположим, что вы хотите вычесть 386 – 9.4. Первый шаг — вычесть 4 из 6 в столбце единиц, что даст вам 2:
Однако когда вы переходите к столбцу десятков, вы обнаружите, что вам нужно вычесть 8–9. Поскольку 8 меньше 9, вам нужно заимствовать значения из столбца сотен. Сначала зачеркните цифру 3 и замените ее цифрой 2, потому что 3 – 1 = 2:
Затем поместите 1 перед 8, изменив его на 18, потому что 8 + 10 = 18:
Теперь вы можете вычесть в столбце десятков: 18 – 9 = 9:
Последний шаг прост: 2 – 0 = 2:
Следовательно, 386 – 94 = 292.
В некоторых случаях в столбце непосредственно слева может не быть ничего, что можно было бы одолжить. Предположим, например, что вы хотите вычесть 1002 – 39.8. Начиная со столбца единиц, вы обнаружите, что вам нужно вычесть от 2 до 8. Поскольку 2 меньше 8, вам нужно заимствовать из следующего столбца слева.
Вычеркните число, которое вы берете взаймы, вычтите 1 и напишите ответ над числом, которое вы вычеркнули.
Добавьте 10 к верхнему числу в столбце, в котором вы работали.
Например, предположим, что вы хотите вычесть 386 – 9.4. Первый шаг — вычесть 4 из 6 в столбце единиц, что даст вам 2:
Однако когда вы переходите к столбцу десятков, вы обнаружите, что вам нужно вычесть 8–9. Поскольку 8 меньше 9, вам нужно заимствовать значения из столбца сотен. Сначала зачеркните цифру 3 и замените ее цифрой 2, потому что 3 – 1 = 2:
Затем поместите 1 перед 8, изменив его на 18, потому что 8 + 10 = 18:
Теперь вы можете вычесть в столбце десятков: 18 – 9 = 9:
Последний шаг прост: 2 – 0 = 2:
Следовательно, 386 – 94 = 292.
В некоторых случаях в столбце непосредственно слева может не быть ничего, что можно было бы одолжить. Предположим, например, что вы хотите вычесть 1002 – 39.8. Начиная со столбца единиц, вы обнаружите, что вам нужно вычесть от 2 до 8. Поскольку 2 меньше 8, вам нужно заимствовать из следующего столбца слева. Но цифра в колонке десятков — 0, так что вы не можете взять оттуда, потому что шкаф, так сказать, пуст:
Когда заимствование из следующего столбца невозможно, вам нужно заимствовать из ближайшего ненулевого столбца слева.
В этом примере столбец, из которого вам нужно заимствовать, — это столбец тысяч. Сначала зачеркните 1 и замените его на 0. Затем поставьте 1 перед 0 в столбце сотен:
Теперь зачеркните 10 и замените на 9.. Поставьте 1 перед 0 в столбце десятков:
Наконец, вычеркните 10 в столбце десятков и замените его на 9. Затем поставьте 1 перед 2:
Наконец, вы можете начать вычитать в столбце единиц: 12 – 8 = 4:
Затем вычтите в столбце десятков: 9 – 9 = 0:
Затем вычтите в столбце сотен: 9 – 3 = 6:
Поскольку в столбце тысяч ничего не осталось, вам не нужно больше ничего вычитать. Следовательно, 1002 – 398 = 604.
Но цифра в колонке десятков — 0, так что вы не можете взять оттуда, потому что шкаф, так сказать, пуст:
Когда заимствование из следующего столбца невозможно, вам нужно заимствовать из ближайшего ненулевого столбца слева.
В этом примере столбец, из которого вам нужно заимствовать, — это столбец тысяч. Сначала зачеркните 1 и замените его на 0. Затем поставьте 1 перед 0 в столбце сотен:
Теперь зачеркните 10 и замените на 9.. Поставьте 1 перед 0 в столбце десятков:
Наконец, вычеркните 10 в столбце десятков и замените его на 9. Затем поставьте 1 перед 2:
Наконец, вы можете начать вычитать в столбце единиц: 12 – 8 = 4:
Затем вычтите в столбце десятков: 9 – 9 = 0:
Затем вычтите в столбце сотен: 9 – 3 = 6:
Поскольку в столбце тысяч ничего не осталось, вам не нужно больше ничего вычитать. Следовательно, 1002 – 398 = 604. 07.2021
07.2021 Цифра справа от цифры, до которой вы округляете, указывает, нужно ли округлять в большую или меньшую сторону, поэтому вам всегда нужно вычислять деление на один дополнительный разряд.
См. следующую диаграмму:
Чтобы округлить десятичную до
Заполните дивиденд с замыкающими нулями, чтобы
Целое число
Один десятичный знак
Один десятичный знак
Два десятичных знака
Два десятичных знака
Три десятичных знака
Примеры вопросов
Разделите следующее: 90,152 / 0,8 = ?
11.44. Для начала напишите задачу как обычно:
Превратите 0,8 в целое число 8, переместив запятую на одно место вправо. При этом запятую в числе 9,1526 переместите на один разряд вправо. Поставьте запятую в частном прямо над тем местом, где она попадает в 91,25:
Теперь вы готовы разделить. Просто будьте осторожны, чтобы правильно выстроить частное, чтобы десятичная точка встала на свое место.
Разделите следующее: 21,9 / 0,015 = ?
1460. Ставьте задачу как обычно:
Обратите внимание, что к делимому добавлены два завершающих нуля, потому что вам нужно переместить десятичные точки в каждом числе на три позиции вправо.
Цифра справа от цифры, до которой вы округляете, указывает, нужно ли округлять в большую или меньшую сторону, поэтому вам всегда нужно вычислять деление на один дополнительный разряд.
См. следующую диаграмму:
Чтобы округлить десятичную до
Заполните дивиденд с замыкающими нулями, чтобы
Целое число
Один десятичный знак
Один десятичный знак
Два десятичных знака
Два десятичных знака
Три десятичных знака
Примеры вопросов
Разделите следующее: 90,152 / 0,8 = ?
11.44. Для начала напишите задачу как обычно:
Превратите 0,8 в целое число 8, переместив запятую на одно место вправо. При этом запятую в числе 9,1526 переместите на один разряд вправо. Поставьте запятую в частном прямо над тем местом, где она попадает в 91,25:
Теперь вы готовы разделить. Просто будьте осторожны, чтобы правильно выстроить частное, чтобы десятичная точка встала на свое место.
Разделите следующее: 21,9 / 0,015 = ?
1460. Ставьте задачу как обычно:
Обратите внимание, что к делимому добавлены два завершающих нуля, потому что вам нужно переместить десятичные точки в каждом числе на три позиции вправо. Опять же, поместите десятичную точку в частном непосредственно над тем местом, где она теперь появляется в делимом, 21900:
Теперь вы готовы разделить. Аккуратно выровняйте частное, чтобы десятичная точка встала на свое место:
Несмотря на то, что деление получается даже после того, как вы вписываете цифру 6 в частное, вам все равно нужно добавить замещающий ноль, чтобы десятичная точка стояла в правильном месте.
Практические вопросы
Разделите эти два десятичных знака: 9,345 / 0,05 = ?
Решите следующее деление: 3,15 / 0,021 = ?
Выполните следующее десятичное деление, округлив до одного знака после запятой: 6,7/10,1.
Найдите решение, округлив до сотых: 9.13/4.25.
Ниже приведены ответы на практические вопросы:
9,345/0,05 = 186,9. Для начала напишите задачу как обычно:
Превратите делитель (0,05) в целое число, переместив запятую на два знака вправо. При этом переместите запятую в делимом (9,345) на два знака вправо. Поместите десятичную точку в частном непосредственно над тем местом, где она теперь появляется в делимом:
Теперь вы готовы разделить.
Опять же, поместите десятичную точку в частном непосредственно над тем местом, где она теперь появляется в делимом, 21900:
Теперь вы готовы разделить. Аккуратно выровняйте частное, чтобы десятичная точка встала на свое место:
Несмотря на то, что деление получается даже после того, как вы вписываете цифру 6 в частное, вам все равно нужно добавить замещающий ноль, чтобы десятичная точка стояла в правильном месте.
Практические вопросы
Разделите эти два десятичных знака: 9,345 / 0,05 = ?
Решите следующее деление: 3,15 / 0,021 = ?
Выполните следующее десятичное деление, округлив до одного знака после запятой: 6,7/10,1.
Найдите решение, округлив до сотых: 9.13/4.25.
Ниже приведены ответы на практические вопросы:
9,345/0,05 = 186,9. Для начала напишите задачу как обычно:
Превратите делитель (0,05) в целое число, переместив запятую на два знака вправо. При этом переместите запятую в делимом (9,345) на два знака вправо. Поместите десятичную точку в частном непосредственно над тем местом, где она теперь появляется в делимом:
Теперь вы готовы разделить.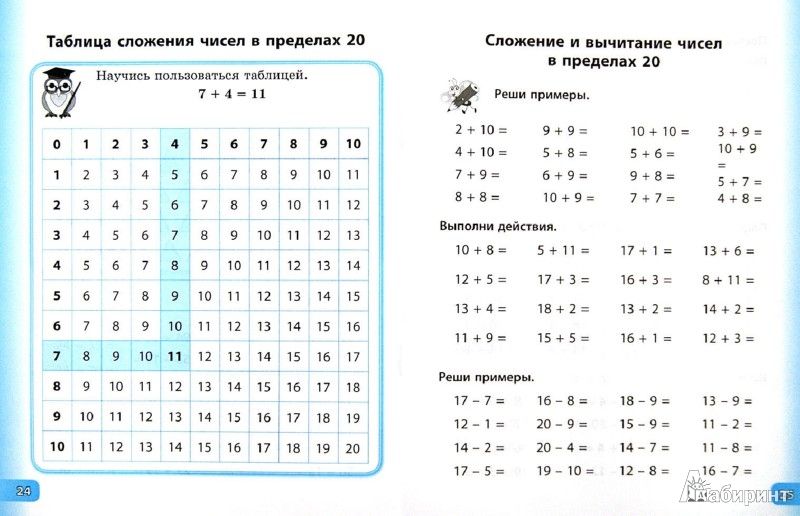 Будьте осторожны, чтобы правильно выстроить частное, чтобы десятичная точка встала на свое место.
3,15 / 0,021 = 150. Запишите задачу как обычно:
Вам нужно переместить десятичную точку в делителе (0,021) на три знака вправо, поэтому добавьте дополнительный нуль в конце делимого (3,15), чтобы расширить его до трех знаков после запятой:
Теперь вы можете переместить обе десятичные точки на три позиции вправо. Поместите запятую в частном над запятой в делимом:
Разделите, стараясь правильно выстроить частное:
Не забудьте вставить в частное замещающий ноль, чтобы десятичная точка оказалась в правильном месте.
6,7/10,1 = 0,7. Для начала напишите задачу как обычно:
Превратите делитель (10.1) в целое число, переместив запятую на одно место вправо. При этом переместите запятую в делимом (6.7) на один разряд вправо:
В задаче предлагается округлить частное до одного десятичного знака, поэтому заполните делимое нулями в конце до двух знаков после запятой:
Теперь вы готовы разделить:
Округлите частное до одного десятичного знака:
90,13/4,25 = 2,15.
Будьте осторожны, чтобы правильно выстроить частное, чтобы десятичная точка встала на свое место.
3,15 / 0,021 = 150. Запишите задачу как обычно:
Вам нужно переместить десятичную точку в делителе (0,021) на три знака вправо, поэтому добавьте дополнительный нуль в конце делимого (3,15), чтобы расширить его до трех знаков после запятой:
Теперь вы можете переместить обе десятичные точки на три позиции вправо. Поместите запятую в частном над запятой в делимом:
Разделите, стараясь правильно выстроить частное:
Не забудьте вставить в частное замещающий ноль, чтобы десятичная точка оказалась в правильном месте.
6,7/10,1 = 0,7. Для начала напишите задачу как обычно:
Превратите делитель (10.1) в целое число, переместив запятую на одно место вправо. При этом переместите запятую в делимом (6.7) на один разряд вправо:
В задаче предлагается округлить частное до одного десятичного знака, поэтому заполните делимое нулями в конце до двух знаков после запятой:
Теперь вы готовы разделить:
Округлите частное до одного десятичного знака:
90,13/4,25 = 2,15. Сначала напишите задачу как обычно:
Превратите делитель (4.25) в целое число, переместив запятую на два знака вправо. При этом переместите запятую в делимом (9.13) на два знака вправо:
В задаче предлагается округлить частное до сотых, поэтому заполните делимое нулями в конце до трех знаков после запятой:
Теперь разделите, тщательно выстраивая частное:
Округлите частное до сотых:
Сначала напишите задачу как обычно:
Превратите делитель (4.25) в целое число, переместив запятую на два знака вправо. При этом переместите запятую в делимом (9.13) на два знака вправо:
В задаче предлагается округлить частное до сотых, поэтому заполните делимое нулями в конце до трех знаков после запятой:
Теперь разделите, тщательно выстраивая частное:
Округлите частное до сотых: Эта концепция дает вам следующую удобную формулу:
Например, для круга с радиусом 5 миллиметров вы можете вычислить диаметр следующим образом:
Окружность
Поскольку круг имеет особую форму, его периметр (длина его «сторон») имеет особое название: окружность (сокращенно C). Ранние математики приложили немало усилий, чтобы выяснить, как измерить длину окружности. Вот формула, которую они нашли:
Примечание. Поскольку 2 x r совпадает с диаметром, вы также можете записать формулу в виде C = π x d.
Символ π называется пи (произносится как «пирог»). Это просто число, приблизительное значение которого выглядит следующим образом (десятичная часть числа пи продолжается бесконечно, поэтому вы не можете получить точное значение числа пи):
Итак, учитывая окружность с радиусом 5 мм, вы можете вычислить примерную длину окружности:
Площадь круга
В формуле площади (A) круга также используется π:
Вот как использовать эту формулу, чтобы найти приблизительную площадь круга с радиусом 5 мм:
Эта концепция дает вам следующую удобную формулу:
Например, для круга с радиусом 5 миллиметров вы можете вычислить диаметр следующим образом:
Окружность
Поскольку круг имеет особую форму, его периметр (длина его «сторон») имеет особое название: окружность (сокращенно C). Ранние математики приложили немало усилий, чтобы выяснить, как измерить длину окружности. Вот формула, которую они нашли:
Примечание. Поскольку 2 x r совпадает с диаметром, вы также можете записать формулу в виде C = π x d.
Символ π называется пи (произносится как «пирог»). Это просто число, приблизительное значение которого выглядит следующим образом (десятичная часть числа пи продолжается бесконечно, поэтому вы не можете получить точное значение числа пи):
Итак, учитывая окружность с радиусом 5 мм, вы можете вычислить примерную длину окружности:
Площадь круга
В формуле площади (A) круга также используется π:
Вот как использовать эту формулу, чтобы найти приблизительную площадь круга с радиусом 5 мм: Эти стратегии помогают развить беглость и более глубокое чувство числа. В этом посте рассматриваются основные советы и приемы обучения стратегиям, которые учащиеся 1-го и 2-го классов учатся использовать при решении уравнений на сложение.
Эти стратегии помогают развить беглость и более глубокое чувство числа. В этом посте рассматриваются основные советы и приемы обучения стратегиям, которые учащиеся 1-го и 2-го классов учатся использовать при решении уравнений на сложение.
 Бумага и карандаш тоже работают, но всегда интересно смешивать вещи, и это будет увлекать ваших учеников при изучении этого важного навыка. Не забудьте модели пропустить счетные метки на 5 с. Имейте в виду, пропуск счета приводит учащихся прямо к умножению.
Бумага и карандаш тоже работают, но всегда интересно смешивать вещи, и это будет увлекать ваших учеников при изучении этого важного навыка. Не забудьте модели пропустить счетные метки на 5 с. Имейте в виду, пропуск счета приводит учащихся прямо к умножению.


 У студентов не так много оперативной памяти, и использовать ее для сложения 8+8 — пустая трата времени. Запоминание их двойников облегчает когнитивную нагрузку вашего ученика, и это то, что мы ищем! Кроме того, как только их двойники запоминаются, учащиеся могут быстро использовать эти знания для решения почти двойных задач.
У студентов не так много оперативной памяти, и использовать ее для сложения 8+8 — пустая трата времени. Запоминание их двойников облегчает когнитивную нагрузку вашего ученика, и это то, что мы ищем! Кроме того, как только их двойники запоминаются, учащиеся могут быстро использовать эти знания для решения почти двойных задач. При введении концепции напишите уравнения, чтобы ваши ученики могли видеть и говорить вслух все, что вы замечаете и делаете.
При введении концепции напишите уравнения, чтобы ваши ученики могли видеть и говорить вслух все, что вы замечаете и делаете. Таким образом, это словарный термин, к которому они будут часто возвращаться в течение первых нескольких лет обучения в школе. Называть это «обернуть факты» удобно для детей и помогает учащимся запомнить, что это значит, но не забывайте часто ссылаться на фактическое название свойства. Это пригодится им в третьем классе, когда они будут изучать свойства умножения.
Таким образом, это словарный термин, к которому они будут часто возвращаться в течение первых нескольких лет обучения в школе. Называть это «обернуть факты» удобно для детей и помогает учащимся запомнить, что это значит, но не забывайте часто ссылаться на фактическое название свойства. Это пригодится им в третьем классе, когда они будут изучать свойства умножения. Затем напишите сумму. Теперь запишите поворот вокруг факта 2 + 5, попросите учащихся смоделировать это новое уравнение, используя свои манипуляции, и напишите сумму. Сумма меняется? Сделайте это несколько раз, используя разные числа. Спросите учащихся, что они замечают. Как переворачивание слагаемых влияет на сумму?
Затем напишите сумму. Теперь запишите поворот вокруг факта 2 + 5, попросите учащихся смоделировать это новое уравнение, используя свои манипуляции, и напишите сумму. Сумма меняется? Сделайте это несколько раз, используя разные числа. Спросите учащихся, что они замечают. Как переворачивание слагаемых влияет на сумму? У нас также есть несколько отличных интерактивных страниц блокнота для дополнительного обзора.
У нас также есть несколько отличных интерактивных страниц блокнота для дополнительного обзора.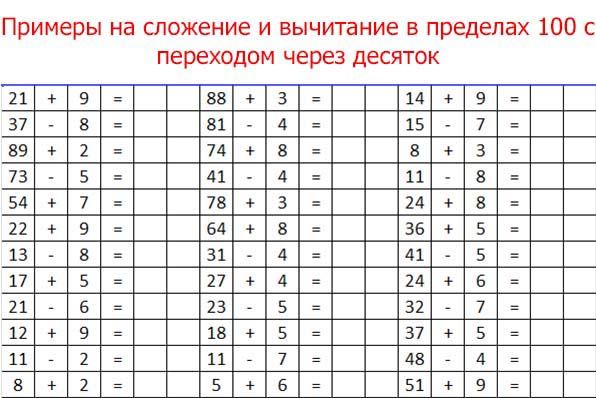
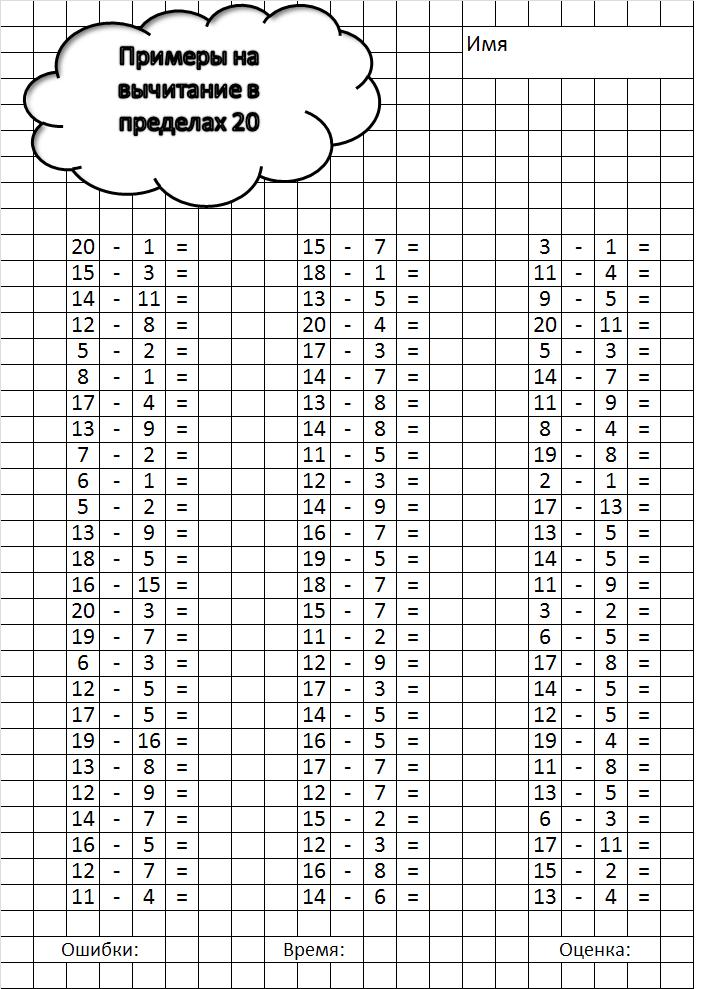 У Мистера Элементарной Математики есть несколько отличных идей, как попрактиковаться в счете.
У Мистера Элементарной Математики есть несколько отличных идей, как попрактиковаться в счете. Отлично! Я израсходовал 30 и у меня осталось 2. Я буду прыгать вперед на единицу. Начните с 55, прыжок 1, 56, прыжок 1, 57». Смоделируйте несколько раз со своими учениками, затем позвольте им попробовать это вместе с вами, а затем постепенно отпустите их, когда они начнут чувствовать себя уверенно. Для старших или отличников используйте 3-значные сложения.
Отлично! Я израсходовал 30 и у меня осталось 2. Я буду прыгать вперед на единицу. Начните с 55, прыжок 1, 56, прыжок 1, 57». Смоделируйте несколько раз со своими учениками, затем позвольте им попробовать это вместе с вами, а затем постепенно отпустите их, когда они начнут чувствовать себя уверенно. Для старших или отличников используйте 3-значные сложения. Сложение 312+453 в уме может быть трудным, но округление этих чисел до 300 и 450 значительно облегчает работу с ними. Ключом к этому навыку является прочное базовое знание округления. Как только ваши ученики освоят округление, объясните, ПОЧЕМУ эта стратегия. Обычный комментарий, который студенты делают при изучении этой стратегии, звучит так: «Но это неправильный ответ». Технически они верны. Поэтому необходимо помочь им понять, почему и когда используются оценки, если вы хотите, чтобы ваши ученики приняли эту стратегию.
Сложение 312+453 в уме может быть трудным, но округление этих чисел до 300 и 450 значительно облегчает работу с ними. Ключом к этому навыку является прочное базовое знание округления. Как только ваши ученики освоят округление, объясните, ПОЧЕМУ эта стратегия. Обычный комментарий, который студенты делают при изучении этой стратегии, звучит так: «Но это неправильный ответ». Технически они верны. Поэтому необходимо помочь им понять, почему и когда используются оценки, если вы хотите, чтобы ваши ученики приняли эту стратегию.
 Девять или меньше? Пусть отдыхает!
Девять или меньше? Пусть отдыхает! 